Evaluating the Polarimetric Radio Occultation Technique Using NEXRAD Weather Radars
Abstract
1. Introduction
2. Materials and Methods
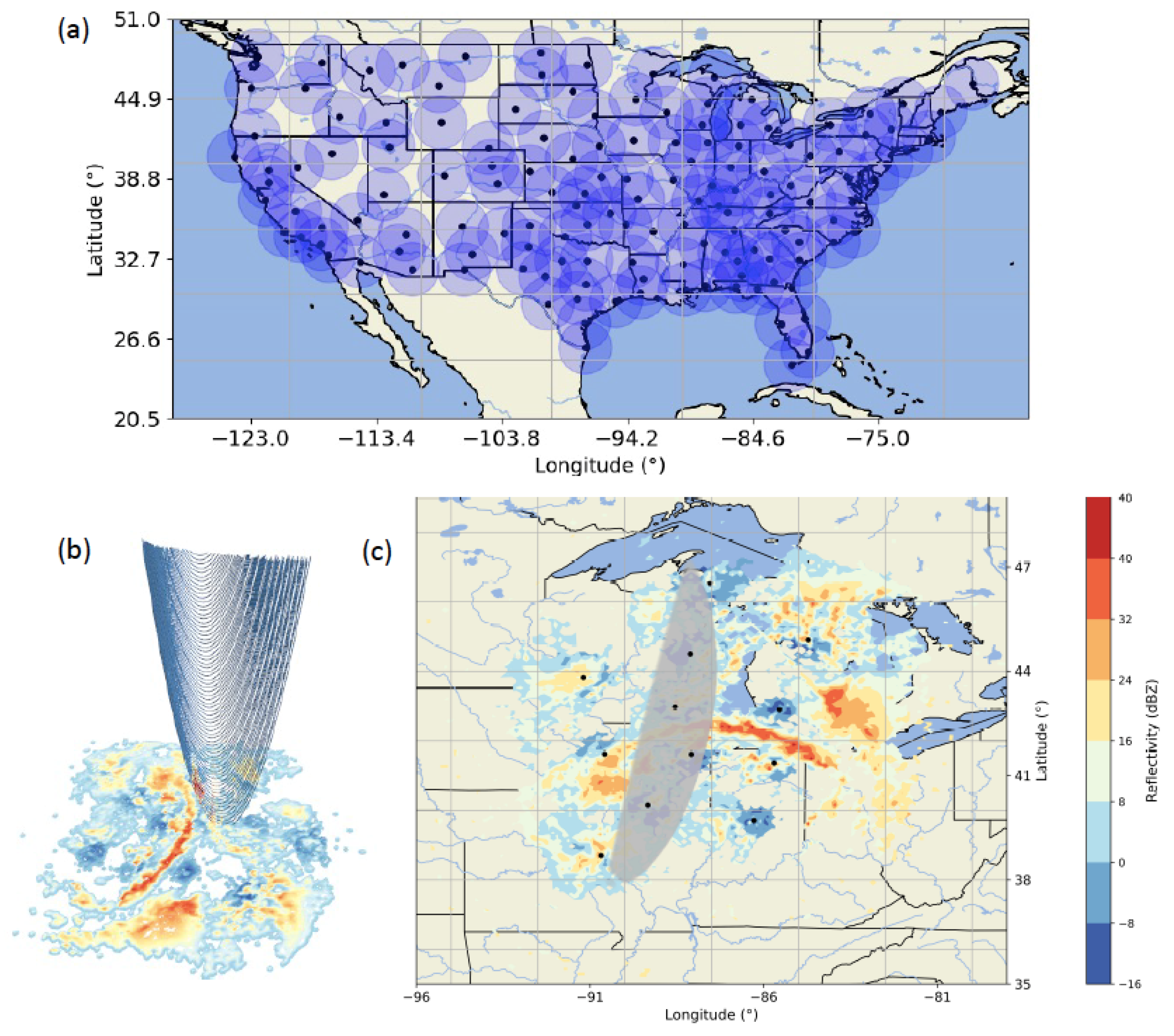
2.1. Polarimetric Radio Occultation Data
2.2. NEXRAD Data
2.3. Coincident Observations between PAZ and NEXRAD
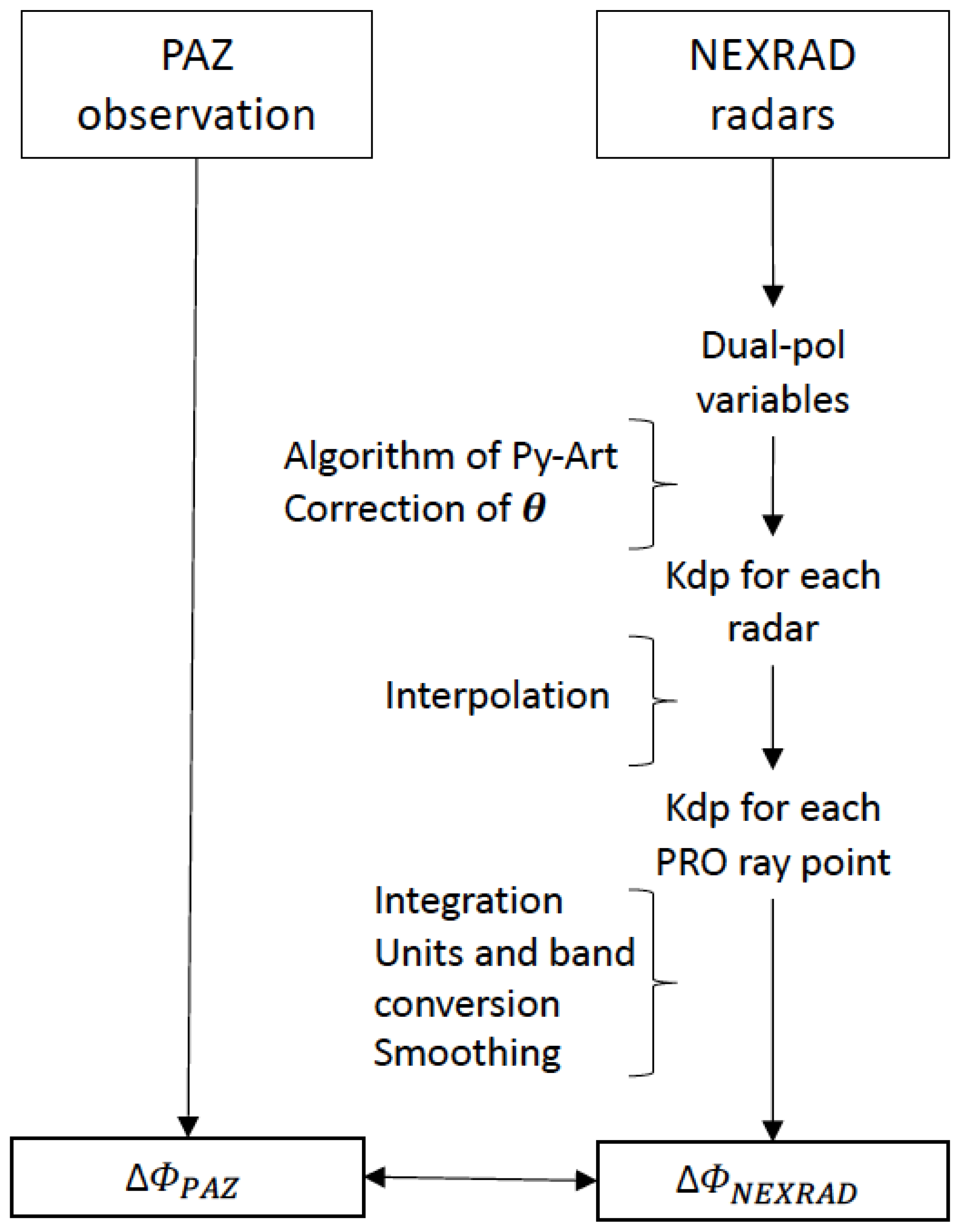
2.4. Calculation of and from NEXRAD
3. Results and Discussions
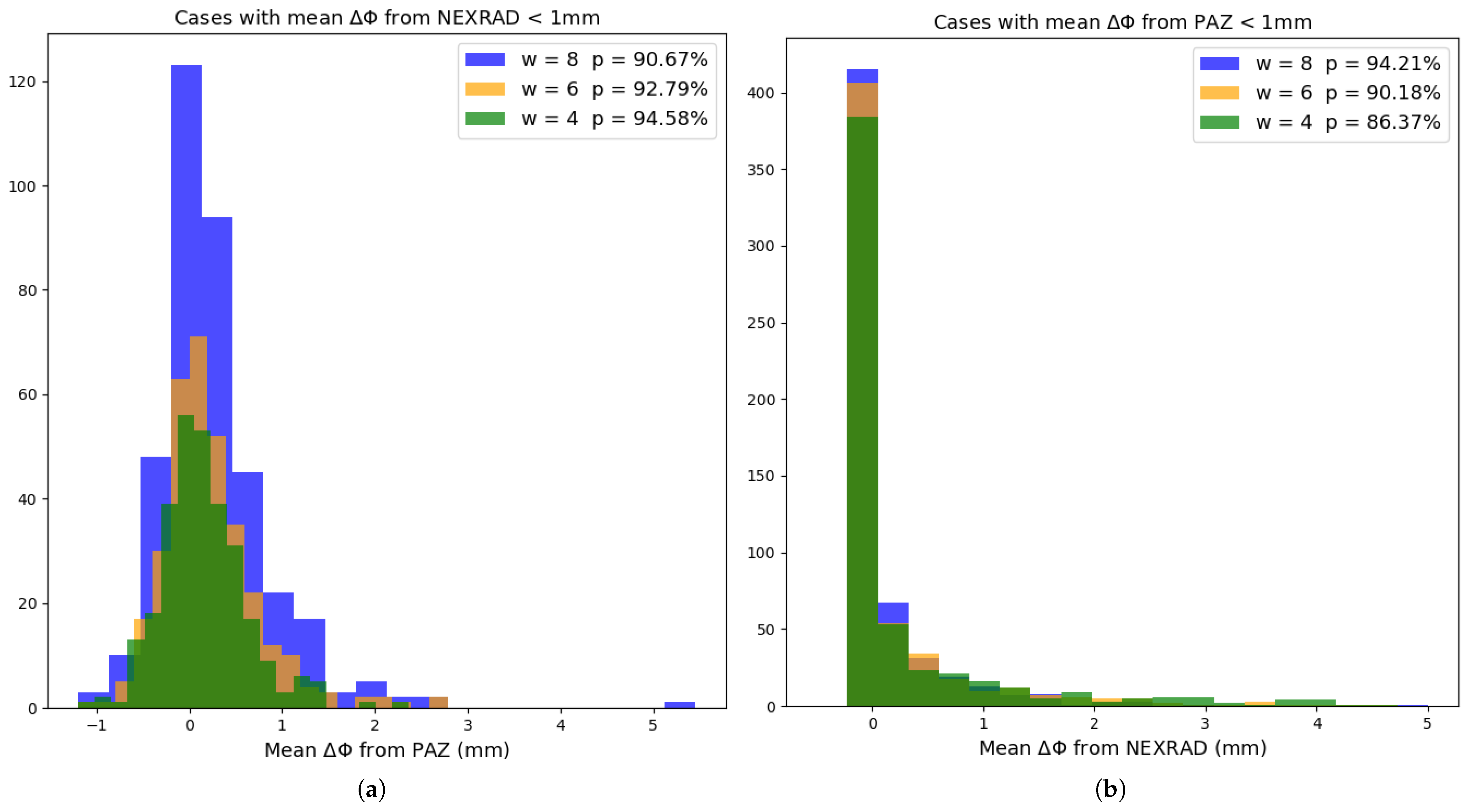
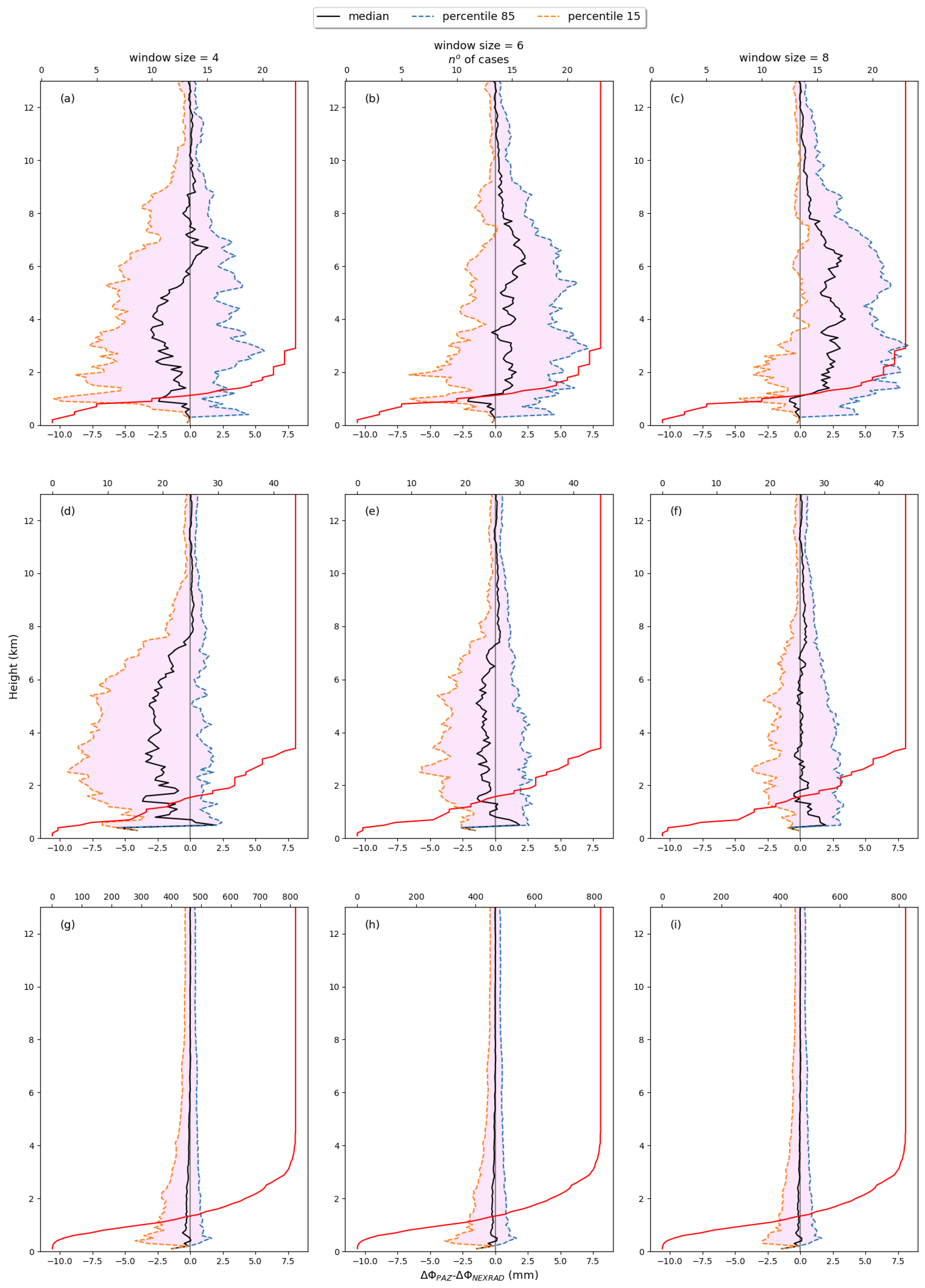
3.1. Sensitivity of to Window Size
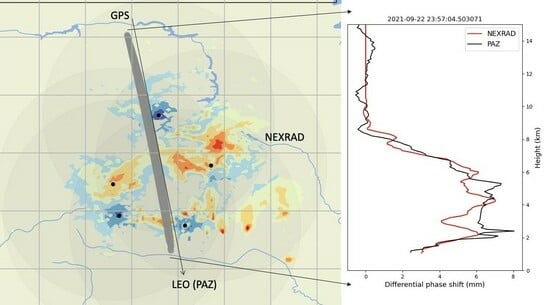
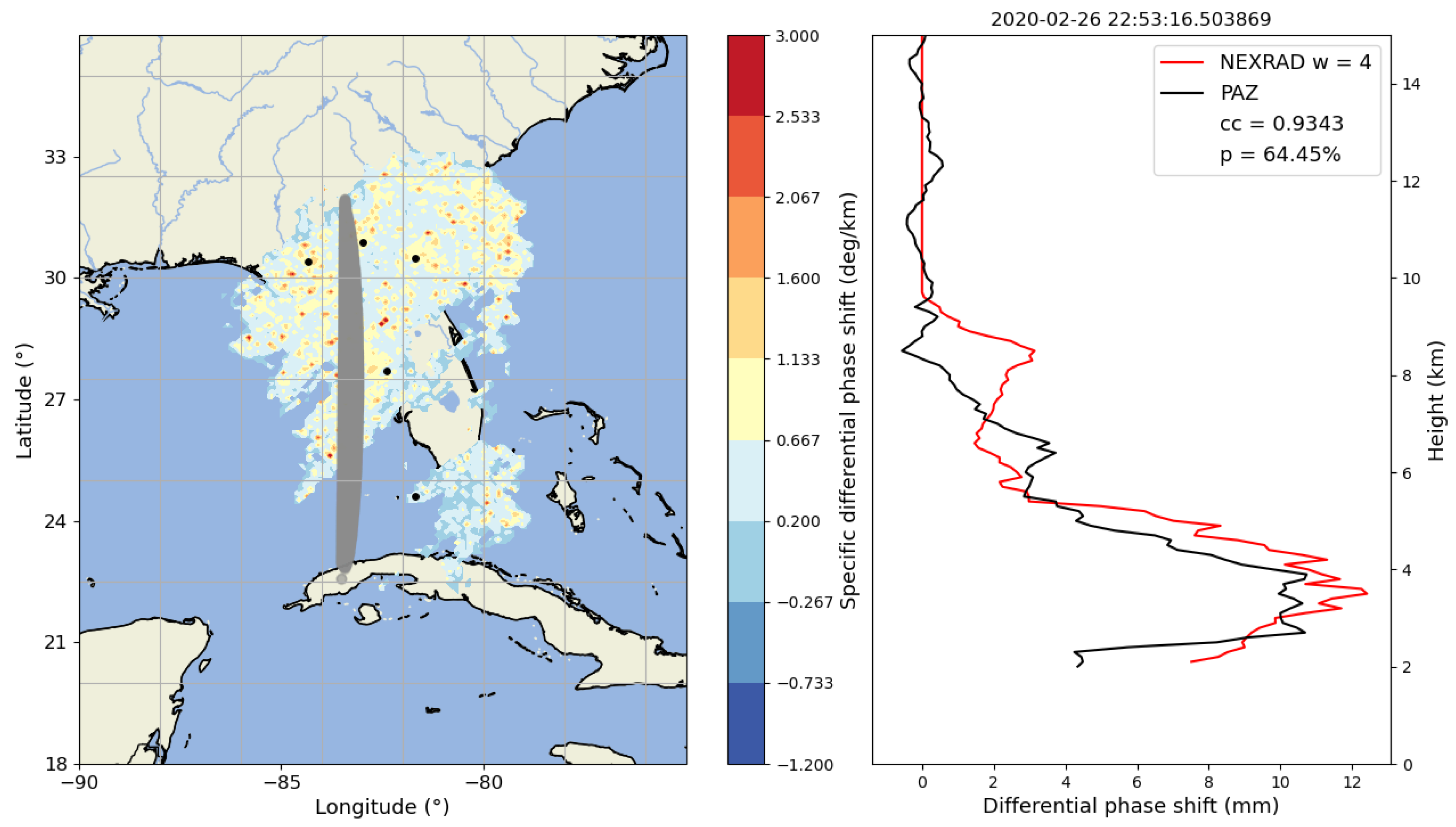
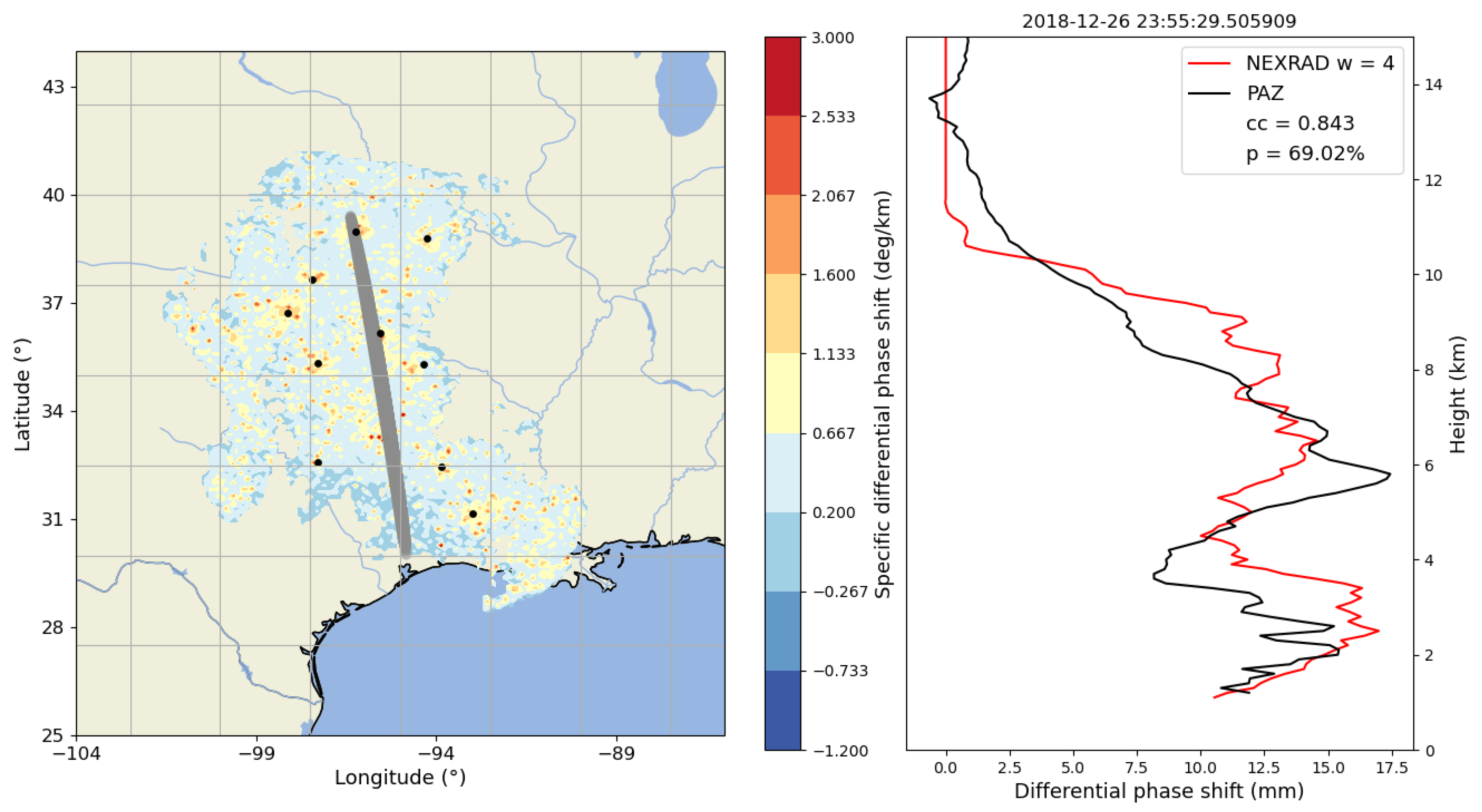
3.2. Illustrative Examples of Vertical Profiles of
3.3. Statistical Analysis of Differences
3.4. Echotop Height Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global Navigation Satellite Systems |
| PRO | Polarimetric Radio Occultation |
| NEXRAD | Next Generation Weather Radars |
| ROHP | Radio Occultation and Heavy Precipitation |
| ICE-CSIC | Institut de Ciéncies de l’Espai-Consejo Superior de Investigaciones Científicas |
| IEEC | Institut d’Estudis Espacials de Catalunya |
| NOAA | National Oceanic and Atmospheric Administration |
| UCAR | University Corporation for Atmospheric Research |
| NASA | National Aeronautics and Space Administration |
| GPS | Global Positioning System |
| LEO | Low Earth Orbit |
| IGOR+ | Integrated GPS Occultation Receiver |
| NWP | Numerical Weather Prediction |
| GPM | Global Precipitation Mission |
| GMI | GPM Microwave Imager |
| PPI | Plan Position Indicator |
| PSD | Particle Size Distribution |
| IMERG | Integrates Multi-satellitE Retrievals for GPM |
| DPR | Dual frequency Precipitation Radar |
| NWS | National Weather Service |
| QC | Quality Control |
References
- Fjeldbo, G.; Eshleman, V.R. The Bistatic Radar-Occultation Method for the Study of Planetary Atmospheres. J. Geophys. Res. 1965, 70, 3217–3225. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmopshere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. Atmos. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Healy, S.B.; Jupp, A.M.; Marquardt, C. Forecast impact experiment with GPS radio occultation measurements. Geophys. Res. Lett. 2005, 32, L3804. [Google Scholar] [CrossRef]
- Cardellach, E.; Tomás, S.; Oliveras, S.; Padullés, R.; Rius, A.; de la Torre Juárez, M.; Turk, F.; Ao, C.; Kursinski, E.R.; Schreiner, B.; et al. Sensitivity of PAZ LEO Polarimetric GNSS Radio-Occultation Experiment to Precipitation Events. IEEE Trans. Geosci. Remote Sens. 2014, 53, 190–206. [Google Scholar] [CrossRef]
- Cardellach, E.; Oliveras, S.; Rius, A.; Tomás, S.; Ao, C.; Franklin, G.W.; Iijima, B.A.; Kuang, D.; Meehan, T.K.; Padullés, R.; et al. Sensing Heavy Precipitation With GNSS Polarimetric Radio Occultations. Geophys. Res. Lett. 2019, 46, 1024–1031. [Google Scholar] [CrossRef]
- Padullés, R.; Ao, C.; Turk, F.; de la Torre Juárez, M.; Iijima, B.; Wang, K.N.; Cardellach, E. Calibration and validation of the Polarimetric Radio Occultation and Heavy Precipitation experiment aboard the PAZ satellite. Atmos. Meas. Tech. 2020, 13, 1299–1313. [Google Scholar] [CrossRef]
- Turk, F.; Padullés, R.; Cardellach, E.; Ao, C.; Wang, K.N.; Morabito, D.D.; de la Torre Juárez, M.; Oyola, M.; Hristova-Veleva, S.; Neelin, J.D. Interpretation of the Precipitation Structure Contained in Polarimetric Radio Occultation Profiles Using Passive Microwave Satellite Observations. J. Atmos. Ocean. Technol. 2021, 38, 1727–1745. [Google Scholar] [CrossRef]
- Padullés, R.; Cardellach, E.; Turk, F.; Ao, C.; de la Torre Juárez, M.; Gong, J.; Wu, D.L. Sensing Horizontally Oriented Frozen Particles With Polarimetric Radio Occultations Aboard PAZ: Validation Using GMI Coincident Observations and Cloudsat a Priori Information. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Padullés, R.; Cardellach, E.; Turk, F. On the global relationship between polarimetric radio occultation differential phase shift and ice water conten. Atmos. Chem. Phys. 2023, 23, 2199–2214. [Google Scholar] [CrossRef]
- Wulfmeyer, V.; Hardesty, R.M.; Turner, D.D.; Behrendt, A.; Cadeddu, M.P.; Di Girolamo, P.; Schlüssel, P.; Baelen, J.V.; Zus, F. A review of the remote sensing of lower tropospheric thermodynamic profiles and its indispensable role for the understanding and the simulation of water and energy cycles. Rev. Geophys. 2015, 53, 819–895. [Google Scholar] [CrossRef]
- Tomás, S.; Padullés, R.; Cardellach, E. Separability of systematic effects in polarimetric GNSS radio occultations for precipitation sensing. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4633–4649. [Google Scholar] [CrossRef]
- Padullés, R.; Cardellach, E.; Oliveras, S. resPrf [Dataset]. 2024. Available online: https://digital.csic.es/handle/10261/348253 (accessed on 18 March 2024).
- Klazura, G.E.; Imy, D.A. A Description of the Initial Set of Analysis Products Aivailable from the NEXRAD WSR-88D System. Bull. Am. Meteorol. Soc. 1993, 74, 1293–1312. [Google Scholar] [CrossRef]
- Crum, T.D.; Saffle, R.E.; Wilson, J.W. An Update on the NEXRAD Program and Future WSR-88D Support to Operations. Weather Forecast. 1998, 13, 253–262. [Google Scholar] [CrossRef]
- NOAA National Weather Service (NWS) Radar Operations Center. NOAA Next Generation Radar (NEXRAD) Level 2 Base Data; National Centers for Environmental Information: Asheville, NC, USA, 1991. [CrossRef]
- Helmus, J.J.; Collis, S.M. The Python ARM Radar Toolkit (Py-Art), a library for working with weather radar data in the Python programmin language. J. Open Res. Softw. 2016, 4, e25. [Google Scholar] [CrossRef]
- Vulpiani, G.; Montopoli, M.; Passeri, L.D.; Gioia, A.G.; Giordano, P.; Marzano, F.S. On the use of dual-polarized C-band radar for operational rainfall retrieval in mountainous areas. J. Appl. Meteorol. Climatol. 2012, 51, 405–425. [Google Scholar] [CrossRef]
- Vulpiani, G.; Baldini, L.; Roberto, N. Characterization of Meditarranean hail-bearing storms using an operational polarimetric X-band radar. Atmos. Meas. Tech. 2015, 8, 4681–4698. [Google Scholar] [CrossRef]
- Reimel, K.J.; Kumjian, M. Evaluation of Kdp Estimation Algorithm Performance in Rain Using a Known-Truth Framework. J. Atmos. Ocean. Technol. 2021, 38, 587–605. [Google Scholar] [CrossRef]
- Griffin, E.M.; Schuur, T.J.; Ryzhkov, A.V. A Polarimetric Analysis of Ice Microphysical Processes in Snow, Using Quasi-Vertical Profiles. J. Appl. Meteorol. Climatol. 2018, 57, 31–50. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Wang, Y.; Chandrasekar, V. Algorithm for Estimation of the Specific Differential Phase. J. Atmos. Ocean. Technol. 2009, 26, 2565–2578. [Google Scholar] [CrossRef]




| Number of Cases | |
|---|---|
| Total | 3208 |
| ≥ area covered | 1076 |
| ≥ 1 mm | 221 |
| ≥ 1.5 mm | 117 |
| ≥ area covered and ≥ 1.5 mm | 51 |
| cc ≥ 0.6 | 290 |
| cc ≥ 0.8 | 127 |
| ≤ 1 mm | 2987 |
| ≤ 1 mm | 2898 |
| ≤ 1 mm and ≤ 1 mm | 2818 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paz, A.; Padullés, R.; Cardellach, E. Evaluating the Polarimetric Radio Occultation Technique Using NEXRAD Weather Radars. Remote Sens. 2024, 16, 1118. https://doi.org/10.3390/rs16071118
Paz A, Padullés R, Cardellach E. Evaluating the Polarimetric Radio Occultation Technique Using NEXRAD Weather Radars. Remote Sensing. 2024; 16(7):1118. https://doi.org/10.3390/rs16071118
Chicago/Turabian StylePaz, Antía, Ramon Padullés, and Estel Cardellach. 2024. "Evaluating the Polarimetric Radio Occultation Technique Using NEXRAD Weather Radars" Remote Sensing 16, no. 7: 1118. https://doi.org/10.3390/rs16071118
APA StylePaz, A., Padullés, R., & Cardellach, E. (2024). Evaluating the Polarimetric Radio Occultation Technique Using NEXRAD Weather Radars. Remote Sensing, 16(7), 1118. https://doi.org/10.3390/rs16071118