Joint Classification of Hyperspectral and LiDAR Data Based on Adaptive Gating Mechanism and Learnable Transformer
Abstract
1. Introduction
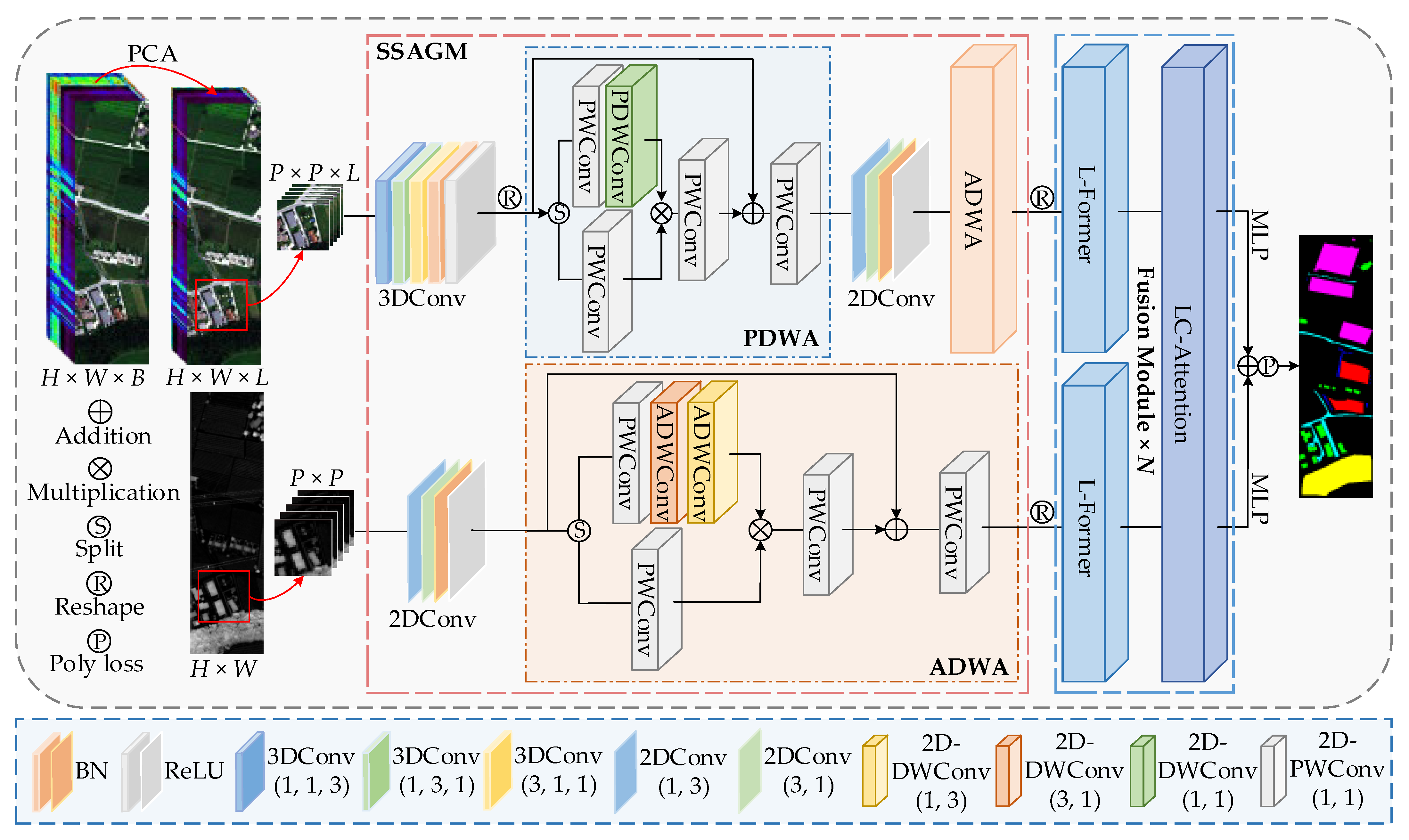
- The Gated Spatial Attention Unit (GSAU) [30] is introduced into the joint classification of HSI and LiDAR-DSM, which is improved to design a dual-branch SSAGM feature extraction module. SSAGM encompasses the point depthwise attention module (PDWA) and the asymmetric depthwise attention module (ADWA). The PDWA primarily aims at extracting the spectral features from HSI, while the ADWA focuses on extracting spatial information from HSI and elevation information from LiDAR-DSM. This approach allows for the omission of the linear layer to emphasize local continuity without compromising complexity.
- The learnable transformer (L-Former) is designed to enhance data dynamics and mitigate performance decline as the depth of the transformer increases. The layer scale is incorporated into the output of each residual block, with different output channels being multiplied by distinct values to further refine the features. Concurrently, a learnable transition matrix is integrated into the self-attention (SA) to develop learnable self-attention (LS-Attention, LSA), which addresses the issue of centralized decomposition and facilitates the training of deeper transformers.
- The learnable transition matrix is integrated into cross-attention, forming learnable cross-attention (LC-Attention). This integration diminishes the similarity among attention maps, thereby augmenting the diversity of the features.
- Poly loss is implemented for classifying to improve the model training. Remote sensing datasets frequently exhibit uneven distributions and potential overlaps among samples of the same type. Furthermore, the features of data differ across various modalities. Poly loss is a versatile loss function suited for multi-modal data fusion classification.
2. Methodology
| Algorithm 1 The algorithm flow of AGMLT | |
| Input | HSI: , LiDAR-DSM: , Labels: , Patches = 11 × 11, PCA = 30. |
| Output | Prediction: . |
| 1: | Initialize: batch size = 64, epochs = 100, learning rate depends on datasets. |
| 2: | PCA: . |
| 3: | Create all sample patches from , , and divide them into the training sets and the test sets . ( contains the labels, and does not contain the labels). |
| 4: | Training AGMLT (begin) |
| 5: | for epoch in range(epochs): |
| 6: | for i, (,,) in enumerate (): |
| 7: | |
| 8: | |
| 9: | , |
| 10: | |
| 11: | |
| 12: | |
| 13: | Training AGMLT (end) and test AGMLT |
| 14: | |
2.1. SSAGM
2.2. L-Former
2.3. LC-Attention
2.4. Poly Loss
3. Experimental Results
3.1. Data Description
- TR
- 2.
- MU
- 3.
- AU
- 4.
- HU
3.2. Experimental Setting
3.2.1. Initial Learning Rate
3.2.2. Depth and Heads
3.3. Performance Comparison
3.3.1. Experimental Results
- TR dataset
| No. | HSI Input | HSI and LiDAR-DSM Input | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DMCN | SpectralFormer | SSFTT | morp- Former | Coupled CNN | MFT_PT | MFT_CT | HCT | AGMLT | ||
| 1 | Mean | 99.65 | 99.1 | 98.84 | 97.89 | 99.18 | 97.65 | 98.2 | 99.57 | 99.47 |
| Std | 0.35 | 0.72 | 0.61 | 0.75 | 0.61 | 0.45 | 0.44 | 0.37 | 0.14 | |
| 2 | Mean | 99.74 | 94.49 | 98.01 | 96.49 | 92.92 | 97.93 | 98.74 | 98.85 | 98.81 |
| Std | 0.49 | 0.39 | 0.5 | 2.57 | 6.24 | 0.48 | 0.64 | 0.28 | 0.37 | |
| 3 | Mean | 99.44 | 97.54 | 100 | 100 | 99.68 | 99.73 | 98.88 | 99.41 | 100 |
| Std | 0.56 | 0.58 | 0 | 0 | 0.32 | 0.27 | 1.12 | 0.59 | 0 | |
| 4 | Mean | 99.99 | 99.92 | 100 | 100 | 99.96 | 99.91 | 99.99 | 100 | 100 |
| Std | 0.01 | 0.08 | 0 | 0 | 0.04 | 0.09 | 0.01 | 0 | 0 | |
| 5 | Mean | 99.97 | 99.65 | 99.99 | 99.97 | 99.84 | 99.92 | 99.96 | 99.99 | 99.97 |
| Std | 0.03 | 0.23 | 0.01 | 0.02 | 0.16 | 0.08 | 0.04 | 0.01 | 0.02 | |
| 6 | Mean | 96.42 | 88.51 | 95.38 | 96.58 | 92.71 | 96.87 | 98.38 | 98.01 | 99.14 |
| Std | 1.12 | 5.55 | 2.23 | 2.84 | 5.06 | 1.46 | 0.9 | 0.98 | 0.2 | |
| OA (%) | Mean | 99.35 | 97.99 | 99.18 | 99.02 | 98.39 | 99.11 | 99.45 | 99.62 | 99.72 |
| Std | 0.17 | 0.64 | 0.12 | 0.28 | 1.28 | 0.19 | 0.1 | 0.14 | 0.04 | |
| AA (%) | Mean | 98.87 | 96.54 | 98.7 | 98.49 | 97.38 | 98.67 | 99.03 | 99.31 | 99.57 |
| Std | 0.35 | 0.51 | 0.22 | 0.42 | 1.94 | 0.3 | 0.32 | 0.32 | 0.07 | |
| K × 100 | Mean | 99.13 | 97.31 | 98.9 | 98.69 | 97.85 | 98.81 | 99.26 | 99.49 | 99.62 |
| Std | 0.58 | 0.49 | 0.17 | 0.38 | 1.72 | 0.12 | 0.14 | 0.18 | 0.05 | |

- 2.
- MU dataset
| No. | HSI Input | HSI and LiDAR-DSM Input | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DMCN | SpectralFormer | SSFTT | morp- Former | Coupled CNN | MFT_PT | MFT_CT | HCT | AGMLT | ||
| 1 | Mean Std | 87.76 2.37 | 88.62 0.36 | 88.16 0.57 | 85.14 2.26 | 86.29 0.78 | 86.42 1.22 | 86.26 2.91 | 90.04 3.34 | 90.52 2.43 |
| 2 | Mean Std | 84.85 6.81 | 78.01 9.75 | 84.27 9.82 | 79.49 6.40 | 87.09 2.12 | 81.96 3.20 | 77.81 13.68 | 82.84 1.45 | 90.56 1.81 |
| 3 | Mean Std | 78.90 3.35 | 81.75 8.58 | 79.53 3.86 | 81.83 2.22 | 76.96 1.58 | 77.24 0.99 | 79.82 2.12 | 77.69 3.65 | 82.46 1.23 |
| 4 | Mean Std | 96.42 1.54 | 94.88 2.49 | 93.89 7.73 | 96.30 0.65 | 94.93 2.56 | 92.79 1.91 | 92.96 1.96 | 94.44 2.74 | 96.76 0.73 |
| 5 | Mean Std | 88.05 3.91 | 88.62 0.36 | 84.34 3.17 | 79.83 5.17 | 77.89 3.72 | 79.12 1.07 | 78.89 2.45 | 86.28 2.47 | 89.69 1.63 |
| 6 | Mean Std | 99.84 0.16 | 99.43 0.57 | 99.68 0.32 | 99.56 0.38 | 99.84 0.19 | 99.24 0.76 | 99.24 0.76 | 99.40 0.60 | 99.87 0.15 |
| 7 | Mean Std | 92.44 3.04 | 91.38 2.04 | 94.30 2.57 | 90.16 2.72 | 92.06 0.96 | 91.22 2.59 | 91.54 3.61 | 92.99 2.98 | 95.10 1.74 |
| 8 | Mean Std | 94.56 2.32 | 92.28 0.85 | 93.03 1.47 | 92.82 2.00 | 77.03 8.71 | 90.24 1.98 | 93.18 2.58 | 94.27 1.28 | 94.62 2.76 |
| 9 | Mean Std | 75.45 3.57 | 76.79 0.93 | 78.93 1.39 | 76.16 6.12 | 75.30 6.98 | 67.32 6.02 | 70.99 5.25 | 75.67 3.28 | 83.61 0.66 |
| 10 | Mean Std | 94.24 5.76 | 93.94 6.06 | 86.68 10.92 | 83.03 10.43 | 92.12 1.21 | 87.88 12.12 | 90.30 0.61 | 95.0 1.31 | 93.93 9.38 |
| 11 | Mean Std | 99.24 0.76 | 99.50 0.52 | 98.32 1.68 | 98.99 0.34 | 97.82 2.18 | 98.99 1.01 | 98.15 1.85 | 90.00 9.00 | 100 0.00 |
| OA (%) | Mean Std | 87.39 1.12 | 87.08 1.24 | 87.06 0.85 | 84.96 1.10 | 83.67 1.46 | 84.33 0.76 | 84.81 1.34 | 87.94 0.48 | 90.16 1.49 |
| AA (%) | Mean Std | 90.09 0.99 | 89.30 1.12 | 89.18 1.64 | 87.57 0.80 | 87.26 1.64 | 86.77 1.52 | 87.19 0.60 | 89.36 1.26 | 92.47 1.33 |
| K × 100 | Mean Std | 83.60 0.21 | 83.14 1.64 | 83.19 0.43 | 80.61 1.31 | 78.86 0.33 | 79.76 0.93 | 80.37 1.59 | 84.24 1.55 | 87.14 1.86 |

- 3.
- AU dataset
| No. | HSI Input | HSI and LiDAR-DSM Input | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DMCN | SpectralFormer | SSFTT | morp- Former | Coupled CNN | MFT_PT | MFT_CT | HCT | AGMLT | ||
| 1 | Mean Std | 98.59 0.56 | 86.10 0.44 | 98.82 0.08 | 97.71 0.21 | 89.59 6.02 | 98.38 0.53 | 98.29 1.31 | 98.75 0.49 | 99.31 0.20 |
| 2 | Mean Std | 98.52 0.44 | 96.10 1.44 | 99.02 0.33 | 98.54 0.25 | 98.55 0.61 | 98.20 0.26 | 98.14 2.86 | 98.66 0.41 | 99.10 0.18 |
| 3 | Mean Std | 87.64 1.51 | 75.99 8.92 | 90.13 1.39 | 89.69 1.46 | 87.65 1.39 | 89.24 2.23 | 88.60 1.20 | 88.45 2.78 | 93.10 2.23 |
| 4 | Mean Std | 99.02 0.58 | 98.66 0.34 | 98.77 0.34 | 98.53 0.11 | 99.39 0.26 | 97.88 0.28 | 98.37 0.35 | 98.93 0.21 | 99.29 0.12 |
| 5 | Mean Std | 71.08 3.99 | 48.88 7.61 | 79.09 5.60 | 84.88 3.06 | 75.54 7.72 | 78.43 0.36 | 86.18 8.12 | 81.08 7.95 | 87.09 5.21 |
| 6 | Mean Std | 47.82 5.15 | 27.56 9.54 | 70.12 3.37 | 75.45 3.58 | 58.62 9.20 | 70.68 3.28 | 71.17 2.02 | 69.00 1.26 | 76.69 3.59 |
| 7 | Mean Std | 64.51 1.86 | 55.50 4.95 | 66.88 1.20 | 71.36 3.58 | 60.73 1.52 | 66.41 6.30 | 67.52 4.04 | 69.52 4.05 | 70.85 1.95 |
| OA (%) | Mean Std | 96.24 1.36 | 93.89 0.27 | 97.08 0.18 | 96.85 0.07 | 95.01 1.31 | 96.35 0.24 | 96.52 0.31 | 96.94 0.33 | 97.80 0.06 |
| AA (%) | Mean Std | 81.03 2.30 | 71.66 2.58 | 86.12 1.93 | 88.03 1.21 | 81.44 2.86 | 85.61 1.11 | 86.89 1.25 | 86.34 1.51 | 89.35 0.92 |
| K × 100 | Mean Std | 94.60 0.42 | 91.22 0.43 | 95.81 0.25 | 95.48 0.10 | 92.79 1.91 | 94.78 0.34 | 95.02 0.44 | 95.61 0.47 | 96.85 0.08 |
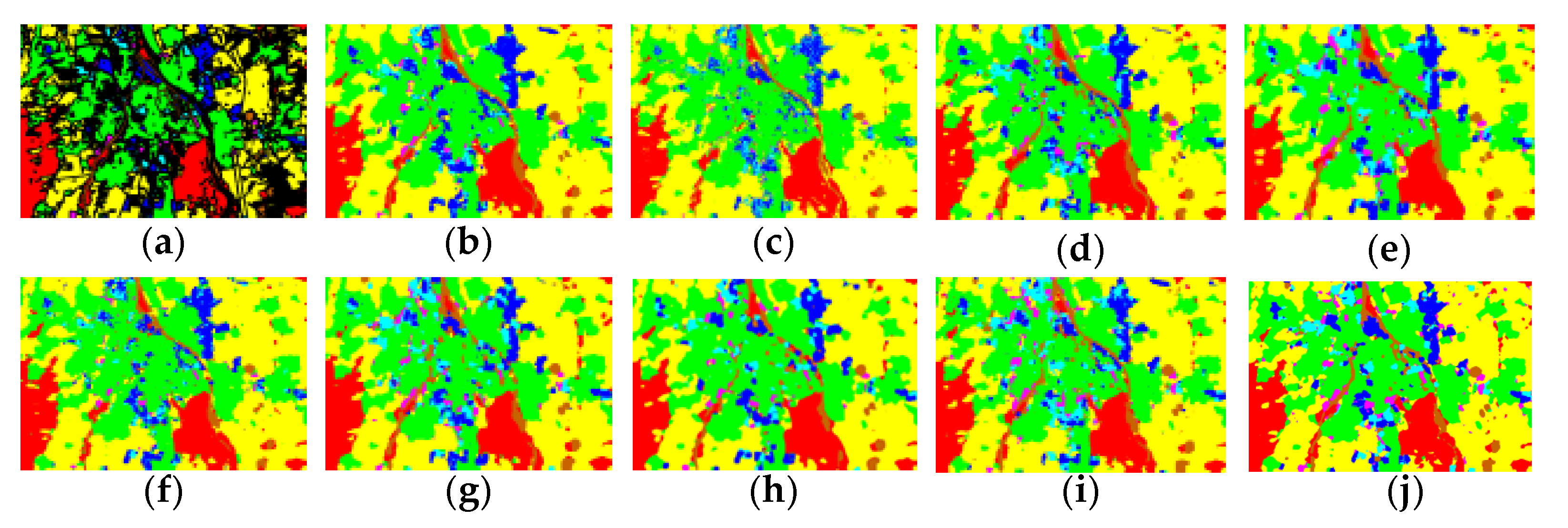
- 4.
- HU dataset
| No. | HSI Input | HSI and LiDAR-DSM Input | ||||||||
| DMCN | SpectralFormer | SSFTT | morp- Former | Coupled CNN | MFT_PT | MFT_CT | HCT | AGMLT | ||
| 1 | Mean Std | 98.35 0.80 | 99.34 0.66 | 99.74 0.26 | 99.18 0.36 | 99.91 0.09 | 99.32 0.68 | 98.94 0.97 | 98.77 1.05 | 99.81 0.08 |
| 2 | Mean Std | 98.54 3.24 | 98.89 1.11 | 99.91 0.09 | 99.19 0.32 | 99.94 0.06 | 99.53 0.85 | 99.49 0.51 | 99.70 0.30 | 99.84 0.16 |
| 3 | Mean Std | 98.05 2.88 | 100 0.00 | 99.96 0.04 | 99.47 0.47 | 99.92 0.08 | 99.76 0.24 | 99.88 0.12 | 99.92 0.08 | 100 0.00 |
| 4 | Mean Std | 98.74 0.98 | 99.72 0.28 | 99.66 0.15 | 99.56 0.16 | 94.56 5.15 | 94.43 0.57 | 98.28 1.72 | 99.56 0.35 | 100 0.00 |
| 5 | Mean Std | 100 0.00 | 99.39 0.61 | 99.92 0.08 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 |
| 6 | Mean Std | 96.89 3.11 | 99.30 0.70 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 |
| 7 | Mean Std | 96.05 1.37 | 98.06 1.94 | 99.63 0.38 | 98.88 0.65 | 99.06 0.75 | 99.31 0.69 | 99.85 0.15 | 99.74 0.26 | 100 0.00 |
| 8 | Mean Std | 94.60 4.45 | 98.33 1.42 | 99.44 0.10 | 98.35 0.25 | 96.81 1.28 | 99.55 0.45 | 99.47 0.53 | 99.87 0.13 | 100 0.00 |
| 9 | Mean Std | 94.34 5.52 | 96.20 2.19 | 99.68 0.32 | 98.65 1.45 | 96.94 2.02 | 99.09 0.91 | 99.13 0.87 | 99.23 0.37 | 100 0.00 |
| 10 | Mean Std | 99.83 0.17 | 99.83 0.17 | 99.77 0.23 | 99.94 0.09 | 99.83 0.17 | 99.81 0.19 | 99.98 0.02 | 99.98 0.02 | 100 0.00 |
| 11 | Mean Std | 99.31 0.69 | 99.48 0.32 | 99.79 0.21 | 100 0.00 | 99.28 0.57 | 99.72 0.28 | 99.49 0.51 | 99.98 0.02 | 100 0.00 |
| 12 | Mean Std | 97.14 2.51 | 99.27 0.23 | 99.63 0.37 | 99.46 0.20 | 99.06 0.56 | 99.81 0.19 | 99.29 0.23 | 99.67 0.33 | 99.57 0.04 |
| 13 | Mean Std | 94.03 5.96 | 95.99 3.64 | 99.93 0.07 | 98.71 1.82 | 99.65 0.35 | 99.86 0.14 | 99.58 0.42 | 99.72 0.28 | 100 0.00 |
| 14 | Mean Std | 99.90 0.10 | 99.92 0.08 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 |
| 15 | Mean Std | 100 0.00 | 99.83 0.17 | 100 0.00 | 100 0.00 | 100 0.00 | 100 0.00 | 99.92 0.08 | 100 0.00 | 100 0.00 |
| OA (%) | Mean Std | 98.84 0.29 | 98.89 0.70 | 99.73 0.14 | 99.36 0.24 | 98.54 0.49 | 99.60 0.15 | 99.46 0.29 | 99.73 0.16 | 99.93 0.02 |
| AA (%) | Mean Std | 99.05 0.38 | 98.90 0.45 | 99.79 0.11 | 99.43 0.29 | 98.85 0.31 | 99.68 0.13 | 99.55 0.24 | 99.78 0.22 | 99.95 0.01 |
| K × 100 | Mean Std | 98.74 0.31 | 98.80 0.32 | 99.71 0.16 | 99.30 0.26 | 98.41 0.53 | 99.57 0.16 | 99.41 0.32 | 99.70 0.16 | 99.93 0.02 |
3.3.2. Consumption and Computational Complexity
4. Discussion
4.1. Ablation Analysis
4.2. Loss Functions
4.3. Training Percentage
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Czaja, W.; Kavalerov, I.; Li, W. Exploring the high dimensional geometry of HSI features. In Proceedings of the 2021 11th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 March 2021; pp. 1–5. [Google Scholar]
- Wang, Z.; Menenti, M. Challenges and opportunities in lidar remote sensing. Front. Remote Sens. 2021, 2, 641723. [Google Scholar] [CrossRef]
- Roy, S.K.; Kar, P.; Hong, D.; Wu, X.; Plaza, A.; Chanussot, J. Revisiting deep hyperspectral feature extraction networks via gradient centralized convolution. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5516619. [Google Scholar] [CrossRef]
- Hestir, E.; Brando, V.; Bresciani, M.; Giardino, C.; Matta, E.; Villa, P.; Dekker, A. Measuring freshwater aquatic ecosystems: The need for a hyperspectral global mapping satellite mission. Remote Sens. Environ. 2015, 167, 181–195. [Google Scholar] [CrossRef]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hyperspectral imaging for military and security applications: Combining myriad processing and sensing techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Wu, X.; Hong, D.; Chanussot, J. UIU-Net: U-Net in U-Net for infrared small object detection. IEEE Trans. Image Process. 2023, 32, 364–376. [Google Scholar] [CrossRef]
- Carrino, T.A.; Crósta, A.P.; Toledo, C.L.B.; Silva, A.M. Hyper-spectral remote sensing applied to mineral exploration in southern peru:A multiple data integration approach in the chapi chiara gold prospect. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 287–300. [Google Scholar]
- Schimleck, L.; Ma, T.; Inagaki, T.; Tsuchikawa, S. Review of Near Infrared Hyperspectral Imaging Applications Related to Wood and Wood Products. Appl. Spectrosc. Rev. 2022, 57, 2098759. [Google Scholar] [CrossRef]
- Liao, X.; Liao, G.; Xiao, L. Rapeseed Storage Quality Detection Using Hyperspectral Image Technology–An Application for Future Smart Cities. J. Test. Eval. 2022, 51, JTE20220073. [Google Scholar] [CrossRef]
- Du, P.; Xia, J.S.; Xue, Z.H. Review of hyperspectral remote sensing image classification. J. Remote Sens. 2016, 20, 236–256. [Google Scholar]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, M.; Wei, C.; Zhong, Y.; Xiang, J. Heterogeneous spectral-spatial network with 3D attention and MLP for hyperspectral image classification using limited training samples. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 8702–8720. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5518615. [Google Scholar] [CrossRef]
- Sang, M.; Zhao, Y.; Liu, G. Improving Transformer-Based Networks with Locality for Automatic Speaker Verification. In Proceedings of the 2023 48th IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–spatial feature tokenization transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Wang, A.; Xing, S.; Zhao, Y.; Wu, H.; Iwahori, Y. A hyperspectral image classification method based on adaptive spectral spatial kernel combined with improved vision transformer. Remote Sens. 2022, 14, 3705. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–spatial hyperspectral image segmentation using subspace multinomial logistic regression and Markov random fields. IEEE Trans. Geosci. Remote Sens. 2011, 50, 809–823. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep hierarchical feature learning on points a metric space. arXiv 2017, arXiv:1706.02413. [Google Scholar]
- Pedergnana, M.; Marpu, P.R.; Dalla Mura, M.; Benediktsson, J.A.; Bruzzone, L. Classification of remote sensing optical and LiDAR data using extended attribute profiles. IEEE J. Sel. Top. Signal Process. 2012, 6, 856–865. [Google Scholar] [CrossRef]
- Rasti, B.; Ghamisi, P.; Gloaguen, R. Hyperspectral and LiDAR fusion using extinction profiles and total variation component analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3997–4007. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Hong, D. Hyperspectral and LiDAR data classification using joint CNNs and morphological feature learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5530416. [Google Scholar] [CrossRef]
- Song, W.; Dai, Y.; Gao, Z. Hashing-based deep metric learning for the classification of hyperspectral and LiDAR data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5704513. [Google Scholar] [CrossRef]
- Xu, X.; Li, W.; Ran, Q. Multisource remote sensing data classification based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2017, 56, 937–949. [Google Scholar] [CrossRef]
- Ding, K.; Lu, T.; Fu, W.; Li, S.; Ma, F. Global–local transformer network for HSI and LiDAR data joint classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5541213. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Y.; Tu, B.; Liu, Y. Local Information interaction transformer for hyperspectral and LiDAR data classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 16, 1130–1143. [Google Scholar] [CrossRef]
- Xu, H.; Zheng, T.; Liu, Y.; Zhang, Z.; Xue, C.; Li, J. A joint convolutional cross ViT network for hyperspectral and light detection and ranging fusion classification. Remote Sens. 2024, 16, 489. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Hong, D. Multimodal fusion transformer for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5515620. [Google Scholar] [CrossRef]
- Zhao, G.; Ye, Q.; Sun, L. Joint classification of hyperspectral and LiDAR data using a hierarchical CNN and transformer. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5500716. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Wang, G.; Liu, X. Multi-scale attention network for single image super-resolution. arXiv 2022, arXiv:2209.14145. [Google Scholar]
- Gulati, A.; Qin, J.; Chiu, C.C. Conformer: Convolution-augmented transformer for speech recognition. arXiv 2020, arXiv:2005.08100. [Google Scholar]
- Hang, R.; Li, Z.; Ghamisi, P.; Hong, D.; Xia, G.; Liu, Q. Classification of hyperspectral and LiDAR data using coupled CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4939–4950. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Zhou, D.; Kang, B.; Jin, X.; Yang, L. DeepViT: Towards deeper vision transformer. arXiv 2021, arXiv:2103.11886v4. [Google Scholar]
- Touvron, H.; Cord, M.; Sablayrolles, A. Going deeper with image transformers. arXiv 2021, arXiv:2103.17239v2. [Google Scholar]
- Leng, Z.Q.; Tan, M.X.; Liu, C.X. PolyLoss: A polynomial expansion perspective of classification loss functions. In Proceedings of the 2022 10th IEEE Conference on International Conference on Learning Representations (ICLR), Virtual, 25–29 April 2022. [Google Scholar]
- Gader, P.; Zare, A.; Close, R.; Aitken, J.; Tuell, G. Muufl Gulfport Hyperspectral and LiDAR Airborne Data Set; Technical Report REP-2013–570; University of Florida: Gainesville, FL, USA, 2013. [Google Scholar]
- Du, X.; Zare, A. Scene Label Ground Truth Map for Muufl Gulfport Data Set; Technical Report 20170417; University of Florida: Gainesville, FL, USA, 2017. [Google Scholar]
- Baumgartner, A.; Gege, P.; Köhler, C.; Lenhard, K.; Schwarzmaier, T. Characterisation methods for the hyperspectral sensor HySpex at DLR’s calibration home base. Proc. SPIE 2012, 8533, 371–378. [Google Scholar]
- Kurz, F.; Rosenbaum, D.; Leitloff, J.; Meynberg, O.; Reinartz, P. Real time camera system for disaster and traffic monitoring. Proceedings of International Conference on SMPR, Tehran, Iran, 18–19 May 2011; pp. 1–6. [Google Scholar]
- Xiang, J.H.; Wei, C.; Wang, M.H.; Teng, L. End-to-End Multilevel Hybrid Attention Framework for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5511305. [Google Scholar] [CrossRef]
- Swalpa, K.R.; Ankur, D.; Shah, C. Spectral–spatial morphological attention transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 61, 5503615. [Google Scholar]




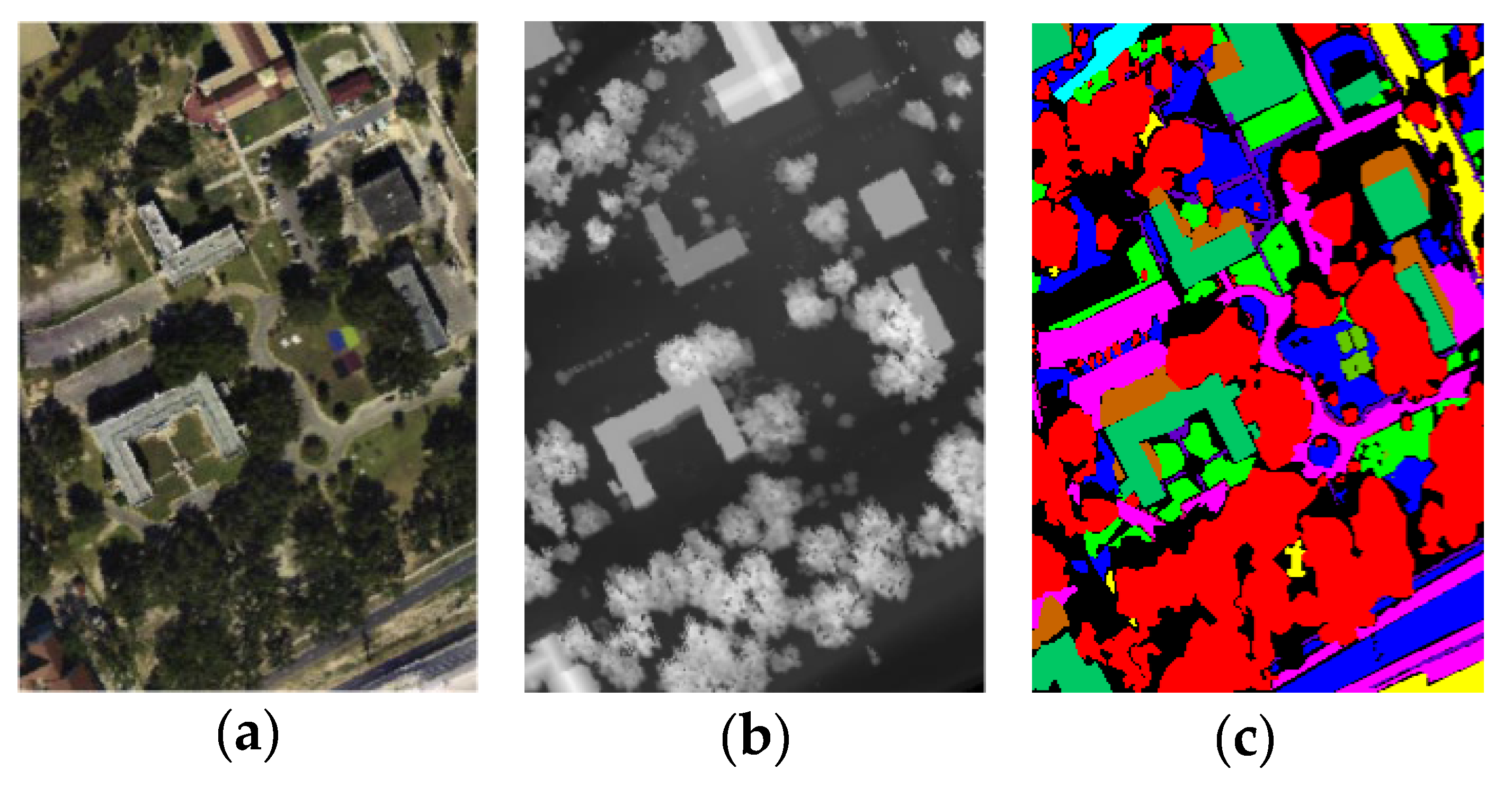




| No. | Color | Class Name | Training Samples | Test Samples |
|---|---|---|---|---|
| 1 | Apple Trees | 129 | 3905 | |
| 2 | Buildings | 125 | 2778 | |
| 3 | Ground | 105 | 374 | |
| 4 | Woods | 154 | 9896 | |
| 5 | Vineyard | 184 | 10,317 | |
| 6 | Roads | 122 | 3052 | |
| Total | 819 | 29,395 | ||
| No. | Color | Class Name | Training Samples | Test Samples |
|---|---|---|---|---|
| 1 | Trees | 150 | 23,096 | |
| 2 | Mostly Grass | 150 | 4120 | |
| 3 | Mixed Ground Surface | 150 | 6732 | |
| 4 | Dirt and Sand | 150 | 1676 | |
| 5 | Road | 150 | 6537 | |
| 6 | Water | 150 | 316 | |
| 7 | Buildings Shadow | 150 | 2083 | |
| 8 | Buildings | 150 | 6090 | |
| 9 | Sidewalk | 150 | 1235 | |
| 10 | Yellow Curb | 150 | 33 | |
| 11 | Cloth Panels | 150 | 119 | |
| Total | 1650 | 52,037 | ||
| No. | Color | Class Name | Training Samples | Test Samples |
|---|---|---|---|---|
| 1 | Forest | 675 | 12,832 | |
| 2 | Residential Area | 1516 | 28,813 | |
| 3 | Industrial Area | 192 | 3659 | |
| 4 | Low Plants | 1342 | 25,515 | |
| 5 | Allotment | 28 | 547 | |
| 6 | Commercial Area | 82 | 1563 | |
| 7 | Water | 16 | 1454 | |
| Total | 3911 | 74,383 | ||
| No. | Color | Class Name | Training Samples | Test Samples |
|---|---|---|---|---|
| 1 | Healthy Grass | 198 | 1053 | |
| 2 | Stressed Grass | 190 | 1064 | |
| 3 | Synthetic Grass | 192 | 505 | |
| 4 | Trees | 188 | 1056 | |
| 5 | Soil | 186 | 1056 | |
| 6 | Water | 182 | 143 | |
| 7 | Residential | 196 | 1072 | |
| 8 | Commercial | 191 | 1053 | |
| 9 | Road | 193 | 1059 | |
| 10 | Highway | 191 | 1036 | |
| 11 | Railway | 181 | 1054 | |
| 12 | Parking Lot l | 192 | 1041 | |
| 13 | Parking Lot 2 | 184 | 285 | |
| 14 | Tennis Court | 181 | 247 | |
| 15 | Running Track | 187 | 473 | |
| Total | 2832 | 12,197 | ||
| Datasets | Initial Learning Rate | ||
|---|---|---|---|
| 0.001 | 0.0005 | 0.0001 | |
| TR | 99.66 ± 0.04 | 99.72 ± 0.04 | 99.58 ± 0.09 |
| MU | 90.16 ± 1.49 | 87.44 ± 1.89 | 87.82 ± 1.03 |
| AU | 97.60 ± 0.16 | 97.80 ± 0.06 | 97.50 ± 0.11 |
| HU | 99.65 ± 0.06 | 99.70 ± 0.05 | 99.93 ± 0.02 |
| Methods | TPs | Tr (s) | Te (s) | Flops | OA (%) | TPs | Tr (s) | Te (s) | Flops | OA (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| TR | MU | |||||||||
| DMCN | 2.77 M | 20.22 | 1.69 | 3.21 G | 99.35 ± 0.17 | 2.77 M | 34.40 | 3.04 | 3.21 G | 87.39 ± 1.12 |
| SpectralFormer | 97.33 K | 46.80 | 3.55 | 192.68 M | 97.99 ± 0.64 | 97.65 K | 93.22 | 6.22 | 192.70 M | 87.08 ± 1.24 |
| SSFTT | 147.84 K | 22.08 | 1.51 | 447.18 M | 99.18 ± 0.12 | 148.16 K | 38.06 | 2.78 | 447.20 M | 87.06 ± 0.85 |
| morpFormer | 62.56 K | 38.36 | 4.38 | 334.43 M | 99.02 ± 0.28 | 62.56 K | 77.67 | 7.11 | 334.43 M | 84.96 ± 1.10 |
| CoupledCNN | 104.18 K | 7.68 | 0.78 | 169.08 M | 98.39 ± 1.28 | 106.11 K | 18.47 | 1.38 | 169.20 M | 83.67 ± 1.46 |
| MFT_PT | 221.29 K | 58.50 | 7.98 | 312.91 M | 99.11 ± 0.19 | 221.61 K | 115.80 | 14.10 | 312.93 M | 84.33 ± 0.76 |
| MFT_CT | 221.29 K | 82.33 | 11.60 | 312.91 M | 99.45 ± 0.10 | 221.61 K | 163.87 | 20.39 | 312.93 M | 84.81 ± 1.34 |
| HCT | 465.62 K | 14.53 | 1.28 | 519.16 M | 99.62 ± 0.14 | 728.09 K | 26.84 | 2.27 | 569.55 M | 87.94 ± 0.48 |
| AGMLT | 837.08 K | 50.44 | 3.97 | 4.91 G | 99.72 ± 0.04 | 837.40 K | 120.48 | 9.55 | 4.91 G | 90.16 ± 1.49 |
| Methods | AU | HU | ||||||||
| DMCN | 2.77 M | 76.96 | 3.82 | 3.21 G | 96.24 ± 1.36 | 2.78 M | 23.49 | 0.93 | 3.21 G | 98.84 ± 0.29 |
| SpectralFormer | 97.39 K | 202.32 | 8.03 | 192.68 M | 93.89 ± 0.27 | 97.91 K | 153.84 | 1.43 | 192.71 M | 98.89 ± 0.70 |
| SSFTT | 147.90 K | 93.01 | 3.97 | 447.18 M | 97.08 ± 0.18 | 148.42 K | 28.37 | 0.37 | 447.22 M | 99.73 ± 0.14 |
| morpFormer | 62.56 K | 185.38 | 10.22 | 334.43 M | 96.85 ± 0.07 | 62.56 K | 134.35 | 1.85 | 334.43 M | 99.36 ± 0.24 |
| CoupledCNN | 104.57 K | 37.86 | 2.03 | 169.11 M | 95.01 ± 1.31 | 107.66 K | 27.98 | 0.37 | 169.30 M | 98.54 ± 0.49 |
| MFT_PT | 221.35 K | 272.02 | 20.03 | 312.91 M | 96.35 ± 0.24 | 221.87 K | 195.11 | 3.32 | 312.95 M | 99.60 ± 0.15 |
| MFT_CT | 221.35 K | 397.32 | 29.77 | 312.91 M | 96.52 ± 0.31 | 221.87 K | 332.68 | 5.50 | 312.95 M | 99.46 ± 0.29 |
| HCT | 727.83 K | 60.74 | 3.42 | 569.52 M | 96.94 ± 0.33 | 728.35 K | 58.33 | 0.87 | 569.58 M | 99.73 ± 0.16 |
| AGMLT | 837.14 K | 258.56 | 12.43 | 4.91 G | 97.80 ± 0.06 | 837.66 K | 170.65 | 1.67 | 4.91 G | 99.93 ± 0.02 |
| SSAGM | L-Former | LC-Attention | OA (%) | AA (%) | K × 100 | |
|---|---|---|---|---|---|---|
| LS | LTM | |||||
| √ | 99.67 ± 0.03 | 99.49 ± 0.04 | 99.56 ± 0.04 | |||
| √ | 99.63 ± 0.01 | 99.38 ± 0.02 | 99.50 ± 0.01 | |||
| √ | √ | √ | 99.34 ± 0.08 | 98.87 ± 0.16 | 99.11 ± 0.11 | |
| √ | √ | √ | 99.55 ± 0.09 | 99.31 ± 0.14 | 99.40 ± 0.11 | |
| √ | 99.62 ± 0.13 | 99.37 ± 0.22 | 99.49 ± 0.18 | |||
| √ | 99.41 ± 0.04 | 98.95 ± 0.17 | 99.21 ± 0.06 | |||
| √ | 99.68 ± 0.02 | 99.46± 0.02 | 99.57 ± 0.02 | |||
| √ | √ | 99.43 ± 0.03 | 98.98 ± 0.13 | 99.24 ± 0.05 | ||
| √ | √ | 99.50 ± 0.09 | 99.12 ± 0.14 | 99.32 ± 0.12 | ||
| √ | √ | 99.46 ± 0.08 | 99.14 ± 0.13 | 99.28 ± 0.11 | ||
| √ | √ | √ | 99.72 ± 0.04 | 99.57 ± 0.07 | 99.62 ± 0.05 | |
| PDWA | ADWA(H) | ADWA(L) | OA (%) | AA (%) | K×100 |
|---|---|---|---|---|---|
| √ | 99.57 ± 0.03 | 99.34 ± 0.05 | 99.43 ± 0.04 | ||
| √ | 99.38 ± 0.06 | 99.04 ± 0.07 | 99.17 ± 0.07 | ||
| √ | 99.63 ± 0.15 | 99.42 ± 0.24 | 99.50 ± 0.20 | ||
| √ | √ | 99.36 ± 0.14 | 98.61 ± 0.20 | 99.14 ± 0.18 | |
| √ | √ | 99.61 ± 0.05 | 99.40 ± 0.07 | 99.48 ± 0.07 | |
| √ | √ | 99.51 ± 0.03 | 99.24 ± 0.05 | 99.34 ± 0.03 | |
| √ | √ | √ | 99.72 ± 0.04 | 99.57 ± 0.07 | 99.62 ± 0.05 |
| OA (%) | AA (%) | K × 100 | Total Params | Flops | |
|---|---|---|---|---|---|
| No Asymmetric Convolution | 99.62 ± 0.08 | 99.01 ± 0.14 | 99.50 ± 0.10 | 904.71 K | 5.39 G |
| With Asymmetric Convolution | 99.72 ± 0.04 | 99.57 ± 0.07 | 99.62 ± 0.05 | 837.08 K | 4.91 G |
| Inputs | OA (%) | AA (%) | K×100 | OA (%) | AA (%) | K × 100 |
|---|---|---|---|---|---|---|
| TR | MU | |||||
| HSI | 99.32 ± 0.03 | 98.95 ± 0.05 | 99.09 ± 0.04 | 89.33 ± 0.92 | 91.83 ± 1.20 | 86.09 ± 1.19 |
| LiDAR-DSM | 97.81 ± 0.64 | 96.55 ± 1.22 | 97.06 ± 0.87 | 68.11 ± 1.61 | 67.26 ± 5.39 | 59.55 ± 1.87 |
| HSI + LiDAR-DSM | 99.72 ± 0.04 | 99.57 ± 0.07 | 99.62 ± 0.05 | 90.16 ± 1.49 | 92.47 ± 1.33 | 87.14 ± 1.86 |
| Inputs | AU | HU | ||||
| HSI | 97.45 ± 0.19 | 89.17 ± 1.21 | 96.35 ± 0.27 | 99.76 ± 0.05 | 99.80 ± 0.05 | 99.73 ± 0.06 |
| LiDAR-DSM | 95.62 ± 1.07 | 95.62 ± 1.07 | 95.62 ± 1.07 | 95.62 ± 1.07 | 95.62 ± 1.07 | 95.62 ± 1.07 |
| HSI + LiDAR-DSM | 97.80 ± 0.06 | 89.35 ± 0.92 | 96.85 ± 0.08 | 99.93 ± 0.02 | 99.95 ± 0.01 | 99.93 ± 0.02 |
| Loss Functions | OA (%) | AA (%) | K × 100 | OA (%) | AA (%) | K × 100 |
|---|---|---|---|---|---|---|
| TR | MU | |||||
| LCE | 99.69 ± 0.05 | 99.49 ± 0.11 | 99.58 ± 0.06 | 89.92 ± 0.77 | 92.84 ± 0.45 | 86.84 ± 0.97 |
| LFC | 99.69 ± 0.09 | 99.54 ± 0.13 | 99.59 ± 0.11 | 90.09 ± 0.29 | 92.09 ± 0.39 | 87.07 ± 0.37 |
| LPC | 99.61 ± 0.05 | 98.99 ± 0.08 | 99.48 ± 0.06 | 89.92 ± 0.40 | 92.47 ± 0.70 | 86.81 ± 0.51 |
| LPF | 99.72 ± 0.04 | 99.57 ± 0.07 | 99.62 ± 0.05 | 90.16 ± 1.49 | 92.47 ± 1.33 | 87.14 ± 1.86 |
| Loss Functions | AU | HU | ||||
| LCE | 97.49 ± 0.27 | 88.34 ± 0.36 | 96.41 ± 0.39 | 99.86 ± 0.05 | 99.89 ± 0.04 | 99.85 ± 0.05 |
| LFC | 97.63 ± 0.28 | 88.26 ± 1.37 | 96.61 ± 0.40 | 99.75 ± 0.05 | 99.79 ± 0.04 | 99.73 ± 0.04 |
| LPC | 97.38 ± 0.25 | 88.42 ± 1.14 | 96.25 ± 0.36 | 99.79 ± 0.05 | 99.75 ± 0.03 | 99.78 ± 0.05 |
| LPF | 97.80 ± 0.06 | 89.35 ± 0.92 | 96.85 ± 0.08 | 99.93 ± 0.02 | 99.95 ± 0.01 | 99.93 ± 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Sun, Y.; Xiang, J.; Sun, R.; Zhong, Y. Joint Classification of Hyperspectral and LiDAR Data Based on Adaptive Gating Mechanism and Learnable Transformer. Remote Sens. 2024, 16, 1080. https://doi.org/10.3390/rs16061080
Wang M, Sun Y, Xiang J, Sun R, Zhong Y. Joint Classification of Hyperspectral and LiDAR Data Based on Adaptive Gating Mechanism and Learnable Transformer. Remote Sensing. 2024; 16(6):1080. https://doi.org/10.3390/rs16061080
Chicago/Turabian StyleWang, Minhui, Yaxiu Sun, Jianhong Xiang, Rui Sun, and Yu Zhong. 2024. "Joint Classification of Hyperspectral and LiDAR Data Based on Adaptive Gating Mechanism and Learnable Transformer" Remote Sensing 16, no. 6: 1080. https://doi.org/10.3390/rs16061080
APA StyleWang, M., Sun, Y., Xiang, J., Sun, R., & Zhong, Y. (2024). Joint Classification of Hyperspectral and LiDAR Data Based on Adaptive Gating Mechanism and Learnable Transformer. Remote Sensing, 16(6), 1080. https://doi.org/10.3390/rs16061080






