Stationary Detection for Zero Velocity Update of IMU Based on the Vibrational FFT Feature of Land Vehicle
Abstract
1. Introduction
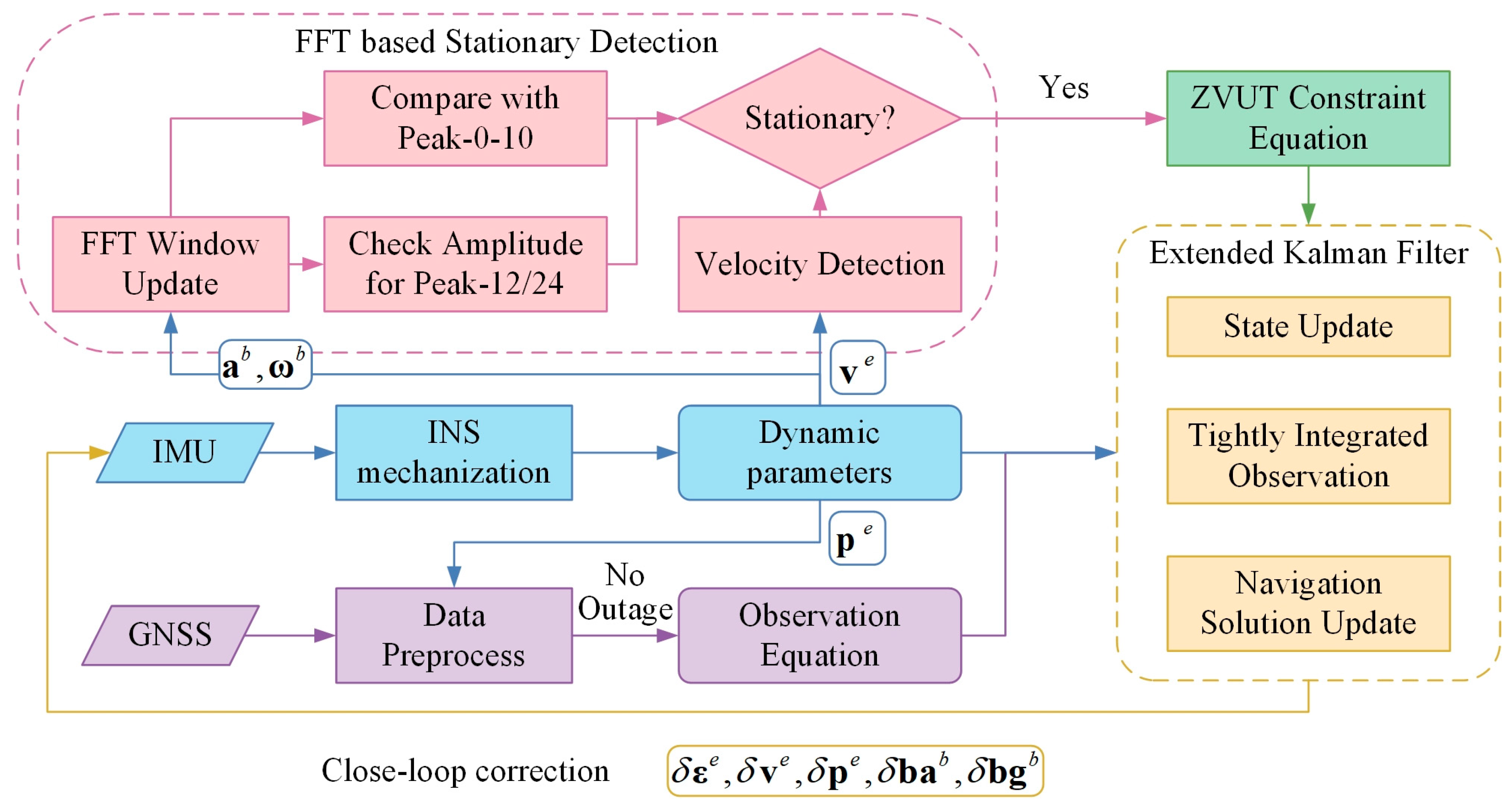
2. Methods
2.1. FFT-Based Vibration Frequency Analysis
2.2. ZVU Constraint in GNSS/IMU Tight Integration
3. Experimental Setup
3.1. Hardware Platform
3.2. Experimental Strategy
4. Experimental Results and Discussion
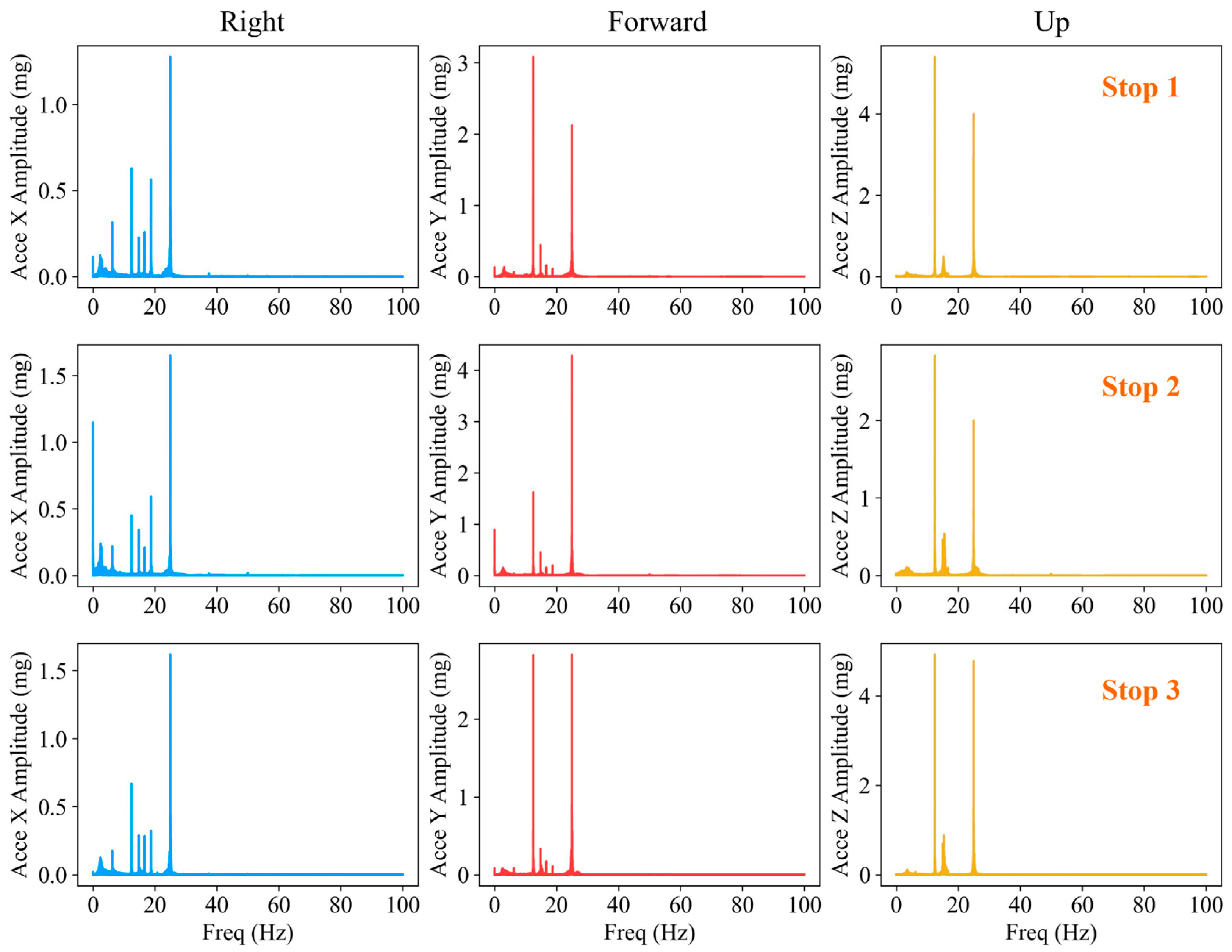
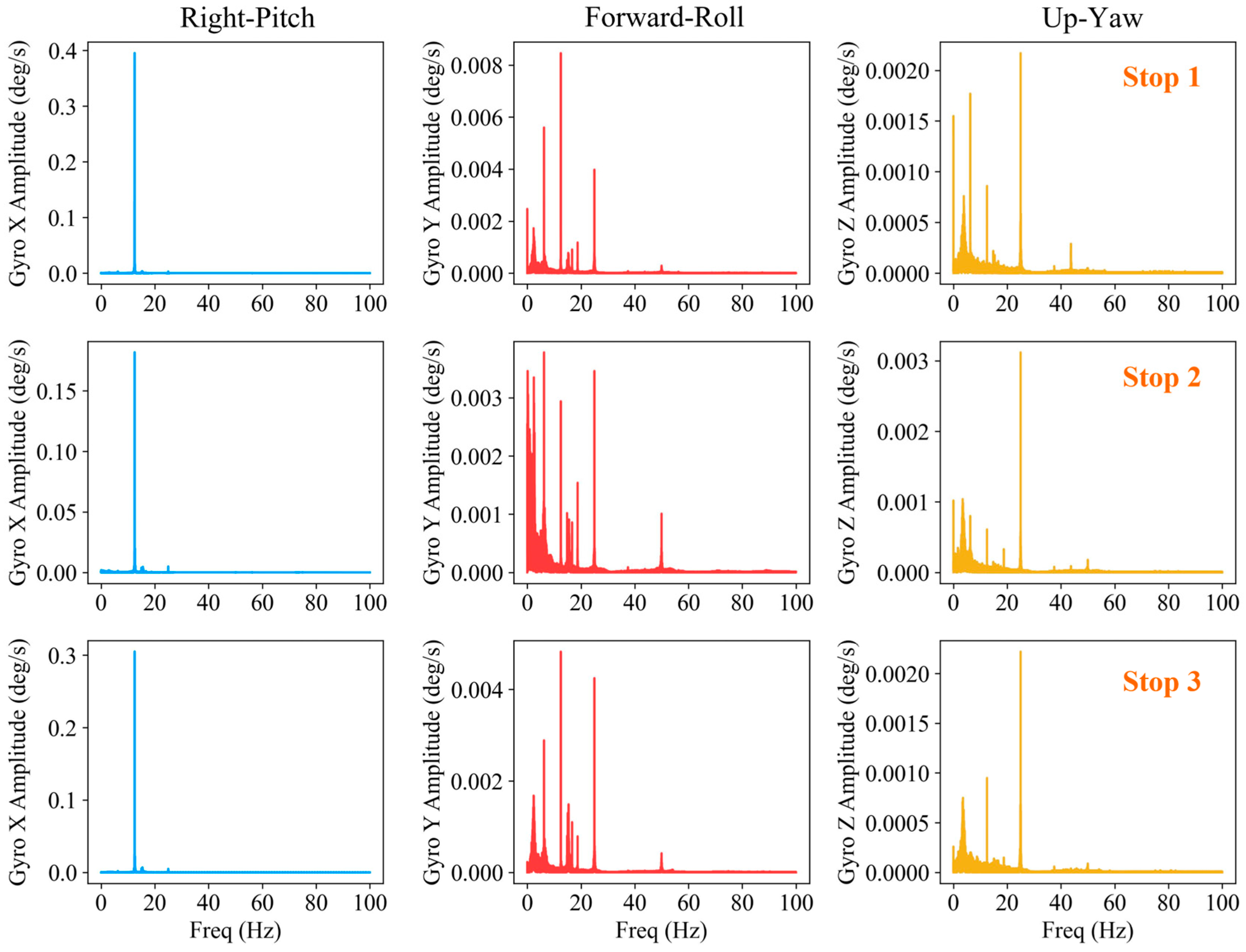
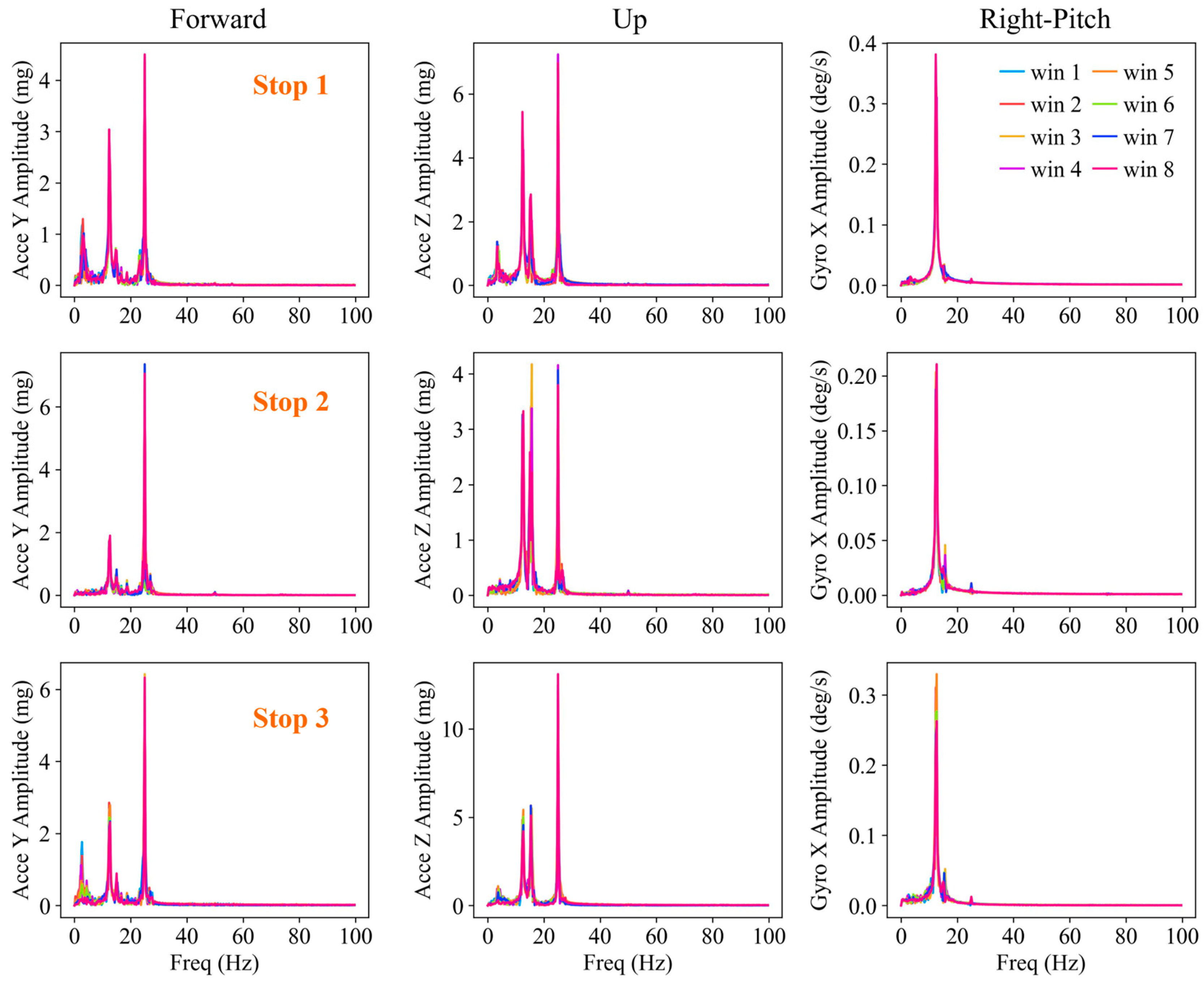
4.1. FFT Features of Acceleration and Angular Velocity for Stationary Idling Vehicle
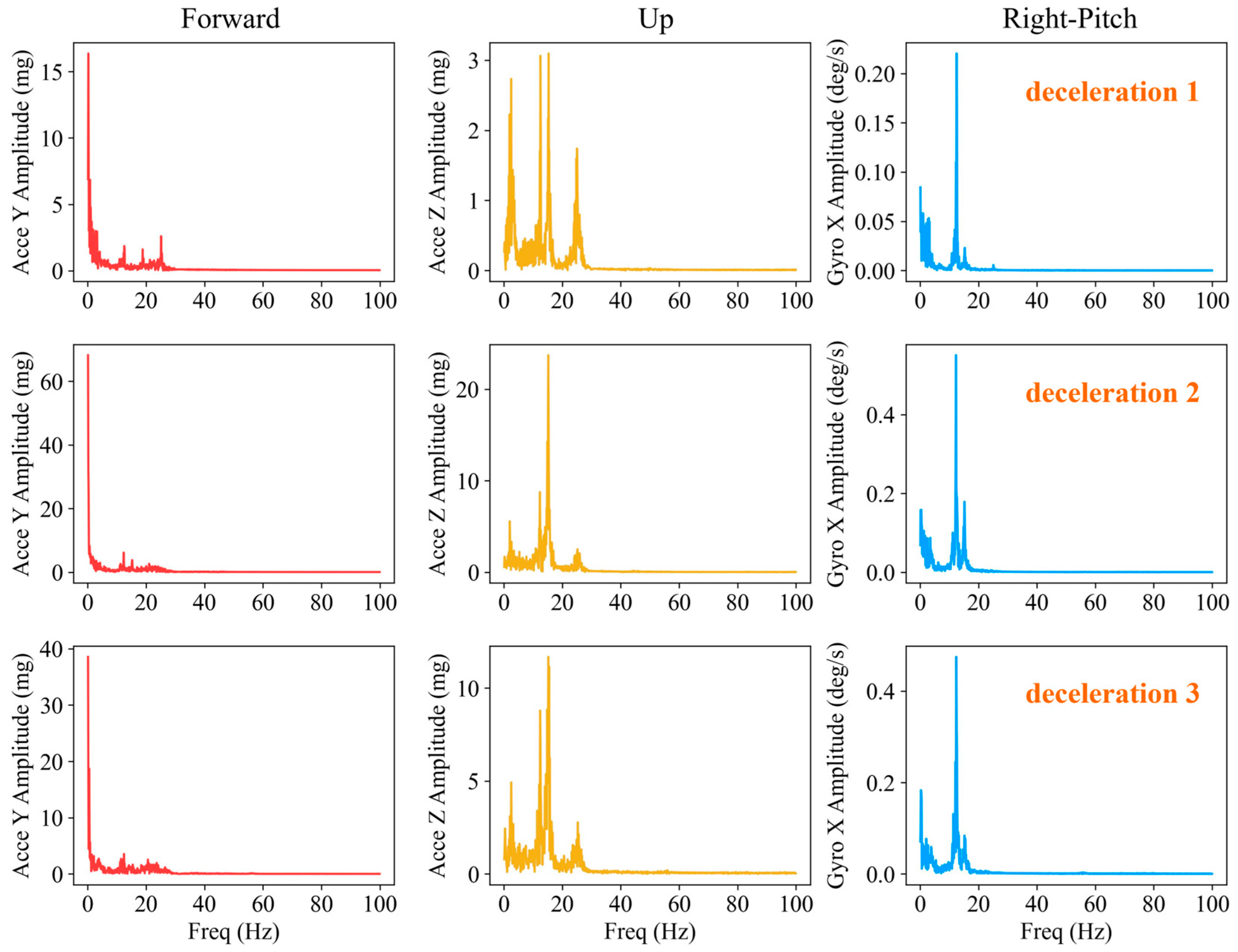
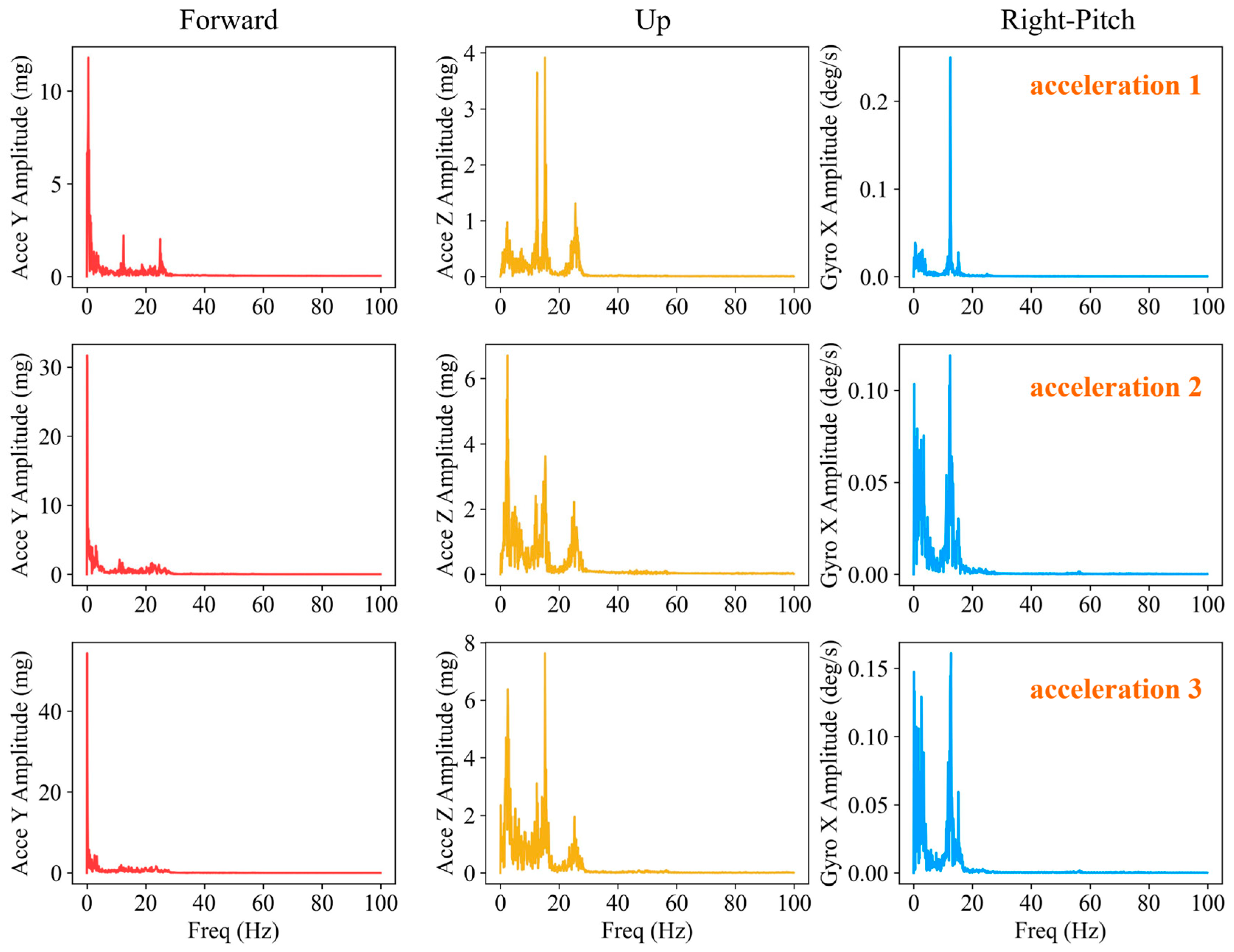
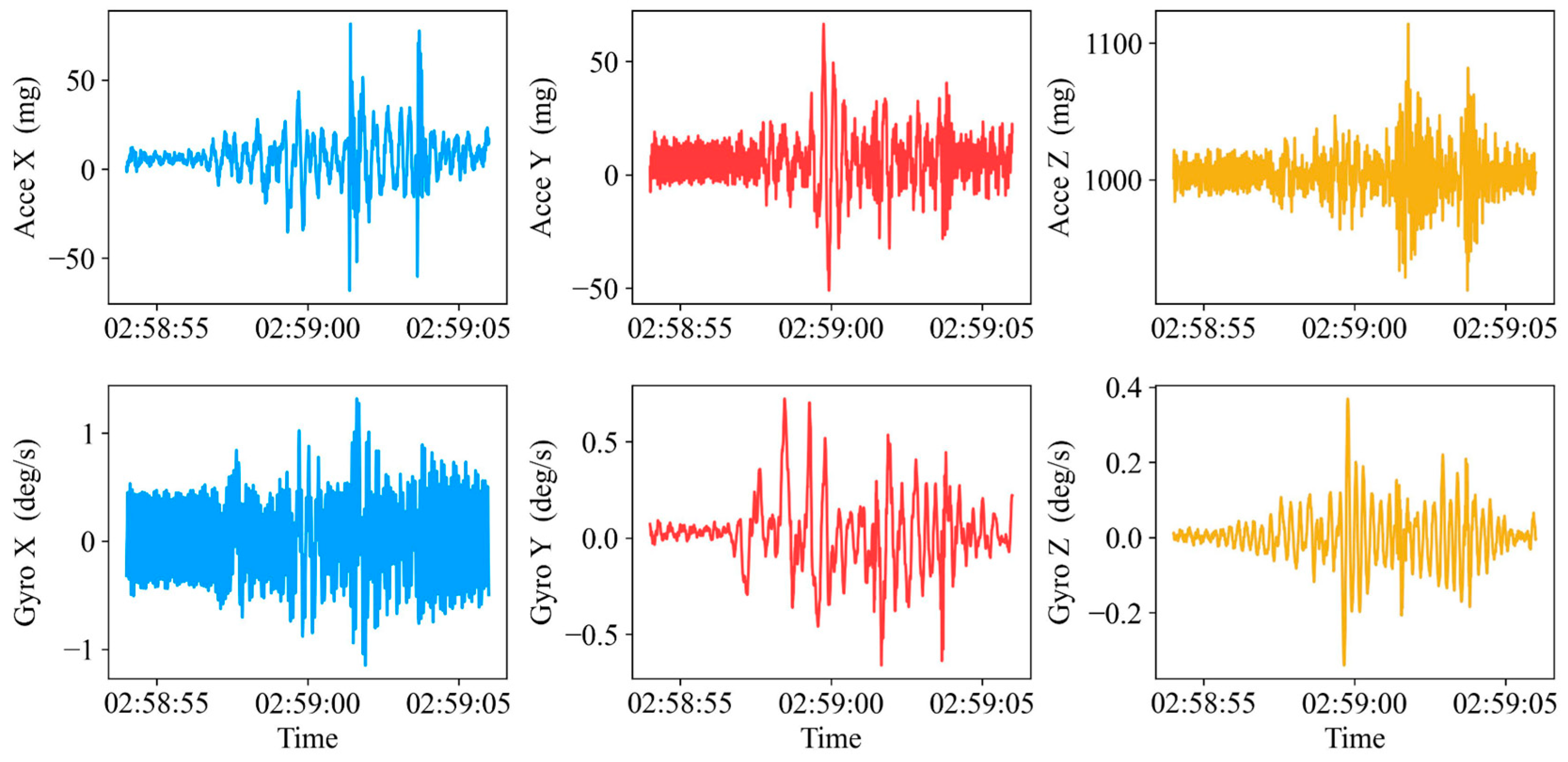
4.2. FFT Features of Acceleration and Angular Velocity in Decelerating and Accelerating
4.3. FFT-Based Stationary Detection Results
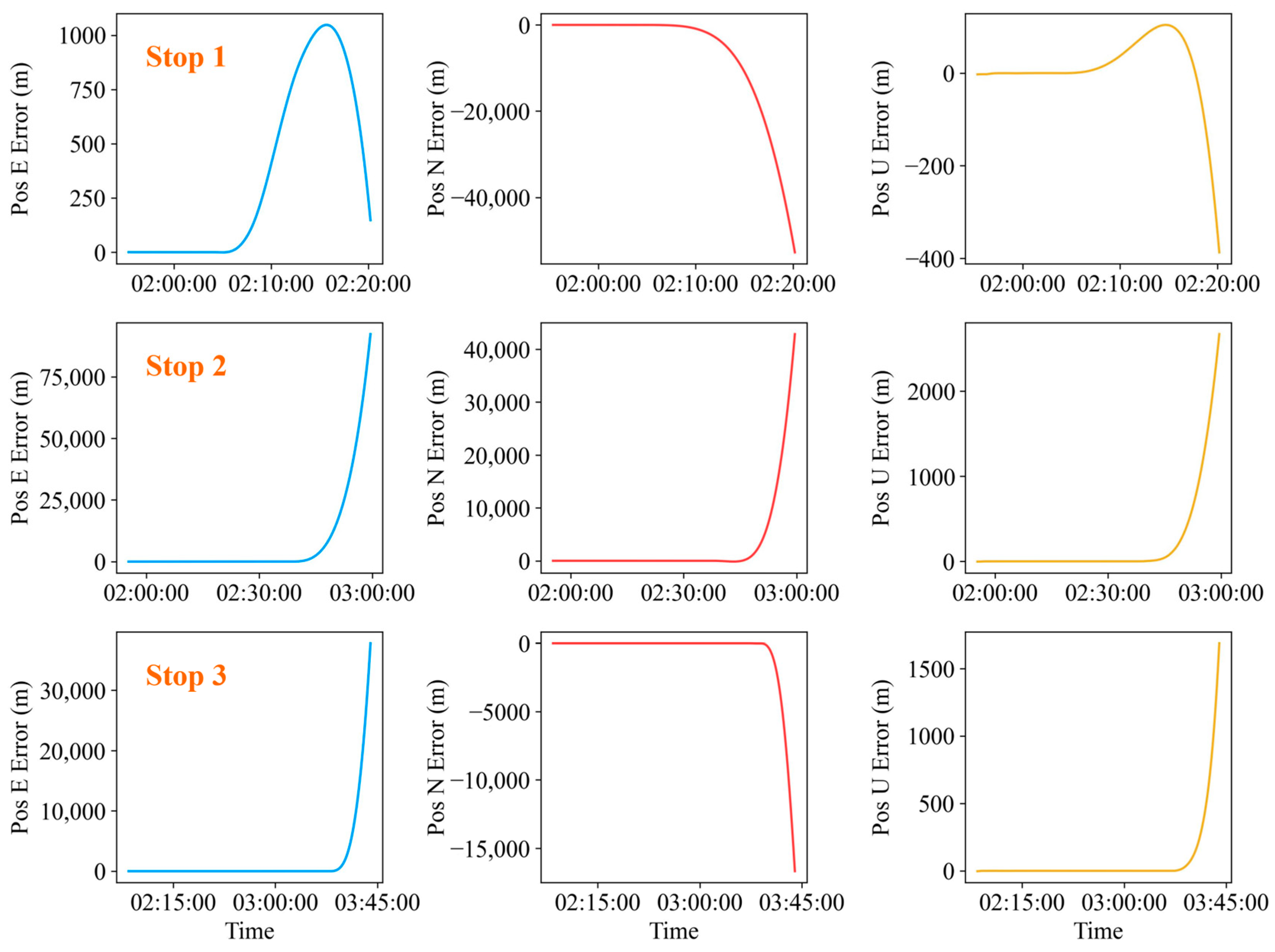
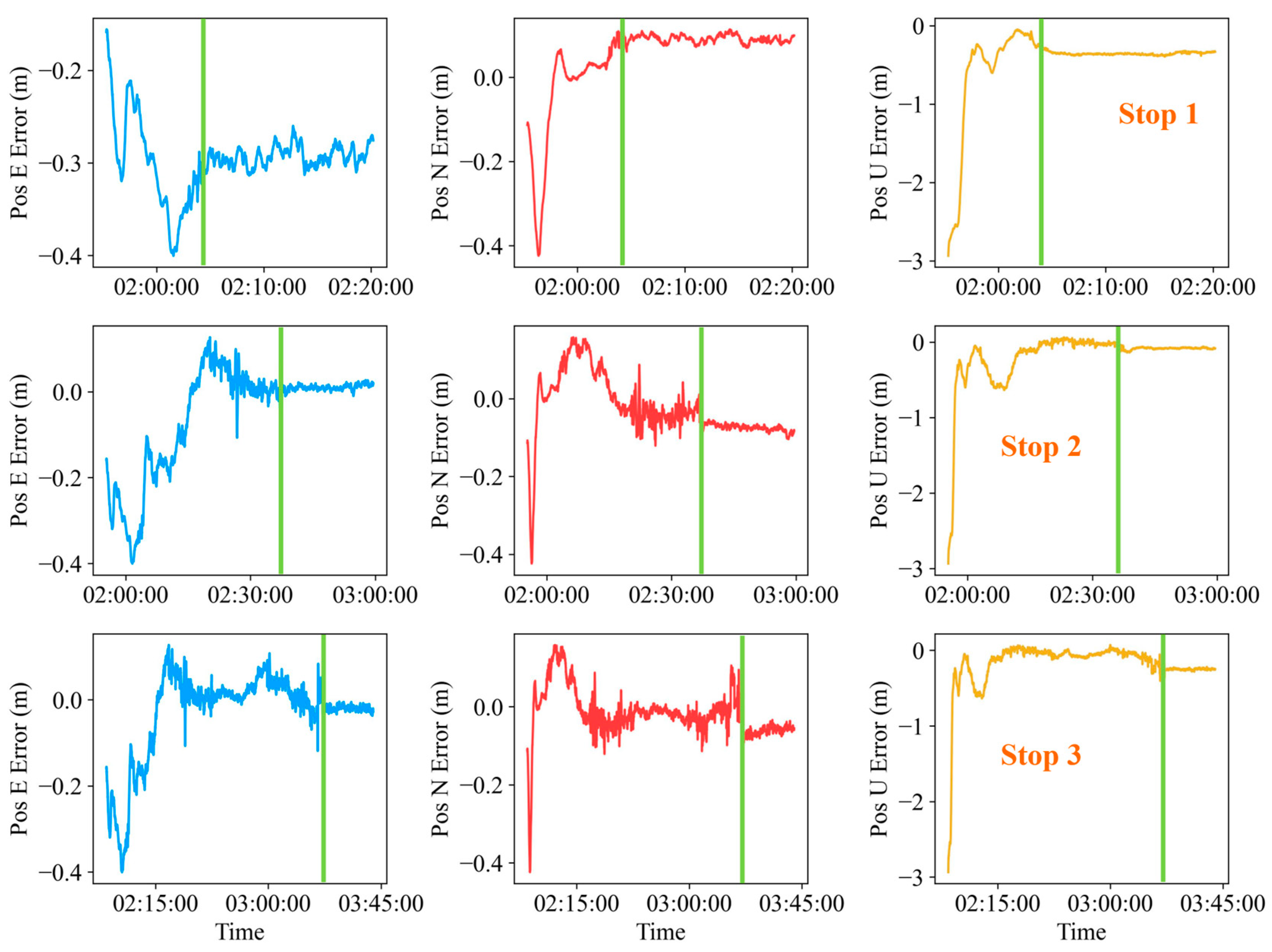
4.4. ZVU-Constrained Positioning Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Titterton, D.; Weston, J.L.; Weston, J. Strapdown Inertial Navigation Technology; IET: London, UK, 2004; Volume 17. [Google Scholar]
- Lawrence, A. Modern Inertial Technology: Navigation, Guidance, and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Abd Rabbou, M.; El-Rabbany, A. Tightly coupled integration of GPS precise point positioning and MEMS-based inertial systems. GPS Solut. 2015, 19, 601–609. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Gao, Z.; Niu, X.; El-sheimy, N. Tight Fusion of a Monocular Camera, MEMS-IMU, and Single-Frequency Multi-GNSS RTK for Precise Navigation in GNSS-Challenged Environments. Remote Sens. 2019, 11, 610. [Google Scholar] [CrossRef]
- Kempe, V. Inertial MEMS: Principles and Practice; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Aggarwal, P. MEMS-Based Integrated Navigation; Artech House: Norwood, MA, USA, 2010. [Google Scholar]
- Li, X.; Wang, H.; Li, S.; Feng, S.; Wang, X.; Liao, J. GIL: A tightly coupled GNSS PPP/INS/LiDAR method for precise vehicle navigation. Satell. Navig. 2021, 2, 26. [Google Scholar] [CrossRef]
- Li, X.; Chang, H.; Wang, X.; Li, S.; Zhou, Y.; Yu, H. An Optimization-Based Tightly-Coupled Integration of PPP, INS and Vision for Precise and Continuous Navigation. IEEE Trans. Veh. Technol. 2023, 1–14. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Niu, X.; Gao, Z. Tightly-Coupled Integration of Multi-GNSS Single-Frequency RTK and MEMS-IMU for Enhanced Positioning Performance. Sensors 2017, 17, 2462. [Google Scholar] [CrossRef] [PubMed]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, 2nd ed.; Artech House: Norwood, MA, USA, 2013; p. 776. [Google Scholar]
- Grewal, M.S.; Weill, L.R.; Andrews, A.P. Global Positioning Systems, Inertial Navigation, and Integration; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Lima Filho, V.C.; Moraes, A. Modeling multifrequency GPS multipath fading in land vehicle environments. GPS Solut. 2020, 25, 3. [Google Scholar] [CrossRef]
- Wang, X.; Li, X.; Shen, Z.; Li, X.; Zhou, Y.; Chang, H. Factor graph optimization-based multi-GNSS real-time kinematic system for robust and precise positioning in urban canyons. GPS Solut. 2023, 27, 200. [Google Scholar] [CrossRef]
- Quan, Y.; Lau, L.; Roberts, G.W.; Meng, X.; Zhang, C. Convolutional Neural Network Based Multipath Detection Method for Static and Kinematic GPS High Precision Positioning. Remote Sens. 2018, 10, 2052. [Google Scholar] [CrossRef]
- Grejner-Brzezinska, D.A.; Yi, Y.; Toth, C.K. Bridging GPS Gaps in Urban Canyons: The Benefits of ZUPTs. Navigation 2001, 48, 216–226. [Google Scholar] [CrossRef]
- Li, Q.; Li, K.; Liang, W. A zero-velocity update method based on neural network and Kalman filter for vehicle-mounted inertial navigation system. Meas. Sci. Technol. 2023, 34, 045110. [Google Scholar] [CrossRef]
- Amin, M.S.; Reaz, M.B.I.; Nasir, S.S.; Bhuiyan, M.A.S. Attitude Heading Reference System based vehicle stationary state detection. In Proceedings of the 2014 International Conference on Electrical Engineering and Information & Communication Technology, Mirpur, Pakistan, 10–12 April 2014; pp. 1–4. [Google Scholar]
- Amin, M.S.; Reaz, M.B.I.; Nasir, S.S.; Bhuiyan, M.A.S.; Ali, M.A.M. A Novel Vehicle Stationary Detection Utilizing Map Matching and IMU Sensors. Sci. World J. 2014, 2014, 597180. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Gong, Y.; Luo, H.; Zhao, F.; Li, Z.; Jiang, J. Heterogeneous Multi-Task Learning for Multiple Pseudo-Measurement Estimation to Bridge GPS Outages. IEEE Trans. Instrum. Meas. 2021, 70, 8500916. [Google Scholar] [CrossRef]
- Ramanandan, A.; Chen, A.; Farrell, J.A.; Suvarna, S. Detection of Stationarity in an Inertial Navigation System. In Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute-of-Navigation (ION GNSS-2010), Portland, OR, USA, 21–24 September 2010; pp. 238–244. [Google Scholar]
- Ramanandan, A.; Chen, A.; Farrell, J.A. Inertial Navigation Aiding by Stationary Updates. IEEE Trans. Intell. Transp. Syst. 2012, 13, 235–248. [Google Scholar] [CrossRef]
- Johnson, S.R.; Subhedar, J.W. Computer optimization of engine mounting systems. In Proceedings of the 3rd International Conference on Vehicle Structural Mechanics, Troy, MI, USA, 1 February 1979. [Google Scholar]
- Lee, J.M.; Yim, H.J.; Kim, J.-H. Flexible Chassis Effects on Dynamic Response of Engine Mount Systems. In Proceedings of the International Conference On Vehicle Structural Mechanics & CAE, Troy, MI, USA, 4–6 April 1995. [Google Scholar]
- Iyer, G.; Prasanth, B.; Wagh, S.; Hudson, D. Idle Vibrations Refinement of a Passenger Car. In Proceedings of the 2011 Symposium on International Automotive Technology, Pune, India, 19–21 January 2011. [Google Scholar]
- Balla, C.K.; Naidu, S.; Ambardekar, M.N. Reduction of Idle Shake in a Small Commercial Vehicle. In Proceedings of the SAE 2015 Noise and Vibration Conference and Exhibition, Tokyo, Japan, 22–25 June 2015. [Google Scholar]
- Qatu, M.S.; Abdelhamid, M.K.; Pang, J.; Sheng, G. Overview of automotive noise and vibration. Int. J. Veh. Noise Vib. 2009, 5, 1–35. [Google Scholar] [CrossRef]
- Wang, X. Vehicle Noise and Vibration Refinement; Woodhead Publishing: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Kalla, B.; Patil, S.; Kumbhar, M. Idle Shake Simulation and Optimization through Digital Car Model. In Proceedings of the SAE 2015 Noise and Vibration Conference and Exhibition, Tokyo, Japan, 22–25 June 2015. [Google Scholar]
- Heideman, M.; Johnson, D.; Burrus, C. Gauss and the history of the fast fourier transform. IEEE ASSP Mag. 1984, 1, 14–21. [Google Scholar] [CrossRef]
- Smith, S. Digital Signal Processing: A Practical Guide for Engineers and Scientists; Newnes: London, UK, 2003. [Google Scholar]
- Cooley, J.W.; Tukey, J.W. An algorithm for machine calculation of complex fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Cooley, J.; Lewis, P.; Welch, P. The finite Fourier transform. IEEE Trans. Audio Electroacoust. 1969, 17, 77–85. [Google Scholar] [CrossRef]
- Sanz Subirana, J.; Juan Zornoza, J.M.; Hernández-Pajares, M. GNSS Data Processing. Fletcher, K., Ed.; European Space Agency, ESA Communications: Noordwijk, The Netherlands, 2013; Volume I. [Google Scholar]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Xu, G.; Xu, Y. GPS: Theory, Algorithms and Applications, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Harris, F.J. On the use of windows for harmonic analysis with the discrete Fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Rohling, H.; Schuermann, J. Discrete time window functions with arbitrarily low sidelobe level. Signal Process. 1983, 5, 127–138. [Google Scholar] [CrossRef]


| PwrPak7-E2 | Item | Value |
|---|---|---|
| Gyroscope | Bias Magnitude | |
| Bias Stability | ||
| Angle Random Walk | ||
| Accelerometer | Bias Magnitude | |
| Bias Stability | ||
| Velocity Random Walk |
| Period | State | Start | End |
|---|---|---|---|
| 1 | Stop | 02:04:07 | 02:20:13 |
| Decelerating | 02:03:56 | 02:04:06 | |
| Accelerating | 02:20:14 | 02:20:24 | |
| 2 | Stop | 02:37:31 | 02:59:32 |
| Decelerating | 02:37:20 | 02:37:30 | |
| Accelerating | 02:59:33 | 02:59:43 | |
| 3 | Stop | 03:21:42 | 03:41:54 |
| Decelerating | 03:21:31 | 03:21:41 | |
| Accelerating | 03:41:55 | 03:42:05 |
| Module | Item | Strategy |
|---|---|---|
| GNSS | Mode | Post-kinematic PPP |
| Observations | IF combination of GPS: C1C-C2W/L1C-L2W; GLO: C1C-C2P/L1C-L2P; Galileo: C1C-C5Q/L1C-L5Q; BDS: C2I-C6I/L2I-L6I | |
| Elevation cutoff | 15° | |
| Measurement weight | Elevation-dependent weight | |
| Satellite products | Multi-GNSS precise orbit and clock products from IGS | |
| Receiver clock offset | White noise process | |
| ISB | Constant mode | |
| Tropospheric delay | Estimate the zenith total delay as a random walk process | |
| Phase windup | Corrected for rover | |
| Ambiguity resolution | Float | |
| IMU | Alignment | GNSS Doppler velocity |
| Integration | Solution | Tightly coupled |
| Stop Period | Freq Range (Hz) | Acce Y | Acce Z | Gyro X | |||
|---|---|---|---|---|---|---|---|
| Freq (Hz) | Amp (mg) | Freq (Hz) | Amp (mg) | Freq (Hz) | Amp (deg/s) | ||
| 1 | 0~10 | 3.071 | 0.133 | 3.305 | 0.105 | 6.247 | 0.003 |
| 10~20 | 12.495 | 3.085 | 12.495 | 5.402 | 12.495 | 0.395 | |
| 20~30 | 24.991 | 2.124 | 24.991 | 3.994 | 24.991 | 0.003 | |
| 2 | 0~10 | 0.001 | 0.890 | 3.332 | 0.107 | 0.100 | 0.002 |
| 10~20 | 12.496 | 1.622 | 12.496 | 2.839 | 12.496 | 0.182 | |
| 20~30 | 24.991 | 4.283 | 24.991 | 2.001 | 24.991 | 0.005 | |
| 3 | 0~10 | 6.248 | 0.085 | 3.573 | 0.113 | 6.248 | 0.002 |
| 10~20 | 12.496 | 2.821 | 12.496 | 4.927 | 12.496 | 0.305 | |
| 20~30 | 24.991 | 2.829 | 24.991 | 4.782 | 24.991 | 0.005 | |
| Mean | 0~10 | 3.106 | 0.369 | 3.404 | 0.108 | 4.198 | 0.002 |
| 10~20 | 12.495 | 2.509 | 12.495 | 4.389 | 12.495 | 0.294 | |
| 20~30 | 24.991 | 3.078 | 24.991 | 3.592 | 24.991 | 0.004 | |
| STD | 0~10 | 2.550 | 0.369 | 0.121 | 0.003 | 2.898 | 5 × 10−4 |
| 10~20 | 4 × 10−4 | 0.637 | 4 × 10−4 | 1.113 | 4 × 10−4 | 0.087 | |
| 20~30 | 2 × 10−4 | 0.899 | 2 × 10−4 | 1.171 | 2 × 10−4 | 0.001 | |
| Stop Period | Duration (s) | Correct (s) | Rate |
|---|---|---|---|
| 1 | 966 | 965 | 99.9% |
| 2 | 1321 | 1314 | 99.5% |
| 3 | 1212 | 1208 | 99.7% |
| Total | 3499 | 3487 | 99.7% |
| Stop Period | East (cm) | North (cm) | Up (cm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMS | STD | Max | RMS | STD | Max | RMS | STD | Max | |
| 1 | 0.99 | 0.98 | 2.92 | 1.39 | 0.92 | 3.16 | 0.31 | 0.29 | 0.87 |
| 2 | 1.00 | 0.44 | 2.17 | 0.70 | 0.42 | 2.16 | 2.24 | 0.21 | 2.72 |
| 3 | 1.29 | 0.47 | 2.45 | 0.73 | 0.63 | 2.12 | 1.36 | 0.25 | 2.08 |
| Average | 1.09 | 0.63 | 2.51 | 0.94 | 0.66 | 2.48 | 1.30 | 0.25 | 1.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Nie, W.; Suvorkin, V.; Rovira-Garcia, A.; Zhang, W.; Xu, T.; Xu, G. Stationary Detection for Zero Velocity Update of IMU Based on the Vibrational FFT Feature of Land Vehicle. Remote Sens. 2024, 16, 902. https://doi.org/10.3390/rs16050902
Li M, Nie W, Suvorkin V, Rovira-Garcia A, Zhang W, Xu T, Xu G. Stationary Detection for Zero Velocity Update of IMU Based on the Vibrational FFT Feature of Land Vehicle. Remote Sensing. 2024; 16(5):902. https://doi.org/10.3390/rs16050902
Chicago/Turabian StyleLi, Mowen, Wenfeng Nie, Vladimir Suvorkin, Adria Rovira-Garcia, Wei Zhang, Tianhe Xu, and Guochang Xu. 2024. "Stationary Detection for Zero Velocity Update of IMU Based on the Vibrational FFT Feature of Land Vehicle" Remote Sensing 16, no. 5: 902. https://doi.org/10.3390/rs16050902
APA StyleLi, M., Nie, W., Suvorkin, V., Rovira-Garcia, A., Zhang, W., Xu, T., & Xu, G. (2024). Stationary Detection for Zero Velocity Update of IMU Based on the Vibrational FFT Feature of Land Vehicle. Remote Sensing, 16(5), 902. https://doi.org/10.3390/rs16050902







