Abstract
With the advancement of intelligent perception in multirobot systems, cooperative localization in dynamic environments has become a critical component. However, existing multirobot cooperative localization systems still fall short in meeting high-precision localization requirements in Global Navigation Satellite System (GNSS)-denied environments. In this paper, we propose a factor-graph-based resilient cooperative localization (FG-RCL) algorithm for multirobot systems. This algorithm integrates measurements from visual sensors and Ultra-WideBand (UWB) to achieve accurate cooperative state estimation—overcoming the visibility issues of visual sensors within limited fields of view. We utilize the Joint Probabilistic Data Association (JPDA) algorithm to calculate the corresponding probabilities of multiple visual detection measurements between robots and assign them to their respective edges in the factor graph, thereby addressing the data association challenges in visual detection measurements. Finally, simulation results demonstrate that the proposed algorithm significantly reduces the influence of visual detection measurement interference on the performance of cooperative localization. Experimental results indicate that the proposed algorithm outperforms UWB-based and vision-based methods in terms of localization accuracy. The system is implemented using a factor-graph-based optimization approach, and it exhibits scalability and enables plug-and-play for sensors. Furthermore, it demonstrates resilience in abnormal situations.
1. Introduction
For multirobot systems, many applications frequently encounter the challenge of cooperative localization, including formation control [1], cooperative transportation [2], and search-and-rescue missions [3]. The issue of cooperative localization in multirobot systems refers to the detection and localization of mobile robots (often with limited sensor data, such as the relative distance or bearing) relative to other robots or landmarks. This is crucial in multirobot systems as it requires cooperation among the entire team and group. Currently, state estimation for multiple robots in outdoor environments heavily relies on a Global Navigation Satellite System (GNSS) [4]. However, GNSS-based methods are restricted to outdoor environments due to limitations to satellite signals. Furthermore, these methods only provide meter-level accuracy, which falls short for tasks requiring high-precision localization of robots. Other methods involve the use of motion capture systems or traditional Ultra-WideBand (UWB) localization systems for indoor scenarios without satellite signals [5,6,7]. They rely on physical anchors or base station deployment in applications to achieve cooperative localization. Therefore, these solutions are unsuitable for unknown environments, such as large areas or indoors, where deploying or modifying infrastructure is challenging. This limitation restricts the overall performance and application potential of multirobot systems and makes their usage more difficult and expensive.
With the advancement of autonomous perception in robots, visible light sensors, LiDAR, ultrasonic sensors, and numerous other novel sensors are being applied to cooperative localization [8,9,10]. The data provided by these sensors can improve localization accuracy and enable motion tracking, providing efficient and robust state estimation for robots in both indoor and outdoor and known and unknown environments [11]. This is due to their ability to detect and understand the surrounding environment, even if their primary installation purposes might not be for localization. For instance, high-precision maps constructed using LiDAR create a digital surface model represented by discrete points, which includes spatial information required for target localization [12]. However, LiDAR, ultrasonic sensors, and optical detectors are usually costly and less easily deployable compared to camera-based visual sensors. Therefore, there is growing interest in cooperative localization methods employing cameras. Vision-based simultaneous localization and mapping (SLAM) techniques can provide relative positions of robots in the surrounding environment [13]. Additionally, other robots can also be directly detected based on the images captured by the onboard camera, and distance and bearing measurements can be extracted from visual devices. However, they suffer from the disadvantages of a small field of view, short range, and susceptibility to nearby object occlusion. Due to the limitations to the observation angle of visual sensors, relative state estimation outside the field of view of onboard cameras has become a challenging issue. Therefore, a sensor with omni-directional perception capabilities and that is easy to carry, such as UWB modules, is needed to assist the camera with relative measurements. This paper introduces a cooperative localization system based on visual and UWB technologies that can be applied to multirobot frameworks.
There are typically two modes for multirobot cooperative localization: centralized and decentralized. Compared to the centralized framework, decentralized methods reduce the complexity of computation and communication during the cooperative process. In the decentralized framework, each member runs an estimator locally: propagating its state by fusing measurements from its local onboard sensors and relative observations received from team members [14]. In multirobot systems, solving the relative distance and bearing problems in a decentralized manner is preferable and scalable. Huang et al. [15] introduced an adaptive recursive decentralized cooperative localization method for multirobot systems with varying measurement accuracy. Wang et al. [16] proposed a fully decentralized cooperative localization algorithm based on covariance union to address inconsistent state estimation caused by spurious sensor data. Ref. [17] presented a resilient decentralized localization algorithm for tracking inter-robot correlation.
The existing decentralized cooperative localization methods for multirobot systems usually utilize traditional filtering algorithms to fuse measurements from different sensors and their prior information, overcoming the limitations of individual sensor technologies to obtain more accurate estimations. For example, commonly used filtering methods include the extended Kalman filter, unscented Kalman filter, and particle filter [18]. However, with the development of multirobot systems, the nonlinearities in navigation and localization systems have become increasingly serious. Filtering methods often require appropriate modeling of the problem and are susceptible to outliers, which leads to the fact that traditional filtering techniques are inadequate for the high-precision requirements of cooperative localization systems. Factor-graph-based multi-source fusion methods have opened up new avenues for cooperative localization in multirobot systems. Unlike traditional filter-based fusion methods, they optimize the complete set of states by considering both historical measurements and system updates simultaneously. These systems can seamlessly integrate new sensors and have the feature of plug-and-play, which effectively solve the nonlinearities in cooperative localization and asynchronous issues in data transmission. Xu et al. [19] presented a decentralized visual–inertial–UWB swarm state estimation system that flexibly integrates or discards sensor measurements and provides estimations through backend graph optimization. In factor-graph-based cooperative localization systems, if a sensor becomes unavailable due to signal loss or sensor failure, the system simply avoids adding relevant factors without requiring special procedures or coordination. In this case, historical information is used to encode all measurement values and states into a factor graph, and sensor fusion is solved through iterative optimization methods. In [20], a factor-graph-assisted distributed cooperative localization algorithm was developed to address ranging localization errors in cooperative nodes. This algorithm integrated a Fisher information matrix between adjacent agent nodes to evaluate ranging performance of the agent node to adjacent nodes. In this paper, we formulate multirobot cooperative localization as a graph optimization problem to efficiently achieve accurate state estimation through a factor-graph-based decentralized cooperative localization method.
Vision-based multirobot cooperative localization often requires accurate recognition of robots to track associated metrics for estimation of the association states [21]. However, real-world environments are far from perfect and often contain various sources of interference that make the task of correct data association challenging. Xunt et al. [22] proposed a system that focuses on relative pose estimation for multirobot systems but established data association through special patterns formed by infrared LED boards. Nguyen et al. [23] proposed a cooperative localization method using a coupled probabilistic data association filter to handle nonlinear measurements. However, this method is implemented based on a filtering structure. While considerable work has been done on multirobot cooperative localization, there is limited research on factor-graph-based methods using visual information for cooperative localization. To solve the problem of association uncertainty in cooperative localization, some researches have explored the use of data association algorithms in factor graphs. Gulati et al. [24] utilized data association filters to calculate the correspondence probabilities between multiple topologies of two robot states, which reduced interference in topological factors. Xu et al. [25] introduced a cooperative localization method based on omni-directional cameras, UWB sensors, and maps from multiple unmanned aerial vehicles that associates visual data through the global nearest neighbor algorithm. Although these methods can effectively track a single target, they face challenges in achieving satisfactory results when dealing with data association for multiple targets. Compared to [25], we use monocular camera and do not have the computational burden of dealing with a large number of distorted images. Meanwhile, in this paper, the Joint Probabilistic Data Association (JPDA) algorithm is used to solve the data association problem in multirobot cooperative localization. It can track multiple targets simultaneously with high tracking performance, and a target can be correlated with multiple measurements in the association gate. By fusing the measurements from the front-end with the back-end through graph optimization based on a factor graph, accurate localization is achieved while improving the resilience of the system in the face of abnormal situations.
We propose a factor-graph-based resilient cooperative localization algorithm (FG-RCL) for multirobot system. The main contributions of this paper are as follows:
- We propose a resilient and accurate cooperative localization system that fuses visual information and UWB measurements without relying on external onboard sensors or computing power.
- The system can handle data association problems in the visual measurement process of multirobot cooperative localization.
- The accuracy and robustness of the proposed algorithm are demonstrated through simulation results and experiments on a public dataset.
The remaining content of this paper is organized as follows. Section 2 first provides some basic concepts and system frameworks. Then, construction of the cost factors and the use of the JPDA algorithm to solve the data association problem of visual detection measurements are introduced. Section 3 presents simulation and experimental results. Finally, Section 4 and Section 5 discuss and summarize our work.
2. Materials and Methods
2.1. Notation
In this paper, we use , , and to represent the sets of natural numbers, non-negative integers, and positive integers, respectively. represents the m-dimensional real vector space of . For a vector or matrix, we use to represent its transpose. For vector , represents its Euclidean norm. For matrix , represents the matrix block in the bottom right corner of matrix , e.g, . We use to represent an antisymmetric matrix, e.g, for , there is
We add a left superscript to to indicate that the vector is relative to the reference frame , e.g, . and , along with the the left superscript and subscript, represent the rotation matrix and transformation matrix, respectively, between two frames. For example, and are the rotation matrix and transformation matrix, respectively, from frame to .
Quaternions can also be used to represent rotation. A quaternion is a four-dimensional complex number composed of one real part and three imaginary parts:
The multiplication of rotation matrices represents the rotation between reference frames, and the corresponding quaternion operations are as follows:
We denote as the body reference frame of the robot, as the world reference frame, and as the camera reference frame. Without specifying it, the left subscript body reference frame is implicit: for example, represents the rotation quaternion from the camera frame reference to the body frame at time k, i.e., .
2.2. System Overview
We assume a multirobot system containing N robots, where the i-th robot is denoted as Robot i, . For simplicity, unless otherwise specified, Robot i will be discussed in the following content. If the self-motion estimation of Robot j works normally and can communicate reliably with Robot i, then Robot j is within the available set of Robot i.
For the team of robots described in this paper, the sensors of each robot include cameras and UWBs. The cooperative localization system is formulated as a nonlinear optimization problem. Figure 1 shows the proposed factor graph structure. Hollow circles serve as vertices, which represent the poses to be optimized. There are three types of edges connecting poses: namely, (1) the local state estimation factor, which refers to incremental estimation of the own motion state of the robot through VO, thereby forming pose constraints for the robot at two moments before and after; (2) the UWB factor, which represents the relative distance constraint between two robots at the same time; (3) the visual detection factor, which represents the relative visual measurement constraint of one robot being detected by another robot. For each edge, the measurement, information matrix, and the Jacobian matrix of the error function relative to the state variables should be implemented.
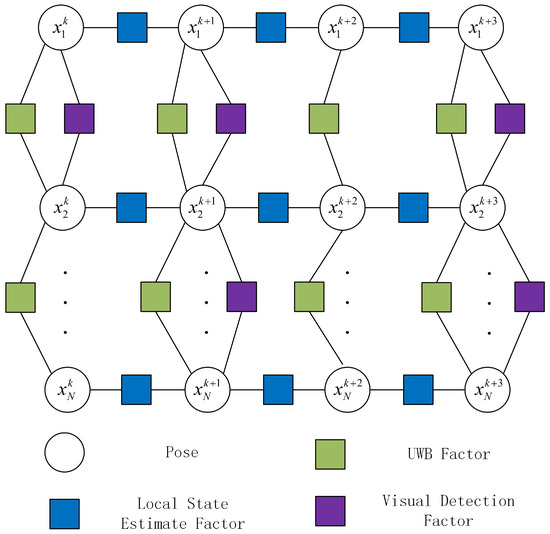
Figure 1.
Factor graph for multirobot state estimation. Local state estimation factor refers to the incremental estimation of the own motion state of the robot through VO, thereby forming pose constraints for the robot at two moments before and after. UWB factor represents the relative distance constraint between two robots at the same time. Visual detection factor represents the relative visual measurement constraint of one robot being detected by another robot.
Usually, is used to describe a set of rigid body motions in 3D space. The pose of a robot on is represented as , where and represent the orientation quaternion and the position of the body frame relative to the world frame, respectively. represents the transformation of quaternions into rotation matrices, which can be seen in [26]. Obviously, the main goal of our work is to estimate the transform .
The proposed framework is divided into a front-end and a back-end that run independently on each robot. At the front-end, the raw data are processed separately through local state estimation (LE), visual detection (VD), and UWB modules. On the back-end, state estimation is performed using a graph optimization method. We use sliding windows to construct cost functions based on the measurements of LE, VD, and UWB at each new time step. The state of Robot i to be estimated includes the robot’s orientation quaternion and position at time step k. We define the state estimate of Robot i at each time step k as , so the optimized full state vector of Robot i in the sliding window is defined as:
where N is the total number of robots, and m is the number of keyframes in the sliding window.
LE, VD, and UWB provide observations coupling two continuous states in a sliding window. Using all the observations obtained from LE, VD, and UWB, the cost function can be constructed at time step k as
where L is the set of all local state estimation factors; V is the set of all visual detection factors; U is the set of all UWB factors; denotes the residuals of the local state estimation factors, which ensures local consistency of the state of Robot i; denotes the residuals of the visual detection factors; denotes the residuals of the UWB factors; and , , and are the covariance matrices of the measurement errors.
2.3. Construction of the Cost Factors
Our proposed FG-RCL algorithm divides the measurements into two stages: (1) a local measurement stage, where local state estimation results are obtained through visual odometry (VO) or proprioceptive sensors; (2) a relative measurement stage, where the relative measurement results of available robots are obtained by cameras and UWBs and are then used with local state estimation results for fusion based on graph optimization.
2.3.1. Local State Estimation Factor
In local state estimation, the VO algorithm is used. The transformation matrix can be obtained based on the state vector of Robot i in the world reference frame at time step k, so measurement of the transformation matrix is obtained as
where is the transformation matrix of Robot i from the world reference frame to the camera reference frame.
Then, we can use the Gaussian model to represent the local measurements as
where is the Gaussian white noise conforming to .
The measurement noise is modeled as an independent zero-mean Gaussian distribution with the following covariance:
In this paper, the residual of the local measurement denotes the residual of the VO result, as shown in Equation (12). The multiplication of and denotes the transformation matrix of Robot i from time step to k in the world reference frame. The result is then multiplied with the local measurement to denote the residual of the local measurement.
We divide the measurement residual into two parts according to the relative rotation and displacement and find the Jacobi matrix for the rotational component and the translational component , respectively.
The variable takes the partial derivatives of , , , and to obtain
The variable takes the partial derivatives of , , , and to obtain
After completing local state estimation in the first stage, it is also necessary to detect and track the relative measurements between robots in the second stage.
2.3.2. Visual Detection Factor
Relative measurements can be obtained by detecting and tracking targets using vision sensors. In this paper, a monocular camera is employed for target detection. When Robot j appears in the field of view of Robot i, Robot i utilizes an object detection algorithm (such as YOLO) to detect Robot j. It is assumed that the center coordinate of the detection bounding box in the pixel coordinate frame of the camera is . The position information of the detected Robot j is broadcast by the communication module and then received by Robot i. The visual detection measurement can be calculated as the direction relative to the detected robot.
where denotes the function that obtains the direction relative to the detected robot from the coordinates of the bounding box center, and its specific form can be referenced in [27]. is the rotation matrix of Robot i from the world reference frame to the camera reference frame. The relative vector is frame invariant, and is the Gaussian white noise that conforms to .
The measurement noise is modeled as an independent zero-mean Gaussian distribution with the following covariance:
The residual of the visual detection measurements is
The Jacobian matrices of the measurement residual based on visual detection over and are
2.3.3. UWB Factor
From the UWB module, the relative distance between each pair of nodes can be obtained. The relative distance measurements between Robot i and Robot j can also be modeled using Gaussian noise as
where is the Gaussian white noise conforming to .
The measurement noise is modeled as an independent zero-mean Gaussian distribution with the following covariance:
The residual of the relative distance measurements between Robot i and Robot j is
The Jacobian matrices of the residual of relative distance measurements over and are
2.4. Data Association for Visual Detection Measurements
The JPDA is a well-known Bayesian target tracking filter. Instead of using a single measurement to update the state, it takes into account all measurements within the associated region of the predicted measurements of the target. JPDA considers each measurement within the cross-correlation region as potentially coming from clutter or multiple targets at the intersection and then assigns weights to the validated measurements [28]. Here, we only provide a brief overview of calculating the corresponding probabilities of multiple visual detection measurements at a time step.
Assume that the set of validated measurements is represented as
where is the j-th validated measurement, and is the number of measurements in the validation region at time step k.
The cumulative set of measurements before time step k is
All possible sources for each measurement can be indicated by creating a validation matrix. Define the validation matrix as
where is a binary element 0 or 1. If the j-th visual measurement is associated with the target Robot t, then the corresponding validation matrix element is 1; otherwise, it is 0. Hence, there is
The main purpose of the JPDA is to calculate the probability of associating each validated measurement with a target that could have generated it. There are the following assumptions: (1) each measurement can only come from one target source; (2) each target can only generate at most one true measurement.
According to the above rules, we can get the feasible matrix , where is the number of feasible matrices. Calculating the probability of a joint event requires scanning each feasible matrix row by row. If , then the Gaussian distribution function of the validated measurements is
where denotes the joint event based on the feasible matrix , c is a normalization constant, is the number of false measurements, is the probability mass function of the number of false measurements, is the probability density distribution function of the true measurement, is the association indicator of the measurement, and is the detection indicator of the target. denotes the probability of the detection of the target and is set manually according to the actual situation.
The association probability between measurement j and target t is obtained from the joint association probability, i.e.:
The final state estimate at time step k in terms of can be written as
where is the updated state of target t based on the events associated with the j-th validated measurement.
Therefore, using the JPDA filter, we can calculate the sum of the probabilities of all feasible events at time step k to obtain the association probability of the validated measurement relative to the target t and then assign weights to the measurements based on the association probabilities.
To solve the problem of data association in visual detection measurement, we implement JPDA next to the factor graph. Thus, the probabilities obtained from the JPDA filter are used as weights for the factors.
We assume that is the probability of the s-th validated measurement of Robot i with respect to Robot j; normalizing it yields
For measurements of Robot i relative to Robot j, each measurement has a certain probability. We can rewrite the visual detection measurement as
Therefore, the corresponding visual detection factor is
Data association based on visual detection can be understood from Figure 2. When Robot i detects both Robot j and Robot l, there may be multiple object detection bounding boxes or clutter measurements relative to a single target. Therefore, Robot i has multiple relative measurements relative to Robot j or Robot l. In this case, it is necessary to perform data association on these measurements. We use JPDA to enable Robot i to track measurements relative to multiple target robots. Firstly, a validation region is given for these measurements to exclude some invalid measurements. Robot i has four valid measurements relative to Robot j and three valid measurements relative to Robot l. The variables and are the predictions of visual detection measurements of Robot i relative to Robot l and Robot j, respectively. The variables and are the validation measurements in the validation region of Robot i relative to Robot l and Robot j, respectively. In particular, is in the intersection portion of the validation region, indicating that it may come from Robot i relative to Robot l or Robot j. Then, JPDA is used to calculate the probability for each validated measurement. In Figure 2, the size of the rectangle in the validation region represents the probability of measurement. The probabilities of these calculations are used in the above equation. Therefore, only validated relative measurements can contribute to a final solution based on weights.
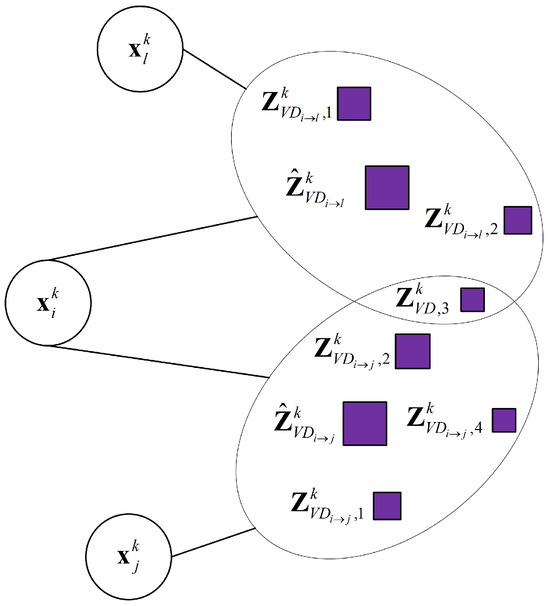
Figure 2.
Implementation of data association based on visual detection in factor graph.
3. Results
3.1. Simulation Results
The simulations are implemented using three robots traveling 200 steps on the same ground plane. Each robot carries a camera and UWB. Assume that the mean Gaussian noise of all sensors is zero, and the covariances of VO and UWB are diag [0.01, 0.01] and diag [0.1, 0.1], and their measurement frequencies are 20 Hz and 80 Hz, respectively. We randomly generate 1–4 visual detection measurements for each robot with a covariance of diag [0.1, 0.1] and measurement frequency of 20 Hz consistent with VO. The initial estimates of all parameters are zero when solving the optimization problem using the Gauss–Newton method.
We can measure the performance of the cooperative localization algorithm by calculating the root mean square deviation (RMSE). There are four cases as follows:
- (1)
- Ground truth trajectory;
- (2)
- No visual detection measurement interference: the estimated trajectory by fusing VO, visual detection, and UWB measurements;
- (3)
- Visual detection measurement interference without data association: the estimated trajectory by fusing VO and UWB measurements and multiple visual detection factors for each state (assuming there are visual detection measurement interferences) without using the data association algorithm for visual detection measurement interference;
- (4)
- The proposed FG-RCL algorithm: the estimated trajectory by fusing VO and UWB measurements and multiple visual detection factors for each state (assuming there is visual detection measurement interference) with probability assignment using the JPDA.
The ground truths of the three robots and their estimated trajectories in various situations are shown in Figure 3. It can be seen that the trajectories of the proposed algorithm (Case 4) are closest to the ground truth. However, this case performs slightly worse compared to Case 2, which uses only one visual detection measurement with a probability of one. But Case 2 also assumes that there is no visual detection measurement interference, which is not true in real environments. Case 3 does not use data association to cope with the interference in the visual detection measurements, and it can be seen from Figure 3 that the estimated trajectories are the worst: even resulting in extreme deviations from normal values.
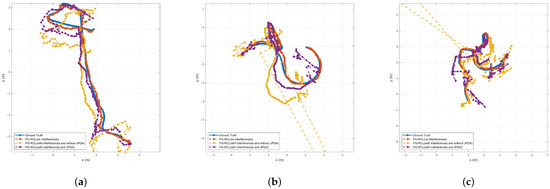
Figure 3.
The ground truths and estimated trajectories of three simulated robots. Case 1 is the ground truth. Case 2 is unrealistic because it has no visual detection measurement interference; it results in estimated trajectories close to the ground truth. Case 3 has visual detection measurement interference and does not use JPDA, resulting in the worst estimated trajectories. Case 4 has visual detection measurement interferences (simulated real-world case) and uses JPDA to assign weights. Although it is worse than Case 2, the results are more effective than Case 3. (a) Robot 1. (b) Robot 2. (c) Robot 3.
As shown in Figure 4, the localization performance of the system is further verified by the RMSEs of three robots in each case. In Case 3, the RMSE is the highest, and some outliers even deviate significantly from the normal range of values, with the location error of Robot 3 being far more than 18 m at 63–67 epochs. This is because visual detection measurement interference can add false information to the fusion process of the factor graph, which significantly increases the localization error. Although Case 2 has the smallest RMSE and the best execution effect, it cannot reflect the real environment because it does not add any false information to the factor graph. Therefore, it can be seen from the RMSE of Case 4 in Figure 4 that using JPDA to handle visual detection measurement interference is an effective solution for real environments.
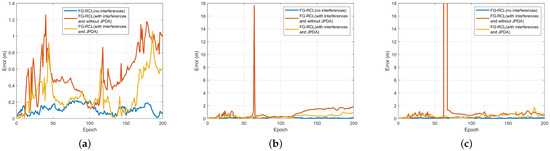
Figure 4.
RMSEs of three robots. (a) Robot 1. (b) Robot 2. (c) Robot 3.
Figure 5 compares the total number of visual detection measurements for all epochs of three robots with the number of visual detection measurements selected by JPDA. The visual detection measurements processed by data association provide more effective measurement information and avoid the interference of visual detection measurement that provides false information to the factor graph, thus allowing accurate estimation of the final state.
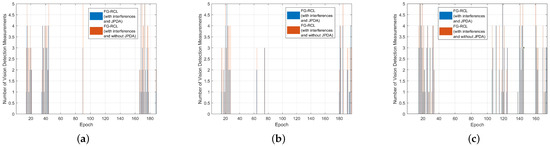
Figure 5.
The total number of visual detection measurements and the number of validated measurements after JPDA. (a) Robot 1. (b) Robot 2. (c) Robot 3.
3.2. Experimental Results
In this section, we use the AirMuseum dataset to evaluate the proposed FG-RDL algorithm [29]. We first describe the dataset and then compare the localization performance of the algorithms in indoor scenes.
The AirMuseum dataset was obtained from the former Air Museum at ONERA Meudon, France. An overview of the experimental site for a 40 m × 80 m warehouse is shown in Figure 6a. Three ground robots (referred to as Robot A, Robot B, and Robot C) are used in the dataset, as shown in Figure 6b. Each robot is equipped with a stereo camera and an inertial measurement unit (IMU). The stereo camera is equipped with a 4 mm focal length lens and a 26 cm baseline and uses a resolution of 640 × 512 pixels with a frame rate of 20 images per second. The robots are connected together via WiFi in the 5 GHz band. Clock synchronization is performed using the Public Network Time Protocol (NTP) reference. Data are collected directly as .bag files using the ROS. The dataset uses Structure-from-Motion algorithms to establish an accurate reconstruction of the environment and to extract a reliable ground truth from it.

Figure 6.
Experimental site and ground robots. (a) Experimental site. (b) Robot B and Robot C.
Robot B and Robot C are both equipped with a backward-facing AprilTag marker for direct observation between robots. Each AprilTag marker can be detected in an undistorted image using detection algorithms. If the tag is detected by a robot, it obtains inter-robot measurements, which can be directly used as an additional constraint for the relative poses between robots.
We use Scenario 2 of this dataset to validate the algorithm proposed in this paper. Images from the camera cam101 at a rate of 20 Hz are utilized for visual odometry state estimation of individual robots using ORB-SLAM2 [30]. Since the dataset does not contain UWB measurements, we generate them using the ground truth and taking into account actual features. Specifically, we simulate a UWB network wherein each robot carries a UWB node. Subsequently, visual measurements from the detection module and distance measurements from the UWB module are used together for the estimation of the relative measurement stage. It is assumed that information transfer between the robots is performed through communication modules broadcasting data with synchronized timestamps at a frequency of 100 Hz.
To verify the effectiveness of the proposed sensor fusion method, we constructed different localization scenarios that discarded UWB measurement and visual detection measurement data. Figure 7 shows the ground truths and estimated trajectories of the three robots. It can be seen that the estimated trajectory of the FG-RCL algorithm, which integrates visual detection measurement and UWB measurement, is closest to the ground truth. The estimated trajectories relying only on visual detection measurement are the worst. This is due to the presence of many obstacles in the scene used for the dataset, which resulted in a small number of visual detection measurements being acquired between the robots.

Figure 7.
Comparison of estimated trajectories with ground truths of three robots. (a) Robot A. (b) Robot B. (c) Robot C.
Figure 8 and Figure 9 show a comparison of the position error and orientation error, respectively, between the proposed algorithm and the ground truth. Table 1 shows the average RMSEs of the position and orientation. In the three-robot scenario, the average RMSE for the position when using the proposed algorithm can reach 0.6 m. With the dataset used in this section, the cooperative localization method [5], which relies only on UWB, has an average RMSE of 1.27 m in the horizontal position and an average RMSE of 3.22° in the orientation angle for the three robots. Compared with the UWB-only based method, the FG-RCL algorithm improves localization accuracy by 54.41%. On the other hand, the vision-only-based cooperative localization in [8] has an average RMSE of 0.65 m in the horizontal position and an average RMSE of 7.01° in the orientation angle for the three robots. Compared to the vision-only-based method, the FG-RCL algorithm improves the localization accuracy by 11.67%. FG-RCL not only has higher accuracy, but it also has the ability to handle situations wherein other robots are located outside the field of view. The proposed algorithm outperforms the other two methods in terms of both relative estimation reliability and localization accuracy.
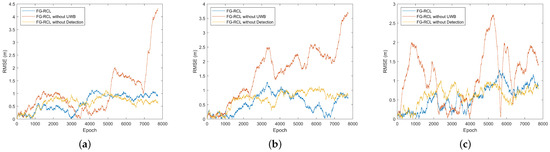
Figure 8.
RMSEs of positions of three robots. (a) Robot A. (b) Robot B. (c) Robot C.
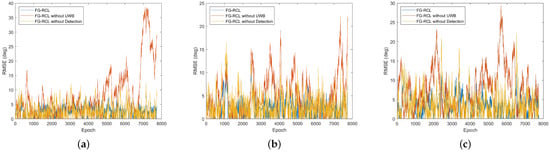
Figure 9.
RMSEs of orientations of three robots. (a) Robot A. (b) Robot B. (c) Robot C.

Table 1.
Comparison of average RMSEs using the proposed algorithm.
In addition, Figure 10 presents the relative states of other robots estimated by Robot A to demonstrate the consistency of our proposed algorithm. The decentralized vision–UWB cooperative localization system based on a factor graph is not limited by FoV or GNSS, which means it may be widely adopted by multirobot applications in different environments.
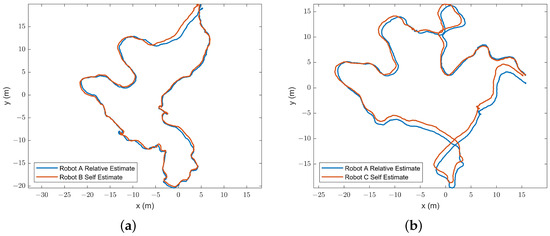
Figure 10.
Comparison of relative estimated trajectories. Robot A obtains the states of Robot B and Robot C by relative state estimation and compares them with its own estimated state. (a) Relative estimated trajectories of Robot A&B. (b) Relative estimated trajectories of Robot A&C.
4. Discussion
This paper proposes a resilient cooperative localization algorithm based on a factor graph. In this method, a factor graph model of the resilient cooperative localization system is established, and the mathematical model for constructing the cost function is derived in detail. The measurement, information matrix, error function, and Jacobian matrix of the error function relative to relevant state variables are provided. This method solves the problem of visual detection measurement data association in factor graphs by using the JPDA algorithm. This paper divides the front-end into a local measurement stage and a relative measurement stage, and it implements optimized fusion based on a factor graph in the back-end. Each robot operates independently to achieve decentralized cooperative localization. Therefore, this solution can realize plug-and-play of sensors, scalability, and resilience in complex environments.
The FG-RCL algorithm is applicable to multirobot cooperative localization in GNSS-denied environments. Specifically, when visual detection measurements have interference, erroneous visual information can affect the optimization of the global function during the factor graph fusion process, leading to an unsatisfactory final estimation state. Although this paper uses the JPDA algorithm to solve the problem of multi-target data association during visual detection measurement, it is still based on the correct recognition of targets. When the cooperative localization system fails to acquire visual information for a long time or is subjected to strong environmental interference, it can cause deviation in the localization results. For example, when the system is in a low-light environment, insufficient lighting seriously weakens the recognition efficiency of the visual object detection module; meanwhile, small targets cannot be recognized effectively, making the system miss part of the relative visual measurement results.
In the future, the FG-RCL algorithm can be combined with sensor selection algorithms, such as consistency-checking-based sensor optimization methods [31], to address the problems of sensor deviation and noise model updates in the factor graph framework during the fusion process.
In addition, for cooperative localization systems, a robust communication network is essential. In a perfect communication scenario, wireless communication networks can be established through point-to-point methods to achieve localization at lower cost and complexity. However, if the system suffers from occasional message loss due to external events, this situation can lead to communication failure within the network. It is best to use corresponding resilient measures to make the cooperative localization system more robust in this situation.
5. Conclusions
In this paper, we propose an FG-RCL algorithm for the fusion of visual and UWB measurements. We derive the mathematical model for the construction of the cost function in detail and use the JPDA algorithm to solve the data association problem in visual detection measurements. The front-end of the system is divided into local measurement and relative measurement stages, and then optimized fusion based on a factor graph is implemented in the back-end. Each robot operates independently to achieve decentralized cooperative localization. This solution enables plug-and-play of sensors along with scalability and resilience to complex environments. The simulation results show that interference from visual detection measurements degrade the performance of cooperative localization algorithms. However, through the data association against this interference performed by the proposed algorithm, its RMSE is better than that of a system without weighted visual detection factors. We also verify the effectiveness of the proposed algorithm through real datasets, and the estimation results for position and orientation show that it can accurately achieve multirobot cooperative localization.
Author Contributions
Conceptualization, D.W.; methodology, D.W.; software, D.W.; validation, B.G.; formal analysis, S.Z.; investigation, Y.L.; resources, B.L.; data curation, B.G.; writing—original draft preparation, D.W.; writing—review and editing, S.Z.; visualization, S.Z.; supervision, Y.L.; project administration, B.L.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under grants 62173276, 62171735, and 62101458 and in part by the Natural Science Basic Research Program of Shaanxi under grants 2021JQ-122 and 2023-JC-QN-0760.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interests.
References
- Alonso-Mora, J.; Montijano, E.; Nägeli, T.; Hilliges, O.; Schwager, M.; Rus, D. Distributed multi-robot formation control in dynamic environments. Auton. Robot. 2019, 43, 1079–1100. [Google Scholar] [CrossRef]
- Ebel, H.; Luo, W.; Yu, F.; Tang, Q.; Eberhard, P. Design and experimental validation of a distributed cooperative transportation scheme. IEEE Trans. Autom. Sci. Eng. 2020, 18, 1157–1169. [Google Scholar] [CrossRef]
- Wang, L.; Cheng, D.; Gao, F.; Cai, F.; Guo, J.; Lin, M.; Shen, S. A collaborative aerial-ground robotic system for fast exploration. In Proceedings of the 2018 International Symposium on Experimental Robotics (ISER), Buenos Aires, Argentina, 5–8 November 2018; pp. 59–71. [Google Scholar]
- Xu, H.; Wang, C.; Bo, Y.; Jiang, C.; Liu, Y.; Yang, S.; Lai, W. An Aerial and Ground Multi-Agent Cooperative Location Framework in GNSS-Challenged Environments. Remote Sens. 2022, 14, 5055. [Google Scholar] [CrossRef]
- Guo, K.; Li, X.; Xie, L. Ultra-wideband and odometry-based cooperative relative localization with application to multi-UAV formation control. IEEE Trans. Cybern. 2019, 50, 2590–2603. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lin, M.; Xie, X.; Gao, Y.; Deng, F.; Lam, T.L. Asymptotically Efficient Estimator for Range-Based Robot Relative Localization. IEEE/ASME Trans. Mechatron. 2023, 28, 3525–3536. [Google Scholar] [CrossRef]
- Xu, X.; Liu, X.; Zhao, B.; Yang, B. An extensible positioning system for locating mobile robots in unfamiliar environments. Sensors 2019, 19, 4025. [Google Scholar] [CrossRef]
- Saska, M.; Baca, T.; Thomas, J.; Chudoba, J.; Preucil, L.; Krajnik, T.; Faigl, J.; Loianno, G.; Kumar, V. System for deployment of groups of unmanned micro aerial vehicles in gps-denied environments using onboard visual relative localization. Auton. Robots 2017, 41, 919–944. [Google Scholar]
- Yan, Z.; Guan, W.; Wen, S.; Huang, L.; Song, H. Multirobot cooperative localization based on visible light positioning and odometer. IEEE Trans. Instrum. Meas. 2021, 70, 7004808. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, Y.; Chen, L.; Cheng, H.; Tu, W.; Cao, D.; Li, Q. RDC-SLAM: A real-time distributed cooperative SLAM system based on 3D LiDAR. IEEE Trans. Intell. Transp. Syst. 2021, 23, 14721–14730. [Google Scholar] [CrossRef]
- Shalihan, M.; Cao, Z.; Pongsirijinda, K.; Guo, L.; Lau, B.P.L.; Liu, R.; Yuen, C.; Tan, U.X. Moving Object Localization based on the Fusion of Ultra-WideBand and LiDAR with a Mobile Robot. In Proceedings of the 2023 IEEE International Conference on Robotics and Biomimetics (ROBIO), Samui, Thailand, 4–9 December 2023; pp. 1–8. [Google Scholar]
- Héry, E.; Xu, P.; Bonnifait, P. Consistent decentralized cooperative localization for autonomous vehicles using LiDAR, GNSS, and HD maps. J. Field Robot. 2021, 38, 552–571. [Google Scholar] [CrossRef]
- Tian, Y.; Chang, Y.; Arias, F.H.; Nieto-Granda, C.; How, J.P.; Carlone, L. Kimera-multi: Robust, distributed, dense metric-semantic slam for multi-robot systems. IEEE Trans. Robot. 2022, 38, 2022–2038. [Google Scholar] [CrossRef]
- Sahawneh, L.R.; Brink, K.M. Factor Graphs-Based Multi-Robot Cooperative Localization: A Study of Shared Information Influence on Optimization Accuracy and Consistency. In Proceedings of the 2017 International Technical Meeting of the Institute of Navigation, Monterey, CA, USA, 30 January–2 February 2017; pp. 819–838. [Google Scholar]
- Huang, Y.; Xue, C.; Zhu, F.; Wang, W.; Zhang, Y.; Chambers, J.A. Adaptive recursive decentralized cooperative localization for multirobot systems with time-varying measurement accuracy. IEEE Trans. Instrum. Meas. 2021, 70, 8501525. [Google Scholar] [CrossRef]
- Wang, X.; Sun, S.; Li, T.; Liu, Y. Fault tolerant multi-robot cooperative localization based on covariance union. IEEE Robot. Autom. Lett. 2021, 6, 7799–7806. [Google Scholar] [CrossRef]
- Wang, D.; Qi, H.; Lian, B.; Liu, Y.; Song, H. Resilient Decentralized Cooperative Localization for Multisource Multirobot System. IEEE Trans. Instrum. Meas. 2023, 72, 8504713. [Google Scholar] [CrossRef]
- Araki, B.; Gilitschenski, I.; Ogata, T.; Wallar, A.; Schwarting, W.; Choudhury, Z.; Rus, D. Range-based cooperative localization with nonlinear observability analysis. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 1864–1870. [Google Scholar]
- Xu, H.; Wang, L.; Zhang, Y.; Qiu, K.; Shen, S. Decentralized visual-inertial-UWB fusion for relative state estimation of aerial swarm. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 8776–8782. [Google Scholar]
- Hu, E.; Deng, Z.; Hu, M.; Yin, L.; Liu, W. Cooperative indoor positioning with factor graph based on fim for wireless sensor network. Future Gener. Comput. Syst. 2018, 89, 126–136. [Google Scholar] [CrossRef]
- Zhang, G.; Ng, H.F.; Wen, W.; Hsu, L.T. 3D mapping database aided GNSS based collaborative positioning using factor graph optimization. IEEE Trans. Intell. Transp. Syst. 2020, 22, 6175–6187. [Google Scholar] [CrossRef]
- Xunt, Z.; Huang, J.; Li, Z.; Ying, Z.; Wang, Y.; Xu, C.; Gao, F.; Cao, Y. CREPES: Cooperative RElative Pose Estimation System. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 5274–5281. [Google Scholar]
- Nguyen, T.; Mohta, K.; Taylor, C.J.; Kumar, V. Vision-based multi-MAV localization with anonymous relative measurements using coupled probabilistic data association filter. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 3349–3355. [Google Scholar]
- Gulati, D.; Zhang, F.; Malovetz, D.; Clarke, D.; Knoll, A. Robust cooperative localization in a dynamic environment using factor graphs and probability data association filter. In Proceedings of the International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017. [Google Scholar]
- Xu, H.; Zhang, Y.; Zhou, B.; Wang, L.; Yao, X.; Meng, G.; Shen, S. Omni-swarm: A decentralized omnidirectional visual–inertial–uwb state estimation system for aerial swarms. IEEE Trans. Robot. 2022, 38, 3374–3394. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Cao, M.; Yuan, S.; Lyu, Y.; Nguyen, T.H.; Xie, L. Viral-fusion: A visual-inertial-ranging-lidar sensor fusion approach. IEEE Trans. Robot. 2021, 38, 958–977. [Google Scholar] [CrossRef]
- Wang, D.; Lian, B.; Tang, C. UGV-UAV robust cooperative positioning algorithm with object detection. IET Intell. Transp. Syst. 2021, 15, 851–862. [Google Scholar] [CrossRef]
- Fortmann, T.; Bar-Shalom, Y.; Scheffe, M. Sonar tracking of multiple targets using joint probabilistic data association. IEEE J. Oceanic Eng. 1983, 8, 173–184. [Google Scholar] [CrossRef]
- Dubois, R.; Eudes, A.; Frémont, V. AirMuseum: A heterogeneous multi-robot dataset for stereo-visual and inertial Simultaneous Localization And Mapping. In Proceedings of the 2020 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Karlsruhe, Germany, 14–16 September 2020; pp. 166–172. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Chen, H.A.N.; Ling, P.E.I.; Danping, Z.O.U.; Kun, L.I.U.; Yexuan, L.I.; Yu, C.A.O. An optimal selection of sensors in multi-sensor fusion navigation with factor graph. In Proceedings of the 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS), Wuhan, China, 22–23 March 2018; pp. 1–8. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).