Abstract
Playing a crucial role in ocean activities, internal solitary waves (ISWs) are of significant importance. Currently, the use of deep learning for detecting ISWs in synthetic aperture radar (SAR) imagery is gaining growing attention. However, these approaches often demand a considerable number of labeled images, which can be challenging to acquire in practice. In this study, we propose an innovative method employing a pyramidal conditional generative adversarial network (PCGAN). At each scale, it employs the framework of a conditional generative adversarial network (CGAN), comprising a generator and a discriminator. The generator works to produce internal wave patterns as authentically as possible, while the discriminator is designed to differentiate between images generated by the generator and reference images. The architecture based on pyramids adeptly captures the encompassing as well as localized characteristics of internal waves. The incorporation of upsampling further bolsters the model’s ability to recognize fine-scale internal wave stripes. These attributes endow the PCGAN with the capacity to learn from a limited amount of internal wave observation data. Experimental results affirm that the PCGAN, trained with just four internal wave images, can accurately detect internal wave stripes in the test set. Through comparative experiments with other segmentation models, we demonstrate the effectiveness and robustness of PCGAN.
1. Introduction
Internal solitary waves in the ocean are captivating phenomena within the field of oceanography, occurring beneath the ocean’s surface and widely present in stably stratified oceans [1,2]. With amplitudes reaching up to 240 m [3], these waves carry substantial energy and have significant impacts on offshore drilling operations [4,5]. Simultaneously, they play a crucial role in the intricate interplay of energy within the marine ecosystem [6]. Hence, it is imperative to precisely ascertain the positions of oceanic internal waves.
Internal waves propagate beneath the ocean surface, and the marine environment is complex and dynamic, making it challenging to directly obtain parameters of internal waves. Utilizing multiple underwater gliders, as indicated in [7], allows for the reconstruction of three-dimensional regional oceanic temperature and salinity fields in the northern South China Sea. Observations of oceanic internal waves can be conducted through temperature and salinity profiles, providing corresponding parameters [8]. However, the data on internal waves obtained through this method remains very limited. Fortunately, ISWs induce convergence and divergence effects, leading to alterations in surface roughness and sun-glint reflection. This phenomenon results in the manifestation of alternating bright and dark stripes on satellite images. Since the early 1980s, this pattern has been detected in synthetic aperture radar (SAR) [9,10]. SAR remains unaffected by cloud cover and can capture high-resolution ocean surface imagery ranging from a few meters to tens of meters, irrespective of weather conditions, day or night [11]. Consequently, SAR has emerged as a robust tool for monitoring oceanic internal waves [12]. Automated segmentation of oceanic internal wave stripes within SAR images is necessary to ascertain the positions of the stripes and subsequently investigate their propagation or invert the parameters of oceanic internal waves.
Over the past few decades, there has been significant research into algorithms and techniques aimed at the automated detection of internal wave signatures from SAR imagery, employing fundamental image-processing methods. Rodenas and Garello [13] conducted oceanic internal wave detection and wavelength estimations using wavelet analysis. They introduced the creation of a suitable wavelet basis for the identification and localization of nonlinear wave signatures within SAR ocean image profiles. Subsequently, the application of continuous wavelet transform is employed to estimate energies and wavelengths within soliton peaks from the identified internal wave trains. Ref. [14] employs a 2D wavelet transform based on multiscale gradient detection for automated detection and orientation of oceanic internal waves in SAR images. Furthermore, it introduces a coastline detection approach to achieve sea-land separation, thereby enhancing the effectiveness of internal wave detection within the SAR image context. Simonin et al. [15] introduce a framework that combines wavelet analysis, linking, edge discrimination, and parallelism analysis for the automated identification of potential internal wave packets within SAR images. The framework has been demonstrated and tested using six satellite images of the Eastern Atlantic, affirming its capability to determine the signature type and wavelength of the internal wave. The study conducted by Zhang et al. [16] investigates the utilization of compact polarimetric (CP) SAR in detecting and identifying oceanic internal solitary waves (ISWs). CP SAR images are generated and 26 CP features are extracted from full-polarimetric Advanced Land Observing Satellite (ALOS) Phase Array type L-band SAR (PALSAR) images. The effectiveness of different polarization features in distinguishing ISWs from the sea surface is evaluated using Jeffries and Euclidean distances. Expanding upon this, an enhancement to the detection capabilities of ISWs is introduced through the implementation of a K-means clustering algorithm utilizing compact polarimetric (CP) features. Qi’s research [17] employed the Gabor transform to extract wave characteristics. The study further utilized the K-means clustering algorithm for stripe segmentation within SAR images. To distinguish the light and dark wave stripes from the background, morphological processing techniques were applied.
With the evolution of neural networks, machine-learning-based models for internal wave detection have been extensively explored in recent years. Machine learning has the capability to automatically extract deep features, providing a more convenient and effective approach. For instance, Wang et al. [18] developed a method for detecting oceanic internal waves, employing a deep learning framework known as PCANet. This method combines binary hashing, principal component analysis (PCA), and block-wise histograms. Following this, a linear support vector machine (SVM) classification model is utilized to accurately identify the locations of oceanic internal waves using a rectangular frame. In the study by Bao et al. [19], the Faster R-CNN framework is employed to achieve the detection of oceanic internal waves within SAR images. This model adeptly navigates the challenge of misidentifying features like ship wakes, prone to aliasing, while simultaneously accurately delineating regions responsible for generating internal waves.
However, the aforementioned deep learning-based methodologies are limited to detecting the positions of oceanic internal waves through rectangular bounding boxes; these approaches are unable to characterize the precise locations of the distinct stripes.
Ref. [20] presents a comprehensive algorithm designed to detect and identify oceanic internal waves. To address the pervasive speckle noise in SAR images, the initial step involves the application of the Gamma Map filtering technique. Subsequently, the classification of SAR images and identification of those containing oceanic internal waves are accomplished through feature fusion and SVM. Ultimately, the Canny edge detection method is employed for the detection and recognition of oceanic internal wave stripes within the SAR images. Within the framework proposed by Vasavi [21], U-Net is applied to carry out feature extraction and segmentation tasks, delving into wave parameters such as frequency, amplitude, latitude, and longitude. Following this, the Korteweg-de Vries (KdV) solver is applied, taking the internal wave parameters as inputs and providing density and velocity plots corresponding to the internal waves as outputs. Li et al. [22] applied a modified U-Net framework to extract ISW-signature information from Himawari-8 images in challenging imaging scenarios. They opted for -balanced cross-entropy as the loss function, deviating from the traditional cross-entropy, and achieved remarkable results. Zheng et al. [23] proposed an algorithm utilizing the SegNet architecture for segmenting oceanic internal waves. This approach proficiently detects the presence of oceanic internal waves within SAR images and determines the specific positions of both light and dark stripes. In [24], an algorithm for segmenting oceanic internal waves’ stripes was introduced, relying on Mask R-CNN. Additionally, they employed a separation and matching approach within the sector region (SMMSR). This method not only accomplishes the localization of internal waves but also allows for the extraction of crucial parameters, encompassing the width and directional angle, associated with every discernible light and dark stripe. In [25], Middle Transformer U2-net (MTU2-net) was introduced as an innovative model, combining a transformer and a unique loss function to enhance its ability to detect ISWs.
The aforementioned intelligent detection methods operate through a training process. The majority of machine-learning-based approaches for internal wave detection rely on substantial training datasets to ensure precise detection outcomes. However, obtaining a large number of labeled internal wave images remains a challenge. In addition to traditional data augmentation methods, there have been studies focused on training neural networks with a small number of samples. For instance, in [26], different-sized convolutional kernels were employed to extract features from a small sample set comprehensively. Ref. [27] employs a random forest-like strategy, achieving superior classification accuracy without overfitting, even with much smaller training datasets than commonly studied in deep learning literature for image classification tasks. In [28], a multi-scale model was applied to detect oil spills on the sea surface, achieving accurate detection results with very few training samples. In [29], a training strategy involving mutual guidance was used to create a powerful hyperspectral image classification framework trained on a small dataset.
Inspired by these methods, we apply the concept of training on a small dataset to the task of internal wave detection. Given the finer and less distinct features of oceanic internal wave stripes, we introduce a pyramidal conditional generative adversarial network (PCGAN) to achieve stripe segmentation of oceanic internal waves with limited training data. PCGAN is composed of a series of adversarial networks at different scales. At each scale, it undergoes training from coarse to fine using observed internal wave images and detection maps. At each scale, PCGAN includes an adversarial network consisting of a generator and a discriminator. The generator’s role is to capture the characteristics of the observed image and produce an internal wave detection map that closely mimics reality. Meanwhile, the discriminator is tasked with differentiating between real images and those generated by the generator. Each generator’s output becomes the input for the subsequent, more detailed-scale generator, as well as the current-scale discriminator. The training process is independently conducted at each scale, following the structure of a Conditional Generative Adversarial Network. This article’s primary contributions can be outlined as follows:
- (1)
- We introduce a pioneering Pyramidal Conditional Generative Adversarial Networks (PCGAN) structure designed for internal wave stripe extraction. This model integrates lightweight networks for both generators and discriminators.
- (2)
- We independently train adversarial network structures at every scale, allowing a cascade of internal wave features to flow from coarse to fine in the data processing.
- (3)
- We enhance the model’s capability to extract finer details of internal wave stripes from the images by incorporating upsampling.
- (4)
- We manually labeled a diverse set of internal wave images to train and validate the model’s performance across various characteristics.
The subsequent sections are organized as follows: Section 2 provides a detailed overview of the model architecture and training specifics of PCGAN. In Section 3, we present the experimental configurations and assessments conducted. Following that, Section 4 delves into a comprehensive discussion of the results of the experiments. Lastly, Section 5 summarizes the conclusions derived from the presented approach and its effectiveness.
2. Materials and Methods
2.1. Basic GAN and Its Variants
The foundational GANs model, initially presented by Goodfellow et al. in 2014 [30], operates as a framework for training deep generative models through a two-player minimax game. The primary objective of GANs is to train a generator distribution, denoted as , to closely align with the distribution of real data, represented by . In the context of GANs, the model entails the learning of a generator network G responsible for generating samples by transforming a latent noise vector z into a corresponding sample . This generator is subjected to training through an adversarial interplay with a discriminator network D, which is designed to discriminate between samples originating from the authentic data distribution and those generated by the distribution . The core objective of the original GANs is articulated through the following objective function:
Conditional Generative Adversarial Networks (CGAN) [31] are a modification of the basic GAN that integrates conditional information to effectively guide the generation process. In CGAN, both the discriminator and generator are augmented with conditional vectors, denoted as y, which can encompass auxiliary details like class labels or image descriptions. This inclusion empowers the generator to produce samples with enhanced accuracy by considering specific conditions. The objective function of CGAN can be represented as follows:
The error function of conventional GANs might face challenges during training, stemming from their potential discontinuity concerning the generator’s parameters. As an alternative, the Wasserstein Generative Adversarial Network (WGAN) [32] adopts the Earth-Mover distance, also known as Wasserstein-1 distance, denoted as . This distance metric is loosely defined as the minimal cost needed to transport mass for converting the distribution q into the distribution p, where the cost is determined by the product of mass and transport distance. Subject to reasonable assumptions, exhibits continuity everywhere and differentiability almost everywhere.
The WGAN loss function is formulated through the Kantorovich-Rubinstein duality to achieve:
Since its introduction in 2014, GAN and its variants have achieved notable success in generative image modeling and demonstrated exceptional performance in semantic segmentation [33,34,35,36]. Adversarial learning has also been shown to be suitable for small-data training [37,38,39]. To obtain an effective method for high-precision internal wave detection in practical scenarios, the latter part of the current section presents an approach to detect internal wave stripes using a Pyramidal Conditional Generative Adversarial Network (PCGAN) trained with a restricted amount of data.
2.2. The PCGAN for the Extraction ISW
Firstly, the initial internal wave remote sensing image is denoted as , the corresponding labeled image as , and the internal wave identification map generated by our PCGAN is represented as . Both and are binary images, where 0 indicates the presence of internal waves, and 1 indicates the absence of internal waves at the oceanic surface. Pyramidal representations spanning multiple scales are constructed for , , and , commencing from the primitive scale.
We first represent the image , in the form of an image pyramid by up and downsampling. Here, and denote the representations obtained after n successive downsamplings of the original images. In each downsampling step, the image size is reduced to of the previous level, where the coefficient r is typically set to 2. Correspondingly, and are obtained by upsampling the original image, and their image sizes are times those of and . The collection of representations across scales forms the pyramidal representation set used in the PCGAN for internal wave detection, adopting a coarse-to-fine strategy.
Our proposed approach introduces a pyramid-based conditional generative adversarial network, a hierarchical structure composed of a series of discriminators and generators operating at various scales. Here, and denote the discriminator and generator at the n-th downsampling layer, respectively. The corresponding generated image by is denoted as . Symmetrically, at the m-th upsampling layer, they are denoted as , , and . Illustrating the PCGAN architecture (Figure 1), the core structure is represented in the central pyramidal section. Arrows on both sides indicate the flow of data from coarse to fine, while the upper corners depict the general structure of the generator and discriminator at each scale. The internal wave remote sensing image and its corresponding labeled image serve as the input, while the internal wave detection map represents the result generated by the entire PCGAN framework.
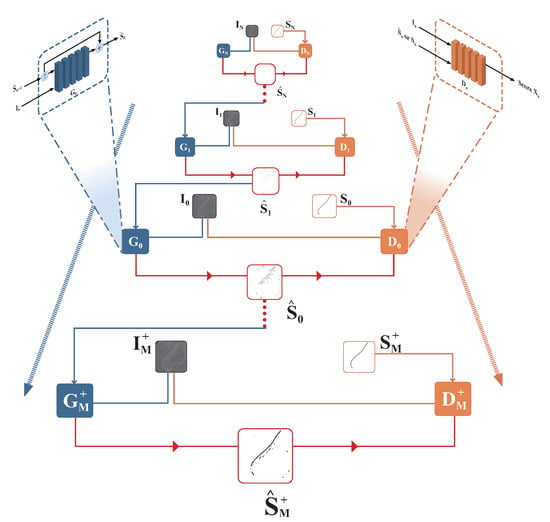
Figure 1.
The fundamental structure of PCGAN for stripe extraction in oceanic internal waves, with a brief showcase of the generator and discriminator at the corners. Arrows on both sides illustrate the data flow from coarse to fine. Blue represents the generators, while orange represents the discriminators.
At every scale, taking the internal wave remote sensing image and the previously generated internal wave detection map as inputs, the generator produces the current-scale generated internal wave detection map . Simultaneously, discriminator is presented with inputs in the form of either the pair or , leading to the generation of respective discrimination scores . The generator aims to produce results that are as realistic as possible to deceive the discriminator, while the discriminator’s goal is to distinguish between the generated detection results and the reference internal wave detection map.
2.3. Discriminator Architecture of PCGAN
Figure 2 illustrates the structural design of the discriminator of PCGAN. The structure consists of five convolutional blocks, with the final block containing only a convolutional layer. In the preceding four blocks, batch normalization (BN) is applied after the convolutional layer, followed by activation using the LeakyReLU function.
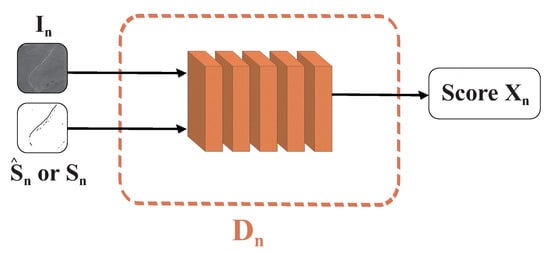
Figure 2.
The structural design of the discriminator of PCGAN.
The discriminator takes either the produced pair or the real pair as the input and produces a discrimination score . The score is determined by computing the mean from the feature map produced by the last convolutional layer of . Additionally, it serves as an indication of the likelihood that the image pair originates from a real image, with values closer to 1 indicating a higher probability of being from a real image. At each scale, the discriminator strives to assign a high score to the genuine image , classifying it as real, and a low score to the generated image , categorizing it as fake, thereby distinguishing between the two.
2.4. Generator Architecture of PCGAN
The structure of the generator of PCGAN is illustrated in Figure 3. It takes the observed remote sensing image at the current scale along with the extraction result generated by the generator at the previous scale as inputs. Then, the detection map is upsampled by a factor of r, resulting in , having identical dimensions as . Subsequently, the pair is concatenated along the channel dimension and then processed by the convolutional network . Similar to the discriminator, the convolutional network is composed of five convolutional modules. Each module consists of a convolutional layer, a BN layer, and an activation layer. The convolutional network’s output is pixel-wise blended with , meaning that the grayscale values of features are combined. This process yields the output of the generator for stripe extraction of the internal wave, denoted as:
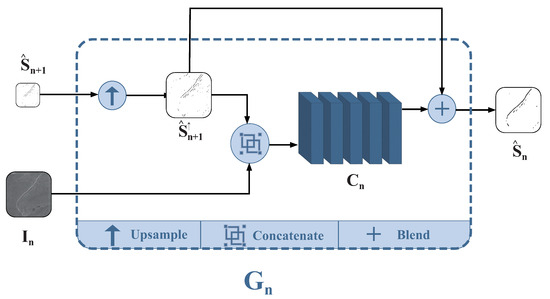
Figure 3.
The structural design of the generator of PCGAN.
Here, the upward arrow ↑ indicates the image after upsampling. At the coarsest scale, to ensure consistency in channels, is set as a blank image of the same size as .
By utilizing the detection image from the previous layer , the generator aims to enhance its expressive capacity and generate internal wave detection images that are as realistic as possible, thereby obtaining better scores in the discriminator.
2.5. The Training Process of PCGAN
The model PCGAN is trained hierarchically from the coarsest scale to the finest scale, with a CGAN trained at each scale. Once the training at a previous scale is completed, the generated internal wave detection images are utilized for training at the next scale. The loss function is based on WGAN-GP (Wasserstein GAN with gradient penalty) and incorporates an L1-norm regularization term, formulated as follows:
where
where and are balancing parameters, the specific values for these parameters will be discussed in Section 3.4. Furthermore, is a random variable sampled uniformly from either or . refers to the error function of WGAN, which provides more stable training compared to the logarithmic formulation in Equation (2). represents the -norm regularization term, which imposes a penalty based on the pixel-wise dissimilarity between the ground truth and the produced . denotes the gradient penalty term, which prevents the gradients of the model from vanishing or exploding.
The training process of PCGAN, as shown in Algorithm 1, accepts ocean internal wave images along with their corresponding stripe label images as input, and outputs the trained generators and discriminators at various scales. For example, given a training image and its corresponding label image pair , and the scale number is set to upsample and downsample once, we first generate an image pyramid , , and . Training starts from the coarsest layer. Firstly, the output of is computed by , where is set to be a fully zero image with the same size as . And takes , as input. Next, update the parameters of and sequentially according to Equation (5). Secondly, concatenate and as the input to to obtain the output . Update and using Equation (5). Finally, similar to other scales, generate and then train and sequentially. Following this, the pair repeats the training process, iteratively updating the parameters of PCGAN. After completing the designated training epochs, the next image pairs in the training set will undergo the same training steps as .
| Algorithm 1 Training of PCGAN for Stripe Extraction of Oceanic Internal Waves |
|
3. Experiments and Results
3.1. Data Preparation
Figure 4 depicts a flow chart outlining the standard process of extracting ISW information from a SAR image [40]. The image, captured at 21:56 UTC on 8 March 2019, undergoes preprocessing steps from SAR image correction to geometric correction. Following this, the enhanced image is processed, leading to the manual extraction of the position information of ISWs. However, manual extraction is time-consuming. Our proposed PCGAN is designed to address the final step in Figure 4, employing machine learning techniques to automatically extract the accurate position of the wave crest of ISWs from local images.

Figure 4.
The extraction process of ISW information from SAR images. The red boxes in the first three images indicate the specific location in the last two images.
To achieve this goal, the original SAR images are obtained from the northern section of the South China Sea, globally acknowledged as the “natural experimental field” for investigating oceanic Internal Solitary Waves [41]. Figure 5 shows the distribution of internal waves in the region from 2010 to 2020 in June and July [40]. Specifically, we use Sentinel-1A/B SAR images with the interferometric wide swath (IW), featuring an image width of 250 km and a spatial resolution of 20 m.
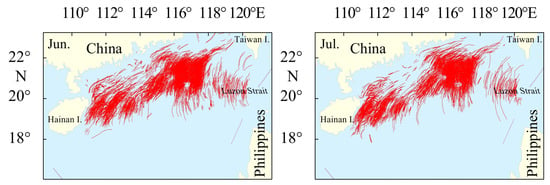
Figure 5.
The distribution of internal waves (represented by red lines) in the northern region of the South China Sea from June to July in the years 2010 to 2020.
From the original SAR images, we initially compiled a dataset consisting of 86 local images containing internal waves for model training and validation. The dimensions of these images varied from 150 to 950 pixels in width and height. To ensure consistency, all these images were uniformly resized to 512 × 512 pixels and subsequently subjected to manual annotation.
From Figure 6 depicted below, we have selected four pairs of images for model training using a limited sample size. Each pair comprises the original SAR image containing internal waves and its corresponding labeled image, which serves as the ground truth for our training process.
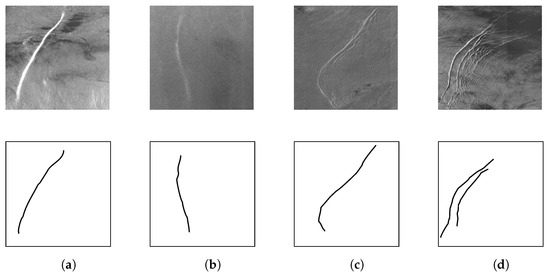
Figure 6.
PCGAN’s training set, comprising four pairs of images with distinct features. (a) high contrast, (b) low contrast, (c) minor coda, (d) more coda.
The upper row of images in Figure 6 highlights the diverse features of internal waves, illustrating their distinctive characteristics. This inherent diversity within the images contributes to a comprehensive and diverse training process. Among these images, Figure 6a presents a heightened color contrast, whereas Figure 6b showcases a lower contrast. In Figure 6c, there exists a minor coda presence, whereas Figure 6d displays more prominent coda interference (‘coda’ means the secondary or trailing part of the stripes that follows the primary wave); however, only the most pronounced portion is annotated in the label image. This ensures that the model also prioritizes the primary wave within the internal wave image.
Eighty-two (82) additional images, featuring distinct content but matching the size of the four images in the training set, were compiled to form the initial test set. To further validate the effectiveness and generalization of the model, an extra 40 images from the South China Sea and Andaman Sea were incorporated into the test set. Importantly, these images were not resized, ensuring that they differ in image size from the training set. Subsequently, all image pairs in both the testing and training datasets underwent normalization, scaling their values to the range of .
3.2. Experimental Environment and Basic Parameters
On a 64-bit Ubuntu 18.04.6 system, we utilized the PyTorch 1.12.1 machine learning framework for implementing and testing the model. The setup included the CUDA toolkit 9.1.85 software and an NVIDIA A100 GPU.
PCGAN underwent a training regimen comprising 5000 epochs, with each scale iteration set to 1. For the training of individual generators () and discriminators (), we harnessed the Adam optimizer, employing and . A learning rate of was designated for each network, while a minibatch size was 1.
At each scale, both the generator and discriminator convolutional neural networks consist of five convolutional layers. These convolutional layers have a filter size of , a stride of 1, and padding set to TRUE, ensuring that the dimensions of the input and output images remain unchanged. The kernel depth and activation functions for each convolutional layer are detailed in Table 1, which categorizes them into the initial layer (Layer 1), the middle layers (Layers 2 to 4), and the final layer (Layer 5).

Table 1.
The kernel depth and activation functions for each convolutional layer.
Here, the generator and discriminator share the same parameters in the initial layer and the middle layers. They only differ in the final layer, where the generator’s kernel depth is set to c, which needs to match the input image’s channel. In our task, the input is an RGB three-channel SAR image, so c is set to 3. LReLU represents the Leaky ReLU function.
3.3. Evaluation Criteria
To assess the efficacy of the proposed model and make comparisons with other models, we use four commonly used evaluation indicators for segmentation models: MIoU, F1-Score, MACC, and FWIoU. MACC calculates the average of all class accuracies (6). The F1-Score, calculated as the harmonic mean of Recall and Precision (as shown in Formulas (7) and (8)), is a widely employed performance metric in binary classification tasks. MIoU (Mean Intersection over Union) measures the overlap between the predicted segmentation regions by the model and the actual labels. The process involves calculating the Intersection over Union (IoU) for each class, which in our task includes the internal wave class and the background class. Subsequently, the average of IoUs across these two classes is computed (as Formula (10)). FWIoU (Frequency Weighted Intersection over Union) is an enhanced metric derived from MIoU, which considers the occurrence frequency of each class. It is the weighted average of the IoUs for these two classes (11).
Here, the number of pixels correctly recognized as “internal wave” is denoted by TP (true positive), while FN (false negative) represents the pixels erroneously missed and not identified as “internal wave”. FP (false positive) corresponds to the number of pixels misclassified as “internal wave” by the model, although they are labeled as “non-internal wave” in the ground truth dataset. Lastly, TN (true negative) represents the accurate identification of pixels as “non-internal wave”, indicating the background pixels that were correctly classified.
3.4. Selection of Balancing Parameters
To determine the optimal balance parameters for the input image, we also conducted a series of preliminary experiments. The -norm constraint parameter () and the weight assigned to the gradient penalty in the WGAN-GP loss term () were set to 5, 10, and 20, respectively. The model underwent training with the identical training dataset, and subsequent evaluation was carried out on the test dataset. Table 2 displays the average MIoU values corresponding to these parameter combinations on the test set. The highest values is highlighted in the cell with a gray background.

Table 2.
Average MIoUs of different balancing parameters.
Based on the metrics, we opted to set the values of both balance parameters to 10 during the subsequent training process.
3.5. Selection of the Number of Upsample and Downsample Layers
To ascertain the ideal count of upsampling and downsampling layers, we conducted a series of preliminary experiments. Table 3 presents the training duration and MIoU values for the model with different configurations, where the upsampling and downsampling layers are set to 0, 1, and 2. Both the testing and training datasets comprise images, with the model trained for 5000 epochs. It can be observed that while the two-layer upsampling shows a slight advantage in evaluation metrics over the one-layer upsampling, its training time is nearly four times that of the one-layer upsampling model. Moreover, due to memory constraints, the model with two upsampling layers can only handle images of half the size compared to the one-layer model. Therefore, we opt for one layer of upsampling.

Table 3.
Performance metrics and training duration across different scales.
After determining the number of upsampling layers, we reverted the dimensions of both the training and testing set back to the original size. Table 4 displays the average model MIoU scores under different downsampling layer configurations. The highest values is highlighted in the cell with a gray background. As the number of downsampling layers increases, the size of the internal wave images to be identified, denoted as , becomes progressively smaller, making it challenging to provide meaningful overall information. In such a context, the increasing number of downsampling layers N does not significantly enhance the model’s detection capability.

Table 4.
Fixed upsampling layers at one, different MIoU scores for various downsampling layers.
Therefore, guided by the outcomes of the preliminary experiments, we fix the number of upsampling layers M to 1, and choose 2 for the number of downsampling layers N.
3.6. Experimental Results and Comparative Analysis
In this segment, we conducted a performance comparison between PCGAN and four other methods, encompassing two traditional approaches: Adaptive Thresholding (AT) [42] and Canny edge detection [43], as well as two deep learning methodologies: Conditional Generative Adversarial Network (CGAN) and U-Net [44]. For a fair comparison, we utilize the identical training set, comprising only four pairs of images as depicted in Figure 6, to separately train these three deep learning models. Additionally, we use identical hyperparameters and conduct training for 5000 epochs.
Table 5 presents an assessment of the performance of AT, Canny, CGAN, U-net, and PCGAN on individual internal wave images, employing the metrics outlined in Section 3.3. Furthermore, Figure 7 visually presents the detection outcomes for four distinct test scenarios, providing insights into the comparative performance of the detection models. Figure 8 illustrates the recognition results of four internal wave images with different sizes, all from the Andaman Sea and featuring multiple wave crests within a single image. Table 6 provides the average metrics across all test images of the same size and compares the performance of the five methods. Table 7 presents the average metrics for an additional set of 40 images from the Andaman Sea and the South China Sea with varying sizes across three deep learning methods. In the table, the highest values for each metric are highlighted in cells with a gray background.

Table 5.
The performance of internal wave detection on nine representative images in the test set.
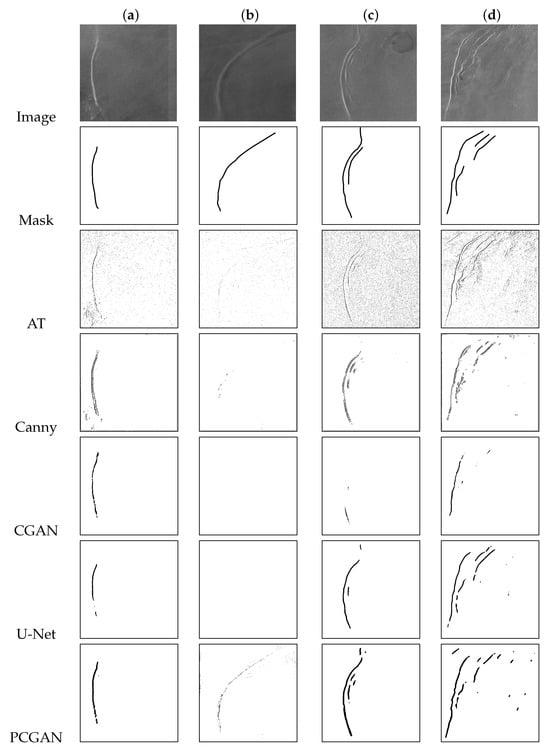
Figure 7.
Under four scenarios depicting high contrast (a), low contrast (b), minor coda presence (c), and more significant coda interference (d), the recognition results of five detection models (AT, Canny, CGAN, U-net, PCGAN).

Figure 8.
Results of detecting internal waves in four representative images using three machine-learning methods (CGAN, U-Net, and PCGAN) with various image sizes. (a): 316 × 436 pixels; (b): 668 × 664 pixels; (c): 328 × 820 pixels; (d): 400 × 552 pixels.

Table 6.
The mean metrics for test images with the same size across the five methods.

Table 7.
The mean metrics for test images with different sizes across the three deep learning methods.
Figure 9 displays box plots illustrating the four evaluation metrics discussed in Section 3.3 for the five detection methods. While our method may have a slightly lower maximum value compared to CGAN and U-Net, it outperforms other models in terms of both mean performance and stability.
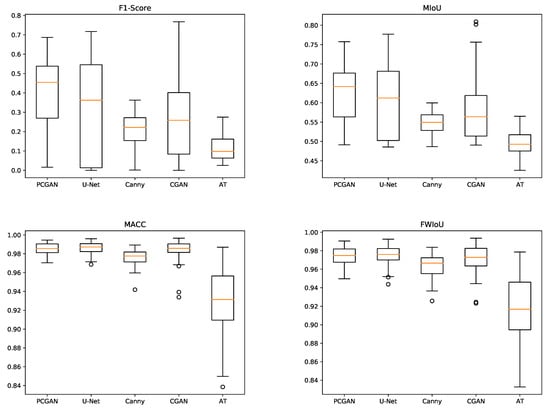
Figure 9.
Boxplots of the five detection methods (AT, Canny, CGAN, U-net, and PCGAN) across four evaluation metrics (F1-Score, MIoU, MACC, and FWIoU). The box signifies the middle 50% of the data, while the orange line inside represents the median. Whiskers extend to illustrate the overall extent of the dataset, and dots denote certain outliers.
4. Discussion
4.1. Descriptive Assessment
Figure 7 showcases SAR images with distinct features along with the detection results obtained using five different models. In (a), there is a high contrast between the stripes and the background, while in (b), the stripes are similar to the background, resulting in low contrast. In (c), in addition to simple stripes, there is a minor coda presence, and in (d), there is a more pronounced coda wave interference.
In these scenarios, as depicted in Figure 7c, compared to other models, PCGAN captures finer details of internal waves, exhibiting a closer resemblance to the mask image. For Figure 7b, where the features of the internal wave image are less pronounced, other models perform poorly, while PCGAN provides a notably superior detection result. In Figure 7a,d, even in situations where CGAN and U-Net yield subpar results, PCGAN still produces detection results that closely align with the reference data.
In Figure 8, the recognition results of internal wave images with four different sizes are demonstrated under three distinct deep learning methods. These images all contain multiple wave crest lines. It can be observed from the figure that, in terms of recognition completeness and continuity, PCGAN is noticeably superior to the other two methods, exhibiting a closer resemblance to the reference data.
This qualitative evidence supports the superior performance of PCGAN over other approaches to comprehensiveness and stability.
4.2. Measurable Assessment
The performance metrics for nine internal wave images across the five segmentation methods are displayed in Table 5. In each column, the evaluation criteria with the highest scores are shaded in gray. Overall, the table indicates that PCGAN achieves higher values across the assessment metrics.
Table 6 provides the mean performance metrics of the five detection models, providing a comprehensive overview of their collective performance across the entire set of test images of the same size. PCGAN exhibits slightly lower MACC than U-Net, which can be attributed to the fact that internal wave stripes are often narrow and occupy only a small fraction of the entire image, potentially compromising the efficacy of the MACC metric. For the remaining three metrics, PCGAN consistently achieves higher average scores compared to the other four detection models.
Table 7 presents the average metrics for 40 images of different sizes under three deep learning methods, with 20 from the South China Sea and 20 from the Andaman Sea. From the results, it can be observed that PCGAN outperforms the other two models in all four evaluation metrics. This demonstrates the superior generalization capability of PCGAN, enabling it to handle images from different maritime regions and varying sizes effectively.
The data utilized for generating the boxplots in Figure 9 encompass all test images. Although PCGAN did not perform the best in terms of the maximum values across the four evaluation metrics, it consistently demonstrates higher median evaluation scores and greater overall detection robustness. This provides quantitative evidence that PCGAN improves internal wave detection across a range of contexts.
Through the above discussion, both visual and numerical assessments have validated the advantages of the pyramid architecture, reducing the model’s demand for extensive training data. Remarkably, PCGAN demonstrated exceptional proficiency in internal wave detection even with just four training data pairs. Consequently, PCGAN stands as an effective solution for addressing internal wave detection with constraints on training data availability.
5. Conclusions
In this research, a Pyramidal Conditional Generative Adversarial Network (PCGAN) was designed to facilitate the learning of an internal wave stripe extraction model, even when the training dataset is limited. The PCGAN possesses strong capabilities for extracting wave stripes due to the following features:
- (1)
- Pyramid Structure: The PCGAN incorporates a pyramid structure, integrating multiple scales of conditional generative adversarial networks. This architecture ensures a stable and efficient training process.
- (2)
- Data Flow: The model employs a data flow from coarse to fine across different scales, enabling it to effectively capture both global and local information.
- (3)
- Upsampling Enhancement: The introduction of upsampling significantly enhances the model’s ability to extract fine features, particularly effective in capturing wave crests.
- (4)
- Parameter Optimization: To achieve optimal performance, a series of preliminary experiments were conducted to fine-tune the model parameters.
Subsequently, the model’s performance on the training set was showcased and compared with other models. The experimental results conclusively affirm that, even when trained with only four sets of training data, the well-trained PCGAN excels in accurate stripe extraction of oceanic internal waves. Furthermore, it demonstrates robust stability and generalization capabilities.
Furthermore, there are areas for potential improvement in future research. For instance, enhancing the continuity of stripe generation and reducing noise in image generation, as well as enhancing the capability to recognize internal waves in remote sensing images from larger areas and more complex environments. Subsequent studies will also explore the use of extracted internal wave stripes for investigating internal wave propagation and inverting parameters.
Author Contributions
Conceptualization, B.D., S.B., J.M. and M.G.; methodology, B.D., S.B., J.M. and M.G.; software, B.D.; validation, B.D.; formal analysis, S.B., J.M. and M.G.; investigation, B.D. and S.B.; resources, S.B. and J.M.; data curation, B.D., S.B., J.M. and M.G.; writing—original draft preparation, B.D.; writing—review and editing, S.B., J.M. and M.G.; visualization, B.D.; supervision, S.B., J.M. and M.G.; project administration, S.B.; funding acquisition, S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (62161044, 11962025), Science and Technology Project of Inner Mongolia (2021GG0140), Natural Science Foundation of Inner Mongolia (2022ZD05, 2023MS06003), Key Laboratory of Infinite-dimensional Hamiltonian System and Its Algorithm Application (IMNU), Ministry of Education (2023KFYB06).
Data Availability Statement
The availability of these data is subject to 3rd Party Data Restrictions. The data were acquired from (third party) and can be accessed (from the authors) with the authorization of (third party).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript (arranged in the order as they appear in the text):
| ISW | Internal solitary wave |
| SAR | synthetic aperture radar |
| PCGAN | pyramidal conditional generative adversarial network |
| CGAN | conditional generative adversarial network |
| CP | compact polarimetric |
| ALOS | Advanced Land Observing Satellite |
| PALSAR | Phase Array type L-band SAR |
| PCA | principal component analysis |
| SVM | support vector machine |
| KdV | Korteweg-de Vries |
| SMMSR | separation and matching approach within the sector region |
| GAN | Generative Adversarial Network |
| WGAN | Wasserstein Generative Adversarial Network |
| BN | batch normalization |
| GP | Gradient Penalty |
| IW | interferometric wide swath |
| MIoU | Mean Intersection over Union |
| IoU | Intersection over Union |
| FWIoU | Frequency Weighted Intersection over Union |
| AT | Adaptive Thresholding |
References
- Garrett, C.; Munk, W. Internal waves in the ocean. Annu. Rev. Fluid Mech. 1979, 11, 339–369. [Google Scholar] [CrossRef]
- Gerkema, T.; Zimmerman, J. An Introduction to Internal Waves; Lecture Notes; Royal NIOZ: Texel, The Netherlands, 2008; Volume 207, p. 207. [Google Scholar]
- Huang, X.; Chen, Z.; Zhao, W.; Zhang, Z.; Zhou, C.; Yang, Q.; Tian, J. An extreme internal solitary wave event observed in the northern South China Sea. Sci. Rep. 2016, 6, 30041. [Google Scholar] [CrossRef] [PubMed]
- Osborne, A.; Burch, T.; Scarlet, R. The influence of internal waves on deep-water drilling. J. Pet. Technol. 1978, 30, 1497–1504. [Google Scholar] [CrossRef]
- Kurup, N.V.; Shi, S.; Shi, Z.; Miao, W.; Jiang, L. Study of nonlinear internal waves and impact on offshore drilling units. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; Volume 44335, pp. 831–840. [Google Scholar]
- Wang, Y.H.; Dai, C.F.; Chen, Y.Y. Physical and ecological processes of internal waves on an isolated reef ecosystem in the South China Sea. Geophys. Res. Lett. 2007, 34, L18609. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, S.; Wang, Y.; Wang, S.; Gao, Z.; Luo, C. Three-dimensional regional oceanic element field reconstruction with multiple underwater gliders in the Northern South China Sea. Appl. Ocean. Res. 2020, 105, 102405. [Google Scholar] [CrossRef]
- Ma, W.; Wang, Y.; Yang, S.; Wang, S.; Xue, Z. Observation of internal solitary waves using an underwater glider in the northern south china sea. J. Coast. Res. 2018, 34, 1188–1195. [Google Scholar] [CrossRef]
- Fu, L.L. Seasat Views Oceans and Sea Ice with Synthetic-Aperture Radar; California Institute of Technology, Jet Propulsion Laboratory: Pasadena, CA, USA, 1982; Volume 81. [Google Scholar]
- Alpers, W. Theory of radar imaging of internal waves. Nature 1985, 314, 245–247. [Google Scholar] [CrossRef]
- Berens, P. Introduction to synthetic aperture radar (SAR). In Advanced Radar Signal and Data Processing; RTO: Neuilly-sur-Seine, France, 2006; pp. 3-1–3-16. [Google Scholar]
- Li, X.; Morrison, J.; Pietrafesa, L.; Ochadlick, A. Analysis of oceanic internal waves from airborne SAR images. J. Coast. Res. 1999, 15, 884–891. [Google Scholar]
- Rodenas, J.A.; Garello, R. Wavelet analysis in SAR ocean image profiles for internal wave detection and wavelength estimation. IEEE Trans. Geosci. Remote Sens. 1997, 35, 933–945. [Google Scholar] [CrossRef]
- Ródenas, J.A.; Garello, R. Internal wave detection and location in SAR images using wavelet transform. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1494–1507. [Google Scholar] [CrossRef]
- Simonin, D.; Tatnall, A.; Robinson, I. The automated detection and recognition of internal waves. Int. J. Remote Sens. 2009, 30, 4581–4598. [Google Scholar] [CrossRef]
- Zhang, H.; Meng, J.; Sun, L.; Zhang, X.; Shu, S. Performance analysis of internal solitary wave detection and identification based on compact polarimetric SAR. IEEE Access 2020, 8, 172839–172847. [Google Scholar] [CrossRef]
- Qi, K.T.; Zhang, H.S.; Zheng, Y.G.; Zhang, Y.; Ding, L.Y. Stripe segmentation of oceanic internal waves in SAR images based on Gabor transform and K-means clustering. Oceanologia 2023, 65, 548–555. [Google Scholar] [CrossRef]
- Wang, S.; Dong, Q.; Duan, L.; Sun, Y.; Jian, M.; Li, J.; Dong, J. A fast internal wave detection method based on PCANet for ocean monitoring. J. Intell. Syst. 2019, 28, 103–113. [Google Scholar] [CrossRef]
- Bao, S.; Meng, J.; Sun, L.; Liu, Y. Detection of ocean internal waves based on Faster R-CNN in SAR images. J. Oceanol. Limnol. 2020, 38, 55–63. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Zhang, H.S.; Wang, Y.Q. Stripe detection and recognition of oceanic internal waves from synthetic aperture radar based on support vector machine and feature fusion. Int. J. Remote Sens. 2021, 42, 6706–6724. [Google Scholar] [CrossRef]
- Vasavi, S.; Divya, C.; Sarma, A.S. Detection of solitary ocean internal waves from SAR images by using U-Net and KDV solver technique. Glob. Trans. Proc. 2021, 2, 145–151. [Google Scholar] [CrossRef]
- Li, X.; Liu, B.; Zheng, G.; Ren, Y.; Zhang, S.; Liu, Y.; Gao, L.; Liu, Y.; Zhang, B.; Wang, F. Deep-learning-based information mining from ocean remote-sensing imagery. Natl. Sci. Rev. 2020, 7, 1584–1605. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Zhang, H.S.; Qi, K.T.; Ding, L.Y. Stripe segmentation of oceanic internal waves in SAR images based on SegNet. Geocarto Int. 2022, 37, 8567–8578. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Qi, K.T.; Zhang, H.S. Stripe segmentation of oceanic internal waves in synthetic aperture radar images based on Mask R-CNN. Geocarto Int. 2022, 37, 14480–14494. [Google Scholar] [CrossRef]
- Barintag, S.; An, Z.; Jin, Q.; Chen, X.; Gong, M.; Zeng, T. MTU2-Net: Extracting Internal Solitary Waves from SAR Images. Remote Sens. 2023, 15, 5441. [Google Scholar] [CrossRef]
- Song, B.; Sheng, R. Crowd counting and abnormal behavior detection via multiscale GAN network combined with deep optical flow. Math. Probl. Eng. 2020, 2020, 6692257. [Google Scholar] [CrossRef]
- Olson, M.; Wyner, A.J.; Berk, R. Modern neural networks generalize on small data sets. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 3623–3632. [Google Scholar]
- Li, Y.; Lyu, X.; Frery, A.C.; Ren, P. Oil spill detection with multiscale conditional adversarial networks with small-data training. Remote Sens. 2021, 13, 2378. [Google Scholar] [CrossRef]
- Tai, X.; Li, M.; Xiang, M.; Ren, P. A mutual guide framework for training hyperspectral image classifiers with small data. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5510417. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 1050, 10. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Han, Z.; Wei, B.; Mercado, A.; Leung, S.; Li, S. Spine-GAN: Semantic segmentation of multiple spinal structures. Med. Image Anal. 2018, 50, 23–35. [Google Scholar] [CrossRef]
- Liu, K.; Ye, Z.; Guo, H.; Cao, D.; Chen, L.; Wang, F.Y. FISS GAN: A generative adversarial network for foggy image semantic segmentation. IEEE/CAA J. Autom. Sin. 2021, 8, 1428–1439. [Google Scholar] [CrossRef]
- Li, H. Image semantic segmentation method based on GAN network and ENet model. J. Eng. 2021, 2021, 594–604. [Google Scholar] [CrossRef]
- Sun, S.; Mu, L.; Wang, L.; Liu, P.; Liu, X.; Zhang, Y. Semantic segmentation for buildings of large intra-class variation in remote sensing images with O-GAN. Remote Sens. 2021, 13, 475. [Google Scholar] [CrossRef]
- Liu, L.; Muelly, M.; Deng, J.; Pfister, T.; Li, L.J. Generative modeling for small-data object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6073–6081. [Google Scholar]
- Zhu, Q.X.; Hou, K.R.; Chen, Z.S.; Gao, Z.S.; Xu, Y.; He, Y.L. Novel virtual sample generation using conditional GAN for developing soft sensor with small data. Eng. Appl. Artif. Intell. 2021, 106, 104497. [Google Scholar] [CrossRef]
- He, Y.L.; Li, X.Y.; Ma, J.H.; Lu, S.; Zhu, Q.X. A novel virtual sample generation method based on a modified conditional Wasserstein GAN to address the small sample size problem in soft sensing. J. Process. Control 2022, 113, 18–28. [Google Scholar] [CrossRef]
- Meng, J.; Sun, L.; Zhang, H.; Hu, B.; Hou, F.; Bao, S. Remote sensing survey and research on internal solitary waves in the South China Sea-Western Pacific-East Indian Ocean (SCS-WPAC-EIND). Acta Oceanol. Sin. 2022, 41, 154–170. [Google Scholar] [CrossRef]
- Zhao, Z.; Klemas, V.; Zheng, Q.; Yan, X.H. Remote sensing evidence for baroclinic tide origin of internal solitary waves in the northeastern South China Sea. Geophys. Res. Lett. 2004, 31, L06302-1. [Google Scholar] [CrossRef]
- Bradley, D.; Roth, G. Adaptive thresholding using the integral image. J. Graph. Tools 2007, 12, 13–21. [Google Scholar] [CrossRef]
- Rong, W.; Li, Z.; Zhang, W.; Sun, L. An improved CANNY edge detection algorithm. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 577–582. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).