Corn Grain Yield Prediction Using UAV-Based High Spatiotemporal Resolution Imagery, Machine Learning, and Spatial Cross-Validation
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Field Data
2.2.1. Weather
2.2.2. Management
2.2.3. Imagery
2.2.4. Yield
2.3. Corn Growth Stage
2.3.1. Growing Degree Days
2.3.2. Estimation
2.4. Feature Extraction
2.4.1. Yield
2.4.2. Imagery and Vegetation Indices
2.4.3. Data Fusion
2.5. Yield Prediction Experiments
2.5.1. Evaluation Metrics
Root Mean Squared Error
Coefficient of Determination
Correlation Coefficient
2.5.2. Model Hyperparameters
- RF: bag size = 100%; number of trees = 100; number of attributes/features = 2 for HRe and 1 for LRe; leaf minimum number of instances = 1; minimum variance for a split = 0.001 (i.e., ); unlimited tree depth; number of decimal places = 2; and random number generation seed = 1.
- LR: the M5 attribute/feature selection method was chosen; ridge parameter = ; and number of decimal places = 4.
2.5.3. Location-Only Standard K-Fold Cross-Validation
2.5.4. Standard K-Fold Cross-Validation
2.5.5. Spatial Cross-Validation
Leave-One-Field-Out Cross-Validation
K-Means-Based Cross-Validation
3. Results
3.1. Imagery Type Analysis
3.1.1. Vegetation Index Ranking
- In general, MS imagery leads to better performance than RGB imagery. We can see two RGB VIs that were among the top five best-ranked VIs: in early season for LOFO-CV-LRe and IKAW4 in the late season for rev-LOFO-CV-HRe.
- For rev-LOFO-CV, we can see that red-edge-based VIs do better from middle to late season.
- NIR-based VIs do especially well earlier in the season, which makes sense, since the NIR reflectance decreases around the middle of the growing season [18]. NDVI is also among the top-ranked VIs in early season.
- Another noteworthy VI is the , which is relatively high ranking for the LOFO-CV experiments using HRe data.
- We can also see that the red-edge raw-band is frequently among the top five highest-ranked VIs, suggesting we could save computational costs and skip the VI calculation step by using the red-edge band directly.
- Over the entire growing season, the three VIs among the top five best ranking performance for each of HRe, LRe, LOFO-CV, and rev-LOFO-CV, are , , and NG.
- Approximately 70% of these VIs included the blue band in their definition, whereas the top five best-ranked VIs rarely included the blue band in their definition. In fact, the middle of the season had no blue-based VIs that were ranked among the top five. Interestingly, was ranked among the top five best VIs for LOFO-CV-HRe, suggesting the blue band still has prediction power when combined with other MS bands.
- Approximately 30% of the raw-bands, all of which were RGB, were among the worst-performing VIs.
- Nearly all the worst-performing VIs (95%) were RGB-based. There were no NIR-based VIs in the early and middle seasons among the five worst VIs. Only in late season for rev-LOFO-LRe were there two NIR-based VIs among the worst VIs. On the other hand, for red-edge-based VIs, there were no red-edge-based VIs among the worst during late season. Only in the early and middle seasons for LOFO-CV-HRe was there a red-edge-based VI among the five worst.
3.1.2. MS Imagery vs. RGB Imagery
3.2. Effects of Spatial Autocorrelation on Performance
3.3. ML Model Comparison
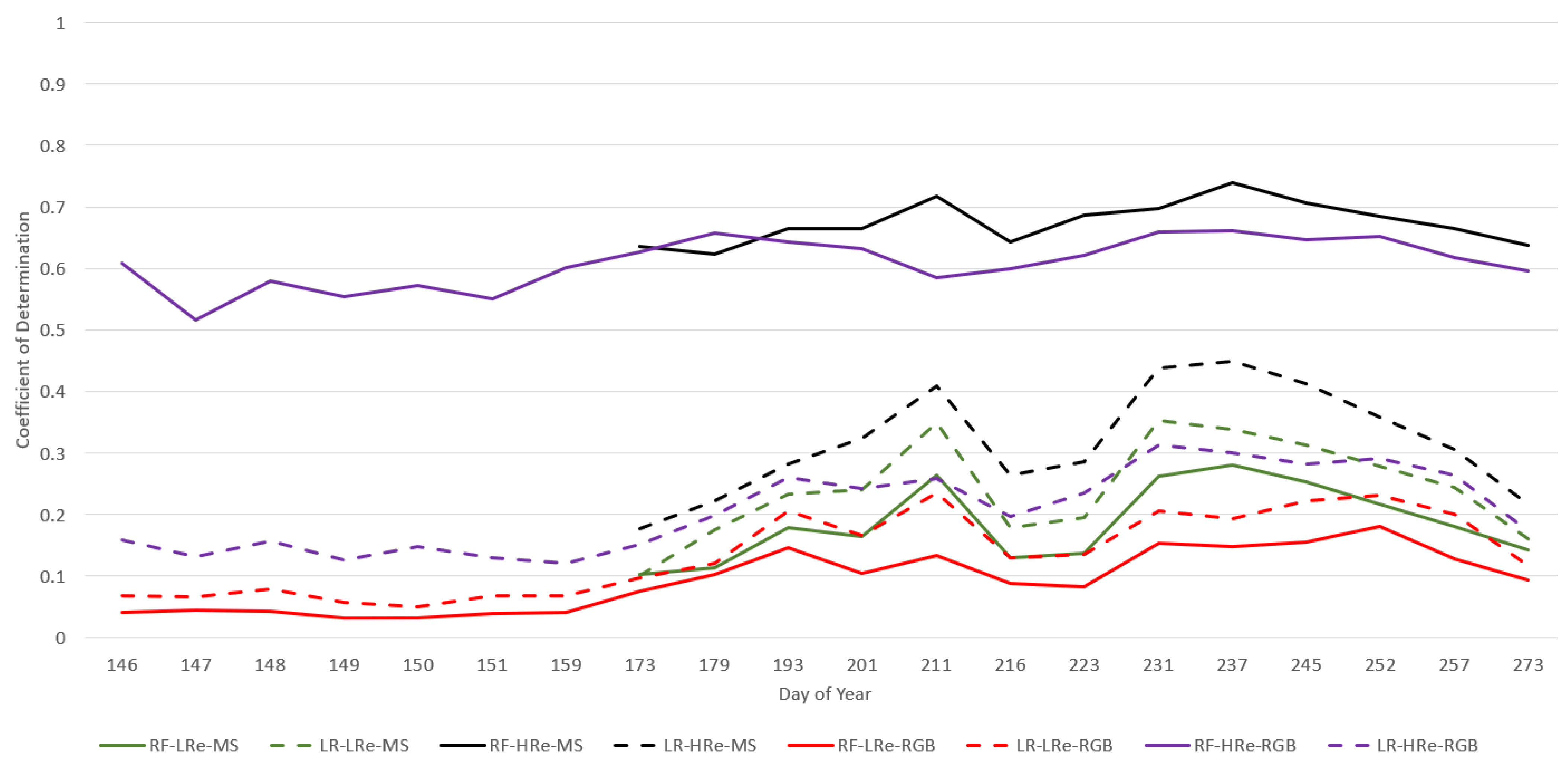
3.4. High vs. Low Spatial Resolution Imagery Analysis
3.5. Evaluation Method Comparison
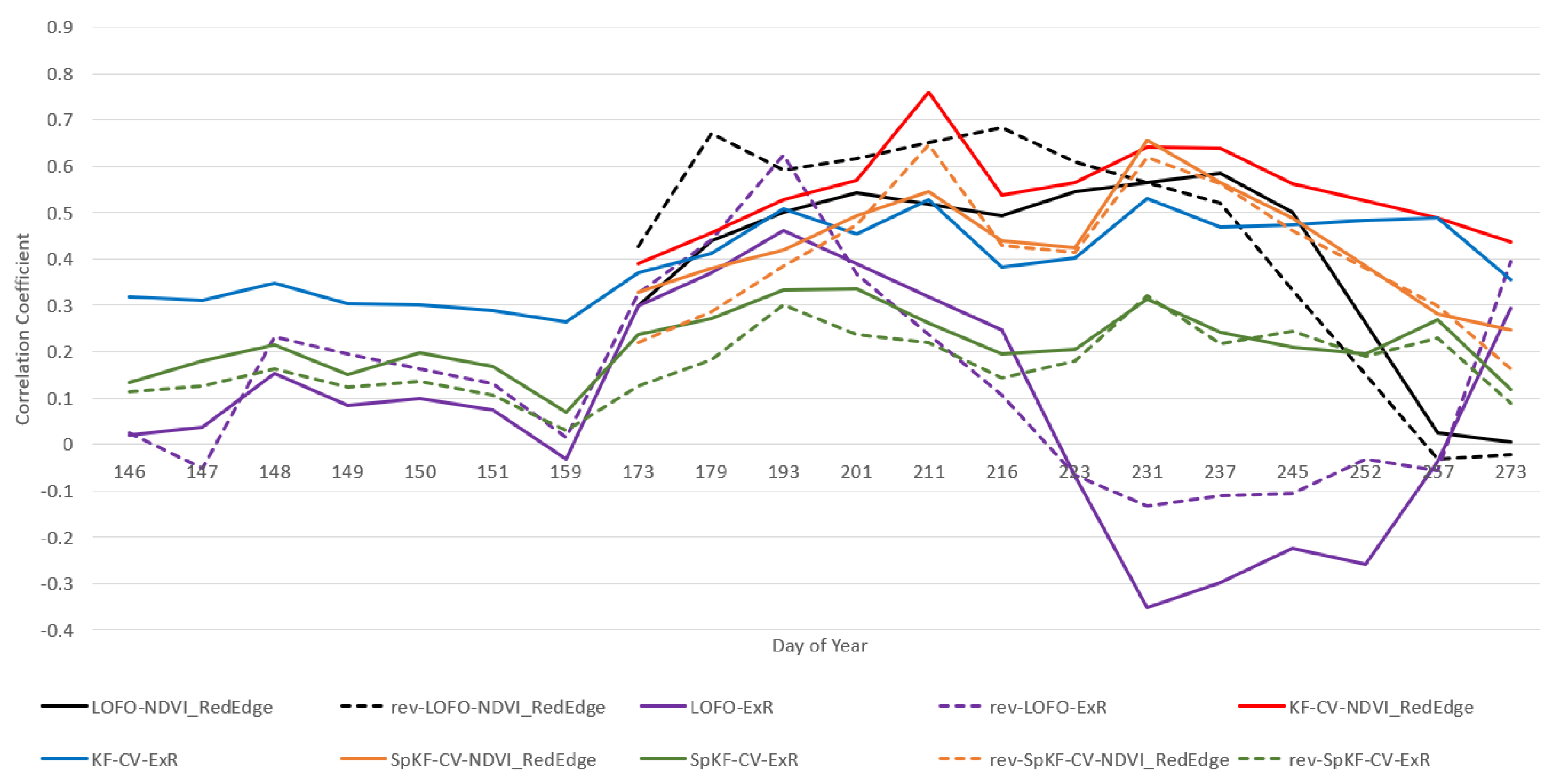
3.5.1. LOFO-CV vs. rev-LOFO-CV
- We can see that for the RGB VI (ExR) for LOFO-CV and rev-LOFO-CV in Figure 2 and Figure 3, earlier in the season there is no large distinction between both evaluation methods other than the peak performance achieved for DoY 193 by rev-LOFO-CV, although, LOFO-CV does generally better than rev-LOFO-CV later in the season. An observable difference between LR and RF is that negative CC performance is achieved by LR-LOFO-CV later in the season, whereas RF has positive CC performance.
- For both the and ExR, the peak performance achieved is by rev-LOFO-CV.
- There is also some bias that could be introduced in the two types of LOFO-CV experiments, since imagery missions were occasionally conducted 1 to 3 days apart (delayed) from the other fields for some weeks, especially at the end of the season. In fact, LOFO-CV and rev-LOFO-CV do most poorly at the end of the season for both ExR and , which may be attributed to these delays in field imagery acquisition missions.
- There are also days when one field was missing, meaning the two LOFO CV methods (rev-LOFO-CV and LOFO-CV) may have a bias in the results involving experiments with missing fields due to the reduced number of folds.
3.5.2. LOFO-CV vs. SpKF-CV
3.5.3. SpKF-CV vs. rev-SpKF-CV
3.6. Imagery Acquisition Date Analysis
3.7. Data Processing Time Analysis
3.7.1. Imagery Acquisition
3.7.2. Imagery and Yield Pre-Processing
- For RGB imagery, six orthomosaics were typically created (one for each field). Sometimes, Field 11 was split into two orthomosaics for a single UAV mission (this was conducted for five missions from August onward), so the orthomosaic with the most imagery and the least amount of noise was chosen for further processing for that DoY. On average, it took 2.4 and 3.1 h to generate orthomosaics for the smaller fields and Field 11, respectively.
- For MS imagery, twelve () orthomosaics were typically created, one for each band and one for NDVI, and two sets of six orthomosaics (one set for Field 11 and another set for the smaller fields) were generated. On average (ignoring a 74.2 h outlier), it took 6.8 and 4.8 h to generate the six single-band orthomosaics for the smaller fields and Field 11, respectively.
3.7.3. Machine Learning
4. Discussion
4.1. Comparison of Approaches
- Requirement 1. The prediction models used to predict yield.
- Abbreviations: LR = linear regression; MLR = multiple LR; GBDT = gradient-boosting decision trees; LASSO = Least Absolute Shrinkage and Selection Operator regression; RR = ridge regression; ENR = elastic net regression; PLSR = partial least square regression; DRF = distributed RF; ERT = extremely randomized trees; GBM = gradient-boosting machine; GLM = generalized linear model; KNN = k-nearest neighbours; CU = cubist; SR = stepwise regression; SMLR = stepwise multiple linear regression; CNN = convolutional neural network; SGB = stochastic gradient boosting; ELM = extreme learning machine; 0-R = ZeroR; DT = decision tree; LME = linear mixed effects; LGBMR = LightGBM regression; RF = random forest; SVM = support vector machine; VI-based = basic regression or correlation models applied to VIs; ANN = artificial neural network (with one hidden layer); and DNN = deep neural network (any ANN with more than one hidden layer)
- Requirement 2. The sensing platforms used to acquire the imagery.
- Abbreviations: SAT = satellite; AIR = airborne/aircraft; UAV = unmanned aerial vehicle; and HAN = hand-held/tractor-mounted
- Requirement 3. The type of imagery used.
- Requirement 4. Imagery spatial resolution.
- Requirement 5. Imagery temporal resolution (number of acquisitions per season).
- Requirement 6. The list of the different types of features included in the models.
- Abbreviations: IMG = imagery; TOP = topography; SOI = soil; MNG = management; GEN = genotype information; WEA = weather; LOC = location; LAI = leaf area index; and BIO = biomass
- Requirement 7. Indicates whether imagery-based plant height was used in the yield prediction model.
- Requirement 8. Number of extracted VIs.
- Requirement 9. Number of extracted TIs.
- Requirement 10. Number of available spectral bands.
- Requirement 11. The yield-sampling technique used to obtain the yield dataset.
- Abbreviations: HA = harvester; YM = yield monitor; and MA = manual
- Requirement 12. Number of raw yield samples.
- Requirement 13. Total study site size (in hectares).
- Requirement 14. Number of growing seasons in the study.
- Requirement 15. Growing season period.
- Requirement 16. The spatial resolution of the predictions made by the yield prediction models (the size of the area a prediction covers).
- Requirement 17. The temporal resolution of the predictions made by the yield prediction models (how frequent were predictions made), where:
- ‘multi’ indicates predictions are made every image acquisition;
- ‘annually’ indicates predictions are made once per season/year;
- ‘once’ indicates predictions are made only once.
- Requirement 18. The prediction scale of the study, where we refer to a study’s scale as
- pixel-level if the study makes model predictions using multiple input samples from a management unit (a small plot or a field);
- field-level if the study makes model predictions using only a single input sample from a management unit.
- Requirement 19. Model evaluation methods applied.
- Requirement 20. Hyperparameter tuning methods applied.
- Requirement 21. Indicates whether temporal structure/features was/were fed to (or used in) the models. Examples of such features include (a) two imagery features derived each from two different dates, and (b) a single feature of accumulated (or averaged) imagery pixels for some location over the growth season.
- Requirement 22. Indicates whether spatial structure/features was/were fed to (or used in) the models. Examples of such features include (a) raw 2D imagery, or (b) statistical aggregations (such as maximum reflectance or a TI) over a spatial region.
- Requirement 23. Indicates whether the spatial generalizability of the models was evaluated/considered.
- Requirement 24. Indicates whether the temporal generalizability of the models was evaluated/considered.
5. Conclusions
- Reproducing the present work’s results using (a) 2023 UAV imagery from Area X.O, and (b) actual satellite imagery instead of simulated satellite imagery.
- Including an additional benchmark ZeroR model that simply outputs the average of the training data’s yields to give more insight into how poor models are performing.
- Evaluating additional ML models, especially spatially aware models such as generalized least squares [40].
- Evaluating and examining the effects on performance of applying various spatial sampling schemes (systematic random, simple random, and clustered random [46]) before applying CV.
- Performing hyperparameter tuning.
- Combining features from multiple DoYs in datasets to add a temporal dimension to the study.
- Performing a temporal generalizability analysis.
- Investigating the effects of number of features on RF performance.
- Expanding on the VI ranking analysis by splitting the mid season in two.
- Exploring multi-band/VI feature models for yield prediction.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Vegetation Index | Description | Equation | Reference |
|---|---|---|---|
| NIR-red difference vegetation index | [93] | ||
| NIR-green difference vegetation index | [93] | ||
| NDVI | normalized difference vegetation index | [16,94] | |
| blue normalized difference vegetation index | [94] | ||
| green normalized difference | |||
| vegetation index | [94] | ||
| RDVI | renormalized difference vegetation index | [16] | |
| WDRVI | wide range vegetation index | , where | [13,95] |
| SAVI | soil-adjusted vegetation index | , where | [81] |
| MSAVI | improved SAVI | [96,97] | |
| OSAVI | optimized soil-adjusted vegetation index | , where | [80] |
| NIR-red simple ratio index | [98] | ||
| NIR-green simple ratio index | [95] | ||
| MSR | modified simple ratio index | [96,98] | |
| GCI or GCVI | green chlorophyll (vegetation) index | [12,99] | |
| NG | normalized green index | [18] | |
| MCARI2 | improved MCARI | [96] | |
| MTVI2 | modified triangular vegetation index (TVI) 2 (improved TVI) | [96] |
| Vegetation Index | Description | Equation | Reference |
|---|---|---|---|
| r | red chromatic coordinate | [18,100] | |
| g | green chromatic coordinate | [18,100] | |
| b | blue chromatic coordinate | [18,100] | |
| MSR with NIR band replaced by green | present work | ||
| green-red simple ratio index | [93,100] | ||
| red-green simple ratio index | [101] | ||
| green-blue simple ratio index | [100] | ||
| red-blue simple ratio index | [100] | ||
| green-red difference vegetation index | [93] | ||
| normalized red-green difference vegetation index | [102] | ||
| normalized green-blue difference vegetation index | [102] | ||
| VIg | vegetation index green or green-red vegetation index | [18,93,100,101] | |
| TVIg | Tucker index | [93] | |
| NGRDI | normalized green-red difference index | [101] | |
| IKAW1 | Kawashima index 1 | [100,103] | |
| IKAW2 | Kawashima index 2 | [103] | |
| IKAW3 | Kawashima index 3 | [103] | |
| IKAW4 | Kawashima index 4 | [103] | |
| IKAW5 | Kawashima index 5 | [103] | |
| CIVE | color index of vegetation extraction, where band reflectance values range from 0 to 255 | [100,104] | |
| CIVEn | color index of vegetation extraction, where the normalized bands are used | [18] | |
| ExR | excess red vegetation index | [100,101] | |
| ExG | excess green vegetation index | [18,100] | |
| ExB | excess blue vegetation index | [100,101] | |
| ExGR | excess green minus excess red | ExG − ExR | [101] |
| principal component analysis index | 0.994 · + 0.961 · + 0.914 · | [100,101] | |
| GLI | green leaf index | [100,101,105] | |
| VARI | visible atmospherically resistant index | [100,101,106] |
| Vegetation Index | Description | Equation | Reference |
|---|---|---|---|
| red-edge-red simple ratio index | present work | ||
| red-edge-red difference vegetation index | present work | ||
| NIR-red-edge simple ratio index | present work | ||
| NIR-red-edge difference vegetation index | present work | ||
| or NDRE | NDVI with red band replaced by red-edge | [99] | |
| MSR with red band replaced by red-edge | [99] | ||
| TCARI | transformed chlorophyll absorption in reflectance index | [16] | |
| MCARI | modified chlorophyll absorption ratio index | [96,97] | |
| TCI | triangular chlorophyll index | [97] |
| Requirement | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Reference | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| [77] | LR, KNN, RF, SVM, DNN | UAV | RGB, MS | ∼3 cm | 2 | IMG | n | 26 | 0 | 7 | HA | 64 | ∼0.68 |
| [91] | LR, LASSO, RR, ENR, PLSR | UAV | RGB | U | 12 | IMG | y | 15 | 0 | 3 | HA | U | U |
| [79] | RF, MLR, GBDT | UAV | MS | U | 5 | IMG | n | 26 | 0 | 5 | HA, MA | 32 | 0.8 |
| [85] | LR, MLR | UAV | MS | 2.1 cm | 5 | IMG | y | 10 | 0 | 4 | MA | 48 | ∼0.16 |
| [22] | GBM, DNN, DRF, ERT, GLM | UAV | HS, LiDAR | 3 cm, 900 pts/ | 1 | IMG | y | U | U | 269 | MA | 369 | U |
| [66] | LR | UAV, HAN | MS | U | 4 to 5 | IMG | n | 3 | 0 | 10 | HA | U | U |
| [74] | RF, LR, KNN, SVM, ANN, 0-R | UAV | MS | <5 m × 0.45 m | 1 | IMG | n | 33 | 0 | 4 | U | 88 | ∼0.02 |
| [27] | RF | UAV | MS | 5.45 cm | 9 | IMG | n | 12 | 8 | 5 | MA | 57 | ∼0.56 |
| [78] | PLSR, VI-based | UAV | MS | <1 m | 7 | IMG | n | 14 | 0 | 11 | MA | 151 | ∼0.19 |
| [29] | ANN, RF, SVM, SR | UAV | RGB, MS | 1 cm, 5 cm | 11, 6 | IMG | y | 35 | 4 | 8 | MA | 20 | U |
| [87] | RF, LR, RR, LASSO, ENR | UAV | RGB | U | 25 | IMG | y | 12 | 0 | 3 | HA | U | U |
| [75] | RR, RF, SVM | UAV | HS | 2.45 cm | 11 | IMG | n | 81 | 0 | 274 | MA | 1429 | ∼1.2 |
| [76] | ANN, RF, SVM, ELM | UAV | RGB | 1.8 cm | 11 | IMG | n | 8 | 0 | 3 | U | 20 | ∼0.16 |
| [72] | LR, MLR | UAV, SAT | RGB, MS | SAT: 10 m, UAV: 0.5 cm | 4 | IMG, BIO, LAI | y | 2 | 0 | 7 | U | 5 | U |
| [28] | ANN, MLR | AIR | MS | 1.5 m | 1 | IMG, TOP | n | 4 | 4 | U | YM | 673 | 30 |
| [86] | ANN, SMLR, VI-based | AIR | HS | 2 m | 3 | IMG | n | 4 | 0 | 71 | MA | 192 | ∼92.2 |
| [24] | SR, RF, ANN, SVM, SGB, CU | AIR | MS, LiDAR | 30 cm, 76 cm | 1 | IMG, TOP, SOI | n | 6 | 0 | 4 | YM | U | 17.5 |
| [6] | CNN, LASSO, RF, LGBMR | AIR | MS | 10 cm | 13 | IMG, LOC, WEA, MNG | n | 5 | 0 | 4 | YM | U | U |
| [90] | LR, RF, SVM, SGB, ANN, CU | AIR, UAV | RGB, MS, LiDAR | ≤35 cm, 12 cm, 76 cm | biweekly and 3 | IMG, TOP | n | 6 | 0 | 7 | YM, MA | U | 76.9 |
| [32] | RF, LR | UAV | RGB, MS | <4 cm | 20, 13 | IMG | n | 33 | 0 | 5 | YM | 18,106 | ∼25.9 |
| [89] | CNN | UAV | HS | ∼4 cm | 5 | IMG | n | 0 | 0 | 240 | U | 172 | ∼0.48 |
| [30] | LME | UAV | RGB, MS | ≤5 cm | 12 | IMG | n | 6 | 0 | 6 | YM | 54–288 | 1.1 |
| [88] | PLSR | UAV | RGB | ≤1.01 cm | 2 | IMG | y | 6 | 0 | 3 | MA | 59 | ∼0.06 |
| [82] | ANN | UAV | RGB, MS | ≤2.15 cm | 2 | IMG | n | 6 | 0 | 7 | MA | 80 | ∼0.24 |
| [92] | RF | UAV | MS | 2.1 cm | 3 | IMG, MNG | n | 15 | 0 | 5 | YM | U | 2.6 |
| [67] | LR | UAV | RGB | 5 cm | 3 | IMG | n | 1 | 0 | 3 | YM | 14,705 | 36 |
| [9] | DNN, CNN, DNN+CNN, RF, XGBoost | UAV | MS | 7.4 cm | 1 | IMG, MNG, GEN | n | 8 | 0 | 5 | HA | ∼4500 | ∼1.6 |
| [73] | ANN, M5P and REPTree DT, RF, SVM, MLR | UAV | RGB, MS, thermal | U, 10 cm, U | 3 | IMG, MNG | n | U | 0 | 7 | MA | 72 | ∼0.24 |
| present work | RF, LR | UAV | RGB, MS | <4 cm | 20, 13 | IMG, LOC | n | 55 | 0 | 8 | YM | 18,106 | ∼25.9 |
| Requirement | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Reference | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| [77] | 1 | 2021 | 12.5 m × 8.5 m | multi | field-level | 5F-CV | grid search + 5F-CV | n | n | n | n |
| [91] | 1 | 2019 | ∼10.64 | once | field-level | holdout method, 10F-CV | grid search | y | n | n | n |
| [79] | 3 | 2017 to 2019 | ∼11.64 m ×38 m | multi | field-level | holdout method | U | n | n | n | n |
| [85] | 1 | 2021 | 32.8 | multi | field-level | U | U | n | n | n | n |
| [22] | 1 | 2020 | U | once | field-level | holdout method | random grid search | n | partial | n | n |
| [66] | 2 | 2020 to 2021 | U | multi | field-level | basic linear regression | None | n | U | n | n |
| [74] | 2 | 2017 to 2019 | 5 m × 0.45 m | once | field-level | 10F-CV | None | n | n | n | n |
| [27] | 1 | 2020 | (5 m × 10 m) and (5 m × 6 m) | multi and annually | field-level | leave-one-out CV | U | y | partial | n | n |
| [78] | 1 | 2015 | ∼12 | multi | field-level | holdout method | None | n | n | n | n |
| [29] | 1 | 2019 | U | multi | field-level | 10F-CV | grid search | n | partial | n | n |
| [87] | 1 | 2019 | ∼170.24 | multi and annually | field-level | 10F-CV | U | y | partial | n | n |
| [75] | 1 | 2020 | ∼1.38 m × 6.1 m | multi and annually | field-level | 4F-CV | grid search | y | n | n | n |
| [76] | 1 | 2019 | 10 m × 8 m | multi and annually | field-level | leave-one-out CV | U | y | n | n | n |
| [72] | 1 | 2021 | field-level | multi | field-level | holdout method | None | n | n | n | n |
| [28] | 1 | 1998 | 9 m | once | pixel-level | holdout method | U | n | partial | n | n |
| [86] | 1 | 2000 | 1 m | annually | pixel-level | 10F-CV | holdout method + Although the Clementine Data Mining System tuning | n | n | n | n |
| [24] | 1 | 2013 | U | once | pixel-level | holdout method | grid search + 10F-CV | n | n | n | n |
| [6] | 2 | 2020 to 2021 | 51.2 m, 20 cm | once | pixel-level | holdout method (stratified+spatial) | U and inspired by Imagenet | y | y | y | y |
| [90] | 3 | 2016 to 2018 | 6.32 m × 2 m | once | pixel-level | holdout method + 10F-CV | U | y | n | n | n |
| [32] | 1 | 2021 | 2.5 m | multi | pixel-level | 10F-CV | None | n | partial | n | n |
| [89] | 1 | 2015 | ∼3 m | U | pixel-level | U | U | n | y | n | n |
| [30] | 1 | 2019 | 1 m | multi and annually | pixel-level | leave-one-out CV | None | y | n | n | n |
| [88] | 1 | 2018 | 1 m × 1.25 m | once | pixel-level | leave-one-out CV | None | n | n | n | n |
| [82] | 1 | 2018 | 4.8 m × 25 m | multi | pixel-level | holdout method | holdout method + U | n | partial | n | n |
| [92] | 1 | 2020 | ∼3 m | multi and annually | pixel-level | holdout method | None | y | partial | n | n |
| [67] | 1 | 2016 | 4.6 m | multi | pixel-level | holdout method | None | n | n | n | n |
| [9] | 3 | 2017 to 2019 | ∼2.96 m | once | pixel-level | holdout method + 5F-CV (stratified) | Optuna framework, CNN inspired by ResNet18 | n | y | U | n |
| [73] | 2 | 2020 to 2021 | 4.05 | multi | pixel-level | 10F-CV (stratified) | None | n | n | n | n |
| present work | 1 | 2021 | 2.5 m | multi | pixel-level | 10F-CV, spatial CV | None | n | partial | y | n |
References
- Saiz-Rubio, V.; Rovira-Más, F. From smart farming towards agriculture 5.0: A review on crop data management. Agronomy 2020, 10, 207. [Google Scholar] [CrossRef]
- Vasisht, D.; Kapetanovic, Z.; Won, J.; Jin, X.; Diego, S.; Chandra, R.; Kapoor, A.; Sinha, S.N.; Sudarshan, M.; Stratman, S. Farmbeats: An iot platform for data-driven agriculture. In Proceedings of the 14th {USENIX} Symposium on Networked Systems Design and Implementation ({NSDI} 17), Boston, MA, USA, 25–27 February 2017; pp. 515–529. [Google Scholar]
- Quan, X.; Doluschitz, R. Unmanned aerial vehicle (UAV) technical applications, standard workflow, and future developments in maize production–water stress detection, weed mapping, nutritional status monitoring and yield prediction. Landtechnik 2021, 76, 36–51. [Google Scholar]
- Filippi, P.; Jones, E.J.; Wimalathunge, N.S.; Somarathna, P.D.; Pozza, L.E.; Ugbaje, S.U.; Jephcott, T.G.; Paterson, S.E.; Whelan, B.M.; Bishop, T.F. An approach to forecast grain crop yield using multi-layered, multi-farm data sets and machine learning. Precis. Agric. 2019, 20, 1015–1029. [Google Scholar] [CrossRef]
- Elijah, O.; Rahman, T.A.; Orikumhi, I.; Leow, C.Y.; Hindia, M.N. An overview of Internet of Things (IoT) and data analytics in agriculture: Benefits and challenges. IEEE Internet Things J. 2018, 5, 3758–3773. [Google Scholar] [CrossRef]
- Baghdasaryan, L.; Melikbekyan, R.; Dolmajain, A.; Hobbs, J. Deep density estimation based on multi-spectral remote sensing data for in-field crop yield forecasting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 2014–2023. [Google Scholar]
- Yang, Q.; Shi, L.; Han, J.; Zha, Y.; Zhu, P. Deep convolutional neural networks for rice grain yield estimation at the ripening stage using UAV-based remotely sensed images. Field Crop. Res. 2019, 235, 142–153. [Google Scholar] [CrossRef]
- Kharel, T.P.; Maresma, A.; Czymmek, K.J.; Oware, E.K.; Ketterings, Q.M. Combining spatial and temporal corn silage yield variability for management zone development. Agron. J. 2019, 111, 2703–2711. [Google Scholar] [CrossRef]
- Danilevicz, M.F.; Bayer, P.E.; Boussaid, F.; Bennamoun, M.; Edwards, D. Maize yield prediction at an early developmental stage using multispectral images and genotype data for preliminary hybrid selection. Remote Sens. 2021, 13, 3976. [Google Scholar] [CrossRef]
- Cheng, T.; Zhu, Y.; Li, D.; Yao, X.; Zhou, K. Hyperspectral Remote Sensing of Leaf Nitrogen Concentration in Cereal Crops. In Hyperspectral Indices and Image Classifications for Agriculture and Vegetation: Hyperspectral Remote Sensing of Vegetation, 2nd ed.; Thenkabail, P.S., Lyon, J.G., Huete, A., Eds.; CRC Press: Boca Raton, FL, USA, 2018; Volume 2, Chapter 6. [Google Scholar]
- Ortenberg, F. Hyperspectral Sensor Characteristics: Airborne, Spaceborne, Hand-Held, and Truck-Mounted; Integration of Hyperspectral Data with LiDAR. In Fundamentals, Sensor Systems, Spectral Libraries, and Data Mining for Vegetation: Hyperspectral Remote Sensing of Vegetation, 2nd ed.; Thenkabail, P.S., Lyon, J.G., Huete, A., Eds.; CRC Press: Boca Raton, FL, USA, 2018; Volume 1, Chapter 2. [Google Scholar]
- Jeffries, G.R.; Griffin, T.S.; Fleisher, D.H.; Naumova, E.N.; Koch, M.; Wardlow, B.D. Mapping sub-field maize yields in Nebraska, USA by combining remote sensing imagery, crop simulation models, and machine learning. Precis. Agric. 2019, 21, 678–694. [Google Scholar] [CrossRef]
- Sibley, A.M.; Grassini, P.; Thomas, N.E.; Cassman, K.G.; Lobell, D.B. Testing remote sensing approaches for assessing yield variability among maize fields. Agron. J. 2014, 106, 24–32. [Google Scholar] [CrossRef]
- Canata, T.F.; Wei, M.C.F.; Maldaner, L.F.; Molin, J.P. Sugarcane Yield Mapping Using High-Resolution Imagery Data and Machine Learning Technique. Remote Sens. 2021, 13, 232. [Google Scholar] [CrossRef]
- Kharel, T.P.; Ashworth, A.J.; Owens, P.R.; Buser, M. Spatially and temporally disparate data in systems agriculture: Issues and prospective solutions. Agron. J. 2020, 112, 4498–4510. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Niu, Y.; Han, W. Mapping maize water stress based on UAV multispectral remote sensing. Remote Sens. 2019, 11, 605. [Google Scholar] [CrossRef]
- Deng, L.; Mao, Z.; Li, X.; Hu, Z.; Duan, F.; Yan, Y. UAV-based multispectral remote sensing for precision agriculture: A comparison between different cameras. Isprs J. Photogramm. Remote Sens. 2018, 146, 124–136. [Google Scholar] [CrossRef]
- Marcial-Pablo, M.d.J.; Gonzalez-Sanchez, A.; Jimenez-Jimenez, S.I.; Ontiveros-Capurata, R.E.; Ojeda-Bustamante, W. Estimation of vegetation fraction using RGB and multispectral images from UAV. Int. J. Remote Sens. 2019, 40, 420–438. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Kulbacki, M.; Segen, J.; Knieć, W.; Klempous, R.; Kluwak, K.; Nikodem, J.; Kulbacka, J.; Serester, A. Survey of drones for agriculture automation from planting to harvest. In Proceedings of the 2018 IEEE 22nd International Conference on Intelligent Engineering Systems (INES), Las Palmas de Gran Canaria, Spain, 21–23 June 2018; pp. 000353–000358. [Google Scholar]
- Zhou, X.; Kono, Y.; Win, A.; Matsui, T.; Tanaka, T.S. Predicting within-field variability in grain yield and protein content of winter wheat using UAV-based multispectral imagery and machine learning approaches. Plant Prod. Sci. 2021, 24, 137–151. [Google Scholar] [CrossRef]
- Dilmurat, K.; Sagan, V.; Moose, S. AI-driven maize yield forecasting using unmanned aerial vehicle-based hyperspectral and LiDAR data fusion. Isprs Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 3, 193–199. [Google Scholar] [CrossRef]
- Maresma, A.; Chamberlain, L.; Tagarakis, A.; Kharel, T.; Godwin, G.; Czymmek, K.J.; Shields, E.; Ketterings, Q.M. Accuracy of NDVI-derived corn yield predictions is impacted by time of sensing. Comput. Electron. Agric. 2020, 169, 105236. [Google Scholar] [CrossRef]
- Khanal, S.; Fulton, J.; Klopfenstein, A.; Douridas, N.; Shearer, S. Integration of high resolution remotely sensed data and machine learning techniques for spatial prediction of soil properties and corn yield. Comput. Electron. Agric. 2018, 153, 213–225. [Google Scholar] [CrossRef]
- Qiao, M.; He, X.; Cheng, X.; Li, P.; Luo, H.; Zhang, L.; Tian, Z. Crop yield prediction from multi-spectral, multi-temporal remotely sensed imagery using recurrent 3D convolutional neural networks. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102436. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Yang, B.; Zhu, W.; Rezaei, E.E.; Li, J.; Sun, Z.; Zhang, J. The Optimal Phenological Phase of Maize for Yield Prediction with High-Frequency UAV Remote Sensing. Remote Sens. 2022, 14, 1559. [Google Scholar] [CrossRef]
- Serele, C.Z.; Gwyn, Q.H.J.; Boisvert, J.B.; Pattey, E.; McLaughlin, N.; Daoust, G. Corn yield prediction with artificial neural network trained using airborne remote sensing and topographic data. In Proceedings of the IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No. 00CH37120). IEEE, Honolulu, HI, USA, 24–28 July 2000; Volume 1, pp. 384–386. [Google Scholar]
- Guo, Y.; Zhang, X.; Chen, S.; Wang, H.; Jayavelu, S.; Cammarano, D.; Fu, Y. Integrated UAV-Based Multi-Source Data for Predicting Maize Grain Yield Using Machine Learning Approaches. Remote Sens. 2022, 14, 6290. [Google Scholar] [CrossRef]
- Sunoj, S.; Cho, J.; Guinness, J.; van Aardt, J.; Czymmek, K.J.; Ketterings, Q.M. Corn grain yield prediction and mapping from Unmanned Aerial System (UAS) multispectral imagery. Remote Sens. 2021, 13, 3948. [Google Scholar] [CrossRef]
- Lyle, G.; Bryan, B.A.; Ostendorf, B. Post-processing methods to eliminate erroneous grain yield measurements: Review and directions for future development. Precis. Agric. 2014, 15, 377–402. [Google Scholar] [CrossRef]
- Killeen, P.; Kiringa, I.; Yeap, T. Corn Grain Yield Prediction Using UAV-based High Spatiotemporal Resolution Multispectral Imagery. In Proceedings of the 2022 IEEE International Conference on Data Mining Workshops (ICDMW), Orlando, FL, USA, 28 November–1 December 2022; pp. 1054–1062. [Google Scholar]
- Semivariogram and Covariance Functions. Available online: https://pro.arcgis.com/en/pro-app/latest/help/analysis/geostatistical-analyst/semivariogram-and-covariance-functions.htm (accessed on 10 September 2021).
- Chu Su, P. Statistical Geocomputing: Spatial Outlier Detection in Precision Agriculture. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2011. [Google Scholar]
- Whelan, B.; McBratney, A.; Viscarra Rossel, R. Spatial prediction for precision agriculture. In Proceedings of the Third International Conference on Precision Agriculture, Minnesota, MN, USA, 23–26 June 1996; Wiley Online Library: Hoboken, NJ, USA, 1996; pp. 331–342. [Google Scholar]
- Whelan, B.; McBratney, A.; Minasny, B. Vesper 1.5–spatial prediction software for precision agriculture. In Proceedings of the Precision Agriculture, Proc. 6th Int. Conf. on Precision Agriculture, ASA/CSSA/SSSA, Madison, WI, USA, 16–19 July 2000; Citeseer: Forest Grove, OR, USA, 2002; Volume 179. [Google Scholar]
- Vallentin, C.; Dobers, E.S.; Itzerott, S.; Kleinschmit, B.; Spengler, D. Delineation of management zones with spatial data fusion and belief theory. Precis. Agric. 2020, 21, 802–830. [Google Scholar] [CrossRef]
- Griffin, T.W. The Spatial Analysis of Yield Data. In Geostatistical Applications for Precision Agriculture; Margareth, O.A., Ed.; Springer Science & Business Media: Dordrecht, Netherlands, 2010; Chapter 4. [Google Scholar]
- Jeong, J.H.; Resop, J.P.; Mueller, N.D.; Fleisher, D.H.; Yun, K.; Butler, E.E.; Timlin, D.J.; Shim, K.M.; Gerber, J.S.; Reddy, V.R.; et al. Random forests for global and regional crop yield predictions. PLoS ONE 2016, 11, e0156571. [Google Scholar] [CrossRef]
- Hawinkel, S.; De Meyer, S.; Maere, S. Spatial regression models for field trials: A comparative study and new ideas. Front. Plant Sci. 2022, 13, 858711. [Google Scholar] [CrossRef]
- Ruß, G.; Brenning, A. Data mining in precision agriculture: Management of spatial information. In Proceedings of the International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems, Dortmund, Germany, 28 June–2 July 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 350–359. [Google Scholar]
- Salazar, J.J.; Garland, L.; Ochoa, J.; Pyrcz, M.J. Fair train-test split in machine learning: Mitigating spatial autocorrelation for improved prediction accuracy. J. Pet. Sci. Eng. 2022, 209, 109885. [Google Scholar] [CrossRef]
- Schratz, P.; Muenchow, J.; Iturritxa, E.; Richter, J.; Brenning, A. Hyperparameter tuning and performance assessment of statistical and machine-learning algorithms using spatial data. Ecol. Model. 2019, 406, 109–120. [Google Scholar] [CrossRef]
- Roberts, D.R.; Bahn, V.; Ciuti, S.; Boyce, M.S.; Elith, J.; Guillera-Arroita, G.; Hauenstein, S.; Lahoz-Monfort, J.J.; Schröder, B.; Thuiller, W.; et al. Cross-validation strategies for data with temporal, spatial, hierarchical, or phylogenetic structure. Ecography 2017, 40, 913–929. [Google Scholar] [CrossRef]
- Ramezan, C.A.; Warner, T.A.; Maxwell, A.E. Evaluation of sampling and cross-validation tuning strategies for regional-scale machine learning classification. Remote Sens. 2019, 11, 185. [Google Scholar] [CrossRef]
- Wadoux, A.M.C.; Heuvelink, G.B.; De Bruin, S.; Brus, D.J. Spatial cross-validation is not the right way to evaluate map accuracy. Ecol. Model. 2021, 457, 109692. [Google Scholar] [CrossRef]
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving performance of spatio-temporal machine learning models using forward feature selection and target-oriented validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
- Nikparvar, B.; Thill, J.C. Machine learning of spatial data. Isprs Int. J. Geo-Inf. 2021, 10, 600. [Google Scholar] [CrossRef]
- Kelleher, J.D.; Mac Namee, B.; D’Arcy, A. Fundamentals of Machine Learning for Predictive Analytics; The MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Beigaitė, R.; Mechenich, M.; Žliobaitė, I. Spatial Cross-Validation for Globally Distributed Data. In Proceedings of the International Conference on Discovery Science, Montpellier, France, 10–12 October 2022; Springer: Cham, Germany, 2022; pp. 127–140. [Google Scholar]
- Barbosa, A.; Trevisan, R.; Hovakimyan, N.; Martin, N.F. Modeling yield response to crop management using convolutional neural networks. Comput. Electron. Agric. 2020, 170, 105197. [Google Scholar] [CrossRef]
- Barbosa, A.; Marinho, T.; Martin, N.; Hovakimyan, N. Multi-Stream CNN for Spatial Resource Allocation: A Crop Management Application. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Davis, I.C.; Wilkinson, G.G. Crop yield prediction using multipolarization radar and multitemporal visible/infrared imagery. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology Viii, Stockholm, Sweden, 11–13 September 2006; Volume 6359, pp. 134–145. [Google Scholar]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Hartling, S.; Esposito, F.; Fritschi, F.B. Soybean yield prediction from UAV using multimodal data fusion and deep learning. Remote Sens. Environ. 2020, 237, 111599. [Google Scholar] [CrossRef]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep gaussian process for crop yield prediction based on remote sensing data. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Bose, P.; Kasabov, N.K.; Bruzzone, L.; Hartono, R.N. Spiking neural networks for crop yield estimation based on spatiotemporal analysis of image time series. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6563–6573. [Google Scholar] [CrossRef]
- Nevavuori, P.; Narra, N.; Linna, P.; Lipping, T. Crop yield prediction using multitemporal UAV data and spatio-temporal deep learning models. Remote Sens. 2020, 12, 4000. [Google Scholar] [CrossRef]
- MicaSense RedEdge-M Multispectral Camera User Manual. Available online: https://www.geotechenv.com/Manuals/Leptron_Manuals/RedEdge-M_User_Manual.pdf (accessed on 3 October 2022).
- Lee, C. Corn Growth and Development. Available online: https://graincrops.ca.uky.edu/files/corngrowthstages_2011.pdf (accessed on 23 January 2024).
- Determining Corn Growth Stages. Available online: https://www.dekalbasgrowdeltapine.com/en-us/agronomy/corn-growth-stages-and-gdu-requirements.html (accessed on 15 October 2020).
- Predict Leaf Stage Development in Corn Using Thermal Time. Available online: https://www.agry.purdue.edu/ext/corn/news/timeless/VStagePrediction.html (accessed on 5 May 2023).
- Gilmore, E., Jr.; Rogers, J. Heat units as a method of measuring maturity in corn 1. Agron. J. 1958, 50, 611–615. [Google Scholar] [CrossRef]
- Heat Unit Concepts Related to Corn Development. Available online: https://www.agry.purdue.edu/ext/corn/news/timeless/heatunits.html (accessed on 4 December 2023).
- Abendroth, L.J.; Elmore, R.W.; Boyer, M.J.; Marlay, S.K. Understanding corn development: A key for successful crop management. In Proceedings of the Integrated Crop Management Conference, Ames, IA, USA, 1–2 December 2010. [Google Scholar]
- Monsanto Company. Corn Growth Stages and GDU Requirements. In Agronomic Spotlight; Monsanto Company: St. Louis, MO, USA, 2015. [Google Scholar]
- Oglesby, C.; Fox, A.A.; Singh, G.; Dhillon, J. Predicting In-Season Corn Grain Yield Using Optical Sensors. Agronomy 2022, 12, 2402. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, J.; Sudduth, K.A.; Kitchen, N.R. Estimation of maize yield and effects of variable-rate nitrogen application using UAV-based RGB imagery. Biosyst. Eng. 2020, 189, 24–35. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Flach, P. Machine Learning: The Art and Science of Algorithms That Make Sense of Data; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Ploton, P.; Mortier, F.; Réjou-Méchain, M.; Barbier, N.; Picard, N.; Rossi, V.; Dormann, C.; Cornu, G.; Viennois, G.; Bayol, N.; et al. Spatial validation reveals poor predictive performance of large-scale ecological mapping models. Nat. Commun. 2020, 11, 4540. [Google Scholar] [CrossRef] [PubMed]
- Sapkota, S.; Paudyal, D.R. Growth Monitoring and Yield Estimation of Maize Plant Using Unmanned Aerial Vehicle (UAV) in a Hilly Region. Sensors 2023, 23, 5432. [Google Scholar] [CrossRef] [PubMed]
- Baio, F.H.R.; Santana, D.C.; Teodoro, L.P.R.; Oliveira, I.C.d.; Gava, R.; de Oliveira, J.L.G.; Silva Junior, C.A.d.; Teodoro, P.E.; Shiratsuchi, L.S. Maize Yield Prediction with Machine Learning, Spectral Variables and Irrigation Management. Remote Sens. 2022, 15, 79. [Google Scholar] [CrossRef]
- Ramos, A.P.M.; Osco, L.P.; Furuya, D.E.G.; Gonçalves, W.N.; Santana, D.C.; Teodoro, L.P.R.; da Silva Junior, C.A.; Capristo-Silva, G.F.; Li, J.; Baio, F.H.R.; et al. A random forest ranking approach to predict yield in maize with uav-based vegetation spectral indices. Comput. Electron. Agric. 2020, 178, 105791. [Google Scholar] [CrossRef]
- Fan, J.; Zhou, J.; Wang, B.; de Leon, N.; Kaeppler, S.M.; Lima, D.C.; Zhang, Z. Estimation of maize yield and flowering time using multi-temporal UAV-based hyperspectral data. Remote Sens. 2022, 14, 3052. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Wu, Z.; Wang, S.; Sun, H.; Senthilnath, J.; Wang, J.; Robin Bryant, C.; Fu, Y. Modified red blue vegetation index for chlorophyll estimation and yield prediction of maize from visible images captured by UAV. Sensors 2020, 20, 5055. [Google Scholar] [CrossRef]
- Kumar, C.; Mubvumba, P.; Huang, Y.; Dhillon, J.; Reddy, K. Multi-Stage Corn Yield Prediction Using High-Resolution UAV Multispectral Data and Machine Learning Models. Agronomy 2023, 13, 1277. [Google Scholar] [CrossRef]
- Herrmann, I.; Bdolach, E.; Montekyo, Y.; Rachmilevitch, S.; Townsend, P.A.; Karnieli, A. Assessment of maize yield and phenology by drone-mounted superspectral camera. Precis. Agric. 2020, 21, 51–76. [Google Scholar] [CrossRef]
- Barzin, R.; Pathak, R.; Lotfi, H.; Varco, J.; Bora, G.C. Use of UAS multispectral imagery at different physiological stages for yield prediction and input resource optimization in corn. Remote Sens. 2020, 12, 2392. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Huete, A. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- García-Martínez, H.; Flores-Magdaleno, H.; Ascencio-Hernández, R.; Khalil-Gardezi, A.; Tijerina-Chávez, L.; Mancilla-Villa, O.R.; Vázquez-Peña, M.A. Corn grain yield estimation from vegetation indices, canopy cover, plant density, and a neural network using multispectral and RGB images acquired with unmanned aerial vehicles. Agriculture 2020, 10, 277. [Google Scholar] [CrossRef]
- Overview of Agriculture Indices. Available online: https://support.micasense.com/hc/en-us/articles/227837307-Overview-of-Agricultural-Indices (accessed on 22 March 2022).
- Wu, G.; Miller, N.D.; De Leon, N.; Kaeppler, S.M.; Spalding, E.P. Predicting Zea mays flowering time, yield, and kernel dimensions by analyzing aerial images. Front. Plant Sci. 2019, 10, 1251. [Google Scholar] [CrossRef]
- Saravia, D.; Salazar, W.; Valqui-Valqui, L.; Quille-Mamani, J.; Porras-Jorge, R.; Corredor, F.A.; Barboza, E.; Vásquez, H.V.; Casas Diaz, A.V.; Arbizu, C.I. Yield Predictions of Four Hybrids of Maize (Zea mays) Using Multispectral Images Obtained from UAV in the Coast of Peru. Agronomy 2022, 12, 2630. [Google Scholar] [CrossRef]
- Uno, Y.; Prasher, S.; Lacroix, R.; Goel, P.; Karimi, Y.; Viau, A.; Patel, R. Artificial neural networks to predict corn yield from compact airborne spectrographic imager data. Comput. Electron. Agric. 2005, 47, 149–161. [Google Scholar] [CrossRef]
- Chatterjee, S.; Adak, A.; Wilde, S.; Nakasagga, S.; Murray, S.C. Cumulative temporal vegetation indices from unoccupied aerial systems allow maize (Zea mays L.) hybrid yield to be estimated across environments with fewer flights. PLoS ONE 2023, 18, e0277804. [Google Scholar] [CrossRef] [PubMed]
- Fathipoor, H.; Arefi, H.; Shah-Hosseini, R.; Moghadam, H. Corn forage yield prediction using unmanned aerial vehicle images at mid-season growth stage. J. Appl. Remote Sens. 2019, 13, 034503. [Google Scholar] [CrossRef]
- Yang, W.; Nigon, T.; Hao, Z.; Paiao, G.D.; Fernández, F.G.; Mulla, D.; Yang, C. Estimation of corn yield based on hyperspectral imagery and convolutional neural network. Comput. Electron. Agric. 2021, 184, 106092. [Google Scholar] [CrossRef]
- Khanal, S.; Klopfenstein, A.; Kushal, K.; Ramarao, V.; Fulton, J.; Douridas, N.; Shearer, S.A. Assessing the impact of agricultural field traffic on corn grain yield using remote sensing and machine learning. Soil Tillage Res. 2021, 208, 104880. [Google Scholar] [CrossRef]
- Adak, A.; Murray, S.C.; Božinović, S.; Lindsey, R.; Nakasagga, S.; Chatterjee, S.; Anderson, S.L.; Wilde, S. Temporal vegetation indices and plant height from remotely sensed imagery can predict grain yield and flowering time breeding value in maize via machine learning regression. Remote Sens. 2021, 13, 2141. [Google Scholar] [CrossRef]
- Vong, C.N.; Conway, L.S.; Zhou, J.; Kitchen, N.R.; Sudduth, K.A. Corn Emergence Uniformity at Different Planting Depths and Yield Estimation Using UAV Imagery. In Proceedings of the 2022 ASABE Annual International Meeting. American Society of Agricultural and Biological Engineers, Houston, TX, USA, 17–20 July 2022; p. 1. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Yang, C.; Everitt, J.H.; Bradford, J.M.; Murden, D. Airborne hyperspectral imagery and yield monitor data for mapping cotton yield variability. Precis. Agric. 2004, 5, 445–461. [Google Scholar] [CrossRef]
- Maresma, Á.; Ariza, M.; Martínez, E.; Lloveras, J.; Martínez-Casasnovas, J.A. Analysis of vegetation indices to determine nitrogen application and yield prediction in maize (Zea mays L.) from a standard UAV service. Remote Sens. 2016, 8, 973. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote estimation of crop chlorophyll content using spectral indices derived from hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 423–437. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Xie, Q.; Dash, J.; Huang, W.; Peng, D.; Qin, Q.; Mortimer, H.; Casa, R.; Pignatti, S.; Laneve, G.; Pascucci, S.; et al. Vegetation Indices Combining the Red and Red-Edge Spectral Information for Leaf Area Index Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1482–1493. [Google Scholar] [CrossRef]
- Zeng, L.; Peng, G.; Meng, R.; Man, J.; Li, W.; Xu, B.; Lv, Z.; Sun, R. Wheat Yield Prediction Based on Unmanned Aerial Vehicles-Collected Red–Green–Blue Imagery. Remote Sens. 2021, 13, 2937. [Google Scholar] [CrossRef]
- Saberioon, M.; Amin, M.; Anuar, A.; Gholizadeh, A.; Wayayok, A.; Khairunniza-Bejo, S. Assessment of rice leaf chlorophyll content using visible bands at different growth stages at both the leaf and canopy scale. Int. J. Appl. Earth Obs. Geoinf. 2014, 32, 35–45. [Google Scholar] [CrossRef]
- Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D.A. Color indices for weed identification under various soil, residue, and lighting conditions. Trans. ASAE 1995, 38, 259–269. [Google Scholar] [CrossRef]
- KAWASHIMA, S.; NAKATANI, M. An Algorithm for Estimating Chlorophyll Content in Leaves Using a Video Camera. Ann. Bot. 1998, 81, 49–54. [Google Scholar] [CrossRef]
- Kataoka, T.; Kaneko, T.; Okamoto, H.; Hata, S. Crop growth estimation system using machine vision. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Port Island, Kobe, Japan, 20–24 July 2003; Volume 2, p. 1079. [Google Scholar]
- Louhaichi, M.; Borman, M.M.; Johnson, D.E. Spatially located platform and aerial photography for documentation of grazing impacts on wheat. Geocarto Int. 2001, 16, 65–70. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
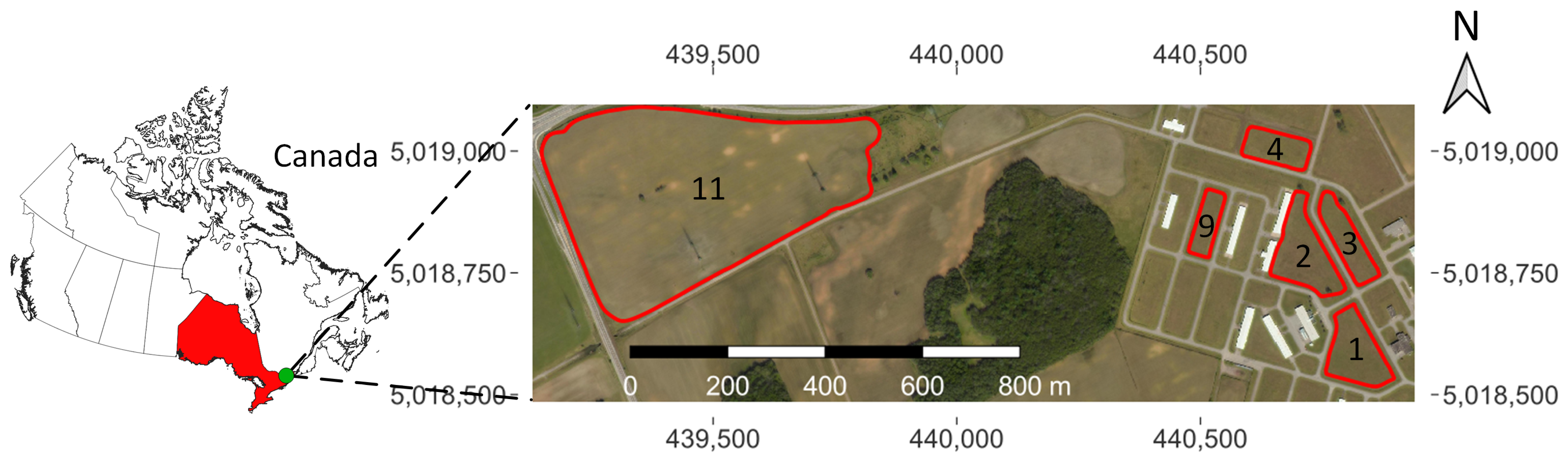



| Herbicide Rates | Fertilizer Rates | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Field |
Tilling
Technique |
Seeding
Rates (kS/ac) |
Acuron 1.5 L +
Crush 0.8 L (gal/ac) |
7-32-23
(lbs/ac) |
40-0-0
5.5 UAS (lbs/ac) |
Urea 60/40
with LP (lbs/ac) |
3-18-18
(gal/ac) |
UAN 32%
(gal/ac) (Side-Dressing) |
LP
(lbs/ac) |
| 1 | CT | 33.7 | 12.3 | 150 | 300 | 0 | 0 | 20.1 | 0 |
| 2 | IST | 33.7 | 12.4 | 125 | 0 | 300 | 10.4 | 20.3 | 4409 |
| 3 | CT | 33.8 | 12.1 | 150 | 300 | 0 | 0 | 20.3 | 4409 |
| 4 1 | CT | 33.6 | 12.2 | 125 | 0 | 0 | 0 | 20.0 | 4409 |
| 9 | IST | 33.8 | 12.4 | 128 | 0 | 327 | 10.6 | 20.0 | 4409 |
| 11 2 | IST | 31.8 | 12.1 | 125 | 0 | 362 | 10.2 | 20.0 | 4409 |
| Field Activity | Date/Period (2021) |
|---|---|
| Tilling 1 | 28 April to 6 May |
| Planting | 14 May |
| Herbicide Spraying | 27 May to 28 May |
| Side-dressing | 23 June to 7 July |
| Harvesting | 5 November to 6 November |
| Image | Acquisition | Flight | |
|---|---|---|---|
| Camera | Type | Period (2021) | Height (m) |
| EVO 2 Gimbal | RGB | 26 May to 8 June | 50 |
| Zenmuse X4S | RGB | 22 June to 1 October | 40 |
| Mica Sense Red-Edge M | MS | 22 June to 1 October | 40 |
| DoY | 145 | 152 | 154 | 157 | 159 | 164–170 | 179–186 | 190–197 | 201 | 204 | 226 | 230 | 237 | 264 |
| AGDD | 191 | 264 | 294 | 360 | 415 | 506–596 | 769–897 | 957–1108 | 1195 | 1249 | 1668 | 1739 | 1923 | 2315 |
| GS | VE | V1 | V2 | V3 | V4 | V5–7 | V8–10 | V11–13 | VT | R1 | R2 | R3 | R4 | R5 |
| Early Season | Mid Season | Late Season | Entire Season | |||||
|---|---|---|---|---|---|---|---|---|
| HRe | LRe | HRe | LRe | HRe | LRe | HRe | LRe | |
| LOFO-CV | OSAVI RDVI SAVI MCARI2 MTVI2 | NDVI | red-edge (raw) NG | red-edge (raw) GCI NG | GCI red-edge (raw) | NG GCI | NG | NG GCI |
| reverse LOFO-CV | MSAVI NDVI MCARI2 | NDVI OSAVI RDVI SAVI | red-edge (raw) NG | red-edge (raw) NG GCI | MCARI TCARI IKAW4 OSAVI | MCARI TCI TCARI | MCARI red-edge (raw) NG | MCARI NG |
| Early Season | Mid Season | Late Season | Entire Season | |||||
|---|---|---|---|---|---|---|---|---|
| HRe | LRe | HRe | LRe | HRe | LRe | HRe | LRe | |
| LOFO-CV | MCARI red (raw) IKAW2 blue (raw) green (raw) | IKAW2 blue (raw) green (raw) b | TCARI IKAW2 IKAW5 ExB | IKAW2 CIVE blue (raw) IPCA | NGRDI IPCA | IKAW2 blue (raw) green (raw) IPCA | IKAW5 ExB IKAW2 | ExB IKAW2 blue (raw) IPCA |
| reverse LOFO-CV | green (raw) blue (raw) b IPCA | IKAW1 green (raw) b IPCA | red (raw) green (raw) blue (raw) | green (raw) b IKAW1 IPCA | ExB IKAW5 red (raw) | blue (raw) WDRVI NDVI red (raw) | ExB green (raw) blue (raw) red (raw) | IPCA green (raw) blue (raw) red (raw) |
| DoY | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Imagery
Type | Model | 146 | 147 | 148 | 149 | 150 | 151 | 159 | 173 | 179 | 193 | 201 | 216 | 223 | 231 | 237 | 245 | 252 | 257 | 273 |
| RGB | LR | 0.08 | 0.14 | 0.19 | 0.15 | 0.15 | 0.14 | 0.01 | 0.12 | 0.20 | 0.37 | 0.20 | 0.07 | 0.07 | 0.04 | 0.02 | 0.03 | 0.08 | 0.12 | 0.23 |
| RGB | RF | 0.02 | 0.08 | 0.07 | 0.08 | 0.06 | 0.07 | 0.01 | 0.03 | 0.03 | 0.15 | 0.06 | 0.01 | 0.03 | 0.02 | 0.01 | 0.02 | 0.03 | 0.04 | 0.08 |
| MS | LR | - | - | - | - | - | - | - | 0.31 | 0.41 | 0.32 | 0.34 | 0.23 | 0.15 | - | 0.14 | 0.11 | - | 0.09 | 0.25 |
| MS | RF | - | - | - | - | - | - | - | 0.08 | 0.14 | 0.11 | 0.14 | 0.10 | 0.07 | - | 0.06 | 0.06 | - | 0.05 | 0.08 |
| Field | ||||||||
|---|---|---|---|---|---|---|---|---|
| Imagery Type | Imagery Resolution | Evaluation Type | 1 | 2 | 3 | 4 | 9 | 11 |
| MS | HRe | SpKF-CV | 0.24 | 0.13 | 0.27 | 0.17 | 0.18 | 0.32 |
| MS | LRe | SpKF-CV | 0.19 | 0.11 | 0.22 | 0.12 | 0.14 | 0.25 |
| RGB | HRe | SpKF-CV | 0.17 | 0.10 | 0.17 | 0.12 | 0.14 | 0.19 |
| RGB | LRe | SpKF-CV | 0.13 | 0.09 | 0.12 | 0.10 | 0.10 | 0.16 |
| MS | HRe | rev-SpKF-CV | 0.13 | 0.13 | 0.25 | 0.18 | 0.05 | 0.26 |
| MS | LRe | rev-SpKF-CV | 0.12 | 0.14 | 0.23 | 0.17 | 0.03 | 0.23 |
| RGB | HRe | rev-SpKF-CV | 0.08 | 0.09 | 0.11 | 0.09 | 0.04 | 0.12 |
| RGB | LRe | rev-SpKF-CV | 0.07 | 0.10 | 0.09 | 0.09 | 0.02 | 0.12 |
| Imagery Processing Step | Imagery Type | Smaller Fields Execution Time (min) | Field 11 Execution Time (h) |
|---|---|---|---|
| Orthomosaic Cropping | RGB | 1.6 | 0.07 |
| Orthomosaic Cropping | MS | 2.2 | 0.26 |
| VI Raster Creation | RGB | 66 | 5.6 |
| VI Raster Creation | MS | 12.1 | 1.1 |
| Yield + Imagery Data Fusion | RGB | 72 | 5.5 |
| Yield + Imagery Data Fusion | MS | 30 | 2.1 |
| Evaluation Method | Imagery Type | LRe Execution Time (min) | HRe Execution Time (min) |
|---|---|---|---|
| KF-CV | RGB | 0.11 | 0.12 |
| KF-CV | MS | 0.12 | 0.13 |
| LOFO-CV and rev-LOFO-CV | RGB | 1.0 | 1.5 |
| LOFO-CV and rev-LOFO-CV | MS | 1.2 | 2.0 |
| SpKF-CV and rev-SpKF-CV | RGB | 5.6 | 8.8 |
| SpKF-CV and rev-SpKF-CV | MS | 11.9 | 20.2 |
| CV Type | Resolution | Field Size | LR Execution Time (s) | RF Execution Time (min) |
|---|---|---|---|---|
| KF-CV | HRe | big | 1 | 6.0 |
| KF-CV | HRe | small | 1 | 1.3 |
| KF-CV | LRe | big | 1 | 6.5 |
| KF-CV | LRe | small | 0 | 1.2 |
| location-only | N/A | big | 0 | 1.4 |
| location-only | N/A | small | 0 | 0.17 |
| LOFO-CV | HRe | all | 0 | 0.28 |
| LOFO-CV | LRe | all | 0 | 0.37 |
| rev-LOFO-CV | HRe | all | 0 | 0.12 |
| rev-LOFO-CV | LRe | all | 0 | 0.13 |
| rev-SpKF-CV | HRe | big | 5 | 1.6 |
| rev-SpKF-CV | HRe | small | 2 | 0.22 |
| rev-SpKF-CV | LRe | big | 2 | 1.3 |
| rev-SpKF-CV | LRe | small | 1 | 0.22 |
| SpKF-CV | HRe | big | 3 | 5.0 |
| SpKF-CV | HRe | small | 2 | 1.1 |
| SpKF-CV | LRe | big | 2 | 5.1 |
| SpKF-CV | LRe | small | 1 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Killeen, P.; Kiringa, I.; Yeap, T.; Branco, P. Corn Grain Yield Prediction Using UAV-Based High Spatiotemporal Resolution Imagery, Machine Learning, and Spatial Cross-Validation. Remote Sens. 2024, 16, 683. https://doi.org/10.3390/rs16040683
Killeen P, Kiringa I, Yeap T, Branco P. Corn Grain Yield Prediction Using UAV-Based High Spatiotemporal Resolution Imagery, Machine Learning, and Spatial Cross-Validation. Remote Sensing. 2024; 16(4):683. https://doi.org/10.3390/rs16040683
Chicago/Turabian StyleKilleen, Patrick, Iluju Kiringa, Tet Yeap, and Paula Branco. 2024. "Corn Grain Yield Prediction Using UAV-Based High Spatiotemporal Resolution Imagery, Machine Learning, and Spatial Cross-Validation" Remote Sensing 16, no. 4: 683. https://doi.org/10.3390/rs16040683
APA StyleKilleen, P., Kiringa, I., Yeap, T., & Branco, P. (2024). Corn Grain Yield Prediction Using UAV-Based High Spatiotemporal Resolution Imagery, Machine Learning, and Spatial Cross-Validation. Remote Sensing, 16(4), 683. https://doi.org/10.3390/rs16040683










