Seismic Landslide Susceptibility Assessment Using Newmark Displacement Based on a Dual-Channel Convolutional Neural Network
Abstract
1. Introduction
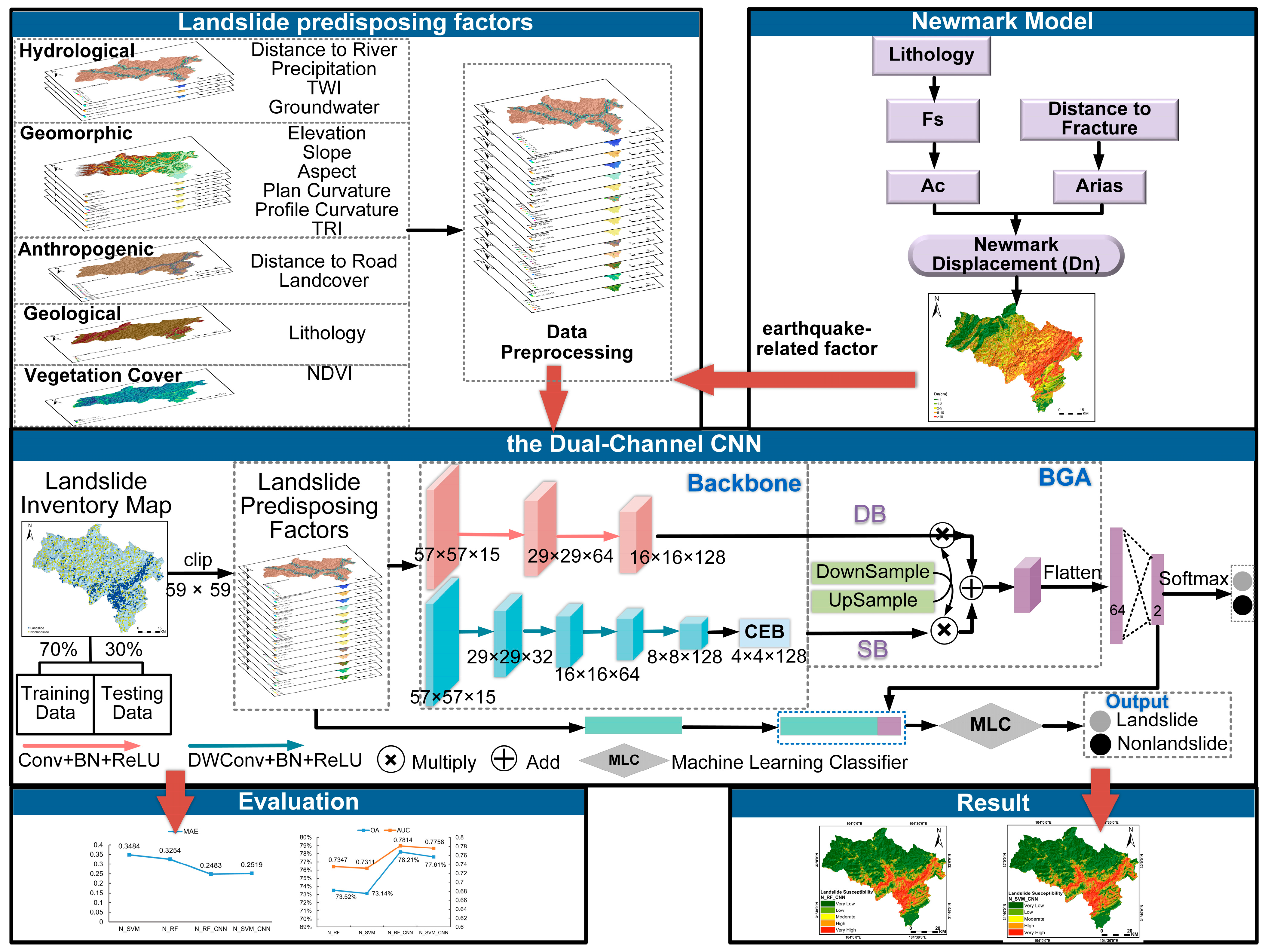
2. Proposed Methods
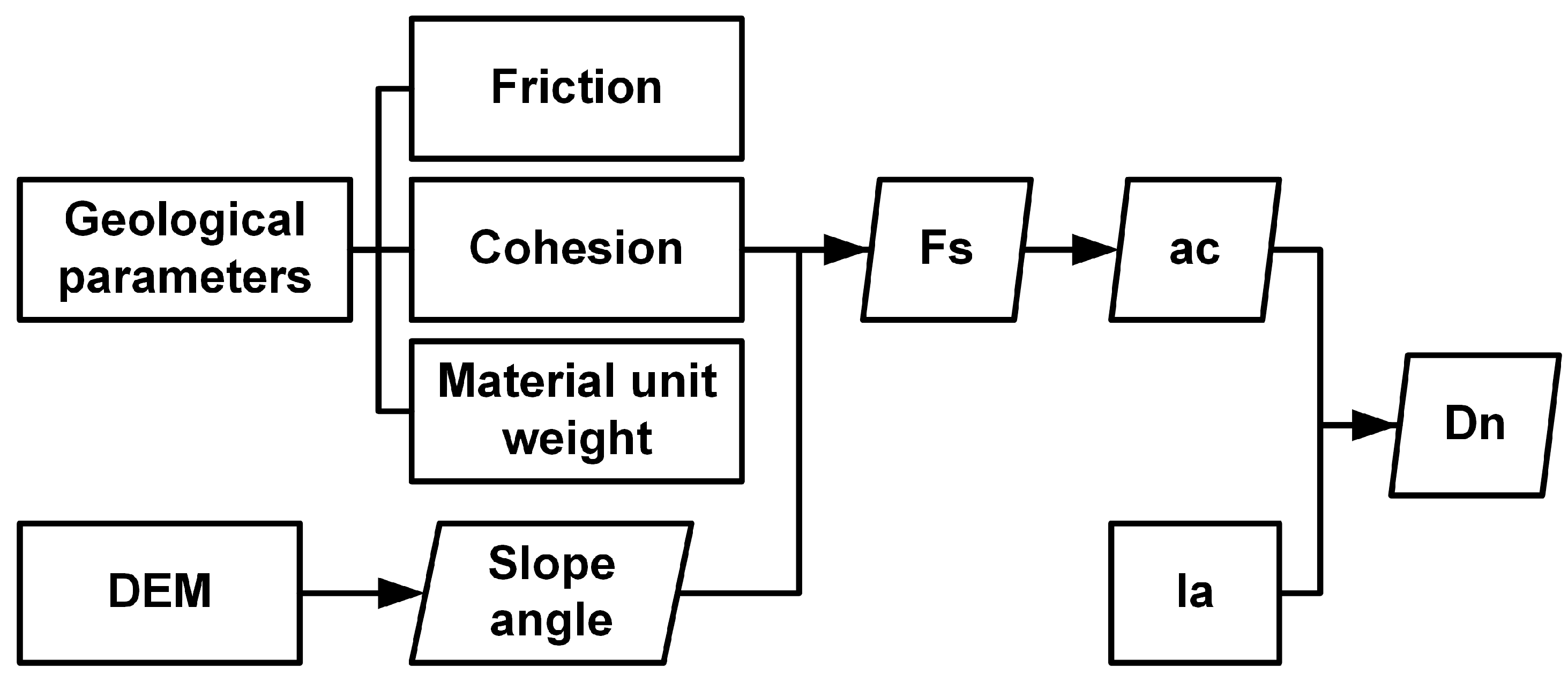
2.1. Newmark Model Theory
2.1.1. Static Factor of Safety (Fs) Calculation
2.1.2. Critical Acceleration (ac) Calculation
2.1.3. Newmark Displacement (Dn) Calculation
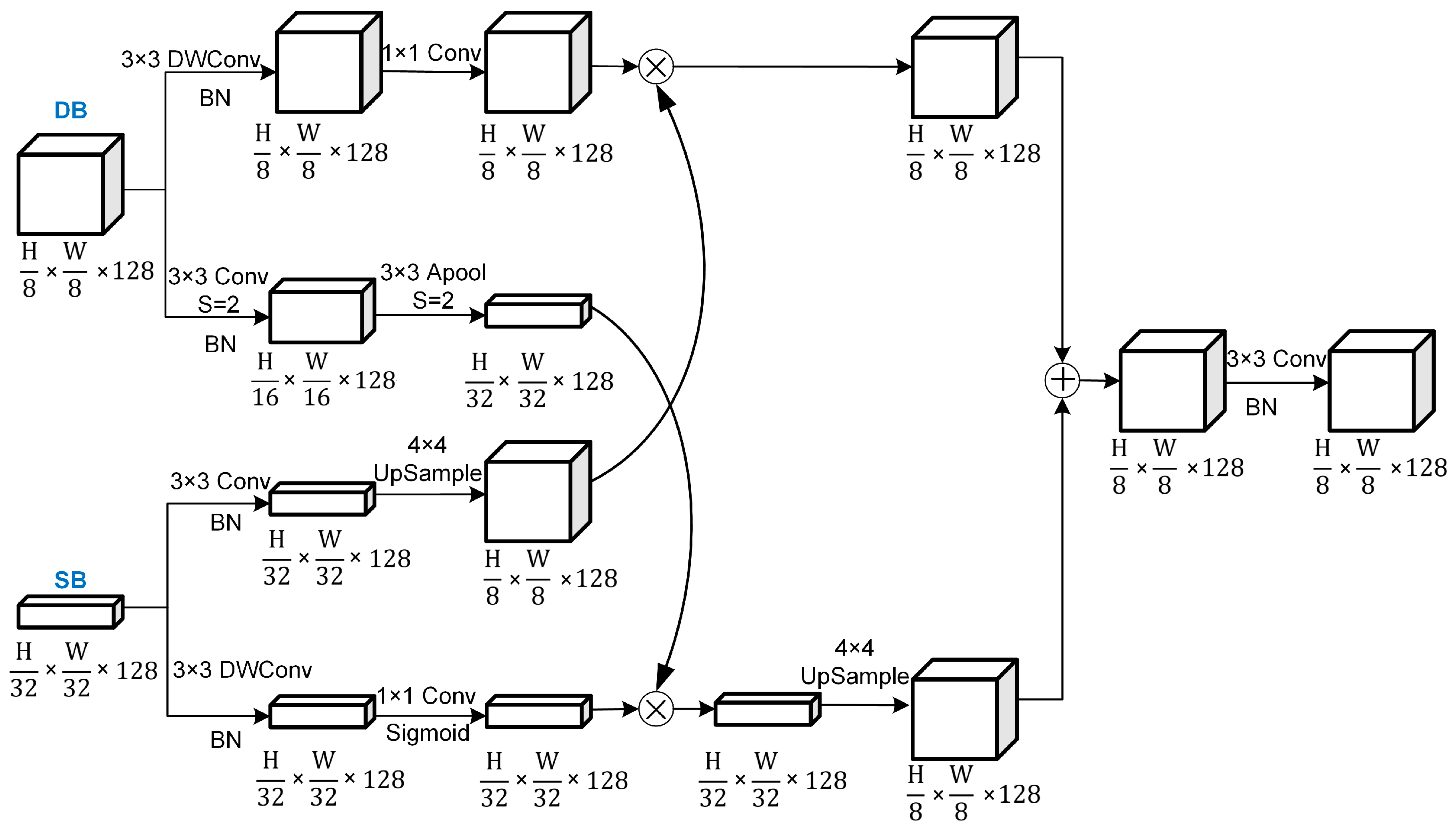
2.2. Dual-Channel CNN
2.3. Evaluation Indicators
3. Study Area and Data
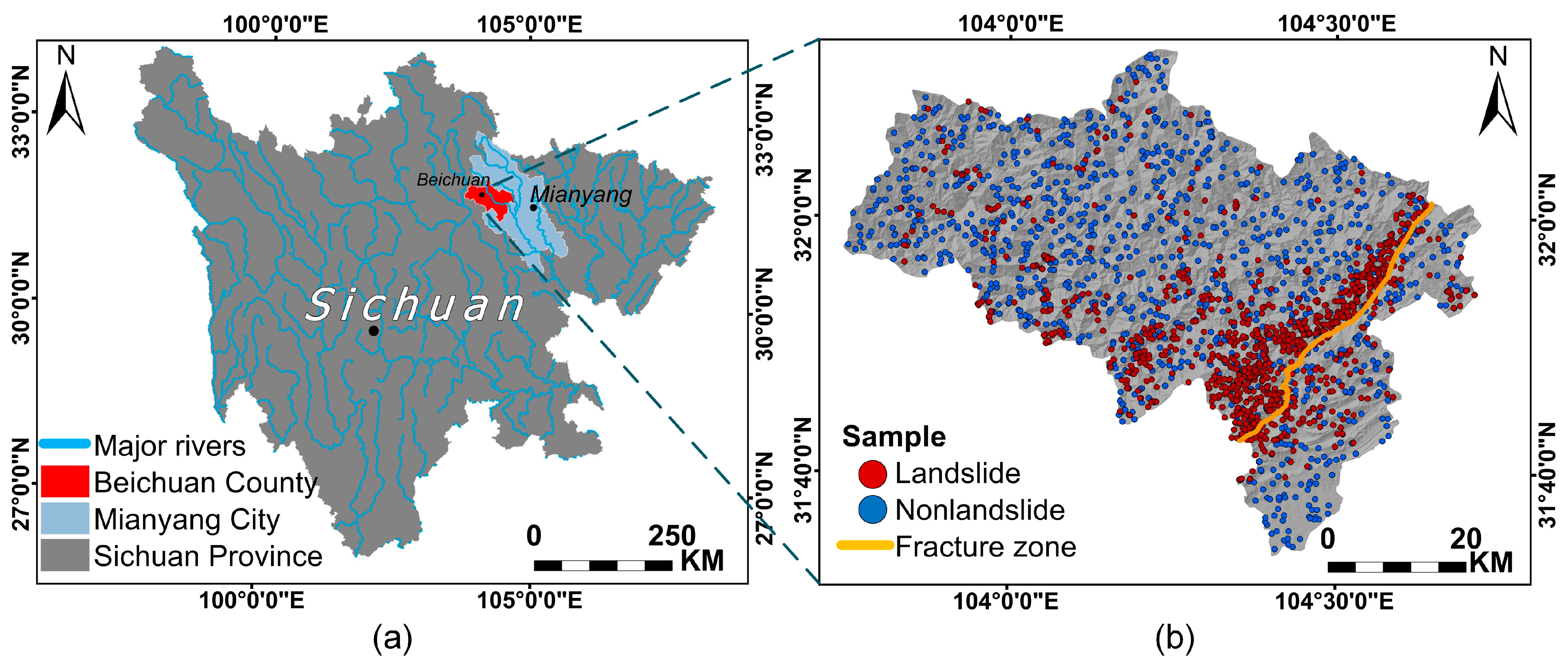
3.1. Study Area
3.2. Landslide Inventory Map
3.3. Landslide Predisposing Factors
4. Experiments and Result
4.1. Multicollinearity Analysis
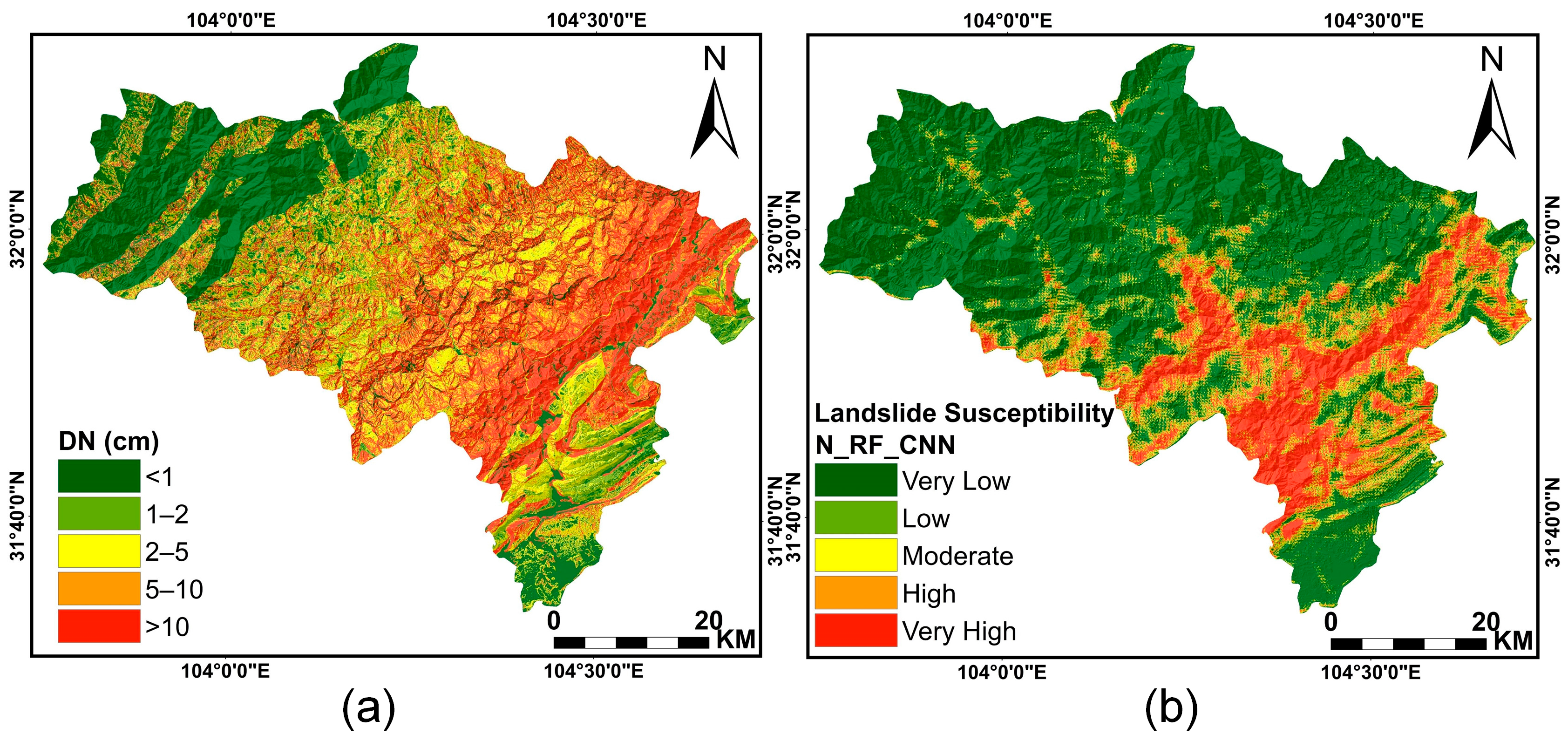
4.2. Seismic Landslide Susceptibility Maps
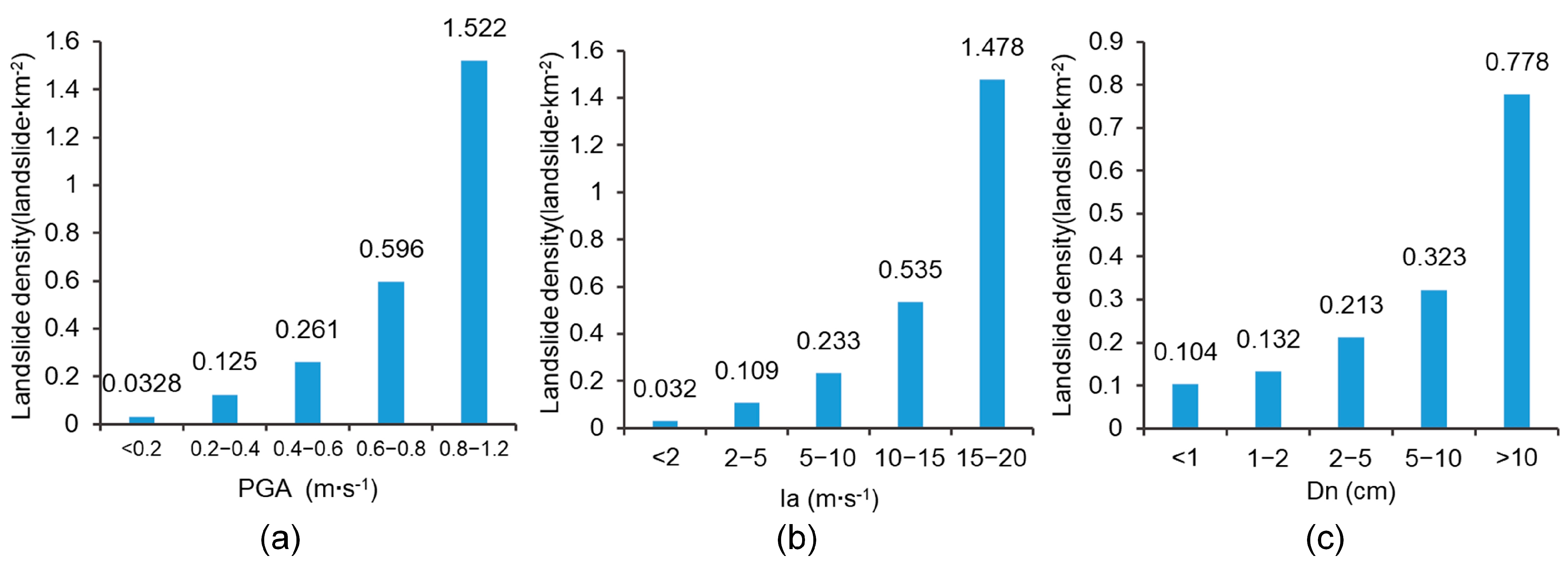
4.2.1. Comparison with Different Earthquake-Related Factors
- These regions are traversed by the Tongkou River and other water systems.
- The terrain in these areas experiences significant fluctuations.
- The locations are situated within valleys and are densely populated with towns. The presence of human-made structures inevitably amplifies the degree of susceptibility.
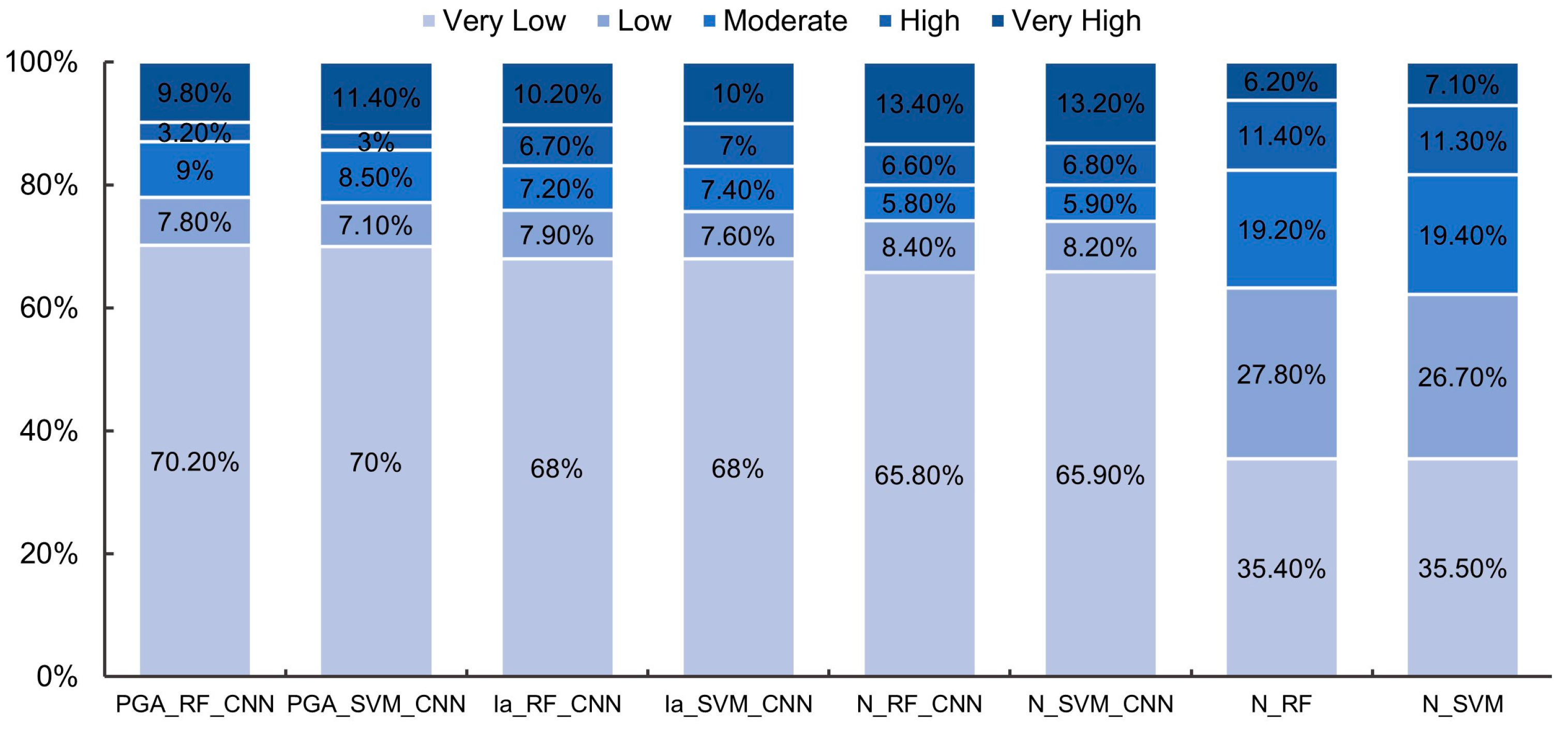
4.2.2. Comparison with Different ML Algorithms
4.3. Evaluation and Validation
4.3.1. Comparison with Different Earthquake-Related Factors
4.3.2. Comparison with Different ML Algorithms
5. Discussion
5.1. Feasibility of Dn as Earthquake-Related Factors for Seismic LSA
5.2. Feasibility of Improved CNN Model for Seismic LSA
5.3. Problems and Improvement Directions
6. Conclusions
- Seismic landslides are the largest secondary hazards after earthquakes. Beichuan was chosen for the study to provide a rapid LSA in similar areas in the future. The seismic landslide susceptibility maps obtained using the methods proposed in this study reveal that the study area exhibits a very high level of landslide susceptibility with a concentrated distribution. The distribution of landslides is mainly influenced by the seismogenic fracture zone, posing a significant threat to human life and property, which requires attention.
- Traditional PGA and Ia contain limited seismic information and fail to fully convey the impact of earthquakes on landslides and may even underestimate the effects. In contrast, Dn can comprehensively convey the mechanical properties of rock–soil mass and the influence of earthquakes.
- It is evident that the improved dual-channel CNN effectively integrates the strengths of both traditional ML and CNNs when compared to traditional ML, providing a new approach for fusing high-level features with multiple predisposing factors in LSA.
- In this paper, a new seismic LSA method is proposed, which can comprehensively take the environmental predisposing factors and the earthquake-related factors into account. Globally, seismic landslides are frequent and have caused enormous damage to people. This method can provide timely and effective support for landslide early warning and landslide risk assessment in post-earthquake disaster areas, thus reducing the losses of people and property.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shafique, M. Spatial and Temporal Evolution of Co-Seismic Landslides after the 2005 Kashmir Earthquake. Geomorphology 2020, 362, 107228. [Google Scholar] [CrossRef]
- Shahabi, H.; Ahmadi, R.; Alizadeh, M.; Hashim, M.; Al-Ansari, N.; Shirzadi, A.; Wolf, I.D.; Ariffin, E.H. Landslide Susceptibility Mapping in a Mountainous Area Using Machine Learning Algorithms. Remote Sens. 2023, 15, 3112. [Google Scholar] [CrossRef]
- Zhao, P.; Masoumi, Z.; Kalantari, M.; Aflaki, M.; Mansourian, A. A GIS-Based Landslide Susceptibility Mapping and Variable Importance Analysis Using Artificial Intelligent Training-Based Methods. Remote Sens. 2022, 14, 211. [Google Scholar] [CrossRef]
- Jin, J.; Cui, Y.; Xu, C.; Zheng, J.; Miao, H. Application of Logistic Regression Model for Hazard Assessment of Landslides Caused by the 2012 Yiliang Ms 5.7 Earthquake in Yunnan Province, China. J. Mt. Sci. 2023, 20, 657–669. [Google Scholar] [CrossRef]
- Mosaffaie, J.; Salehpour Jam, A.; Sarfaraz, F. Landslide Risk Assessment Based on Susceptibility and Vulnerability. Environ. Dev. Sustain. 2023, preview. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, B.; Han, S.; Fan, X.; Zou, T.; Zhou, Z.; Gong, H. Research on Landslide Hazard Spatial Prediction Models Based on Deep Neural Networks: A Case Study of Northwest Sichuan, China. Environ. Earth Sci. 2022, 81, 258. [Google Scholar] [CrossRef]
- Karakas, G.; Kocaman, S.; Gokceoglu, C. Multi-Hazard Susceptibility Assessment with Hybrid Machine Learning Methods for Tut Region (Adiyaman, Turkiye). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-M-1, 529–536. [Google Scholar] [CrossRef]
- Song, Y.; Gong, J.; Gao, S.; Wang, D.; Cui, T.; Li, Y.; Wei, B. Susceptibility Assessment of Earthquake-Induced Landslides Using Bayesian Network: A Case Study in Beichuan, China. Comput. Geosci. 2012, 42, 189–199. [Google Scholar] [CrossRef]
- Li, X.; Xu, W.; Gao, M. Probabilistic Seismic Hazard Analysis Based on Arias Intensity in the North–South Seismic Belt of China. Bull. Seism. Soc. Am. 2022, 112, 1149–1160. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of Earthquakes on Dams and Embankments. Géotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Gupta, K.; Satyam, N. Co-Seismic Landslide Hazard Assessment of Uttarakhand State (India) Based on the Modified Newmark Model. J. Asian Earth Sci. X 2022, 8, 100120. [Google Scholar] [CrossRef]
- Jin, K.P.; Yao, L.K.; Cheng, Q.G.; Xing, A.G. Seismic Landslides Hazard Zoning Based on the Modified Newmark Model: A Case Study from the Lushan Earthquake, China. Nat. Hazards 2019, 99, 493–509. [Google Scholar] [CrossRef]
- Shinoda, M.; Miyata, Y.; Kurokawa, U.; Kondo, K. Regional Landslide Susceptibility Following the 2016 Kumamoto Earthquake Using Back-Calculated Geomaterial Strength Parameters. Landslides 2019, 16, 1497–1516. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide Hazard Mapping at Selangor, Malaysia Using Frequency Ratio and Logistic Regression Models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Shirzadi, A.; Chapi, K.; Shahabi, H.; Solaimani, K.; Kavian, A.; Ahmad, B.B. Rock Fall Susceptibility Assessment along a Mountainous Road: An Evaluation of Bivariate Statistic, Analytical Hierarchy Process and Frequency Ratio. Environ. Earth Sci. 2017, 76, 152. [Google Scholar] [CrossRef]
- Singh, K.; Kumar, V. Hazard Assessment of Landslide Disaster Using Information Value Method and Analytical Hierarchy Process in Highly Tectonic Chamba Region in Bosom of Himalaya. J. Mt. Sci. 2018, 15, 808–824. [Google Scholar] [CrossRef]
- He, Q.; Wang, M.; Liu, K. Rapidly Assessing Earthquake-Induced Landslide Susceptibility on a Global Scale Using Random Forest. Geomorphology 2021, 391, 107889. [Google Scholar] [CrossRef]
- Liu, R.; Li, L.; Pirasteh, S.; Lai, Z.; Yang, X.; Shahabi, H. The Performance Quality of LR, SVM, and RF for Earthquake-Induced Landslides Susceptibility Mapping Incorporating Remote Sensing Imagery. Arab. J. Geosci. 2021, 14, 259. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, H.; Hong, H. A Comparative Study of Composite Kernels for Landslide Susceptibility Mapping: A Case Study in Yongxin County, China. Catena 2019, 183, 104217. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, C.; Nie, R.; Yang, Z.; Li, W.; Dai, X.; Cheng, J.; Zhang, J.; Ma, L.; Fu, X.; et al. A Comparative Analysis of Certainty Factor-Based Machine Learning Methods for Collapse and Landslide Susceptibility Mapping in Wenchuan County, China. Remote Sens. 2022, 14, 3259. [Google Scholar] [CrossRef]
- Castro-Miguel, R.; Legorreta-Paulín, G.; Bonifaz-Alfonzo, R.; Aceves-Quesada, J.F.; Castillo-Santiago, M.Á. Modeling Spatial Landslide Susceptibility in Volcanic Terrains through Continuous Neighborhood Spatial Analysis and Multiple Logistic Regression in La Ciénega Watershed, Nevado de Toluca, Mexico. Nat. Hazards 2022, 113, 767–788. [Google Scholar] [CrossRef]
- Jin, J.; Chen, G.; Meng, X.; Zhang, Y.; Shi, W.; Li, Y.; Yang, Y.; Jiang, W. Prediction of River Damming Susceptibility by Landslides Based on a Logistic Regression Model and InSAR Techniques: A Case Study of the Bailong River Basin, China. Eng. Geol. 2022, 299, 106562. [Google Scholar] [CrossRef]
- Chen, C.; Shen, Z.; Weng, Y.; You, S.; Lin, J.; Li, S.; Wang, K. Modeling Landslide Susceptibility in Forest-Covered Areas in Lin’an, China, Using Logistical Regression, a Decision Tree, and Random Forests. Remote Sens. 2023, 15, 4378. [Google Scholar] [CrossRef]
- Mandal, K.; Saha, S.; Mandal, S. Applying Deep Learning and Benchmark Machine Learning Algorithms for Landslide Susceptibility Modelling in Rorachu River Basin of Sikkim Himalaya, India. Geosci. Front. 2021, 12, 101203. [Google Scholar] [CrossRef]
- Chen, Y.; Ming, D.; Ling, X.; Lv, X.; Zhou, C. Landslide Susceptibility Mapping Using Feature Fusion-Based CPCNN-ML in Lantau Island, Hong Kong. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3625–3639. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, M.; Liu, K. Comparisons of Convolutional Neural Network and Other Machine Learning Methods in Landslide Susceptibility Assessment: A Case Study in Pingwu. Remote Sens. 2023, 15, 798. [Google Scholar] [CrossRef]
- Xi, C.; Han, M.; Hu, X.; Liu, B.; He, K.; Luo, G.; Cao, X. Effectiveness of Newmark-Based Sampling Strategy for Coseismic Landslide Susceptibility Mapping Using Deep Learning, Support Vector Machine, and Logistic Regression. Bull. Eng. Geol. Environ. 2022, 81, 174. [Google Scholar] [CrossRef]
- Wang, Y.; Song, C.; Lin, Q.; Li, J. Occurrence Probability Assessment of Earthquake-Triggered Landslides with Newmark Displacement Values and Logistic Regression: The Wenchuan Earthquake, China. Geomorphology 2016, 258, 108–119. [Google Scholar] [CrossRef]
- GB/T 50218-2014; Ministry of Water Resources of the People’s Republic of China (2014) Standard for Engineering Classification of Rock Masses. Standards Press of China: Beijing, China, 2014. (In Chinese)
- Wang, T.; Wu, S.; Shi, J.; Xin, P. Case Study on Rapid Assessment of Regional Seismic Landslide Hazard Based on Simplified Newmark Displacement Model: Wenchuan MS 8.0 Earthquake. J. Eng. Geol. 2013, 21, 16–24. (In Chinese) [Google Scholar] [CrossRef]
- Jibson, R.W. Regression Models for Estimating Coseismic Landslide Displacement. Eng. Geol. 2007, 91, 209–218. [Google Scholar] [CrossRef]
- Arias, A. Measure of Earthquake Intensity. In Seismic Design for Nuclear Power Plants; Hansen Robert, J., Ed.; Massachusetts Institute of Technology Press: Cambridge, MA, USA, 1970; pp. 438–483. [Google Scholar]
- Wang, X.; Nie, G.; Ma, M. Evaluation Model of Landslide Hazards Induced by the 2008 Wenchuan Earthquake Using Strong Motion Data. Earthq. Sci. 2011, 24, 311–319. [Google Scholar] [CrossRef][Green Version]
- Pham, B.T.; Nguyen-Thoi, T.; Qi, C.; Phong, T.V.; Dou, J.; Ho, L.S.; Le, H.V.; Prakash, I. Coupling RBF Neural Network with Ensemble Learning Techniques for Landslide Susceptibility Mapping. Catena 2020, 195, 104805. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.; Yao, X.; Dai, F. Three (Nearly) Complete Inventories of Landslides Triggered by the May 12, 2008 Wenchuan Mw 7.9 Earthquake of China and Their Spatial Distribution Statistical Analysis. Landslides 2014, 11, 441–461. [Google Scholar] [CrossRef]
- Bui, D.T.; Tsangaratos, P.; Nguyen, V.-T.; Liem, N.V.; Trinh, P.T. Comparing the Prediction Performance of a Deep Learning Neural Network Model with Conventional Machine Learning Models in Landslide Susceptibility Assessment. Catena 2020, 188, 104426. [Google Scholar] [CrossRef]
- Panahi, M.; Gayen, A.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial Prediction of Landslide Susceptibility Using Hybrid Support Vector Regression (SVR) and the Adaptive Neuro-Fuzzy Inference System (ANFIS) with Various Metaheuristic Algorithms. Sci. Total Environ. 2020, 741, 139937. [Google Scholar] [CrossRef]
- Thi Ngo, P.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of Deep Learning Algorithms for National Scale Landslide Susceptibility Mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Xie, J.; Wen, Z.; Gao, M. Characteristics of near-fault vertical and horizontal ground motion from the 2008 Wenchuan earthquake. Chin. J. Ceophysics 2008, 53, 1796–1805. (In Chinese) [Google Scholar]
- Zhang, T.; Zhou, X.P.; Liu, X.F. Reliability Analysis of Slopes Using the Improved Stochastic Response Surface Methods with Multicollinearity. Eng. Geol. 2020, 271, 105617. [Google Scholar] [CrossRef]
- Yuan, R.; Deng, Q.; Cunningham, D.; Han, Z.; Zhang, D.; Zhang, B. Newmark Displacement Model for Landslides Induced by the 2013 Ms 7.0 Lushan Earthquake, China. Front. Earth Sci. 2016, 10, 740–750. [Google Scholar] [CrossRef]
- Gupta, K.; Satyam, N.; Gupta, V. Probabilistic Physical Modelling and Prediction of Regional Seismic Landslide Hazard in Uttarakhand State (India). Landslides 2023, 20, 901–912. [Google Scholar] [CrossRef]
- Peng, D.; Yueren, X.; Qinjian, T.; Weiheng, Z.; Shuang, L. The Spatial Distribution and Attribute Parameter Statistics of Landslides Triggered by the May 12th 2008 MW7. 9 Wenchuan Earthquake. Inst. Geol. China Earthq. Adm. 2020, 34, 29–49. [Google Scholar]
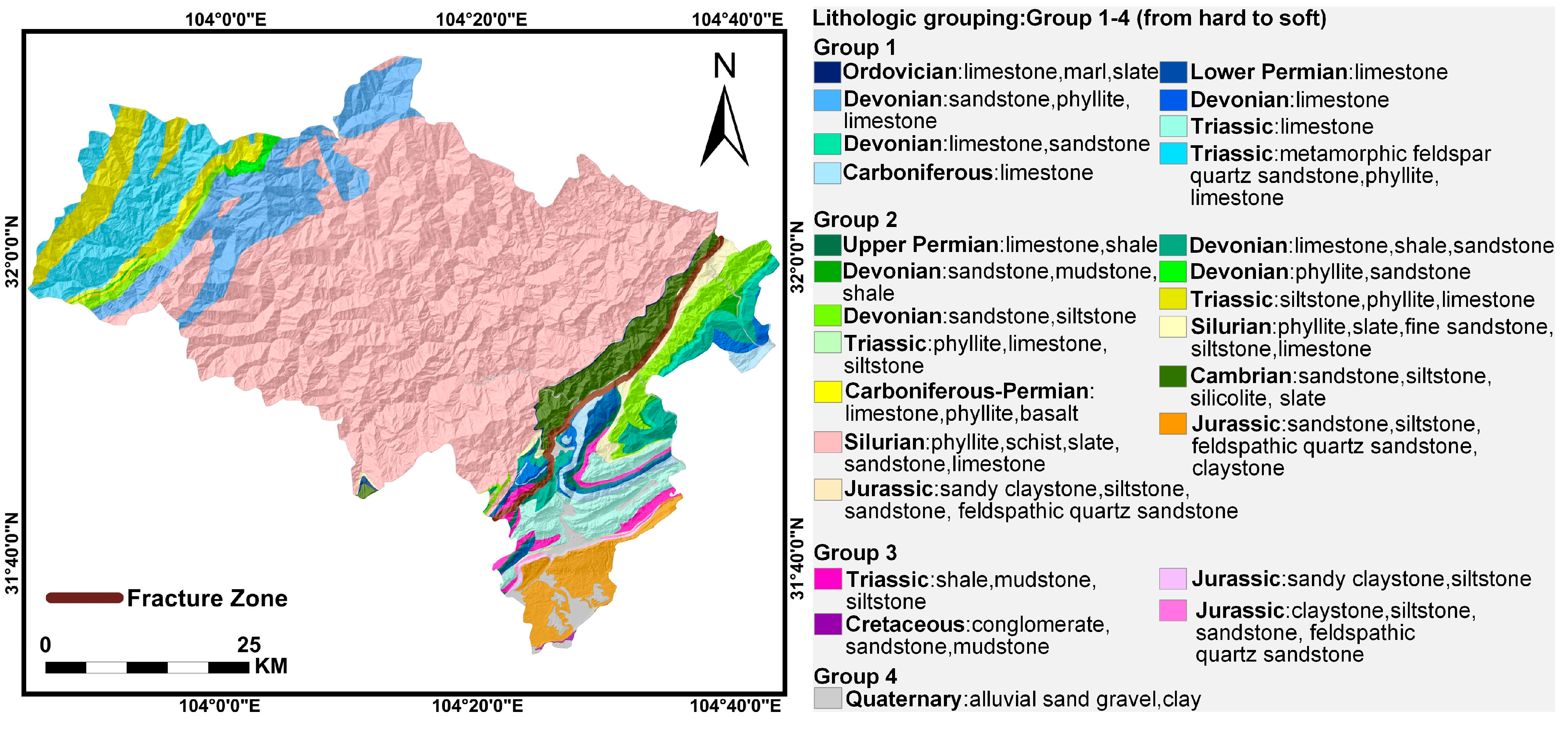




| Group 1 | Group 2 | Group 3 | Group 4 | |
|---|---|---|---|---|
| /KPa | 100 | 80 | 50 | 40 |
| (KN/m3) | 26 | 25 | 22 | 15 |
| /() | 25 | 15 | 12 | 10 |
| Type | Predisposing Factors | Data Source | Time |
|---|---|---|---|
| Hydrological | Distance to river Mean annual precipitation TWI Groundwater | Calculated with the river network CHIRPS Calculated with DEM GRACE-FO Data | 2010 2004–2008 2009 2004–2008 |
| Geomorphic | Elevation Slope Aspect Plan curvature Profile curvature TRI | ASTER GDEM Calculated with DEM Calculated with DEM Calculated with DEM Calculated with DEM Calculated with DEM | 2009 |
| Geological | Lithology | National Geological Library (China) | 2008 |
| Vegetation Cover | NDVI | Geospatial Data Cloud | 2004–2008 |
| Anthropogenic | Distance to road Landcover | Calculated with the road network National Earth System Science Data Center (China) | 2008 |
| Earthquake-related | Newmark displacement (Dn) | - | 2008 |
| Predisposing Factors | TOL | VIF |
|---|---|---|
| Lithology | 0.84 | 1.194 |
| Landcover | 0.64 | 1.557 |
| Mean annual precipitation | 0.59 | 1.695 |
| Elevation | 0.34 | 2.943 |
| NDVI | 0.70 | 1.434 |
| Distance to road | 0.63 | 1.597 |
| Groundwater | 0.93 | 1.072 |
| TRI | 0.73 | 1.365 |
| TWI | 0.76 | 1.309 |
| Distance to river | 0.67 | 1.504 |
| Plan curvature | 0.78 | 1.280 |
| Profile curvature | 0.78 | 1.290 |
| Aspect | 0.96 | 1.040 |
| Slope | 0.93 | 1.074 |
| Dn | 0.74 | 1.323 |
| Very Low | Low | Moderate | High | Very High | |
|---|---|---|---|---|---|
| PGA_RF_CNN | 8% | 7% | 16% | 9% | 60% |
| PGA_SVM_CNN | 9% | 7% | 15% | 8% | 61% |
| Ia_RF_CNN | 5% | 4% | 10% | 17% | 64% |
| Ia_SVM_CNN | 6% | 4% | 8% | 15% | 67% |
| N_RF_CNN | 4% | 4% | 5% | 12% | 75% |
| N_SVM_CNN | 4% | 3% | 5% | 12% | 76% |
| N_RF | 5% | 6% | 13% | 24% | 53% |
| N_SVM | 4% | 7% | 13% | 29% | 47% |
| OA | AUC | MAE | |
|---|---|---|---|
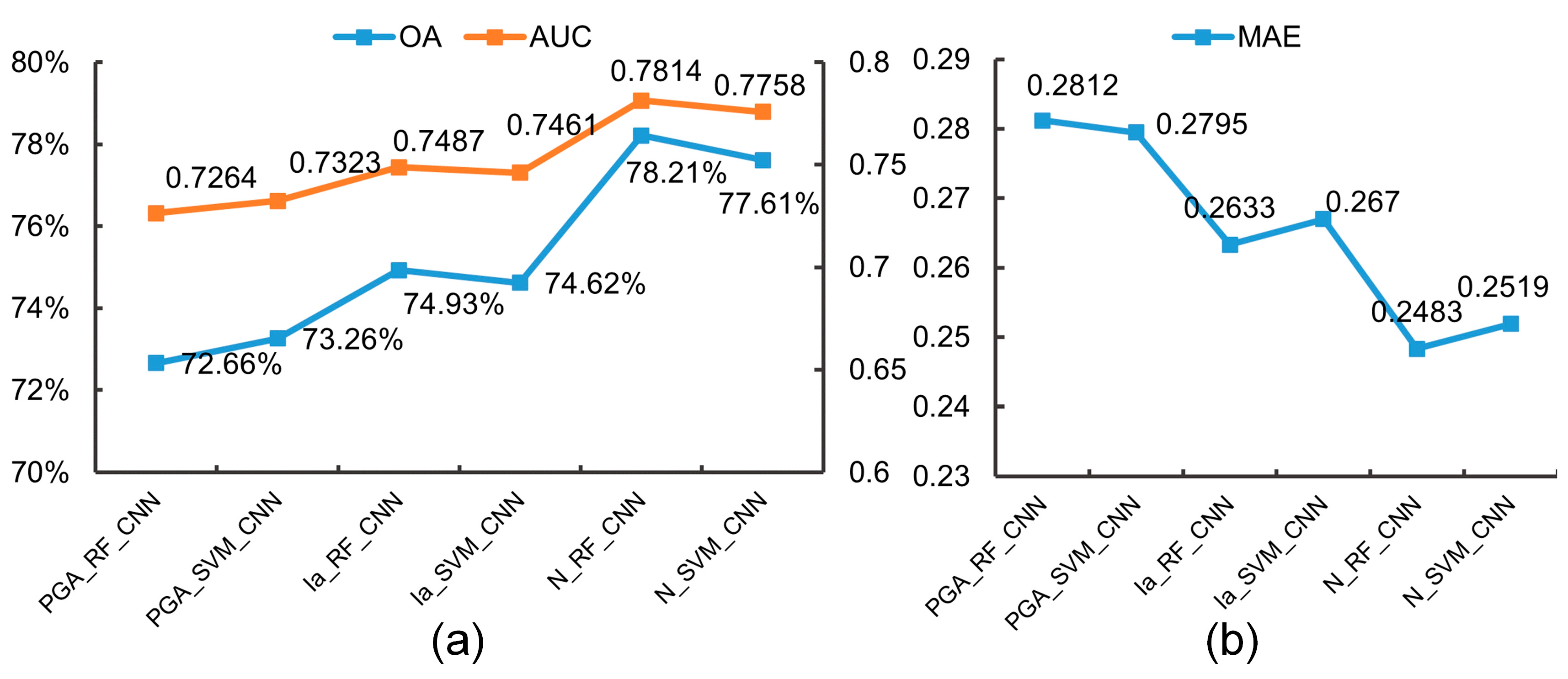
| PGA_RF | 70.39% | 0.7029 | 0.3375 |
| PGA_SVM | 71.81% | 0.7273 | 0.3549 |
| PGA_RF_CNN | 72.66% | 0.7264 | 0.2812 |
| PGA_SVM_CNN | 73.26% | 0.7323 | 0.2795 |
| Ia_RF | 72.45% | 0.7136 | 0.3344 |
| Ia_SVM | 72.36% | 0.7228 | 0.3544 |
| Ia_RF_CNN | 74.93% | 0.7487 | 0.2633 |
| Ia_SVM_CNN | 74.62% | 0.7461 | 0.267 |
| N_RF | 73.52% | 0.7347 | 0.3254 |
| N_SVM | 73.14% | 0.7311 | 0.3484 |
| N_RF_CNN | 78.21% | 0.7814 | 0.2483 |
| N_SVM_CNN | 77.61% | 0.7758 | 0.2519 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Ming, D.; Zhang, L.; Niu, Y.; Chen, Y. Seismic Landslide Susceptibility Assessment Using Newmark Displacement Based on a Dual-Channel Convolutional Neural Network. Remote Sens. 2024, 16, 566. https://doi.org/10.3390/rs16030566
Li Y, Ming D, Zhang L, Niu Y, Chen Y. Seismic Landslide Susceptibility Assessment Using Newmark Displacement Based on a Dual-Channel Convolutional Neural Network. Remote Sensing. 2024; 16(3):566. https://doi.org/10.3390/rs16030566
Chicago/Turabian StyleLi, Yan, Dongping Ming, Liang Zhang, Yunyun Niu, and Yangyang Chen. 2024. "Seismic Landslide Susceptibility Assessment Using Newmark Displacement Based on a Dual-Channel Convolutional Neural Network" Remote Sensing 16, no. 3: 566. https://doi.org/10.3390/rs16030566
APA StyleLi, Y., Ming, D., Zhang, L., Niu, Y., & Chen, Y. (2024). Seismic Landslide Susceptibility Assessment Using Newmark Displacement Based on a Dual-Channel Convolutional Neural Network. Remote Sensing, 16(3), 566. https://doi.org/10.3390/rs16030566






