Exploring the Limits of Species Identification via a Convolutional Neural Network in a Complex Forest Scene through Simulated Imaging Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
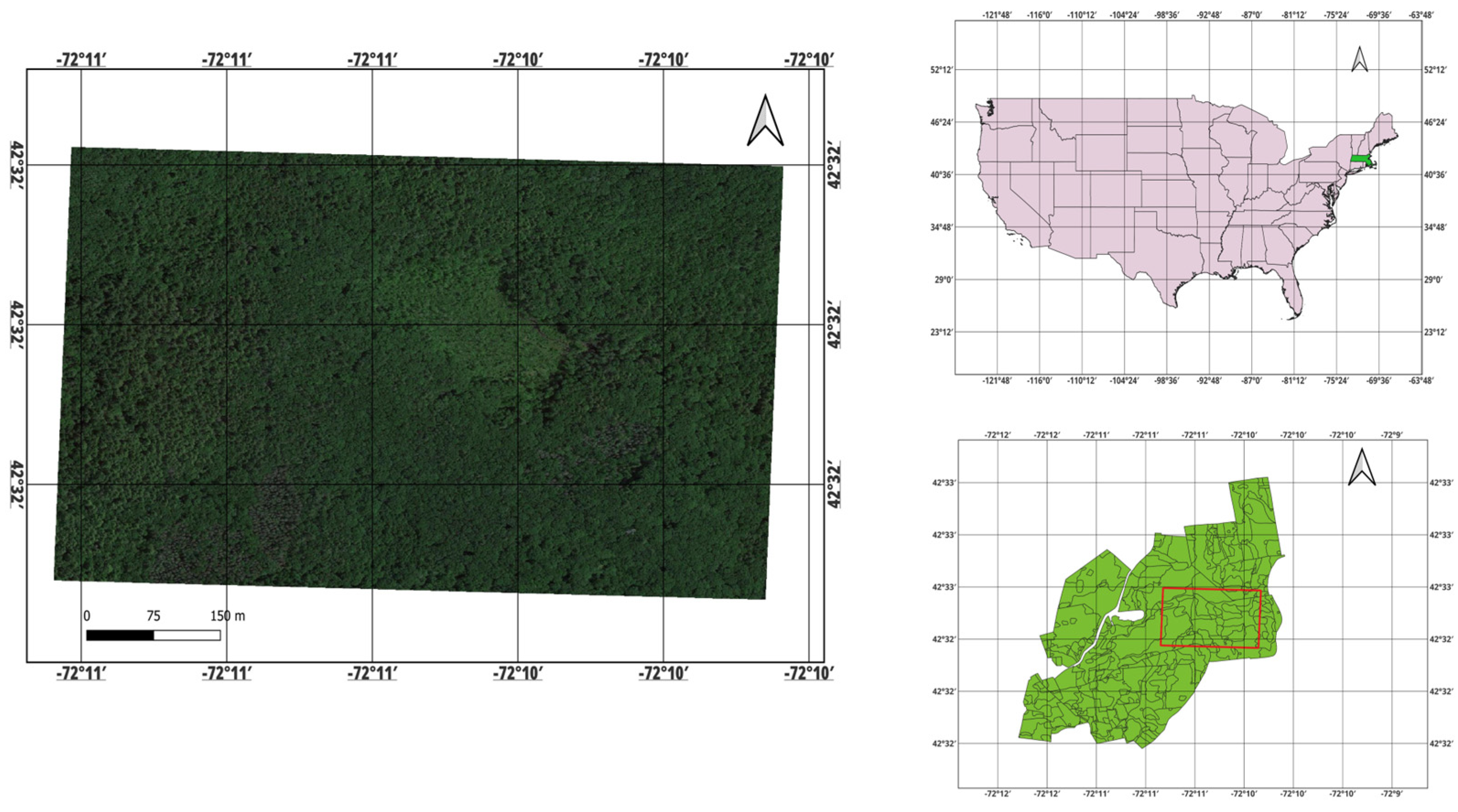
2.1. Study Area
Field Data in the Study Area
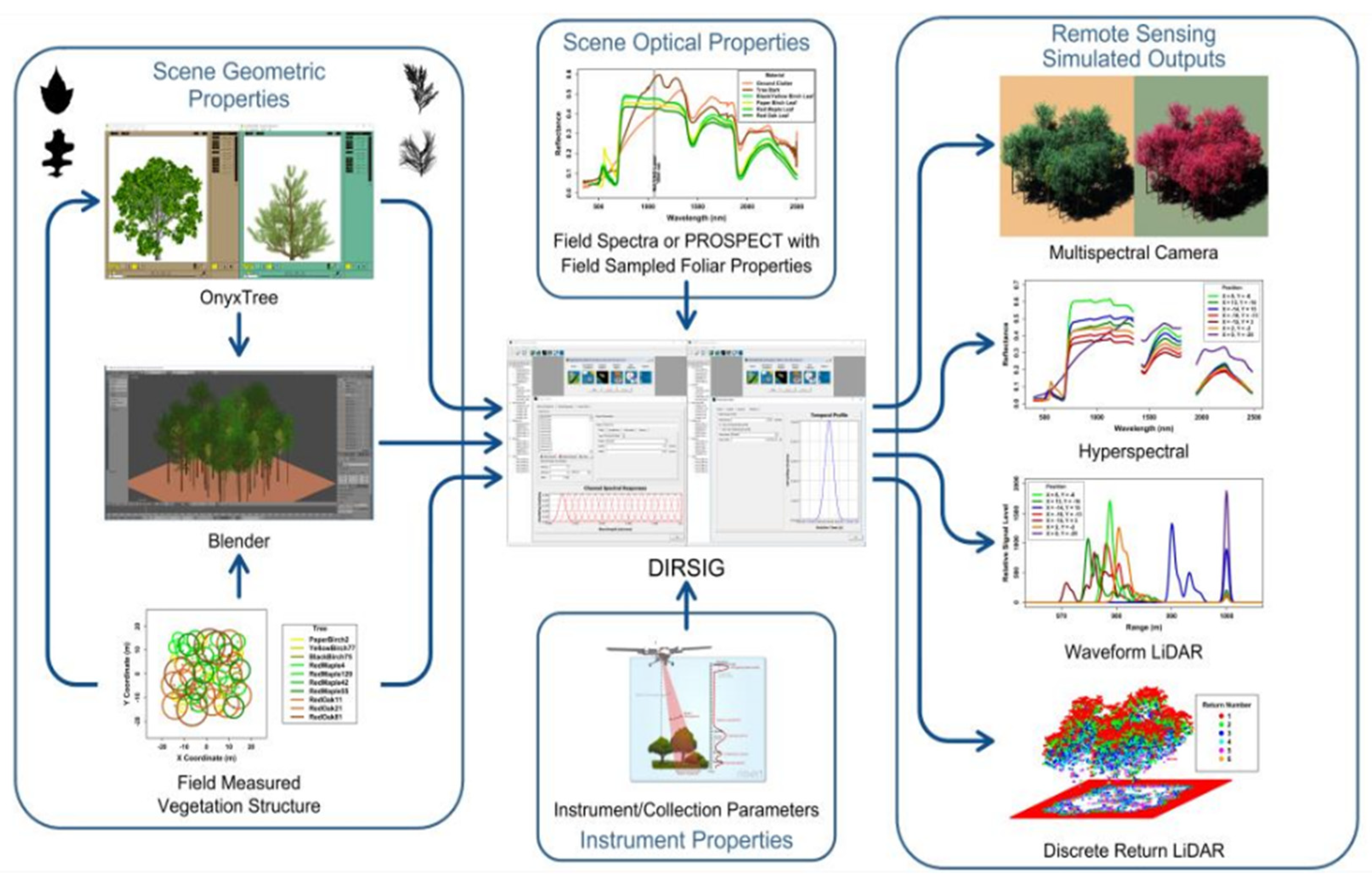
2.2. DIRSIG Simulation Development
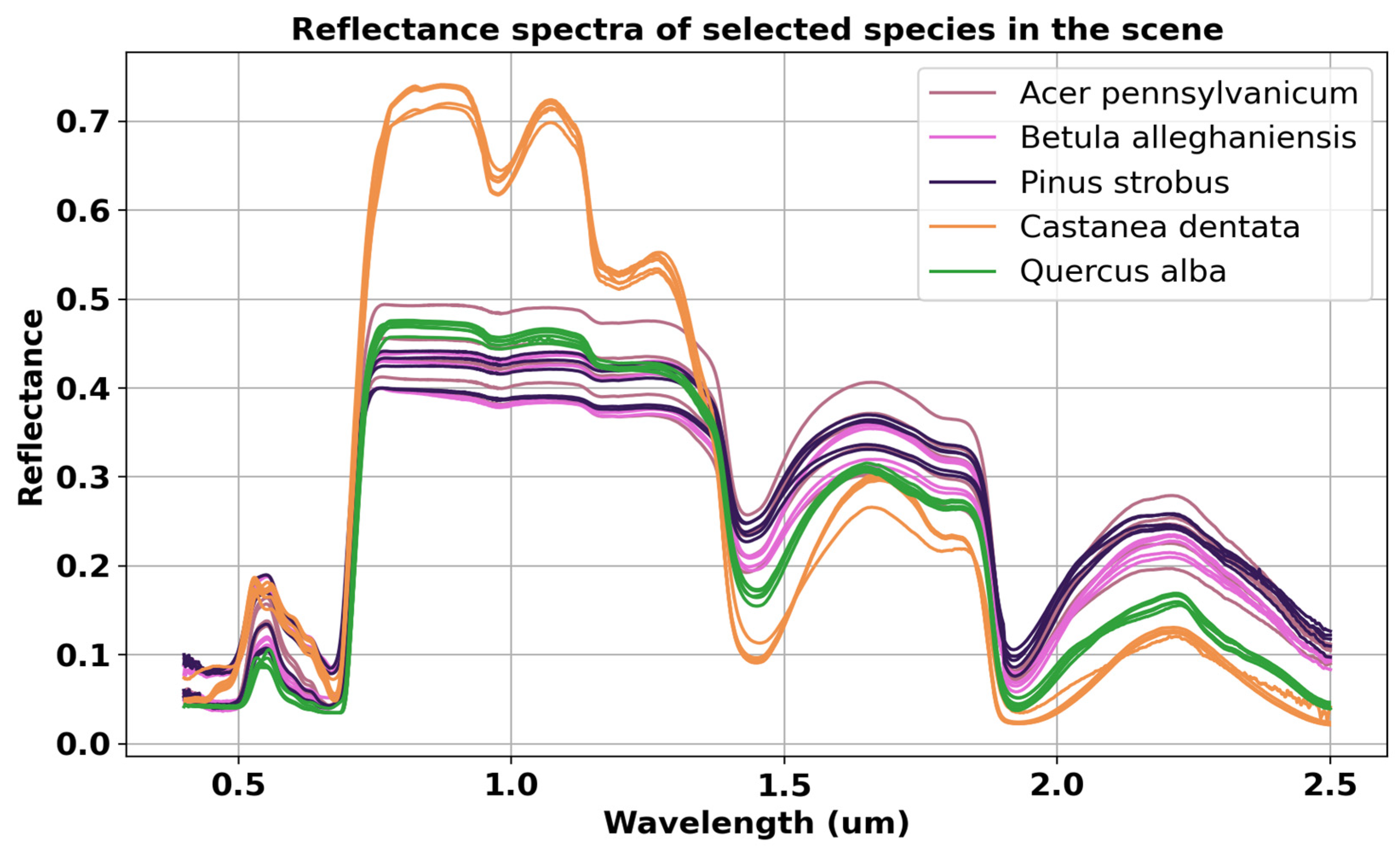
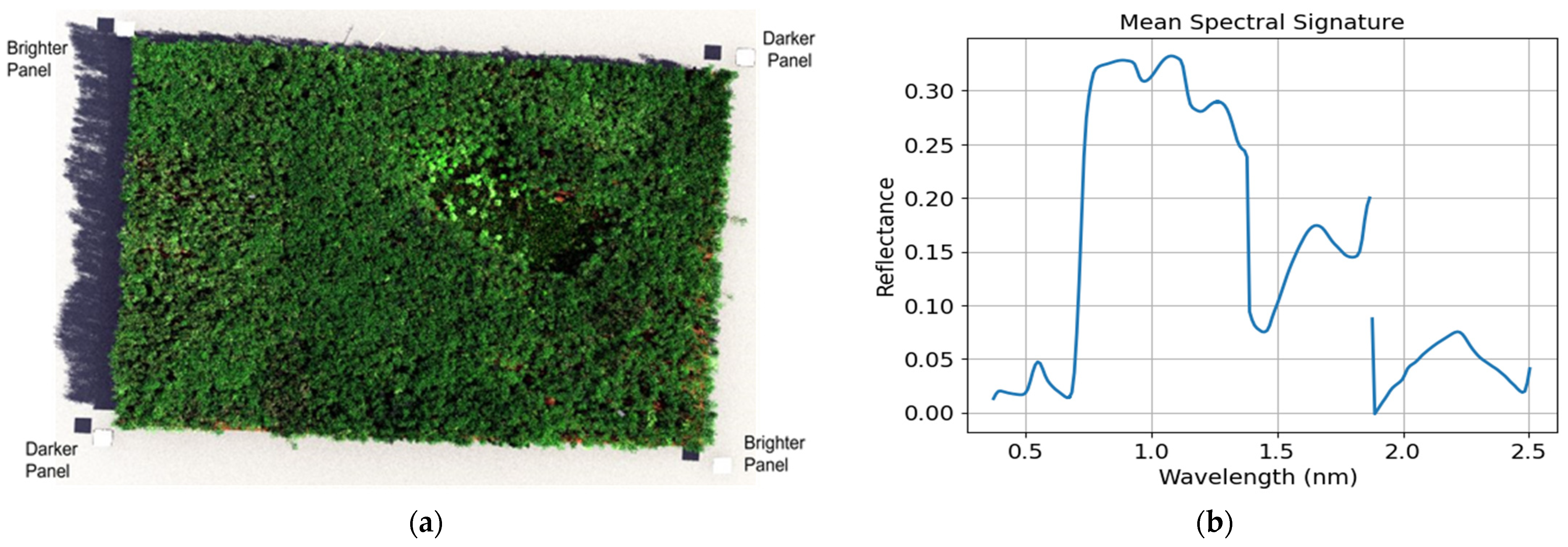
- Scene: A DIRSIG scene is a collection of geolocated, geometric object models that include suitable optical characteristics, texture mapping, and other related attributes. We modeled 80 geometric properties of Harvard Forest vegetation (tree heights, shapes, curvatures) using the OnyxTREE software. Embedding spectral variations in the reflectance and transmittance spectra were created using PROSPECT model (pypi.org/project/prosail, accessed on 25 January 2024) by randomly adjusting leaf parameters. The geographic locations, height, and diameter at breast height (DBH) values of all plants were collected from field data and the Harvard Forest Data Archive (https://harvardforest.fas.harvard.edu/, accessed on 25 January 2024). Figure 3 illustrates the diagram of the inputs used to develop the Harvard Forest scene.
- Atmosphere: DIRSIG uses MODTRAN4 (4v3r1) to define atmospheric conditions, including downwelling radiance, atmospheric transmission, and temperature profiles [22]. For this analysis, we used a prebuilt atmospheric model (FourCurveAtmosphere) to calculate downwelling radiance and atmospheric transmission, based on standard vertical column profiles for a midlatitude summer (MLS) environment (http://dirsig.cis.rit.edu/docs/new/four_curve_atm_plugin.html, accessed on 25 January 2024). We know that remote sensing data acquisition and analysis can be atmospherically sensitive, so for this analysis, we opted to use the same atmospheric model for all types of simulations to avoid any conflict.
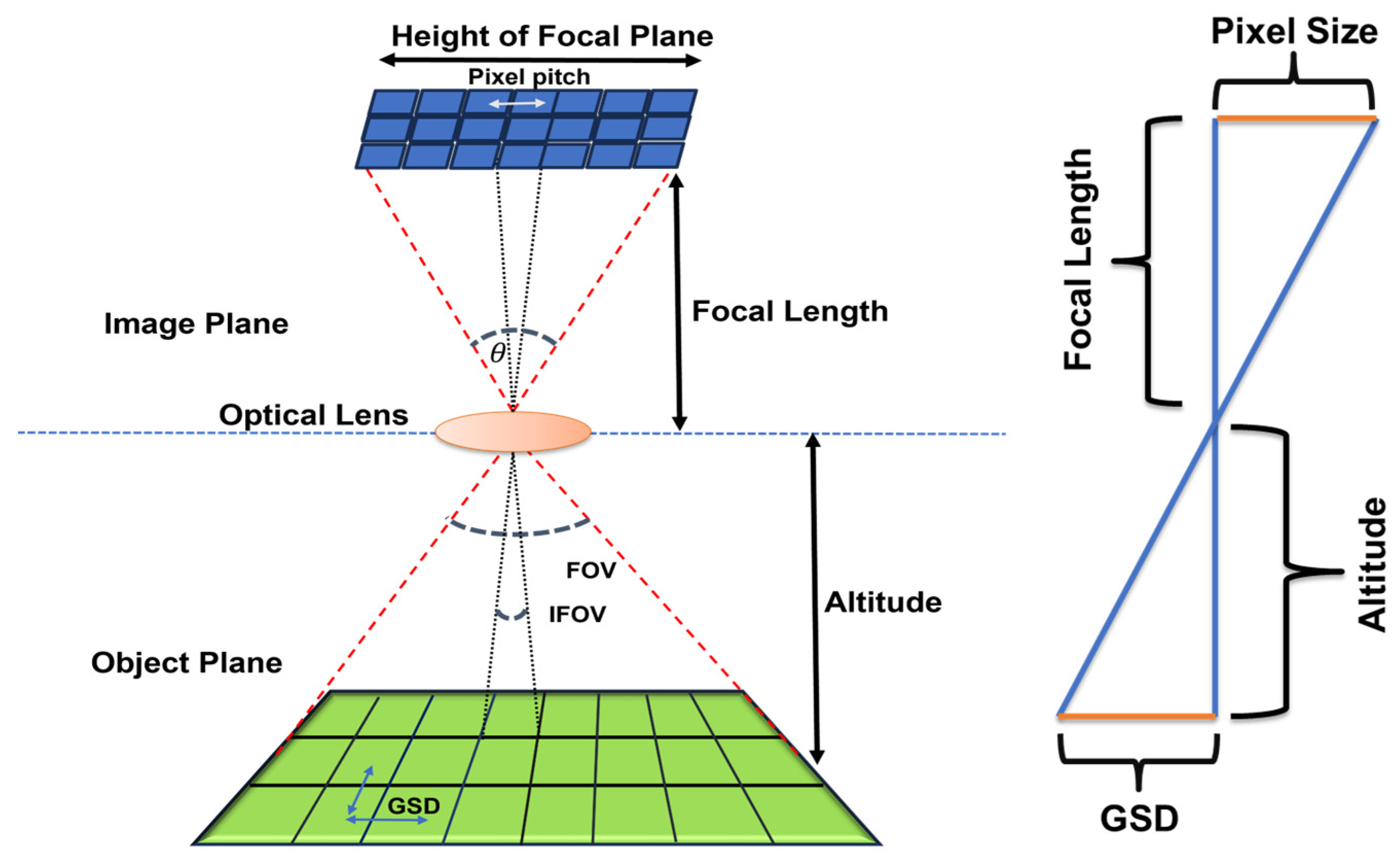
- Imaging System: The imaging system or sensor entails a methodical description of the imaging platform, encompassing the scanning technique, optical focal length, arrangement of the detector array, spectral response function, point spread function (PSF), noise properties, and other related attributes. We used AVIRIS Classic hyperspectral sensor to simulate image samples of the Harvard Forest scene. A summary of the imaging spectrometer specifications is provided in Table 2.
- Platform Motion: The characterization of platform motion and/or position involves gathering information regarding factors such as the altitude at which it operates, its velocity, and any potential irregularities or vibrations (jitter). We used a Scene-ENU (East–North–UP) coordinate system. Since we used a fixed/static frame array sensor, platform velocity was not required.
- Collection Details: The collection of supplementary data concerning the date and time of the task(s) impacts the sun–target–sensor geometry, along with other relevant variables. We simulated at-nadir images to avoid any sun geometry correction and took a single shot to capture the whole scene. A complete flowchart of the scene simulation is shown in Figure 4.
2.3. Preprocessing
2.4. Computing Scene for Different Ground Sampling Distance
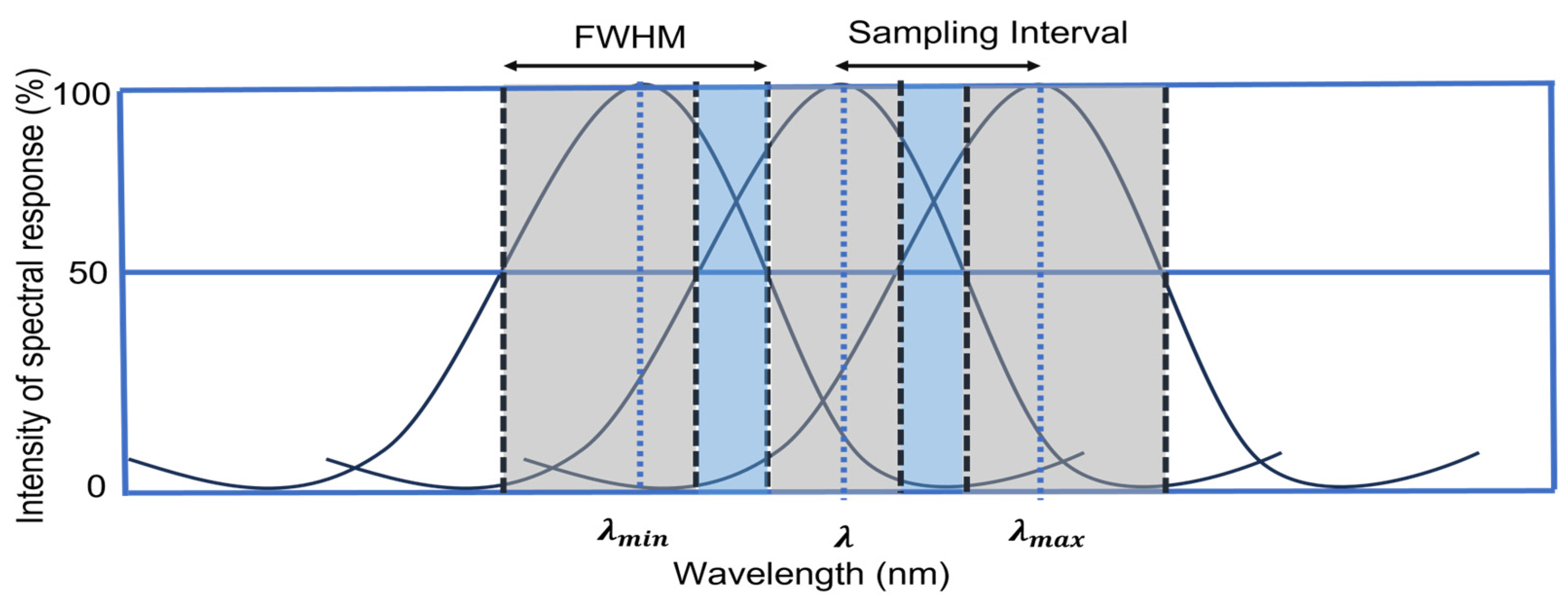
2.5. Computing Scenes across Different Spectral Resolutions
2.6. Computing Scenes at Different Scale Resolutions
2.7. Deep Learning Algorithm
2.8. CNN Training and Testing
2.9. Accuracy Metrics
- True Positive (TP): Accurately labeled positive samples by the classifier.
- True Negative (TN): Accurately labeled negative samples by the classifier.
- False Positive (FP): Incorrectly labeled negative samples as positive.
- False Negative (FN): Incorrectly labeled positive samples as negative.
3. Results and Discussion
3.1. Simulated Scenes for Different GSD
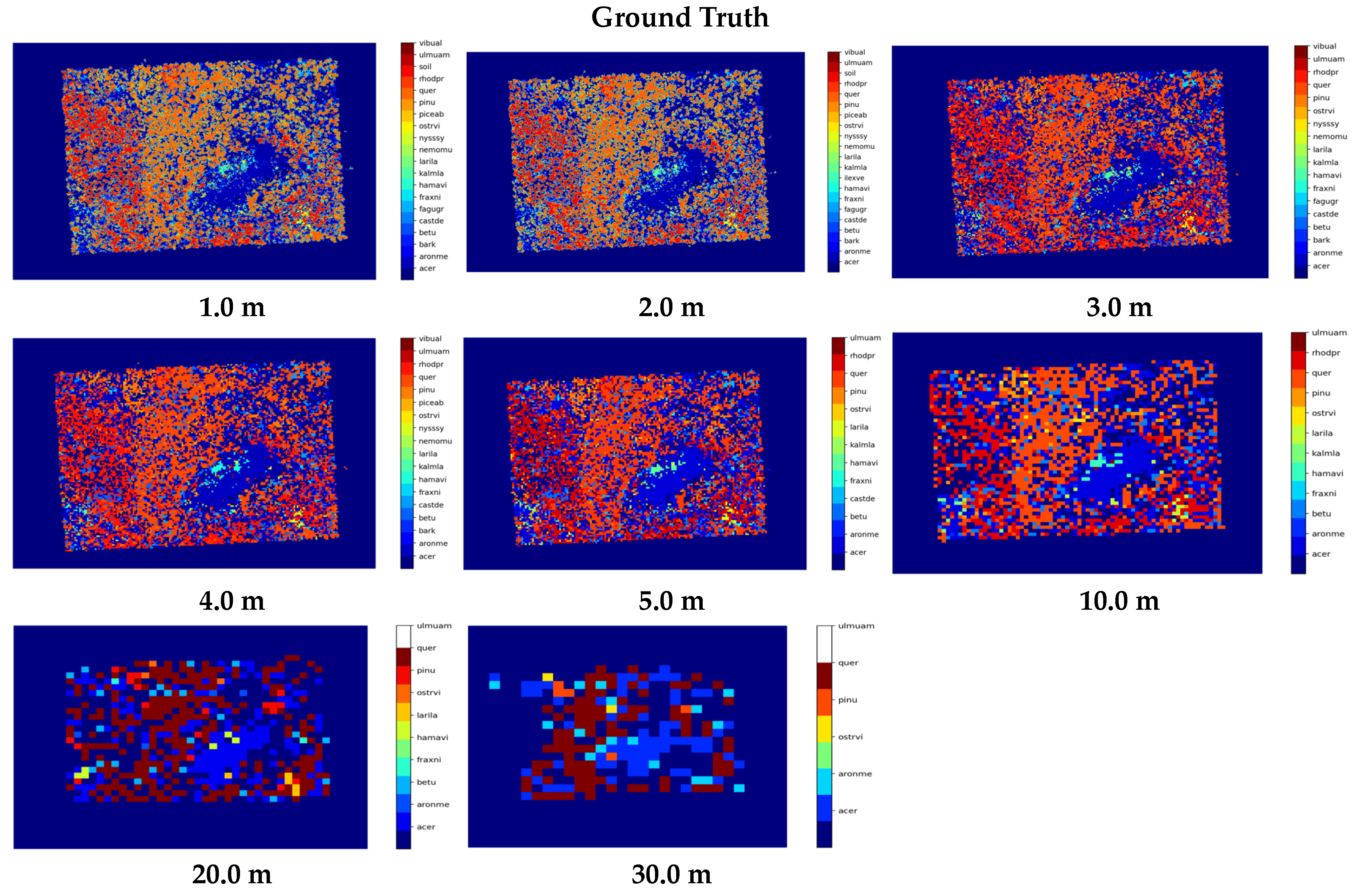
3.2. Ground Truth Map for Different GSD Values
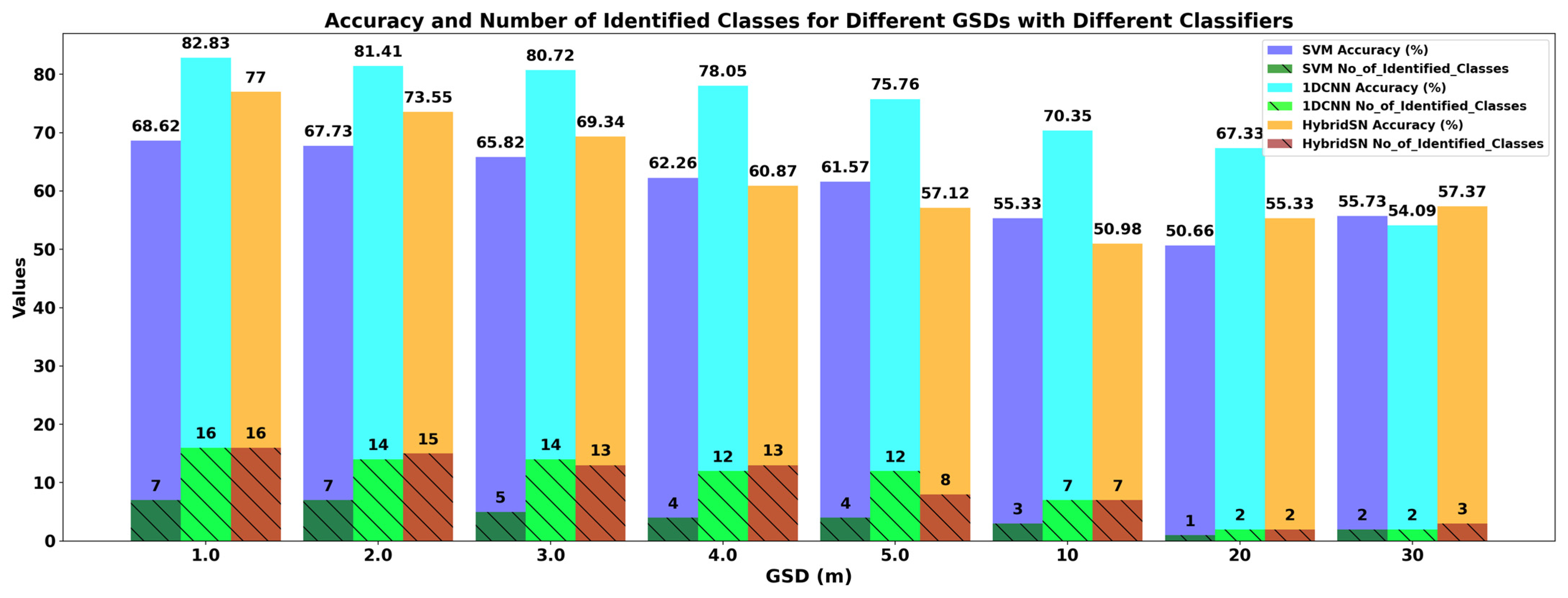
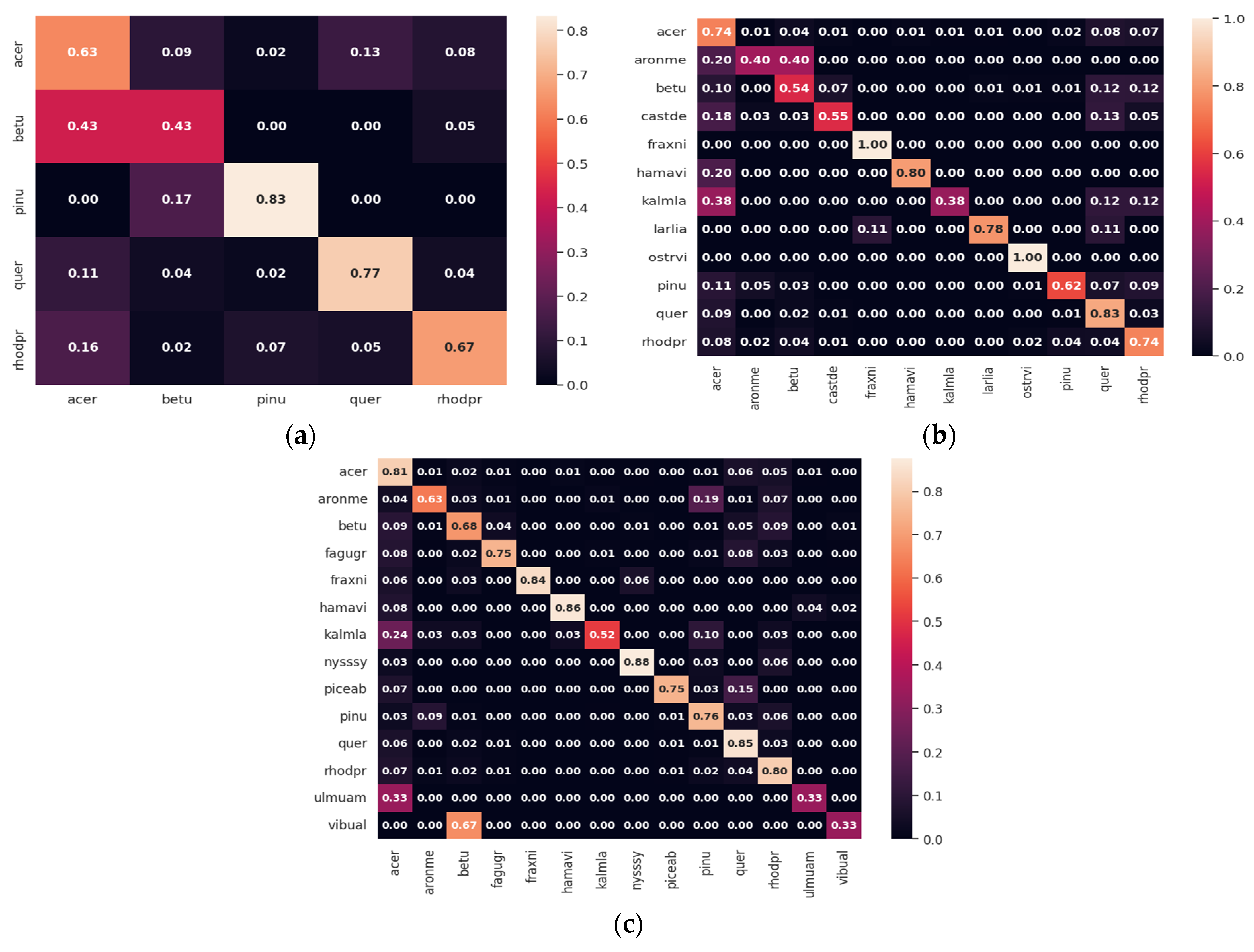
3.3. Classification Performance for Imagery of Different GSDs
3.4. Classification Performance for Imagery of Different Spectral Resolutions
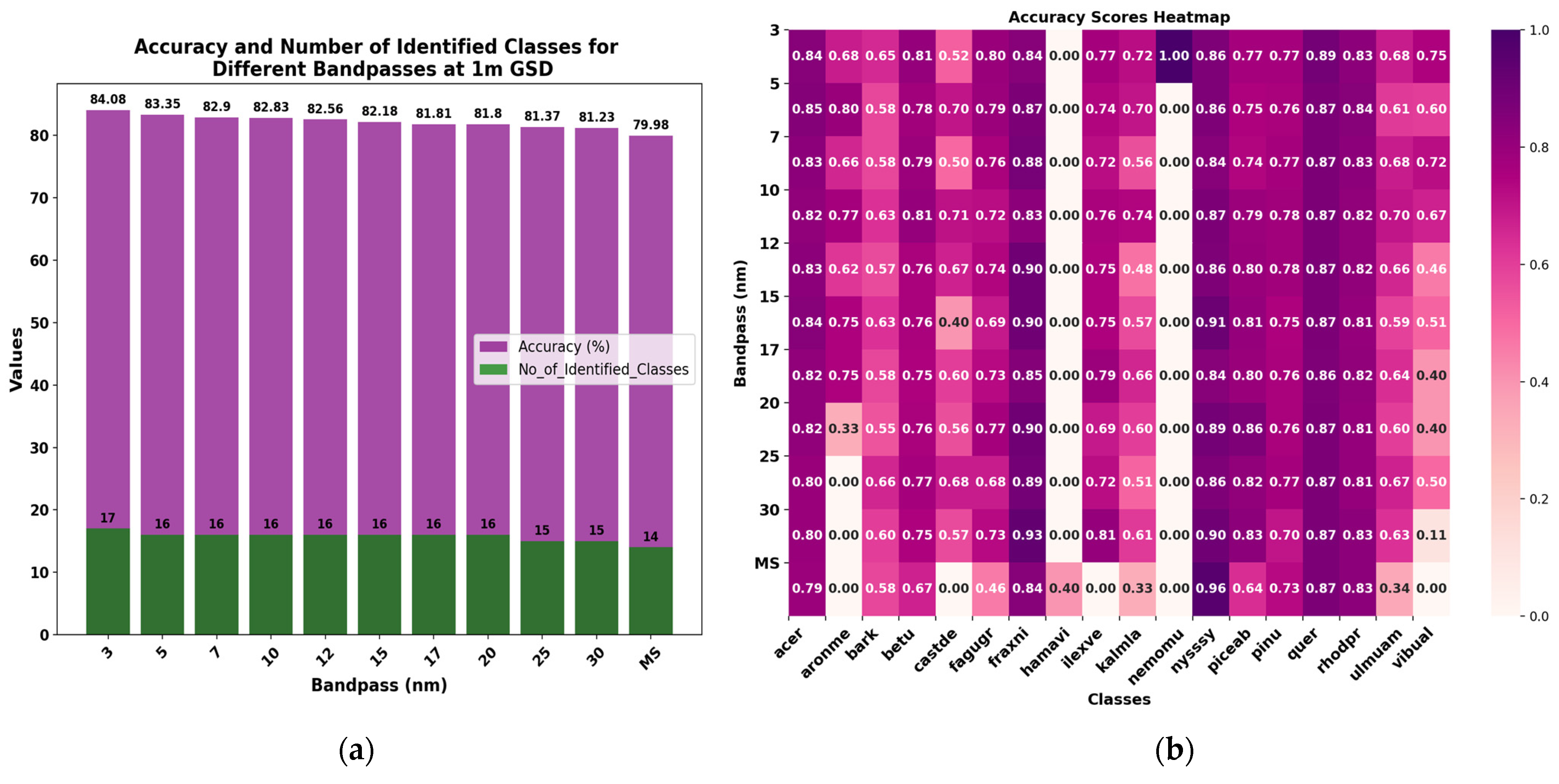
3.4.1. Different Spectral Resolutions at 1 m GSD
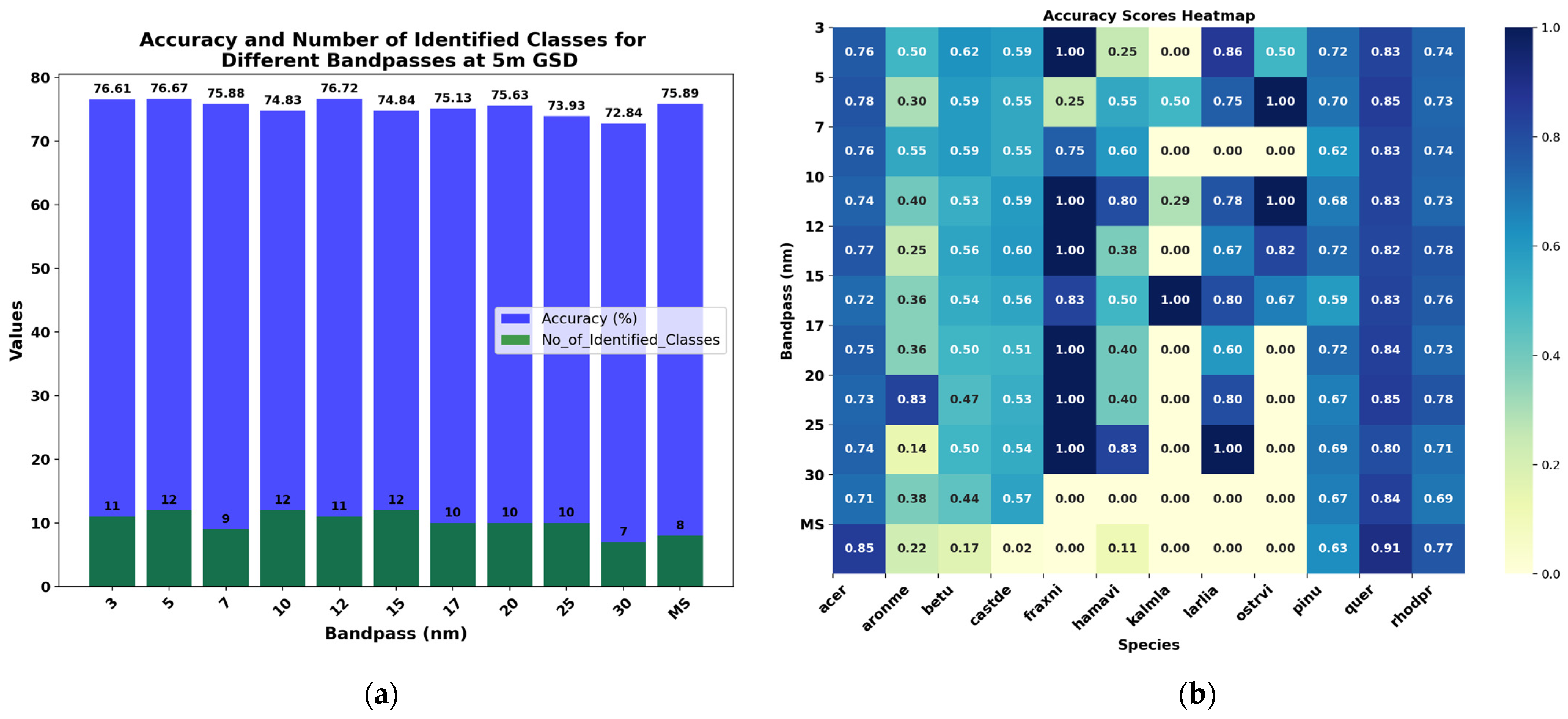
3.4.2. Evaluating Different Spectral Resolutions at GSD = 5 m and GSD = 10 m
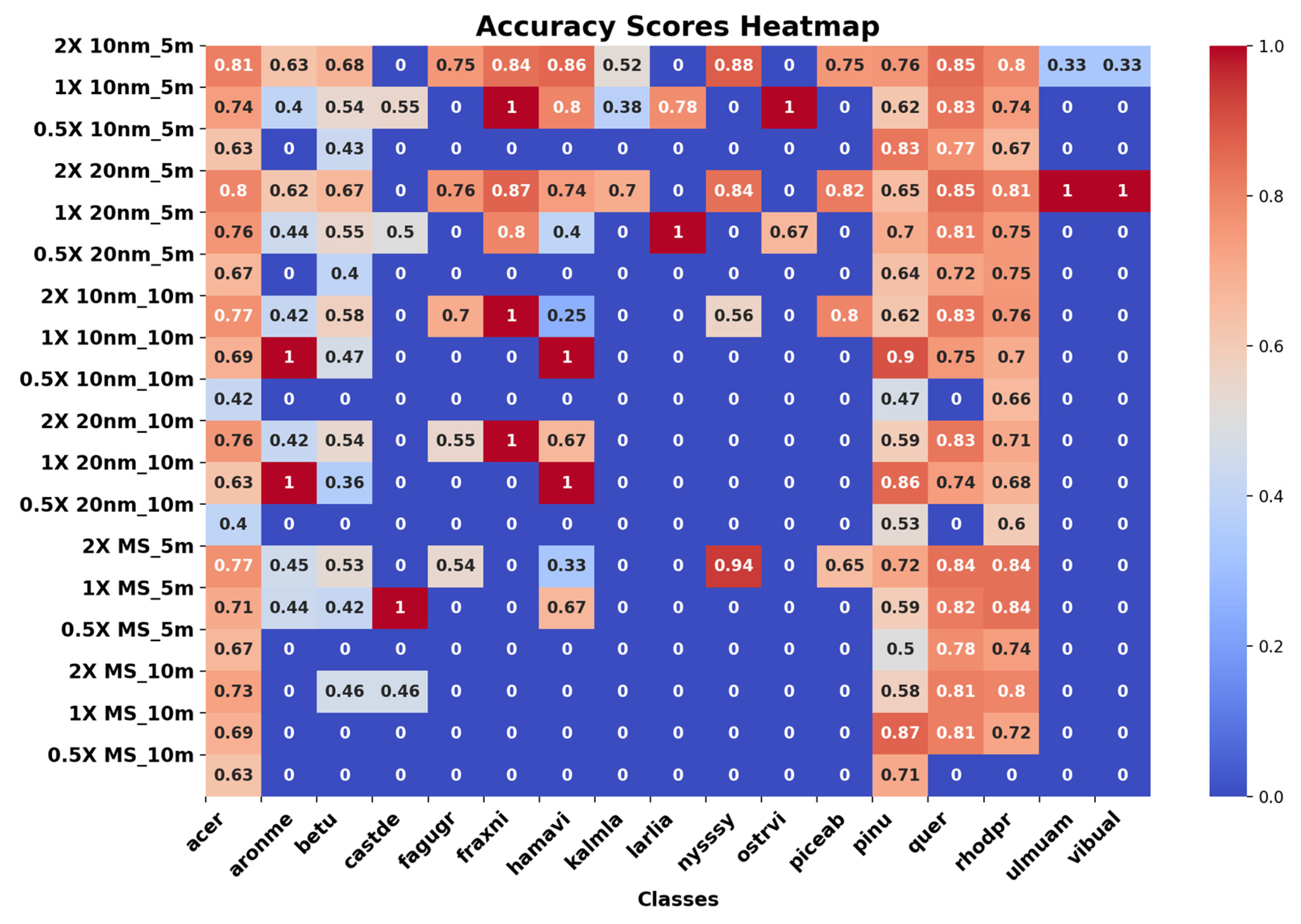
3.5. Classification Performance for Different Sensor-Scale-Resolution Imagery
3.5.1. Different Scale Resolutions at GSD = 5 m and 10 nm and 20 nm Spectral Resolutions
3.5.2. Evaluating Different Scale Resolutions for Other Experimental Setups
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nemani, R.R.; Running, S.W.; Pielke, R.A.; Chase, T.N. Global vegetation cover changes from coarse resolution satellite data. J. Geophys. Res. Atmos. 1996, 101, 7157–7162. [Google Scholar] [CrossRef]
- Myneni, R.B.; Dong, J.; Tucker, C.J.; Kaufmann, R.K.; Kauppi, P.E.; Liski, J.; Zhou, L.; Alexeyev, V.; Hughes, M. A large carbon sink in the woody biomass of Northern forests. Proc. Natl. Acad. Sci. USA 2001, 98, 14784–14789. [Google Scholar] [CrossRef] [PubMed]
- Swatantran, A.; Dubayah, R.; Roberts, D.; Hofton, M.; Blair, J.B. Mapping biomass and stress in the Sierra Nevada using lidar and hyperspectral data fusion. Remote Sens. Environ. 2011, 115, 2917–2930. [Google Scholar] [CrossRef]
- Ørka, H.O.; Dalponte, M.; Gobakken, T.; Naesset, E.; Ene, L.T. Characterizing forest species composition using multiple remote sensing data sources and inventory approaches. Scand. J. For. Res. 2013, 28, 677–688. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of studies on tree species classification from remotely sensed data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in Automatic Individual Tree Crown Detection and Delineation—Evolution of LiDAR Data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef]
- Zemek, F. Airborne Remote Sensing: Theory and Practice in Assessment of Terrestrial Ecosystems; Global Change Research Centre AS CR: Brno, Czech Republic, 2014. [Google Scholar]
- Wang, K.; Wang, T.; Liu, X. A Review: Individual Tree Species Classification Using Integrated Airborne LiDAR and Optical Imagery with a Focus on the Urban Environment. Forests 2019, 10, 1. [Google Scholar] [CrossRef]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree Species Classification with Random Forest Using Very High Spatial Resolution 8-Band WorldView-2 Satellite Data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Cochrane, M. Using vegetation reflectance variability for species level classification of hyperspectral data. Int. J. Remote Sens. 2000, 21, 2075–2087. [Google Scholar] [CrossRef]
- Van Leeuwen, M.; Frye, H.A.; Wilson, A.M. Understanding limits of species identification using simulated imaging spectroscopy. Remote Sens. Environ. 2021, 259, 112405. [Google Scholar] [CrossRef]
- Huang, J.; Wang, Y.; Zhang, D.; Yang, L.; Xu, M.; He, D.; Zhuang, X.; Yao, Y.; Hou, J. Design and demonstration of airborne imaging system for target detection based on area-array camera and push-broom hyperspectral imager. Infrared Phys. Technol. 2021, 116, 103794. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Cwiek, M.; Zak, L.; Lakota, T.; Tulczyjew, L.; Kawulok, M. Towards on-board hyperspectral satellite image segmentation: Understanding robustness of deep learning through simulating acquisition conditions. Remote Sens. 2021, 13, 1532. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Moreno, J.; Camps-Valls, G. Gaussian processes uncertainty estimates in experimental Sentinel-2 LAI and leaf chlorophyll content retrieval. ISPRS J. Photogramm. Remote Sens. 2013, 86, 157–167. [Google Scholar] [CrossRef]
- Xu, X.; Lu, J.; Zhang, N.; Yang, T.; He, J.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.; Tian, Y. Inversion of rice canopy chlorophyll content and leaf area index based on coupling of radiative transfer and Bayesian network models. ISPRS J. Photogramm. Remote Sens. 2019, 150, 185–196. [Google Scholar] [CrossRef]
- Nur, N.B.; Bachmann, C.M. Comparison of soil moisture content retrieval models utilizing hyperspectral goniometer data and hyperspectral imagery from an unmanned aerial system. J. Geophys. Res. Biogeosci. 2023, 128, e2023JG007381. [Google Scholar] [CrossRef]
- Masemola, C.; Cho, M.A.; Ramoelo, A. Towards a semi-automated mapping of Australia native invasive alien Acacia trees using Sentinel-2 and radiative transfer models in South Africa. ISPRS J. Photogramm. Remote Sens. 2020, 166, 153–168. [Google Scholar] [CrossRef]
- Miraglio, T.; Adeline, K.; Huesca, M.; Ustin, S.; Briottet, X. Joint Use of PROSAIL and DART for Fast LUT Building: Application to Gap Fraction and Leaf Biochemistry Estimations over Sparse Oak Stands. Remote Sens. 2020, 12, 2925. [Google Scholar] [CrossRef]
- Goodenough, A.A.; Brown, S.D. DIRSIG5: Next-generation remote sensing data and image simulation framework. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4818–4833. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Yin, T.; Yan, G.; Gastellu-Etchegorry, J.-P.; Li, L.; Zhang, W.; Mu, X.; Norford, L.K. LESS: LargE-Scale remote sensing data and image simulation framework over heterogeneous 3D scenes. Remote Sens. Environ. 2019, 221, 695–706. [Google Scholar] [CrossRef]
- Wald, I.; Woop, S.; Benthin, C.; Johnson, G.S.; Ernst, M. Embree: A kernel framework for efficient CPU ray tracing. ACM Trans. Graph. (TOG) 2014, 33, 1–8. [Google Scholar] [CrossRef]
- North, P.R. Three-dimensional forest light interaction model using a Monte Carlo method. IEEE Trans. Geosci. Remote Sens. 1996, 34, 946–956. [Google Scholar] [CrossRef]
- Wu, J.; Van Aardt, J.; Asner, G.; Mathieu, R.; Kennedy-Bowdoin, T.; Knapp, D.; Wessels, K.; Erasmus, B.; Smit, I. Connecting the dots between laser waveforms and herbaceous biomass for assessment of land degradation using small-footprint waveform lidar data. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. II-334–II-337. [Google Scholar]
- Wu, J.; Van Aardt, J.; Asner, G.P. A comparison of signal deconvolution algorithms based on small-footprint LiDAR waveform simulation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2402–2414. [Google Scholar] [CrossRef]
- Wu, J.; Van Aardt, J.; McGlinchy, J.; Asner, G.P. A robust signal preprocessing chain for small-footprint waveform lidar. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3242–3255. [Google Scholar] [CrossRef]
- Romanczyk, P.; van Aardt, J.; Cawse-Nicholson, K.; Kelbe, D.; McGlinchy, J.; Krause, K. Assessing the impact of broadleaf tree structure on airborne full-waveform small-footprint LiDAR signals through simulation. Can. J. Remote Sens. 2013, 39, S60–S72. [Google Scholar] [CrossRef]
- Yao, W.; Kelbe, D.; Leeuwen, M.V.; Romanczyk, P.; Aardt, J.V. Towards an improved LAI collection protocol via simulated and field-based PAR sensing. Sensors 2016, 16, 1092. [Google Scholar] [CrossRef]
- Yao, W.; van Aardt, J.; van Leeuwen, M.; Kelbe, D.; Romanczyk, P. A simulation-based approach to assess subpixel vegetation structural variation impacts on global imaging spectroscopy. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4149–4164. [Google Scholar] [CrossRef]
- Maschler, J.; Atzberger, C.; Immitzer, M. Individual tree crown segmentation and classification of 13 tree species using airborne hyperspectral data. Remote Sens. 2018, 10, 1218. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Zortea, M.; Zanotta, D.C.; Shimabukuro, Y.E.; de Souza Filho, C.R. Mapping tree species in tropical seasonal semi-deciduous forests with hyperspectral and multispectral data. Remote Sens. Environ. 2016, 179, 66–78. [Google Scholar] [CrossRef]
- Fricker, G.A.; Ventura, J.D.; Wolf, J.A.; North, M.P.; Davis, F.W.; Franklin, J. A convolutional neural network classifier identifies tree species in mixed-conifer forest from hyperspectral imagery. Remote Sens. 2019, 11, 2326. [Google Scholar] [CrossRef]
- Ghosh, A.; Fassnacht, F.E.; Joshi, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar] [CrossRef]
- Guo, X.; Li, H.; Jing, L.; Wang, P. Individual tree species classification based on convolutional neural networks and multitemporal high-resolution remote sensing images. Sensors 2022, 22, 3157. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, T.-H.; Kiang, J.-F. Comparison of CNN algorithms on hyperspectral image classification in agricultural lands. Sensors 2020, 20, 1734. [Google Scholar] [CrossRef] [PubMed]
- Wible, R.; Patki, K.; Krause, K.; van Aardt, J. Toward a Definitive Assessment of the Impact of Leaf Angle Distributions on LiDAR Structural Metrics. In Proceedings of the SilviLaser Conference 2021, Vienna, Austria, 28–30 September 2021; pp. 307–309. [Google Scholar]
- Schott, J.R.; Brown, S.D.; Raqueno, R.V.; Gross, H.N.; Robinson, G. An advanced synthetic image generation model and its application to multi/hyperspectral algorithm development. Can. J. Remote Sens. 1999, 25, 99–111. [Google Scholar] [CrossRef]
- Schott, J.R.; Raqueno, R.V.; Salvaggio, C. Incorporation of a time-dependent thermodynamic model and a radiation propagation model into IR 3D synthetic image generation. Opt. Eng. 1992, 31, 1505–1516. [Google Scholar] [CrossRef]
- Green, R.O.; Conel, J.E.; Roberts, D.A. Estimation of aerosol optical depth, pressure elevation, water vapor, and calculation of apparent surface reflectance from radiance measured by the airborne visible/infrared imaging spectrometer. In Proceedings of the Imaging Spectrometry of the Terrestrial Environment, Orlando, FL, USA, 11–16 April 1993; pp. 2–11. [Google Scholar]
- Sanders, L.C.; Schott, J.R.; Raqueno, R. A VNIR/SWIR atmospheric correction algorithm for hyperspectral imagery with adjacency effect. Remote Sens. Environ. 2001, 78, 252–263. [Google Scholar] [CrossRef]
- Conel, J.E.; Green, R.O.; Vane, G.; Bruegge, C.J.; Alley, R.E.; Curtiss, B.J. AIS-2 radiometry and a comparison of methods for the recovery of ground reflectance. In Proceedings of the 3rd Airborne Imaging Spectrometer Data Analysis Workshop, Pasadena, CA, USA, 2–4 June 1987. [Google Scholar]
- Kotawadekar, R. 9—Satellite data: Big data extraction and analysis. In Artificial Intelligence in Data Mining; Binu, D., Rajakumar, B.R., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 177–197. [Google Scholar] [CrossRef]
- Malenovsky, Z. Quantitative Remote Sensing of Norway Spruce (Picea Abies (L.) Karst.): Spectroscopy from Needles to Crowns to Canopies; Wageningen University and Research: Wageningen, The Netherlands, 2006. [Google Scholar]
- Safonova, A.; Tabik, S.; Alcaraz-Segura, D.; Rubtsov, A.; Maglinets, Y.; Herrera, F. Detection of fir trees (Abies sibirica) damaged by the bark beetle in unmanned aerial vehicle images with deep learning. Remote Sens. 2019, 11, 643. [Google Scholar] [CrossRef]
- Egli, S.; Höpke, M. CNN-based tree species classification using high resolution RGB image data from automated UAV observations. Remote Sens. 2020, 12, 3892. [Google Scholar] [CrossRef]
- Agarap, A.F. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Gulli, A.; Pal, S. Deep Learning with Keras; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Rodarmel, C.; Shan, J. Principal component analysis for hyperspectral image classification. Surv. Land Inf. Sci. 2002, 62, 115–122. [Google Scholar]
- Nweke, H.F.; Teh, Y.W.; Al-Garadi, M.A.; Alo, U.R. Deep learning algorithms for human activity recognition using mobile and wearable sensor networks: State of the art and research challenges. Expert Syst. Appl. 2018, 105, 233–261. [Google Scholar] [CrossRef]
- Wagle, S.A.; Harikrishnan, R.; Ali, S.H.M.; Faseehuddin, M. Classification of plant leaves using new compact convolutional neural network models. Plants 2021, 11, 24. [Google Scholar] [CrossRef] [PubMed]
- Mather, P.M.; Koch, M. Computer Processing of Remotely-Sensed Images: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zhang, H.; Zhang, L.; Shen, H. A super-resolution reconstruction algorithm for hyperspectral images. Signal Process. 2012, 92, 2082–2096. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Clark, R.N. Spectroscopic determination of leaf biochemistry using band-depth analysis of absorption features and stepwise multiple linear regression. Remote Sens. Environ. 1999, 67, 267–287. [Google Scholar] [CrossRef]




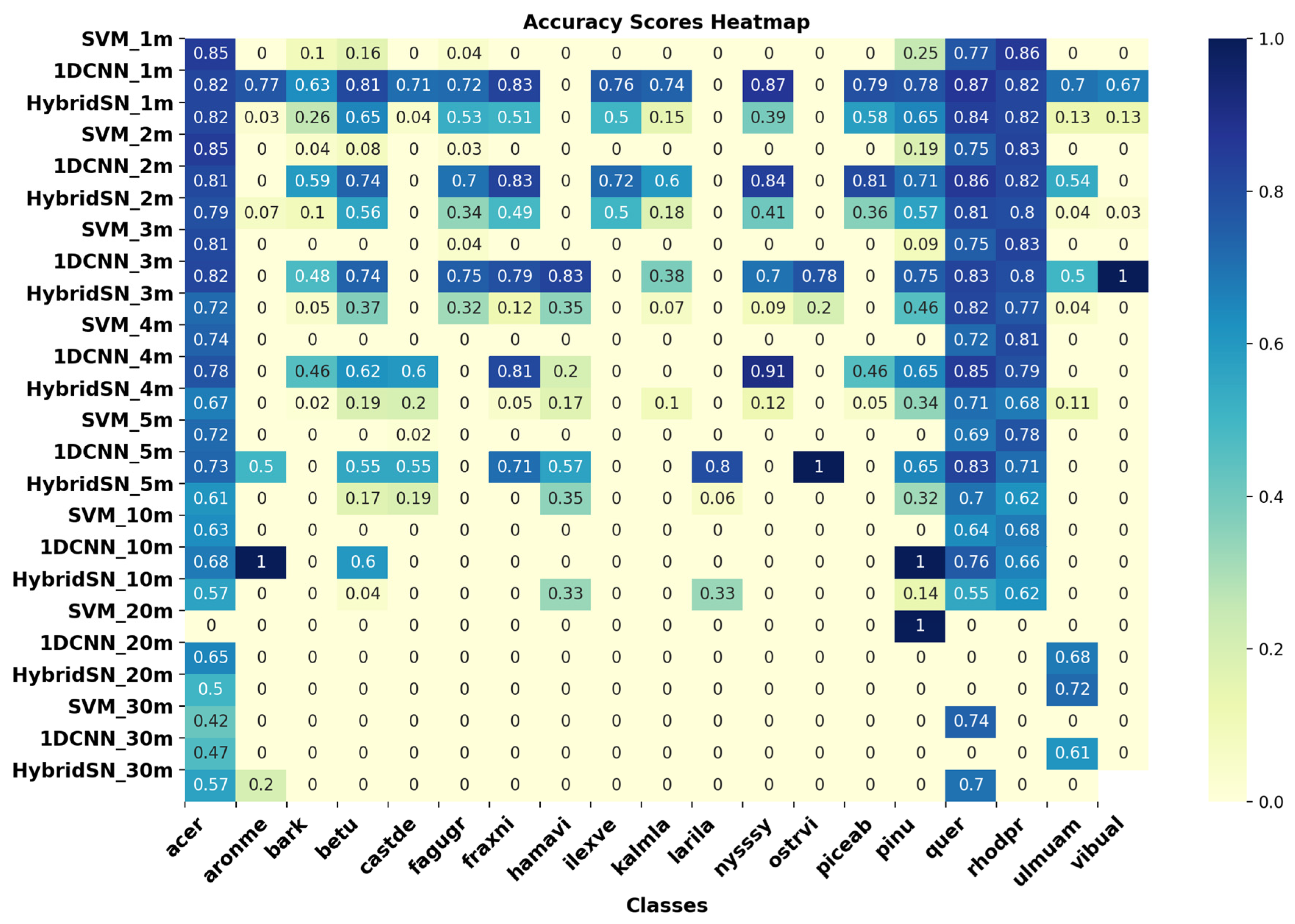
| Class | Scientific Name | Genus | Common Name | Type | Number of Individuals |
|---|---|---|---|---|---|
| acer | Acer pennsylvanicum | Acer | Moosewood Maple | Tree | 354 |
| Acer rubrum | Acer | Red Maple | Tree | 10,760 | |
| aronme | Aronia melanocarpa | Aronia | Black Chokeberry | Subcanopy | 413 |
| betual | Betula alleghaniensis | Betula | Yellow Birch | Subcanopy | 4452 |
| Betula lenta | Betula | Black Birch | Tree | 1479 | |
| Betula papyrifera | Betula | Paper Birch | Tree | 711 | |
| Betula populifolia | Betula | Grey Birch | Tree | 131 | |
| castde | Castanea dentata | Castanea | American Chestnut | Subcanopy | 782 |
| fagugr | Fagus grandifolia | Fagus | Beech | Tree | 3879 |
| fraxni | Fraxinus nigra | Fraxinus | Black Ash | Tree | 38 |
| hamavi | Hamamelis virginiana | Hamamelis | Witch-hazel | Subcanopy | 1967 |
| ilexve | Ilex verticillata | Ilex | Winterberry | Subcanopy | 9875 |
| kalmla | Kalmia latifolia | Kalmia | Mountain Laurel | Subcanopy | 3929 |
| larila | Larix laricina | Larix | Tamarack | Subcanopy | 1 |
| lyonli | Lyonia ligustrina | Lyonia | Maleberry | Subcanopy | 1178 |
| nemomu | Nemopanthus mucronatus | Nemopanthus | Mountain Holley | Subcanopy | 599 |
| nysssy | Nyssa sylvatica | Nyssa | Tupelo | Tree | 181 |
| ostrvi | Ostrya virginiana | Ostrya | Hornbeam | Tree | 24 |
| piceab | Picea abies | Picea | Norway Spruce | Tree | 1458 |
| pinu | Pinus resinosa | Pinus | Red Pine | Tree | 973 |
| Pinus strobus | Pinus | Eastern White Pine | Tree | 3070 | |
| quer | Quercus alba | Quercus | White Oak | Tree | 46 |
| Quercus rubra | Quercus | Northern Red Oak | Tree | 4122 | |
| rhodpr | Rhododendron prinophyllum | Rhododendron | Rhododendron | Subcanopy | 127 |
| tsugca | Tsuga canadensis | Tsuga | Eastern Hemlock | Tree | 24,266 |
| ulmuam | Ulmus americana | Ulmus | Elm | Tree | 1 |
| vaccco | Vaccinium corymbosum | Vaccinium | Blueberry bush | Subcanopy | 3533 |
| vibual | Viburnum alnifolium | Viburnum | Hobblebush | Subcanopy | 76 |
| soil | - | - | - | ||
| bark | - | - | - |
| Hyperspectral Imager | AVIRIS Classic |
|---|---|
| Spectral Bands | 224 |
| Spectral Range | 380–2500 |
| Spectral Sampling | 10 nm FWHM (Gaussian) |
| Pixel Array | 667 × 552 |
| Pixel Size | 200 microns |
| Focal Length | 197.60 mm |
| Flying Height | 1–30 km |
| GSD | 1–30 m |
| Spectral Sampling | Total No. of Bands |
|---|---|
| 3 nm | 714 |
| 5 nm | 425 |
| 7 nm | 306 |
| 10 nm | 224 |
| 12 nm | 178 |
| 15 nm | 143 |
| 17 nm | 126 |
| 20 nm | 108 |
| 25 nm | 83 |
| 30 nm | 69 |
| Multispectral (MS) | 8 |
| Scale Resolution | Pixel Array Dimension | Pixel Size/Pitch (Microns) |
|---|---|---|
| 0.5X | 334 × 276 | 400.00 |
| 1X | 667 × 552 | 200.00 |
| 2X | 1334 × 1104 | 100.00 |
| GSD | Number of Samples (Pixels) | Total | |
|---|---|---|---|
| Train | Test | ||
| 1.0 m | 216,561 | 92,812 | 309,373 |
| 1.5 m | 93,618 | 40,122 | 133,740 |
| 2.0 m | 51,825 | 22,211 | 74,036 |
| 2.5 m | 32,738 | 14,031 | 46,769 |
| 3.0 m | 22,538 | 9660 | 32,198 |
| 4.0 m | 12,428 | 5327 | 17,755 |
| 5.0 m | 7849 | 3365 | 11,214 |
| 10 m | 1770 | 759 | 2529 |
| 20 m | 350 | 150 | 500 |
| 30 m | 140 | 61 | 201 |
| GSD | Overall Accuracy (OA) (%) | Kappa Coefficient (%) | F1 Score (%) | Precision | Recall | ||
|---|---|---|---|---|---|---|---|
| Macro Average (%) | Weighted Average (%) | Macro Average (%) | Weighted Average (%) | ||||
| 1.0 m | 82.83 | 77.51 | 83 | 40 | 85 | 59 | 83 |
| 2.0 m | 81.41 | 75.35 | 81 | 35 | 83 | 46 | 81 |
| 3.0 m | 80.72 | 74.18 | 81 | 38 | 82 | 56 | 81 |
| 4.0 m | 78.05 | 70.56 | 78 | 34 | 80 | 42 | 78 |
| 5.0 m | 75.76 | 65.89 | 75 | 37 | 77 | 56 | 75 |
| 10 m | 70.35 | 58.17 | 70 | 27 | 76 | 43 | 70 |
| 20 m | 67.33 | 37.58 | 67 | 16 | 79 | 15 | 67 |
| 30 m | 54.09 | 18.70 | 54 | 21 | 62 | 18 | 54 |
| GSD | Overall Accuracy (OA) (%) | Kappa Coefficient (%) | F1 Score (%) | Precision | Recall | ||
|---|---|---|---|---|---|---|---|
| Macro Average (%) | Weighted Average (%) | Macro Average (%) | Weighted Average (%) | ||||
| 1.0 m | 76.94 | 69.81 | 77 | 45 | 76 | 33 | 77 |
| 2.0 m | 73.55 | 64.85 | 74 | 42 | 72 | 29 | 74 |
| 3.0 m | 69.34 | 58.70 | 69 | 40 | 68 | 24 | 69 |
| 4.0 m | 60.87 | 46.90 | 61 | 37 | 59 | 20 | 61 |
| 5.0 m | 57.12 | 41.51 | 57 | 27 | 55 | 23 | 57 |
| 10 m | 50.98 | 31.47 | 51 | 26 | 48 | 24 | 51 |
| 20 m | 55.33 | 16.97 | 55 | 12 | 49 | 14 | 55 |
| 30 m | 57.37 | 30.37 | 57 | 24 | 59 | 24 | 57 |
| GSD | Overall Accuracy (OA) (%) | Kappa Coefficient (%) | F1 Score (%) | Precision | Recall | ||
|---|---|---|---|---|---|---|---|
| Macro Average (%) | Weighted Average (%) | Macro Average (%) | Weighted Average (%) | ||||
| 1.0 m | 68.62 | 57.33 | 68.62 | 0.28 | 67 | 15 | 69 |
| 2.0 m | 67.73 | 55.41 | 67.73 | 23 | 65 | 14 | 68 |
| 3.0 m | 65.82 | 52.37 | 65.82 | 22 | 60 | 15 | 66 |
| 4.0 m | 62.26 | 47.23 | 62.26 | 17 | 56 | 13 | 62 |
| 5.0 m | 61.57 | 45.72 | 61.57 | 18 | 53 | 17 | 62 |
| 10 m | 55.33 | 35.96 | 55.33 | 14 | 48 | 16 | 55 |
| 20 m | 50.66 | 10.00 | 50.66 | 7 | 26 | 14 | 51 |
| 30 m | 55.73 | 15.01 | 55.73 | 21 | 50 | 23 | 56 |
| Bandpass | Overall Accuracy (OA) (%) | Kappa Coefficient (%) | F1 Score (%) | Precision | Recall | ||
|---|---|---|---|---|---|---|---|
| Macro Average (%) | Weighted Average (%) | Macro Average (%) | Weighted Average (%) | ||||
| 3 nm | 84.08 | 79.46 | 84 | 48 | 85 | 63 | 84 |
| 5 nm | 83.35 | 78.32 | 83 | 45 | 84 | 58 | 83 |
| 7 nm | 82.90 | 77.67 | 83 | 44 | 84 | 56 | 83 |
| 10 nm | 82.83 | 77.51 | 83 | 40 | 85 | 59 | 83 |
| 12 nm | 82.56 | 77.22 | 83 | 40 | 84 | 55 | 83 |
| 15 nm | 82.18 | 76.76 | 82 | 40 | 84 | 55 | 82 |
| 17 nm | 81.81 | 76.19 | 82 | 38 | 84 | 55 | 82 |
| 20 nm | 81.80 | 76.18 | 82 | 37 | 84 | 53 | 84 |
| 25 nm | 81.37 | 75.65 | 81 | 36 | 84 | 53 | 81 |
| 30 nm | 81.23 | 75.39 | 81 | 35 | 84 | 51 | 81 |
| MS | 79.98 | 73.56 | 80 | 31 | 83 | 42 | 80 |
| Bandpass | Overall Accuracy (OA) (%) | Kappa Coefficient (%) | F1 Score (%) | Precision | Recall | ||
|---|---|---|---|---|---|---|---|
| Macro Average (%) | Weighted Average (%) | Macro Average (%) | Weighted Average (%) | ||||
| 3 nm | 76.61 | 68.20 | 77 | 37 | 80 | 57 | 77 |
| 5 nm | 76.67 | 68.52 | 77 | 35 | 79 | 54 | 77 |
| 7 nm | 75.88 | 67.22 | 76 | 31 | 80 | 43 | 76 |
| 10 nm | 74.83 | 65.84 | 75 | 41 | 77 | 64 | 75 |
| 12 nm | 76.72 | 68.55 | 77 | 37 | 79 | 53 | 77 |
| 15 nm | 74.84 | 65.98 | 75 | 35 | 78 | 56 | 75 |
| 17 nm | 75.13 | 66.18 | 75 | 31 | 78 | 46 | 75 |
| 20 nm | 75.63 | 67.11 | 76 | 31 | 79 | 50 | 76 |
| 25 nm | 73.93 | 64.36 | 74 | 32 | 79 | 54 | 74 |
| 30 nm | 72.84 | 62.49 | 72 | 25 | 77 | 31 | 72 |
| MS | 75.89 | 66.52 | 76 | 26 | 83 | 39 | 76 |
| Bandpass | Overall Accuracy (OA) (%) | Kappa Coefficient (%) | F1 Score (%) | Precision | Recall | ||
|---|---|---|---|---|---|---|---|
| Macro Average (%) | Weighted Average (%) | Macro Average (%) | Weighted Average (%) | ||||
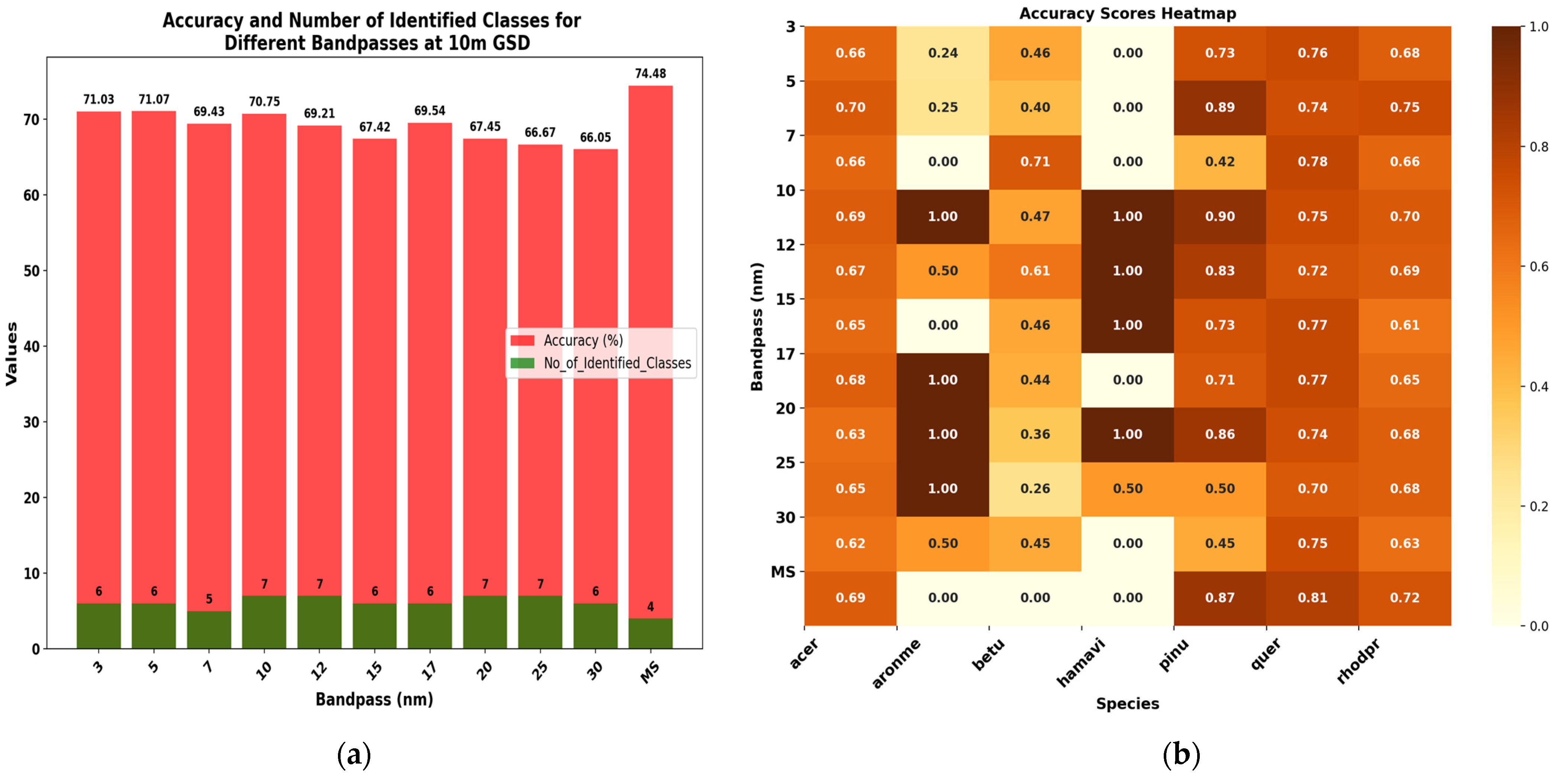
| 3 nm | 71.03 | 60.01 | 71 | 25 | 73 | 29 | 71 |
| 5 nm | 71.07 | 59.43 | 71 | 26 | 71 | 31 | 71 |
| 7 nm | 69.43 | 57.00 | 69 | 26 | 75 | 29 | 69 |
| 10 nm | 70.75 | 58.93 | 71 | 30 | 75 | 50 | 71 |
| 12 nm | 69.21 | 56.74 | 69 | 27 | 74 | 42 | 69 |
| 15 nm | 67.42 | 54.34 | 67 | 27 | 73 | 38 | 67 |
| 17 nm | 69.54 | 57.41 | 70 | 29 | 74 | 39 | 70 |
| 20 nm | 67.45 | 53.90 | 67 | 26 | 73 | 44 | 67 |
| 25 nm | 66.67 | 52.78 | 67 | 25 | 73 | 36 | 67 |
| 30 nm | 66.05 | 52.06 | 66 | 25 | 72 | 31 | 66 |
| MS | 74.48 | 62.96 | 74 | 27 | 82 | 28 | 74 |
| Scale Resolution | Overall Accuracy (OA) (%) | Kappa Coefficient (%) | F1 Score (%) | Precision | Recall | ||
|---|---|---|---|---|---|---|---|
| Macro Average (%) | Weighted Average (%) | Macro Average (%) | Weighted Average (%) | ||||
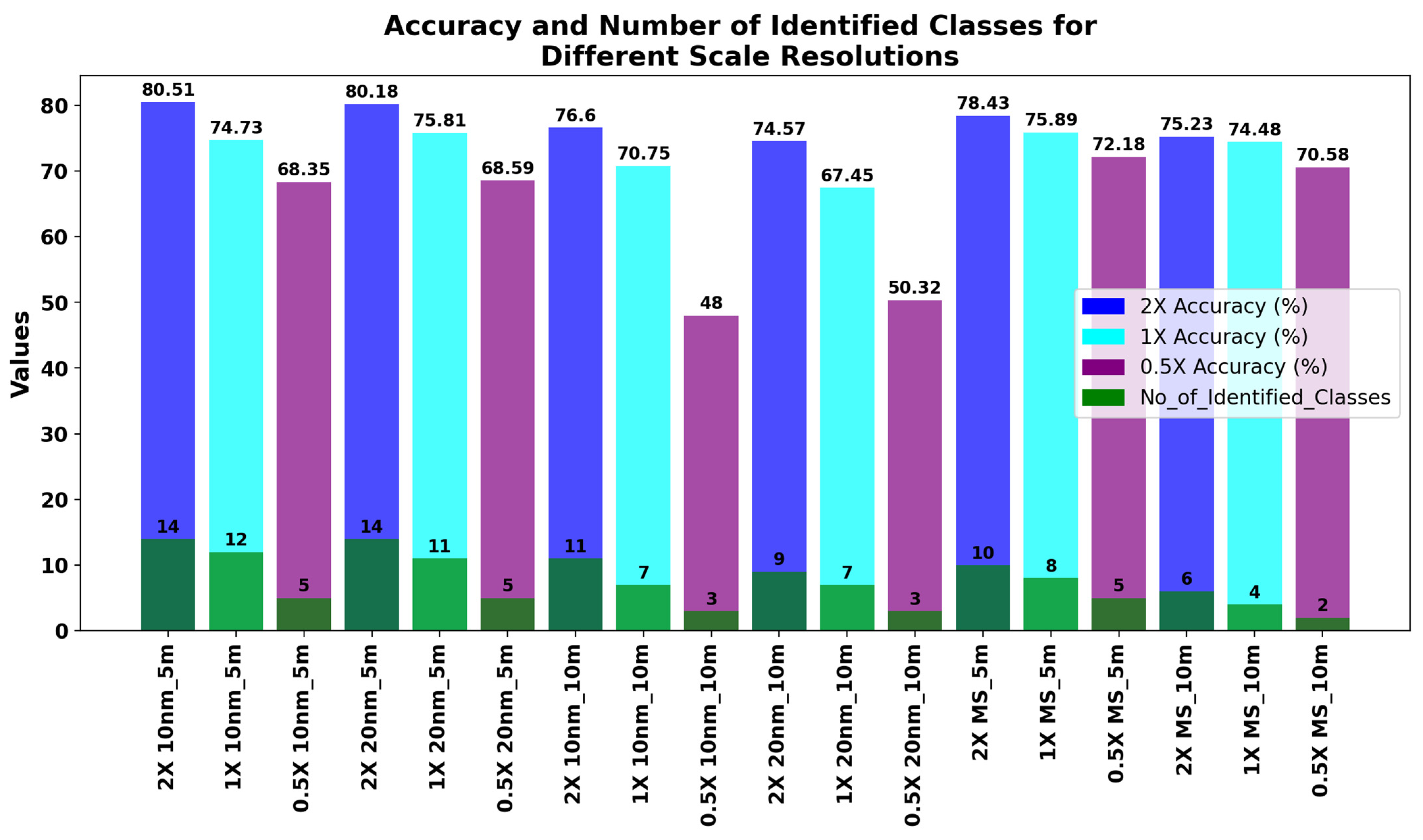
| 2X 10 nm_5 m | 81.00 | 74.23 | 81 | 40 | 82 | 55 | 81 |
| 1X 10 nm_5 m | 74.73 | 65.84 | 75 | 41 | 77 | 64 | 75 |
| 0.5X 10 nm_5 m | 68.35 | 55.20 | 68 | 22 | 75 | 28 | 68 |
| 2X 20 nm_5 m | 80.18 | 73.57 | 80 | 38 | 82 | 62 | 80 |
| 1X 20 nm_5 m | 75.81 | 67.11 | 76 | 34 | 79 | 53 | 76 |
| 0.5X 20 nm_5 m | 68.59 | 57.35 | 70 | 24 | 77 | 27 | 70 |
| Pixel Count per Class for Different Scale Resolutions | |||
|---|---|---|---|
| Class | 0.5X | 1X | 2X |
| acer | 845 | 3603 | 15,010 |
| aronme | 18 | 108 | 599 |
| bark | - | - | 24 |
| betu | 178 | 746 | 3182 |
| castde | - | 229 | 12 |
| fagugr | - | - | 989 |
| fraxni | 10 | 42 | 157 |
| hamavi | 12 | 67 | 343 |
| kalmla | 10 | 54 | 183 |
| larlia | 13 | 57 | 25 |
| nysssy | - | - | 216 |
| ostrvi | 13 | 71 | 4 |
| piceab | - | - | 365 |
| pinu | 98 | 421 | 1706 |
| quer | 882 | 3446 | 13,335 |
| rhodpr | 489 | 2340 | 9855 |
| ulmuam | 2 | 30 | 130 |
| vibual | - | - | 120 |
| Scale Resolution | Overall Accuracy (OA) (%) | Kappa Coefficient (%) | F1 Score (%) | Precision | Recall | ||
|---|---|---|---|---|---|---|---|
| Macro Average (%) | Weighted Average (%) | Macro Average (%) | Weighted Average (%) | ||||
| 2X 10 nm_10 m | 76.60 | 68.32 | 77 | 33 | 79 | 49 | 77 |
| 1X 10 nm_10 m | 70.75 | 58.93 | 71 | 30 | 75 | 50 | 71 |
| 0.5X 10 nm_10 m | 48.00 | 22.32 | 49 | 20 | 52 | 19 | 49 |
| 2X 20 nm_10 m | 74.57 | 65.57 | 75 | 33 | 78 | 43 | 75 |
| 1X 20 nm_10 m | 67.45 | 53.90 | 67 | 26 | 73 | 44 | 73 |
| 0.5X 20 nm_10 m | 50.32 | 26.67 | 50 | 21 | 54 | 19 | 50 |
| 2X MS_5 m | 78.43 | 70.88 | 78 | 28 | 82 | 37 | 78 |
| 1X MS_5 m | 75.89 | 66.52 | 76 | 26 | 83 | 39 | 76 |
| 0.5X MS_5 m | 72.18 | 60.32 | 73 | 23 | 83 | 24 | 73 |
| 2X MS_10 m | 75.23 | 65.73 | 75 | 27 | 81 | 29 | 75 |
| 1X MS_10 m | 74.48 | 62.96 | 74 | 27 | 82 | 28 | 74 |
| 0.5X MS_10 m | 70.58 | 37.49 | 68 | 20 | 75 | 19 | 68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaity, M.D.; van Aardt, J. Exploring the Limits of Species Identification via a Convolutional Neural Network in a Complex Forest Scene through Simulated Imaging Spectroscopy. Remote Sens. 2024, 16, 498. https://doi.org/10.3390/rs16030498
Chaity MD, van Aardt J. Exploring the Limits of Species Identification via a Convolutional Neural Network in a Complex Forest Scene through Simulated Imaging Spectroscopy. Remote Sensing. 2024; 16(3):498. https://doi.org/10.3390/rs16030498
Chicago/Turabian StyleChaity, Manisha Das, and Jan van Aardt. 2024. "Exploring the Limits of Species Identification via a Convolutional Neural Network in a Complex Forest Scene through Simulated Imaging Spectroscopy" Remote Sensing 16, no. 3: 498. https://doi.org/10.3390/rs16030498
APA StyleChaity, M. D., & van Aardt, J. (2024). Exploring the Limits of Species Identification via a Convolutional Neural Network in a Complex Forest Scene through Simulated Imaging Spectroscopy. Remote Sensing, 16(3), 498. https://doi.org/10.3390/rs16030498







