Abstract
Long-term exposure to high concentrations of fine particles can cause irreversible damage to people’s health. Therefore, it is of extreme significance to conduct large-scale continuous spatial fine particulate matter (PM2.5) concentration prediction for air pollution prevention and control in China. The distribution of PM2.5 ground monitoring stations in China is uneven with a larger number of stations in southeastern China, while the number of ground monitoring sites is also insufficient for air quality control. Remote sensing technology can obtain information quickly and macroscopically. Therefore, it is possible to predict PM2.5 concentration based on multi-source remote sensing data. Our study took China as the research area, using the Pearson correlation coefficient and GeoDetector to select auxiliary variables. In addition, a long short-term memory neural network and random forest regression model were established for PM2.5 concentration estimation. We finally selected the random forest regression model (R2 = 0.93, RMSE = 4.59 μg m−3) as our prediction model by the model evaluation index. The PM2.5 concentration distribution across China in 2021 was estimated, and then the influence factors of high-value regions were explored. It is clear that PM2.5 concentration is not only related to the local geographical and meteorological conditions, but also closely related to economic and social development.
1. Introduction
The inception of China’s urbanization development can be traced back to the 1950s when it was primarily driven by heavy industrialization strategies [1]. And, the ensuing urbanization process in China has been characterized by extensive and large-scale expansion. However, this rapid urban growth has also given rise to a host of environmental challenges due to the disregard for natural resource preservation and environmental protection. Among these challenges, haze composed of sulfur dioxide and inhalable particulate matter has emerged as a prominent issue. Of particular concern is fine particulate matter (PM2.5), which can readily infiltrate the human respiratory system, posing significant health risks [2,3]. The Global Air Quality Report 2021, published by IQAir, is the first global air quality report on PM2.5 released under the new standards after the World Health Organization Air Quality Guidelines were updated. According to the report, the average annual concentration of PM2.5 in China has decreased by 21% since 2018. Compared with 2020, 66% of cities saw a decrease in PM2.5 concentration, but none met the Air Quality Guideline’s annual average PM2.5 concentration standard of 5 µg m−3 [4]. The concentration of PM2.5 in China’s most polluted cities was even more than 20 times the standard. Therefore, an accurate understanding of the spatiotemporal distribution of PM2.5 concentrations and the factors affecting them serve as a fundamental prerequisite for the effective implementation of atmospheric pollution control measures.
To monitor atmospheric environmental qualities, the Chinese government has established 1436 monitoring sites in 338 cities, forming a preliminary environmental monitoring network. These observation stations rely on delicate automated instruments to conduct real-time monitoring of surface atmospheric pollutants, providing essential baseline data to support atmospheric pollution prevention and control. However, the spatial distribution of ground-based monitoring stations is uneven, with a larger number of stations distributed in the southeastern regions and urban areas. These result in an incomplete and discontinuous representation of China’s environmental quality through its ground-based monitoring network [5]. The rapid development of satellite remote sensing technology has provided new insights for monitoring environmental quality. Satellite remote sensing technology offers advantages such as wide coverage, low monitoring costs, and continuous dynamic monitoring, which can effectively compensate for the limitations of ground-based monitoring stations [6,7].
Aerosol optical depth (AOD), an indicator of atmospheric turbidity, refers to the integral of the extinction coefficient of a medium in the vertical direction [8]. Many studies have demonstrated a strong correlation between AOD and near-surface PM2.5 concentrations [9,10,11]. Satellite-based PM2.5 estimation generally involves two steps. First, the retrieval of satellite observation data is used to obtain AOD distribution products, then the estimation model of PM2.5 concentration is established based on AOD data and other auxiliary data.
In early studies, scholars mainly used traditional linear regression models to explore the relationship between PM2.5 and satellite-derived AOD [10]. However, the complex temporal and spatial distribution of PM2.5 and the diversity of influencing factors limit the accuracy of simple linear regression models. Therefore, scholars have gradually added factors such as meteorological and land-related factors, leading to the development of multivariate regression models, such as the mixed-effects model [12], two-stage model [13,14], geographically weighted regression model [15,16], and geographically and temporally weighted regression model [17,18,19]. These models have further improved the accuracy of PM2.5 concentration retrieval by incorporating multiple factors and considering their spatial and temporal variations. However, these regression models still cannot fully capture the complex relationships between PM2.5 and a wide range of factors. In recent years, machine learning and deep learning models have been introduced to PM2.5 retrieval research. Compared with the support vector machine model [20] and other machine learning models, the random forest (RF) model [21,22,23] requires fewer parameters and has a higher prediction accuracy and better robustness when dealing with large numbers of data [24,25,26]. And, the RF model is better at processing data without dimensionality reduction [27]. By establishing a recurrent neural network [28], long short-term memory (LSTM) network [29,30], convolutional neural network (CNN) [30,31], and other deep learning models, the spatial and temporal heterogeneity of PM2.5 concentration distribution has been better captured and its prediction accuracy further improved. Many scholars build LSTM models based on hourly or daily data to explore the temporal correlations between PM2.5 concentration and its controlling variables for its excellent ability to capture time dependencies [29,30,32]. The application of the LSTM network based on annual data needs further exploration. Therefore, we evaluated the performances of the RF regression model and LSTM neural network in annual PM2.5 concentration estimation.
An important step of model construction is the selection of independent variables. Factor analysis, Pearson’s correlation coefficient, information gain, and other statistical methods are widely used in feature selection [33,34]. The Pearson’s correlation coefficient is easy to interpret and quantifies the linear relationship between two continuous variables [35], but it does not consider the spatial pattern characteristics of geographic data. The geographical detector model with a q-statistic is a statistical method used to detect spatial heterogeneity and reveal its driving factors [36,37]. This method is good at detecting the relationship of spatial variables between independent variables of type and dependent variables of numerical type without a linear hypothesis. We can use the optimal parameters-based geographical detector (OPGD) model to optimize the process of spatial data discretization and spatial scales for spatial analysis and determine the best parameters for the geographical detector model [38]. Due to its excellence, the geographical detector model has been widely used to identify contributing factors of soil pollution [39,40], air pollution [41], land use transformation [42], and so on. In this study, we combined Pearson’s correlation coefficient and GeoDetector to avoid multicollinearity and improve the representativeness of the selected variables.
Therefore, this study took China as the research area, used the Pearson’s correlation coefficient and GeoDetector to select auxiliary variables, and established two PM2.5 concentration estimation models, that is, the LSTM neural network and RF regression model. After selecting the optimal model by the model evaluation index, the PM2.5 concentration distribution in China in 2021 was estimated and then the influence factors of high-value regions were explored.
2. Materials
All data products used in this study are shown in Table 1.

Table 1.
Summary of the data sources and details.
2.1. Ground-Level PM2.5
The hourly average PM2.5 concentration data of the 2014 monitoring stations (Figure 1) in China from January 2014 to December 2021 were downloaded from the official website of the China Environmental Monitoring Center (CNEMC, https://air.cnemc.cn:18007/, accessed on 22 March 2022). Then, the annual average PM2.5 concentration data from 2014 to 2021 of all ground monitoring stations with geographical location information were obtained. The spatial distribution of monitoring stations generally presented heterogeneity with a larger number of stations in the east of China (Figure 1).
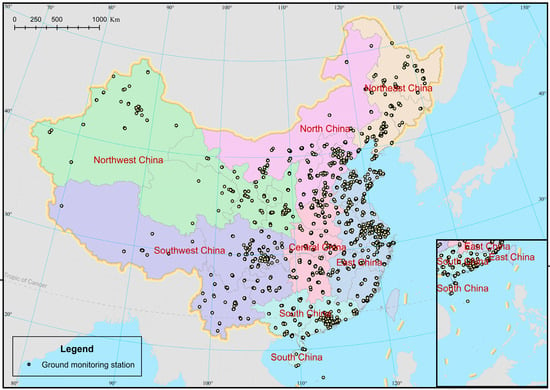
Figure 1.
The spatial distribution of PM2.5 ground monitoring stations in 2021.
2.2. Moderate Resolution Imaging Spectroradiometer (MODIS) AOD Product
MODIS is a passive satellite sensor [43] and was launched on Terra and Aqua spacecraft. With 36 spectral bands and a viewing swath width of 2330 km, MODIS can capture data of the whole world every one to two days, which can be used for atmospheric, terrestrial, and oceanic change research [44,45]. Compared to the dark target and deep blue algorithms, the multi-angle implementation of atmospheric correction (MAIAC) algorithm can meet the requirements for providing aerosol retrieval products with higher spatial resolution [46,47]. The MCD19A2 data product is an AOD gridded Level 2 product for MODIS Terra and Aqua, based on the MAIAC algorithm, providing 1 km resolution of daily AOD data at 550 nm [48,49].
ENVI IDL was used to conduct daily MODIS AOD data product geometric correction, reprojection, mosaic, and other preprocessing operations, and the ArcGIS 10.3 spatial analysis tool was used to synthesize the MODIS AOD annual images of China from 2014 to 2021.
Validation of the MODIS AOD against ground-level AOD was conducted to ensure the satellite-derived AOD data were reliable, accurate, and could be used for the prediction of PM2.5 concentration. Aerosol Robotic Network (AERONET) data are widely used to verify satellite-derived AOD products due to their high accuracy [50,51]. AERONET has set up a total of 81 stations in China. Because of their different setting times and running statuses, the available data of each monitoring station varied greatly in terms of category and coverage time range. AERONET Level 1.5 data (quality-assured) at 21 stations (Table A1) across China providing ground-level AOD data at 440 and 870 nm from 2014 to 2021 were used to verify the MODIS AOD products.
To compare with the MODIS AOD values, AERONET AOD data with a wavelength of 550 nm were interpolated from AERONET AOD at 440 and 870 nm [15,52]. Compared with AEROET AOD observations (Figure A1), the MODIS AOD (retrievals falling within the expected error range, EE = 78.52%, RMSE = 0.187) showed high accuracy, which was sufficient to support our research.
2.3. Auxiliary Data
Previous studies have shown that meteorological and land cover-related factors have significant positive or negative effects on PM2.5 concentration [53,54,55,56,57,58]. Therefore, a total of six meteorology-related variables including surface pressure (P), boundary layer height (BLH), surface air temperature (TEMP), surface air relative humidity (RHU), precipitation (PRE), wind speed (WS) were selected for our study. We also chose three land cover-related variables including the normalized difference vegetation index (NDVI), digital elevation model (DEM), and land use and land cover change (LUCC) as auxiliary variables for PM2.5 retrieval and mapping.
2.3.1. Auxiliary Meteorological Variables
Meteorological factors interact with the PM2.5 concentration through different mechanisms including the dispersion, growth, chemical components, optical properties, and deposition of PM2.5 [59,60]. Therefore, meteorological conditions including the P, BLH, TEMP, RHU, PRE, and WS contribute significantly to the variation in PM2.5 concentrations [59,61,62].
The three monthly auxiliary meteorological factors including BLH, P, and WS were downloaded from the official website of the fifth generation European Center for Medium Weather Forecasting atmospheric reanalysis of the global climate (ERA5), with a spatial resolution of 0.5° × 0.5°. The global atmospheric reanalysis climate dataset ERA5 includes various meteorological factors from 1979 to the present. The other three auxiliary meteorological factors, TEMP, RHU, and PRE, were obtained through the Essential Climate Variable (ECV) data products with a resolution of 0.25° × 0.25°. The ECV data product was reanalyzed based on the ERA-Interim and ERA5 datasets. Atmospheric reanalysis refers to the reprocessing and analysis of historical meteorological observational data through modeling and assimilation analysis techniques to obtain long-term historical atmospheric data with complete spatial coverage [63,64].
The temporal resolution of the auxiliary meteorological data was monthly, and the annual data of each meteorological variable from 2014 to 2021 were obtained by averaging using the ArcGIS 10.3 spatial analysis tool.
2.3.2. Auxiliary Land Use-Related Variables
The leaf surfaces of vegetation including grass and trees have a considerable capacity to reduce PM2.5 via dispersion and deposition [65,66]. Generally, an increase in PM2.5 concentration is closely related to a decrease in vegetation greenness [67]. To indicate vegetation greenness, the MODIS MOD13A3 data product provided by MODIS was selected for the NDVI variable. MOD13A3 is a three-level gridded product with a sinusoidal projection, which provides 1 km monthly NDVI and other environmental variables. MODIS NDVI is centered on the blue, red, and near-infrared wavelengths of 469, 645, and 858 nm, respectively.
In our study, the MOD13A3 NDVI data product was selected and the MRT tool was used to mosaic and reproject the remote sensing images. Then, ArcGIS 10.3 was used to obtain yearly NDVI images of China by maximum value composites from the year 2014 to 2021.
Elevation acts as a constraining variable for PM2.5 transmission. Scholars have found that the Yan Mountains in the north and Taihang Mountains in the west can trap PM2.5 from the lower elevations in the south and stop transmission to the higher elevations in the northern part of the Beijing–Tianjin–Hebei region [68,69]. And, there is a positive correlation between urbanization and PM2.5 concentration [70,71]. Generally, the PM2.5 concentrations on natural vegetation are much lower than those on artificial surfaces [72]. The annual DEM product at a 250 m resolution and LUCC data at a 30 m resolution were downloaded from the official website of the China Resource and Environment Science and Data Center (RESDC).
3. Methods
3.1. Research Framework
Our study was constructed in several steps (Figure 2). Firstly, the ten factors in Table 1 were used as independent variables, while PM2.5 concentrations were adopted as the dependent variable. Since MODIS AOD, meteorological, and land-related data are raster data, it was necessary to extract their values to each PM2.5 ground observation point using the spatial analysis tool in ArcGIS 10.3. The PM2.5 dataset containing environmental elements from 2014 to 2021 in China was then obtained.
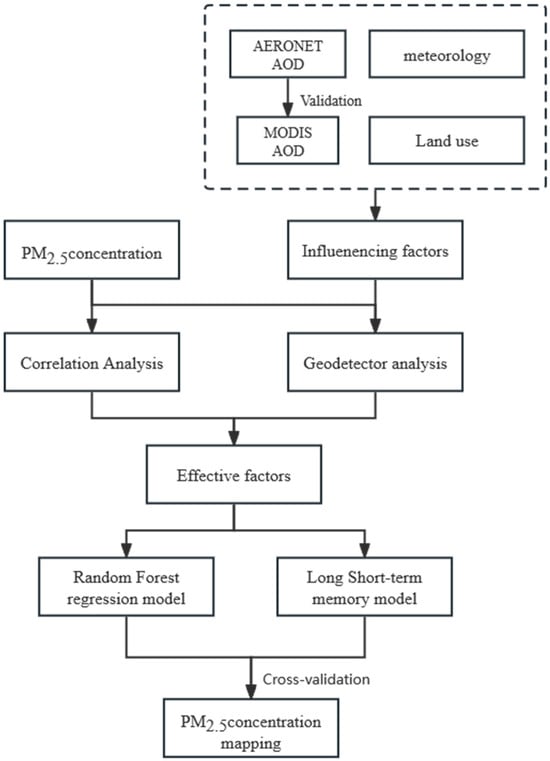
Figure 2.
The research framework.
Secondly, we used Pearson’s correlation coefficient and GeoDetector to determine the effective factors. Only one factor was retained when the Pearson correlation coefficient of two variables was greater than 0.8 and the variance inflation factor (VIF) was greater than 5 [73]. And, we excluded those variables with a p-value greater than 0.01 in GeoDetector analysis. Then, according to the model evaluation indexes, we compared the RF and LSTM models and selected the optimal PM2.5 predicting model to estimate PM2.5 concentration distribution based on multi-source satellite products across China in 2021.
3.2. GeoDetector Analysis
GeoDetector is a statistical method used to detect the degree of spatial stratified heterogeneity and reveal the driving factors. The coupled degree of the spatial distribution of independent and dependent variables can be statistically measured by the q-statistic, which increases as the strength of the stratified heterogeneity increases [36,37].
The GeoDetector method uses the q-statistic, ranging from 0 to 1, to reflect the spatial correlation of the factors and by the following equation [37]:
where is the number of units in the study area, is the number of strata of factor , is the number of units in strata of factor , is the total variance of in the study area, and is the variance of within strata of factor .
3.3. RF Regression Model
Based on the bagging idea of ensemble learning, RF is an algorithm that integrates multiple trees, and a decision tree is its basic unit [27]. Each node inside the regression decision tree represents the judgment of a certain factor, different branches of the tree represent different judgment results, and leaf nodes represent sample sets with the same judgment results [74].
The results of random forest regression are based on the mean of each decision tree :
where is the independent variable, is an independent and identically distributed random variable, is the number of decision trees, and is the output of each decision tree based on and .
The training samples of each decision tree are randomly selected by the bootstrap method, and the features are selected and optimized randomly during node segmentation [75]. Therefore, the random forest is not prone to overfitting and has good anti-noise ability [76].
We used Python’s scikit-learn machine learning library to build a random forest regression model.
3.4. LSTM
The LSTM model is an improved approach to recurrent neural networks (RNNs) [77]. An RNN adds the relationship between before and after time series based on a fully connected neural network, which can solve the problems related to time series, but the explosion and disappearance of the gradient may occur at distant nodes [78]. LSTM is designed to solve this problem. The LSTM consists of memory cells and a gate mechanism. Each memory cell contains a cell state and three gates: the forget gate, input gate, and output gate (Figure 3). The three gates have sigmoid activation function control which changes in their cell state.
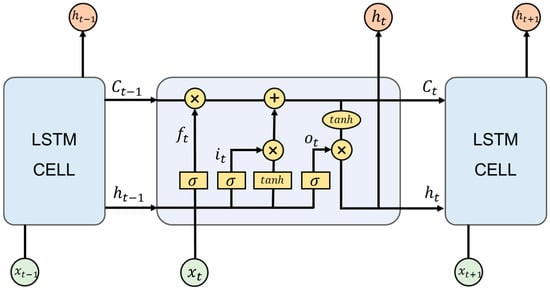
Figure 3.
LSTM cell structure including forget, input, and output gates.
The forget gate can be computed as the following:
where represents the forget gate vector, and are the weight and bias vectors of the forget gate, is the output result at the last moment, is the input at the current moment, represents connecting two vectors into a longer vector, and represents the activation function.
The input gate and output gate can be computed as the following:
where , , and are vectors of the input gate, output gate, and cell state, respectively, is the vector of output, , and are the weights of the corresponding gate, , , and represent the bias vector of the corresponding gate, and is a kind of activation function.
The LSTM model was implemented in the Python Keras module. We fed data into the model after min–max normalization. In order to achieve the optimal performance of the model, the optimizer of the LSTM model was Adam, the batch size was set to 72, and epochs were set to 50. The time step was 3, which meant that the data in the previous three years were used to predict the PM2.5 concentration.
3.5. Model Validation
Three cross-validation (CV) methods were chosen in terms of sample-based CV, temporal CV, and spatial CV to evaluate the performance of the models. For the sample-based CV process, the dataset was divided into 10 folds randomly. One fold was used for validation and the model was trained using the remaining nine folds, which were then rotated until ten folds were used for validation again. Temporal CV involved excluding one year for validation, with the remaining years utilized for model fitting. In spatial CV, the dataset was partitioned into calibration and validation groups based on China’s geographical divisions (Figure 1). The workflows for the temporal CV and spatial CV were similar to the sample-based CV, differing only in the methods employed for dividing calibration and validation sets.
This study selected indicators of the coefficient of determination (), root mean square error (RMSE), and mean absolute error (MAE):
where and are the observed and predicted data, and are the averages of the observed and predicted data, and m is the number of the sample.
4. Results
4.1. Descriptive Statistics
From 2014 to 2021, the annual average PM2.5 concentration at the ground monitoring stations decreased steadily and reached the lowest value of 32.64 μg m−3 in 2021 (Table 2) during the study periods. The annual average PM2.5 concentration dropped by 29.98 μg m−3 in the eight years. According to Figure 4, in 2016, 2017, and 2020, there were some abnormally high values of PM2.5 concentration with values over 170 μg m−3. In addition, the PM2.5 concentrations across China changed the least in 2015 and 2021. While the minimum PM2.5 concentration rose to approximately 6 μg m−3 during the COVID-19 lockdown period, the annual average concentration across China continued to decrease, albeit at a slower rate.

Table 2.
Summary of ground monitoring sites from 2014 to 2021.
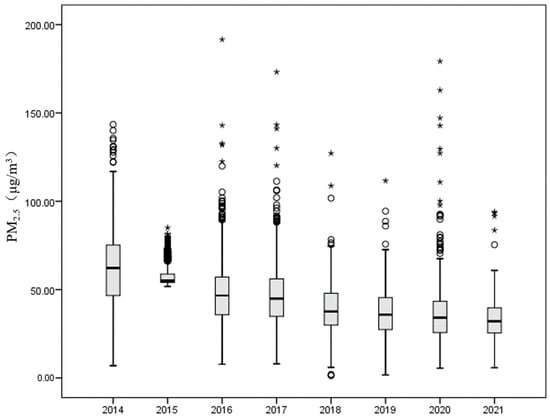
Figure 4.
Boxplots of ground-level PM2.5 from 2014 to 2021. Points at a greater distance from the median than 1.5 times the interquartile range are plotted individually as asterisks (*).
The spatial distributions of the annual average concentration of PM2.5 at each station from 2014 to 2021 are shown in Figure 5. The ground-level PM2.5 concentration during these eight years showed obvious spatial stratified heterogeneity with the high value centering around North China. North China had a relatively high PM2.5 concentration, followed by parts of the central region. By contrast, the concentrations of PM2.5 in the eastern coastal region and Southwest China were at a low level.
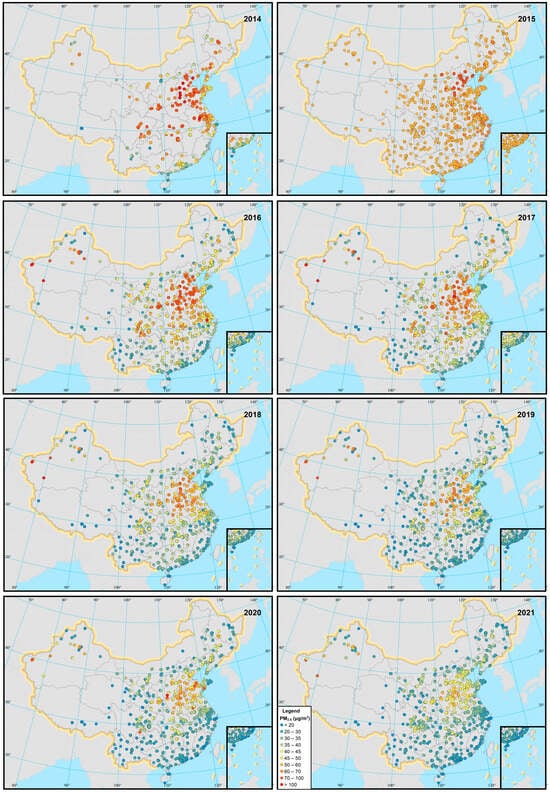
Figure 5.
The annual average PM2.5 concentration distributions of sites from 2014 to 2021.
4.2. Variable Selection
Pearson’s correlation coefficient analysis was used to assess the correlation between each dependent variable and PM2.5 concentration. The results of the Pearson’s correlation coefficient showed that the relationship between independent variables and PM2.5 concentration was moderately positive and weakly negative (Figure 6), especially for the AOD (r = 0.45, p < 0.01) and PRE (r = −0.25, p < 0.01). In addition, considering the issue of covariance among the independent variables, we used the VIF to make judgments. Table 3 shows a strong covariance between P and DEM (P ~ 16.91, DEM ~ 13.43). Differences in atmospheric pressure in years would be more sensitive than in the DEM data, so the variable P was chosen and the variable DEM was excluded.
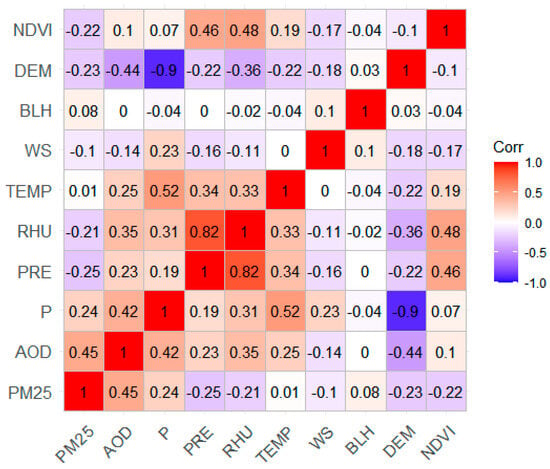
Figure 6.
Correlation matrix of all variables.

Table 3.
Table of variance inflation factors.
GeoDetector analysis was used to compute the contribution of each factor toward PM2.5 concentration. It was necessary to categorize all continuous variables by natural break classification to conduct the GeoDetector analysis. In this study, AOD and TEMP were divided into eight categories, while P, BLH, RHU, PRE, WS, and NDVI were separated into ten categories. The results (Table 4) indicated that all the dependent variables, except for LUCC (q = 0.076, p > 0.05), contributed to the spatial heterogeneity of the PM2.5 concentrations. Among them, TEMP (q = 0.34, p < 0.01), PRE (q = 0.23, p < 0.01), and AOD (q = 0.17, p < 0.01) ranked in the top three.

Table 4.
Results of factor detection by GeoDetector.
Therefore, the eight explanatory variables, AOD, NDVI, surface pressure, precipitation, surface air relative humidity, surface air temperature, wind speed, and boundary layer height, were finally selected to invert the PM2.5 concentration distribution in China.
4.3. Model Fitting and Validation
Scatterplots illustrate the models’ accuracy in estimating PM2.5 concentrations across China, with the results of three CV methods presented in Figure 7. Compared to spatial CV and temporal CV, both the RF and LSTM models exhibited better performance in sample-based CV with higher R2 values of 0.93 and 0.75, respectively. While the RF model performed optimally in sample-based CV, its performance exhibited a decline in spatial and temporal CV with R2 decreasing to 0.54 and 0.64, respectively. The LSTM model exhibited relatively stable performance across three types of CVs, with R2 and RMSE values ranging from 0.64 to 0.75 and 6.40 μg m−3 to 7.85 μg m−3.
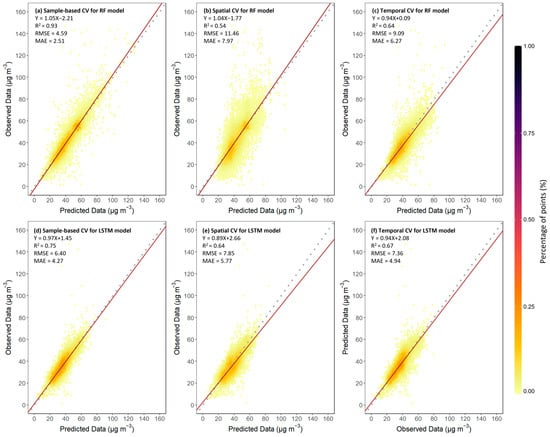
Figure 7.
The density scatterplots of model validation results. (a) Sample-based CV for the RF model, (b) Spatial CV for the RF model, (c) Temporal CV for the RF model, (d) Sample-based CV for the LSTM model, (e) Spatial CV for the LSTM model, and (f) Temporal CV for the LSTM model. The colors of points represent the percentages of the total number of points in the value range. The solid red line denotes the line of best fit using linear regression and the gray dashed line represents the 1:1 line. The units of the RMSE and MAE are μg m−3.
The overall accuracy was assessed through a sample-based CV (Figure 7). The RF model outperformed the LSTM model with a higher R2, lower RMSE, and MAE (R2 = 0.93, RMSE = 4.59 μg m−3, MAE = 2.51 μg m−3), and the data points of the RF were more concentrated. Though the LSTM model took the time series into consideration, the model performance did not increase. In addition, the predictive ability of both models for high-value points was significantly weaker than that for low values. The high values tended to be underestimated, while the median values (20–80 μg m−3) were often predicted more accurately.
4.4. Spatial Distribution of PM2.5 Concentrations
According to the model validation results, we chose the RF model to estimate the annual average PM2.5 concentration at a 10 km spatial resolution in 2021 (Figure 8).
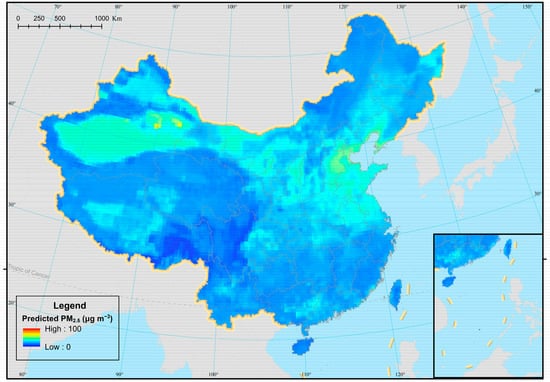
Figure 8.
PM2.5 concentration spatial distribution of China in 2021.
In 2021, the annual predicted average PM2.5 concentration in China was 26.93 ± 18.78 μg m−3, lower than the average observed concentration (32.64 μg m−3). Spatially, the PM2.5 concentrations showed a clear trend of gradual increase from the south to the north. Highly PM2.5 concentrated areas over 50 μg m−3 were predominately located in North and Northwest China. Approximately 29.8% of China’s land area had average concentrations ranging between 30 and 50 μg m−3. Conversely, low-value regions were concentrated in Southwest China and in southeast coastal areas, with the annual average PM2.5 falling between 10 and 30 μg m−3.
It was clear that the 30th parallel north divides China’s high and low PM2.5 concentration areas in a north–south direction except for the Qinghai–Tibetan Plateau. The east–west split line between high- and low-value zones was consistent with the Heihe–Tengchong Line. The spatial distribution of highly polluted areas of China was consistent with the distribution of deserts in the Xinjiang Uygur Autonomous Region and the Beijing–Tianjin–Hebei (BTH) region. In addition, high PM2.5 concentration zones were scattered in southeastern Inner Mongolia and northern Shaanxi Province. The low PM2.5 concentration areas were mainly located in the Qinghai–Tibetan Plateau, southern coastal areas, and Greater Khingan Mountain region. The lowest PM2.5 concentration zone was near the Hengduan Mountain range with around 10 μg m−3 in 2021.
5. Discussion
5.1. Comparison with Recent Studies
Overall, our model used to estimate PM2.5 concentration across China obtained satisfactory performance. Our feature selection method combining GeoDetector and Pearson’s correlation coefficient provided statistical support for identifying effective factors, which contributed to the improvement in model accuracy. Moreover, RF regression models can avoid complex structures and consume less computational resources [79]; thus the RF regression model outperformed the LSTM neural network in annual average PM2.5 concentration prediction.
The time effect in predicting model construction did not improve the precision and accuracy of the model, and the R2 for the LSTM was only 0.75. Referring to previous studies [38,80,81], this may have been caused by the low temporal resolution of data. We used annual data for prediction, and as a result, the time characteristics of each variable were smoothed. Kang et al. [82] built an LSTM model based on the hourly air quality concentration data and meteorological data of Shanghai from January to October 2017, which showed an excellent performance with an R2 value of 0.98 and RMSE of 2.98 μg m−3. In contrast, prediction performance by RF on a monthly or yearly scale is better than that on a daily scale [83].
We conducted three CV methods to assess the accuracy of the models. The models displayed relatively lower precision in temporal and spatial CV, primarily due to the diversity of the PM2.5 concentrations at the temporal and spatial scales [25]. Upon the introduction of spatiotemporal information into the regression model, the results of the three CV methods might have become stable [83]. According to the model performance, the random forest model was finally selected to monitor the temporal and spatial distribution of the annual average PM2.5 concentration across China in 2021. The accuracy of the model in this study on a national scale, characterized by a relatively higher validation R2 value and lower RMSE, outperformed many statistical regression models (Table 5), including geographical weighted regression (GWR), geographically and temporally weighted regression (GTWR), and adaptive spatiotemporal regression (ASTR) models. And, many scholars [25,83] only conducted a collinearity test to determine its effective factors without considering nonlinear relationships between factors, whereas our study took advantage of the GeoDetector to fill this gap for higher model accuracy.

Table 5.
The model performance compared with other studies.
There is however still room for predicting capability improvement. When input data are subdivided into classes representing different aerosol types [84] and the estimation models take the synergy of space–time information into account [83], the models may perform better. Although the traditional GWR model and GTWR model make use of spatial information, the performance of the models is still not as good as our model for the limitation of regression ability (Table 5). In this study, we considered geographical stratified heterogeneity to determine the contributing factors, which effectively improved the accuracy of PM2.5 estimation. A further study with more focus on aggregating spatial information into a machine learning regression model [85] should be performed to investigate this. Therefore, socioeconomic factors including population, light at night, road density, and industrial emissions play an important role in the distribution of air pollutants [23,86]. Therefore, incorporating socioeconomic variables into a prediction model is a direction for our future work.
5.2. Heavy PM2.5 Pollution Area Analysis
The average annual PM2.5 concentration in the Xinjiang region was 29.33 ± 18.72 μg m−3, ranging from 14.47 μg m−3 to 71.95 μg m−3. The NDVI and PRE values there were relatively low, which was unbeneficial to particulate matter deposition. The deserts in the Xinjiang region are widely distributed to provide rich material sources for the formation of fine particles, and the specific topographic features hinder the diffusion of PM2.5, so the concentration of PM2.5 in the Xinjiang region is relatively high [89]. The Qinghai–Tibetan Plateau, which is bound by the Kunlun Mountains, Qilian Mountains, and Hengduan Mountains, is only separated from the Xinjiang Province by a mountain, but it was a large low-value area of PM2.5 concentration in China in 2021. Similarly, the unfavorable geographical conditions for PM2.5 transportation and dispersion also result in high pollution in northern Shaanxi Province [90].
The variation in PM2.5 concentration is not only related to the local geographical conditions, but also closely related to economic development situations [91,92]. The BTH region was a PM2.5 heavily polluted area with an average annual concentration of 35.64 ± 16.28 μg m−3, ranging from 19.33 μg m−3 to 47.92 μg m−3. Although this region has favorable meteorological and topographical conditions, its high proportion of energy-consuming industries with exhaust gas emission, continuous heating systems in winter, vehicular emission, and rapid urbanization all contribute to heavy PM2.5 pollution [91,92,93,94]. Therefore, in order to reduce the level of PM2.5 concentration, the BTH region should make full use of natural advantages such as wind power to develop new cleaning energy, as well as improve the energy and industrial structure, together with continuing to promote technological innovation [95].
The causes of high-value areas are different. Therefore, the Chinese government needs to formulate guidelines and policies based on the actual causes of pollution.
6. Conclusions
In this study, a machine learning-based PM2.5 predicting model was established. The Pearson’s correlation coefficient and GeoDetector were used to select independent variables to monitor PM2.5 concentrations in China. The results showed that the RF model had a better performance compared with the LSTM model with an R2 value of 0.94 and RMSE of 4.59 μg m−3. The spatial distribution of PM2.5 across China in 2021 (Figure 8) was generated using the RF model. In 2021, the annual average PM2.5 concentration was 26.93 ± 18.78 μg m−3. Spatially, the PM2.5 concentration showed a clear trend of a gradual increase from the south to the north.
In the future, a high temporal and spatial resolution dataset can be used to improve the model’s performance. Furthermore, the spatial heterogeneous distribution of PM2.5 ground monitoring stations with more sites distributed in the southeast of China could make the results more representative of eastern China. This shortcoming could be resolved by introducing economic and demographic variables.
Author Contributions
Conceptualization, Y.Y. and Z.W.; data curation, H.G.; formal analysis, Y.Y.; funding acquisition, C.C., M.X. and X.Y.; investigation, K.W.; methodology, Y.Y. and Z.W.; project administration, C.C., M.X. and X.Y.; resources, Z.W.; software, Y.Y.; supervision, C.C., X.Y. and Z.S.; validation, J.L.; visualization, X.G.; writing—original draft, Y.Y.; writing—review and editing, Z.W., C.C., M.X. and Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Forestry Technological Developments and Monitoring and Assessment of Terrestrial Ecosystem Research (No. 2020132108).
Data Availability Statement
Data are contained within this article.
Acknowledgments
We would like to thank the China National Environmental Monitoring Center, the Level-1 and Atmosphere Archive & Distribution System, the National Aeronautics and Space Administration, the European Centre for Medium-Range Weather Forecasts, and the Resource and Environmental Science and Data Center, Chinese Academy of Sciences, for their data support.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A

Table A1.
Information on the AERONET monitoring sites across China.
Table A1.
Information on the AERONET monitoring sites across China.
| Site | Longitude (°E) | Latitude (°N) | Source |
|---|---|---|---|
| AOE_Baotou | 109.629 | 40.852 | https://aeronet.gsfc.nasa.gov/, accessed on 23 September 2023. |
| Beijing | 116.381 | 39.977 | |
| Beijing_PKU | 116.31 | 39.992 | |
| Beijing-CAMS | 116.317 | 39.933 | |
| Beijing_RADI | 116.379 | 40.005 | |
| Hong_Kong_PolyU | 114.180 | 22.303 | |
| Hong_Kong_Sheung | 114.117 | 22.483 | |
| Kashi | 75.930 | 39.504 | |
| Lingshan_Mountain | 115.496 | 40.054 | |
| NAM_CO | 90.962 | 30.773 | |
| QOMS_CAS | 86.948 | 28.365 | |
| SONET_Harbin | 126.614 | 45.705 | |
| SONET_Hefei | 117.162 | 31.905 | |
| SONET_Nanjing | 118.957 | 32.115 | |
| SONET_Xingtai | 114.360 | 37.182 | |
| SONET_Zhoushan | 122.188 | 29.994 | |
| Taihu | 120.215 | 31.421 | |
| XiangHe | 119.962 | 39.754 | |
| XingLong | 117.578 | 40.396 | |
| XuZhou-CUMT | 117.142 | 34.217 | |
| Yanqihu | 116.674 | 40.408 |
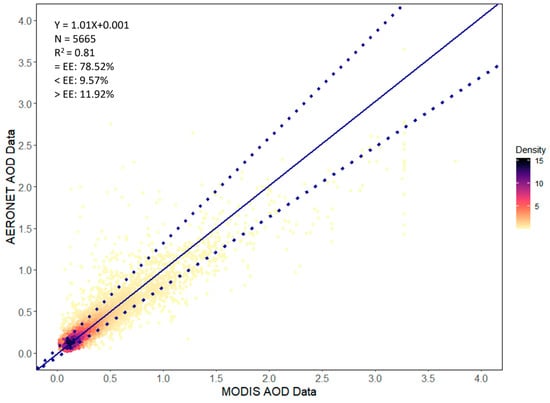
Figure A1.
The validation of the MODIS AOD and AERONET Level 1.5 AOD data with a wavelength of 550 nm. N, R2, and EE represent the number of matches, correlation coefficient, and expected error (EE = ±(0.05 + 0.2AOD)), respectively. The colors of points represent the density in the value range. The blue solid line and blue dashed lines represent the linear regression of the scattered dots and expected retrieval error lines, respectively.
References
- Gu, C.L.; Hu, L.Q.; Cook, I.G. China’s urbanization in 1949–2015: Processes and driving forces. Chin. Geogr. Sci. 2017, 27, 847–859. [Google Scholar] [CrossRef]
- Barzeghar, V.; Sarbakhsh, P.; Hassanvand, M.S.; Faridi, S.; Gholampour, A. Long-term trend of ambient air PM10, PM2.5, and O3 and their health effects in Tabriz city, Iran, during 2006–2017. Sustain. Cities Soc. 2020, 54, 101988. [Google Scholar] [CrossRef]
- Thangavel, P.; Park, D.; Young-Chul, L. Recent Insights into Particulate Matter (PM2.5)-Mediated Toxicity in Humans: An Overview. Int. J. Environ. Res. Public. Health 2022, 19, 7511. [Google Scholar] [CrossRef] [PubMed]
- IQAir. 2021 World Air Quality Report; IQAir: Goldach, Switzerland, 2022. [Google Scholar]
- Liu, J.; Weng, F.; Li, Z. Satellite-based PM2.5 estimation directly from reflectance at the top of the atmosphere using a machine learning algorithm. Atmos. Environ. 2019, 208, 113–122. [Google Scholar] [CrossRef]
- Bai, K.; Li, K.; Sun, Y.; Wu, L.; Zhang, Y.; Chang, N.-B.; Li, Z. Global synthesis of two decades of research on improving PM2.5 estimation models from remote sensing and data science perspectives. Earth-Sci. Rev. 2023, 241, 104461. [Google Scholar] [CrossRef]
- Li, F.; Yigitcanlar, T.; Nepal, M.; Nguyen, K.; Dur, F. Machine learning and remote sensing integration for leveraging urban sustainability: A review and framework. Sustain. Cities Soc. 2023, 96, 104653. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Lyapustin, A.; Sun, L.; Peng, Y.; Xue, W.; Su, T.; Cribb, M. Reconstructing 1-km-resolution high-quality PM2.5 data records from 2000 to 2018 in China: Spatiotemporal variations and policy implications. Remote Sens. Environ. 2021, 252, 112136. [Google Scholar] [CrossRef]
- He, Q.; Gao, K.; Zhang, L.; Song, Y.; Zhang, M. Satellite-derived 1-km estimates and long-term trends of PM2.5 concentrations in China from 2000 to 2018. Environ. Int. 2021, 156, 106726. [Google Scholar] [CrossRef]
- Shao, P.; Xin, J.; An, J.; Kong, L.; Wang, B.; Wang, J.; Wang, Y.; Wu, D. The empirical relationship between PM2.5 and AOD in Nanjing of the Yangtze River Delta. Atmos. Pollut. Res. 2017, 8, 233–243. [Google Scholar] [CrossRef]
- Xin, J.; Zhang, Q.; Wang, L.; Gong, C.; Wang, Y.; Liu, Z.; Gao, W. The empirical relationship between the PM2.5 concentration and aerosol optical depth over the background of North China from 2009 to 2011. Atmos. Res. 2014, 138, 179–188. [Google Scholar] [CrossRef]
- Lee, H.J.; Liu, Y.; Coull, B.A.; Schwartz, J.; Koutrakis, P. A novel calibration approach of MODIS AOD data to predict PM2.5 concentrations. Atmos. Chem. Phys. 2011, 11, 7991–8002. [Google Scholar] [CrossRef]
- Guo, W.; Zhang, B.; Wei, Q.; Guo, Y.; Yin, X.; Li, F.; Wang, L.; Wang, W. Estimating ground-level PM2.5 concentrations using two-stage model in Beijing-Tianjin-Hebei, China. Atmos. Pollut. Res. 2021, 12, 101154. [Google Scholar] [CrossRef]
- Zeng, Q.L.; Li, Y.M.; Tao, J.H.; Fan, M.; Chen, L.F.; Wang, L.H.; Wang, Y.C. Full-coverage estimation of PM2.5 in the Beijing-Tianjin-Hebei region by using a two-stage model. Atmos. Environ. 2023, 309, 119956. [Google Scholar] [CrossRef]
- Ma, Z.W.; Hu, X.F.; Huang, L.; Bi, J.; Liu, Y. Estimating Ground-Level PM2.5 in China Using Satellite Remote Sensing. Environ. Sci. Technol. 2014, 48, 7436–7444. [Google Scholar] [CrossRef]
- Tang, Y.B.; Xie, S.F.; Huang, L.K.; Liu, L.L.; Wei, P.Z.; Zhang, Y.B.; Meng, C.Y. Spatial Estimation of Regional PM2.5 Concentrations with GWR Models Using PCA and RBF Interpolation Optimization. Remote Sens. 2022, 14, 5626. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, L.X.; Qin, K.; Zhang, Y.F.; Shen, Y.Y.; Zhou, Y. A Geographically and Temporally Weighted Regression Model for Ground-Level PM2.5 Estimation from Satellite-Derived 500 m Resolution AOD. Remote Sens. 2016, 8, 262. [Google Scholar] [CrossRef]
- Wu, L.; Bai, Y.; Zhang, Y.; Li, J.; Han, Y.; Qin, K. Estimate PM2.5 Concentration in 500 m Resolution from Satellite Data and Ground Observation. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5716–5719. [Google Scholar]
- Zhao, H.B.; Liu, Y.X.; Gu, T.S.; Zheng, H.; Wang, Z.Y.; Yang, D.Y. Identifying Spatiotemporal Heterogeneity of PM2.5 Concentrations and the Key Influencing Factors in the Middle and Lower Reaches of the Yellow River. Remote Sens. 2022, 14, 2643. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, H.; Qin, Z.D.; Zhang, G.S. A novel hybrid-Garch model based on ARIMA and SVM for PM2.5 concentrations forecasting. Atmos. Pollut. Res. 2017, 8, 850–860. [Google Scholar] [CrossRef]
- Huang, K.; Xiao, Q.; Meng, X.; Geng, G.; Wang, Y.; Lyapustin, A.; Gu, D.; Liu, Y. Predicting monthly high-resolution PM2.5 concentrations with random forest model in the North China Plain. Environ. Pollut. 2018, 242, 675–683. [Google Scholar] [CrossRef]
- Li, X.Y.; Li, L.; Chen, L.G.; Zhang, T.; Xiao, J.Y.; Chen, L.Q. Random Forest Estimation and Trend Analysis of PM2.5 Concentration over the Huaihai Economic Zone, China (2000–2020). Sustainability 2022, 14, 8520. [Google Scholar] [CrossRef]
- Stafoggia, M.; Bellander, T.; Bucci, S.; Davoli, M.; de Hoogh, K.; de’ Donato, F.; Gariazzo, C.; Lyapustin, A.; Michelozzi, P.; Renzi, M.; et al. Estimation of daily PM10 and PM2.5 concentrations in Italy, 2013–2015, using a spatiotemporal land-use random-forest model. Environ. Int. 2019, 124, 170–179. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Y.H.; Chen, M.X.; Wang, L.; Zhao, S.H.; Pu, X.; Chen, X.G. Estimation of monthly 1 km resolution PM2.5 concentrations using a random forest model over “2 + 26” cities, China. Urban. Clim. 2021, 35, 100734. [Google Scholar] [CrossRef]
- Guo, B.; Zhang, D.M.; Pei, L.; Su, Y.; Wang, X.X.; Bian, Y.; Zhang, D.H.; Yao, W.Q.; Zhou, Z.X.; Guo, L.Y. Estimating PM2.5 concentrations via random forest method using satellite, auxiliary, and ground-level station dataset at multiple temporal scales across China in 2017. Sci. Total Env. 2021, 778, 146288. [Google Scholar] [CrossRef]
- Bagheri, H. A machine learning-based framework for high resolution mapping of PM2.5 in Tehran, Iran, using MAIAC AOD data. Adv. Space Res. 2022, 69, 3333–3349. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Dai, X.; Liu, J.; Li, Y. A recurrent neural network using historical data to predict time series indoor PM2.5 concentrations for residential buildings. Indoor Air 2021, 31, 1228–1237. [Google Scholar] [CrossRef]
- Li, J.; Xu, G.; Cheng, X. Combining spatial pyramid pooling and long short-term memory network to predict PM2.5 concentration. Atmos. Pollut. Res. 2022, 13, 101309. [Google Scholar] [CrossRef]
- Wen, C.C.; Liu, S.; Yao, X.J.; Peng, L.; Li, X.; Hu, Y.; Chi, T.H. A novel spatiotemporal convolutional long short-term neural network for air pollution prediction. Sci. Total Environ. 2019, 654, 1091–1099. [Google Scholar] [CrossRef] [PubMed]
- Kabir, S.; Ul Islam, R.; Hossain, M.S.; Andersson, K. An integrated approach of Belief Rule Base and Convolutional Neural Network to monitor air quality in Shanghai. Expert. Syst. Appl. 2022, 206, 117905. [Google Scholar] [CrossRef]
- Casallas, A.; Ferro, C.; Celis, N.; Guevara-Luna, M.A.; Mogollón-Sotelo, C.; Guevara-Luna, F.A.; Merchán, M. Long short-term memory artificial neural network approach to forecast meteorology and PM2.5 local variables in Bogotá, Colombia. Model. Earth Syst. Environ. 2021, 8, 2951–2964. [Google Scholar] [CrossRef]
- Sun, D.; Shi, S.; Wen, H.; Xu, J.; Zhou, X.; Wu, J. A hybrid optimization method of factor screening predicated on GeoDetector and Random Forest for Landslide Susceptibility Mapping. Geomorphology 2021, 379, 107623. [Google Scholar] [CrossRef]
- Lee, S.; Talib, J.A. Probabilistic landslide susceptibility and factor effect analysis. Environ. Geol. 2005, 47, 982–990. [Google Scholar] [CrossRef]
- Mukaka, M.M. A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar] [PubMed]
- Wang, J.F.; Li, X.H.; Christakos, G.; Liao, Y.L.; Zhang, T.; Gu, X.; Zheng, X.Y. Geographical Detectors-Based Health Risk Assessment and its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Wang, J.F.; Zhang, T.L.; Fu, B.J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Ge, Y.; Xu, C. An optimal parameters-based geographical detector model enhances geographic characteristics of explanatory variables for spatial heterogeneity analysis: Cases with different types of spatial data. GISci. Remote Sens. 2020, 57, 593–610. [Google Scholar] [CrossRef]
- Qiao, Y.; Wang, X.; Han, Z.; Tian, M.; Wang, Q.; Wu, H.; Liu, F. Geodetector based identification of influencing factors on spatial distribution patterns of heavy metals in soil: A case in the upper reaches of the Yangtze River, China. Appl. Geochem. 2022, 146, 105459. [Google Scholar] [CrossRef]
- Shi, H.; Wang, P.; Zheng, J.; Deng, Y.; Zhuang, C.; Huang, F.; Xiao, R. A comprehensive framework for identifying contributing factors of soil trace metal pollution using Geodetector and spatial bivariate analysis. Sci. Total Environ. 2023, 857, 159636. [Google Scholar] [CrossRef]
- Zhao, R.; Zhan, L.; Yao, M.; Yang, L. A geographically weighted regression model augmented by Geodetector analysis and principal component analysis for the spatial distribution of PM2.5. Sustain. Cities Soc. 2020, 56, 102106. [Google Scholar] [CrossRef]
- Gong, Y.; You, G.; Chen, T.; Wang, L.; Hu, Y. Rural Landscape Change: The Driving Forces of Land Use Transformation from 1980 to 2020 in Southern Henan, China. Sustainability 2023, 15, 2565. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Barnes, W.L.; Maymon, P.W.; Montgomery, H.E.; Ostrow, H. MODIS: Advanced facility instrument for studies of the Earth as a system. IEEE Trans. Geosci. Remote Sens. 1989, 27, 145–153. [Google Scholar] [CrossRef]
- Wang, J.; Bretz, M.; Dewan, M.A.A.; Delavar, M.A. Machine learning in modelling land-use and land cover-change (LULCC): Current status, challenges and prospects. Sci. Total Environ. 2022, 822, 153559. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Liu, M.; Tao, M.; Zhou, W.; Lu, X.; Xiong, Y.; Li, F.; Wang, Q. The role of satellite remote sensing in mitigating and adapting to global climate change. Sci. Total Environ. 2023, 904, 166820. [Google Scholar] [CrossRef] [PubMed]
- Qin, W.; Fang, H.; Wang, L.; Wei, J.; Zhang, M.; Su, X.; Bilal, M.; Liang, X. MODIS high-resolution MAIAC aerosol product: Global validation and analysis. Atmos. Environ. 2021, 264, 118684. [Google Scholar] [CrossRef]
- Tao, M.; Wang, J.; Li, R.; Wang, L.; Wang, L.; Wang, Z.; Tao, J.; Che, H.; Chen, L. Performance of MODIS high-resolution MAIAC aerosol algorithm in China: Characterization and limitation. Atmos. Environ. 2019, 213, 159–169. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Laszlo, I.; Kahn, R.; Korkin, S.; Remer, L.; Levy, R.; Reid, J.S. Multiangle implementation of atmospheric correction (MAIAC): 2. Aerosol algorithm. J. Geophys. Res.-Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.J.; Korkin, S.; Huang, D. MODIS Collection 6 MAIAC algorithm. Atmos. Meas. Tech. 2018, 11, 5741–5765. [Google Scholar] [CrossRef]
- Bibi, H.; Alam, K.; Chishtie, F.; Bibi, S.; Shahid, I.; Blaschke, T. Intercomparison of MODIS, MISR, OMI, and CALIPSO aerosol optical depth retrievals for four locations on the Indo-Gangetic plains and validation against AERONET data. Atmos. Environ. 2015, 111, 113–126. [Google Scholar] [CrossRef]
- Soni, K.; Parmar, K.S.; Kapoor, S.; Kumar, N. Statistical variability comparison in MODIS and AERONET derived aerosol optical depth over Indo-Gangetic Plains using time series modeling. Sci. Total Environ. 2016, 553, 258–265. [Google Scholar] [CrossRef]
- Li, B.G.; Yuan, H.S.; Feng, N.; Tao, S. Comparing MODIS and AERONET aerosol optical depth over China. Int. J. Remote Sens. 2009, 30, 6519–6529. [Google Scholar] [CrossRef]
- Chen, C.C.; Wang, Y.R.; Yeh, H.Y.; Lin, T.H.; Huang, C.S.; Wu, C.F. Estimating monthly PM2.5 concentrations from satellite remote sensing data, meteorological variables, and land use data using ensemble statistical modeling and a random forest approach. Environ. Pollut. 2021, 291, 118159. [Google Scholar] [CrossRef]
- Jiang, M.; Sun, W.W.; Yang, G.; Zhang, D.A.F. Modelling Seasonal GWR of Daily PM2.5 with Proper Auxiliary Variables for the Yangtze River Delta. Remote Sens. 2017, 9, 346. [Google Scholar] [CrossRef]
- Jiang, T.T.; Chen, B.; Nie, Z.; Ren, Z.H.; Xu, B.; Tang, S.H. Estimation of hourly full-coverage PM2.5 concentrations at 1-km resolution in China using a two-stage random forest model. Atmos. Res. 2021, 248, 105146. [Google Scholar] [CrossRef]
- Lu, D.B.; Mao, W.L.; Xiao, W.; Zhang, L. Non-Linear Response of PM2.5 Pollution to Land Use Change in China. Remote Sens. 2021, 13, 1612. [Google Scholar] [CrossRef]
- Lu, D.B.; Xu, J.H.; Yue, W.Z.; Mao, W.L.; Yang, D.Y.; Wang, J.Z. Response of PM2.5 pollution to land use in China. J. Clean. Prod. 2020, 244, 118741. [Google Scholar] [CrossRef]
- Zheng, C.W.; Zhao, C.F.; Zhu, Y.N.; Wang, Y.; Shi, X.Q.; Wu, X.L.; Chen, T.M.; Wu, F.; Qiu, Y.M. Analysis of influential factors for the relationship between PM2.5 and AOD in Beijing. Atmos. Chem. Phys. 2017, 17, 13473–13489. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, D.; Zhao, C.; Kwan, M.-P.; Cai, J.; Zhuang, Y.; Zhao, B.; Wang, X.; Chen, B.; Yang, J.; et al. Influence of meteorological conditions on PM2.5 concentrations across China: A review of methodology and mechanism. Environ. Int. 2020, 139, 105558. [Google Scholar] [CrossRef] [PubMed]
- Tai, A.P.K.; Mickley, L.J.; Jacob, D.J. Correlations between fine particulate matter (PM2.5) and meteorological variables in the United States: Implications for the sensitivity of PM2.5 to climate change. Atmos. Environ. 2010, 44, 3976–3984. [Google Scholar] [CrossRef]
- Shakya, D.; Deshpande, V.; Goyal, M.K.; Agarwal, M. PM2.5 air pollution prediction through deep learning using meteorological, vehicular, and emission data: A case study of New Delhi, India. J. Clean. Prod. 2023, 427, 139278. [Google Scholar] [CrossRef]
- Zavorueva, E.N.; Zavoruev, V.V. The influence of climatic factors on the concentration of particulate matter in the atmosphere of Drokino and Minino villages (Krasnoyarsk krai) during the heating season. In Proceedings of the 25th International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, Novosibirsk, Russia, 30 June–5 July 2019. [Google Scholar]
- Gleixner, S.; Demissie, T.; Diro, G.T. Did ERA5 Improve Temperature and Precipitation Reanalysis over East Africa? Atmosphere 2020, 11, 996. [Google Scholar] [CrossRef]
- Hamm, A.; Arndt, A.; Kolbe, C.; Wang, X.; Thies, B.; Boyko, O.; Reggiani, P.; Scherer, D.; Bendix, J.; Schneider, C. Intercomparison of Gridded Precipitation Datasets over a Sub-Region of the Central Himalaya and the Southwestern Tibetan Plateau. Water 2020, 12, 3271. [Google Scholar] [CrossRef]
- Nowak, D.J.; Hirabayashi, S.; Bodine, A.; Hoehn, R. Modeled PM2.5 removal by trees in ten U.S. cities and associated health effects. Environ. Pollut. 2013, 178, 395–402. [Google Scholar] [CrossRef]
- Jeanjean, A.P.R.; Monks, P.S.; Leigh, R.J. Modelling the effectiveness of urban trees and grass on PM2.5 reduction via dispersion and deposition at a city scale. Atmos. Environ. 2016, 147, 1–10. [Google Scholar] [CrossRef]
- Lim, C.-H.; Ryu, J.; Choi, Y.; Jeon, S.W.; Lee, W.-K. Understanding global PM2.5 concentrations and their drivers in recent decades (1998–2016). Environ. Int. 2020, 144, 106011. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Chen, J.; Wen, J.; Tian, H.; Liu, X. Composition and sources of PM2.5 around the heating periods of 2013 and 2014 in Beijing: Implications for efficient mitigation measures. Atmos. Environ. 2016, 124, 378–386. [Google Scholar] [CrossRef]
- Yang, Q.; Yuan, Q.; Yue, L.; Li, T. Investigation of the spatially varying relationships of PM2.5 with meteorology, topography, and emissions over China in 2015 by using modified geographically weighted regression. Environ. Pollut. 2020, 262, 114257. [Google Scholar] [CrossRef]
- Superczynski, S.D.; Christopher, S.A. Exploring Land Use and Land Cover Effects on Air Quality in Central Alabama Using GIS and Remote Sensing. Remote Sens. 2011, 3, 2552–2567. [Google Scholar] [CrossRef]
- Liang, L.; Wang, Z.; Li, J. The effect of urbanization on environmental pollution in rapidly developing urban agglomerations. J. Clean. Prod. 2019, 237, 117649. [Google Scholar] [CrossRef]
- Zeng, L.; Hang, J.; Wang, X.; Shao, M. Influence of urban spatial and socioeconomic parameters on PM2.5 at subdistrict level: A land use regression study in Shenzhen, China. J. Environ. Sci. 2022, 114, 485–502. [Google Scholar] [CrossRef]
- Kock, N.; Lynn, G. Lateral collinearity and misleading results in variance-based SEM: An illustration and recommendations. J. Assoc. Inf. Syst. 2012, 13. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees. In The Wadsworth & Brooks/Cole; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Misha, D.; David, M.; Nando De, F. Narrowing the Gap: Random Forests in Theory and in Practice. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 665–673. [Google Scholar]
- Ziegler, A.; König, I.R. Mining data with random forests: Current options for real-world applications. WIREs Data Min. Knowl. Discov. 2014, 4, 55–63. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- DiPietro, R.; Hager, G.D. Chapter 21—Deep learning: RNNs and LSTM. In Handbook of Medical Image Computing and Computer Assisted Intervention; Zhou, S.K., Rueckert, D., Fichtinger, G., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 503–519. [Google Scholar]
- Zhao, C.; Wang, Q.; Ban, J.; Liu, Z.; Zhang, Y.; Ma, R.; Li, S.; Li, T. Estimating the daily PM2.5 concentration in the Beijing-Tianjin-Hebei region using a random forest model with a 0.01° × 0.01° spatial resolution. Environ. Int. 2020, 134, 105297. [Google Scholar] [CrossRef]
- Gao, X.; Li, W.D. A graph-based LSTM model for PM2.5 forecasting. Atmos. Pollut. Res. 2021, 12, 101150. [Google Scholar] [CrossRef]
- Song, F.; Tie, Z.; Huang, Z.; Ding, C. PM2.5 Concentration Prediction Model Based on KNN-LSTM. Comput. Syst. Appl. 2020, 29, 193–198. [Google Scholar]
- Kang, J.; Tan, J.; Fang, L.; Xiao, Y. Short-term PM2.5 concentration prediction based on XGBoost and LSTM variable weight combination model: A case study of Shanghai. China Environ. Sci. 2021, 41, 4016–4025. [Google Scholar]
- Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
- Falah, S.; Kizel, F.; Banerjee, T.; Broday, D.M. Accounting for the aerosol type and additional satellite-borne aerosol products improves the prediction of PM2.5 concentrations. Environ. Pollut. 2023, 320, 121119. [Google Scholar] [CrossRef]
- Guan, S.; Zhang, X.; Zhao, W.; Duan, Y.; Yang, S.; Yao, Y.; Jia, K. A similarity distance-based space-time random forest model for estimating PM2.5 concentrations over China. Atmos. Environ. 2023, 313, 120043. [Google Scholar] [CrossRef]
- Pacca, L.; Antonarakis, A.; Schröder, P.; Antoniades, A. The effect of financial crises on air pollutant emissions: An assessment of the short vs. medium-term effects. Sci. Total Environ. 2020, 698, 133614. [Google Scholar] [CrossRef]
- Yang, Q.; Yuan, Q.; Yue, L.; Li, T.; Shen, H.; Zhang, L. Mapping PM2.5 concentration at a sub-km level resolution: A dual-scale retrieval approach. ISPRS J. Photogramm. Remote Sens. 2020, 165, 140–151. [Google Scholar] [CrossRef]
- Guo, B.; Wang, X.; Pei, L.; Su, Y.; Zhang, D.; Wang, Y. Identifying the spatiotemporal dynamic of PM2.5 concentrations at multiple scales using geographically and temporally weighted regression model across China during 2015–2018. Sci. Total Env. 2021, 751, 141765. [Google Scholar] [CrossRef]
- Liu, Y.X.; Teng, Y.; Liang, S.; Li, X.L.; Zhao, J.W.; Shan, M.; Chen, L.; Yu, H.; Mao, J.; Zhang, H.; et al. Establishment of PM10 and PM2.5 emission inventories from wind erosion source and simulation of its environmental impact based on WEPS-Models3 in southern Xinjiang, China. Atmos. Environ. 2021, 248, 118122. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, L.; Ma, W.; Wang, N.; Wen, F.; Liu, Q. Spatiotemporal estimation of the PM2.5 concentration and human health risks combining the three-dimensional landscape pattern index and machine learning methods to optimize land use regression modeling in Shaanxi, China. Environ. Res. 2022, 208, 112759. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, C.; Wang, S.; Li, S. Impacts of energy consumption structure, energy intensity, economic growth, urbanization on PM2. 5 concentrations in countries globally. Appl. Energy 2018, 230, 94–105. [Google Scholar] [CrossRef]
- Wang, Z.; Li, W.; Han, L. Study on the change in energy production structure under the energy coordinated development strategy of Beijing-Tianjin-Hebei urban agglomeration, China. Acta Ecol. Sin. 2019, 39, 1203–1211. [Google Scholar]
- Dai, Q.; Chen, J.; Wang, X.; Dai, T.; Tian, Y.; Bi, X.; Shi, G.; Wu, J.; Liu, B.; Zhang, Y.; et al. Trends of source apportioned PM2.5 in Tianjin over 2013–2019: Impacts of Clean Air Actions. Environ. Pollut. 2023, 325, 121344. [Google Scholar] [CrossRef]
- Wu, Q.L.; Guo, R.X.; Luo, J.H.; Chen, C. Spatiotemporal evolution and the driving factors of PM2.5 in Chinese urban agglomerations between 2000 and 2017. Ecol. Indic. 2021, 125, 107491. [Google Scholar] [CrossRef]
- Chen, J.; Wang, S.; Zhou, C.; Li, M. Does the path of technological progress matter in mitigating China’s PM2.5 concentrations? Evidence from three urban agglomerations in China. Environ. Pollut. 2019, 254, 113012. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).