Angle Expansion Estimation and Correction Based on the Lindeberg–Feller Central Limit Theorem Under Multi-Pulse Integration
Abstract
1. Introduction
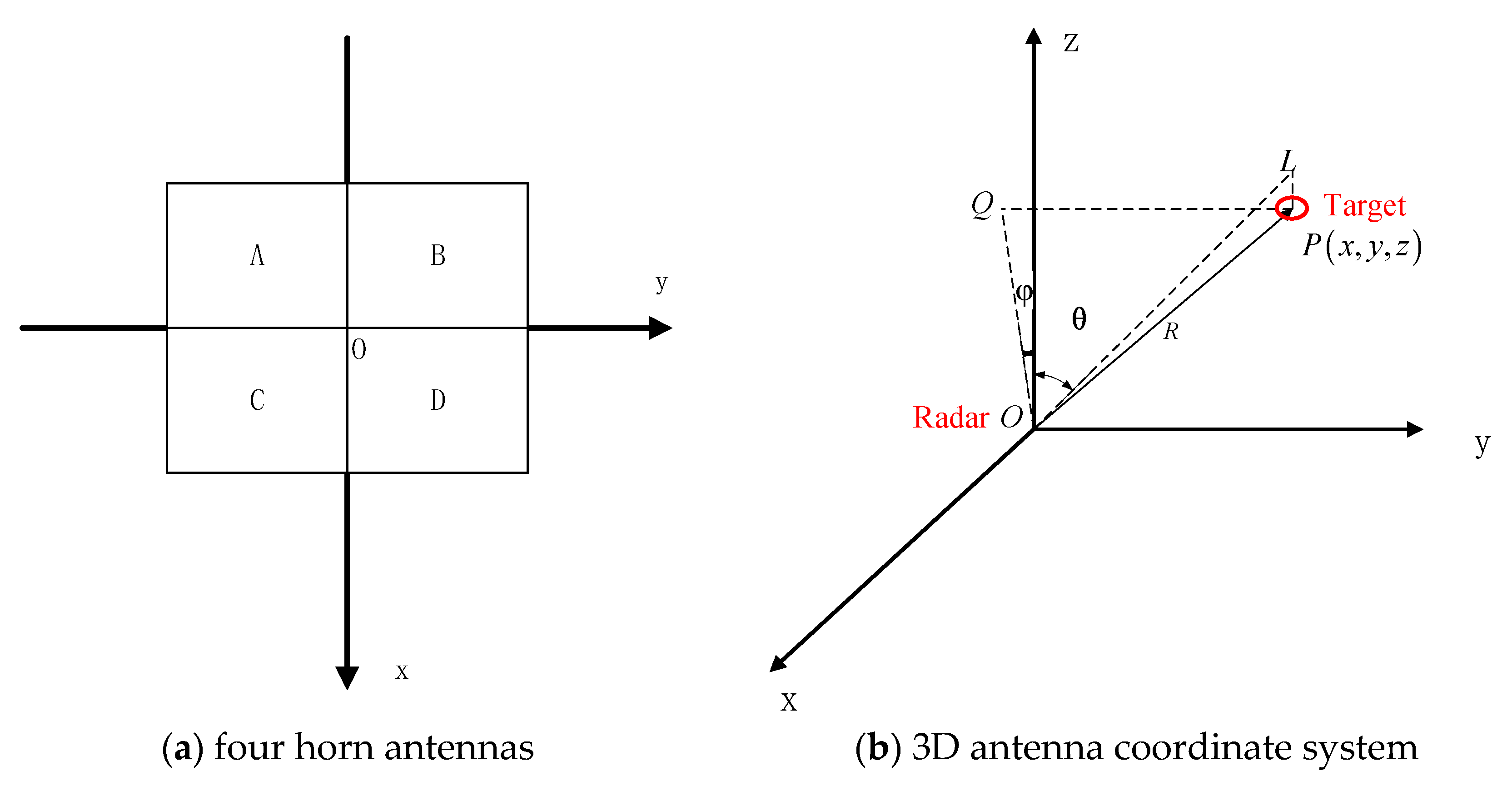
2. Amplitude Comparison Angle Measurement Under Multi-Pulse Integration
2.1. Amplitude Comparison Monopulse Angle Measurement Principles
2.2. Multi-Pulse Integration Angle Measurement Model
3. Angle Expansion Model Based on the Lindeberg–Feller Central Limit Theorem
3.1. Lindeberg–Feller Central Limit Theorem
3.2. Uniform Linear Motion in Three-Dimensional Space
3.2.1. Multi-Pulse Angle Error Model for Uniform Linear Motion
3.2.2. Angle Expansion Model Under Amplitude Fluctuation for Uniform Linear Motion
3.3. Uniformly Accelerated Linear Motion in a Three-Dimensional Space
3.3.1. Multi-Pulse Angle Error Model for Uniformly Accelerated Linear Motion
3.3.2. Angle Expansion Model Under Amplitude Fluctuation in Uniformly Accelerated Linear Motion
- From the mean component, it can be observed that the angular error after multi-pulse integration is greater than the angular error at the central moment , with the difference being ; as increases, this deviation gradually grows.
- From the variance component, it is evident that the greater the target fluctuation, the greater the impact of integration on angular error measurement; as the number of integrated pulses increases, the impact on angular error measurement also increases.
- Overall, when the quadratic term coefficient of angular error variation in Equation (58), it can be reduced to Equation (42) in Section 3.2 under uniform velocity conditions.
4. Angle Correction Algorithm Based on Multi-Pulse Integration and Long-Term Estimation
4.1. Uniform Linear Motion in Three-Dimensional Space
4.2. Uniformly Accelerated Linear Motion in a Three-Dimensional Space
5. Simulation Experiment Verification
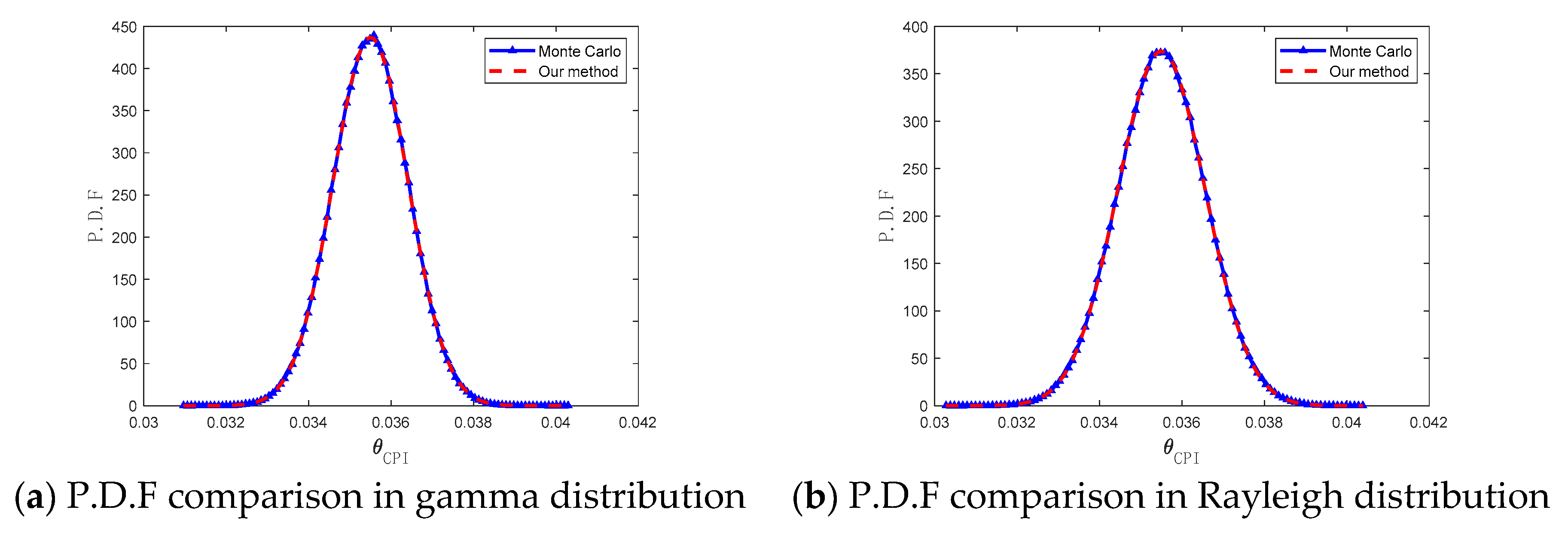
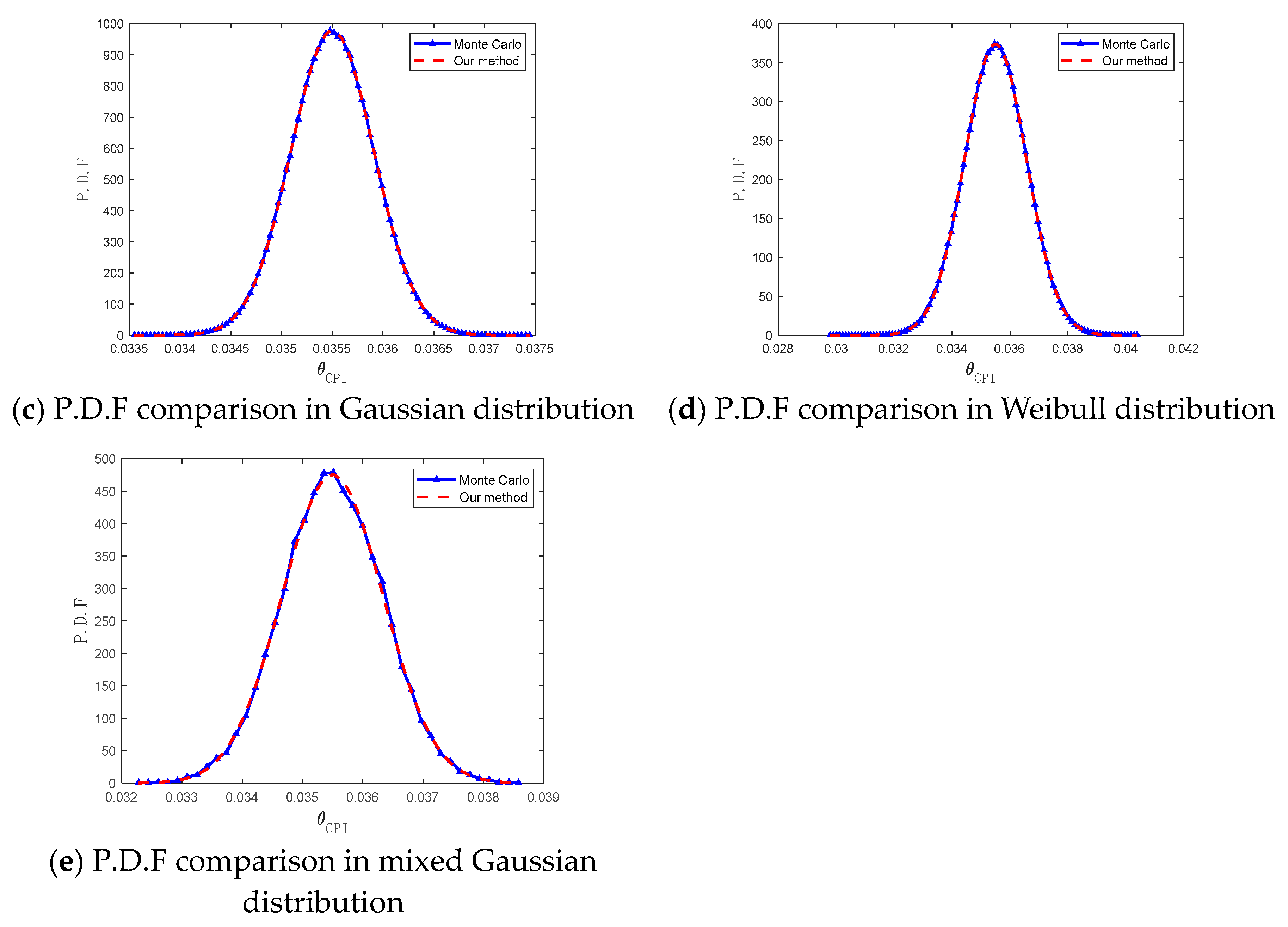
5.1. Gaussian Approximation of Angle Expansion Models
5.1.1. Uniform Linear Motion in a Three-Dimensional Space
5.1.2. Uniformly Accelerated Linear Motion in a Three-Dimensional Space
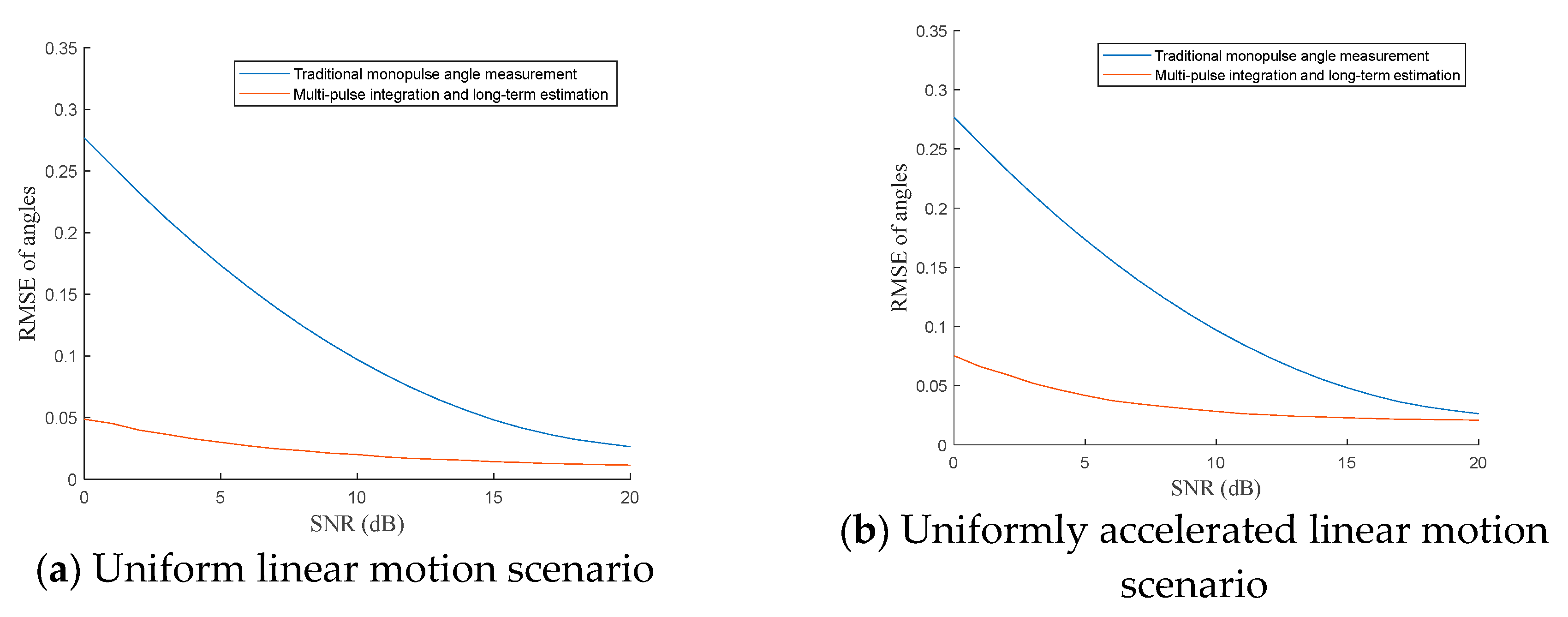
5.2. The Angle Measurement Accuracy of the Angle Correction Algorithm
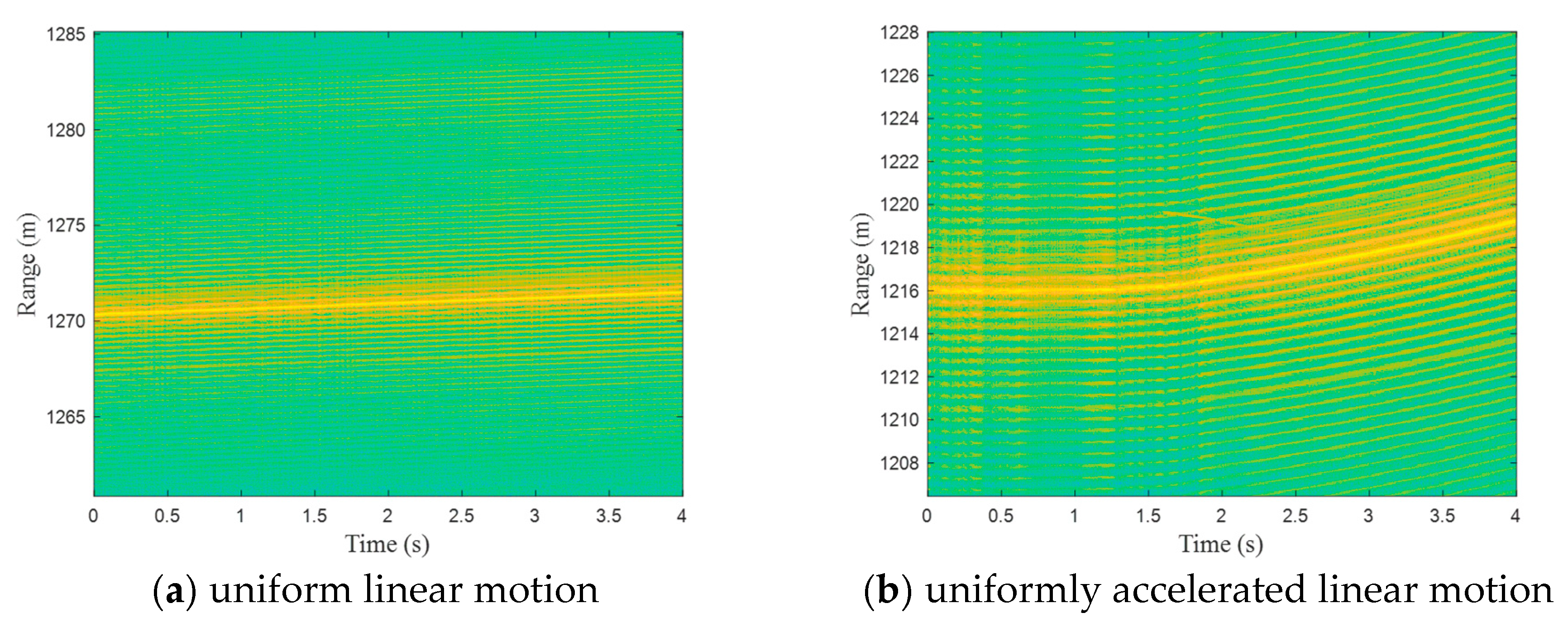
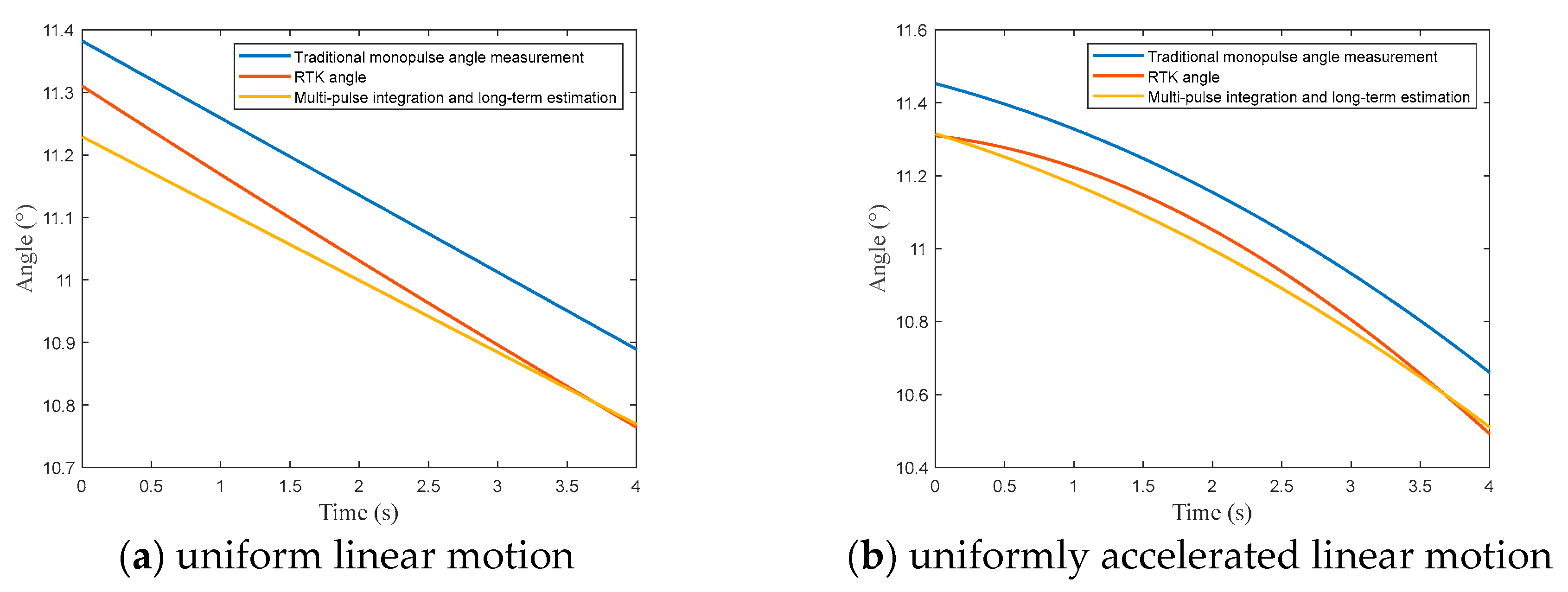
6. Verification with Measured Data
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Xiong, X.; Deng, Z.; Qi, W.; Dou, Y. High-precision angle estimation based on phase ambiguity resolution for high resolution radars. Sci. China Inf. Sci. 2019, 62, 040307. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, B. Altitude measurement of low-angle target in complex terrain for very high-frequency radar. IET Radar Sonar Navig. 2015, 9, 967–973. [Google Scholar] [CrossRef]
- Joshi, S.K.; Baumgartner, S.V.; da Silva, A.B.C.; Krieger, G. Direction-of-arrival angle and position estimation for extended targets using multichannel airborne radar data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4022705. [Google Scholar] [CrossRef]
- Okay, F.Y.; Özdemir, S. Real-time Aircraft Tracking System: A Survey and A Deep Learning Based Model. In Proceedings of the 2021 International Symposium on Networks, Computers and Communications (ISNCC), Dubai, United Arab Emirates, 31 October–2 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Lo, K. Theoretical analysis of the sequential lobing technique. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 282–293. [Google Scholar] [CrossRef]
- Lank, G.; Pollon, G. Exact Angular Accuracy of an Amplitude Comparison Sequential-Lobing Processor. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 393–398. [Google Scholar] [CrossRef]
- Kirkpatrick, G. Development of A Monopulse Radar System. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 807–818. [Google Scholar] [CrossRef]
- Leonov, A. History of monopulse radar in the USSR. IEEE Aerosp. Electron. Syst. Mag. 1998, 13, 7–13. [Google Scholar] [CrossRef]
- Sinsky, A.; Lew, E. Comparative analysis of a phase and an amplitude processor for amplitude monopulse systems. IEEE Trans. Antennas Propag. 1983, 31, 519–522. [Google Scholar] [CrossRef]
- Sebt, M.; Goodarzi, M.; Darvishi, H. Geometric Arithmetic Mean Method for Low Altitude Target Elevation Angle Tracking. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 5111–5119. [Google Scholar] [CrossRef]
- Darvishi, H.; Sebt, M. Adaptive hybrid method for low-angle target tracking in multipath. IET Radar Sonar Navig. 2018, 12, 931–937. [Google Scholar] [CrossRef]
- Park, D.; Yang, E.; Ahn, S.; Chun, J. Adaptive beamforming for low-angle target tracking under multipath interference. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2564–2577. [Google Scholar] [CrossRef]
- Xu, Z.; Xiong, Z.; Wu, J.; Xiao, S. Symmetrical difference pattern monopulse for low-angle tracking with array radar. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2676–2684. [Google Scholar] [CrossRef]
- Seifer, A. Monopulse-radar angle tracking in noise or noise jamming. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 622–638. [Google Scholar] [CrossRef]
- Han, H.; Xu, X.; Wang, H.; Dai, H. Analysis of Cross-polarization Jamming for Phase Comparison Monopulse Radars. In Proceedings of the 2019 IEEE 2nd International Conference on Electronic Information and Communication Technology (ICEICT), Harbin, China, 20–22 January 2019; pp. 404–407. [Google Scholar]
- Chen, X.; Shu, T.; Yu, K.; Yu, W. Enhanced ADBF Architecture for Monopulse Angle Estimation in Multiple Jammings. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2684–2687. [Google Scholar] [CrossRef]
- Yu, K.; Murrow, D. Adaptive digital beamforming for angle estimation in jamming. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 508–523. [Google Scholar]
- Gogineni, S.; Nehorai, A. Monopulse MIMO Radar for Target Tracking. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 755–768. [Google Scholar] [CrossRef]
- Zhang, X.; Willett, P.; Bar-Shalom, Y. Detection and Localization of Multiple Unresolved Extended Targets via Monopulse Radar Signal Processing. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 455–472. [Google Scholar] [CrossRef]
- Fu, M.; Gao, C.; Li, Y.; Deng, Z.; Chen, D. Monopulse-Radar Angle Estimation of Multiple Targets Using Multiple Observations. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 968–983. [Google Scholar] [CrossRef]
- Huang, Q.; Fan, H.; Cai, F.; Xiao, H. Joint Estimation of Unresolved Leader–Follower in the Presence of Dense False Signals Using Monopulse Radar. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 9635–9649. [Google Scholar] [CrossRef]
- Palamà, R.; Fioranelli, F.; Ritchie, M.; Inggs, M.; Lewis, S.; Griffiths, H. Measurements and discrimination of drones and birds with a multi-frequency multistatic radar system. IET Radar Sonar Navig. 2021, 15, 841–852. [Google Scholar] [CrossRef]
- Wang, R.; Cai, J.; Hu, C.; Zhou, C.; Zhang, T. A Novel Radar Detection Method for Sensing Tiny and Maneuvering Insect Migrants. Remote Sens. 2020, 12, 3238. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, T.; Hu, C.; Cai, J.; Li, W. Digital detection and tracking of tiny migratory insects using vertical-looking radar and ascent and descent rate observation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5101615. [Google Scholar] [CrossRef]
- Wang, J.; Guo, P.; Lei, P.; Wei, S. Influence and compensation of target motion on monopulse estimation in PD radar. In Proceedings of the IEEE 10th International Conference on Signal Processing, Beijing, China, 24–28 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2312–2315. [Google Scholar]
- Medina, P.K.; Merino, S.; Galton, F. The Central Limit Theorem. In Mathematical Finance and Probability: A Discrete Introduction; Springer: Berlin/Heidelberg, Germany, 2003; pp. 221–246. [Google Scholar]
- Chow, Y.S.; Teicher, H.; Chow, Y.S.; Teicher, H. Central limit theorems. Probab. Theory Indep. Interchang. Martingales 1988, 295–335. [Google Scholar]
- Rio, E. About the Lindeberg method for strongly mixing sequences. ESAIM Probab. Stat. 1997, 1, 35–61. [Google Scholar] [CrossRef]
- Klenke, A.; Klenke, A. Characteristic Functions and the Central Limit Theorem. Probab. Theory A Compr. Course 2020, 327–366. [Google Scholar]
- Adachi, A.; Kobayashi, T.; Yamauchi, H. A Methodology for Estimating the Parameters of a Gamma Raindrop Size Distribution Model from Polarimetric Radar Measurements at Attenuating Frequency Based on the Self-Consistency Principle. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 17–22 April 2016; p. EPSC2016-5381. [Google Scholar]
- Blair, W.D.; Brandt-Pearce, M. Monopulse DOA estimation of two unresolved Rayleigh targets. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 452–469. [Google Scholar] [CrossRef]
- Ehrman, L.M.; Blair, W.D. Using target RCS when tracking multiple Rayleigh targets. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 701–716. [Google Scholar] [CrossRef]
- Buller, W.; Wilson, B.; van Nieuwstadt, L.; Ebling, J. Statistical modelling of measured automotive radar reflections. In Proceedings of the 2013 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Minneapolis, MN, USA, 6–9 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 349–352. [Google Scholar]
- Zhang, Y.; Shen, J.; Tuo, X.; Yang, H.; Zhang, Y.; Huang, Y. Scanning radar forward-looking superresolution imaging based on the Weibull distribution for a sea-surface target. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5116111. [Google Scholar] [CrossRef]
- Pierce, R.D. RCS characterization using the alpha-stable distribution. In Proceedings of the Proceedings of the 1996 IEEE National Radar Conference, Ann Arbor, MI, USA, 13–16 May 1996; IEEE: Piscataway, NJ, USA, 1996; pp. 154–159. [Google Scholar]
- Seybold, J.S.; Weeks, K.L. Arithmetic versus geometric mean of target radar cross section. Microw. Opt. Technol. Lett. 1996, 11, 265–270. [Google Scholar] [CrossRef]
- Wang, L.; Xie, G.; Qian, F.; Jin, Y.; Gao, K. A novel model for analyzing the statistical properties of targets’ RCS. IEEE Signal Process. Lett. 2021, 29, 583–586. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Xia, X.; Shui, P.; Zhang, Y.; Li, X.; Xu, X. An empirical model of shape parameter of sea clutter based on X-band island-based radar database. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3503205. [Google Scholar] [CrossRef]




| Parameters | Parameter Values | Parameters | Parameter Values |
|---|---|---|---|
| Number of TR components | 96 | Subpulse pulse width | 3 us |
| Peak array emission power | 12 kW | Subpulse bandwidth | 125 MHz |
| Carrier center frequency | 16.5 GHz | Frequency hopping interval | 100 MHz |
| System damage | 9 dB | Bandwidth | 1 GHz |
| Difference slope | 0.13 | Range resolution | 0.2 m |
| Launch gain | 49.6 dB | System noise temperature | 809 K |
| Receive gain | 48.8 dB |
| Parameter | Parameter Values |
|---|---|
| Target 3D velocity [vx, vy, vz] | [0 m/s, 20 m/s, −10 m/s] |
| Target starting position [x, y, z] | [0 m, 4 m, 400 m] |
| Fluctuation Scenario 1: Gamma distribution fluctuation | Mean: 15; Variance: 45 |
| Fluctuation Scenario 2: Rayleigh distribution fluctuation | Mean: 8.77; Variance: 21.03 |
| Fluctuation Scenario 3: Gaussian distribution fluctuation | Mean: 10; Variance: 4 |
| Fluctuation Scenario 4: Weibull distribution fluctuation | Mean: 6.2; Variance: 10.57 |
| Fluctuation Scenario 5: Mixed Gaussian distribution fluctuation | Weight matrix: [0.3, 0.4, 0.3] Mean matrix: [10, 20, 30] Variance matrix: [4, 9, 9] |
| Scenario No. | KS Distance |
|---|---|
| Scenario 1: Gamma distribution | 1.2 × 10−3 |
| Scenario 2: Rayleigh distribution | 1.4 × 10−3 |
| Scenario 3: Gaussian distribution | 1.2 × 10−3 |
| Scenario 4: Weibull distribution | 1.3 × 10−3 |
| Scenario 5: Mixed Gaussian distribution | 2.8 × 10−3 |
| Scenario No. | KS Distance |
|---|---|
| Scenario 1: Gamma distribution | 1.4 × 10−3 |
| Scenario 2: Rayleigh distribution | 1.6 × 10−3 |
| Scenario 3: Gaussian distribution | 1.8 × 10−3 |
| Scenario 4: Weibull distribution | 1.6 × 10−3 |
| Scenario 5: Mixed Gaussian distribution | 3.1 × 10−3 |
| Parameters | Parameter Values | Parameters | Parameter Values |
|---|---|---|---|
| Number of TR components | 64 | Pulse width | 3 us |
| Carrier center frequency | 3 GHz | Bandwidth | 20 MHz |
| Difference slope | 0.2 | Range resolution | 10 m |
| Uav Parameters | Numerical Values |
|---|---|
| Model number | DJI Warp and Weft M300 (RTK) |
| Weight | 6.3 kg |
| Maximum flying speed | 17 m/s |
| RTK position accuracy | 1 cm (horizontal), 1.5 cm (vertical) |
| Scene 1: Uniform linear motion | Horizontal flight with a total speed of about 13 m/s |
| Scenario 2: Uniformly accelerated linear motion | Horizontal flight, acceleration of about 2 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, J.; Wang, R.; Yang, H. Angle Expansion Estimation and Correction Based on the Lindeberg–Feller Central Limit Theorem Under Multi-Pulse Integration. Remote Sens. 2024, 16, 4535. https://doi.org/10.3390/rs16234535
Cai J, Wang R, Yang H. Angle Expansion Estimation and Correction Based on the Lindeberg–Feller Central Limit Theorem Under Multi-Pulse Integration. Remote Sensing. 2024; 16(23):4535. https://doi.org/10.3390/rs16234535
Chicago/Turabian StyleCai, Jiong, Rui Wang, and Handong Yang. 2024. "Angle Expansion Estimation and Correction Based on the Lindeberg–Feller Central Limit Theorem Under Multi-Pulse Integration" Remote Sensing 16, no. 23: 4535. https://doi.org/10.3390/rs16234535
APA StyleCai, J., Wang, R., & Yang, H. (2024). Angle Expansion Estimation and Correction Based on the Lindeberg–Feller Central Limit Theorem Under Multi-Pulse Integration. Remote Sensing, 16(23), 4535. https://doi.org/10.3390/rs16234535







