Abstract
The latest satellite in the Landsat series, Landsat-9, was successfully launched on 27 September 2021, equipped with the Operational Land Imager-2 (OLI-2) sensor, continuing the legacy of OLI/Landsat-8. To evaluate the uncertainties in water surface reflectance derived from OLI-2, this study conducts a comprehensive performance assessment of six atmospheric correction (AC) methods—DSF, C2RCC, iCOR, L2gen (NIR-SWIR1), L2gen (NIR-SWIR2), and Polymer—using in-situ measurements from 14 global sites, including 13 AERONET-OC stations and 1 MOBY station, collected between 2021 and 2023. Error analysis shows that L2gen (NIR-SWIR1) (RMSE ≤ 0.0017 sr−1, SA = 6.33°) and L2gen (NIR-SWIR2) (RMSE ≤ 0.0019 sr−1, SA = 6.38°) provide the best results across four visible bands, demonstrating stable performance across different optical water types (OWTs) ranging from clear to turbid water. Following these are C2RCC (RMSE ≤ 0.0030 sr−1, SA = 5.74°) and Polymer (RMSE ≤ 0.0027 sr−1, SA = 7.76°), with DSF (RMSE ≤ 0.0058 sr−1, SA = 11.33°) and iCOR (RMSE ≤ 0.0051 sr−1, SA = 12.96°) showing the poorest results. By comparing the uncertainty and consistency of Landsat-9 (OLI-2) with Sentinel-2A/B (MSI) and S-NPP/NOAA20 (VIIRS), results show that OLI-2 has similar uncertainties to MSI and VIIRS in the blue, blue-green, and green bands, with RMSE differences within 0.0002 sr−1. In the red band, the OLI-2 uncertainties are lower than those of MSI but higher than those of VIIRS, with an RMSE difference of about 0.0004 sr−1. Overall, OLI-2 data processed using L2gen provide reliable surface reflectance and show high consistency with MSI and VIIRS, making it suitable for integrating multi-satellite observations to enhance global coastal water color monitoring.
1. Introduction
Since the successful launch of Landsat-1 on 23 July 1972 [1], the Landsat program has provided a half-century-long record of Earth observations [2,3], making a significant contribution to the advancement of Earth sciences [4]. Although Landsat series satellites were initially designed for terrestrial observations, they have also been widely used in aquatic ecosystem observations, including inland lakes [5,6,7,8], rivers [9,10,11], and coastal water [12,13,14,15] monitoring. Especially after the launch of Landsat-8 in 2013, its onboard Operational Land Imager (OLI) not only enhanced the signal-to-noise ratio but also increased one spectral band centered at 443 nm to improve the radiometric quality over water [2,16]. Landsat-9, as a continuation of the Landsat program, was successfully launched on 21 September 2021, carrying an Operational Land Imager-2 (OLI-2) with the same spatial resolution (30 m) and swath as OLI. Compared with OLI/Landsat-8, OLI-2/Landsat-9 increases the radiometric resolution from 12-bit to 14-bit and improves the signal-to-noise ratio (SNR) by 7–30% in all bands, implying that the quality of OLI-2/Landsat-9 products in aquatic ecosystems is expected to catch up with or exceed that of OLI [2,17], which makes it full of potential in coastal zone, inland lake, and river applications.
The prerequisite for obtaining high-quality water color products is to obtain accurate remote sensing reflectance () over water, which requires not only a satellite sensor with good performance but also excellent atmospheric correction (AC) methods. The atmospheric contribution occupies most of the signals received by water color satellite sensors at the top of atmosphere (TOA), accounting for up to 90% of the total signal [18]. To obtain accurate water-leaving reflectance information, the atmospheric contribution should be estimated and subtracted from the total TOA signal measured by the sensor. This process is called AC [19], and the AC process is one of the main sources of uncertainties in water color products. Currently, the “black pixel” AC method proposed by Gordon and Wang [20] is primarily utilized for oceanic (Case I) water, which assumes the ocean in the near-infrared (NIR) band is black, namely, the water-leaving reflectance is zero, due to strong water absorption in the NIR. Although the black pixel AC method performs well in Case I waters and has been used by the National Aeronautics and Space Administration (NASA) as an official AC method [21], it fails in coastal (Case II) waters with strong particulate scattering, where the non-negligible of the NIR band invalidates the black pixel assumption.
Fortunately, numerous AC methods have been developed and used in Case II water environments such as coastal zones, inland lakes, and rivers. Popular approaches include bio-optical model-based algorithms like Level 2 generator (L2gen) [22], dark spectral fitted algorithms (DSF) [23], and the machine learning-based AC algorithms Case 2 Regional Coast Color (C2RCC) [24], spectral matching algorithms like the Polynomial-based algorithms (Polymer) [25], image-based algorithms like cloud shadow algorithms [26] and image correction for atmospheric effects (iCOR) [27], etc. In addition, two commonly used generalized algorithms, ARCSI [28] and LaSRC [29], designed for landscape, have also been used in a few coastal monitoring cases.
The performance of different AC methods has been evaluated by researchers in various regions. For example, Pahlevan et al. (2017) [30] evaluated three band combinations of L2gen applied to Landsat-8, NIR–SWIR1, NIR–SWIR2, and SWIR1–SWIR2, using in-situ measurements from the Aerosol Robotic Network-Ocean Color (AERONET-OC) (for Landsat-8/9, the NIR, SWIR1, and SWIR2 bands correspond to wavelengths of 865 nm, 1609 nm, and 2201 nm, respectively). The evaluation showed that the NIR–SWIR1 combination had the lowest uncertainty, followed by the NIR–SWIR2 combination, with both having RMSE ≤ 0.0010 sr−1. The SWIR1–SWIR2 combination had the highest uncertainty, with RMSE ≤ 0.0032 sr−1. Wei et al. (2018) [31] analyzed the performance of DSF, L2gen (NIR–SWIR1), and cloud shadow approaches using Landsat-8 data in coral reef and coastal turbid waters. They found that L2gen (NIR–SWIR1) and the cloud shadow approaches produced highly consistent results with the in-situ measurements in shallow coral reefs and optically deep waters. Pahlevan et al. (2018, 2019) [32,33] used OLI/Landsat-8 data processed by L2gen, together with AERONET-OC in-situ measurements, to evaluate the uncertainty of ETM+/Landsat-7 and TM/Landsat-5, and made adjustments to their calibration gains. Ilori et al. (2019) [32] evaluated the performance of four AC methods (ARCSI, LaSRC, DSF, and L2gen (NIR–SWIR1)) for Landsat-8 data using in-situ measurements provided by AERONET-OC in coastal waters. Their findings confirm that the two general AC methods, ARCSI and LaSRC, perform significantly worse in coastal environments compared to the two AC methods (DSF and L2gen (NIR–SWIR1)) specifically designed for water, and the L2gen produces products with the lowest uncertainty. Additionally, Yan et al. (2023) [34] conducted a global assessment of five AC methods (DSF, C2RCC, iCOR, L2gen (NIR–SWIR1), and Polymer) applicable to Landsat-8 data using in-situ measurements from AERONET-OC, Marine Optical Buoy (MOBY), and SeaWiFS Bio-optical Archive and Storage System (SeaBASS). They assessed the performance of these AC methods by classifying optical water types (OWTs) based on spectral similarity. Their results indicate that L2gen (NIR–SWIR1) has the highest accuracy, with and RMSE ≤ 0.0018 sr−1, across four visible bands, and it produces the most accurate in five different OWTs, ranging from clear to turbid water. Van et al. (2023) [35] proposed a machine learning atmospheric correction method, AC-Net, which can be applied to tropical inland water bodies, achieving an RMSE of 0.0039 sr−1 and a SA of 19.5°. Kabir et al. (2023) [2] conducted a comparative analysis of the top-of-atmosphere reflectance () from OLI/Landsat-8 and OLI-2/Landsat-9, as well as processed using L2gen. The results show that the difference between the two sensors is within 0.8% in the visible-near-infrared bands and around 2% in the SWIR1 and SWIR2 bands. In the visible range, the median difference in is between 1.5% and 2.5%, indicating high consistency between OLI-2/Landsat-9 and OLI/Landsat-8 in aquatic ecosystem monitoring. Based on previous studies, it can be concluded that there is still a lack of assessing uncertainties in various AC methods for Landsat-9 data in global water types, which can provide recommendations for the suitability of different AC methods and help improve AC methods, reducing unnecessary errors and ensuring the quality of OLI-2/Landsat-9 data in coastal and inland water research and applications [2].
Considering the long revisit period of one single high-spatial-resolution satellite (approximately 16 days for the Landsat series) [36] and the significant limited amount of effective data due to clouds and haze [37], the joint use of multiple on-orbit spaceborne sensors becomes crucial in dynamic coastal areas, which not only improves the temporal resolution but also improves the spatial coverage of the valid data pixels. Li et al. (2020) [38] demonstrated that after the deployment of OLI-2/Landsat-9, combined with OLI/Landsat-8 and MultiSpectral Instrument (MSI)/Sentinel-2A/B, the revisit period can be reduced to 2.3 days, greatly enhancing the continuity of coastal water quality monitoring. This places high demands on the consistency between Sentinel-2A/B and Landsat-8/9. In fact, many efforts have been made to ensure consistency between the Landsat and Sentinel series, such as the similar design of the MSI and OLI sensors. However, differences in satellite orbits, illumination conditions, and sensor viewing angles pose challenges to this consistency. Studies [39,40] have focused on evaluating the consistency between Landsat and Sentinel data. For example, Trevisiol et al. (2024) [40] proposed harmonization coefficients for the European continent, which were used to align Landsat-9 with Landsat-8/Sentinel-2 and cross-validate the consistency of surface reflectance and four derived vegetation indices. The results showed a very high similarity between Landsat-9 and Landsat-8, as well as good interoperability between Landsat-9 and Sentinel-2. However, there is currently a lack of research assessing the differences in suitability between Landsat-9 and other commonly used medium-to-high spatial resolution satellite remote sensing sensors for coastal water quality inversion, such as MSI/Sentinel-2A/B, Visible Infrared Imaging Radiometer Suite (VIIRS)/S-NPP, and NOAA-20, in coastal water environments [41,42,43].
Therefore, to assess the uncertainty of Landsat-9 in global coastal and inland waters, determine the optimal AC method for Landsat-9, and evaluate the consistency differences between Landsat-9 and operational satellites such as Sentinel-2A/B, S-NPP, and NOAA-20, this study utilized global in-situ datasets from AERONET-OC and MOBY to evaluate the six most widely validated and proven effective AC methods (DSF, C2RCC, iCOR, L2gen (NIR-SWIR1), L2gen (NIR-SWIR2), and Polymer) for OLI-2/Landsat-9 data in ocean color remote sensing. The in-situ measurements were also categorized into different OWTs based on measured to explore the performance of AC methods in various optical water environments. Additionally, the study compared the consistency and uncertainty differences between OLI-2/Landsat-9 and two on-orbit spaceborne sensors of MSI/Sentinel-2A/B and VIIRS/S-NPP/NOAA-20, providing insights into the uncertainty levels of Landsat-9 data, and its assessment of consistency differences among Landsat-9, Sentinel-2, S-NPP, and NOAA-20 can facilitate data integration and enhance interoperability.
2. Materials and Methods
2.1. Satellite Data
Satellite remote sensing data acquired by the OLI-2 sensor aboard Landsat-9, MSI sensors on Sentinel-2A and Sentinel-2B, and VIIRS sensors on S-NPP and NOAA-20 were utilized in this study.
Landsat-9, as the ninth satellite in the NASA and United States Geological Survey (USGS) joint Landsat satellite remote sensing program, was successfully launched on 27 September 2021. It has a revisit period of 16 days, and carries the OLI-2 sensor, which is an improved version of OLI onboard Landsat-8. The OLI-2 has similar spectral bands and spatial resolution as OLI (see Table 1), and the radiometric resolution of OLI-2 (14-bit) is higher than OLI (12-bit), which further enhances the application potential of OLI-2 in coastal water bodies [3]. In this study, a total of 102 scenes of Landsat-9 Level 1 data from 2021 to 2023 were downloaded from the USGS website (https://earthexplorer.usgs.gov/ (accessed on 15 June 2024)). The OLI-2/Landsat-9 data used in this study are official reprocessed products with adjustments to reduce calibration differences with OLI (https://www.usgs.gov/landsat-missions/landsat-mission-headlines (accessed on 15 June 2024)).

Table 1.
Comparison of similar bands for the OLI-2, MSI, and VIIRS, with SR denoting spatial resolution in meters.
Sentinel-2A and Sentinel-2B are two satellites launched by the European Space Agency (ESA) under the Copernicus program in 2015 and 2017, respectively [44]. Both are equipped with the MSI sensor, which has a 12-bit radiometric resolution and 13 spectral bands with ground resolutions of 10 m, 20 m, and 60 m. In this study, the MSI data with four visible bands similar to those of OLI-2 were used and analyzed, and the spectral ranges and ground resolutions are shown in Table 1. All top-of-atmosphere radiance data from the four MSI bands were resampled to a ground resolution of 60 m. Warren et al. (2019) [45] analyzed the MSI data processed using 6 AC methods, including DSF, C2RCC, iCOR, L2gen, Polymer, and Sen2Cor in European nearshore waters, and concluded that Polymer is the most effective one. A similar conclusion was also reached by SòRIA et al. (2022) [46]. Thus, Polymer was chosen in the atmospheric correction process of Sentinel-2 data in this study.
S-NPP was launched jointly by NOAA and NASA in 2011, while NOAA-20 was launched by NOAA in 2017, and both are equipped with the VIIRS sensor. The VIIRS sensor has a 12-bit radiometric resolution and 22 spectral bands, including one panchromatic diurnal band, 16 bands with a spatial resolution of 750 m, and six bands at a resolution of 375 m. This study selected four visible bands of VIIRS that closely match OLI-2 for comparative analysis, and the details are provided in Table 1. The VIIRS Level 2 data used in this study were downloaded from website (https://oceancolor.gsfc.nasa.gov (accessed on 20 June 2024)). The data were atmospherically corrected using the L2gen method, which has been widely evaluated and proven to be accurate and reliable [47,48].
2.2. In-Situ Data
In-situ measurements from AERONET-OC and MOBY were used in this study. The AERONET program, established by NASA and PHOTONS (PHOtométrie pour le Traitement Opérationnel de Normalisation Satellitaire; Univ. of Lille 1, CNES, and CNRS-INSU), has been operational for over 25 years. It is a global aerosol monitoring network supported by national agencies, institutes, universities, individual scientists, and partners. The program provides standardized, publicly accessible field data for research, satellite validation, and other applications. AERONET-OC, a component of the AERONET program, measures water-leaving reflectance using sun photometers installed on offshore platforms [49,50]. The reliability and accuracy of AERONET-OC data have been well validated, and the data have been widely used in assessing the uncertainties of spaceborne remote sensing data [34,51,52].
MOBY is a mooring system operated by NOAA near the coast of Lanai Island, Hawaii. It has operated since 1997 and provides a continuous time series of normalized water-leaving reflectance (). MOBY has been used to calibrate multiple satellite sensors, including Sea-viewing Wide Field of View Sensor (SeaWiFS), MODIS, Medium Resolution Imaging Spectrometer (MERIS), VIIRS, and Ocean and Land Colour Instrument (OLCI) [53,54,55].
In-situ data from a total of 14 stations from AERONET-OC and MOBY spanning from 2021 to 2023 were used in this study. The locations of the stations are shown in Figure 1, and detailed information is presented in Table 2. For the AERONET-OC data categorized into three quality levels, the highest quality Level 2.0 data were used in this study. For MOBY data classified into four levels, the “Good” quality data were chosen. Following Pahlevan et al. (2021) [51], the provided by AERONET-OC and MOBY was divided by the top-of-atmosphere solar irradiance () [56] to obtain the as shown in Equation (1), where denotes the wavelength:
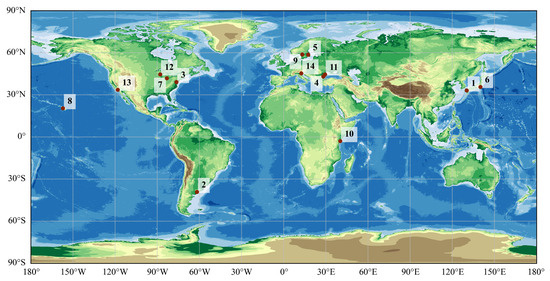
Figure 1.
Locations of 14 global field measurements stations used in this study.

Table 2.
The latitude and longitude information and the Principal Investigators (PIs) for 14 stations used in this study, as well as the number of matchup data points (N).
2.3. Atmospheric Correction Methods
The top-of-atmosphere reflectance () received by spaceborne ocean color sensors at the top of the atmosphere primarily consists of contributions from Rayleigh scattering by atmospheric molecules (), aerosol scattering (), and water-leaving reflectance () [20,57] as shown in the following equation:
where t is the atmospheric diffuse transmittance. The atmospheric correction process involves removing the atmospheric contributions from the total top-of-atmosphere reflectance received by the sensor, thereby isolating the . Dividing by gives the . During the atmospheric correction procedure, the contribution of Rayleigh scattering can be estimated accurately [19]. However, the diverse composition of atmospheric aerosols makes it challenging to accurately estimate aerosol contributions, which could account for up to 90% of the total reflectance over water [18].
Various AC methods estimating aerosol contributions over water bodies have been developed. The commonly used methods of DSF, C2RCC, iCOR, L2gen, and Polymer applicable for Landsat-9 data were analyzed in this study. A brief introduction to these atmospheric correction methods is provided in Table 3.

Table 3.
Brief description of atmospheric correction methods used in this study.
These atmospheric correction methods can be classified into two categories: two-step and one-step methods. The two-step methods include DSF, iCOR, L2gen, and Polymer, where Rayleigh scattering and gas absorption are removed first, followed by the aerosol contributions. The one-step method is C2RCC, which is based on a machine learning approach that takes the top-of-atmosphere reflectance as input and performs atmospheric correction through a pre-trained neural network, directly outputting [51]. Among these methods, iCOR and Polymer outputs , which is then divided by to obtain , while the other methods directly output .
In terms of aerosol correction methods, the DSF method automatically selects the lowest spectral reflectance within one scene to determine the atmospheric path reflectance by assuming that the atmosphere is homogeneous and that black pixels definitely exist [30,62]. C2RCC uses a neural network that has been well trained with a dataset of surface water reflectance and top-of-atmosphere radiance obtained through radiative transfer simulations [24]. The iCOR algorithm commonly utilizes land pixels to perform the dark target method and multi-parameter inversion of aerosol optical thickness, employing the MODTRAN radiative transfer model for atmospheric modeling to correct for atmospheric scattering and absorption in satellite imagery [27]. In the L2gen method, an iterative method based on a bio-optical model, is used to estimate aerosol reflectance in the NIR or SWIR bands, which is then further extrapolated to the visible spectrum by selecting the appropriate aerosol models from pre-defined aerosol look-up tables [57,63]. Polymer is a spectral matching algorithm based on two models: one is a polynomial model that simulates atmospheric contributions and sun glint, and the other is a water-leaving reflectance model that simulates water reflectance through chlorophyll-a concentration and backscattering coefficients. According to the spectral similarity proposed by Ruddick et al. (2006) [64], the model is extended to the NIR bands to ensure its applicability in turbid waters. Through iterative adjustments of the parameters in both models, Polymer ensures optimal spectral fitting [25,65].
Additionally, L2gen combines an iterative bio-optical model with the NIR/SWIR atmospheric correction method, which requires the reflectance ratio between two NIR or SWIR bands to retrieve aerosol contributions. It has been demonstrated that combinations of the NIR–SWIR1 or NIR–SWIR2 bands work effectively for Landsat-8 data [30]. Since both Landsat-9 and Landsat-8 have similar spectral band configurations, these two different band combinations were also respectively used with L2gen to verify their performance for Landsat-9 data in this study, and they are referred to as L2gen (NIR–SWIR1) and L2gen (NIR–SWIR2) hereafter.
2.4. Procedure for Comparing Satellite and In-Situ Measurements
In this study, in-situ measurements were first utilized to evaluate uncertainties in water surface reflectance obtained from OLI-2/Landsat-9 processed by six atmospheric correction methods, including DSF, C2RCC, iCOR, L2gen (NIR–SWIR1), L2gen (NIR–SWIR2), and Polymer. Following this, a comparison of the consistency and uncertainty differences between OLI-2/Landsat-9 and two on-orbit sensors, MSI/Sentinel-2A/B and VIIRS/S-NPP/NOAA-20, was conducted. The flowchart of this study is illustrated in Figure 2.
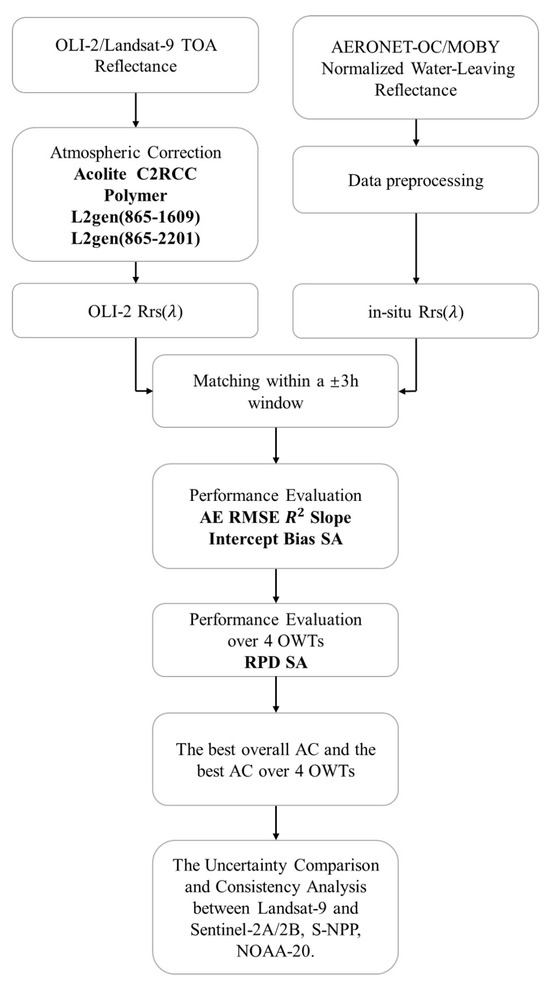
Figure 2.
Research flowchart of this study.
When matching satellite data with in-situ measurements, the Landsat-9 data pixels flagged by clouds, land, stray light, and sun glint were masked out, and the median of valid data pixels within a spatial window and h temporal window was used. If the number of valid pixels within the window exceeded half (namely greater than 12 in this study), the matchup data were retained; otherwise, they were discarded. The same procedure was also applied to MSI and VIIRS data.
2.5. Evaluation Indicators
To assess the performance of atmospheric correction methods for Landsat-9 data over water bodies, evaluation metrics including Root Mean Square Error (RMSE), Absolute Error (AE), Bias, Relative Percentage Difference (RPD), Correlation Coefficient (), and spectral angle (SA) were used. Among these, the SA reflects the consistency of the spectral shape between satellite and in-situ measurements [65], and SA is an indicator commonly used in atmospheric correction for its insensitivity to amplitude variations. It has been widely applied in the evaluation of atmospheric correction methods for satellites such as Landsat-8 (OLI), Sentinel-3 (OLCI), and HY-1C (CZI, Coastal Zone Imager) [34,41,66]. The evaluation indicators are defined as follows:
In the above equations, represents the remote sensing reflectance obtained from satellite data after atmospheric correction, represents the in-situ measured , N is the number of matchup data, i denotes an individual data point, n represents the total number of spectral bands, and j indicates a single band.
3. Results
3.1. Error Statistical Analysis of Different AC Methods
Figure 3 shows the scatter plots comparing the values at 443 nm, 482 nm, 561 nm, and 655 nm bands derived from OLI-2/Landsat-9 data using six AC methods (DSF, C2RCC, iCOR, L2gen (NIR-SWIR1), L2gen (NIR-SWIR2), and Polymer) with in-situ measurements. Figure 4 presents the variations in error metrics (, AE, RMSE, and Bias) of the six atmospheric correction methods with wavelength. Table 4 lists values of the error metrics for the six AC methods.
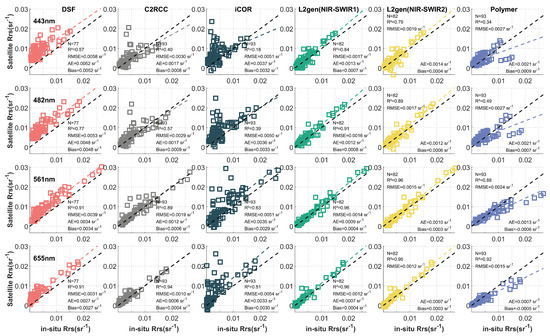
Figure 3.
Scatter plots of OLI/Landsat-9 processed by six atmospheric correction methods (DSF, C2RCC, iCOR, L2gen(NIR-SWIR1), L2gen(NIR-SWIR2), Polymer) versus in-situ measurements in four visible bands (443 nm, 482 nm, 561 nm, 665 nm). The black dashed line represents the 1:1 line, while the colored dashed lines represent the regression lines for the scatter points.
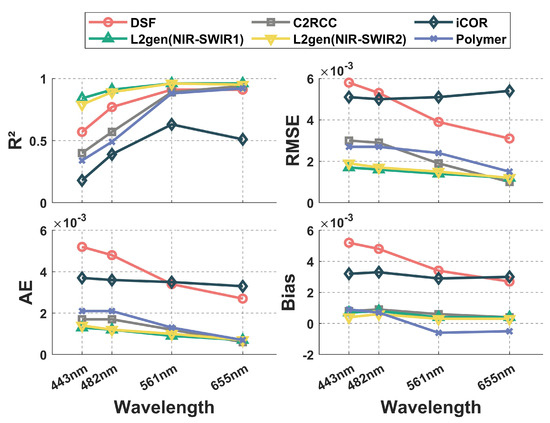
Figure 4.
Variations of four accuracy metrics (, AE, RMSE, and Bias) with wavelength for six atmospheric correction methods. The results of six atmospheric correction methods DSF, C2RCC, iCOR, L2gen(NIR-SWIR1), L2gen(NIR-SWIR2), and Polymer are indicated in red, gray, blur, green, yellow, and purple, respectively.

Table 4.
Statistical numbers of OLI-2 derived using six AC methods (DSF, C2RCC, iCOR, L2gen (NIR-SWIR1), L2gen (NIR-SWIR2)), and Polymer compared to in-situ data in the visible bands. The statistical metrics include the Correlation Coefficient (), slope and intercept of the regression line, Root Mean Square Error (RMSE), Absolute Error (AE), Bias, spectral angle (SA), and the number of matchups (N). The values indicating the best performance are highlighted in bold.
It is evident that the number of matchup points between satellite and in-situ measurements varies across the different AC methods. The C2RCC, iCOR, and Polymer have the highest number of matching points of 93, L2gen has 82, and DSF has the fewest of 77. The number of valid matchup data points between field measurements and Landsat-9 data varies with different atmospheric correction methods, which is mainly related to the effectiveness of AC methods and cloud thresholds used by different AC methods [64].
Analyzing results from Figure 3 and Figure 4, and Table 4, it is clear that the L2gen (NIR-SWIR1) and L2gen (NIR-SWIR2) methods perform best with the smallest errors. As shown in Figure 3 and Table 4, for the L2gen (NIR-SWIR1) method, the values range from 0.84 to 0.96, and the RMSE values are between and . For the L2gen (NIR-SWIR2) method, the values range from 0.79 to 0.96, and the RMSE values are between and . These two methods exhibit similar accuracy and generally have lower errors than the other four methods. Figure 4 further clearly illustrates that the L2gen (NIR-SWIR1) method has relatively higher values and lower RMSE and AE values, indicating slightly better performance than the L2gen (NIR-SWIR2) method. However, it is worth noting that, as shown in Figure 3, both the L2gen (NIR-SWIR1) and L2gen (NIR-SWIR2) methods tend to overestimate values when , and this overestimation becomes more pronounced as the value increases. Compared to DSF and iCOR, the C2RCC and Polymer methods have relatively smaller errors. The values range from 0.40 to 0.94 for the C2RCC method, and from 0.34 to 0.92 for the Polymer method. The RMSE values are between and for C2RCC, and between and for Polymer. Although the error statistics between these two methods seem similar, C2RCC generally performs slightly better than Polymer as shown in Figure 4. Additionally, Figure 3 shows that Polymer tends to underestimate when , while the C2RCC method does not show such a significant deviation. Therefore, based on the statistical results of the matchup data in this study, C2RCC generally outperforms Polymer for OLI-2/Landsat-9 data. DSF and iCOR exhibit the highest errors among the atmospheric correction methods, with DSF recording values from 0.57 to 0.91 and RMSE values ranging from to . The iCOR results have values between 0.18 and 0.63 and RMSE values from to . These errors are significantly larger compared to the other four atmospheric correction methods. Additionally, both methods demonstrate notable overestimations across all spectral bands from 443 nm to 655 nm.
In addition, it is shown in Figure 4 that the six AC methods examined in this study perform differently across visible spectral bands for OLI-2/Landsat-9 data. Among them, the performance difference across varying spectral bands is relatively larger for C2RCC, Polymer, and DSF, and smaller for iCOR, L2gen (NIR-SWIR1), and L2gen (NIR-SWIR2). Their statistical errors of RMSE, AE, and Bias increase with the varying wavelength from red to blue, and errors in the blue-green bands (443 nm, 482 nm) are significantly larger than those in the yellow-red ones (561 nm, 655 nm). Similar results were also demonstrated in evaluating Sentinel-2 and Landsat-8 data by Pahlevan et al. (2021) [51]. This could be attributed to errors introduced by misusing an aerosol type different from the actual one when extrapolating aerosol contributions from the NIR/SWIR, to visible spectral bands during the atmospheric correction procedure [67].
Considering that the errors of results processed by the six AC methods vary with wavelength, SA, which can reflect the similarity in spectral shapes between the satellite-derived and in-situ , was further calculated and compared in this study. The smaller the SA value, the higher the similarity in the spectral shape of the satellite-derived and in-situ .
Figure 5 shows the SA of the results processed by the six AC methods used in this study. Significant differences in SA can be observed among different AC methods. The C2RCC and L2gen exhibit the smallest median SA values, with C2RCC at and L2gen showing and for its two spectral combinations, reflecting a more concentrated SA distribution with a relatively narrow interquartile range. This is followed by Polymer, with median SA values of , then comes DSF with a median SA of . The iCOR has the largest median SA of , with the longest box plot indicating poor stability.
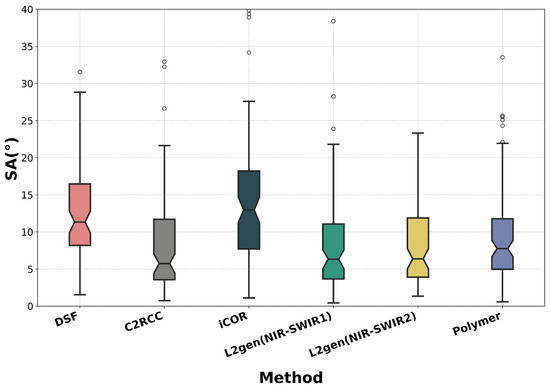
Figure 5.
Box plot of spectral angles for six AC methods (DSF, C2RCC, iCOR, L2gen(NIR-SWIR1), L2gen(NIR-SWIR2), and Polymer) used in this study. The box represents the interquartile range (IQR), containing 25% to 75% of the spectral angle values. The bottom and top edges of the box correspond to the first quartile (Q1) and third quartile (Q3), respectively. The line inside the box represents the median of the spectral angles. The whiskers extend to values 1.5 times the IQR beyond the box. The upper whisker extends to the maximum value within 1.5 × IQR above the box’s top edge (Q3), and the lower whisker extends to the minimum value within 1.5 × IQR below the box’s bottom edge (Q1). Black dots beyond the whiskers represent outliers.
To sum up, among the six AC methods used in this study, the L2gen method using two spectral band combinations of NIR–SWIR1 and NIR–SWIR2 performs better than the others across the four spectral bands for Landsat-9 data. L2gen (NIR-SWIR1) achieves the highest , lowest RMSE, AE, and a relatively small SA across all four visible bands. L2gen (NIR–SWIR2) exhibits the smallest Bias. Overall, L2gen (NIR–SWIR1) and L2gen (NIR–SWIR2) demonstrate similar superior performance, with L2gen (NIR–SWIR1) slightly outperforming L2gen (NIR–SWIR2). This is consistent with the findings of Yan et al. (2023) using Landsat-8 data [34].
Following the L2gen methods, the C2RCC and Polymer methods also demonstrate similar performance for Landsat-9 data. Compared to L2gen, C2RCC and Polymer show slightly worse precision in the yellow-red spectral bands (561 nm, 655 nm), while at blue-green wavelengths (443 nm, 482 nm), their performance deteriorates significantly, with noticeably lower values and significantly higher RMSE, AE, and Bias [34,45]. By comparison, C2RCC performs slightly better than Polymer.
Finally, the iCOR and DSF methods demonstrate the poorest performance across all four visible spectral bands for Landsat-9 data, consistently overestimating . This aligns with previous evaluation studies for Landsat-8 [34] and Sentinel-2 [68] data.
Figure 6 displays the Landsat-9 482 nm images processed by various AC methods. The two L2gen combinations along with C2RCC and Polymer yield similar images. The results indicate that the DSF method produces higher values, while iCOR shows substantial differences compared to the other methods, aligning with the error analysis presented earlier. Except L2gen and DSF, images processed by the three other methods exhibit striping and spatial non-uniformity on the eastern edge. This striping on the eastern edge is also observed in Landsat-8 imagery [39].
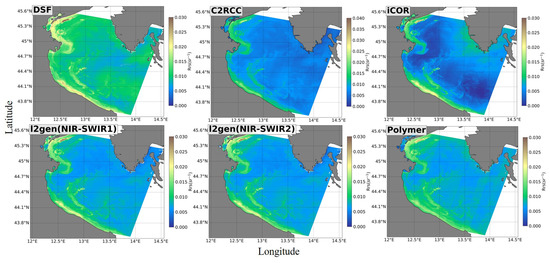
Figure 6.
Images from Landsat-9 at 482 nm on 9 April 2022, at the Venise site, processed using six atmospheric correction methods: DSF, C2RCC, iCOR, L2gen (NIR-SWIR1), L2gen (NIR-SWIR2), and Polymer demonstrate variations in measurements.
3.2. Performance Variations in AC Methods in Different OWTs
The performance of AC methods usually varies with OWTs [51]. In this section, to evaluate the performance of the six AC methods in different OWTs, the water bodies of matchup data in this study were further classified into four OWTs, including both clear and turbid waters, based on in-situ measured spectra following the optical water classification method of Wei et al. (2016) [69]. The performance of the six AC methods over different OWTs is then demonstrated.
To eliminate the magnitude differences in the original data while preserving their spectral shape characteristics, the in-situ measured spectra were first normalized to obtain according to Equation (9), represents the normalized spectrum, n denotes the total number of wavelengths, and represents the individual wavelengths of 443 nm, 482 nm, 561 nm, and 655 nm. Then, an unsupervised clustering method of Kmeans++ was applied to classify the normalized spectra into different OWTs. The in-situ data in this study were categorized into four OWTs (OWT1 to OWT4), corresponding to water types 4, 8, 15, and 17 from the 23 global water types derived by Wei et al. (2016). As shown in Figure 7, it can be seen that the four OWTs in this study cover both clear and turbid waters:
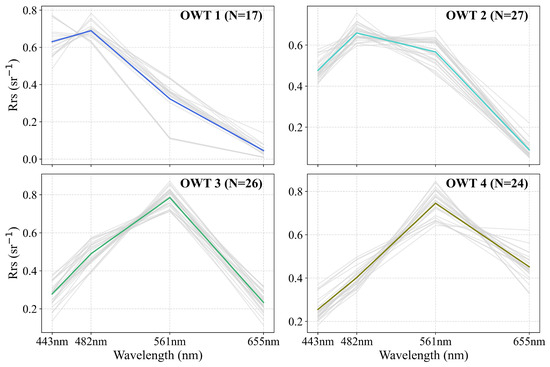
Figure 7.
Normalized spectra of four OWTs in this study. The colored lines represent the average spectra for each OWT, while the gray lines represent the normalized in-situ measured spectra.
Figure 8 presents scatter plots comparing in-situ with OLI-2/Landsat-9 data processed by six AC methods over four OWTs. The accuracy of the six AC methods across four OWTs is further ranked in Figure 9 based on RPD values, which are also listed in Table 5. The larger the RPD value, the higher the uncertainty, resulting in a lower ranking. Figure 10 demonstrates the median derived from OLI-2/Landsat-9 processed by six AC methods in four OWTs, and the corresponding median in-situ measurements are also plotted as references. The SA between satellite data and field measurements is also given in Table 5.
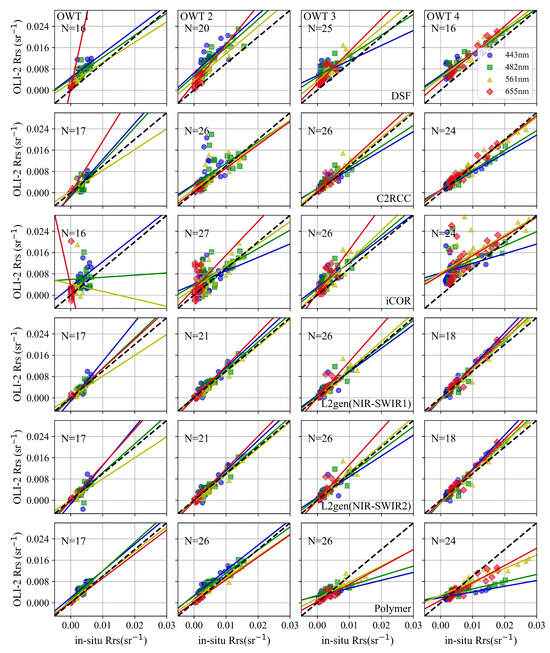
Figure 8.
Scatter plots between OLI-2/Landsat-9 and in-situ data for six AC methods across four visible wavelengths (443 nm, 482 nm, 561 nm, and 665 nm) over four OWTs (OWT1, OWT2, OWT3, and OWT4). The subplots in the same column represent one specific water quality type (OWT1 to OWT4, from left to right), and the subplots in different rows correspond to varying atmospheric correction methods (DSF, C2RCC, iCOR, L2gen(NIR-SWIR1), L2gen(NIR-SWIR2), and Polymer from top to bottom). Four different wavelengths of 443 nm, 482 nm, 561 nm, and 655 nm are indicated by blue, green, yellow, and red, respectively. The dashed line represents the 1:1 line, while the solid lines are the regression lines at individual wavelengths.
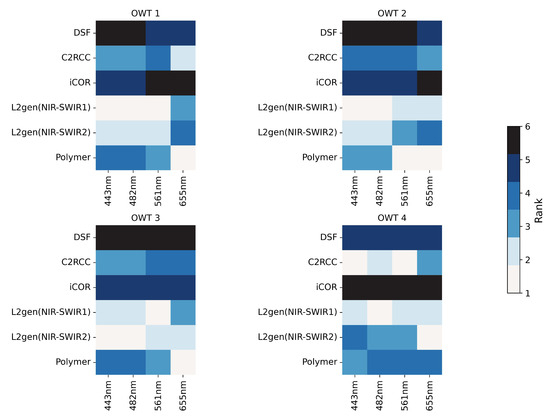
Figure 9.
A heatmap of the relative RPD rankings for six AC methods across four OWTs and wavelengths. Lighter colors indicate smaller errors and better performance. The horizontal axis represents the wavelengths, while the vertical axis represents the AC methods. The color scale on the right indicates the ranking.

Table 5.
The Relative Percentage Difference (RPD), median spectral angle (SA), and the number of matches (N) of Landsat-9 data processed by six atmospheric correction methods in four OWTs and wavelengths.
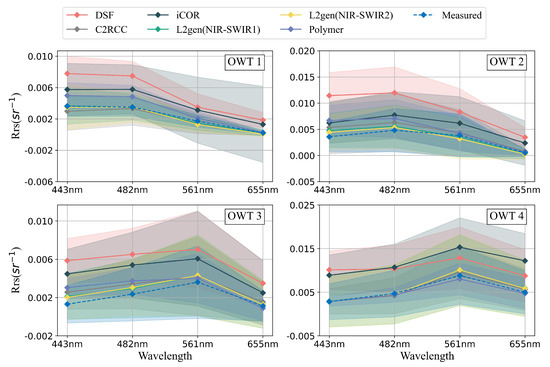
Figure 10.
Comparison of the spectrum from different AC methods with in-situ data across four OWTs. The vertical axis represents , and the horizontal axis represents the wavelength. The lines in red, gray, blur, green, yellow, purple, and light blue show results derived from DSF, C2RCC, iCOR, L2gen (NIR-SWIR1), L2gen (NIR-SWIR2), Polymer and in-situ measurements.
For the Polymer method, the matchup data points scatter close to the 1:1 line in OWT1 and OWT2. However, in OWT3 and OWT4, significant underestimations occur when . On the other hand, the C2RCC method results generally agree well with field data across the four OWTs, except for some outliers in OWT2 in Figure 8. This results in C2RCC performing slightly better than Polymer as shown in Section 3.1 of this study. Notably, Figure 9 and Figure 10, and Table 5 show that C2RCC performs best in turbid waters of OWT4 in the spectral range from 443 nm to 561 nm among the six AC methods. This might be attributed to the large number of turbid water cases included in the C2RCC training dataset [21]. DSF and iCOR show significantly higher uncertainty than the other four AC methods, both across different bands and OWTs. Additionally, DSF is more suited to turbid waters than to clear water bodies, aligning with the previous findings for Sentinel-2 and Sentinel-3 [68,70].
From Figure 8, Figure 9 and Figure 10, and Table 5, L2gen (NIR-SWIR1) and L2gen (NIR-SWIR2) consistently rank in the top two across four spectral bands in OWT1, OWT2, and OWT3. However, in turbid waters of OWT4, a slight overestimation for at 561 nm and 655 nm can be observed in Figure 8 and Figure 10. The L2gen (NIR-SWIR1) slightly outperforms L2gen (NIR-SWIR2) in OWT1, OWT2, and OWT4, while L2gen (NIR-SWIR2) shows a smaller RPD in the moderately turbid water of OWT3. This is consistent with the findings of Pahlevan et al. (2017) [39] that L2gen (NIR-SWIR2) produces more robust in moderately turbid waters.
Overall, compared with the other four AC methods, L2gen performs more stably and consistently across four OWTs and four visible bands for Landsat-9 data, despite a slight overestimation for at 561 nm and 655 nm in OWT4. Both Polymer and C2RCC can be used in clear waters (OWT1, OWT2, and OWT3), but they exhibit more uncertainties compared to L2gen. C2RCC is particularly suited for more turbid waters like OWT4 in this study. Both DSF and iCOR exhibit significant overestimation of and higher uncertainty across all four OWTs compared to the four other AC methods.
From Figure 11, it is evident that Landsat-9 data processed using L2gen (NIR-SWIR1) exhibit high consistency with in-situ measurements across various OWTs, demonstrating Landsat-9’s robust capability to accurately capture spectral characteristics. However, it is also worth noting that relatively higher uncertainty exhibits at the blue band, which should be taken into consideration when interpreting results in this spectral region.
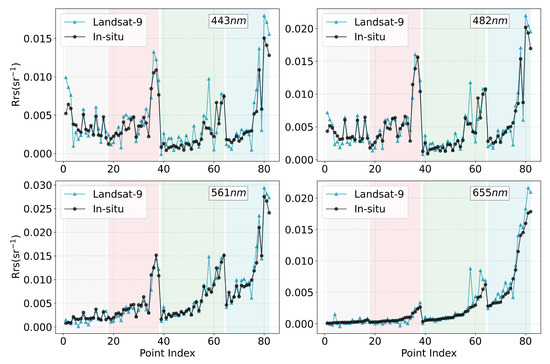
Figure 11.
Sequence analysis of in-situ compared to Landsat-9 processed using L2gen (NIR-SWIR1). Four distinct background colors are used to represent the four OWTs, labeled sequentially from OWT1 to OWT4. Within each category, data points are sorted by the values at 561 nm to illustrate the spectral variations under varying aquatic conditions.
4. Discussion
4.1. Uncertainties of Matchup Analysis
This study evaluates the performance of six commonly used AC methods for OLI-2/Landsat-9 data with in-situ measurements from AERONET-OC and MOBY. In terms of satellite-derived surface reflectance, apart from errors caused by the AC procedure, uncertainties might also be introduced by the spatial and temporal window sizes in the matchup process.
Given the scale of the satellite observations, adopting an box in the matching experiments helps mitigate potential navigation errors in the satellite data, reduces the impact of small-scale spatial variability, and increases the number of successful matches [71]. However, although spaceborne sensors with extensive coverage can effectively average geophysical variability within a pixel, in-situ stations such as AERONET-OC and MOBY may not fully capture these variations, thereby introducing some uncertainty [64,72]. There is currently no consensus on the optimal selection of box size. Bailey et al. (2006) used SeaWiFS as an example to calculate the minimum sample size required to obtain reliable results, finding that a box was reasonable while also noting that a box did not significantly affect the results. Considering that a larger box might introduce geophysical variations that could affect the outcomes, a box was ultimately recommended.
In addition, instead of using the coefficient of variation (CV) threshold for data validity assessment, this study opted for the median error to mitigate the influence of outliers. Recent research by Barnes et al. (2019) [47], which examined the impact of CV thresholds and other data screening techniques using VIIRS and MODIS, found that these techniques did not substantially enhance validation statistics and could lead to unnecessary data loss. Given the relatively scarce data availability from Landsat-9, which has a 16-day revisit cycle and was launched just over two years prior to the study, the CV threshold was not employed for spatial uniformity testing, and median error was used instead. A time window of h, which is commonly recommended in evaluating the ocean color remote sensing data [15,21], was used during the matching process. However, most of the in-situ measurements used in this study come from coastal waters as shown in Figure 1. Previous studies have demonstrated that factors such as rainfall, wind, tides, river plumes, or human activities can lead to rapid changes in the optical properties of coastal waters [73,74,75]. It was also observed that values measured at the AERONET-OC Venise site could vary up to 15% within 3 h [52].
To ensure the quality of the experiment, this study only used quality-controlled AERONET-OC Level 2 data and MOBY “Good” level data, which resulted in a loss of some matched data points. This study strongly recommends expanding the network of stations to increase the amount of in-situ data, ensuring broad geographic coverage and enabling evaluation of sensor performance in complex optical waters, particularly in rapidly changing environments such as estuaries, optically shallow waters, and eutrophic waters. Additionally, increasing the amount of data would also facilitate the use of smaller time windows, thereby reducing uncertainties in the matching process. In addition to increasing the number of in-situ measurements, efforts should be made to enhance data sharing. Existing platforms like AERONET and SeaBASS [55] provide excellent examples, and the recently established WISPstation network has also expanded the range of available data [76]. It is important to note that data formats and quality often differ across platforms, requiring significant time for users to standardize formats and select appropriate data. Therefore, strengthening international collaboration, establishing standardized data collection processes and processing protocols, and unifying data storage formats would greatly benefit the evaluation of uncertainties in both historical and future remote sensing sensor data, and improve retrieval performance.
4.2. Analysis of Error Sources of Different AC Methods
It is shown in this study that the L2gen AC methods with two NIR-SWIR band combinations (NIR-SWIR1 and NIR-SWIR2) achieve the best performance. Since both methods share the same underlying atmospheric correction procedure and use the same 865 nm NIR band combined with different SWIR bands, they produce very similar outcomes. The superior performance of L2gen may be attributed to the following reasons: (1) Besides a strict data pre-filtering excluding pixels potentially affected by clouds or sun glint, the aerosol model used in L2gen is built based on extensive in-situ aerosol optical properties from AERONET, and the in-situ measurements used in this evaluation are primarily from AERONET-OC sites. (2) Using the NIR and SWIR bands of 865 nm, 1609 nm, and 2201 nm with high SNR in atmospheric correction, the band combinations between NIR and SWIR can satisfy the black pixel assumption for most cases in coastal water. As shown in this study, the NIR-SWIR1 combination performs better than the NIR-SWIR2 in OWT1 and OWT2, while the latter produces more robust in moderately turbid water of OWT3, which is consistent with previous studies [39]. However, in highly turbid water of OWT4, the L2gen with both NIR-SWIR band combinations tends to slightly overestimate as the values increase over 0.01 sr−1.
The C2RCC ranks second after the L2gen in performance. It filters out fewer data pixels, resulting in the highest number of matchups. However, it shows higher uncertainties in the 443 nm and 482 nm bands compared to L2gen, while its performance improves in the 561 nm and 655 nm bands. Notably, C2RCC achieves the lowest uncertainty in turbid water (OWT4) but ranks third to fourth in the other three water types (OWT1 to OWT3). This might be due to the fact that the training dataset for C2RCC does not cover all actual atmospheric aerosol types and includes sufficient training for sediment-rich waters but insufficient training for other OWTs, as machine learning methods such as C2RCC strongly depend on the datasets in their training process [21].
Polymer ranks fourth overall among the six AC methods in this study. It also filters out fewer data pixels like C2RCC, resulting in a high number of matchups. Its performance in longer wavelengths is significantly better than in shorter ones. However, unlike C2RCC, Polymer is not suitable for sediment-rich waters, ranking fourth in OWT4, which is consistent with Liu et al.’s (2022) [21] findings. The relatively poorer performance of Polymer may be due to the following reasons: (1) It assumes an Angstrom coefficient of 1.0 for aerosol spectral optical properties, while the actual range is 0.5–1.3 [64], and strong absorbing aerosols near coasts or inland may also lead to biases, particularly in these environments [21]. (2) Its bio-optical water reflectance model, which estimates the water-leaving reflectance based on the chlorophyll-a concentration and backscattering coefficients, is effective in clear waters (OWT1 and OWT2) where phytoplankton dominates. However, in turbid waters, the presence of large amounts of sediments can make the model’s applicability challenging. It has been addressed in work by Wang et al. (2020) [77] that treating the aerosol scattering exponent as a variable instead of a fixed value and using IOP (Inherent Optical Property)-based surface water reflectance models can improve the performance of Polymer in turbid waters.
The DSF ranks poorly due to its reliance on the black pixel assumption, which presumes atmospheric homogeneity and depends on the presence of non-reflective land pixels in the image. This assumption often fails in coastal areas where such pixels are scarce, leading to systematic overestimations of and high SA values, indicating poor spectral fidelity [45]. However, the performance of DSF improves in turbid waters, likely due to the increased presence of reflective sediments and closer proximity to land, which align with its design assumptions. Furthermore, the lack of adjacency correction in DSF may result in the contamination of water pixels by adjacent land, exacerbating errors in processed images [34].
The iCOR algorithm often overestimates reflectance due to its reliance on land pixels for aerosol estimation. In coastal satellite imagery, where these land pixels are frequently sparse, iCOR struggles to accurately utilize them to estimate aerosol optical thickness (AOT), often resorting to default AOT values that do not represent actual atmospheric conditions accurately [45]. The strength of iCOR lies in its unique consideration of adjacency effects, which effectively reduces land pixel contamination in inland water bodies such as rivers and lakes. Moreover, because it does not require an in-depth understanding of radiative transfer or absolute sensor calibration, it is easier to implement [27].
L2gen(NIR-SWIR1) is identified as the best-performing method for Landsat-9, with the RMSE ≤ 0.0017 sr−1. Yan et al. (2023) [34] compared DSF, C2RCC, iCOR, L2gen(NIR-SWIR2), and Polymer, concluding that L2gen(NIR-SWIR2) performs the best with the RMSE ≤ 0.0018 sr−1. Similarly, Ilori et al. (2019) [32] evaluated DSF, L2gen(NIR-SWIR1), LaSRC, and ARCSI, recommending L2gen(NIR-SWIR1) as the most reliable method with an RMSE of ≤0.0015 sr−1. These consistent findings underscore the robustness of L2gen for both Landsat-8 and Landsat-9.
4.3. Consistency Analysis of OLI-2/Landsat-9 with Other On-Orbit Remote Sensing Sensors
The long revisit period of approximately 16 days for the Landsat-9 data limits its applications in dynamic coastal areas; therefore, a joint use of multiple on-orbit spaceborne sensors, such as MSI/Sentinel-2 or VIIRS/S-NPP/NOAA-20, is usually necessary [40]. The uncertainty of MSI data has been assessed multiple times [39,45,51]. For VIIRS, as the successor to MODIS, the uncertainty and consistency of its products have also been validated and evaluated by the scientific community several times since it was launched in 2012 [47,48]. Notably, Pardo et al. (2023) [48] used datasets in the Atlantic Ocean to compare VIIRS data with Sentinel-3 and MODIS. However, there is still a lack of consistency assessments between MSI, VIIRS, and OLI-2 data in aquatic systems.
In this study, a time window of ±3 h was chosen to match the MSI, VIIRS, and OLI-2 data, as well as the in-situ measurements from AERONET-OC. Note that, with the long revisit period of 16 days for the OLI-2/Landsat-9 data, it is difficult to obtain concurrent matchups for MSI, VIIRS, and OLI-2 data on the same day. Thus, the OLI-2 data were matched up with MSI and VIIRS, respectively. Since VIIRS has a revisit period of about one day, 52 valid matchups were obtained between OLI-2 and VIIRS. MSI, with a revisit period of six days, resulted in only 23 matchups with OLI-2. Figure 12 presents the statistics of the overpass time differences of OLI-2 versus MSI and VIIRS matchup points obtained in this study. It can be seen that the matchup data between MSI and OLI-2 are nearly simultaneous within 30 min, while the time differences between VIIRS and OLI-2 are greater, with a median average of 2.4 h.
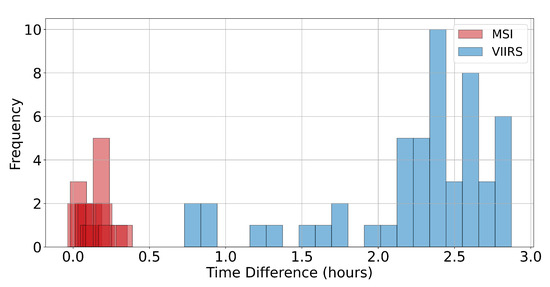
Figure 12.
Statistics of the overpass time differences between MSI, VIIRS, and OLI-2. The horizontal axis represents the absolute value of the overpass time difference, and the vertical axis shows the number of matchups. Although a h time window was used, the actual overpass times of MSI and OLI-2 are within 0.5 h of each other, while most VIIRS overpasses differ from OLI-2 by 2 to 3 h.
Figure 13 demonstrates the scatter plots between satellite data (MSI, VIIRS, and OLI-2) and in-situ measured . Results show that the performance of OLI-2 is generally comparable to MSI and VIIRS. The RMSE errors in Table 6 further support this observation. Specifically, in the first three visible bands of 443 nm, 482 nm, and 561 nm, the RMSE values of OLI-2, MSI, and VIIRS are very close, with a difference of less than 0.0002 sr−1. However, at 655 nm, the uncertainty of the OLI-2 data is lower than that of MSI but higher than that of VIIRS, with a difference of approximately 0.0004 sr−1 between them.
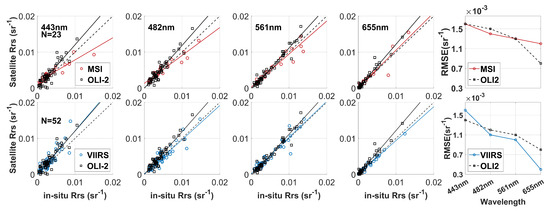
Figure 13.
Comparison of satellite from OLI-2, MSI, and VIIRS with in-situ measured at the 443 nm, 482 nm, 561 nm, and 655 nm bands. The overpass times of MSI/VIIRS and OLI-2 were within h, and each satellite was matched with the nearest in-situ measurements using a matchup time window of h. The dashed line represents the 1:1 line, the black solid line indicates the regression line for OLI-2, and the red and blue solid lines represent the regression lines for MSI and VIIRS, respectively. The subplots in the last column show the variations in RMSE with wavelength for the three spaceborne sensors.

Table 6.
Error statistics of RMSE (sr−1) for OLI-2, MSI, and VIIRS versus in-situ data.
These differences could be partly attributed to spatial coverage and time differences between the satellite and in-situ data, which lead to variations in water optical properties, and partly to the use of different atmospheric correction methods—Polymer for MSI data and L2gen for VIIRS and OLI-2. Nevertheless, the RMSE differences between the three sensors are much smaller than those observed in the previous evaluation experiment between L2gen and other AC methods such as DSF, C2RCC, and Polymer using Landsat-9 data. For these three sensors on board different satellites, the uncertainty differences are within an acceptable range, suggesting that OLI-2 data have the potential to be effectively combined with MSI and VIIRS data for comprehensive applications.
The spatial distributions of data at four visible spectral bands from OLI-2/Landsat-9, MSI/Sentinel-2B, and VIIRS/S-NPP for the Venise station (2 February 2022) and Section-7 station (12 May 2022), as well as the corresponding frequency distributions, demonstrate general consistency among the three sensors, with similar spatial patterns and closely matching frequency distributions shown in Figure 14 and Figure 15. However, the OLI-2 (30 m) and MSI (60 m) data show finer details compared to VIIRS (750 m), with the latter displaying small jagged edges along image boundaries. Moreover, the values at 561 nm and 655 nm from the three sensors exhibit rather similar spatial patterns of variation in coastal waters, while at 443 nm and 482 nm, the OLI-2 values are slightly higher than those of VIIRS. We speculate that the differences are caused by the use of different band combinations in estimating aerosol contributions despite using the same L2gen atmospheric correction procedure.
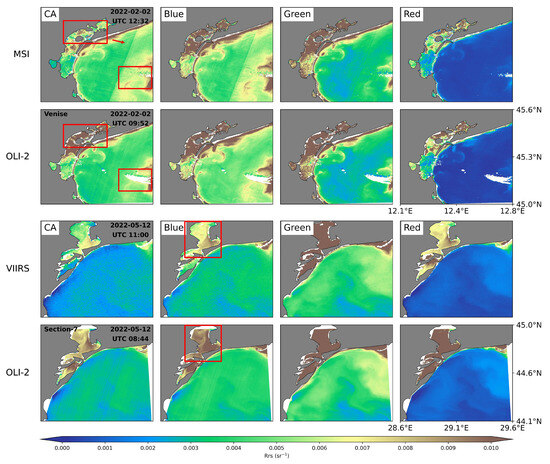
Figure 14.
The spatial distributions of data at four visible spectral bands from OLI-2/Landsat-9, MSI/Sentinel-2B and VIIRS/S-NPP at the Venise station on 2 February 2022, and the Section-7 station on 12 May 2022. CA, blue, green, and red correspond to the 443 nm, 482 nm, 561 nm, and 655 nm bands, respectively. The spatial resolution of OLI-2, MSI and VIIRS is 30 m, 60 m, and 750 m.
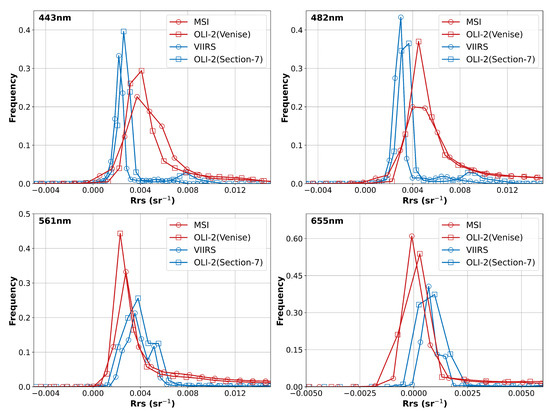
Figure 15.
Frequency distribution of within the scenes.
It is also worth noting that the overpass time difference is over two hours, during which the varying water optical properties could contribute to the observed differences. We observe that the discrepancies in lakes (marked in a red rectangle) are more significant than those in coastal waters, which we speculate could also result from the variable water optical properties in the lake, where the impact of multiple land activities is more pronounced. The noticeable cloud displacement within the red rectangle could also lead to inconsistencies in the frequency distributions. Additionally, as indicated by the red arrow in Figure 14, the MSI data suffer from pronounced striping effects at 443 nm and 482 nm, which could potentially be improved by utilizing the concurrent, smoother OLI-2 data.
5. Conclusions
The performance of the latest Landsat-9, launched in 2021, is highly anticipated for global inland and coastal aquatic ecosystem monitoring, and its application depends on reliable atmospheric correction processing. In this study, the performance of six atmospheric correction methods (DSF, C2RCC, iCOR, L2gen(NIR-SWIR1), L2gen(NIR-SWIR2), and Polymer) available for Landsat-9 data was evaluated and compared using global in-situ data from AERONET-OC and MOBY. The results show that L2gen(NIR-SWIR1) demonstrates the lowest uncertainty (RMSE ≤ 0.0017 sr−1, SA = 6.33°) across the four optical water types. L2gen (NIR-SWIR2) follows closely (RMSE ≤ 0.0019 sr−1, SA = 6.38°), followed by C2RCC (RMSE ≤ 0.0030 sr−1, SA = 5.74°) and Polymer (RMSE ≤ 0.0027 sr−1, SA = 7.76°). Finally, iCOR (RMSE ≤ 0.0051 sr−1, SA = 12.96°) and DSF (RMSE ≤ 0.0058 sr−1, SA = 11.33°) exhibit relatively high uncertainties. This provides a reference for selecting optimal atmospheric correction methods for Landsat-9 data applications in aquatic systems.
Additionally, the uncertainty and consistency of OLI-2/Landsat-9 in the visible bands were compared with concurrent on-orbit sensors MSI/Sentinel-2A/B and VIIRS/S-NPP/NOAA-20. The results suggest that they exhibit relatively high consistency, making it possible to form a multi-satellite observation system. This enables researchers to track and analyze dynamic changes in the inland and coastal water environment conveniently, providing timely decision-making tools and guidance for addressing ecological issues such as algal blooms and pollution diffusion.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs16234517/s1, Table S1. Summary of the Landsat-9 images; Table S2. Summary of the Sentinel-2A/B images; Table S3. Summary of the S-NPP/NOAA-20 images.
Author Contributions
Conceptualization was contributed by S.H. and Y.G.; A.S. conducted the experiments and validated the results, as well as prepared the original draft; P.L. and C.L. assisted in method debugging; G.Y. and F.Z. performed the review and editing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (Grant No. 2022YFC3103402), the Zhejiang Provincial Natural Science Foundation of China (Grant No. LD24D060002), the Hainan Provincial Joint Project of Sanya Yazhou Bay Science and Technology City (Grant No. 2021CXLH0020), the National Natural Science Foundation of China (Grant No. U23A2033), the Key R&D Program of Zhejiang Province (Grant No. 2024C03034), and the Ocean Decade action “Kuroshio Edge Exchange and the Shelf Ecosystem” (Grant No. CSK-2/08/2023).
Data Availability Statement
The data used in this study can be found in the Supplementary Materials.
Acknowledgments
The authors extend their appreciation to the United States Geological Survey (USGS) for providing Landsat-9 data, the National Aeronautics and Space Administration (NASA) for AERONET-OC and S-NPP/NOAA-20 data, the European Space Agency (ESA) for Sentinel-2A/B data, and the National Oceanic and Atmospheric Administration (NOAA) for MOBY data. The authors also thank the Hainan Observation and Research Station of Ecological Environment and Fishery Resource in Yazhou Bay for their support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wulder, M.A.; Roy, D.P.; Radeloff, V.C.; Loveland, T.R.; Anderson, M.C.; Johnson, D.M.; Healey, S.; Zhu, Z.; Scambos, T.A.; Pahlevan, N.; et al. Fifty years of Landsat science and impacts. Remote Sens. Environ. 2022, 280, 113195. [Google Scholar] [CrossRef]
- Kabir, S.; Pahlevan, N.; O’Shea, R.E.; Barnes, B.B. Leveraging Landsat-8/-9 underfly observations to evaluate consistency in reflectance products over aquatic environments. Remote Sens. Environ. 2023, 296, 113755. [Google Scholar] [CrossRef]
- Masek, J.G.; Wulder, M.A.; Markham, B.; McCorkel, J.; Crawford, C.J.; Storey, J.; Jenstrom, D.T. Landsat 9: Empowering open science and applications through continuity. Remote Sens. Environ. 2020, 248, 111968. [Google Scholar] [CrossRef]
- Goward, S.N.; Williams, D.L. Landsat and earth systems science: Development of terrestrial monitoring. Photogramm. Eng. Remote Sens. 1997, 63, 887–900. [Google Scholar]
- Cao, Z.; Ma, R.; Duan, H.; Pahlevan, N.; Melack, J.; Shen, M.; Xue, K. A machine learning approach to estimate chlorophyll-a from Landsat-8 measurements in inland lakes. Remote Sens. Environ. 2020, 248, 111974. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, M.; Tang, X. Eutrophication assessment of seasonal urban lakes in China Yangtze River Basin using Landsat 8-derived Forel-Ule index: A six-year (2013–2018) observation. Sci. Total Environ. 2020, 745, 135392. [Google Scholar] [CrossRef] [PubMed]
- Maleki, S.; Mohajeri, S.H.; Mehraein, M.; Sharafati, A. Lake evaporation in arid zones: Leveraging Landsat 8’s water temperature retrieval and key meteorological drivers. J. Environ. Manag. 2024, 355, 120450. [Google Scholar] [CrossRef]
- Marchese, F.; Genzano, N.; Nolde, M.; Falconieri, A.; Pergola, N.; Plank, S. Mapping and characterizing the Kīlauea (Hawaii) lava lake through Sentinel-2 MSI and Landsat-8 OLI observations of December 2020–February 2021. Environ. Model. Softw. 2022, 148, 105273. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, W.; Tian, Y.Q.; Yu, Q. Monitoring dissolved organic carbon by combining Landsat-8 and Sentinel-2 satellites: Case study in Saginaw River estuary, Lake Huron. Sci. Total Environ. 2020, 718, 137374. [Google Scholar] [CrossRef]
- Li, H.; Li, H.; Wang, J.; Hao, X. Revealing the river ice phenology on the Tibetan Plateau using Sentinel-2 and Landsat 8 overlapping orbit imagery. J. Hydrol. 2023, 619, 129285. [Google Scholar] [CrossRef]
- Osadchiev, A.; Sedakov, R. Spreading dynamics of small river plumes off the northeastern coast of the Black Sea observed by Landsat 8 and Sentinel-2. Remote Sens. Environ. 2019, 221, 522–533. [Google Scholar] [CrossRef]
- Min, Y.; Cui, L.; Li, J.; Han, Y.; Zhuo, Z.; Yin, X.; Zhou, D.; Ke, Y. Detection of large-scale Spartina alterniflora removal in coastal wetlands based on Sentinel-2 and Landsat 8 imagery on Google Earth Engine. Int. J. Appl. Earth Obs. Geoinf. 2023, 125, 103567. [Google Scholar] [CrossRef]
- Pacheco, A.; Horta, J.; Loureiro, C.; Ferreira, Ó. Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef]
- Zeng, J.; Sun, Y.; Cao, P.; Wang, H. A phenology-based vegetation index classification (PVC) algorithm for coastal salt marshes using Landsat 8 images. Int. J. Appl. Earth Obs. Geoinf. 2022, 110, 102776. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, X.; Qiu, S.; Xu, X.; Wang, X.; Chang, Q.; Wu, J.; Li, B. Quantifying latitudinal variation in land surface phenology of Spartina alterniflora saltmarshes across coastal wetlands in China by Landsat 7/8 and Sentinel-2 images. Remote Sens. Environ. 2022, 269, 112810. [Google Scholar] [CrossRef]
- Xu, Y.; Feng, L.; Zhao, D.; Lu, J. Assessment of Landsat atmospheric correction methods for water color applications using global AERONET-OC data. Int. J. Appl. Earth Obs. Geoinf. 2020, 93, 102192. [Google Scholar] [CrossRef]
- Micijevic, E.; Barsi, J.; Haque, M.O.; Levy, R.; Anderson, C.; Thome, K.; Czapla-Myers, J.; Helder, D. Radiometric performance of the Landsat 9 Operational Land Imager over the first 8 months on orbit. In Proceedings of the Earth Observing Systems XXVII, San Diego, CA, USA, 23–25 August 2022; SPIE: Bellingham, DC, USA, 2022; Volume 12232, pp. 249–256. [Google Scholar]
- Gordon, H.R.; Clark, D.K.; Hovis, W.A.; Austin, R.W.; Yentsch, C.S. Ocean color measurements. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 1985; Volume 27, pp. 297–333. [Google Scholar]
- Gordon, H.R. Atmospheric correction of ocean color imagery in the Earth Observing System era. J. Geophys. Res. Atmos. 1997, 102, 17081–17106. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef]
- Liu, H.; Li, Q.; Zhu, P.; Hu, Z.; Yang, C.; Wang, Y.; Cui, A.; Wang, Z.; Wu, G. A glimpse of ocean color remote sensing from moon-based Earth observations. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Bailey, S.W.; Franz, B.A.; Werdell, P.J. Estimation of near-infrared water-leaving reflectance for satellite ocean color data processing. Opt. Express 2010, 18, 7521–7527. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Atmospheric correction of Sentinel-3/OLCI data for mapping of suspended particulate matter and chlorophyll-a concentration in Belgian turbid coastal waters. Remote Sens. Environ. 2021, 256, 112284. [Google Scholar] [CrossRef]
- Brockmann, C.; Doerffer, R.; Peters, M.; Kerstin, S.; Embacher, S.; Ruescas, A. Evolution of the C2RCC neural network for Sentinel 2 and 3 for the retrieval of ocean colour products in normal and extreme optically complex waters. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; Volume 740, p. 54. [Google Scholar]
- Steinmetz, F.; Deschamps, P.Y.; Ramon, D. Atmospheric correction in presence of sun glint: Application to MERIS. Opt. Express 2011, 19, 9783–9800. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Casey, B.; Arnone, R.A.; Weidemann, A.D.; Parsons, R.; Montes, M.J.; Gao, B.C.; Goode, W.; Davis, C.O.; Dye, J. Water and bottom properties of a coastal environment derived from Hyperion data measured from the EO-1 spacecraft platform. J. Appl. Remote Sens. 2007, 1, 011502. [Google Scholar]
- De Keukelaere, L.; Sterckx, S.; Adriaensen, S.; Knaeps, E.; Reusen, I.; Giardino, C.; Bresciani, M.; Hunter, P.; Neil, C.; Van der Zande, D.; et al. Atmospheric correction of Landsat-8/OLI and Sentinel-2/MSI data using iCOR algorithm: Validation for coastal and inland waters. Eur. J. Remote Sens. 2018, 51, 525–542. [Google Scholar] [CrossRef]
- Clewley, D.; Bunting, P.; Shepherd, J.; Gillingham, S.; Flood, N.; Dymond, J.; Lucas, R.; Armston, J.; Moghaddam, M. A python-based open source system for geographic object-based image analysis (GEOBIA) utilizing raster attribute tables. Remote Sens. 2014, 6, 6111–6135. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Pahlevan, N.; Schott, J.R.; Franz, B.A.; Zibordi, G.; Markham, B.; Bailey, S.; Schaaf, C.B.; Ondrusek, M.; Greb, S.; Strait, C.M. Landsat 8 remote sensing reflectance (Rrs) products: Evaluations, intercomparisons, and enhancements. Remote Sens. Environ. 2017, 190, 289–301. [Google Scholar] [CrossRef]
- Wei, J.; Lee, Z.; Garcia, R.; Zoffoli, L.; Armstrong, R.A.; Shang, Z.; Sheldon, P.; Chen, R.F. An assessment of Landsat-8 atmospheric correction schemes and remote sensing reflectance products in coral reefs and coastal turbid waters. Remote Sens. Environ. 2018, 215, 18–32. [Google Scholar] [CrossRef]
- Ilori, C.O.; Pahlevan, N.; Knudby, A. Analyzing performances of different atmospheric correction techniques for Landsat 8: Application for coastal remote sensing. Remote Sens. 2019, 11, 469. [Google Scholar] [CrossRef]
- Pahlevan, N.; Balasubramanian, S.V.; Sarkar, S.; Franz, B.A. Toward long-term aquatic science products from heritage Landsat missions. Remote Sens. 2018, 10, 1337. [Google Scholar] [CrossRef]
- Yan, N.; Sun, Z.; Huang, W.; Jun, Z.; Sun, S. Assessing Landsat-8 atmospheric correction schemes in low to moderate turbidity waters from a global perspective. Int. J. Digit. Earth 2023, 16, 66–92. [Google Scholar] [CrossRef]
- Van Nguyen, M.; La, O.; Nguyen, H.; Heriza, D.; Lin, B.Y.; Ryadi, G.; Lin, C.H.; Pham, V.Q. Landsat 8 OLI atmospheric correction neural network for inland waters in tropical regions. Int. J. Environ. Sci. Technol. 2024, 1–20. [Google Scholar] [CrossRef]
- Li, J.; Roy, D.P. A global analysis of Sentinel-2A, Sentinel-2B and Landsat-8 data revisit intervals and implications for terrestrial monitoring. Remote Sens. 2017, 9, 902. [Google Scholar] [CrossRef]
- Wu, Z.; Snyder, G.; Vadnais, C.; Arora, R.; Babcock, M.; Stensaas, G.; Doucette, P.; Newman, T. User needs for future Landsat missions. Remote Sens. Environ. 2019, 231, 111214. [Google Scholar] [CrossRef]
- Li, J.; Chen, B. Global revisit interval analysis of Landsat-8-9 and Sentinel-2A-2B data for terrestrial monitoring. Sensors 2020, 20, 6631. [Google Scholar] [CrossRef]
- Pahlevan, N.; Sarkar, S.; Franz, B.A.; Balasubramanian, S.V.; He, J. Sentinel-2 MultiSpectral Instrument (MSI) data processing for aquatic science applications: Demonstrations and validations. Remote Sens. Environ. 2017, 201, 47–56. [Google Scholar] [CrossRef]
- Trevisiol, F.; Mandanici, E.; Pagliarani, A.; Bitelli, G. Evaluation of Landsat-9 interoperability with Sentinel-2 and Landsat-8 over Europe and local comparison with field surveys. ISPRS J. Photogramm. Remote Sens. 2024, 210, 55–68. [Google Scholar] [CrossRef]
- Gilerson, A.; Malinowski, M.; Agagliate, J.; Herrera-Estrella, E.; Tzortziou, M.; Tomlinson, M.C.; Meredith, A.; Stumpf, R.P.; Ondrusek, M.; Jiang, L.; et al. Development of VIIRS-OLCI chlorophyll-a product for the coastal estuaries. Front. Mar. Sci. 2024, 11, 1476425. [Google Scholar] [CrossRef]
- Jiang, G.; Loiselle, S.A.; Yang, D.; Ma, R.; Su, W.; Gao, C. Remote estimation of chlorophyll a concentrations over a wide range of optical conditions based on water classification from VIIRS observations. Remote Sens. Environ. 2020, 241, 111735. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, M.; Ma, R.; Zhang, Y.; Duan, H.; Jiang, L.; Xue, K.; Xiong, J.; Hu, M. A decade-long chlorophyll-a data record in lakes across China from VIIRS observations. Remote Sens. Environ. 2024, 301, 113953. [Google Scholar] [CrossRef]
- Li, S.; Song, K.; Li, Y.; Liu, G.; Wen, Z.; Shang, Y.; Lyu, L.; Fang, C. Performances of atmospheric correction processors for sentinel-2 MSI imagery over typical lakes across China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 2065–2078. [Google Scholar] [CrossRef]
- Warren, M.A.; Simis, S.G.; Martinez-Vicente, V.; Poser, K.; Bresciani, M.; Alikas, K.; Spyrakos, E.; Giardino, C.; Ansper, A. Assessment of atmospheric correction algorithms for the Sentinel-2A MultiSpectral Imager over coastal and inland waters. Remote Sens. Environ. 2019, 225, 267–289. [Google Scholar] [CrossRef]
- Sòria-Perpinyà, X.; Delegido, J.; Urrego, E.P.; Ruíz-Verdú, A.; Soria, J.M.; Vicente, E.; Moreno, J. Assessment of sentinel-2-MSI atmospheric correction processors and in situ spectrometry waters quality algorithms. Remote Sens. 2022, 14, 4794. [Google Scholar] [CrossRef]
- Barnes, B.B.; Cannizzaro, J.P.; English, D.C.; Hu, C. Validation of VIIRS and MODIS reflectance data in coastal and oceanic waters: An assessment of methods. Remote Sens. Environ. 2019, 220, 110–123. [Google Scholar] [CrossRef]
- Pardo, S.; Tilstone, G.H.; Brewin, R.J.; Dall’Olmo, G.; Lin, J.; Nencioli, F.; Evers-King, H.; Casal, T.G.; Donlon, C.J. Radiometric assessment of OLCI, VIIRS, and MODIS using fiducial reference measurements along the Atlantic Meridional Transect. Remote Sens. Environ. 2023, 299, 113844. [Google Scholar] [CrossRef]
- Zibordi, G.; Holben, B.; Hooker, S.B.; Mélin, F.; Berthon, J.F.; Slutsker, I.; Giles, D.; Vandemark, D.; Feng, H.; Rutledge, K.; et al. A network for standardized ocean color validation measurements. Eos, Trans. Am. Geophys. Union 2006, 87, 293–297. [Google Scholar] [CrossRef]
- Zibordi, G.; Mélin, F.; Berthon, J.F.; Holben, B.; Slutsker, I.; Giles, D.; D’Alimonte, D.; Vandemark, D.; Feng, H.; Schuster, G.; et al. AERONET-OC: A network for the validation of ocean color primary products. J. Atmos. Ocean. Technol. 2009, 26, 1634–1651. [Google Scholar] [CrossRef]
- Pahlevan, N.; Mangin, A.; Balasubramanian, S.V.; Smith, B.; Alikas, K.; Arai, K.; Barbosa, C.; Bélanger, S.; Binding, C.; Bresciani, M.; et al. ACIX-Aqua: A global assessment of atmospheric correction methods for Landsat-8 and Sentinel-2 over lakes, rivers, and coastal waters. Remote Sens. Environ. 2021, 258, 112366. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, C. Evaluation of remote sensing reflectance derived from the Sentinel-2 multispectral instrument observations using POLYMER atmospheric correction. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5764–5771. [Google Scholar] [CrossRef]
- Clark, D.K.; Feinholz, M.; Yarbrough, M.; Johnson, B.C.; Brown, S.W.; Kim, Y.S.; Barnes, R.A. Overview of the radiometric calibration of MOBY. In Proceedings of the Earth Observing Systems VI, San Diego, CA, USA, 1–3 August 2002; SPIE: Bellingham, DC, USA, 2002; Volume 4483, pp. 64–76. [Google Scholar]
- Clark, D.; Gordon, H.; Voss, K.; Ge, Y.; Broenkow, W.; Trees, C. Validation of atmospheric correction over the oceans. J. Geophys. Res. Atmos. 1997, 102, 17209–17217. [Google Scholar] [CrossRef]
- Valente, A.; Sathyendranath, S.; Brotas, V.; Groom, S.; Grant, M.; Jackson, T.; Chuprin, A.; Taberner, M.; Airs, R.; Antoine, D.; et al. A compilation of global bio-optical in situ data for ocean-colour satellite applications–version three. Earth Syst. Sci. Data Discuss. 2022, 2022, 1–61. [Google Scholar] [CrossRef]
- Thuillier, G.; Floyd, L.; Woods, T.; Cebula, R.; Hilsenrath, E.; Hersé, M.; Labs, D. Solar irradiance reference spectra for two solar active levels. Adv. Space Res. 2004, 34, 256–261. [Google Scholar] [CrossRef]
- Ruddick, K.G.; De Cauwer, V.; Park, Y.J.; Moore, G. Seaborne measurements of near infrared water-leaving reflectance: The similarity spectrum for turbid waters. Limnol. Oceanogr. 2006, 51, 1167–1179. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.H., Jr.; Hoke, M.L.; et al. MODTRAN5: 2006 update. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XII, Kissimmee, UK, 17–20 April 2006; SPIE: Bellingham, DC, USA, 2006; Volume 6233, pp. 508–515. [Google Scholar]
- Ahmad, Z.; Fraser, R.S. An iterative radiative transfer code for ocean-atmosphere systems. J. Atmos. Sci. 1982, 39, 656–665. [Google Scholar] [CrossRef]
- Vanhellemont, Q. Adaptation of the dark spectrum fitting atmospheric correction for aquatic applications of the Landsat and Sentinel-2 archives. Remote Sens. Environ. 2019, 225, 175–192. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Atmospheric correction of metre-scale optical satellite data for inland and coastal water applications. Remote Sens. Environ. 2018, 216, 586–597. [Google Scholar] [CrossRef]
- Franz, B.A.; Bailey, S.W.; Kuring, N.; Werdell, P.J. Ocean color measurements with the Operational Land Imager on Landsat-8: Implementation and evaluation in SeaDAS. J. Appl. Remote Sens. 2015, 9, 096070. [Google Scholar] [CrossRef]
- Steinmetz, F.; Ramon, D. Sentinel-2 MSI and Sentinel-3 OLCI consistent ocean colour products using POLYMER. In Proceedings of the Remote Sensing of the Open and Coastal Ocean and Inland Waters, Honolulu, HI, USA, 24–26 September 2018; SPIE: Bellingham, DC, USA, 2018; Volume 10778, pp. 46–55. [Google Scholar]
- Zhang, M.; Hu, C.; Cannizzaro, J.; English, D.; Barnes, B.B.; Carlson, P.; Yarbro, L. Comparison of two atmospheric correction approaches applied to MODIS measurements over North American waters. Remote Sens. Environ. 2018, 216, 442–455. [Google Scholar] [CrossRef]
- Keshava, N. Distance metrics and band selection in hyperspectral processing with applications to material identification and spectral libraries. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1552–1565. [Google Scholar] [CrossRef]
- Zhao, X.; Ma, Y.; Xiao, Y.; Liu, J.; Ding, J.; Ye, X.; Liu, R. Atmospheric correction algorithm based on deep learning with spatial-spectral feature constraints for broadband optical satellites: Examples from the HY-1C Coastal Zone Imager. ISPRS J. Photogramm. Remote Sens. 2023, 205, 147–162. [Google Scholar] [CrossRef]
- Pahlevan, N.; Roger, J.C.; Ahmad, Z. Revisiting short-wave-infrared (SWIR) bands for atmospheric correction in coastal waters. Opt. Express 2017, 25, 6015–6035. [Google Scholar] [CrossRef] [PubMed]
- Pereira-Sandoval, M.; Ruescas, A.; Urrego, P.; Ruiz-Verdú, A.; Delegido, J.; Tenjo, C.; Soria-Perpinyà, X.; Vicente, E.; Soria, J.; Moreno, J. Evaluation of atmospheric correction algorithms over Spanish inland waters for sentinel-2 multi spectral imagery data. Remote Sens. 2019, 11, 1469. [Google Scholar] [CrossRef]
- Wei, J.; Lee, Z.; Shang, S. A system to measure the data quality of spectral remote-sensing reflectance of aquatic environments. J. Geophys. Res. Ocean. 2016, 121, 8189–8207. [Google Scholar] [CrossRef]
- Renosh, P.R.; Doxaran, D.; Keukelaere, L.D.; Gossn, J.I. Evaluation of atmospheric correction algorithms for sentinel-2-MSI and sentinel-3-OLCI in highly turbid estuarine waters. Remote Sens. 2020, 12, 1285. [Google Scholar] [CrossRef]
- Gordon, H. Phytoplankton pigment concentrations in the middle Atlantic blight: Comparison between shipdeterminations and Coastal Zone Color Scanner estimates. Appl. Opt. 1983, 27, 862–871. [Google Scholar] [CrossRef]
- Bailey, S.W.; Werdell, P.J. A multi-sensor approach for the on-orbit validation of ocean color satellite data products. Remote Sens. Environ. 2006, 102, 12–23. [Google Scholar] [CrossRef]
- Choi, J.K.; Park, Y.J.; Ahn, J.H.; Lim, H.S.; Eom, J.; Ryu, J.H. GOCI, the world’s first geostationary ocean color observation satellite, for the monitoring of temporal variability in coastal water turbidity. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Nezlin, N.P.; DiGiacomo, P.M. Satellite ocean color observations of stormwater runoff plumes along the San Pedro Shelf (southern California) during 1997–2003. Cont. Shelf Res. 2005, 25, 1692–1711. [Google Scholar] [CrossRef]
- Shi, W.; Wang, M. Satellite observations of flood-driven Mississippi River plume in the spring of 2008. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Bresciani, M.; Pinardi, M.; Free, G.; Luciani, G.; Ghebrehiwot, S.; Laanen, M.; Peters, S.; Della Bella, V.; Padula, R.; Giardino, C. The use of multisource optical sensors to study phytoplankton spatio-temporal variation in a Shallow Turbid Lake. Water 2020, 12, 284. [Google Scholar] [CrossRef]
- Wang, J.; Lee, Z.; Wei, J.; Du, K. Atmospheric correction in coastal region using same-day observations of different sun-sensor geometries with a revised POLYMER model. Opt. Express 2020, 28, 26953–26976. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).