Abstract
Glacier meltwater is an indispensable water supply for billions of people living in the catchments of major Asian rivers. However, the role of glaciers on river runoff regulation is seldom investigated due to the lack of annual glacier mass balance observation. In this study, we employed an albedo-based model with a daily land surface albedo dataset to derive the annual glacier mass balance over the Tuotuo River Basin (TRB). During 2000–2022, an annual glacier mass balance range of −0.89 ± 0.08 to 0.11 ± 0.11 m w.e. was estimated. By comparing with river runoff records from the hydrometric station, the contribution of glacier mass change to river runoff was calculated to be 0.00–31.14% for the studied period, with a mean value of 9.97%. Moreover, we found that the mean contribution in drought years is 20.07%, which is approximately five times that in wet years (4.30%) and twice that in average years (9.49%). Therefore, our results verify that mountain glaciers act as a significant buffer against drought in the TRB, at least during the 2000–2022 period.
1. Introduction
The Tibetan Plateau (TP), which is the largest modern glacierized area except for the polar regions (Arctic and Antarctic), is the source region of some major Asian rivers, such as the Yangtze River, Yellow River, and Indus River [1,2]. During recent decades, most glaciers in this plateau experienced terminus retreat, area reduction, and surface thinning due to the quick and continuous rise of the regional air temperature [3,4,5,6,7]. In general, the increasing rate of air temperature in the TP is approximately twice that of the global average air temperature [7]. A decadal mean glacier mass loss of more than −15 Gt per year has been estimated for the plateau since 2000 by comparing glacier surface topographic data in different years [3,4,6]. Moreover, an accelerating rate of glacier mass loss has been detected over several glacierized regions in the interior TP (e.g., the Geladandong Mountain [8] and the Puruogangri ice field [9]), as well as some glaciers in the southeast TP [10] and the Pamir Mountains [11]. Glacier meltwater caused by negative mass change has been reported to be a significant water supply for the runoff of some major Asian rivers during recent decades [3,12]. For all the river basins in the TP and its surroundings, the largest amount of glacier meltwater (5.1 Gt per year) was detected for the Brahmaputra River between 2000 and 2016 [3]. Until now, most of the existing glacier mass balance estimates are simply averaged values of the specific mass change over a time frame of several years to several decades. Little is known about the influence of glaciers on river runoff regulation because of the paucity of observations or estimates of annual glacier mass balance in the TP.
Field measurement is a traditional and effective method for obtaining annual glacier mass balance at the spatial scale of an individual glacier. However, fieldwork in the glacierized regions of the TP is seriously hampered by severe weather conditions (e.g., cold and windy) and high altitudes. To date, in situ observations of the annual glacier mass balance have been conducted for no more than twenty glaciers in the TP [2,13]. Considering the capability of global coverage and short revisit time (several days to several weeks), satellite remote sensing is a promising technique for extracting the basin-wide annual glacier mass balance. Monthly observations of global gravity have been conducted by satellite gravity missions since 2002. Due to the low spatial resolution (~300 km) of satellite gravity data, it is challenging to distinguish glacier mass balance from the water storage changes in soil, lakes, and other sources [14,15]. With the generation of highly accurate and high spatial-resolution digital elevation models from satellite photogrammetry and SAR interferometry, glacier surface elevation changes with a time interval of about one year have been precisely measured by comparing two sets of glacier surface topographic data from adjacent years [16,17]. The conversion from these observed surface elevation changes to annual glacier mass balance is still very difficult due to limitations in reasonable conversion factors and the accurate correction of systematic biases (e.g., seasonal variation and radar signal penetration depth) [9,18].
Satellite multispectral and hyperspectral remote sensing images have proven to be valuable data sources for extracting land surface albedo, which is an essential parameter of surface radiation or energy balance [19,20]. For glacierized regions, the absorbed solar radiation, which can result in mass loss by heating glacial materials, is mainly affected by surface albedo, which is the ratio of reflected solar radiation to incoming solar radiation [21,22]. A strong linearly positive correlation has been detected between glacier surface albedo and the field-measured glacier mass balance over several glaciers in the Alps and the TP [23,24,25,26]. By employing satellite surface albedo data and in situ observations of glacier mass balance, Zhang et al. [26] established a linear albedo-based model for the Dongkemadi Glacier. Moreover, this albedo-based model has been successfully applied to estimate the annual glacier mass balance time series for other glacierized regions in the interior TP [26].
In this study, we aim to extract the annual glacier mass balances for the whole glacierized regions in the Tuotuo River Basin (TRB) and, consequently, quantitatively assess the influence of basin-wide glacier mass change on river runoff. The annual glacier mass balances were obtained by employing the linear albedo-based model proposed by Zhang et al. [26] and the glacier surface albedo data acquired from satellite hyperspectral remote sensing images. River runoff data were extracted from the records of the Tuotuohe hydrometric station. According to the simplest form of the water balance equation, river runoff is also directly affected by the two climatic factors of precipitation and evaporation. Here, the impact of regional climatic variation on river runoff was discussed using the precipitation and evaporation collected from climate reanalysis datasets.
2. Study Area
The TRB, located in the middle-eastern portion of the Tibetan Plateau, is a sub-basin of the source region of the Yangtze River (Figure 1). The area of the TRB is approximately 15,920 km2. Glaciers in the TRB generally belong to the continental or cold type [27] because the climate setting of the TRB is dominated by continental climatic conditions [7]. According to the second Chinese glacier inventory [28], the number of glaciers is 98 for the TRB. The GLIMS (Global Land Ice Measurements from Space) identifier of the largest glacier in the TRB is G091104E33504N, with an area of approximately 54 km2 [28]. As demonstrated in Figure 1, most of these glaciers are distributed at the northern slope of the Tanggula Mountain Range, especially in the surrounding regions of the Geladandong Mountain. Considering the spatial distribution of the glacierized regions, three study sites (A, B, and C) were selected to estimate the annual glacier mass balance of the TRB.
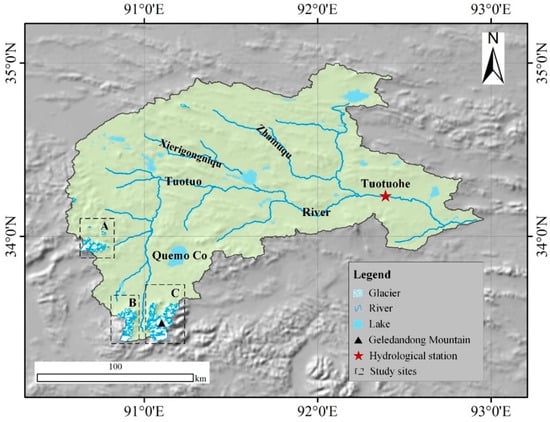
Figure 1.
The geographic location of the Tuotuo River Basin (Olivine Yellow) and the three study sites (A, B, and C). Glacier boundaries were obtained from the second Chinese glacier inventory. The location of the Tuotuohe hydrometric station is indicated as a red five-pointed star.
As illustrated in Figure 1, there are some tributaries that flow into the Tuotuo River. The two largest tributaries of this river are Xierigongniqu and Zhamuqu, and both of them are located in the northern part of the TRB. It is noteworthy that the Tuotuo River originates in the Geladandong Mountain (Figure 1), indicating that glacier meltwater is an important supply for this river. The largest lake, located in the southeastern part of the TRB, is named Quemo Co, with an area of approximately 100 km2 in 2021 [29]. The Tuotuohe hydrometric station (Figure 1) was built downstream of the Tuotuo River in June 1958. River runoff has been observed by this hydrometric station for more than 60 years. During recent decades, a significantly increasing trend has been detected for the runoff of the Tuotuo River [30,31].
3. Data and Method
3.1. Annual Minimum Regional-Average Surface Albedo Extraction
The amount of glacier mass loss caused by snow or ice melting is affected by surface albedo because snow and ice can be heated by the absorbed solar radiation [21,22]. Furthermore, the annual minimum regional-average surface albedo (AMRSA) has been found to be correlated with the glacier mass balance for the same year [23,24,25,26]. The regional-average glacier surface albedo for a day in the melt season is significantly smaller than that for a day in the accumulation season because ice albedo is much less than snow albedo [32,33]. Here, the Moderate Resolution Imaging Spectroradiometer (MODIS) land surface albedo products in were collected the months of June, July, August, and September to estimate the AMRSAs in 2000–2022 for the three study sites in the TRB.
The MODIS is an essential instrument of the Earth Observation System operated by the National Aeronautics and Space Administration (NASA). Until now, two MODIS sensors have been launched with the satellites Terra on 18 December 1999, and Aqua on 4 May 2002. The spectral resolution of the MODIS sensor includes 36 bands ranging from 0.415 to 14.235 μm. The spatial resolution of the acquired MODIS data is determined by the spectral band (250 m for bands 1–2, 500 m for bands 3–7, and 1000 m for bands 8–36). For the complement in orbit of the two flying satellites and the viewing swath width of 2330 km, the Earth’s surface can be almost completely observed by the two MODIS sensors every day. In recent years, NASA released some MODIS level-2 or level-3 products of the daily land surface albedo. Here, we used the level-3 daily black-sky snow surface albedo products of the MOD10A1 and MYD10A1 to estimate the regional-average glacier surface albedo for the three study sites. The MODIS level-3 albedo products we used are characterized by cloud-free coverage, with a spatial resolution of 500 m [34].
The pixel value of the downloaded MODIS level-3 daily surface albedo products is an integer type, ranging from 0 to 100 (%) [35]. Therefore, the surface albedo of every pixel was separately calculated by dividing the pixel’s value by 100. The other data preprocesses, such as map reprojection and spatial sub-setting, were conducted using the MODIS Reprojection Tool. In order to alleviate data gaps in the used MODIS data, the MOD10A1 and MYD10A1 surface albedo data acquired on the same day were merged into one image [26]. The regional-average glacier surface albedo was calculated with the merged image for every day. It is noteworthy that we only used the MOD10A1 surface albedo products during 2000–2021. The MYD10A1 surface albedo data were not available for these two years because the Aqua satellite was launched on May 4, 2002. The regional-average glacier surface albedo was calculated with the glacial pixels for the three study sites. The boundaries of the glacierized regions were obtained from the second Chinese glacier inventory [28].
For a certain year, when the regional-average glacier surface albedo was estimated for all the days between June 1 and September 30, a mean filter in time with a 10-day moving window was used for noise suppression [26]. The AMRSA for this year was thus estimated as the minimum value of the filtered daily regional-average glacier surface albedo time series.
3.2. Annual Glacier Mass Balance Estimation and Error Analysis
According to the relationship between the AMRSA and the field-measured mass balance over the Dongkemadi Glacier, an albedo-based model was established using a simple linear regression method by Zhang et al. [26].
Here, represents the annual glacier mass balance for the same year as the extracted . The parameters of (4.385) and (−2.339) are the slope and intercept of the created regression line, respectively.
The above linear equation has been verified to be an effective model for estimating the annual glacier mass balance over the interior regions of the Tibetan Plateau [26]. In this study, this linear albedo-based model was employed to estimate the annual glacier mass balance time series for 2000–2022 with the extracted AMRSAs for the three study sites separately. For all the glacierized regions in the TRB, the annual glacier mass balance for a certain year was calculated as the area-weighted mean value of the modeled results over the three study sites.
The uncertainty of the estimated annual glacier mass balance was assessed by employing the standard law of error propagation. Therefore, the error of the annual glacier mass balance estimate in a certain year can be calculated with the following equation.
where and are the errors of the two parameters of the liner albedo-based model. As suggested by Zhang et al. [26], is ±0.231 and is ±0.099. , which is the error of the extracted AMRSA, mainly originates from the errors of the MODIS daily snow surface albedo products used. In this study, the AMRSA’s error was estimated by dividing the error of the snow albedo data by the root mean square of the number of glacier pixels [24,36].
For the estimated annual glacier mass balance for the entire glacierized regions in the TRB, its error () was also assessed with the standard law of error propagation.
where , , and are the errors in the estimated annual glacier mass balances for study sites A, B, and C, respectively. is the total area of the glacierized regions of the three study sites. is the glacier area of study site A, is the glacier area of study site B, and is the glacier area of study site C.
3.3. Annual River Runoff Calculation
The runoff of the Tuotuo River has been recorded by the Tuotuohe hydrometric station since June 1958. In the early decades of establishing this hydrometric station, river runoff was observed for all the months of every year. However, from 1986 to now, river runoff has only been recorded by this hydrometric station between May and October. This means the data gap of river runoff exists in the other six months of January, February, March, April, November, and December.
In this study, the observed runoff datasets of the Tuotuo River between 1970 and 2022 were collected from the Qinghai Provincial Hydrology and Water Resources Measurement and Reporting Center. In order to quantitatively analyze the influence of annual glacier mass change on river runoff in 2000–2022, annual river runoffs for this time period need to be estimated first. Considering no available runoff record for six months in the years 1986–2022, the intra-annual variation of river runoff was analyzed by using the runoff records in 1970–1985 to fill these data gaps. As listed in Table 1, more than 95% of annual river runoff occurs between May and October for most years between 1970 and 1985. Moreover, the average value of the ratio of runoff between May and October to annual runoff during this period was calculated to be 0.956. Here, the annual runoff for the years 1986–2022 was thus estimated by dividing the observed total river runoff between May and October by this coefficient (0.956).

Table 1.
Comparison between annual river runoffs and those between May and October for the years between 1970 and 1985.
3.4. Annual Basin-Wide Precipitation and Evaporation Calculation
According to the simplest form of the water balance equation, runoff is directly affected by the two climatic factors of precipitation and evaporation.
where is runoff, is precipitation, is evaporation, and is the water storage variation of soil, glaciers, lakes, groundwater, and so on.
In order to quantitatively assess the effect of regional climate on river runoff, the records of precipitation and evaporation between 1970 and 2022 were collected from fifth-generation ECMWF reanalysis datasets (ERA5). Here, the specific version of the reanalysis climatic datasets used is the ERA5 monthly averaged data on single levels from 1940 to the present. The temporal and horizontal resolutions of these ERA5 climatic datasets are monthly and 0.25°, respectively [37]. The file format of our downloaded ERA5 datasets is NetCDF (Network Common Data Form). For a particular month, the basin-wide average precipitation or evaporation of the TRB (unit mm) was calculated with the pixels of more than half of their areas located in the TRB. Moreover, the basin-wide total precipitation or evaporation (unit Gt) was calculated by multiplying the basin-wide average value and the TRB’s area together. Finally, when monthly basin-wide precipitation or evaporation was completely calculated for all the months between 1970 and 2022, annual precipitation or evaporation was estimated as a sum of the calculated values for the twelve months (from January to December) each year. Note that the absolute value of the downloaded evaporation data was used in this study because the ERA5 original data are negative.
4. Results
4.1. Temporal and Spatial Variation of the AMRSAs
The extracted AMRSAs of the three study sites in the TRB between 2000 and 2022 are illustrated in Figure 2. Overall, a pronounced decreasing trend was detected for the AMRSAs of all three study sites during the studied time period. For 2000–2012, the mean values of the AMRSAs were 0.45, 0.48, and 0.50 for study sites A, B, and C, respectively (Table 2). However, the time-averaged AMRSAs dropped to 0.37, 0.40, and 0.42 for the three study sites between 2013 and 2022. Moreover, as illustrated in Table 2 and Figure 2, the maximum value of the AMRSAs was 0.57 during the period of 2000–2012 (for study site C in 2008), whereas it decreased to 0.50 between 2013 and 2022 (for study site B in 2017). Similarly, the minimum value of the AMRSAs (0.35) in 2000–2012 (for study site A in 2006) is relatively larger than that (0.30) in 2013–2022 (for study site B in 2016). The temporal variations of the AMRSAs were quantitatively analyzed using the linear regression analysis method. A decreasing trend of approximately −0.05 per decade (p < 0.05) was estimated for the three study sites in 2000–2022.
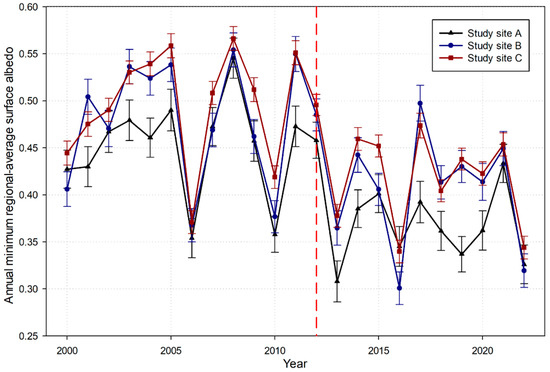
Figure 2.
The extracted annual minimum regional-average surface albedo time series for the three study sites in the TRB between 2000 and 2022. The red vertical dashed line indicates the year 2012.

Table 2.
The mean, maximum, and minimum values of the extracted annual minimum regional-average surface albedo in 2000–2012 and 2013–2022 for the three study sites.
The spatial difference in the extracted AMRSAs in the TRB is characterized by the fact that the AMRSA of study site A is generally smaller than those of study sites B and C (Figure 2). For example, in 2013, the AMRSA of study site A was 0.31, which is obviously smaller than those of study sites B (0.36) and C (0.38). For the periods of 2000–2012 and 2013–2022, the mean values of the AMRSAs for study site A (0.45 and 0.37) are clearly smaller than those for study sites B (0.48 and 0.40) and C (0.50 and 0.42). Furthermore, the decreasing trend of the AMRSAs between 2000 and 2022 for study site A (−0.054 per decade, p < 0.05) is slightly more serious than those for study site B (−0.048 per decade, p < 0.05) and study site C (−0.050 per decade, p < 0.05). It is noteworthy that the AMRSA’s decreasing trend from 2000 to 2022 for study site C (−0.050 per decade) is slightly more severe than that for study site B (−0.048 per decade), although both the AMRSA’s mean values for 2000–2012 and 2013–2022 at study site C are relatively larger than those at study site B (Table 2).
4.2. Annual Glacier Mass Balances
The modeled annual glacier mass balance time series between 2000 and 2022 are listed in Table 3. A pronounced glacier mass loss has been estimated for most years during the study period across the three study sites. Study site A especially experienced glacier mass losses for almost all the years during the period of 2000–2022. A slight glacier mass gain of 0.05 ± 0.16 m w.e. was only detected in 2008 at this study site. For the other two study sites, slight glacier mass gains were extracted in the years 2003 (0.01 ± 0.16 m w.e.), 2005 (0.02 ± 0.16 m w.e.), 2008 (0.09 ± 0.16 m w.e.), and 2011 (0.07 ± 0.16 m w.e.) at study site B and in the years 2004 (0.03 ± 0.16 m w.e.), 2005 (0.11 ± 0.16 m w.e.), 2008 (0.14 ± 0.16 m w.e.), and 2011 (0.08 ± 0.16 m w.e.) at study site C. Overall, glacier mass gains have only been estimated for several years between 2000 and 2012. As listed in Table 3, the three study sites experienced an apparent glacier mass loss for all the years between 2013 and 2022 (ranging from −0.16 ± 0.15 to −1.02 ± 0.12 m w.e.). Consequently, the estimated annual glacier mass balances clearly reveal accelerated glacier mass loss for all three study sites from 2000 to 2022.

Table 3.
The modeled annual glacier mass balances (m w.e.) for the three study sites and the whole glacierized regions of the Tuotuo River Basin (TRB) between 2000 and 2022.
For all the glacierized regions of the TRB, a slight glacier mass gain was only obtained in the three years of 2005 (0.03 ± 0.10 m w.e.), 2008 (0.11 ± 0.11 m w.e.), and 2011 (0.01 ± 0.10 m w.e.). An obvious glacier mass loss was observed for most years between 2000 and 2022 (Table 3). The most substantial glacier mass loss of −0.89 ± 0.08 m w.e. was detected for the year 2016. A discrepancy in glacier mass balance was also found for the periods of 2000–2012 and 2013–2022. The mean value of annual glacier mass balances for 2013–2022 was −0.57 ± 0.09 m w.e., approximately three times that of 2000–2012 (−0.21 ± 0.10 m w.e.). By applying the linear regression analysis method, an accelerating trend in annual glacier mass loss of −0.22 m w.e. per decade (p < 0.05) was calculated for the whole set of glaciers in the TRB in 2000–2022. Moreover, accelerated glacier mass losses of −0.24 m w.e. per decade (p < 0.05), −0.21 m w.e. per decade (p < 0.05), and −0.22 m w.e. per decade (p < 0.05) were found in 2000–2022 for study sites A, B, and C, respectively.
4.3. Runoff of the Tuotuo River
Between 2000 and 2022, annual river runoff of 0.73 Gt to 2.54 Gt was recorded by the Tuotuohe hydrometric station (Figure 3). The mean value of annual river runoff was calculated to be 1.49 Gt for this studied period. As illustrated in Figure 3, a possible increasing annual river runoff has been observed for the Tuotuo River in recent decades. Using the linear regression analysis method, we estimated that the increasing rate of annual river runoff was 0.19 Gt per decade from 2000 to 2022; however, p (0.23) is larger than 0.05. This large p value is likely associated with the violent fluctuation in the annual runoff of the Tuotuo River. For example, we observed an annual river runoff of more than 2.50 Gt in the year 2018 (2.53 Gt), but it dropped to 0.96 Gt in the next year (2019). This means that the annual river runoff in 2018 was approximately three times that in 2019. Although the linearly increasing trend of annual river runoff failed to achieve statistical significance (p > 0.05), it is noteworthy that the mean value of annual river runoff in 2013–2022 (1.55 Gt) is obviously larger than that in 2000–2012 (1.45 Gt).
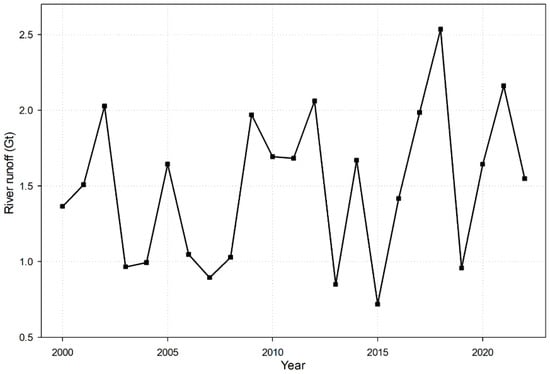
Figure 3.
The observed annual runoff of the Tuotuo River between 2000 and 2022.
4.4. Temporal Variations of Precipitation and Evaporation
Annual basin-wide average precipitation ranging from 479.88 to 635.85 mm and annual basin-wide average evaporation ranging from 395.67 to 434.90 mm were estimated for the TRB between 2000 and 2022 (Figure 4). Annual precipitation was relatively larger than annual evaporation during this period. A mean value of 577.53 mm was calculated for annual precipitation in 2000–2022, and that of annual evaporation was 414.26 mm. The temporal variation of both annual precipitation and annual evaporation was characterized by violent fluctuations. As demonstrated in Figure 4, both annual precipitation and annual evaporation increased and decreased sharply during this period. For example, annual precipitation in the year 2012 was 617.69 mm, which then decreased to 479.88 mm in 2013 and increased to 620.33 mm in 2014.
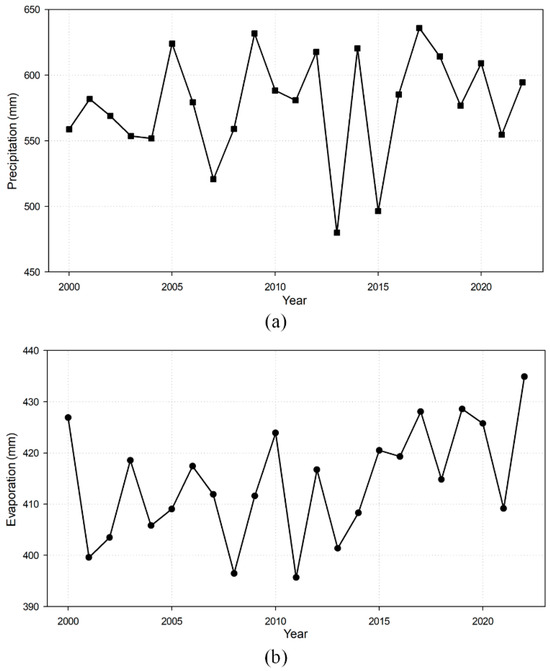
Figure 4.
Annual basin-wide average precipitation (a) and evaporation (b) for the Tuotuo River Basin between 2000 and 2022.
Although the temporal fluctuation is relatively severe, a possible increasing trend was found for both annual precipitation and annual evaporation from 2000 to 2022. During the first few years of the 21st century, annual precipitation was around 560 mm, whereas it has increased to about 600 mm in recent years (Figure 4a). Annual evaporation has increased from less than 410 mm to approximately 420 mm in recent decades (Figure 4b). By employing the linear regression analysis method, a long-term increasing rate of 10.03 mm per decade (p = 0.45 > 0.05) and 6.85 mm per decade (p < 0.05) was estimated for annual precipitation and annual evaporation between 2000 and 2022, respectively. This result indicates that the linearly increasing trend failed to achieve statistical significance for annual precipitation.
5. Discussion
5.1. Influence of Glacier Mass Change on River Runoff
In order to quantitatively assess the impact of glacier mass change on the annual runoff of the Tuotuo River, the unit of annual glacier mass balance (m w.e.) was first converted to Gt by multiplying the modeled estimates with the total area of the glacierized regions. For all the glaciers in the TRB, annual glacier mass changes ranging from −0.31 ± 0.03 to 0.04 ± 0.04 Gt were estimated between 2000 and 2022. As illustrated in Figure 5, the temporal variation of annual glacier mass change is similar to that of annual river runoff during this period. Specifically, a more seriously negative annual glacier mass change is much more likely to be detected for the years with less annual river runoff and vice versa. This indicates that glacier mass change likely helps to regulate the annual runoff of the Tuotuo River.
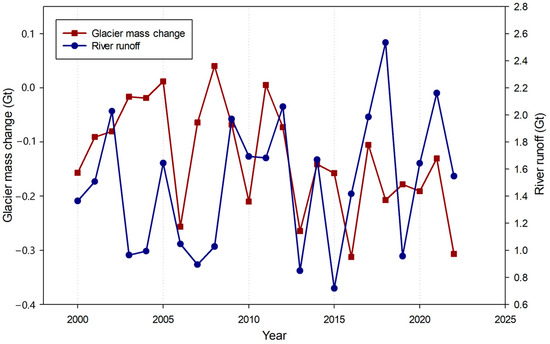
Figure 5.
Comparison between annual glacier mass change and annual river runoff for the Tuotuo River Basin during the period of 2000–2022.
The contribution of glacier mass change to river runoff was calculated by dividing annual river runoff into the absolute value of annual glacier mass loss for every year. For the years of positive glacier mass change (e.g., 0.04 ± 0.04 Gt in 2008), the value of contribution was set to zero. Therefore, the yearly contribution of glacier mass change to river runoff ranging from 0.00% to 31.14% was estimated for the TRB in 2000–2022 (Table 4). The maximum value of 31.14% was detected for the year (2013) with the second smallest annual river off (0.85 Gt). Moreover, a contribution of more than 20% was also estimated for the three years of 2006 (24.51%), 2015 (21.92%), and 2016 (22.05%). The mean value of contribution for all the years between 2000 and 2022 was 9.97% over the TRB, much larger than that in 2000–2018 over the whole source region of the Yangtze River (1.9% in Liu et al. [12]). This discrepancy is mainly attributed to the fact that most glacierized regions of the source region of the Yangtze River are distributed over the TRB (see Figure 1 in Liu et al. [12]). The contribution of glacier mass change to river runoff was detected to be accelerating at a rate of 4.8% per decade between 2000 and 2022. However, this estimated linear temporal tendency failed to achieve statistical significance (p = 0.08 > 0.05). The estimation of annual glacier mass balance time series with a longer studied period is needed to investigate whether glacier meltwater will become increasingly important for the river runoff of the TRB in the future.

Table 4.
The contribution of glacier mass change to the runoff of the Tuotuo River in 2000–2022.
According to the annual total precipitation of the TRB (Figure 4a), the years between 2000 and 2022 were classified into three types: drought, wet, and average. The mean value and standard deviation were first calculated for the annual precipitation time series in 2000–2022. When annual precipitation exceeded the sum of mean value and standard deviation, the year was classified as wet type (2005, 2009, 2014, and 2017). The drought-type years (2007, 2013, and 2015) were identified as having annual precipitation less than the difference between mean value and standard deviation. The other years for this period were classified as average type. As listed in Table 4, the maximum contribution of glacier mass change to river runoff was obtained in a drought-type year (2013), and the minimum value was detected in the three wet-type (2005) and average-type (2008 and 2011) years. The mean value of the contribution of glacier mass change to river runoff in drought-type years (20.07%) is approximately five times that in wet-type years (4.30%) and twice that in average-type years (9.49%). Consequently, our results provide verification of the role of glaciers as a buffer against drought in the TRB. This finding is supported by Pritchard [1] who reported that glacier meltwater is a significant buffer against drought for people living in the catchments of major Asian rivers such as the Ganges River and the Brahmaputra River. Moreover, the importance of glacier meltwater during drought years was also verified in the northeast TP. An extreme glacier mass loss of −1.188 m w.e. (approximately three times the decadal mean mass balance) was observed during a heavy drought year (2023) in the Qilian Mountains [38].
5.2. Influence of Climatic Change on River Runoff
In order to quantitatively assess the impact of climatic variation on river runoff, the unit of annual precipitation and annual evaporation was converted from mm to Gt by multiplying it by the total area of the TRB. Moreover, the amount of annual precipitation minus annual evaporation (PME) was calculated for all the years between 2000 and 2022 (Figure 6). Like the temporal variation of annual precipitation and annual evaporation, the fluctuation of the PME was serious during this period. PME values of 3.20, 1.25, 3.38, 1.21, and 2.64 Gt were extracted for the years 2012, 2013, 2014, 2015, and 2016, respectively. For the long-term trend of the PME, an increasing rate of 0.05 Gt per decade (p = 0.81 > 0.05) was estimated by employing the linear regression analysis method. Obviously, this large p value indicates that the linear increasing trend of PME in 2000–2022 failed to achieve statistical significance.
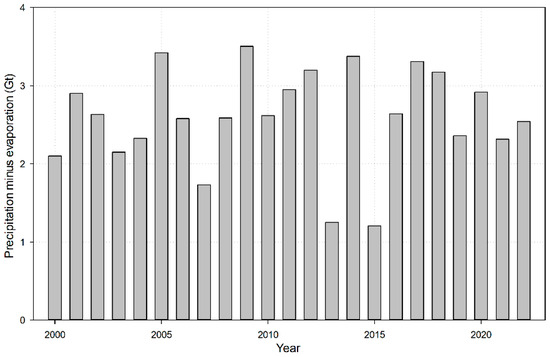
Figure 6.
The amount of annual precipitation minus annual evaporation in 2000–2022.
As exhibited in Figure 7, the annual runoff of the Tuotuo River was positively correlated with the PME between 2000 and 2022 (R = 0.72, p < 0.05). This indicates that the temporal variation of river runoff is mainly determined by regional climatic change, although glaciers are an effective buffer against drought. Notably, annual river runoff is clearly less than the PME for every year during this studied period. According to the water balance theory, a large amount of water resources should have been provided by the PME for the soil, lake, and groundwater of the TRB during the studied period. A continuous expansion or rise of water level was observed for some lakes over the TRB (e.g., Quemo Co) in recent decades [29,39]. This temporal feature of lake water resources is partly or mainly related to the increased PME [40,41].
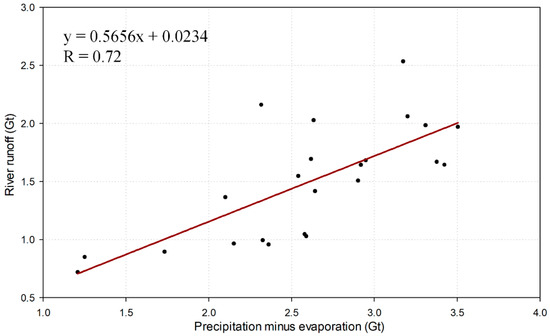
Figure 7.
Relationship between river runoff and the difference in precipitation and evaporation over the Tuotuo River Basin during the period of 2000–2022.
6. Conclusions
In this study, we quantitatively extracted the annual glacier mass balance and its contribution to river runoff in the TRB. By using an albedo-based model with the year’s minimum regional-average surface albedo derived from the MODIS daily land surface albedo products, we estimated annual glacier mass balance ranges from −0.89 ± 0.08 m w.e. to 0.11 ± 0.11 m w.e. between 2000 and 2022. Annual river runoff between 0.73 Gt and 2.54 Gt during the studied period was calculated using the records of the Tuotuo hydrometric station. The contribution of glacier mass change to river runoff was calculated by dividing annual river runoff into the absolute value of annual glacier mass loss for every year. Overall, the contribution of glacier mass change to river runoff was calculated to be 0.00–31.14% for the studied period, with a mean value of 9.97%.
According to the annual precipitation of the TRB, the years between 2000 and 2022 were classified into three types: drought, wet, and average. The mean value of the contribution of glacier mass change to river runoff was 20.07%, 9.49%, and 4.30% for the drought-type year, average-type year, and wet-type year, respectively. Consequently, our results provide verification of the role of glaciers as a buffer against drought in the TRB, at least in the 2000–2022 period. By using the method of linear regression analysis, the increasing trend of 4.8% per decade was estimated for the contribution of glacier mass loss to river runoff from 2000–2022. However, this linear tendency failed to achieve statistical significance (p = 0.08 > 0.05). In the future, a long-term annual glacier mass balance time series is needed to investigate whether glacier meltwater will become increasingly important for the river runoff in the TRB.
Author Contributions
Conceptualization, L.L.; methodology, Z.Z.; validation, X.Z. and Z.Z.; formal analysis, L.L. and X.Z.; writing—original draft preparation, X.Z. and Z.Z.; writing—review and editing, L.L.; funding acquisition, L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 42274028 and 41704023.
Data Availability Statement
All the daily surface albedo data are openly available in the Earthdata (https://earthdata.nasa.gov).
Acknowledgments
The authors would like to thank the National Snow and Ice Data Center (NSIDC) for providing the MODIS daily surface albedo products and the European Centre for Medium-Range Weather Forecasts (ECMWF) for providing the ERA5 monthly averaged data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pritchard, H.D. Asia’s shrinking glaciers protect large populations from drought stress. Nature 2019, 569, 649–654. [Google Scholar] [CrossRef] [PubMed]
- Yao, T.D.; Bolch, T.; Chen, D.L.; Gao, J.; Immerzeel, W.; Piao, S.L.; Su, F.G.; Thompson, L.; Wada, Y.; Wang, L.; et al. The imbalance of the Asian water tower. Nat. Rev. Earth Environ. 2022, 3, 618–632. [Google Scholar] [CrossRef]
- Brun, F.; Berthier, E.; Wagnon, P.; Kääb, A.; Treichler, D. A spatially resolved estimate of High Mountain Asia glacier mass balances from 2000 to 2016. Nat. Geosci. 2017, 10, 668–673. [Google Scholar] [CrossRef]
- Hugonnet, R.; McNabb, R.; Berthier, E.; Menounos, B.; Nuth, C.; Girod, L.; Farinotti, D.; Huss, M.; Dussaillant, I.; Brun, F.; et al. Accelerated global glacier mass loss in the early twenty-first century. Nature 2021, 592, 726–731. [Google Scholar] [CrossRef] [PubMed]
- Rounce, D.R.; Hock, R.; Maussion, F.; Hugonnet, R.; Kochtitzky, W.; Huss, M.; Berthier, E.; Brinkerhoff, D.; Compagno, L.; Copland, L.; et al. Global glacier change in the 21st century: Every increase in temperature matters. Science 2023, 379, 78–83. [Google Scholar] [CrossRef]
- Shean, D.E.; Bhushan, S.; Montesano, P.; Rounce, D.R.; Arendt, A.; Osmanoglu, B. A systematic, regional assessment of High Mountain Asia glacier mass balance. Front. Earth Sci. 2020, 7, 363. [Google Scholar] [CrossRef]
- Yao, T.D.; Thompson, L.; Yang, W.; Yu, W.S.; Gao, Y.; Guo, X.J.; Yang, X.X.; Duan, K.Q.; Zhao, H.B.; Xu, B.Q.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, L.M.; Zhang, Z.M.; Wang, H.S.; Ding, X. Recent accelerating glacier mass loss of the Geladandong Mountain, inner Tibetan Plateau, estimated from ZiYuan-3 and TanDEM-X measurements. Remote Sens. 2020, 12, 472. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, L.M.; Jiang, H.J.; Wang, H.S.; Ma, N.; Xu, H.Z. Accelerated glacier mass loss (2011-2016) over the Puruogangri ice field in the inner Tibetan Plateau revealed by bistatic InSAR measurements. Remote Sens. Environ. 2019, 231, 111241. [Google Scholar] [CrossRef]
- Wu, K.; Liu, S.; Jiang, Z.; Xu, J.; Wei, J.; Guo, W. Recent glacier mass balance and area changes in the Kangri Karpo Mountains from DEMs and glacier inventories. Cryosphere 2018, 12, 103–121. [Google Scholar] [CrossRef]
- Lambrecht, A.; Mayer, C.; Wendt, A.; Floricioiu, D.; Völksen, C. Elevation change of Fedchenko Glacier, Pamir Mountains, from GNSS field measurements and TanDEM-X elevation models, with a focus on the upper glacier. J. Glaciol. 2018, 64, 1–12. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, L.M.; Wang, H.S.; Ding, X.L.; Xu, H.Z. Estimation of glacier mass loss and its contribution to river runoff in the source region of the Yangtze River during 2000-2018. J. Hydrol. 2020, 589, 125207. [Google Scholar] [CrossRef]
- WGMS. Fluctuations of Glaciers Database; World Glacier Monitoring Service (WGMS): Zurich, Switzerland, 2024. [Google Scholar]
- Wang, H.S.; Jia, L.L.; Steffen, H.; Wu, P.; Jiang, L.M.; Hsu, H.; Xiang, L.W.; Wang, Z.Y.; Hu, B. Increased water storage in North America and Scandinavia from GRACE gravity data. Nat. Geosci. 2013, 6, 38–42. [Google Scholar] [CrossRef]
- Xiang, L.W.; Wang, H.S.; Steffen, H.; Wu, P.; Jia, L.L.; Jiang, L.M.; Shen, Q. Groundwater storage changes in the Tibetan Plateau and adjacent areas revealed from GRACE satellite gravity data. Earth Planet. Sci. Lett. 2016, 449, 228–239. [Google Scholar] [CrossRef]
- Beraud, L.; Cusicanqui, D.; Rabatel, A.; Brun, F.; Vincent, C.; Six, D. Glacier-wide seasonal and annual geodetic mass balances from Pléiades stereo images: Application to the Glacier d’Argentière, French Alps. J. Glaciol. 2023, 69, 525–537. [Google Scholar] [CrossRef]
- Falaschi, D.; Bhattacharya, A.; Guillet, G.; Huang, L.; King, O.; Mukherjee, K.; Rastner, P.; Yao, T.D.; Bolch, T. Annual to seasonal glacier mass balance in High Mountain Asia derived from Pléiades stereo images: Examples from the Pamir and the Tibetan Plateau. Cryosphere 2023, 17, 5435–5458. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y. Impact of resolution and radar penetration on glacier elevation changes computed from DEM differencing. J. Glaciol. 2012, 58, 419–422. [Google Scholar] [CrossRef]
- Liang, X.Z.; Xu, M.; Gao, W.; Kunkel, K.; Slusser, J.; Dai, Y.J.; Min, Q.L.; Houser, P.R.; Rodell, M.; Schaaf, C.B.; et al. Development of land surface albedo parameterization based on Moderate Resolution Imaging Spectroradiometer (MODIS) data. J. Geophys. Res. 2005, 110, D11107. [Google Scholar] [CrossRef]
- Wang, D.D.; Liang, S.L.; He, T.; Yu, Y.Y.; Schaaf, C.; Wang, Z.S. Estimating daily mean land surface albedo from MODIS data. J. Geophys. Res. 2015, 120, 4825–4841. [Google Scholar] [CrossRef]
- Huintjes, E.; Neckel, N.; Hochschild, V.; Schneider, C. Surface energy and mass balance at Purogangri ice cap, central Tibetan Plateau, 2001–2011. J. Glaciol. 2015, 61, 1048–1060. [Google Scholar] [CrossRef]
- Li, S.H.; Yao, T.D.; Yang, W.; Yu, W.S.; Zhu, M.L. Glacier energy and mass balance in the Inland Tibetan Plateau: Seasonal and interannual variability in relation to atmospheric changes. J. Geophys. Res. 2018, 123, 6390–6409. [Google Scholar] [CrossRef]
- Brun, F.; Dumont, M.; Wagnon, P.; Berthier, E.; Azam, M.F.; Shea, J.M.; Sirguey, P.; Rabatel, A.; Ramanathan, A. Seasonal changes in surface albedo of Himalayan glaciers from MODIS data and links with the annual mass balance. Cryosphere 2015, 9, 341–355. [Google Scholar] [CrossRef]
- Dumont, M.; Gardelle, J.; Sirguey, P.; Guillot, A.; Six, D.; Rabatel, A.; Arnaud, Y. Linking glacier annual mass balance and glacier albedo retrieved from MODIS data. Cryosphere 2012, 6, 1527–1539. [Google Scholar] [CrossRef]
- Williamson, S.N.; Copland, L.; Thomson, L.; Burgess, D. Comparing simple albedo scaling methods for estimating Arctic glacier mass balance. Remote Sens. Environ. 2020, 246, 111858. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Jiang, L.M.; Liu, L.; Sun, Y.F.; Wang, H.S. Annual glacier-wide mass balance (2000–2016) of the interior Tibetan Plateau reconstructed from MODIS albedo products. Remote Sens. 2018, 10, 1031. [Google Scholar] [CrossRef]
- Huang, M.H. On the temperature distribution of glaciers in China. J. Glaciol. 1990, 36, 210–216. [Google Scholar]
- Guo, W.Q.; Liu, S.Y.; Xu, J.L.; Wu, L.Z.; Shangguan, D.H.; Yao, X.J.; Wei, J.F.; Bao, W.J.; Yu, P.C.; Liu, Q.; et al. The second Chinese glacier inventory: Data, methods and results. J. Glaciol. 2015, 61, 357–372. [Google Scholar] [CrossRef]
- Yang, Z.C.; Duan, S.B.; Dai, X.A.; Sun, Y.W.; Liu, M. Mapping of lakes in the Qinghai-Tibet Plateau from 2016 to 2021: Trend and potential regularity. Int. J. Digit. Earth 2022, 15, 1692–1714. [Google Scholar] [CrossRef]
- Bing, L.F.; Shao, Q.Q.; Liu, J.Y. Runoff characteristics in flood and dry seasons based on wavelet analysis in the source regions of the Yangtze and Yellow rivers. J. Geogr. Sci. 2012, 22, 261–272. [Google Scholar] [CrossRef]
- Luo, Y.; Qin, N.S.; Zhou, B.; Li, J.J.; Wang, C.X.; Liu, J.; Pang, Y.S. Runoff characteristics and hysteresis to precipitation in Tuotuo River Basin in source region of Yangtze River during 1961-2011. Bull. Soil Water Conserv. 2019, 39, 22–28. [Google Scholar]
- Gardner, A.S.; Sharp, M.J. A review of snow and ice albedo and the development of a new physically based broadband albedo parameterization. J. Geophys. Res. 2010, 115, F01009. [Google Scholar] [CrossRef]
- Wiscombe, W.J.; Warren, S.G. A model for the spectral albedo of snow. I: Pure snow. J. Atmos. Sci. 1980, 37, 2712–2733. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. Accuracy assessment of the MODIS snow products. Hydrol. Process. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Liu, J.; Gao, F.; Strahler, A.H. Aqua and Terra MODIS albedo and reflectance anisotropy products. In Land Remote Sensing and Global Environmental Change; Kramer, H.J., Ed.; Springer: New York, NY, USA, 2010; pp. 549–561. [Google Scholar]
- Sirguey, P.; Still, H.; Cullen, N.J.; Dumont, M.; Arnaud, Y.; Conway, J.P. Reconstructing the mass balance of Brewster Glacier, New Zealand, using MODIS-derived glacier-wide albedo. Cryosphere 2016, 10, 2465–2484. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 monthly averaged data on single levels from 1940 to present. In Copernicus Climate Change Service (C3S) Climate Data Store (CDS); Copernicus Products: Brussels, Belgium, 2023. [Google Scholar]
- Chen, J.A.; Xue, X.Y.; Du, W.T. Short communication: Extreme glacier mass loss triggered by high temperature and drought during hydrological year 2022/2023 in Qilian Mountains. Res. Cold Arid Reg. 2024, 16, 1–4. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Yao, T.D.; Xie, H.J.; Yang, K.; Zhu, L.P.; Shum, C.K.; Bolch, T.; Yi, S.; Allen, S.; Jiang, L.G.; et al. Response of Tibetan Plateau lakes to climate change: Trends, patterns, and mechanisms. Earth Sci. Rev. 2020, 208, 103269. [Google Scholar] [CrossRef]
- Lei, Y.B.; Yang, K. The cause of rapid lake expansion in the Tibetan Plateau: Climate wetting or warming? Rev. Water. 2017, 4, e1236. [Google Scholar] [CrossRef]
- Song, C.Q.; Huang, B.; Richards, K.; Ke, L.H.; Hien Phan, V. Accelerated lake expansion on the Tibetan Plateau in the 2000s: Induced by glacial melting or other processes? Water Resour. Res. 2014, 50, 3170–3186. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).