Experimental Analysis of Terahertz Wave Scattering Characteristics of Simulated Lunar Regolith Surface
Abstract
1. Introduction
2. Lunar Regolith Surface Characterization
2.1. Surface Roughness Spectrum
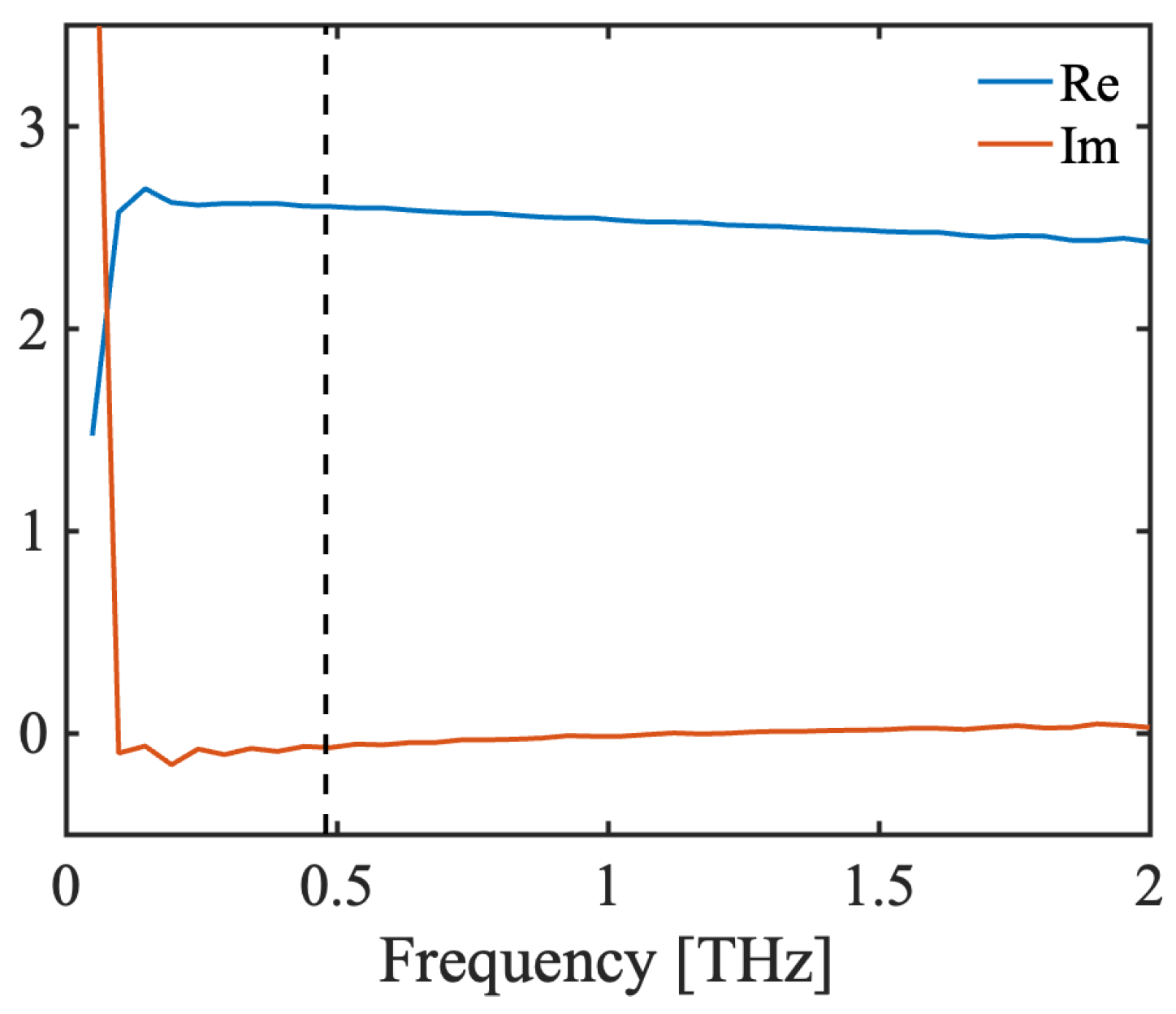
2.2. Dielectric Property
3. Experimental Measurements from the Rough Surface at 325 GHz to 500 GHz
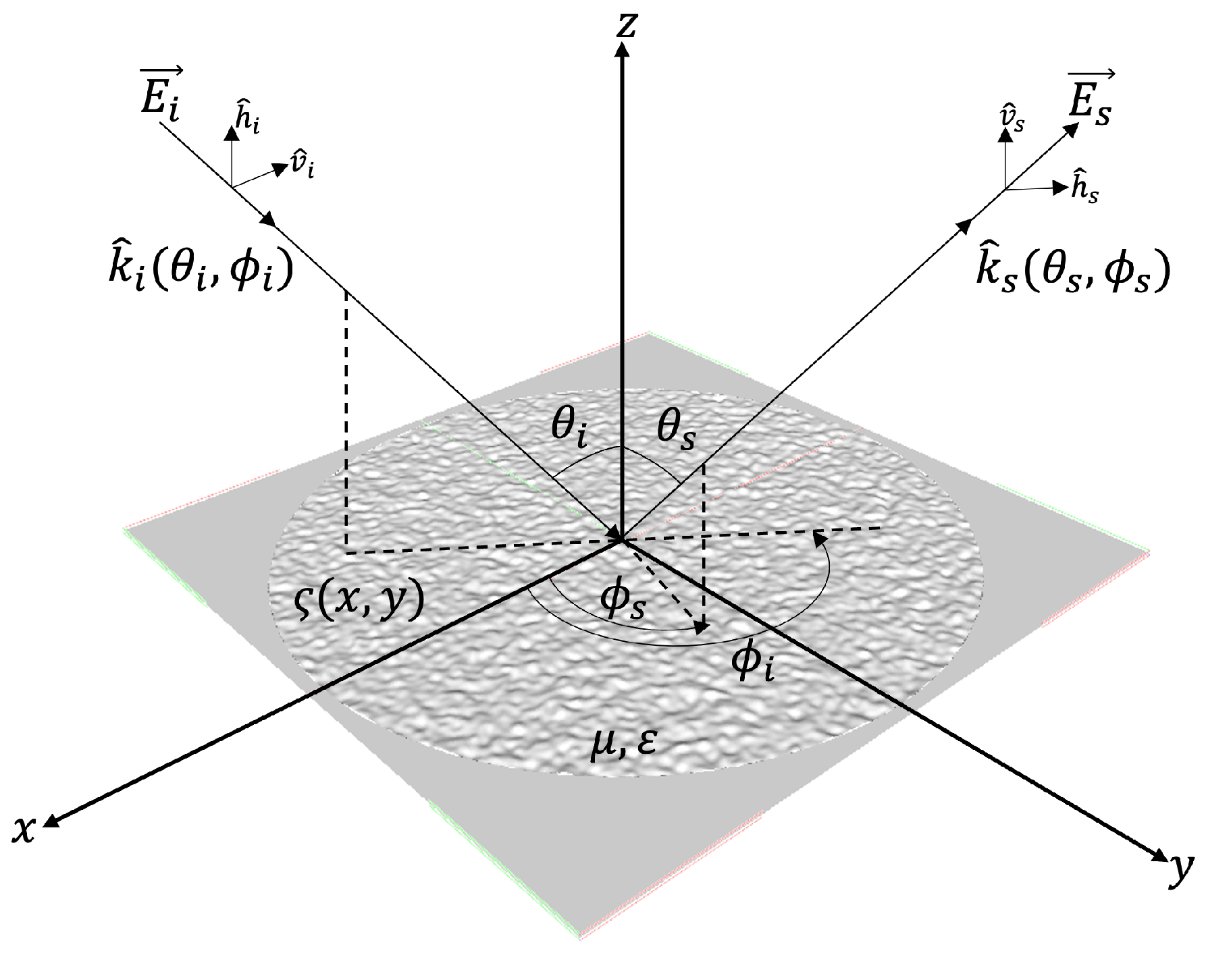
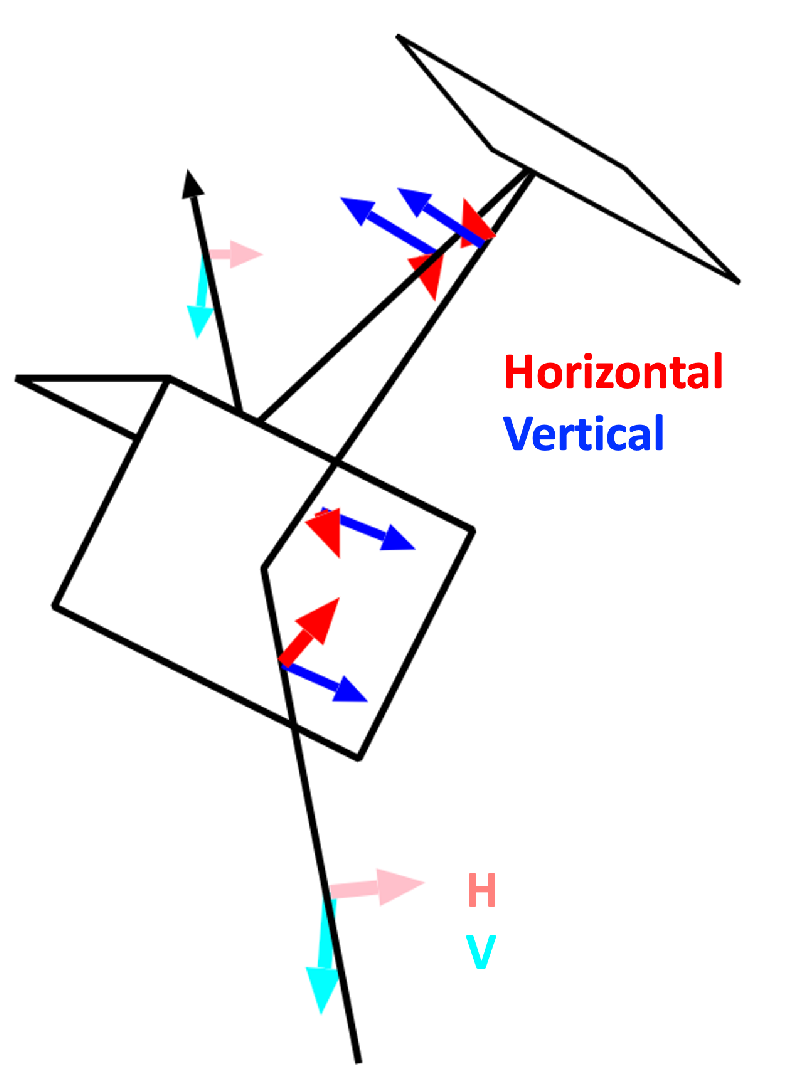
3.1. Wave Scattering Geometry
3.2. Scattering Target
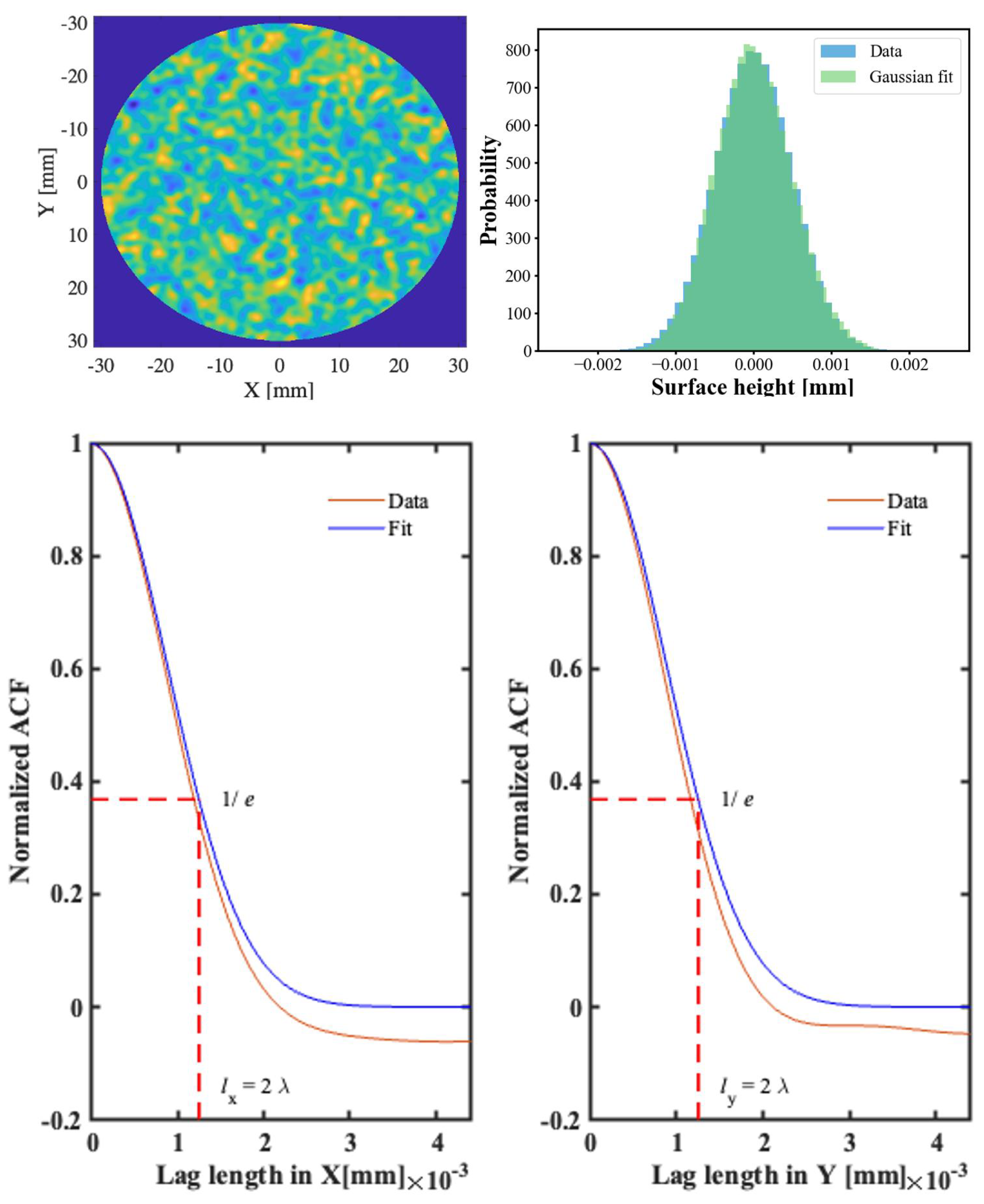
3.2.1. Rough Surface Generation
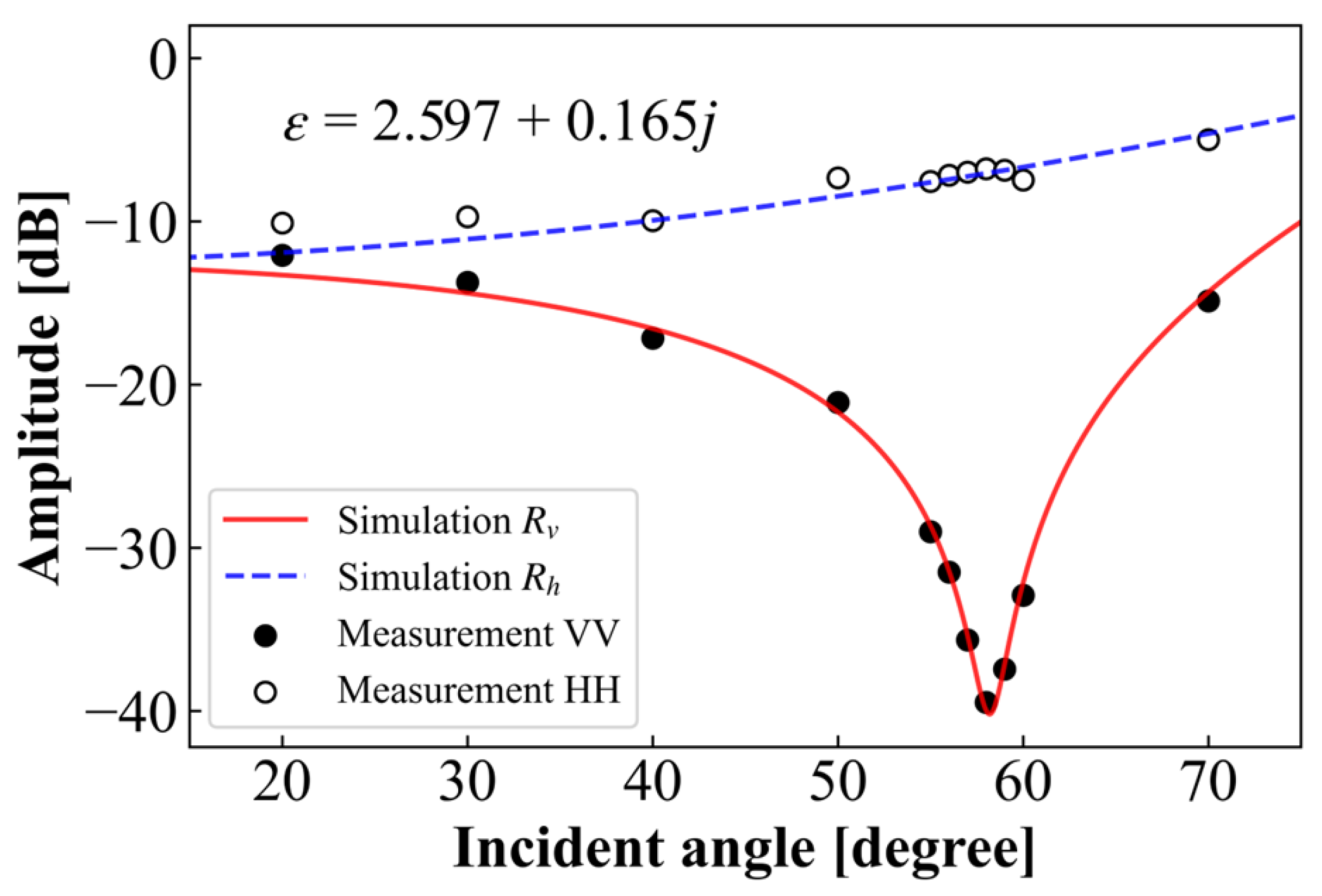
3.2.2. Validation of Dielectric Property and Surface Roughness
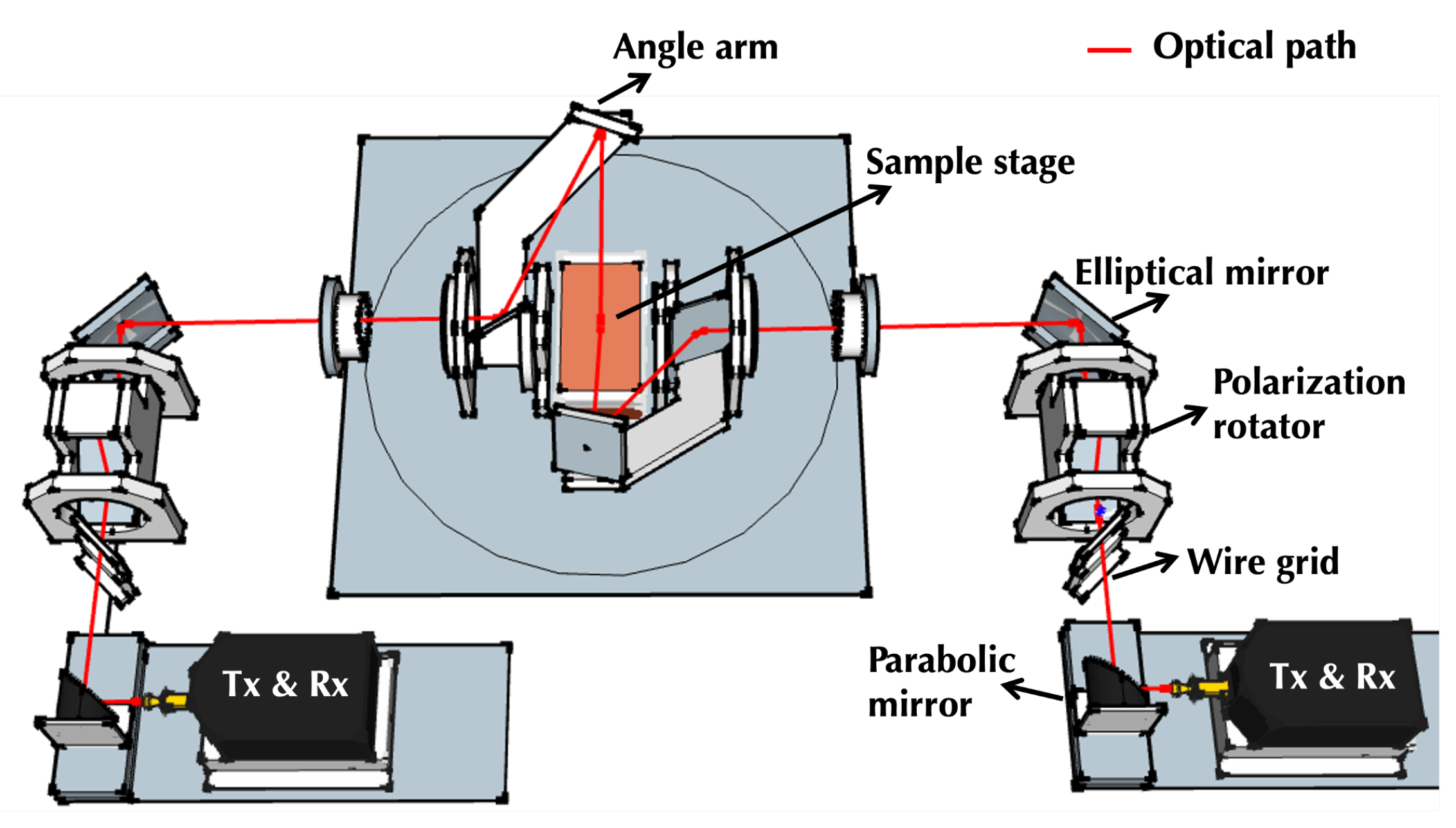
3.3. Experimental Setup
3.3.1. System Configuration
3.3.2. System Calibration
4. Results and Discussion
4.1. Backscattering
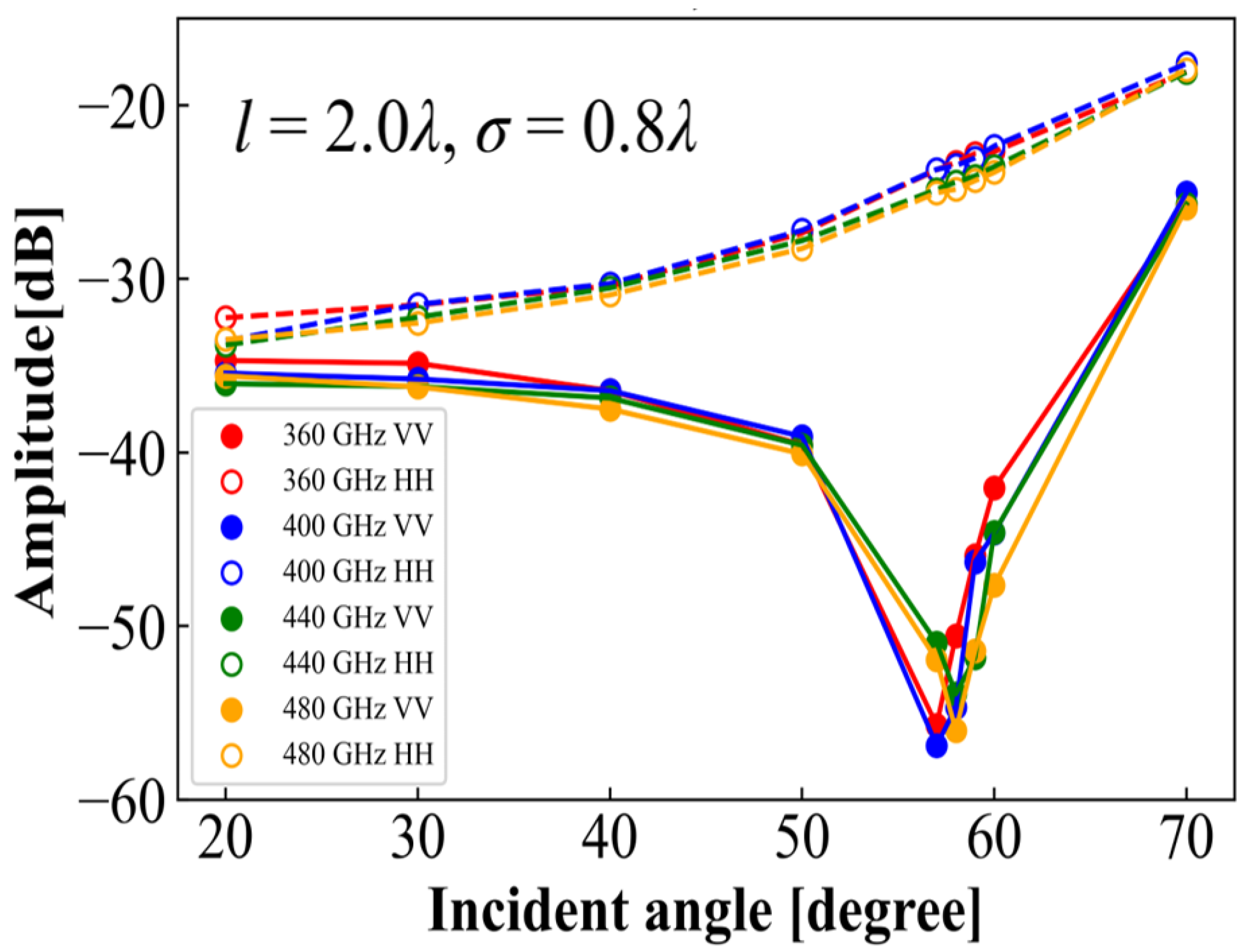
4.1.1. Frequency Dependence
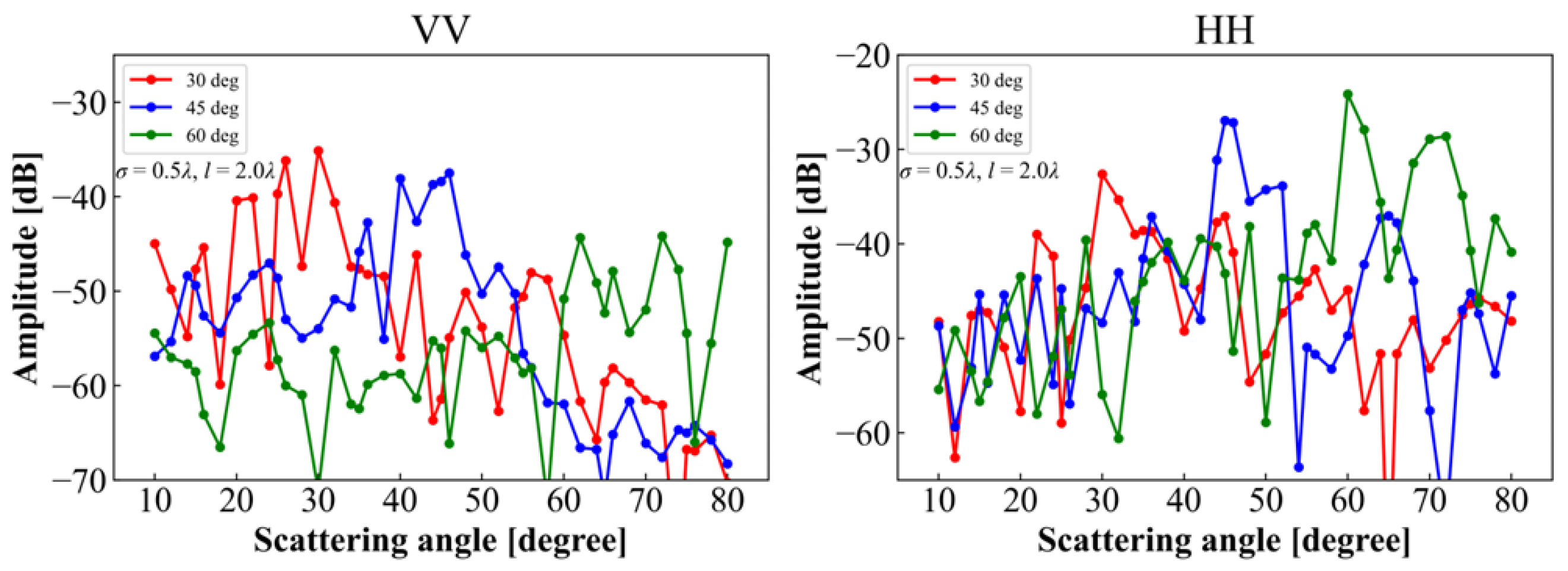
4.1.2. Angular Dependence
4.1.3. Polarization Dependence
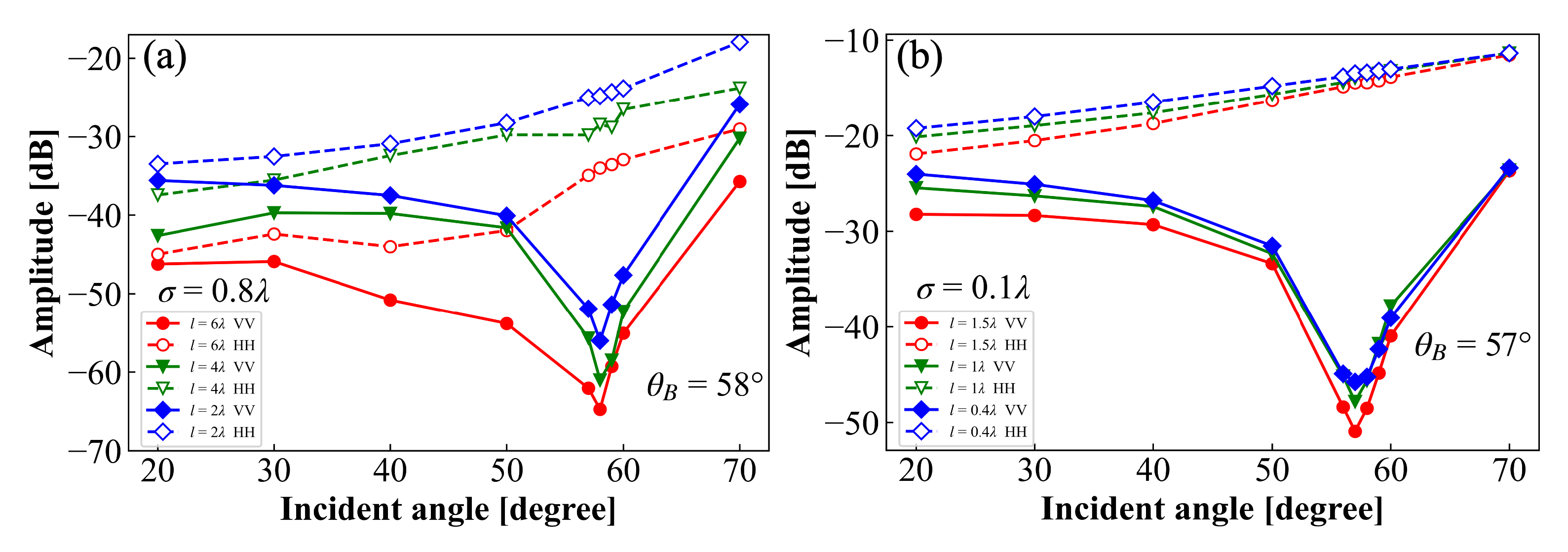
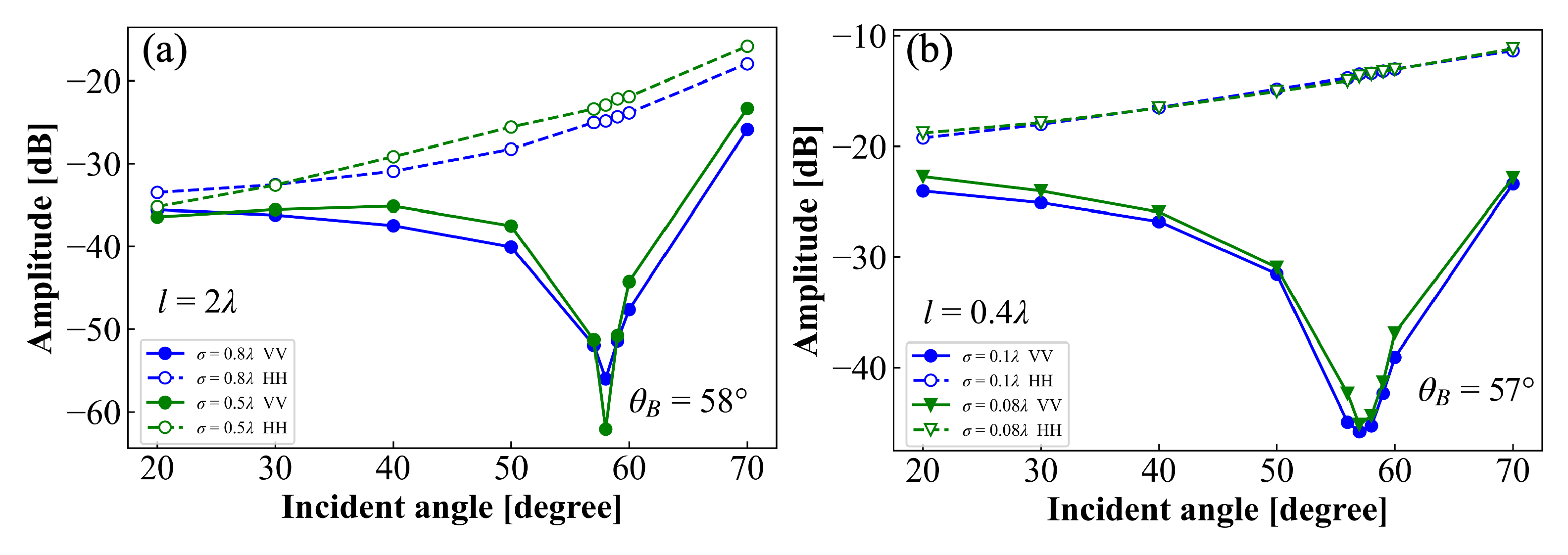
4.1.4. Brewster Effect
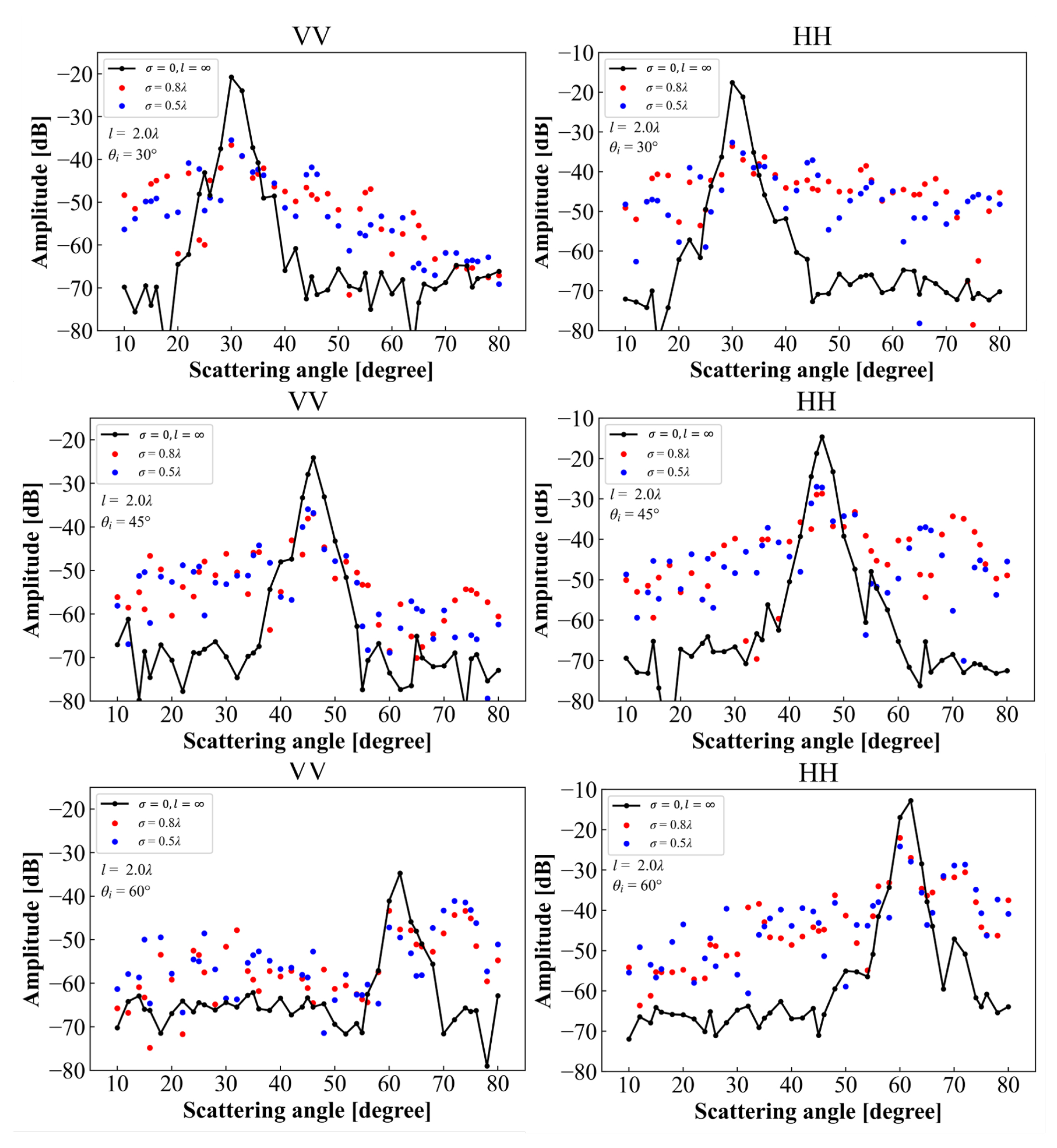
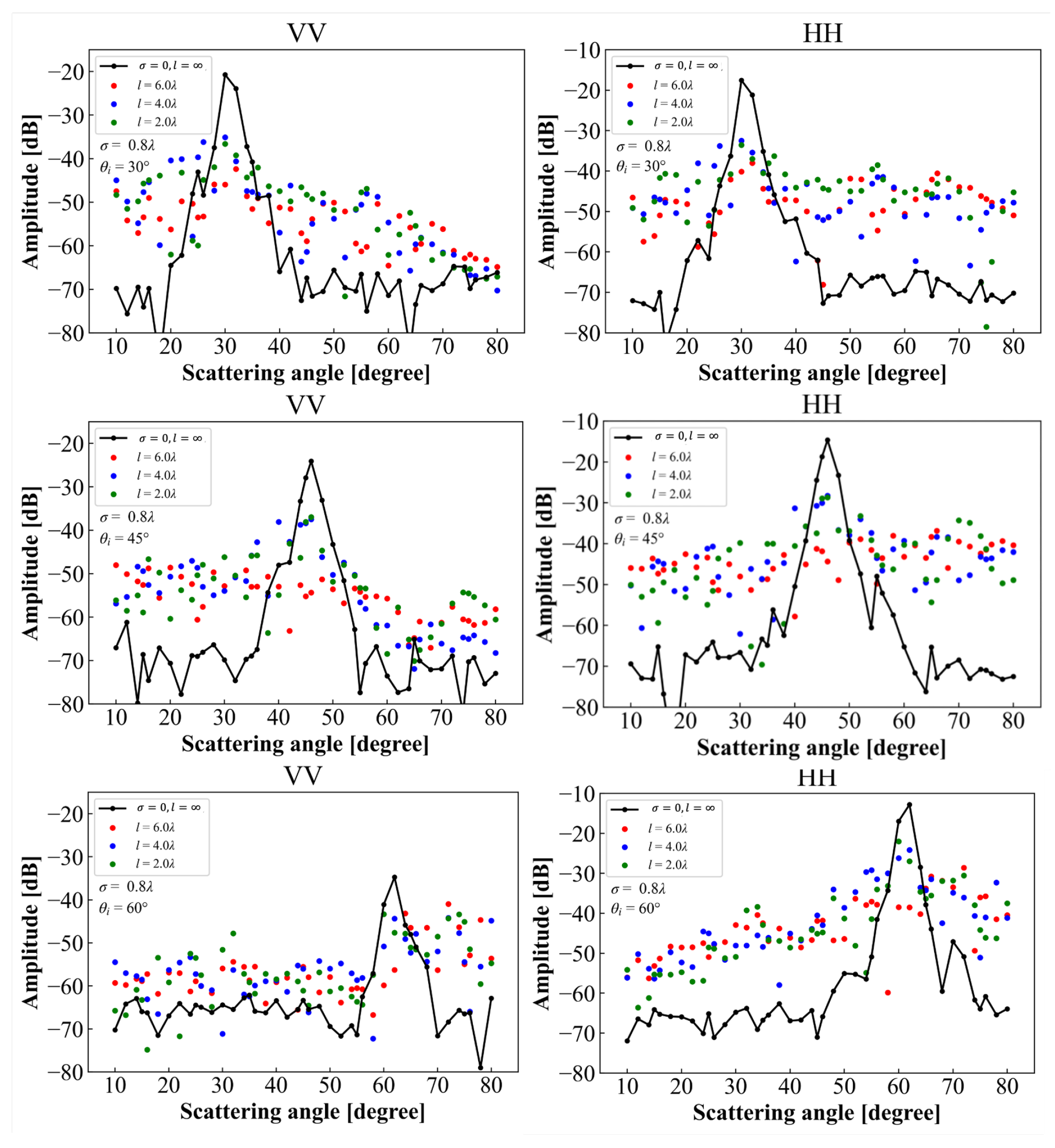
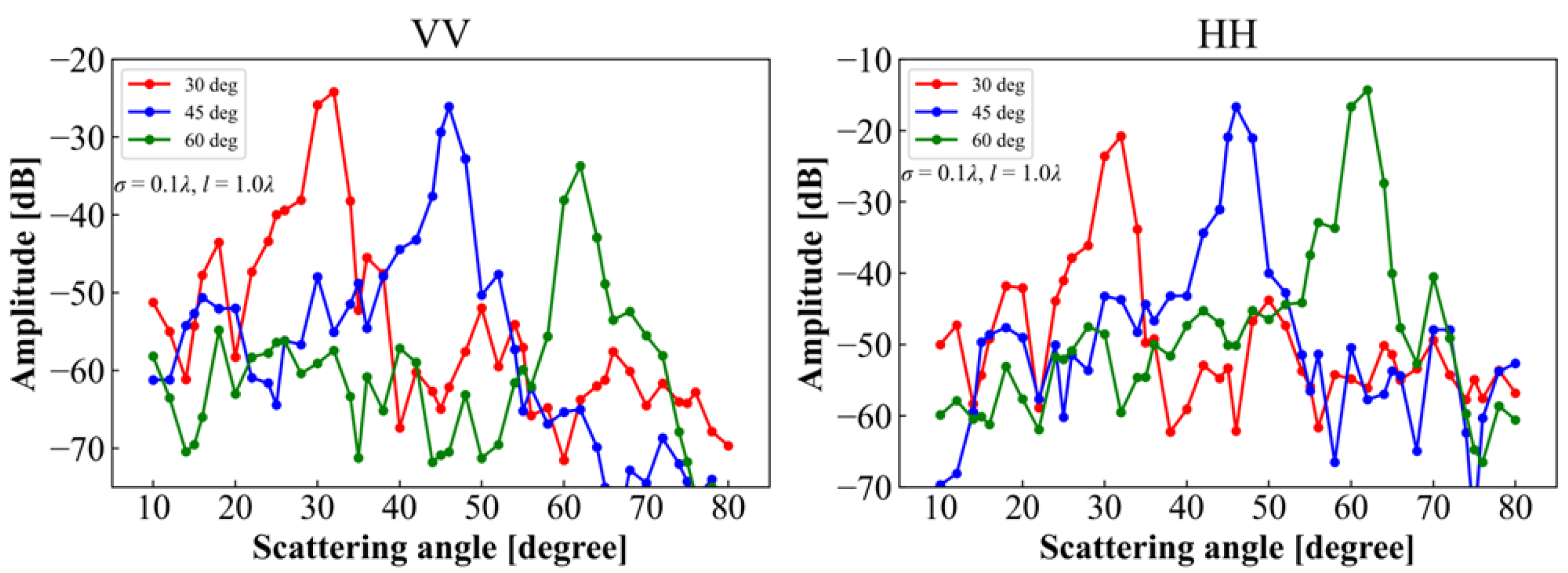
4.2. Bistatic Scattering
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melosh, H.J. Planetary Surface Processes; Cambridge University Press: Cambridge, UK, 2011; Volume 13. [Google Scholar]
- Evans, J. Radar studies of planetary surfaces. Annu. Rev. Astron. Astrophys. 1969, 7, 201–248. [Google Scholar] [CrossRef]
- Williams, J.P.; Paige, D.; Greenhagen, B.; Sefton-Nash, E. The global surface temperatures of the Moon as measured by the Diviner Lunar Radiometer Experiment. Icarus 2017, 283, 300–325. [Google Scholar] [CrossRef]
- de Arruda Moreira, G.; Guerrero-Rascado, J.L.; Bravo-Aranda, J.A.; Foyo-Moreno, I.; Cazorla, A.; Alados, I.; Lyamani, H.; Landulfo, E.; Alados-Arboledas, L. Study of the planetary boundary layer height in an urban environment using a combination of microwave radiometer and ceilometer. Atmos. Res. 2020, 240, 104932. [Google Scholar] [CrossRef]
- Horgan, B.H.; Cloutis, E.A.; Mann, P.; Bell, J.F., III. Near-infrared spectra of ferrous mineral mixtures and methods for their identification in planetary surface spectra. Icarus 2014, 234, 132–154. [Google Scholar] [CrossRef]
- Goetz, A.F. Three decades of hyperspectral remote sensing of the Earth: A personal view. Remote Sens. Environ. 2009, 113, S5–S16. [Google Scholar] [CrossRef]
- Davidsson, B.J.; Rickman, H.; Bandfield, J.L.; Groussin, O.; Gutiérrez, P.J.; Wilska, M.; Capria, M.T.; Emery, J.P.; Helbert, J.; Jorda, L.; et al. Interpretation of thermal emission. I. The effect of roughness for spatially resolved atmosphereless bodies. Icarus 2015, 252, 1–21. [Google Scholar] [CrossRef]
- Näränen, J.; Kaasalainen, S.; Peltoniemi, J.; Heikkilä, S.; Granvik, M.; Saarinen, V. Laboratory photometry of planetary regolith analogs. II. Surface roughness and extremes of packing density. Astron. Astrophys. 2004, 426, 1103–1109. [Google Scholar] [CrossRef]
- Johnson, P.E.; Vogler, K.J.; Gardner, J.P. The effect of surface roughness on lunar thermal emission spectra. J. Geophys. Res. Planets 1993, 98, 20825–20829. [Google Scholar] [CrossRef]
- Honniball, C.; Lucey, P.; Li, S.; Shenoy, S.; Orlando, T.; Hibbitts, C.; Hurley, D.; Farrell, W. Molecular water detected on the sunlit Moon by SOFIA. Nat. Astron. 2021, 5, 121–127. [Google Scholar] [CrossRef]
- Davidsson, B.J.; Hosseini, S. Implications of surface roughness in models of water desorption on the Moon. Mon. Not. R. Astron. Soc. 2021, 506, 3421–3429. [Google Scholar] [CrossRef]
- Spencer, J.R. A rough-surface thermophysical model for airless planets. Icarus 1990, 83, 27–38. [Google Scholar] [CrossRef]
- Giese, B.; Kührt, E. Theoretical interpretation of infrared measurements at Deimos in the framework of crater radiation. Icarus 1990, 88, 372–379. [Google Scholar] [CrossRef]
- Emery, J.; Sprague, A.; Witteborn, F.; Colwell, J.; Kozlowski, R.; Wooden, D. Mercury: Thermal modeling and mid-infrared (5–12 μm) observations. Icarus 1998, 136, 104–123. [Google Scholar] [CrossRef]
- Müller, M. Surface properties of asteroids from mid-infrared observations and thermophysical modeling. arXiv 2012, arXiv:1208.3993. [Google Scholar]
- Hayne, P.O.; Aharonson, O.; Schörghofer, N. Micro cold traps on the Moon. Nat. Astron. 2021, 5, 169–175. [Google Scholar] [CrossRef]
- Bandfield, J.L.; Hayne, P.O.; Williams, J.P.; Greenhagen, B.T.; Paige, D.A. Lunar surface roughness derived from LRO Diviner Radiometer observations. Icarus 2015, 248, 357–372. [Google Scholar] [CrossRef]
- Fa, W.; Wieczorek, M.A. Regolith thickness over the lunar nearside: Results from Earth-based 70-cm Arecibo radar observations. Icarus 2012, 218, 771–787. [Google Scholar] [CrossRef]
- Liu, N.; Fa, W.; Jin, Y.Q. No water–ice invertable in PSR of Hermite-a crater based on mini-RF data and two-layers model. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1485–1489. [Google Scholar] [CrossRef]
- Wang, S.; Yamada, T.; Kasai, Y. TSUKIMI: Forward modeling for lunar terahertz exploration. In Proceedings of the 44th COSPAR Scientific Assembly, Athens, Greece, 16–24 July 2022; Volume 44, p. 291. [Google Scholar]
- Siegel, P.H. Terahertz technology. IEEE Trans. Microw. Theory Tech. 2002, 50, 910–928. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Long, D.G. Microwave Radar and Radiometric Remote Sensing; University of Michigan Press: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Ma, J.; Shrestha, R.; Moeller, L.; Mittleman, D.M. Invited article: Channel performance for indoor and outdoor terahertz wireless links. APL Photonics 2018, 3, 051601. [Google Scholar] [CrossRef]
- Piesiewicz, R.; Jansen, C.; Mittleman, D.; Kleine-Ostmann, T.; Koch, M.; Kurner, T. Scattering analysis for the modeling of THz communication systems. IEEE Trans. Antennas Propag. 2007, 55, 3002–3009. [Google Scholar] [CrossRef]
- Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Chen, K.S. Radar Scattering and Imaging of Rough Surfaces: Modeling and Applications with MATLAB®; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Grossman, E.N.; Popovic, N.; Chamberlin, R.A.; Gordon, J.; Novotny, D. Submillimeter wavelength scattering from random rough surfaces. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 546–562. [Google Scholar] [CrossRef]
- Fung, A.K.; Liu, W.; Chen, K.; Tsay, M. An improved IEM model for bistatic scattering from rough surfaces. J. Electromagn. Waves Appl. 2002, 16, 689–702. [Google Scholar] [CrossRef]
- Krywonos, A.; Harvey, J.E.; Choi, N. Linear systems formulation of scattering theory for rough surfaces with arbitrary incident and scattering angles. J. Opt. Soc. Am. A 2011, 28, 1121–1138. [Google Scholar] [CrossRef]
- Ma, J.; Shrestha, R.; Zhang, W.; Moeller, L.; Mittleman, D.M. Terahertz wireless links using diffuse scattering from rough surfaces. IEEE Trans. Terahertz Sci. Technol. 2019, 9, 463–470. [Google Scholar] [CrossRef]
- Amarasinghe, Y.; Zhang, W.; Zhang, R.; Mittleman, D.M.; Ma, J. Scattering of terahertz waves by snow. J. Infrared Millim. Terahertz Waves 2020, 41, 215–224. [Google Scholar] [CrossRef]
- Alissa, M.; Friederich, B.; Sheikh, F.; Czylwik, A.; Kaiser, T. Experimental investigation of terahertz scattering: A study of non-Gaussianity and lateral roughness influence. IEEE Access 2020, 8, 170672–170680. [Google Scholar] [CrossRef]
- Heiken, G.; Vaniman, D.; French, B.M. Lunar Sourcebook: A User’s Guide to the Moon; Number 1259; CUP Archive: Cambridge, UK, 1991. [Google Scholar]
- Li, Q.; Shi, J.; Chen, K.S. A generalized power law spectrum and its applications to the backscattering of soil surfaces based on the integral equation model. IEEE Trans. Geosci. Remote Sens. 2002, 40, 271–280. [Google Scholar]
- Neu, J.; Schmuttenmaer, C.A. Tutorial: An introduction to terahertz time domain spectroscopy (THz-TDS). J. Appl. Phys. 2018, 124, 231101. [Google Scholar] [CrossRef]
- Formlabs. Durable Resin V2 Technical Data Sheet. 2020. Available online: https://formlabs-media.formlabs.com/datasheets/Durable_Resin_Technical.pdf (accessed on 26 January 2018).
- Yang, Y.; Chen, K.S.; Li, Z.L. A note on brewster effect for lossy inhomogeneous rough surfaces. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6722–6730. [Google Scholar] [CrossRef]
- Greffet, J.J. Theoretical model of the shift of the Brewster angle on a rough surface. Opt. Lett. 1992, 17, 238–240. [Google Scholar] [CrossRef] [PubMed]
- Kawanishi, T.; Ogura, H.; Wang, Z. Scattering of an electromagnetic wave from a slightly random dielectric surface: Yoneda peak and Brewster angle in incoherent scattering. Waves Random Media 1997, 7, 351. [Google Scholar] [CrossRef]
- Vid’Machenko, A.; Morozhenko, A. The application of the brewster angle data for the lunar surface mapping by the real part of the refractive index. Sol. Syst. Res. 2006, 40, 462–467. [Google Scholar] [CrossRef]



| Parameter | Specification | Unit |
|---|---|---|
| Frequency | 325∼500 | GHz |
| Polarization | HH/VV/HV/VH | - |
| Waveform | Linear frequency modulation | - |
| Sampling | 8001 | Point |
| Average | 10 | Time |
| Incident angle | 20∼70 | Degree |
| Material | Resin V2 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Hiramatsu, K. Experimental Analysis of Terahertz Wave Scattering Characteristics of Simulated Lunar Regolith Surface. Remote Sens. 2024, 16, 3819. https://doi.org/10.3390/rs16203819
Wang S, Hiramatsu K. Experimental Analysis of Terahertz Wave Scattering Characteristics of Simulated Lunar Regolith Surface. Remote Sensing. 2024; 16(20):3819. https://doi.org/10.3390/rs16203819
Chicago/Turabian StyleWang, Suyun, and Kazuma Hiramatsu. 2024. "Experimental Analysis of Terahertz Wave Scattering Characteristics of Simulated Lunar Regolith Surface" Remote Sensing 16, no. 20: 3819. https://doi.org/10.3390/rs16203819
APA StyleWang, S., & Hiramatsu, K. (2024). Experimental Analysis of Terahertz Wave Scattering Characteristics of Simulated Lunar Regolith Surface. Remote Sensing, 16(20), 3819. https://doi.org/10.3390/rs16203819





