Abstract
Carbon dioxide is one of the most influential greenhouse gases affecting human life. CO2 data can be obtained through three methods: ground-based, airborne, and satellite-based observations. However, ground-based monitoring is typically composed of sparsely distributed stations, while airborne monitoring has limited coverage and spatial resolution; they cannot fully reflect the spatiotemporal distribution of CO2. Satellite remote sensing plays a crucial role in monitoring the global distribution of atmospheric CO2, offering high observation accuracy and wide coverage. However, satellite remote sensing still faces spatiotemporal constraints, such as interference from clouds (or aerosols) and limitations from satellite orbits, which can lead to significant data loss. Therefore, the reconstruction of satellite-based CO2 data becomes particularly important. This article summarizes methods for the reconstruction of satellite-based CO2 data, including interpolation, data fusion, and super-resolution reconstruction techniques, and their advantages and disadvantages, it also provides a comprehensive overview of the classification and applications of super-resolution reconstruction techniques. Finally, the article offers future perspectives, suggesting that ideas like image super-resolution reconstruction represent the future trend in the field of satellite-based CO2 data reconstruction.
1. Introduction
Climate change is one of the most significant challenges for the planet’s future [,,]. It has enormous ecological, social, and economic impacts across the globe, including an increase in extreme weather events, rising sea levels, melting glaciers, reduced biodiversity, and food security. Carbon dioxide (CO2) is one of the greenhouse gases with the most significant impact on human life [,,]. Continuing increases in CO2 concentrations will significantly accelerate temperature rise [,,]. The Earth’s annual carbon emissions have exceeded its natural absorptive capacity, resulting in rising atmospheric CO2 concentrations [,]. Over the past few decades, as the global economy and population have grown, human activities have led to a steady rise in CO2 emissions, which are still increasing at a rate of more than 2 ppm/yr (ppm: parts per million, yr: year) []. If uncontrolled, the global average CO2 concentrations are projected to exceed 415 ppmv (parts per million by volume, meaning 415 volume units of CO2 per one million volume units of air) by 2030, contributing to more extreme weather events.
In response to climate change, governments have set policies and targets for greenhouse gas emissions reductions to keep CO2 levels at specific levels []. On 12 December 2015, 197 countries joined the Paris Agreement, which aimed to keep global temperatures below 2 °C [,]. In September 2018, the United Nations Framework Convention on Climate Change convened in Katowice, Poland. The conference aimed to develop rules and guidelines for implementing the Paris Agreement and accelerate global action to reduce emissions to meet the challenge of climate change []. To effectively control and reduce CO2 emissions and achieve the double carbon target, carbon monitoring is first needed to understand the characteristics and trends of the spatial and temporal distributions of atmospheric CO2. However, the spatial distribution of CO2 is not uniform and is closely related to human activities. Therefore, obtaining accurate CO2 monitoring data is essential for understanding the spatial and temporal distribution characteristics of CO2.
Satellite carbon dioxide data reconstruction uses satellite observation data and ancillary data to infer and estimate the spatial distribution and spatial–temporal variations in CO2 in the Earth’s atmosphere through data processing and analysis methods. The method makes up for the shortcomings of satellite observation, improves the precision and coverage of observation, and supports CO2 concentration data on a global scale.
Currently, there are three main ways to monitor CO2: ground based, airborne, and satellite based.
Ground-based monitoring is one of the critical methods for obtaining the spatial and temporal distributions of CO2 and is one of the older means of CO2 monitoring. In this method, the carbon dioxide concentration is monitored in real-time by ground stations or towers, such as the National Oceanic and Atmospheric Administration—Earth System Research Laboratory (NOAA-ESRL) [] and the Total Column Carbon Observing Network (TCCON) []. This method has the advantage of high accuracy and high temporal resolution and therefore is often analyzed in comparison with results from satellite data inversion. However, the global ground-based monitoring network consists of sparsely distributed stations with limited coverage, low spatial resolution, and no real-time capability, so it cannot fully reflect the spatial and temporal distributions of CO2 []. Therefore, in the late 1970s, airborne monitoring methods were introduced.
Airborne monitoring is a method of monitoring the CO2 concentration in the Earth’s atmosphere in real-time [,,]. Airborne refers to meteorological observations conducted from platforms that are flying or floating in the air. This method has the advantages of global coverage, high spatial and temporal resolution, long-term observation, and uncrewed operation. It helps to understand climate and environmental change trends. However, technical challenges, atmospheric disturbances, and calibration verification are disadvantages that must be overcome to ensure data accuracy and validity.
Satellite-based monitoring is a real-time or continuous monitoring of the CO2 concentration in the Earth’s atmosphere by launching a dedicated satellite in space and utilizing high-resolution remote sensing technology [,,]. Satellite monitoring has the advantages of being free from time and space constraints, comprehensive coverage, stable observation, long-term time series, and three-dimensional observation, and its observation accuracy is gradually improving []. However, it costs the most and is limited by shortcomings such as technical complexity, data processing challenges, and weather impacts, which need to be addressed to maximize its monitoring potential.
With the launching of more and more carbon satellites, the work of validating a large amount of CO2 data has gradually begun. At present, scholars mainly validate the accuracy of CO2 products inverted by different satellites by combining real-time ground station data, aircraft route measurement data, and model simulation data [,]. However, due to the limitations of the validation methods, the calibration of satellite CO2 data usually focuses only on evaluating the data accuracy and the study of the temporal variation characteristics of the errors, neglecting the characterization of the spatial distribution of the errors. In addition, due to the existence of aerosols and the limitation of satellite orbit, there are a lot of data missing in the process of satellite inversion, so the reconstruction of satellite CO2 data becomes particularly important [].
To deeply discuss strategies for addressing uncertainties and errors in carbon satellite data reconstruction, a comprehensive approach encompassing data processing, model validation, and error correction is essential. Firstly, optimizing data calibration and noise reduction techniques can enhance the quality of the raw observational data. Secondly, improving retrieval algorithms, such as through multi-model validation and error propagation analysis, can increase the processing accuracy. Additionally, integrating multi-source data and analyzing temporal sequences can enhance the spatial and temporal coverage of observations, mitigating the impact of data gaps. Concurrently, combining ground validation and simulation experiments for model calibration ensures result reliability. Finally, quantifying uncertainties through sensitivity analysis and statistical methods provides confidence intervals for the data results. These measures collectively reduce uncertainties and errors in the reconstruction process, thereby improving the accuracy and utility of CO2 data.
In the field of carbon remote sensing, many researchers and scholars have summarized the work of the time and published excellent review papers.
In 2015, Schimel et al. [] assessed the current development of terrestrial ecosystems and the carbon cycle through satellite observations. They presented the available satellite remote sensing data products such as vegetation index, surface temperature, chlorophyll fluorescence, land surface elevation, and their limitations. In addition, the article discusses the applications of satellite remote sensing technology in monitoring the carbon cycle and climate change and predicts future trends in satellite remote sensing technology and data products. Those trends include improving data resolution and accuracy, enhancing the real-time and spatial and temporal coverage of data, developing technologies such as multi-source data fusion and machine learning, and strengthening the integration of satellite observations with ground-based observations and model simulations to better understand the dynamics of terrestrial ecosystems.
In 2016, Yue et al. [] synthesized the latest research results and development trends of space and ground-based CO2 concentration measurement technologies, outlining the research progress of CO2 inversion algorithms, spatial interpolation methods, and ground-based observation data. In addition, they elaborated on the latest research results of CO2 concentration measurement techniques and the application of these techniques in global climate change and carbon cycle research and looked forward to future research directions.
In 2019, Xiao et al. [] provided an overview of the terrestrial carbon cycle and carbon fluxes. They outlined critical milestones in the remote sensing of the terrestrial carbon cycle and synthesized the platforms/sensors, methods, research results, and challenges faced in the remote sensing of carbon fluxes. In addition, they explored the uncertainty and validity of carbon flux and stock estimates and provided an outlook on future research directions for the remote sensing of the terrestrial carbon cycle.
In 2021, Pan et al. [] assessed the ability of CO2 satellites to serve as an objective, independent, and potentially low-cost and external data source while comparing the significance of nighttime optical satellite data for proxy CO2 monitoring to distinguish the importance of direct CO2 satellite monitoring.
In 2022, Kerimov et al. [] reviewed the application of machine learning models to greenhouse gas emissions estimation and modeling. They provided an overview of the methodology for applying machine learning in greenhouse gas emissions estimation and the main challenges faced.
As mentioned above, several past reviews have focused on CO2 monitoring, the carbon cycle, and carbon emissions. Although these reviews have covered the outlook of mapping the spatial and temporal distributions of CO2, they still lack content on CO2 data reconstruction methods. Therefore, a study focusing on satellite CO2 data reconstruction methods is urgently needed to help researchers interested in this field understand the latest developments in satellite CO2 data reconstruction.
This paper takes interpolation, data fusion, and super-resolution reconstruction as the main topics, systematically combs the satellite CO2 data reconstruction methods, and constructs high-resolution and high-precision CO2 data so that the readers can quickly understand the research hotspots of CO2 spatial and temporal distributions.
The contributions of this paper include the following:
(1) This paper provides a comprehensive review of CO2 monitoring methods and data sources.
(2) This paper describes in detail the comparative analysis of satellite CO2 data reconstruction methods on the basis of limited CO2 measurement data, with interpolation, data fusion, and super-resolution reconstruction as horizontal tasks, and traditional methods and machine/deep learning methods as vertical tasks. Combining these two types of analyses allows for a comprehensive evaluation and comparison of different CO2 data reconstruction methods. To the knowledge of the authors of this paper, this is the first review of CO2 reconstruction methods.
(3) This paper proposes the future development direction of satellite CO2 data reconstruction, namely, CO2 data with a longer period, a larger spatial range, a higher spatial resolution, and higher data accuracy can be obtained by super-resolution reconstruction and other methods.
This paper is divided into four main parts. As shown in Figure 1, the first part primarily introduces the research background and the necessity of reconstructing CO2 data. Through a summary of previous reviews, it also summarizes the innovative aspects and major contributions of this review. The second part discusses the monitoring methods for CO2 and the sources of data. In this part, Citespace, a tool for visualization and analysis of scientific literature, is used to visualize the development trend and research focus in this field. The third part delves into the specific applications of interpolation and data fusion methods in the reconstruction of CO2 data to achieve high-precision CO2 data reconstruction. The fourth part provides an in-depth exploration of super-resolution reconstruction methods and offers suggestions for the future development of carbon dioxide data reconstruction. The authors of this paper believe that this review will serve as an important reference for the reconstruction of satellite-based CO2 data.
Figure 1.
Schematic diagram of the structure of this paper.
2. Data Sources and Analysis in the Field
2.1. Data Sources
2.1.1. Ground-Based Monitoring
Ground-based monitoring is an essential method for obtaining the spatial and temporal distributions of CO2. Major ground-based CO2 monitoring networks include WDCGG (World Data Centre for Greenhouse Gases), GLOBALVIEW-CO2, NOAA-ESRL, COCCON, and TCCON.
WDCGG, established by the World Meteorological Organization, focuses on the global collection, storage, and sharing of greenhouse gas data. The WDCGG dataset includes information from multiple sources: on one hand, it contains a substantial amount of in situ measurement data from ground-based observation stations, which directly measure atmospheric CO2 concentrations at the ground level; on the other hand, WDCGG also integrates remote sensing data from satellite instruments, which measure atmospheric CO2 concentrations above the ground stations. This integration of remote sensing data complements ground-based observations by capturing a broader spatial distribution and the vertical profiles of atmospheric CO2 concentrations.
GLOBALVIEW-CO2 is a dataset maintained by international collaborative organizations, aiming to provide CO2 measurement data on a global scale. This dataset primarily consists of CO2 measurement data from ground-based observation stations, provided by fixed stations located around the world, recording atmospheric CO2 concentrations at the ground level. Unlike WDCGG, the GLOBALVIEW-CO2 dataset does not include remote sensing data, relying solely on ground-based observations to monitor and analyze global CO2 levels.
NOAA-ESRL is a research laboratory within the National Oceanic and Atmospheric Administration of the United States. In climate change, NOAA-ESRL contributes to data support through the Global Greenhouse Gas Reference Network [,]. The network comprises 106 stations, primarily in developed countries, including 8 high-tower stations and 4 baseline observatories. These stations provide discrete weekly CO2 sample collection, continuous in situ CO2 measurements, and measurements of other gases. Data from NOAA-ESRL are widely used to study temporal and spatial trends in global CO2 concentrations and sources and sinks of CO2. In addition, NOAA-ESRL has developed the CarbonTracker data assimilation system. The system utilizes continuous CO2 time series data from around the globe in conjunction with Earth system models to infer global CO2 sources and sinks, as well as CO2 uptake and release processes.
COCCON (Collaborative Carbon Column Observing Network) is a global observation network focused on high-precision ground-based measurements of atmospheric greenhouse gases, such as carbon dioxide and methane []. It aims to provide accurate column concentration data to support and validate satellite observations, particularly in areas where satellite measurements are affected by cloud cover or complex terrain. Using the micro Fourier Transform Infrared Spectrometer, a portable and low-cost yet high-precision instrument, COCCON measures the solar spectrum to determine the total column concentrations of CO2, CH4, and carbon monoxide. These measurements offer high temporal and spatial resolution, making COCCON a valuable resource for calibrating satellite data, improving climate models, studying the carbon cycle, and informing climate policy. Through its global network, COCCON addresses gaps in satellite observations and plays a crucial role in advancing greenhouse gas monitoring and climate change research.
TCCON, as a global CO2 observation network comprised of ground-based measurement sites, has a key objective of providing comprehensive information on global CO2 concentration changes through high-precision and high-resolution measurements []. As shown in Figure 2, this network gathers observational sites from around the world, spanning multiple countries and regions including North America, South America, Europe, Asia, Australia, and Antarctica. Each site is equipped with high-precision ground-based infrared spectrometers. The measurement data from the TCCON network exhibit exceptional accuracy and high temporal resolution, allowing for the provision of CO2 concentration change information at hourly or even shorter intervals for research purposes. These data are also widely utilized to investigate important questions such as the spatial distribution of CO2 in the atmosphere, seasonal variations, and variations among different regions [,].
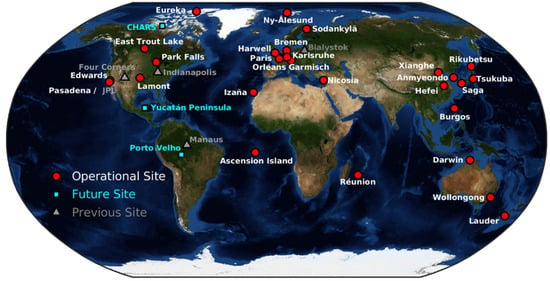
Figure 2.
Global TCCON site location distribution (https://tccondata.org/accessed on 1 October 2024).
While ground-based monitoring is a crucial means to understand changes in atmospheric CO2 concentrations, its advantages lie in high precision and high temporal resolution. Therefore, it is often used for comparative analysis with satellite and airborne data, particularly for validating satellite data retrieval results. However, this approach also has some limitations, including limited spatial coverage. Ground monitoring stations are sparsely distributed and cannot comprehensively cover the entire globe, especially in remote and oceanic regions where monitoring data are relatively scarce. This limitation may impact the accuracy of global CO2 concentration change analysis. In conclusion, accurately depicting the spatiotemporal distribution of CO2 solely relying on ground observations can be quite challenging.
2.1.2. Airborne Monitoring
Researchers have successfully supplemented ground-based monitoring with the use of airborne monitoring methods. This approach involves measuring atmospheric CO2 concentrations and vertical distribution using commercial flights or specially equipped research aircraft. It provides vital information about the distribution of CO2 and carbon cycling in the atmosphere.
On the one hand, commercial flights typically use Automatic Air Sampling Equipment or Continuous CO2 Measuring Equipment to collect air samples or continuously measure CO2 concentrations. On the other hand, research aircraft can carry various instruments to measure atmospheric CO2 concentration and vertical distribution, such as the Laser Absorption Spectrometer [] and the Infrared Absorption Spectrometer [].
Airborne monitoring can provide high-resolution data because the aircraft can collect information at different altitudes and times, resulting in more detailed spatiotemporal information. Atmospheric CO2 monitoring has become an important part of the global atmospheric monitoring network. More detailed data can be obtained through projects such as the Integrated Aircraft Trace Gases Observation Network [], the National Oceanic and Atmospheric Administration (NOAA)’s European Laboratory for Atmospheric Research Carbon Cycle Greenhouse Gas Aircraft Program, and NASA’s Airborne Greenhouse Gas Emissions Observation System. IAGOS (In-service Aircraft for a Global Observing System) is also a global program that utilizes sensors and instruments on commercial flights to measure atmospheric composition and meteorological parameters. IAGOS aims to collect atmospheric data on a global scale by installing sensors on regular commercial flights to supplement data from ground stations and satellite observations. IAGOS provides data on the concentration of carbon dioxide in the upper atmosphere. These data can be used to study the concentration and vertical distribution of CO2 in the atmosphere and to assess the impact of global climate change.
Airborne monitoring also has some limitations. Firstly, the coverage and sampling frequency of airborne monitoring are constrained by flight routes and schedules. Despite the establishment of a global aviation monitoring network, the number of monitoring stations and sampling frequencies remains limited due to factors such as cost. Additionally, since airborne monitoring instruments are installed on commercial aircraft, they can be influenced by factors such as weather, flight altitude, and aircraft type, which can affect the accuracy and reliability of the monitoring data.
2.1.3. Satellite Monitoring
During the past two decades, continuous advances in sensor technology and inversion methods have led to the maturation of satellite remote sensing for CO2 detection. Optical sensors onboard satellites are widely used for atmospheric CO2 observations. Currently, many satellites and instruments have been successfully launched into space, including the Scanning Imaging Absorption Spectrometer for Atmospheric Component Mapping (SCIAMACHY) [], the Atmospheric Infrared Sounder (AIRS) [], the Greenhouse Gas Observing Satellite (GOSAT) [], the Orbiting Carbon Observatory (OCO-2, OCO-3) [,,], and TanSat []. Future satellite launch programs for monitoring CO2 are in the pipeline. Table 1 summarizes the CO2 monitoring satellites that have been launched and those planned for launch until 2028 worldwide.

Table 1.
Carbon dioxide monitoring satellites launched and planned (to be launched by 2028) globally.
Europe has been an early pioneer in satellite remote sensing for greenhouse gases. On 28 February 2002, the European Space Agency (ESA) launched the Environmental Satellite carrying the instrument SCIAMACHY. It had three observation modes: limb, nadir, and occultation. It was the first satellite sensor capable of detecting changes in boundary layer CO2 concentrations. SCIAMACHY confirmed the feasibility of measuring near-surface CO2 concentrations in the near-infrared spectral range []. The retrieval algorithm for SCIAMACHY involved a combination of radiative transfer models and atmospheric inversion techniques to derive CO2 concentrations from the observed spectra. This approach was critical in validating the satellite’s capability to detect CO2 variations at different altitudes. Furthermore, ESA has initiated the European Copernicus anthropogenic CO2 monitoring mission. These satellites not only provide precise observations with high resolution and high signal-to-noise ratios but also can simultaneously image various parameters [].
On 23 January 2009, Japan successfully launched the GOSAT satellite, becoming the world’s first satellite specifically designed for the detection of atmospheric greenhouse gases, including CO2 and CH4 []. GOSAT employs the Fourier Transform Spectroscopy (FTS) method, which involves using a Michelson interferometer to capture spectral data across a broad range of wavelengths. The retrieval algorithm processes these data using radiative transfer models and inversion techniques to estimate CO2 and CH4 concentrations. Following GOSAT, the GOSAT-2 satellite was successfully launched on 29 October 2018, equipped with higher-performance sensors to provide more accurate greenhouse gas concentration data. However, both GOSAT and GOSAT-2 had limitations in terms of their ability to continuously sample the atmosphere due to their coarse spatial resolution. To enhance the spatial coverage capability for atmospheric greenhouse gases, Japan initiated the GOSAT-GW project, which adopted a grating-based spectral detection mode similar to OCO, Sentinel-5, and TanSat.
The United States’ first carbon satellite, OCO, experienced a launch failure in 2009 due to a payload rocket malfunction. However, in July 2014, OCO-2 was successfully launched []. NASA (National Aeronautics and Space Administration) released the initial global CO2 concentration distribution maps for OCO-2 on 8 December 2014, covering the period from 1 October 2014 to 11 November 2014. The retrieval algorithm for OCO-2 utilizes a combination of high-resolution spectroscopic measurements and advanced inversion techniques to derive CO2 concentrations from the captured solar absorption spectra. Following OCO-2, OCO-3 was successfully launched on 4 May 2019 and installed on the International Space Station, continuing the CO2 observation mission. Compared to OCO-2, OCO-3 has a larger observation range, meaning it can cover a wider swath of the Earth’s surface in each orbit, and it operates in the orbit of the space station. Each orbit allows for target and snapshot observations of any point at different times. Additionally, it can provide continuous observations of CO2 and Solar-Induced Fluorescence data from dawn to dusk within a day, significantly enhancing its observational capabilities for local and point source targets [].
Satellite resolution plays a crucial role in the remote sensing detection of point sources such as power plants. To achieve this goal, commercial satellite companies in Canada and the United States have initiated greenhouse gas satellite remote sensing programs with high spatial resolution [,]. Canada’s GHGSat company has launched three satellites in 2016, 2020, and 2021. These satellites are capable of capturing greenhouse gas remote sensing data with a resolution of 25 m and an accuracy of 4 ppm for Column-Averaged Dry Air Mole Fraction of CO2 () and 18 parts per billion for Column-Averaged Dry Air Mole Fraction of CH4 (). This innovative solution provides high-precision estimation for point source emissions. Meanwhile, Planet Labs, a private Earth imaging company based in the United States, plans to launch two Carbon Mapper satellites in 2024. These satellites will collect high signal-to-noise ratio spectral data with a resolution of 30 m, an 18 km swath, and a range of 400–2500 nanometers. These data can provide high-precision and greenhouse gas scientific data, with the capability to detect emissions from sources as small as 50 kg/h and as large as 300 t/h CO2. This detection capability is sufficient for effectively monitoring over of the world’s coal-fired power plants, making a significant contribution to greenhouse gas emission monitoring.
In recent years, China has made significant progress in the field of greenhouse gas remote sensing detection. First, on 22 December 2016, China successfully launched its first carbon satellite, TanSat, which has achieved a series of important results in global atmospheric CO2 concentration and chlorophyll fluorescence monitoring, among other aspects. The Institute of Atmospheric Physics of the Chinese Academy of Sciences, using the carbon retrieval system IAPCAS (Institute of Atmospheric Physics Carbon Retrieval Algorithm System), which was independently developed by their team, obtained from the TanSat satellite []. The IAPCAS retrieval algorithm integrates spectral data with radiative transfer models to provide accurate CO2 measurements. Following that, on 15 November 2017, the Fengyun-3D (FY-3D) meteorological satellite was successfully launched at the Taiyuan Satellite Launch Center. FY-3D carries the Greenhouse Gas Monitoring Instrument, which measures global CO2 and CH4 column concentrations using shortwave infrared interferometry. The retrieval algorithm for FY-3D processes interferometric data to estimate greenhouse gas concentrations with high precision. Furthermore, on 9 May 2018, the Gaofen-5 (GF-5) satellite was successfully launched at the Taiyuan Satellite Launch Center. The GF-5 satellite carries the Greenhouse Gases Monitor Instrument, primarily designed for quantitative monitoring of the distribution and changes in CO2 and CH4 concentrations globally. The Chinese GF-5B satellite (Gaofen-5B), launched on 7 September 2021, is a crucial part of China’s high-resolution Earth observation system. It features advanced remote sensing instruments, including multi-spectral, hyperspectral, infrared, and ultraviolet sensors, for precise monitoring of the atmosphere, land, and oceans. The retrieval algorithms for GF-5B are tailored to handle complex datasets from these various sensors, ensuring accurate greenhouse gas measurements. In the future, the Fengyun-3 No.08 polar-orbiting satellite is planned to be launched, which will carry a high-spectral-resolution greenhouse gas monitoring instrument. This instrument will achieve high-precision quantitative inversion of global atmospheric greenhouse gases through continuous high-resolution measurements in the near-infrared and shortwave infrared spectral bands. Here, high-resolution refers to the ability to distinguish and resolve fine details within the spectral bands, enabling the accurate detection and analysis of trace gas concentrations.
2.2. Datasets
Various datasets are used to measure and monitor global atmospheric CO2 concentrations. Currently, researchers utilize ground-based, satellite, and other ancillary datasets.
- (1)
- Ground-based datasets
Ground-based data refer to the continuous monitoring and recording of CO2 concentrations in the atmosphere by setting up meteorological stations, observatories, and other equipment on the Earth’s surface. These datasets contain extensive observations of atmospheric CO2 concentrations, typically on hourly, daily, monthly, or yearly time scales. They cover variations in atmospheric CO2 concentrations across different regions globally. Additionally, these data are usually maintained and published collectively by multiple institutions and organizations. Data processing and quality control also undergo rigorous standardization and calibration procedures. As shown in Table 2, there are currently three main ground-based datasets: TCCON, WDCGG, and GLOBALVIEW-CO2.
TCCON sites use Fourier Transform Spectrometers (FTSs) to make hyperspectral observations with a spectral resolution of 0.02 and a temporal resolution of about 90 s. Spectral data are recorded for direct solar radiation in the 4000 to 9000 range. The spectra measured for CO2 include two CO2 weak absorption bands located at 6220 and 6339 , and one absorption band located at 7885 . The spectral data are standardized, stable, and obtained in continuous observation mode at the TCCON site. The accuracy of the atmospheric products inverted from the FTS observation spectra reaches 0.8 ppm under clear or less cloudy conditions. The sites are selected according to a uniform criterion, and most are located within 100 km of human activity impacts.
WDCGG was established by the World Meteorological Organization and is dedicated to the collection, storage, and sharing of greenhouse gas data on a global scale []. The dataset includes various sources of data: first, ground-based observations, which involve direct measurements at observation sites, such as the atmospheric CO2 concentration measurements initiated by the Mauna Loa Observatory in Hawaii in 1958 []; second, mobile observations, which include measurements from ships, aircraft, and high-altitude balloons. These mobile platforms help capture spatial variations and vertical distributions of atmospheric CO2 concentrations; and finally, the remote sensing of data involves measurements of the atmosphere from satellite instruments, providing supplementary information to ground-based and mobile observations. By the late 1970s, NOAA’s Global Monitoring Division had conducted extensive measurements of atmospheric CO2 concentrations worldwide, encompassing both ground-based and mobile observations. In 1989, the International Meteorological Organization established the Global Atmosphere Watch, which now includes 51 countries that collectively establish observation sites and contribute data, integrating ground-based, mobile, and remote sensing technologies to provide a comprehensive view of atmospheric CO2 levels.
The GLOBALVIEW-CO2 dataset, provided by NOAA-ESRL, integrates observational data from multiple stations worldwide, offering long-term CO2 concentration data []. This dataset is essential for researching atmospheric carbon cycling, climate change, and identifying sources of CO2 emissions.

Table 2.
Current major ground-based carbon observation datasets.
Table 2.
Current major ground-based carbon observation datasets.
| Database | Brief Introduction | Reference |
|---|---|---|
| TCCON | TCCON is recognized as a standard network for CO2 | [] |
| WDCGG | WDCGG focuses on the collection, management and dissemination of observational data | [] |
| GLOBALVIEW-CO2 | The observation platforms include ground-based stations, tall towers, ships, and aircraft | [] |
- (2)
- Satellite datasets
Currently, the inversion of using satellite shortwave infrared observations has become the most effective method for obtaining CO2 data. This effectiveness refers to the ability of satellite datasets to provide comprehensive, global coverage and frequent observations, which ground-based or airborne datasets cannot achieve. Satellites can monitor remote and inaccessible areas, offering a more complete and consistent picture of CO2 distribution on a global scale. As shown in Table 3, the available satellite data include ENVISAT (with SCIAMACHY), the GOSAT series, the OCO series, and TanSat, which simultaneously provide products from different inversion algorithms.

Table 3.
Major satellite carbon observation datasets.
The SCIAMACHY spectral data employ three main algorithms to estimate the concentration of CO2 in the atmosphere []. These algorithms are the Differential Optical Absorption Spectroscopy (DOAS) algorithm, the Weighting Function Modified DOAS (WFM-DOAS) algorithm, and the Band-Enhanced Sensitivity Differential (BESD) algorithm. The DOAS algorithm is based on the absorption characteristics of the spectrum. It utilizes the absorption properties of different gas molecules at various wavelengths of light to infer the concentrations of gases in the atmosphere. The WFM-DOAS algorithm builds upon the DOAS approach by considering the propagation path of light through the atmosphere. This helps enhance measurement precision and also takes into account the vertical distribution of gases in the atmosphere, which can impact the results. The BESD algorithm is particularly useful for measuring low-concentration gases like methane and CO2. This method relies on the absorption and emission characteristics of gas molecules in the atmosphere. By measuring the spectral emissions from the atmosphere, it can estimate the concentrations of methane and CO2. These algorithms collectively provide valuable tools for assessing atmospheric gas concentrations, with each having its own strengths and applications.
The GOSAT is positioned in a sun-synchronous orbit at an inclination of 98° with an orbit altitude of approximately 666 kilometers. It completes one orbit approximately every 100 min, resulting in a revisit time of once every three days, with its local time of overpass being 13:00 []. The GOSAT satellite series includes GOSAT, GOSAT-2, and the planned GOSAT-GW. GOSAT utilizes the Thermal And Near-infrared Sensor for Carbon Observation (TANSO)—FTS and the TANSO-2 OCC for measurements. GOSAT-2, on the other hand, employs the TANSO-2 FTS-2 and TANSO-2 OCC-2 instruments for its observations. Satellite data products are categorized into four levels. Level 1 includes raw data, such as radiance measurements. Level 2 provides column-averaged concentrations of greenhouse gases like CO2 and CH4. Level 3 aggregates data spatially and temporally into gridded maps of gas concentrations. Level 4 comprises higher-level products, including model outputs like regional CO2 flux data. These data level descriptions are consistent across the GOSAT series, with each new satellite improving upon its predecessor’s capabilities.
The OCO series of satellites includes OCO-2 and OCO-3. OCO-2 is a NASA-sponsored Earth observation satellite program whose primary goal is to detect CO2 column concentrations with high accuracy, precision, and spatial resolution. OCO-2’s CO2 products offer excellent precision and accuracy and can characterize CO2 sources, sinks, and regional variations. In 2014, OCO-2 was launched into a sun-synchronous EOSA-train orbit at 705 km, becoming the first satellite in the A-train constellation. Each orbit has a period of 98.8 min, with a transit time of 13:36 local time and a revisit period of 16 days. OCO-2 carries a three-band grating imaging spectrometer to capture the solar reflected light spectrum in the 0.765 µm, 1.61 µm, and 2.06 µm bands. The spectrometer collects eight consecutive observation images at a frequency of 3 Hz at the bottom of the sky, with each image covering a 2 km by 1 km area on the Earth’s surface. OCO-3 is specialized in measuring gases such as CO2 and methane in the atmosphere. The data products of the OCO series satellites are divided into two levels: Level 1 and Level 2. Level 1 data products contain raw radiometric and image data from OCO-2 and OCO-3. Level 2 data products mainly cover vertical profiles of the CO2 column concentration and apparent absorption rate, which are crucial for studying the global carbon cycle and climate change.
TanSat is China’s first satellite dedicated to observing CO2 from space. Launched on 22 December 2016, TanSat was placed into a sun-synchronous orbit at an altitude of 700 km with an inclination angle of 98.2°, and its local overpass time is 13:30. The satellite carries two main instruments: the Aerosol and Cloud Gas Sensor (ACGS) and the Cloud and Aerosol Polarization Imager (CAPI). ACGS is a grating spectrometer designed to record the solar backscatter spectra for retrieving CO2 and oxygen concentrations. CAPI is a multi-band imaging spectrometer covering spectral ranges from ultraviolet to near-infrared in five bands (365–408 nm, 660–685 nm, 862–877 nm, 1360–1390 nm, and 1628–1654 nm). It is used to gather information about aerosols and clouds, with the 660–685 nm and 1628–1654 nm bands specifically employed for scattering detection. Using inversion algorithms developed by the Institute of Atmospheric Physics, Chinese Academy of Sciences, data from the carbon satellite have been inverted to obtain global CO2 distributions. Comparisons with observation data from TCCON at the Sudan Gurusha and Karlsruhe stations indicate absolute biases of 2.1 ppm and 2.9 ppm, respectively []. Additionally, the ACOS (Atmospheric CO2 Observations from Space) inversion algorithm has been applied to retrieve CO2 column concentrations from the carbon satellite data, yielding a product bias of 0.85 ppm []. Furthermore, the Department of Ecological and Environmental Informatics at the State Key Laboratory of Resources and Environmental Information System in China has developed a carbon satellite inversion algorithm that combines the SCIAMACHY radiative transfer model with optimization estimation methods. Validation against TCCON data shows a bias of 2.62 ppm and a standard deviation of 1.41 ppm [].
- (3)
- Auxiliary datasets
The CO2-supporting datasets provide information at the national, regional, and city levels, documenting emissions from sources such as coal combustion, oil, natural gas, cement production, and iron and steel production. These datasets are instrumental in analyzing climate change trends, formulating mitigation policies, and assessing national progress in reducing emissions. Standard anthropogenic CO2 emission datasets, listed in Table 4, are based on various methodologies and data sources.

Table 4.
Common auxiliary datasets for CO2.
The CHRED (China High Resolution Emission Database) is an energy consumption database published by the China Energy Research Institute. It provides data on energy consumption across various regions of China, supporting research on energy policy, regional energy planning, and environmental analysis []. This dataset includes information on energy consumption by provinces and prefecture-level administrative units, covering a range of energy types such as coal, crude oil, natural gas, and electricity. It may also include consumption data by different industries and uses, as well as related economic and environmental indicators. Researchers, policymakers, and environmental protection agencies can use the CHRED dataset to analyze energy consumption, environmental impacts, and economic benefits across China.
A team of researchers from Peking University (PKU) has released a series of global emissions inventory datasets that cover various pollutants and time scales []. The datasets include global emissions data for CO2, CO, and PM2.5. These global emissions inventory data were developed using a bottom–up approach, estimating pollutant emissions on a pollutant-by-pollutant basis. The dataset has a spatial resolution of 0.1° by 0.1°, providing detailed geographic information, and covers the period from 1960 to 2014 with a monthly temporal resolution. It represents 64 to 88 individual emission sources, encompassing different sectors and fuel combinations.
The ODIAC (Open-Data Inventory for Anthropogenic Carbon dioxide) dataset estimates anthropogenic CO2 emissions in various regions of the globe using satellite observations, energy statistics, and ground-based data []. With a resolution of 1 km, this dataset can be used to study the spatial distribution, as well as temporal and spatial variations, and trends in global carbon emissions [].
The EDGAR (Emissions Database for Global Atmospheric Research) dataset provides global anthropogenic emissions data with a resolution of 0.1° × 0.1°, offering high accuracy, spatial and temporal resolution, and timeliness [].
Additionally, CARMA [], WDI [], MEIC [], and CEADS [] are standard auxiliary CO2 datasets that enhance the transparency of global carbon emissions and support mitigation actions. These datasets aggregate information from multiple sources, including government reports, energy statistics, and other publicly available data.
2.3. Citespace-Based Reconstruction Analysis of Satellite CO2 Data
Citespace is a tool for visualizing and analyzing scientific literature, primarily used for studying knowledge evolution and academic collaboration networks within academic fields [,]. It assists researchers in identifying research hotspots, key authors, field collaborations, and trends in knowledge evolution, thereby facilitating academic research and decision-making. In this section, Citespace 6.1.R2 is employed to visualize and analyze literature related to global satellite CO2 data reconstruction and to review research on satellite CO2 data reconstruction over the past 20 years, focusing on keyword mapping and author contributions.
With the increase in CO2 emissions, satellite CO2 data reconstruction has become widely utilized. Figure 3 illustrates that the number of papers in the field of satellite CO2 reconstruction has shown an overall increasing trend from 2005 to 2024, with the most significant rise occurring between 2021 and 2022. This indicates that satellite CO2 data reconstruction has garnered considerable attention in recent years and is highly valued by scholars.
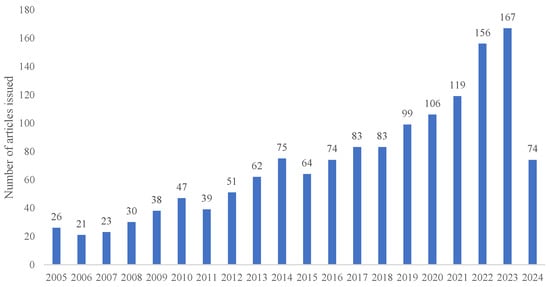
Figure 3.
Number of papers issued on satellite CO2 data reconstruction (total per year until May 2024).
This paper searched the Web of Science using the keywords “carbon dioxide” and “reconstruction”, collecting about 1437 relevant articles from the past two decades. The size of each circle in the keyword map is proportional to the frequency of the keyword. The hierarchy of the circles represents the passage of time, with the circles moving from the inside to the outside, indicating a progression from the past to the present. Red circles highlight key nodes, demonstrating that the relevant literature in the field has attracted significant attention. Connecting lines show associations between different keywords (data source: Web of Science Core Collection).
As shown in Figure 4, the CO2 node is the most prominent and frequent keyword on the map, followed by “satellite”, “remote sensing”, “reconstruction”, “assimilation”, and “model”. These high-frequency keywords reflect the core concepts, key technologies, and research directions in the reconstruction of satellite CO2 data, highlighting the hotspots and concerns in the field. This information helps researchers gain a deeper understanding of the field’s development trends and knowledge structure.
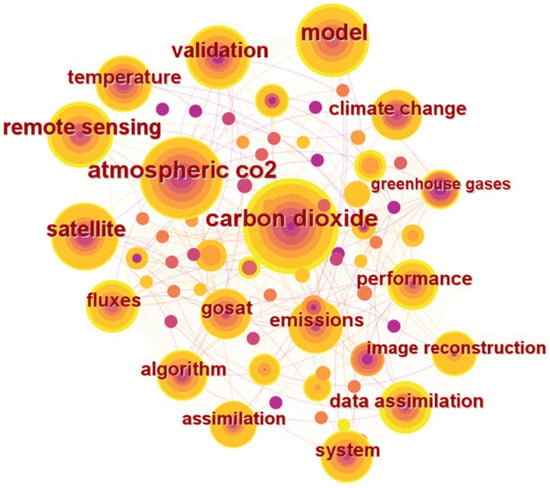
Figure 4.
Keyword mapping analysis of carbon satellite data reconstruction based on Citespace.
In the author mapping, as shown in Figure 5, authors such as Frederic Chevallier, Tomohiro Oda, and others appear with high frequency in Citespace’s author mapping. The high frequency of these authors reflects their academic reputation, leadership, collaborative networks, and key innovations, as well as the significance of their academic contributions and activities in the field of satellite CO2 data reconstruction. Readers can stay informed about the research frontiers in this field by following the progress and work of these prominent authors.

Figure 5.
Author mapping analysis in the field of carbon satellite data reconstruction based on Citespace.
It can be observed from Figure 6 that China and the United States lead in paper contributions. Compared to developing countries, developed nations have made more rapid progress in the field of satellite remote sensing and have paid greater attention to satellite CO2 data reconstruction, resulting in a higher volume of published papers. This trend indicates that countries worldwide are focusing on advancing this field, highlighting it as a significant area of development at the international level.
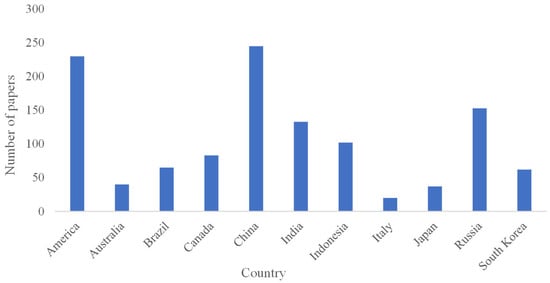
Figure 6.
Number of papers on CO2 in selected countries in the period January 2020 to May 2024.
3. Satellite CO2 Reconstruction Methods
Scholars have conducted CO2 data reconstruction studies across multiple satellites and developed a series of high-precision CO2 datasets over extended periods, considering the spatial and temporal coverage as well as the data accuracy of various CO2 satellites.
Interpolation is a method used to estimate information about a function’s value or its derivative at discrete points. It involves estimating approximate values at other points based on a finite number of known points. Interpolation techniques can be used to fill in unobserved spatial data within a single image or unobserved temporal data across multiple images over a fixed observation area. Kriging is a specific interpolation method that not only utilizes known data points but also models the spatial correlation structure between these points to make more accurate predictions. It achieves this by fitting a semivariogram to quantify the spatial correlation and then using this model to appropriately weight the known data points when estimating values at unknown locations. In CO2 data reconstruction, Kriging can estimate CO2 concentrations at locations without measurements by leveraging the spatial patterns observed in known data. However, not all CO2 data reconstruction methods use Kriging. Some methods may employ other statistical or machine learning techniques that do not involve the spatial correlation modeling characteristic of Kriging.
Data fusion is an information processing technique where computers analyze and synthesize observational data from multiple sensors collected over time under specific guidelines to perform decision-making or assessment tasks. It typically targets a specific observation area and integrates information from sources such as satellite carbon remote sensing, meteorological data, and Digital Elevation Models (DEMs) to address missing spatiotemporal data.
In this section, interpolation and data fusion methods will be explored in depth to enhance the spatial resolution of CO2 data, fill observational gaps, and improve data accuracy. This approach will provide more comprehensive information and support for CO2 concentration research and applications.
3.1. Data Reconstruction Based on Interpolation
Interpolation involves estimating values between several discrete data points using specific methods. These data points are often collected over a defined time or spatial range, though data may not be available at every point within that range. The goal of interpolation is to fill in these gaps to create a more continuous and complete dataset. It is important to note that interpolation methods generate estimates for unknown data points rather than actual measurements. Consequently, the interpolation error should be evaluated for each case, and the uncertainty of the data must be considered. Table 5 compares different interpolation techniques to provide a comprehensive understanding. In different interpolation methods, the local trend, the information of coordinates, and the stratification have specific meanings. The local trend refers to systematic changes or trends within a local area of data, which can be linear or nonlinear and are usually caused by local factors rather than the overall trend of the data. The information of coordinates refers to the specific spatial locations of data points, which are used to determine the spatial relationships and distances between data points, and are fundamental for calculating spatial correlation and performing interpolation. Stratification involves dividing data into multiple subsets or layers based on certain criteria, such as geographic, geological, or statistical characteristics. This method is particularly useful for areas with significantly different characteristics, as the data within each layer may have distinct statistical properties and spatial variability structures. During interpolation, stratification can enhance the model’s accuracy and reliability by ensuring the data within each layer are more homogeneous and consistent.

Table 5.
Comparison of different Kriging interpolation methods.
Kriging interpolation methods include several variants for estimating attribute values at unknown locations. For example, Simple Kriging (SK) assumes that the attribute values follow a normal distribution with a constant mean; Ordinary Kriging (OK) takes into account local trends and semivariance functions; Universal Kriging (UK) is suitable for cases with external trends. In Kriging interpolation methods, external trends refer to systematic changes or trends present in the data, which are typically caused by known external factors rather than random spatial variation. These external trends can be explained and described by one or more known external variables. Simple Co-Kriging (SCK) and Ordinary Co-Kriging (OCK) are suitable for multi-attribute interpolation, considering covariance and local spatial trends, respectively. Probability Kriging (PCK) considers the probability distribution of the attribute values. At the same time, Simple Collocated Co-Kriging (SCCK) and Ordinary Collocated Co-Kriging (OCCK) are used in multi-attribute contexts and consider correlations and local trends between attributes. The selection of the appropriate Kriging method depends on the data characteristics and requirements and can provide accurate and reliable spatial interpolation results.
In satellite CO2 reconstruction, Kriging interpolation is used in the field of carbon satellite data reconstruction []. Interpolation methods based on discrete data points can be used to fill in missing or blank parts of satellite observations to obtain a complete picture of the CO2 distribution []. These methods utilize statistical properties and spatial correlations between known observations to infer CO2 concentrations at unobserved locations.
In order to accurately reflect the spatial and temporal distributions of CO2, both temporal and spatial interpolation are essential. However, capturing spatial and temporal variability in satellite data reconstruction is challenging using only spatial interpolation methods. In contrast, spatiotemporal interpolation methods can capture spatiotemporal variability more accurately, and the model’s accuracy can be assessed by cross-validation in space and time. Next, spatial interpolation and combined spatiotemporal interpolation methods will be introduced.
3.1.1. Spatially Interpolated Data Reconstruction
Traditional statistical methods have widely utilized spatial Kriging interpolation to generate data products. However, interpolation methods that utilize only spatial correlation do not consider the time-dependent structure of CO2 data. As a result, temporal variations in dynamic CO2, including annual growth and seasonal cycles, need to be adequately considered []. The following Table 6 lists the results obtained by researchers in recent years in satellite data reconstruction using spatial interpolation methods.

Table 6.
Papers related to spatial interpolation.
In 2008, Tomosada et al. [] used a spatial statistical approach to obtain CO2 column concentrations from GOSAT data. In 2012, Hammerling et al. [] used a spatial interpolation approach to generate maps at high spatial and temporal resolutions without the need to use atmospheric transport models and estimates of CO2 uptake and emissions. In 2014, Jing et al. [] combined the GOSAT and SCIAMACHY satellite measurements to propose a filling method to model the spatial correlation structure of the CO2 concentration to solve the problem of limited CO2 data provided by a single satellite due to cloud effects, in order to more accurately characterize the spatial and temporal distributions of atmospheric CO2 concentration. In 2020, Shrutilipi Bhattacharjee et al. [] proposed a method to fill in the spatial correlation structure of the modeled CO2 concentration based on the Kriging grid interpolation method of the spatial interpolation technique, which interpolates the CO2 source points in the emission inventory and the types in the land use/cover information with the CO2 column concentration separately, and then combines the interpolation results of the two to obtain a more accurate prediction of the CO2 column concentration. Meanwhile, the researchers also demonstrated that the method can be applied to predict the CO2 column concentration in other regions.
Although spatial interpolation can be used to reconstruct satellite CO2 data to address the problem of insufficient CO2 data, it has some limitations. First, interpolation methods rely on estimating values between known measurement points, but they may introduce errors, especially when data are sparse or when extrapolation beyond the range of measurements is required. Second, interpolation methods do not accurately capture the true spatial and temporal variability because they do not account for spatial and temporal autocorrelations in the data. This can lead to the generation of biased or noisy maps, particularly in situations where measurement points are sparse, resulting in a loss of information rather than overly smooth fields. In contrast, spatiotemporal interpolation methods can better address these issues.
3.1.2. Spatiotemporal Interpolation Data Reconstruction
Spatiotemporal interpolation methods can capture spatiotemporal variability more accurately and can also be used to assess the accuracy of models by cross-validating them in space and time. Additionally, spatiotemporal interpolation methods can utilize multiple data sources, including satellite observations, ground-based observations, and model simulations, to enhance spatiotemporal resolution and accuracy. However, these methods primarily focus on estimating values between existing data points, whereas data fusion methods aim to integrate data from different sources to create a more comprehensive and consistent representation. Data fusion typically involves calibrating and merging data sources to reduce systematic errors and improve the overall reliability of the results, potentially providing higher precision and consistency when handling different types of data. The following Table 7 lists some excellent articles on satellite CO2 data reconstruction using spatiotemporal interpolation methods in recent years for the readers’ convenience.

Table 7.
Papers related to spatiotemporal interpolation.
In 2015, Tadić et al. [] proposed a flexible moving-window Kriging method, which can serve as an effective technique for imputing missing data and reconstructing datasets. This method was demonstrated to generate high spatial and temporal resolution maps using satellite data, and its feasibility was validated using CO2 data from the GOSAT satellite and the GOME-2 instrument. In 2017, Zeng et al. [] employed spatiotemporal geostatistical methods, effectively utilizing the spatial and temporal correlations between observational data, to establish a global land-based mapping dataset of total CO2 amounts from satellite measurements. They conducted cross-validation and verification at the TCCON sites. The results revealed a correlation coefficient of 0.94 between the dataset and observational values, with an overall bias of 0.01 ppmv.
Due to the limited spatial and temporal resolution of concentrations, more data sources must be available. If spatial and temporal interpolation is performed using fewer observational data sources, the uncertainty of the interpolated data will increase significantly. In the future, finding suitable data sources with high-quality, long-time series of CO2 concentrations is another critical task. To create the longest possible time series and to improve the accuracy by utilizing multiple measurements when possible, Zhonghua He’s team [] developed an accuracy-weighted spatiotemporal Kriging method for integrating and mapping observed by multiple satellites, which fills in the data gaps from multiple satellites and generates continuous global 1° × 1° spatiotemporally resolved data every eight days from 2003 to 2016.
To better reconstruct the satellite CO2 data and to observe the spatiotemporal variations of CO2, an extended Gstat package was proposed. It reuses the spacetime class to estimate the spatiotemporal covariance/half-variance model and performs spatiotemporal interpolation. However, it is challenging to select reliable and reasonable semivariance models and their parameters in spatiotemporal Kriging interpolation. Inappropriate choices of models and parameters may lead to significantly inaccurate and inefficient interpolation results. To better understand the multi-fractal scale behavior, Ma et al. [] investigated the characteristics of the multi-fractal scale behavior of the time series of atmospheric concentration in China from 2010 to 2018 in terms of spatial distribution. They gained insights into the dynamical mechanisms of the CO2 concentration changes and proposed an improved spatiotemporal interpolation method (spatiotemporal thin-plate spline interpolation) to realize the spatiotemporal interpolation of the atmospheric concentration. In 2023, Sheng et al. [] generated a global terrestrial dataset with a grid resolution of 1° and a temporal resolution of 3 days, covering the period from 2009 to 2020 based on the spatiotemporal geostatistical method.
In summary, although interpolation methods can, to a certain extent, solve some of the missing data problems and maintain the spatial continuity of the data, some interpolation methods rely heavily on the number and quality of samples, meaning that they primarily depend on the distribution and accuracy of existing data points to estimate values at unmeasured locations. This can lead to several issues: firstly, if the number of samples is insufficient, the interpolation results may not adequately reflect the true spatial variability of the data, thereby reducing estimation accuracy. Secondly, if the sample quality is poor, these errors may be propagated into the interpolation results, further affecting their reliability. Additionally, these methods sometimes neglect the spatial characteristics of the geographic data, such as topographic variations or environmental conditions, which can lead to results that do not accurately represent the real situation, causing discrepancies from the actual data. In addition, due to the limitations of the data itself, interpolation reconstruction often fails to improve the data accuracy significantly. Therefore, when applying interpolation methods, it is necessary to carefully choose appropriate variants and parameters and make adjustments and corrections according to the actual situation.
3.2. Data Reconstruction Based on Data Fusion
Data fusion combines data from different data sources, sensors, or observation methods to obtain more comprehensive, accurate, and reliable information [].
Data fusion methods and techniques are diverse. Their advantage lies in their ability to fully utilize information from multiple data sources, thereby increasing the accuracy and confidence of the data while reducing uncertainty. Data fusion can also fill gaps and compensate for deficiencies while providing more comprehensive spatial and temporal coverage. The following Figure 7 shows the categorization of data fusion methods to help readers understand better. In Figure 7, Vvting aggregates predictions from multiple models by selecting the most frequent outcome, thereby enhancing accuracy through consensus. Weighted voting refines this approach by assigning different weights to each model’s predictions based on their accuracy, thus giving more influence to the more reliable models [].
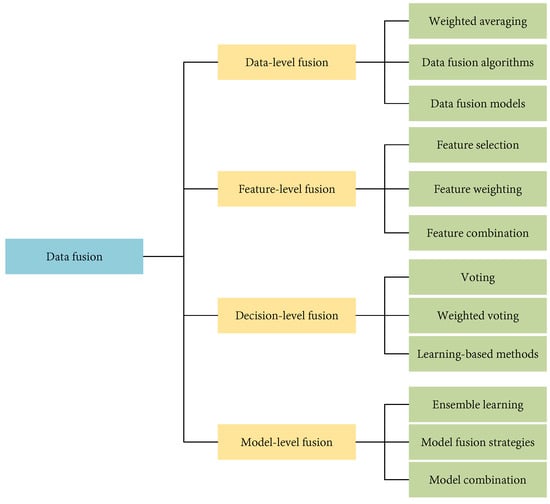
Figure 7.
Classification of data fusion methods.
Fusion methods are categorized into data-level fusion, feature-level fusion, decision-level fusion, and model-level fusion. Data-level fusion enhances the coverage and credibility of data by combining raw data from different sources. Feature-level fusion extracts features from different data sources and improves the expressiveness of the data. Extracting features means identifying and extracting variables or information that are useful for a specific task. For example, in image data, this might include extracting edge, texture, or shape features; in time series data, it could involve extracting trends, periodicities, or anomalies. The process of feature extraction typically includes steps such as data preprocessing, feature selection, and feature calculation. Enhancing the expressiveness of the data means integrating and optimizing features extracted from different data sources to make the data more accurate in representing and reflecting the actual situation. This can be achieved by increasing the detail and richness of the data, enabling subsequent analyses or models to better capture the underlying patterns and complexities of the data. Decision-level fusion integrates the decision results from different data sources to improve the credibility of classification and decision-making. Model-level fusion integrates outputs from different models to enhance overall model performance. First, different models may excel at handling specific types of data or tasks, and by combining their outputs, we can leverage each model’s strengths and address the weaknesses of individual models, improving overall prediction accuracy and robustness. Second, a single model might overfit the training data, leading to poor performance on new data. Model fusion helps mitigate this risk by incorporating diverse learning strategies and perspectives, thus enhancing generalization. Additionally, different models may react differently to noise and outliers in the data; combining multiple models can reduce the errors introduced by any single model and increase overall result stability. Finally, various models might use different feature sets, algorithms, or training methods, and model fusion can effectively utilize these diverse information sources to better handle complex data. In summary, model-level fusion combines the strengths of multiple models to improve prediction accuracy and overall model performance. Choosing the appropriate fusion method depends on the problem requirements and the nature of the data.
In satellite CO2 reconstruction, due to the presence of heavy clouds (or aerosols) and the limitation of satellite orbits, there is a large amount of missing data in satellite inversion, which limits the study of global CO2 sources and sinks. Therefore, satellite CO2 reconstruction using data fusion methods is a potential endeavor. Data fusion can improve the spatial resolution and temporal coverage, increase the data precision and accuracy, and enhance the spatial coverage. By integrating information from different data sources, data fusion can generate more detailed, continuous, and comprehensive maps of CO2 distribution, contributing to an in-depth understanding and study of the carbon cycle process.
Data fusion can be performed based on statistics, modeling, and learning algorithms. The choice of the specific method depends on the nature of the data, the purpose of the fusion, and the application requirements. These three approaches are described below to help understand satellite CO2 data reconstruction better.
3.2.1. Data Fusion Method Based on Statistics
The use of statistical-based data fusion methods is a commonly used data fusion technique that integrates information from multiple data sources by applying statistical principles and methods to obtain more accurate and reliable estimates. Table 8 shows the results achieved by researchers in recent years in satellite CO2 data reconstruction using statistics-based data fusion methods.

Table 8.
Data fusion method based on statistics.
In 2013, Reuter et al. [] applied an ensemble median merging algorithm (EMMA) and used grid-weighted averaging to fuse CO2 data, resulting in a new dataset. In 2014, Jing et al. [] fused measurements from GOSAT and SCIAMACHY and proposed a data imputation method based on spatial correlation structures of CO2 concentrations. This method enabled the creation of high-spatiotemporal-resolution global land CO2 distribution maps. Hai et al. [], in the same year, employed dimensionality reduction Kalman smoothing and a spatial random effects model to merge CO2 observational data from GOSAT, AIRS, and OCO-2 satellites. In 2015, Zhou et al. [] introduced an improved fixed-rank Kriging method based on GOSAT and AIRS data. The results demonstrated a better correlation between the fused dataset and meteorological analysis data. In 2017, Zhao et al. [] introduced a method called High-Precision Surface Albedo Model Data Fusion (HSAM-DF). This approach utilized geological–chemical model CO2 concentration outputs as a driving field and ground-based CO2 concentration observations as accuracy control conditions to merge two types of CO2 data. In 2023, Meng et al. [] used inversion data from GOSAT and OCO-2 to create a global continuous spatiotemporal dataset called “Mapping-”. Mapping- revealed the spatiotemporal characteristics of global similar to those observed in the CarbonTracker model data.
Statistically based data fusion methods can derive spatial and temporal distributions of . These distributions are more accurate, have higher resolution, and span longer periods than the results generated based solely on a single satellite dataset.
3.2.2. Data Fusion Method Based on Model Simulation
Model-based simulation is a common approach to data fusion, mainly using chemical transport models (CTMs) to simulate atmospheric CO2. CTMs can infer the distribution of CO2 concentrations and fluxes in various regions of the globe and, at the same time, correct the simulation results using observational data to improve their accuracy. Commonly used CTMs include CarbonTracker and GEOS-Chem. They obtain optimized carbon flux and CO2 concentration distributions in various regions of the globe by assimilating data such as bottle-sampled CO2, continuous CO2 series from towers, and detected by satellites. These two commonly used chemical transport models are described in detail next.
- (1)
- GEOS-Chem
GEOS-Chem is a global chemical transport model dedicated to simulating chemical reactions and transporting substances in the atmosphere []. The model employs a high-resolution, three-dimensional grid to reflect atmospheric changes in space and time accurately. It fully accounts for many critical atmospheric processes, including radiation, convection, turbulence, wet and dry deposition, and chemical reactions. GEOS-Chem is particularly notable for its broad applications in atmospheric composition modeling, generating simulations of gases such as CO2, CH4, CO, and isoprene with spatial and temporal continuity. It has been extensively used to evaluate satellite-detected data as well as ground-based observations.
GEOS-Chem is a 3D Eulerian transport model with a spatial resolution of 4° × 5°, containing 47 vertical levels, with coverage extending from the surface to a height of 0.01 hectopascal. During assimilation, the model uses a four-dimensional variational (4D-Var) approach by iterating the model’s equations to minimize the cost function J:
where N is the number of time steps of the observation data, c is the optimized model state, is the observation data at the ith time step, is the observation operator, the model state c is transferred to the observation space, is the observation error covariance matrix at the ith time step, is the background estimation, and is the background error covariance matrix.
Before the reconstruction of satellite CO2 data, it is critical to assess the applicability of chemical transport models in CO2 simulations through ground-based observations of atmospheric CO2 and satellite-measured XCO2 []. Several studies have investigated the contribution of terrestrial ecosystems to atmospheric CO2 concentrations through chemical model simulations. In 2011, Feng et al. [] evaluated the accuracy of a global chemical transport model for CO2 simulations from 2003 to 2006 using ground-based observations, aircraft measurements, and AIRS satellite data. In 2013, Lei et al. [] compared and assessed the spatial and temporal variations in atmospheric CO2 between June 2009 and May 2010 using XCO2 from two datasets, GOSAT and GEOS-Chem, and analyzed the CO2 differences between the Chinese land region and the U.S. land region to demonstrate the satellite observations and model simulations’ rationality and uncertainty. In 2017, Li et al. [] evaluated regional chemical modeling simulations of CO2 concentrations in 2012 using GOSAT observations and ground-based measurements.
Due to limitations in data availability and precision, the spatiotemporal patterns of XCO2 have not been well characterized at the regional scale. Researchers have utilized XCO2 data from GOSAT to investigate the spatiotemporal patterns of XCO2 in the Chinese region. They employed a high-resolution nested grid GEOS-Chem model to construct XCO2 []. In 2017, Zhang et al. [] compared the results of XCO2 derived from the fusion of TCCON measurements with the GEOS-Chem model to the satellite observations. They found that the global OCO-2 XCO2 estimates were closer to the HASM XCO2. The primary methodological workflow can be seen in Figure 8.
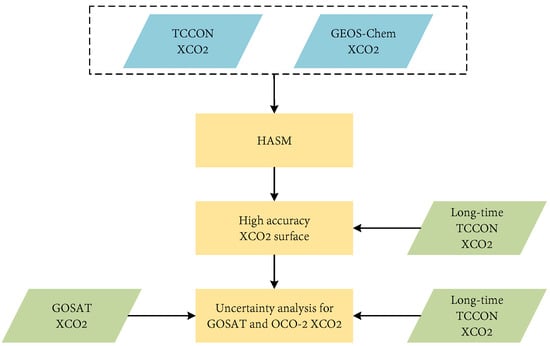
Figure 8.
Flowchart for obtaining high-precision XCO2 and evaluating the effectiveness of GOSAT and OCO-2 satellite observations (Zhang et al. []).
GEOS-Chem is essential in atmospheric chemistry, air quality research, climate change, and pollution management. However, CTM simulations require a higher level of certainty, primarily due to the limited knowledge of a priori fluxes, errors in the simulated atmospheric transport processes, and inaccuracies in the observational CO2 data being assimilated, particularly satellite-acquired data.
Errors in the representation of atmospheric transport in chemical transport models have long been recognized as a major source of uncertainty in atmospheric CO2 inversion analyses. Improving transport models is critical for enhancing the accuracy of CO2 inversions. Current efforts to improve model transport focus on two key areas: refining the parameterization of unresolved transport, particularly in coarse offline CTMs, and increasing the spatial and temporal resolutions of model simulations to better capture atmospheric transport processes. As transport models evolve, it will be crucial to regularly evaluate their ability to accurately represent large-scale atmospheric dynamics [].
- (2)
- CarbonTracker
CarbonTracker is a CO2 measurement and modeling system developed by NOAA to track CO2 sources and sinks globally []. The CarbonTracker model typically uses the Transport Model 5 chemical transport model to simulate the atmospheric transport of CO2 and other trace gases. It integrates ground-based observatories, airborne observations, satellite observations, and model simulations to provide high-resolution estimates of CO2 concentration and spatial distribution through data assimilation techniques. The current release is CarbonTracker 2022, which covers the period from January 2000 to December 2020 with global surface–atmosphere CO2 flux estimates.
In CO2 flux inversion, errors induced by atmospheric transport models can contribute to the uncertainty in inferring surface fluxes, in addition to biases in retrieval. Furthermore, model grid cells are often relatively coarse and may have different representational capabilities compared to satellite observations. Therefore, analyzing the differences between the simulated CO2 and satellite-derived results and assessing the uncertainty in model transport outcomes is crucial. To better understand CO2 trends in the Asian region, Farhan Mustafa and colleagues conducted a comparison in 2020 between obtained from CarbonTracker and obtained from GOSAT and OCO-2 satellite observations []. The results revealed good consistency between CarbonTracker and the other two satellite datasets, allowing the use of any of these datasets to understand CO2 in the context of carbon budgets, climate change, and air quality.
CarbonTracker reconstructs atmospheric carbon emission and absorption processes by integrating multiple observations and simulation models. Satellite CO2 data are crucial in this process, as they provide high temporal and spatial resolution observations that can compensate for the lack of ground-based observations, monitor carbon emission sources and sinks, and validate and improve models. However, due to the coarse spatial resolution, data extracted by CarbonTracker may not capture the spatial heterogeneity of CO2.
In the field of carbon dioxide reconstruction, in addition to commonly used physical models like GEOS-Chem and CarbonTracker, many other models are widely applied. Numerical Weather Prediction (NWP) models, such as WRF, provide high-precision meteorological background data and can be coupled with Chemical Transport Models (CTMs) like CAMS (Copernicus Atmospheric Monitoring Service) to enhance the simulation of CO2 transport [,]. Radiative Transfer Models (RTMs), such as MODTRAN and SCIATRAN, simulate the propagation of light through the atmosphere, providing a crucial foundation for satellite remote sensing inversion []. Additionally, General Circulation Models (GCMs), like the GISS model, aim to simulate atmospheric circulation in the global climate system and are often combined with CTMs for long-term climate analysis []. By integrating observational data across varying temporal and spatial scales, these models enable the accurate reconstruction of atmospheric CO2 distribution and trends, providing essential scientific support for addressing climate change.
3.2.3. Data Fusion Method Based on Learning Algorithms
Data fusion methods based on learning algorithms belong to emerging technologies. They utilize neural networks, integrated learning, Convolutional Neural Networks, Generative Adversarial Networks, and transfer learning to learn and fuse information from multiple data sources automatically []. Learning algorithms are widely used in action recognition [], image enhancement [,], and semantic segmentation [,]. These methods reveal complex relationships between data by training on a large amount of data, extracting feature representations, and merging information from different data sources to obtain more accurate and comprehensive data fusion results [].
Machine learning methods utilize existing observations and associated features as inputs, and models are trained to learn data relationships to predict and fill in missing data [,]. Deep learning methods, on the other hand, utilize deep neural network models for satellite data reconstruction. These deep learning models have multiple hidden layers to learn more advanced feature representations from the data [,,]. The success of machine learning and deep learning methods in satellite CO2 data reconstruction depends on adequate training data and appropriate feature engineering.
With the assistance of multi-source data, even simple multiple linear regression models can obtain good fitting results. However, due to the complexity of CO2 transport processes between terrestrial ecosystems, marine ecosystems, and the atmosphere, linear models face the challenge of having an inadequate fitting ability. To overcome this challenge, studies have been conducted in recent years to apply machine learning to derive continuous distributions and to reconstruct satellite CO2 data. Table 9 summarizes the results of data fusion methods based on learning algorithms achieved by researchers in satellite CO2 data reconstruction in recent years.

Table 9.
Data fusion method based on data fusion.
In 2019, Siabi et al. [] employed a Multi-layer Perceptron (MLP) model to establish a nonlinear relationship between OCO-2 satellite XCO2 and various data sources, successfully filling the gaps in satellite observation data. In 2020, Phuong Nguyen et al. [] creatively combined compressed sensing and deep learning into a single framework to merge GOSAT and OCO-2 XCO2 data. Compared to the original data, the fused dataset exhibited Root Mean Square Errors ranging from 1.31 ppm to 4.12 ppm, enhancing the spatiotemporal resolution of long-term analysis. He et al. [] developed a LightGBM (Light Gradient Boosting Machine)-based CO2 reconstruction model that achieved strong objective fitting accuracy. This model filled gaps in OCO-2 inversion data for the Chinese region from 2015 to 2018, with a cross-validation R² of 0.95 and an RMSE (Root Mean Square Error) of 0.91 ppm.
In 2022, Li et al. [] proposed a high spatial and temporal resolution and spatial and temporal continuum method for reconstructing atmospheric CO2 concentration. As shown in Figure 9, they integrated data from OCO-2 satellite observations by selecting environmental factors that affect atmospheric CO2 concentration and used an extreme random tree (ERT) model for training to determine the relationship between environmental factors and the atmospheric CO2 concentration. With this method, they generated spatiotemporally continuous atmospheric CO2 concentration data on a global continental scale. Validation results show that these reconstructed CO2 data exhibit satisfactory performance.
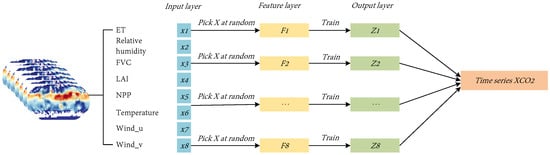
Figure 9.
Schematic of the extremely randomized tree model for the estimation of CO2.
In 2022, Wang et al. [] successfully reconstructed the daily variation in the CO2 column concentration in the Beijing–Tianjin–Hebei region with full spatial coverage by analyzing the sources of atmospheric CO2 and various factors affecting the spatial distribution of CO2, using multi-source satellite data and a random forest model. Compared with direct CO2 satellite observation data, these reconstructed CO2 data can achieve daily global coverage and have richer application value. In addition, in 2022, Zhang et al. [] proposed an innovative geographically weighted neural network (GWNN) model by combining a neural network model with a geographically weighted regression (GWR) model, which can effectively capture the spatial heterogeneity of CO2 and further improve the model’s accuracy.
There are a few longer time scales and more comprehensive studies of multiple satellites in China. In 2023, Zhang et al. [] planned to use machine learning techniques to create a long-term, monthly dataset with missing data filled in and analyze its spatial and temporal variability in depth. As shown in Figure 10, the spatial gradient of CO2 is not very significant due to its long lifetime in the atmosphere and continuous accumulation. When dealing with filled with missing data, it is more challenging to construct a machine learning model, which requires careful consideration of its spatial variation and influencing factors. To this end, Zhang et al. [] utilized near-infrared CO2 observation satellites, including SCIAMACHY, GOSAT, and OCO-2, as well as a variety of auxiliary data such as emissions, vegetation, and meteorology. In a framework based on Convolutional Neural Networks, deep convolution and attention mechanisms are employed while focusing on the correlation between nearest neighbors. The specific methodology is described below.
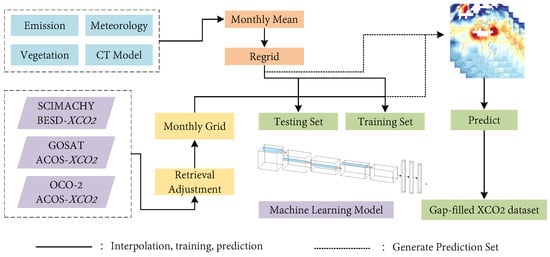
Figure 10.
The workflow of Zhang et al.’s [] study.
- (1)
- Data preprocessingwhere is the data in a given monthly grid, and is the inverse square of the precision, which is the uncertainty in the standard deviation for the SCIAMACHY dataset and the a posteriori error in for GOSAT and OCO-2. Zhang et al. [] chose data with an ‘xco2_quality_flag’ value of 0 and excluded outliers of more than four times the standard deviation each month.
In the CarbonTracker model, Zhang et al. [] used auxiliary data to calculate by employing 25 levels of CO2 profile data as constraints and reference values for the machine learning model. In this process, they used a pressure weighting function, which is formulated as follows:
where and are the bottom and top pressures of the i-th layer, respectively. is the CO2 mixing ratio in the dry air of layer i. is the column density of dry air per unit pressure. , g, and are the specific humidity, gravitational acceleration, and molar mass of the dry air, respectively. To minimize discontinuities, monthly averaging was performed by Zhang et al. []. Meanwhile, CT- was used as a spatial constraint only. Then, all auxiliary variables were aggregated to a resolution of 0.25° × 0.25°. To increase the resolution, bilinear interpolation was used.
- (2)
- Machine learning model
In this study, to utilize the observed data, Zhang et al. [] selected the first N nearest-neighbor data points of each valid XCO2 data point and used the corresponding XCO2 values as inputs. Meanwhile, to combine the influencing factors, they selected a size of 7 × 7 in the region centered on each XCO2 observation. To handle the C auxiliary variables, they designed a data block with dimensions (7, 7, 18), where 7 represents the spatial dimensions of the data block and 18 represents the number of channels. Through experiments, they found that Convolutional Neural Networks (CNNs) performed more effectively with these high-dimensional data. Considering the different characteristics of the channels, they concluded that a uniform convolutional kernel was not suitable and decided to use depthwise separable convolution and attention mechanisms to achieve better results.
As shown in Figure 11, Zhang et al. [] proposed a machine learning network with the structure shown below. This architecture first took a data block consisting of each variable as input. A double convolution–activation operation was performed after channel and spatial attention processing, followed by spreading. Distance and values of N points around each valid grid point were used as inputs. To integrate the time and latitude variations, the time, latitude, and global CO2 background values were also introduced as auxiliary inputs.
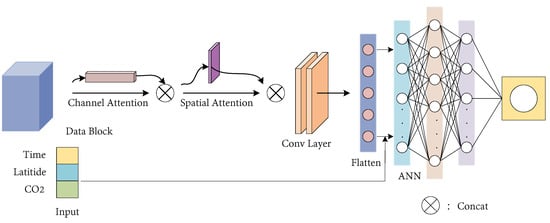
Figure 11.
The architecture of the machine learning model (Zhang et al. []).
- (3)
- Model training
Zhang et al. [] used MAE (Mean Absolute Error) and RMSE as monitoring metrics in model training. To assess the accuracy of the model, they randomly divided all valid data and kept 30% of the whole dataset as the validation set, which was not involved in training but was used to validate the model’s performance. Meanwhile, predictive ability is also a critical assessment method. Zhang et al. [] generated a long-term dataset using a model trained for prediction and evaluated it against satellite observations, model simulations, and ground-based observations.
Data fusion methods based on learning algorithms in satellite CO2 data reconstruction can significantly improve data accuracy and processing efficiency. For the carbon satellite data reconstruction methods, this paper provides a comparative analysis of the reconstruction results (Table 10), making them easier for readers to further understand and reference.

Table 10.
Comparative analysis of the reconstruction results.
Based on the research conducted by the authors of this paper, it has been observed that the currently popular deep learning algorithms are scarcely applied in the field of CO2 data fusion. As shown in Table 11, we compiled a list of deep learning algorithms that can potentially be used in the field of data fusion, providing readers with a reference for further exploration.

Table 11.
The mainstream deep learning algorithms in data fusion.
In the field of CO2 data fusion, the vast majority of current research papers primarily focus on the fusion of multiple data sources, with very limited mention of methods for the fusion of multiple heterogeneous data sources. Multiple data source fusion predominantly concerns the integration of data from the same data types, whereas the fusion of multiple heterogeneous data sources comprehensively integrates data from different types and characteristics. Therefore, in the domain of satellite CO2 data reconstruction, the fusion of multiple heterogeneous data sources allows for a more comprehensive consideration of the strengths and limitations of various data sources, ultimately providing more accurate and reliable CO2 concentration information.
3.3. Summary of Satellite CO2 Reconstruction Methods
In the field of satellite CO2 data reconstruction, both interpolation methods and data fusion methods play crucial roles. Interpolation methods are employed to address missing data in the spatial and temporal dimensions, utilizing techniques such as Kriging interpolation and temporal interpolation to fill in the gaps. Data fusion methods, on the other hand, integrate CO2 concentration data from different sources, including satellite data, ground station data, and model-generated data, thereby enhancing the spatiotemporal coverage and accuracy of the data. This fusion can be achieved through combining satellite data with ground station data, and model data with satellite data, as well as integrating data from multiple sensors. Looking ahead, with the continuous advancement of technology, satellite CO2 data reconstruction is expected to become more precise, comprehensive, and effective in monitoring and understanding the spatiotemporal variations in CO2 concentration in the Earth’s atmosphere.
4. Super-Resolution Reconstruction Methods
Image super-resolution reconstruction aims to reconstruct a natural and clear high-resolution (HR) image from one or more low-resolution (LR) images. Image super-resolution algorithms can be broadly categorized into three groups based on their research methods: interpolation-based super-resolution algorithms, reconstruction-based super-resolution algorithms, and learning-based super-resolution algorithms [].
In remote sensing, super-resolution reconstruction methods are widely used to enhance the detail and clarity of satellite images. These methods benefit various fields such as geology, climatology, environmental science, agriculture, oceanography, and urban planning [,,,]. In the following sections, we will elaborate on the three classification methods of super-resolution reconstruction and discuss the application and potential of super-resolution reconstruction technology in satellite CO2 data reconstruction.
4.1. Interpolation-Based Image Super-Resolution Algorithm
The interpolation method is a simple and fast image super-resolution algorithm that effectively improves image resolution. Its classification topological framework is shown in Figure 12. The two super-resolution reconstruction methods, traditional interpolation and guided interpolation, are described below. Traditional interpolation methods (such as nearest-neighbor, bicubic, and bilinear interpolation) are based on geometric calculations of pixel values without involving image feature extraction and analysis. These methods are generally faster but may be less effective in handling complex image structures; their commonality is that they rely on straightforward mathematical operations based on pixel values for interpolation. In contrast, guided interpolation methods (such as edge-guided, gradient-guided, and wavelet transform interpolation) use specific image features (like edges, gradients, or frequency components) to guide the interpolation process, thereby enhancing the preservation of image details and edges. Their commonality lies in their reliance on image feature analysis to improve the interpolation results. Table 12 compares each reconstruction algorithm based on the interpolation method.
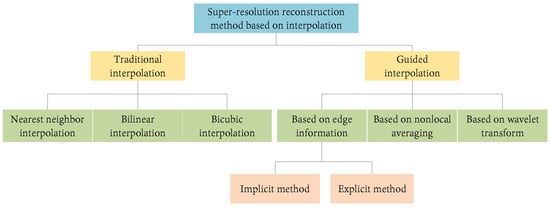
Figure 12.
Classification of image super-resolution algorithms based on interpolation.

Table 12.
Comparison of image reconstruction algorithms based on interpolation.
- (1)
- Traditional interpolation algorithm
Traditional interpolation methods do not consider the structural information of the image but are based on simple geometric operations of pixel values. For example, nearest-neighbor interpolation directly assigns the grey value of the nearest pixel as the interpolation result; bilinear interpolation calculates new pixel values through linear interpolation based on the nearest four pixels; and bicubic interpolation uses more complex cubic interpolation functions to achieve smoother results.
Nearest-neighbor interpolation [,] assigns the grey value of the pixel closest in Euclidean distance to the interpolating point as its interpolated grey value. The formula is as follows:
where are floating point numbers in the interval, and is the pixel value of the low-resolution image at .
Although nearest-neighbor interpolation is a simple interpolation algorithm with a low level of complexity and ease of implementation, it tends to produce aliasing artifacts and discontinuities in image intensity. This is because it does not take into account the influence of other neighboring pixels on the target interpolated point, especially when applied to higher-resolution images. To address the issue of aliasing artifacts caused by the neglect of interactions between adjacent pixels in nearest-neighbor interpolation, researchers introduced bilinear interpolation [,,].
The bilinear method primarily addresses the image interpolation problem by linearly interpolating four adjacent pixel points in both vertical and horizontal directions. The formula is as follows:
Although the bilinear interpolation method has improved the resolution of image greyscale discontinuity problems, the interpolated image may still exhibit noticeable detail degradation, especially when high-frequency information is severely affected.
Researchers extended bilinear interpolation to propose bicubic interpolation. Bicubic interpolation expands the neighborhood from four adjacent pixels to sixteen adjacent pixels and employs weighted averaging after applying cubic interpolation polynomials for image interpolation and reconstruction. This method uses cubic polynomials as the interpolation functions:
w is the weight or distance parameter used in the interpolation process. is a piecewise cubic function that provides weights in different ranges depending on the value of w. The interpolation formula is as follows:
wherein
A is a row vector containing the values of the function S at the points , u, , and ; B is a matrix containing the specific values of the function G around the points ; and C is a column vector containing the values of the function S at the points , v, , and .
The double-cubic interpolation method fully considers the influence of each pixel on the target interpolation point, which improves the reconstruction quality but increases the computational complexity and volume significantly.
Because these algorithms are designed based on the assumption of local smoothness in images, they may not perform well in regions with high-frequency information, such as edges or textured areas, where pixel intensity changes are abrupt. In these regions, traditional interpolation algorithms may fail to produce satisfactory results. Additionally, as the magnification factor increases, issues like ringing artifacts and aliasing effects can arise. Therefore, researchers have proposed guided interpolation methods to address these challenges.
- (2)
- Guided interpolation algorithm
Guided interpolation methods utilize specific image information (such as edges or gradients) to enhance the interpolation effects. For example, edge-guided interpolation identifies edges in the image and aims to preserve their sharpness during interpolation; gradient-guided interpolation uses gradient information to guide the process, ensuring that areas with significant gradient changes (such as edges) are handled better; and wavelet transform interpolation employs wavelet transforms to decompose the image and guide interpolation using frequency domain information, thereby preserving more details.
Edge-guided interpolation methods [,,] are primarily used to enhance edge information in RGB (Red, Green, Blue) color images, addressing the perceptual impact of human vision characteristics on image edges. Li et al. [] introduced the edge-guided NEDI (New Edge-Directed Interpolation) algorithm, which utilizes the local covariance of edges in the LR image to reconstruct edge information similar to that in the HR image, thus improving edge sharpening. However, this algorithm is computationally intensive and has limited practical applications. Building on the NEDI algorithm, Zhang et al. [] proposed an adaptive interpolation method to optimize the structural information between LR and HR images, leading to more comprehensive image structural and edge information.
Gradient-guided interpolation [,] uses first- and second-order gradient information from the neighborhood to adjust gradient and pixel distributions. It combines edge-guided interpolation with bicubic interpolation for image reconstruction.
Wavelet transform interpolation [,,] leverages the wavelet transform’s ability to capture local details. It decomposes image features into different scales for analysis, then overlays and fuses these features, and uses wavelet inverse transform to enhance resolution. Ford et al. [] used one-dimensional wavelet signals for nonuniform image sampling reconstruction, while Nguyen et al. [] extended this approach to two-dimensional signals and reconstructed LR images within a multi-resolution framework.
Most interpolation-based image super-resolution algorithms are relatively simple and computationally efficient, but they cannot recover lost high-frequency details and have limited accuracy. Therefore, interpolation-based super-resolution algorithms are often used as preprocessing methods, where the interpolated image serves as the initial super-resolution result, which is then combined with other methods to further enhance the high-frequency information.
4.2. Reconstruction-Based Image Super-Resolution Algorithm
Reconstruction-based super-resolution methods are widely used in image processing and are primarily categorized into frequency domain and spatial domain approaches []. These methods reconstruct the high-resolution image by extracting necessary feature information from multiple low-resolution images and estimating the HR image details.
4.2.1. Frequency Domain Method
Image super-resolution algorithms based on frequency domain reconstruction are used to improve the resolution of images by eliminating spectral aliasing in the frequency domain. Patti et al. [] first proposed to eliminate the spectral aliasing of LR images in the Fourier transform frequency domain and Fourier transform of multiple LR images to realize super-resolution image reconstruction. The frequency domain method improves the computing speed and image accuracy. However, the frequency domain-based method cannot utilize the a priori knowledge in the image null domain and is only suitable for the overall translation and spatially invariant model, which makes it difficult to solve the image noise problem. Thus, most of the research mainly focuses on studying image super-resolution algorithms based on null domain reconstruction.
4.2.2. Spatial Domain Method
Image super-resolution algorithms based on spatial domain reconstruction can conveniently and flexibly incorporate various prior knowledge and use this prior information as a constraint condition to ensure that the iterative solution process converges to an optimal or local optimal solution. Spatial domain-based image super-resolution algorithms mainly include nonuniform interpolation [], iterative back-projection [], convex set projection [], and maximum a posteriori probability methods []. Table 13 comprehensively presents the characteristics and performance of reconstruction-based image reconstruction methods in terms of prior information dependence, the feasibility of unique solutions, computational complexity, processing speed, algorithm flexibility, and reconstructed image quality.

Table 13.
Comparison of image reconstruction algorithms based on reconstruction.
- (1)
- Nonuniform interpolation
The nonuniform interpolation method [] works by fitting or interpolating the feature information from nonuniformly distributed LR images to generate uniformly distributed HR image features, thereby achieving super-resolution reconstruction. While this algorithm is effective for reconstruction, it depends heavily on having sufficient a priori information, which can limit its flexibility.
- (2)
- Iterative inverse projection method
Irani et al. [] proposed the iterative back-projection approach. The iterative back-projection algorithm first estimates a high-resolution image as the initial solution, then generates a low-resolution image by simulating noise interference, and finally projects the difference between the real low-resolution image y and back onto . The low-resolution image and the iterative image are shown in Equation:
where represents the simulated low-resolution image, H is the projection matrix, is the initial estimation of the high-resolution image, n represents noise, is the final result image obtained after the first iteration, represents the back-projection matrix, and y represents the actual observed low-resolution image after back-projection. To compare the two images y and , if their values are equal, it indicates that the two images are the same, and the iteration stops. If the values of y and are not equal, the error between the two images needs to be back-projected onto , and is updated and corrected accordingly. This process continues until the error meets the desired criteria.
The iterative back-projection method addresses the issue of high dependence on a priori information in super-resolution image reconstruction algorithms and effectively improves the quality of the reconstructed images. However, it does not guarantee the uniqueness of the reconstructed image.
- (3)
- Projections onto Convex Sets
Stark and Oskoui [] were the first to apply the Convex Projection Over the Union of Sets (POCS) algorithm to image super-resolution reconstruction. The POCS method maps the LR image into a set of HR images through interpolation, applies constraints based on prior knowledge to this set, and then iteratively projects the initial value to find a solution that satisfies the constraints. The iterative process of the convex set projection algorithm is shown in the following equation:
where denotes the first iteration of the high-resolution image, and denotes the projection matrix of any pixel point of the high-resolution image projected onto the convex set.
The POCS algorithm can maintain the edge contour region relatively well. However, the algorithm has high computational complexity, slow convergence speed, and strong dependence on a priori information in each iteration.
- (4)
- Maximum a posteriori probability method
Schultz and his team [] introduced an algorithm based on maximum a posteriori (MAP) estimation. The maximum a posteriori method treats the high-resolution image and the low-resolution image as two random variables, framing the image super-resolution reconstruction problem as a probability estimation problem to ultimately estimate the final high-resolution image. The maximum a posteriori estimation algorithm process is as follows. First, assume that the known image A is the original low-resolution image, image B is the reconstructed high-resolution image, and is the objective function:
Finally, by simplifying using logarithmic operations, Equation (16) can be converted into Equation (17) below:
where denotes the conditional probability corresponding to the high-resolution image B, and denotes the a priori probability of the high-resolution image. MAP estimation can effectively utilize the internal information of known images and produce high-quality reconstructed images. However, its drawbacks include complexity, computational intensity, and the suboptimal handling of image details in the reconstructed result.
Reconstruction-based image super-resolution algorithms rely on solving the degradation model. Many of these algorithms incorporate a priori distribution information of the image as a constraint, which generally results in higher performance compared to interpolation-based methods. However, the reconstruction process primarily utilizes internal image information, which can lead to a lack of high-frequency details in the reconstructed image.
4.3. Learning-Based Image Super-Resolution Algorithm
Learning-based image super-resolution methods involve using machine learning techniques on a database of low-resolution and high-resolution image pairs to model the mapping relationship between these images. These methods can be categorized into four main approaches: example based, neighborhood embedding based, sparse representation based, and deep learning based. The first three categories are considered shallow learning algorithms, while deep learning-based approaches represent a more advanced, complex form of learning.
4.3.1. Shallow Learning-Based Image Super-Resolution Algorithm
Shallow learning-based image super-resolution algorithms utilize relatively simple neural network structures to achieve high-quality reconstruction of low-resolution images. These algorithms generally recover details by learning image features through convolution and pooling layers, and then map these features to a high-resolution image using upsampling or inverse convolution operations. The primary shallow learning-based image super-resolution methods include example-based learning, neighborhood embedding, and sparse representation-based techniques.
- (1)
- Example-based learning method
The example-based learning method as developed by Freeman and others relies on a single-image reconstruction algorithm using Markov networks [,]. This approach involves applying degradation operations to original high-resolution images to create a training image feature library. It then learns prior information from these HR images to recover high-frequency details and features. The process is as follows.
For each input low-resolution block y, the algorithm selects the 16 most similar high-resolution blocks as distinct states of the hidden node x. The distribution is modeled as a conditional probability distribution, which is formulated as follows:
where the compatibility functions and represent the relationships between the adjacent nodes’ high-resolution blocks and between the same node’s high-resolution and low-resolution blocks, respectively, with Z being a normalization constant. To define compatibility functions, nodes in the sampled image ensure that high-resolution blocks overlap with each other. Let i and j be two neighboring blocks, be the 1st candidate block for block i, and be the mth candidate block for block j. If (the 1st candidate block for node i) and have consistent pixels in their overlapping regions, they are considered mutually compatible. Let be the corresponding low-resolution block for . The compatibility matrix is defined as
where and represent noise parameters. The optimal high-resolution block is the block that maximizes the probability in the Markov network. Belief Propagation is introduced to iteratively calculate the probability distribution, and an approximate solution can be obtained in 3 to 4 iterations.
Algorithms based on example learning can effectively utilize sample libraries to increase the high-frequency information of an image. However, the amount of searching needed in sample libraries is huge and computationally expensive. If there is a mismatch, it can reconstruct details that do not match the overall characteristics of the image.
- (2)
- Neighborhood-based embedding method
The neighborhood embedding method involves solving the k-nearest-neighbor representation coefficients of input low-resolution image blocks within the low-resolution image block sample set []. Finally, these coefficients are used to linearly combine the neighbors in the high-resolution image block sample set to obtain the corresponding output high-resolution image block.
In 2004, Chang et al. [] utilized the same local structural linear properties of LR and HR images to obtain the weights of neighboring points for the final reconstructed image, substantially avoiding the overfitting problem in the modeling process. Chang et al. assumed that the low-resolution image chunks have similar local geometrical properties to the corresponding high-resolution image chunks for the near-neighbor embedding-based super-resolution reconstruction of the image. The low-resolution test image y is divided into overlapping image blocks of size , and features are extracted to form a feature vector , , where Q is the total number of chunks of the LR test image. For each of them, the following operation is performed.
Step 1: In the low-resolution feature vector , of the training set, find the K low-resolution nearest neighbors of based on the Euclidean distance , where denotes the set of K nearest neighbors.
Step 2: According to the LLE (Locally Linear Embedding) algorithm [], a method used for dimensionality reduction, data are mapped to a lower-dimensional space while preserving the local relationships between the data points. It computes the reconstruction weights such that the reconstruction error is minimized and required to satisfy the constraints , and for any , . In Formula (21), the double vertical bars denote the norm, used to measure the size or length of a vector or matrix:
Step 3: Keeping the weights unchanged, reconstruct the high-resolution block using the K nearest-neighbor high-resolution training blocks corresponding to :
For the , superimposed low-frequency portion, which is then merged into the target high-resolution image x, local consistency and smoothing constraints are imposed on the neighboring blocks by taking the mean value at the overlapping pixels again.
Neighborhood embedding methods reduce the dependence of reconstructed images on the sample set. However, the number of nearest neighbors is fixed and lacks flexibility, which is prone to over-learning or under-learning phenomena, leading to blurred reconstruction results.
- (3)
- Sparse representation-based methods
The sparse representation method focuses on dictionary learning and sparse coding as the core to realize a practical improvement in the image reconstruction efficiency and reconstruction quality []. The sparse coding is used to represent the image blocks. Then, the HR image block and LR image block are captured from the sample image to form an ultra-complete dictionary. The sparse linear representation of the sample image is obtained according to the dictionary, and finally, the HR image is reconstructed according to the sparse coefficients.
Yang et al. [] proposed image super-resolution reconstruction based on sparse representations, where low-resolution image blocks are considered to have sparse representations for an overcomplete dictionary composed of prototype signal atoms. The authors used sparsity as a priori information to regularize the super-resolution reconstruction problem by randomly selecting 100,000 pairs of original image blocks from training images with similar statistical properties to be used as dictionaries and . consists of high-resolution blocks, and consists of low-resolution blocks. The problem is described as finding the sparsest representation of a low-resolution block under dictionary . The problem is summarized as follows:
where represents the sparse representation of the low-resolution image block , represents the norm, which is the number of nonzero elements in , s.t. is the abbreviation for subject to, which means constrained by or satisfying the following conditions, F is the feature extraction operator, and is the allowable error. Donoho [] pointed out that when is sparse enough, it can be equivalently minimized using the norm:
Introducing the Lagrange factor, the problem is described as
The parameter balances the sparsity of the solution and the approximation to . This is a linear regression problem involving the norm. Once the optimal coefficients are determined, the HR block is computed.
Traditional sparse representation methods reconstruct image structures by independently considering the sparsity of image blocks. This approach can lead to a loss in fine texture details and spatial structural features. To address this issue, Timofte et al. [] combined neighborhood embedding with sparse coding, reducing computational complexity while constraining the relationship between image blocks and their neighborhood information. Li et al. [] introduced a self-learning super-resolution algorithm that merges nonlocal self-similarity with sparse coding, effectively reducing the model training time and enhancing robustness. Zeng et al. [] proposed using principal component analysis and hierarchical clustering to train a dictionary model, which differs from traditional sparse representation methods, aiming to improve the quality of reconstructed images.
The super-resolution reconstruction algorithm based on sparse representation avoids the artificial selection of the number of nearest neighbors, resulting in better reconstruction effects. However, challenges remain in terms of algorithm efficiency and the rapid acquisition of more compliant dictionaries from a large set of training images.
In conclusion, shallow learning-based image super-resolution algorithms offer advantages in computational efficiency and simplicity, making them suitable for specific scenarios. However, they may require improvements for tasks involving complex texture and detail reconstruction, for which deep learning methods are often more effective.
4.3.2. Deep Learning-Based Image Super-Resolution Algorithm
Deep learning-based image super-resolution algorithms employ deep neural network architectures to achieve high-quality image reconstruction. These algorithms excel in processing complex textures, preserving details, and generating high-resolution images by leveraging the representation learning capabilities of deep learning. They provide advanced solutions for image super-resolution reconstruction.
In 2014, Dong et al. [] made a groundbreaking contribution to the field by introducing deep learning techniques for image super-resolution. They developed the first Convolutional Neural Network-based super-resolution model, called SRCNN (Super-Resolution Convolutional Neural Network). While SRCNN improved the speed and reconstruction quality compared to traditional methods, it faced challenges such as computational complexity and slow training convergence due to its pre-upsampling model architecture. Additionally, the relatively simple SRCNN structure struggled to fully utilize contextual information in images.
- (1)
- Inverse Convolution Layer
To address the high computational cost and complex real-time application issues of SRCNN, Dong et al. [] proposed an improved and accelerated model in 2016 called FSRCNN (Fast SRCNN). FSRCNN includes a feature extraction layer, a contraction layer, a nonlinear mapping layer, an expansion layer, and an inverse convolution layer. The main improvement in FSRCNN is the replacement of the SRCNN pre-upsampling model framework with a post-upsampling framework. Up-sampling is performed by the deconvolutional layer at the end of the network, which helps to reduce the computational complexity. Additionally, FSRCNN enhances the computational efficiency by modifying feature dimensions and sharing parameters in the mapping layer, which also contributes to the improved quality of the reconstructed image.
- (2)
- Subpixel layer
To reduce computational complexity and enhance efficiency, Shi et al. [] introduced a fast and effective super-resolution network model called ESPCN (Efficient Sub-Pixel CNN) in 2016. Like FSRCNN, ESPCN employs a post-upsampling framework. However, it utilizes a sub-pixel convolutional layer for up-sampling the image. The ESPCN network consists of a hidden layer with two convolutional layers and a sub-pixel convolutional layer. Initially, it extracts features from the low-resolution input image using the hidden layers. Subsequently, it reconstructs the high-resolution image through the sub-pixel convolutional layer. This approach facilitates fast and efficient end-to-end learning, yielding better reconstruction results compared to the FSRCNN model.
- (3)
- Residual network
In 2016, He et al. [] introduced the concept of a residual network (ResNet) to address the degradation problem in deep Convolutional Neural Networks caused by excessively deep architectures. They developed a ResNet structure by stacking multiple residual blocks as illustrated in Figure 13. Residual networks utilize skip connections between residual blocks to enhance the transfer of image feature information across layers and alleviate the vanishing gradient issue in deep networks. However, since feature information extracted by each residual block must pass through these skip connections to reach the subsequent modules, it can become increasingly complex as it propagates deeper into the network. This complexity might result in the loss of simpler features from earlier layers.
Figure 13.
Structure of the residual network.
To address the challenges associated with residual networks, researchers have proposed various novel architectures based on the original ResNet framework. In 2016, Kim et al. [] applied ResNet (Figure 14a) to image super-resolution, introducing the Very Deep Super-Resolution (VDSR) network model. Recognizing the similarity in low-frequency information between low-resolution and high-resolution images, VDSR used residual learning to focus on high-frequency details. This approach significantly reduced training time and improved training speed.
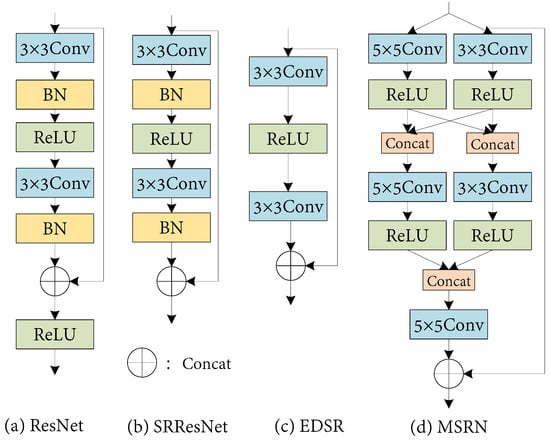
Figure 14.
Four improved residual networks.
In 2017, Lim et al. [] built upon the SRResNet structure [] (Figure 14b) to develop the Enhanced Deep Super-Resolution (EDSR) network. They made a notable improvement by removing the batch normalization (BN) layers from the SRResNet architecture (Figure 14c), which had previously compromised the image quality. The removal of BN layers not only enhanced image quality but also reduced memory usage by approximately 40%, allowing for deeper networks with similar computational resources. Lim et al. also addressed the training instability using residual scaling, leading to significant improvements in image quality.
In 2018, Li et al. [] introduced the Multi-Scale Residual Network (MSRN) to address limitations in utilizing low-resolution image features and handling multi-scale tasks with a single model. The MSRN incorporated Multi-Scale Residual Blocks (Figure 14d), which combined ResNet with convolutional kernels of varying scales to capture diverse image features. This design allowed MSRN to fuse local multi-scale features with global features, enhancing the performance and quality of the reconstructed image.
In 2021, Lan et al. [] observed that many CNN-based models did not fully exploit low-level features, leading to suboptimal performance. To address this, they introduced two new models: the Cascading Residual Network (CRN) and the Enhanced Residual Network (ERN). The CRN featured a cascading mechanism with multiple locally shared groups to improve feature fusion and gradient propagation, enhancing feature extraction efficiency. The ERN employed a dual global pathway structure to capture long-distance spatial features from the input, resulting in a more robust feature representation. Both CRN and ERN achieved comparable or superior performance to EDSR while using fewer parameters.
ResNet excels in extracting feature information from low-resolution input images in super-resolution networks through both local and global residual learning. It effectively addresses various training and gradient issues associated with very deep networks. Consequently, many super-resolution network models have adopted the concept of residual learning to enhance network performance. Additionally, subsequent super-resolution models have integrated residual learning with other network design strategies to achieve improved super-resolution reconstruction results.
- (4)
- Attention mechanisms
As network structures deepen, residual networks may struggle to capture correlations between the image space, structure, and texture. This often results in training focusing on low-value image regions, which can degrade the quality of reconstructed images.
To address these challenges, several advancements have been made. In 2018, Hu et al. [] introduced the Squeeze-and-Excitation Network, which incorporates “squeeze-and-excitation” blocks to model interdependencies between channels, enhancing feature learning capabilities. Zhang et al. [] integrated channel attention mechanisms (Figure 15) with residual networks to create deeper networks that reduce interference from low-frequency information in LR images. They proposed the ResNet in ResNet residual structure to bypass low-frequency information, adaptively scaling features in each channel to improve the processing efficiency and model robustness. Woo et al. [] developed the Convolutional Block Attention Module by combining channel and spatial attention modules, which strengthened the network’s ability to focus on crucial image regions.
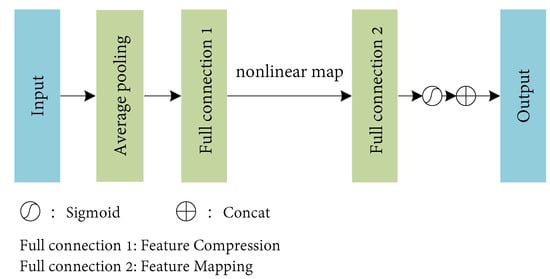
Figure 15.
Channel attention mechanism.
In 2019, Dai et al. [] introduced the Second-Order Attention Network, incorporating second-order channel attention mechanisms to capture feature correlations through covariance normalization. This approach improved feature-related learning and expression capabilities. Xu et al. [] proposed a binocular image reconstruction algorithm guided by a dual-layer attention mechanism and disparity attention mechanism, tailored to enhance image quality under varying conditions. This method preserved fine details in underwater images despite external factors. Lu et al. [] further advanced high-frequency image reconstruction by incorporating hybrid attention mechanisms and long–short skip connections, which improved the edge information and texture structure.
Compared to other CNN-based network models, those utilizing attention mechanisms differentiate between essential and less important regions in the image. By assigning higher weights to critical regions, these models enhance feature extraction and obtain more effective image information.
- (5)
- Recurrent Neural Networks
Recurrent neural networks (RNNs) can achieve infinite memory depth through successive network updates []. In super-resolution, RNNs apply the same module multiple times in a recursive manner, leveraging parameter sharing within the internal module. This allows the network to learn higher-level features without introducing excessive parameters, thereby enhancing network performance.
Kim et al. [] introduced the DRCN (Deeply Recursive Convolutional Network) algorithm, which utilizes RNNs for super-resolution image reconstruction. By repeatedly applying convolution and recursion, DRCN continuously learns the differences between low-resolution and high-resolution images. This approach enables image information to circulate and recurse within the network, aiming to recover high-frequency image details and address the challenge of increasing parameter counts. Han et al. [] proposed the DSRN (Dual-State Recurrent Network), viewing many deep super-resolution network structures as finite expansions of single-state RNNs with various recursive functions. The RNN structure in DSRN operates at different spatial resolutions, employing two recurrent states for LR and HR spaces. Through a delayed feedback mechanism, it exchanges cyclic signals between these spaces, effectively utilizing features from both domains to produce the final reconstructed image.
In 2019, Li et al. [] introduced the SRFBN (Super-Resolution Feedback Network), an image super-resolution feedback network. SRFBN refines high-level information into low-level representations and progressively generates the final HR image, achieving improved performance with fewer parameters. As depicted in Figure 16, SRFBN employs a feedback mechanism with hidden states in a constrained RNN. It also incorporates a curriculum learning strategy, where target HR images of increasing reconstruction difficulty are sequentially fed into the network for continuous iteration. This strategy allows the network to gradually learn complex degradation models and adapt more effectively to challenging tasks.
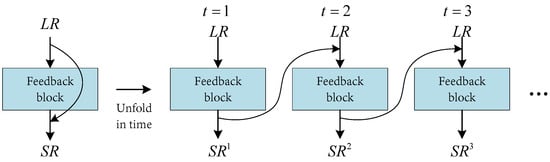
Figure 16.
SRFBN feedback mechanism.
The characteristic of parameter sharing in RNNs enables them to learn higher-level features without introducing excessive parameters. However, RNNs still face gradient and training issues common to deep networks. To address these challenges, RNNs are often integrated with advanced network designs and learning strategies, such as ResNet, multi-supervised learning, and curriculum learning. These combinations help alleviate gradient and training problems, leading to improved network performance.
- (6)
- Generating Adversarial Networks
Super-resolution image reconstruction algorithms based on Generative Adversarial Networks (GANs) have demonstrated excellent performance in terms of image reconstruction quality, network complexity, and computational speed. Adversarial methods in AI have the advantage of generating high-quality and realistic images, making them particularly effective in super-resolution image reconstruction. In 2014, Goodfellow et al. [] introduced the concept of Generative Adversarial Networks (Figure 17), depicted in the structure below. Figure 17 depicts a Generative Adversarial Network with two main components: the generator and the discriminator. The generator converts low-resolution input into high-resolution output, while the discriminator evaluates whether these outputs are real or fake. If the discriminator deems the data real, the generator is successful; otherwise, the generator needs improvement. This adversarial process continuously loops, allowing the generator to progressively produce more realistic data. In 2017, Ledig et al. introduced the SRGAN (Super-Resolution Generative Adversarial Network) algorithm, which was pioneering in applying adversarial training to super-resolution image reconstruction. SRGAN employs a generator network to produce high-resolution images and a discriminator network to distinguish between these reconstructed HR images and the original HR images. The generator and discriminator are trained in an adversarial manner, which enhances the reconstruction of fine image details. Unlike traditional methods that use Mean Square Error loss, SRGAN utilizes a perceptual loss function. This approach improves the recovery of image details, resulting in high-fidelity and high-quality reconstructed images.
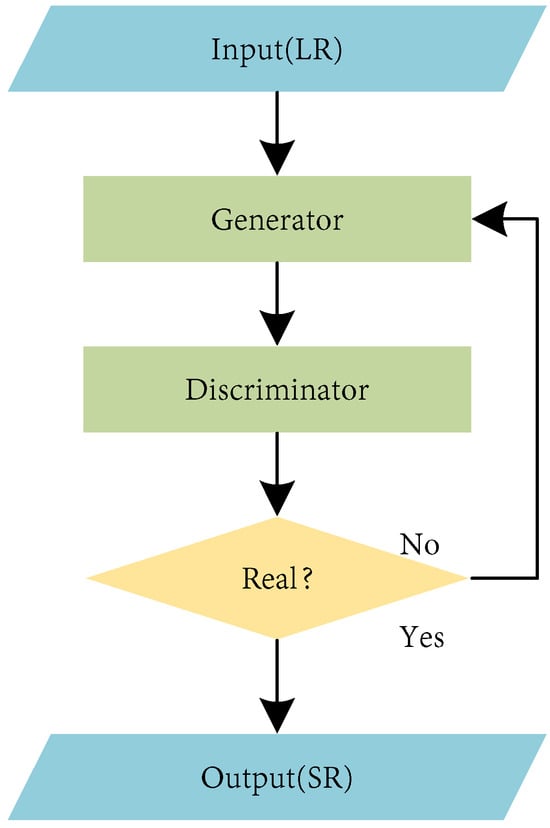
Figure 17.
Generative Adversarial Networks.
Although the SRGAN algorithm preserves more image detail features, the use of BN layers in the network introduces a large number of parameters, consuming a significant amount of runtime memory and potentially degrading network performance. In response to this issue, Lim et al. [] proposed the EDSR algorithm by removing the BN layers. They found that this modification did not negatively impact network training, reduced the number of network parameters, and improved the preservation of image texture information. Wang et al. [] introduced the Enhanced Super-Resolution Generative Adversarial Network (ESRGAN) algorithm to enhance network generalization. They employed residual scaling to accelerate deep network training and reduce computational parameters. This resulted in reconstructed HR images with richer texture features and colors that closely resembled the original HR images. Shang et al. [] improved the ESRGAN algorithm by using small kernel convolutions instead of large filters for detail feature extraction. This change maintained network performance while reducing computational complexity and handling noisy input more effectively.
Overall, researchers have tried to apply super-resolution techniques in scenarios with limited computational and storage resources by designing lightweight network models and applying search methods. Although some methods have achieved performance improvements, there is still a need to balance model performance and computational complexity.
4.4. Potential of Super-Resolution Reconstruction in Satellite CO2
After discussing various super-resolution reconstruction methods, we will specifically explore their potential applications to carbon dioxide datasets, highlighting the unique challenges and opportunities these methods present in the field of climate monitoring. Super-resolution reconstruction not only improves the spatial resolution of satellite meteorological images but also enables meteorologists and climate scientists to observe and predict weather patterns, climate change, and precipitation distribution. It provides more reliable data for meteorological disaster monitoring and climate modeling. Therefore, it is possible to improve the spatial resolution of the data using image super-resolution reconstruction.
However, the application of super-resolution reconstruction methods to satellite CO2 reconstruction is limited primarily due to the complexity and sparsity of the data, challenges of applying these algorithms to atmospheric science data, high-precision requirements, computational costs, and the difficulty of cross-disciplinary applications. Super-resolution techniques are mainly used in image processing, while satellite CO2 reconstruction involves complex physical and chemical processes. Applying the super-resolution reconstruction method to satellite CO2 data is a work with great potential, and the super-resolution reconstruction method can construct a long series satellite CO2 dataset with high precision and high resolution, which can provide vital data support for the better application of satellite CO2 data to the study of the small-scale carbon source-sink pattern. At the same time, we can combine super-resolution reconstruction techniques with multi-source heterogeneous data fusion techniques to provide more comprehensive, accurate, and reliable CO2 concentration information.
In 2022, Ru Xiang and colleagues [] proposed a method using bicubic interpolation to perform the super-resolution reconstruction of CO2 data from the GOSAT satellite to enhance the spatial resolution and accuracy of the data. As shown in Figure 18, to objectively and quantitatively evaluate the quality of the reconstructed results, high-precision in situ measurement data are required. However, due to the limited and sparse distribution of TCCON stations, it is not possible to provide CO2 measurements globally, especially in regions such as oceans, deserts, polar areas, and other sparsely populated areas. Therefore, additional high-precision OCO-2 satellite observation data are needed to assess the quality of the reconstructed GOSAT data. Recognizing the spatial continuity of CO2 data, Ru Xiang and colleagues performed preprocessing on the GOSAT data by filling the missing pixel values with the average values of their surrounding 8 pixels. They then used bicubic interpolation to reconstruct the GOSAT data. To better evaluate the reconstructed data at a global scale, OCO-2 data were processed into data of different resolutions using Kriging interpolation. The specific workflow was as follows.
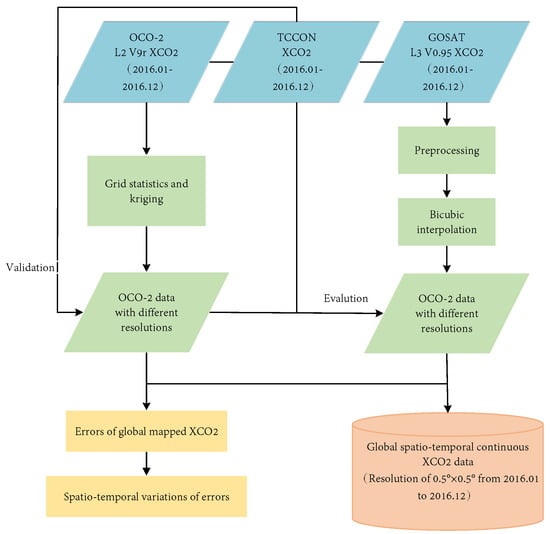
Figure 18.
Research process of reconstruction of GOSAT XCO2 observations using bicubic interpolation [].
- (1)
- Data preprocessing
Ru Xiang et al. employed a neighborhood mean method to fill in the missing data in the GOSAT L3 product. As shown in Figure 19, they used a combination of gridded statistics and Kriging to generate OCO-2 monthly-scale data at various spatial resolutions. Addressing the temporal scale issue of TCCON data, they obtained TCCON monthly-scale data for different sites by averaging the daily data.
Figure 19.
Data preprocessing process [].
- (2)
- Super-resolution reconstruction with double cubic interpolation
Bicubic interpolation is a commonly used super-resolution method, producing better interpolation results compared to bilinear interpolation or nearest-neighbor interpolation. The value of a pixel point can be obtained by taking the weighted average of the sixteen nearest sampled pixels within a rectangular grid. This method requires the use of two cubic polynomial interpolation functions, one for each direction. The value of the pixel after super-resolution reconstruction is calculated using the following formula:
where is the XCO2 value of pixel P after reconstruction, are the coordinates of pixel P, and is the value of the nearest pixel of pixel P at the corresponding position in the original data. There are 16 pixels in total, and i and j are the indexes of these 16 pixels, representing the weight of the 16 pixels, respectively, which can be computed by the following formula:
where denotes the weight of each pixel, and x denotes the distance of each pixel to the corresponding position of pixel P in the original data. The double triple convolutional interpolation kernel is typically configured with the parameter a set to −0.5, as this value provides the best fit for the intended applications.
- (3)
- Verification of the accuracy of GOSAT reconstruction results based on TCCON, OCO-2.
In the evaluation, the MAE, MSE, and Average Relative Error (AVER) are used to describe the accuracy of data. The following formulas define them:
where denotes the TCCON-measured XCO2 value, and is the satellite-observed XCO2 value at the corresponding TCCON site location.
The OCO-2 observations were preprocessed and then processed into XCO2 data at different resolutions. The original and reconstructed GOSATs were evaluated using this method. ME, MAE and RMSE were used to characterize the differences between the original reconstructed GOSAT and OCO-2 with the following equations:
where denotes the XCO2 value of the preprocessed OCO-2 data, and is either the original GOSAT data or the reconstructed GOSAT data.
The reconstructed GOSAT data improved the resolution from 2.5° to 0.5°. The mean error in the reconstructed data for January 2016 was 1.335 ppmv, with no loss in precision compared to the original data. The errors in the original data caused errors in the reconstructed data, and the average error had significant temporal variation.
The reconstruction of the GOSAT XCO2 data by the double cubic interpolation method can improve the data resolution, but more is needed to improve the data accuracy effectively. Due to the problem of the method itself, the accuracy of the reconstructed data largely depends on the accuracy of the original data. The information contained in the reconstructed results is also affected by the original data, which cannot produce additional CO2 source or sink information, and there are some edge areas with missing data after reconstruction. Ru Xiang et al. used the SRCNN network model to reconstruct the GOSAT XCO2 data to improve the resolution and accuracy of the data.
The network structure of the model has three main layers, including three main processes of resolution reconstruction: data feature extraction, nonlinear mapping, and the final data reconstruction process. Unlike the SRCNN structure in the image domain, Ru Xiang et al. used the low-resolution and low-precision GOSAT XCO2 data as the input to the model. After undergoing the main processes of the model, the output is CO2 data with the resolution and precision of OCO-2, involving both resolution and precision reconstruction. The rest of the model structure is consistent with the standard SRCNN network model.
Therefore, the process of reconstructing GOSAT XCO2 data based on the SRCNN model mainly includes feature extraction of the original GOSAT XCO2 data, mapping the low-resolution and low-precision GOSAT features into high-resolution and high-precision OCO-2 features, and reconstructing the data based on these features.
The model’s network structure does not involve an up-scaling or down-scaling process for the data. The input to the model is the low-resolution GOSAT XCO2 data, which are upsampled using bicubic interpolation to match the output resolution. Thus, the SRCNN model focuses solely on improving the accuracy of the satellite CO2 data, requiring GOSAT and OCO-2 XCO2 data with the same resolution. To address the size of training samples, Ru Xiang and his team used bicubic-interpolated GOSAT XCO2 data (0.5°) and preprocessed OCO-2 XCO2 data (0.5°) to obtain a larger training dataset. Through experimental comparisons, they selected the ReLU activation function for the first two layers of the SRCNN model due to its good convergence speed and fitting performance, and the Adam optimization algorithm as the model’s optimization method.
The results indicate that, compared to the original data, the data reconstructed by the SRCNN model better preserve the distribution characteristics of the original data, although the overall spatial continuity is not very high. When compared to OCO-2 data, the results reconstructed by the SRCNN model exhibit higher data accuracy, with an improvement of approximately 0.5 ppmv over the original data. The data with improved accuracy are primarily distributed in the Southern Hemisphere.
With the continuous advancement of deep learning technology [,,], the importance of satellite carbon dioxide reconstruction is becoming increasingly evident. In the future, it will be possible to obtain high-resolution, gap-free, long-term XCO2 data, which holds profound significance for the study and resolution of global environmental issues.
5. Summary and Outlook
Satellite CO2 data reconstruction work has a wide range of applications in today’s society and has received significant attention from researchers in related fields. In order to help beginners understand the satellite CO2 reconstruction methods and follow up on the research hotspots, this paper summarizes the related research on satellite CO2 data reconstruction, which aims to provide global CO2 concentration data by filling the gaps in the satellite observations or increasing the accuracy and coverage of the observations. In this article, the authors first introduce the necessity of satellite CO2 data reconstruction, as well as the monitoring methods and data sources for carbon dioxide. Secondly, the article discusses the specific applications of interpolation and data fusion methods in the reconstruction of CO2 data. Finally, the authors delve into the topic of super-resolution reconstruction technology and its specific applications in the field of satellite CO2 data reconstruction.
In recent years, researchers have made significant achievements in CO2 data reconstruction. Interpolation and data fusion methods have become the mainstream methods of carbon satellite data reconstruction, and super-resolution reconstruction technology has gradually developed in the field of data reconstruction. However, there are still many challenges and directions to pursue in further research.
(1) Although interpolation can, to some extent, solve the problem of partially missing data and ensure the spatial continuity of the data, part of the interpolation method overly relies on the number and quality of sample points and ignores the geographic characteristics of the data. Therefore, combining the interpolation and deep learning methods is a future research hotspot. The fusion of multi-modal data, modeling uncertainty, and adaptive interpolation methods will receive more attention to enhance the accuracy of interpolation results.
(2) The reconstructed results of the data fusion method have an extended time coverage. However, the method needs to focus more on improving the data resolution, and the reconstructed data often loses accuracy. Based on this, researchers can consider using migration learning to optimize and enhance the model in the sparse data region. Furthermore, multi-source heterogeneous data fusion can comprehensively integrate different types and characteristics of data sources, providing more comprehensive, accurate, and reliable CO2 concentration information, which is also a future trend in this field.
(3) The low resolution of satellite CO2 data makes them difficult to be directly applied to the study of small-scale carbon sources and sinks. Therefore, the idea of image super-resolution reconstruction is also one of the future trends.
6. Declaration of Generative AI and AI-Assisted Technologies in the Writing Process
During the preparation of this work the authors used ChatGPT in order to improve language and readability. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of this publication.
Author Contributions
Conceptualization, K.H. and M.X.; Methodology, K.H., Z.L., P.S., K.M. and Y.X.; Formal analysis, Z.L., S.W., Y.W., H.W. and L.D.; Investigation, Z.L., P.S., K.M., S.W., Y.W., H.W. and L.D.; Writing—original draft preparation, Z.L. and K.M.; Writing—review, K.H., Z.L. and Y.Z.; Writing—editing, Z.L., P.S., K.M. and Y.X.; Visualization, Z.L., P.S. and K.M.; Supervision, K.H. and M.X.; Project administration, K.H. and M.X.; Collect material, Y.X., S.W., Y.W., H.W., L.D. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
Research in this article is supported by the National Natural Science Foundation of China (42275156).
Data Availability Statement
The datasets used in the paper are publicly available and do not require any authorization or permission. The TCCON dataset is available at https://tccondata.org/, accessed on 25 July 2024. The WDCGG dataset is available at https://gaw.kishou.go.jp/, accessed on 25 July 2024. The GLOBALVIEW-CO2 dataset is available at https://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=1111, accessed on 25 July 2024. The SCIAMACHY WFMD dataset is available at https://www.iup.uni-bremen.de/sciamachy/, accessed on 25 July 2024. The SCIAMACHY BESD dataset is available at https://www.iup.uni-bremen.de/deu/, accessed on 25 July 2024. The GOSAT ACOS dataset is available from https://search.earthdata.nasa.gov/, accessed on 25 July 2024. The GOSAT SRFP dataset is available at https://catalogue.ceda.ac.uk/, accessed on 25 July 2024. The GOSAT NIES dataset is available at https://data2.gosat.nies.go.jp/, accessed on 25 July 2024. The GOSAT OCFP dataset is available from https://catalogue.ceda.ac.uk/, accessed on 25 July 2024. The GOSAT-2 FP dataset is available at https://prdct.gosat-2.nies.go.jp/, accessed on 25 July 2024. The TanSat OCFP dataset is available from https://catalogue.ceda.ac.uk/, accessed on 25 July 2024. The TanSat ACGS dataset is available at http://www.cgga.org.cn/, accessed on 25 July 2024. The OCO-2 ACOS dataset is available at https://search.earthdata.nasa.gov/, accessed on 25 July 2024. The OCO-2 FOCAL dataset is available at https://catalogue.ceda.ac.uk/, accessed on 25 July 2024. The OCO-3 ACOS dataset is available at https://search.earthdata.nasa.gov, accessed on 25 July 2024. The PKU dataset is available at https://opendata.pku.edu.cn/dataverse.xhtml, accessed on 25 July 2024. The ODIAC dataset is available at https://db.cger.nies.go.jp/dataset/ODIAC/, accessed on 25 July 2024. The EDGAR dataset is available at https://meta.icos-cp.eu/collections/unv31HYRKgullLjJ99O5YCsG, accessed on 25 July 2024.
Conflicts of Interest
Authors Shiqian Wang, Yuanyuan Wang, Han Wang and Li Di were employed by the State Grid Henam Electric Power Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACGS | Aerosol and cloud gas sensor |
| ACOS | Atmospheric CO2 observations from space |
| AIRS | Atmospheric infrared sounder |
| BESD | Building energy and sustainable design |
| BN | Batch normalization |
| CAPI | Cloud and aerosol polarization imager |
| CHRED | China High Resolution Emission Database |
| COCCON | Collaborative carbon column observing network |
| CRN | Cascading Residual Network |
| CTM | Chemical transport model |
| DOAS | Differential optical absorption spectroscopy |
| DRCN | Deep recursive convolutional network |
| DSRN | Deep super-resolution network |
| EDGAR | Emissions database for global atmospheric research |
| EDSR | Enhanced deep super-resolution |
| EMMA | Ensemble median algorithm |
| ENVISAT | Environmental satellite |
| ERN | Enhanced Residual Network |
| ERT | Extreme random tree |
| ESA | European space agency |
| ESPCN | Efficient sub-pixel convolutional network |
| ESRL | Earth system research laboratory |
| FTS | Fourier transform spectrometers |
| GOSAT | Greenhouse gases observing satellite |
| GWNN | Geographically weighted neural network |
| GWR | Geographically weighted regression |
| HR | High-resolution |
| HSAM-DF | High-precision surface albedo model data fusion |
| IAGOS | In-service aircraft for a global observing system |
| IAPCAS | Institute of atmospheric physics carbon retrieval algorithm system |
| LightGBM | Light gradient boosting machine |
| LLE | Locally linear embedding |
| LR | Low-resolution |
| MAE | Mean Absolute Error |
| MAP | Maximum a posteriori |
| MSRN | Multi-scale residual network |
| MLP | Multi-layer perceptron |
| NASA | National aeronautics and space administration |
| NOAA | National oceanic and atmospheric administration |
| OCC | Optical camera communication |
| OCCK | Ordinary co-located co-Kriging |
| OCK | Ordinary co-Kriging |
| OCO | Orbiting carbon observatory |
| ODIAC | Open-data inventory for anthropogenic carbon dioxide |
| PCK | Principal component Kriging |
| PKU | Peking university |
| POCS | Projection onto convex sets |
| ppb | Parts per billion |
| ppmv | Parts per million by volume |
| ResNet | Residual network |
| RMSE | Root Mean Square Error |
| RNNs | Recurrent neural networks |
| SCCK | Simple co-located co-Kriging |
| SCIAMACHY | Scanning imaging atmospheric absorption spectrometer |
| SCK | Simple co-Kriging |
| SK | Simple Kriging |
| SRCNN | Super-Resolution Convolutional Neural Network |
| SRGAN | Super-Resolution Generative Adversarial Network |
| TANSO | Thermal and near-infrared sensor for carbon observation |
| UK | Universal Kriging |
| WDCGG | World Data Centre for Greenhouse Gases |
| TCCON | Total carbon column observing network |
| VDSR | Very deep super-resolution |
| Column-averaged CO2 dry air mole fraction |
References
- Meehl, G.A.; Washington, W.M. El Niño-like climate change in a model with increased atmospheric CO2 concentrations. Nature 1996, 382, 56–60. [Google Scholar] [CrossRef]
- West, T.O.; Marland, G. A synthesis of carbon sequestration, carbon emissions, and net carbon flux in agriculture: Comparing tillage practices in the United States. Agric. Ecosyst. Environ. 2002, 91, 217–232. [Google Scholar] [CrossRef]
- Buchwitz, M.D.; De Beek, R.; Noël, S.; Burrows, J.; Bovensmann, H.; Schneising, O.; Khlystova, I.; Bruns, M.; Bremer, H.; Bergamaschi, P.; et al. Atmospheric carbon gases retrieved from SCIAMACHY by WFM-DOAS: Version 0.5 CO and CH4 and impact of calibration improvements on CO2 retrieval. Atmos. Chem. Phys. 2006, 6, 2727–2751. [Google Scholar] [CrossRef]
- Bonan, G.B.; Doney, S.C. Climate, ecosystems, and planetary futures: The challenge to predict life in Earth system models. Science 2018, 359, eaam8328. [Google Scholar] [CrossRef]
- Soh, W.K.; Yiotis, C.; Murray, M.; Parnell, A.; Wright, I.J.; Spicer, R.A.; Lawson, T.; Caballero, R.; McElwain, J.C. Rising CO2 drives divergence in water use efficiency of evergreen and deciduous plants. Sci. Adv. 2019, 5, eaax7906. [Google Scholar] [CrossRef]
- Wigley, T.; Jones, P.; Kelly, P. Scenario for a warm, high-CO2 world. Nature 1980, 283, 17–21. [Google Scholar] [CrossRef]
- DeVries, T. Atmospheric CO2 and sea surface temperature variability cannot explain recent decadal variability of the ocean CO2 sink. Geophys. Res. Lett. 2022, 49, e2021GL096018. [Google Scholar] [CrossRef]
- Kikstra, J.S.; Nicholls, Z.R.; Smith, C.J.; Lewis, J.; Lamboll, R.D.; Byers, E.; Sandstad, M.; Meinshausen, M.; Gidden, M.J.; Rogelj, J.; et al. The IPCC Sixth Assessment Report WGIII climate assessment of mitigation pathways: From emissions to global temperatures. Geosci. Model Dev. 2022, 15, 9075–9109. [Google Scholar] [CrossRef]
- Ramanathan, V.; Feng, Y. On avoiding dangerous anthropogenic interference with the climate system: Formidable challenges ahead. Proc. Natl. Acad. Sci. USA 2008, 105, 14245–14250. [Google Scholar] [CrossRef]
- Fujimori, S.; Wu, W.; Doelman, J.; Frank, S.; Hristov, J.; Kyle, P.; Sands, R.; Van Zeist, W.J.; Havlik, P.; Domínguez, I.P.; et al. Land-based climate change mitigation measures can affect agricultural markets and food security. Nat. Food 2022, 3, 110–121. [Google Scholar] [CrossRef]
- Jacobson, T.A.; Kler, J.S.; Hernke, M.T.; Braun, R.K.; Meyer, K.C.; Funk, W.E. Direct human health risks of increased atmospheric carbon dioxide. Nat. Sustain. 2019, 2, 691–701. [Google Scholar] [CrossRef]
- Fernández-Martínez, M.; Sardans, J.; Chevallier, F.; Ciais, P.; Obersteiner, M.; Vicca, S.; Canadell, J.; Bastos, A.; Friedlingstein, P.; Sitch, S.; et al. Global trends in carbon sinks and their relationships with CO2 and temperature. Nat. Clim. Chang. 2019, 9, 73–79. [Google Scholar] [CrossRef]
- Yunfeng, Y.; Laike, Y. China’s foreign trade and climate change: A case study of CO2 emissions. Energy Policy 2010, 38, 350–356. [Google Scholar] [CrossRef]
- Fawzy, S.; Osman, A.I.; Doran, J.; Rooney, D.W. Strategies for mitigation of climate change: A review. Environ. Chem. Lett. 2020, 18, 2069–2094. [Google Scholar] [CrossRef]
- Knutti, R.; Rogelj, J.; Sedláček, J.; Fischer, E.M. A scientific critique of the two-degree climate change target. Nat. Geosci. 2016, 9, 13–18. [Google Scholar] [CrossRef]
- Kuyper, J.; Schroeder, H.; Linnér, B.O. The Evolution of the UNFCCC. Annu. Rev. Environ. Resour. 2018, 43, 343–368. [Google Scholar] [CrossRef]
- Andrews, E.; Sheridan, P.J.; Ogren, J.A.; Hageman, D.; Jefferson, A.; Wendell, J.; Alástuey, A.; Alados-Arboledas, L.; Bergin, M.; Ealo, M.; et al. Overview of the NOAA/ESRL federated aerosol network. Bull. Am. Meteorol. Soc. 2019, 100, 123–135. [Google Scholar] [CrossRef]
- Wunch, D.; Wennberg, P.O.; Osterman, G.; Fisher, B.; Naylor, B.; Roehl, C.M.; O’Dell, C.; Mandrake, L.; Viatte, C.; Kiel, M.; et al. Comparisons of the orbiting carbon observatory-2 (OCO-2) XCO2 measurements with TCCON. Atmos. Meas. Tech. 2017, 10, 2209–2238. [Google Scholar] [CrossRef]
- Hu, K.; Feng, X.; Zhang, Q.; Shao, P.; Liu, Z.; Xu, Y.; Wang, S.; Wang, Y.; Wang, H.; Di, L.; et al. Review of Satellite Remote Sensing of Carbon Dioxide Inversion and Assimilation. Remote Sensing 2024, 16, 3394. [Google Scholar] [CrossRef]
- Yang, E.G.; Kort, E.A.; Ott, L.E.; Oda, T.; Lin, J.C. Using Space-Based CO2 and NO2 Observations to Estimate Urban CO2 Emissions. J. Geophys. Res. Atmos. 2023, 128, e2022JD037736. [Google Scholar] [CrossRef]
- Kort, E.A.; Frankenberg, C.; Miller, C.E.; Oda, T. Space-based observations of megacity carbon dioxide. Geophysical Research Letters 2012, 39. [Google Scholar] [CrossRef]
- Hakkarainen, J.; Ialongo, I.; Tamminen, J. Direct space-based observations of anthropogenic CO2 emission areas from OCO-2. Geophys. Res. Lett. 2016, 43, 400–411. [Google Scholar] [CrossRef]
- De Sy, V.; Herold, M.; Achard, F.; Asner, G.P.; Held, A.; Kellndorfer, J.; Verbesselt, J. Synergies of multiple remote sensing data sources for REDD+ monitoring. Curr. Opin. Environ. Sustain. 2012, 4, 696–706. [Google Scholar] [CrossRef]
- Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making REDD a reality. Environ. Res. Lett. 2007, 2, 045023. [Google Scholar] [CrossRef]
- Turner, W.; Spector, S.; Gardiner, N.; Fladeland, M.; Sterling, E.; Steininger, M. Remote sensing for biodiversity science and conservation. Trends Ecol. Evol. 2003, 18, 306–314. [Google Scholar] [CrossRef]
- Peiro, H.; Crowell, S.; Schuh, A.; Baker, D.F.; O’Dell, C.; Jacobson, A.R.; Chevallier, F.; Liu, J.; Eldering, A.; Crisp, D.; et al. Four years of global carbon cycle observed from the Orbiting Carbon Observatory 2 (OCO-2) version 9 and in situ data and comparison to OCO-2 version 7. Atmos. Chem. Phys. 2022, 22, 1097–1130. [Google Scholar] [CrossRef]
- Houweling, S.; Krol, M.; Bergamaschi, P.; Frankenberg, C.; Dlugokencky, E.; Morino, I.; Notholt, J.; Sherlock, V.; Wunch, D.; Beck, V.; et al. A multi-year methane inversion using SCIAMACHY, accounting for systematic errors using TCCON measurements. Atmos. Chem. Phys. 2014, 14, 3991–4012. [Google Scholar] [CrossRef]
- Boesch, H.; Liu, Y.; Palmer, P.I.; Tamminen, J.; Anand, J.S.; Cai, Z.; Che, K.; Chen, H.; Chen, X.; Liang, F.; et al. Monitoring Greenhouses Gases over China Using Space-Based Observations. J. Geod. Geoinf. Sci. 2020, 3, 14. [Google Scholar]
- Crisp, D. Measuring atmospheric carbon dioxide from space with the Orbiting Carbon Observatory-2 (OCO-2). Int. Soc. Opt. Photonics 2015, 9607, 960702. [Google Scholar]
- Schimel, D.; Pavlick, R.; Fisher, J.B.; Asner, G.P.; Saatchi, S.; Townsend, P.; Miller, C.; Frankenberg, C.; Hibbard, K.; Cox, P. Observing terrestrial ecosystems and the carbon cycle from space. Glob. Chang. Biol. 2015, 21, 1762–1776. [Google Scholar] [CrossRef]
- Yue, T.; Zhang, L.; Zhao, M.; Wang, Y.; Wilson, J. Space-and ground-based CO2 measurements: A review. Sci. China Earth Sci. 2016, 59, 2089–2097. [Google Scholar] [CrossRef]
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F.; et al. Remote sensing of the terrestrial carbon cycle: A review of advances over 50 years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Pan, G.; Xu, Y.; Ma, J. The potential of CO2 satellite monitoring for climate governance: A review. J. Environ. Manag. 2021, 277, 111423. [Google Scholar] [CrossRef]
- Kerimov, B.; Chernyshev, R. Review of Machine Learning Methods in the Estimation of Greenhouse Gas Emissions; Ivane Javakhishvili Tbilisi State University: Tbilisi, Georgia, 2022. [Google Scholar]
- Maddy, E.S.; Barnet, C.D.; Goldberg, M.; Sweeney, C.; Liu, X. CO2 retrievals from the Atmospheric Infrared Sounder: Methodology and validation. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Sweeney, C.; Karion, A.; Wolter, S.; Newberger, T.; Guenther, D.; Higgs, J.A.; Andrews, A.E.; Lang, P.M.; Neff, D.; Dlugokencky, E.; et al. Seasonal climatology of CO2 across North America from aircraft measurements in the NOAA/ESRL Global Greenhouse Gas Reference Network. J. Geophys. Res. Atmos. 2015, 120, 5155–5190. [Google Scholar] [CrossRef]
- Vogel, F.R.; Frey, M.; Staufer, J.; Hase, F.; Broquet, G.; Xueref-Remy, I.; Chevallier, F.; Ciais, P.; Sha, M.K.; Chelin, P.; et al. XCO2 in an emission hot-spot region: The COCCON Paris campaign 2015. Atmos. Chem. Phys. 2019, 19, 3271–3285. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.C.; Blavier, J.F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.; Sherlock, V.; Wennberg, P.O. The total carbon column observing network. Philos. Trans. R. Soc. Math. Eng. Sci. 2011, 369, 2087–2112. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.C.; Wennberg, P.O.; Wofsy, S.C.; Stephens, B.B.; Fischer, M.L.; Uchino, O.; Abshire, J.B.; Bernath, P.; Biraud, S.C.; et al. Calibration of the Total Carbon Column Observing Network using aircraft profile data. Atmos. Meas. Tech. 2010, 3, 1351–1362. [Google Scholar] [CrossRef]
- Yang, D.; Boesch, H.; Liu, Y.; Somkuti, P.; Cai, Z.; Chen, X.; Di Noia, A.; Lin, C.; Lu, N.; Lyu, D.; et al. Toward high precision XCO2 retrievals from TanSat observations: Retrieval improvement and validation against TCCON measurements. J. Geophys. Res. Atmos. 2020, 125, e2020JD032794. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, J.; Xi, Z.; Ma, W.; Li, J. Simultaneous detection of atmospheric CO2 and H2O using a DFB diode laser based absorption spectrometer. Spectrochim. Acta Part A Mol. Biomol. 2022, 281, 121628. [Google Scholar] [CrossRef]
- Wehr, R.; Kassi, S.; Romanini, D.; Gianfrani, L. Optical feedback cavity-enhanced absorption spectroscopy for in situ measurements of the ratio 13 C: 12 C in CO2. Appl. Phys. B 2008, 92, 459–465. [Google Scholar] [CrossRef]
- Jiang, F.; Wang, H.; Chen, J.; Machida, T.; Zhou, L.; Ju, W.; Matsueda, H.; Sawa, Y. Carbon balance of China constrained by CONTRAIL aircraft CO2 measurements. Atmos. Chem. Phys. 2014, 14, 10133–10144. [Google Scholar] [CrossRef]
- Bovensmann, H.; Burrows, J.; Buchwitz, M.; Frerick, J.; Noel, S.; Rozanov, V.; Chance, K.; Goede, A. SCIAMACHY: Mission objectives and measurement modes. J. Atmos. Sci. 1999, 56, 127–150. [Google Scholar] [CrossRef]
- Aumann, H.H.; Chahine, M.T.; Gautier, C.; Goldberg, M.D.; Kalnay, E.; McMillin, L.M.; Revercomb, H.; Rosenkranz, P.W.; Smith, W.L.; Staelin, D.H.; et al. AIRS/AMSU/HSB on the Aqua mission: Design, science objectives, data products, and processing systems. IEEE Trans. Geosci. Remote Sens. 2003, 41, 253–264. [Google Scholar] [CrossRef]
- Hamazaki, T.; Kuze, A.; Kondo, K. Sensor system for Greenhouse gas Observing Satellite (GOSAT). Proc. SPIE 2004, 5543. [Google Scholar] [CrossRef]
- Crisp, D.; Atlas, R.M.; Breon, F.M.; Brown, L.; Burrows, J.; Ciais, P.; Connor, B.; Doney, S.; Fung, I.; Jacob, D.; et al. The orbiting carbon observatory (OCO) mission. Adv. Space Res. 2004, 34, 700–709. [Google Scholar] [CrossRef]
- Crisp, D.; Pollock, H.R.; Rosenberg, R.; Chapsky, L.; Lee, R.A.; Oyafuso, F.A.; Frankenberg, C.; O’Dell, C.W.; Bruegge, C.J.; Doran, G.B.; et al. The on-orbit performance of the Orbiting Carbon Observatory-2 (OCO-2) instrument and its radiometrically calibrated products. Atmos. Meas. Tech. 2017, 10, 59–81. [Google Scholar] [CrossRef]
- Eldering, A.; Taylor, T.E.; O’Dell, C.W.; Pavlick, R. The OCO-3 mission: Measurement objectives and expected performance based on 1 year of simulated data. Atmos. Meas. Tech. 2019, 12, 2341–2370. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Yao, L.; Chen, X.; Cai, Z.; Yang, D.; Yin, Z.; Gu, S.; Tian, L.; Lu, N.; et al. The TanSat mission: Preliminary global observations. Sci. Bull. 2018, 63, 1200–1207. [Google Scholar] [CrossRef]
- Buchwitz, M.; Schneising, O.; Burrows, J.; Bovensmann, H.; Reuter, M.; Notholt, J. First direct observation of the atmospheric CO2 year-to-year increase from space. Atmos. Chem. Phys. 2007, 7, 4249–4256. [Google Scholar] [CrossRef]
- Rusli, S.P.; Hasekamp, O.; Fu, G.; Aan de Brugh, J.; Meijer, Y.; Landgraf, J. Anthropogenic CO2 monitoring satellite mission: The need for multi-angle polarimetric observations. Atmos. Meas. Tech. 2021, 14, 1167–1190. [Google Scholar] [CrossRef]
- Yokota, T.; Yoshida, Y.; Eguchi, N.; Ota, Y.; Tanaka, T.; Watanabe, H.; Maksyutov, S. Global concentrations of CO2 and CH4 retrieved from GOSAT: First preliminary results. Sola 2009, 5, 160–163. [Google Scholar] [CrossRef]
- Eldering, A.; Wennberg, P.O.; Crisp, D.; Schimel, D.S.; Gunson, M.R.; Chatterjee, A.; Liu, J.; Schwandner, F.M.; Sun, Y.; O’Dell, C.W.; et al. The Orbiting Carbon Observatory-2 early science investigations of regional carbon dioxide fluxes. Science 2017, 358, eaam5745. [Google Scholar] [CrossRef]
- Taylor, T.E.; Eldering, A.; Merrelli, A.; Kiel, M.; Somkuti, P.; Cheng, C.; Rosenberg, R.; Fisher, B.; Crisp, D.; Basilio, R.; et al. OCO-3 early mission operations and initial (vEarly) XCO2 and SIF retrievals. Remote Sens. Environ. 2020, 251, 112032. [Google Scholar] [CrossRef]
- Ligori, M.; Bradbury, L.M.; Spina, R.; Zee, R.E.; Germain, S. GHGSat Constellation: The Future of Monitoring Greenhouse Gas Emissions. In Proceedings of the Small Satellite Conference, Logan, UT, USA, 3–8 August 2019. [Google Scholar]
- Duren, R.M.; Guido, J.; Herner, J.; Rao, S.; Green, R.O.; de Belloy, M.; Schingler, R.; Ardila, D.R.; Thorpe, A.K.; Cusworth, D.; et al. Carbon Mapper: Global tracking of methane and CO2 point-sources. In Proceedings of the AGU Fall Meeting Abstracts, Virtual, 1–17 December 2020; Volume 2020, p. A247-01. [Google Scholar]
- Yang, D.; Liu, Y.; Cai, Z.; Chen, X.; Yao, L.; Lu, D. First Global Carbon Dioxide Maps Produced from TanSat Measurements. Adv. Atmos. Sci. 2018, 35, 621–623. [Google Scholar] [CrossRef]
- Jin, C.; Xue, Y.; Jiang, X.; Zhao, L.; Yuan, T.; Sun, Y.; Wu, S.; Wang, X. A long-term global XCO2 dataset: Ensemble of satellite products. Atmos. Res. 2022, 279, 106385. [Google Scholar] [CrossRef]
- Keeling, C.D.; Bacastow, R.B.; Bainbridge, A.E.; Ekdahl Jr, C.A.; Guenther, P.R.; Waterman, L.S.; Chin, J.F. Atmospheric carbon dioxide variations at Mauna Loa observatory, Hawaii. Tellus 1976, 28, 538–551. [Google Scholar] [CrossRef]
- Takagi, H.; Saeki, T.; Oda, T.; Saito, M.; Valsala, V.; Belikov, D.; Saito, R.; Yoshida, Y.; Morino, I.; Uchino, O.; et al. On the benefit of GOSAT observations to the estimation of regional CO2 fluxes. Sola 2011, 7, 161–164. [Google Scholar] [CrossRef]
- TCCON. Available online: https://tccondata.org/ (accessed on 25 July 2024).
- WDCGG. Available online: https://gaw.kishou.go.jp/ (accessed on 25 July 2024).
- GLOBALVIEW-CO2. Available online: https://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=1111 (accessed on 25 July 2024).
- SCIAMACHY WFMD. Available online: https://www.iup.uni-bremen.de/sciamachy/ (accessed on 25 July 2024).
- SCIAMACHY BESD. Available online: https://www.iup.uni-bremen.de/deu/ (accessed on 25 July 2024).
- GOSAT ACOS. Available online: https://search.earthdata.nasa.gov/ (accessed on 25 July 2024).
- GOSAT SRFP. Available online: https://catalogue.ceda.ac.uk/ (accessed on 25 July 2024).
- GOSAT NIES. Available online: https://data2.gosat.nies.go.jp/ (accessed on 25 July 2024).
- GOSAT OCFP. Available online: https://catalogue.ceda.ac.uk/ (accessed on 25 July 2024).
- GOSAT-2 FP. Available online: https://prdct.gosat-2.nies.go.jp/ (accessed on 25 July 2024).
- TanSat OCFP. Available online: https://catalogue.ceda.ac.uk/ (accessed on 25 July 2024).
- TanSat ACGS. Available online: http://www.cgga.org.cn/ (accessed on 25 July 2024).
- OCO-2 ACOS. Available online: https://search.earthdata.nasa.gov/ (accessed on 25 July 2024).
- OCO-2 FOCAL. Available online: https://catalogue.ceda.ac.uk/ (accessed on 25 July 2024).
- OCO-3 ACOS. Available online: https://search.earthdata.nasa.gov (accessed on 25 July 2024).
- Buchwitz, M.; Reuter, M.; Bovensmann, H.; Pillai, D.; Heymann, J.; Schneising, O.; Rozanov, V.; Krings, T.; Burrows, J.; Boesch, H.; et al. Carbon Monitoring Satellite (CarbonSat): Assessment of atmospheric CO2 and CH4 retrieval errors by error parameterization. Atmos. Meas. Tech. 2013, 6, 3477–3500. [Google Scholar] [CrossRef]
- Kuze, A.; Suto, H.; Nakajima, M.; Hamazaki, T. Thermal and near infrared sensor for carbon observation Fourier-transform spectrometer on the Greenhouse Gases Observing Satellite for greenhouse gases monitoring. Appl. Opt. 2009, 48, 6716–6733. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Y.; Boesch, H.; Yao, L.; Di Noia, A.; Cai, Z.; Lu, N.; Lyu, D.; Wang, M.; Wang, J.; et al. A new TanSat XCO2 global product towards climate studies. Adv. Atmos. Sci. 2021, 38, 8–11. [Google Scholar] [CrossRef]
- Wang, S.; van der A, R.J.; Stammes, P.; Wang, W.; Zhang, P.; Lu, N.; Zhang, X.; Bi, Y.; Wang, P.; Fang, L. Carbon dioxide retrieval from TanSat observations and validation with TCCON measurements. Remote Sens. 2020, 12, 2204. [Google Scholar] [CrossRef]
- Bao, Z.; Zhang, X.; Yue, T.; Zhang, L.; Wang, Z.; Jiao, Y.; Bai, W.; Meng, X. Retrieval and validation of XCO2 from TanSat target mode observations in Beijing. Remote Sens. 2020, 12, 3063. [Google Scholar] [CrossRef]
- PKU. Available online: https://opendata.pku.edu.cn/dataverse.xhtml (accessed on 25 July 2024).
- ODIAC. Available online: https://db.cger.nies.go.jp/dataset/ODIAC/ (accessed on 25 July 2024).
- EDGAR. Available online: https://meta.icos-cp.eu/collections/unv31HYRKgullLjJ99O5YCsG (accessed on 25 July 2024).
- Cai, B.; Liang, S.; Zhou, J.; Wang, J.; Cao, L.; Qu, S.; Xu, M.; Yang, Z. China high resolution emission database (CHRED) with point emission sources, gridded emission data, and supplementary socioeconomic data. Resour. Conserv. Recycl. 2018, 129, 232–239. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, J.; Peng, J.; Cao, Q. The uncertainty of nighttime light data in estimating carbon dioxide emissions in China: A comparison between DMSP-OLS and NPP-VIIRS. Remote Sens. 2017, 9, 797. [Google Scholar] [CrossRef]
- Oda, T.; Maksyutov, S.; Andres, R.J. The Open-source Data Inventory for Anthropogenic CO2, version 2016 (ODIAC2016): A global monthly fossil fuel CO2 gridded emissions data product for tracer transport simulations and surface flux inversions. Earth Syst. Sci. Data 2018, 10, 87–107. [Google Scholar] [CrossRef]
- An, N.; Mustafa, F.; Bu, L.; Xu, M.; Wang, Q.; Shahzaman, M.; Bilal, M.; Ullah, S.; Feng, Z. Monitoring of atmospheric carbon dioxide over Pakistan using satellite dataset. Remote Sens. 2022, 14, 5882. [Google Scholar] [CrossRef]
- Karstens, U. Global Anthropogenic CO2 Emissions for 2006–2019 Based on EDGARv4.3 and BP Statistics 2019 (Version 2.0). ICOS ERIC-Carbon Portal, [Online]. 2019; p. 1000. Available online: https://meta.icos-cp.eu/collections/unv31HYRKgullLjJ99O5YCsG (accessed on 26 June 2019).
- Afsah, S.; Ness, E. Carbon Monitoring for Action (CARMA): Climate Campaign Built on Questionable Data—A Due Diligence Report on CARMA’s Data and Methodology. 2008. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1133432 (accessed on 27 July 2024).
- Galbraith, J.K.; Choi, J.; Halbach, B.; Malinowska, A.; Zhang, W. A comparison of major world inequality data sets: LIS, OECD, EU-SILC, WDI, and EHII. In Income Inequality around the World; Emerald Group Publishing Limited: Bingley, UK, 2016; pp. 1–48. [Google Scholar]
- Zheng, B.; Cheng, J.; Geng, G.; Wang, X.; Li, M.; Shi, Q.; Qi, J.; Lei, Y.; Zhang, Q.; He, K. Mapping anthropogenic emissions in China at 1 km spatial resolution and its application in air quality modeling. Sci. Bull. 2021, 66, 612–620. [Google Scholar] [CrossRef]
- Han, P.; Lin, X.; Zeng, N.; Oda, T.; Zhang, W.; Liu, D.; Cai, Q.; Crippa, M.; Guan, D.; Ma, X.; et al. Province-level fossil fuel CO2 emission estimates for China based on seven inventories. J. Clean. Prod. 2020, 277, 123377. [Google Scholar] [CrossRef]
- Chen, C.; Leydesdorff, L. Patterns of connections and movements in dual-map overlays: A new method of publication portfolio analysis. J. Assoc. Inf. Sci. Technol. 2014, 65, 334–351. [Google Scholar] [CrossRef]
- Chen, C.; Dubin, R.; Kim, M.C. Emerging trends and new developments in regenerative medicine: A scientometric update (2000–2014). Expert Opin. Biol. Ther. 2014, 14, 1295–1317. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, H.; Hayashi, K.; Saeki, T.; Maksyutov, S.; Nasuno, I.; Shimono, Y.; Kanekon, S.; Ajiro, M.; Matsumoto, Y.; Yokota, T.; et al. Global mapping of greenhouse gases retrieved from GOSAT Level 2 products by using a kriging method. Int. J. Remote Sens. 2015, 36, 1509–1528. [Google Scholar] [CrossRef]
- Gräler, B.; Pebesma, E.J.; Heuvelink, G.B. Spatio-temporal interpolation using gstat. R J. 2016, 8, 204. [Google Scholar] [CrossRef]
- Schneising, O.; Reuter, M.; Buchwitz, M.; Heymann, J.; Bovensmann, H.; Burrows, J. Terrestrial carbon sink observed from space: Variation of growth rates and seasonal cycle amplitudes in response to interannual surface temperature variability. Atmos. Chem. Phys. 2014, 14, 133–141. [Google Scholar] [CrossRef]
- Tomosada, M.; Kanefuji, K.; Matsumoto, Y.; Tsubaki, H. Application of the Spatial Statistics to the Retrieved CO2 Column Abundances Derived from GOSAT Data. In Proceedings of the WSEAS International Conference, Corfu Island, Greece, 26–28 October 2008. [Google Scholar]
- Hammerling, D.M.; Michalak, A.M.; Kawa, S.R. Mapping of CO2 at high spatiotemporal resolution using satellite observations: Global distributions from OCO-2. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Jing, Y.; Shi, J.; Wang, T.; Sussmann, R. Mapping global atmospheric CO2 concentration at high spatiotemporal resolution. Atmosphere 2014, 5, 870–888. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Chen, J. Prediction of satellite-based column CO2 concentration by combining emission inventory and LULC information. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8285–8300. [Google Scholar] [CrossRef]
- Tadić, J.M.; Qiu, X.; Yadav, V.; Michalak, A.M. Mapping of satellite Earth observations using moving window block kriging. Geosci. Model Dev. 2015, 8, 3311–3319. [Google Scholar] [CrossRef]
- Zeng, Z.C.; Lei, L.; Strong, K.; Jones, D.B.; Guo, L.; Liu, M.; Deng, F.; Deutscher, N.M.; Dubey, M.K.; Griffith, D.W.; et al. Global land mapping of satellite-observed CO2 total columns using spatio-temporal geostatistics. Int. J. Digit. Earth 2017, 10, 426–456. [Google Scholar] [CrossRef]
- He, Z.; Lei, L.; Zhang, Y.; Sheng, M.; Wu, C.; Li, L.; Zeng, Z.C.; Welp, L.R. Spatio-temporal mapping of multi-satellite observed column atmospheric CO2 using precision-weighted kriging method. Remote Sens. 2020, 12, 576. [Google Scholar] [CrossRef]
- Ma, Y.; He, X.; Wu, R.; Shen, C. Spatial Distribution of Multi-Fractal Scaling Behaviours of Atmospheric XCO2 Concentration Time Series during 2010–2018 over China. Entropy 2022, 24, 817. [Google Scholar] [CrossRef] [PubMed]
- Sheng, M.; Lei, L.; Zeng, Z.C.; Rao, W.; Song, H.; Wu, C. Global land 1∘ mapping dataset of XCO2 from satellite observations of GOSAT and OCO-2 from 2009 to 2020. Big Earth Data 2023, 7, 170–190. [Google Scholar] [CrossRef]
- Castanedo, F. A Review of Data Fusion Techniques. Sci. World J. 2013, 2013, 704504. [Google Scholar] [CrossRef] [PubMed]
- Kuncheva, L.I.; Rodríguez, J.J. A weighted voting framework for classifiers ensembles. Knowl. Inf. Syst. 2014, 38, 259–275. [Google Scholar] [CrossRef]
- Reuter, M.; Bösch, H.; Bovensmann, H.; Bril, A.; Buchwitz, M.; Butz, A.; Burrows, J.; O’Dell, C.; Guerlet, S.; Hasekamp, O.; et al. A joint effort to deliver satellite retrieved atmospheric CO2 concentrations for surface flux inversions: The ensemble median algorithm EMMA. Atmos. Chem. Phys. 2013, 13, 1771–1780. [Google Scholar] [CrossRef]
- Jing, Y.; Shi, J.; Wang, T. Fusion of space-based CO2 products and its comparison with other available CO2 estimates. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 2363–2366. [Google Scholar] [CrossRef]
- Nguyen, H.; Katzfuss, M.; Cressie, N.; Braverman, A. Spatio-temporal data fusion for very large remote sensing datasets. Technometrics 2014, 56, 174–185. [Google Scholar] [CrossRef]
- Zhou, C.; Shi, R.; Gao, W. Data fusion of CO2 retrieved from GOSAT and AIRS using regression analysis and fixed rank kriging. In Remote Sensing and Modeling of Ecosystems for Sustainability XII; SPIE: Bellingham, WA, USA, 2015; Volume 9610, pp. 315–323. [Google Scholar]
- Zhao, M.; Yue, T.; Zhang, X.; Sun, J.; Jiang, L.; Wang, C. Fusion of multi-source near-surface CO2 concentration data based on high accuracy surface modeling. Atmos. Pollut. Res. 2017, 8, 1170–1178. [Google Scholar]
- Henze, D.K.; Hakami, A.; Seinfeld, J.H. Development of the adjoint of GEOS-Chem. Atmos. Chem. Phys. 2007, 7, 2413–2433. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, B.; Xu, G.; Yan, J.; Che, M.; Chen, J.; Fang, S.; Lin, X.; Sun, S. Comparing simulated atmospheric carbon dioxide concentration with GOSAT retrievals. Sci. Bull. 2015, 60, 380–386. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Yang, Y.; Yantosca, R.M.; Kawa, S.R.; Paris, J.D.; Matsueda, H.; Machida, T. Evaluating a 3-D transport model of atmospheric CO2 using ground-based, aircraft, and space-borne data. Atmos. Chem. Phys. 2011, 11, 2789–2803. [Google Scholar] [CrossRef]
- Lei, L.; Guan, X.; Zeng, Z.; Zhang, B.; Ru, F.; Bu, R. A comparison of atmospheric CO2 concentration GOSAT-based observations and model simulations. Sci. China Earth Sci. 2014, 57, 1393–1402. [Google Scholar] [CrossRef]
- Li, R.; Zhang, M.; Chen, L.; Kou, X.; Skorokhod, A. CMAQ simulation of atmospheric CO2 concentration in East Asia: Comparison with GOSAT observations and ground measurements. Atmos. Environ. 2017, 160, 176–185. [Google Scholar] [CrossRef]
- Bie, N.; Lei, L.; He, Z.; Zeng, Z.; Liu, L.; Zhang, B.; Cai, B. Specific patterns of XCO2 observed by GOSAT during 2009–2016 and assessed with model simulations over China. Sci. China Earth Sci. 2020, 63, 384–394. [Google Scholar] [CrossRef]
- Zhang, L.L.; Yue, T.X.; Wilson, J.P.; Zhao, N.; Zhao, Y.P.; Du, Z.P.; Liu, Y. A comparison of satellite observations with the XCO2 surface obtained by fusing TCCON measurements and GEOS-Chem model outputs. Sci. Total Environ. 2017, 601, 1575–1590. [Google Scholar] [CrossRef]
- Byrne, B.; Baker, D.F.; Basu, S.; Bertolacci, M.; Bowman, K.W.; Carroll, D.; Chatterjee, A.; Chevallier, F.; Ciais, P.; Cressie, N.; et al. National CO2 budgets (2015–2020) inferred from atmospheric CO2 observations in support of the global stocktake. Earth Syst. Sci. Data 2023, 15, 963–1004. [Google Scholar] [CrossRef]
- Anthony, L.F.W.; Kanding, B.; Selvan, R. Carbontracker: Tracking and Predicting the Carbon Footprint of Training Deep Learning Models. arXiv 2020, arXiv:2007.03051. [Google Scholar]
- Mustafa, F.; Bu, L.; Wang, Q.; Ali, M.A.; Bilal, M.; Shahzaman, M.; Qiu, Z. Multi-year comparison of CO2 concentration from NOAA carbon tracker reanalysis model with data from GOSAT and OCO-2 over Asia. Remote Sens. 2020, 12, 2498. [Google Scholar] [CrossRef]
- Agustí-Panareda, A.; Barré, J.; Massart, S.; Inness, A.; Aben, I.; Ades, M.; Baier, B.C.; Balsamo, G.; Borsdorff, T.; Bousserez, N.; et al. The CAMS greenhouse gas reanalysis from 2003 to 2020. Atmos. Chem. Phys. 2023, 23, 3829–3859. [Google Scholar] [CrossRef]
- Ballav, S.; Naja, M.; Patra, P.K.; Machida, T.; Mukai, H. Assessment of spatio-temporal distribution of CO2 over greater Asia using the WRF–CO2 model. J. Earth Syst. Sci. 2020, 129, 1–16. [Google Scholar] [CrossRef]
- Khanipour, P.; Löffler, M.; Reichert, A.M.; Haase, F.T.; Mayrhofer, K.J.; Katsounaros, I. Electrochemical real-time mass spectrometry (EC-RTMS): Monitoring electrochemical reaction products in real time. Angew. Chem. Int. Ed. 2019, 58, 7273–7277. [Google Scholar] [CrossRef]
- Yuan, L.; Zhang, X.C.J.; Busteed, P.; Flanagan, D.C. Simulating the potential effects of elevated CO2 concentration and temperature coupled with storm intensification on crop yield, surface runoff, and soil loss based on 25 GCMs ensemble: A site-specific case study in Oklahoma. Catena 2022, 214, 106251. [Google Scholar] [CrossRef]
- Gao, J.; Weng, L.; Xia, M.; Lin, H. MLNet: Multichannel feature fusion lozenge network for land segmentation. J. Appl. Remote Sens. 2022, 16, 016513. [Google Scholar] [CrossRef]
- Hu, K.; Jin, J.; Shen, C.; Xia, M.; Weng, L. Attentional weighting strategy-based dynamic GCN for skeleton-based action recognition. Multimed. Syst. 2023, 29, 1941–1954. [Google Scholar] [CrossRef]
- Hu, K.; Weng, C.; Zhang, Y.; Jin, J.; Xia, Q. An overview of underwater vision enhancement: From traditional methods to recent deep learning. J. Mar. Sci. Eng. 2022, 10, 241. [Google Scholar] [CrossRef]
- Hu, K.; Weng, C.; Shen, C.; Wang, T.; Weng, L.; Xia, M. A multi-stage underwater image aesthetic enhancement algorithm based on a generative adversarial network. Eng. Appl. Artif. Intell. 2023, 123, 106196. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, E.; Xia, M.; Weng, L.; Lin, H. Mcanet: A multi-branch network for cloud/snow segmentation in high-resolution remote sensing images. Remote Sens. 2023, 15, 1055. [Google Scholar] [CrossRef]
- Lu, C.; Xia, M.; Lin, H. Multi-scale strip pooling feature aggregation network for cloud and cloud shadow segmentation. Neural Comput. Appl. 2022, 34, 6149–6162. [Google Scholar] [CrossRef]
- Hu, K.; Lu, M.; Li, Y.; Gong, S.; Wu, J.; Zhou, F.; Jiang, S.; Yang, Y. A Federated Incremental Learning Algorithm Based on Dual Attention Mechanism. Appl. Sci. 2022, 12, 10025. [Google Scholar] [CrossRef]
- Hu, K.; Wu, J.; Li, Y.; Lu, M.; Weng, L.; Xia, M. Fedgcn: Federated learning-based graph convolutional networks for non-euclidean spatial data. Mathematics 2022, 10, 1000. [Google Scholar] [CrossRef]
- Ji, H.; Xia, M.; Zhang, D.; Lin, H. Multi-Supervised Feature Fusion Attention Network for Clouds and Shadows Detection. ISPRS Int. J. Geo-Inf. 2023, 12, 247. [Google Scholar] [CrossRef]
- Chen, K.; Xia, M.; Lin, H.; Qian, M. Multi-scale Attention Feature Aggregation Network for Cloud and Cloud Shadow Segmentation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar]
- Dai, X.; Xia, M.; Weng, L.; Hu, K.; Lin, H.; Qian, M. Multi-Scale Location Attention Network for Building and Water Segmentation of Remote Sensing Image. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–19. [Google Scholar]
- Hu, K.; Li, M.; Xia, M.; Lin, H. Multi-scale feature aggregation network for water area segmentation. Remote Sens. 2022, 14, 206. [Google Scholar] [CrossRef]
- Siabi, Z.; Falahatkar, S.; Alavi, S.J. Spatial distribution of XCO2 using OCO-2 data in growing seasons. J. Environ. Manag. 2019, 244, 110–118. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, P.; Shivadekar, S.; Laya Chukkapalli, S.S.; Halem, M. Satellite Data Fusion of Multiple Observed XCO2 using Compressive Sensing and Deep Learning. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2073–2076. [Google Scholar] [CrossRef]
- He, C.; Ji, M.; Li, T.; Liu, X.; Tang, D.; Zhang, S.; Luo, Y.; Grieneisen, M.L.; Zhou, Z.; Zhan, Y. Deriving Full-Coverage and Fine-Scale XCO2 Across China Based on OCO-2 Satellite Retrievals and CarbonTracker Output. Geophys. Res. Lett. 2022, 49, e2022GL098435. [Google Scholar] [CrossRef]
- Li, J.; Jia, K.; Wei, X.; Xia, M.; Chen, Z.; Yao, Y.; Zhang, X.; Jiang, H.; Yuan, B.; Tao, G.; et al. High-spatiotemporal resolution mapping of spatiotemporally continuous atmospheric CO2 concentrations over the global continent. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102743. [Google Scholar] [CrossRef]
- Wang, W.; He, J.; Feng, H.; Jin, Z. High-Coverage Reconstruction of XCO2 Using Multisource Satellite Remote Sensing Data in Beijing–Tianjin–Hebei Region. Int. J. Environ. Res. Public Health 2022, 19, 10853. [Google Scholar] [CrossRef]
- Zhang, L.; Li, T.; Wu, J. Deriving gapless CO2 concentrations using a geographically weighted neural network: China, 2014–2020. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103063. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, G. Mapping contiguous XCO2 by machine learning and analyzing the spatio-temporal variation in China from 2003 to 2019. Sci. Total. Environ. 2023, 858, 159588. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Han, K.; Xiao, A.; Wu, E.; Guo, J.; Xu, C.; Wang, Y. Transformer in transformer. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS 2021), Online, 6–14 December 2021; Volume 34, pp. 15908–15919. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. arXiv 2020, arXiv:2012.07436. [Google Scholar] [CrossRef]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. Timesnet: Temporal 2d-variation modeling for general time series analysis. arXiv 2022, arXiv:2210.02186. [Google Scholar]
- Das, A.; Kong, W.; Leach, A.; Sen, R.; Yu, R. Long-term Forecasting with TiDE: Time-series Dense Encoder. arXiv 2023, arXiv:2304.08424. [Google Scholar]
- Li, Y.; Wang, Z.; Zhang, K.; Zhang, W.; Yan, Y. Survey on example learning-based single image super-resolution technique. Comput. Eng. Appl. 2018, 54, 13–21. [Google Scholar]
- Yin, Y.; Robinson, J.; Zhang, Y.; Fu, Y. Joint super-resolution and alignment of tiny faces. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12693–12700. [Google Scholar]
- Huang, Y.; Zheng, F.; Wang, D.; Jiang, J.; Wang, X.; Shao, L. Super-Resolution and Inpainting with Degraded and Upgraded Generative Adversarial Networks. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI-20, Yokohama, Japan, 11–17 July 2020; Bessiere, C., Ed.; International Joint Conferences on Artificial Intelligence Organization: Bremen, Germany, 2020; pp. 645–651. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, K.; Yi, P.; Han, Z.; He, Z. Ultra-dense GAN for satellite imagery super-resolution. Neurocomputing 2020, 398, 328–337. [Google Scholar] [CrossRef]
- Gao, G.; Yu, Y.; Xie, J.; Yang, J.; Yang, M.; Zhang, J. Constructing multilayer locality-constrained matrix regression framework for noise robust face super-resolution. Pattern Recognit. 2021, 110, 107539. [Google Scholar] [CrossRef]
- Blu, T.; Thévenaz, P.; Unser, M. Linear interpolation revitalized. IEEE Trans. Image Process. 2004, 13, 710–719. [Google Scholar] [CrossRef]
- Tao, H.; Tang, X.; Liu, J.; Tian, J. Superresolution remote sensing image processing algorithm based on wavelet transform and interpolation. Proc. SPIE 2003, 4898, 259–263. [Google Scholar]
- Nayak, R.; Patra, D. Image interpolation using adaptive P-spline. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–6. [Google Scholar]
- Zhou, D.; Shen, X.; Dong, W. Image zooming using directional cubic convolution interpolation. IET Image Process. 2012, 6, 627–634. [Google Scholar] [CrossRef]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Li, X.; Orchard, M.T. New edge-directed interpolation. IEEE Trans. Image Process. 2001, 10, 1521–1527. [Google Scholar] [PubMed]
- Dai, S.; Han, M.; Xu, W.; Wu, Y.; Gong, Y. Soft edge smoothness prior for alpha channel super resolution. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Zhang, X.; Wu, X. Image interpolation by adaptive 2-D autoregressive modeling and soft-decision estimation. IEEE Trans. Image Process. 2008, 17, 887–896. [Google Scholar] [CrossRef] [PubMed]
- Jing, G.; Choi, Y.K.; Wang, J.; Wang, W. Gradient guided image interpolation. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 1822–1826. [Google Scholar]
- Sun, J.; Xu, Z.; Shum, H.Y. Image super-resolution using gradient profile prior. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Rasti, P.; Lüsi, I.; Demirel, H.; Kiefer, R.; Anbarjafari, G. Wavelet transform based new interpolation technique for satellite image resolution enhancement. In Proceedings of the 2014 IEEE International Conference on Aerospace Electronics and Remote Sensing Technology, Yogyakarta, Indonesia, 13–14 November 2014; pp. 185–188. [Google Scholar]
- Ford, C.; Etter, D. Wavelet basis reconstruction of nonuniformly sampled data. IEEE Trans. Circuits Syst. II Analog. Digit. Process. 1998, 45, 1165–1168. [Google Scholar] [CrossRef]
- Nguyen, N.; Milanfar, P. A wavelet-based interpolation-restoration method for superresolution (wavelet superresolution). Circuits Syst. Signal Process. 2000, 19, 321–338. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, L.; Lim, K.; Li, Y.; Wang, F.; Lu, J. Review and prospect of image super-resolution technology. J. Front. Comput. Sci. Technol. 2020, 14, 181–199. [Google Scholar]
- Patti, A.J.; Sezan, M.I.; Tekalp, A.M. Superresolution video reconstruction with arbitrary sampling lattices and nonzero aperture time. IEEE Trans. Image Process. 1997, 6, 1064–1076. [Google Scholar] [CrossRef]
- Nasonov, A.V.; Krylov, A.S. Fast super-resolution using weighted median filtering. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2230–2233. [Google Scholar]
- Irani, M.; Peleg, S. Improving resolution by image registration. CVGIP Graph. Model. Image Process. 1991, 53, 231–239. [Google Scholar] [CrossRef]
- Stark, H.; Oskoui, P. High-resolution image recovery from image-plane arrays, using convex projections. JOSA A 1989, 6, 1715–1726. [Google Scholar] [CrossRef] [PubMed]
- Banham, M.R.; Katsaggelos, A.K. Digital image restoration. IEEE Signal Process. Mag. 1997, 14, 24–41. [Google Scholar] [CrossRef]
- Schultz, R.R.; Stevenson, R.L. Extraction of high-resolution frames from video sequences. IEEE Trans. Image Process. 1996, 5, 996–1011. [Google Scholar] [CrossRef]
- Freeman, W.T.; Pasztor, E.C.; Carmichael, O.T. Learning low-level vision. Int. J. Comput. Vis. 2000, 40, 25–47. [Google Scholar] [CrossRef]
- Freeman, W.T.; Jones, T.R.; Pasztor, E.C. Example-based super-resolution. IEEE Comput. Graph. Appl. 2002, 22, 56–65. [Google Scholar] [CrossRef]
- Glasner, D.; Bagon, S.; Irani, M. Super-resolution from a single image. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 349–356. [Google Scholar]
- Chang, H.; Yeung, D.Y.; Xiong, Y. Super-resolution through neighbor embedding. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2004), Washington, DC, USA, 27 June–2 July 2004; Volume 1, p. I. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.; Ma, Y. Image super-resolution as sparse representation of raw image patches. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Donoho, D.L. For most large underdetermined systems of linear equations the minimal 1-norm solution is also the sparsest solution. Commun. Pure Appl. Math. 2006, 59, 797–829. [Google Scholar] [CrossRef]
- Timofte, R.; De Smet, V.; Van Gool, L. A+: Adjusted Anchored Neighborhood Regression for Fast Super-Resolution. In Proceedings of the Computer Vision–ACCV 2014, Singapore, 1–5 November 2014; Cremers, D., Reid, I., Saito, H., Yang, M.H., Eds.; Springer: Cham, Switzerland, 2015; pp. 111–126. [Google Scholar]
- Li, J.; Wu, J.; Deng, H.; Liu, J. A self-learning image super-resolution method via sparse representation and non-local similarity. Neurocomputing 2016, 184, 196–206. [Google Scholar] [CrossRef]
- Zeng, T.; Du, F. Image Super-Resolution Reconstruction Based on Hierarchical Clustering. Acta Opt. Sin. 2018, 38, 0410004. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Springer: Cham, Switzerland, 2014; pp. 184–199. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 391–407. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar] [CrossRef]
- Li, J.; Fang, F.; Mei, K.; Zhang, G. Multi-scale Residual Network for Image Super-Resolution. In Proceedings of the Computer Vision—-ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer: Cham, Swizterland, 2018; pp. 527–542. [Google Scholar]
- Lan, R.; Sun, L.; Liu, Z.; Lu, H.; Su, Z.; Pang, C.; Luo, X. Cascading and enhanced residual networks for accurate single-image super-resolution. IEEE Trans. Cybern. 2020, 51, 115–125. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y.R. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. arXiv 2018, arXiv:1807.02758. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. arXiv 2018, arXiv:1807.06521. [Google Scholar]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.T.; Zhang, L. Second-Order Attention Network for Single Image Super-Resolution. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 11057–11066. [Google Scholar] [CrossRef]
- Xu, Y.B.; Dong, Y. Binocular image super resolution reconstruction algorithm guided by multi-attention mechanism. Electron. Meas. Technol. 2021, 44, 103–108. [Google Scholar]
- Zheng, H.; Liu, C. Multiscale feature reuse mixed attention network for image reconstruction. J. Image Graph. 2021, 26, 2645–2658. [Google Scholar]
- Yi-Yue, Y.; Qian, F.; Ding-Sheng, W. A prediction model for time series based on deep recurrent neural network. Comput. Technol. Dev. 2017, 27, 35–38. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-Recursive Convolutional Network for Image Super-Resolution. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar]
- Han, W.; Chang, S.; Liu, D.; Yu, M.; Witbrock, M.; Huang, T.S. Image Super-Resolution via Dual-State Recurrent Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1654–1663. [Google Scholar]
- Li, Z.; Yang, J.; Liu, Z.; Yang, X.; Jeon, G.; Wu, W. Feedback Network for Image Super-Resolution. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3862–3871. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 27th International Conference on Neural Information Processing Systems—Volume 2 (NIPS’14), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Loy, C.C. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. In Proceedings of the Computer Vision—ECCV 2018 Workshops, Munich, Germany, 8–14 September 2018; Leal-Taixé, L., Roth, S., Eds.; Springer: Cham, Swizterland, 2019; pp. 63–79. [Google Scholar]
- Shang, T.; Dai, Q.; Zhu, S.; Yang, T.; Guo, Y. Perceptual extreme super-resolution network with receptive field block. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 440–441. [Google Scholar]
- Xiang, R.; Yang, H.; Yan, Z.; Mohamed Taha, A.M.; Xu, X.; Wu, T. Super-resolution reconstruction of GOSAT CO2 products using bicubic interpolation. Geocarto Int. 2022, 37, 15187–15211. [Google Scholar] [CrossRef]
- Dai, X.; Chen, K.; Xia, M.; Weng, L.; Lin, H. LPMSNet: Location Pooling Multi-Scale Network for Cloud and Cloud Shadow Segmentation. Remote Sens. 2023, 15, 4005. [Google Scholar] [CrossRef]
- Jiang, S.; Lin, H.; Ren, H.; Hu, Z.; Weng, L.; Xia, M. MDANet: A High-Resolution City Change Detection Network Based on Difference and Attention Mechanisms under Multi-Scale Feature Fusion. Remote Sens. 2024, 16, 1387. [Google Scholar] [CrossRef]
- Li, Y.; Weng, L.; Xia, M.; Hu, K.; Lin, H. Multi-Scale Fusion Siamese Network Based on Three-Branch Attention Mechanism for High-Resolution Remote Sensing Image Change Detection. Remote Sens. 2024, 16, 1665. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).