Remote Sensing Image Denoising Based on Feature Interaction Complementary Learning
Abstract
1. Introduction
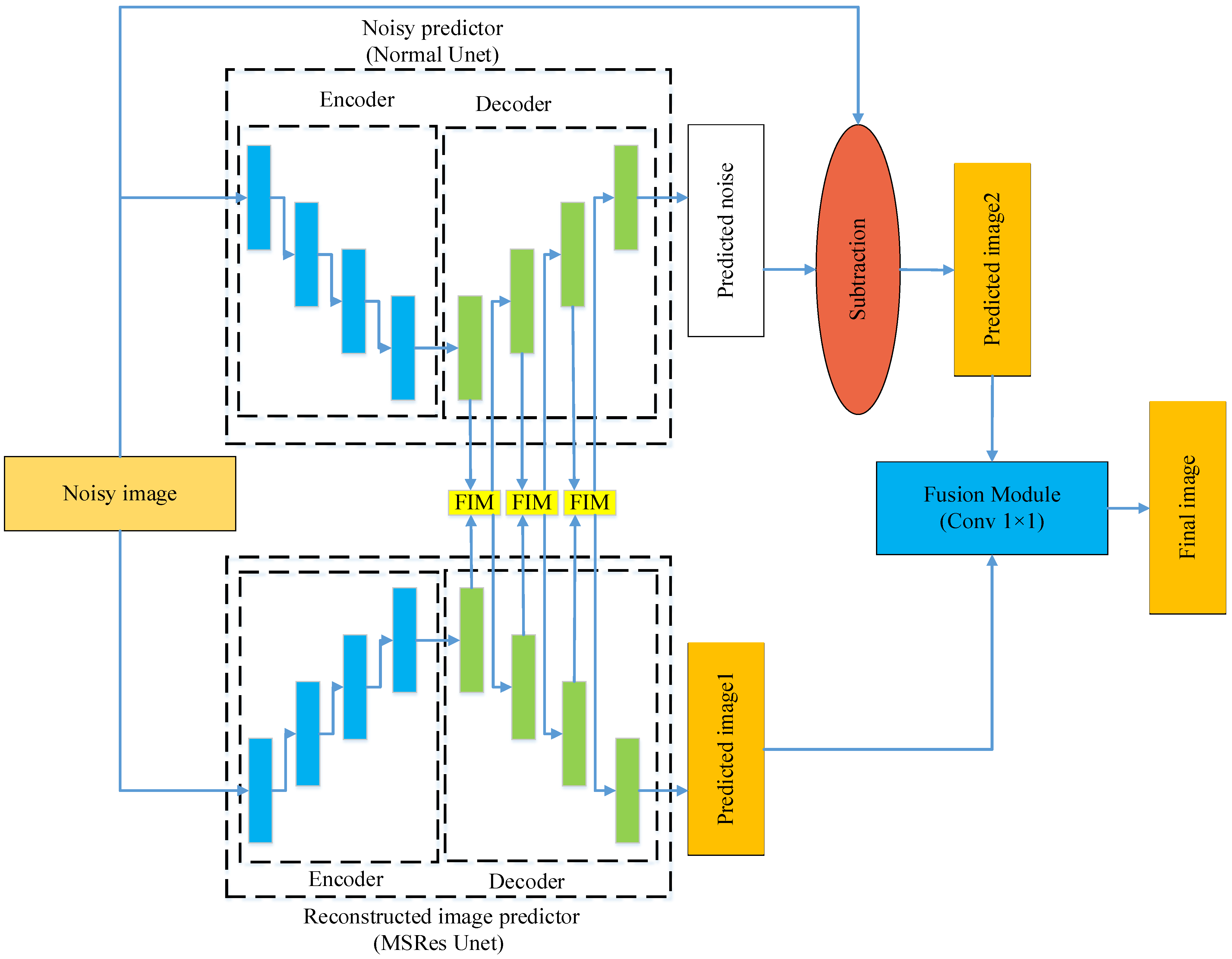
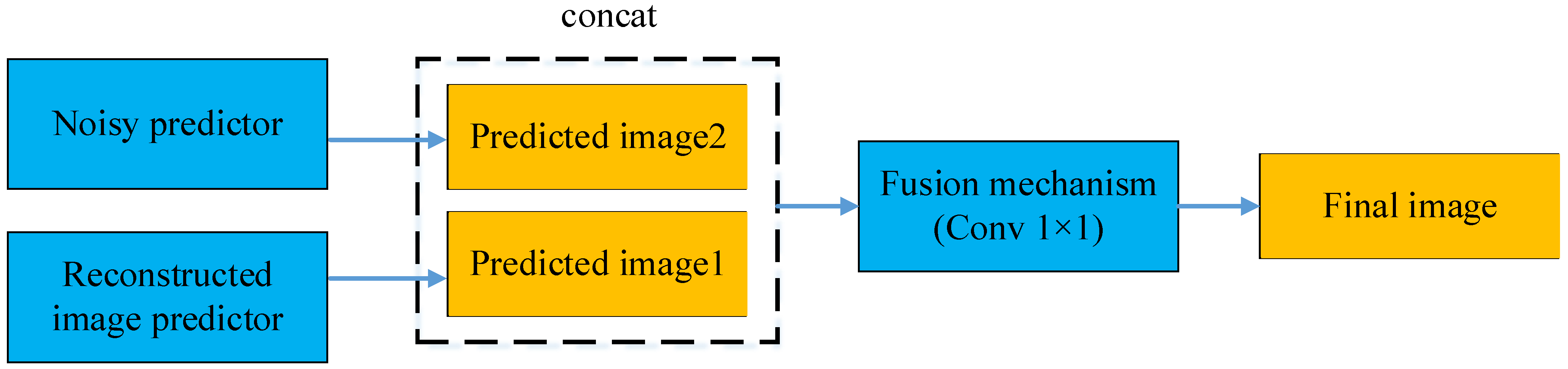
- We proposed a remote sensing image denoising model based on feature interaction complementary learning, which we term the FICL model. The FICL model is comprised of four distinct components: reconstructed image predictor (RIP), noise predictor (NP), feature interaction module (FIM), and fusion module. The model’s original fusion of results also allows for the coupling of features, more fully integrating the strengths of both paradigms.
- We proposed an FIM which facilitates the interaction between the features of the reconstructed image and noise, thereby enhancing the denoising efficacy of the network.
- The proposed FICL model was evaluated on both synthetic Gaussian noise datasets and existing real-world denoising datasets. In comparison with other, more advanced techniques, the FICL method demonstrates superior performance.
2. Materials and Methods
2.1. Complementary Learning
2.2. Feature Interaction Complementary Learning
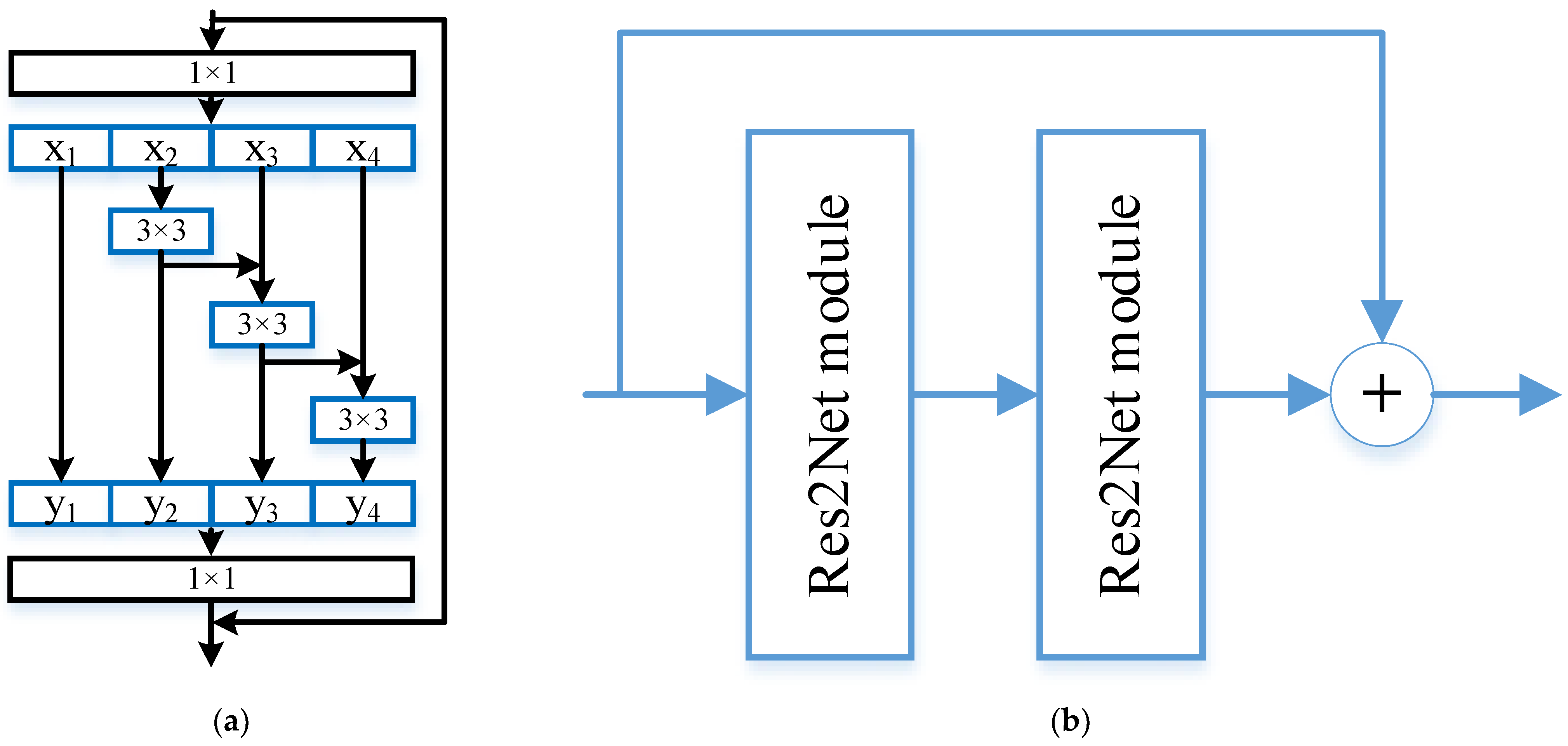
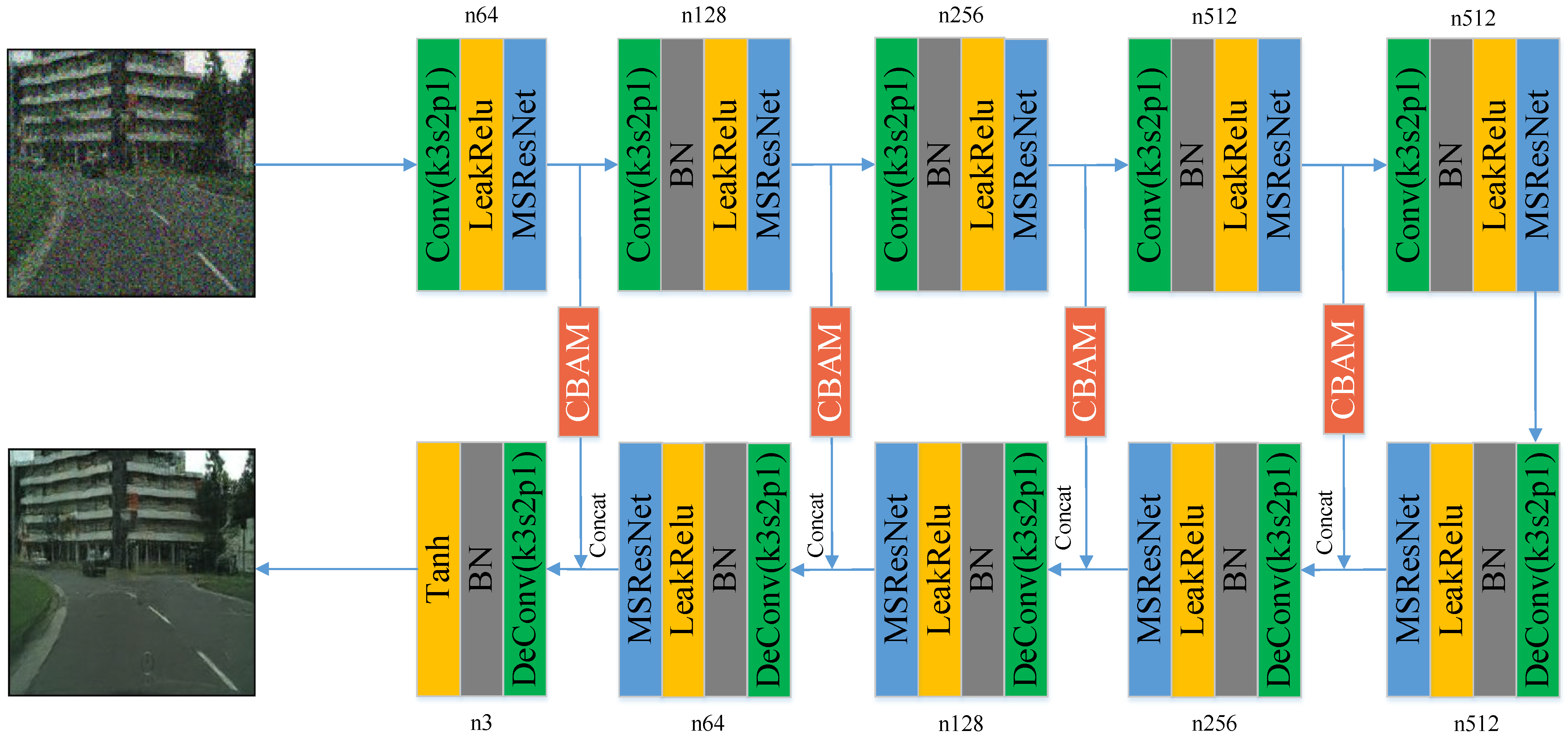
2.2.1. Reconstructed Image Predictor
2.2.2. Noise Predictor
2.2.3. Feature Interaction Module
2.2.4. Fusion Module
2.3. Loss Functions
3. Experiments and Results
3.1. Datasets and Evaluation Metrics
3.1.1. Datasets
- Leveraging existing high-quality images from image databases, these images undergo image processing techniques, encompassing linear transformations, brightness adjustments, among others. Subsequently, synthetic noise is meticulously added in accordance with a predefined noise model, thereby generating noise-corrupted images.
- Multiple images of the same scene are continuously captured. Following this, rigorous image processing procedures are implemented, including image registration and the removal of anomalous images. Ultimately, a weighted average of these processed images is computed to synthesize a ground truth image, serving as the reference for denoising tasks.
3.1.2. Evaluation Metrics
3.2. Experimental Setup
3.2.1. Implementation Details
3.2.2. Compared Methods
3.3. Result and Analysis
3.3.1. Result of Evaluation Metrics
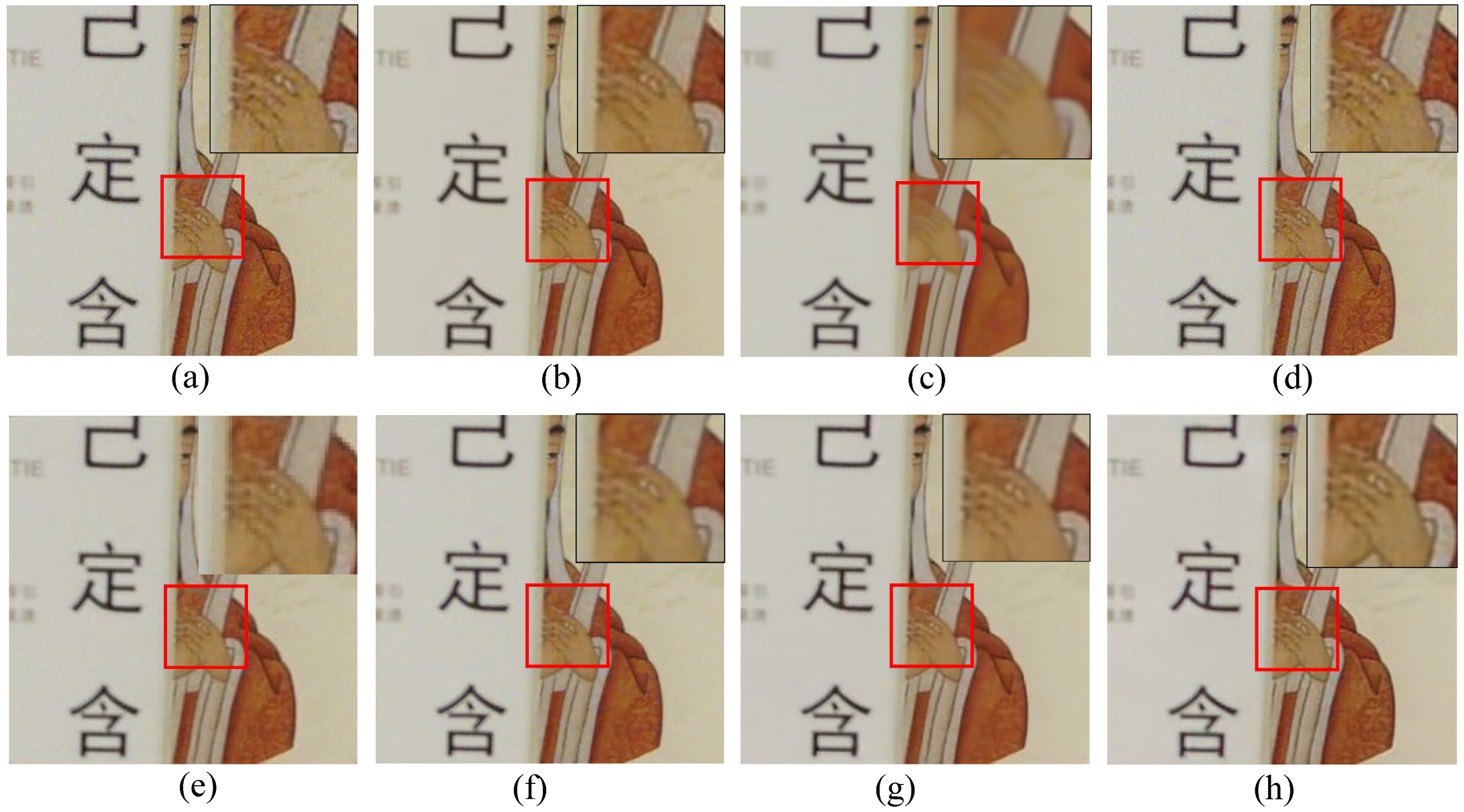
3.3.2. Visual Effects Demonstration
3.3.3. Effect in Application Scenarios
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, X.; Zhang, W.; Su, X.; Xu, Z. Optical Remote Sensing Image Denoising and Super-Resolution Reconstructing Using Optimized Generative Network in Wavelet Transform Domain. Remote Sens. 2021, 13, 1858. [Google Scholar] [CrossRef]
- Qi, J.; Wan, P.; Gong, Z.; Xue, W.; Yao, A.; Liu, X.; Zhong, P. A Self-Improving Framework for Joint Depth Estimation and Underwater Target Detection from Hyperspectral Imagery. Remote Sens. 2021, 13, 1721. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, G.; Yang, H.; Zhao, F.; Han, S.; Chen, R.; Zhang, C.; Yang, X.; Liu, M.; Cheng, J.; et al. Estimation of Apple Flowering Frost Loss for Fruit Yield Based on Gridded Meteorological and Remote Sensing Data in Luochuan, Shaanxi Province, China. Remote Sens. 2021, 13, 1630. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Tang, X.; Huang, Z.; Jiao, L. Vehicle Detection and Tracking in Remote Sensing Satellite Vidio Based on Dynamic Association. In Proceedings of the 2019 10th International Workshop on the Analysis of Multitemporal Remote Sensing Images (Multitemp), Shanghai, China, 5–7 August 2019. [Google Scholar]
- Xia, J.; Wang, Y.; Zhou, M.; Deng, S.; Wang, Z. Variations in Channel Centerline Migration Rate and Intensity of a Braided Reach in the Lower Yellow River. Remote Sens. 2021, 13, 1680. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, M.; Cheng, X.; Shi, L.; Gamba, P.; Wang, H. Dynamic Low-Rank and Sparse Priors Constrained Deep Autoencoders for Hyperspectral Anomaly Detection. IEEE Trans. Instrum. Meas. 2024, 73, 2500518. [Google Scholar] [CrossRef]
- Cheng, X.; Huo, Y.; Lin, S.; Dong, Y.; Zhao, S.; Zhang, M.; Wang, H. Deep Feature Aggregation Network for Hyperspectral Anomaly Detection. IEEE Trans. Instrum. Meas. 2024, 73, 5033016. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral Image Denoising Employing a Spatial-Spectral Deep Residual Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1205–1218. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted Nuclear Norm Minimization with Application to Image Denoising. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2862–2869. [Google Scholar]
- Xu, J.; Osher, S. Iterative Regularization and Nonlinear Inverse Scale Space Applied to Wavelet-Based Denoising. IEEE Trans. Image Process. 2007, 16, 534–544. [Google Scholar] [CrossRef]
- Roth, S.; Black, M.J. Fields of Experts. Int. J. Comput. Vis. 2009, 82, 205–229. [Google Scholar] [CrossRef]
- Anwar, S.; Porikli, F.; Huynh, C.P. Category-Specific Object Image Denoising. IEEE Trans. Image Process. 2017, 26, 5506–5518. [Google Scholar] [CrossRef] [PubMed]
- Luo, E.; Chan, S.H.; Nguyen, T.Q. Adaptive Image Denoising by Targeted Databases. IEEE Trans. Image Process. 2015, 24, 2167–2181. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Yao, Q.; Li, C.; Yokoya, N.; Zhao, Q. Non-Local Meets Global: An Integrated Paradigm for Hyperspectral Denoising. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 15–20 June 2019; pp. 6861–6870. [Google Scholar]
- Kong, X.; Zhao, Y.; Chan, J.C.-W.; Xue, J. Hyperspectral Image Restoration via Spatial-Spectral Residual Total Variation Regularized Low-Rank Tensor Decomposition. Remote Sens. 2022, 14, 511. [Google Scholar] [CrossRef]
- Xu, S.; Cao, X.; Peng, J.; Ke, Q.; Ma, C.; Meng, D. Hyperspectral Image Denoising by Asymmetric Noise Modeling. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5545214. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.; Liu, T.; Tam, J. Graded Image Generation Using Stratified CycleGAN. Med. Image Comput. Comput. Assist. Interv. 2020, 12262, 760–769. [Google Scholar] [CrossRef] [PubMed]
- Lyu, Q.; Guo, M.; Ma, M. Boosting Attention Fusion Generative Adversarial Network for Image Denoising. Neural Comput. Appl. 2021, 33, 4833–4847. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, M.; Lin, S.; Li, Y.; Wang, H. Deep Self-Representation Learning Framework for Hyperspectral Anomaly Detection. IEEE Trans. Instrum. Meas. 2024, 73, 5002016. [Google Scholar] [CrossRef]
- Huo, Y.; Qian, X.; Li, C.; Wang, W. Multiple Instance Complementary Detection and Difficulty Evaluation for Weakly Supervised Object Detection in Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2023, 20, 6006505. [Google Scholar] [CrossRef]
- Zhou, K.; Zhang, M.; Wang, H.; Tan, J. Ship Detection in SAR Images Based on Multi-Scale Feature Extraction and Adaptive Feature Fusion. Remote Sens. 2022, 14, 755. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, M.; Cheng, X.; Zhou, K.; Zhao, S.; Wang, H. Dual Collaborative Constraints Regularized Low-Rank and Sparse Representation via Robust Dictionaries Construction for Hyperspectral Anomaly Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 2009–2024. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, M.; Cheng, X.; Zhou, K.; Zhao, S.; Wang, H. Hyperspectral Anomaly Detection via Sparse Representation and Collaborative Representation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2023, 16, 946–961. [Google Scholar] [CrossRef]
- Huo, Y.; Cheng, X.; Lin, S.; Zhang, M.; Wang, H. Memory-Augmented Autoencoder with Adaptive Reconstruction and Sample Attribution Mining for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5518118. [Google Scholar] [CrossRef]
- Lin, S.; Cheng, X.; Zeng, Y.; Huo, Y.; Zhang, M.; Wang, H. Low-Rank and Sparse Representation Inspired Interpretable Network for Hyperspectral Anomaly Detection. IEEE Trans. Instrum. Meas. 2024, 73, 5033116. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, M.; Lin, S.; Zhou, K.; Zhao, S.; Wang, H. Two-Stream Isolation Forest Based on Deep Features for Hyperspectral Anomaly Detection. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5504205. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a Fast and Flexible Solution for CNN-Based Image Denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef]
- Guo, S.; Yan, Z.; Zhang, K.; Zuo, W.; Zhang, L. Toward Convolutional Blind Denoising of Real Photographs. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1712–1722. [Google Scholar]
- Anwar, S.; Barnes, N. Real Image Denoising with Feature Attention. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3155–3164. [Google Scholar]
- Chang, M.; Li, Q.; Feng, H.; Xu, Z. Spatial-Adaptive Network for Single Image Denoising. In Proceedings of the Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 171–187. [Google Scholar]
- Han, L.; Zhao, Y.; Lv, H.; Zhang, Y.; Liu, H.; Bi, G. Remote Sensing Image Denoising Based on Deep and Shallow Feature Fusion and Attention Mechanism. Remote Sens. 2022, 14, 1243. [Google Scholar] [CrossRef]
- Xu, J.; Yuan, M.; Yan, D.-M.; Wu, T. Deep Unfolding Multi-Scale Regularizer Network for Image Denoising. Comput. Vis. Media 2023, 9, 335–350. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.; Lin, F.; Wu, W.; Chen, Z.-M.; Heidari, A.A.; Chen, H. DSEUNet: A Lightweight UNet for Dynamic Space Grouping Enhancement for Skin Lesion Segmentation. Expert Syst. Appl. 2024, 255, 124544. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, J.; Liu, D. A Remote Sensing Hyperspectral Image Noise Removal Method Based on Multipriors Guidance. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5504805. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Zhu, M.-L.; Zhao, L.-L.; Xiao, L. Image Denoising Based on GAN with Optimization Algorithm. Electronics 2022, 11, 2445. [Google Scholar] [CrossRef]
- Chen, S.; Shi, D.; Sadiq, M.; Cheng, X. Image Denoising with Generative Adversarial Networks and Its Application to Cell Image Enhancement. IEEE Access 2020, 8, 82819–82831. [Google Scholar] [CrossRef]
- Lyu, Q.; Guo, M.; Pei, Z. DeGAN: Mixed Noise Removal via Generative Adversarial Networks. Appl. Soft. Comput. 2020, 95, 106478. [Google Scholar] [CrossRef]
- Wang, Y.; Chang, D.; Zhao, Y. A New Blind Image Denoising Method Based on Asymmetric Generative Adversarial Network. IET Image Process. 2021, 15, 1260–1272. [Google Scholar] [CrossRef]
- Pan, S.; Ma, J.; Fu, X.; Chen, D.; Xu, N.; Qin, G. Denoising Research of Petrographic Thin Section Images with the Global Residual Generative Adversarial Network. Geoenergy Sci. Eng. 2023, 220, 111204. [Google Scholar] [CrossRef]
- Huang, Y.; Xia, W.; Lu, Z.; Liu, Y.; Chen, H.; Zhou, J.; Fang, L.; Zhang, Y. Noise-Powered Disentangled Representation for Unsupervised Speckle Reduction of Optical Coherence Tomography Images. IEEE Trans. Med. Imaging 2021, 40, 2600–2614. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Hong, S.; Xiong, Z.; Cui, X.; Yue, W. A Coarse-to-Fine Multi-Scale Feature Hybrid Low-Dose CT Denoising Network. Signal Process.-Image Commun. 2023, 118, 117009. [Google Scholar] [CrossRef]
- Zheng, Y.; Su, J.; Zhang, S.; Tao, M.; Wang, L. Dehaze-AGGAN: Unpaired Remote Sensing Image Dehazing Using Enhanced Attention-Guide Generative Adversarial Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Chen, X.; Huang, Y. Memory-Oriented Unpaired Learning for Single Remote Sensing Image Dehazing. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3511705. [Google Scholar] [CrossRef]
- Jin, M.; Wang, P.; Li, Y. HyA-GAN: Remote Sensing Image Cloud Removal Based on Hybrid Attention Generation Adversarial Network. Int. J. Remote Sens. 2024, 45, 1755–1773. [Google Scholar] [CrossRef]
- Kas, M.; Chahi, A.; Kajo, I.; Ruichek, Y. DLL-GAN: Degradation-Level-Based Learnable Adversarial Loss for Image Enhancement. Expert Syst. Appl. 2024, 237, 121666. [Google Scholar] [CrossRef]
- Geng, M.; Meng, X.; Yu, J.; Zhu, L.; Jin, L.; Jiang, Z.; Qiu, B.; Li, H.; Kong, H.; Yuan, J.; et al. Content-Noise Complementary Learning for Medical Image Denoising. IEEE Trans. Med. Imaging 2022, 41, 407–419. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Lin, S.; Cheng, X.; Zhou, K.; Zhang, M.; Wang, H. Dual-GAN Complementary Learning for Real-World Image Denoising. IEEE Sens. J. 2024, 24, 355–366. [Google Scholar] [CrossRef]
- Lu, W.; Onofrey, J.A.; Lu, Y.; Shi, L.; Ma, T.; Liu, Y.; Liu, C. An Investigation of Quantitative Accuracy for Deep Learning Based Denoising in Oncological PET. Phys. Med. Biol. 2019, 64, 165019. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhang, Y.; Kalra, M.K.; Lin, F.; Chen, Y.; Liao, P.; Zhou, J.; Wang, G. Low-Dose CT with a Residual Encoder-Decoder Convolutional Neural Network. IEEE Trans. Med. Imaging 2017, 36, 2524–2535. [Google Scholar] [CrossRef]
- Gao, S.-H.; Cheng, M.-M.; Zhao, K.; Zhang, X.-Y.; Yang, M.-H.; Torr, P. Res2Net: A New Multi-Scale Backbone Architecture. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 652–662. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision—ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–19. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5835–5843. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Jiang, K.; Wang, Z.; Yi, P.; Chen, C.; Huang, B.; Luo, Y.; Ma, J.; Jiang, J. Multi-Scale Progressive Fusion Network for Single Image Deraining. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar] [CrossRef]
- Kamgar-Parsi, B.; Kamgar-Parsi, B. Optimally Isotropic Laplacian Operator. IEEE Trans. Image Process. 1999, 8, 1467–1472. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-Visual-Words and Spatial Extensions for Land-Use Classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 3–5 November 2010; pp. 270–279. [Google Scholar] [CrossRef]
- Xu, J.; Li, H.; Liang, Z.; Zhang, D.; Zhang, L. Real-World Noisy Image Denoising: A New Benchmark. arXiv 2018. [Google Scholar] [CrossRef]
- Plotz, T.; Roth, S. Benchmarking Denoising Algorithms with Real Photographs. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Honolulu, HI, USA, 2017; pp. 2750–2759. [Google Scholar]
- Huynh-Thu, Q.; Ghanbari, M. Scope of Validity of PSNR in Image/Video Quality Assessment. Electron. Lett. 2008, 44, 800. [Google Scholar] [CrossRef]









| KERRYPNX | σ = 5 | σ = 10 | σ = 20 | σ = 30 | σ = 40 | σ = 50 |
|---|---|---|---|---|---|---|
| BM3D | 37.46/0.9586 | 33.19/0.9121 | 29.35/0.8323 | 27.44/0.7685 | 26.04/0.7191 | 25.18/0.6826 |
| DnCNN | 38.99/0.9696 | 35.10/0.9300 | 31.39/0.8603 | 29.60/0.8118 | 28.36/0.7729 | 27.33/0.7355 |
| DUMRN | 36.34/0.9652 | 34.47/0.9423 | 31.65/0.8890 | 29.82/0.8394 | 28.51/0.7933 | 27.47/0.7523 |
| CBDNet | 39.08/0.9757 | 35.35/0.9450 | 31.73/0.8887 | 29.69/0.8348 | 28.26/0.7847 | 27.15/0.7383 |
| DGCL | 35.48/0.9602 | 33.60/0.9329 | 30.72/0.8687 | 29.12/0.8191 | 27.91/0.7720 | 26.88/0.7238 |
| FICL (ours) | 39.14/0.9799 | 35.99/0.9570 | 32.48/0.9075 | 30.54/0.8635 | 29.23/0.8252 | 28.24/0.7913 |
| σ = 5 | σ = 10 | σ = 20 | σ = 30 | σ = 40 | σ = 50 | |
|---|---|---|---|---|---|---|
| BM3D | 36.27/0.9659 | 32.17/0.9218 | 28.43/0.8738 | 25.83/0.8411 | 22.57/0.8094 | 20.12/0.7719 |
| DnCNN | 35.67/0.9467 | 32.77/0.8993 | 29.82/0.8302 | 28.39/0.7942 | 27.32/0.7645 | 26.46/0.7409 |
| DUMRN | 33.53/0.9437 | 32.38/0.9240 | 30.31/0.8791 | 28.79/0.8380 | 27.58/0.7992 | 26.58/0.7633 |
| CBDNet | 36.21/0.9523 | 33.19/0.9240 | 30.41/0.8807 | 28.78/0.8337 | 27.47/0.7934 | 26.40/0.7523 |
| DGCL | 32.64/0.9295 | 31.41/0.9042 | 29.42/0.8527 | 28.11/0.8139 | 27.05/0.7754 | 26.08/0.7342 |
| FICL(ours) | 36.34/0.9492 | 33.26/0.9279 | 30.87/0.8852 | 29.35/0.8499 | 28.23/0.8192 | 27.34/0.7912 |
| PSNR | SSIM | |
|---|---|---|
| BM3D | 33.51 | 0.9027 |
| DnCNN | 33.97 | 0.9142 |
| DUMRN | 37.45 | 0.9489 |
| CBDNet | 37.86 | 0.9621 |
| DGCL | 38.11 | 0.9613 |
| FICL (ours) | 38.41 | 0.9652 |
| PSNR | SSIM | |
|---|---|---|
| BM3D | 33.90 | 0.8915 |
| DnCNN | 32.59 | 0.8764 |
| DUMRN | 36.75 | 0.9032 |
| CBDNet | 36.63 | 0.9085 |
| DGCL | 37.33 | 0.9133 |
| FICL (ours) | 37.45 | 0.9146 |
| σ = 0 | σ = 10 | σ = 20 | σ = 30 | σ = 40 | σ = 50 | |
|---|---|---|---|---|---|---|
| Accuracy with noisy | 0.7637 | 0.7637 | 0.7255 | 0.6945 | 0.6324 | 0.5417 |
| Accuracy with denoising | — | — | 0.7613 | 0.7303 | 0.7183 | 0.6992 |
| σ = 5 | σ = 10 | σ = 20 | σ = 30 | σ = 40 | σ = 50 | |
|---|---|---|---|---|---|---|
| Only NP | 38.02/0.9748 | 35.12/0.9514 | 31.91/0.8965 | 30.11/0.8439 | 28.57/0.7862 | 27.14/0.7174 |
| Only RIP | 37.36/0.9736 | 34.99/0.9509 | 31.87/0.9007 | 30.03/0.8556 | 28.76/0.8159 | 27.80/0.7807 |
| Fusion without FIM | 38.20/0.9766 | 35.45/0.9541 | 32.12/0.9036 | 30.23/0.8585 | 28.94/0.8188 | 27.95/0.7825 |
| FICL (ours) | 39.14/0.9799 | 35.99/0.9570 | 32.48/0.9075 | 30.54/0.8635 | 29.23/0.8252 | 28.24/0.7913 |
| σ = 5 | σ = 10 | σ = 20 | σ = 30 | σ = 40 | σ = 50 | |
|---|---|---|---|---|---|---|
| Only NP | 34.36/0.9447 | 32.73/0.9232 | 30.48/0.8766 | 28.93/0.8341 | 27.60/0.7874 | 26.32/0.7287 |
| Only RIP | 33.93/0.9440 | 32.56/0.9221 | 30.39/0.8778 | 28.91/0.8412 | 27.82/0.8096 | 26.94/0.7809 |
| Fusion without FIM | 34.44/0.9473 | 32.92/0.9257 | 30.62/0.8819 | 29.11/0.8452 | 27.99/0.8133 | 27.09/0.7838 |
| FICL (ours) | 36.34/0.9492 | 33.26/0.9279 | 30.87/0.8852 | 29.35/0.8499 | 28.23/0.8192 | 27.34/0.7912 |
| Only NP | Only RIP | Fusion without FIM | FICL | |
|---|---|---|---|---|
| PolyU | 37.47/0.9558 | 36.94/0.9516 | 37.76/0.9596 | 38.41/0.9652 |
| SIDD | 36.60/0.9042 | 36.21/0.9023 | 36.93/0.9087 | 37.45/0.9146 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Dong, Y.; Cheng, X.; Huo, Y.; Zhang, M.; Wang, H. Remote Sensing Image Denoising Based on Feature Interaction Complementary Learning. Remote Sens. 2024, 16, 3820. https://doi.org/10.3390/rs16203820
Zhao S, Dong Y, Cheng X, Huo Y, Zhang M, Wang H. Remote Sensing Image Denoising Based on Feature Interaction Complementary Learning. Remote Sensing. 2024; 16(20):3820. https://doi.org/10.3390/rs16203820
Chicago/Turabian StyleZhao, Shaobo, Youqiang Dong, Xi Cheng, Yu Huo, Min Zhang, and Hai Wang. 2024. "Remote Sensing Image Denoising Based on Feature Interaction Complementary Learning" Remote Sensing 16, no. 20: 3820. https://doi.org/10.3390/rs16203820
APA StyleZhao, S., Dong, Y., Cheng, X., Huo, Y., Zhang, M., & Wang, H. (2024). Remote Sensing Image Denoising Based on Feature Interaction Complementary Learning. Remote Sensing, 16(20), 3820. https://doi.org/10.3390/rs16203820










