Simulating High-Resolution Sun-Induced Chlorophyll Fluorescence Image of Three-Dimensional Canopy Based on Photon Mapping
Abstract
1. Introduction
2. Method
2.1. Formulation of the Light Transport for Fluorescence
2.1.1. A General Formulation of the Light Transport for Fluorescence
2.1.2. Formulation of the Light Transport for the Canopy SIF
2.2. Implementation of the SIF Simulator
2.2.1. Overview of the SIF Simulation Algorithm
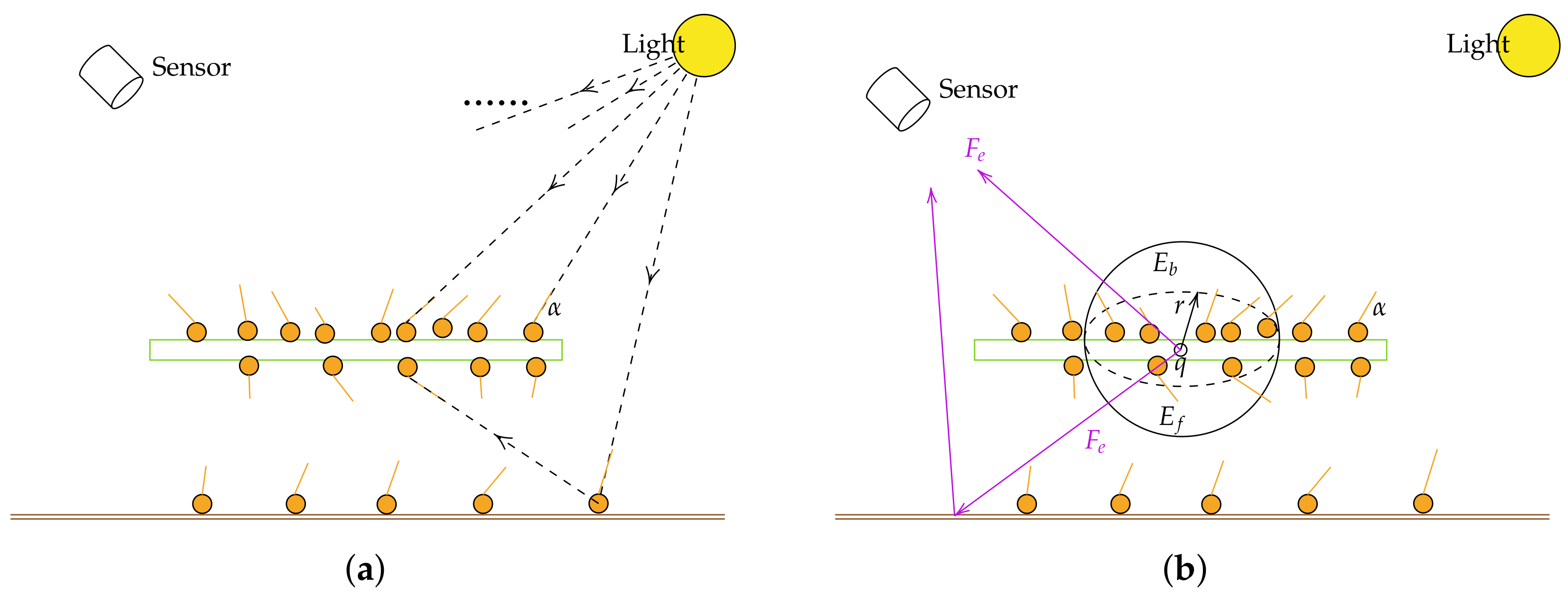
2.2.2. Photon Tracing
2.2.3. Collection of Energy
3. Data
3.1. Abstract Scenes and Simulated Data
3.1.1. Abstract Scenes
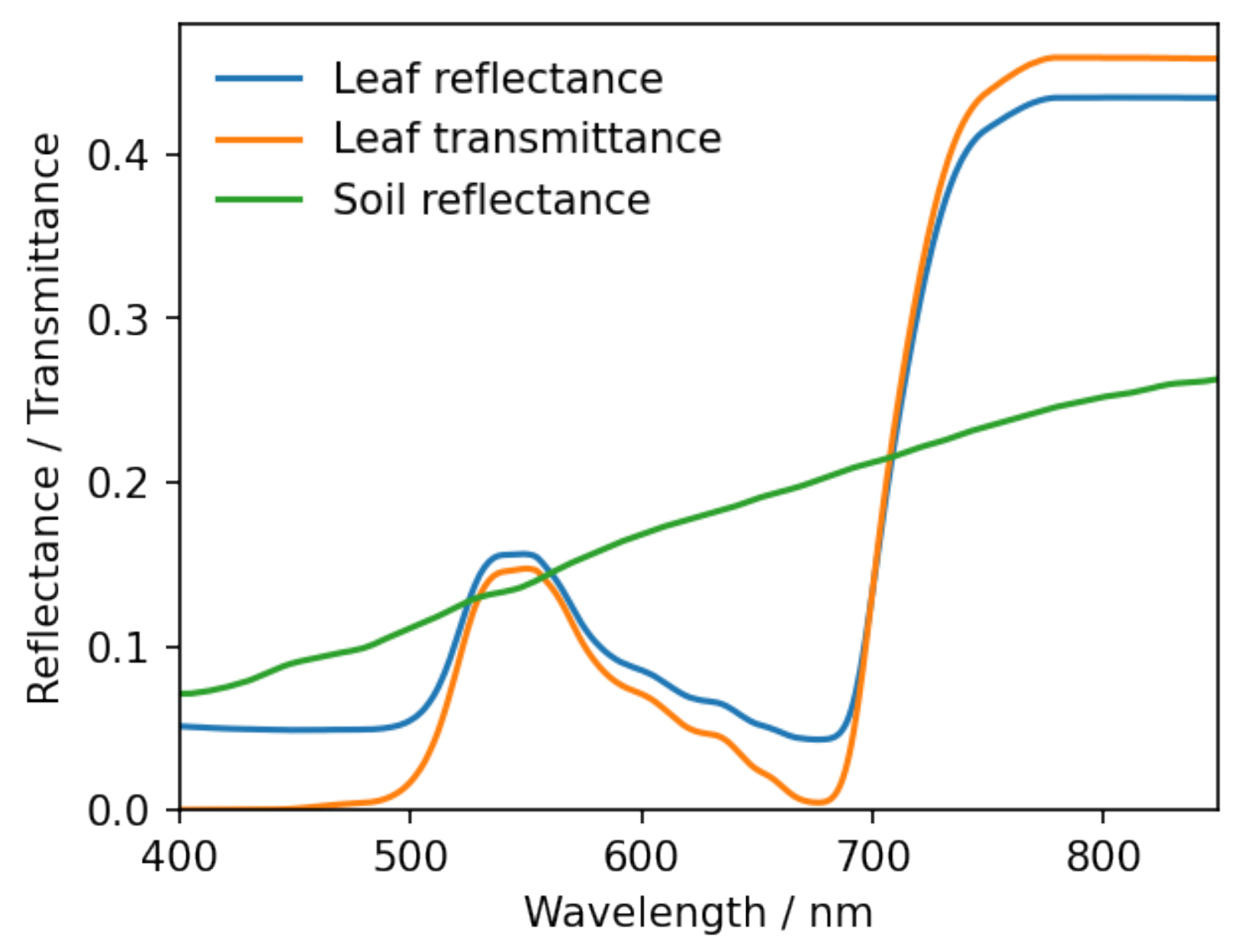
3.1.2. Spectral Data
3.2. Field Data about Soybean
3.2.1. Leaf Spectral Measurements
3.2.2. Canopy Structural Measurements and Abstract Scene Construction
3.2.3. Canopy Spectral Measurements
3.3. Field Data about Corn
3.3.1. Leaf and Stem Spectral Measurements
3.3.2. Structural Measurements and Geometrically Explicit Canopy Generation
4. Results
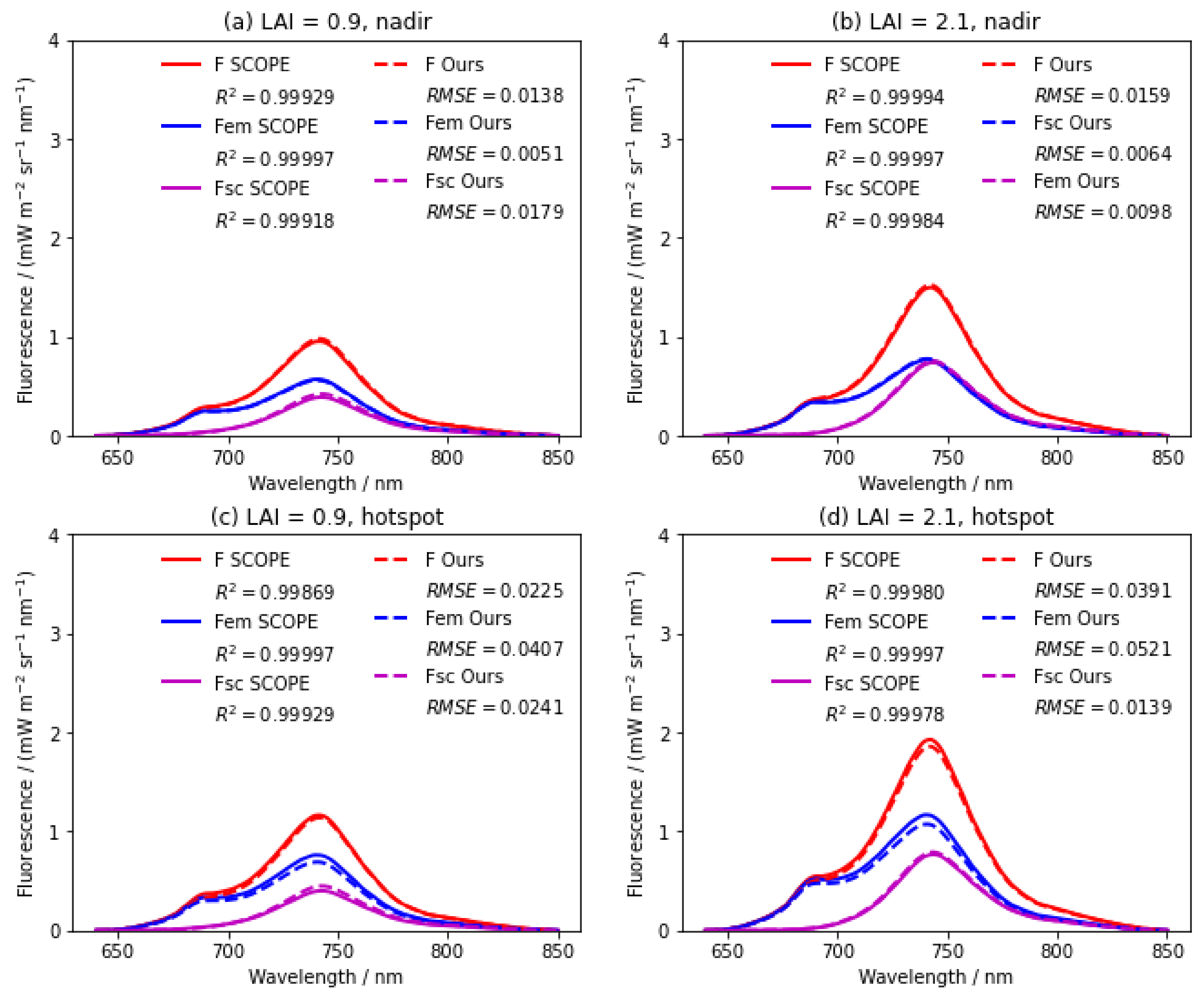
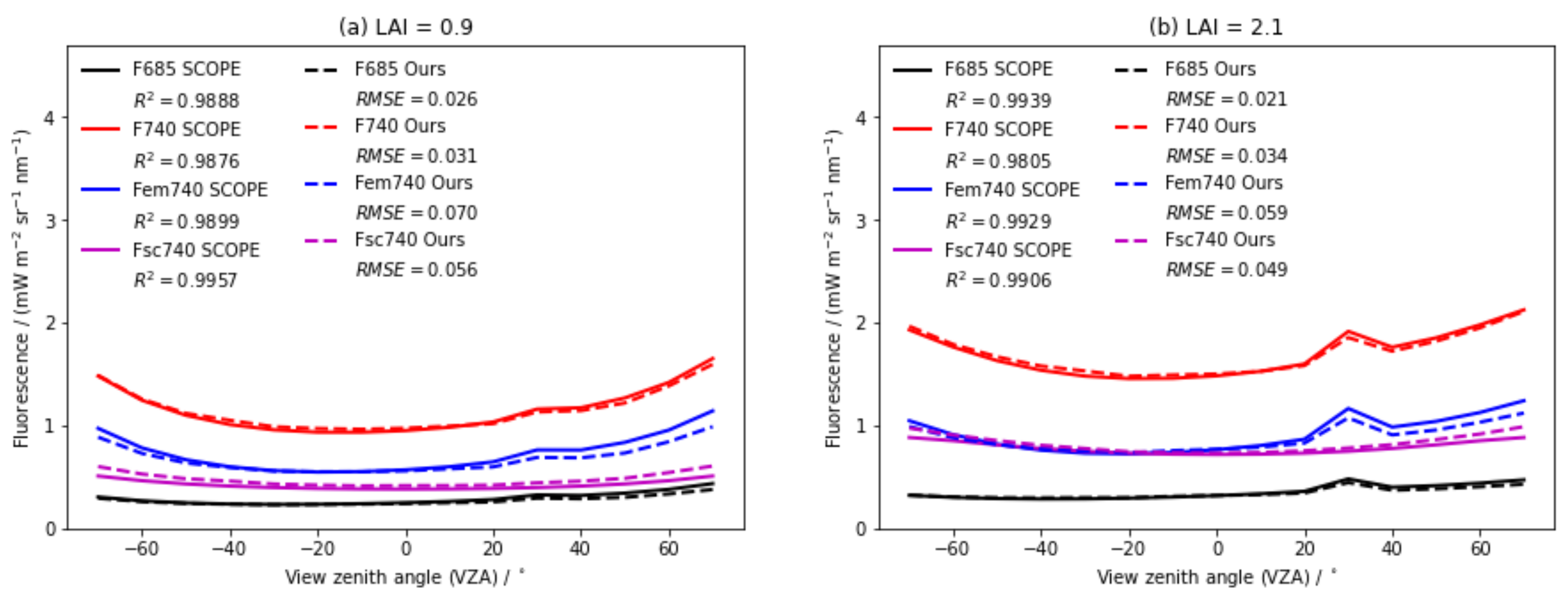
4.1. Comparison with the SCOPE Model
4.1.1. SIF Spectrum
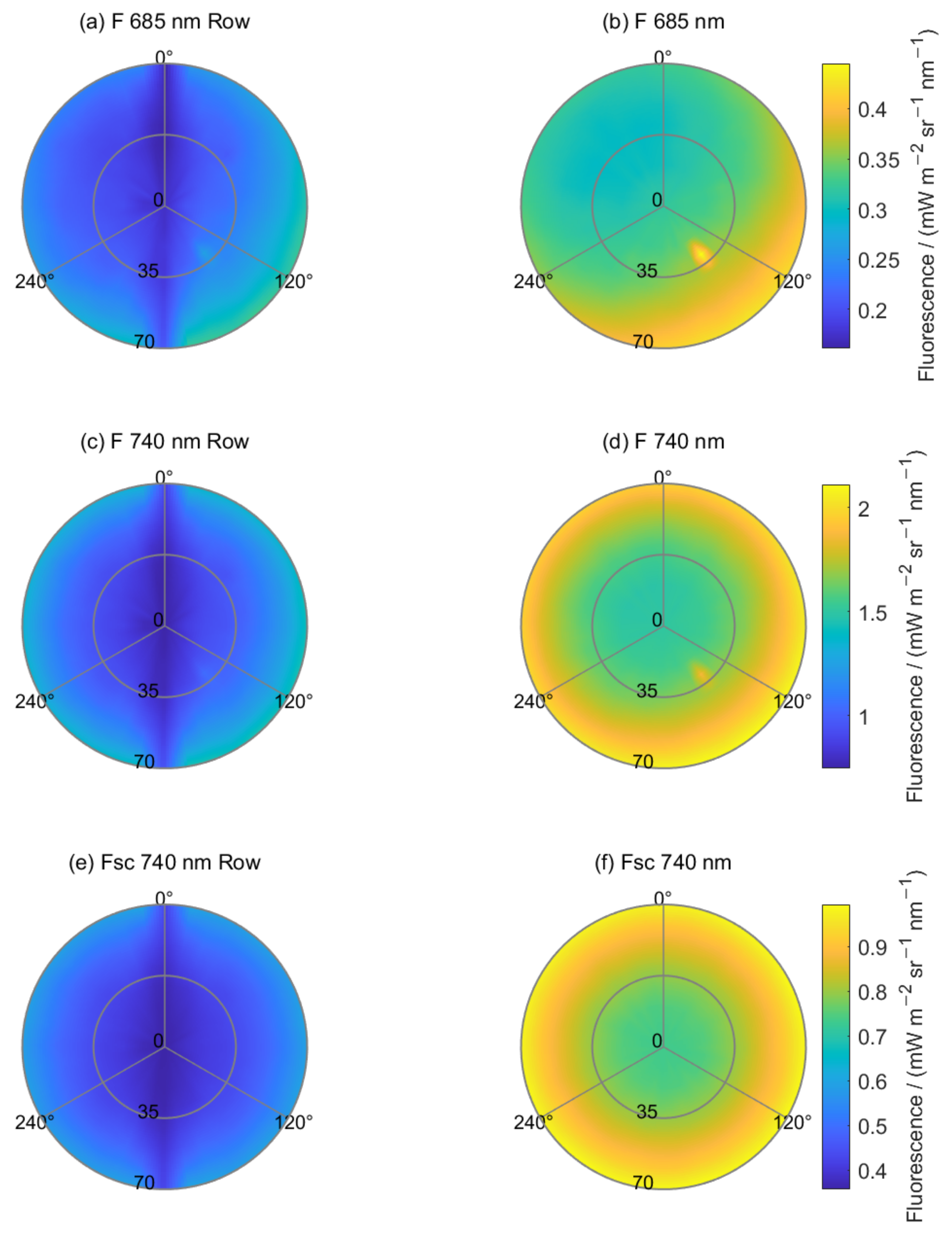
4.1.2. Angular SIF Distributions
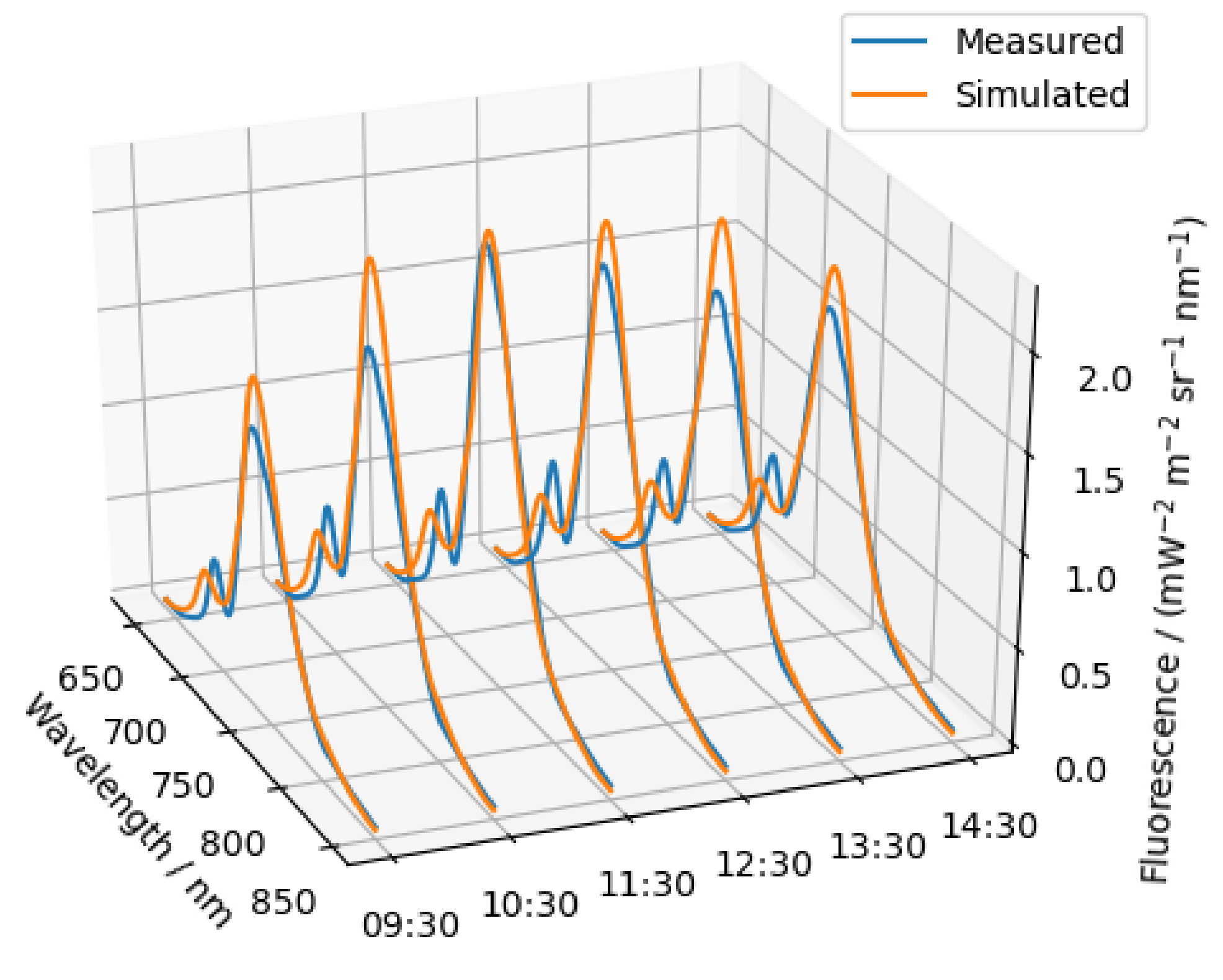
4.2. Comparison with Field Measurements
5. Discussion
5.1. Model Application on the Impact of Row Structure on SIF Distributions
5.2. Model Application on the Realistic Corn Scene
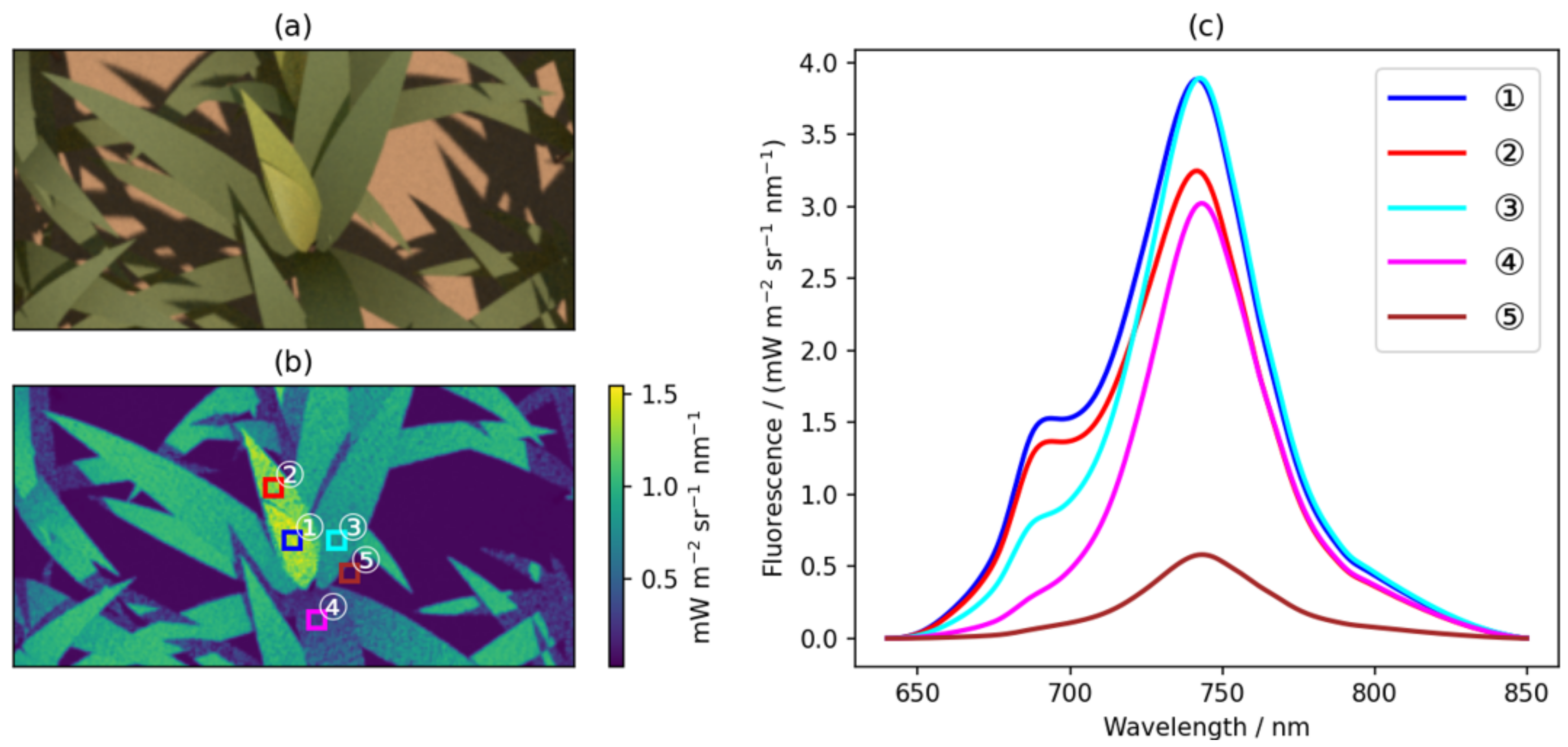
5.2.1. Fluorescence Imaging
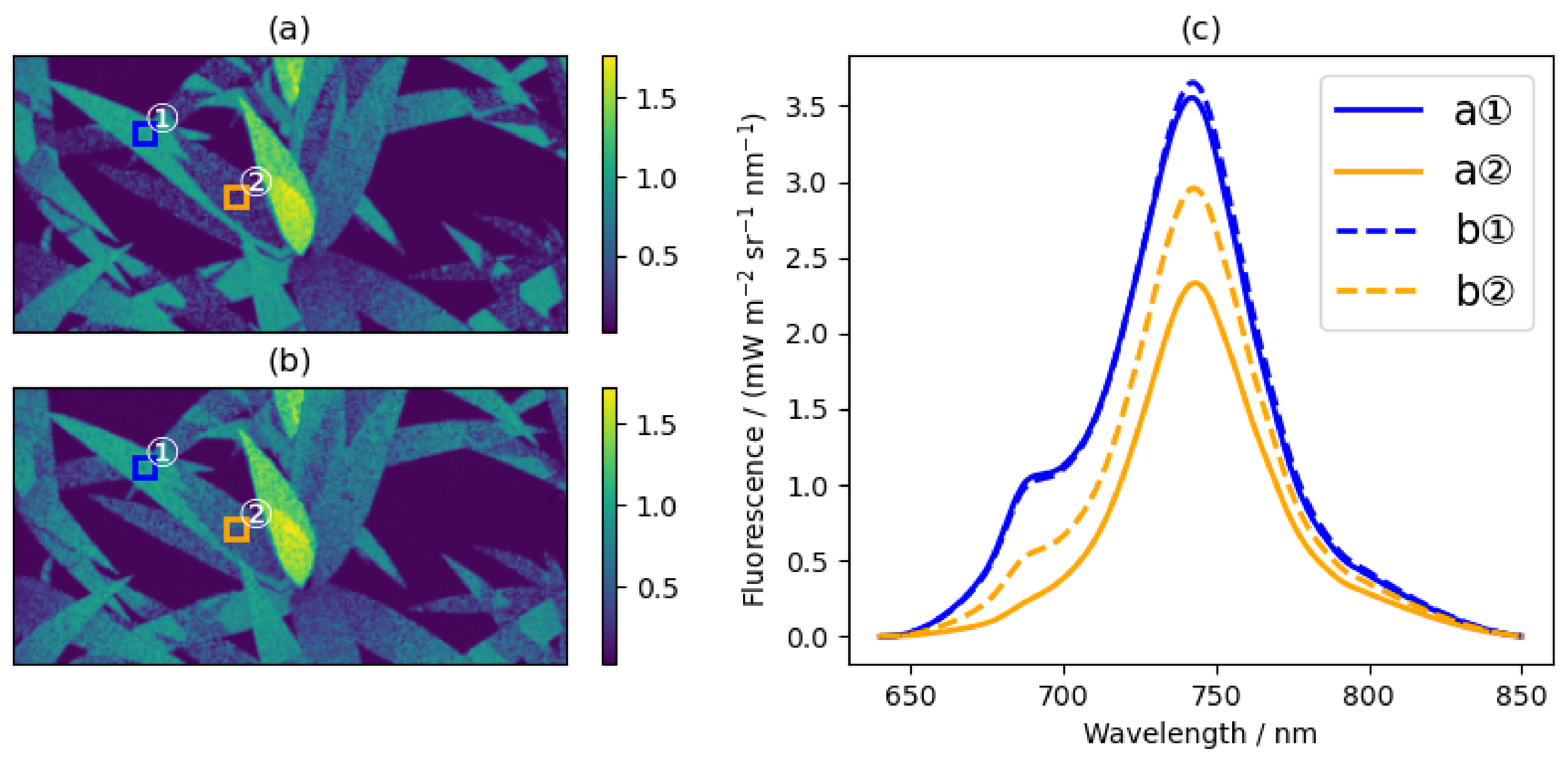
5.2.2. SIF Images under Different Natural Light Conditions
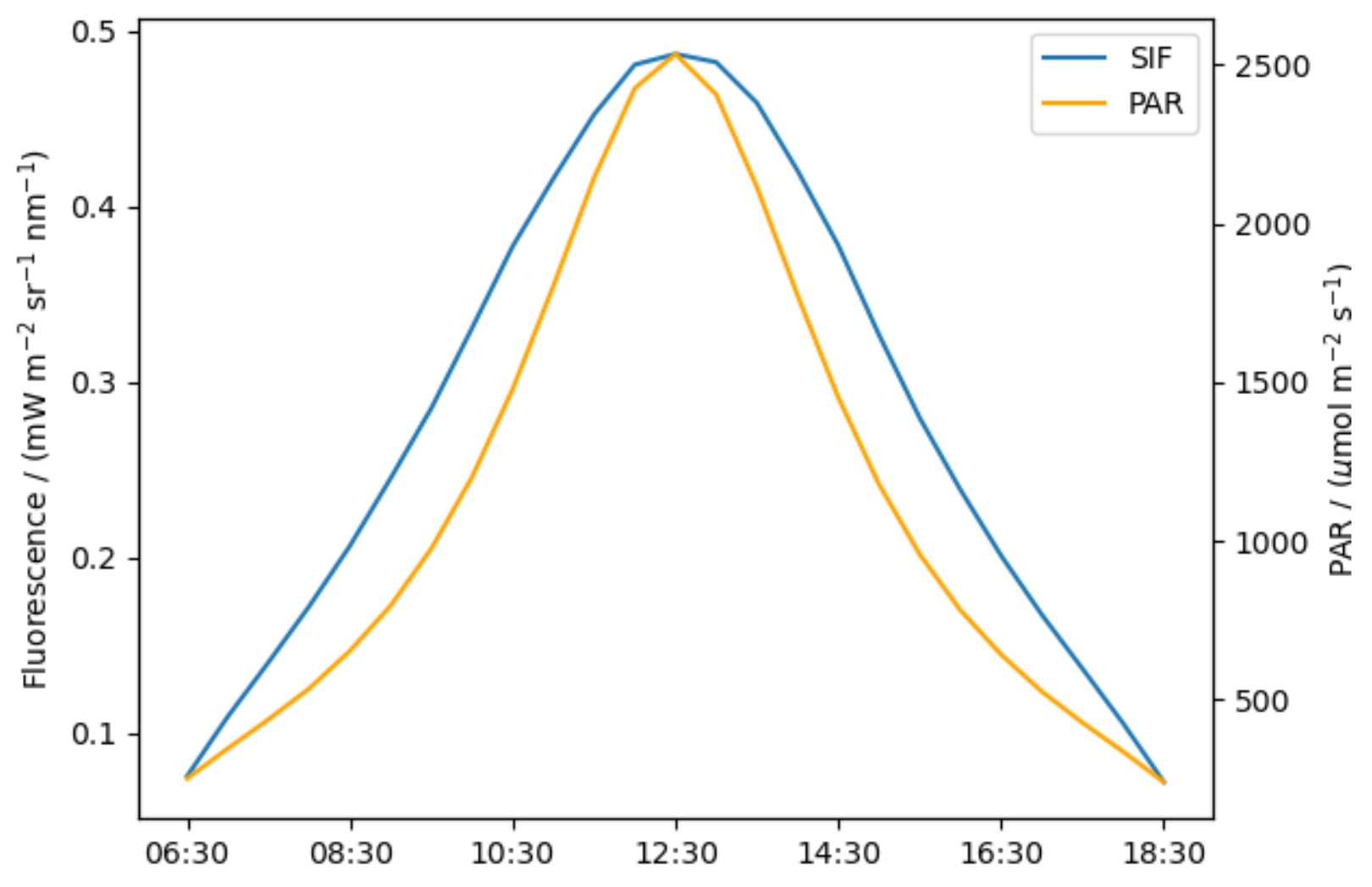
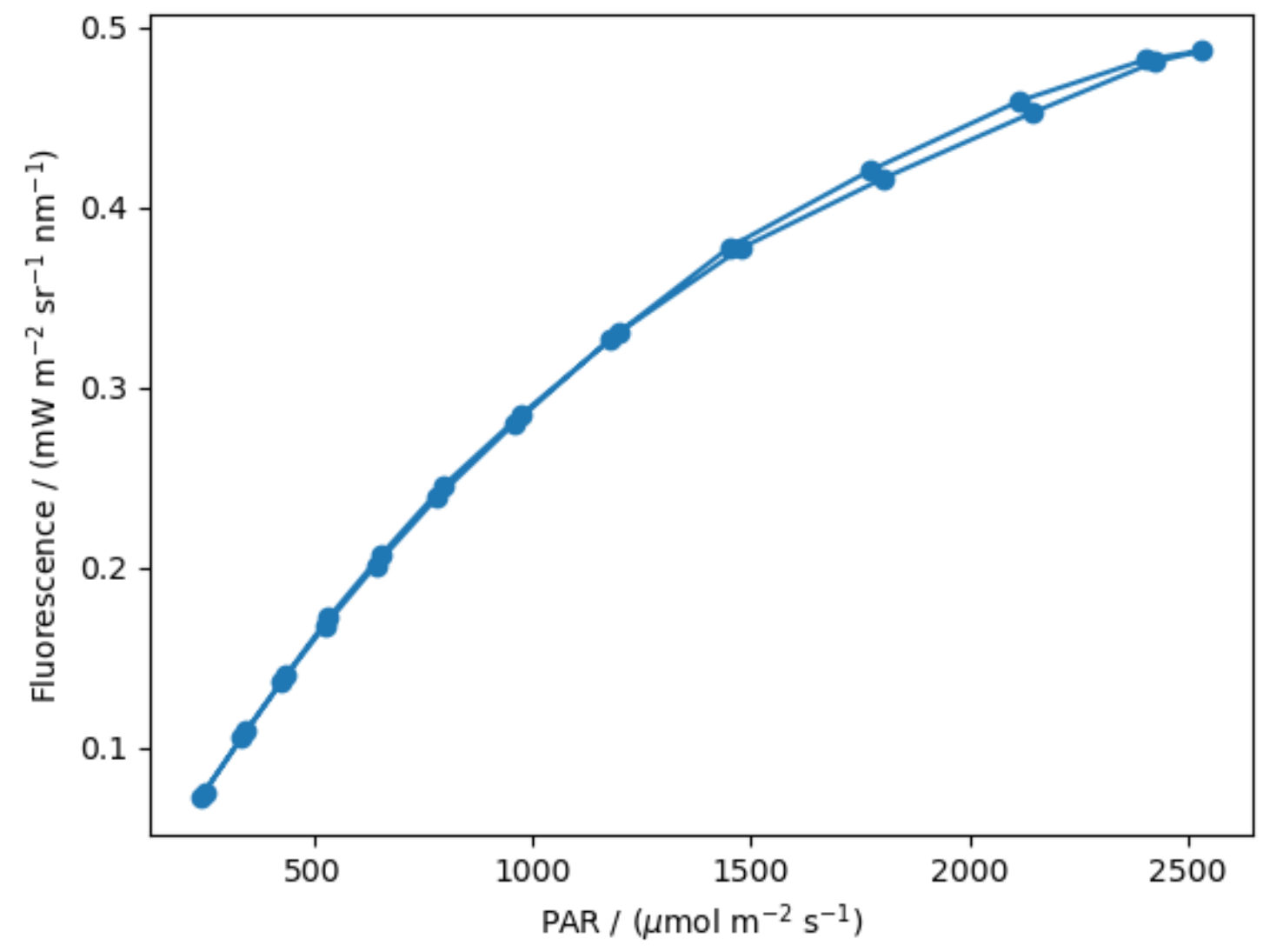
5.2.3. Diurnal Variation of the SIF
5.3. Perspectives
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Dependence of the Fluorescence Correction Factor on Incident Photosynthetic Active Radiation Level
References
- Glassner, A. Principles of Digital Image Synthesis; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar] [CrossRef]
- Louis, J.; Cerovic, Z.G.; Moya, I. Quantitative Study of Fluorescence Excitation and Emission Spectra of Bean Leaves. J. Photochem. Photobiol. B Biol. 2006, 85, 65–71. [Google Scholar] [CrossRef] [PubMed]
- Oerke, E.C. Remote Sensing of Diseases. Annu. Rev. Phytopathol. 2020, 58, 225–252. [Google Scholar] [CrossRef] [PubMed]
- Goetz, A.F.H.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging Spectrometry for Earth Remote Sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Milton, E.J. Review Article Principles of Field Spectroscopy. Int. J. Remote Sens. 1987, 8, 1807–1827. [Google Scholar] [CrossRef]
- Aasen, H.; Van Wittenberghe, S.; Sabater Medina, N.; Damm, A.; Goulas, Y.; Wieneke, S.; Hueni, A.; Malenovský, Z.; Alonso, L.; Pacheco-Labrador, J.; et al. Sun-Induced Chlorophyll Fluorescence II: Review of Passive Measurement Setups, Protocols, and Their Application at the Leaf to Canopy Level. Remote Sens. 2019, 11, 927. [Google Scholar] [CrossRef]
- Miller, J.; Berger, M.; Goulas, Y.; Jacquemoud, S.; Louis, J.; Mohammed, G.; Moise, N.; Moreno, J.; Moya, I.; Pedros, R.; et al. Development of a Vegetation Fluorescence Canopy Model; Technical Report; ESTEC: Noordwijk, The Netherlands, 2005. [Google Scholar]
- Zhang, Y.; Xiao, X.; Jin, C.; Dong, J.; Zhou, S.; Wagle, P.; Joiner, J.; Guanter, L.; Zhang, Y.; Zhang, G.; et al. Consistency between Sun-Induced Chlorophyll Fluorescence and Gross Primary Production of Vegetation in North America. Remote Sens. Environ. 2016, 183, 154–169. [Google Scholar] [CrossRef]
- Mohammed, G.H.; Colombo, R.; Middleton, E.M.; Rascher, U.; van der Tol, C.; Nedbal, L.; Goulas, Y.; Pérez-Priego, O.; Damm, A.; Meroni, M.; et al. Remote Sensing of Solar-Induced Chlorophyll Fluorescence (SIF) in Vegetation: 50 Years of Progress. Remote Sens. Environ. 2019, 231, 111177. [Google Scholar] [CrossRef] [PubMed]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.P.; Yoshida, Y.; Corp, L.A.; Middleton, E.M. First Observations of Global and Seasonal Terrestrial Chlorophyll Fluorescence from Space. Biogeosciences 2011, 8, 637–651. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A.; et al. New Global Observations of the Terrestrial Carbon Cycle from GOSAT: Patterns of Plant Fluorescence with Gross Primary Productivity: Chlorophyll Fluorescence from Space. Geophys. Res. Lett. 2011, 38, L17706. [Google Scholar] [CrossRef]
- Frankenberg, C.; O’Dell, C.; Berry, J.; Guanter, L.; Joiner, J.; Köhler, P.; Pollock, R.; Taylor, T.E. Prospects for Chlorophyll Fluorescence Remote Sensing from the Orbiting Carbon Observatory-2. Remote Sens. Environ. 2014, 147, 1–12. [Google Scholar] [CrossRef]
- Köhler, P.; Frankenberg, C.; Magney, T.S.; Guanter, L.; Joiner, J.; Landgraf, J. Global Retrievals of Solar-Induced Chlorophyll Fluorescence with TROPOMI: First Results and Intersensor Comparison to OCO-2. Geophys. Res. Lett. 2018, 45, 10,456–10,463. [Google Scholar] [CrossRef] [PubMed]
- Du, S.; Liu, L.; Liu, X.; Zhang, X.; Zhang, X.; Bi, Y.; Zhang, L. Retrieval of Global Terrestrial Solar-Induced Chlorophyll Fluorescence from TanSat Satellite. Sci. Bull. 2018, 63, 1502–1512. [Google Scholar] [CrossRef] [PubMed]
- Porcar-Castell, A.; Tyystjärvi, E.; Atherton, J.; van der Tol, C.; Flexas, J.; Pfündel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. Linking Chlorophyll a Fluorescence to Photosynthesis for Remote Sensing Applications: Mechanisms and Challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef] [PubMed]
- Moreno, J.F.; Asner, G.P.; Bach, H.; Belenguer, T.; Bell, A.; Buschmann, C.; Calera, A.; Calpe, J.; Campbell, P.; Cecchi, G.; et al. FLuorescence EXplorer (FLEX): An Optimised Payload to Map Vegetation Photosynthesis from Space. In Proceedings of the 57th International Astronautical Congress, Valencia, Spain, 2–6 October 2006. [Google Scholar] [CrossRef]
- Rascher, U.; Alonso, L.; Burkart, A.; Cilia, C.; Cogliati, S.; Colombo, R.; Damm, A.; Drusch, M.; Guanter, L.; Hanus, J.; et al. Sun-Induced Fluorescence—A New Probe of Photosynthesis: First Maps from the Imaging Spectrometer HyPlant. Glob. Change Biol. 2015, 21, 4673–4684. [Google Scholar] [CrossRef]
- Pinto, F.; Damm, A.; Schickling, A.; Panigada, C.; Cogliati, S.; Müller-Linow, M.; Ballvora, A.; Rascher, U. Sun-Induced Chlorophyll Fluorescence from High-Resolution Imaging Spectroscopy Data to Quantify Spatio-Temporal Patterns of Photosynthetic Function in Crop Canopies. Plant Cell Environ. 2016, 39, 1500–1512. [Google Scholar] [CrossRef]
- Pinto, F.; Müller-Linow, M.; Schickling, A.; Cendrero-Mateo, M.; Ballvora, A.; Rascher, U. Multiangular Observation of Canopy Sun-Induced Chlorophyll Fluorescence by Combining Imaging Spectroscopy and Stereoscopy. Remote Sens. 2017, 9, 415. [Google Scholar] [CrossRef]
- Jiang, Y.; Snider, J.L.; Li, C.; Rains, G.C.; Paterson, A.H. Ground Based Hyperspectral Imaging to Characterize Canopy-Level Photosynthetic Activities. Remote Sens. 2020, 12, 315. [Google Scholar] [CrossRef]
- Araus, J.L.; Kefauver, S.C.; Zaman-Allah, M.; Olsen, M.S.; Cairns, J.E. Translating High-Throughput Phenotyping into Genetic Gain. Trends Plant Sci. 2018, 23, 451–466. [Google Scholar] [CrossRef]
- Watt, M.; Fiorani, F.; Usadel, B.; Rascher, U.; Muller, O.; Schurr, U. Phenotyping: New Windows into the Plant for Breeders. Annu. Rev. Plant Biol. 2020, 71, 689–712. [Google Scholar] [CrossRef]
- Bendig, J.; Malenovsky, Z.; Gautam, D.; Lucieer, A. Solar-Induced Chlorophyll Fluorescence Measured from an Unmanned Aircraft System: Sensor Etaloning and Platform Motion Correction. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3437–3444. [Google Scholar] [CrossRef]
- van der Tol, C.; Verhoef, W.; Timmermans, J.; Verhoef, A.; Su, Z. An Integrated Model of Soil-Canopy Spectral Radiances, Photosynthesis, Fluorescence, Temperature and Energy Balance. Biogeosciences 2009, 6, 3109–3129. [Google Scholar] [CrossRef]
- Zhao, F.; Dai, X.; Verhoef, W.; Guo, Y.; van der Tol, C.; Li, Y.; Huang, Y. FluorWPS: A Monte Carlo Ray-Tracing Model to Compute Sun-Induced Chlorophyll Fluorescence of Three-Dimensional Canopy. Remote Sens. Environ. 2016, 187, 385–399. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Lauret, N.; Yin, T.; Landier, L.; Kallel, A.; Malenovsky, Z.; Bitar, A.A.; Aval, J.; Benhmida, S.; Qi, J.; et al. DART: Recent Advances in Remote Sensing Data Modeling with Atmosphere, Polarization, and Chlorophyll Fluorescence. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2640–2649. [Google Scholar] [CrossRef]
- Hernández-Clemente, R.; North, P.R.J.; Hornero, A.; Zarco-Tejada, P.J. Assessing the Effects of Forest Health on Sun-Induced Chlorophyll Fluorescence Using the FluorFLIGHT 3-D Radiative Transfer Model to Account for Forest Structure. Remote Sens. Environ. 2017, 193, 165–179. [Google Scholar] [CrossRef]
- Sakai, Y.; Kobayashi, H.; Kato, T. FLiES-SIF Ver. 1.0: Three-dimensional Radiative Transfer Model for Estimating Solar Induced Fluorescence. Geosci. Model Dev. 2020. preprint. [Google Scholar] [CrossRef]
- Verrelst, J.; van der Tol, C.; Magnani, F.; Sabater, N.; Rivera, J.P.; Mohammed, G.; Moreno, J. Evaluating the Predictive Power of Sun-Induced Chlorophyll Fluorescence to Estimate Net Photosynthesis of Vegetation Canopies: A SCOPE Modeling Study. Remote Sens. Environ. 2016, 176, 139–151. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Yin, T.; Yan, G.; Gastellu-Etchegorry, J.P.; Li, L.; Zhang, W.; Mu, X.; Norford, L.K. LESS: LargE-Scale Remote Sensing Data and Image Simulation Framework over Heterogeneous 3D Scenes. Remote Sens. Environ. 2019, 221, 695–706. [Google Scholar] [CrossRef]
- Wang, Y.; Kallel, A.; Yang, X.; Regaieg, O.; Lauret, N.; Guilleux, J.; Chavanon, E.; Gastellu-Etchegorry, J.P. DART-Lux: An Unbiased and Rapid Monte Carlo Radiative Transfer Method for Simulating Remote Sensing Images. Remote Sens. Environ. 2022, 274, 112973. [Google Scholar] [CrossRef]
- Jensen, H.W. Realistic Image Synthesis Using Photon Mapping; A K Peters: Natick, MA, USA, 2001. [Google Scholar]
- Baker, N.R. Chlorophyll Fluorescence: A Probe of Photosynthesis In Vivo. Annu. Rev. Plant Biol. 2008, 59, 89–113. [Google Scholar] [CrossRef]
- Kajiya, J.T. The Rendering Equation. ACM SIGGRAPH Comput. Graph. 1986, 20, 143–150. [Google Scholar] [CrossRef]
- Sakas, G.; Müller, S.; Shirley, P. (Eds.) Photorealistic Rendering Techniques; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar] [CrossRef]
- Yazici, Ö. Spectral Raytracing. Available online: https://graphics.cg.uni-saarland.de/courses/ris-2021/slides/Spectral%20Raytracing.pdf (accessed on 8 March 2022).
- Vilfan, N.; van der Tol, C.; Muller, O.; Rascher, U.; Verhoef, W. Fluspect-B: A Model for Leaf Fluorescence, Reflectance and Transmittance Spectra. Remote Sens. Environ. 2016, 186, 596–615. [Google Scholar] [CrossRef]
- Rosema, A.; Snel, J.F.H.; Zahn, H.; Buurmeijer, W.F.; Van Hove, L.W.A. The Relation between Laser-Induced Chlorophyll Fluorescence and Photosynthesis. Remote Sens. Environ. 1998, 65, 143–154. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.; Painter, T.; Dangel, S.; Martonchik, J. Reflectance Quantities in Optical Remote Sensing—Definitions and Case Studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Veach, E. Robust Monte Carlo Methods for Light Transport Simulation. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1998. [Google Scholar]
- Pharr, M.; Jakob, W.; Humphreys, G. Physically Based Rendering: From Theory to Implementation, 3rd ed.; Morgan Kaufmann Publishers: Burlington, MA, USA; Elsevier: Cambridge, MA, USA, 2017. [Google Scholar]
- Jakob, W. Mitsuba Renderer. Available online: www.mitsuba-renderer.org (accessed on 10 September 2023).
- Shirley, P.; Wang, C.; Zimmerman, K. Monte Carlo Techniques for Direct Lighting Calculations. ACM Trans. Graph. 1996, 15, 1–36. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Y.; Yin, T.; Wang, C.; Lauret, N.; Regaieg, O.; Xi, X.; Gastellu-Etchegorry, J.P. Comprehensive LiDAR Simulation with Efficient Physically-Based DART-Lux Model (I): Theory, Novelty, and Consistency Validation. Remote Sens. Environ. 2022, 272, 112952. [Google Scholar] [CrossRef]
- Jarosz, W. Efficient Monte Carlo Methods for Light Transport in Scattering Media. Ph.D. Thesis, UC San Diego, San Diego, CA, USA, 2008. [Google Scholar]
- Zhao, F.; Gu, X.; Verhoef, W.; Wang, Q.; Yu, T.; Liu, Q.; Huang, H.; Qin, W.; Chen, L.; Zhao, H. A Spectral Directional Reflectance Model of Row Crops. Remote Sens. Environ. 2010, 114, 265–285. [Google Scholar] [CrossRef]
- Zhao, F.; Guo, Y.; Verhoef, W.; Gu, X.; Liu, L.; Yang, G. A Method to Reconstruct the Solar-Induced Canopy Fluorescence Spectrum from Hyperspectral Measurements. Remote Sens. 2014, 6, 10171–10192. [Google Scholar] [CrossRef]
- Wu, M.X.; Zhu, Q.J.; Wang, J.D.; Xiang, Y.Q.; Su, L.H.; Zhou, X.D.; Tang, S.H. Approach for Computation of Structural Parameters and Visual Research of Canopy in Summer Corn. Acta Agron. Sin. 2002, 28, 721–726. [Google Scholar]
- Morozumi, T.; Kato, T.; Kobayashi, H.; Sakai, Y.; Tsujimoto, K.; Nakashima, N.; Buareal, K.; Lan, W.; Ninomiya, H. Row Orientation Influences the Diurnal Cycle of Solar-Induced Chlorophyll Fluorescence Emission from Wheat Canopy, as Demonstrated by Radiative Transfer Modeling. Agric. For. Meteorol. 2023, 339, 109576. [Google Scholar] [CrossRef]
- Magney, T.S.; Bowling, D.R.; Logan, B.A.; Grossmann, K.; Stutz, J.; Blanken, P.D.; Burns, S.P.; Cheng, R.; Garcia, M.A.; Köhler, P.; et al. Mechanistic Evidence for Tracking the Seasonality of Photosynthesis with Solar-Induced Fluorescence. Proc. Natl. Acad. Sci. USA 2019, 116, 11640–11645. [Google Scholar] [CrossRef]
- McCartney, E. Optics of the Atmosphere; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Van Wittenberghe, S.; Amin, E.; Pascual-Venteo, A.B.; Pérez-Suay, A.; Tenjo, C.; Sabater, N.; Van Der Tol, C.; Drusch, M.; Moreno, J. Retrieval of Leaf-Level Fluorescence Quantum Efficiency and NPQ-related Xanthophyll Absorption through Spectral Unmixing Strategies for Future VIS-NIR Imaging Spectroscopy. Remote Sens. Environ. 2024, 300, 113879. [Google Scholar] [CrossRef]
- Zhao, X.; Qi, J.; Xu, H.; Yu, Z.; Yuan, L.; Chen, Y.; Huang, H. Evaluating the Potential of Airborne Hyperspectral LiDAR for Assessing Forest Insects and Diseases with 3D Radiative Transfer Modeling. Remote Sens. Environ. 2023, 297, 113759. [Google Scholar] [CrossRef]
- Linn, A.I.; Zeller, A.K.; Pfündel, E.E.; Gerhards, R. Features and Applications of a Field Imaging Chlorophyll Fluorometer to Measure Stress in Agricultural Plants. Precis. Agric. 2021, 22, 947–963. [Google Scholar] [CrossRef]
- Schreiber, U.; Schliwa, U.; Bilger, W. Continuous Recording of Photochemical and Non-Photochemical Chlorophyll Fluorescence Quenching with a New Type of Modulation Fluorometer. Photosynth. Res. 1986, 10, 51–62. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.; Wang, Y.; Regaieg, O.; Yin, T.; Malenovsky, Z.; Zhen, Z.; Yang, X.; Tao, Z.; Landier, L.; Bitar, A.A.; et al. Recent Improvements in the Dart Model for Atmosphere, Topography, Large Landscape, Chlorophyll Fluorescence, Satellite Image Inversion. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 3455–3458. [Google Scholar] [CrossRef]
- Zhao, F.; Li, Z.; Verhoef, W.; Fan, C.; Luan, H.; Yin, T.; Zhang, J.; Liu, Z.; Tong, C.; Bao, Y. Simulation of Solar-Induced Chlorophyll Fluorescence by Modeling Radiative Coupling between Vegetation and Atmosphere with WPS. Remote Sens. Environ. 2022, 277, 113075. [Google Scholar] [CrossRef]











| Scene Index | Leaf Area Index | Average Leaf Angle/Standard Deviation/Degrees | Canopy Height/cm |
|---|---|---|---|
| S1 | 0.9 | 54/23 | 40 |
| S2 | 2.1 | 54/23 | 140 |
| S3 | 2.1 | 54/23 | 140 |
| Parameter | Unit | Description | Value |
|---|---|---|---|
| N | - | Leaf thickness parameter | 1.5 |
| Cab | μg cm−2 | Chlorophyll AB content | 40 |
| Cca | μg cm−2 | Carotenoid content | 10 |
| Cw | cm | Leaf water equivalent layer | 0.009 |
| Cdm | μg cm−2 | Dry matter content | 0.012 |
| fqe | - | Fluorescence quantum yield efficiency at photosystem level | 0.01 |
| F 685 nm | F 740 nm | Fem 740 nm | Fsc 740 nm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Scene | RMSE | RMSE | RMSE | RMSE | |||||||
| LAI = 0.9 | 0.9888 | 0.026 | 0.9876 | 0.031 | 0.9899 | 0.070 | 0.9957 | 0.056 | |||
| LAI = 2.1 | 0.9939 | 0.021 | 0.9805 | 0.034 | 0.9929 | 0.059 | 0.9906 | 0.049 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Xie, D.; Qi, J.; Yan, G.; Mu, X. Simulating High-Resolution Sun-Induced Chlorophyll Fluorescence Image of Three-Dimensional Canopy Based on Photon Mapping. Remote Sens. 2024, 16, 3783. https://doi.org/10.3390/rs16203783
Luo Y, Xie D, Qi J, Yan G, Mu X. Simulating High-Resolution Sun-Induced Chlorophyll Fluorescence Image of Three-Dimensional Canopy Based on Photon Mapping. Remote Sensing. 2024; 16(20):3783. https://doi.org/10.3390/rs16203783
Chicago/Turabian StyleLuo, Yaotao, Donghui Xie, Jianbo Qi, Guangjian Yan, and Xihan Mu. 2024. "Simulating High-Resolution Sun-Induced Chlorophyll Fluorescence Image of Three-Dimensional Canopy Based on Photon Mapping" Remote Sensing 16, no. 20: 3783. https://doi.org/10.3390/rs16203783
APA StyleLuo, Y., Xie, D., Qi, J., Yan, G., & Mu, X. (2024). Simulating High-Resolution Sun-Induced Chlorophyll Fluorescence Image of Three-Dimensional Canopy Based on Photon Mapping. Remote Sensing, 16(20), 3783. https://doi.org/10.3390/rs16203783






