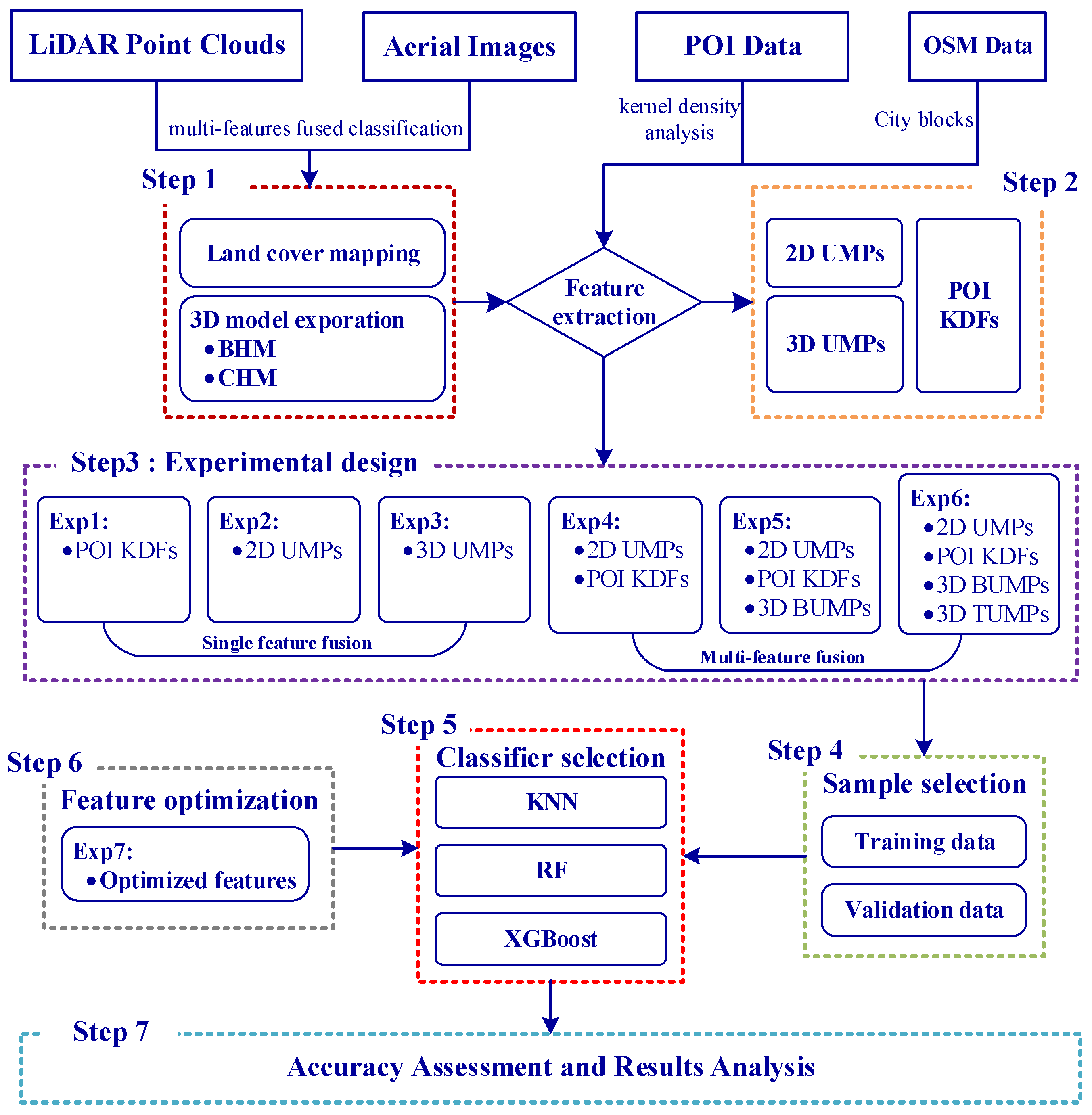
3.5.1. Sample Selection
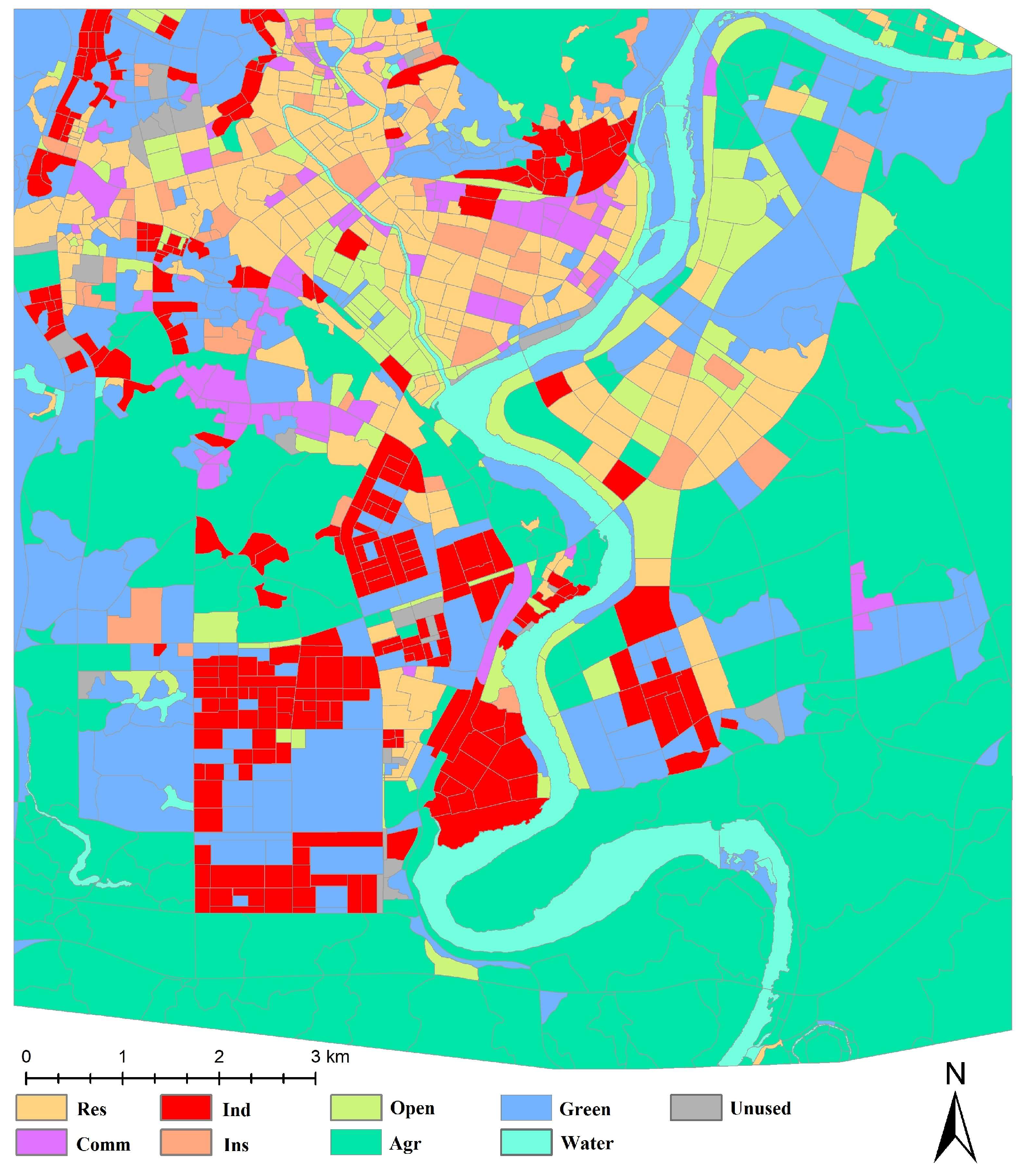
Our study area was characterized by a diverse range of functionalities, including residential housing, factories, hotels, shopping centers, and urban villages. Leveraging airborne images and high-precision Google Maps, we meticulously classified the study area into two distinct zones: built-up and non-built-up. This classification was based on a nuanced understanding of the social and economic characteristics of each city block, as well as the composition of the underlying surfaces. Within the built-up zones, there were identifiable segments such as residential areas, commercial districts, industrial sectors, institutional services, and open spaces. Conversely, the non-built-up zones encompass agricultural zones, green spaces, water, and unused zones. A detailed breakdown of these functional categories within the study area is presented in
Table 6, providing a comprehensive overview of the diverse landscape and land cover patterns.
In machine learning algorithm, the process of selecting classification samples is a pivotal step that has a direct impact on the construction of models and the quality of the classification results. The sample dataset comprises both training data and validation data. The training data are employed to construct the learning model, whereas the validation data are utilized to assess the model’s capacity to discriminate new samples. The testing error on the validation data provides an approximation of the generalization error and is used to select the learning model. To avoid the impact of sample quantity and proportion imbalance on classifier training [
45], we selected the sample dataset for each UFZ based on the spectral responses of objects on aerial images and existing geographic data. This process, combined with the delineation of city blocks and nine UFZs, resulted in the selection of sample datasets covering the entire study area and all categories. The number of samples for each UFZ was determined based on the proportion of each UFZ within the entire study area. The selection of the sample dataset involves several steps: Initially, we randomly generated sample dataset that spanned the entire study area without including any feature attribute information. Subsequently, we combined high-resolution Google Earth images with aerial images taken at similar times to label the sample dataset with specific categories. We then employed random sampling once again to divide the sample dataset into two sets: 70% training data and non-overlapping 30% validation data. Finally, we extracted the attribute information contained within the input features of each classification experiment and assigned it to the corresponding training and validation data. Following these steps, we prepared the sample dataset for Exp.1–6, with each sample data containing its associated input feature information.
Figure 6 displays the number of training and validation data samples for UFZ classification, indirectly indicating the approximate proportion of each UFZ within the study area.
3.5.2. Classifier Selection
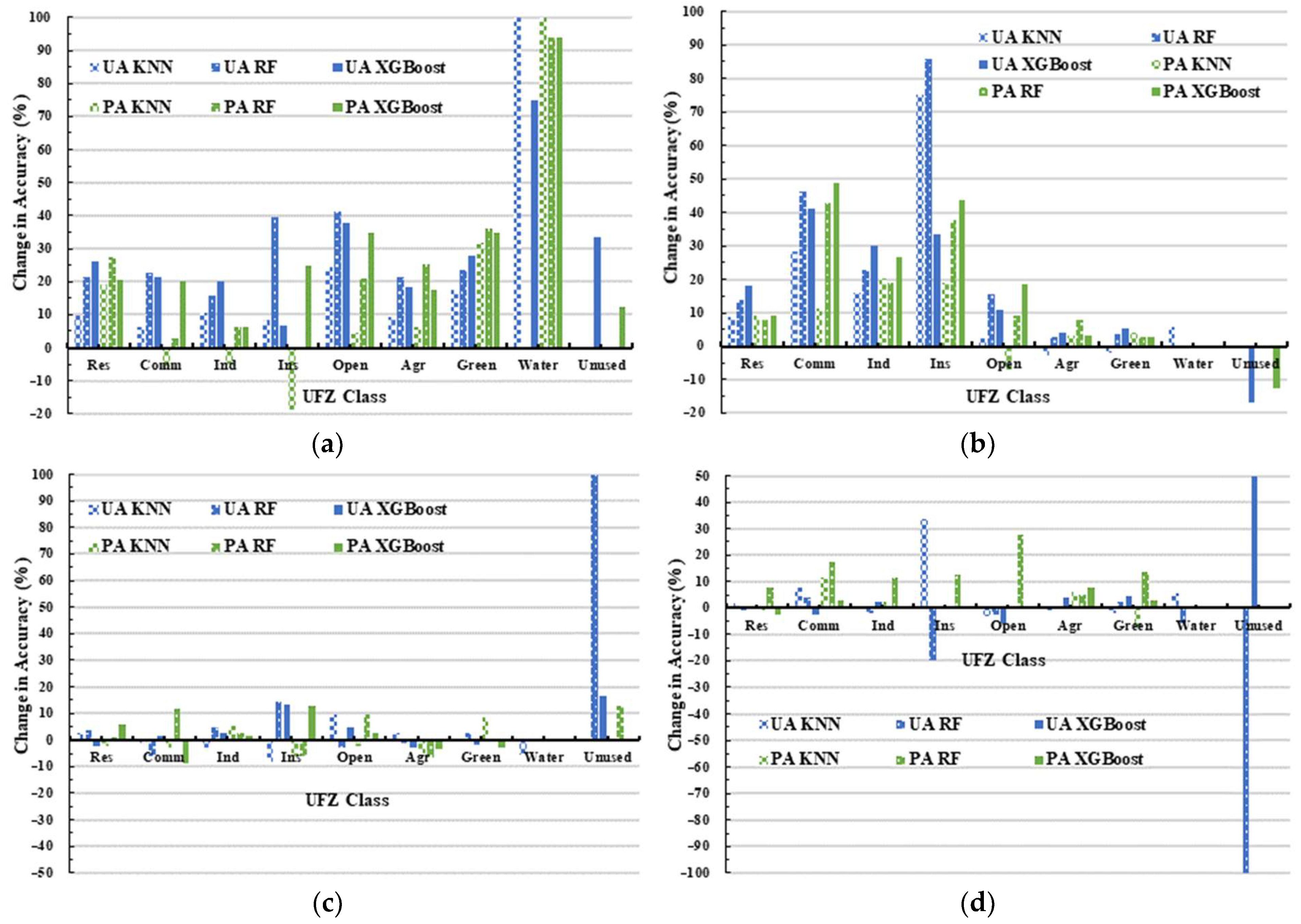
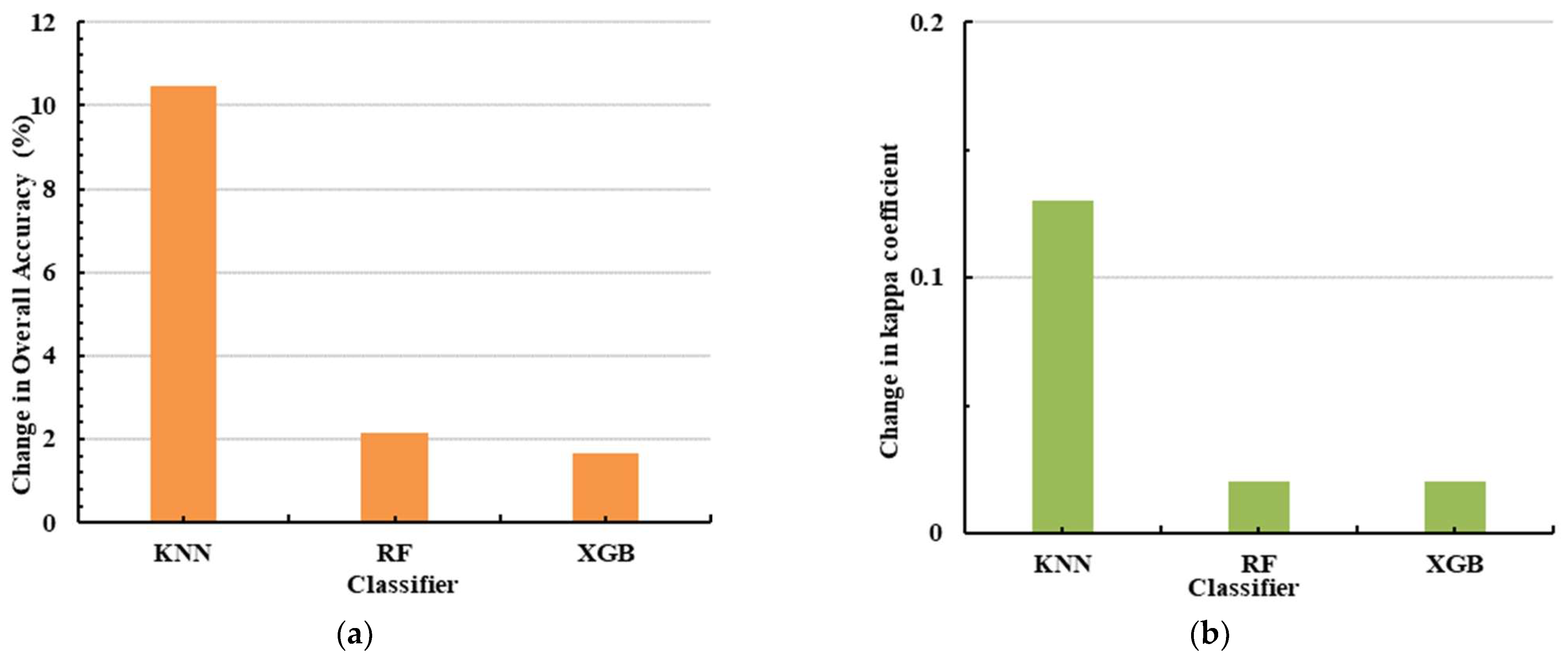
In this research, we carefully chose three machine learning algorithms for UFZ classification: KNN, RF, and XGBoost. Our objective was twofold. Firstly, we sought to evaluate the robustness and consistency of the classification experiments through a comprehensive analysis of the results obtained from these three classifiers. Secondly, we aimed to identify and select the classifier that delivered the highest classification performance to produce the UFZ classification map. The UFZ classification, leveraging these three classifiers, was executed within the Python 3.7 environment.
The KNN classifier is a widely used and powerful non-parametric machine learning algorithm in pattern recognition [
46,
47]. It stands out for its user-friendly nature, interpretability, robust predictive capabilities, resilience to outliers, and its unique ability to assess the uniformity of sample distribution based on the accuracy of the algorithm. Consequently, KNN is often integrated with other classifiers in the realm of remote sensing data classification research [
25,
48,
49,
50]. KNN is an instance-based lazy learning algorithm that does not require pre-training on a large set of samples to build a classifier. Instead, it stores all available instances and measures the similarity between samples based on distance calculations. The fundamental principle of KNN involves comparing the features of a new input sample, which lacks a classification label, to the features of every sample in the training data. It identifies the K-nearest (most similar) data and assigns the most frequently occurring class among these data as the classification label for the new input data [
51]. The selection of the K value holds paramount importance in the classification process, given that both excessively large and small K values can potentially result in problems like over-regularization or an exaggerated emphasis on local distinctions [
52]. In this study, we diligently conducted numerous trials to ascertain the optimal
K value for achieving the highest classification accuracy by exploring values within a range of 0 <
K < 50. To achieve this, we introduced an iterative algorithm that calculated the classification accuracy for each iteration. This was accomplished through cross-validation, using both training and validation data, and selecting the
K value that corresponded to the highest validation data accuracy as the best choice.
The RF classifier stands out as a non-parametric pattern recognition algorithm that operates as an ensemble classifier based on decision trees and bagging. Its classification predictions are reached by aggregating the results from a multitude of individual decision trees, essentially taking a collective vote from this ensemble of trees [
53,
54]. RF demonstrates remarkable capability in managing high-dimensional input samples without the need for dimensionality reduction. It operates without the requirement for any a priori assumptions regarding data distribution, ensuring efficiency even in experiments with limited sample sizes. Despite these attributes, it consistently delivers robust and reliable classification results. Furthermore, RF possesses the capability to assess the importance of input variables, adding to its versatility and utility in various classification research studies [
53,
55]. These characteristics render RF exceptionally effective in the realm of remote sensing data classification, spanning a wide array of data types including multispectral, hyperspectral, LiDAR, and multisource remote sensing data [
56,
57,
58]. The fundamental principle of RF involves a series of steps: Starting with N samples and M feature variables, RF employs bootstrap sampling to randomly, and with replacement, draw 2N/3 independent samples from the original training data. These samples serve as the foundation for constructing individual decision trees, collectively forming the random forests. Within each tree, m feature variables (where m < M) are randomly and repeatedly selected to guide the branching process. The splitting of nodes within these trees is determined using the Gini criterion, a measure that identifies the variable offering the most optimal partitioning for the nodes [
49]. The remaining data, known as out-of-bag (OOB) data, are used to evaluate the error rate of the random forest and to calculate the importance of each feature [
57]. Through a series of iterations, OOB data are progressively used to eliminate less impactful features and select the most valuable ones. After OOB predicts results for all samples and compares them to the actual values, the OOB error rate is calculated. The classification of new sample data is determined by majority voting among the results from all constructed decision trees [
59]. When confronted with a substantial number of input features, the heightened intercorrelation among variables can lead to a decline in both classification accuracy and computational efficiency. Consequently, the process of feature optimization becomes imperative, as it ensures the preservation of the most influential features that enhance classification accuracy while simultaneously eliminating the less pertinent ones. RF incorporates two significant parameters: the number of decision trees (ntree) and the number of randomly selected feature variables at each node split (mtry). Generally, ntree configuration is considered more critical since a higher number of trees increases model complexity but decreases efficiency [
56,
59]. For most RF applications, the recommended range for ntree values extends from 0 to 1000, with mtry often being set as the square root of the total number of input features [
24,
25,
57]. In this study, we set mtry as the square root of the number of input features, while the ntree range was established from 0 to 1000 with 100-interval iterations to compute the model’s accuracy, thus determining the optimal ntree value.
XGBoost is a gradient boosting algorithm based on decision trees, falling within the realm of gradient boosting tree models. XGBoost undergoes iterative data processing across multiple rounds, generating a weak classifier at each iteration. The training of each classifier is rooted in the classification residuals acquired from the preceding iteration. These weak classifiers are distinguished by their simplicity, low variance, and high bias, exemplified by models like CART classifiers, and they are also amenable to linear classification. The training procedure consistently enhances classification accuracy by mitigating bias. The final classifier is crafted through an additive model, wherein each weak classifier obtained in every round of training is assigned weights and aggregated together [
60]. XGBoost boasts several advantages, including regularization to reduce overfitting, parallel processing capabilities, customization of optimization goals and evaluation criteria, as well as handling sparse and missing values. Research has demonstrated that XGBoost provides high predictive accuracy and processing efficiency in remote sensing data analysis and classification applications [
61,
62,
63]. XGBoost is frequently implemented alongside cross-validation and grid search, which are two crucial components in machine learning. The combination of cross-validation and grid search is the most commonly employed method for model optimization and parameter evaluation [
64,
65]. In machine learning, using the same dataset for both model training and estimation can result in inaccurate error estimation. To mitigate this issue, cross-validation methods are employed, offering more precise estimates of generalization error that closely reflect the actual performance of the model. In practical applications, k-fold cross-validation is commonly utilized, with k = 10 being a typical and empirically favored choice [
66,
67,
68]. Grid search is an algorithm that leverages cross-validation to identify the optimal model parameters. It operates as an exhaustive search method, meticulously exploring candidate parameter choices to unearth the most favorable results. This algorithm systematically cycles through and evaluates every conceivable parameter combination, effectively automating the process of hyperparameter tuning [
69]. In our research, we incorporated the k-fold cross-validation and grid search methods to enhance the efficiency of tuning multiple parameters while minimizing their interdependencies. The following parameters were optimized in our study to enhance model accuracy. Learning rate, representing the rate of learning, enhances model robustness by systematically reducing weights at each step. Our study meticulously examined its values, encompassing 0.0001, 0.001, 0.01, 0.1, 0.2, and 0.3, in order to pinpoint the optimal setting; n_estimators, denoting the quantity of decision trees, was fine-tuned within a range spanning from 1 to 1000, with iterations conducted at intervals of 1. The iterative process persisted until no further enhancements were evident in cross-validation error over 50 iterations; max_depth and min_child_weight are pivotal parameters exerting substantial influence on the ultimate results. We systematically adjusted their values, spanning from 1 to 10, with iterations occurring at 1-interval intervals; gamma, the controller of post-pruning tree behavior, designates the minimum loss reduction necessary for additional splits at a leaf node. Higher values reflect a more conservative approach. Our study meticulously examined a range of values, spanning from 0 to 0.5, with iterations conducted at 0.1 intervals; subsample, a parameter governing the random selection of training data for each tree, plays a key role in the algorithm’s balance between conservatism and susceptibility to overfitting. Our study encompassed values ranging from 0.6 to 1, with iterations occurring at 0.1 intervals to identify the most suitable setting; colsample_bytree, responsible for column sampling during tree construction, dictates the ratio of columns randomly chosen for each tree, and we explored a range of values from 0.6 to 1, conducting iterations at 0.1 intervals; reg_alpha, serving as the L1 regularization term for weights, bolsters the algorithm’s computational efficiency in high-dimensional training samples. Our study delved into values ranging from 10
−5, 10
−2, 0.1, and 1 to 100 for this parameter.
3.5.3. Feature Optimization
When dealing with a substantial number of input features, the increased intercorrelation among variables can lead to a decline in classification accuracy and computational efficiency. Therefore, it is imperative to optimize these numerous input features, preserving those that significantly contribute to the model’s classification accuracy and eliminating the less influential ones, to achieve optimal precision. In the realm of classification research, RF algorithm is frequently employed to assess variable importance. There are two primary methods for evaluating variable importance: Mean Decrease Impurity (MDI), often referred to as GINI importance, evaluates the value of a node by quantifying the reduction in impurity during its division. Mean Decrease in Accuracy (MDA), based on OOB error, examines the effect on classification accuracy when specific feature values are randomly interchanged within OOB data. Notably, MDA tends to yield results with greater accuracy than MDI [
53,
54].
The MDA of
is calculated by averaging the difference in OOB error estimation before and after permutation across all trees [
70]. A higher MDA value indicates greater variable importance. The formula for calculating the importance of feature
(the
dimension of the sample) is as follows:
where
represents the number of random trees
that represent the sample, with
representing the class label.
denotes the sample resulting from the random exchange of the
-th dimension (feature) of
;
is the OOB sample dataset for random tree
and
represents the sample dataset formed after exchanging the
-th dimension;
represents the prediction (class) for sample
;
is the indicator function, returning 1 if the prediction matches the true class label, and 0 otherwise.
In our research, we employed the MDA method to evaluate variable importance and implement feature optimization to pinpoint the optimal features for a refined classification experiment (Exp.7).
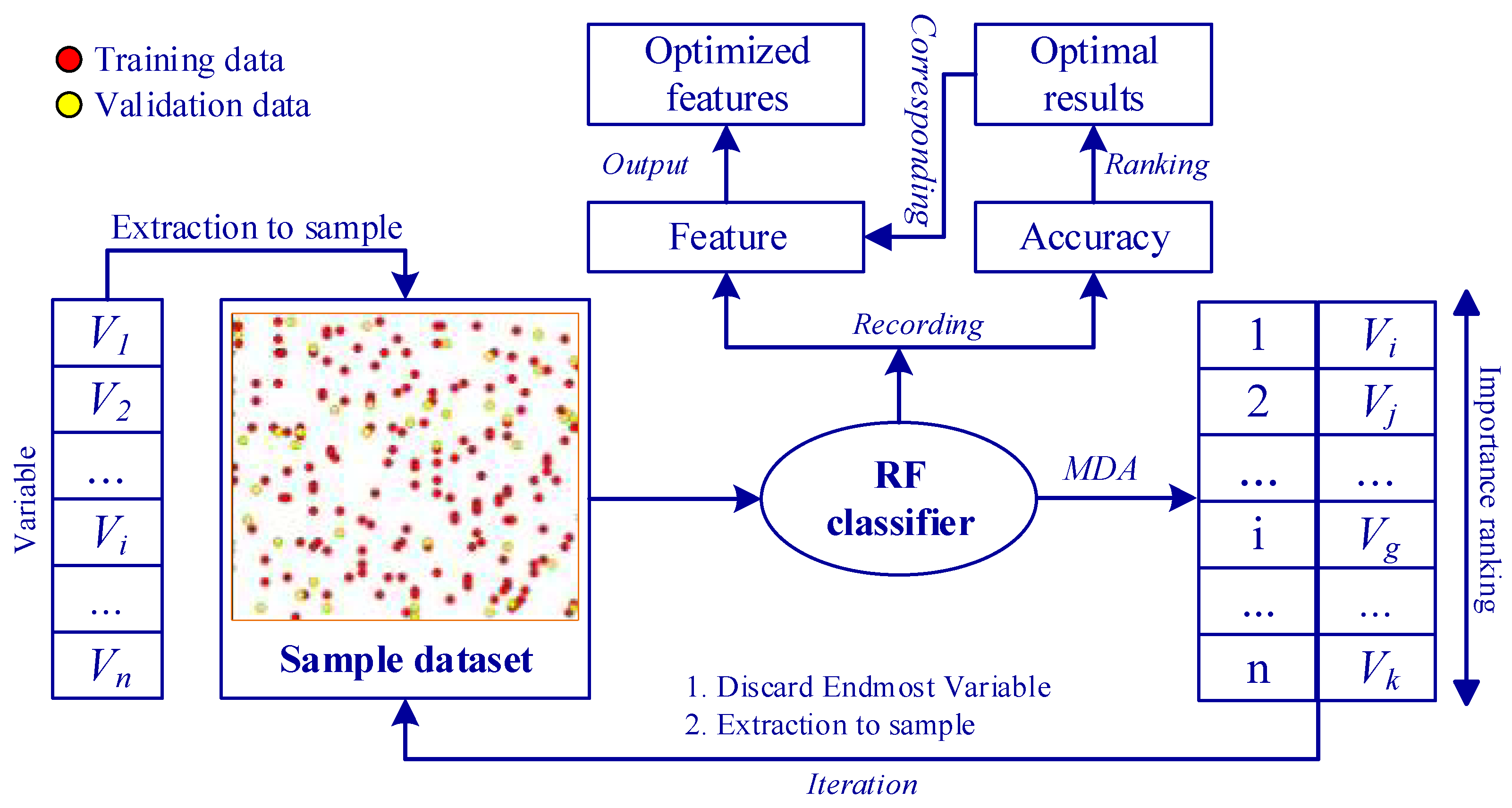
Figure 7 illustrates the workflow of feature optimization via the RF classifier, particularly when managing high-dimensional input features. To begin with, we extracted the attribute values of all features (variables) to their corresponding samples, denoted as
. The sample dataset was then trained using the RF classifier. Subsequently, variables were ranked based on their MDA values, and the least important ones were identified. These least important variables were then excluded from the input variables, and the attribute values of the remaining variable amalgamation were reintroduced into the sample dataset. Another round of training was executed with the RF classifier. This process was iterated until the number of input variables reached zero. Throughout the iterations, we recorded the variables involved in RF training and the resulting classification accuracy. Finally, we ranked all the recorded accuracies, found the best classification result and its corresponding variables, and then output the optimal variable combination for Exp.7. In this paper, we introduced the variable importance proportion (VIP), which represents the feature contribution to classification by indicating the proportion of each variable’s importance relative to the overall variable importance.