Evaluating the Reconstructed All-Weather Land Surface Temperature for Urban Heat Island Analysis
Abstract
1. Introduction
2. Study Area and Datasets
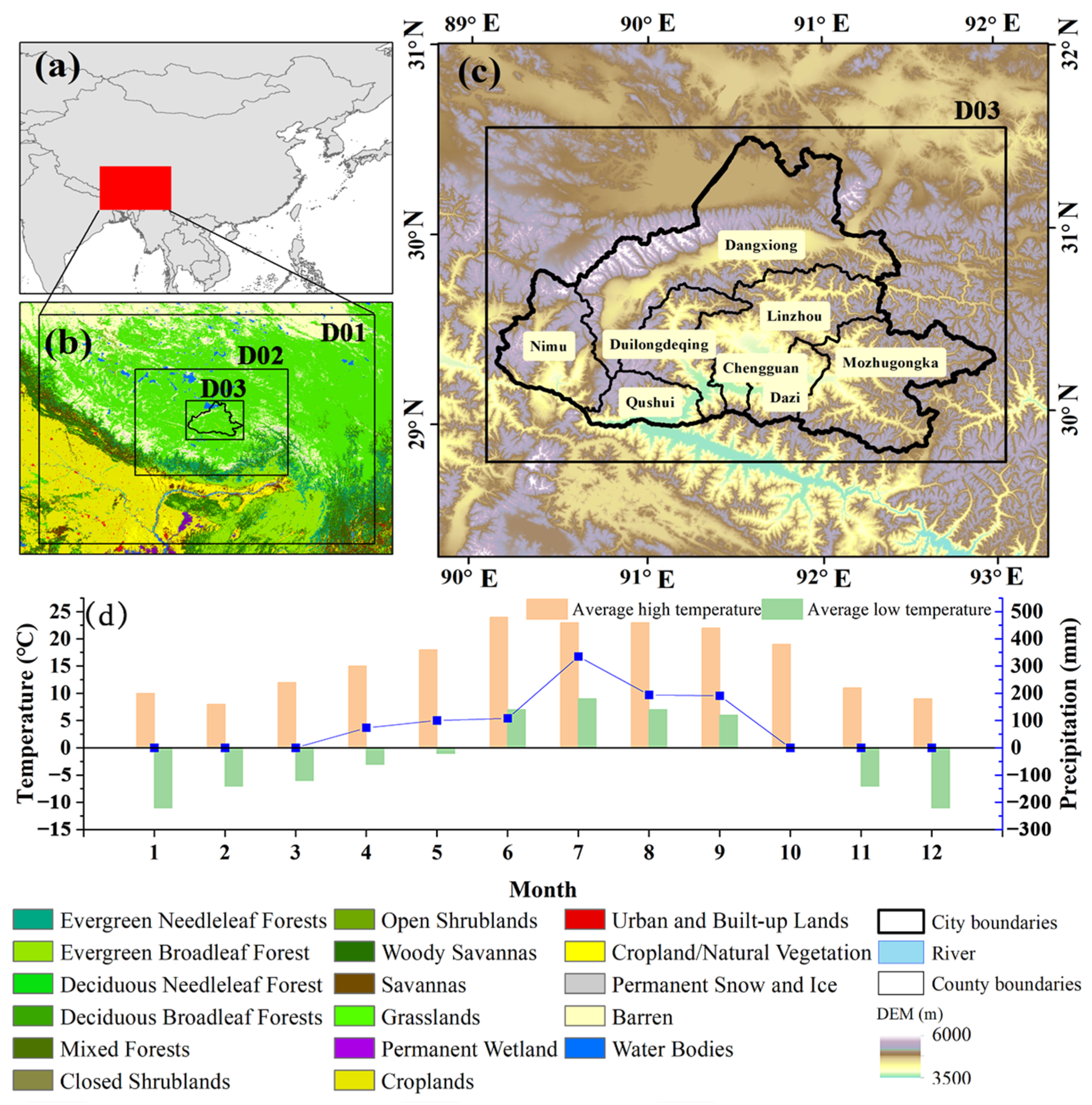
2.1. Study Area
2.2. Datasets
2.2.1. Modis Data
2.2.2. FNL Data
2.2.3. Other Data
3. Methodology
3.1. All-Weather LST Reconstruction
3.1.1. WRF Configuration
3.1.2. LST Reconstruction
3.1.3. Accuracy Verification Metrics
3.2. Analysis of the UHI Effect
4. Results
4.1. All-Weather LST Reconstruction
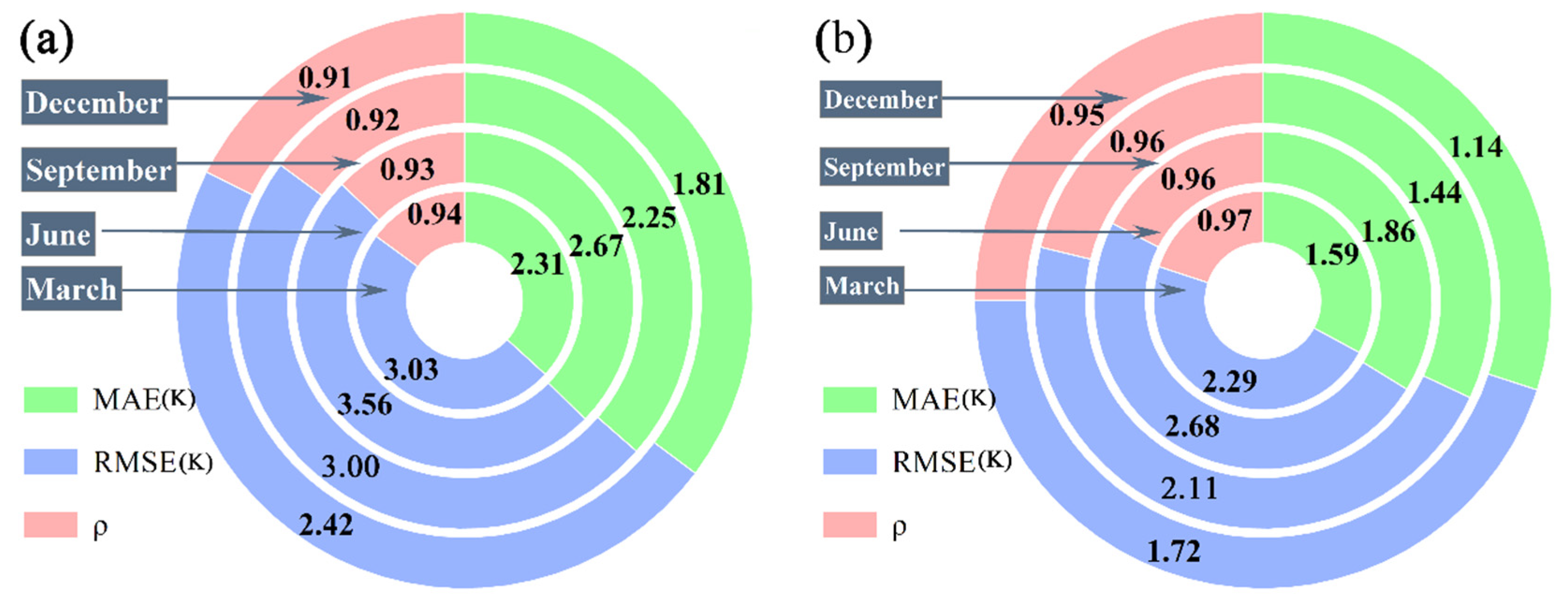
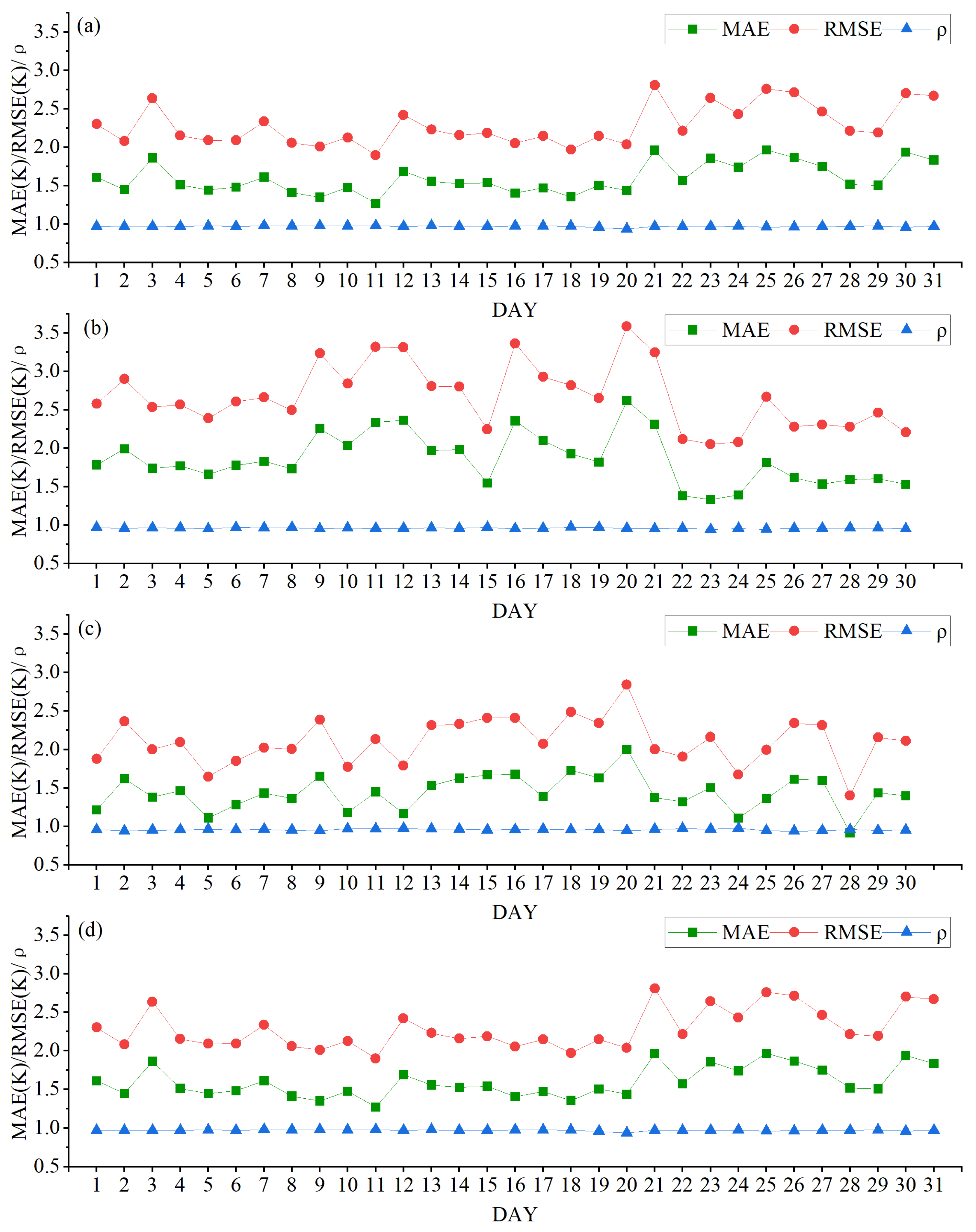
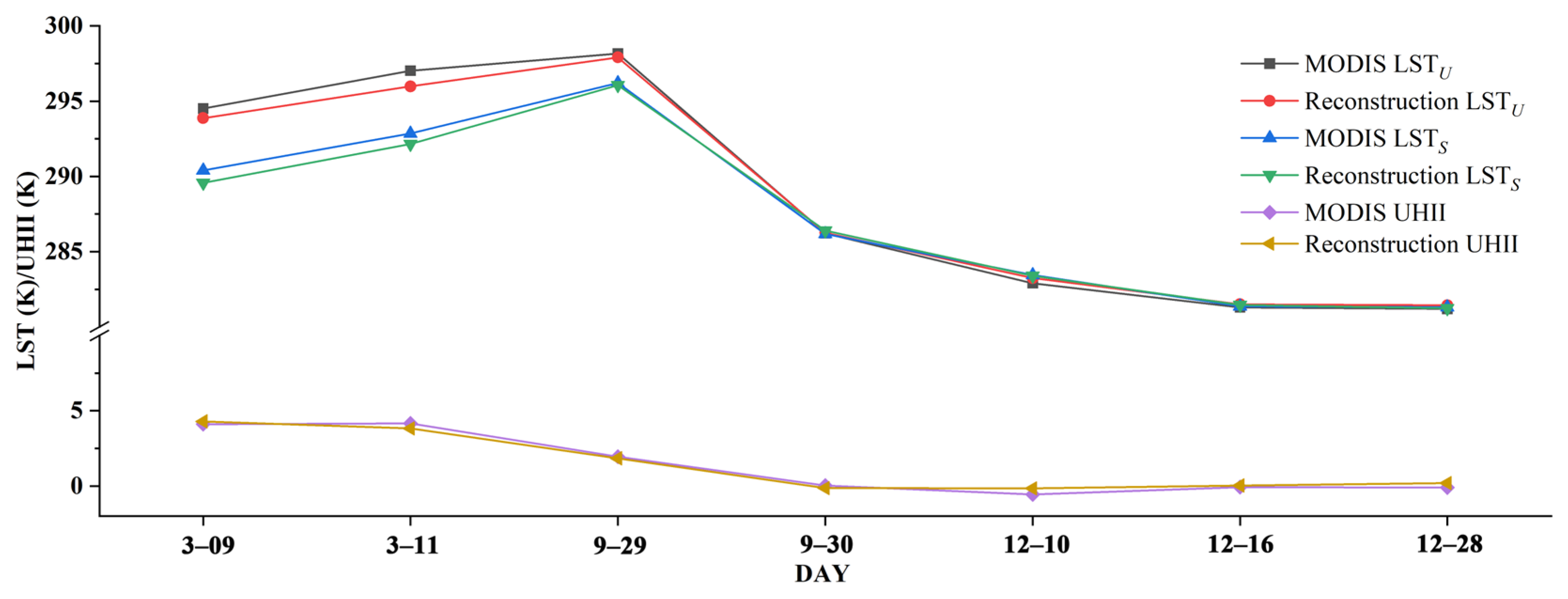
4.2. Accuracy of the All-Weather LST
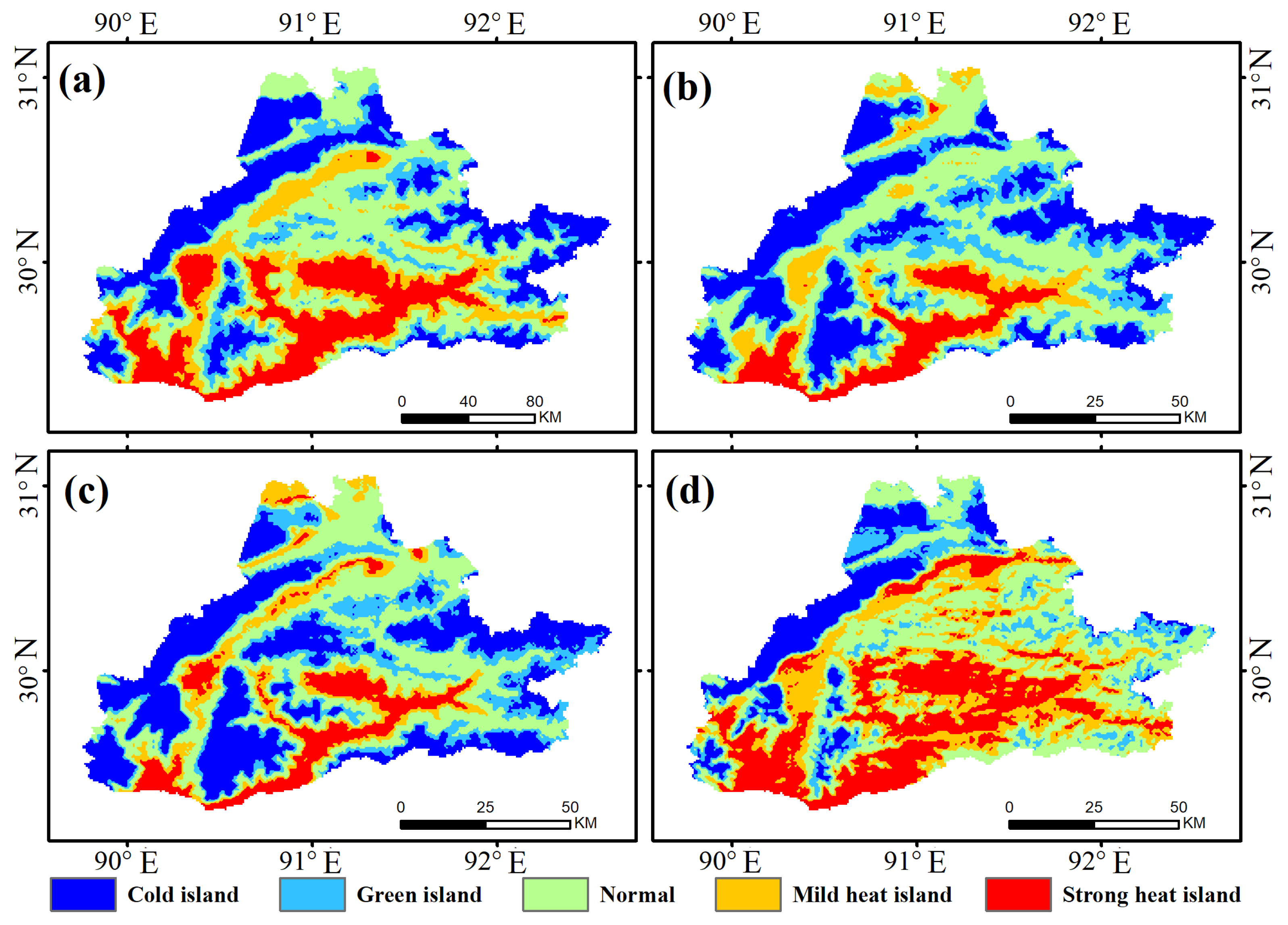
4.3. Analysis of the Urban Heat Island Intensity
5. Discussion
6. Conclusions
- (1)
- The all-weather LST reconstructed in this study can effectively compensate for the missing pixels in MODIS LST and exhibits high spatiotemporal continuity. Many spatial distribution details are accurately restored. This provides a new method for the reconstruction of all-weather LST.
- (2)
- The reconstructed LST in this study demonstrates high accuracy, with an average RMSE of 2.20 K, average MAE of 1.51 K, and ρ greater than 0.9. This provides fundamental research data for studies related to the thermal environment.
- (3)
- In terms of the seasonal analysis, the UHI effect is most frequently observed during the spring and winter seasons in the Lhasa region, with the winter season showing a relatively stable UHII value. In terms of the spatial distribution, the areas with the highest proportion of strong heat islands are primarily observed during the spring and winter seasons, followed by the summer and autumn seasons.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Zhang, X.; Gou, P.; Zhang, F.; Huang, Y.; Wang, Z.; Li, G.; Xing, J. Reconstruction of all-weather land surface temperature based on a combined physical and data-driven model. Environ. Sci. Pollut. Res. 2023, 30, 78865–78878. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, P.K.; Han, D.; Ramirez, M.R.; Islam, T. Machine Learning Techniques for Downscaling SMOS Satellite Soil Moisture Using MODIS Land Surface Temperature for Hydrological Application. Water Resour. Manag. 2013, 27, 3127–3144. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, X.; Chen, W.; Yang, B.; Chen, Z.; Tang, H.; Wang, Z.; Bi, P.; Yang, L.; Li, G.; et al. Cloud-Free Land Surface Temperature Reconstructions Based on MODIS Measurements and Numerical Simulations for Characterizing Surface Urban Heat Islands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6882–6898. [Google Scholar] [CrossRef]
- Bartkowiak, P.; Castelli, M.; Crespi, A.; Niedrist, G.; Zanotelli, D.; Colombo, R.; Notarnicola, C. Land Surface Temperature Reconstruction Under Long-Term Cloudy-Sky Conditions at 250 m Spatial Resolution: Case Study of Vinschgau/Venosta Valley in the European Alps. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2037–2057. [Google Scholar] [CrossRef]
- Ding, L.; Zhou, J.; Li, Z.-L.; Ma, J.; Shi, C.; Sun, S.; Wang, Z. Reconstruction of Hourly All-Weather Land Surface Temperature by Integrating Reanalysis Data and Thermal Infrared Data From Geostationary Satellites (RTG). IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Leng, P. A framework for the retrieval of all-weather land surface temperature at a high spatial resolution from polar-orbiting thermal infrared and passive microwave data. Remote Sens. Environ. 2017, 195, 107–117. [Google Scholar] [CrossRef]
- Jia, A.; Ma, H.; Liang, S.; Wang, D. Cloudy-sky land surface temperature from VIIRS and MODIS satellite data using a surface energy balance-based method. Remote Sens. Environ. 2021, 263, 112566. [Google Scholar] [CrossRef]
- Long, D.; Yan, L.; Bai, L.; Zhang, C.; Shi, C. Generation of MODIS-like land surface temperatures under all-weather conditions based on a data fusion approach. Remote Sens. Environ. 2020, 246, 111863. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Liang, S.; Wang, D. A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1-km all-weather land surface temperature. Remote Sens. Environ. 2021, 260. [Google Scholar] [CrossRef]
- Liu, W.; Cheng, J.; Wang, Q. Estimating Hourly All-Weather Land Surface Temperature from FY-4A/AGRI Imagery Using the Surface Energy Balance Theory. IEEE Trans. Geosci. Remote Sens. 2023, 61. [Google Scholar] [CrossRef]
- Zhou, S.; Cheng, J.; Shi, J. A Physical-Based Framework for Estimating the Hourly All-Weather Land Surface Temperature by Synchronizing Geostationary Satellite Observations and Land Surface Model Simulations. IEEE Trans. Geosci. Remote Sens. 2022, 60, 112437. [Google Scholar] [CrossRef]
- Fu, P.; Xie, Y.; Weng, Q.; Myint, S.; Meacham-Hensold, K.; Bernacchi, C. A physical model-based method for retrieving urban land surface temperatures under cloudy conditions. Remote Sens. Environ. 2019, 230, 111191. [Google Scholar] [CrossRef]
- Urquhart, E.A.; Hoffman, M.J.; Murphy, R.R.; Zaitchik, B.F. Geospatial interpolation of MODIS-derived salinity and temperature in the Chesapeake Bay. Remote Sens. Environ. 2013, 135, 167–177. [Google Scholar] [CrossRef]
- Dalawi, A.N.; Lakestani, M.; Ashpazzadeh, E. Solving Fractional Optimal Control Problems Involving Caputo-Fabrizio Derivative Using Hermite Spline Functions. Iran. J. Sci. 2023, 47, 545–566. [Google Scholar] [CrossRef]
- Wenjun, Y.; Tonghua, W.; Zhuotong, N.; Lin, Z.; Zhiwei, W. A novel interpolation method for MODIS land surface temperature data on the Tibetan Plateau. Proc. SPIE 2014, 9260, 92600Y. [Google Scholar]
- Huang, C.; Duan, S.-B.; Jiang, X.-G.; Han, X.-J.; Leng, P.; Gao, M.-F.; Li, Z.-L. A physically based algorithm for retrieving land surface temperature under cloudy conditions from AMSR2 passive microwave measurements. Int. J. Remote Sens. 2019, 40, 1828–1843. [Google Scholar] [CrossRef]
- Prigent, C.; Jimenez, C.; Aires, F. Toward “all weather,” long record, and real-time land surface temperature retrievals from microwave satellite observations. J. Geophys. Res.-Atmos. 2016, 121, 5699–5717. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Jin, M.; Dickinson, R.E. A generalized algorithm for retrieving cloudy sky skin temperature from satellite thermal infrared radiances. J. Geophys. Res.-Atmos. 2000, 105, 27037–27047. [Google Scholar] [CrossRef]
- Kadaverugu, R. A comparison between WRF-simulated and observed surface meteorological variables across varying land cover and urbanization in south-central India. Earth Sci. Inform. 2023, 16, 147–163. [Google Scholar] [CrossRef]
- Zhang, X.D.; Zhou, J.; Liang, S.L.; Chai, L.N.; Wang, D.D.; Liu, J. Estimation of 1-km all-weather remotely sensed land surface temperature based on reconstructed spatial-seamless satellite passive microwave brightness temperature and thermal infrared data. Isprs J. Photogramm. Remote Sens. 2020, 167, 321–344. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, W.; Ma, M.; Yu, W.; Fan, L.; Huang, Y.; Sun, X.; Lang, Q. An Integrated Method for the Generation of Spatio-Temporally Continuous LST Product With MODIS/Terra Observations. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Han, W.; Duan, S.-B.; Tian, H.; Lian, Y. Estimation of land surface temperature from AMSR2 microwave brightness temperature using machine learning methods. Int. J. Remote Sens. 2023, 22, 1–12. [Google Scholar] [CrossRef]
- Zhao, W.; Duan, S.-B. Reconstruction of daytime land surface temperatures under cloud-covered conditions using integrated MODIS/Terra land products and MSG geostationary satellite data. Remote Sens. Environ. 2020, 247, 111931. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Y.; Pan, X.; Ding, Y.; Hu, J.; Dai, Y. Multiinformation Fusion Network for Mapping Gapless All-Sky Land Surface Temperature Using Thermal Infrared and Reanalysis Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Liu, K.; Su, H.B.; Li, X.K.; Chen, S.H. Development of a 250-m Downscaled Land Surface Temperature Data Set and Its Application to Improving Remotely Sensed Evapotranspiration Over Large Landscapes in Northern China. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Wang, S.; Fu, G. Modelling soil moisture using climate data and normalized difference vegetation index based on nine algorithms in alpine grasslands. Front. Environ. Sci. 2023, 11, 1130448. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Yu, T.; Zhang, Y.; Liu, Q.; Chen, X.; Zhan, Y. A Method of Using WRF-Simulated Surface Temperature to Estimate Daily Evapotranspiration. J. Appl. Meteorol. Climatol. 2020, 59, 901–914. [Google Scholar] [CrossRef]
- Diaz, L.R.; Santos, D.C.; Käfer, P.S.; Rocha, N.S.d.; Costa, S.T.L.d.; Kaiser, E.A.; Rolim, S.B.A. Land Surface Temperature Retrieval Using High-Resolution Vertical Profiles Simulated by WRF Model. Atmosphere 2021, 12, 1436. [Google Scholar] [CrossRef]
- Leng, P.; Yang, Z.; Yan, Q.-Y.; Shang, G.-F.; Zhang, X.; Han, X.-J.; Li, Z.-L. A framework for estimating all-weather fine resolution soil moisture from the integration of physics-based and machine learning-based algorithms. Comput. Electron. Agric. 2023, 206, 107673. [Google Scholar] [CrossRef]
- Liu, Z.H.; Zhan, W.F.; Lai, J.M.; Hong, F.L.; Quan, J.L.; Bechtel, B.; Huang, F.; Zou, Z.X. Balancing prediction accuracy and generalization ability: A hybrid framework for modelling the annual dynamics of satellite-derived land surface temperatures. Isprs J. Photogramm. Remote Sens. 2019, 151, 189–206. [Google Scholar] [CrossRef]
- Yu, L.X.; Liu, Y.; Yang, J.C.; Liu, T.X.; Bu, K.; Li, G.S.; Jiao, Y.; Zhang, S.W. Asymmetric daytime and nighttime surface temperature feedback induced by crop greening across Northeast China. Agric. For. Meteorol. 2022, 325, 109136. [Google Scholar] [CrossRef]
- Lu, Y.S.; He, T.; Xu, X.L.; Qiao, Z. Investigation the Robustness of Standard Classification Methods for Defining Urban Heat Islands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11386–11394. [Google Scholar] [CrossRef]
- Sheng, L.; Tang, X.L.; You, H.Y.; Gu, Q.; Hu, H. Comparison of the urban heat island intensity quantified by using air temperature and Landsat land surface temperature in Hangzhou, China. Ecol. Indic. 2017, 72, 738–746. [Google Scholar] [CrossRef]
- Lin, L.; Meng, L.N.; Mei, Y.D.; Zhang, W.T.; Liu, H.; Xiang, W.L. Spatial-temporal patterns of summer urban islands and their economic implications in Beijing. Environ. Sci. Pollut. Res. 2022, 29, 33361–33371. [Google Scholar] [CrossRef] [PubMed]
- de Speville, C.D.; Seviour, W.J.M.; Lo, Y.T.E. Predicting future UK nighttime urban heat islands using observed short-term variability and regional climate projections. Environ. Res. Lett. 2023, 18, 104044. [Google Scholar] [CrossRef]
- Zhong, Y.L.; Chen, S.Q.; Mo, H.H.; Wang, W.W.; Yu, P.F.; Wang, X.M.; Chuduo, N.; Ba, B. Contribution of urban expansion to surface warming in high-altitude cities of the Tibetan Plateau. Clim. Change 2022, 175, 1–22. [Google Scholar] [CrossRef]
- Zhong, Y.L.; Yu, H.; Wang, W.W.; Yu, P.F. Impacts of future urbanization and rooftop photovoltaics on the surface meteorology and energy balance of Lhasa, China. Urban Clim. 2023, 51, 101668. [Google Scholar] [CrossRef]
- Wang, S.; Tan, X.; Fan, F. Changes in Impervious Surfaces in Lhasa City, a Historical City on the Qinghai-Tibet Plateau. Sustainability 2023, 15, 5510. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, W.; Chen, Z.; Yang, F.; Meng, C.; Gou, P.; Zhang, F.; Feng, J.; Li, G.; Wang, Z. Construction of cloud-free MODIS-like land surface temperatures coupled with a regional weather research and forecasting (WRF) model. Atmos. Environ. 2022, 283, 119190. [Google Scholar] [CrossRef]
- Huang, D.; Gao, S. Impact of different reanalysis data on WRF dynamical downscaling over China. Atmos. Res. 2018, 200, 25–35. [Google Scholar] [CrossRef]
- O’Loughlin, F.E.; Paiva, R.C.D.; Durand, M.; Alsdorf, D.E.; Bates, P.D. A multi-sensor approach towards a global vegetation corrected SRTM DEM product. Remote Sens. Environ. 2016, 182, 49–59. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, X.; Han, C.; Ma, Y. A performance evaluation of various physics schemes on the predictions of precipitation and temperature over the Tibet Autonomous Region of China. Atmos. Res. 2023, 292, 106878. [Google Scholar] [CrossRef]
- Quan, J.; Chen, Y.; Zhan, W.; Wang, J.; Voogt, J.; Li, J. A hybrid method combining neighborhood information from satellite data with modeled diurnal temperature cycles over consecutive days. Remote Sens. Environ. 2014, 155, 257–274. [Google Scholar] [CrossRef]
- Ciren, L.; Ga, Z.; Bu, L.; Ciren, P. Temporal and Spatial Distribution of Urban Heat Islands Around Lhasa City. Resour. Sci. 2012, 34, 2364–2373. [Google Scholar]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Duan, S.B.; Lian, Y.H.; Zhao, E.Y.; Chen, H.; Han, W.J.; Wu, Z.H. A Novel Approach to All-Weather LST Estimation Using XGBoost Model and Multisource Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, B.; Shi, J. Reconstructing spatial-temporal continuous MODIS land surface temperature using the DINEOF method. J. Appl. Remote Sens. 2017, 11, 046016. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Asrar, G.R.; Zhu, Z. Creating a seamless 1km resolution daily land surface temperature dataset for urban and surrounding areas in the conterminous United States. Remote Sens. Environ. 2018, 206, 84–97. [Google Scholar] [CrossRef]
- Wang, M.; Shen, P. Investigation of Indoor Asymmetric Thermal Radiation in Tibet Plateau: Case Study of a Typical Office Building. Buildings 2022, 12, 129. [Google Scholar] [CrossRef]
- Zou, H.B.; Wu, S.S.; Shan, J.S. Sensitivity of Lake-Effect Convection to the Lake Surface Temperature over Poyang Lake in China. J. Meteorol. Res. 2022, 36, 342–359. [Google Scholar] [CrossRef]



| Name | Source | Time period |
|---|---|---|
| MODIS LST | MODIS data website (https://ladsweb.modaps.eosdis.nasa.gov/, accessed on 8 June 2023) | March, June, September, and December of 2020 |
| FNL | National Centers for Environmental Prediction (https://rda.ucar.edu/, accessed on 8 June 2023) | |
| DEM | Resource and Environment Science Data Center (https://www.resdc.cn/, accessed on 8 June 2023) | |
| LAT | Based on DEM data | |
| NDVI | MODIS data website (https://ladsweb.modaps.eosdis.nasa.gov/, accessed on 8 June 2023) |
| Option Name | Parameterization | ID |
|---|---|---|
| Cumulus | Kain–Fritsch | 3 |
| Planetary Boundary layer | Mellor–Yamada–Janjic | 2 |
| Longwave Radiation | RRTMG | 4 |
| Shortwave Radiation | RRTMG | 4 |
| Surface Layer | Mellor–Yamada–Janjic | 2 |
| Microphysics | New Thompson | 8 |
| Land Surface | Noah-MP | 4 |
| Heat Island Intensity | Temperature Range | Temperature Range |
|---|---|---|
| Cold island | Low | TS < μ − σ |
| Green island | Medium low | μ − σ ≤ TS < μ − 0.5σ |
| Normal | Medium | μ − 0.5σ ≤ TS ≤ μ + 0.5σ |
| Subheat island | Medium high | μ + 0.5σ < TS ≤ μ + σ |
| Strong heat island | High | TS > μ + σ |
| Cold island | Low | TS < μ − σ |
| Green island | Medium low | μ − σ ≤ TS < μ − 0.5σ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Meng, C.; Gou, P.; Huang, Y.; Ma, Y.; Ma, W.; Wang, Z.; Hu, Z. Evaluating the Reconstructed All-Weather Land Surface Temperature for Urban Heat Island Analysis. Remote Sens. 2024, 16, 373. https://doi.org/10.3390/rs16020373
Zhang X, Meng C, Gou P, Huang Y, Ma Y, Ma W, Wang Z, Hu Z. Evaluating the Reconstructed All-Weather Land Surface Temperature for Urban Heat Island Analysis. Remote Sensing. 2024; 16(2):373. https://doi.org/10.3390/rs16020373
Chicago/Turabian StyleZhang, Xuepeng, Chunchun Meng, Peng Gou, Yingshuang Huang, Yaoming Ma, Weiqiang Ma, Zhe Wang, and Zhiheng Hu. 2024. "Evaluating the Reconstructed All-Weather Land Surface Temperature for Urban Heat Island Analysis" Remote Sensing 16, no. 2: 373. https://doi.org/10.3390/rs16020373
APA StyleZhang, X., Meng, C., Gou, P., Huang, Y., Ma, Y., Ma, W., Wang, Z., & Hu, Z. (2024). Evaluating the Reconstructed All-Weather Land Surface Temperature for Urban Heat Island Analysis. Remote Sensing, 16(2), 373. https://doi.org/10.3390/rs16020373











