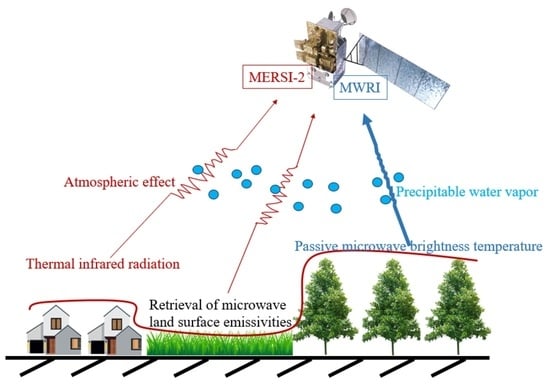
A Physics-Based Method for Retrieving Land Surface Emissivities from FengYun-3D Microwave Radiation Imager Data

Abstract

The passive microwave land surface emissivity (MLSE) plays a crucial role in retrieving various land surface and atmospheric parameters and in Numerical Weather Prediction models. The retrieval accuracy of MLSE depends on many factors, including the consistency of the input data acquisition time. The FengYun-3D (FY-3D) polar-orbiting meteorological satellite, equipped with passive microwave and infrared bands, offers time-consistent data crucial for MLSE retrieval. This study proposes a physics-based MLSE retrieval algorithm using all the input data from the FY-3D satellite. Based on the retrieved MLSE, the spatial distribution of the MLSE is closely correlated with the land cover types and topography. Lower emissivities prevailed over barren or sparsely vegetated regions, river basins, and coastal areas. Higher emissivities dominated densely vegetated regions and mountainous areas. Moderate emissivities dominated grasslands and croplands. Lower-frequency channels showed larger emissivity differences with different polarizations than those of higher-frequency channels in barren or sparsely vegetated regions. The MLSE across densely vegetated land areas, mountainous areas, and deserts showed small seasonal variations. However, woody savannas, grasslands, croplands, and seasonal snow-covered areas showed noticeable seasonal variations. For most land cover types, the differences between vertically and horizontally polarized emissivities remained relatively constant across seasons. However, certain grasslands in eastern Inner Mongolia and southern Mongolia showed clear seasonal variations. It is very difficult to verify the MLSE on a large scale. Consequently, the possible error sources in the retrieved MLSE were analyzed, including the brightness temperature errors (correlation coefficient ranging from 0.92 to 0.99) and the retrieved land surface temperature errors (Root Mean Square Error was 3.34 K and relation coefficient was 0.958).

1. Introduction

Accurate retrieval of passive microwave land surface emissivity (MLSE) data is essential in many fields [1]. A realistic MLSE can potentially improve the initial fields of Numerical Weather Prediction models, thereby enhancing 24 h forecasts of precipitation distribution and intensity [2]. A rapid change in emissivity can indicate precipitation events in certain land cover types when it is not saturated [3,4,5]. Moreover, because MLSE is sensitive to snow, it is often used to monitor snow cover and melting at high latitudes [6] and to detect soil freeze–thaw states [7,8]. MLSE is also vital for retrieving atmospheric parameters. For example, because land surface radiation has high spatial and temporal heterogeneities compared to those of the sea surface, it is difficult to retrieve the column water vapor content (WVC) over land [9]. Zhou et al. [10] developed a physics-based model that primarily uses MLSE to retrieve the column WVC over land. Greenwald et al. [11] proved that the retrieval of the cloud liquid water content may be applicable if the MLSE at 85 GHz is known in advance. Furthermore, MLSE is vital for quantitative retrieval of land surface parameters. For example, as the land surface temperature (LST) is coupled with MLSE in the radiative transfer model, some retrieval algorithms for the LST need to first calculate the MLSE [12,13,14]. In general, an error of 0.01 in the MLSE retrieval at 36.5 GHz may lead to a 3 K error in the LST [12]. Moreover, the relation between the MLSE in the L band and the soil moisture content showed a negative correlation. Consequently, many retrieval models for the soil moisture content have been developed using this relation [15,16,17].

MLSE is affected by many inherent land features, including the soil texture, soil moisture content, land cover type, land surface roughness, vegetation optical depth, and freeze–thaw transition [18,19,20]. In addition, it is influenced by radiation characteristics, such as the frequency and polarization. Consequently, it is difficult to obtain the MLSE at a passive microwave spatial resolution scale through a physical forward model because it is difficult to obtain accurate descriptions of all the aforementioned parameters [21,22]. Compared with modeling activity, a simpler method to obtain the MLSE at a satellite footprint scale involves using the inverse radiative transfer model. This method involves removing atmospheric and LST contributions from the top of the atmospheric brightness temperature data. Prigent et al. [23] measured global MLSE retrievals using Special Sensor Microwave Imager data. Since then, many MLSE products have been obtained from other passive microwave sensors, such as the Advanced Microwave Scanning Radiometer-Earth Observing System [24,25], the Advanced Microwave Sounding Unit [26], the Tropical Rainfall Measuring Mission Microwave Imager [27], Windsat [28], the Advanced Microwave Scanning Radiometer 2 (AMSR2) [29], the FY-3B Microwave Radiation Imager (MWRI) [30], and the FY-3D MWRI [31]. These retrieval models have been proven to offer reliable first-order MLSE measurements [32,33].

To remove the influences of the LST and atmospheric effects from microwave brightness temperature data, the aforementioned algorithms require many input parameters. As these input parameters have strong spatiotemporal heterogeneity, differences in the data acquisition time may produce large errors in the retrieval of the MLSE. Consequently, a physics-based MLSE retrieval algorithm using all the input data from the FY-3D satellite was proposed in this study. The FY-3D, the successor to the FY-3B, has taken over prime operational weather services from the FY-3B. The structure of this paper is as follows. Section 2 details the study area and the data employed. Section 3 outlines the physics-based MLSE retrieval method. Section 4 presents the results of the study. Section 5 presents the discussion. Finally, Section 6 presents the conclusions.

2. Study Area and the Data

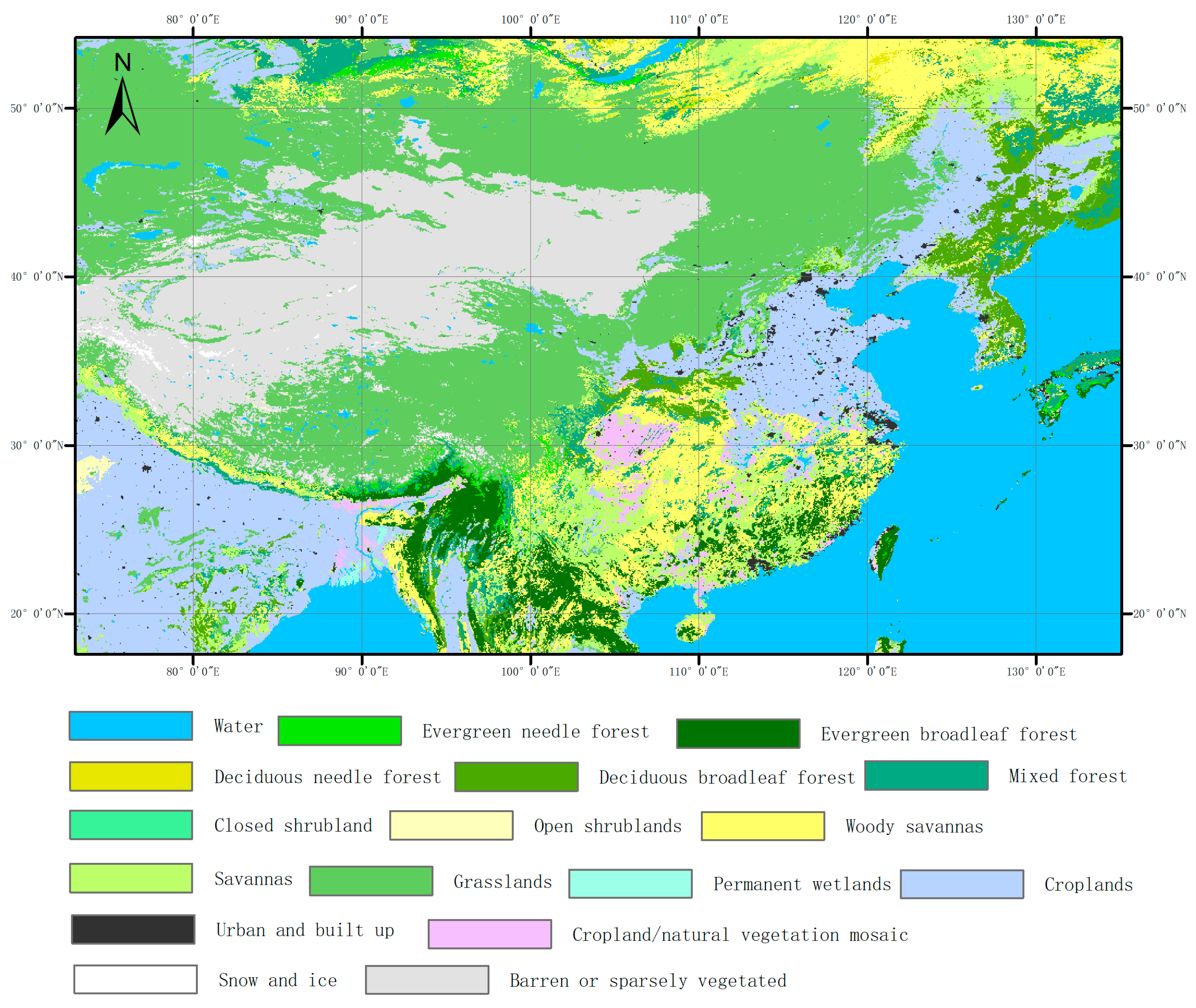
2.1. Study Area

Eastern Asia (73.0°–135.1°E, 17.6°–54.2°N), as shown Figure 1, was selected as the study area. This region has complex terrain features, such as the Himalayan Mountains, Qinghai–Tibet Plateau, plains, hills, and basins. As shown in Figure 1, the complex terrain features and distinct climatic characteristics result in various land use and land cover types, including forests, savannas, croplands, grasslands, shrublands, and barren lands. These land cover types, which range from forests to deserts, can provide completely different MLSE values due to differences in the soil moisture content, soil texture, surface roughness, and vegetation optical depth.

2.2. FY-3D MWRI Data

The FY-3D, the fourth flight unit of the Chinese FY-3 series of satellites, was launched on 15 November 2017. It carries the MWRI instrument for exploring the atmosphere, ocean, and land surface environments. The MWRI operates at five frequencies: 10.65, 18.7, 23.8, 36.5, and 89.0 GHz, with two polarization modes for each frequency. The swath width is approximately 1400 km, with an incidence angle of 53° and overpass times of approximately 02:00 am (descending)/02:00 pm (ascending) local solar time. Detailed characteristics are listed in

Table 1. Detailed characteristics of the FY-3D/MWRI.

Central Frequency (GHz)	Bandwidth (MHz)	Polarization	NEΔT (K)	Range (K)
10.65	180	V, H	0.5	3–340
18.7	200		0.5
23.8	400		0.5
36.5	400		0.5
89	3000		0.8

. The MWRI Level-1 brightness temperature data used in this study were downloaded from the National Satellite Meteorological Center of the China Meteorological Administration (http://satellite.nsmc.org.cn/PortalSite/Data/Satellite.aspx (accessed on 18 July 2022)). Compared to previous MWRI sensors, the bias of the FY-3D MWRI data showed a node-independent difference from the background simulation of the Numerical Weather Prediction [34,35]. In this study, Level-1 brightness temperature data with a spatial resolution of 0.25° were used for the year 2020.

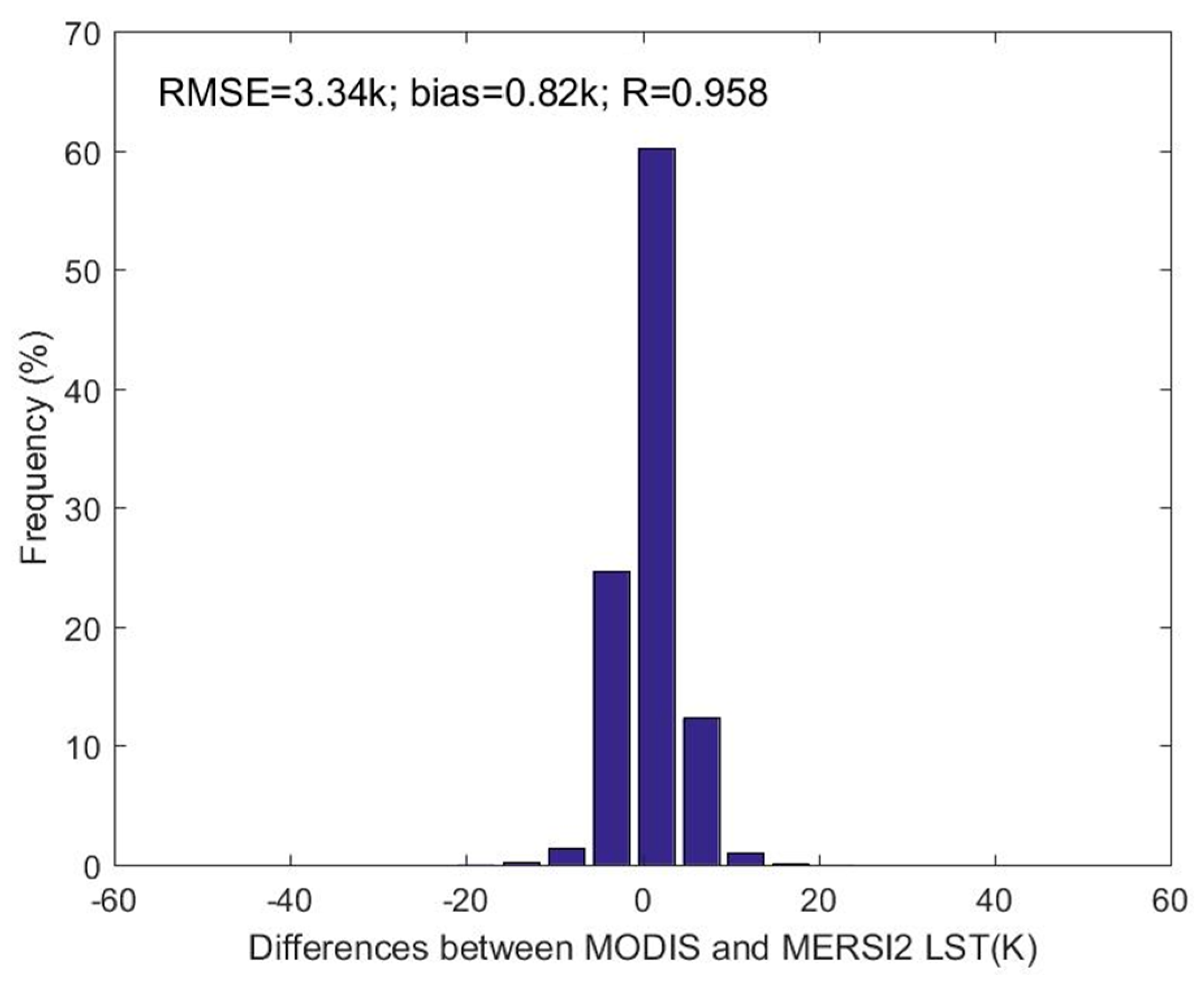
2.3. FY-3D Medium Resolution Spectral Imager-2 (MERSI-2) Data

The MERSI-2 is another inherited instrument carried by the FY-3D. The MERSI-2 is equipped with fifteen visible and near-infrared bands, four shortwave infrared bands, two medium-wave infrared bands, one water vapor band, and three thermal infrared bands. In this study, MERSI-2 Band 24 (10.3–11.3 µm) and Band 25 (11.5–12.5 µm) were chosen for the retrieval of the LST using the split window (SW) algorithm (see Section 3 for details). Additionally, the FY-3D MERSI-2 column WVC products, as produced by Wang et al. [36], were used in this study:

First, it is assumed that the surface reflectance is linearly correlated with the wavelength, and a three-channel ratio involving an absorption channel and two window channels can be used to estimate the transmittance of the absorption channel:

$$T_{wv}={\rho }_{wv}/\left(k_1·{\rho }_{ws}+k_2·{\rho }_{wl}\right)$$

(1)

where $T_{wv}$ is the transmittance of the absorption channel, meaning that three absorption channels have three transmittances ($T_{905}$, $T_{936}, \mathrm{a}\mathrm{n}\mathrm{d} T_{940}$); ${\rho }_{wv}$, ${\rho }_{ws}$, and ${\rho }_{wl}$ are the apparent reflectances of the absorption channel and two window channels (“ws” denotes the shorter wavelength, and “wl” denotes the longer wavelength); and $k_1+k_2=1$. The three-channel ratio method was used when the land pixels were cloud-free. The proportionality constants k₁ and k₂ are calculated as follows:

$$k_1=\left({{\lambda }_{wl}-\lambda }_{wv}\right)/\left({{\lambda }_{wl}-\lambda }_{ws}\right)$$

(2)

$$k_2=\left({{\lambda }_{wv}-\lambda }_{ws}\right)/\left({{\lambda }_{wl}-\lambda }_{ws}\right)$$

(3)

where ${\lambda }_{wv}$ is the wavelength of the absorption channel, ${\lambda }_{ws}$ is the wavelength of the shorter-wavelength channel, and ${\lambda }_{wl}$ is the wavelength of the longer-wavelength channel.

The $T_{wv}$ as a function of the slant total ${WVC}^{\ast }$ was precalculated using MODTRAN under the six standard atmospheric models defined in MODTRAN4.3 [36]. The total slant ${WVC}^{\ast }$ can be derived from the transmittance–water vapor lookup table. The slant total ${WVC}^{\ast }$ is then converted into the vertical column $WVC$ (mm) using the formula:

$$WVC={WVC}^{\ast }/\left[\frac{1}{\cos {\theta }_s}+\frac{1}{\cos {\theta }_v}\right]$$

(4)

where ${\theta }_s$ and ${\theta }_v$ are the solar and view zenith angles, respectively.

Based on the aforementioned WVC retrieval algorithm, three WVC datasets were developed, which were calculated from the combination of 905 nm, 865 nm, and 1030 nm (${WVC}_{905}$), the combination of 936 nm, 865 nm, and 1030 nm (${WVC}_{936}$), and the combination of 940 nm, 865 nm, and 1030 nm (${WVC}_{940}$). Generally, the derived WVC from the three channels differed because the three channels had different absorption coefficients. Consequently, the combined WVC was obtained using the following equation:

$${WVC}_c=P_1·{WVC}_{905}+P_2·{WVC}_{936}+P_3·{WVC}_{940}$$

(5)

where P₁, P₂ and P₃ are the corresponding weighting functions, which can be calculated based on the sensitivity of the transmittance in each channel to the WVC: ${\eta }_i=\left|∆T_{wv,i}/∆WVC\right|$. The weighting functions, $P_i$, are defined as the normalized values of ${\eta }_i$: $P_i={\eta }_i/{(\eta }_1+{\eta }_2+{\eta }_3)$. $P_1+P_2+P_3=1$.

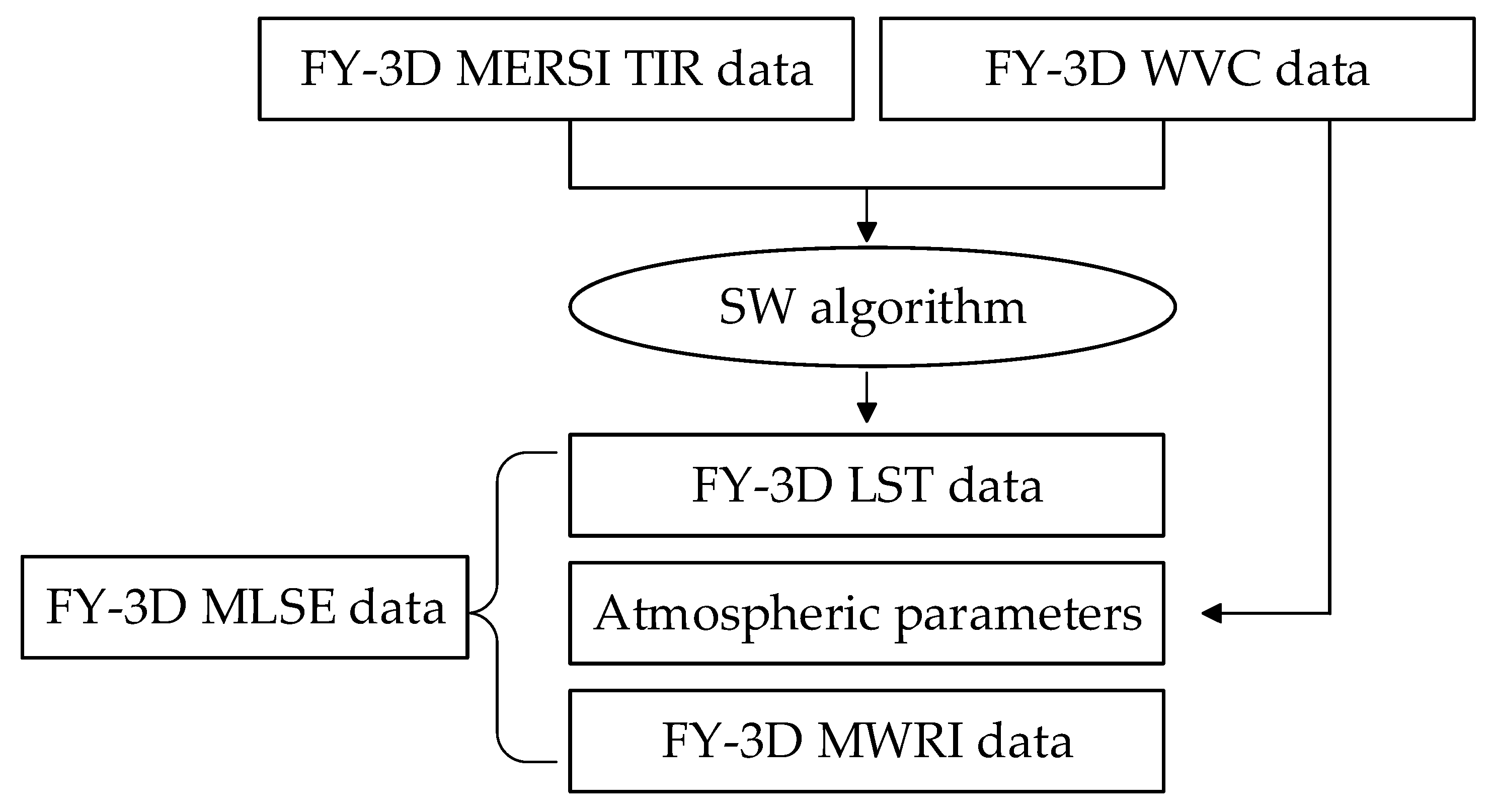
3. Methodology

Based on the radiative transfer model, the brightness temperature at i GHz can be expressed as follows:

$$T_{b,i}=T_{a,i}^{\uparrow }+{\tau }_i\cdot {\epsilon }_i\cdot T_S+\left(1-{\epsilon }_i\right){\tau }_i\left(T_{a,i}^{\downarrow }+T_{sky}\right)$$

(6)

where the first term on the right side of the equation represents the upwelling effective radiation of the atmosphere, the second term represents the surface-emitted radiation attenuated by the atmosphere, and the third term represents the surface-reflected and then the atmosphere-attenuated downwelling effective radiation of the atmosphere and the cosmic background radiation. $T_{b,i}$ is the brightness temperatures at i GHz K); ${\tau }_i$ is the atmospheric transmittances; $T_{a,i}^{\uparrow }$ and $T_{a,i}^{\downarrow }$ are the upwelling and downwelling effective radiating temperatures of the atmosphere (K); ${\epsilon }_i$ is MLSE; $T_S$ is LST (K); and $T_{sky}$ is the cosmic background radiation temperature (approximately 2.7 K). These equations implicitly include the dependence of radiance on the sensor angle. Consequently, ${\epsilon }_i$ can be estimated from the transformation of Equation (6):

$${\epsilon }_i=\frac{T_{b,i}-T_{a,i}^{\uparrow }-\left(T_{a,i}^{\downarrow }+T_{sky}\right){\tau }_i}{{\tau }_i\cdot T_S-\left(T_{a,i}^{\downarrow }+T_{sky}\right){\tau }_i}$$

(7)

where the unknown parameters are $T_s$, ${\tau }_i$, $T_{a,i}^{\uparrow }$, and $T_{a,i}^{\downarrow }$. These atmospheric parameters have been estimated from the WVC [37,38] and are described as follows [37]:

$${\tau }_i=e^{-\left(a_v\times WVC+b_o\right)}$$

(8)

$$T_{a,i}^{\uparrow }\approx T_{a,i}^{\downarrow }\approx \left(1-{\tau }_i\right)\left(a_T·{WVC}^2+b_T·WVC+c_T\right)$$

(9)

where ${\tau }_i$ is the exponential function of the WVC with base e, when ignoring the effect of cloud liquid water. $T_{a,i}^{\uparrow }$ is approximately equal to $T_{a,i}^{\downarrow }$ and is expressed as a function of ${\tau }_i$ and WVC. Han et al. [37] analyzed these relations using a monochromatic radiative transfer model and found that $a_v$, $b_o$, $a_T$, $b_T$, and $c_T$ depend on the frequency.

$T_s$ data can be retrieved from the FY-3D MERSI-2 under clear-sky conditions using the SW algorithm. The SW algorithm, a classical algorithm for retrieving the LST, uses the absorbing differences within the atmosphere between two adjacent thermal infrared channels. This helps eliminate the influence of the atmosphere through a combination of two thermal infrared channels. The general expression for the SW algorithm is as follows:

$$LST=A_0+A_1{T}_{B1}-A_2{T}_{B2}$$

(10)

where $A_0$, $A_1$, $A_2$ are parameters and $T_{B1}$ and $T_{B2}$ are two brightness temperatures in adjacent thermal infrared channels. Scholars have improved the SW algorithm and obtained numerous new expressions [39]. In this study, we used the improved SW algorithm proposed by Wang et al. [40], whose expression of the SW algorithm is reduced as follows:

$$LST=\left[C_{25}\left(B_{24}+D_{24}\right)-C_{24}\left(B_{25}+D_{25}\right)\right]∕\left(C_{25}{A}_{24}-C_{24}{A}_{25}\right)$$

(11)

$$\mathrm{where} \left\{\begin{array}{c}{A}_{24}=0.1419{\epsilon }_{24}{\tau }_{24}\\ A_{25}=0.1195{\epsilon }_{25}{\tau }_{25}\\ B_{24}=0.1419T_{B24}+32.764{\epsilon }_{24}{\tau }_{24}-32.764\\ B_{25}=0.1195T_{B25}+26.775{\epsilon }_{25}{\tau }_{25}-26.775\\ C_{24}=\left(1-{\tau }_{24}\right)\cdot \left[1+\left(1-{\epsilon }_{24}\right){\tau }_{24}\right]\cdot 0.1419\\ C_{25}=\left(1-{\tau }_{25}\right)\cdot \left[1+\left(1-{\epsilon }_{25}\right){\tau }_{25}\right]\cdot 0.1195\\ D_{24}=\left(1-{\tau }_{24}\right)\cdot \left[1+\left(1-{\epsilon }_{24}\right){\tau }_{24}\right]\cdot 32.764\\ D_{25}=\left(1-{\tau }_{25}\right)\cdot \left[1+\left(1-{\epsilon }_{25}\right){\tau }_{25}\right]\cdot 26.775\end{array}\right\}$$

(12)

where ${\epsilon }_M$ is the land surface emissivity of channel M, ${\tau }_M$ is the atmospheric transmittance of channel M, and $T_{BM}$ is the brightness temperature of channel M.

To obtain the LST, it is necessary to first obtain the other two parameters: atmospheric transmittance: ${\tau }_{24}$ and ${\tau }_{25}$; and thermal infrared land surface emissivity ${\epsilon }_{24}$ and ${\epsilon }_{25}$.

Wang et al. [40] found that the thermal infrared atmospheric transmittance shows a decreasing trend with an increase in the WVC based on simulations from MODTRAN. Consequently, they built a cubic polynomial fitting to estimate the atmospheric transmittance in the thermal infrared bands from the WVC [40]:

$${\tau }_{24}=0.0016{WVC}^3-0.0216{WVC}^2-0.0243WVC+0.9635$$

(13)

$${\tau }_{25}=0.0023{WVC}^3-0.0234{WVC}^2-0.0623WVC+0.9555$$

(14)

For the thermal infrared land surface emissivity, because the imaging times and thermal infrared wavelength settings of the MERSI-2 were similar to those of the Moderate Resolution Imaging Spectroradiometer (MODIS, MERSI-2 Band 24 vs. MODIS Band 31 and MERSI-2 Band 25 vs. MODIS Band 32) [24], the values of the Band 24 and 25 emissivities were directly used from the MODIS/Aqua Land Surface Temperature/Emissivity Daily L3 Global 1 km SIN Grid (MYD11A1) products.

Since the thermal infrared land surface emissivity ${\epsilon }_{\lambda }$ and atmospheric transmittance ${\tau }_{\lambda }$ were now known, the LST was calculated based on Equation (11). To match the spatial resolution of the MWRI data, the LST was aggregated to 0.25° using a cubic spline interpolation method.

Due to the greater penetration of lower-frequency radiation in arid regions, brightness temperature data at low frequencies are emitted from the subsurface rather than from the skin surface. Consequently, the passive microwave brightness temperature and infrared-based LST are not from the same physical quantity [30], which may produce inconsistent MLSE values between the day and night when the MLSE is estimated using Equation (7). To minimize this error and obtain more accurate MLSE estimates, a correction factor for the LST was computed based on the monthly mean brightness temperature for daytime and nighttime [29]:

$$T_s^c=T_s\pm \frac{\overline{T_{b,day}}-\overline{T_{b,night}}}{2}$$

(15)

where $\overline{T_{b,day}}$ and $\overline{T_{b,night}}$ are the mean composite brightness temperatures for all the daytimes and night-times for a specific month (K); “+” is used for the daytime and the “−” is used for the nighttime; $T_s^c$ is the corrected effective temperature consistent with passive microwave radiation (K), which was used in this study in arid regions; and $T_s$ is the original LST in arid regions (K). Figure 2 shows a flowchart of the MLSE retrieval algorithm.

4. Results

Figure 3a,b show the spatial distribution of the MLSE with horizontal and vertical polarization at all the frequencies in April 2020 separately (10, 18, 23, 36, and 89 H or V in the figure for short, as shown subsequently). As seen in Figure 3a, a noticeable increase in the MLSE is found with an increasing frequency. However, this pattern is not found in Figure 3b. On the contrary, the MLSE with vertical polarization in the Qinghai–Tibet Plateau decreases with an increasing frequency. In the 10H submap of Figure 3, some unusually high values appeared in the southern Jiangsu Province (marked by a black circle). We checked three kinds of input products and found that the abnormal values appeared in the brightness temperature data at 10.65 GHz. We believe that these brightness temperature data in this region are affected by radio-frequency interference.

5. Discussions

Due to the absence of thermal infrared LST under cloudy conditions, the passive microwave MLSE retrievals in this study were limited to clear-sky conditions. Consequently, the analysis of the spatial and seasonal distributions of the MLSE was based on monthly mean retrievals.

Because of the effect of the radio-frequency interference, the MLSE at 10.65 GHz was excluded from the following discussions. Additionally, as the differences in the MLSE between 18.7 and 23.8 GHz are small, the discussions also exclude 18.7 GHz.

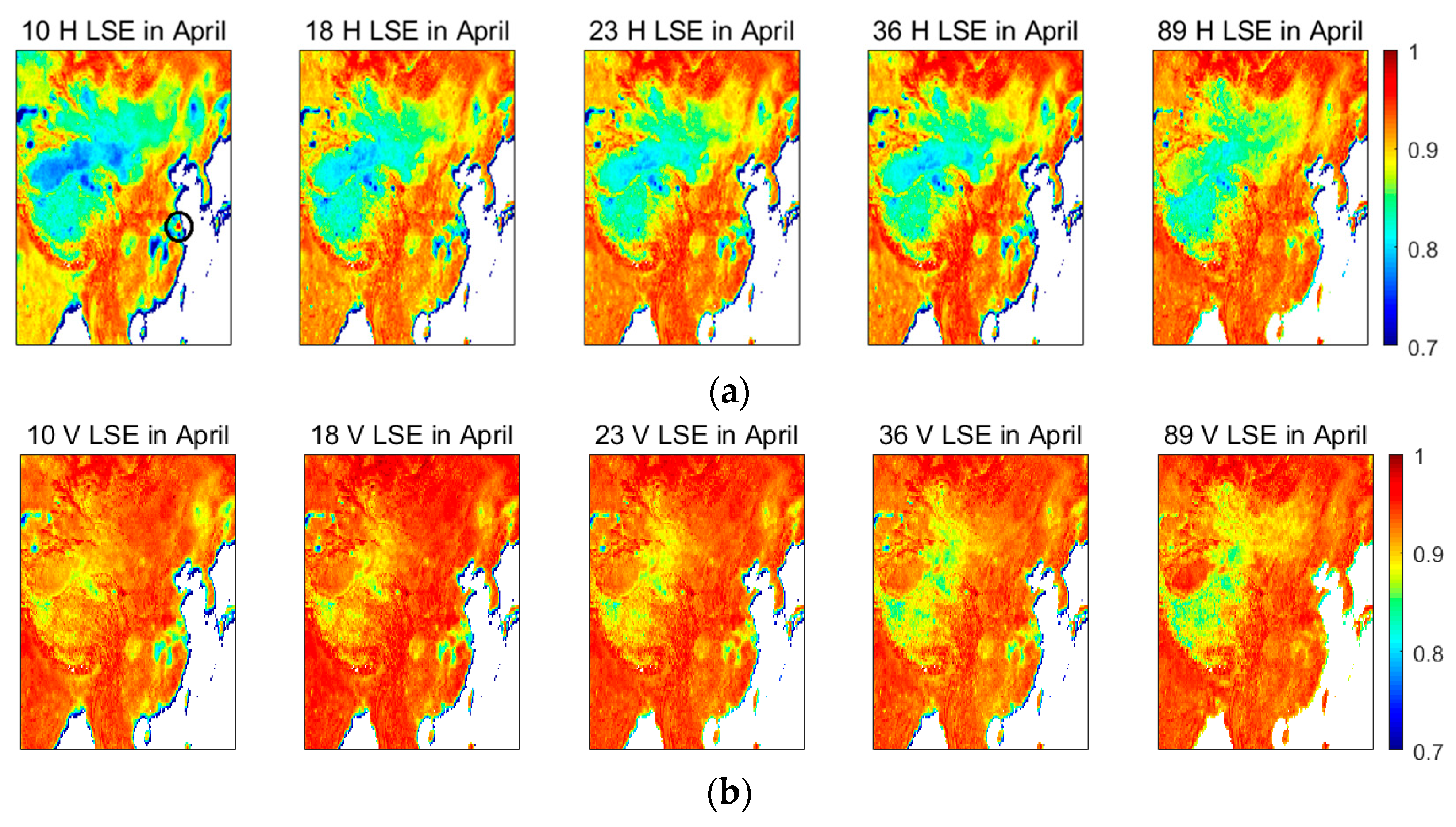
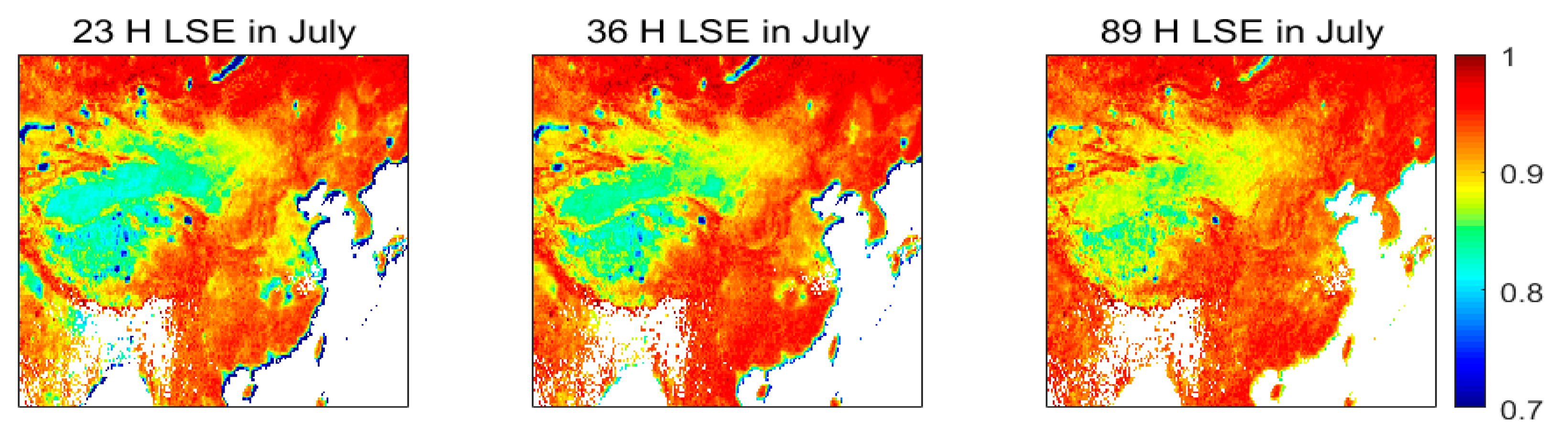
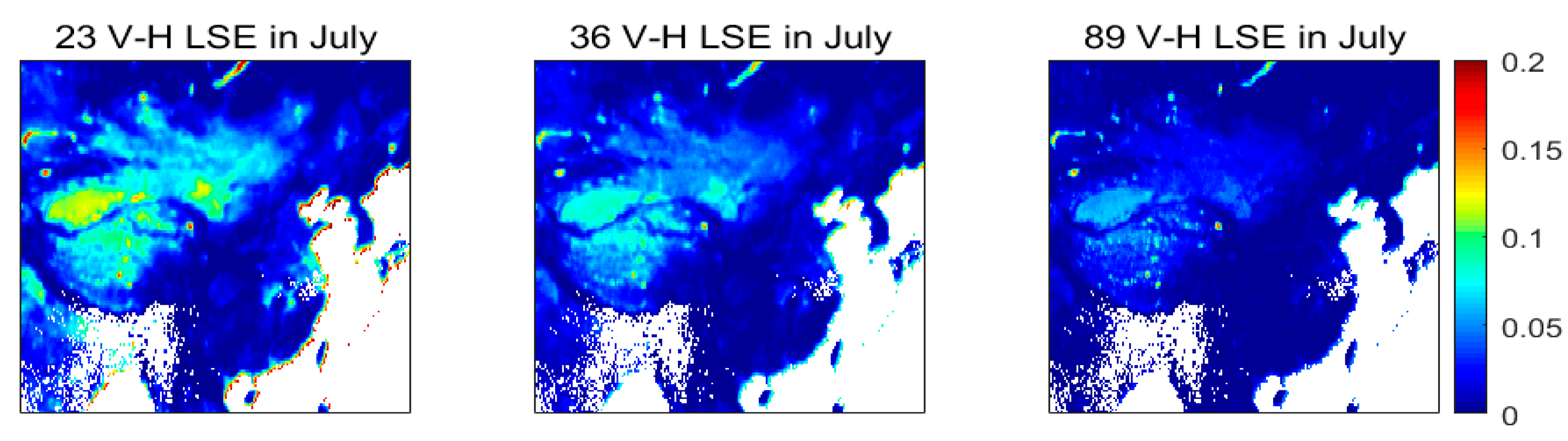
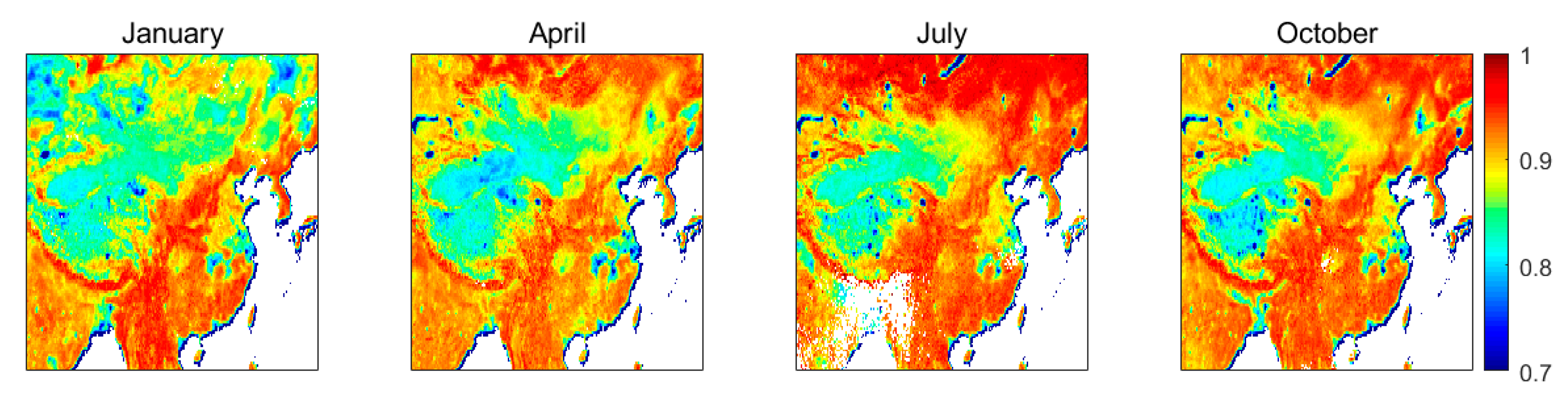
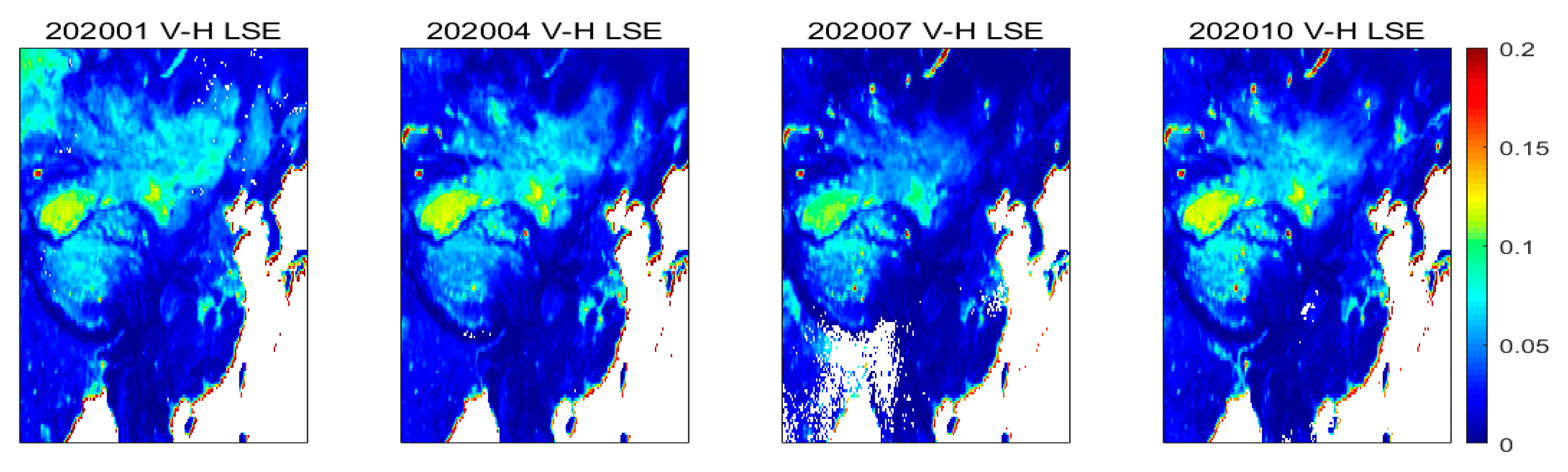
5.1. Spatial Distribution of the Monthly MLSE

Figure 4 presents the monthly mean retrievals of the MLSE at 23.8, 36.5, and 89.0 GHz with horizontal polarization in July 2020. The spatial distribution of the MLSE in the study area is highly related to the land cover types and topography. Lower emissivities are mainly located over barren or sparsely vegetated regions (such as the Taklimakan Desert, Kumtag Desert, and Badain Jaran Desert) due to the low surface roughness. They are also located over river basins (such as the lower reaches of the Yangtze River and Ganges) and coastal areas owing to the large attenuation coefficient of water. In contrast, higher emissivities are mainly located over densely vegetated regions (such as southwest China) and mountainous areas (such as the Himalayan Mountains, Qinling–Taihang Mountains, and Great Khingan) due to the large surface roughness. Moderate emissivities are mainly located over grassland and cropland areas, such as the North China Plain.

Figure 4 also shows that lower-frequency channels are more sensitive to water than higher-frequency channels. For example, in the lower reaches of the Yangtze River, Ganges River basin, and coastal areas, the number of pixels of low emissivities at 23.8 GHz are noticeably more than those at 89.0 GHz. Consequently, low-frequency channels are useful for retrieving the soil moisture and vegetation water content. Moreover, low-frequency emissivities have the potential to monitor precipitation during land and soil droughts.

It is known that the MLSE with vertical and horizontal polarizations show different characteristics because of the differences in their dielectric constant responses. Figure 5 shows the differences between the vertically and horizontally polarized emissivities from 23.8 GHz to 89.0 GHz in July 2020. It is observed that lower-frequency channels show larger differences in emissivities due to polarization than those of higher-frequency channels in barren or sparsely vegetated regions. The Taklimakan and Ala Shan Deserts showed the largest polarization differences, while evergreen rainforests and mountainous areas exhibited the smallest differences. This distinction is useful for identifying land cover and terrain based on polarized emissivity differences.

5.2. Seasonal Distribution of the MLSE

Figure 6 shows the seasonal variation in the emissivities at 36.5 GHz with horizontal polarization in January, April, July, and October 2020, representing winter, spring, summer, and autumn, respectively. It is observed that the MLSEs located over densely vegetated land areas, such as evergreen broadleaf forests in Southeast Asia, deserts, such as the Taklimakan Desert, and river basins, such as the lower reaches of the Yangtze River, exhibit minimum seasonal variations. This is because the surface cover types in evergreen forests and deserts do not change seasonally. However, other areas, such as woody savannas, grasslands, croplands, and seasonal snow cover areas, showed noticeable seasonal variations related to seasonal changes in the vegetation density, snow cover, and melting. Figure 6 also shows that many missing emissivity values existed at low latitudes in July. Because these areas are always covered by clouds, thermal infrared data cannot be used to measure the LST.

Figure 7 shows the seasonal variation in the MLSE differences at 36.5 GHz between vertical and horizontal polarization in 2020. Across most land cover types, the differences between the vertically and horizontally polarized emissivities do not change significantly throughout the seasons. Barren or sparsely vegetated regions (such as Taklimakan Desert, Badain Jaran Desert, Tengger Desert, Uulan Buh Desert, Kubuqi Desert, and Hunshandak Sandy Land), river basins (such as the lower reaches of the Yangtze River), and coastal areas show large polarization differences, while evergreen rainforests and mountainous areas exhibit the smallest polarization differences. However, certain grasslands in eastern Inner Mongolia and southern Mongolia show clear seasonal variations. This was mainly caused by seasonal changes in the rainfall and vegetation density.

5.3. Possible Error Sources of the Retrieved MLSE

To date, no high-precision MWRI emissivity product from the FY-3D satellite is available for verifying our algorithm. Our MLSE retrievals were compared to those of Moncet_MLSE [24] and Hu_MLSE [41] at all five frequencies in China. Similar spatial and seasonal distributions of the MLSE were observed in the three retrievals. However, some differences were also found, which may have been caused by differences in the sensors, algorithms, and data acquisition times. In addition, possible errors in our proposed algorithm might originate from three sources.

5.3.1. Errors from the FY-3D MWRI Brightness Temperature Measurements

To assess the accuracy of the MWRI brightness temperature data, AMSR2 L3 brightness temperature data with a spatial resolution of 0.25°, which was the same as that of the MWRI data, were used. The original spatial resolutions of the five bands of both the MWRI and AMSR2 are listed in

Table 2. Differences in the original resolution of the MWRI and AMSR2.

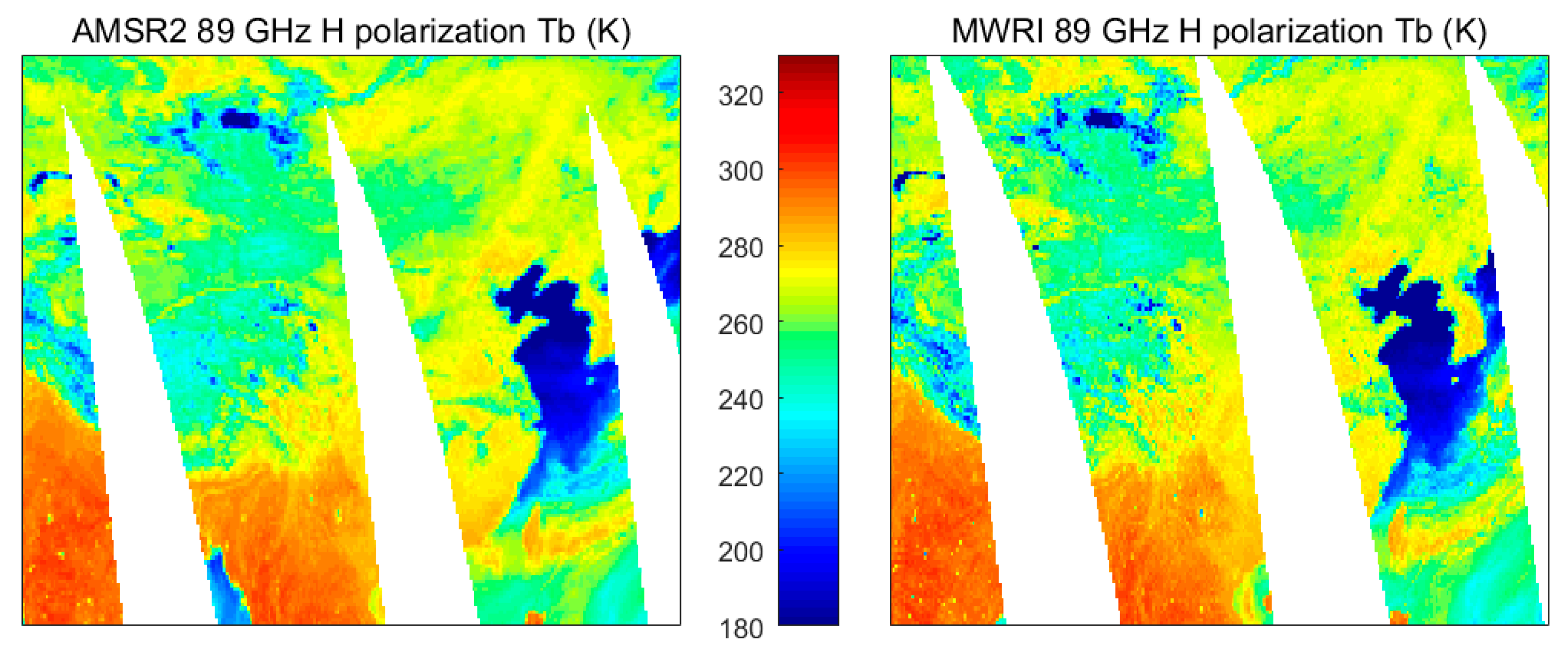
Central Frequency (GHz)	MWRI (km)	AMSR2 (km)
10.65	51 × 85	24 × 42
18.7	30 × 50	14 × 22
23.8	27 × 45	15 × 26
36.5	18 × 30	7 × 12
89	9 × 15	3 × 5

MWRI, Microwave Radiation Imager; AMSR2, Advanced Microwave Scanning Radiometer 2.

. As shown in Table 2, the original spatial resolutions of all the AMSR2 frequencies were much higher than those of the MWRI.

Figure 8 shows the brightness temperature distribution map at 89 GHz with horizontal polarizations of the MWRI and AMSR2 on 1 April 2020. As shown in Figure 8, the brightness temperature distribution trends from both passive microwave radiometers were consistent. The gaps in the MWRI map are larger than those in the AMSR2 map because the swath width of the MWRI is 1400 km, whereas that of the AMSR2 is 1450 km. Two error metrics, the correlation coefficient (R) and bias, were used to evaluate the accuracy of the MWRI brightness temperature across five frequencies and two polarizations, and the results are listed in

Table 3. Accuracy of the Microwave Radiation Imager brightness temperature across five frequencies and two polarizations.

Polarization	Frequency (GHz)	R	Bias (K)
H	10.65	0.99	−2.77
	18.7	0.98	0.25
	23.8	0.97	−3.14
	36.5	0.96	−4.49
	89	0.92	−0.98
V	10.65	0.99	−5.1
	18.7	0.98	−2.88
	23.8	0.97	−4.47
	36.5	0.96	−5.05
	89	0.92	−2.19

. The table shows high correlation coefficients (>0.92), indicating high consistency between the MWRI and AMSR2 across all channels. However, the correlation coefficients decrease (from 0.99 to 0.92) with an increase in the frequency (from 10.65 GHz to 89 GHz) and the decreasing trend have no connection with polarization. The bias of −5.1 to 0.25 K suggests that the MWRI brightness temperature is lower than that of the AMSR2. These differences may be due to variations in the overpass time, incidence angles, bandwidth, and original spatial resolutions between the two sensors, aligning with findings from previous studies [40].

5.3.2. Errors from the FY-3D LST

The MODIS is one of the most reliable global remotely sensed LST products [42,43,44]. Validated via in situ measurements, the MODIS LST in some homogeneous land surfaces showed accuracy within 1 K [45,46]. The MERSI-2 operates with thermal infrared wavelength settings similar to those of the MODIS data, albeit with an imaging time of approximately half an hour later than that of the MODIS. Wang et al. [40] showed a good agreement between the LST from the MODIS and MERSI-2 in the Bohai Sea area of China. Aveni and Blackett [47] evaluated the MODIS and MERSI-2 LST of Mount Etna (Italy) during the active volcanic phase in 2019 and obtained an R² of 0.92.

In this study, the corresponding MODIS LST (MYD11A1) and calculated MERSI-2 LST on 1 April 2020, were compared at the 1 km pixel level. The error frequency map of LST differences is shown in Figure 9, revealing an RMSE of 3.34 K and a correlation coefficient of 0.958. The bias of 0.82 K means that the MODIS LSTs are higher than the MERSI-2 LSTs. The higher RMSE, compared to that reported by Wang et al. [40], mainly comes from the more complicated validation data involving many land cover types, land surface elevations, and climatic zones. The half an hour time gap between the MODIS and MERSI-2 acquisitions may be the main cause of this temperature discrepancy.

5.3.3. Errors from the FY-3D WVC

The Aerosol Robotic Network, a global ground-based aerosol observation network equipped with many sun photometers, has been widely used and validated worldwide. Xie et al. [48] used ground-based WVC data from 369 Aerosol Robotic Network sites to validate the MERSI-2 WVC products. The results showed that all four MERSI-2 WVC datasets (${WVC}_c, {WVC}_{905}, {WVC}_{936}, {\mathrm{a}\mathrm{n}\mathrm{d} WVC}_{940}$) were better than the MODIS WVC dataset due to the serious overestimation found in the MODIS WVC data.

6. Conclusions

In this study, a physics-based algorithm was developed to retrieve MLSE data using passive microwave brightness temperature measurements obtained from the FY-3D MWRI. The algorithm utilized input data, including the brightness temperature, LST, and WVC, obtained exclusively from the FY-3D satellite, ensuring consistency in the data acquisition times. This feature significantly reduced the MLSE retrieval errors caused by inconsistencies in the data acquisition time.

Based on the MLSE retrieved by our algorithm, it was found that the spatial distribution of the MLSE was highly relevant to the land cover types and topography. Lower emissivities were mainly located over barren or sparsely vegetated regions, which have low surface roughness. Similarly, they were also located over river basins and coastal areas, which have large attenuation coefficients. In contrast, higher emissivities were mainly located over densely vegetated regions and mountainous areas, distinguished by their rough surfaces. Moderate emissivities were mainly observed across grasslands and croplands within plains. Moreover, lower-frequency channels were more sensitive to water than higher-frequency channels, which is more evident in the lower reaches of the Yangtze River, Ganges River basin, and coastal areas. Lower-frequency channels showed larger emissivity differences with different polarizations than those of higher-frequency channels in barren or sparsely vegetated regions. The MLSE over densely vegetated land areas and deserts showed small seasonal variations because the surface cover types in these areas do not change seasonally. However, areas with woody savannas, grasslands, croplands, and seasonal snow cover showed noticeable seasonal variations associated with seasonal changes in the vegetation density, snow cover, and melting dynamics. For most land cover types, the differences between the vertically and horizontally polarized emissivities do not change significantly across seasons. However, some grasslands in eastern Inner Mongolia and southern Mongolia show clear seasonal variations. This was mainly caused by seasonal changes in the rainfall and vegetation density.

It is very difficult to verify the MLSE on a large scale. Therefore, this study mainly focused on the derivation of the physics-based MLSE retrieval method and the analysis of the results. Similar spatial and temporal distributions were observed when our MLSE retrievals were compared to those of other MLSE products. Some differences in the MLSE may arise from differences in sensors, algorithms, data acquisition times, and input data measurement errors. In this study, we validated the accuracy of the FY-3D MWRI brightness temperature and MERSI-2 LST measurements. It was found that the correlation coefficients between the MWRI and AMSR2 brightness temperatures ranged from 0.92 to 0.99. Additionally, the accuracy of the retrieved MERSI-2 LST measurements showed an RMSE of 3.34 K and a correlation coefficient of 0.958, compared with those of the MODIS LST measurements.