Identifying Seismic Anomalies via Wavelet Maxima Analysis of Satellite Microwave Brightness Temperature Observations
Abstract
1. Introduction
2. Data and Preprocessing
2.1. Data
2.1.1. Microwave Brightness Temperature (MBT) Data
2.1.2. Remote Sensing Parameters Influencing MBT Data
2.2. Data Processing
3. Comprehensive Methodological Approach
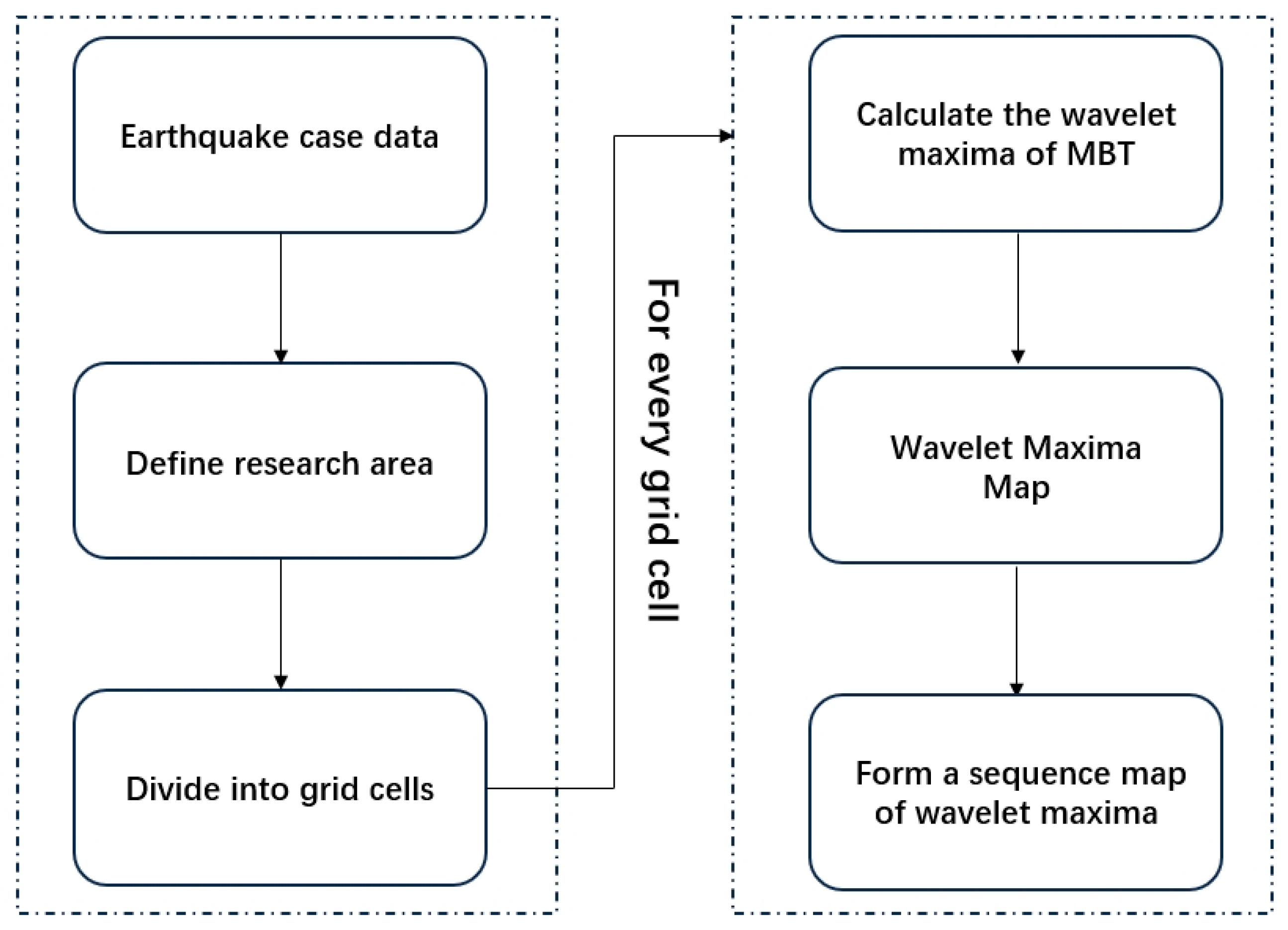
3.1. Wavelet Analysis Method
3.1.1. Continuous Wavelet Base Function
- (1)
- Haar wavelet
- (2)
- Mexico wavelet
- (3)
- Complex Gaussian wavelet
- (4)
- Fushanong wavelet
3.1.2. Wavelet Maxima
3.2. Research Approach
4. Results
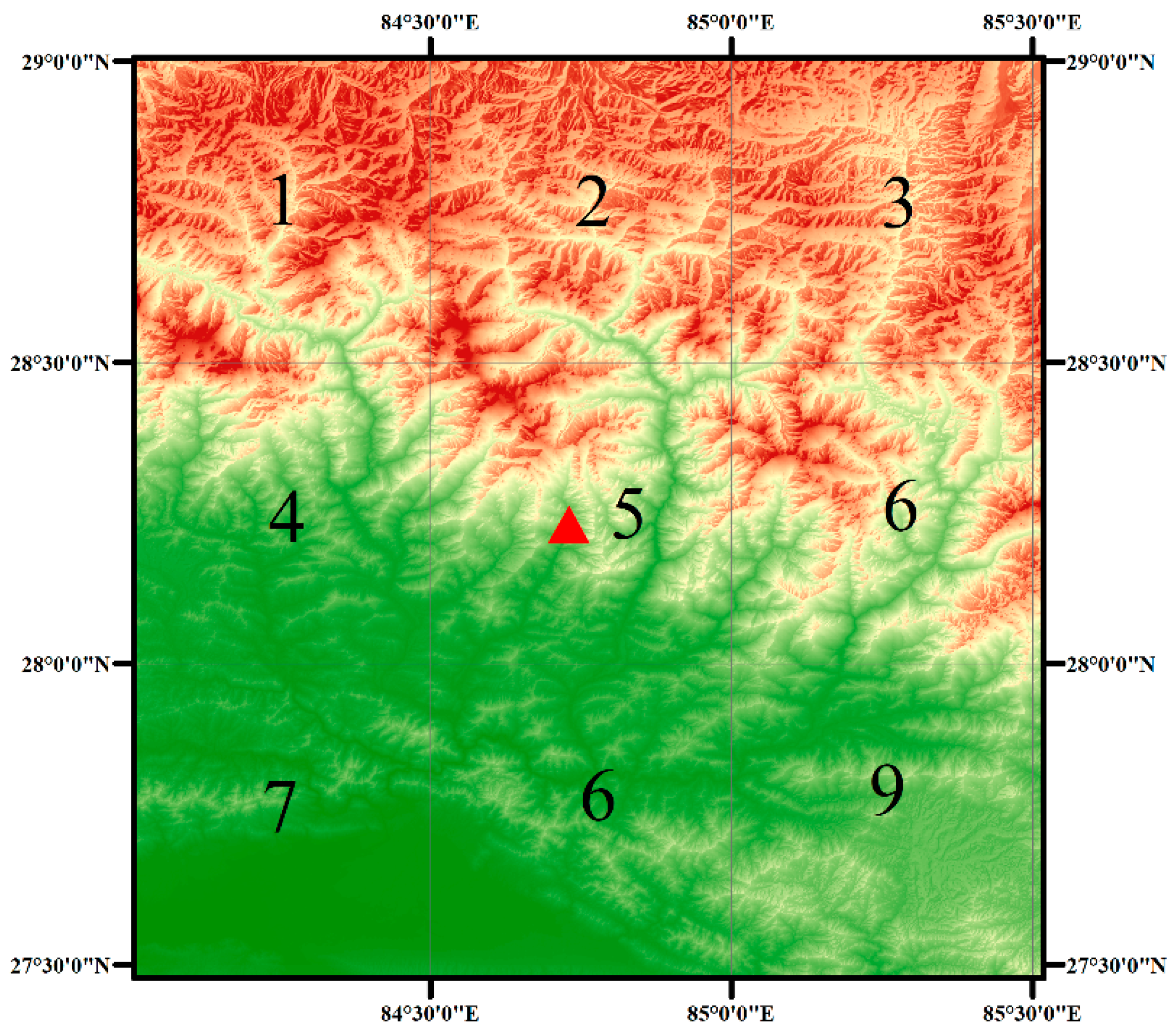
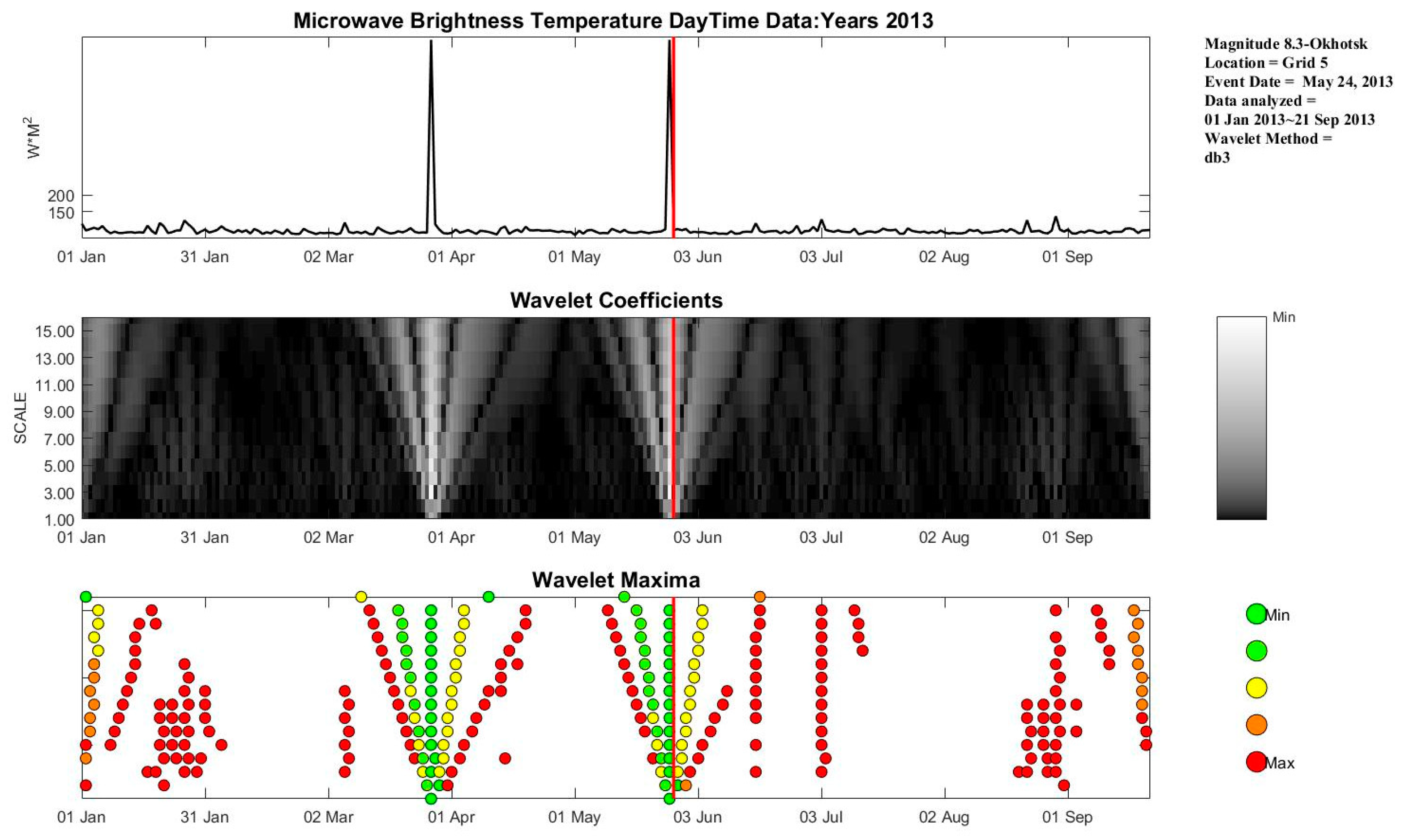
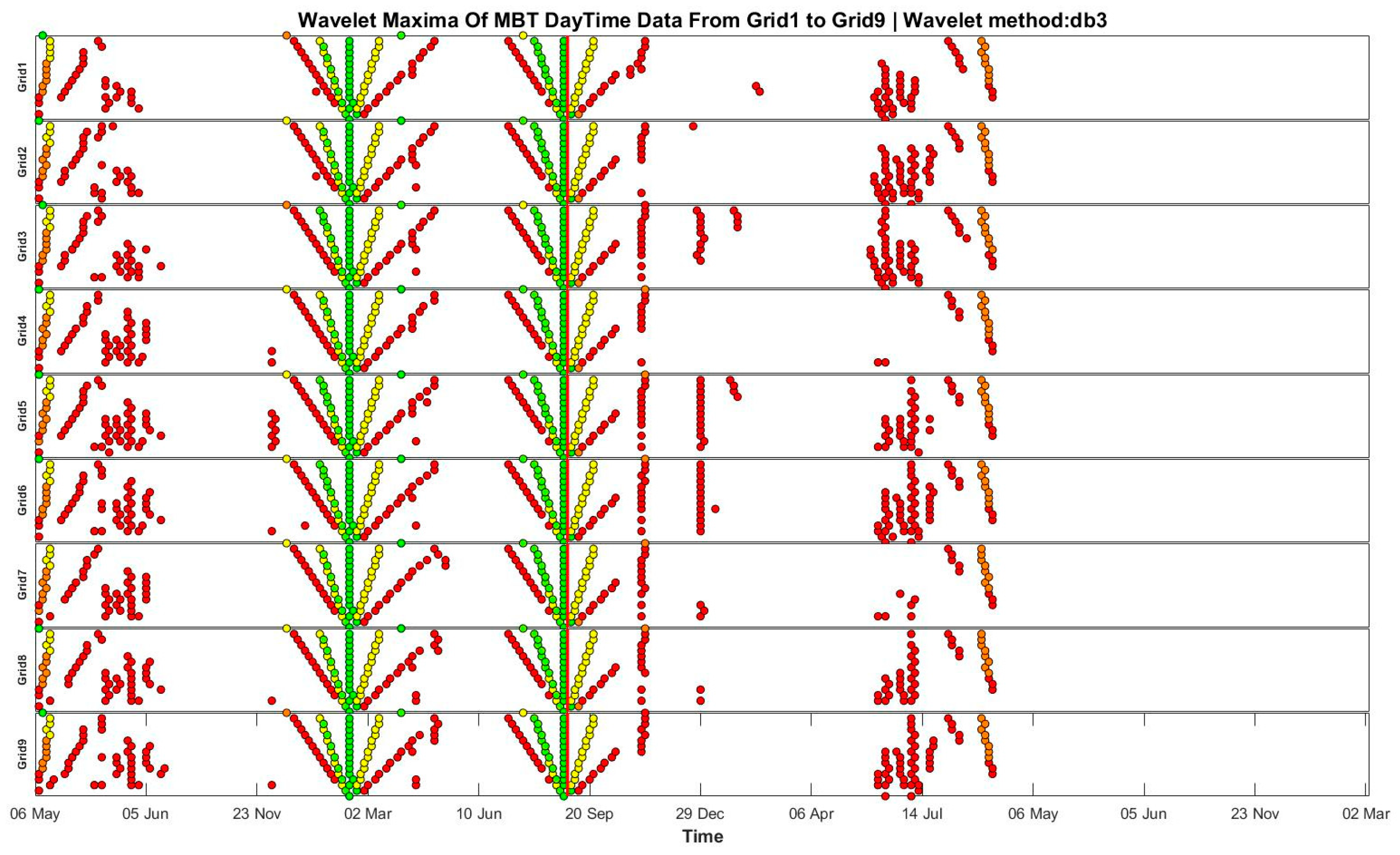
4.1. Ms 8.3 Earthquake in the Sea of Okhotsk
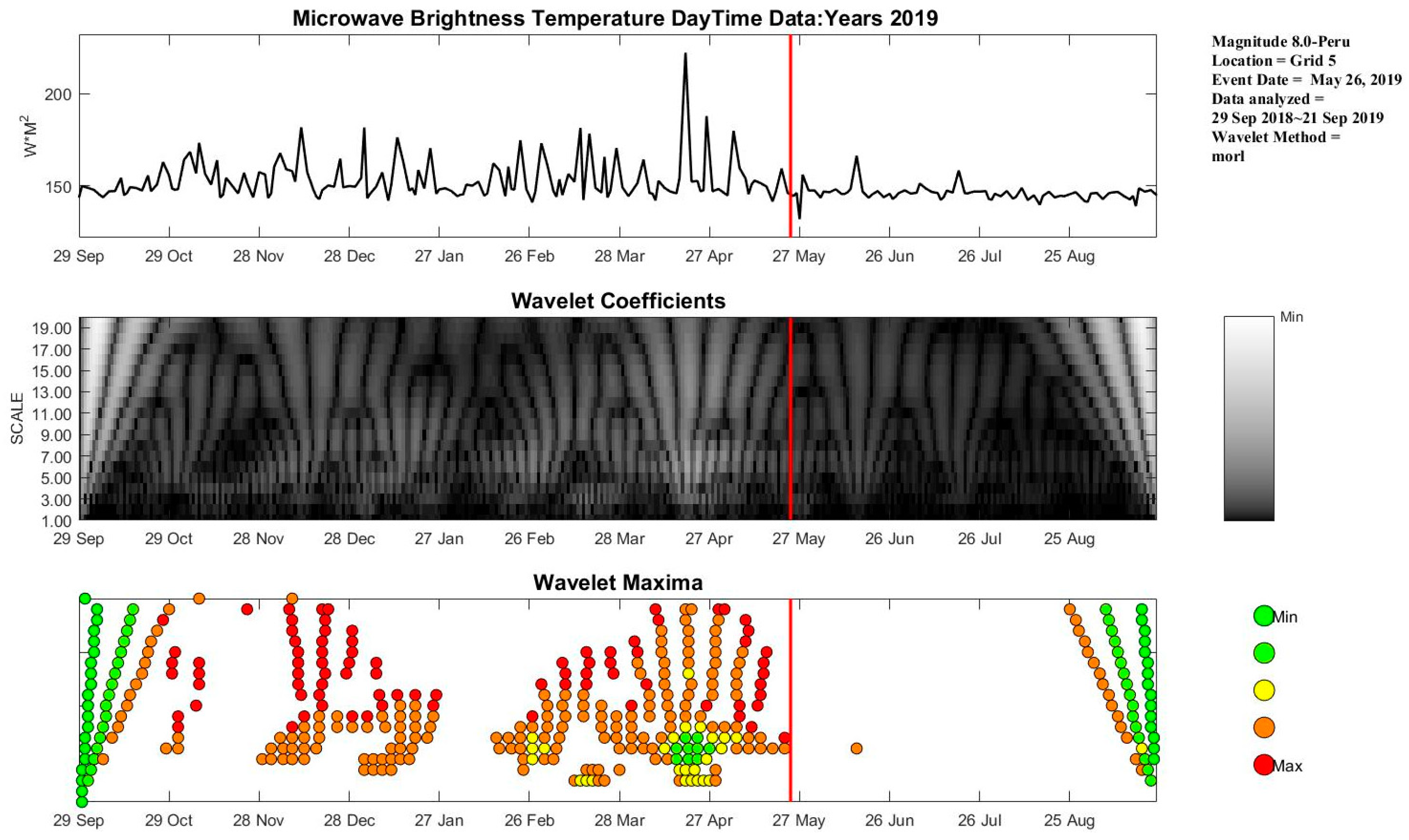
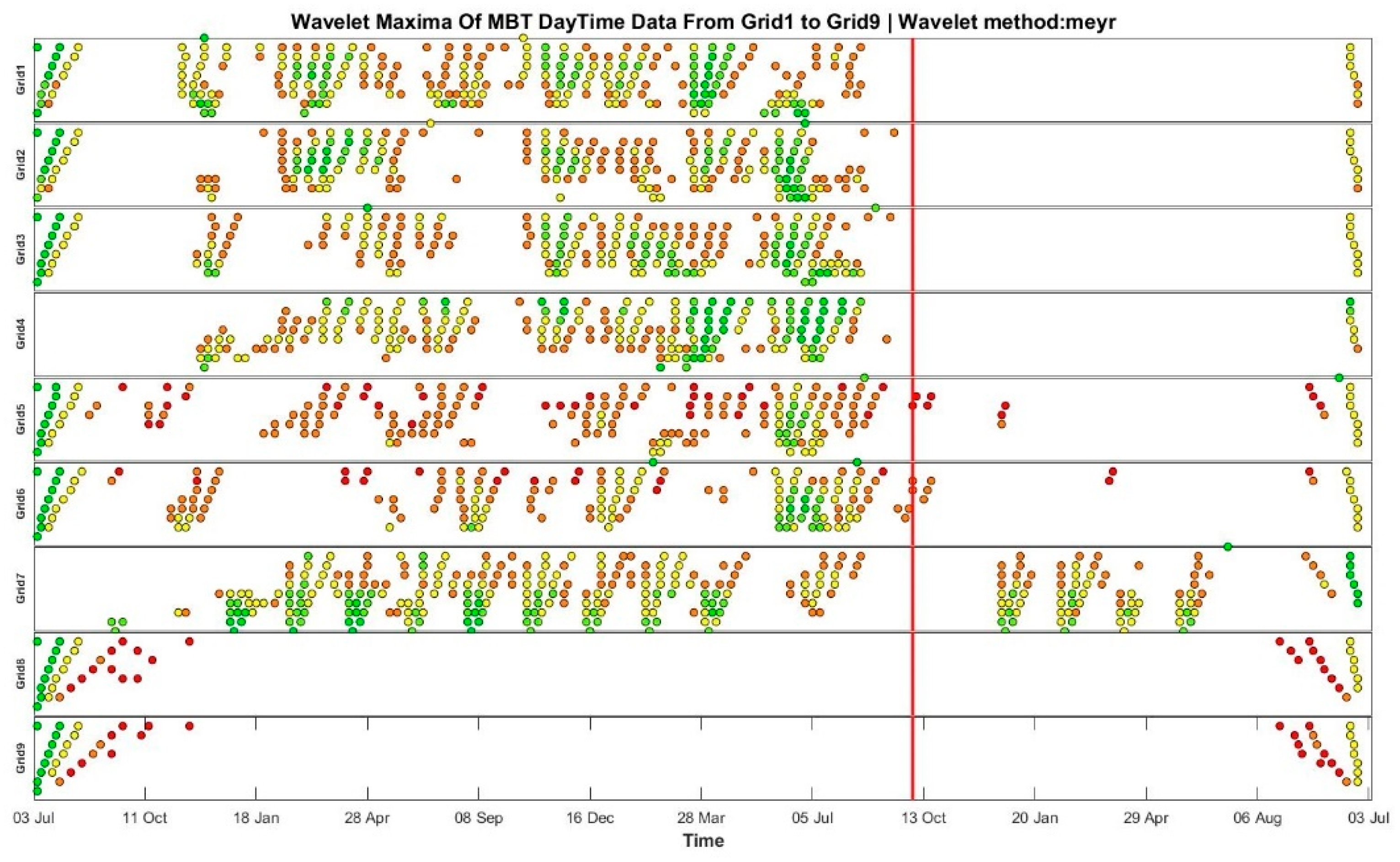
4.2. Ms 8.0 Peru Earthquake
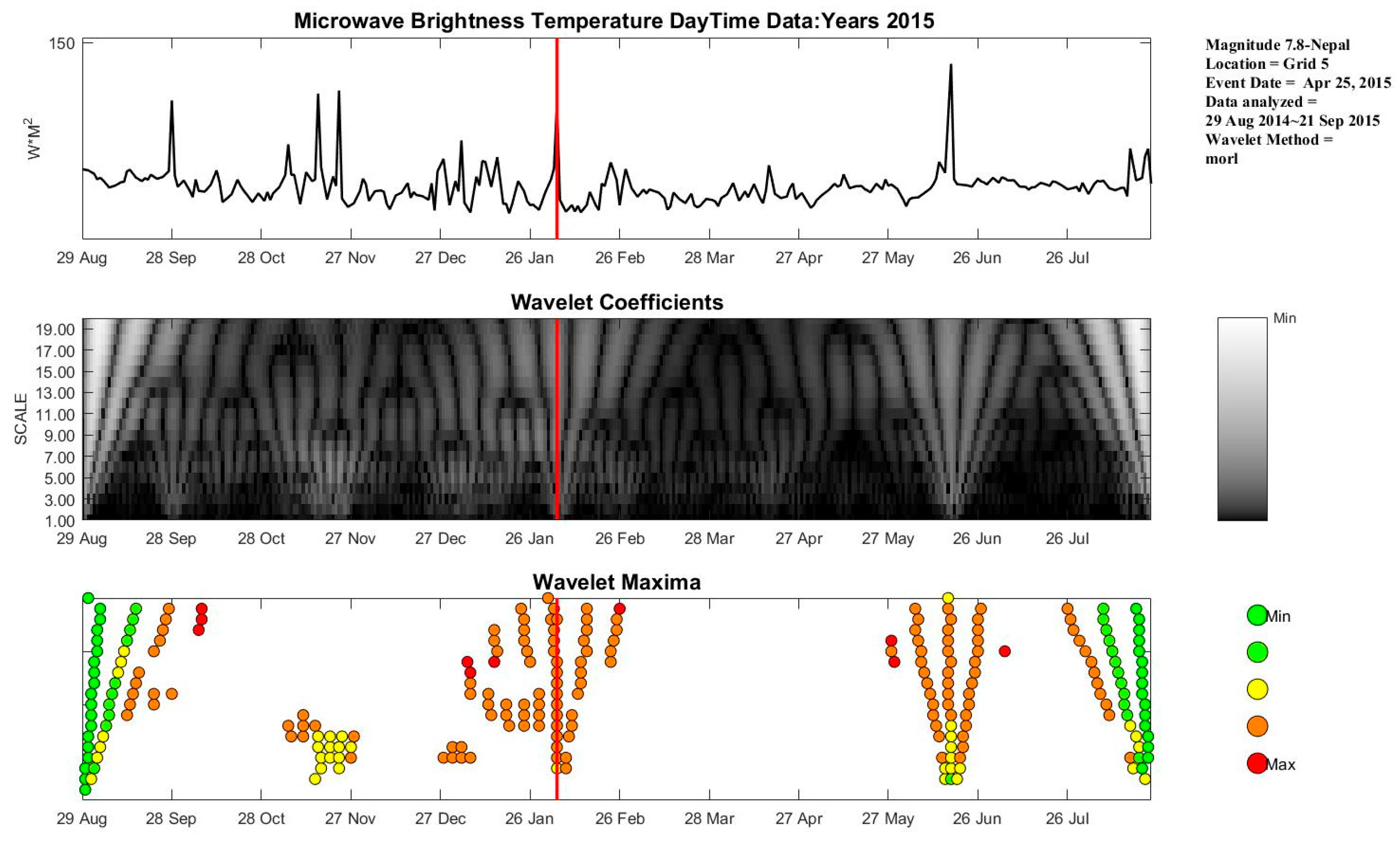
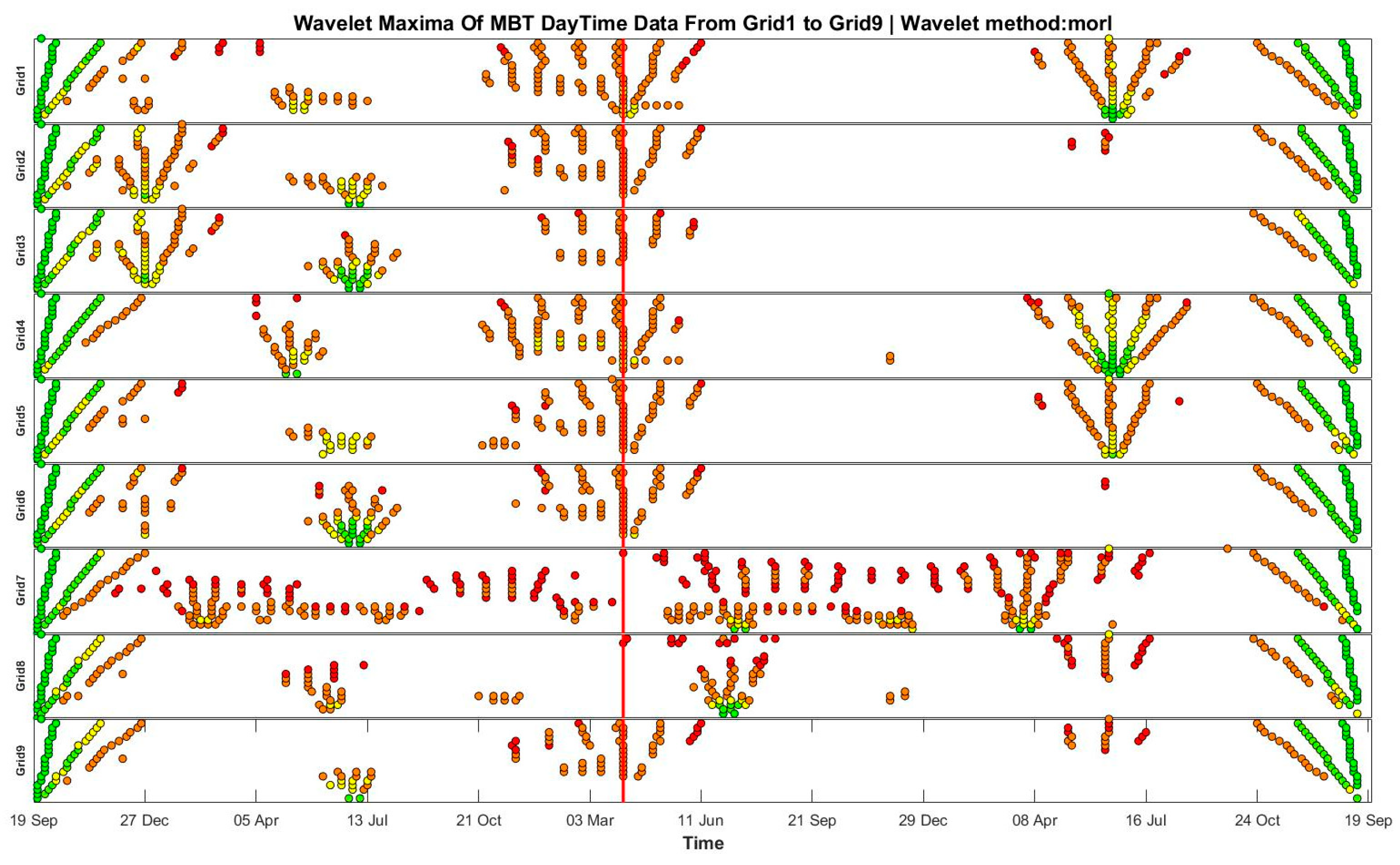
4.3. Ms 7.8 Nepal Earthquake
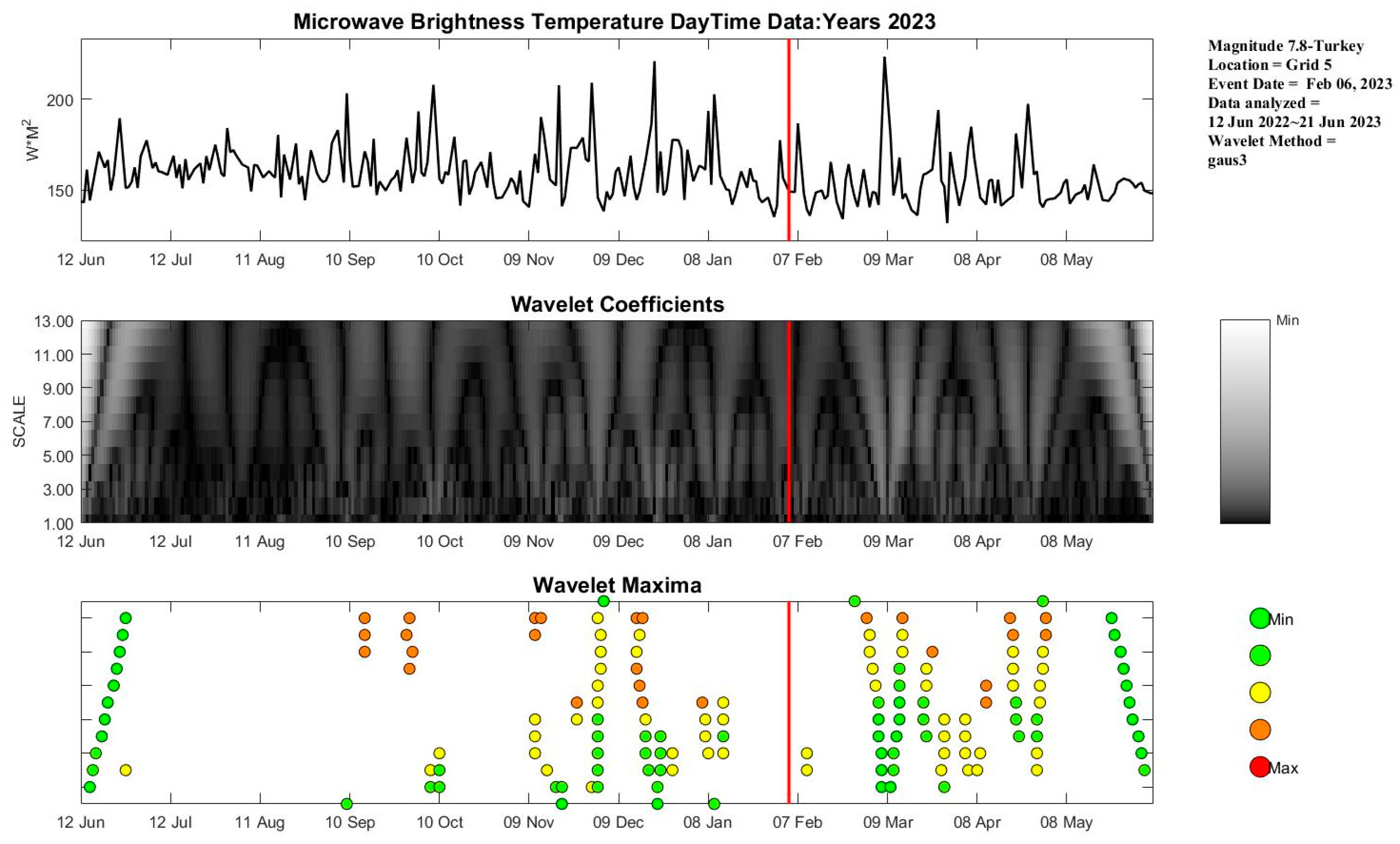
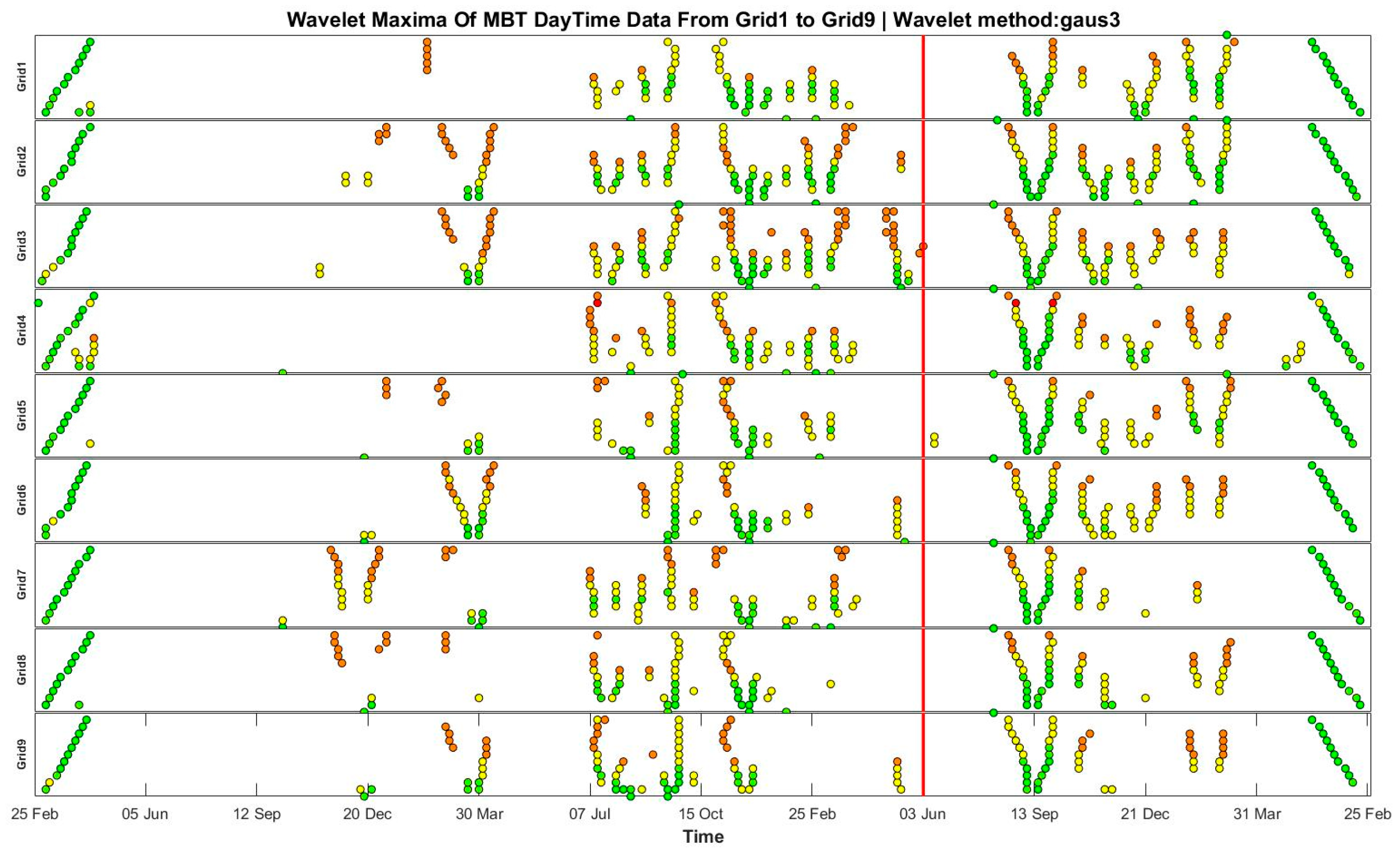
4.4. Ms 7.8 Turkey Earthquake
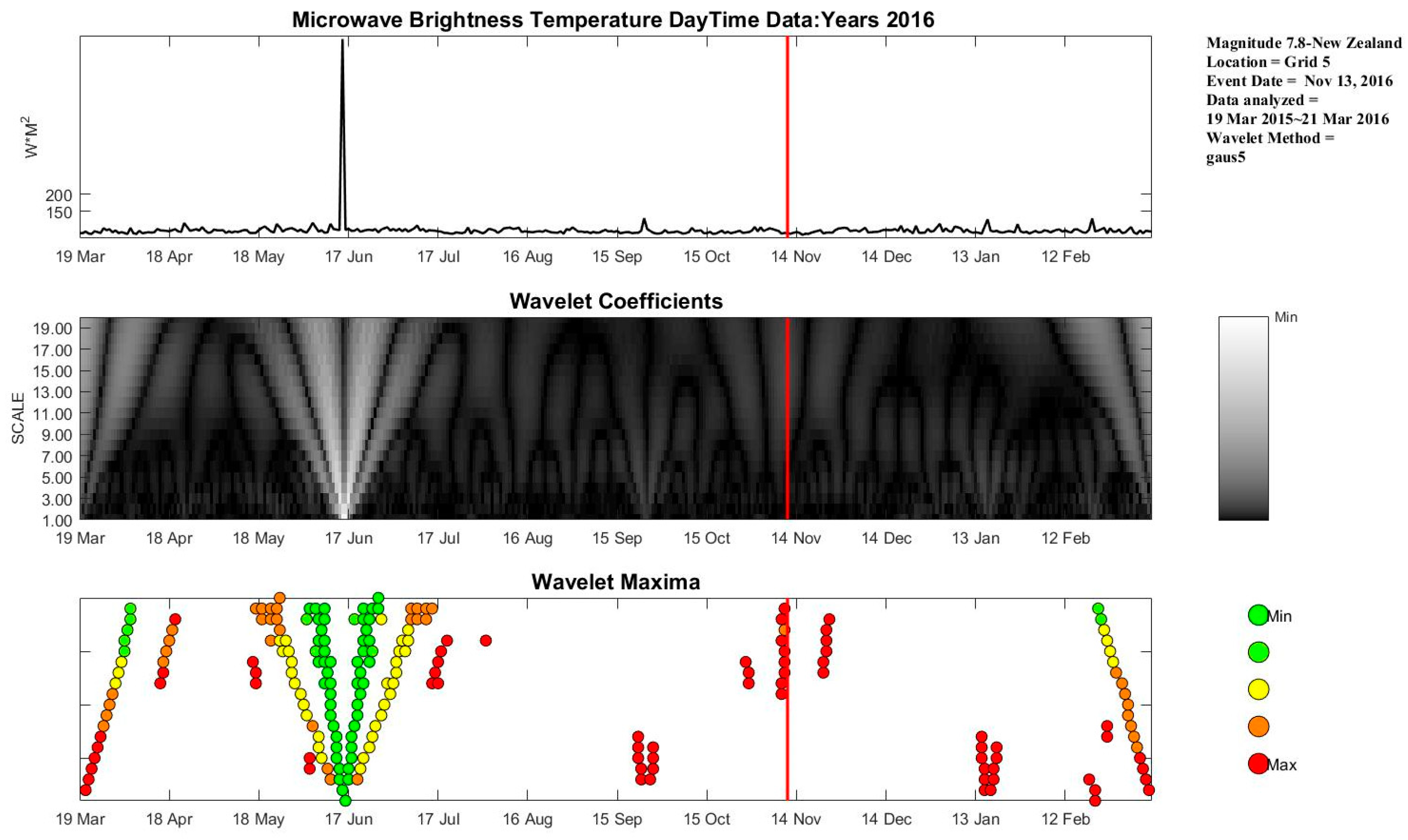
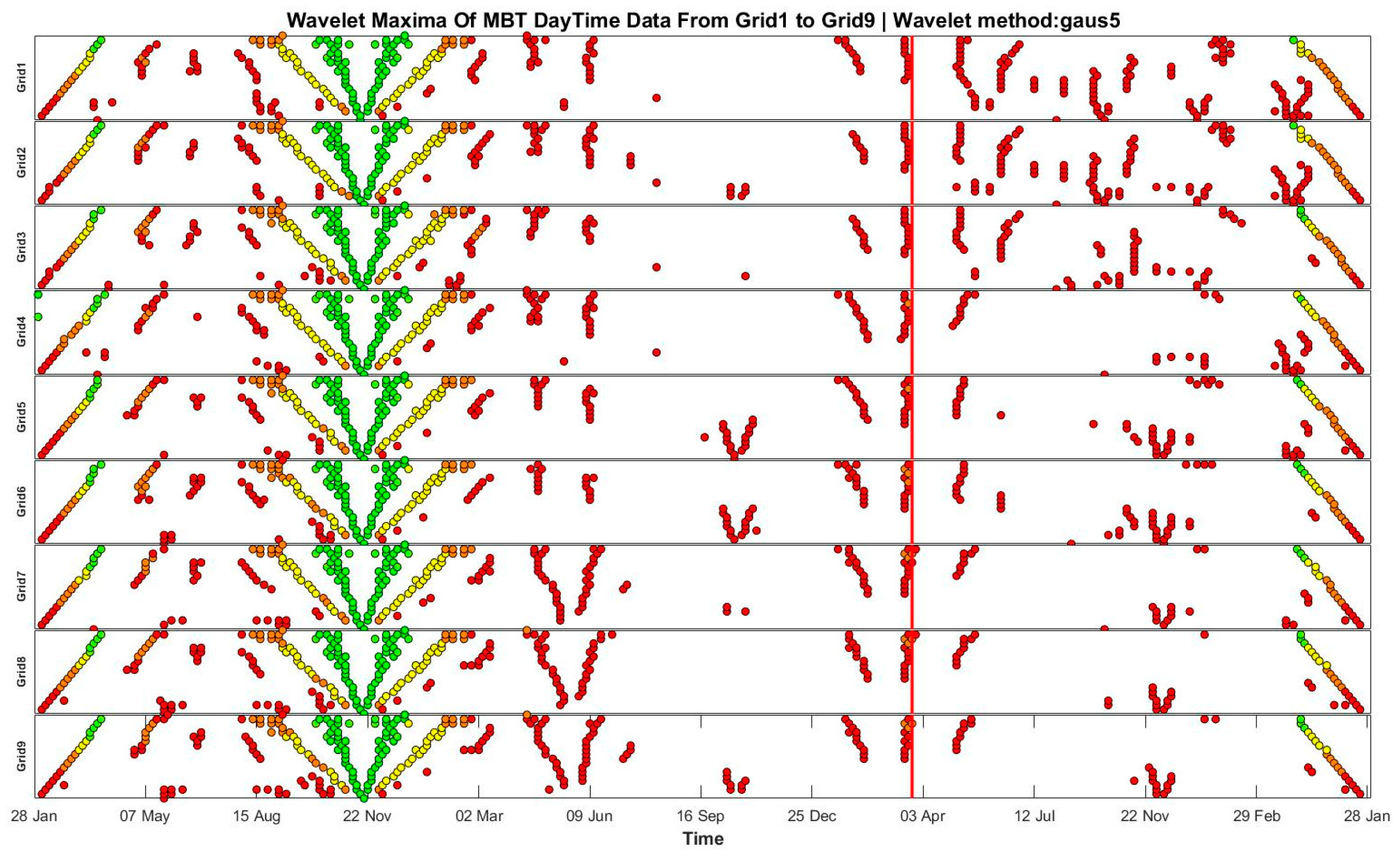
4.5. Ms 7.8 New Zealand Earthquake
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qi, Y.; Wu, L.; Mao, W.; Ding, Y.; Liu, Y.; Wang, X. Characteristic background of microwave brightness temperature (MBT) and optimal microwave channels for searching seismic MBT anomaly in and around the Qinghai-Tibet Plateau. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4504918. [Google Scholar] [CrossRef]
- Maeda, T.; Takano, T. Detection of microwave signals associated with rock failures in an earthquake from satellite-borne microwave radiometer data. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Hao, C.; Yaqiu, J. Preliminary Detection of Rock Fracture Radiation Anomalies in the Yushu Earthquake by Spaceborne Microwave Radiometer. Remote Sens. Technol. Appl. 2020, 29, 29–35. [Google Scholar] [CrossRef]
- Singh, R.P.; Mehdi, W.; Gautam, R.; Senthil Kumar, J.; Zlotnicki, J.; Kafatos, M. Precursory signals using satellite and ground data associated with the Wenchuan Earthquake of 12 May 2008. Int. J. Remote Sens. 2010, 31, 3341–3354. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, S.; Wu, L.; Xu, Z. Two-step method to extract seismic microwave radiation anomaly: Case study of MS8.0 Wenchuan earthquake. Earthq. Sci. 2011, 24, 577–582. [Google Scholar] [CrossRef]
- Jie, Y.; Guangmeng, G. Preliminary analysis of thermal anomalies before the 2010 Baja California M7.2 earthquake. Atmósfera 2013, 26, 473–477. [Google Scholar] [CrossRef]
- Zhang, B.; Qin, K.; Wu, T.; Shi, T.; Fan, W. Statistical Analysis of Microwave Radiation Anomaly Before Earthquake: A Case Study of Kamchatka Peninsula. Acta Seismol. Sin. 2018, 40, 98–107. [Google Scholar] [CrossRef]
- Jing, F.; Singh, R.P.; Cui, Y.; Sun, K. Microwave Brightness Temperature Characteristics of Three Strong Earthquakes in Sichuan Province, China. IEEE J-Stars 2020, 13, 513–522. [Google Scholar] [CrossRef]
- Jing, F.; Singh, R.P.; Shen, X. Land—Atmosphere—Meteorological coupling associated with the 2015 Gorkha (M 7.8) and Dolakha (M 7.3) Nepal earthquakes. Geomat. Nat. Hazards Risk 2019, 10, 1267–1284. [Google Scholar] [CrossRef]
- Qi, Y.; Wu, L.; Ding, Y.; Mao, W. Microwave Brightness Temperature Anomalies Associated With the 2015 Mw 7.8 Gorkha and Mw 7.3 Dolakha Earthquakes in Nepal. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Qi, Y.; Wu, L.; Mao, W.; Ding, Y.; He, M. Discriminating Possible Causes of Microwave Brightness Temperature Positive Anomalies Related With May 2008 Wenchuan Earthquake Sequence. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1903–1916. [Google Scholar] [CrossRef]
- Qi, Y.; Wu, L.; Ding, Y.; Liu, Y.; Chen, S.; Wang, X.; Mao, W. Extraction and Discrimination of MBT Anomalies Possibly Associated with the Mw 7.3 Maduo (Qinghai, China) Earthquake on 21 May 2021. Remote Sens. 2021, 13, 4726. [Google Scholar] [CrossRef]
- Qi, Y.; Wu, L.; He, M.; Mao, W. Spatio-Temporally Weighted Two-Step Method for Retrieving Seismic MBT Anomaly: May 2008 Wenchuan Earthquake Sequence Being a Case. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 382–391. [Google Scholar] [CrossRef]
- Liu, S.J.; Ji, M.Y.; Song, L.M.; Wei, L.H. Microwave Anomaly of Maduo MS7.4 Earthquake Derived by Improved Two-Step Difference Method. Acta Seismol. Sin. 2023, 45, 328–340. [Google Scholar] [CrossRef]
- Liu, S.; Cui, Y.; Wei, L.; Liu, W.; Ji, M. Pre-earthquake MBT anomalies in the Central and Eastern Qinghai-Tibet Plateau and their association to earthquakes. Remote Sens. Environ. 2023, 298, 113815. [Google Scholar] [CrossRef]
- Zhang, Y.-S.; Guo, X.; Wei, C.-X.; Shen, W.-R.; Hui, S.-X. The Characteristics of Seismic Thermal Radiation of Japan Ms9.0 and Myanmar Ms7.2 Earthquake. Chin. J. Geophys. Chin. 2011, 54, 2575–2580. [Google Scholar] [CrossRef]
- Xiong, P.; Shen, X.H.; Bi, Y.X.; Kang, C.L.; Chen, L.Z.; Jing, F.; Chen, Y. Study of outgoing longwave radiation anomalies associated with Haiti earthquake. Nat. Hazards Earth Syst. Sci. 2010, 10, 2169–2178. [Google Scholar] [CrossRef]
- Xiong, P.; Bi, Y.; Shen, X. Study of outgoing longwave radiation anomalies associated with two earthquakes in China using wavelet maxima. In Proceedings of the Hybrid Artificial Intelligence Systems: 4th International Conference, HAIS 2009, Proceedings 4, Salamanca, Spain, 10–12 June 2009; pp. 77–87. [Google Scholar]
- Xiong, P.; Bi, Y.; Shen, X. A wavelet-based method for detecting seismic anomalies in remote sensing satellite Data. In Proceedings of the Machine Learning and Data Mining in Pattern Recognition: 6th International Conference, MLDM 2009, Proceedings 6, Leipzig, Germany, 23–25 July 2009; pp. 569–581. [Google Scholar]
- Xiong, P.; Gu, X.; Shen, X.; Zhang, X.; Kang, C.; Bi, Y. Wavelet-based method for detecting seismic anomalies in DEMETER satellite data. In Proceedings of the Knowledge Science, Engineering and Management: 5th International Conference, KSEM 2011, Proceedings 5, Irvine, CA, USA, 12–14 December 2011; pp. 1–11. [Google Scholar]
- Kim, S.-B.; Huang, H.; Liao, T.-H.; Colliander, A. Estimating Vegetation Water Content and Soil Surface Roughness Using Physical Models of L-Band Radar Scattering for Soil Moisture Retrieval. Remote Sens. 2018, 10, 556. [Google Scholar] [CrossRef]
- Liang, M.; Pause, M.; Prechtel, N.; Schramm, M. Regionalization of Coarse Scale Soil Moisture Products Using Fine-Scale Vegetation Indices—Prospects and Case Study. Remote Sens. 2020, 12, 551. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, Z.; Lv, A. Evaluation of Satellite-Derived Soil Moisture in Qinghai Province Based on Triple Collocation. Water 2020, 12, 1292. [Google Scholar] [CrossRef]
- Mladenova, I.; Jackson, T.; Njoku, E.; Bindlish, R.; Chan, S.; Cosh, M.; Holmes, T.; De Jeu, R.; Jones, L.; Kimball, J.; et al. Remote monitoring of soil moisture using passive microwave-based techniques—Theoretical basis and overview of selected algorithms for AMSR-E. Remote Sens. Environ. 2014, 144, 197–213. [Google Scholar] [CrossRef]
- Qiao, P.; Zhang, J.; Wang, C. Soil moisture retrieving by AMSR-E microwave remote sensing data. J. China Univ. Min. Technol. Chin. Ed. 2007, 36, 262. [Google Scholar]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Jin, Y. Data analysis of the spaceborne SSM/I over crop areas of the Northern China. J. Remote Sens. 1998, 2, 18–25. [Google Scholar]
- Wang, J.R.; Schmugge, T.J. An empirical model for the complex dielectric permittivity of soils as a function of water content. IEEE Trans. Geosci. Remote Sens. 1980, 4, 288–295. [Google Scholar] [CrossRef]
- Mao, W.F.; Wu, L.X.; Liu, S.J.; Xu, Z.Y. Experiment Comparison on Microwave Radiation from Stressed Rock Covered by Materials: Dry or Humid Sands. J. Northeast. Univ. Nat. Sci. 2018, 39, 710. [Google Scholar]
- Liu, S.; Xu, Z.; Wei, J.; Huang, J.; Wu, L. Experimental study on microwave radiation from deforming and fracturing rock under loading outdoor. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5578–5587. [Google Scholar] [CrossRef]
| Type | Description | Vegetation Cover | Soil Moisture |
|---|---|---|---|
| 1 | Ocean | - | - |
| 2 | Land | >0.5 | >6 |
| 3 | Land | >0.5 | ≤6 |
| 4 | Land | ≤0.5 | >6 |
| 5 | Land | ≤0.5 | ≤6 |
| Type | Latitude | Longitude | Depth | Mag | CVH | SM |
|---|---|---|---|---|---|---|
| 1 | 54.892 | 153.221 | 598.10 | 8.3 | 0 | −1 |
| 2 | −5.812 | −75.269 | 122.57 | 8.0 | 1 | 8.27 |
| 3 | 28.231 | 84.731 | 8.22 | 7.8 | 0.656 | 4.505 |
| 4 | 37.226 | 37.014 | 10.00 | 7.8 | 0.479 | 7.435 |
| 5 | −42.737 | 173.054 | 15.11 | 7.8 | 0.014 | 4.849 |
| Type | Frequency (GHz) | Polarization | Wavelet Function | Wavelet Order |
|---|---|---|---|---|
| 1 | 10 | H | Db3 | 16 |
| 2 | 10 | H | Meyr | 10 |
| 3 | 10 | H | Morl | 20 |
| 4 | 36 | H | Gaus3 | 13 |
| 5 | 10 | H | Gaus5 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Xiong, P.; Chen, J.; Zhang, X.; Yang, X. Identifying Seismic Anomalies via Wavelet Maxima Analysis of Satellite Microwave Brightness Temperature Observations. Remote Sens. 2024, 16, 303. https://doi.org/10.3390/rs16020303
Wu H, Xiong P, Chen J, Zhang X, Yang X. Identifying Seismic Anomalies via Wavelet Maxima Analysis of Satellite Microwave Brightness Temperature Observations. Remote Sensing. 2024; 16(2):303. https://doi.org/10.3390/rs16020303
Chicago/Turabian StyleWu, Haochen, Pan Xiong, Jianghe Chen, Xuemin Zhang, and Xing Yang. 2024. "Identifying Seismic Anomalies via Wavelet Maxima Analysis of Satellite Microwave Brightness Temperature Observations" Remote Sensing 16, no. 2: 303. https://doi.org/10.3390/rs16020303
APA StyleWu, H., Xiong, P., Chen, J., Zhang, X., & Yang, X. (2024). Identifying Seismic Anomalies via Wavelet Maxima Analysis of Satellite Microwave Brightness Temperature Observations. Remote Sensing, 16(2), 303. https://doi.org/10.3390/rs16020303







