Abstract
An earthquake is a seismic event resulting from a sudden release of energy in the lithosphere, which produces waves that can propagate through the atmosphere into the ionosphere, causing ionospheric disturbances, and excites an additional electric field in the lower ionosphere. Two large-scale traveling ionospheric disturbances (LSTIDs) at daytime Turkey longitudes were found, with phase speeds of 534 and 305 m/s, respectively, after the second strong earthquake at 10:24 UT on 6 February 2023. During strong earthquakes, the equatorial ionospheric currents including the E-region equatorial electrojet (EEJ) and F-region ionospheric radial current (IRC) might be perturbed. At the Tatuoca station in Brazil, we observed a stronger-than-usual horizontal magnetic field associated with the EEJ, with a magnitude of ~100 nT. EEJ perturbations are mainly controlled by neutral winds, especially zonal winds. In the equatorial F-region, a wave perturbation of the IRC was caused by a balance of the electric field generated by the zonal winds at ~15° MLat, the F-region local winds driven by atmospheric resonance, and the additional polarization electric field. Our findings better the understanding of the complex interplay between seismic events and ionospheric current disturbances.
1. Introduction
The Earth’s ionosphere is the ionized part of the upper atmosphere, about 80–1000 km above the surface. Although the ratio between the charged particles and neutrals is less than 1%, the ionospheric plasma plays an important role in human activities for spacecraft communication, navigation, positioning, etc. Most of the low Earth orbit (LEO) satellites fly in the ionospheric altitudes; thus, the ionosphere plays a crucial role in the near-Earth geospace. Several works have reported that the ionosphere could be remarkably disturbed by lower atmospheric forcing, such as the energy release related to earthquakes, thunderstorms, and volcanic eruptions (e.g., [1,2,3,4,5,6,7,8]). The external driving of the upper atmosphere mainly comes from the energy deposition due to solar wind and magnetosphere coupling (e.g., [9,10,11,12,13,14,15]) and from changes in solar radiation (e.g., [16,17,18,19,20,21,22,23]). During the interaction between solar winds and the geomagnetic field, the energized particles carried by solar winds are deposited into the upper thermosphere along the open field lines, causing changes in the electric field and neutral temperatures through ion–neutral collisions.
Because of the interaction between the interplanetary magnetic field and the Earth geomagnetic field, a large amount of energy and momentum from the solar wind is deposited into the Earth’s upper atmosphere, triggering geomagnetic storms and thereby causing traveling ionospheric/atmospheric disturbances (TIDs/TADs) through Joule heating, ion drag, and storm-time energetic particle precipitation [24]. TIDs /TADs can also be induced by the upward propagation of lower-atmosphere gravity waves [24,25,26,27]. TIDs/TADs can be categorized as large-scale (velocity of 400–1000 m/s, period of 0.5–3 h, and a wavelength of thousands of kms) and medium-scale (velocity of 100–300 m/s, period of 0.25–1 h, and a wavelength of hundreds of kms) [26,28]. During tropospheric thunderstorm events, the electron density at 75–85 km decreases due to enhanced electron attachment to atmospheric molecular O2. However, between 85 and 95 km, the electron density increases due to the ionization of molecular N2 and O2 [29]. During intense volcanic eruptions, large-scale air pollution could be produced in the troposphere, producing a low conducting layer, and the generated waves propagate upward into the ionosphere, causing disturbances as a result of the coupling processes between neutral particles and plasma [30]. Using ionospheric total electron content (TEC) from the Global Navigation Satellite System (GNSS), volcanic-eruption-associated TIDs with phase speeds of 300–350 and 600–700 m/s and amplitudes of 0.5 and 3 TECu (1 TECu equals 1016 electrons/m2) were observed [8].
Earthquakes occur due to the movement of Earth’s lithospheric plates. During an earthquake, a large amount of energy could be released into the atmosphere via the form of acoustic gravity waves and Rayleigh waves, and the ionosphere could be modulated by the generated additional electric field [3,4,31]. During intense earthquakes with a moment magnitude (Mw, a measure of the earthquake’s strength based on the seismic moment) larger than 5, acoustic gravity waves could be generated due to the vertical ground displacement and can propagate upward to affect ionospheric electron density [3]. Low-frequency acoustic waves propagate upward and horizontally with the speed of sound. The earthquake-associated acoustic waves take about a few minutes to tens of minutes to reach the ionosphere because the acoustic waves in the Earth’s atmosphere at altitudes less than 300 km have a speed ranging from 240 to 700 m/s [32]. An additional vertical electric field directly penetrates into the ionosphere, causing the redistribution of charged particles. For instance, a significant enhancement (~88.5 m/s) in the zonal plasma drifts was observed during a major earthquake on 28 March 2005, inducing a downward electric field of ~3 mV/m [3,33]. Because of the atmospheric resonance, the upper ionosphere/atmosphere could be directly affected as well. For example, using electron density observations at altitudes ranging from ~100 to 300–400 km, a previous study found that the earthquake-related electron density perturbations had a nature of 15–30 min quasi-periodic oscillation [34].
The ionosphere at equatorial latitudes is different from that at middle and high latitudes in that the equatorial geomagnetic field is nearly horizontal. Previous studies have demonstrated that the equatorial ionosphere could be modulated by the forcings from lower atmospheric forcing, such as the energy release related to earthquakes, thunderstorms, and volcanic eruptions (e.g., [1,2,3,4,5,6,7,8]); the energy deposition due to solar wind and magnetosphere coupling (e.g., [9,10,11,12,13,14,15]); and changes in solar radiation [16]. The ionospheric currents are key in the energy transfer in the near-Earth geospace. By interacting with a zonal electric field, the horizontal geomagnetic field could give rise to several interesting physical phenomena, for instance, the equatorial electrojet (EEJ), ionospheric radial current (IRC), and equatorial ionization anomaly (two crests of large electron density at ±15° geomagnetic latitude, MLat). The IRC flows vertically at the ionospheric F-layer near the dip equator. It is key in the coupling processes between the E-region and F-region. Previous studies have identified earthquake-related ionospheric signatures at low latitudes [35,36,37,38]. However, comprehensive investigations into the E-F coupling processes, combining ground- and space-based measurements, remain scarce and require more attention. Few studies have explored the potential physical link between earthquakes and equatorial ionospheric currents in the E- and F-layers. In this work, we report the quasi-periodic responses of the E-region EEJ and F-region IRC to the earthquake on 6 February in Turkey (Mw = 7.8). To investigate the perturbations in the equatorial ionospheric currents during earthquakes, two cases using the TIEGCM developed by the High Altitude Observatory of the National Center for Atmospheric Research have been studied. One uses the default TIEGCM with the true geomagnetic conditions input, termed TIEGCM-default. The other also inputs the true geomagnetic conditions, but with an additional upward electric field in the lower ionosphere [3,39] and disturbances in the lower thermosphere [40] at the epicenter, termed TIEGCM-Earthquake. An abnormal upward electric field is generated at the bottom of ionosphere during earthquakes [3,39], and this has been imposed into TIEGCM-Earthquake. Moreover, the energy release during earthquakes might also trigger disturbances in the lower thermosphere, and this has been specified in TIEGCM-Earthquake. The differences between TIEGCM-default and TIEGCM-Earthquake reveal the disturbances in the coupled ionosphere and thermosphere, excluding the effects of geomagnetic activity. A series of works have confirmed the reliability and stability of TIEGCM in reproducing the ionosphere and thermosphere [12,14,41]. For instance, a large degree of similarity between the large-scale structures of DMSP-observed and TIEGCM-modeled electron density at high latitudes has been achieved, ensuring the reliability of the model [14]. The ionospheric currents are key in the energy transfer in the coupled lithosphere–atmosphere–ionosphere system. The associated current disturbances due to the forcings from below might cause changes in the horizontal geomagnetic field, affecting the distributions of plasma. However, there is still a lack of knowledge of the behaviors of the EEJ and IRC during earthquakes. A better knowledge of EEJ and IRC behaviors is critical for a full understanding of the electrodynamical coupling between Earth’s lithosphere–atmosphere–ionosphere (LAI).
2. Results
On 6 February 2023, a series of large earthquakes shook Turkey and Northern Syria [42]. A strong earthquake (Mw = 7.8) occurred at 01:17 UT (04:17 LT) in Turkey (37.15° GLat, 36.95° GLon). Three notable aftershocks (Mw > 5.5) followed within the next 18 min. Nine hours later, at 10:24 UT (13:24 LT), a following earthquake with the same Mw strength occurred. A Mw 6.0 earthquake occurred to the northeast of the first main earthquake. The epicenter was located at 38.00° GLat and 37.15° GLon. The depth of both earthquakes was about 20 km. A large amount of energy was released into the Earth’s atmosphere.
2.1. Large-Scale Travelling Ionospheric Disturbances
To ensure the reliability of models (TIEGCM-default and TIEGCM-Earthquake), the GNSS-observed total electron content (TEC), Swarm C-measured electron density (Ne), and corresponding TIEGCM-default and TIEGCM-Earthquake simulations are depicted in Figure 1a,b. There are several GNSS receivers near the epicenter in Turkey. Swarm B and C satellites fly at an altitude of 540 and 450 km, with an inclination angle of 87.75° and 87.35°, respectively. In Figure 1a, the average TEC from ground-based GNSS receivers is less than 20 TECU, a unit of 1016 el/m2, at nighttime (00–04 and 16–00 UT). In daytime, it peaks at 11 UT, with a TECU of 60, yielding a reverse V-shape. The diurnal variation is greatly related to solar illumination, which can produce ionospheric electrons via photochemical processes. A comparison between magenta and blue lines shows that the large-scale diurnal structures of TEC have been generally reproduced in both TIEGCM-default and TIEGCM-Earthquake, but with differences in magnitude. This is accepted in the model work because of the strong degree of similarity between the observed and modeled large-scale diurnal variations in TEC. The modeled TEC peaks at ~12 UT with a value of 62 and 60 TECU in TIEGCM-default and TIEGCM-Earthquake, respectively. Note here that the GNSS-observed TEC has a value of 55 TECU at ~12 UT but peaks at ~11 UT with a magnitude of 60 TECU. Thus, it can be assumed here that the variability of TEC is better captured in TIEGCM-Earthquake. To further confirm the assumption, a comparison between the Swarm C-observed and corresponding modeled Ne at the orbit of 07:48 UT is presented in Figure 1b. The observed Ne slightly increases from higher to lower latitudes. Two outstanding peaks, termed equatorial ionospheric anomaly (EIA) peaks, occur at −5° and 17° GLat, with a density of 1.45 and 1.7 × 106 cm−3, respectively. A similar profile is captured in TIEGCM-default and TIEGCM-Earthquake. The modeled EIA peaks have densities of 1.75 and 1.78 × 106 cm−3 (1.52 and 1.73 × 106 cm−3) at −5° and 17° GLat in TIEGCM-default (TIEGCM-Earthquake). In summary, the variability of the ionosphere has been better captured in TIEGCM-Earthquake. This indicates that we can use this model to explore the effects of earthquakes in the ionosphere and thermosphere.
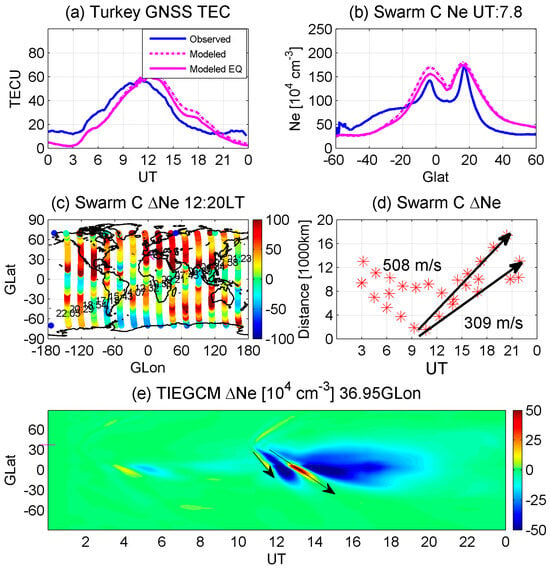
Figure 1.
(a) GNSS-observed (blue line) and TIEGCM-default (magenta dotted line, “modeled”)- and TIEGCM-Earthquake (magenta line, “modeled EQ”)-modeled total electron content (TEC) in Turkey on 6 February 2023. (b) Swarm C-observed and corresponding TIEGCM-default- and TIEGCM-Earthquake-modeled ionospheric electron density (Ne) at 07:48 UT on 6 February. (c) Swarm C-observed dayside ∆Ne with the removal of Ne on 5 February. (d) UT and distance from the epicenter variations in the Swarm C-observed ∆Ne. (e) UT and geographic latitude variations in ∆Ne associated with earthquakes at Turkey longitude. The black arrows indicate LSTIDs.
Figure 1c gives the Swarm C-observed residual Ne (∆Ne) at 12:20 LT. Several enhancements are found at each orbit, which might be related to the large-scale traveling ionospheric disturbances (LSTIDs). LSTIDs are the longitudinal space–time variations in TEC disturbances. They are usually excited at high latitudes during storm time and travel from high to low latitudes [13]. During earthquakes, LSTIDs are triggered at the epicenter and extend to wider longitudes and latitudes. Therefore, the ionospheric currents at the dip equator might be perturbed during earthquakes and are our focus. Note here that determining whether LSTIDs are well reproduced by TIEGCM or not could also confirm the reliability and reasonability of the model. To clearly calculate the phase velocity of the LSTIDs, ∆Ne enhancements in the frame of distance and UT are depicted in Figure 1d.
After the second earthquake, two obvious LSTIDs are found, as indicated by two black arrows. They have phase speeds of 508 and 309 m/s. Figure 1e represents the modeled ∆Ne between TIEGCM-Earthquake and TIEGCM-default at the Turkey longitude of 36.95° GLon, for comparison with the observations in Figure 1d. The first earthquake occurred at nighttime (01:17 UT/04:17 LT), indicating a weak background ionospheric Ne and hence weak Ne disturbance. During the following earthquake at 10:24 UT/13:24 LT (daytime), background ionospheric Ne is greatly produced because of the solar illumination; therefore, a strong perturbation is generated. Two LSTIDs (black arrows) propagate away from the epicenter, with phase speeds of 534 and 305 m/s. The phase speeds of the observed LSTIDs are verified by the model. The disturbances extend to wider latitudes, even to the opposite hemisphere. Then, it might be assumed that the equatorial ionospheric currents could be disturbed, which has a scientific value in the modeling and forecasting of space weather and deserves to be explored.
The anomalous phenomenon of LSTIDs being only clearly observed on the dayside might be related to the following mechanism: During earthquakes, the energy released into the LAI system could trigger large-scale traveling atmospheric disturbances (LSTADs) in the thermosphere [40]. LSTADs propagate from the epicenter to the global scale. On the dayside, the ionospheric electron density is large, and it could be modulated by the LSTADs. Richmond [43] suggested that LSTADs can push the ionosphere upward or downward along magnetic field lines and transport energy from high latitudes to low-latitude regions, producing LSTIDs. However, on the nightside, the ionospheric electron density is significantly weakened due to the absence of solar illumination. This could lead to the weak magnitude of LSTIDs at nighttime.
2.2. E-Region EEJ and F-Region IRC Perturbations
The E-region EEJ disappears at nighttime due to the weak ionospheric conductivity. Therefore, only daytime EEJs are explored in the literature. The E-region EEJ represents a ribbon of intense daytime electric current flowing along the dip equator at ~110 km height and confined to a narrow latitudinal band of ±5°. This intense current would generate a strong deflection in the horizontal magnetic field (ΔH), which could reach a maximum magnitude of hundreds of nT during extreme geomagnetic conditions [44]. The primary reason for the EEJ is the geometry of the geomagnetic field which is almost horizontal at equatorial latitudes and therefore enables enhanced electrical conductivity. As shown in Figure 2a, the ΔH observed at the Tatuoca station on 6 February is significantly stronger, about 98.4% larger, than the ΔH observed in the previous year. Ignoring small-scale perturbations, the daytime ΔH on 6 February decreases to −17.7 nT at 9:48 UT and then increases to the peak value of 105 nT at 14:02 UT; after that, it slowly returns to zero at dusk. The large-scale ΔH forms a structure similar to a reverse V-shape. The ΔH on 5 February has a peak of 58.75 nT at 13:41 UT. This is much weaker than that on 6 February, further indicating the physical significance of EEJ behaviors during the earthquake and geomagnetic activity. To isolate the effects of geomagnetic activity, TIEGCM-default- and TIEGCM-Earthquake-modeled EEJs are given. The modeled EEJ on 5 February has a large degree of similarity to the observations, ensuring the reliability of TIEGCM. A comparison between EEJs on 6 February shows that the TIEGCM-Earthquake-modeled EEJ is much closer to the observation than the TIEGCM-default result. This confirms the reliability of TIEGCM-Earthquake and the great influence of earthquakes on the behaviors of the EEJ. The spherical distance from the epicenter to the Tatuoca station at 110 km above the surface is 9706 km, indicating a cost of 5 h for LSTIDs from the epicenter. The polarization electric field disturbances could be established simultaneously. Considering those two, the daytime EEJ at Tatuoca station could be well perturbed during earthquakes. The residual EEJ (∆EEJ) associated with the earthquake is determined by removing TIEGCM-default results from TIEGCM-Earthquake-modeled EEJ. The wave structure of the daytime ∆EEJ yields a peak value of 20 nT at 16 UT and −10 nT at 12:30 UT.
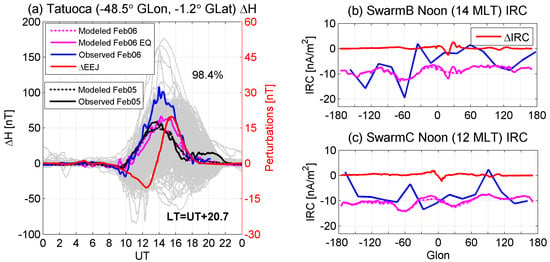
Figure 2.
(a) The temporal variations in ground-observed horizontal magnetic field disturbances (ΔH) and corresponding simulations at Tatuoca in Brazil. The gray, black, and blue full lines are ΔH for the whole year of 2022, 5 February, and 6 February, respectively. The black dotted and magenta dotted lines and magenta solid lines are the TIEGCM-default (“Modeled Feb05” and “Modeled Feb06”) simulations on 5 and 6 February and TIEGCM-Earthquake (“Modeled Feb06 EQ”) on 6 February, respectively. The red line is the perturbations of EEJ, showing the difference between TIEGCM-Earthquake and TIEGCM-default on 6 February. Positive for eastward EEJ. (b,c) The longitudinal distributions of noon F-region IRC from Swarm B and C satellites and the corresponding TIEGCM-default and TIEGCM-Earthquake on 6 February 2023. The red line is the earthquake-linked ∆IRC. IRC is given in nA/m2. Positive for upward IRC.
As outlined above, the E-region ionospheric current from the ground station Tatuoca, EEJ, is greatly perturbed after the earthquakes. The question of whether the F-region IRC will be disturbed or not is still not clear. Because the night IRC is complicated and does not have a typical pattern [6], it is hence not explored in the literature and this work. The low-orbit Swarm provides in situ ionospheric IRC observations, an opportunity to explore the IRC responses. Figure 2b,c depict the Swarm B- and C-observed IRC on 6 February (Swarm A data are unavailable). In Figure 2b, the IRC has a significant wave structure, four peaks (troughs) at −106°, −36°, 59°, and 180° (−130°, −59°, −12°, and 130°) GLon, with intensities of −6.01, 1.97, 1.46, and −1.28 (−15.79, −19.52, −5.77, and −8.58) nA/m2, respectively. The TIEGCM-default simulations have four peaks as well, which are located at −100°, −15°, 80°, and 180° GLon, with intensities of −7, −6, −6, and −6.5 nA/m2, respectively. Different from the TIEGCM-default results, TIEGCM-Earthquake results show a wave shape at 10–30° GLon. This wave pattern is not observed in Swarm observations, because the longitude difference between two following orbits is approximately 23° GLon. Moreover, this data–model discrepancy might be also related to the empirical high-latitude forcing in the model. The high-latitude electric field in TIEGCM is specified by the empirical Weimer model, which would not be able to perfectly capture temporal variations in the ionospheric electric field [14]. The electric field is key in the modulation of ionospheric currents. Thus, the discrepancy between the data and model might be also due to the specified high-latitude electric field. The strong degree of similarity between modeled and observed large-scale structures approves the reliability of TIEGCM. Based on two simulations, the residual IRC (∆IRC) due to the earthquake has a wave pattern similar to the reverse sine function, with a peak intensity of 4 nA/m2. A similar result is found in the Swarm C-observed and corresponding TIEGCM-simulated IRC (Figure 2c). However, the earthquake-associated ∆IRC (2.5 nA/m2) is significantly weaker than that in Figure 2b.
3. Potential Physical Mechanisms
So far, according to Conti et al. [45] and Picozza et al. [46], no good coupling mechanisms or models in the Earth’s lithosphere–atmosphere–ionosphere (LAI) coupled system associated with earthquakes have been established. The “energy source” released during earthquakes includes acoustic waves, electromagnetic waves, and long-wave radiation [3,4,31,32]. The mentioned “energy source” could act as the “driving power” to generate an additional upward electric field at the bottom of the ionosphere [39] and thermospheric disturbances [40], potentially causing disturbances in the ionospheric currents at the dip equator. Nonetheless, some studies have reported that these so-called forcings have less power than that observed during seismic events [45,47]. However, the effects of earthquakes on the ionospheric currents are still unclear and important for understanding space weather.
As is known to all, the ionospheric electric current is a stream of charged particles. It plays an important part in the energy transfer processes in the coupling of the helio-magneto-ionospheric system. For instance, the field-aligned currents at polar latitudes carried by electrons play a role in the energy deposition and momentum transfer from the magnetosphere to the ionosphere [48]. At the dip equator, the ionospheric current system has two important components: the E-region EEJ at 110 km and the F-region IRC at higher altitudes. An earthquake is a huge geohazard event with far-reaching effects, causing a range of geophysical disturbances [3]. The impact of changes in the ionospheric currents on humans is mainly reflected in communication systems, for instance, in the propagation of radio waves, including strength, frequency, polarization, and phase and time delay, and the accuracy of the navigation and positioning. In earthquake events, the perturbations in the ionospheric currents could affect the communications during post-disaster reconstruction. Therefore, the behaviors of the E- and F-region currents and the associated E-F coupling processes during an earthquake are key in the understanding of the variability and electrodynamics of the geospace.
3.1. Drivers for E-Region EEJ
The E-region EEJ is dominated by the collisions between ions and neutrals, , where , , and are the ionospheric cowling conductivity, electric field, neutral winds, and ambient magnetic field, respectively [49]. Note here that the so-called cowling conductivity is the combined Hall and Pedersen conductivity. Recently, the simultaneous responses of the TEC at different latitudes to the penetration electric field events during a disturbance period when Kp equals 4 were explored by Zhang et al. [50]. This confirms that the ionospheric EEJ/CEJ could be simultaneously driven by the penetration electric field. Therefore, the roles of ionospheric conductivity, the electric field, and neutral winds during earthquakes are explored in this section.
3.1.1. Roles of the Ionospheric Conductivity
Figure 3a gives the geographic longitude and latitude variations in COSMIC footprints at 15 UT on 5 and 6 February. This ensures the validity of the comparison between the ionospheric electron density (Ne) values from COSMIC on 5 and 6 February at the same location. To further confirm the above conclusion, the vertical profile of COSMIC-observed Ne at 15 UT is given in Figure 3b. A comparison between Ne values on 5 and 6 February shows that during the earthquake day, a larger electron density is observed. However, in the E-region, there is a relative reduction in plasma density from 5 to 6 February by 3.49%, as given in the bottom right-hand corner.
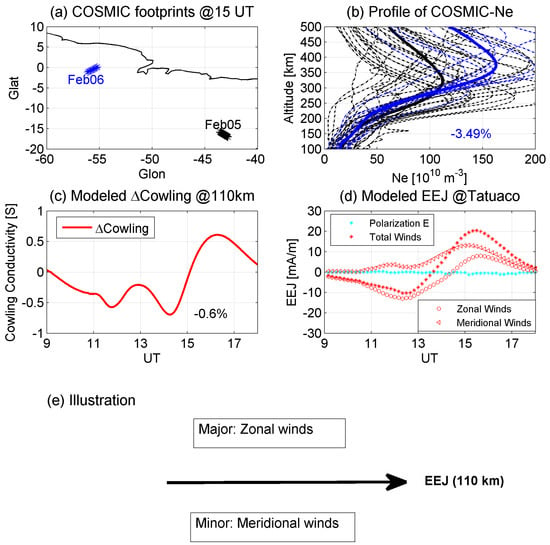
Figure 3.
(a,b) The footprints of COSMIC and the vertical profiles of observed Ne on 5 February (black) and 6 February (blue). The solid and dashed lines are the average value and samples, respectively. The percentage value is the relative Ne changes in the E-region from 5 to 6 February. (c,d) UT variations in ∆Cowling and ∆EEJ owing to different forcings. The cyan star, red star, circle, and triangle are ∆EEJ due to polarization electric field, total neutral winds, zonal winds, and meridional winds, respectively. (e) An illustration of the drivers of the earthquake-linked EEJ perturbations at 110 km.
The ionospheric conductivity is controlled by the ambient magnetic field and Ne [51]. The ambient magnetic field will not change in response to the earthquake effects. Hence, the ionospheric conductivity does not have remarkable perturbations. To further confirm the results, the modeled earthquake-linked residual ionospheric cowling conductivity (∆Cowling) is given in Figure 3c; it is the difference between TIEGCM-Earthquake and TIEGCM-default. ∆Cowling shows a wave pattern that is reduced at 9–15 UT and enhanced at 15–18 UT. However, the average change in ∆Cowling in percentage is −0.6%, consistent with the observations. The observed and modeled results of the weak relative changes in Ne (Figure 3b) and cowling conductivity (Figure 3c) could lead to the hypothesis that the electric field and neutral winds play key roles in the perturbations in the EEJ, which is stronger by 98.4% than the previous one-year EEJ (Figure 2a).
3.1.2. Roles of the Neutral Winds
The roles of the polarization electric field and neutral winds were distinguished by using the following techniques: At first, we ran the model including all forcings (Case 1). Note that an output file for every 10 min of model time is created. Subsequently, at every 10 min, we ran the model with neutral winds off for one model time step (with a higher resolution of ~2 min model time) to obtain much more detailed outputs, termed Case 2. When the neutral winds are excluded from the dynamo calculation module, the EEJ due to the polarization electric field could be output. Thus, we can isolate the polarization electric field effects, and the differences between Cases 1 and 2 are the EEJ induced by total neutral winds. Likewise, when the zonal (meridional) wind was switched off, the associated ∆EEJ would be obtained.
The dayside earthquake-linked ∆EEJ at Tatuoca station driven by different forcings is illustrated in Figure 3d. The ∆EEJ owing to the polarization electric field is approximately zero, indicating its negligible role. A large degree of similarity between the ∆EEJ due to total winds and the ∆EEJ in Figure 2a, including the magnitude and the temporal structure, is found. Evidently, neutral wind changes during earthquakes play a major role in the wave shape of ∆EEJ. During the earthquake, the disturbed winds travel to latitudes of ~2° MLat, which could generate an electric field that penetrates into the E-region dip equator. Hence, the EEJ at 110 km is modulated. When we further compare the ∆EEJs owing to different winds, it is found that zonal winds are the major driver for ∆EEJ during earthquakes, with contributions from meridional winds, as illustrated in Figure 3e. The former account for almost 100% of the ∆EEJ at pre-14 UT, and their contribution smoothly decreases to 40% at post-14 UT. The meridional winds contribute 60% of the ∆EEJ at post-14 UT.
3.2. Drivers for F-Region IRC
Previous studies demonstrated that the equatorial F-region IRC can be expressed as , where , , , and are F-region Pedersen conductivity, vertical polarization electric field (positive for downward), magnetic zonal winds (positive for eastward), and northward geomagnetic field, respectively [52]. As shown in Figure 2b,c and Figure 4a, the noon residual IRC (∆IRC) due to the earthquake has a wave shape. To investigate the potential drivers of the polarization electric field and neutral winds, a similar technique to that presented above was used.
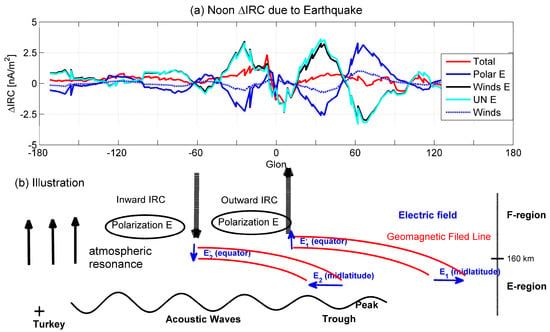
Figure 4.
(a) Longitudinal variations in earthquake-associated ∆IRC due to total forcing (red, “total”), polarization electric field (blue, “Polar E”), winds (blue dotted, “Winds”), and electric fields due to wind dynamo (black, “Winds E”) and zonal wind dynamo (cyan, “UN E”). (b) Illustration of the Turkey earthquake-related disturbances in IRC and the associated potential drivers. E1 and E2 are generated electric fields from wind dynamo.
3.2.1. Local Drivers
During an earthquake, an additional vertical electric field will be generated in the lower boundary of the ionosphere [3,39]. This might drive the perturbations of the electric field at the F-layer, hence driving ∆IRC. Gurram et al. [3] studied the pre-seismic and post-seismic effects on Equatorial Spread F irregularities during two earthquakes in the Indonesian region located around the dip equator. The vertical electric field is generated a few days prior to an earthquake. In the present work, we study the post-seismic effects that are associated with vertical electric fields, acoustic gravity waves, or Rayleigh waves. At the longitudes of ∆the IRC wave shape (−30~30° GLon), a similar reverse wave structure is found in the polarization-electric-field-driven IRC (blue line in Figure 4a). Thus, the polarization electric field due to earthquake might prevent the formation of the wave pattern of the F-region ∆IRC.
During huge geohazard events with far-reaching effects (e.g., earthquakes, volcanic eruptions), the generated acoustic waves penetrate on a global scale, directly producing disturbances in E-region thermospheric winds and electric fields [18]. The perturbations penetrate upward through the atmospheric resonance. The earthquake-linked acoustic waves that penetrate the troposphere at the speed of sound could carry energy into the upper atmosphere through atmospheric resonance. Therefore, the F-region local neutral winds might be perturbed. In Figure 4a, the neutral-wind-driven ∆IRC has a similar wave structure to that driven by polarization electric field, but with a weak intensity. Thus, the neutral winds also play a negative role. Then, which drivers might be responsible for the ∆IRC during an earthquake?
3.2.2. Roles of the Low-Latitude Winds
Apart from the effects at the dip equator, the thermosphere disturbances at 15° MLat could also play a key role in the regulation of the F-region IRC through the ionospheric wind dynamo effects. The daytime F-region electric field is dominated by the E-region dynamo electric field at mid-latitudes, which maps along the geomagnetic field lines from lower to higher altitudes [53]. During a huge geohazard event, the generated acoustic waves may lead to wave perturbations of the E-region thermosphere [7,54]. The generated meridional electric field would penetrate into the F-region along the geomagnetic field lines to dominate the equatorial F-region vertical electric field, hence dominating the IRC.
When the total winds are switched off in the model, we can obtain the ∆IRC due to total winds, as in the discussion of ∆EEJ. In Figure 4a, the ∆IRC due to the electric field from the total wind dynamo also forms a wave shape, which has a strong similarity to that due to total forcing, but with a stronger intensity. This is reasonable because the currents directly driven by neutral winds and the polarization electric field reduce the wave shape of ∆IRC. Thus, it can be concluded that the electric field due to the wind dynamo dominates the regulation of the IRC during earthquakes.
To further answer the question of which component of winds controls the wind dynamo during an earthquake, we also turned off the zonal winds in the model, as in the ∆EEJ analysis. The longitudinal wave pattern of ∆IRC due to the electric field from the zonal wind dynamo is almost the same as that from the total wind dynamo. This demonstrates the dominant roles of zonal winds in the regulation of the IRC during earthquakes via wind dynamo effects.
To clearly show the drivers of ∆IRC, an illustration is also given in Figure 4b. ∆IRC is dominated by electric field from wind dynamo, especially from zonal winds. During earthquakes, the excited acoustic waves travel from the epicenter to a global scale. The generated electric field from wind dynamo maps from the E-region at low latitudes to the F-region at the dip equator along the geomagnetic field lines. This can form an upward/downward electric field at the dip equator, hence forming outward/inward IRC. Through the atmospheric resonance, the E-region wind disturbances could be introduced into the F-region. Both the local winds from atmospheric resonance and the polarization electric field oppose the formation of ∆IRC.
4. Conclusions
On 6 February 2023, strong earthquakes occurred in Turkey and caused large damage to human lives. The effects of an earthquake not only exist at the surface of the Earth but also occur in the near-Earth space, affecting the ionospheric currents. The ionospheric currents play an important role in communication systems, and their behaviors during earthquakes are still unclear. Therefore, we investigated the ionospheric current system at the dip equator during earthquakes. Several interesting results were found:
- Two remarkable LSTIDs are found in the dayside ionospheric electron density, with phase speeds of 508 and 309 m/s, respectively, probably associated with the second earthquakes.
- The equatorial E-region EEJ is disturbed by neutral winds (major effects from zonal winds and minor effects from meridional winds), with ignorable roles from ionospheric conductivity.
- The equatorial F-region IRC perturbations are attributed to three processes. One is that the acoustic waves traveling to the low latitudes might modulate the local E-region winds and then generate a meridional electric field that maps to the dip equator. The second is that the local winds from atmospheric resonance prevent the formation of ∆IRC. The last is that the ionospheric polarization electric field reduces the wave shape of ∆IRC during an earthquake.
Author Contributions
Conceptualization, K.Z.; methodology, K.Z.; data curation, H.X.; writing—original draft preparation, K.Z.; writing—review and editing, H.W., W.W., J.L., S.Z. and Y.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China Basic Science Center (42188101), National Nature Science Foundation of China (No. 41974182 and 42122031), the Fundamental Research Funds for the Central Universities (2042023kf0099), National Key Research and Development Program (2022YFF0503700), and Hubei Provincial Natural Science Foundation of China (2023AFB616). This work is supported by the Project Supported by the Specialized Research Fund for State Key Laboratories and the Project Supported by the Open Fund of Hubei Luojia Laboratory. GNSS TEC data processing and Madrigal database system are provided to the community by MIT under US NSF Grant AGS-1952737, AGS-2033787, and AGS-2149698 support.
Data Availability Statement
The Swarm EEJ and Ne data can be obtained from the European Space Agency (ESA) (http://swarm-diss.eo.esa.int), accessed on 5 February 2023. The COSMIC Ne observations are available at https://data.cosmic.ucar.edu/gnss-ro/cosmic2/provisional/spaceWeather/level2/2023/, accessed on 5 February 2023. The minutely horizontal magnetic field can be downloaded at https://www.intermagnet.org/data-donnee/download-eng.php#view, accessed on 5 February 2023. The GNSS TEC is stored in Madrigal (http://cedar.openmadrigal.org/), accessed on 5 February 2023.
Acknowledgments
We are grateful to the Editor and anonymous reviewers for their assistance in improving the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Aa, E.; Zhang, S.R.; Wang, W.; Erickson, P.J.; Qian, L.; Eastes, R.; Spicher, A. Pronounced Suppression and X-Pattern Merging of Equatorial Ionization Anomalies After the 2022 Tonga Volcano Eruption. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030527. [Google Scholar] [CrossRef] [PubMed]
- Davis, C.J.; Johnson, C.G. Lightning-induced intensification of the ionospheric sporadic E layer. Nature 2005, 435, 799–801. [Google Scholar] [CrossRef] [PubMed]
- Gurram, P.; Kakad, B.; Ravi Kumar, M.; Bhattacharyya, A. Earthquake/Tsunami-Linked Imprints in the Equatorial F Region Zonal Plasma Drifts and Spatial Structures of Plasma Bubbles. J. Geophys. Res. Space Phys. 2019, 124, 504–520. [Google Scholar] [CrossRef]
- Rolland, L.M.; Lognonné, P.; Munekane, H. Detection and modeling of Rayleigh wave induced patterns in the ionosphere. J. Geophys. Res. Space Phys. 2011, 116, A05320. [Google Scholar] [CrossRef]
- Tsugawa, T.; Saito, A.; Otsuka, Y.; Nishioka, M.; Maruyama, T.; Kato, H.; Murata, K.T. Ionospheric disturbances detected by GPS total electron content observation after the 2011 off the Pacific coast of Tohoku Earthquake. Earth Planets Space 2011, 63, 875–879. [Google Scholar] [CrossRef]
- Wang, H.; Xia, H.; Zhang, K. Variations in the Equatorial Ionospheric F Region Current during the 2022 Tonga Volcanic Eruption. Remote Sens. 2022, 14, 6241. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, H.; Zhong, Y.; Xia, H.; Qian, C. The Temporal Evolution of F-Region Equatorial Ionization Anomaly Owing to the 2022 Tonga Volcanic Eruption. Remote Sens. 2022, 14, 5714. [Google Scholar] [CrossRef]
- Zhang, S.R.; Vierinen, J.; Aa, E.; Goncharenko, L.P.; Erickson, P.J.; Rideout, W.; Spicher, A. 2022 Tonga volcanic eruption induced global propagation of ionospheric disturbances via Lamb waves. Front. Astron. Space Sci. 2022, 9, 871275. [Google Scholar] [CrossRef]
- da Silva, C.L.; Salazar, S.D.; Brum, C.G.; Terra, P. Survey of electron density changes in the daytime ionosphere over the Arecibo observatory due to lightning and solar flares. Sci. Rep. 2021, 11, 10250. [Google Scholar] [CrossRef]
- Liu, J.; Wang, W.; Qian, L.; Lotko, W.; Burns, A.G.; Pham, K.; Wilder, F. Solar flare effects in the Earth’s magnetosphere. Nat. Phys. 2021, 17, 807–812. [Google Scholar] [CrossRef]
- Lühr, H.; Marker, S. High-latitude thermospheric density and wind dependence on solar and magnetic activity. In Climate and Weather of the Sun-Earth System (CAWSES); Highlights from a Priority Program; Springer: Dordrecht, The Netherlands, 2013; pp. 189–205. [Google Scholar]
- Maute, A.; Richmond, A.D.; Lu, G.; Knipp, D.J.; Shi, Y.; Anderson, B. Magnetosphere-ionosphere coupling via prescribed field-aligned current simulated by the TIEGCM. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028665. [Google Scholar] [CrossRef]
- Shinbori, A.; Otsuka, Y.; Sori, T.; Tsugawa, T.; Nishioka, M. Temporal and spatial variations of total electron content enhancements during a geomagnetic storm on 27 and 28 September 2017. J. Geophys. Res. Space Phys. 2020, 125, e2019JA026873. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, H.; Liu, J.; Zheng, Z.; He, Y.; Gao, J.; Sun, L.; Zhong, Y. Dynamics of the tongue of ionizations during the geomagnetic storm on 7 September 2015. J. Geophys. Res. Space Phys. 2021, 126, e2020JA029038. [Google Scholar] [CrossRef]
- Zhang, K.; Song, H.; Wang, H.; Liu, J.; Wang, W.; Wan, X.; Jin, Y. Dynamics of the tongue of ionizations during the geomagnetic storm on 7 September 2015: The altitudinal dependences. J. Geophys. Res. Space Phys. 2023, 128, e2023JA031735. [Google Scholar] [CrossRef]
- Huba, J.D.; Drob, D. SAMI3 prediction of the impact of the 21 August 2017 total solar eclipse on the ionosphere/plasmasphere system, Geophys. Res. Lett. 2017, 44, 5928–5935. [Google Scholar] [CrossRef]
- Wang, W.; Dang, T.; Lei, J.; Zhang, S.; Zhang, B.; Burns, A. Physical processes driving the response of the F2 region ionosphere to the 21 August 2017 solar eclipse at Millstone Hill. J. Geophys. Res. Space Phys. 2019, 124, 2978–2991. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, H. The great reduction of equatorial electrojet during the solar eclipse on 14 December 2020. Space Weather 2022, 20, e2022SW003295. [Google Scholar] [CrossRef]
- Colonna, R.; Filizzola, C.; Genzano, N.; Lisi, M.; Tramutoli, V. Optimal Setting of Earthquake-Related Ionospheric TEC (Total Electron Content) Anomalies Detection Methods: Long-Term Validation over the Italian Region. Geosciences 2023, 13, 150. [Google Scholar] [CrossRef]
- Nayak, K.; López-Urías, C.; Romero-Andrade, R.; Sharma, G.; Guzmán-Acevedo, G.M.; Trejo-Soto, M.E. Ionospheric Total Electron Content (TEC) Anomalies as Earthquake Precursors: Unveiling the Geophysical Connection Leading to the 2023 Moroccan 6.8 Mw Earthquake. Geosciences 2023, 13, 319. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X.; Wu, W.; Chen, C.; Wang, M.; Yang, M.; Guo, Y.; Wang, J. The Seismo-Ionospheric Disturbances before the 9 June 2022 Maerkang Ms6.0 Earthquake Swarm. Atmosphere 2022, 13, 1745. [Google Scholar] [CrossRef]
- López-Urias, C.; Vazquez-Becerra, G.E.; Nayak, K.; López-Montes, R. Analysis of Ionospheric Disturbances during X-Class Solar Flares (2021–2022) Using GNSS Data and Wavelet Analysis. Remote Sens. 2023, 15, 4626. [Google Scholar] [CrossRef]
- Grodji, O.D.F.; Doumbia, V.; Amaechi, P.O.; Amory-Mazaudier, C.; N’guessan, K.; Diaby, K.A.A.; Zie, T.; Boka, K. A Study of Solar Flare Effects on the Geomagnetic Field Components during Solar Cycles 23 and 24. Atmosphere 2022, 13, 69. [Google Scholar] [CrossRef]
- Dungey, J.W. Interplanetary magnetic field and the auroral zones. Phys. Rev. Lett. 1961, 6, 47–48. [Google Scholar] [CrossRef]
- Forbes, J.M.; Lu, G.; Bruinsma, S.; Nerem, S.; Zhang, X. Thermosphere density variations due to the 15–24 April 2002 solar events from CHAMP/STAR accelerometer measurements. J. Geophys. Res. 2005, 110, A12S27. [Google Scholar] [CrossRef]
- Liu, J.; Liu, L.; Nakamura, T.; Zhao, B.; Ning, B.; Yoshikawa, A. A case study of ionospheric storm effects during long-lasting southward IMF Bz-driven geomagnetic storm. J. Geophys. Res. Space Phys. 2014, 119, 7716–7731. [Google Scholar] [CrossRef]
- Thome, G.D. Incoherent scatter observations of traveling ionospheric disturbances. J. Geophys. Res. 1964, 69, 4047–4049. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, J.; Wang, W.; Wang, H. The effects of IMF Bz periodic oscillations on thermospheric meridional winds. J. Geophys. Res. Space Phys. 2019, 124, 5800–5815. [Google Scholar] [CrossRef]
- Shao, X.M.; Lay, E.H.; Jacobson, A.R. Reduction of electron density in the night-time lower ionosphere in response to a thunderstorm. Nat. Geosci. 2013, 6, 29–33. [Google Scholar] [CrossRef]
- Pulinets, S.; Davidenko, D.; Pulinets, M. Atmosphere-ionosphere coupling induced by volcanoes eruption and dust storms and role of GEC as the agent of geospheres interaction. Adv. Space Res. 2022, 69, 4319–4334. [Google Scholar] [CrossRef]
- Currie, J.; Waters, C. On the use of geomagnetic indices and ULF waves for earthquake precursor signatures. J. Geophys. Res. Space Phys. 2014, 119, 992–1003. [Google Scholar] [CrossRef]
- Ma, J.Z. Atmospheric layers in response to the propagation of gravity waves under nonisothermal, wind-shear, and dissipative conditions. J. Mar. Sci. Eng. 2016, 4, 25. [Google Scholar] [CrossRef]
- Pulinets, S.; Boyarchuk, K. Ionospheric Precursors of Earthquakes; Springer Science Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Guo, Q.; Chernogor, L.F.; Garmash, K.P.; Rozumenko, V.T.; Zheng, Y. Dynamical processes in the ionosphere following the moderate earthquake in Japan on 7 July 2018. J. Atmos. Sol.-Terr. Phys. 2019, 186, 88–103. [Google Scholar] [CrossRef]
- Pulinets, S. Physical mechanism of the vertical electric field generation over active tectonic faults. Adv. Space Res. 2009, 44, 767–773. [Google Scholar] [CrossRef]
- Pulinets, S.; Budnikov, P.; Karelin, A.; Žalohar, J. Thermodynamic instability of the atmospheric boundary layer stimulated by tectonic and seismic activity. J. Atmos. Sol.-Terr. Phys. 2023, 246, 106050. [Google Scholar] [CrossRef]
- Nayak, K.; Romero-Andrade, R.; Sharma, G.; Zavala, J.L.C.; Urias, C.L.; Soto, M.E.T.; Aggarwal, S.P. A combined approach using b-value and ionospheric GPS-TEC for large earthquake precursor detection: A case study for the Colima earthquake of 7.7 Mw, Mexico. Acta Geod. Geophys. 2023, 58, 515–538. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S.; Zhang, S.; Dai, R. Analysis of potential precursory pattern at Earth surface and the above atmosphere and ionosphere preceding two Mw ≥ 7 earthquakes in Mexico in 2020–2021. Earth Space Sci. 2022, 9, e2022EA002267. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, Y.; Zhao, S.; Liu, J.; Zhang, X.; Huang, J.; Zhao, Z. An electric field penetration model for seismo-ionospheric research. Adv. Space Res. 2017, 60, 2217–2232. [Google Scholar] [CrossRef]
- Heki, K.; Ping, J. Directivity and apparent velocity of the coseismic ionospheric disturbances observed with a dense GPS array. Earth Planet. Sci. Lett. 2005, 236, 845–855. [Google Scholar] [CrossRef]
- Wang, W.; Talaat, E.R.; Burns, A.G.; Emery, B.; Hsieh, S.Y.; Lei, J.; Xu, J. Thermosphere and ionosphere response to subauroral polarization streams (SAPS): Model simulations. J. Geophys. Res. Space Phys. 2012, 117, 1864. [Google Scholar] [CrossRef]
- Maletckii, B.; Astafyeva, E.; Sanchez, S.A.; Kherani, E.A.; de Paula, E.R. The 6 February 2023 Türkiye earthquake sequence as detected in the ionosphere. J. Geophys. Res. Space Phys. 2023, 128, e2023JA031663. [Google Scholar] [CrossRef]
- Richmond, A.D. Gravity wave generation, propagation, and dissipation in the thermosphere. J. Geophys. Res. 1978, 83, 4131–4145. [Google Scholar] [CrossRef]
- Lühr, H.; Rother, M.; Häusler, K.; Alken, P.; Maus, S. The influence of nonmigrating tides on the longitudinal variation of the equatorial electrojet. J. Geophys. Res. 2008, 113, A08313. [Google Scholar] [CrossRef]
- Conti, L.; Picozza, P.; Sotgiu, A. A critical review of ground based observations of earthquake precursors. Front. Earth Sci. 2021, 9, 676766. [Google Scholar] [CrossRef]
- Picozza, P.; Conti, L.; Sotgiu, A. Looking for earthquake precursors from space: A critical review. Front. Earth Sci. 2021, 9, 676775. [Google Scholar] [CrossRef]
- Fraser-Smith, A.C.; McGill, P.R.; Bernardi, A. Comment on “Natural Magnetic Disturbance fields, Not Precursors, Preceding the Loma Prieta Earthquake” by Wallace H. Campbell. J. Geophys. Res. Space Phys. 2011, 116, A08. [Google Scholar] [CrossRef]
- Lühr, H.; Park, J.; Gjerloev, J.W.; Rauberg, J.; Michaelis, I.; Merayo, J.M.; Brauer, P. Field-aligned currents’ scale analysis performed with the Swarm constellation. Geophys. Res. Lett. 2015, 42, 1–8. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Harding, B.J.; Stolle, C.; Matzka, J. Neutral wind profiles during periods of eastward and westward equatorial electrojet. Geophys. Res. Lett. 2021, 48, e2021GL093567. [Google Scholar] [CrossRef]
- Zhang, S.-R.; Nishimura, Y.; Vierinen, J.; Lyons, L.R.; Knipp, D.J.; Gustavsson, B.J.; Waghule, B.V.; Erickson, P.J.; Coster, A.J.; Aa, E.; et al. Simultaneous Global Ionospheric Disturbances Associated with Penetration Electric Fields During Intense and Minor Solar and Geomagnetic Disturbances. Geophys. Res. Lett. 2023, 50, e2023GL104250. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Maute, A. Sq and EEJ—A review on the daily variation of the geomagnetic field caused by ionospheric dynamo currents. Space Sci. Rev. 2017, 206, 299–405. [Google Scholar] [CrossRef]
- Park, J.; Lühr, H. Effects of sudden stratospheric warming (SSW) on the lunitidal modulation of the F-region dynamo. J. Geophys. Res. Space Phys. 2012, 117, A09320. [Google Scholar] [CrossRef]
- Blanc, M.; Richmond, A.D. The ionospheric disturbance dynamo. J. Geophys. Res. 1980, 85, 1669–1686. [Google Scholar] [CrossRef]
- Harding, B.J.; Wu, Y.-J.J.; Alken, P.; Yamazaki, Y.; Triplett, C.C.; Immel, T.J.; Gasque, L.C.; Mende, S.B.; Xiong, C. Impacts of the January 2022 Tonga volcanic eruption on the ionospheric dynamo: ICON-MIGHTI and Swarm observations of extreme neutral winds and currents. Geophys. Res. Lett. 2022, 49, e2022GL098577. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).