A New Determining Method for Ionospheric F2-Region Peak Electron Density Height
Abstract
1. Introduction
2. Methodology
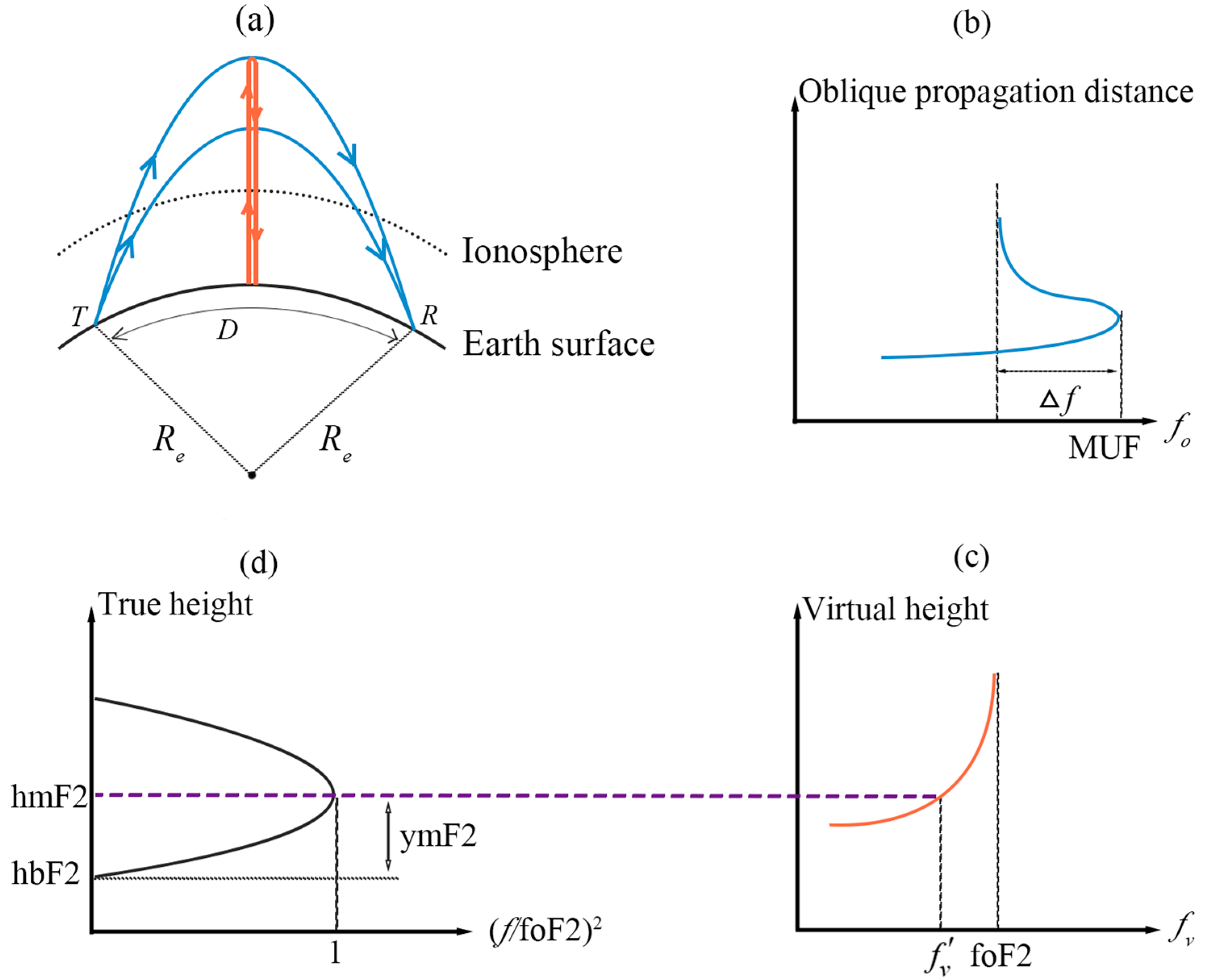
2.1. Physical Principle
2.2. Modeling Method
- (1)
- Data are the core of SML, which should have certain statistical regularity and be similar data with some common properties.
- (2)
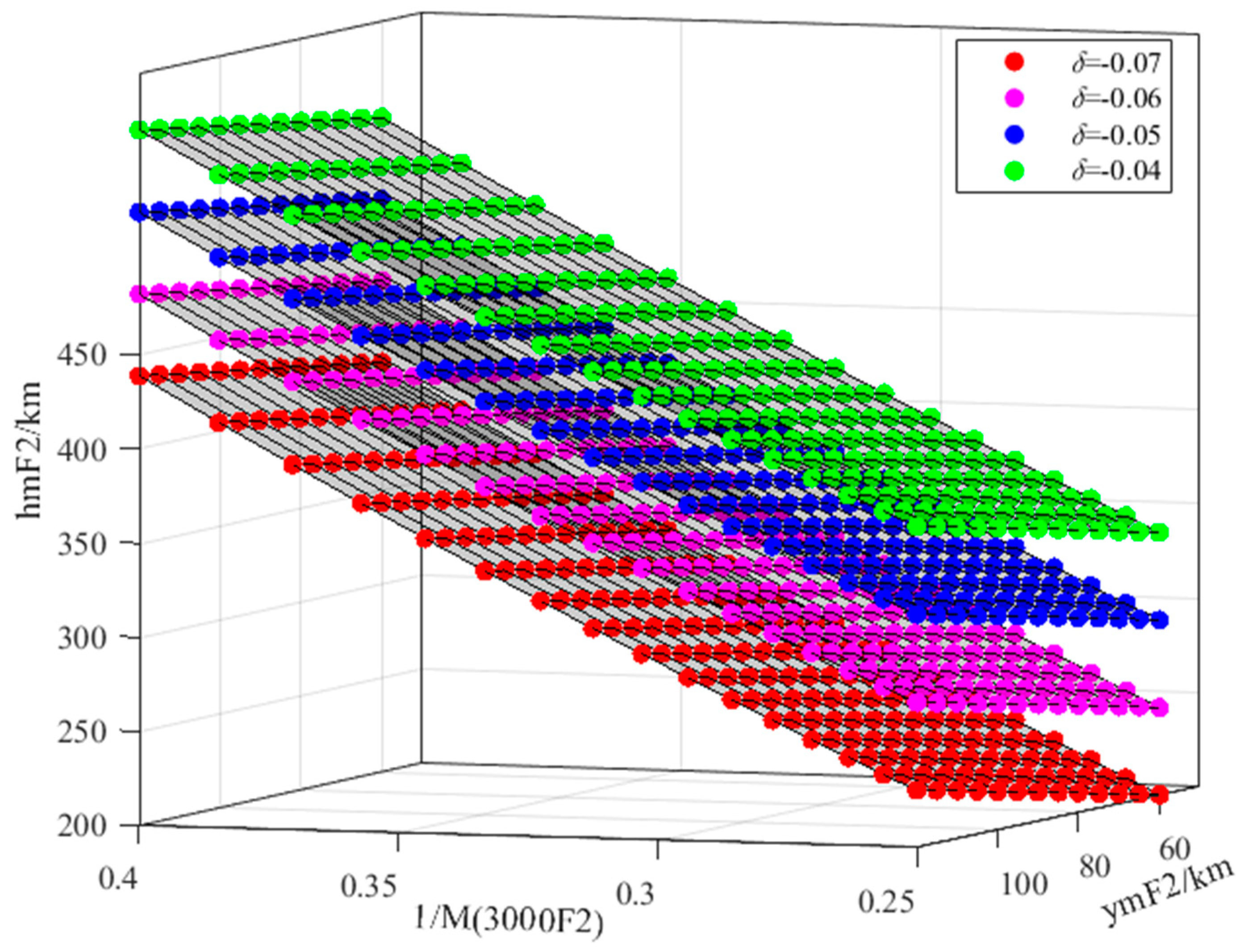
- The model of SML can be understood as a function, that is, to find the relationship between the input and output variables. Through previous analysis, it has been determined that the relationship between hmF2 and 1/M3000F2 is approximately linear (Equation (6)). M(3000)F2 is the input variable, and hmF2 is the output variable. C0(s,t) and C1(s,t) are the intercept and slope of the model, respectively, which are unknown quantities in the model. It needs to be determined by selecting a suitable algorithm.
- (3)
- SML primarily uses supervised learning to determine the model, and the task of supervised learning is to obtain the mapping relationship between input and output through learning. Specifically, the specific values of hyperparameters C0(s,t) and C1(s,t) in Equation (6) need to be determined through supervised learning. Considering that the model can be reduced to a linear function of one variable, the least squares (LS) regression analysis method is chosen in this paper to find the best function matching of the data by obtaining the sum of squares that minimizes the error.
- (4)
- SML needs to set model evaluation criteria to evaluate the merits and demerits of the trained model, in which root mean square error (RMSE) and relative root mean square error (RRMSE) are selected. RMSE can evaluate performance changes and characterize the impact caused by data perturbations, while RRMSE is used to assess the percentage of relative performance changes [26].
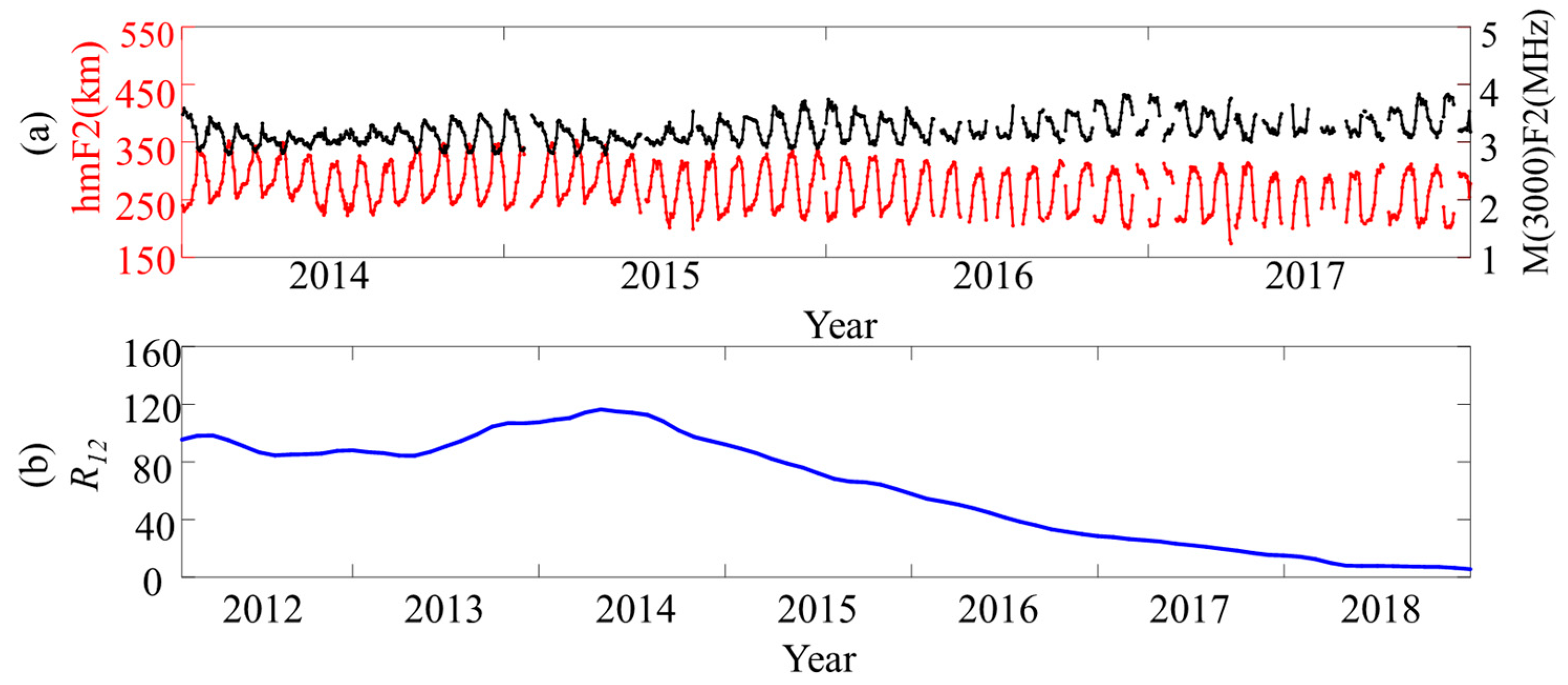
2.3. Data Collecting
2.4. Modeling Process
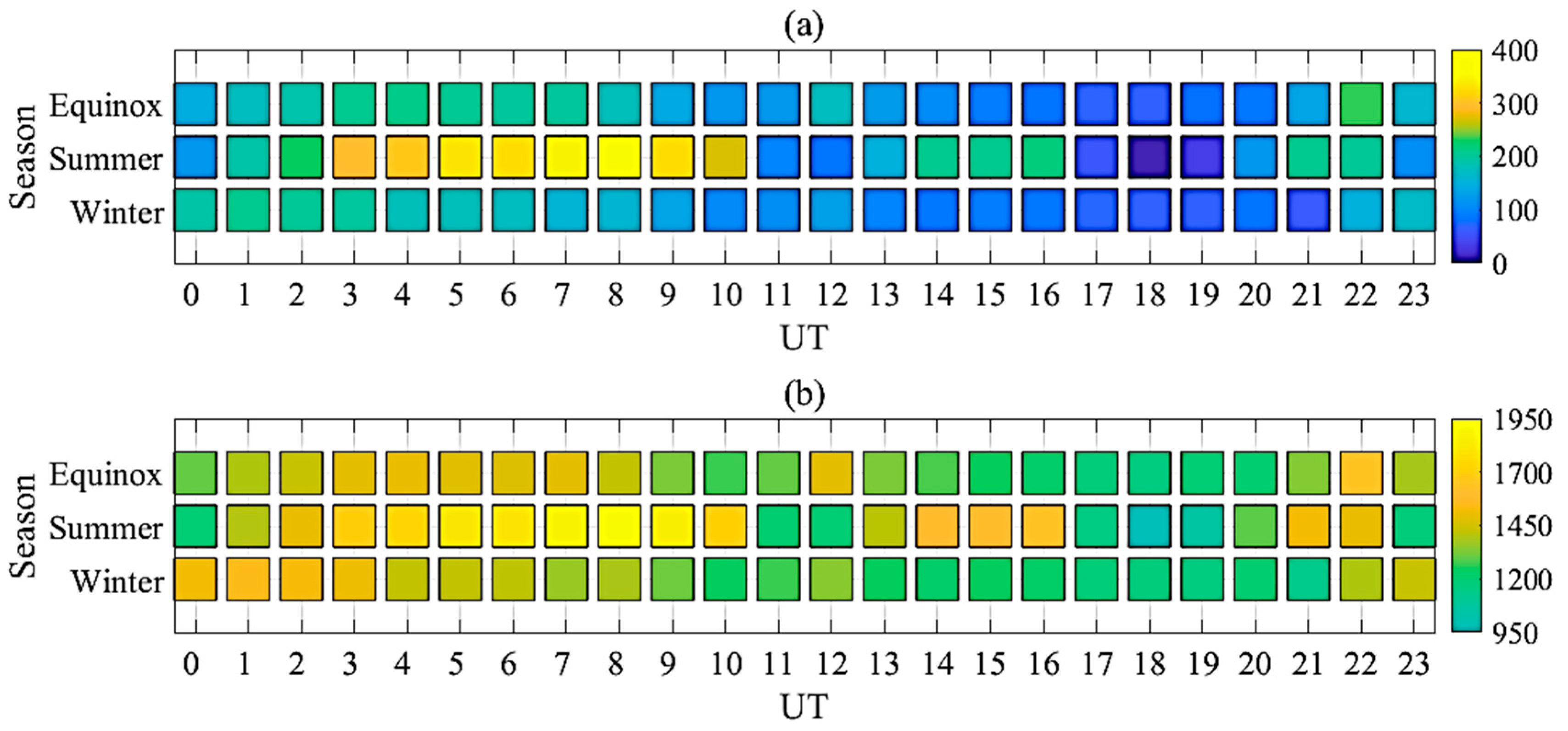
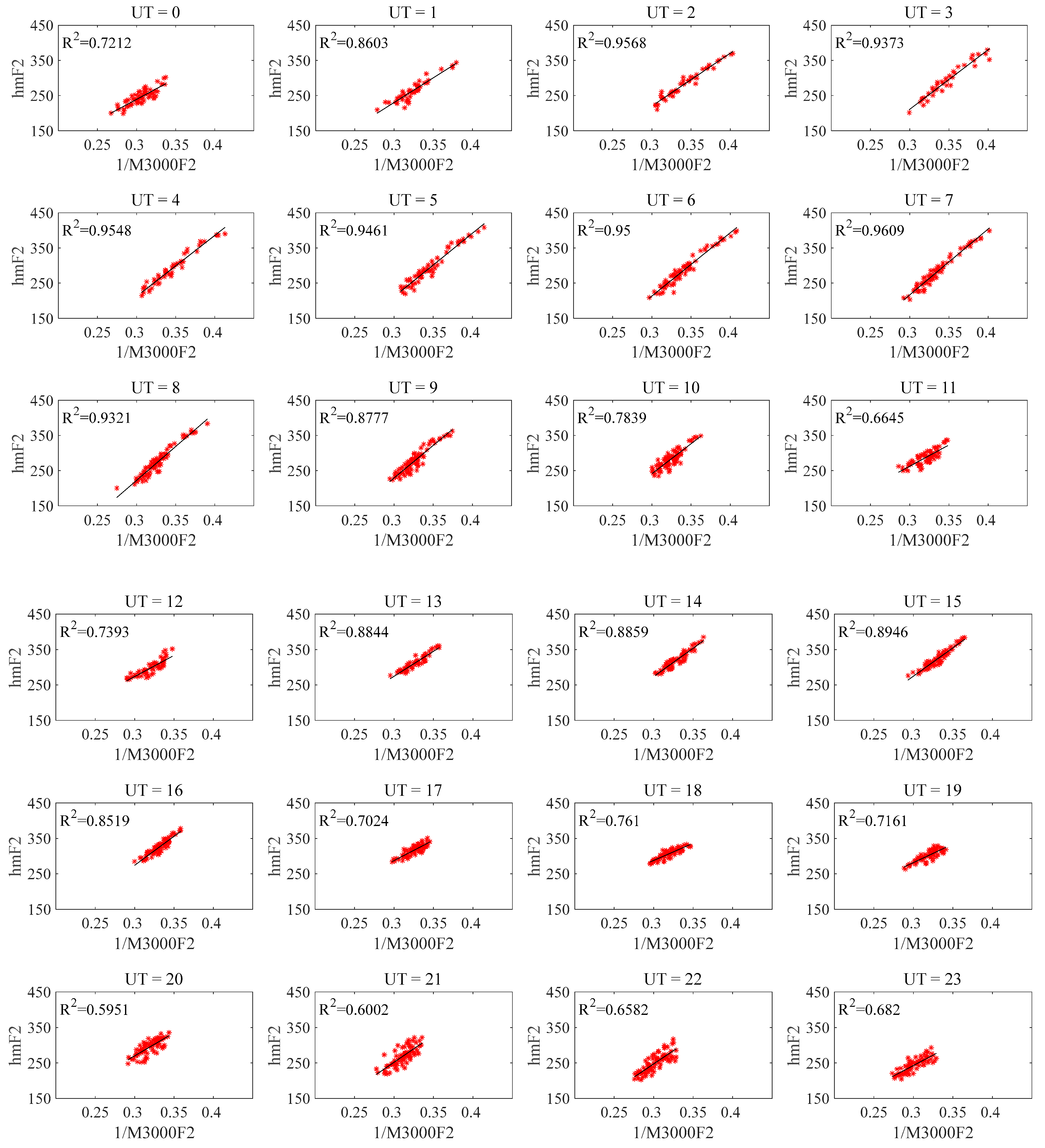
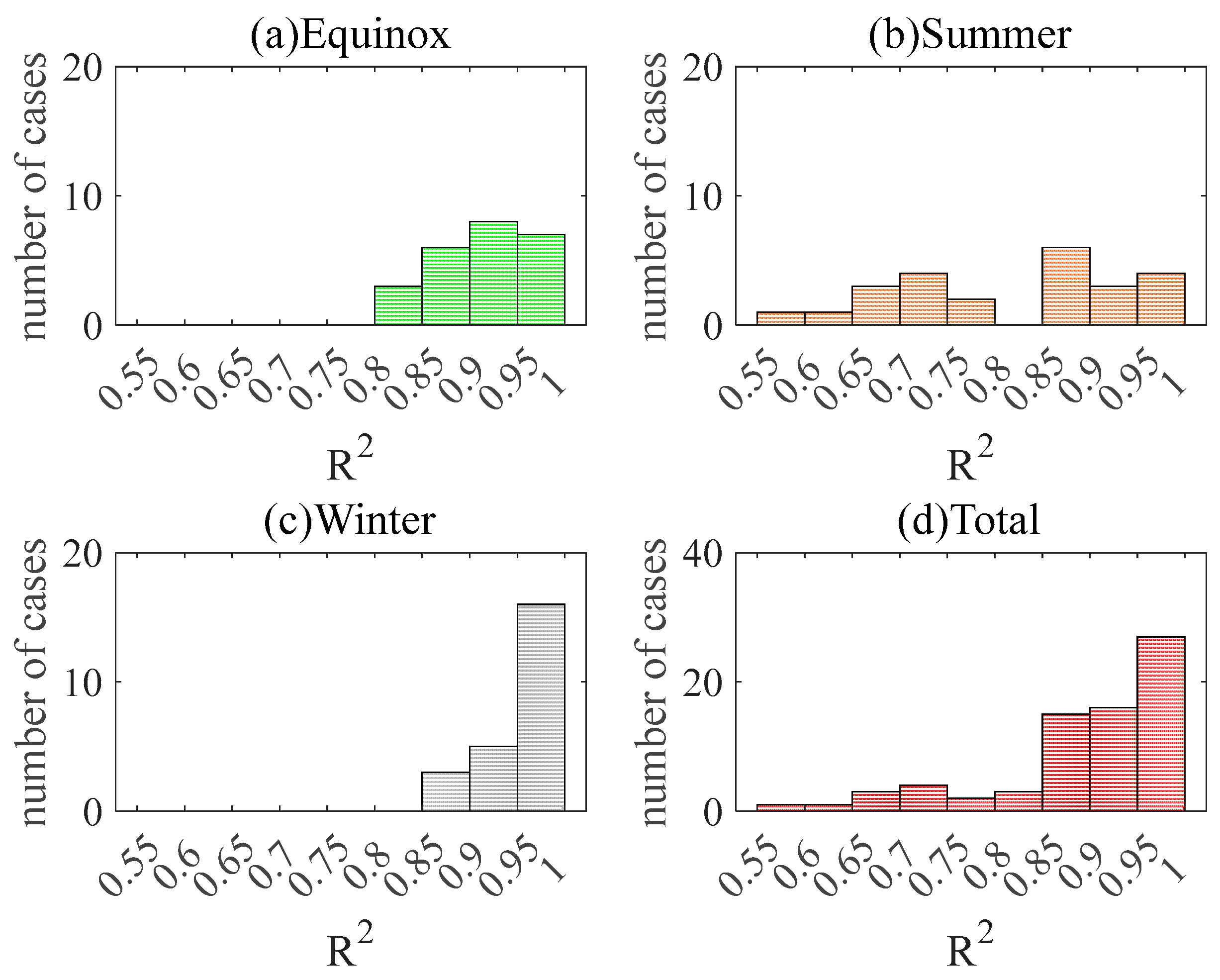
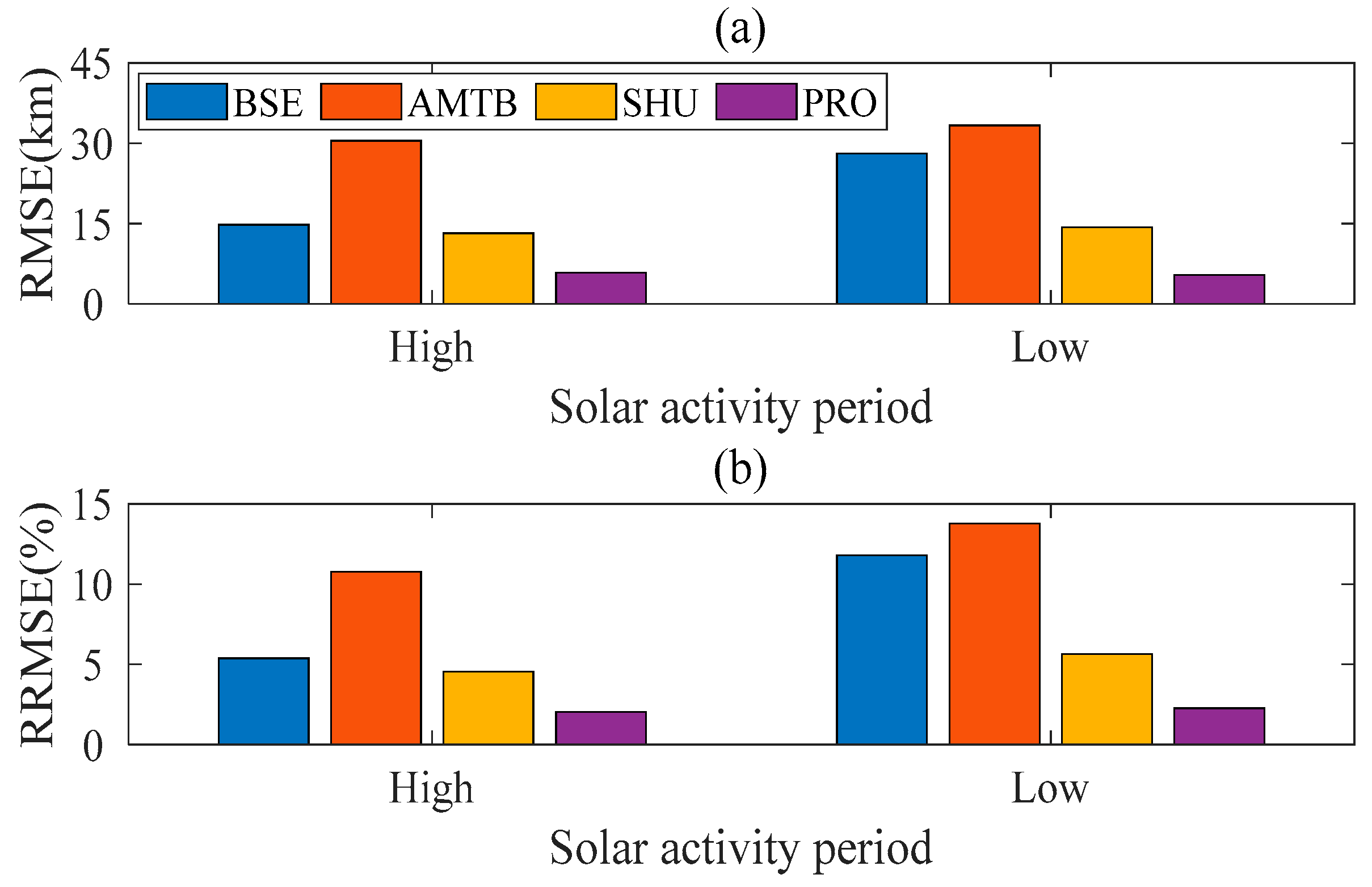
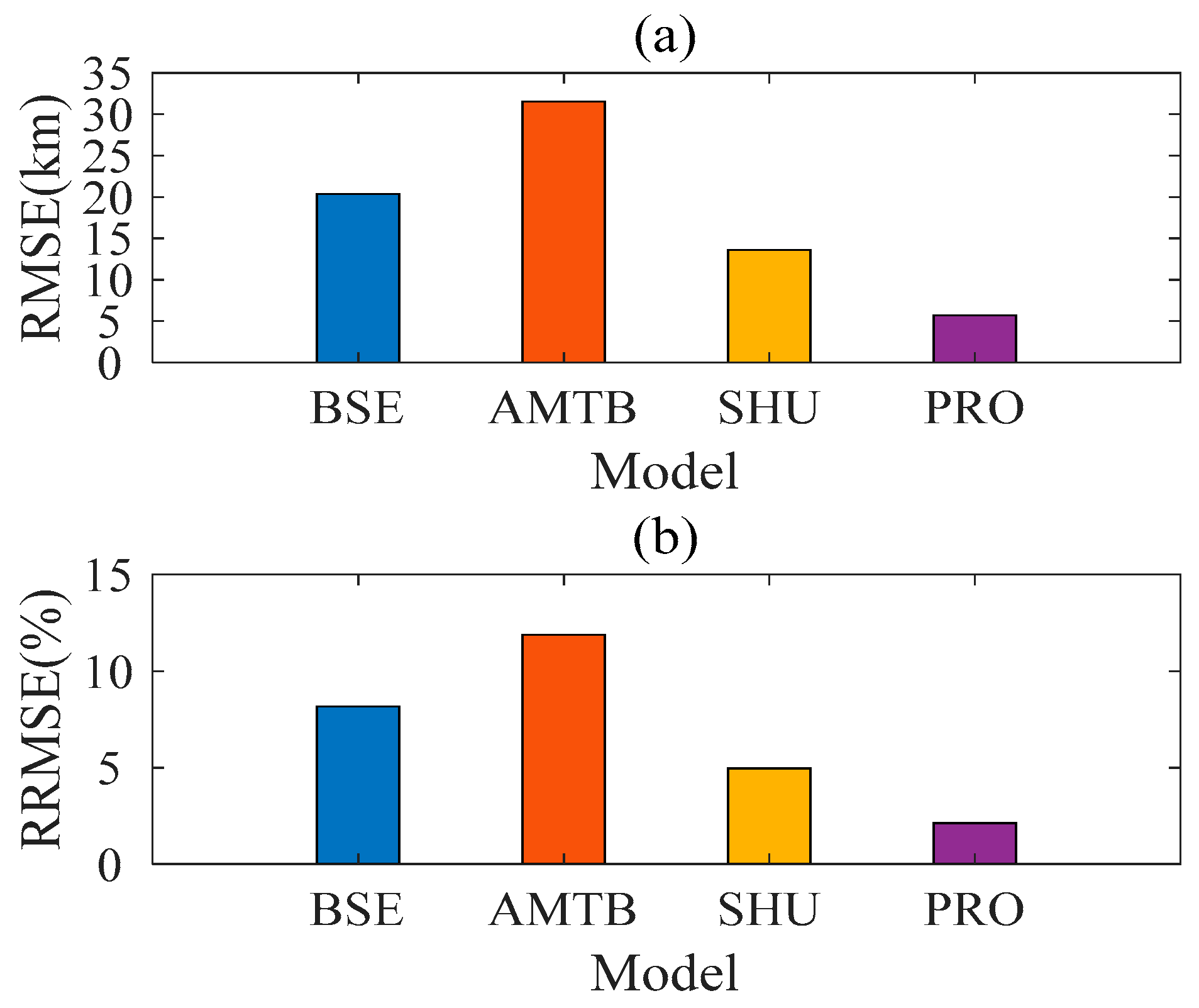
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, B.; Wang, Z.; Shen, Y.; Li, W.; Xu, F.; Li, X. Evaluation of foF2 and hmF2 Parameters of IRI-2016 Model in Different Latitudes over China under High and Low Solar Activity Years. Remote Sens. 2022, 14, 860. [Google Scholar] [CrossRef]
- Wang, J.; Yang, C.; An, W. Regional Refined Long-Term Predictions Method of Usable Frequency for HF Communication Based on Machine Learning Over Asia. IEEE Trans. Antennas Propag. 2022, 70, 4040–4055. [Google Scholar] [CrossRef]
- Wang, J.; Shi, Y.; Yang, C.; Zhang, Z.; Zhao, L. A Short-Term Forecast Method of Maximum Usable Frequency for HF Communication. IEEE Trans. Antennas Propag. 2023, 71, 5189–5198. [Google Scholar] [CrossRef]
- Fagre, M.; Zossi, B.S.; Chum, J.; Yiğit, E.; Elias, A.G. Ionospheric high frequency wave propagation using different IRI hmF2 and foF2 models. J. Atmos. Sol. Terr. Phys. 2019, 196, 105141. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Q.; Shi, Y.; Yang, C.; Wang, J. A Reconstruction Method for Ionospheric foF2 Spatial Mapping over Australia. Atmosphere 2023, 14, 1399. [Google Scholar] [CrossRef]
- Schunk, R.; Nagy, A. Ionospheres: Physics, Plasma Physics, and Chemistry; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Elias, A.G.; Zossi, B.S.; Yiğit, E.; Saavedra, Z.; Barbas, B.F.H. Earth’s magnetic field effect on MUF calculation and consequences for hmF2 trend estimates. J. Atmos Sol. Terr. Phy. 2017, 163, 114–119. [Google Scholar] [CrossRef]
- Huang, H.; Moses, M.; Volk, A.E.; Elezz, O.A.; Kassamba, A.A.; Bilitza, D. Assessment of IRI-2016 hmF2 model options with digisonde, COSMIC and ISR observations for low and high solar flux conditions. Adv. Space Res. 2021, 68, 2093–2103. [Google Scholar] [CrossRef]
- Sezen, U.; Sahin, O.; Arikan, F.; Arikan, O. Estimation of hmF2 and foF2 Communication Parameters of Ionosphere F2 -Layer Using GPS Data and IRI-Plas Model. IEEE Trans. Antennas Propag. 2013, 61, 5264–5273. [Google Scholar] [CrossRef]
- Maruyama, T.; Ma, g.; Tsugawa, T.; Supnithi, P.; Komolmis, T. Ionospheric peak height at the magnetic equator: Comparison between ionosonde measurements and IRI. Adv. Space Res. 2017, 60, 375–380. [Google Scholar] [CrossRef]
- Thu, H.; Mazaudier, C.; Huy, M.; Thanh, D.; Viet, H.; Thi, N.; Hozumi, K.; Truong, T. Comparison between IRI-2012, IRI-2016 models and F2 peak parameters in two stations of the EIA in Vietnam during different solar activity periods. Adv. Space Res. 2021, 68, 2076–2092. [Google Scholar] [CrossRef]
- Bilitza, D.; Pezzopane, M.; Truhlik, V.; Altadill, D.; Reinisch, B.W.; Pignalberi, A. The International Reference Ionosphere model: A review and description of an ionospheric benchmark. Rev. Geophys. 2020, 60, e2022RG000792. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, C.; Liu, T.; Yang, G.; Zhao, Z. Effect of the ionospheric virtual height on the joint positioning accuracy of multi-station over-the-horizon radar system. Chin. J. Radio Sci. 2022, 37, 761–767. [Google Scholar]
- Fatima, T.; Ameen, M.A.; Jabbar, M.A.; Baig, M.J. The variation of ionosonde-derived hmF2 and its comparisons with International Reference Ionosphere (IRI) and Empirical Orthogonal Function (EOF) over Pakistan longitude sector during solar cycle 22. Adv. Space Res. 2021, 68, 2104–2114. [Google Scholar] [CrossRef]
- Tang, J.; Ji, S.; Wang, J.; Wang, X. Assimilation methods of ionospheric short-term forecast for selecting frequency in short wave communication. Chin. J. Radio Sci. 2022, 28, 499–504. [Google Scholar]
- Adebesin, B.O.; Adeniyi, J.O. F2-layer height of the peak electron density (hmF2) dataset employed in Inferring Vertical Plasma Drift–Data of Best fit. Data Brief 2015, 19, 59–66. [Google Scholar] [CrossRef]
- Shimazaki, T. World-wide daily variations in the height of the electron density of the ionospheric F2-layer. J. Radio Res. Lab. 1955, 2, 85–97. [Google Scholar]
- Bradley, P.A.; Dudeney, J.R. A simple model of the vertical distribution of electron concentration in the ionosphere. J. Atmos. Solar. Terr. Phys. 1973, 35, 2131–2146. [Google Scholar] [CrossRef]
- Dudeney, J.R. A Simple Empirical Method for Estimating the Height and Semi-Thickness of the F2-Layer at the Argentine Islands Graham Land; Science Report 88; British Antarctic Survey: London, UK, 1975. [Google Scholar]
- Bilitza, D.; Eyfrig, R.; Sheikh, A.M. A global model for the height of the F2-peak using M3000 values from the CCIR numerical map. ITU Telecommun. J. 1979, 49, 549–553. [Google Scholar]
- Adebesin, B.O.; Adeniyi, J.O.; Afolabi, P.A.; Ikubanni, S.O.; Adebiyi, S.E. Modelling M(3000)F2 at an African equatorial location for better IRI-model prediction. Radio Sci. 2022, 57, 1–19. [Google Scholar] [CrossRef]
- Oyekola, O.S. Comparison of IRI-2016 model-predictions of F2-layer peak density height options with the ionosonde-derived hmF2 at the equatorial station during different phases of solar cycle. Adv. Space Res. 2019, 64, 2064–2076. [Google Scholar] [CrossRef]
- Brunini, C.; Conte, J.F.; Azpilicueta, F.; Bilitza, D. A different method to update monthly median hmF2 values. Adv. Space Res. 2013, 51, 2322–2332. [Google Scholar] [CrossRef]
- Sugiyama, M. Statistical Machine Learning; China Machine Press: Beijing, China, 2016. [Google Scholar]
- Lu, X.; Song, J. Big Data Mining and Statistical Machine Learning; China Renmin University Press: Beijing, China, 2016. [Google Scholar]
- Wang, J.; Shi, Y.; Yang, C. Investigation of Two Prediction Models of Maximum Usable Frequency for HF Communication Based on Oblique- and Vertical-Incidence Sounding Data. Atmosphere 2022, 13, 1122. [Google Scholar] [CrossRef]
- Lloyd, H. A Treatise on Magnetism General and Terrestrial by Humphrey Lloyd; Longmans, Green and Company: London, UK, 1874. [Google Scholar]
- Bello, S.A.; Abdullah, M.; Hamid, N.S.A.; Yusuf, K.A.; Yoshikawa, A.; Fujimoto, A. Fujimoto, Robust least square modelling for selected daytime ionospheric parameters using geomagnetic observations at low latitudes. Adv. Space Res. 2023, 72, 1615–1633. [Google Scholar] [CrossRef]
- Altadill, D.; Magdaleno, S.; Torta, J.M.; Blanch, E. Global empirical models of the density peak height and of the equivalent scale height for quiet conditions. Adv. Space Res. 2013, 52, 1756–1769. [Google Scholar] [CrossRef]
- Shubin, V.N. Global median model of the F2-layer peak height based on ionospheric radio-occultation and ground-based Digisonde observations. Adv. Space Res. 2015, 56, 916–928. [Google Scholar] [CrossRef]


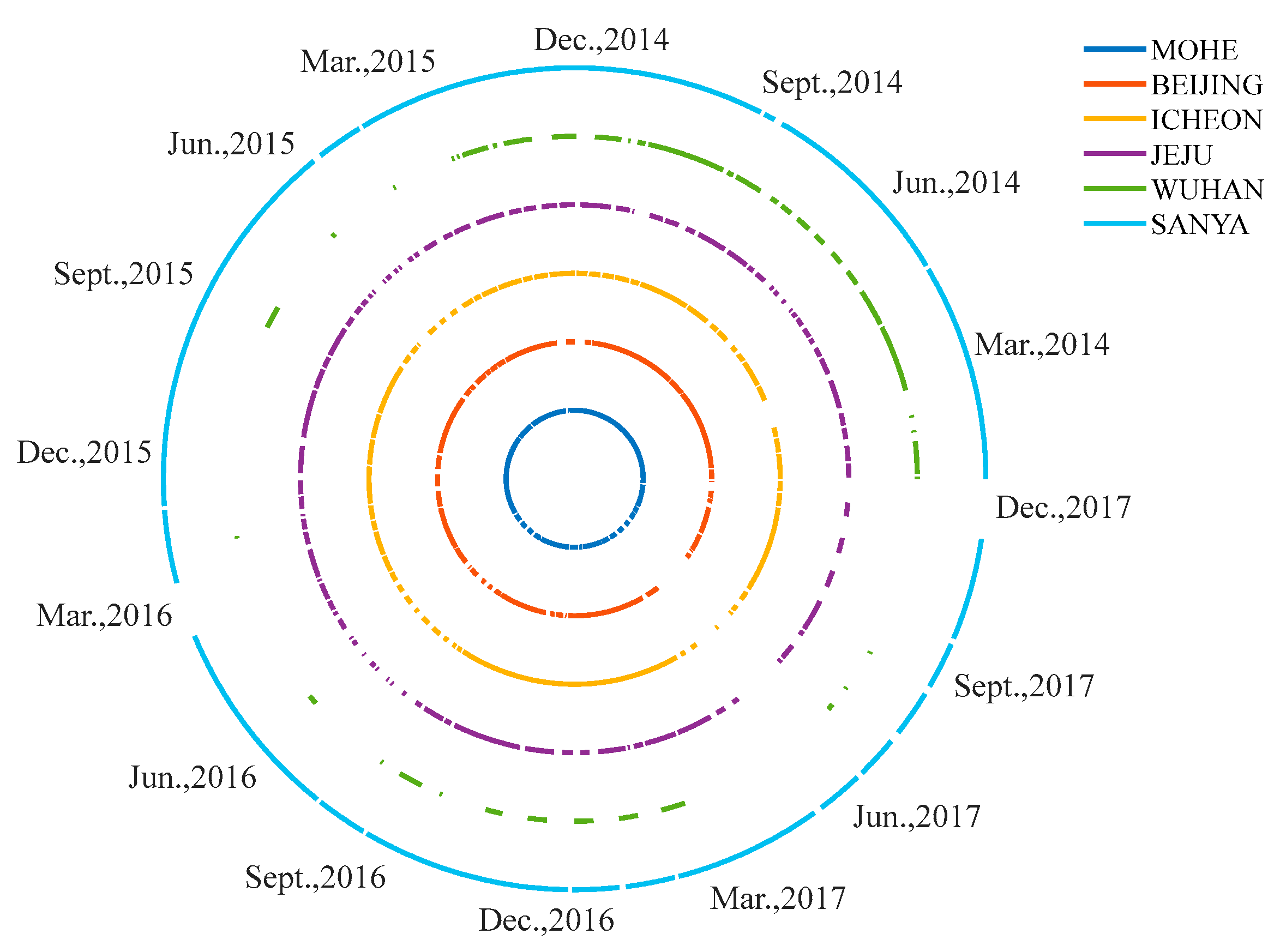



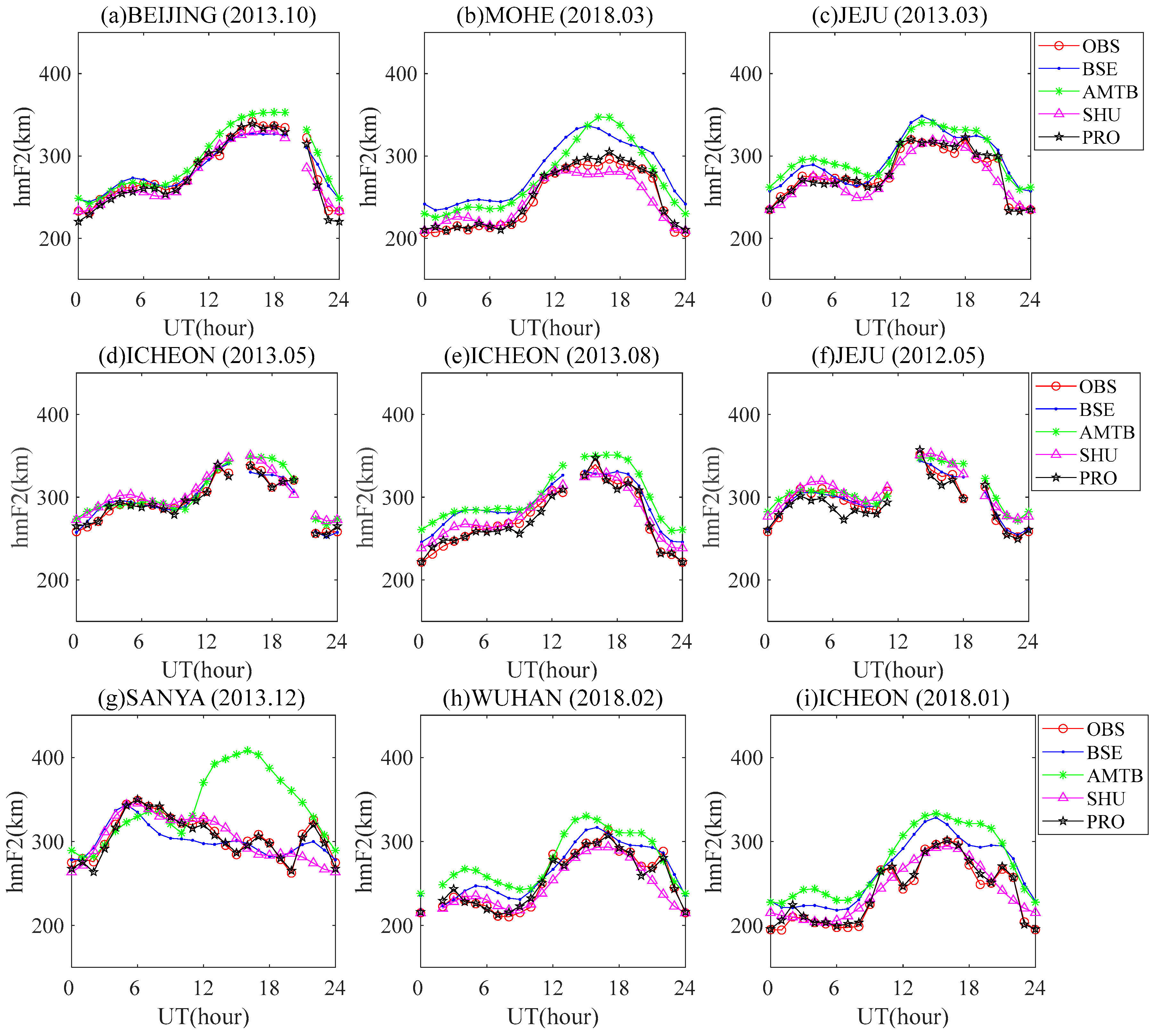

| Season | Station | Year | Month | Solar Activity Year |
|---|---|---|---|---|
| Equinox | Beijing | 2013 | 10 | High |
| Mohe | 2018 | 3 | Low | |
| Jeju | 2013 | 3 | High | |
| Summer | Icheon | 2013 | 5 | High |
| Icheon | 2013 | 8 | High | |
| Jeju | 2012 | 5 | High | |
| Winter | Sanya | 2013 | 12 | High |
| Wuhan | 2018 | 12 | Low | |
| Icheon | 2018 | 1 | Low |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Yu, Q.; Shi, Y.; Yang, C.; Ji, S.; Zheng, Y. A New Determining Method for Ionospheric F2-Region Peak Electron Density Height. Remote Sens. 2024, 16, 531. https://doi.org/10.3390/rs16030531
Wang J, Yu Q, Shi Y, Yang C, Ji S, Zheng Y. A New Determining Method for Ionospheric F2-Region Peak Electron Density Height. Remote Sensing. 2024; 16(3):531. https://doi.org/10.3390/rs16030531
Chicago/Turabian StyleWang, Jian, Qiao Yu, Yafei Shi, Cheng Yang, Shengyun Ji, and Yu Zheng. 2024. "A New Determining Method for Ionospheric F2-Region Peak Electron Density Height" Remote Sensing 16, no. 3: 531. https://doi.org/10.3390/rs16030531
APA StyleWang, J., Yu, Q., Shi, Y., Yang, C., Ji, S., & Zheng, Y. (2024). A New Determining Method for Ionospheric F2-Region Peak Electron Density Height. Remote Sensing, 16(3), 531. https://doi.org/10.3390/rs16030531











