WenSiM: A Relative Accuracy Assessment Method for Land Cover Products Based on Optimal Transportation Theory

Abstract

Land cover (LC) products play a crucial role in various fields such as change detection, resource management, and urban planning. The diversity in methods and principles used to create different products poses a challenge for researchers in choosing the most suitable one for research needs. Mainstream evaluation methods typically consider only a portion of the accuracy information from the product and require a significant effort in creating validation datasets. Here, we propose a relative accuracy assessment method for LC products based on optimal transport theory, which provides a comprehensive evaluation by utilizing a broader range of accuracy information within the product. The method can directly compute the similarity between the target product and the reference truth at a global scale, addressing the issue of quantitatively assessing product accuracy in the absence of a validation dataset. To validate the effectiveness of the method, we select Beijing as the study area to assess the accuracy of four LC products. The results suggest that the method allows for precise quantification of product accuracy, aligning closely with validation outcomes, which can provide valuable guidance to researchers in both product creation and selection.

1. Introduction

Land cover (LC) products, as common remote sensing products, depict the interactions between human activities and the natural environment, which are widely applied in environmental change monitoring, ecosystem assessment, and sustainable development planning [1,2,3]. With the rapid advancement of satellite remote sensing technology and the continuous improvement in data accessibility, LC products continue to evolve and be updated. However, due to differences in the classification algorithms and schemes of products, researchers find it challenging to directly assess the quality of these products [4]. The accuracy assessment and rational selection of LC products have become key issues in research [5,6]. It is a widely held view that the absolute ground truth does not exist, making it impossible to directly compare remote sensing products with it [7].

Previous research has found that a validation dataset can be created for the study area using a full-sampling method and make the dataset I reference truth to evaluate the overall accuracy of LC products. But the high cost of creating the dataset has made the full-sampling method rarely used directly [8]. To strike a balance between cost and accuracy, a variety of studies have proposed two major categories of accuracy assessment methods: direct assessment methods and indirect assessment methods. The direct assessment method involves first obtaining samples through random sampling and then creating a validation dataset through field surveys or visual interpretation based on high-resolution satellite images such as Google Earth [9]. Finally, a confusion matrix is computed to determine the overall accuracy of the product [10]. Although the method saves costs, the number and methods of sampling can introduce errors and lead to unstable results. Furthermore, most validation datasets are not interoperable, making it difficult for researchers to select the highest-quality one. Moreover, the rationale of relying solely on one validation dataset to assess the accuracy of all LC products need to be questioned [11]. To avoid the creation of validation datasets, indirect evaluation methods that compare the similarity between products have been reported. Unlike direct assessment, the indirect assessment method evaluates relative accuracy by analyzing differences between products, primarily through regional consistency and spatial consistency analysis [12,13,14]. Specifically, regional consistency involves statistically assessing the composition of different land cover types within the study area [15]. Spatial consistency compares whether different products have the same land cover type at the same location through pixel-by-pixel spatial overlay analysis [16]. The number of matching pixels indicates spatial consistency between products, implying the degree of similarity [17]. However, it is important to note that the method primarily provides qualitative assessments and may not offer a definitive ranking of product quality. The methods for assessing the accuracy of LC products described above can be summarized in Figure 1 based on their distinctive characteristics and developmental trajectories. As can be seen from the figure, the full-sampling method is rarely used due to its high cost. Although direct assessment methods and indirect assessment methods are cost-effective, they result in the loss of a significant amount of information accuracy.

This paper argues that the accuracy information determined by LC products can be divided into two types: spatial position information and global feature information. Most studies that assess LC product accuracy have only focused on spatial position information, which means the classification correctness of each pixel, disregarding the distribution of features formed by all pixels [18,19]. Every land cover type exhibits distinctive morphologic characteristics, which are expressed through the arrangement of pixels. Therefore, even with the absolute ground truth, the methods depicted in Figure 1 are still unable to fully exploit the accuracy information of products and the ground truth for a comprehensive assessment. This paper extends the research of Tan et al. [20], which primarily took account of the global features of pixels to quantitatively compare the similarity of remote sensing products. However, the similarity index proposed in Tan’s study also only considers a portion of the accuracy information in the products and may be challenging to explain in some application scenarios. In this paper, we attempt to utilize more accuracy information to assess LC products and ensure that the new similarity index maintains strict mathematical logic and interpretability, revealing both commonalities and differences among products. The new metric will assist researchers in making optimal selections quickly from LC products.

The primary innovations and contributions of this paper include:

• Proposal of a relative accuracy assessment method for LC products based on optimal transport theory. The method considers a broader range of accuracy information to compute the Wasserstein similarity (WenSiM) between the target product and the reference ground truth at a global level without the need for registration and validation datasets.
• Evaluation of the classification accuracy of four LC products in Beijing. Through a comparative analysis of WenSiM and the results obtained from mainstream approaches, the effectiveness of the relative accuracy assessment method is validated.

2. Data

2.1. Data Preprocessing

This study made use of Dynamic World [21], ESA WorldCover v100 [22], FROM_GLC10 [23], and SinoLC_1 [24] in Beijing to conduct accuracy assessments. ESRI World Cover [25] was chosen as the reference ground truth because of the highest overall official validation accuracy.

Table 1. Basic information of the five LC products.

	ESRI_GLC10	DW_GLC10	ESA_GLC10	FROM_GLC10	SinoLC_1
Institution	Esri	WRI	ESA	THU	WHU
Resolution (m)	10	10	10	10	1
Coverage	Global	Global	Global	Global	National (China)
Classification scheme	10 classes	9 classes	11 classes	10 classes	11 classes
Version and timeline	2020	2020	2020	2017	2020
Overall accuracy (%)	85.96	77.80	74.40	72.76	73.61 55.55 (Beijing)

Notes: ESRI = Environmental Systems Research Institute; WRI = World Resources Institute; ESA = European Space Agency; THU = Tsinghua University; WHU = Wuhan University.

shows the basic information for every LC product.

In contrast to common data preprocessing procedures, this study only dealt with resampling and reclassifying the products without requiring georeferencing. According to Table 1, only the SinoLC_1 product had a resolution of 1 m. To facilitate a more comprehensive comparison of each product’s accuracy and ensure fairness in the process, we standardized the resolutions of the five products to 10 m. It is also important to emphasize that, although the FROM_GLC10 was produced in 2017, existing research has demonstrated that, compared to classification errors in LC products, land cover changes in large regions within a five-year timeframe can be negligible [26,27]. Additionally, for the DW_GLC10, as a continuously updated image collection, the study utilized the confusion matrix results obtained during the testing process as its overall accuracy. Finally, the land cover categories for products were reclassified into forestland, cropland, grassland, wetland, settlements, and other land according to the classification rules of the Intergovernmental Panel on Climate Change (IPCC), with specific classification criteria and details provided in

Table A1. The detailed definitions of IPCC land categories.

Land Categories	Detailed Definitions
Forestland	All land with woody vegetation consistent with thresholds; Systems with vegetation that are expected to exceed the threshold of the forestland.
Cropland	Arable and tillage land; Agro-forestry systems where vegetation falls below the thresholds.
Grassland	Rangelands and pastureland that is not considered cropland; Systems with vegetation that fall below the threshold and are not expected to exceed the threshold without human intervention; All grassland from wildlands to recreational areas, as well as agricultural and silvi-pastural systems.
Wetlands	Land that is covered by or saturated with water for all or part of the year; Reservoirs, natural rivers and lakes.
Settlements	All developed land, including transportation infrastructure and human settlements.
Other land	Bare soil, rock, ice, and all unmanaged land areas that do not fall into any of the other five categories.

and

Table A2. Conversion relations between five LC products and the IPCC land cover classification.

IPCC	ESRI_GLC10	DW_GLC10	ESA_GLC10	FROM_GLC10	SinoLC_1
Forestland	Trees	Trees	Tree cover	Forest	Tree cover
	Scrub and shrub		Shrubland	Shrubland	Shrubland
			Mangroves
Cropland	Crops	Crops	Cropland	Cropland	Cropland
Grassland	Grass	Grass	Grassland	Grassland	Grassland
Wetlands	Water	Water	Permanent water bodies	Waterbodies	Water
	Flooded vegetation	Flooded vegetation	Herbaceous wetland	Wetlands	Wetlands
Settlements	Built area	Built	Built up	Impervious	Roads
					Built up
Other land	Bare ground	Bare	Bare and sparse vegetation	Barren land	Barren and spare vegetation
	Snow and ice	Snow and ice	Snow and ice	Snow and ice	Snow and ice
	Clouds		Moss and Lichen	Tundra	Moss and lichen

.

2.2. Study Area

The study area was Beijing (Lat 39°56′N, Long 116°20′E), which covers an area of 1,641,054 hectares and is renowned as both an ancient capital and a modern international city. The city is surrounded by mountains on its western, northern, and northeastern sides, whereas the southeastern part consists of a plain that slopes toward the Bohai Sea. Detailed geographic information about Beijing, as well as the visual comparative effects of LC products in Changping District, are depicted in Figure 2.

3. Methods

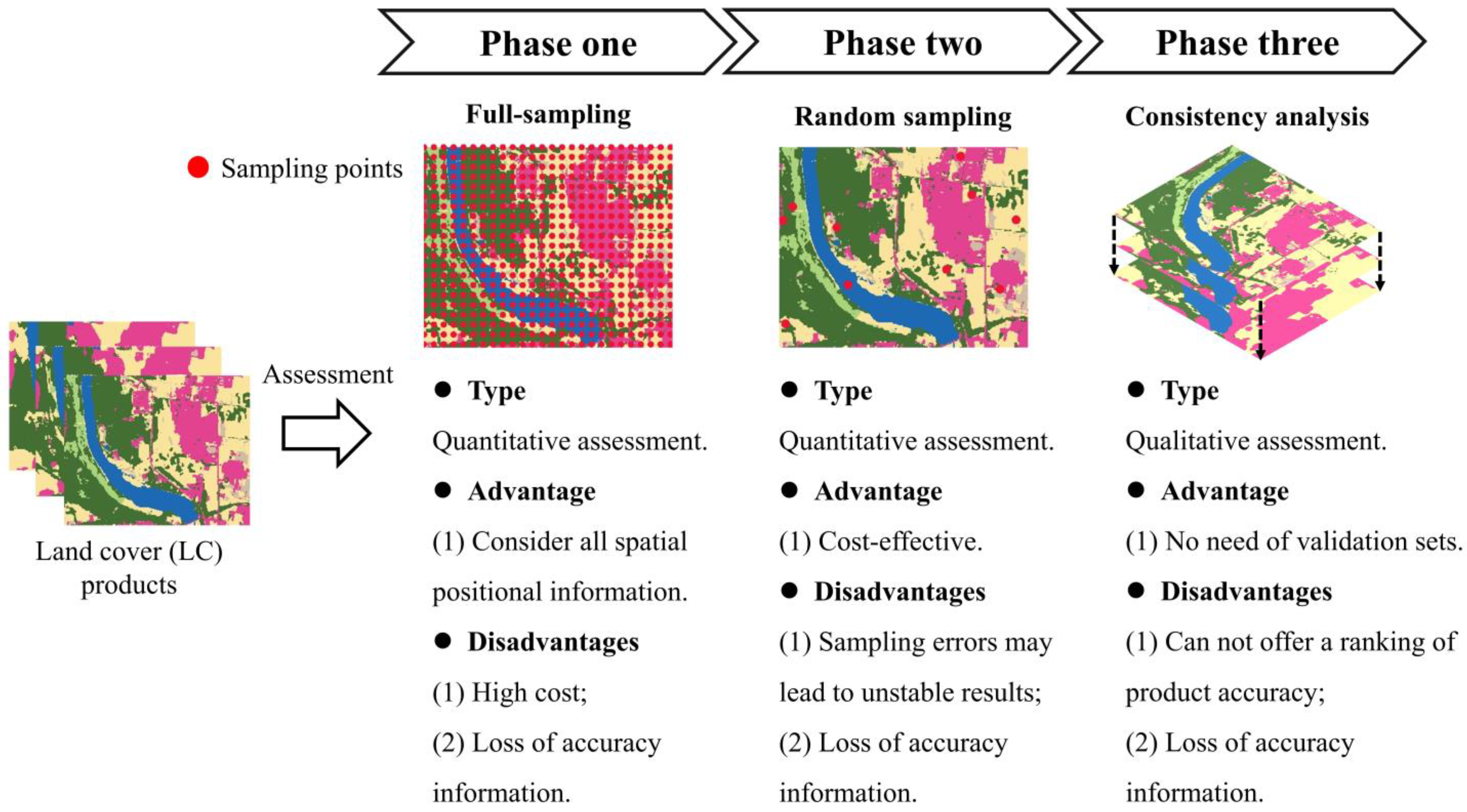
The section begins by highlighting the theoretical underpinnings of the relative accuracy assessment method. Following that, the section elaborates on the characteristics and computational process of the WenSiM index. Finally, the section introduces the creation of a validation dataset for the study area by using stratified sampling theory.

3.1. Wasserstein-p Distance

The Wasserstein distance (earth mover’s distance, EMD) is a type of histogram similarity measure [28,29]. Compared to other similarity measures, like the Kullback–Leibler (KL) divergence and the Jensen–Shannon (JS) divergence, the Wasserstein distance has the advantage of being able to assess the similarity between two probability distributions that do not overlap at all. In addition, its value represents the minimum “cost” when two distributions are transformed into each other.

Let $\mathsf{\varphi }$ be a metric space. For this study, we considered $\mathsf{\varphi }$ to be compact d-dimensional Euclidean spaces, i.e., $\mathsf{\varphi }={\left[\mathrm{0,1}\right]}^d$. Let ${\varphi }_{\mu }$ and ${\varphi }_{\nu }$ denote the set of Borel probability measures defined on $\mathsf{\varphi }$. The Wasserstein-p distance for $p\in \left[\left.1,\infty \right)\right.$ between two distributions $P_{\mu }\in {\varphi }_{\mu }$ and $P_{\nu }\in {\varphi }_{\nu }$ can be defined as Equation (1) with the cost functions $c\left(x,y\right)=d^p\left(x,y\right)$.

$$W_p\left(P_{\mu },P_{\nu }\right)\triangleq {\left\{\underset{\gamma \in \Gamma \left(P_{\mu },P_{\nu }\right)}{\inf }{\int }_{{\varphi }_{\mu }\times {\varphi }_{\nu }}^{}{d}^p\left(x,y\right)d\gamma \left(x,y\right)\right\}}^{\frac{1}{p}}$$

(1)

Here, $\Gamma \left(P_{\mu },P_{\nu }\right)$ is the set of all transportation plans $\gamma \left(x,y\right)$ whose marginals are $P_{\mu }$ and $P_{\nu }$, respectively, $\gamma \in \Gamma \left(P_{\mu },P_{\nu }\right)$. Additionally, $d^p\left(x,y\right)$ represents the “cost” associated with transforming $x$ in probability distribution $P_{\mu }$ into $y$ in $P_{\nu }$, and $p$ is the dimension size of the probability distribution. Thus, the Wasserstein p-distance reflects the “cost” of the optimal transportation plan.

According to Brenier’s theorem [30], if $P_{\mu }$ and $P_{\nu }$ (with respect to the Lebesgue measure) are absolutely continuous probability measures, the Wasserstein p-distance can be equivalently calculated using Equation (2).

$$W_p\left(P_{\mu },P_{\nu }\right)={\left\{\underset{f\in \mathit{MP}\left(P_{\mu },P_{\nu }\right)}{\inf }{\int }_{{\varphi }_{\mu }}^{}{d}^p\left(f\left(x\right),x\right)d{P}_{\mu }\left(x\right)\right\}}^{\frac{1}{p}}$$

(2)

where $MP\left(P_{\mu },P_{\nu }\right)=\left\{f:{\varphi }_{\mu }\to {\varphi }_{\nu }\left|f_{\#P_{\mu }}=P_{\nu }\right.\right\}$ and $f_{\#P_{\mu }}$ is used to indicate the pushforward of measure $P_{\mu }$.

Since LC products consist of pixels, they belong to a special two-dimensional discrete probability distribution and can be calculated numerically using a matrix. Thus, we focused on how to calculate the Wasserstein distance of absolute discrete probability measures in various dimensions.

The process of calculating higher-dimensional Wasserstein distance is difficult and complicated. But the development of the sliced Wasserstein distance provides a closed-form solution to the Wasserstein-p distance calculation problem [31]. By reducing the probability distribution to one dimension through random projection, computing the Wasserstein distance becomes fast and straightforward [32,33].

The idea behind the sliced Wasserstein distance is to obtain the marginal distribution family (i.e., one-dimensional distribution) of high-dimensional probability distribution through linear random projection and then calculate the Wasserstein distance of two marginal distributions. The method transforms the challenging high-dimensional optimal transport problem into several one-dimensional optimal transport problems with closed-form solutions. Then, the sliced Wasserstein-p distance between two probability distributions $P_{\mu }$ and $P_{\nu }$ can be defined as in Equation (3).

$${\tilde{W}}_p\left(P_{\mu },P_{\nu }\right)={\left[{\int }_{\theta \in \mathsf{\Omega }}^{}{W}_p^p\left(P_{\mu }^{\theta },P_{\nu }^{\theta }\right)d\theta \right]}^{\frac{1}{p}}$$

(3)

where $P_{\mu }^{\theta }$ and $P_{\nu }^{\theta }$ denote all projections of marginal distributions $P_{\mu }$ and $P_{\nu }$ on the direction $\theta$, respectively, and $\mathsf{\Omega }$ is the set of all possible directions on the unit sphere. It has also been proven that ${\tilde{W}}_p$ satisfies sub-additivity and coincidence axioms, making it a genuine metric [34].

Due to the various direction selections, calculating the corresponding projections during the actual process is still very complicated. To address the challenge of projection complexity while keeping the sample complexity constant, Deshpande et al. [35] proposed a method to first find the most meaningful projection direction. The result obtained by Equation (4) in the projection direction $\theta$ is known as the max sliced Wasserstein distance.

$${\tilde{W}}_{2-max}\left(P_{\mu },P_{\nu }\right)={\left[\underset{\theta \in \mathsf{\Omega }}{\max }{W}_2^2\left(P_{\mu }^{\theta },P_{\nu }^{\theta }\right)\right]}^{\frac{1}{2}}$$

(4)

${\tilde{W}}_{2-max}$ is an effective measure that overcomes the limitations of projection complexity. It can directly compute the difference between two-dimensional distributions. Therefore, in this study, it was employed to calculate the Wasserstein distance between LC products and the reference ground truth within the study area.

3.2. Wasserstein Similarity Index

This study divided the accuracy information carried by the LC products into two types: global feature information and spatial position information. Although the Wasserstein distance is effective in quantifying the similarity between products and the reference truth from a global feature perspective, its interpretability is affected because the total weight is evenly distributed among all pixels. Therefore, we normalized ${\tilde{W}}_{2-max}$ to ensure that the global feature similarity $\mathcal{F}$ had a strict mathematical significance and was independent of the size of the study area.

The existence of target product A and reference truth B was assumed, whose matrix spaces are denoted as $A_{\mu }$ and $B_{\nu }$, respectively. In the study area, there was a total of $k$ land cover types, and the transformed numerical matrices satisfied $P_{\mu }\in A_{\mu }$ and $P_{\nu }\in B_{\nu }$. Then, $\mathcal{F}$ can be defined as Equation (5).

$${\mathcal{F}}_i=1-\frac{{\tilde{W}}_{2-max}^{\left(i\right)}}{D^{\left(i\right)}}$$

(5)

where ${\mathcal{F}}_i$ represents the global feature similarity for the type $i$($i=\mathrm{1,2},\cdots ,k$) in the study area, with $0<{\mathcal{F}}_i\le 1$. $D^{\left(i\right)}$ denoting the maximum centroid distance for the pixels of the land cover type $i$ in A and B, which can be defined with Equation (6).

$$D^{\left(i\right)}=max\left\{d\left(n_A^{\left(i\right)},n_B^{\left(i\right)}\right)\right\}$$

(6)

where $n_A^{\left(i\right)}$ and $n_B^{\left(i\right)}$ represent the pixels of the land cover type $i$ in A and B, respectively. $d$ denotes the centroid distance for the pixels of land cover type $i$ in A and B. When the pixels in the two products are distributed in the diagonal corners of the area, the maximum centroid distance can be computed.

After considering the global feature information of the products comprehensively, there is also a need for an evaluation metric to assess spatial positional information. This study used the correlation coefficient to quantify the spatial position similarity between the target product and the reference truth. The correlation coefficient $K$ can be defined with Equation (7), primarily reflecting the commonalities and differences in category composition between the product and the truth [36].

$$K=\frac{{\sum }_{i=1}^k\left(P_{\mu }^{\left(i\right)}-{\overline{P}}_{\mu }\right)\left(P_{\nu }^{\left(i\right)}-{\overline{P}}_{\nu }\right)}{\sqrt{{\sum }_{i=1}^k{\left(P_{\mu }^{\left(i\right)}-{\overline{P}}_{\mu }\right)}^2{\sum }_{i=1}^k{\left(P_{\nu }^{\left(i\right)}-{\overline{P}}_{\nu }\right)}^2}}$$

(7)

Here, $P_{\mu }^{\left(i\right)}$ and $P_{\nu }^{\left(i\right)}$ represent the areas of type $i$($i=\mathrm{1,2},\cdots ,k$) for A and B, respectively. ${\overline{P}}_{\mu }$ and ${\overline{P}}_{\nu }$ are the average areas of each type in A and B, respectively within the study area.

With $\mathcal{F}$ and $K$ serving as measures for different types of accuracy information, this study further introduced the Wasserstein similarity (WenSiM) between the target product A and reference truth B. The index comprehensively extracts accuracy information to reflect the overall similarity, and it is defined as follows:

$$WenSiM=\frac{1}{k}{\sum }_{i=1}^{k}K{\mathcal{F}}_i$$

(8)

where the $WenSiM$ satisfies the condition $0<WenSiM\le 1$ and $WenSiM=1$ only when $K={\mathcal{F}}_i=1$, indicating that the target product and the reference truth are entirely identical in both spatial position and global features within the study area.

The WenSiM index fully takes use of more accuracy information to evaluate LC products. While maintaining properties such as symmetry, non-negativity, and identity, the WenSiM also possesses strict mathematical significance and interpretability. It is an excellent metric for accurately and rapidly assessing LC product accuracy. The detailed calculation process is summarized in Algorithm 1.

Algorithm 1. $WenSiM$($P_{\mu }$, $P_{\nu }$, $k$, $\theta$, $\mathsf{\Omega }$)

1: Initialize $\theta$, $\mathsf{\Omega }$

2: Data preprocessing for $(P_{\mu }$, $P_{\nu })$

3: Repeat

4:    $(A^{\left(i\right)}, B^{\left(i\right)}, P_{\mu }^{\left(i\right)}, P_{\nu }^{\left(i\right)},n_A^{\left(i\right)},n_B^{\left(i\right)})\leftarrow (P_{\mu }$, $P_{\nu })$

5:    $D^{\left(i\right)}, K\leftarrow {(A}^{\left(i\right)}, B^{\left(i\right)},n_A^{\left(i\right)},n_B^{\left(i\right)})$

6:    ${\tilde{W}}_{2-max}^{\left(i\right)}\leftarrow (P_{\mu }^{\left(i\right)}, P_{\nu }^{\left(i\right)}, \theta , \mathsf{\Omega })$

7:     ${\mathcal{F}}^{\left(i\right)}\leftarrow \left({{\tilde{W}}_{2-max}^{\left(i\right)}, D}^{\left(i\right)}\right)$

8:    ${WenSiM}^{\left(i\right)}\leftarrow (K, {\mathcal{F}}^{\left(i\right)})$

9:    $i\leftarrow i+1$

10: Until $i>k$

11: $WenSiM\leftarrow ({WenSiM}^{\left(i\right)}, k)$

12: Output $WenSiM$

3.3. Production of Validation Dataset

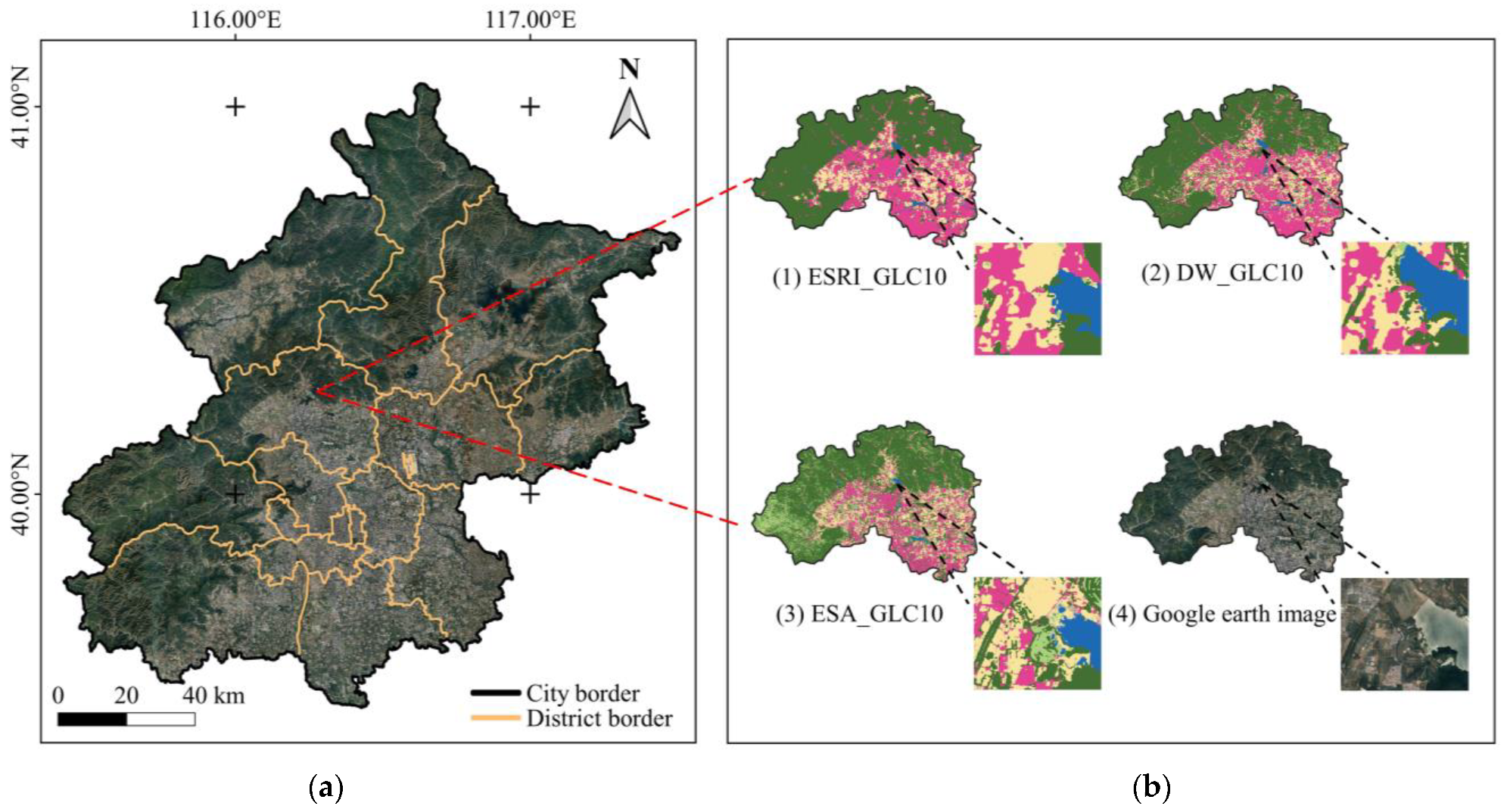
The evaluation method proposed in this paper can directly assess the accuracy of LC products without registration and validation datasets. In order to demonstrate the effectiveness and rationality of the WenSiM index, it is necessary to create a validation dataset to analyze the consistency between validation accuracy and assessment results.

Sampling is a crucial step in creating a validation dataset, as the sample size and sample variance determine the accuracy of the dataset. Although increasing the sample size is beneficial for improving accuracy, it also comes with the added cost of production. The optimal sampling scheme aims to obtain the most reliable validation results with the lowest cost [37]. Therefore, once the sample size is determined, the key to improving the accuracy lies in reducing sample variance [38].

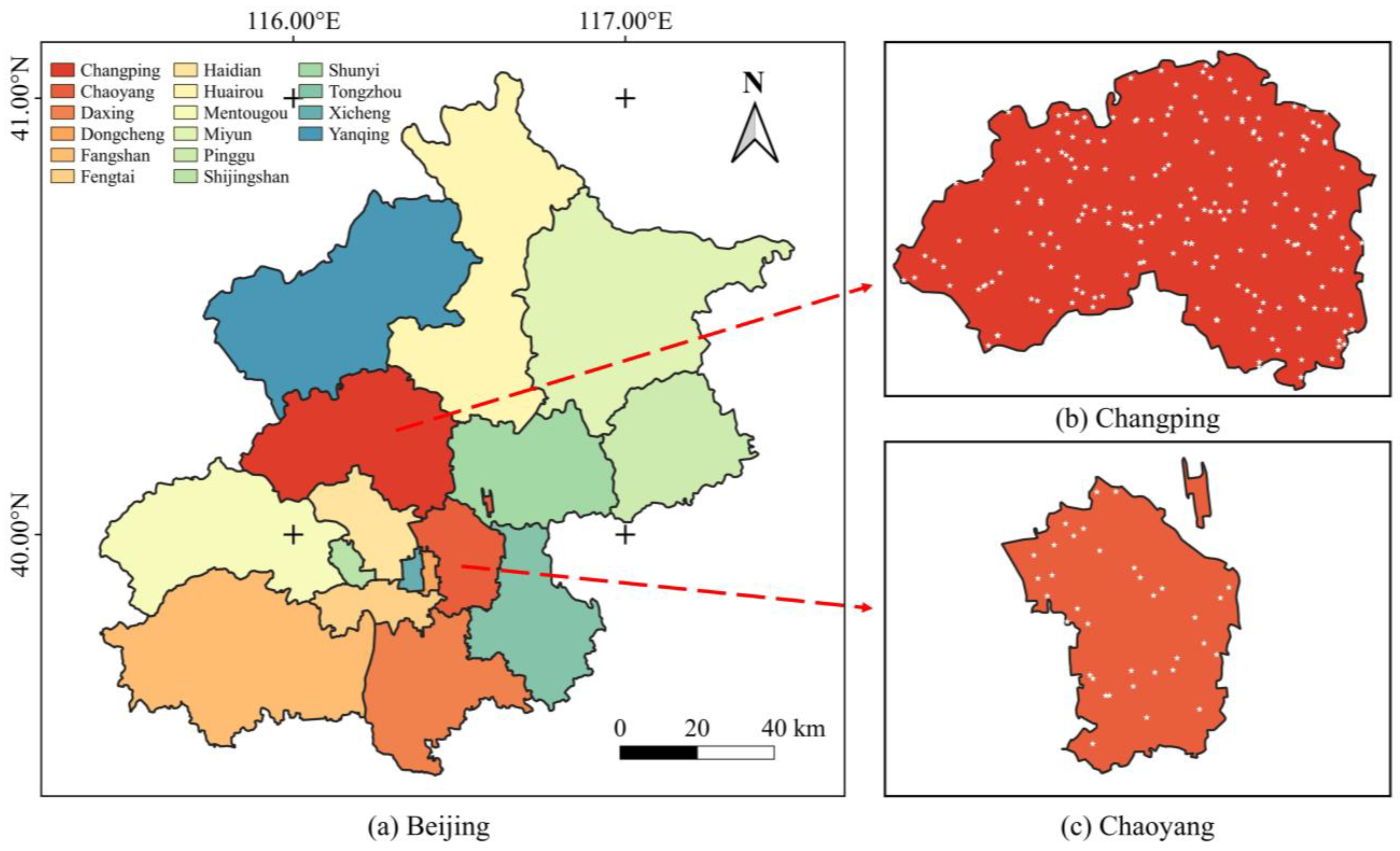
Stratified sampling (SS) is a great method to reduce variance and improve sampling accuracy when the sample size is constant [39,40]. To implement SS, it is crucial to confirm that every object in the sampling range shares similar properties. Subsequently, researchers can use a particular characteristic or rule to divide the population into $L$ non-repeating sub-groups, each referred to as a layer. Finally, samples for each layer can be acquired through random sampling.

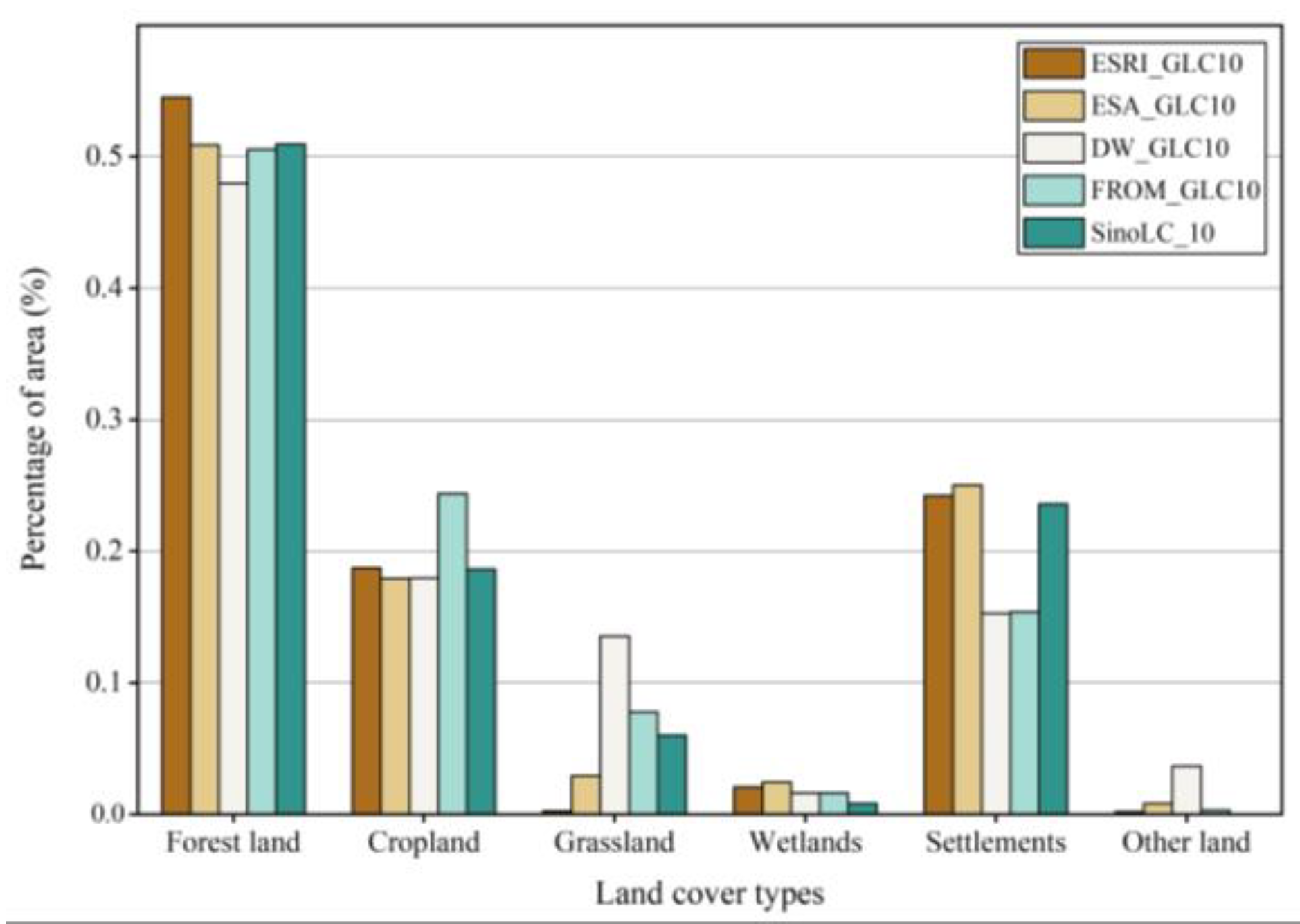
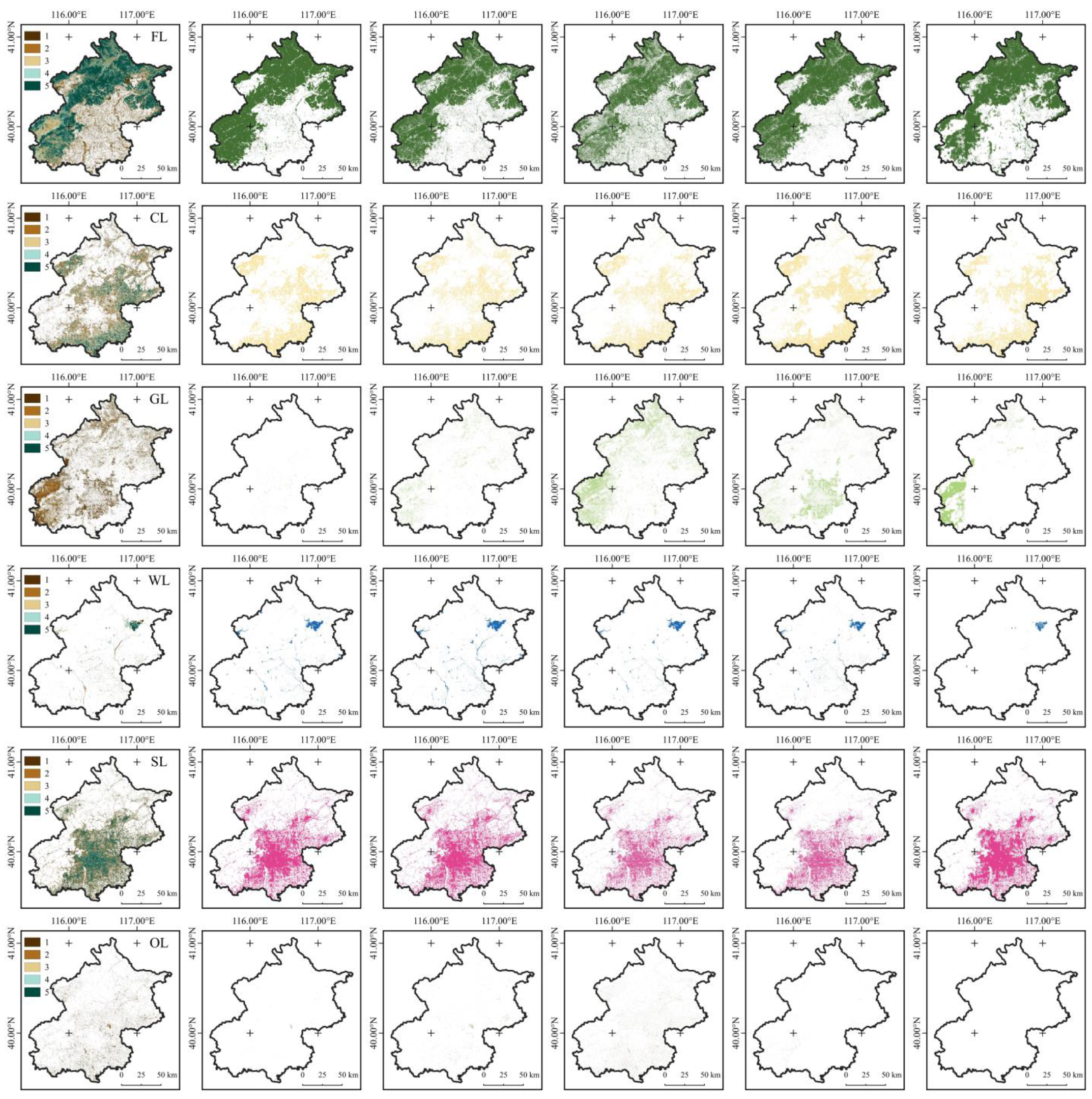
LC products possess both geographical and administrative attributes, allowing them to be divided into multiple levels using administrative boundaries. Therefore, researchers can divide the study area into $L$ layers based on the characteristic. After getting sampling points through SS, an unbiased estimate of the variance $V\left(y_{ss}\right)$ of all samples can be calculated by using Equation (9).

$$\left(y_{ss}\right)=\sum _{l=1}^L{W}_l^2·V\left(y_l\right)=\sum _{l=1}^L{W}_l^2·\frac{1-f_l}{m_l}{S}_l^2=\sum _{l=1}^L\frac{W_l^2{S}_l^2}{m_l}-\sum _{l=1}^L\frac{W_l{S}_l^2}{M_{ss}}$$

(9)

where $y_{ss}$ represents all samples, and $M_{ss}$ is the total population size. $W_l=\frac{M_l}{M_{ss}}$ and $f_l=\frac{m_l}{M_l}$ are the weight parameter and the sampling ratio of layer $l (l=1,2,\dots ,L)$, respectively. $m_l$ and $M_l$ denote the number of samples and pixels in layer $l$, respectively; $y_l$ is the sample mean of layer $l$; and the population variance of layer $l$ can be written as $S_l^2$.

To minimize the objective function $V\left(y_{ss}\right)$, it is essential to choose an appropriate sample size and allocation method. This study adopted the Neyman optimal allocation method, which maximizes sampling accuracy by achieving a proportional distribution between $m_l$ and $W_l{S}_l$. $V_{min}\left(y_{ss}\right)$ can be computed by Equation (10), where $m_{ss}$ is used to indicate the total number of samples.

$$V_{min}\left(y_{ss}\right)=\frac{1}{m_{ss}}{\left(\sum _{l=1}^L{W}_l{S}_l\right)}^2-\frac{1}{M_{ss}}\sum _{l=1}^L{W}_l{S}_l^2$$

(10)

The production method is based on SS theory and considers factors such as economic cost and sample quality, which involves scientifically selecting sample points to ensure that the accuracy meets research requirements. However, it is important to emphasize that the sample points selected through SS only reflect the spatial position information of the pixels and do not effectively reveal the global features formed by the pixels’ interactions.

4. Results

This section is divided into two parts: the computation results of the Wasserstein similarity and the validation results obtained through the validation dataset within the study area. Ultimately, the section computes the confusion matrix to obtain the validation accuracy of each product and compares the results with the WenSiM and official validation accuracy.

4.1. Wasserstein Similarity Results

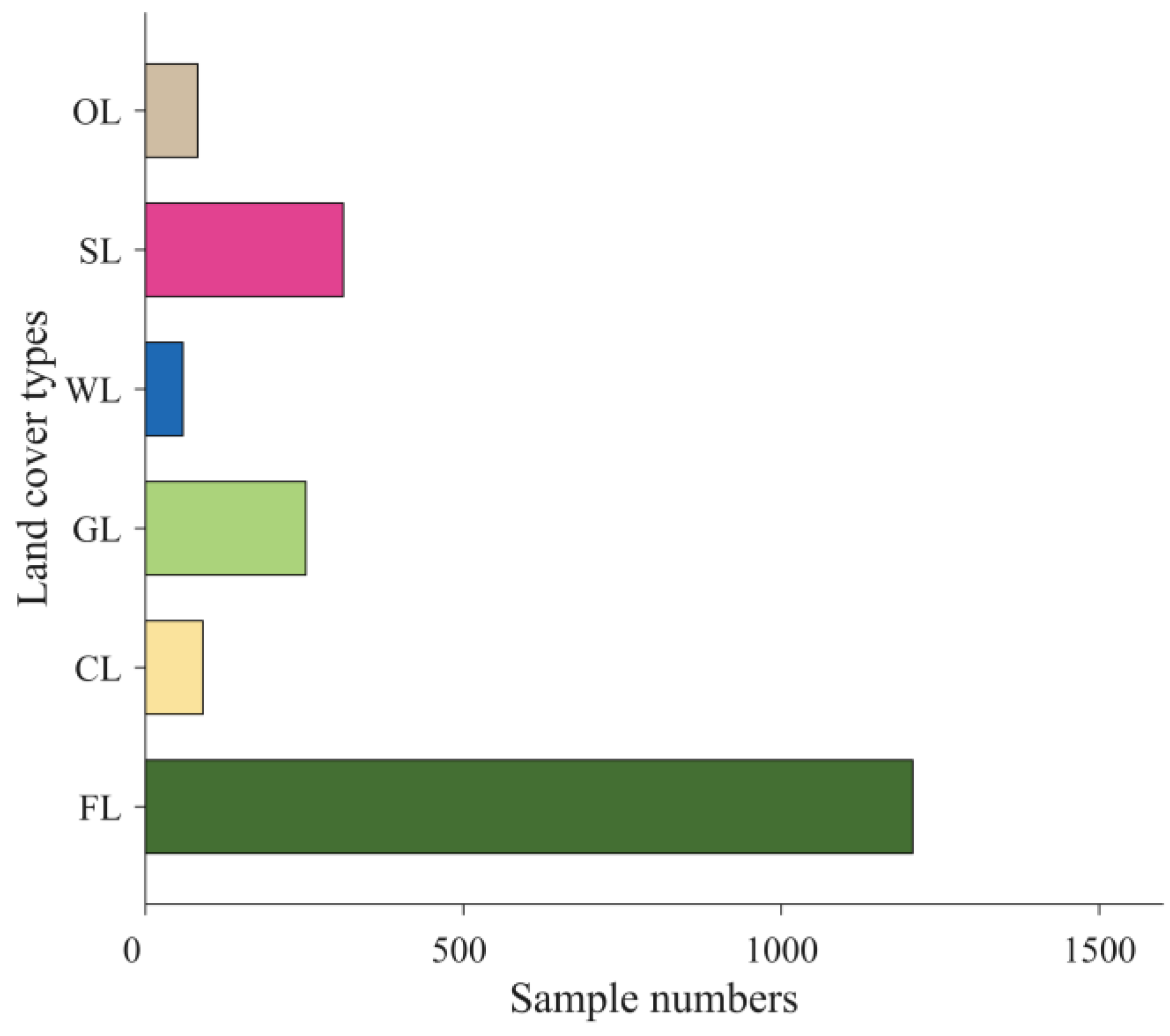
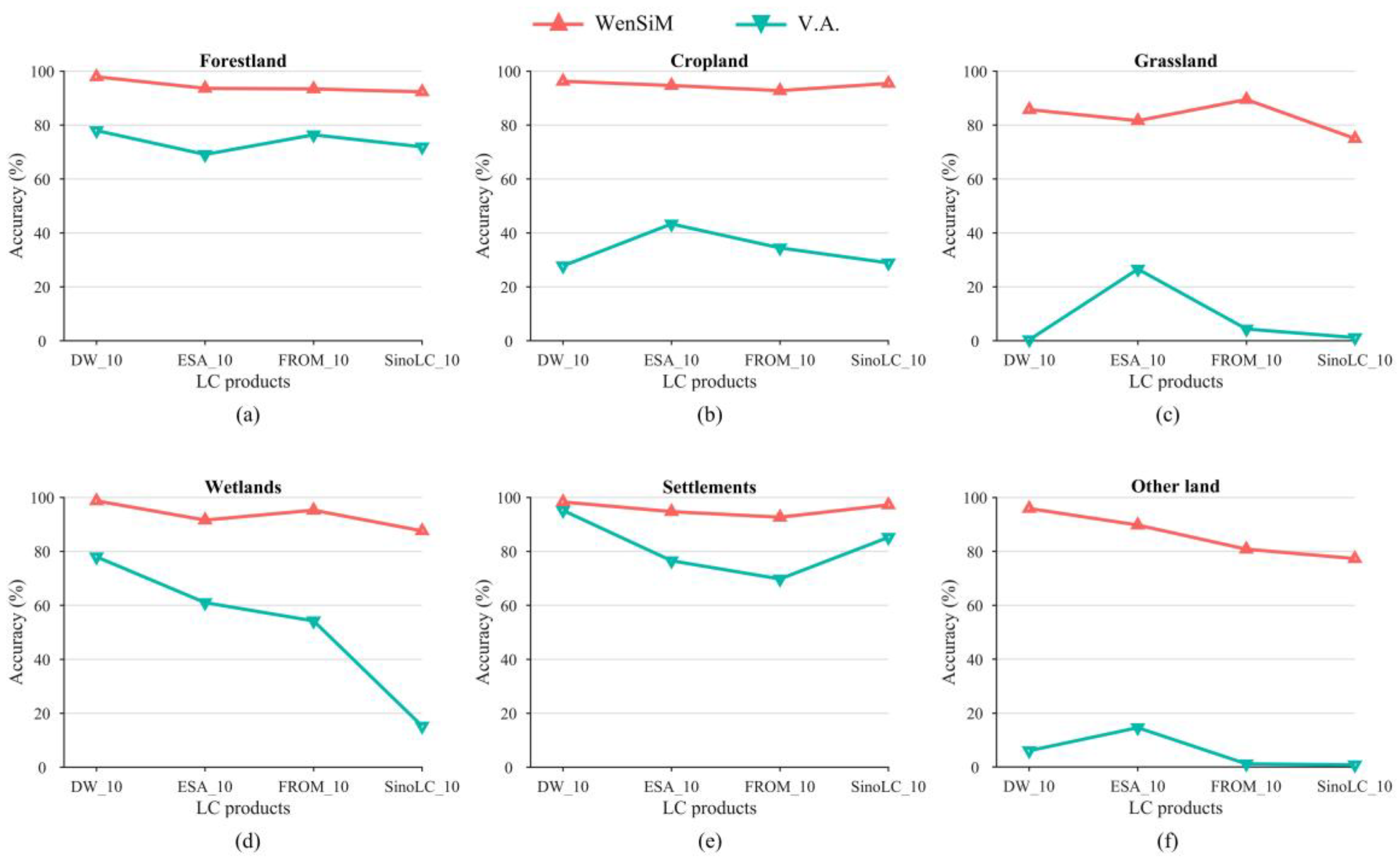
On completing data preprocessing, the product’s classification scheme was modified to the IPCC format, categorizing the types into forestland, cropland, grassland, wetlands, settlements, and other land. Since the absolute ground truth did not exist, the paper selected ESRI_GLC10, with the highest overall official validation accuracy from Table 1, as the reference truth. Accuracy assessment of DW_GLC10, ESA_GLC10, FROM_GLC10, and SinoLC_10 was performed by computing the WenSiM between the remaining products and the reference truth. The results for global feature similarity and correlation coefficients are shown in

Table 2. The global feature similarity between four LC products and ESRI_GLC10 in Beijing.

Types	DW_GLC10	ESA_GLC10	FROM_GLC10	SinoLC_10
FL (%)	98.05	97.57	97.17	93.00
CL (%)	96.37	98.66	96.51	96.15
GL (%)	85.86	85.06	93.09	75.55
WL (%)	98.86	95.45	99.10	88.26
SL (%)	98.45	98.72	96.40	97.95
OL (%)	96.02	93.52	84.06	77.89

Note: FL = forestland; CL = cropland; GL = grassland; WL = wetlands; SL = settlements; OL = other land. The bold results represent the maximum values of all products.

and

Table 3. The correlation coefficient between four LC products and ESRI_GLC10 in Beijing.

	DW_GLC10	ESA_GLC10	FROM_GLC10	SinoLC_10
ESRI_GLC10	0.9985	0.9596	0.9611	0.9925

The bold results represent the maximum values.

, respectively.

What stands out in the tables is that DW_GLC10 exhibited the strongest correlation with the reference truth, with the highest global feature similarity in forestland and other land of 98.05% and 96.02%, respectively. It also can be seen from the data in Table 2 that ESA_GLC10 had the most similar global features with the reference truth in cropland and settlements, with a value of 98.66%, and in wetlands, at 98.72%. The max similarity results for grassland of 93.09% and wetlands of 99.10% were from FROM_GLC10.

Table 4. The WenSiM results between four LC products and ESRI_GLC10 in Beijing.

Types	DW_GLC10	ESA_GLC10	FROM_GLC10	SinoLC_10
FL (%)	97.90	93.63	93.40	92.31
CL (%)	96.23	94.68	92.76	95.43
GL (%)	85.73	81.63	89.47	74.99
WL (%)	98.71	91.60	95.25	87.60
SL (%)	98.30	94.73	92.65	97.22
OL (%)	95.88	89.74	80.80	77.31
OS (%)	95.46	91.00	90.72	87.48

Note: FL = forestland; CL = cropland; GL = grassland; WL = wetlands; SL = settlements; OL = other land; OS = overall WenSiM. The bold results represent the maximum values of all products.

displays the WenSiM results obtained from the preliminary analysis of global feature similarity and correlation coefficients. Following the results, researchers can evaluate the product accuracy at different levels, such as for each land cover type or the overall product, to meet the various requirements. From the data in Table 4, it is apparent that FROM_GLC10 exhibited the highest WenSiM to the reference ground truth in grassland, with a value of 89.47%. The single most striking observation to emerge from the results is that DW_GLC10 was the most similar to ESA_GLC10 in all aspects except grassland. In summary, for the overall WenSiM results in Table 4, the products can be ranked in order of the overall WenSiM results as follows: DW_GLC10 > ESA_GLC10 > FROM_GLC10 > SinoLC_10.

4.2. Validation Results

Following the SS theory outlined in Section 3.3, the study initially divided Beijing into 16 layers, corresponding to each administrative district. Subsequently, a total of 2001 samples were randomly selected within the study area.

Table A3. Stratified sampling calculation parameters.

District	${\mathit{M}}_{\mathit{l}}$	${\overline{\mathit{y}}}_{\mathit{l}}$	${\mathit{S}}_{\mathit{l}}^2$	${\mathit{W}}_{\mathit{l}}$	${\mathit{W}}_{\mathit{l}}{\mathit{S}}_{\mathit{l}}$	${\mathit{m}}_{\mathit{l}}$
Changping	23,067,539	2.408	1.323	0.082	0.09430	197
Chaoyang	7,925,627	4.401	0.363	0.028	0.01697	35
Daxing	17,461,322	3.221	0.720	0.062	0.05264	110
Dongcheng	713,476	4.879	0.092	0.003	0.00077	2
Fangshan	33,808,138	2.095	1.284	0.120	0.13612	285
Fengtai	5,195,318	4.264	0.478	0.018	0.01276	27
Haidian	7,322,717	3.972	0.679	0.026	0.02145	45
Huairou	36,841,342	1.417	0.896	0.131	0.12396	259
Mentougou	24,734,083	1.269	0.764	0.088	0.07681	161
Miyun	38,531,881	1.742	1.065	0.137	0.14133	295
Pinggu	16,263,416	1.998	1.140	0.058	0.06171	129
Shijingshan	1,436,001	3.957cc	0.763	0.005	0.00446	9
Shunyi	17,292,399	3.288	0.758	0.061	0.05349	112
Tongzhou	15,341,172	3.359	0.695	0.055	0.04544	95
Xicheng	856,827	4.965	0.012	0.003	0.00034	1
Yanqing	34,618,782	1.576	0.861	0.123	0.11415	239

Notes: $M_l$ = the number of pixels in layer $l$; ${\overline{y}}_l$ = the sample mean of layer $l$; $S_l^2$ = the population variance of layer $l$; $W_l$ = the weight parameter of layer $l$; $m_l$ = the number of samples of layer $l.$

shows the sampling results and computational parameters for each district.

Table A4. Sample numbers for each land cover type in each layer.

District	FL	CL	GL	WL	SL	OL
Changping	125	5	20	3	37	7
Chaoyang	6	1	3	2	22	1
Daxing	38	5	30	0	36	1
Dongcheng	0	0	0	0	2	0
Fangshan	185	4	33	3	54	6
Fengtai	5	2	0	0	17	3
Haidian	15	3	1	1	22	3
Huairou	210	12	15	1	14	7
Mentougou	139	10	4	0	2	6
Miyun	186	17	27	24	20	21
Pinggu	73	1	33	9	11	2
Shijingshan	5	0	0	1	3	0
Shunyi	28	6	35	6	32	5
Tongzhou	28	7	24	5	27	4
Xicheng	0	0	0	0	1	0
Yanqing	164	17	27	4	11	16
Total	1207	90	252	59	311	82

Notes: FL = forestland; CL = cropland; GL = grassland; WL = wetlands; SL = settlements; OL = other land.

displays the sample numbers for each land cover type in each layer. Figure 3 illustrates the visual distribution of districts in Beijing, as well as the distribution of sample points in Changping and Chaoyang districts.

In the follow-up phase of the study, multiple experts were invited to determine the land cover types of the sample points based on Google Earth and Sentinel-2 high-resolution remote sensing images. For samples with disputed categorizations, experts engaged in collective discussions and voting to assign the type with the highest number of votes, ensuring that the accuracy of the validation dataset met the task requirements. Figure 4 below illustrates the number of samples for each land cover type in the validation dataset.

After the validation dataset was created, the confusion matrices were computed and the quantitative metrics for evaluating the product performance were provided, including user accuracy (U.A.), producer accuracy (P.A.), overall accuracy (O.A.), and the kappa coefficient. The results of the confusion matrices for each product can be found in

Table A5. Confusion matrix for ESRI_GLC10 according to the validation dataset.

Classification	FL	CL	GL	WL	SL	OL	Total	P.A. (%)
FL	983	127	0	2	94	1	1207	81.44
CL	51	25	0	1	13	0	90	27.78
GL	25	157	15	0	47	8	252	5.95
WL	7	4	1	42	5	0	59	71.19
SL	5	13	0	0	291	2	311	93.57
OL	35	14	0	4	27	2	82	2.44
Total	1106	340	16	49	477	13	2001
U.A. (%)	88.88	7.35	93.75	85.71	61.01	15.38
O.A. (%)	67.87
Kappa	0.4816

Note: FL = forestland; CL = cropland; GL = grassland; WL = wetlands; SL = settlements; OL = other land.

,

Table A6. Confusion matrix for DW_GLC10 according to the validation dataset.

Classification	FL	CL	GL	WL	SL	OL	Total	P.A. (%)
FL	941	131	42	2	89	2	1207	77.96
CL	40	25	5	1	16	3	90	27.78
GL	19	170	1	3	55	4	252	0.40
WL	3	3	0	46	6	1	59	77.97
SL	5	5	0	0	296	5	311	95.18
OL	29	11	0	4	33	5	82	6.10
Total	1037	345	48	56	495	20	2001
U.A. (%)	90.74	7.25	2.08	82.14	59.80	25.00
O.A. (%)	65.67
Kappa	0.4610

Note: FL = forestland; CL = cropland; GL = grassland; WL = wetlands; SL = settlements; OL = other land.

,

Table A7. Confusion matrix for ESA_GLC10 according to the validation dataset.

Classification	FL	CL	GL	WL	SL	OL	Total	P.A. (%)
FL	834	112	222	0	18	21	1207	69.10
CL	20	39	20	0	5	6	90	43.33
GL	52	107	67	1	9	16	252	26.59
WL	5	6	3	36	0	9	59	61.02
SL	30	20	1	0	238	22	311	76.53
OL	19	15	13	3	20	12	82	14.63
Total	960	299	326	40	290	86	2001
U.A. (%)	86.88	13.04	20.55	90.00	82.07	13.95
O.A. (%)	61.27
Kappa	0.4118

Note: FL = forestland; CL = cropland; GL = grassland; WL = wetlands; SL = settlements; OL = other land.

,

Table A8. Confusion matrix for FROM_GLC10 according to the validation dataset.

Classification	FL	CL	GL	WL	SL	OL	Total	P.A. (%)
FL	922	176	77	1	25	6	1207	76.39
CL	41	31	9	0	9	0	90	34.44
GL	34	182	11	1	24	0	252	4.36
WL	3	15	5	32	4	0	59	54.24
SL	10	55	25	0	217	4	311	69.77
OL	27	25	8	2	19	1	82	1.22
Total	1037	484	135	36	298	11	2001
U.A. (%)	88.91	6.40	8.15	88.89	72.82	9.09
O.A. (%)	60.67
Kappa	0.3894

Note: FL = forestland; CL = cropland; GL = grassland; WL = wetlands; SL = settlements; OL = other land.

and

Table A9. Confusion matrix for SinoLC_10 according to the validation dataset.

Classification	FL	CL	GL	WL	SL	OL	Total	P.A. (%)
FL	868	130	123	3	83	0	1207	71.91
CL	47	26	6	0	11	0	90	28.89
GL	45	154	3	1	49	0	252	1.19
WL	30	13	0	9	7	0	59	15.25
SL	16	28	2	0	265	0	311	85.21
OL	32	19	3	0	28	0	82	0
Total	1038	370	137	13	443	0	2001
U.A. (%)	83.62	7.03	2.19	69.23	59.82	0
O.A. (%)	58.52
Kappa	0.3474

Note: FL = forestland; CL = cropland; GL = grassland; WL = wetlands; SL = settlements; OL = other land.

. For clarity, this paper refers to the accuracy computed from the validation dataset as the validation accuracy (V.A.), whereas the accuracy reported by the production agencies is referred to as the official validation accuracy (O.V.A.).

Table 5. The V.A. and O.V.A. of four LC products in Beijing.

Accuracy (%)	DW_GLC10	ESA_GLC10	FROM_GLC10	SinoLC_10
V.A. (FL)	77.96	69.09	76.39	71.91
V.A. (CL)	27.78	43.33	34.44	28.89
V.A. (GL)	0.40	26.59	4.37	1.19
V.A. (WL)	77.97	61.01	54.23	15.25
V.A. (SL)	95.18	76.53	69.77	85.21
V.A. (OL)	6.10	14.63	1.22	0.85
V.A. (O.A.)	65.67	61.23	60.67	58.52
O.V.A. (O.A.)	77.80	75.00	72.76	55.55

Note: V.A. = validation accuracy; FL = forestland; CL = cropland; GL = grassland; WL = wetlands; SL = settlements; OL = other land; O.A. = overall accuracy; V.O.A. = official validation accuracy. The bold results represent the maximum values of all products.

displays the V.A. and O.V.A. for every product in the study area.

The most surprising aspect of Table 5 is that DW_GLC10 and ESA_GLC10 achieved the highest validation accuracy across all land cover types. As shown in the table, the peak validation accuracy for forestland of 77.96%, wetlands of 77.97%, and settlements of 95.18% came from DW_GLC10. ESA_GLC10 had the highest validation accuracy for cropland of 43.33%, grassland of 26.59%, and other land of 14.63%. Additionally, DW_GLC10 had the maximum overall V.A. of 65.67% and O.V.A. of 77.80%. To further demonstrate the superiority of the WenSiM metric, Figure 5 and Figure 6 present a comparison of the WenSiM, V.A., and O.V.A. results.

Looking at the figures, it is apparent that the WenSiM consistently had higher values compared to the V.A. and O.V.A. Figure 5 shows that the WenSiM exhibited similar trends to the V.A. for forestland, wetlands, and settlements, whereas it differed significantly for cropland, grassland, and other land categories. What is interesting about the trend in Figure 6 is that the overall WenSiM, V.A. and O.V.A. displayed the same accuracy assessment results: DW_GLC10 > ESA_GLC10 > FROM_GLC10 > SinoLC_10.

5. Discussion

This section initially delves into latent information within the results of the WenSiM and validation. Through a comparison with mainstream methods, the section further analyzes the strengths and weaknesses of the relative accuracy assessment method based on optimal transport theory. Finally, the section provides a reasonable accuracy assessment and ranking of LC products within the study area.

5.1. Analysis and Comparison of Assessment Results

Due to the fact that both the relative accuracy assessment method and the direct assessment method require the reference ground truth for accuracy evaluation, it is imperative to engage in a discussion about the scientific basis for the selection standards. Firstly, a number of recent studies have already demonstrated the rationality of using a validation dataset as the reference ground truth [41,42,43]. Although the V.A. and O.V.A. do not fully exploit all accuracy information, they are still considered the primary indicators for effectively assessing LC product accuracy [44]. Therefore, it is scientific to choose O.V.A. as the standard for selecting the reference ground truth. Moreover, the results of the V.A. and O.V.A. can also serve as important references for evaluating the WenSiM index.

As shown in Figure 5, nearly all quantitative results of the validation accuracy were lower than those of the WenSiM, which is because the WenSiM results encompass more accuracy information about the products. Figure 6 demonstrates that the overall WenSiM, V.A., and O.V.A. results had consistent trends, further confirming the effectiveness of the WenSiM index. The reason for the low V.A. of grassland and other land was attributed to the limitations of direct evaluation method.

The 10 m resolution LC product had hundreds of millions of pixels in Beijing. Considering cost constraints, it was not feasible to validate the true land cover type for each pixel. Despite the fact that the sample proportion chosen in this study surpassed that of other validation datasets, it remained insufficient for a region of this magnitude. The situation had the potential to create imbalanced sampling data ratios among different classes, ultimately leading to an unreasonable accuracy assessment [45].

On the one hand, when there is an imbalance in land cover composition within a study area, the direct evaluation method, with random sampling, will inevitably result in insufficient or even zero samples for certain land cover categories. This phenomenon may lead to unstable validation accuracy for those land cover types. On the other hand, the direct evaluation method only considers the spatial position information of sample points to quantify product accuracy, which can unavoidably yield lower results.

The indirect evaluation method achieves cost-effective utilization of spatial position information for all pixels by comparing the consistency between products [46]. The study categorized spatial consistency into five levels from high to low. Taking forestland as an example, level 5 indicates that the classification results of all LC products at that pixel were forest land, whereas level 1 means that only one LC product classified the pixel as forestland. Figure 7 and Figure 8 present the regional consistency analysis results and the spatial consistency analysis results, respectively, for the five LC products.

Looking at Figure 7, it is apparent that there was a significant difference for each product in grassland and other land, whereas the differences are relatively small in the forestland and wetlands. Interestingly, a noticeable grouping effect was observed in the regional consistency in cropland and settlements. Except for FROM_GLC10, the products exhibited stronger consistency in cropland. The consistency results of settlements in ESRI_GLC10, ESA_GLC10, and SinoLC_10 were similar, whereas DW_GLC10 was more consistent with FROM_GLC10.

Figure 8 shows that the spatial consistency analysis not only revealed the distribution of land cover types in the study area but also indirectly assessed the classification accuracy of the products. For instance, the analysis results indicate that forestland was mainly distributed in the northern and southwestern parts of Beijing. Through visual interpretation, SinoLC_10 exhibited the highest spatial consistency in forestland, which suggests that SinoLC_10 had a higher classification accuracy in forestland.

The indirect evaluation method can effectively mitigate issues arising from low samples, preventing insufficient utilization of spatial location information in products. However, the method lacks on-site validation and the ability to quantify product accuracy, providing only qualitative suggestions for product selection [47].

5.2. Advantages and Limitations of Wasserstein Similarity

Land cover types often exhibit anomalous morphologies, manifesting as anomalous pixels. Anomalous pixels carry accuracy information that is markedly different from other pixels of the same type, representing unique features. The causes of anomalous pixels can be attributed to three main factors.

• The random distribution of the actual class;
• Errors introduced during development;
• Misclassification resulting from insufficient accuracy in the classification algorithms.

Therefore, anomalous pixels primarily reflect the commonalities and differences between products. The direct evaluation method, due to the randomness of sampling, cannot effectively utilize the accuracy information of anomalous pixels. Although the indirect evaluation method considers the spatial position information of anomalous pixels, it falls short in quantifying the accuracy information. This paper provides the first method to take into account various types of accuracy information, with a specific emphasis on anomalous pixels, to quantify product accuracy globally.

The advantages of Wasserstein similarity are primarily evident in two application scenarios. Firstly, when the absolute ground truth is available, serving as a reference for LC products, the method reasonably evaluates the products by thoroughly exploring their accuracy information. This results in more comprehensive findings compared to other approaches. Secondly, when the absolute ground truth is unattainable, WenSiM enables a cost-effective evaluation of new LC products. Unlike direct evaluation methods, the method selects the product with the highest overall accuracy as the reference truth for computing WenSiM, eliminating the need for a validation dataset. In contrast to indirect evaluation methods, it allows for a quantitative assessment of product accuracy and provides a clear ranking of accuracy for each product at different levels.

However, the method also has some limitations. Firstly, the presence of anomalous pixels can make the evaluation results overly stringent. Secondly, when performing assessments on an extensive scale, such as at the global or super-regional level, the large number of pixels can lead to slower computation speeds. Furthermore, in the absence of the absolute ground truth, the evaluation results are influenced by the choice of reference truth. If the criteria are chosen arbitrarily, the reliability of the results may significantly decrease. Therefore, the criteria for selecting the reference truth should be flexibly determined in applications. In the future, the method could be expanded for the accuracy assessment of a broader range of remote sensing products, such as land surface temperature and digital elevation models, thereby aiding researchers in rapidly selecting the most suitable products based on task requirements [48,49].

After elucidating the characteristics of the accuracy evaluation method based on optimal transportation theory, the final evaluation ranking was obtained by combining the WenSiM with the validation results: DW_GLC10 > ESA_GLC10 > FROM_GLC10 > SinoLC_10.

6. Conclusions

The paper set out to find a relative accuracy assessment method based on optimal transport theory for LC products and demonstrates its effectiveness through a research case. Three key conclusions are drawn from the paper. First, the method enables a rapid quantification of LC product accuracy without the need for registration and validation datasets. Second, the WenSiM index derived from the method measures the similarity between the target product and the reference truth at a global scale, utilizing a broader range of accuracy information and resulting in more accurate assessment. Third, this study evaluated the accuracy of four LC products in Beijing, with results closely aligning with validation outcomes. Although the method is limited by the small number of cases, it possesses universality and can be extended to the accuracy assessment of various remote sensing products in global regions. This would be a fruitful area for further work, with the goal of providing researchers with a fast and reliable accuracy assessment tool for the selection and production of remote sensing products.