Abstract
The estimation of the target number and individual tracks are two major tasks in multi-target tracking. The main shortcoming of traditional tracking methods is the cumbersome data association between measurements and targets. The cardinalized probability hypothesis density filter (CPHD) proposed in recent years can achieve the requirement for multitarget tracking. This kind of filter jointly estimates the cardinality distribution and the posterior density, which can achieve a more stable estimate of the target number. However, targets with complex micro-Doppler signatures (drones, birds, etc.) may generate target-dependent false alarms, which is contrary to the traditional uniform distribution assumption. In this case, the estimates of traditional CPHD filter will suffer from the abnormal transfer of PHD mass, causing the degradation of filtering performance. This paper studies the individual tracking of group targets with an improved GM-CPHD filter. First, the target-dependent false alarms are modeled with a general independent and identically distributed (I.I.D.) cluster process. Second, the update equations of cardinality and PHD density in target-dependent false alarms are derived. Finally, a practical solution using the Gaussian mixture method is proposed. The effectiveness of the proposed filter is verified by the simulation and experimental results.
1. Introduction
Bird flocks and drone swarms are typical group targets at low altitude. They are usually composed of a large number of coordinated individuals. Group targets with swarm intelligence is a hot research topic for radar target tracking. Their activities may pose severe threats to the security of artificial equipment [1]. For example, intrusive birds or drones in airports can lead to serious strike damage to the airplane [2]. Therefore, the effective observation of group targets is of great importance to the security of man-made facilities.
Radar is one major type of equipment for observing group targets at low altitudes. Significant progress has been made in the past several decades. For example, radar can be used to measure the features of bird formations, detecting the birds near the airport at night [3], and monitoring the birds’ flight activities during migration seasons near wind farms [4].
For extended target tracking, the goal is to estimate the kinematic state and the shape parameters simultaneously [5]. For multiple target tracking, the goal is to estimate the target number and output the individual tracks. These two parameters are key to the evaluation of the target’s intention and threat assessment. The main idea of traditional multitarget tracking is to decompose it into independent single-target tracking procedures. The major issue is the association between measurements and tracking in clutters. For example, ref. [6] proposes an efficient joint probabilistic association filter (JPDAF) that can deal with several hundred targets; ref. [7] proposes a new adaptive framework for multiple extended target tracking in the presence of data association uncertainty and heavy clutter. The number of targets is usually assumed as known and constant. Otherwise, the tracking filter must update the multiple states jointly in high dimensional space.
Approximation approach is essential for computing the posterior Bayesian density. For example, ref. [8] proposed a novel probabilistic multi-hypothesis tracking (PMHT) method to deal with multiple extended targets. In [9], an expectation maximization belief propagation (GEMBP) filter is proposed for the cases in which targets are dependent.
Alternative methods avoid explicit associations between measurements and targets. For example, the theoretically optimal random finite sets (RFS) approach can be implemented in the Bayesian filtering framework. The probability hypothesis density (PHD) filter is developed to alleviate the computational intractability in the optimal filter [10,11]. The PHD filter propagates the first-order statistical moment of the posterior multiple target state. It also encapsulates the underlying models of target motions, births, deaths, and false alarms. The major practical solution for the PHD filter is the Gaussian mixture approach [12]. The predicted density is modeled as a Gaussian mixture distribution. The closed-form recursions for the update equations can be derived.
The major assumption of the traditional PHD recursion is the Poisson process model for the states of clutters and multi-targets. The cardinality distribution is approximated from the Poisson distribution. The variance of cardinality distribution may increase when there are missed detections. To solve the problem, Mahler and Vo relaxed the Poisson restriction to a more generalized I.I.D. cluster process [13,14]. The cardinalized PHD (CPHD) filter is derived under this assumption. This kind of filter propagates the PHD density and the cardinality distribution jointly. A huge amount of modified CPHD filters have been proposed in recent years [15,16,17,18]. However, if the observation model cannot match the actual distribution (the false alarms may be target-dependent, etc.), the filtering performance will suffer from the abnormal transfer of PHD mass [19,20,21].
For the PHD filtering in the target-dependent false alarms, current results focus more on the modeling of the false alarm distribution. For example, ref. [22] gives the probability generating functional (PGFL) of likelihood density in target-dependent false alarms without a specific implementation solution. This paper proposes a novel GM-CPHD filter. First, this paper analyses the characteristics of the false alarm distribution of typical drones based on real data. Then we propose to model the false alarms as an I.I.D. cluster process. The PGFL under the I.I.D. cluster process model is derived and the recursion of cardinality and PHD density are presented. Finally, a practical GM-CPHD solution is proposed. The simulation and experimental results prove that the proposed method has a more stable performance than the traditional GM-CPHD filter.
The rest of this article is organized as follows. Section 2 analyzes the characteristics of the target-dependent false alarms caused by micro-motion. The basic observation model is presented. Section 3 derives the update equation of the cardinality distribution and the PHD density in target-dependent false alarms and the GM-CPHD solution is proposed. Section 4 verifies the effectiveness of this paper’s algorithm by using simulation and experimental data. Finally, Section 5 concludes the whole paper.
2. Problem Formulation and Basic Models
Birds and drones with complex micro-Doppler signatures have distributed Doppler spectra. This may lead to the generation of target-dependent false measurements around the targets. Traditional uniform distribution cannot model these kinds of false alarms. Degradation of performance may occur if the tracking filter fails to match the actual distribution of likelihood density.
This study analyzed the features of number and spatial distribution of target-dependent false alarms based on the real data. The basic assumptions and the observation model are proposed. The PGFL of likelihood density is given, which provides theoretical support for the derivation of subsequent CPHD filter update expressions.
2.1. Target-Dependent False Alarms
For a high-resolution radar, the cross section of one individual is usually too small to be detected directly from the range profile. Therefore, radar echoes should be accumulated over a specific period of time, after which the measurements are detected on the range-Doppler plane. The range-Doppler plane exhibits distributed spectra for a target with complex micro-Doppler signatures. This will lead to the detection of false alarms around the target.
In recent years, many research teams have collected and analyzed the real data of birds and drones using various radar devices [23,24,25,26,27]. Micro-Doppler signatures have been studied for target recognition. However, there is little research dedicated to studying the impact of Doppler distribution on target detection and tracking. In this paper, the research team has collected real radar data of different types of drones using a Ka-band monopulse radar. The distributions of state-dependent false alarms are analyzed.
The illustrations of a DJI Matrix 300 drone and the detection results of one frame are shown in Figure 1a and Figure 1b, respectively. The red circles in Figure 1b represent the detection results on the range-Doppler plane using a CFAR detector. The yellow-orange color represents the target’s energy and the blue-green area means the background noise. This drone remained hovering at an altitude of about 200 m during the experiment. The stripe of the distributed spectrum is expanded to the whole sampled Doppler domain and several false alarms are detected on the Doppler spectra. The detection result on the range-Doppler plane and the overall number of measurements of one hundred successive coherent processing intervals (CPIs) are shown in Figure 2. The number of false alarms fluctuates over time.
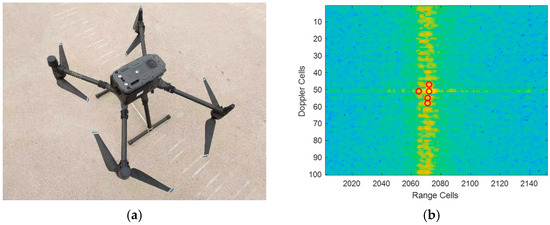
Figure 1.
(a) The DJI Matrix 300 drone. (b) The detection result of one coherent processing interval.
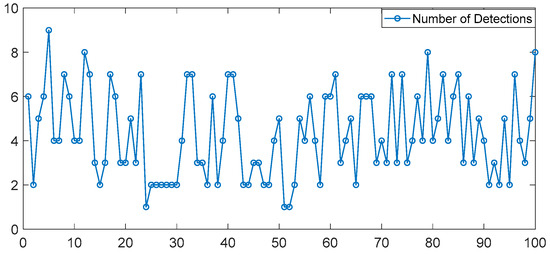
Figure 2.
The overall numbers of measurements of 100 successive CPIs.
We analyzed the dependent relations between different time steps using the autocorrelation function. We use simulation software to generate a pseudo-random sequence of integers, which is uniformly distributed between 1 and 9. The length of the sequence is 100, as shown in Figure 3. The autocorrelation results of the random sequence and the drone’s measurement sequence are calculated. The results are shown in Figure 4, in which the autocorrelation results have been normalized. The autocorrelation result of the drone’s measurement sequence is very close to that of the pseudo-random sequence, and the correlation coefficient between two adjacent time steps is about 0.83. Therefore, it can be assumed that the drone’s measurement sequence and the pseudo-random sequence have similar properties. This is crucial to the modeling of target-dependent false alarms.
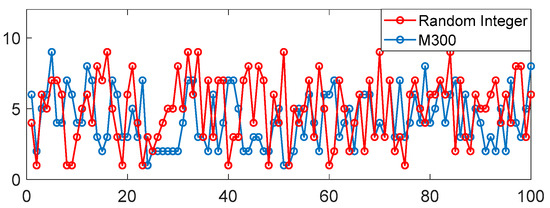
Figure 3.
The numbers of measurements and a random integer sequence.
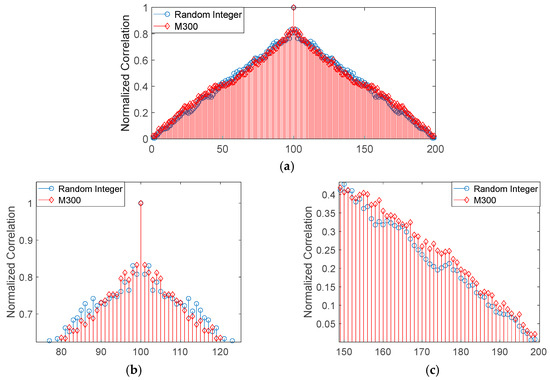
Figure 4.
(a) Autocorrelation results of the drone’s measurement sequence and the pseudo-random sequence. (b) Zoomed-in area of the results. (c) Another zoomed-in area of the results.
The spatial distribution of the measurements of the DJI M300 drone are shown in Figure 5. The true measurements and false measurements are labeled in the figures. The number of detected measurements varies at different time steps, but in general they are distributed around the region where the target is located. Their distribution area shows typical state-dependent features, and they can be described by a cluster process. In this paper we assume that the measurements of one target during observation are modeled by an I.I.D. cluster process.
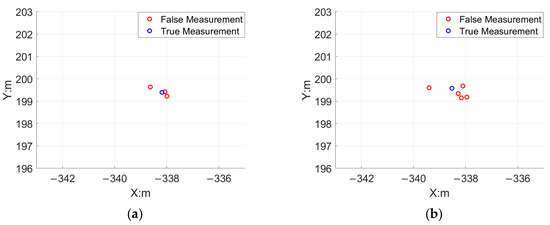
Figure 5.
(a) The spatial distribution of measurements at one time step. (b) The spatial distribution of measurements at another time step.
From these results, it is clear that the micro-Doppler phenomenon of rotating blades can introduce target-dependent false alarms. Traditional uniform models cannot model this kind of false alarm. Based on the analysis of real data collected from several types of drones, the following empirical conclusions can be used as the basic assumptions of this paper:
- The target-dependent false alarms generated from one target can be modeled by an I.I.D. cluster process.
- True measurements and false alarms of the same target are very close to each other in three-dimensional space. It can be assumed that their spatial distributions are identical.
- The number of false alarms between two adjacent time steps are independent.
Therefore, the model of target-dependent false alarms must be considered in order to derive the CPHD update equations.
2.2. Observation Model with Target-Dependent False Alarms
The observation model and the corresponding likelihood expression are one of the key steps in deriving the Bayesian posterior recursion. The traditional PHD and CPHD filters assume that false alarms are uniformly distributed in the observation space. This assumption is inconsistent with the actual distribution of the group targets (bird flocks and drone swarms, etc.). In this subsection, based on the analysis in the previous subsection, the observation model with the target-dependent false alarms is proposed. The probability generating functionals are derived for the subsequent discussion of the novel CPHD filter.
Suppose there are targets in the observation space at time k. Their states are denoted by the random set The following assumptions are consistent at any time k:
- 4.
- Disappearance of existing targets: the disappearance probability of any target at time k + 1 is denoted by . The number of disappeared targets is denoted by .
- 5.
- Appearance of new targets: completely new targets will enter the observation area at time k + 1;
There are targets at time step k + 1 whose number and states are both random. Therefore, is a typical random finite set. The measurement set at time k + 1 is the superposition of multiple sets:
where is the true measurement of the i-th target. If this target is detected with probability , there will be one state vector within ; otherwise, if this target is not detected, . is the superposition of target-dependent false alarms and target-independent clutters:
where is the set of target-dependent false alarms generated from the i-th target. This random finite set can be modeled by an I.I.D. cluster process, whose spatial distribution is dependent on the ground truth of the target. is the set of uniformly distributed clutter. The random vectors within , , and are independent. If there are no targets, then .
To formulate the update equations of the proposed method, we need to introduce the definition of PGFL. Let be the probability distribution of a finite random set , its PGFL is defined as:
where and is any real-valued function. For the intuitive meaning of the PGFL, see [10]. This is crucial for the derivation of posterior densities. For the true measurement set, the PGFL of the likelihood function is derived in [10]:
where being the PGFL of single target likelihood function. The PGFL of the likelihood function of with target-dependent false alarms can be written as [22]:
where . is the likelihood of one target-dependent false alarm. is the expected number of false measurements under the Poisson assumption, where and are the expectation of target-independent and target-dependent false alarms, respectively. Therefore, the PGFL of the complete likelihood function is:
In this paper, we relax the relaxed the first-order assumption on the number of targets and replace the Poisson false alarm processes by the I.I.D. cluster processes. Before the derivation of the likelihood function, we will introduce the definition of the I.I.D. cluster process. For a random nonnegative integer , its probability distribution is . The probability generating function (PGF) of (defined on ) is:
The PGF gets the name from the fact that
where denotes the n-th derivative of [13]. Then, an I.I.D. cluster process is one that has a PGFL of the form:
where is the PGF of an arbitrary probability distribution and is the PGFL of a single probability density . Under the I.I.D. cluster process assumption, the process of target transition and observation are described by the single probability density and target number. Therefore, the PGFL of the likelihood function can be rewritten as:
where and are the probability generating function of the cardinality distribution of target-independent clutter and target-dependent false alarms, respectively. , and are the PGFLs of clutter, true measurement, and target-dependent false alarm, respectively. We will derive the full recursions of cardinality distribution and PHD density in the following Section.
3. The Novel GM-CPHD Filter
3.1. CPHD Filter Predictor
In this subsection we derive the predicted cardinality distribution and PHD density given the set of multitargets’ states . A surviving target may transit to a new state , whose Markov transition density is denoted by . The state transition model is described by the following equation:
The predicted PHD density for existing targets at time k is denoted by:
New targets may appear in the observation area at time k + 1. The predicted PHD for new targets is denoted by . Therefore, the complete predicted PHD density is:
To derive the closed-form formulas for the predicted PGFs, we follow the I.I.D cluster process prior assumption proposed in [13]: the PGF of has the form , where is the PGF of the cardinality distribution of and . Then the predicted PGF of the predicted cardinality distribution is:
where . is the PGF of the cardinality distribution for new targets and is the PGF for the surviving targets. The cardinality distribution corresponding to is:
for all non-negative integers n. This expression is the convolution of the cardinality distributions of the birth and surviving targets.
3.2. CPHD Filter Corrector with Target-Dependent False Alarms
The posterior PHD at time k + 1 is denoted by . To derive the updated equation formula of PHD, we need to first define the two-variable PGFL :
where .Then the denominator of the Bayesian update equation can be expressed as the iterated functional derivatives of ; the numerator can be expressed as iterated functional derivatives of . The first step for deriving the posterior PHD is:
Then the posterior PHD at time k + 1 is derived by:
For more details, see the appendices in [10]. The functional derivatives of an I.I.D. cluster process can be computed according to the chain and liner functional rules:
where , , and are the sensor likelihood function with respect to the background clutter, target-dependent false alarms, and true measurements, respectively. Therefore, we have:
The summation is taken over all the possible partitions of . Let and , the derivative can be simplified as:
where being the elementary symmetric function of order I in , whose definition is . Therefore, , ,. The update equation of can be written as:
According to [13], the PGF of the cardinality distribution has the following property: . Therefore, we can get the PGF of the cardinality distribution with target-dependent false alarms:
where and . After the derivation of the updated cardinality distribution, we compute with respect to variable h. According to the linear functional rule, we have:
The summation is taken over all the possible partitions of This derivation uses the conclusion in [13]: unless or . Now let and , we have:
where . Substitute into , we have:
Here means that the i-th variable is weeded out from the set . According to the conclusion:, this equation can be simplified as:
where and . The additional parts in the update recursion mainly includes , and compared with traditional CPHD filter. According to the assumption in Chapter 2, we can assume that . Therefore, the final result can be further simplified. It can be concluded that the CPHD filter has a higher computational burden than the traditional PHD filter as the recursion equations for the posterior cardinality and density are coupled. In the next subsection, we propose a closed-form solution to the CPHD recursion using the Gaussian mixture approach, as in [28,29].
3.3. Closed-Form Gaussian Mixture Solution
In this paper we follow the traditional assumptions in GM-CPHD filer:
- 1.
- The posterior PHD density at time k and the birth density at time k + 1 are both Gaussian mixture densities:
- 2.
- The transition density and likelihood density for each target are linear-Gaussian;
- 3.
- The probability of surviving and detection are both constants;
- 4.
- Target-independent clutters and target-dependent false alarms are independent cluster processes.
Under these assumptions, the predicted cardinality distribution and PHD density has the following forms:
where being the binomial coefficient . The update equations of cardinality distribution and PHD density can be written as:
where is the inner product of two vectors:. is the elementary symmetric function of order j. is the vector of all the Gaussian components. The expressions of other components are given below.
3.4. Clustering, Pruning and Merging
The proposed novel GM-CPHD filter in this paper needs to consider all the possible partitions of the measurement set. One specific association relationship will be established for one specific partition possibility. This will increase the computation burden significantly. In [15], it has been proved that one reasonable partition can approximate all the possible cases. Therefore, the gating method is often used in PHD filters. In [30], it is also shown that for a measurement set , there exists only one partition case in which any pair of measurements satisfies:
The value of the threshold is set according to the distance between two neighboring targets. The gating method can refer to the approaches proposed in [14,31].
Pruning is necessary for Gaussian mixture approach to reduce the number of Gaussian components. Otherwise, the computation burden would increase rapidly. Components with weak weights will be discarded and only the components whose weights are large enough will be preserved. Besides, if two Gaussian components are spatially close enough, they will be merged into one component. The merging criterion can be described as:
where and being the mean value of the i-th and j-th Gaussian components. is a predetermined covariance matrix and is the threshold. The merged component has a weighted mean value and averaged covariance value.
3.5. Initialization of Gaussian Components
For RFS filters, the initialization step is crucial for the performance of filters. The first step of initialization is the merging of measurements, as a bird or drone may generate multiple measurements. If two measurements are spatially close enough, then they will be merged into one. After the merging process, the number of targets can be set according to the number of merged measurements within the group.
Group targets are usually clusters composed of similar individuals. Therefore, it is suitable to assume that the weights of all the targets are equal. For example, for a drone swarm with ten individuals, the initial weight of each target is . The state of each Gaussian component can be set according to the merging results.
4. Simulation and Experimental Results
In this section, we present one simulation result and one experimental result in three-dimensional space. We first present the details of simulation scenario and the devices employed for experiment. Then we present the results using the method proposed in this paper. Finally, we discuss and analyze the performance and the advantages of our method.
4.1. Simulation Result
4.1.1. Simulation Scenario and Setups
To simulate the collective behavior of a formation target, we resort to a decentralized model proposed in [32]. The research team made several modifications of the decentralized model and it has been successfully implemented in other papers. The applied forces of each individual include a distance-based repulsion , a middle-range velocity alignment , and a global constraint :
is the distance between two individuals. is the equilibrium distance above which there is no repulsion, and is the lower bound to avoid over-excitation. is the upper threshold for the alignment and is the upper bound of global constraint. , and are the spring constant, the constraint coefficient, and the constraint coefficient, respectively.
The velocity evolution of each individual at time i + 1 is:
where is the self-propelling velocity, is the group velocity conditioned on the outer environment, and 𝜏 is the characteristic time needed to reach the velocity .
In this subsection, we simulate a line-formation of ten targets moving in a coordinated turn. The distance between the neighboring targets is 20 m. All the members will keep their rank during the simulation. Important simulation parameters are given in Table 1.

Table 1.
Parameters for coordinated formation simulation.
The simulation trajectories of 10 targets are presented in Figure 6. Different colors indicate different trajectories. For example, the purple line represents the fourth target’s trajectory. The simulation time is about 66 s and the lines of different colors represent different trajectories.
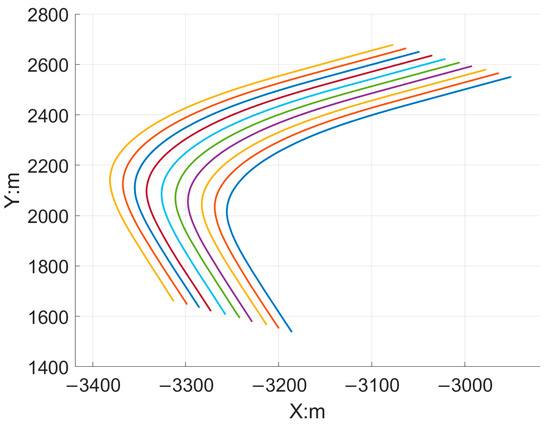
Figure 6.
Illustration of the trajectories of the simulation formation targets.
After the generation of simulation trajectories, we generate the measurements of the radar. First, we assume that the data rate of tracking radar is 5 Hz and the beamwidth is ± 1.2°. The bandwidth of radar is 200 MHz and it can resolve the formation into different individuals.
The non-ideal measurements are generated based on the ideal measurements. First, the Gaussian noise is added to the true measurements. The variance of noise is 1.5 in each dimension. Then the state-dependent false measurements are generated according to the Poisson processes with mean value . Each target-dependent false alarm is Gaussian distributed and whose mean value is the state of its parent target. The covariance matrix is identical to the Gaussian noise added to the ideal measurement. Then the target-independent background clutters are added to the measurement set. The background clutter rate is 5 × 10−6/m3.
The simulated measurements are shown in Figure 7. Each target has multiple measurements at each sampling time step. False alarms will seriously disturb the association step of the traditional tracking filtering, generating a large number of false tracks.
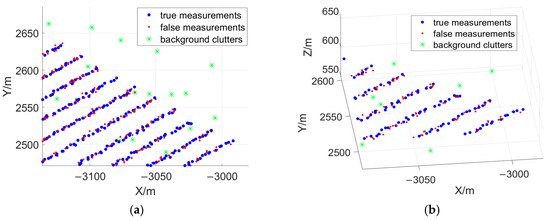
Figure 7.
(a) The illustration of non-ideal measurements observed by the radar. (b) The zoomed-in results of false measurements, true measurements, and background clutters.
4.1.2. Analysis of Performance
The simulated measurements are processed by the novel GM-CPHD filter proposed in this paper and the traditional GM-CPHD filter proposed in [28]. The upper limit of Gaussian components is 100; the probability of survival is 0.95 and the probability of detection for each target is 0.98. The pruning threshold is 10−5 and the merging threshold is 5 m. It can be recognized from Figure 8 that the false measurements reduced significantly after the filtering. The filter proposed in this paper can adopt the coordinate turn, while the traditional CPHD filter loses two targets’ states during tracking.
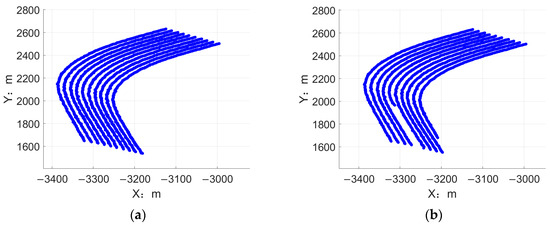
Figure 8.
(a) The filtering results of the proposed method. (b) The filtering results of the traditional GM-CPHD method.
Several criterions have been proposed to evaluate the performance of tracking filters [33,34]. In order to further analyze the performance of the algorithm, we compared the results of the novel method with traditional CPHD filtering methods: (1) the cardinalities after filtering and (2) the OSPA distances after filtering.
Figure 9 represents the cardinality statistics after filtering. The cardinalities of the proposed method’s results are coincident with the ground truth, while the traditional GM-CPHD filter has many fluctuations in the initial 200 time steps. One target is lost from the 210th time step onwards, and a second target is lost from the 280th time step. Only eight targets’ states are outputted at the end of the simulation.
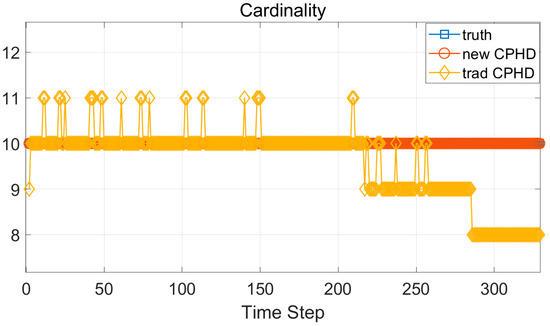
Figure 9.
The cardinality statistics of the two filters.
To evaluate the accuracy of estimated states, the common method is to calculate the OSPA distance defined in [14,33]. There are two sets, and , whose cardinality is m and n, respectively. For m ≤ n, the OSPA distance between and is:
where is the cutoff function, c is the cutoff parameter, and p is the OSPA metric order parameter. In this paper we set p = 1 and c = 100.
The OSPA distances of the two different filters are shown in Figure 10. Due to the error in the cardinality estimation, the OSPA results of traditional GM-CPHD filter has outliers when there are spurious states or missed detections (see Figure 10a). This is consistent with the time steps where the cardinality deviates from the ground truth. From the 210th time step onwards, the OSPA distance never reduces to a lower level because the estimated number of targets is less than the true number.
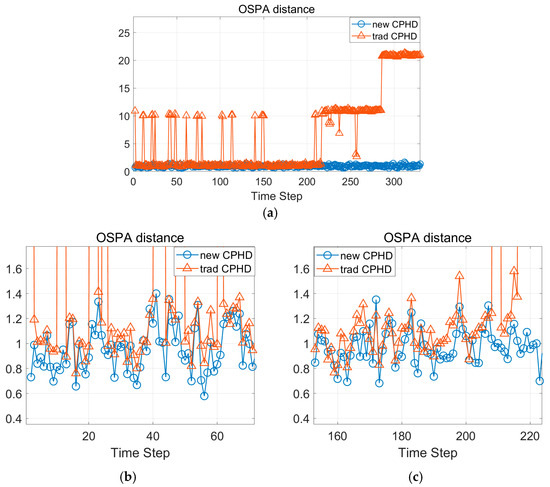
Figure 10.
(a) The OSPA distances of the two filters. (b) Zoomed-in area of the results. (c) Another zoomed-in area of the results.
The zoomed-in results are shown in Figure 10b,c. It show that for most of the time steps, the novel GM-CPHD filter proposed in this paper can achieve higher accuracy than the traditional GM-CPHD filter, which is because the method proposed in this paper takes into account the target-dependent false alarms, and it can achieve a robust filtering of individuals within a group target.
4.2. Experimental Results
In this subsection, we analyze the performance of the proposed GM-CPHD filter through real experimental data. First, we describe the collaborative radar system used to collect real data. Then we present and discuss the results of multitarget filtering. Comparison with traditional filter, this shows the robustness of the proposed method.
4.2.1. Experiment Program and Radar System
The research team carried out the experiment of observing the drone swarm in August 2023. The quadrotors in this experiment are commonly used in drone light shows. Dozens of quadrotors can form different formations under the control of ground stations. The research team designed a coordinated turn of a formation. Ten drones were divided into two groups, each containing five drones, forming a line formation with a spacing of 6 m. The height difference between the two groups is 10 m. The radius of the coordinated turn is 50 m and the turn rate is 0.5 r/min. This process was recorded by the RTK locators carried by the drones. The ground truths of tracks are reconstituted using the RTK records. Figure 11a shows the quadrotors used for the experiment. Figure 11b shows the launching of ten drones, during which different colored light bulbs were illuminated.

Figure 11.
(a) Multiple drones before taking off. (b) Ten drones were taking off from the ground.
The radar system is installed in Dongying, Shandong province, China. This system is designed for observing and studying the behaviors of bird flocks. The main devices of the collaborative radar system include a Ku-band high-resolution phased array radar and a X-band monopulse radar. Both radars obtain high range resolutions by synthesizing multiple stepped chirp pulses. The synthesized bandwidths are 1 GHz and 800 MHz for the phased array radar and monopulse radar, respectively. The synthesized beamwidth of phased array antenna is 0.6° in elevation and 0.5° in azimuth. The beamwidth of X-band monopulse is 1.5°. Therefore, this system has the capability to resolve the different members within a group target.
The procedure of drone swarm observation is as follows. The phased array radar is working in the track-while-scan mode. When the targets fall into the observation space of phased array radar, the detection results will be displayed on the plan position indicator (PPI) installed in the control room. Then the radar operator should judge whether the target is worth observing, after which the operator chooses the target on the PPI and issues the guidance information to the monopulse radar and the photoelectric pod. After the target acquisition procedure in the designated area, the radar beam would aim at the group target according to guidance information. Raw data are collected, and the proposed algorithm will be tested.
The illustrations of devices are given in Figure 12a,b. The detection results of the phased array radar during the experiment are given in Figure 12c, where a yellow dot means filtering results, a yellow solid line means a track, and a blue short line means a new detection. The transmitted power is strong enough to observe a large number of birds and insects at night. The drone formation can be observed by the photoelectric pod, as shown in Figure 12d.

Figure 12.
(a) Illustration of the phased array radar. (b) Illustration of the monopulse radar. (c) Detection results and tracks illustrated on the PPI of phased array radar. (d) Drone formation captured by the photoelectric pod.
4.2.2. Analysis of Performance
The quadrotors used in this experiment have typical micro-Doppler signatures. This leads to the distributed Doppler spectra and target-dependent false alarms. Figure 13 shows the range profile of the drone swarm and the corresponding range-Doppler plane. Ten drones can be recognized from the range-Doppler plane, as shown in Figure 13b, where the yellow-orange color represents the target’s energy and the blue-green area means the background noise. Nevertheless, the farthest target on the edge of the beam was too weak to be detected. A total of eleven measurements were generated for the remaining nine detected targets, including two target-dependent false alarms in the Doppler domain for the fourth drone and the seventh drone. The number of measurements at each time step during the observation (about 17 s) is given in the figure below; it can be seen that the number of measurements is more than 10 for most of the time steps.
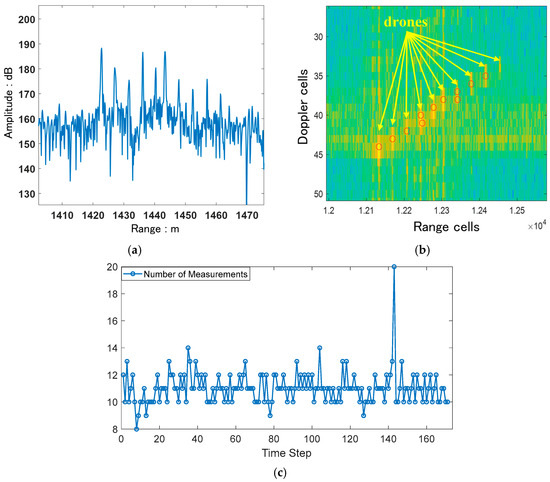
Figure 13.
(a) Range profile of the ten drones. (b) The range-Doppler plane and detection results of ten drones. (c) Number of measurements during tracking.
The measured data exceeds 17 s and contains more than 170 sampling time steps. The maximum number of Gaussian components for CPHD filtering is 100. The probability of target detection is 0.98 and the probability of target survival is 0.95. The pruning threshold for Gaussian weight is 10−3, and the fusion threshold is 3 m. Comparison of the cardinality distribution with traditional CPHD is given in Figure 14. The results of the novel CPHD filter proposed in this paper are coincident with the ground truth most of the time (55% of the time steps). The cardinalities are larger than the truth by 1 for about one third of the time steps (33%), and less than 1% of the time steps are larger than the truth by 2 and above. The traditional CPHD filter can output the true value for 35.3% of the time steps. The result is larger than the truth by 1 for 40.6% of the time steps and is larger than 2 for 12.9% of the time steps. This shows that the algorithm proposed in this paper has a more stable cardinality estimation performance.
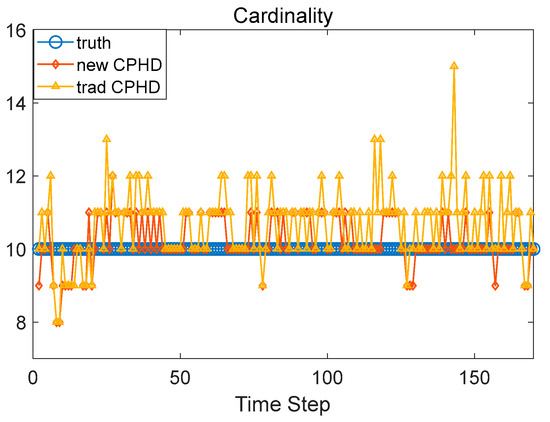
Figure 14.
The cardinality statistics of the two filters.
A comparison of the OSPA distances of the method proposed in this paper with the traditional GM-CPHD is given in Figure 15. Since the cardinality estimation of traditional CPHD filtering is more unstable, there are significant outliers in the OSPA distance of the traditional filtering method, which is due to the inaccurate estimation of the number of targets. In addition, there is a deviation between the RTK localization value recorded by the drone and the localization value calibrated by the monopulse radar, resulting in an error in the OSPA distance that is slightly larger than 10. When the number of targets is estimated correctly, the method proposed in this paper shows a small improvement in filtering accuracy over the traditional method.
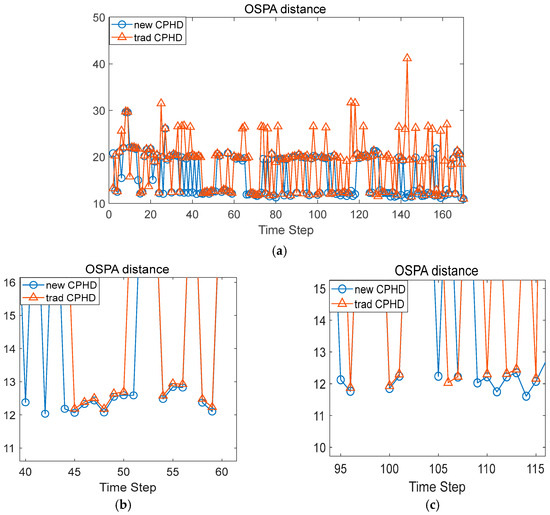
Figure 15.
(a) The OSPA distances of the two filters. (b) Zoomed-in area of the results. (c) Another zoomed-in area of the results.
A simple nearest neighbor association method is used to correlate the filtering results into different trajectories of 10 targets; it can be seen from Figure 16 that the trajectory results obtained by this paper’s method are better than those of the traditional GM-CPHD method, in which different colors represent different tracks after the filtering. It can be seen from Figure 16b that there are short and false tracks using the traditional method.
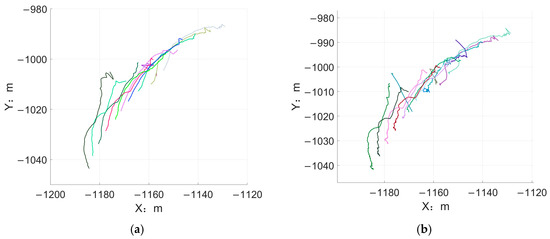
Figure 16.
(a) Trajectories obtained from the proposed method; (b) Trajectories obtained from the traditional method.
5. Conclusions
This paper proposes a novel GM-CPHD filter for group targets. The update recursion of the cardinality distribution and PHD density in state-dependent false alarms is derived and simplified to meet the practical applications. The effectiveness of the proposed method is verified by the simulation and experimental data. The cardinalities and OSPA distances are analyzed compared with the traditional GM-CPHD filter. It can be concluded that the method proposed in this paper can achieve robust tracking of multi-targets and can obtain more stable multi-target estimation performance than the traditional GM-CPHD filters. Future work will focus on tracking multiple maneuvering targets.
Author Contributions
Conceptualization, Q.J., C.H. and R.W.; methodology, Q.J. and R.W.; software, Q.J., L.D. and L. J.; validation, Q.J. and L. D.; experiment, Q.J., L.D. and L.J.; writing—original draft preparation, Q.J. and L.D.; writing—review and editing, R.W., C.H. and Q.J.; funding acquisition, R.W. and C.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded in part by the National Natural Science Foundation of China under Grant 62225104, 62001021, and 62201049, and in part by the National Key R&D Program of China under Grant 2023YFC3341100.
Data Availability Statement
The data supporting the conclusions of this article are not readily available because the data are part of the ongoing studies funded by the projects mentioned above.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Van Doren, B.M.; Horton, K.G. A continental system for forecasting bird migration. Science 2018, 361, 1115–1118. [Google Scholar] [CrossRef] [PubMed]
- Metz, I.C.; Ellerbroek, J.; Mühlhausen, T.; Kügler, D.; Hoekstra, J.M. The bird strike challenge. Aerospace 2020, 7, 26. [Google Scholar] [CrossRef]
- Phillips, A.C.; Majumdar, S.; Washburn, B.E.; Mayer, D.; Swearingin, R.M.; Herricks, E.E.; Guerrant, T.L.; Beckerman, S.F.; Pullins, C.K. Efficacy of avian radar systems for tracking birds on the airfield of a large international airport. Wildl. Soc. Bull. 2018, 42, 467–477. [Google Scholar] [CrossRef]
- Plonczkier, P.; Simms, I.C. Radar monitoring of migrating pink-footed geese: Behavioural responses to offshore wind farm development. J. Appl. Ecol. 2012, 49, 1187–1194. [Google Scholar] [CrossRef]
- Yang, S.; Baum, M. Tracking the Orientation and Axes Lengths of an Elliptical Extended Object. IEEE Trans. Signal Process. 2019, 67, 4720–4729. [Google Scholar] [CrossRef]
- Horridge, P.; Maskell, S. Real-Time Tracking of Hundreds of Targets with Efficient Exact JPDAF Implementation. In Proceedings of the 2006 9th International Conference on Information Fusion, Florence, Italy, 10–13 July 2006; pp. 1–8. [Google Scholar]
- Li, Q.; Gan, R.; Liang, J.; Godsill, S.J. An Adaptive and Scalable Multi-Object Tracker Based on the Non-Homogeneous Poisson Process. IEEE Trans. Signal Process. 2023, 71, 105–120. [Google Scholar] [CrossRef]
- Wieneke, M.; Koch, W. A PMHT approach for extended objects and object groups. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2349–2370. [Google Scholar] [CrossRef]
- Lau, R.A.; Williams, J.L. Tracking a coordinated group using expectation maximization. In Proceedings of the 2013 IEEE Eighth International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Melbourne, Australia, 2–5 April 2013. [Google Scholar]
- Mahler, R. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Mahler, R. Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007. [Google Scholar]
- Vo, B.N.; Ma, W.K. The Gaussian Mixture Probability Hypothesis Density Filter. IEEE Trans. Signal Process. 2006, 54, 4091–4104. [Google Scholar] [CrossRef]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N.; Cantoni, A. Analytic Implementations of the Cardinalized Probability Hypothesis Density Filter. IEEE Trans. Signal Process. 2007, 55, 3553–3567. [Google Scholar] [CrossRef]
- Lundquist, C.; Granström, K.; Orguner, U. An Extended Target CPHD Filter and a Gamma Gaussian Inverse Wishart Implementation. IEEE J. Sel. Top. Signal Process. 2013, 7, 472–483. [Google Scholar] [CrossRef]
- Beard, M.; Vo, B.T.; Vo, B.N.; Arulampalam, S. A Partially Uniform Target Birth Model for Gaussian Mixture PHD/CPHD Filtering. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2835–2844. [Google Scholar] [CrossRef]
- Melo, F.E.D.; Maskell, S. A CPHD Approximation Based on a Discrete-Gamma Cardinality Model. IEEE Trans. Signal Process. 2019, 67, 336–350. [Google Scholar] [CrossRef]
- García-Fernández, Á.F.; Svensson, L. Trajectory PHD and CPHD Filters. IEEE Trans. Signal Process. 2019, 67, 5702–5714. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.N. The para-normal Bayes multi-target filter and the spooky effect. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 173–180. [Google Scholar]
- Franken, D.; Schmidt, M.; Ulmke, M. “Spooky Action at a Distance” in the Cardinalized Probability Hypothesis Density Filter. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1657–1664. [Google Scholar] [CrossRef]
- Ouyang, C.; Ji, H.B.; Tian, Y. Improved Gaussian Mixture CPHD Tracker for Multitarget Tracking. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1177–1191. [Google Scholar] [CrossRef]
- Mahler, R.; El-Fallah, A. PHD filtering in known target-dependent clutter. In Proceedings of the Signal Processing Sensor Fusion, and Target Recognition XIX, Orlando, FL, USA, 27 April 2010; pp. 203–214. [Google Scholar]
- Palamà, R.; Fioranelli, F.; Ritchie, M.; Inggs, M.R.; Lewis, S.; Griffiths, H. Measurements of Multistatic X&L Band Radar Signatures of UAVS. In Proceedings of the 2019 International Radar Conference (RADAR), Toulon, France, 23–27 September 2019; pp. 1–5. [Google Scholar]
- Beasley, P.; Ritchie, M.; Griffiths, H.; Miceli, W.; Inggs, M.; Lewis, S.; Kahn, B. Multistatic Radar Measurements of UAVs at X-band and L-band. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar]
- Rahman, S.; Robertson, D.A. Radar micro-Doppler signatures of drones and birds at K-band and W-band. Sci. Rep. 2018, 8, 17396. [Google Scholar] [CrossRef] [PubMed]
- Björklund, S. Target Detection and Classification of Small Drones by Boosting on Radar Micro-Doppler. In Proceedings of the 2018 15th European Radar Conference (EuRAD), Madrid, Spain, 26–28 September 2018; pp. 182–185. [Google Scholar]
- Jahangir, M.; Atkinson, G.M.; Antoniou, M.; Baker, C.J.; Sadler, J.P.; Reynolds, S.J. Measurements of Birds and Drones with L-Band Staring Radar. In Proceedings of the 2021 21st International Radar Symposium (IRS), Berlin, Germany, 21–22 June 2021; pp. 1–10. [Google Scholar]
- Vo, B.T.; Vo, B.N.; Cantoni, A. The Cardinalized Probability Hypothesis Density Filter for Linear Gaussian Multi-Target Models. In Proceedings of the 2006 40th Annual Conference on Information Sciences and Systems, Princeton, NJ, USA, 22–24 March 2006; pp. 681–686. [Google Scholar]
- Ulmke, M.; Erdinc, O.; Willett, P. Gaussian mixture cardinalized PHD filter for ground moving target tracking. In Proceedings of the 2007 10th International Conference on Information Fusion, Quebec, QC, Canada, 9–12 July 2007; pp. 1–8. [Google Scholar]
- Granstrom, K.; Lundquist, C.; Orguner, O. Extended Target Tracking using a Gaussian-Mixture PHD Filter. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3268–3286. [Google Scholar] [CrossRef]
- Li, T.; Corchado, J.M.; Chen, H. Distributed Flooding-then-Clustering: A Lazy Networking Approach for Distributed Multiple Target Tracking. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 2415–2422. [Google Scholar]
- Vásárhelyi, G.; Virágh, C.; Somorjai, G.; Tarcai, N.; Szörenyi, T.; Nepusz, T.; Vicsek, T. Outdoor flocking and formation flight with autonomous aerial robots. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 3866–3873. [Google Scholar]
- Ristic, B.; Vo, B.N.; Clark, D.; Vo, B.T. A Metric for Performance Evaluation of Multi-Target Tracking Algorithms. IEEE Trans. Signal Process. 2011, 59, 3452–3457. [Google Scholar] [CrossRef]
- Wang, X.; Zhai, W.; Zhang, X.; Wang, X.; Amin, M.G. Enhanced Automotive Sensing Assisted by Joint Communication and Cognitive Sparse MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4782–4799. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).