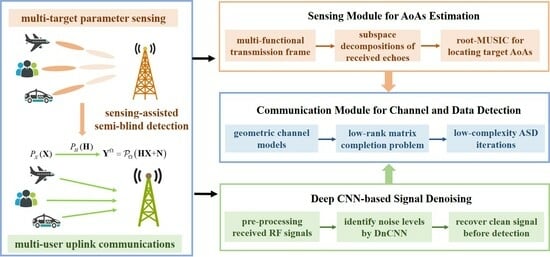
Sensing and Deep CNN-Assisted Semi-Blind Detection for Multi-User Massive MIMO Communications
Abstract
1. Introduction
1.1. Background
1.2. Problem Being Addressed
1.3. Existing Solutions
1.4. Motivations and Objectives
1.5. Our Proposal and Contributions
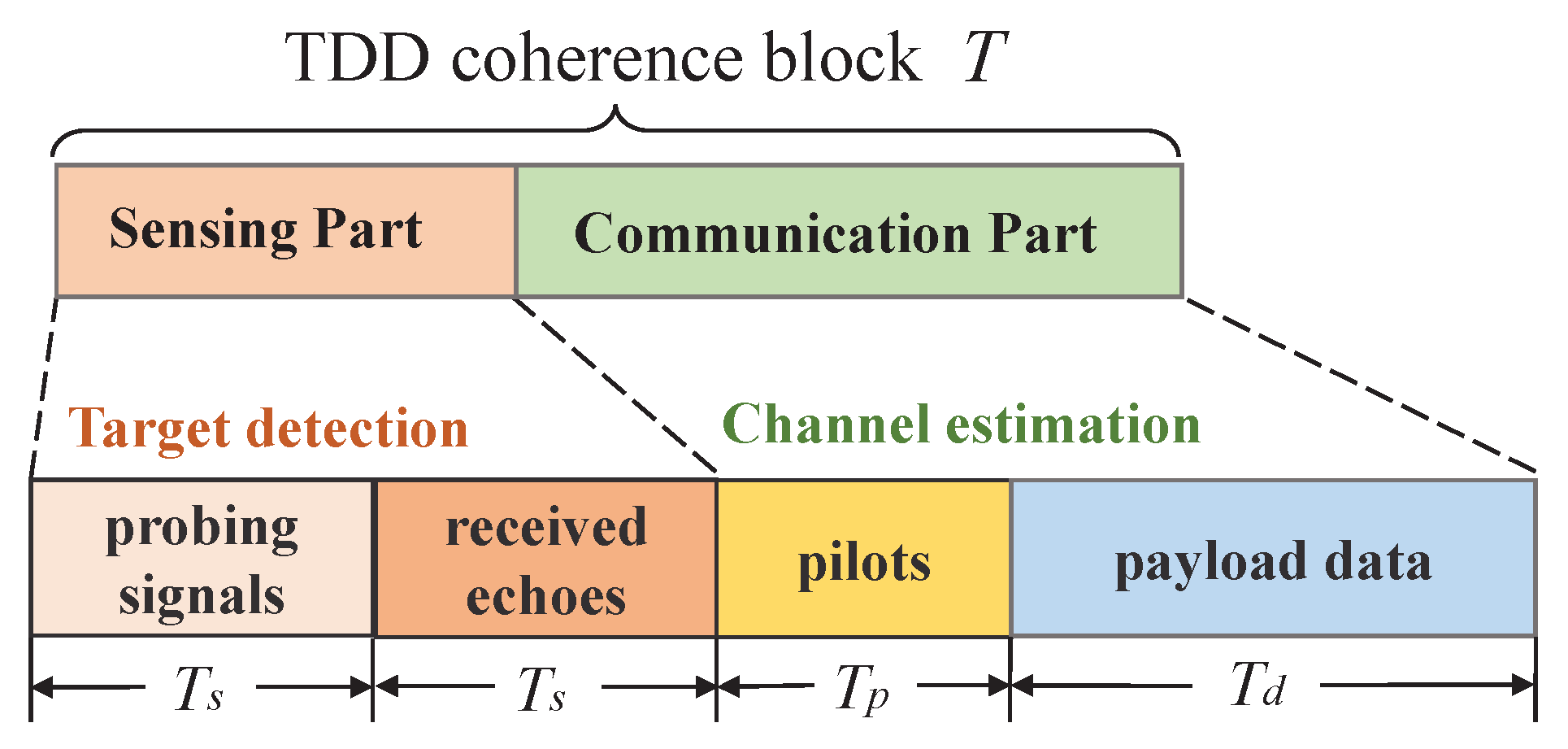
- A novel time-division duplex (TDD) transmission frame capable of coordinating the radar and communication operations is designed, based on which the root multiple signal classification (MUSIC) algorithm is firstly applied to environment sensing and then the extracted target angle information is utilized for refining the subsequent communication detection results.
- A generic representation for analog combining with phase shifters is considered, and the signal recovery problem is transformed into a low-rank matrix completion. To obtain the matrix factorizations with lower complexity, an iterative algorithm modified from ASD is proposed without any prior knowledge of noise statistics. In addition, different from the conventional pilot-only method, the semi-blind detection scheme is employed with reduced training overhead.
- A pre-trained denoising convolutional neural network (DnCNN) is adopted to preprocess the received signals before performing the semi-blind detection, which attempts to handle Gaussian noise removal with unknown noise level and shows powerful ability of improved accuracy especially in low SNR regions.
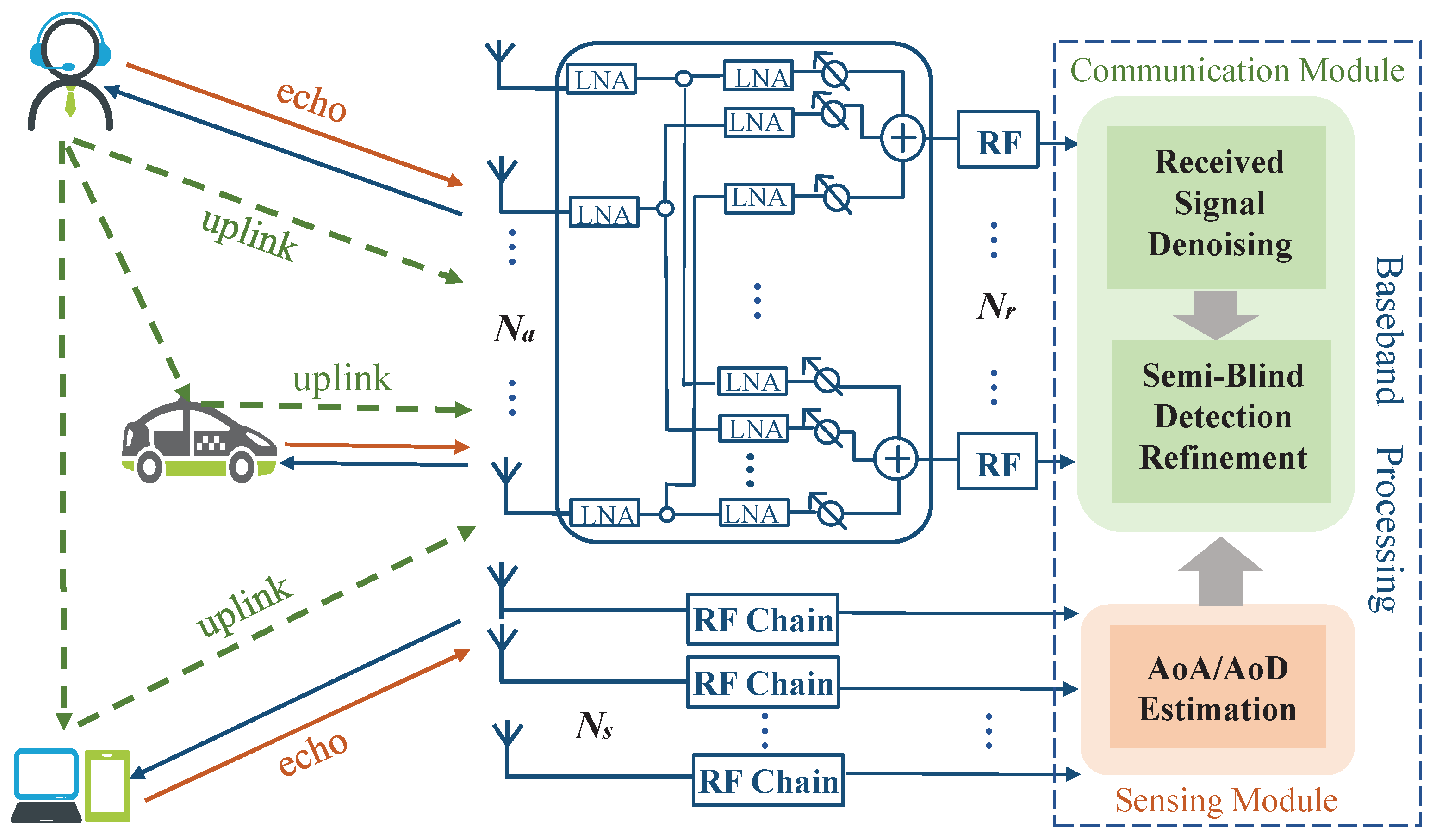
2. System Model and Background
2.1. Sensing Model
2.2. Uplink Communication Model
2.3. The Conventional LMMSE Estimator
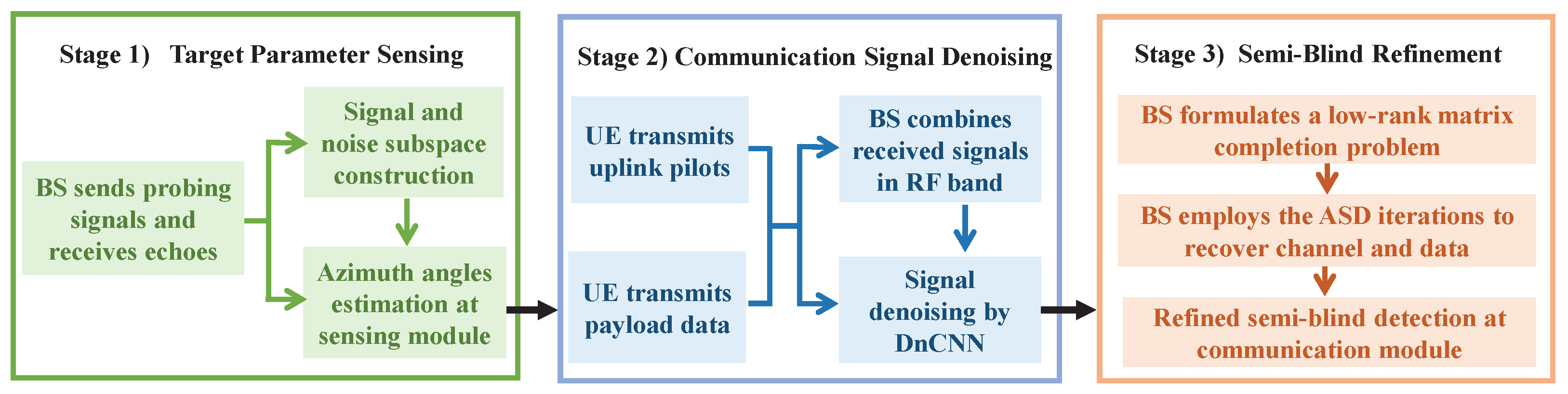
3. Proposed Sensing and Deep CNN-Assisted Semi-Blind Detection Scheme
3.1. Target Parameter Sensing
3.2. Low-Rank Matrix Completion
3.3. Refined Semi-Blind Detection
3.3.1. Ambiguity Removal
| Algorithm 1 The proposed sensing-assisted semi-blind detection with reduced pilot overhead | |
| 1: | Input , , |
| 2: | Randomly initialize and . |
| 3: | Set and . |
| 4: | repeat |
| 5: | Step (1) Update to as follows |
| 6: | Compute |
| and . | |
| 7: | . |
| 8: | . |
| 9: | Step (2) Update to as follows |
| 10: | Compute |
| and . | |
| 11: | . |
| 12: | Step (3) Update t to . |
| 13: | until Convergence |
| 14: | Get . |
| 15: | Output |
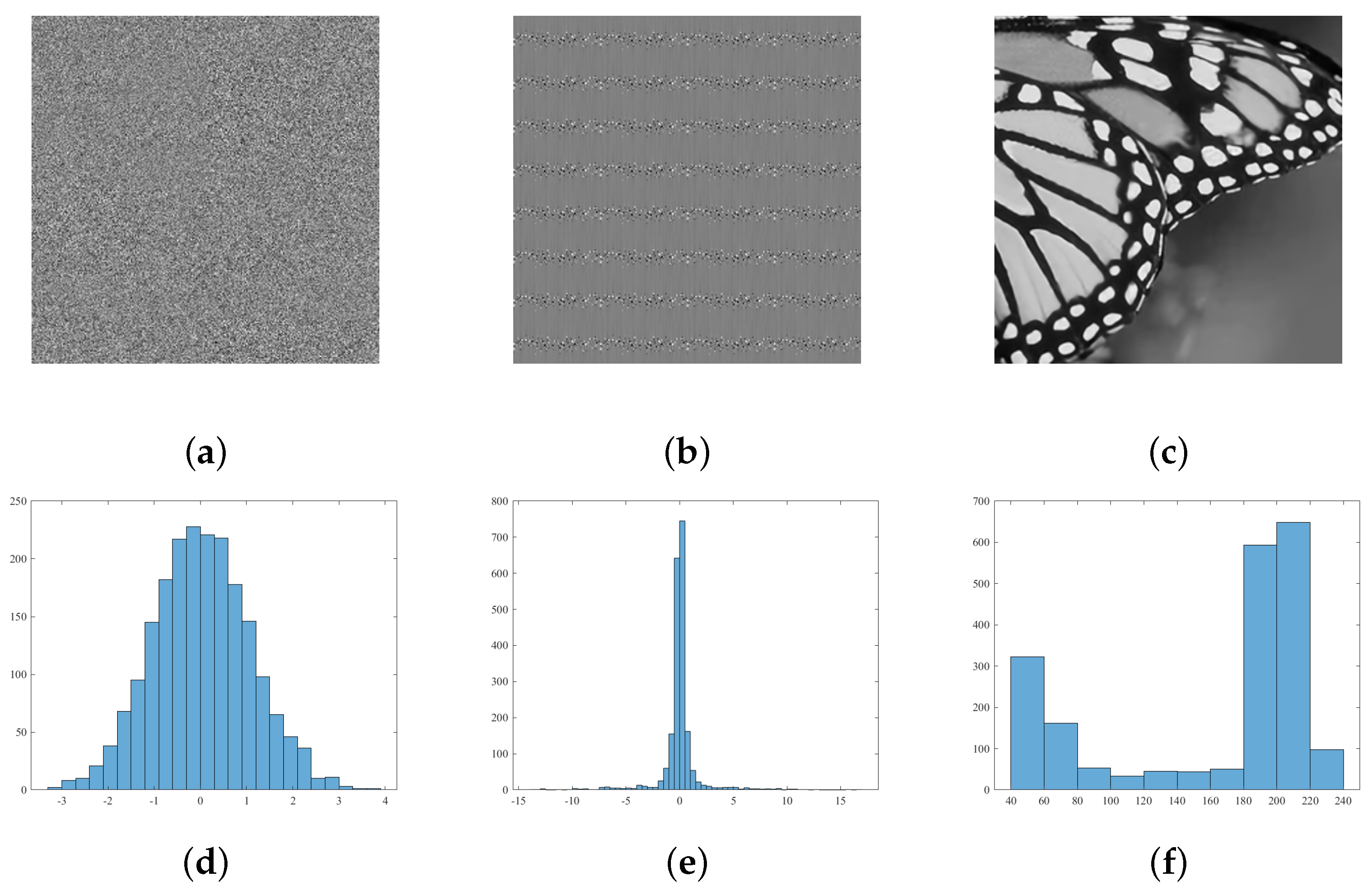
3.3.2. Signal Denoising
4. Simulation Results
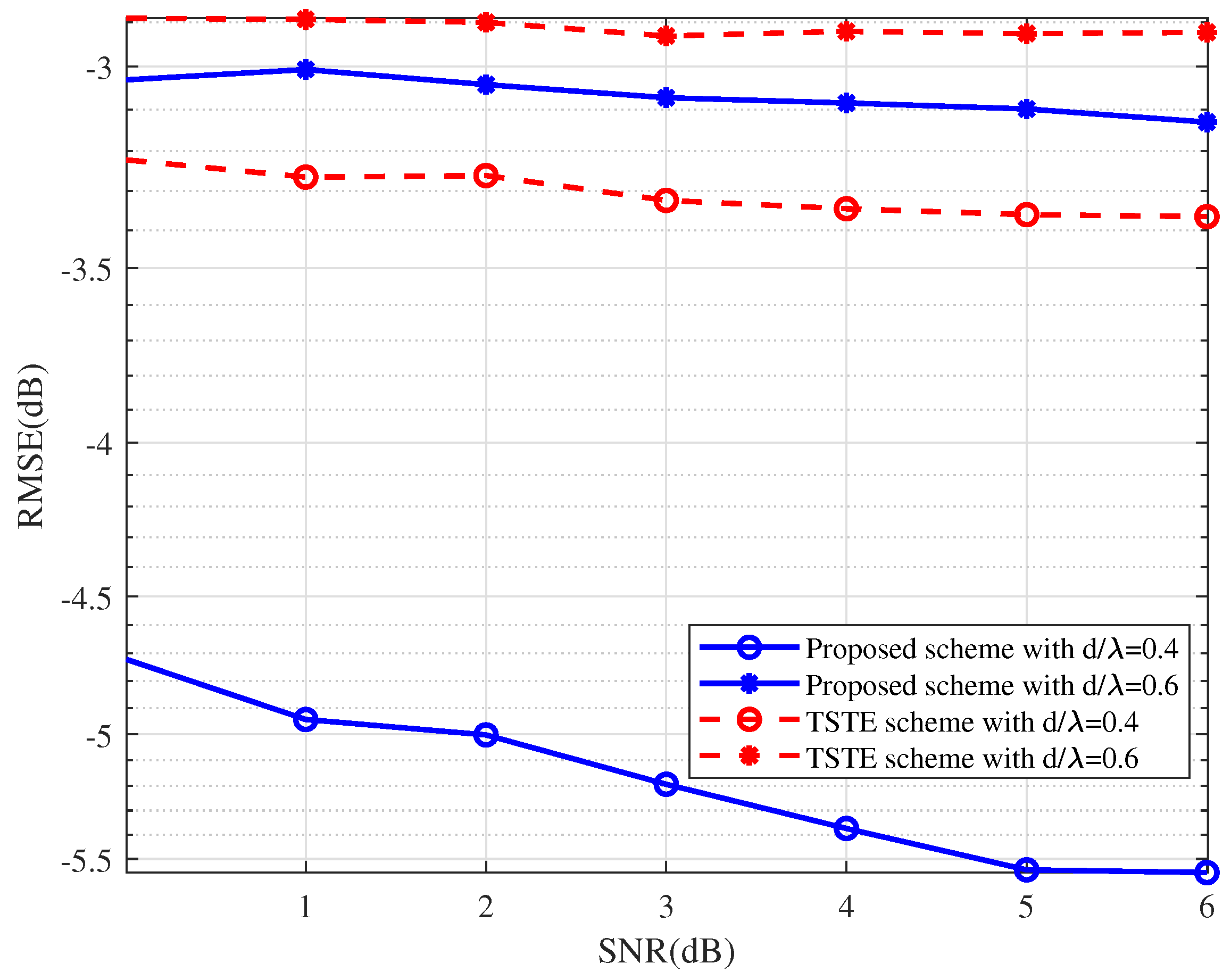
4.1. The Proposed Transmission Frame
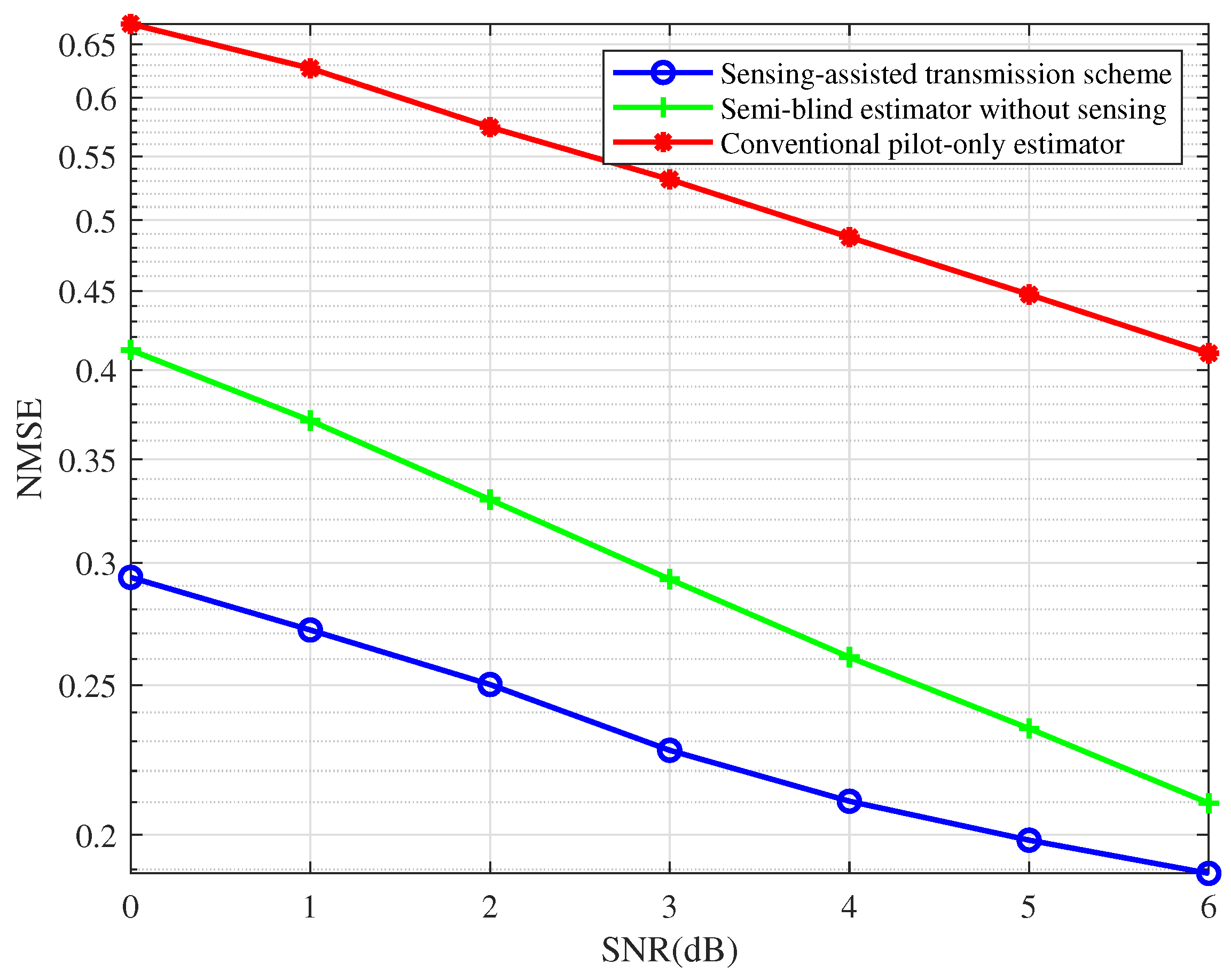
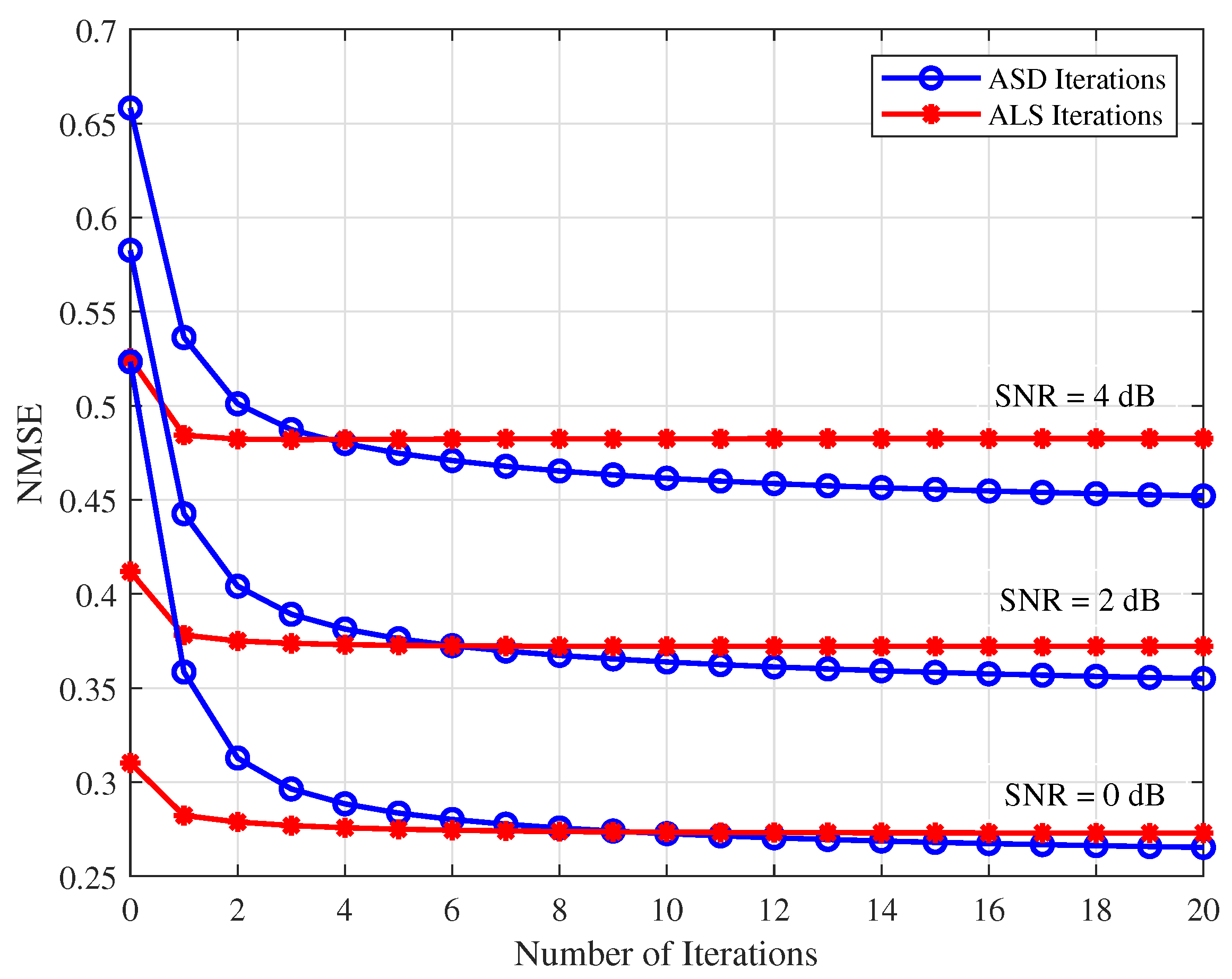
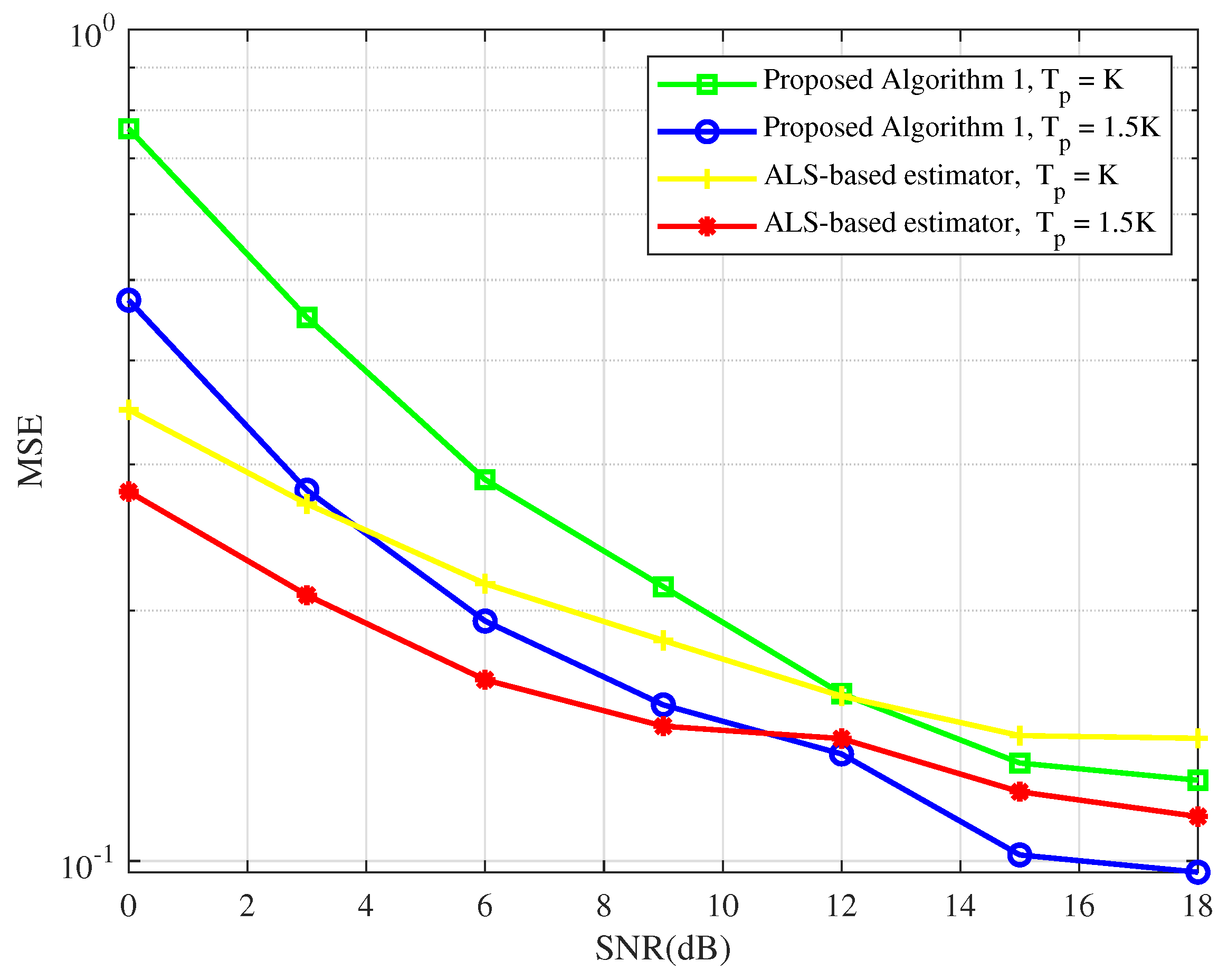
4.2. Refined Semi-Blind Detection
4.3. Signal Denoising by DnCNN
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tong, W.; Li, G.Y. Nine challenges in artificial intelligence and wireless communications for 6G. IEEE Wirel. Commun. 2022, 29, 140–145. [Google Scholar] [CrossRef]
- Li, X.; Liu, F.; Zhou, Z.; Zhu, G.; Wang, S.; Huang, K.; Gong, Y. Integrated sensing, communication, and computation over-the-Air: MIMO beamforming design. IEEE Trans. Wirel. Commun. 2023, 22, 5383–5398. [Google Scholar] [CrossRef]
- Koubaa, A.; Ammar, A.; Abdelkader, M.; Alhabashi, Y.; Ghouti, L. AERO: AI-enabled remote sensing observation with onboard edge computing in UAVs. Remote Sens. 2023, 15, 1873. [Google Scholar] [CrossRef]
- Zhu, Y.; Guo, H.; Lau, V.K.N. Bayesian channel estimation in multi-user massive MIMO with extremely large antenna array. IEEE Trans. Signal Process. 2021, 69, 5463–5478. [Google Scholar] [CrossRef]
- Guo, J.; Wen, C.-K.; Jin, S.; Li, G.Y. Overview of deep learning-based CSI feedback in massive MIMO systems. IEEE Trans. Commun. 2022, 70, 8017–8045. [Google Scholar] [CrossRef]
- Zhang, R.; Cheng, L.; Wang, S.; Lou, Y.; Wu, W.; Ng, D.W.K. Tensor decomposition-based channel estimation for hybrid mmWave massive MIMO in high-mobility scenarios. IEEE Trans. Commun. 2022, 70, 6325–6340. [Google Scholar] [CrossRef]
- Wei, X.; Hu, C.; Dai, L. Deep learning for beamspace channel estimation in millimeter-wave massive MIMO systems. IEEE Trans. Commun. 2021, 69, 182–193. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Ma, M.; Lavi, O.; Shlezinger, N.; Eldar, Y.C.; Swindlehurst, A.L.; Juntti, M. Deep unfolding hybrid beamforming designs for THz massive MIMO systems. IEEE Trans. Signal Process. 2023, 71, 3788–3804. [Google Scholar] [CrossRef]
- Mirzaei, J.; ShahbazPanahi, S.; Sohrabi, F.; Adve, R. Hybrid analog and digital beamforming design for channel estimation in correlated massive MIMO systems. IEEE Trans. Signal Process. 2021, 69, 5784–5800. [Google Scholar] [CrossRef]
- Wei, X.; Dai, L. Channel estimation for extremely large-scale massive MIMO: Far-field, near-field, or hybrid-field? IEEE Commun. Lett. 2022, 26, 177–181. [Google Scholar] [CrossRef]
- Chafaa, I.; Negrel, R.; Belmega, E.V.; Debbah, M. Self-supervised deep learning for mmWave beam steering exploiting sub-6 GHz channels. IEEE Trans. Wirel. Commun. 2022, 21, 8803–8816. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, J.A.; Huang, X.; Guo, Y.J.; Hanzo, L. Simultaneous beam and user selection for the beamspace mmWave/THz massive MIMO downlink. IEEE Trans. Commun. 2023, 71, 1785–1797. [Google Scholar] [CrossRef]
- Cheng, Z.; Liao, B. QoS-aware hybrid beamforming and DOA estimation in multi-carrier dual-function radar-communication systems. IEEE J. Sel. Areas Commun. 2022, 40, 1890–1905. [Google Scholar] [CrossRef]
- Liu, F.; Cui, Y.; Masouros, C.; Xu, J.; Han, T.X.; Eldar, Y.C.; Buzzi, S. Integrated sensing and communications: Toward dual-functional wireless networks for 6G and beyond. IEEE J. Sel. Areas Commun. 2022, 40, 1728–1767. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, F.; Jing, X.; Mu, J. Integrating sensing and communications for ubiquitous IoT: Applications, trends, and challenges. IEEE Netw. 2021, 35, 158–167. [Google Scholar] [CrossRef]
- Wang, J.; Varshney, N.; Gentile, C.; Blandino, S.; Chuang, J.; Golmie, N. Integrated Sensing and Communication: Enabling Techniques, Applications, Tools and Data Sets, Standardization, and Future Directions. IEEE Internet Things J. 2022, 9, 23416–23440. [Google Scholar] [CrossRef]
- Graff, A.; Chen, Y.; González-Prelcic, N.; Shimizu, T. Deep learning-based link configuration for radar-aided multiuser mmWave vehicle-to-infrastructure communication. IEEE Trans. Veh. Technol. 2023, 72, 7454–7468. [Google Scholar] [CrossRef]
- Wang, X.; Zhai, W.; Zhang, X.; Wang, X.; Amin, M.G. Enhanced automotive sensing assisted by joint communication and cognitive sparse MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4782–4799. [Google Scholar] [CrossRef]
- Hassan, K.; Masarra, M.; Zwingelstein, M.; Dayoub, I. Channel estimation techniques for millimeter-wave communication systems: Achievements and challenges. IEEE Open J. Commun. Soc. 2020, 1, 1336–1363. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, L.; Tang, M.; Tan, W.; Zhao, J. Channel estimation for mmWave massive MIMO systems with mixed-ADC architecture. IEEE Open J. Commun. Soc. 2023, 4, 606–613. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Tian, Z.; Leus, G.; Zhang, G. Super-resolution channel estimation for arbitrary arrays in hybrid millimeter-wave massive MIMO systems. IEEE J. Sel. Top. Signal Process. 2019, 13, 947–960. [Google Scholar] [CrossRef]
- Fan, D.; Gao, F.; Liu, Y.; Deng, Y.; Wang, G.; Zhong, Z.; Nallanathan, A. Angle domain channel estimation in hybrid millimeter wave massive MIMO systems. IEEE Trans. Wirel. Commun. 2018, 17, 8165–8179. [Google Scholar] [CrossRef]
- Zhou, L.; Dai, J.; Xu, W.; Chang, C. Sparse channel estimation for intelligent reflecting surface assisted massive MIMO systems. IEEE Trans. Green Commun. Netw. 2022, 6, 208–220. [Google Scholar] [CrossRef]
- Wang, Y.; Qi, C.; Li, P.; Lu, Z.; Lu, P. Channel estimation for wideband mmWave MIMO OFDM system exploiting block sparsity. IEEE Commun. Lett. 2022, 26, 897–901. [Google Scholar] [CrossRef]
- Chu, H.; Zheng, L.; Wang, X. Semi-blind millimeter-wave channel estimation using atomic norm minimization. IEEE Commun. Lett. 2018, 22, 2535–2538. [Google Scholar] [CrossRef]
- Han, F.; Wang, X.; Deng, H. A very-low pilot scheme for mmWave hybrid massive MIMO-OFDM systems. IEEE Wirel. Commun. Lett. 2021, 10, 2061–2064. [Google Scholar] [CrossRef]
- Liang, S.; Wang, X.; Ping, L. Semi-blind detection in hybrid massive MIMO systems via low-rank matrix completion. IEEE Trans. Wirel. Commun. 2019, 18, 5242–5254. [Google Scholar] [CrossRef]
- Li, X.; Fang, J.; Li, H.; Wang, P. Millimeter wave channel estimation via exploiting joint sparse and low-rank structures. IEEE Trans. Wirel. Commun. 2018, 17, 1123–1133. [Google Scholar] [CrossRef]
- Vlachos, E.; Alexandropoulos, G.C.; Thompson, J. Massive MIMO channel estimation for millimeter wave systems via matrix completion. IEEE Signal Process. Lett. 2018, 25, 1675–1679. [Google Scholar] [CrossRef]
- Masood, K.F.; Hu, R.; Tong, J.; Xi, J.; Guo, Q.; Yu, Y. A low-complexity three-stage estimator for low-rank mmWave channels. IEEE Trans. Veh. Technol. 2021, 70, 5920–5931. [Google Scholar] [CrossRef]
- Nguyen, L.T.; Kim, J.; Shim, B. Low-rank matrix completion: A contemporary survey. IEEE Access 2019, 7, 94215–94237. [Google Scholar] [CrossRef]
- Giampouras, P.V.; Rontogiannis, A.A.; Koutroumbas, K.D. Alternating iteratively reweighted least squares minimization for low-rank matrix factorization. IEEE Trans. Signal Process. 2019, 67, 490–503. [Google Scholar] [CrossRef]
- Chi, Y.; Lu, Y.M.; Chen, Y. Nonconvex optimization meets low-rank matrix factorization: An overview. IEEE Trans. Signal Process. 2019, 67, 5239–5269. [Google Scholar] [CrossRef]
- Tanner, J.; Wei, K. Low rank matrix completion by alternating steepest descent methods. Appl. Comput. Harmon. Anal. 2016, 40, 417–429. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Petropulu, A.P.; Griffiths, H.; Hanzo, L. Joint radar and communication design: Applications, state-of-the-art, and the road ahead. IEEE Trans. Commun. 2020, 68, 3834–3862. [Google Scholar] [CrossRef]
- Yuan, W.; Wei, Z.; Li, S.; Yuan, J.; Ng, D.W.K. Integrated sensing and communication-assisted orthogonal time frequency space transmission for vehicular networks. IEEE J. Sel. Top. Signal Process. 2021, 15, 1515–1528. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, M.; Gao, Y.; Feng, Z. MIMO radar aided mmWave time-varying channel estimation in MU-MIMO V2X communications. IEEE Trans. Wirel. Commun. 2021, 20, 7581–7594. [Google Scholar] [CrossRef]
- He, H.; Wen, C.-K.; Jin, S.; Li, G.Y. Deep learning-based channel estimation for beamspace mmWave massive MIMO systems. IEEE Wirel. Commun. Lett. 2018, 7, 852–855. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing, Volume III: Practical Algorithm Development; Prentice Hall: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- Gizzini, A.K.; Chafii, M.; Nimr, A.; Fettweis, G. Enhancing least square channel estimation using deep learning. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference: VTC2020-Spring, Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Liu, A.; Lau, V. Phase only RF precoding for massive MIMO systems with limited RF chains. IEEE Trans. Signal Process. 2014, 62, 4505–4515. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]

| Existing Works | System Models | Receiver Techniques | Limitations or Features |
|---|---|---|---|
| [19,20,21] | mmWave MIMO communications | non-blind detection based on pilots only | Pilot overhead can be enlarged greatly with massive antennas. |
| [22,23,24] | mmWave MIMO communications | CS leveraging the channel sparsity | Gird-based estimator may lead to effects of basis mismatch. |
| [25] | mmWave MIMO communications | atomic norm minimization | High-dimensional optimizations may cause substantial computational complexity. |
| [26] | mmWave MIMO communications | semi-blind detection aided with payload data | Neglect of geometric structure of channel distributions. |
| [27] | massive MIMO communications | LS leveraging the channel low-rankness | Underexploitation of realistic channel characteristic with multiple propagation paths. |
| [28,29,30] | mmWave MIMO communications | multiple stages exploiting both the low-rankness and sparsity | High computational complexity when generalized to large-scale problems. |
| [35] | joint radar and communications | multiple signal classification (MUSIC) for angle estimation | Joint signal processing strategy can simultaneously detect targets while estimating the communication channel. |
| [36] | joint radar and communications | maximum likelihood (ML) estimator | Sensing parameter estimation can promote the dynamic topology construction of surrounding environments. |
| [37] | joint radar and communications | LS detection vs. DL-based denoiser | Efficient estimation with fewer training resources by eliminating noise before recovering channels. |
| Abbreviations | Expansion |
|---|---|
| ALS | Alternating Least Squares |
| AoA | Angle-of-Arrival |
| AoD | Angle-of-Departure |
| BS | Base Station |
| CNN | Convolutional Neural Network |
| CS | Compressed Sensing |
| DnCNN | Denoising Convolutional Neural Network |
| DL | Deep Learning |
| LMMSE | Linear Minimum Mean Squared Error |
| LoS | Line-of-Sight |
| LS | Least Squares |
| mmWave | Millimeter Wave |
| MIMO | Multiple-Input Multiple-Output |
| MU-MIMO | Multi-User MIMO |
| MUSIC | Multiple Signal Classification |
| NMSE | Normalized Mean Squared Error |
| RF | Radio Frequency |
| RMSE | Root Mean Squared Error |
| SNR | Signal-to-Noise Ratio |
| SVD | Singular Value Decomposition |
| TDD | Time-Division Duplex |
| UE | User Equipment |
| ULA | Uniform Linear Array |
| Approaches | Averaged Computational Cost | Total Cost until Convergence | ||
|---|---|---|---|---|
| performance | memory | time | memory | time |
| proposed ASD | 0.216 Kb | 3.11 ms | 10.22 Kb | 22.80 ms |
| R-ALS | 8.644 Kb | 43.22 ms | 46.61 Kb | 86.96 ms |
| LMMSE | 0.636 Kb | 3.50 ms | / | / |
| SNR Value | −5 dB | −4 dB | −3 dB | |||
|---|---|---|---|---|---|---|
| Selected Model | NMSE-Y | NMSE | NMSE-Y | NMSE | NMSE-Y | NMSE |
| Without DnCNN | 3.1727 | 1.6561 | 2.5430 | 1.2967 | 1.9962 | 0.9956 |
| DnCNN-15 | 1.5223 | 1.0362 | 1.1352 | 0.8159 | 0.8320 | 0.6679 |
| DnCNN-25 | 0.8566 | 0.8875 | 0.8618 | 0.8951 | 0.8888 | 0.9199 |
| DnCNN-B | 0.9424 | 0.9635 | 0.9265 | 0.9488 | 0.8888 | 0.9042 |
| SNR Value | −2 dB | −1 dB | 0 dB | |||
| Selected Model | NMSE-Y | NMSE | NMSE-Y | NMSE | NMSE-Y | NMSE |
| Without DnCNN | 1.6025 | 0.8733 | 1.2425 | 0.7477 | 0.9951 | 0.6051 |
| DnCNN-15 | 0.6335 | 0.6242 | 0.4998 | 0.5947 | 0.4312 | 0.5720 |
| DnCNN-25 | 0.9070 | 0.9363 | 0.9314 | 0.9552 | 0.9356 | 0.9610 |
| DnCNN-B | 0.9350 | 0.8631 | 0.8218 | 0.8875 | 0.7700 | 0.8672 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, F.; Zeng, J.; Zheng, L.; Zhang, H.; Wang, J. Sensing and Deep CNN-Assisted Semi-Blind Detection for Multi-User Massive MIMO Communications. Remote Sens. 2024, 16, 247. https://doi.org/10.3390/rs16020247
Han F, Zeng J, Zheng L, Zhang H, Wang J. Sensing and Deep CNN-Assisted Semi-Blind Detection for Multi-User Massive MIMO Communications. Remote Sensing. 2024; 16(2):247. https://doi.org/10.3390/rs16020247
Chicago/Turabian StyleHan, Fengxia, Jin Zeng, Le Zheng, Hongming Zhang, and Jianhui Wang. 2024. "Sensing and Deep CNN-Assisted Semi-Blind Detection for Multi-User Massive MIMO Communications" Remote Sensing 16, no. 2: 247. https://doi.org/10.3390/rs16020247
APA StyleHan, F., Zeng, J., Zheng, L., Zhang, H., & Wang, J. (2024). Sensing and Deep CNN-Assisted Semi-Blind Detection for Multi-User Massive MIMO Communications. Remote Sensing, 16(2), 247. https://doi.org/10.3390/rs16020247