Monte Carlo Full-Waveform Inversion of Cross-Hole Ground-Penetrating Radar Data Based on Improved Residual Network

Abstract

A full-waveform inversion (FWI) of ground-penetrating radar (GPR) data can be used to effectively obtain the parameters of a shallow subsurface. Introducing the Markov chain Monte Carlo (MCMC) algorithm into the FWI can reduce the dependence on the initial model and obtain the global optimal solution, but it requires a large number of computations. In order to better detect underground targets based on ground-penetrating radar data, this paper proposes a joint scheme of an improved ResNet and an MCMC full-waveform inversion. This scheme combines the Bayesian MCMC algorithm and an improved ResNet to accurately invert the target dielectric permittivity. The introduction of deep learning networks into the forward calculation part of the MCMC inversion algorithm replaced the complex forward simulation process, greatly improving the inversion speed. It is worth noting that the neural network model was an approximation of complex forward modeling, and, therefore, it contained modeling errors. The MCMC method could quantify and explain modeling errors during the inversion process, reducing the impact of modeling errors on the inversion results. Finally, a simulation dataset was constructed for training and testing, and the errors were statistically analyzed. The results showed that this method can accurately reconstruct underground medium targets, and it has strong robustness and efficiency.

1. Introduction

Ground-penetrating radar (GPR) is a nondestructive detection technique for underground targets that has been extensively used in various fields [1,2,3]. In the early stages of GPR technology, migration techniques were mainly used to detect underground targets [4]. However, the migration methods only used part of the wavefield information, and these methods were unable to obtain the dielectric parameters of the targets.

Full-waveform inversion (FWI) is an effective technique that can be used to quantitatively describe underground media parameters by matching observational data and simulated data [5,6]. FWI was initially proposed for seismic prospecting to solve acoustic and elastic wave equations [7,8,9]. It was subsequently quickly modified for GPR exploration to estimate the permittivity and conductivity of a subsurface medium using Maxwell’s equations [10,11,12,13,14,15]. However, due to the high nonlinearity of the FWI method, the inversion results are usually highly dependent on the initial model and easily trapped in local optima [16].

Introducing the MCMC algorithm based on Bayes’ theory into full-waveform inversion can solve these problems. An MCMC inversion does not need an accurate initial model, and its inversion result is a posterior probability density distribution that does not fall into local optima. Mosegaard et al. [17] introduced the extended Metropolis algorithm to sample the posterior probability density, a method that proved advantageous for dealing with highly nonlinear inverse problems. In this framework, an approach known as a “black box” algorithm was employed to sample the prior probability density, bypassing the need to solve a definitive mathematical expression of prior information. Hansen et al. [18,19] recommended the sequential Gibbs sampler, a black box algorithm designed to manage the perturbation step size when sampling prior data. Cordua [20] was the first to utilize the extended Metropolis algorithm for the full-waveform inversion of ground-penetrating radar (GPR) data, successfully obtaining a posterior probability density. Nevertheless, inversion techniques based on the Bayesian method continue to grapple with the issue of hefty computational demands.

In recent years, deep learning technology has been increasingly applied in the fields of seismic and electromagnetic signal processing [21,22]. In the field of inversion, a large amount of data is usually utilized to train networks that can directly estimate model parameters from data. These methods are based on the theory that any ordinary function can be approximated using a standard feedforward neural network equipped with a single hidden layer, ample weights, any bounded non-constant activation functions, and a linear output layer [23]. Some deep learning networks have been proposed to solve the full-waveform inversion problem, such as the permittivity inversion network (PINet) [24] and the ground-penetrating radar inversion network (GPRInvNet) [25].

In addition, increasing the width and depth of a neural network can greatly improve its performance. However, due to the gradient degradation problem, when the network depth reaches a certain number of layers, the network performance reaches saturation. However, increasing the training depth can actually decrease the network performance. A residual network (ResNet) overcomes this drawback. ResNets were proposed by He [26] in 2015, and their biggest feature is the insertion of jump connection structures between network layers, which can train deeper networks and improve accuracy. Due to its excellent performance, ResNet has gained high popularity in object detection [27,28] and land-cover mapping [29]. Cao et al. used a novel deep residual network to predict the internal moisture content of AC pavement from ground-penetrating radar (GPR) measurements [30]. However, for deep learning networks that directly estimate underground parameters from observational data, it is difficult to measure the impact of network modeling errors [31].

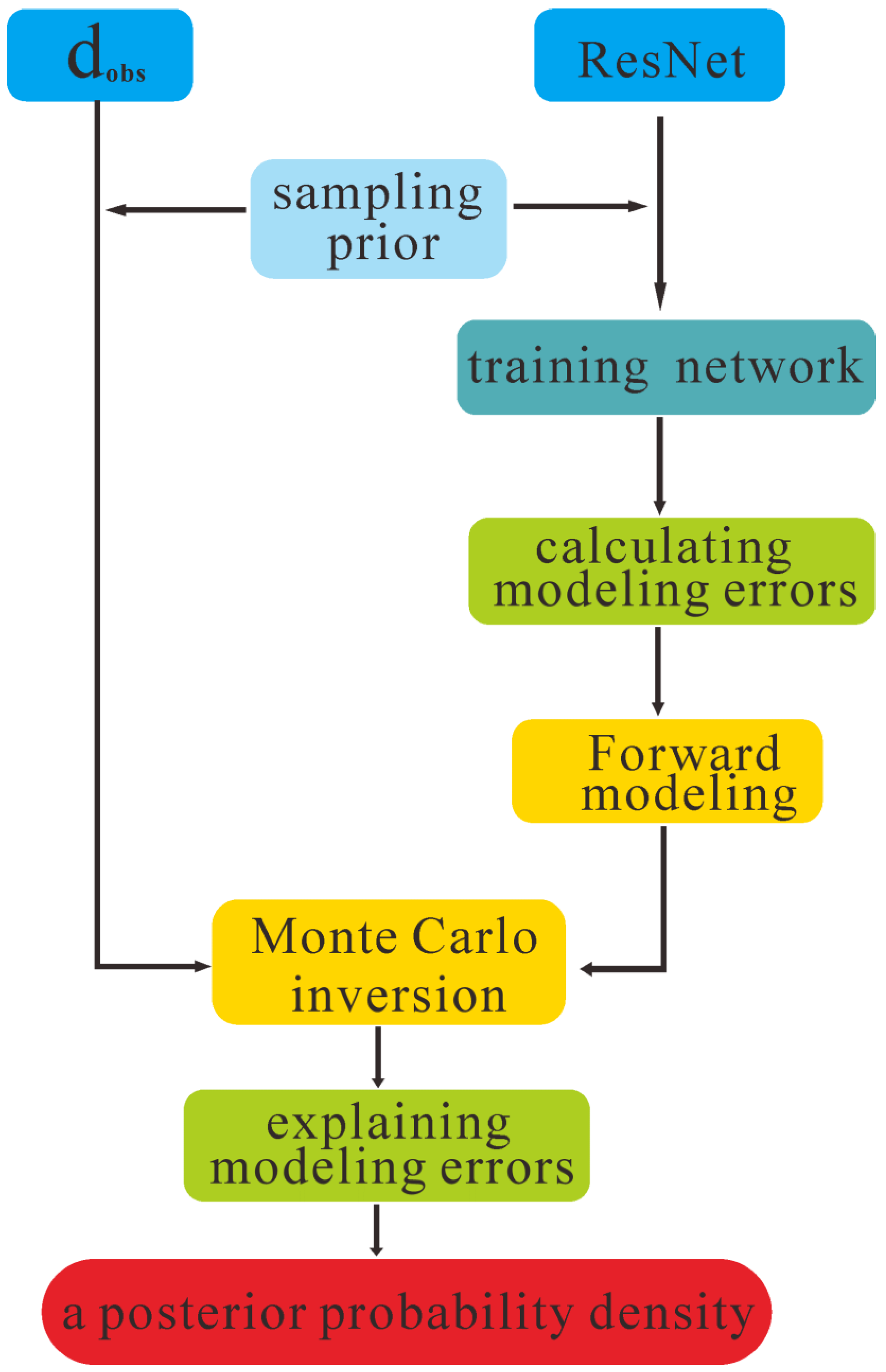
To solve the problems of full-waveform inversion methods, this article proposes a method that combines a ResNet and the MCMC algorithm. Unlike other methods that directly estimate the model parameters from observational data using a deep learning network, this method combines the MCMC algorithm with a deep learning network, which replaces the forward calculation based on the Maxwell equation. An improved ResNet is proposed instead of a forward model based on the 2D finite-difference time-domain (FDTD) solution of Maxwell’s equations. This network contains four residual blocks, which can achieve mapping from two-dimensional dielectric constant images to one-dimensional waveform data with low modeling errors and a fast calculation. The modeling errors of the deep learning network can be statistically quantified during the MCMC inversion process, improving the result of the inversion.

2. Methods

2.1. The Theory of Probability Inversion

In geophysical inversion challenges, the underground properties can be depicted by a set of characteristics, labeled $\mathbf{m}$, while the collected information is denoted by data, $\mathbf{d}$. Therefore, the direct link between $\mathbf{m}$ and $\mathbf{d}$ can be illustrated as [32]:

$$\mathbf{d}=f(\mathbf{m})$$

(1)

Here, $f$ signifies a conversion function determined by a specific physical correlation. The associated reverse function can be detailed as follows:

$$\mathbf{m}=f^{-1}(\mathbf{d})$$

(2)

Within this equation, obtaining the reverse function $f^{-1}$ is intricate due to its complexity or potential non-existence. In our study, the relative dielectric permittivity indicates the underground characteristics $\mathbf{m}$, which aim to invert, with the observed data $\mathbf{d}$, which are the full-waveform data of the GPR cross-hole.

Considering a probabilistic inversion approach, the respective reverse equation is:

$${\sigma }_M(\mathbf{m})=k{\rho }_M(\mathbf{m})L(\mathbf{m})$$

(3)

Here, ${\rho }_M(\mathbf{m})$ defines the prior probability density, denoting the pre-existing knowledge about the model attributes. ${\sigma }_M(\mathbf{m})$ is a posterior probability distribution, which presents the solution of the inversion.$k$ represents a normalization factor. $L(\mathbf{m})$ stands for the likelihood function, which offers a metric illustrating the extent to which the simulated data align with the observed data. Its equation is:

$$L(\mathbf{m})={\displaystyle \int d\mathbf{d}}\frac{{\rho }_D\left(g(\mathbf{m})\right)\theta (\mathbf{d}|\mathbf{m})}{{\mu }_D(\mathbf{d})}$$

(4)

In this equation, ${\rho }_D\left(g(\mathbf{m})\right)$ highlights uncertainties primarily associated with the data collection tool. $\theta (\mathbf{d}|\mathbf{m})$ is the modeling error caused by the imperfect forward method. Meanwhile, ${\mu }_D(\mathbf{d})$ elaborates on the consistent information status, ensuring stability in parameterization even if the coordinate system undergoes changes. Frequently, ${\mu }_D(\mathbf{d})$ is considered a constant.

It is worth noting that the use of an approximate forward model introduces modeling errors, which are determined by $\theta (\mathbf{d}|\mathbf{m})$. If the modeling errors are ignored, the data portion that should be considered (modeling) errors will be considered data. This may cause modeling errors to map to a posterior distribution, which may lead to the distortion of the inversion results. Hansen et al. [30] described a sampling method that uses statistical methods to describe modeling errors $\theta (\mathbf{d}|\mathbf{m})$, and explaining the modeling errors in the inversion process can eliminate the impact of model errors on the inversion results. In this article, model errors $\theta (\mathbf{d}|\mathbf{m})$ represent the error caused by the neural network methods. Neural networks are approximations of accurate forward formulas; they contain errors. The Equation (4) can be used to explain model errors, reducing the impact of model errors on inversion results.

2.2. Full-Waveform Forward Model

In the forward modeling process, there are multiple approaches to emulate the wavefield of the GPR signal. For this study, we opted for the 2D FDTD technique to interpret Maxwell’s equations within the transverse electric mode.

This FDTD approach reproduces the vertical component of the electric field for the data observed. For the transmission of electromagnetic waves, the transverse electric or TE models of Maxwell’s equations on the (x, z) axis in Cartesian coordinates can be defined as [33]:

$$\frac{\partial E_x}{\partial t}=\frac{1}{\epsilon }\left(-\frac{\partial H_y}{\partial z}-\sigma E_x\right)$$

(5)

$$\frac{\partial E_z}{\partial t}=\frac{1}{\epsilon }\left(\frac{\partial H_y}{\partial x}-\sigma E_x\right)$$

(6)

$$\frac{\partial H_y}{\partial t}=\frac{1}{\mu }\left(\frac{\partial E_z}{\partial x}-\frac{\partial E_x}{\partial z}\right)$$

(7)

In these equations, $E_x$ and $E_z$ denote the horizontal and vertical segments of the electric field, respectively; $\epsilon$ symbolizes the dielectric permittivity; $\sigma$ signifies the electrical conductivity; $H_y$ stands for the magnetic field perpendicular to the wave plane; and $\mu$ stands for the magnetic permeability, which, for the following discussion, was assumed to be constant and equal to the free-space permeability.

For the computations, we employed FDTD strategies [34], utilizing the staggered grid finite difference methodology with precision up to the second order in both space and duration to elucidate Equations (5)–(7).

A generalized perfectly matched layer (GPML) enveloped the FDTD grid boundaries to mitigate any artificial reverberations at the model space boundaries. Near the terrestrial surface, electromagnetic pulses were predominantly influenced by electrical conductivity and dielectric permittivity.

The dielectric permittivity predominantly governed the phases, while the electrical conductivity majorly controlled the signal amplitudes. In this research, we focused predominantly on the effects of dielectric permittivity. Throughout the examples shared in this study, the dielectric permittivity was the variable of interest, while the electrical conductivity was maintained constant.

The Process of Monte Carlo sampling of inverse problems based on the Resnet network as Figure 1 shows. ${\mathrm{d}}_{obs}$ represents observed data. This article uses samples based on prior information to train neural networks. Use the trained network to replace the forward model in Monte Carlo inversion. Finally, the observed data were inverted to obtain a posterior probability distribution.

2.3. Solving the Forward Problem Using ResNet

Residual networks were proposed by He [26] in 2015. Their biggest feature is the use of skip connections between network layers, which can train deeper networks than before and result in higher accuracy. The residual block is the basic unit in a residual network, and its structure is shown in Figure 2.

The residual block is composed of two convolutional layer groups, and skip connections are made to the input and output positions. According to the residual block structure, the residual learning formula can be expressed as:

$$x_L=x_l+{\displaystyle \sum _{i=1}^{L-1}F(x_i,w_i)}$$

(8)

where $x_L$ is the L-layer feature and $F(x_i,w_i)$ is the residual function. $w_i$ is the parameter of the i-th layer. Therefore, the model is in the form of a residual within any element. When the residual is $F(x_i,w_i)=0$, the stacked layer only performs identity mapping; at least, the network performance will not decrease. In fact, the residual will not be 0, which will enable the stacked layer to learn new features based on the input features and, thus, result in a better performance.

In this article, the improved ResNet proposed mainly consisted of a convolutional layer, a batch normalization (BN) layer, a pooling layer, and a fully connected layer that used convolutional neural networks to extract target features. The network structure is shown in Figure 3.

A description of each layer in the model is as follows:

(1) Input layer. The improved ResNet input was 66 × 26 2D images. These images reflected the distribution of underground dielectric permittivity. Firstly, the value of the dielectric constant was normalized, and a convolutional neural network with a convolutional kernel of 7 × 7 was used to extract features.

(2) Feature extraction layer. The improved ResNet used four residual blocks to extract the features of the input data. Each residual block contained two convolutions with convolution kernels with a size of 3 × 3. Except for the maximum pooling layer step size of 1 in the first residual block, there was a maximum pooling layer step size of 2 in all the other residual blocks. The activation functions in the feature extraction layer were all ReLU.

(3) Output layer. The output layer first went through two fully connected layers to output 1 × 460 one-dimensional data. These one-dimensional data represented the full-waveform data of the ground-penetrating radar. The activation function of the fully connected layer was the tanh function.

Four residual blocks can provide 512 channels, and the structure is not too complex. Because the original intention of using neural networks to replace formula methods is to speed up calculations, efficiency is one of our priority considerations. The adaptive moment estimation (Adam) optimizer was selected to train the network, with an initial learning rate set to 0.01.

3. Experimental Validation

To test the effectiveness of the method proposed in this paper, we simulated reference model data of the dielectric permittivity created by a multivariate Gaussian probability distribution. The width and depth of this reference model were 5.2 m and 12 m, respectively, with a pixel size of 0.2 m × 0.2 m. Therefore, the parameters of this two-dimensional image were 26 × 60. In this model, it was assumed that the electrical conductivity was a constant of 3 mS/m. The average value and variance of the dielectric permittivity in the reference model were 4.0 and 0.75, which was the prior information. A high dielectric permittivity region was located in approximately 10 positions at the bottom of the model. Our inversion goal was to invert the position of this high dielectric constant.

The recording geometry of this model is shown in Figure 4. The red dots in the figure represent the transmitters, the black dots represent the receivers, and the spacing between the receivers is 1.5 m. Considering the influence of the waveguide [35], data with an angle greater than 45° between the transmitter–receiver and the horizontal plane were omitted. The parameters of this recording geometry were similar to those reported by Cordua et al. [20].

The full-waveform synthetic data were created using the FDTD algorithm. The FDTD model used a regular grid of 0.1 × 0.1 m to solve Maxwell’s equations, and the time interval is 4 ns.

The recording geometry could receive a total of 20 waveforms. There were five waveforms in the figure generated by the transmitter located at a depth of 3 m in the left borehole. In order to simulate a noisy environment, we added Gaussian-distributed data uncertainties to the waveform data. The signal-to-noise ratio of the signal was 20, and the relationship between the noise-free waveforms and the noisy waveforms is shown in Figure 5.

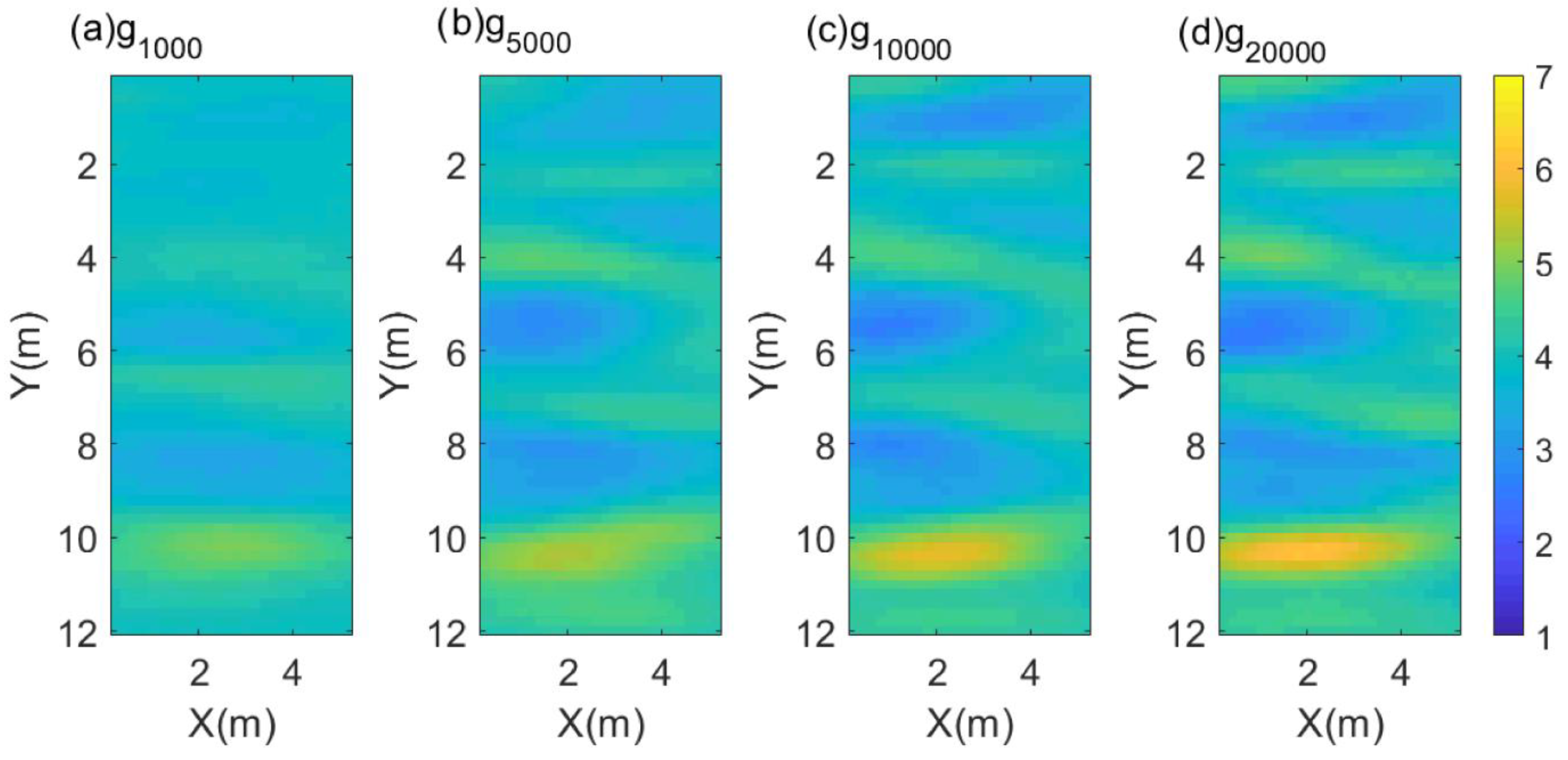
For the reference model and observational data, the input of the neural network was a 26 × 60 two-dimensional image, and the output of the neural network was 1 × 460 one-dimensional waveform data. We used different sizes of training data to train the neural network and test its accuracy, and the models in the training data were generated using a prior probability density. The training datasets were (1000, 5000 10,000 20,000), and the corresponding neural network models for this dataset were $g_{1000}$, $g_{5000}$, $g_{10000}$, and $g_{20000}$. Figure 6 shows the four model samples generated in the training dataset; the distribution of dielectric permittivity in the model sample was random.

After training the neural network model for different sizes, the forward model based on the neural network method was obtained. The root mean squared error (RMSE) of each network model is shown in

Table 1. RMSE of different forward models.

Forward Model	${\mathit{g}}_{1000}$	${\mathit{g}}_{5000}$	${\mathit{g}}_{10000}$	${\mathit{g}}_{20000}$
RMSE	0.94983	0.64377	0.51268	0.37907

, which is evaluated from the entire test set.

Because the neural network model was an approximation of the Maxwell equation, it may have generated modeling errors. In order to test the forward performance of the neural network model, a sample model was randomly selected to compute observation waveforms based on the 2D FDTD method. Neural network models were used to obtain simulated waveforms, and the comparison results are shown in Figure 7. The error of $g_{1000}$ was relatively large, and the waveform-matching effect was poor. However, as the training frequency increased, the waveforms of the neural network model became closer to the observation waveforms and $g_{20000}$ was already very similar to the observed data.

In order to reduce the impact of modeling errors on the inversion results, we statistically analyzed the modeling errors of the neural network. The error statistics method is similar to Hansen et al. [36]. The statistical results are shown in Figure 8. Figure 8 shows the 1D distribution of the modeling errors of the neural networks with different training sizes created by 3000 realizations. Obviously, the modeling errors decreased as the neural network training size increased. Figure 9 further shows the covariance models of the neural networks with different training sizes. As the training size increased, the correlated covariance model gradually decreased.

Using the trained neural network instead of the forward model, we used the extended Metropolis algorithm to obtain a posterior probability density. The inversion results of the four neural network forward models are shown in Figure 10. The first column is the true model, and the remaining four columns are the inversion results. The inversion target is mainly the high dielectric constant distribution at a depth of 10 m. It can be seen that when the network is trained more than 5000 times, the high dielectric constant begins to appear at a depth of 10 m. As the training size increases, the distribution of the high dielectric constant becomes closer to the reference model. Figure 10 indicates that, as the training size increased, the inversion results using the neural network methods became more accurate, and the features contained in the inversion model gradually aligned with the reference model. It proved the effectiveness of using neural network methods for MCMC.

Figure 11 shows the mean of the posterior distribution of the inversion results. The results of the mean model indicated that, even if the neural network was trained only 1000 times, its mean could reflect the distribution characteristics of the underground dielectric permittivity. As the training size increased, the details of the mean of the inversion results increased and became closer to the reference model.

Figure 12 shows the inversion results using a trained neural network without considering the modeling errors. The first column is the true model, and the remaining four columns are the inversion results. In the inversion results, without explaining the modeling errors, although there is a distribution of high dielectric constant underground, it is not concentrated at a depth of 10 m underground, which is inconsistent with the characteristics of the reference model. Compared with Figure 10, the inversion results without considering modeling errors in Figure 12 performed worse than those considering modeling errors. When the modeling errors were not explained, the inversion results were different from the reference model, and even when the training size was 20,000, the inversion results were not ideal.

The mean of the inversion results without considering modeling errors is shown in Figure 13. The mean of the inversion results can more intuitively reflect the impact of modeling errors on the inversion results. Compared with Figure 10, the distribution positions of the high dielectric permittivity in Figure 13 are significantly different from the reference model.

We subtracted the inversion results from the reference model to obtain the residual distribution, as shown in Figure 14. Regardless of whether the modeling errors were explained or not, as the size of the training neural network increased, the residual of the inversion results decreased, which is consistent with our analysis of the inversion results in Figure 10 and Figure 12. When the training frequency was the same, the residual of the inversion results considering modeling errors was significantly smaller than that without considering modeling errors, which proves the effectiveness of the Monte Carlo inversion method in explaining modeling errors, thus improving the accuracy of the inversion results.

In order to analyze the efficiency of the neural network methods, we conducted 100 tests on different, forward models in the extended metropolitan algorithm and recorded the calculation time, as shown in

Table 2. Computation time analysis of different forward models.

Forward Model	${\mathit{g}}_{\mathbf{F}\mathbf{W}\mathbf{I}}$	${\mathit{g}}_{1000}$	${\mathit{g}}_{5000}$	${\mathit{g}}_{10000}$	${\mathit{g}}_{20000}$
Calculation Time (s)	265.30	1.09	0.96	1.02	0.98

. Compared to the full-waveform forward model, the forward model based on neural networks had a significantly improved computational efficiency.

4. Discussion and Future Work

This article uses residual networks and full-waveform data from ground-penetrating radar for inversion. We analyzed the errors and efficiency of the network methods. Regarding our current work, we have two tasks in the future.

(1) At present, our data mainly focus on processing simulated data. We will study how to apply this method to some complex models, as the field data situation may be more complex. The underground structure of field data is variable and requires inversion based on different actual situations. The ultimate goal is to apply this method to field data processing. To apply this method to the industry, a large number of field-data-processing cases are required, which is a challenge for our next scientific study.

(2) There were some obvious distortion points in the simulated waveform generated by the neural network with the 1000 training size. As the size of the training neural network increased, the distortion significantly disappeared in the simulated waveform. In the future, research can be conducted on the training frequency and accuracy of the network to further optimize the network structure.

5. Conclusions

This article combines a ResNet and the MCMC method to solve the full-waveform inversion problem of cross-hole ground-penetrating radar. We replaced the complex forward model based on the 2D FDTD solution of Maxwell’s equations with a ResNet. We used neural networks with different training sizes to invert the dielectric permittivity. The inversion results indicated that, although a neural network with a training size of 1000 could not reflect the correct features of the reference model when the training size was greater than 5000, the inversion results of the neural network contained features consistent with the reference model. The analysis of the inversion results showed that, as the size of the training increased, the accuracy of the inversion results increased.

By utilizing the advantages of the Monte Carlo methods, the modeling errors of neural networks can be quantified and explained. By comparing the inversion results of explaining modeling errors and not explaining modeling errors, we found that modeling errors had a significant impact on the inversion results, and the residual analysis also proved this. Explaining modeling errors can effectively improve the accuracy of inversion results. In terms of computational efficiency, compared with accurate full-waveform forward models, the forward model based on a ResNet had a significantly improved computational efficiency. The combination of the MCMC method and a ResNet is an effective method for solving inversion problems that greatly improves computational efficiency while obtaining reliable inversion results.