SAR-to-Optical Image Translation via an Interpretable Network
Abstract
1. Introduction
- A thermodynamic perspective is taken on the S2O image translation task, and accordingly, we propose a novel S2O-TDN that follows a clear and interpretable design principle. This is the first time that thermodynamic theories are brought into S2O image translation networks.
- Inspired by the third order finite difference equation (TFD), i.e., the TFD residual block was used to build the backbone network. Motivated by the first law of thermodynamics (FLT), i.e., the FLT-guided branch was developed. They help the proposed S2O-TDN to learn a better nonlinear mapping between inter-domain features for S2O image translation while preserving the geometric structures by mitigating the pixel diffusion problem.
- The proposed S2O-TDN model was experimentally tested on the currently popular SEN1-2 dataset with improved objective metrics and visual image quality. Optical images were generated with a finer structure and improved geometry.
2. Related Work
2.1. SAR-to-Optical Image Translation
2.2. Neural Partial Differential Equations
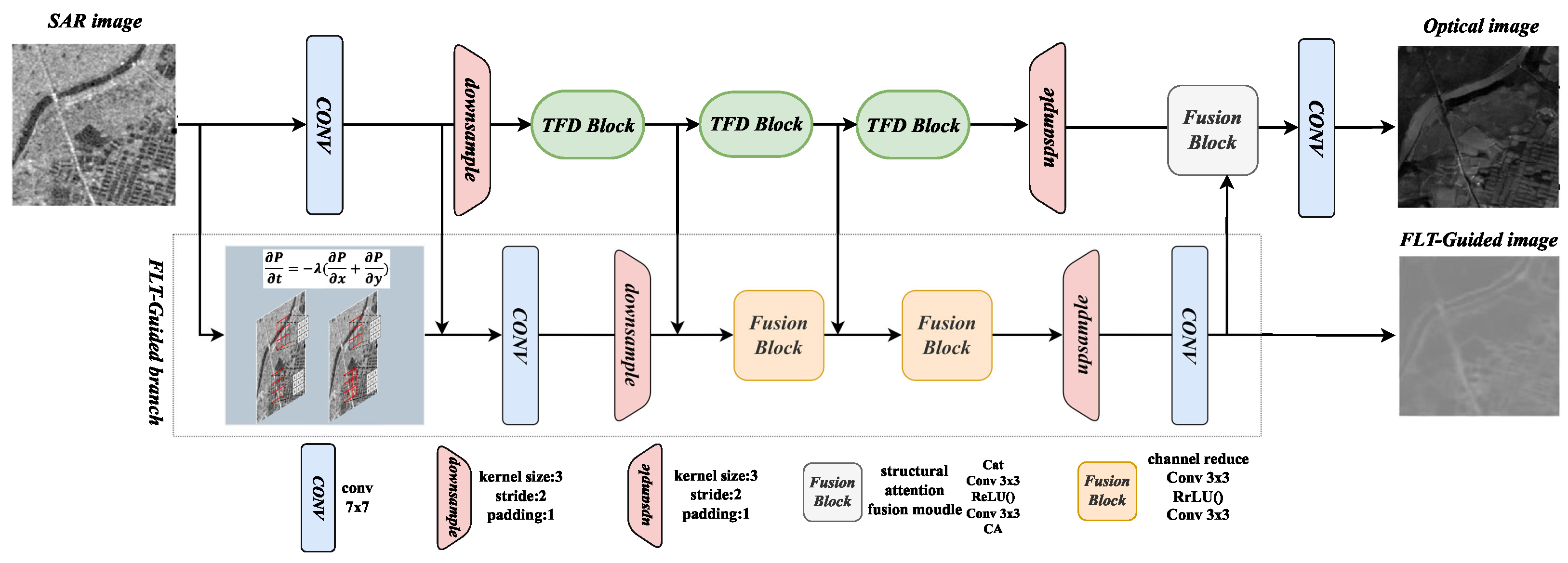
3. Method
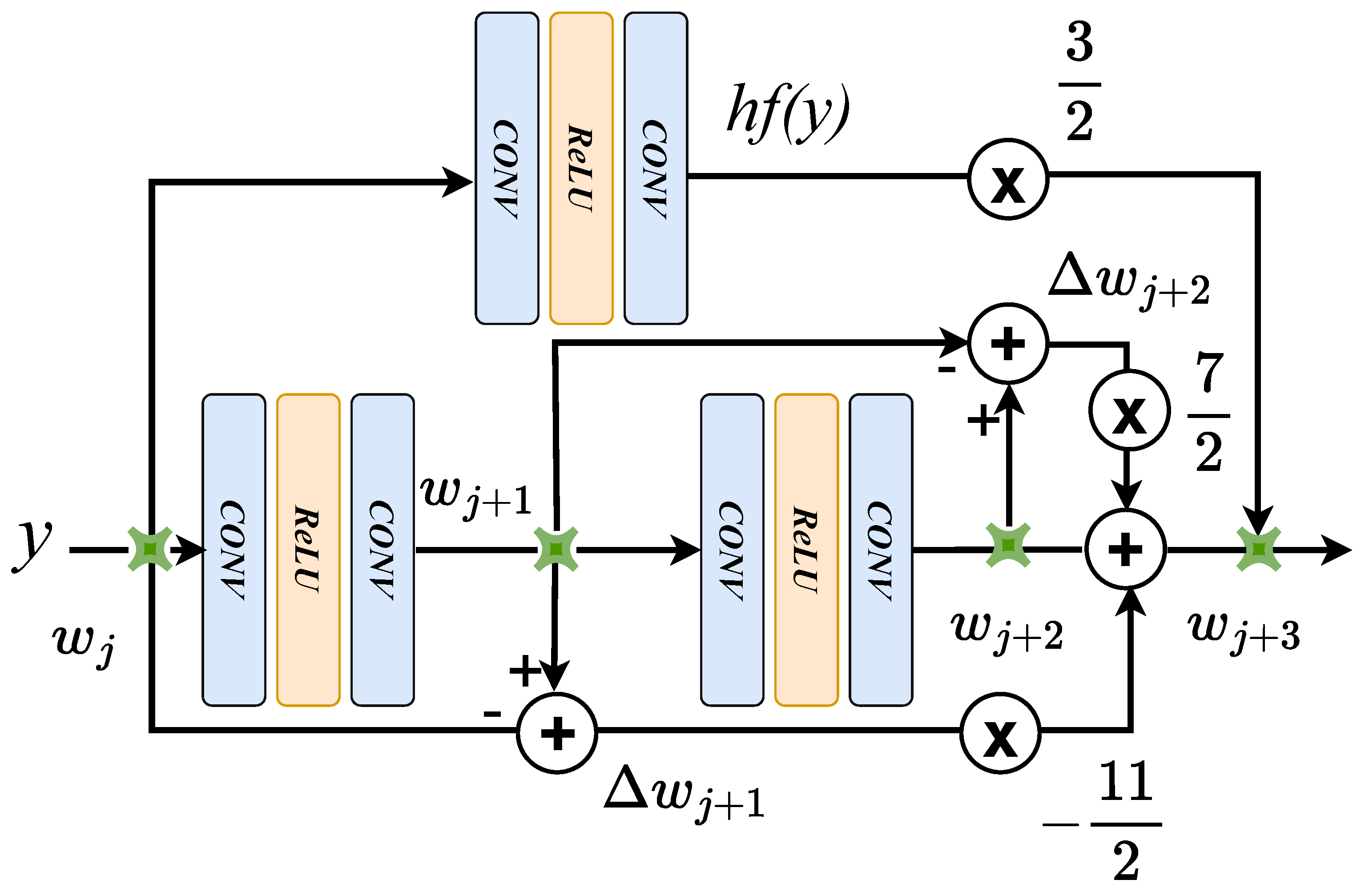
3.1. Third-Order Finite Difference Residual Structure
3.2. The First Law of the Thermodynamics Guided Branch
3.3. The Overall Structure of S2O-TDN
3.4. Loss Function
4. Experimental Results and Analysis
4.1. Datasets
4.2. Implementation Details
4.3. Quantitative Results
4.4. Visual Results
4.4.1. Comparison of Optical Images
4.4.2. Comparison of Structural Information
5. Discussion
5.1. Impact of the Key Components of S2O-TDN
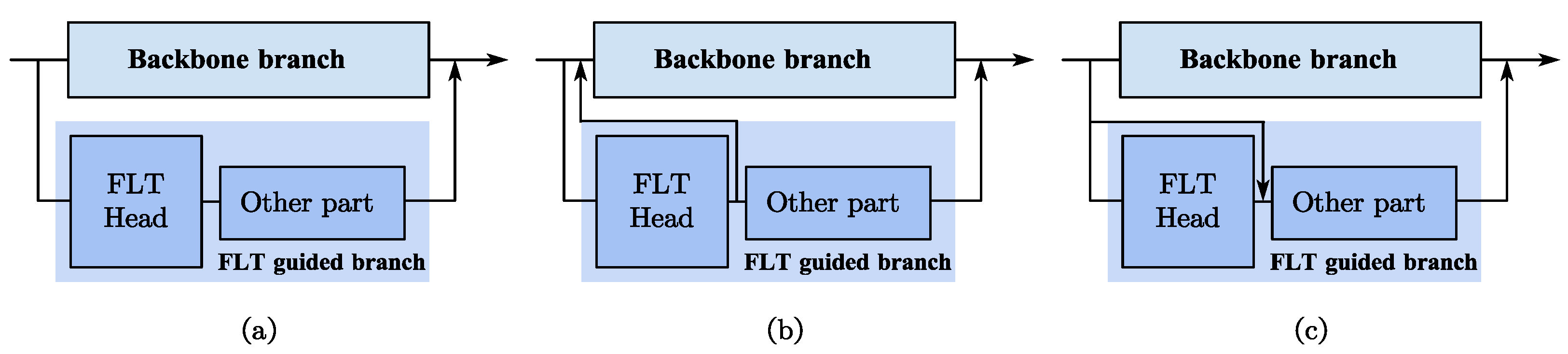
5.2. Variant Designs of the FLT-Guided Branch
5.3. Model Complexity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, X.; Zhao, J.; Wei, Z.; Wang, N.; Gao, X. SAR-to-optical image translation based on improved CGAN. Pattern Recognit. 2022, 121, 108208. [Google Scholar] [CrossRef]
- Auer, S.; Hinz, S.; Bamler, R. Ray-tracing simulation techniques for understanding high-resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1445–1456. [Google Scholar] [CrossRef]
- Pu, W. Deep SAR Imaging and Motion Compensation. IEEE Trans. Image Process. 2021, 30, 2232–2247. [Google Scholar] [CrossRef]
- Simard, M.; Degrandi, G. Analysis of speckle noise contribution on wavelet decomposition of SAR images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1953–1962. [Google Scholar] [CrossRef]
- Guo, Z.; Guo, H.; Liu, X.; Zhou, W.; Wang, Y.; Fan, Y. Sar2color: Learning Imaging Characteristics of SAR Images for SAR-to-Optical Transformation. Remote Sens. 2022, 14, 3740. [Google Scholar] [CrossRef]
- Jordan, R.; Huneycutt, B.; Werner, M. The SIR-C/X-SAR Synthetic Aperture Radar system. IEEE Trans. Geosci. Remote Sens. 1995, 33, 829–839. [Google Scholar] [CrossRef]
- Gray, A.; Vachon, P.; Livingstone, C.; Lukowski, T. Synthetic aperture radar calibration using reference reflectors. IEEE Trans. Geosci. Remote Sens. 1990, 28, 374–383. [Google Scholar] [CrossRef]
- Villano, M.; Krieger, G.; Papathanassiou, K.P.; Moreira, A. Monitoring dynamic processes on the earth’s surface using synthetic aperture radar. In Proceedings of the 2018 IEEE International Conference on Environmental Engineering (EE), Milan, Italy, 12–14 March 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Fu, S.; Xu, F.; Jin, Y.Q. Reciprocal translation between SAR and optical remote sensing images with cascaded-residual adversarial networks. Sci. China Inf. Sci. 2021, 64, 1–15. [Google Scholar] [CrossRef]
- Grohnfeldt, C.; Schmitt, M.; Zhu, X. A conditional generative adversarial network to fuse sar and multispectral optical data for cloud removal from sentinel-2 images. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1726–1729. [Google Scholar]
- Tomiyasu, K. Tutorial review of synthetic-aperture radar (SAR) with applications to imaging of the ocean surface. Proc. IEEE 1978, 66, 563–583. [Google Scholar] [CrossRef]
- Paolo, F.; Lin, T.t.T.; Gupta, R.; Goodman, B.; Patel, N.; Kuster, D.; Kroodsma, D.; Dunnmon, J. xView3-SAR: Detecting Dark Fishing Activity Using Synthetic Aperture Radar Imagery. In Proceedings of the Advances in Neural Information Processing Systems 35, NeurIPS 2022, New Orleans, LA, USA, 28 November 2022; Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., Oh, A., Eds.; Curran Associates, Inc.: Nice, France, 2022; Volume 35, pp. 37604–37616. [Google Scholar]
- Huang, L.; Yang, J.; Meng, J.; Zhang, J. Underwater Topography Detection and Analysis of the Qilianyu Islands in the South China Sea Based on GF-3 SAR Images. Remote Sens. 2020, 13, 76. [Google Scholar] [CrossRef]
- Argenti, F.; Bianchi, T.; Lapini, A.; Alparone, L. Simplified MAP despeckling based on Laplacian-Gaussian modeling of undecimated wavelet coefficients. In Proceedings of the 19th IEEE European Signal Processing Conference, Barcelona, Spain, 29 August–2 September 2011; pp. 1140–1144. [Google Scholar]
- Bayramov, E.; Buchroithner, M.; Kada, M.; Zhuniskenov, Y. Quantitative Assessment of Vertical and Horizontal Deformations Derived by 3D and 2D Decompositions of InSAR Line-of-Sight Measurements to Supplement Industry Surveillance Programs in the Tengiz Oilfield (Kazakhstan). Remote Sens. 2021, 13, 2579. [Google Scholar] [CrossRef]
- Merkle, N.; Auer, S.; Müller, R.; Reinartz, P. Exploring the potential of conditional adversarial networks for optical and SAR image matching. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1811–1820. [Google Scholar] [CrossRef]
- Wang, P.; Patel, V.M. Generating high quality visible images from SAR images using CNNs. In Proceedings of the 2018 IEEE Radar Conference, Oklahoma City, OK, USA, 23–27 April 2018; pp. 570–575. [Google Scholar]
- Wang, H.; Zhang, Z.; Hu, Z.; Dong, Q. SAR-to-Optical Image Translation with Hierarchical Latent Features. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5233812. [Google Scholar] [CrossRef]
- Wei, J.; Zou, H.; Sun, L.; Cao, X.; Li, M.; He, S.; Liu, S. Generative Adversarial Network for SAR-to-Optical Image Translation with Feature Cross-Fusion Inference. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 6025–6028. [Google Scholar] [CrossRef]
- Quan, D.; Wei, H.; Wang, S.; Lei, R.; Duan, B.; Li, Y.; Hou, B.; Jiao, L. Self-Distillation Feature Learning Network for Optical and SAR Image Registration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4706718. [Google Scholar] [CrossRef]
- Zhao, Y.; Celik, T.; Liu, N.; Li, H.C. A Comparative Analysis of GAN-Based Methods for SAR-to-Optical Image Translation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3512605. [Google Scholar] [CrossRef]
- Zhang, M.; He, C.; Zhang, J.; Yang, Y.; Peng, X.; Guo, J. SAR-to-Optical Image Translation via Neural Partial Differential Equations. In Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence, IJCAI-22, Messe Wien, Vienna, Austria, 23–29 July 2022; Raedt, L.D., Ed.; International Joint Conferences on Artificial Intelligence Organization: Eindhoven, The Netherlands, 2022; Volume 7, pp. 1644–1650. [Google Scholar] [CrossRef]
- Fuentes Reyes, M.; Auer, S.; Merkle, N.; Henry, C.; Schmitt, M. SAR-to-Optical Image Translation Based on Conditional Generative Adversarial Networks—Optimization, Opportunities and Limits. Remote Sens. 2019, 11, 2067. [Google Scholar] [CrossRef]
- Ebel, P.; Schmitt, M.; Zhu, X.X. Cloud Removal in Unpaired Sentinel-2 Imagery Using Cycle-Consistent GAN and SAR-Optical Data Fusion. In Proceedings of the IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2065–2068. [Google Scholar] [CrossRef]
- Fornaro, G.; Reale, D.; Serafino, F. Four-Dimensional SAR Imaging for Height Estimation and Monitoring of Single and Double Scatterers. IEEE Trans. Geosci. Remote Sens. 2009, 47, 224–237. [Google Scholar] [CrossRef]
- Laine, M.; Vuorinen, A. Basics of thermal field theory. Lect. Notes Phys. 2016, 925, 1701-01554. [Google Scholar]
- Zhang, M.; Wu, Q.; Guo, J.; Li, Y.; Gao, X. Heat Transfer-Inspired Network for Image Super-Resolution Reconstruction. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Fu, S.; Xu, F. Differentiable SAR Renderer and Image-Based Target Reconstruction. IEEE Trans. Image Process. 2022, 31, 6679–6693. [Google Scholar] [CrossRef]
- Chen, S.W.; Cui, X.C.; Wang, X.S.; Xiao, S.P. Speckle-Free SAR Image Ship Detection. IEEE Trans. Image Process. 2021, 30, 5969–5983. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, B.; Wang, Y.; Cui, Z.; Chen, L. SAR-to-Optical Image Translating Through Generate-Validate Adversarial Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4506905. [Google Scholar] [CrossRef]
- Hwang, J.; Shin, Y. SAR-to-Optical Image Translation Using SSIM Loss Based Unpaired GAN. In Proceedings of the 2022 13th International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 19–21 October 2022; pp. 917–920. [Google Scholar] [CrossRef]
- Pan, Y.; Khan, I.A.; Meng, H. SAR-to-optical image translation using multi-stream deep ResCNN of information reconstruction. Expert Syst. Appl. 2023, 224, 120040. [Google Scholar] [CrossRef]
- Romano, G.; Diaco, M.; Barretta, R. Variational formulation of the first principle of continuum thermodynamics. Contin. Mech. Thermodyn. 2010, 22, 177–187. [Google Scholar] [CrossRef]
- Cai, R.G.; Kim, S.P. First law of thermodynamics and Friedmann equations of Friedmann-Robertson-Walker universe. J. High Energy Phys. 2005, 2005, 050. [Google Scholar] [CrossRef]
- Guo, J.; He, C.; Zhang, M.; Li, Y.; Gao, X.; Song, B. Edge-Preserving Convolutional Generative Adversarial Networks for SAR-to-Optical Image Translation. Remote Sens. 2021, 13, 3575. [Google Scholar] [CrossRef]
- Tang, H.; Xu, D.; Yan, Y.; Corso, J.J.; Torr, P.; Sebe, N. Multi-Channel Attention Selection GANs for Guided Image-to-Image Translation. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020. [Google Scholar]
- Dong, G.; Liu, H. Global Receptive-Based Neural Network for Target Recognition in SAR Images. IEEE Trans. Cybern. 2021, 51, 1954–1967. [Google Scholar] [CrossRef]
- Zuo, Z.; Li, Y. A SAR-to-Optical Image Translation Method Based on PIX2PIX. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 3026–3029. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, N.; Li, Y.; Gao, X. Deep latent low-rank representation for face sketch synthesis. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3109–3123. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, N.; Li, Y.; Gao, X. Neural probabilistic graphical model for face sketch synthesis. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2623–2637. [Google Scholar] [CrossRef]
- Gomez, R.; Liu, Y.; De Nadai, M.; Karatzas, D.; Lepri, B.; Sebe, N. Retrieval guided unsupervised multi-domain image to image translation. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 3164–3172. [Google Scholar]
- Li, S.; Günel, S.; Ostrek, M.; Ramdya, P.; Fua, P.; Rhodin, H. Deformation-Aware Unpaired Image Translation for Pose Estimation on Laboratory Animals. In Proceedings of the 2020 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–18 June 2020; pp. 13155–13165. [Google Scholar] [CrossRef]
- Doi, K.; Sakurada, K.; Onishi, M.; Iwasaki, A. GAN-Based SAR-to-Optical Image Translation with Region Information. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 17 February 2020; pp. 2069–2072. [Google Scholar] [CrossRef]
- Xiong, Q.; Li, G.; Yao, X.; Zhang, X. SAR-to-Optical Image Translation and Cloud Removal Based on Conditional Generative Adversarial Networks: Literature Survey, Taxonomy, Evaluation Indicators, Limits and Future Directions. Remote Sens. 2023, 15, 1137. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, X.; Liu, M.; Zou, X.; Zhu, L.; Ruan, X. Comparative analysis of edge information and polarization on sar-to-optical translation based on conditional generative adversarial networks. Remote Sens. 2021, 13, 128. [Google Scholar] [CrossRef]
- Li, H.; Gu, C.; Wu, D.; Cheng, G.; Guo, L.; Liu, H. Multiscale Generative Adversarial Network Based on Wavelet Feature Learning for SAR-to-Optical Image Translation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, J.; Lu, X. Feature-guided SAR-to-optical image translation. IEEE Access 2020, 8, 70925–70937. [Google Scholar] [CrossRef]
- Wang, L.; Xu, X.; Yu, Y.; Yang, R.; Gui, R.; Xu, Z.; Pu, F. SAR-to-optical image translation using supervised cycle-consistent adversarial networks. IEEE Access 2019, 7, 129136–129149. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, J.; Li, M.; Zhou, H.; Yu, T. Quality Assessment of SAR-to-Optical Image Translation. Remote Sens. 2020, 12, 3472. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, W.; Yang, J.; Li, W. SAR Target Recognition Using cGAN-Based SAR-to-Optical Image Translation. Remote Sens. 2022, 14, 1793. [Google Scholar] [CrossRef]
- Wei, J.; Zou, H.; Sun, L.; Cao, X.; He, S.; Liu, S.; Zhang, Y. CFRWD-GAN for SAR-to-Optical Image Translation. Remote Sens. 2023, 15, 2547. [Google Scholar] [CrossRef]
- Du, W.L.; Zhou, Y.; Zhu, H.; Zhao, J.; Shao, Z.; Tian, X. A Semi-Supervised Image-to-Image Translation Framework for SAR–Optical Image Matching. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Zhang, M.; Zhang, R.; Zhang, J.; Guo, J.; Li, Y.; Gao, X. Dim2Clear Network for Infrared Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, R.; Yang, Y.; Bai, H.; Zhang, J.; Guo, J. ISNet: Shape Matters for Infrared Small Target Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 877–886. [Google Scholar]
- Zhang, M.; Yue, K.; Zhang, J.; Li, Y.; Gao, X. Exploring Feature Compensation and Cross-Level Correlation for Infrared Small Target Detection. In Proceedings of the 30th ACM International Conference on Multimedia, New York, NY, USA, 10–14 October 2022; MM ‘22. pp. 1857–1865. [Google Scholar] [CrossRef]
- Zhang, M.; Bai, H.; Zhang, J.; Zhang, R.; Wang, C.; Guo, J.; Gao, X. RKformer: Runge-Kutta Transformer with Random-Connection Attention for Infrared Small Target Detection. In Proceedings of the 30th ACM International Conference on Multimedia, New York, NY, USA, 10–14 October 2022; MM ‘22. pp. 1730–1738. [Google Scholar] [CrossRef]
- Ghiasi, A.; Kazemi, H.; Borgnia, E.; Reich, S.; Shu, M.; Goldblum, M.; Wilson, A.G.; Goldstein, T. What do Vision Transformers Learn? A Visual Exploration. arXiv 2022, arXiv:2212.06727. [Google Scholar]
- Hu, Y.; Yang, J.; Chen, L.; Li, K.; Sima, C.; Zhu, X.; Chai, S.; Du, S.; Lin, T.; Wang, W.; et al. Planning-Oriented Autonomous Driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 17853–17862. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Zhang, M.; Xin, J.; Zhang, J.; Tao, D.; Gao, X. Curvature Consistent Network for Microscope Chip Image Super-Resolution. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 10538–10551. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wu, Q.; Zhang, J.; Gao, X.; Guo, J.; Tao, D. Fluid Micelle Network for Image Super-Resolution Reconstruction. IEEE Trans. Cybern. 2022, 53, 578–591. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Tao, D. FAMED-Net: A fast and accurate multi-scale end-to-end dehazing network. IEEE Trans. Image Process. 2019, 29, 72–84. [Google Scholar] [CrossRef] [PubMed]
- Weinan, E. A proposal on machine learning via dynamical systems. Commun. Math. Stat. 2017, 1, 1–11. [Google Scholar]
- Lu, Y.; Zhong, A.; Li, Q.; Dong, B. Beyond finite layer neural networks: Bridging deep architectures and numerical differential equations. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 3276–3285. [Google Scholar]
- Yin, S.; Yang, X.; Lu, R.; Deng, Z.; Yang, Y.H. Visual Attention and ODE-inspired Fusion Network for image dehazing. Eng. Appl. Artif. Intell. 2024, 130, 107692. [Google Scholar] [CrossRef]
- Yin, S.; Hu, S.; Wang, Y.; Wang, W.; Yang, Y.H. Adams-based hierarchical features fusion network for image dehazing. Neural Netw. 2023, 163, 379–394. [Google Scholar] [CrossRef]
- Chen, R.T.Q.; Rubanova, Y.; Bettencourt, J.; Duvenaud, D. Neural Ordinary Differential Equations. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, NIPS 2018, Red Hook, NY, USA, 3–8 December 2018; pp. 6572–6583. [Google Scholar]
- He, X.; Mo, Z.; Wang, P.; Liu, Y.; Yang, M.; Cheng, J. Ode-inspired network design for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1732–1741. [Google Scholar]
- Han, J.; Shoeiby, M.; Petersson, L.; Armin, M.A. Dual Contrastive Learning for Unsupervised Image-to-Image Translation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021. [Google Scholar]
- Tang, H.; Liu, H.; Xu, D.; Torr, P.H.S.; Sebe, N. AttentionGAN: Unpaired Image-to-Image Translation using Attention-Guided Generative Adversarial Networks. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 1972–1987. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Change Loy, C.; Lin, D. Polynet: A pursuit of structural diversity in very deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(cvpr), Honolulu, HI, USA, 21–26 July 2017; pp. 718–726. [Google Scholar]



| Method | PSNR | SSIM | |
|---|---|---|---|
| Pix2pix | Test 1 | 17.18 | 0.3452 |
| Test 2 | 15.93 | 0.2664 | |
| Test 3 | 16.46 | 0.2715 | |
| CycleGAN | Test 1 | 16.51 | 0.3422 |
| Test 2 | 15.13 | 0.2956 | |
| Test 3 | 15.91 | 0.2896 | |
| S-CycleGAN | Test 1 | 18.05 | 0.4082 |
| Test 2 | 15.67 | 0.2899 | |
| Test 3 | 16.53 | 0.2841 | |
| FGGAN | Test 1 | 18.56 | 0.4438 |
| Test 2 | 15.67 | 0.3625 | |
| Test 3 | 16.53 | 0.3302 | |
| EPCGAN | Test 1 | 18.89 | 0.4491 |
| Test 2 | 16.54 | 0.3615 | |
| Test 3 | 17.46 | 0.3454 | |
| AttentionGAN | Test 1 | 12.50 | 0.3239 |
| Test 2 | 14.70 | 0.1914 | |
| Test 3 | 15.18 | 0.2374 | |
| S2O-TDN | Test 1 | 19.16 | 0.4736 |
| Test 2 | 17.93 | 0.4053 | |
| Test 3 | 18.26 | 0.3705 |
| Method | PSNR | SSIM | |
|---|---|---|---|
| Base | Test 1 | 18.19 | 0.4351 |
| Test 2 | 16.99 | 0.3696 | |
| Test 3 | 16.96 | 0.3329 | |
| +FLT-guided | Test 1 | 16.61 | 0.4529 |
| Test 2 | 17.29 | 0.3702 | |
| Test 3 | 17.53 | 0.3480 | |
| +TFD | Test 1 | 18.59 | 0.4441 |
| Test 2 | 17.60 | 0.3825 | |
| Test 3 | 17.96 | 0.3596 | |
| +Poly2 +FLT-guided | Test 1 | 18.78 | 0.4644 |
| Test 2 | 17.87 | 0.3986 | |
| Test 3 | 17.33 | 0.3541 | |
| +RK2 +FLT-guided | Test 1 | 18.54 | 0.4408 |
| Test 2 | 17.12 | 0.3814 | |
| Test 3 | 16.69 | 0.3329 | |
| +TFD +FLT-guided | Test 1 | 19.16 | 0.4736 |
| Test 2 | 17.94 | 0.4053 | |
| Test 3 | 18.26 | 0.3705 |
| Method | PSNR | SSIM | |
|---|---|---|---|
| Ordinary conv | Test 1 | 18.23 | 0.4370 |
| Test 2 | 17.34 | 0.3872 | |
| Test 3 | 17.69 | 0.3585 | |
| FLT Head | Test 1 | 19.16 | 0.4736 |
| Test 2 | 17.94 | 0.4053 | |
| Test 3 | 18.26 | 0.3705 |
| Method | PSNR | SSIM | |
|---|---|---|---|
| FLT Head | Test 1 | 19.16 | 0.4736 |
| Test 2 | 17.94 | 0.4053 | |
| Test 3 | 18.26 | 0.3705 | |
| Roberts filters | Test 1 | 16.35 | 0.3578 |
| Test 2 | 16.28 | 0.3144 | |
| Test 3 | 15.84 | 0.2917 | |
| Prewitt filters | Test 1 | 18.37 | 0.4527 |
| Test 2 | 17.11 | 0.3918 | |
| Test 3 | 17.84 | 0.3429 | |
| Sobel filters | Test 1 | 17.98 | 0.4219 |
| Test 2 | 17.35 | 0.4011 | |
| Test 3 | 17.78 | 0.3315 |
| Method | PSNR | SSIM | |
|---|---|---|---|
| S2O-TDN | Test 1 | 19.16 | 0.4736 |
| Test 2 | 17.94 | 0.4053 | |
| Test 3 | 18.26 | 0.3705 | |
| S2O-TDN(b) | Test 1 | 19.21 | 0.4827 |
| Test 2 | 17.74 | 0.3969 | |
| Test 3 | 18.18 | 0.3659 | |
| S2O-TDN(c) | Test 1 | 18.96 | 0.4505 |
| Test 2 | 17.80 | 0.3944 | |
| Test 3 | 17.88 | 0.3613 |
| Method | Paramrers (M) | FLOPs (G) | Execution Time (s) |
|---|---|---|---|
| Pix2pix | 54.40 | 17.84 | 2.263 |
| CycleGAN | 11.37 | 56.01 | 0.805 |
| FG-GAN | 45.58 | 62.04 | 3.572 |
| EPCGAN | 2.515 | 64.53 | 0.859 |
| S2O-TDN | 2.063 | 62.12 | 0.783 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Zhang, P.; Zhang, Y.; Yang, M.; Li, X.; Dong, X.; Yang, L. SAR-to-Optical Image Translation via an Interpretable Network. Remote Sens. 2024, 16, 242. https://doi.org/10.3390/rs16020242
Zhang M, Zhang P, Zhang Y, Yang M, Li X, Dong X, Yang L. SAR-to-Optical Image Translation via an Interpretable Network. Remote Sensing. 2024; 16(2):242. https://doi.org/10.3390/rs16020242
Chicago/Turabian StyleZhang, Mingjin, Peng Zhang, Yuhan Zhang, Minghai Yang, Xiaofeng Li, Xiaogang Dong, and Luchang Yang. 2024. "SAR-to-Optical Image Translation via an Interpretable Network" Remote Sensing 16, no. 2: 242. https://doi.org/10.3390/rs16020242
APA StyleZhang, M., Zhang, P., Zhang, Y., Yang, M., Li, X., Dong, X., & Yang, L. (2024). SAR-to-Optical Image Translation via an Interpretable Network. Remote Sensing, 16(2), 242. https://doi.org/10.3390/rs16020242







