Rao and Wald Tests for Moving Target Detection in Forward Scatter Radar
Abstract
1. Introduction
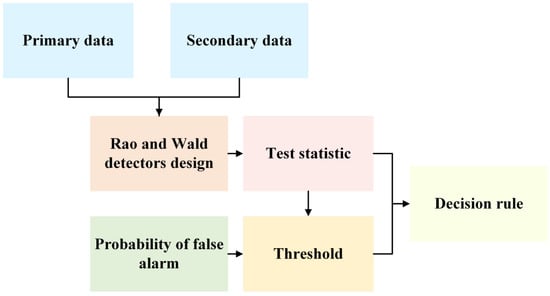
2. Design of Adaptive Detectors with Secondary Data
2.1. Adaptive Complex Parameter Rao Detector with Secondary Data
2.2. Adaptive Complex Parameter Wald Detector with Secondary Data
3. Design of Adaptive Detectors without Secondary Data
3.1. Adaptive Complex Parameter Rao Detector without Secondary Data
3.2. Adaptive Complex Parameter Wald Detector without Secondary Data
4. The Equivalence of the Wald Test, Rao Test, and GLRT
4.1. The Equivalence of the Wald Test, Rao Test, and GLRT with Secondary Data
4.2. The Equivalence of the Wald Test, Rao Test, and GLRT without Secondary Data
5. Numerical Evaluation
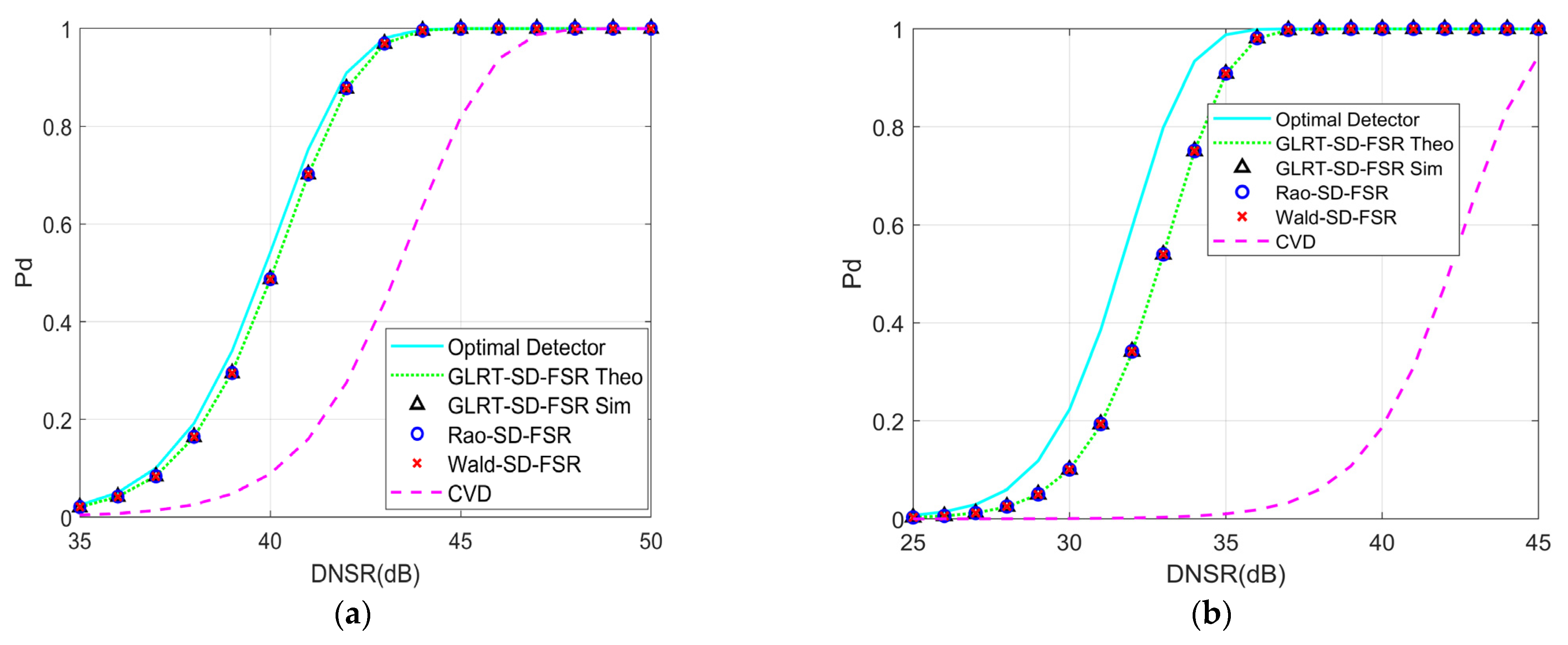
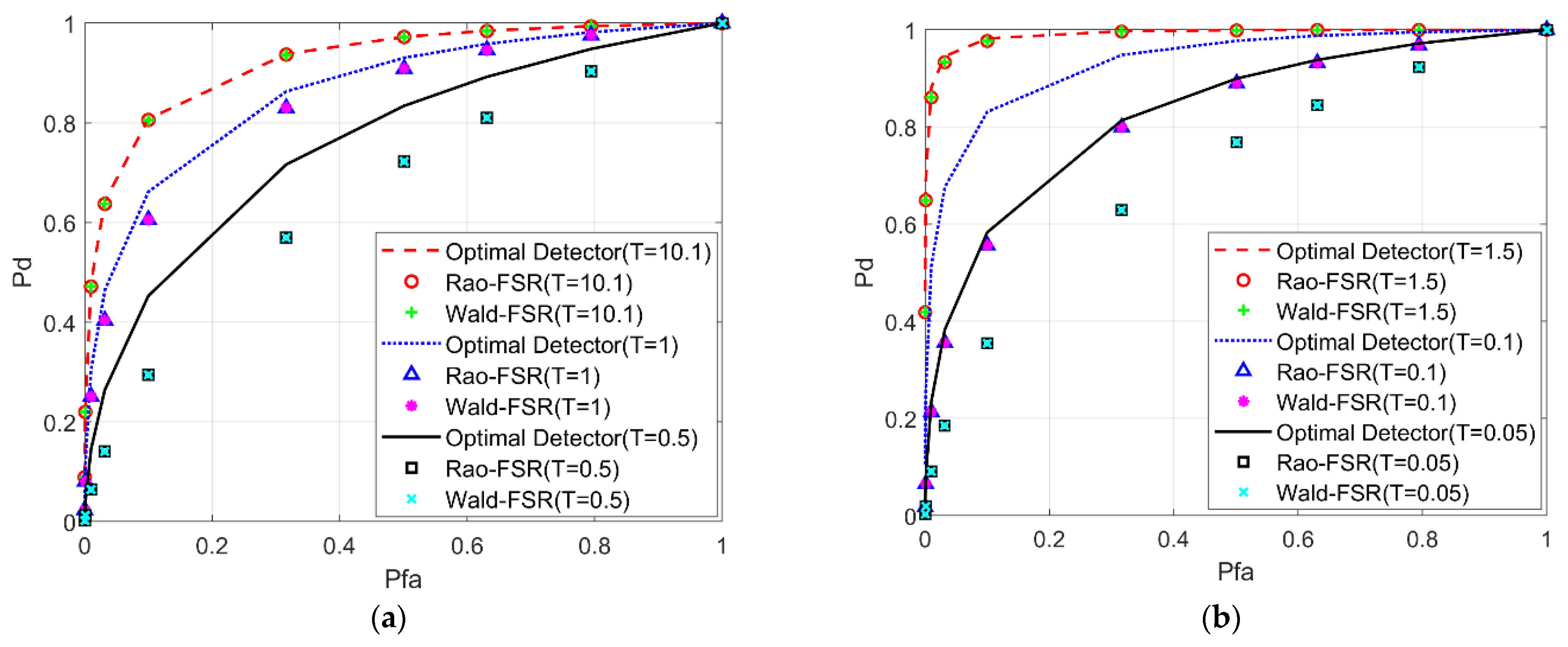
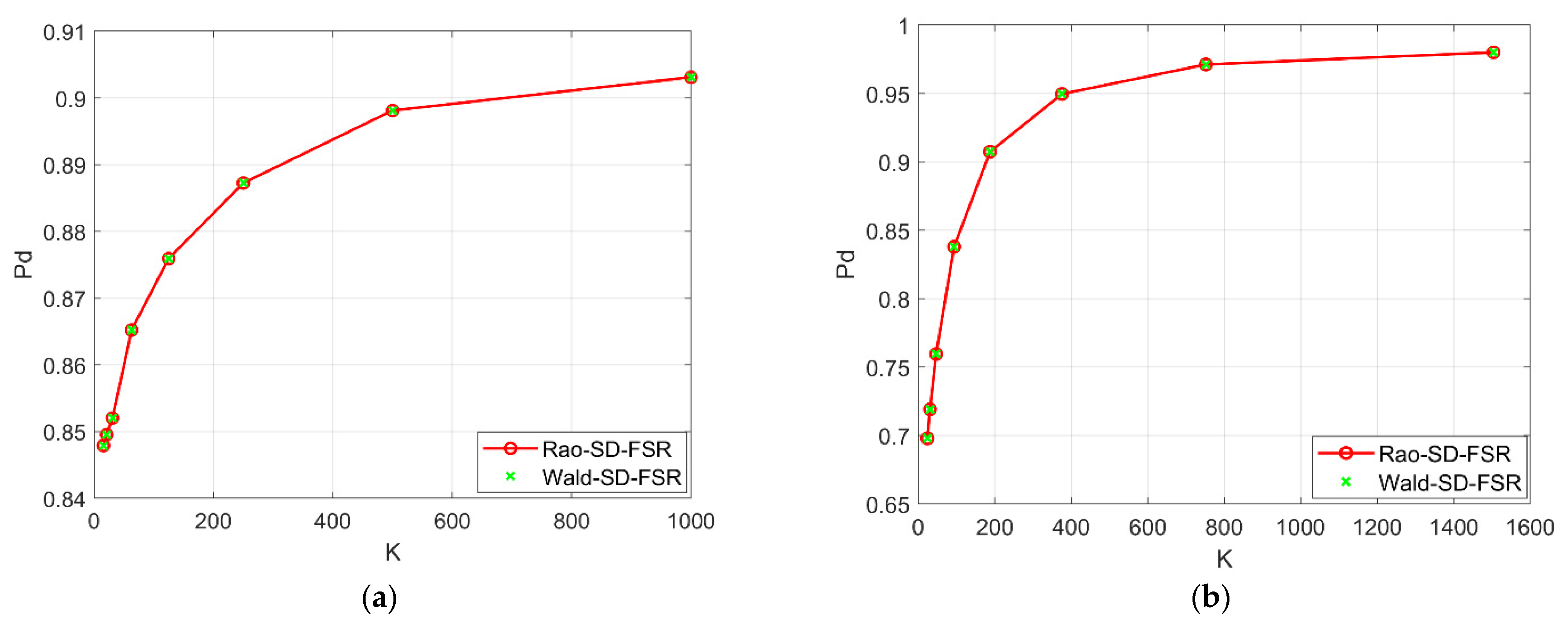
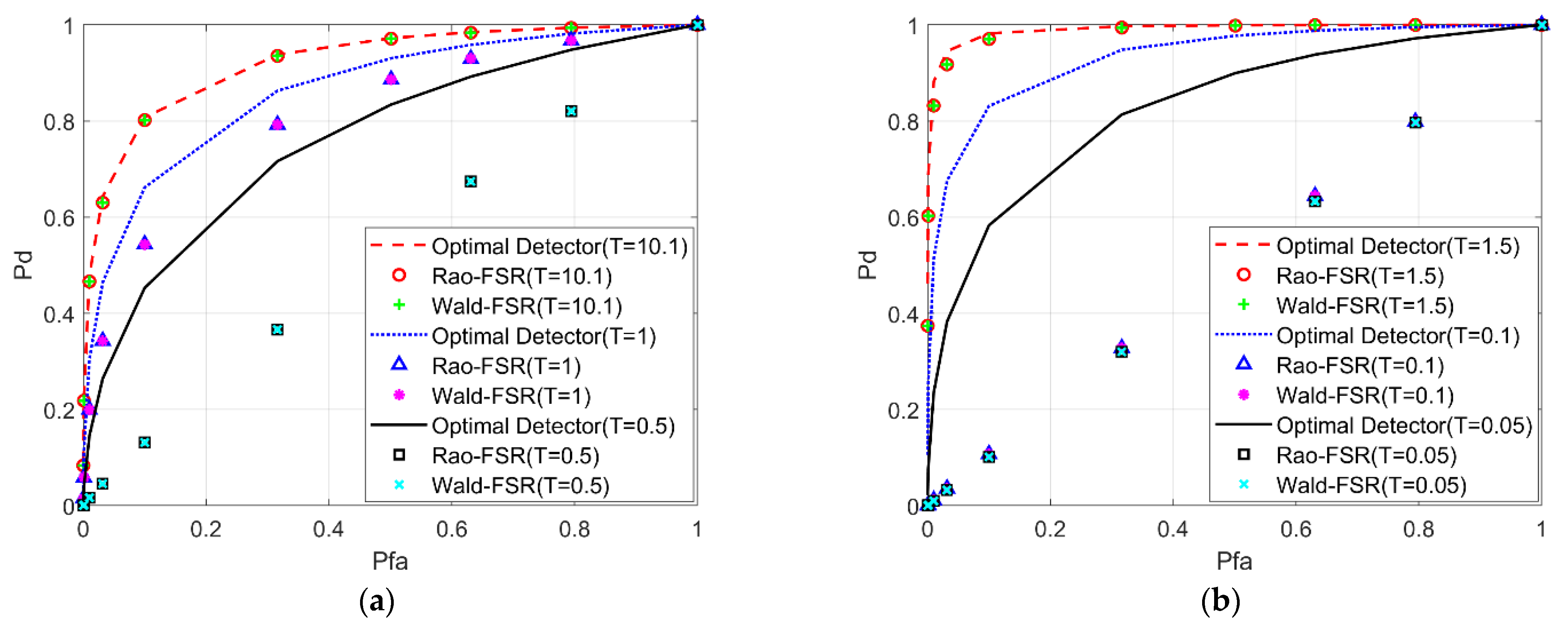
5.1. Performance Analysis of the Proposed Detectors with Secondary Data
5.2. Performance Analysis of the Proposed Detectors without Secondary Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mertens, M.; Koch, W.; Kirubarajan, T. Exploiting Doppler Blind Zone Information for Ground Moving Target Tracking with Bistatic Airborne Radar. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 130–148. [Google Scholar] [CrossRef]
- Sun, H. Conceptual Study on Bistatic Shipborne High Frequency Surface Wave Radar. IEEE Trans. Aerosp. Electron. Syst. Mag. 2018, 33, 4–13. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, T.; Zhang, L. Longtime Coherent Integration Algorithm for High-Speed Maneuvering Target Detection Using Space-Based Bistatic Radar. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5100216. [Google Scholar] [CrossRef]
- Vu, V.T.; Pettersson, M.I. Nyquist Sampling Requirements for Polar Grids in Bistatic Time-Domain Algorithms. IEEE Trans. Signal Process. 2015, 63, 457–465. [Google Scholar] [CrossRef]
- Boyle, R.J.; Wasylkiwskyj, W. Comparison of Monostatic and Bistatic Bearing Estimation Performance for Low RCS Targets. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 962–968. [Google Scholar] [CrossRef]
- Falconi, M.T.; Lombardo, P.; Pastina, D.; Marzano, F.S. A Closed-Form Model for Long- and Short-Range Forward Scatter Radar Signals from Rectangular Conductive Targets. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1370–1390. [Google Scholar] [CrossRef]
- Suberviola, I.; Mayordomo, I.; Mendizabal, J. Experimental Results of Air Target Detection with a GPS Forward-Scattering Radar. IEEE Geosci. Remote Sens. Lett. 2012, 9, 47–51. [Google Scholar] [CrossRef]
- Pairon, T.; Craeye, C.; Oestges, C. Improved Physical Optics Computation Near the Forward Scattering Region: Application to 2-D Scenarios. IEEE Trans. Antennas Propag. 2021, 69, 417–428. [Google Scholar] [CrossRef]
- Clemente, C.; Soraghan, J.J. GNSS-Based Passive Bistatic Radar for Micro-Doppler Analysis of Helicopter Rotor Blades. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 491–500. [Google Scholar] [CrossRef]
- Garvanov, I.; Kabakchiev, C.; Behar, V.; Daskalov, P. Air target detection with a GPS forward-scattering radar. In Proceedings of the 2016 19th International Symposium on Electrical Apparatus and Technologies (SIELA), Bourgas, Bulgaria, 29 May–1 June 2016. [Google Scholar]
- Ustalli, N.; Pastina, D.; Lombardo, P. Target Motion Parameters Estimation in Forward Scatter Radar. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 226–248. [Google Scholar] [CrossRef]
- Ai, X.; Zheng, Y.; Xu, Z.; Zhao, F.; Xiao, S. Characteristics of Target Crossing the Baseline in FSR: Experiment Results. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3503105. [Google Scholar] [CrossRef]
- Zheng, Y.; Ai, X.; Xu, Z.; Zhao, F.; Yang, Y. Parameter Estimation Based on Crossing Time Difference and Doppler Rate in FSR Network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4027105. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Z.; Chen, Y.; Zheng, S.; Ge, J. Forward Scatter Radar Meets Satellite: Passive Sensing of Aerial Target Using Satellite Communication Waveforms. Remote Sens. 2022, 14, 1375. [Google Scholar] [CrossRef]
- Colone, F. DVB-T-Based Passive Forward Scatter Radar: Inherent Limitations and Enabling Solutions. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1084–1104. [Google Scholar] [CrossRef]
- Contu, M.; De Luca, A.; Hristov, S.; Daniel, L.; Stove, A.; Gashinova, M.; Cherniakov, M.; Pastina, D.; Lombardo, P.; Baruzzi, A.; et al. Passive Multifrequency Forward-Scatter Radar Measurements of Airborne Targets Using Broadcasting Signals. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1067–1087. [Google Scholar] [CrossRef]
- Hamdollahzadeh, M.; Amiri, R.; Behnia, F. Moving Target Localization in Bistatic Forward Scatter Radars: Performance Study and Efficient Estimators. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1582–1594. [Google Scholar] [CrossRef]
- Kanona, M.E.A.; Ahmed, A.M.; Mirghani, M.E.; Hassan, M.K.; Abdalla, A.G.E.; Hamza, M.E. Performance Analysis of Hybrid Pre-Processing Techniques of Ground Target Classification in FSR using Neural Network. In Proceedings of the 2020 International Conference on Computer, Control, Electrical, and Electronics Engineering (ICCCEEE), Khartoum, Sudan, 26 February–1 March 2021. [Google Scholar]
- Raja Abdullah, R.S.A.; Mohd Ali, A.; Rasid, M.F.A.; Abdul Rashid, N.E.; Ahmad Salah, A.; Munawar, A. Joint Time-Frequency Signal Processing Scheme in Forward Scattering Radar with a Rotational Transmitter. Remote Sens. 2016, 8, 1028. [Google Scholar] [CrossRef]
- Hu, C.; Sizov, V.; Antoniou, M.; Gashinova, M.; Cherniakov, M. Optimal Signal Processing in Ground-Based Forward Scatter Micro Radars. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3006–3026. [Google Scholar] [CrossRef]
- Ustalli, N.; Lombardo, P.; Pastina, D. Detection Performance of a Forward Scatter Radar Using a Crystal Video Detector. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1093–1114. [Google Scholar] [CrossRef]
- Ustalli, N.; Lombardo, P.; Pastina, D. Generalized Likelihood Ratio Detection Schemes for Forward Scatter Radar. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2951–2970. [Google Scholar] [CrossRef]
- Liu, W.; Liu, J.; Hao, C.; Gao, Y.; Wang, Y.-L. Multichannel Adaptive Signal Detection: Basic Theory and Literature Review. Sci. China Inf. Sci. 2022, 65, 121301. [Google Scholar] [CrossRef]
- Liu, W.; Liu, J.; Liu, T.; Chen, H.; Wang, Y.-L. Detector Design and Performance Analysis for Target Detection in Subspace Interference. IEEE Signal Process. Lett. 2023, 30, 618–622. [Google Scholar] [CrossRef]
- Addabbo, P.; Besson, O.; Orlando, D.; Ricci, G. Adaptive Detection of Coherent Radar Targets in the Presence of Noise Jamming. IEEE Trans. Signal Process. 2019, 67, 6498–6510. [Google Scholar]
- Orlando, D.; Ricci, G.; Scharf, L.L. A Unified Theory of Adaptive Subspace Detection Part I: Detector Designs. IEEE Trans. Signal Process. 2022, 70, 4925–4938. [Google Scholar] [CrossRef]
- Xue, J.; Ma, M.; Liu, J.; Pan, M.; Xu, S.; Fang, J. Wald- and Rao-Based Detection for Maritime Radar Targets in Sea Clutter with Lognormal Texture. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5119709. [Google Scholar] [CrossRef]
- Sun, M.; Liu, W.; Liu, J.; Hao, C. Complex Parameter Rao Wald Gradient and Durbin Tests for Multichannel Signal Detection. IEEE Trans. Signal Process. 2021, 70, 117–131. [Google Scholar] [CrossRef]
- Nomakuchi, K. A Note on The Uniformly Most Powerful Tests in The Presence of Nuisance Parameters. Ann. Inst. Stat. Math. 1992, 44, 141–145. [Google Scholar] [CrossRef]
- Ciuonzo, D.; De Maio, A.; Orlando, D. A Unifying Framework for Adaptive Radar Detection in Homogeneous Plus Structured Interference—Part II: Detectors Design. IEEE Trans. Signal Process. 2016, 64, 2907–2919. [Google Scholar] [CrossRef]
- Naderpour, M.; Ghobadzadeh, A.; Tadaion, A.; Gazor, S. Generalized Wald Test for Binary Composite Hypothesis Test. IEEE Signal Process. Lett. 2015, 22, 2239–2243. [Google Scholar] [CrossRef]
- Wang, Z.; Li, G.; Chen, H. Adaptive Persymmetric Subspace Detectors in the Partially Homogeneous Environment. IEEE Trans. Signal Process. 2020, 68, 5178–5187. [Google Scholar] [CrossRef]
- Shikhaliev, A.P.; Himed, B. GLR, Rao, and Wald Tests for Distributed Parametric Detection in Subspace Interference. IEEE Trans. Signal Process. 2023, 71, 388–400. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Li, Y.; Chen, H.; Peng, M. Adaptive Subspace Signal Detection in Structured Interference Plus Compound Gaussian Sea Clutter. Remote Sens. 2022, 14, 2274. [Google Scholar] [CrossRef]
- Liu, J.; Li, J. Robust Detection in MIMO Radar with Steering Vector Mismatches. IEEE Trans. Signal Process. 2019, 67, 5270–5280. [Google Scholar] [CrossRef]
- Jing, X.; Su, H.; Shen, L.; Mao, Z.; Jia, C. Adaptive Radar Detection in the Clutter and Noise Cover Pulse Jamming Environment. Signal Process. 2023, 205, 108852. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, W.; Zaimbashi, A.; Li, H. Persymmetric Adaptive Array Detection of Spread Spectrum Signals. IEEE Trans. Inf. Theory 2020, 66, 7828–7834. [Google Scholar] [CrossRef]
- De Maio, A.; Han, S.; Orlando, D. Adaptive Radar Detectors Based on the Observed FIM. IEEE Trans. Signal Process. 2018, 66, 3838–3847. [Google Scholar] [CrossRef]
- Xue, J.; Xu, S.; Liu, J. Persymmetric Detection of Radar Targets in Nonhomogeneous and Non-Gaussian Sea Clutter. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5103709. [Google Scholar] [CrossRef]
- Hjorungnes, A.; Gesbert, D. Complex-Valued Matrix Differentiation: Techniques and Key Results. IEEE Trans. Signal Process. 2007, 55, 2740–2746. [Google Scholar] [CrossRef]
- De Maio, A. A New Derivation of the Adaptive Matched Filter. IEEE Signal Process. Lett. 2004, 11, 792–793. [Google Scholar] [CrossRef]
- Kelly, E.J. An Adaptive Detection Algorithm. IEEE Trans. Aerosp. Electron. Syst. 1986, AES-22, 115–127. [Google Scholar] [CrossRef]
- De Maio, A. Rao Test for Adaptive Detection in Gaussian Interference with Unknown Covariance Matrix. IEEE Trans. Signal Process. 2007, 55, 3577–3584. [Google Scholar] [CrossRef]
- Besson, O. Rao, Wald, and Gradient Tests for Adaptive Detection of Swerling I Targets. IEEE Trans. Signal Process. 2023, 71, 3043–3052. [Google Scholar] [CrossRef]


| Parameters | Symbol | Value |
|---|---|---|
| Carrier Frequency | 2.4 GHz | |
| Horizontal Dimension | 4 m | |
| Vertical Dimension | 1 m | |
| Target Velocity | 25 m/s | |
| Base Line | 4000 m, 600 m | |
| Distance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Chen, H.; Li, Y.; Wang, D. Rao and Wald Tests for Moving Target Detection in Forward Scatter Radar. Remote Sens. 2024, 16, 211. https://doi.org/10.3390/rs16020211
Wang Z, Chen H, Li Y, Wang D. Rao and Wald Tests for Moving Target Detection in Forward Scatter Radar. Remote Sensing. 2024; 16(2):211. https://doi.org/10.3390/rs16020211
Chicago/Turabian StyleWang, Zeyu, Hongmeng Chen, Yachao Li, and Dewu Wang. 2024. "Rao and Wald Tests for Moving Target Detection in Forward Scatter Radar" Remote Sensing 16, no. 2: 211. https://doi.org/10.3390/rs16020211
APA StyleWang, Z., Chen, H., Li, Y., & Wang, D. (2024). Rao and Wald Tests for Moving Target Detection in Forward Scatter Radar. Remote Sensing, 16(2), 211. https://doi.org/10.3390/rs16020211