Abstract
Ensuring the safety of autonomous vehicles (AVs) in complex and high-risk traffic scenarios remains a critical unresolved challenge. Current AV planning methods exhibit limitations in generating robust driving trajectories that effectively avoid collisions, highlighting the urgent need for improved planning strategies to address these issues. This paper introduces a novel iterative optimization framework that incorporates safety-critical trajectory generation to enhance AV planning. The use of the HighD dataset, which is collected using the wide-area remote sensing capabilities of unmanned aerial vehicles (UAVs), is fundamental to the framework. Remote sensing enables large-scale real-time observation of traffic conditions, providing precise data on vehicle dynamics, road structures, and surrounding environments. To generate safety-critical trajectories, the decoder within the conditional variational auto-encoder (CVAE) is innovatively designed through a data-mechanism integration method, ensuring that these trajectories strictly adhere to vehicle kinematic constraints. Furthermore, two parallel CVAEs (Dual-CVAE) are trained collaboratively by a shared objective function to implicitly model the multi-vehicle interactions. Inspired by the concept of “learning to collide”, adversarial optimization is integrated into the Dual-CVAE (Adv. Dual-CVAE), facilitating efficient generation from normal to safety-critical trajectories. Building upon this, these generated trajectories are then incorporated into an iterative optimization framework, significantly enhancing the AV’s planning ability to avoid collisions. This framework decomposes the optimization process into stages, initially addressing normal trajectories and progressively tackling more safety-critical and collision trajectories. Finally, comparative case studies of enhancing AV planning are conducted and the simulation results demonstrate that the proposed method can efficiently enhance AV planning by generating safety-critical trajectories.
1. Introduction
The safety of autonomous vehicles (AVs) is crucial for their development and commercial deployment [,,]. Enhanced AV planning in special driving conditions, particularly in critical and challenging traffic environments, has become a pressing necessity [,]. These challenging conditions require AVs to plan a safe trajectory in unpredictable and demanding situations, a key factor in boosting the reliability of these systems []. Without addressing these safety challenges in AV planning, the commercial deployment of AVs will not only be restricted but also confined to specific operational environments []. Moreover, safety deficiencies could lead to fatal traffic accidents, thereby negatively impacting public acceptance of AVs on public roads.
Ensuring the safety of AVs largely depends on developing an AV planning system capable of handling various collision-prone traffic scenarios. Recent research has made significant strides in AV planning technologies. For instance, Niklas et al. [] proposed a fine-tuning optimization method that effectively reduces collision risks in specific scenarios, while Chowdhury et al. [] explored reinforcement learning approaches to enhance AV planning capabilities in dynamic environments. However, these methods often struggle with the inherent rarity of safety-critical trajectories. Liu et al. [] emphasized the need for fine-tuning optimization under specific accident-prone conditions, but the lack of diverse safety-critical data limits the universality of AV planning solutions. Moreover, while traditional optimization techniques provide valuable insights for enhancing AVs’ planning, they often fail to adapt to the complexities of near-collision situations. The more challenging the traffic scenario, the harder it becomes to improve AVs’ planning. Zhang et al. [] further highlighted that as complex situations increase, the limitations of existing traditional optimization methods become more apparent, rendering them ineffective in addressing near-collision scenarios.
Ensuring the safety of an AV’s planning depends not only on developing a comprehensive set of safety-critical driving trajectories for various traffic situations but also on refining the AV to effectively mitigate and avoid collision scenarios [,,,]. More specifically, these safety-critical driving trajectories are crucial in real-world contexts as they highlight the scenarios where AV planning is most vulnerable, thus identifying areas for potential enhancement []. Once these vulnerabilities are identified, it becomes necessary to employ advanced methods to enhance AV planning, particularly for addressing complex near-collision situations and significant collision challenges [].
Remote sensing technology, particularly when employed through unmanned aerial vehicles (UAVs), has emerged as a crucial tool for collecting safety-critical driving trajectories in the past decade []. This technology utilizes high-altitude aerial photography to provide a bird’s-eye view, significantly reducing data acquisition costs while capturing a broader and more diverse set of trajectory data. As a result, it markedly increases the likelihood of obtaining safety-critical trajectories. The HighD dataset, enriched with critical trajectories through remote sensing, exemplifies this approach []. Additionally, synthesizing different scenarios in simulation can serve as a viable alternative. Despite its flexibility and controllability, simulation can become prohibitively expensive when a large set of scenarios is required for enhancing autonomous vehicles (AVs) []. However, some simulators fail to generate realistic vehicle maneuvers, leading to trajectories that violate physical constraints []. Moreover, the human-designed rules for simulation data may result in distribution drift and over-adversarial behaviors [].
Traditionally, various methods for improving AV planning have been developed based on safety-critical trajectories. These methods primarily include direct optimization techniques [,,], reinforcement learning approaches [,,], and game-theoretic strategies [,,], all aimed at strategically addressing specific challenging scenarios to prevent collisions [,,]. Rempe et al. [] improved rule-based AV planning by parameter tuning under accident-prone driving scenarios. Although these improvements achieve a good effect under specific and limited collision events, the applicability of AV planning is constrained by the scarcity of safety-critical trajectories.
As depicted in Figure 1a, traffic scenarios with accidents are rare in real-world driving, leading to a scarcity of collision trajectories. Despite the advantages of UAVs in enhancing data richness over vehicle-mounted sensors, they cannot address the inherent rarity of safety-critical trajectories. This scarcity poses significant challenges to the development of safety-oriented AV planning. Besides the collected collision trajectories, a more effective alternative involves the traditional direct generation of a substantial volume of requisite safety-critical driving trajectories through data-driven methods, as depicted in Figure 1c. In contrast to image and text generation, producing vehicle trajectories requires adherence to kinematic constraints, interactions and high generation efficiency. Additionally, extreme collision scenarios present significant challenges in enhancing AV planning. As illustrated in Figure 1b, traditional direct optimization methods are likely to fail in these complex situations. It is essential to note that the rarity and complexity of collision events contribute to the difficulty of improving AV planning.
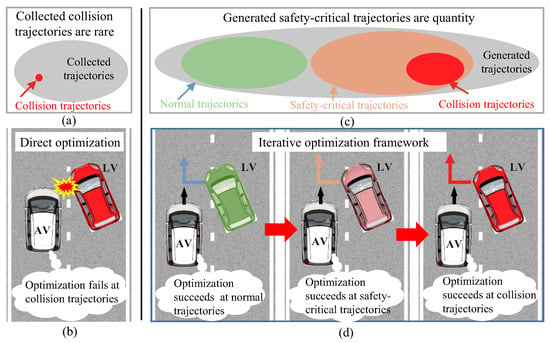
Figure 1.
Motivated illustration of the proposed enhancing of AV planning: (a) the proportion of collision trajectories in natural driving data; (b) the conventional direct optimization method; (c) the proposed safety-critical trajectory generation; (d) the proposed iterative optimization framework.
There are several challenges in improving collision avoidance of AV planning that are associated with the following special characteristics:
- (1)
- Safety-critical trajectory generation: The first challenge involves generating safety-critical driving trajectories by data-driven methods. Initially, these methods struggle to adhere to vehicle kinematic constraints. Furthermore, although multi-vehicle interactions are common in traffic scenarios, existing solutions seldom account for them during trajectory generation. More importantly, safety-critical trajectories are rare in collected natural driving datasets, which significantly lowers the efficiency of their generation.
- (2)
- Optimizing AV planning in safety-critical trajectories: AV planning needs to effectively handle complicated near-collision scenarios, which are from generated safety-critical trajectories. However, the more challenging these scenarios are, the more difficult it becomes to improve AV planning, directly affecting the optimization algorithms. This increased complexity poses significant challenges for the method designed to optimize AV planning.
To address the above challenges in enhancing safety for AV planning, an iterative optimization framework incorporating safety-critical trajectory generation is presented in this paper. The primary objective is to develop an approach that can effectively enhance the safety of AV planning across various challenging vehicle trajectories. The essence of enhancing safety is to design a novel iterative optimization framework, where safety-critical trajectories are generated from data-driven traffic methods. The contributions and novelty of this paper can be summarized in three key aspects:
- (1)
- The Adv. Dual-CVAE is introduced to efficiently generate safety-critical trajectories, enhancing the variety of challenging scenarios for improving AV safety. Specifically, the decoder in the CVAE [] is designed through data-mechanism integration, enabling the generation of trajectories that adhere to vehicle kinematic constraints. The Dual-CVAE uses a shared objective function to interactively generate vehicle trajectories during training. By integrating adversarial optimization, the Adv. Dual-CVAE significantly boosts the generation efficiency, enabling a shift from generating normal to safety-critical trajectories.
- (2)
- An iterative optimization framework is proposed to ensure that the AV planning improvements remain effective. The framework segments the optimization process into stages, beginning with normal trajectories and methodically advancing to increasingly address safety-critical ones and direct collision trajectories, as demonstrated in Figure 1d.
- (3)
- The study of enhancing AV planning is carried out, involving distinct AVs in cut-in and car-following scenarios.
This article is organized as follows. Section 2 introduces the problem statement and the overview of the proposed framework. In Section 3, a novel adversarial Dual-CVAE is designed. In Section 4, the iterative optimization framework is proposed. Section 5 reports the results. Finally, Section 7 concludes this article.
2. Problem Statement
2.1. Naturalistic Driving Dataset Collected by Remote Sensing
Remote sensing technologies, especially those involving UAVs, have revolutionized data acquisition for naturalistic driving datasets by broadening the scope and diversity of collected vehicle trajectories [,]. This advancement significantly enhances the foundation for safety-critical research in autonomous driving. Unlike traditional vehicle-mounted sensors that require extensive travel to accumulate data, UAVs can swiftly cover large areas, capturing dynamic traffic conditions and temporary hazardous events from a bird’s-eye view []. This panoramic perspective not only reflects driving behaviors more comprehensively but also provides valuable vehicle interaction data []. Furthermore, the application of remote sensing dramatically reduces trajectory collection costs and enhances the convenience and speed of gathering specific regional dataset [].
Given the relative rarity of accidents in natural driving data, there is a significant scarcity of safety-critical driving trajectories. Remote sensing not only increases the chances of capturing such data but also supports the direct generation of essential safety-critical trajectories through data-driven methods []. Additionally, UAVs furnish a rich array of terrain information, aiding in the precise reconstruction and simulation of various driving scenarios []. This capability is crucial for the rapid iteration and optimization of autonomous driving algorithms.
In this paper, we utilize the highD dataset, a high-precision, large-scale traffic dataset renowned for its comprehensive coverage of naturalistic driving events on German highways []. The dataset encompasses over 110,000 post-processed trajectories of various vehicles, including cars and trucks, meticulously captured via UAVs’ video recording, as shown in Figure 2a. These trajectories provide detailed vehicular data such as size, type, driving direction, position, velocity, acceleration, and the number of lane changes. The data of each vehicle are tagged with a unique identifier (ID) and automatically extracted using advanced computer vision algorithms, as shown in Figure 2b.
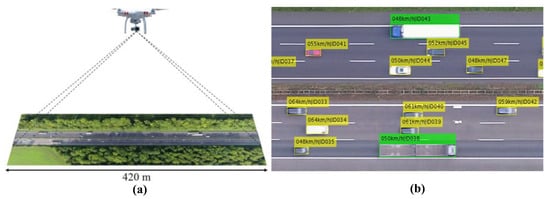
Figure 2.
HighD dataset acquisition and representation: (a) data collection setup showing a UAV equipped with advanced sensors capturing a 420 m stretch of highway traffic, providing a comprehensive bird’s-eye view; (b) an example of processed data from the highD dataset, illustrating detailed vehicular dynamics on a German highway. The visualization includes vehicle IDs, types, and dynamic parameters such as position, velocity, and lane changes, captured and annotated using computer vision algorithms.
The highD dataset is distinguished by its exceptional data accuracy, with an error margin of less than 10 cm, ensuring the reliability of the information. It also includes contextual vehicle information surrounding the target vehicle, along with descriptions of diverse driving scenarios, such as cut-in and car-following. By leveraging the rich data available in the highD dataset, this work aims to provide a comprehensive understanding of safety-critical trajectory generation and enhance AV planning.
2.2. Safety-Critial Trajectory Generation by Adv. Dual-CVAE
Generating safety-critical trajectories in typical traffic scenarios, including car-following and cut-in, is pivotal for the development of AV planning. In typical traffic scenarios, there are two vehicles: a leading vehicle (LV) and a following vehicle (FV). The trajectories of two vehicles are represented as , where and denote the trajectories of the LV and FV, respectively. Specifically, is the sequence of states for the LV, and is the sequence of states for the FV. Each state and at time t is structured identically, comprising the position and speed .
Generating safety-critical trajectories usually involves learning a distribution from the collected natural driving data , where is the learning parameter, and the new trajectories are often generated by sampling from this distribution . To learn this distribution , the corresponding optimization problem can be formulated as:
where ensures that the generated trajectories adhere to vehicle kinematic constraints, and reflects that the generated trajectories satisfy the muti-vehicle interaction.
In the collected natural driving trajectories dataset, those safety-critical trajectories are exceedingly sparse, as shown in Figure 3a. Even if the traffic model successfully learns the distribution , safety-critical trajectories still reside in the distribution’s long tail. This results in their generation efficiency being significantly low, as illustrated in Figure 3b.
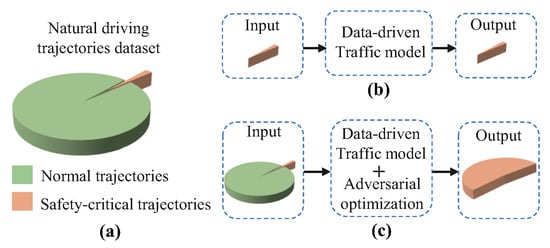
Figure 3.
Motivational illustration of the proposed safety-critical trajectory generation: (a) the proportion of safety-critical trajectories in the natural driving dataset is very low, indicating that such trajectories are scarce; (b) the conventional data-driven traffic model struggles to generate additional safety-critical trajectories due to limitations in data diversity; (c) the proposed data-driven traffic model incorporating adversarial optimization effectively generates a greater number of safety-critical trajectories, addressing the scarcity issue.
To enhance the efficiency of generating safety-critical trajectories, our core idea is to integrate adversarial optimization into the data-driven traffic model, encouraging its shift from producing normal driving trajectories to safety-critical ones, as illustrated in Figure 3c. Specifically, the objective of adversarial optimization is to minimize the distance of generated trajectories (e.g., cause a collision). Concurrently, the prior within the traffic model is constrained to ensure the plausibility of these safety-critical trajectories. Thus, efficient generation of safety-critical trajectories is formulated as following:
where denotes the prior threshold within the traffic model, and can be obtained by solving the optimization problem (1).
2.3. Traditional Optimization Solution for AV Planning
Traditionally, optimizing the solution for AV planning under the generated safety-critical trajectories is a critical step towards ensuring the robustness and reliability of AVs. As illustrated in Figure 4, this involves a comprehensive process that uses the generated safety-critical trajectories to enhance AV planning.
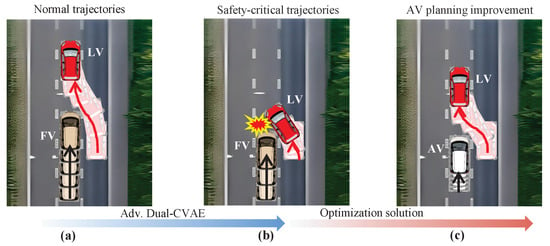
Figure 4.
Traditional progression of AV planning optimization using safety-critical trajectories: (a) collection of normal trajectories including LV and FV from the highD dataset, (b) generation of safety-critical trajectories by the Adv. Dual-CVAE, (c) implementation of enchanted AV planning where the FV trajectory is replaced by an AV, demonstrating enhanced collision avoidance capabilities.
Initially, as shown in Figure 4a, a large volume of normal trajectories, including those of the LV and the FV, is collected from cut-in and car-following scenarios within the highD dataset. Subsequently, as depicted in Figure 4b, the Adv. Dual-CVAE generates a variety of safety-critical trajectories based on the normal trajectories from the highD dataset. Following this, challenging collision trajectories are identified among the safety-critical ones. In the AV planning improvement, as demonstrated in Figure 4c, the LV trajectory remains unchanged in generated collision ones, while the FV trajectory is replaced with that of an AV. This substitution creates a challenging traffic scenario for the AV. In this scenario, optimizing the parameters for AV planning enables the avoidance of collisions, thereby ensuring robust and reliable AV operation under diverse and challenging traffic conditions.
Time-to-Collision (TTC) classifies driving trajectories as normal or safety-critical, considering that lower TTC values indicate a higher collision risk []. Through the generation of trajectories using the Adv. Dual-CVAE based on the highD dataset, three categories of trajectories are obtained: normal trajectories ( or ), safety-critical trajectories (), and collision trajectories (). Subsequently, the most challenging collision trajectories are selected to aid improvements in AV planning. Considering that there are no AVs in the generated pair of collision trajectories, we assume that the trajectory remains unchanged, serving as the LV in scenarios that are challenging for the AV, as illustrated in Figure 4c. The generated FV trajectory is then replaced by the AV trajectory . Then, the AV needs to consider avoiding collisions under the aggressive LV trajectory . By optimizing parameters, a traditional optimization problem can be formulated as follows:
where is the AV planning, serves as an optimization variable and also as the parameter in AV planning, and is the optimized objective for avoiding a collision.
To effectively address the potential failure of solving a traditional optimization problem (3) when encountering overly challenging collision trajectories, an iterative optimization framework is designed. The core concept of this framework is to gradually enhance AV planning through an iterative approach.
2.4. Iterative Optimization Framework
The overall framework of the proposed enhancing of planning for autonomous driving via the iterative optimization framework incorporating safety-critical trajectory generation is depicted in Figure 5. The Adv. Dual-CVAE is designed to first generate a large volume of normal trajectories from the highD dataset, which are then transformed into safety-critical trajectories and collision trajectories through adversarial optimization.
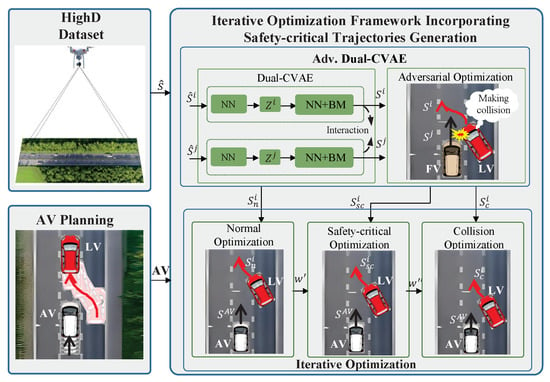
Figure 5.
Optimization solution for AV planning under generation of safety-critical trajectories. The figure illustrates four main components: First, the highD dataset provides the data foundation for trajectory generation. Second, the AV Planning module supplies specific autonomous driving planning algorithms. Third, the Iterative Optimization Framework Incorporating Safety-critical Trajectory Generation generates adversarial driving trajectories through Adv. Dual-CVAE. Finally, the Iterative Optimization improves AV planning step by step based on trajectories with varying levels of danger. Note that NN refers to Neural Network and BM stands for the Bicycle Model.
Following this, the generated safety-critical trajectories are seamlessly integrated into an iterative optimization framework, which strategically breaks down the optimization process into stages—starting with normal trajectories and methodically advancing to more complex scenarios like safety-critical and direct collision trajectories—thereby, significantly enhancing the AV’s planning capability to robustly avoid collisions.
3. Safety-Critical Trajectory Generation by Adv. Dual-CVAE
In this section, the safety-critical trajectories are generated by using the Adv. Dual-CVAE, which is illustrated in Figure 6. Initially, a data-driven traffic model, named Dual-CVAE is established, which can learn traffic distribution from the highD dataset and generate various vehicle trajectories. Subsequently, the efficiency of generating safety-critical trajectories is further enhanced through the employment of adversarial optimization.
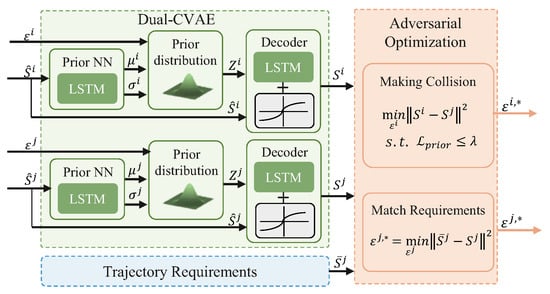
Figure 6.
Overall schematic of the proposed Adv. Dual-CVAE.
3.1. Data-Driven Traffic Model by Dual-CVAE
To generate safety-critical trajectories in typical traffic scenarios by solving the optimization problem (1), the distribution is taught to generate trajectories conditioned on the fixed given trajectories (defined similar to ). Consequently, the CVAE emerges as an apt model for facilitating this generation process, due to its proficiency in handling conditional distributions and generating diverse outcomes.
To effectively generate trajectories , the CVAE model employs a prior network designed around Long Short-Term Memory (LSTM) networks []. This network structure is particularly adept at capturing the temporal dependencies inherent in vehicle trajectories, which is crucial for generating the next states of vehicles based on their given trajectories. The LSTM-based prior network processes the given trajectories , which consists of sequences of vehicle states, and outputs the parameters for the Gaussian distribution: mean and standard deviation . These parameters, mean and standard deviation , define the conditional probability distribution in the CVAE model, which describes the statistical characteristics of vehicle trajectories under specific conditions, thereby facilitating the generation of diverse and realistic trajectories.
Once the parameters of the Gaussian distribution are determined by the LSTM prior network, the latent vectors can be obtained by prior distribution with a reparameterization trick:
where is a random vector, and random numbers and samples from the standard Gaussian distribution during training. The outputs of traffic prior distribution is a Gaussian as follows:
where is the standard Gaussian distribution function.
3.1.1. Decoder of CVAE for Data-Mechanism Integration
To address the vehicle kinematic constraints in the optimization problem (1), a decoder by data-mechanism integration is innovatively designed. The decoder firstly utilizes an LSTM neural network, which sequentially processes the sampled latent vectors , allowing for the step-by-step decoding of vehicle states. This decoding approach is crucial as it facilitates the integration of vehicle kinematic constraints at each step, ensuring that the generated trajectory adheres to constraints. Specifically, the LSTM decoder computes the next state based on state at time t, as follows:
where is the LSTM decoder with parameter , and the state differencing between and is as follows:
where is the time step.
To ensure the kinematic feasibility of the generated trajectories, the output of the LSTM decoder is constrained by the bicycle model, which is one of the simple kinematic models []. As illustrated in Figure 7, the bicycle model simplifies the complex vehicle dynamics as follows:
where is the vehicle yaw angle, is the center of gravity sideslip angle, is the rear wheelbase, and a is the acceleration. and are the front wheelbase and the front wheel steering angle in Figure 7, respectively.
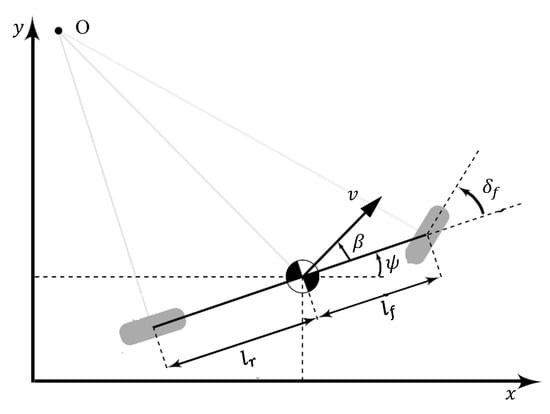
Figure 7.
The simple bicycle model. The dark color is the vehicle mass point, and the light gray color is the wheel.
Given an acceleration threshold , the velocity threshold can be quickly obtained through the kinematic model (8). Similarly, given a front wheel steering angle threshold , the threshold of the center of gravity sideslip angle can be obtained by:
Then, by substituting , , and into (8), the thresholds of the state changing rate are obtained, and the state at time is determined by:
Thus, the trajectories can adhere to vehicle kinematic constraints by LSTM and the vehicle kinematic model. This model incorporates kinematic constraints directly into the decoding process, enabling the generation of realistic trajectories.
3.1.2. Dual-CVAE for Multi-Vehicle Interactions
To address the multi-vehicle interaction constraints in the optimization problem (1), which are difficult to explicitly express, the Dual-CVAE architecture is proposed. By employing two parallel CVAE models that are collaboratively trained, this architecture implicitly captures the multi-vehicle interactions. More specifically, during the training process, each CVAE is tasked with generating the trajectory of a single vehicle and simultaneously learns the interactive effects with others through a shared objective function .
The training of the Dual-CVAE involves optimizing the objective function over pairs of trajectory data , where represents the actual observed trajectories in the collected dataset. The Dual-CVAE’s objective is structured to minimize the following composite loss function, which includes contributions from both CVAE models:
Here, and are the reconstruction loss and the Kullback–Leibler (KL) divergence, respectively. More specifically, the reconstruction loss ensures that the generated trajectories closely match the real-world data. The KL divergence quantifies the discrepancy between the predicted latent distribution and the prior distribution.
3.2. Adversarial Optimization of Dual-CVAE
To enhance the efficiency of generating safety-critical trajectories with Dual-CVAE, the adoption of adversarial optimization is crucial. In the naturalistic driving dataset, the rarity of safety-critical trajectories leads to lower generation efficiency. However, adversarial optimization effectively addresses this challenge, as illustrated in Figure 6. Specifically, we fix the FV’s trajectory, as a baseline or potential trajectory, and then have the LV’s trajectory perform an adversarial attack to attempt a collision with .
Following the strategic setup of adversarial optimization, the matching requirements play a pivotal role in refining the trajectory generation process. The FV’s trajectory can be generated to match the requirements by following the optimization problem:
where in (4) is the optimization variable.
The following task of adversarial optimization is given by the optimization problem (2). Given the trajectory requirements and the historical trajectories of two vehicles and , encompassing both normal and safety-critical trajectories, the Dual-CVAE is tasked with generating trajectories and through adversarial optimization. The generation of is designed to make it collide with (representing a safety-critical trajectory), while aims to match the requirements .
The adversarial objective is set to minimize the distance between the generated trajectories and :
The traffic prior is constrained to the plausibility:
Then, by substituting (13) and (14) into (2), the efficient Dual-CVAE trajectory generation problem can be solved and the optimal input can be obtained. Note that is the optimization variable in (2). Thus, the efficient generation of safety-critical trajectories and can be obtained by Dual-CVAE after being given the inputs , , , and .
4. Iterative Optimization Framework Incorporating Safety-Critical Trajectory Generation
In the previous chapter, the scarcity of safety-critical trajectories in the natural driving dataset were effectively addressed by designing the Adv. Dual-CVAE. However, as the complexity of these trajectories increases, so does the difficulty of enhancing AV planning to cope with these safety-critical trajectories. Traditional optimization methods (3) gradually decrease in their likelihood of successfully resolving these highly challenging collision trajectories for AV planning.
To address the challenge of directly solving the complex optimization problem (3), a natural approach is to adaptively adjust the optimization problem if the final solution proves difficult. To implement this, an iterative optimization framework is established, where each iteration involves constructing and reformulating the optimization problem based on the previous iterations.
Intuitively, the iterative optimization framework effectively enables a gradual discovery of optimal AV planning strategies to avoid collisions. Specifically, AV planning can be successfully solved within normal trajectories, using the optimal solution of this iterative step as the initial set of parameters for the next iteration. Subsequently, normal trajectories are replaced with safety-critical trajectories, allowing AV planning to be adequately addressed within these more challenging scenarios. The optimal solution of this stage then serves as the initial parameters for the next iteration. Ultimately, in collision trajectories, the framework optimizes parameters for AV planning, thereby incrementally solving the more challenging optimization problem. Throughout this process, AV planning concurrently addresses normal safety-critical and collision trajectories, enabling robust performance across various environments.
In the iterative optimization framework, the process starts by addressing AV planning within normal trajectories. The initial optimization problem is formulated as follows:
where is the generated normal trajectories by Dual-CVAE, and represents that is the initial parameter setting for AV planning in the optimization process. The objective, , minimizes the negative squared distance between the generated trajectory and the AV’s trajectory , facilitating collision avoidance, and the optimal solution of the current optimization problem (15) is .
Upon successful optimization within normal trajectories, the framework advances to incorporate safety-critical trajectories:
where is the generated safety-critical trajectories generated by the Adv. Dual-CVAE, denotes that is the initial parameter in the current optimization process, and the optimal solution of the optimization problem (16) is .
Similarly, at the final stage of the iterative optimization framework, AV planning will be completed within collision trajectories, where the optimization problem is formulated as follows:
where indicates the generated collision trajectories, and the optimization progresses from to , further refining the AV’s planning capabilities under increasingly complex scenarios. This systematic progression ensures a methodical enhancement of AV’s ability to handle a range of traffic conditions effectively, thereby optimizing its robust performance in diverse environments. The following pseudocode is presented to demonstrate our proposed iterative optimization framework, which is illustrated in Algorithm 1.
| Algorithm 1 Iterative Optimization Framework Incorporating Safety-critical Trajectory Generation for AV Planning |
|
5. Results
In this section, we firstly introduce the implementation of the proposed method, then illustrate the training result of Adv. Dual-CVAE. Next, we conduct a comprehensive study to improve the AV planning.
5.1. Experiment’s Setup
5.1.1. Case Study Scenarios and Dataset
In our experiments, we focus on cut-in and car-following scenarios, as illustrated in Figure 8. Chosen for their prevalence in daily driving and their significant impact on traffic safety, these scenarios are pivotal for both generating safety-critical trajectories and enhancing AV planning efficacy.
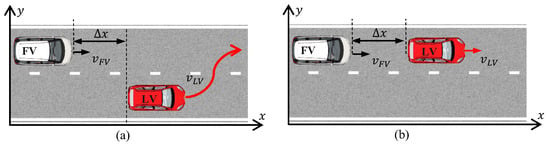
Figure 8.
Typical traffic scenarios: (a) cut-in; (b) car-following.
As depicted in Figure 8, the traffic scenarios involve an LV traveling at speed and an FV at speed , separated by a longitudinal distance . Notably, both the LV and FV trajectories are generated using the Adv. Dual-CVAE. For the enhancement of AV planning, the LV’s trajectory is kept constant, while the FV’s trajectory is substituted with the AV’s planned trajectory, as shown in Figure 4. This configuration allows for targeted improvement to AV planning, optimizing responses to the safety-critical trajectory presented by the LV.
These natural trajectories in traffic scenarios are collected in the highD dataset, which includes 12,000 car-following and 4397 cut-in two-vehicle trajectories. For car-following scenarios, 2 s of given trajectories are used to generate 13 s of trajectories . Similarly, two seconds of a given cut-in trajectory is utilized to generate the subsequent trajectories.
5.1.2. Model Parameter Setting
The parameter settings for the Adv. Dual-CVAE and AV planning are crucial for the effectiveness of the models. For the Adv. Dual-CVAE, the model utilizes a latent vector with a dimension of 10. To minimize the loss function, the ADAM optimizer [] is utilized with a learning rate of 0.001. The configuration specifies a batch size of 200 and a training epoch of 50. We use python 3.8 and Pytorch 2.0 for generating safety-critical trajectories. Experiments are done on a computer with i5-13490f CPU and 4060ti GPU.
The settings for AV planning are those used for a rule-based model, focusing primarily on adaptive cruise planning. Specifically, in the car-following scenario, the AV continuously tracks the LV using the Intelligent Driver Model (IDM) [], which is as follows:
where is the AV acceleration, is the AV’s maximum acceleration, and b is the comfortable braking deceleration. is the desired AV’s velocity. is the acceleration exponent. is the minimum possible spacing when the AV is stopped. is the desired time headway. The parameters used in (18), namely , and , collectively form the set of AV planning parameters in the car-following scenario. In the cut-in scenario, at time , the AV follows the LV that is executing a cut-in maneuver. The following strategy employed by the AV is based on the IDM planning with AV planning parameters , and . It should be noted that at the beginning of the iterative optimization, the initial parameters of the AV planning for car-following and cut-in are randomly initialized.
5.1.3. Evaluation Metrics
To determine the proportion of safety-critical trajectories in the natural driving dataset, we analyzed the highD dataset, focusing on car-following and cut-in scenarios as shown in Figure 9. In the cut-in scenario, safety-critical trajectories account for only 0.15% of the highD dataset. Meanwhile, in the car-following scenario, they represent a mere 0.57%, which confirms that safety-critical trajectories are indeed rare in the natural driving dataset.
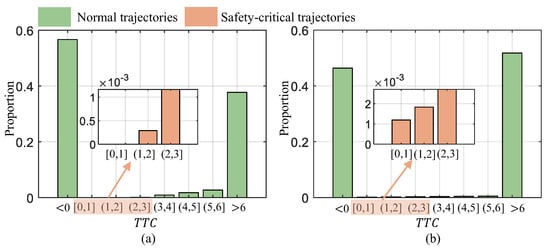
Figure 9.
Proportion of safety-critical trajectories in the highD dataset: (a) cut-in; (b) car-following.
Three metrics are assessed quantitatively for our Adv. Dual-CVAE model. The root mean square difference (RMSE) evaluates the deviation between the original and the generated trajectories []. The safety-critical rate and collision rate are designed to evaluate generation efficiency:
where and are the number of generated safety-critical and collision trajectories, respectively. is the total number of trajectories.
To assess the collision avoidance capabilities of AV planning by optimization methods, we design the metric of collision avoidance rate as follows:
where is the test number of AV planning to avoid collisions with LV. is the total test number.
5.2. Training Result and Analysis of Adv. Dual-CVAE
5.2.1. Evaluation of Dual-CVAE Training
To assess the training process of Dual-CVAE, we qualitatively analyze the convergence of the loss value (11a), which is shown in Figure 10. As the number of epochs increases, the loss values exhibit a gradual decrease. Specifically, the loss approaches zero after 100 epochs for both the cut-in and car-following scenarios. This convergence indicates that Dual-CVAE has successfully completed the training process.
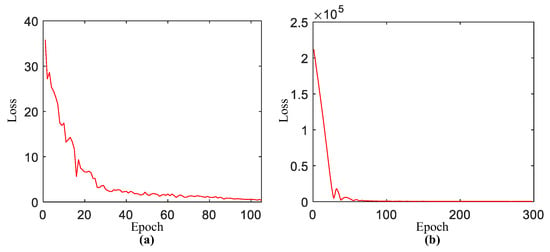
Figure 10.
The loss value of Dual-CVAE model: (a) cut-in; (b) car-following.
To assess the performance of Dual-CVAE, we introduce the traditional CVAE as the baseline []. Then, the RMSEs of the relative position in car-following and cut-in scenarios are calculated by:
and the RMSEs of the relative velocity in car-following and cut-in are calculated as follows:
Table 1 reveals that Dual-CVAE achieves a lower RMSE than traditional CVAE, with improvements of 96.24% and 97.93% in relative position and velocity, respectively. These reductions suggest that Dual-CVAE’s kinematic constraints and multi-vehicle dynamics enhance the accuracy of the generated trajectory.

Table 1.
RMSE value of comparative setting combinations.
5.2.2. Comparative Efficiency of Safety-Critical Trajectory Generation by Adv. Dual-CVAE
In cut-in and car-following scenarios, the trajectories generated by our Dual-CVAE model incorporating adversarial optimization (Adv. Dual-CVAE) versus the Dual-CVAE (Base Dual-CVAE) model are compared in Figure 11 and Figure 12. The Adv. Dual-CVAE model more readily produces safety-critical or collision trajectories under an identical input (normal trajectories with ), indicating its enhanced efficacy in simulating potential collision scenarios.
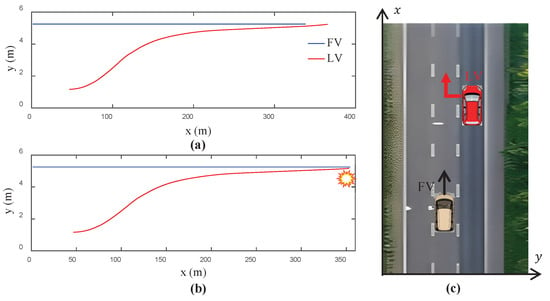
Figure 11.
Trajectories’ generation with the same input (normal trajectories with ): (a) Base Dual-CVAE; (b) Adv. Dual-CVAE; (c) cut-in.
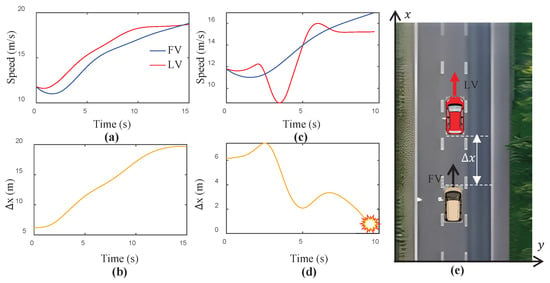
Figure 12.
Generating trajectories with the same input (normal trajectories with ): (a,b) Base Dual-CVAE; (c,d) Adv. Dual-CVAE; (e) car-following scenario.
To evaluate the generation efficiency of Base Dual-CVAE versus Adv. Dual-CVAE in traffic scenarios, we computed the safety-critical rate and collision rate across various TTC thresholds. More specifically, both Base and Adv. Dual-CVAE receive identical inputs and as demonstrated in Figure 6. However, for Base Dual-CVAE, the inputs and are random, whereas in Adv. Dual-CVAE, and are derived via adversarial optimization. To ensure a fair comparison, the trajectory requirements are sourced from the naturalistic driving dataset. Table 2 shows that Adv. Dual-CVAE achieves a higher generation efficiency for safety-critical and collision trajectories than Base Dual-CVAE, highlighting the benefits of incorporating adversarial optimization.

Table 2.
Generation efficiency of comparative setting combinations.
5.3. Comparative Analysis of Iterative Optimization in AV Collision Avoidance across Driving Scenarios
To evaluate the iterative optimization framework incorporating safety-critical trajectory generation, we utilized the Adv. Dual-CVAE to generate normal, safety-critical, and collision trajectories within cut-in and car-following scenarios. In these generated trajectories, the LVs are used for interaction with the AV. Moreover, we iteratively improve the AV algorithm in MATLAB 2019a. The results of the AV improvements based on iterative optimization are depicted in Figure 13 and Figure 14. Before iterative optimization, the AV is seen to potentially collide with the LV. After optimization, there is a noticeable separation between the trajectories, suggesting successful avoidance maneuvers by the AV.
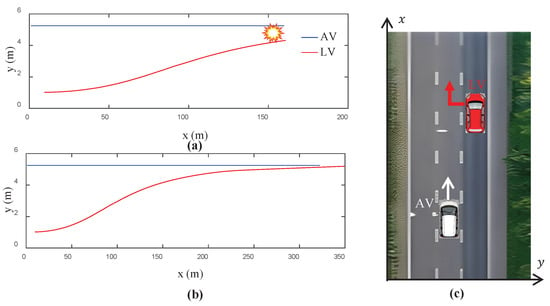
Figure 13.
Results of iterative optimization for AV planning in a cut-in scenario: (a) before iterative optimization, depicting a collision between the AV and LV using the generated collision trajectory; (b) after iterative optimization, showing the improved AV strategy successfully avoiding a collision; (c) the cut-in scenario on a highway from the highD dataset.
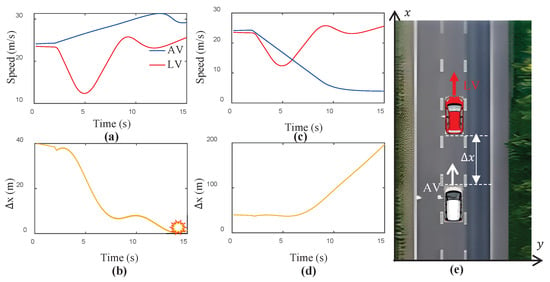
Figure 14.
Iterative optimization results in a car-following scenario: (a,b) AV collisions with LV at safety-critical trajectories; (c,d) AV avoids collision after iterative optimization; (e) the car-following scenario from the highD dataset.
To evaluate the collision avoidance capabilities of different optimization methods on generated trajectories, we computed the collision avoidance rate (20) under different generated trajectories. More specifically, two approaches are adopted to enhance AV planning: the first approach was traditional direct optimization, as outlined in (1); the second approach is iterative optimization, detailed in (15)–(17). The comparative results for various generated trajectories and scenarios are presented in Table 3, which highlights a pronounced enhancement in the collision avoidance rate when using iterative optimization compared to traditional direct optimization, particularly in handling complex driving scenarios.

Table 3.
Result of iterative optimization framework versus the traditional direct optimization in cut-in and car-following scenarios.
In the cut-in scenario, iterative optimization not only maintains a 100% collision avoidance rate in normal trajectories but also achieves significant gains in managing safety-critical and collision trajectories, with improvements of 24.79% and 28.23%, respectively. This indicates that iterative optimization is particularly effective in adapting AV behavior in sudden, critical traffic situations.
In the car-following scenario, the AV planning’s collision avoidance capability is improved even more significantly. While traditional direct optimization already shows high effectiveness in this scenario, iterative optimization further refines this, pushing the collision avoidance rate to nearly 100% across all trajectory types. This marginal but critical increase in safety-critical and collision trajectory—from 86.60% to 99.87% and from 86.19% to 99.86%, respectively—demonstrates the added robustness provided by the iterative approach. This suggests that iterative optimization helps the AV planning system to improve its responses to dynamic and potentially hazardous tailgating scenarios.
To provide a more intuitive display of the iterative optimization, we present the collision avoidance rate of AV planning at each iteration, as shown in Figure 15. In the cut-in scenario (Figure 15a), the initial normal optimization step shows a high collision avoidance rate of 99.9% for normal trajectories but significantly lower rates for safety-critical (11.0%) and collision trajectories (9.6%). This indicates that while AVs can handle standard conditions well, they struggle significantly under more challenging scenarios initially. As the optimization progresses to the safety-critical stage, the collision avoidance rate improves substantially to 100.0% for normal trajectories, 74.5% for safety-critical trajectories, and 71.0% for collision trajectories, demonstrating the iterative method’s effectiveness in enhancing AV capabilities under more complex conditions. In the final collision optimization stage, collision avoidance rates reach 100.0%, 80.6%, and 77.6% for normal, safety-critical, and collision trajectories, respectively, highlighting the model’s ability to optimize AV planning progressively to handle the most challenging scenarios.
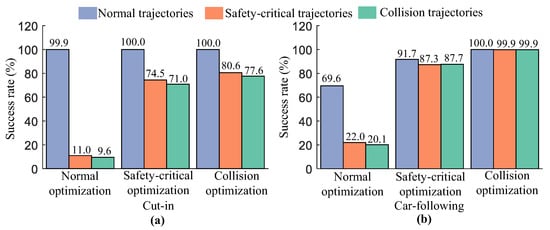
Figure 15.
Success rates of AV planning in avoiding collisions across different trajectory types during iterative optimization: (a) cut-in scenario; (b) car-following scenario.
In the car-following scenario (Figure 15b), the collision avoidance rate of AV planning aligns with that observed in the cut-in scenario, indicating that iterative optimization significantly enhances AV safety in car-following scenarios as well. Notably, during the final collision optimization stage, the collision avoidance rate of avoiding collisions for AV planning in the cut-in scenario (77.6%) is lower than in the car-following scenario (99.9%). This difference can be attributed to the comparative simplicity of the car-following scenario, where rule-based AV algorithms more easily address the challenges, whereas, in the more complex cut-in scenario, the limitations of AV planning safety become apparent.
6. Discussion
While our proposed methods effectively address the core challenge of generating safety-critical trajectories to enhance AV planning, there are limitations that warrant further discussion. Our approach assumes sufficient time is available to improve AV algorithms, focusing primarily on identifying challenging scenarios that significantly test AV planning capabilities. This focus is crucial for advancing AV safety and performance; however, it introduces certain constraints regarding real-time applicability.
To evaluate the real-time applicability of our methods, we conducted a series of experiments measuring the computation time for each module in both car-following and cut-in scenarios. Each module was executed 10 times, and the results were averaged to ensure reliability. As presented in Table 4, the Dual-CVAE and Advanced Dual-CVAE models demonstrated strong real-time performance, with trajectory generation times of 0.008 s and 0.522 s for car-following scenarios, and 0.003 s and 0.084 s for cut-in scenarios, respectively. These results indicate that the trajectory generation components of our models are capable of operating effectively within real-time environments.

Table 4.
Real-time applicability analysis of our method.
However, the iterative optimization process, particularly during safety-critical and collision phases, exhibited significantly higher computation times—reaching up to 29.894 s in car-following scenarios and 13.839 s in cut-in scenarios. Therefore these iterative processes are suitable for offline analysis. This disparity highlights the necessity for further improvement to enhance their suitability for real-time applications. Speeding up the iterative optimization process remains a key area for improvement to ensure the practicality of real-time deployment.
7. Conclusions
This paper presents an innovative iterative optimization framework that significantly enhances autonomous vehicle (AV) planning by integrating safety-critical trajectory generation. The proposed Dual-CVAE model employs two parallel conditional variational auto-encoders trained collaboratively to implicitly model multi-vehicle interactions while ensuring adherence to vehicle kinematic constraints. By incorporating adversarial optimization into the Dual-CVAE (resulting in the Adv. Dual-CVAE), we efficiently generate a diverse spectrum of trajectories, including critical scenarios essential for AV systems. The iterative optimization framework progressively addresses increasingly challenging situations, from normal driving conditions to collision-prone scenarios, markedly improving the AV’s collision avoidance capabilities. Comparative case studies validate the effectiveness of our method, demonstrating substantial improvements in collision avoidance rates across various challenging traffic situations, including a 24.79% and 28.23% increase in safety-critical and collision trajectories in cut-in scenarios, and a 13.27% and 13.67% improvement in car-following scenarios.
Future research will focus on evaluating and enhancing the real-time performance of the proposed methods, which is vital for practical deployment. Potential approaches include the development of more efficient optimization algorithms to reduce computational time, leveraging high-performance computing resources or specialized hardware such as GPUs for acceleration, and exploring real-time optimization techniques and online learning algorithms to promptly update AV planning strategies. Addressing these challenges will further enhance the practicality and impact of the framework in real-world autonomous driving applications.
Author Contributions
Conceptualization, Z.L., X.G. and H.G.; methodology, Z.L., X.G. and H.G.; software, Z.L. and H.G.; validation, Y.L., Z.L., X.G. and H.G.; formal analysis, Z.L.; investigation, X.G.; resources, X.G. and Y.L.; writing—original draft preparation, Z.L.; writing—review and editing, X.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (No. 2020AAA0108105), in part by the Major Science and Technology Projects of Jilin Province and Changchun City under Grant 20220301033GX, in part by Shanghai Automobile Industry Technology Development Foundation (2105), and in part by the Development and Reform Commission Foundation of Jilin Province (No. 2023C034-3).
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found here: https://levelxdata.com/highd-dataset/ (accessed on 15 July 2024).
Acknowledgments
We appreciate the critical and constructive comments and suggestions from the reviewers that helped improve the quality of this manuscript. We also would like to offer our sincere thanks to those who participated in the data processing and provided constructive comments for this study.
Conflicts of Interest
Author Yeting Lin was employed by the company SAIC Motor R&D Innovation Headquarters. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Feng, S.; Sun, H.; Yan, X.; Zhu, H.; Zou, Z.; Shen, S.; Liu, H.X. Dense reinforcement learning for safety validation of autonomous vehicles. Nature 2023, 615, 620–627. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Yan, X.; Sun, H.; Feng, Y.; Liu, H.X. Intelligent driving intelligence test for autonomous vehicles with naturalistic and adversarial environment. Nat. Commun. 2021, 12, 748. [Google Scholar] [CrossRef]
- Giannaros, A.; Karras, A.; Theodorakopoulos, L.; Karras, C.; Kranias, P.; Schizas, N.; Kalogeratos, G.; Tsolis, D. Autonomous vehicles: Sophisticated attacks, safety issues, challenges, open topics, blockchain, and future directions. J. Cybersecur. Priv. 2023, 3, 493–543. [Google Scholar] [CrossRef]
- Feng, S.; Feng, Y.; Sun, H.; Zhang, Y.; Liu, H.X. Testing scenario library generation for connected and automated vehicles: An adaptive framework. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1213–1222. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Z.; Zhang, Z.; Liu, J.; Li, W.; Wu, Y.; Li, X.; Yu, H.; Cao, D. Integrated post-impact planning and active safety control for autonomous vehicles. IEEE Trans. Intell. Veh. 2023, 8, 2062–2076. [Google Scholar] [CrossRef]
- He, X.; Huang, W.; Lv, C. Toward trustworthy decision-making for autonomous vehicles: A robust reinforcement learning approach with safety guarantees. Engineering 2024, 33, 77–89. [Google Scholar] [CrossRef]
- Teng, S.; Hu, X.; Deng, P.; Li, B.; Li, Y.; Ai, Y.; Yang, D.; Li, L.; Xuanyuan, Z.; Zhu, F.; et al. Motion planning for autonomous driving: The state of the art and future perspectives. IEEE Trans. Intell. Veh. 2023, 8, 3692–3711. [Google Scholar] [CrossRef]
- Hanselmann, N.; Renz, K.; Chitta, K.; Bhattacharyya, A.; Geiger, A. King: Generating safety-critical driving scenarios for robust imitation via kinematics gradients. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2022; pp. 335–352. [Google Scholar]
- Chowdhury, J.; Shivaraman, V.; Sundaram, S.; Sujit, P. Graph-based Prediction and Planning Policy Network (GP3Net) for scalable self-driving in dynamic environments using Deep Reinforcement Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 11606–11614. [Google Scholar]
- Liu, H.; Wei, H.; Zuo, T.; Li, Z.; Yang, Y.J. Fine-tuning ADAS algorithm parameters for optimizing traffic safety and mobility in connected vehicle environment. Transp. Res. Part C Emerg. Technol. 2017, 76, 132–149. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Liniger, A.; Borrelli, F. Optimization-based collision avoidance. IEEE Trans. Control Syst. Technol. 2020, 29, 972–983. [Google Scholar] [CrossRef]
- Wang, J.; Pun, A.; Tu, J.; Manivasagam, S.; Sadat, A.; Casas, S.; Ren, M.; Urtasun, R. Advsim: Generating safety-critical scenarios for self-driving vehicles. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9909–9918. [Google Scholar]
- Wang, Z.; Li, X.; Wei, D.; Wang, L.; Huang, Y. Efficient Generation of Safety-Critical Scenarios Combining Dynamic and Static Scenario Parameters. IEEE Trans. Intell. Veh. 2024. [Google Scholar] [CrossRef]
- Pek, C.; Althoff, M. Fail-safe motion planning for online verification of autonomous vehicles using convex optimization. IEEE Trans. Robot. 2020, 37, 798–814. [Google Scholar] [CrossRef]
- Sharma, O.; Sahoo, N.C.; Puhan, N.B. Recent advances in motion and behavior planning techniques for software architecture of autonomous vehicles: A state-of-the-art survey. Eng. Appl. Artif. Intell. 2021, 101, 104211. [Google Scholar] [CrossRef]
- Ding, W.; Xu, C.; Arief, M.; Lin, H.; Li, B.; Zhao, D. A survey on safety-critical driving scenario generation—A methodological perspective. IEEE Trans. Intell. Transp. Syst. 2023, 24, 6971–6988. [Google Scholar] [CrossRef]
- Ajanović, Z.; Regolin, E.; Shyrokau, B.; Ćatić, H.; Horn, M.; Ferrara, A. Search-based task and motion planning for hybrid systems: Agile autonomous vehicles. Eng. Appl. Artif. Intell. 2023, 121, 105893. [Google Scholar] [CrossRef]
- Zhang, C.; Tang, Z.; Zhang, M.; Wang, B.; Hou, L. Developing a more reliable aerial photography-based method for acquiring freeway traffic data. Remote Sens. 2022, 14, 2202. [Google Scholar] [CrossRef]
- Krajewski, R.; Bock, J.; Kloeker, L.; Eckstein, L. The highD dataset: A drone dataset of naturalistic vehicle trajectories on german highways for validation of highly automated driving systems. In Proceedings of the 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2118–2125. [Google Scholar]
- Rempe, D.; Philion, J.; Guibas, L.J.; Fidler, S.; Litany, O. Generating Useful Accident-Prone Driving Scenarios via a Learned Traffic Prior. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 17305–17315. [Google Scholar]
- Chen, B.; Chen, X.; Wu, Q.; Li, L. Adversarial evaluation of autonomous vehicles in lane-change scenarios. IEEE Trans. Intell. Transp. Syst. 2021, 23, 10333–10342. [Google Scholar] [CrossRef]
- Yan, X.; Feng, S.; Sun, H.; Liu, H.X. Distributionally consistent simulation of naturalistic driving environment for autonomous vehicle testing. arXiv 2021, arXiv:2101.02828. [Google Scholar]
- Abeysirigoonawardena, Y.; Shkurti, F.; Dudek, G. Generating adversarial driving scenarios in high-fidelity simulators. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8271–8277. [Google Scholar]
- Zhu, S.; Aksun-Guvenc, B. Trajectory planning of autonomous vehicles based on parameterized control optimization in dynamic on-road environments. J. Intell. Robot. Syst. 2020, 100, 1055–1067. [Google Scholar] [CrossRef]
- Diachuk, M.; Easa, S.M. Motion planning for autonomous vehicles based on sequential optimization. Vehicles 2022, 4, 344–374. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, R.; Wu, T.; Weng, R.; Han, M.; Zhao, Y. Safe reinforcement learning with stability guarantee for motion planning of autonomous vehicles. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5435–5444. [Google Scholar] [CrossRef]
- Aradi, S. Survey of deep reinforcement learning for motion planning of autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 23, 740–759. [Google Scholar] [CrossRef]
- Fisac, J.F.; Bronstein, E.; Stefansson, E.; Sadigh, D.; Sastry, S.S.; Dragan, A.D. Hierarchical game-theoretic planning for autonomous vehicles. In Proceedings of the 2019 International conference on robotics and automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9590–9596. [Google Scholar]
- Yan, Y.; Peng, L.; Shen, T.; Wang, J.; Pi, D.; Cao, D.; Yin, G. A multi-vehicle game-theoretic framework for decision making and planning of autonomous vehicles in mixed traffic. IEEE Trans. Intell. Veh. 2023, 8, 4572–4587. [Google Scholar] [CrossRef]
- Li, C.; Trinh, T.; Wang, L.; Liu, C.; Tomizuka, M.; Zhan, W. Efficient game-theoretic planning with prediction heuristic for socially-compliant autonomous driving. IEEE Robot. Autom. Lett. 2022, 7, 10248–10255. [Google Scholar] [CrossRef]
- Pinto, L.; Davidson, J.; Sukthankar, R.; Gupta, A. Robust adversarial reinforcement learning. In Proceedings of the International Conference on Machine Learning. PMLR, Sydney, Australia, 6–11 August 2017; pp. 2817–2826. [Google Scholar]
- Li, N.; Oyler, D.W.; Zhang, M.; Yildiz, Y.; Kolmanovsky, I.; Girard, A.R. Game theoretic modeling of driver and vehicle interactions for verification and validation of autonomous vehicle control systems. IEEE Trans. Control Syst. Technol. 2017, 26, 1782–1797. [Google Scholar] [CrossRef]
- Tian, R.; Li, N.; Kolmanovsky, I.; Yildiz, Y.; Girard, A.R. Game-theoretic modeling of traffic in unsignalized intersection network for autonomous vehicle control verification and validation. IEEE Trans. Intell. Transp. Syst. 2020, 23, 2211–2226. [Google Scholar] [CrossRef]
- Lopez-Martin, M.; Carro, B.; Sanchez-Esguevillas, A.; Lloret, J. Conditional variational autoencoder for prediction and feature recovery applied to intrusion detection in iot. Sensors 2017, 17, 1967. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhu, L. A review on unmanned aerial vehicle remote sensing: Platforms, sensors, data processing methods, and applications. Drones 2023, 7, 398. [Google Scholar] [CrossRef]
- Abdollahi, A.; Pradhan, B.; Alamri, A. VNet: An end-to-end fully convolutional neural network for road extraction from high-resolution remote sensing data. IEEE Access 2020, 8, 179424–179436. [Google Scholar] [CrossRef]
- Teng, H.; Ota, K.; Liu, A.; Wang, T.; Zhang, S. Vehicles joint UAVs to acquire and analyze data for topology discovery in large-scale IoT systems. Peer-Netw. Appl. 2020, 13, 1720–1743. [Google Scholar] [CrossRef]
- Han, Y.; Liu, H.; Wang, Y.; Liu, C. A comprehensive review for typical applications based upon unmanned aerial vehicle platform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9654–9666. [Google Scholar] [CrossRef]
- Yao, H.; Qin, R.; Chen, X. Unmanned aerial vehicle for remote sensing applications—A review. Remote Sens. 2019, 11, 1443. [Google Scholar] [CrossRef]
- Kim, E.J.; Park, H.C.; Ham, S.W.; Kho, S.Y.; Kim, D.K. Extracting vehicle trajectories using unmanned aerial vehicles in congested traffic conditions. J. Adv. Transp. 2019, 2019, 9060797. [Google Scholar] [CrossRef]
- Jiménez-Jiménez, S.I.; Ojeda-Bustamante, W.; Marcial-Pablo, M.d.J.; Enciso, J. Digital terrain models generated with low-cost UAV photogrammetry: Methodology and accuracy. ISPRS Int. J. Geo-Inf. 2021, 10, 285. [Google Scholar] [CrossRef]
- Nadimi, N.; Ragland, D.R.; Mohammadian Amiri, A. An evaluation of time-to-collision as a surrogate safety measure and a proposal of a new method for its application in safety analysis. Transp. Lett. 2020, 12, 491–500. [Google Scholar] [CrossRef]
- Hochreiter, S. Long Short-term Memory. In Neural Computation; MIT-Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Kong, J.; Pfeiffer, M.; Schildbach, G.; Borrelli, F. Kinematic and dynamic vehicle models for autonomous driving control design. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Republic of Korea, 28 June–1 July 2015; pp. 1094–1099. [Google Scholar]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sun, P.; Wang, X.; Zhu, M. Modeling car-following behavior on freeways considering driving style. J. Transp. Eng. Part A Syst. 2021, 147, 04021083. [Google Scholar] [CrossRef]
- Hou, J.; Yao, D.; Wu, F.; Shen, J.; Chao, X. Online vehicle velocity prediction using an adaptive radial basis function neural network. IEEE Trans. Veh. Technol. 2021, 70, 3113–3122. [Google Scholar] [CrossRef]
- Feng, X.; Cen, Z.; Hu, J.; Zhang, Y. Vehicle trajectory prediction using intention-based conditional variational autoencoder. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 3514–3519. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).