Estimating Rootzone Soil Moisture by Fusing Multiple Remote Sensing Products with Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.1.1. In Situ Soil Moisture Data
2.1.2. Satellite Soil Moisture Data
2.1.3. Land Cover and Vegetation Data
2.1.4. Soil Data
2.1.5. Weather and Climate Data
2.1.6. Topographic Data
2.1.7. Data Preprocessing
2.2. Machine Learning Algorithms
2.2.1. Feed-Forward Artificial Neural Network (ANN)
2.2.2. Random Forest (RF)
2.2.3. Extreme Gradient Boosting (XGBoost)
2.2.4. Categorical Boosting (CatBoost)
2.2.5. Light Gradient Boosting Machine (LightGBM)
2.3. Model Training and Evaluation
3. Results
3.1. Performance of Machine Learning Algorithms
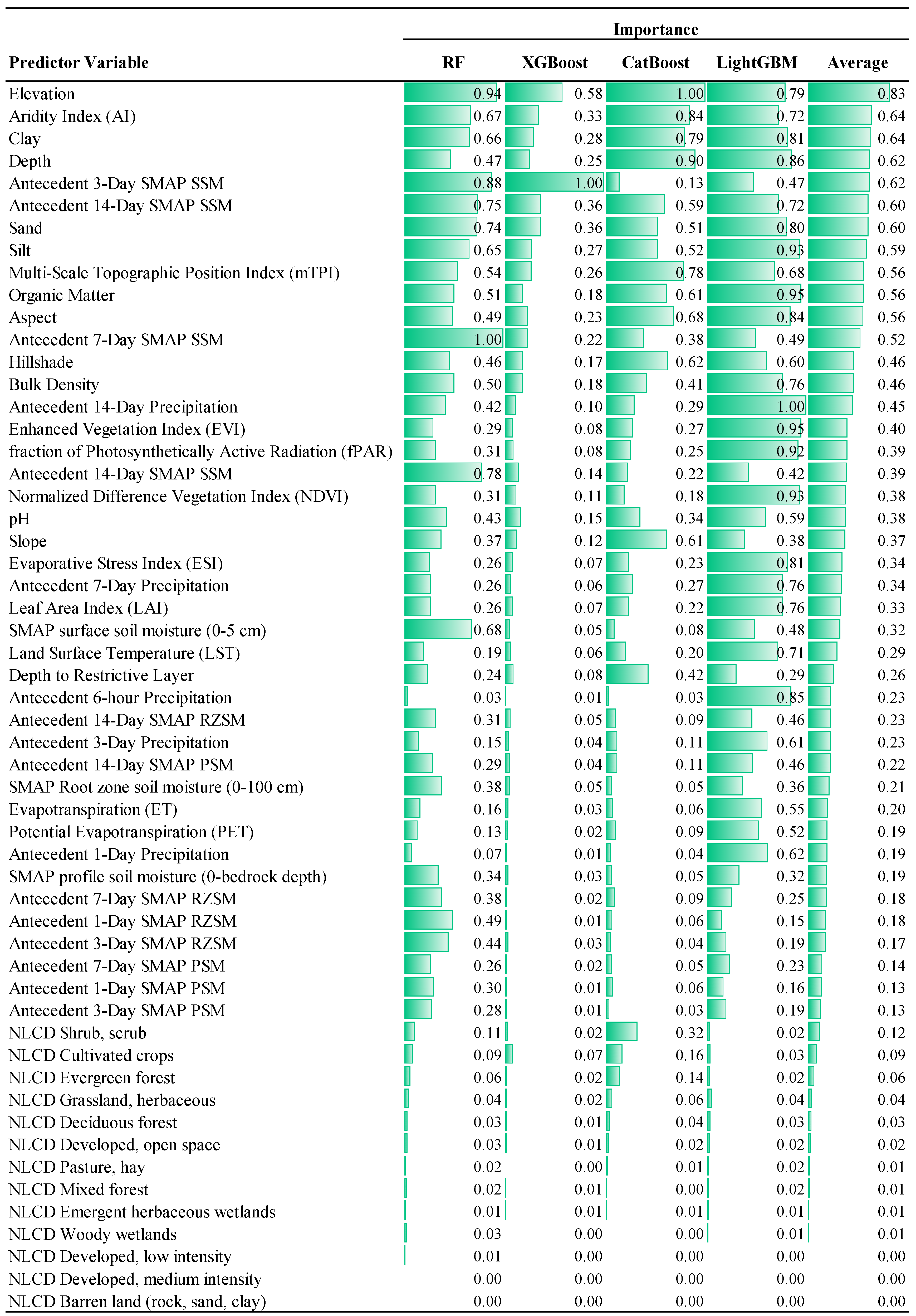
3.2. Importance of Predictor Variables
4. Discussion
5. Conclusions
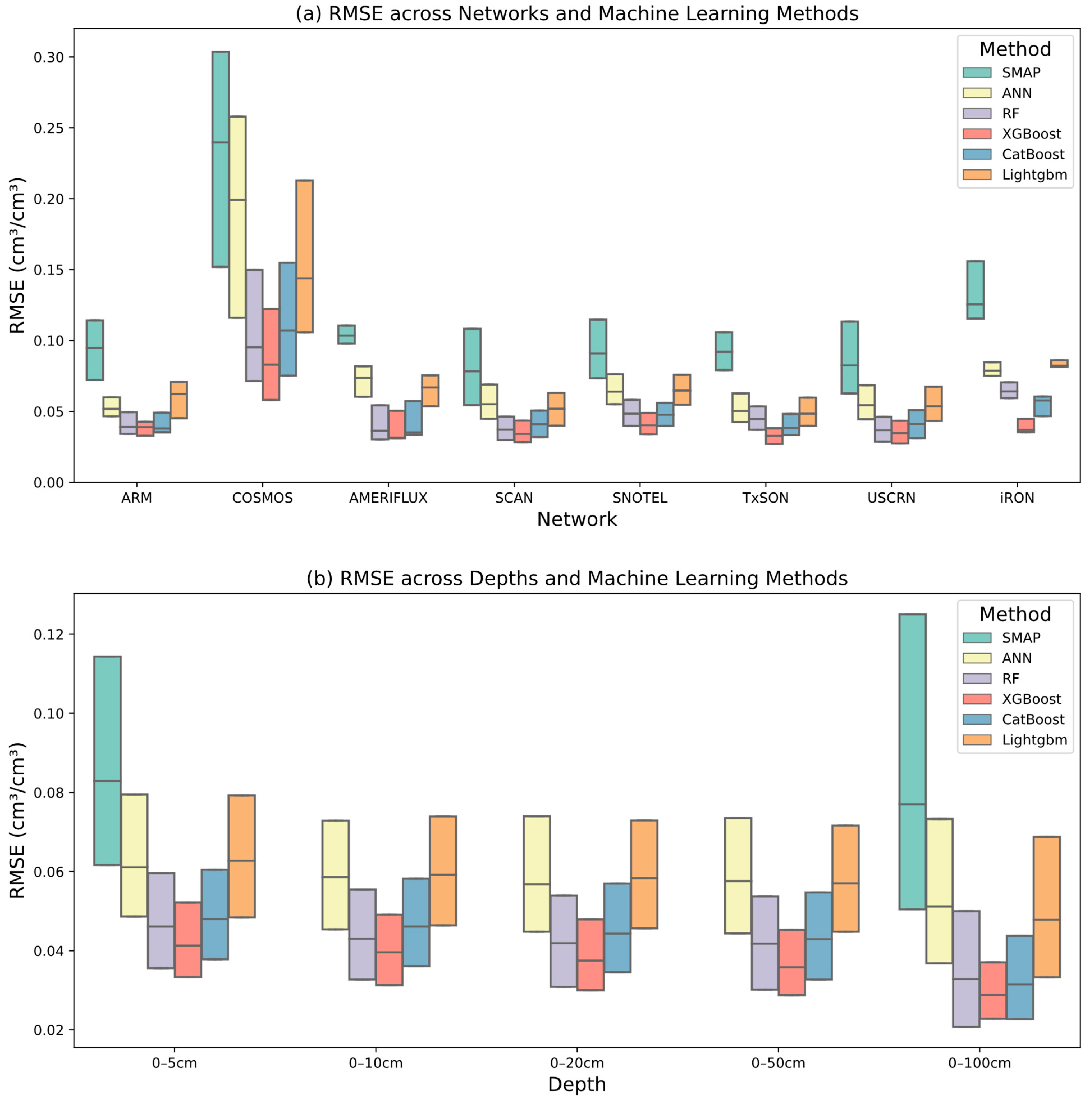
- For the dataset considered, XGBoost provides more accurate soil moisture estimates than the other machine learning models considered. XGBoost also provides better accuracy than directly using SMAP as an estimate of point soil moisture. XGBoost achieves the lowest mean RMSE of 0.042 cm3/cm3 compared to random forest (0.048 cm3/cm3), CatBoost (0.050 cm3/cm3), ANN (0.067 cm3/cm3), LightGBM (0.066 cm3/cm3), and SMAP (0.101 cm3/cm3) for the testing locations. XGBoost produces the best accuracy when considering the entire testing dataset, and it produces the best accuracy when separately considering each in situ soil moisture network and each depth.
- All the machine learning algorithms perform more poorly when comparing to data from the COSMOS network than to the other in situ data networks. The COSMOS measurements have a larger footprint (~700 m diameter) than the point measurements in the other networks. This inconsistency as well as the inconsistency between the COSMOS footprint and the 70 m resolution used to represent the predictor variables likely contributes to the poorer performance at the COSMOS sites.
- The machine learning algorithms typically provide more accurate estimates as the depth of the estimate increases. For example, XGBoost produces a median RMSE of around 0.041 cm3/cm3 for a 0–5 cm depth and 0.029 cm3/cm3 for a 0–100 cm depth. The accuracy may improve with depth because deeper soil moisture varies more gradually and predictably than surface soil moisture.
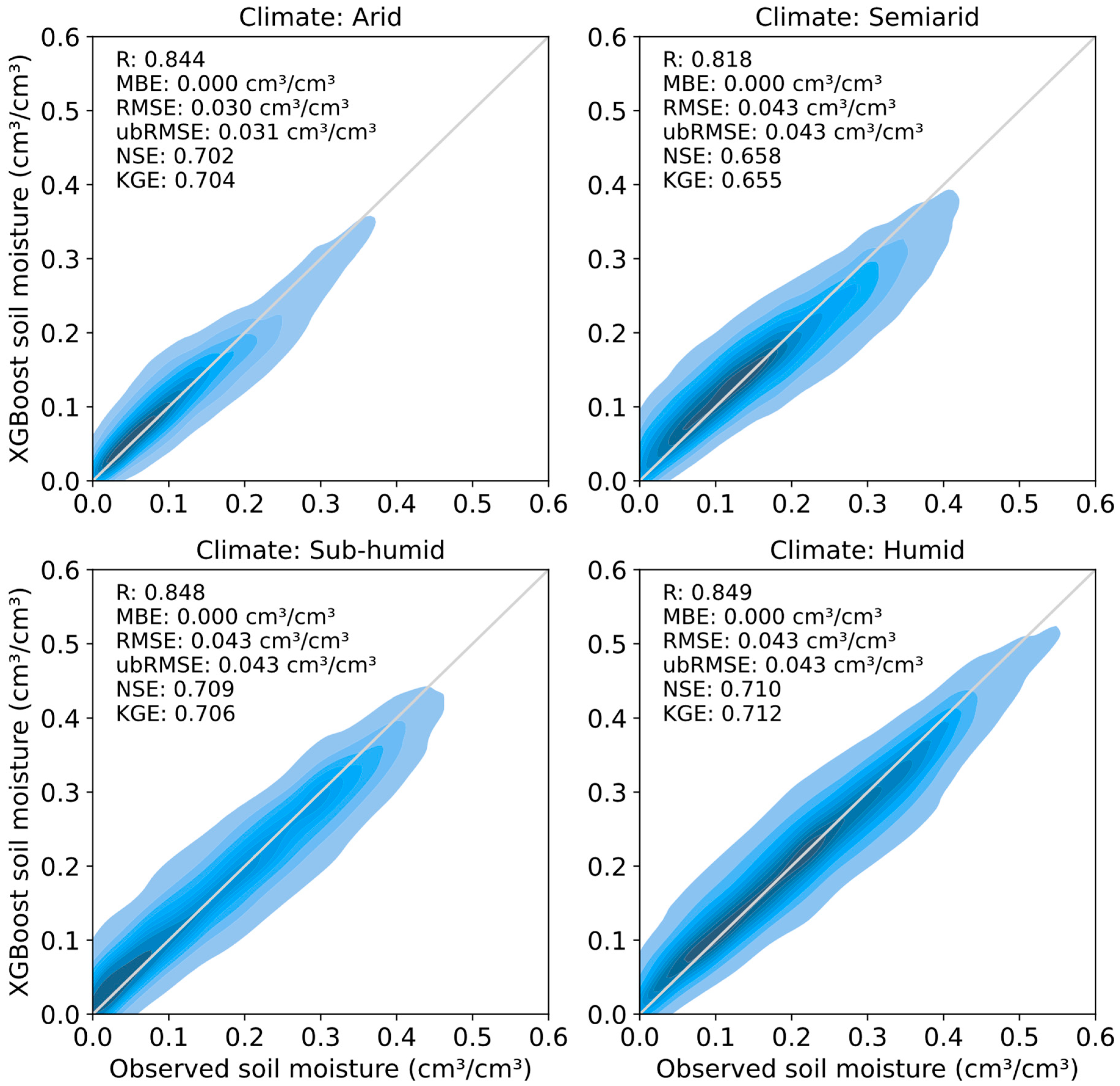
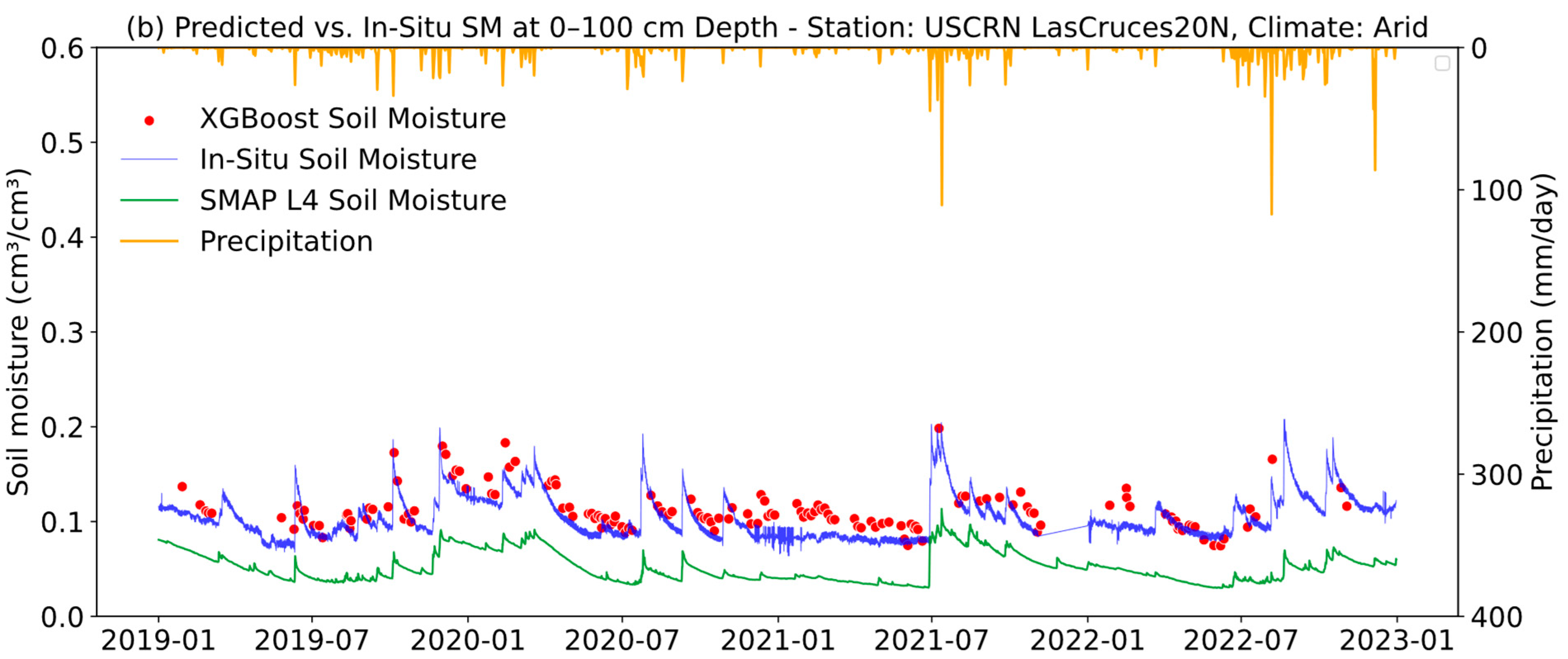
- Although XGBoost exhibits similar accuracy for arid, semiarid, sub-humid, and humid regions, the accuracy is lowest for the semiarid region (semiarid is the only region with NSE and KGE values below 0.70). The accuracy might be lower in semiarid regions due to more complex topographic, soil, and vegetation characteristics. XGBoost can reproduce the typical dynamics of soil moisture in arid regions, where soil moisture remains low except during responses to precipitation events. It can also reproduce the typical behavior in humid regions, where soil moisture remains high except for prolonged periods with low precipitation.
- Feature importance analysis identified elevation as the most important topographic variable when the machine learning models are applied to CONUS, and percent clay is typically the most important soil characteristic. Vegetation plays a lesser role in the models, with EVI being the most important vegetation variable. Land cover classification provides little value to the machine learning algorithms. Among SMAP soil moisture products, surface soil moisture is the most important, with rootzone and profile products having lower importance. Furthermore, 3-day and 14-day antecedent soil moisture variables are more important to the algorithms than the current soil moisture.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A.; Herrero-Jiménez, C.M. Satellite Soil Moisture for Agricultural Drought Monitoring: Assessment of the SMOS Derived Soil Water Deficit Index. Remote Sens. Environ. 2016, 177, 277–286. [Google Scholar] [CrossRef]
- Foster, T.; Mieno, T.; Brozović, N. Satellite-Based Monitoring of Irrigation Water Use: Assessing Measurement Errors and Their Implications for Agricultural Water Management Policy. Water Resour. Res. 2020, 56, e2020WR028378. [Google Scholar] [CrossRef]
- Petropoulos, G.; Srivastava, P.; Piles, M.; Pearson, S. Earth Observation-Based Operational Estimation of Soil Moisture and Evapotranspiration for Agricultural Crops in Support of Sustainable Water Management. Sustainability 2018, 10, 181. [Google Scholar] [CrossRef]
- Zhan, X.; Zheng, W.; Fang, L.; Liu, J.; Hain, C.; Yin, J.; Ek, M. A Preliminary Assessment of the Impact of SMAP Soil Moisture on Numerical Weather Forecasts from GFS and NUWRF Models. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5229–5232. [Google Scholar]
- Koster, R.D.; Suarez, M.J. Impact of Land Surface Initialization on Seasonal Precipitation and Temperature Prediction. J. Hydrometeorol. 2003, 4, 408–423. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J. Soil Moisture Memory in Climate Models. J. Hydrometeorol. 2001, 2, 558–570. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil Moisture for Hydrological Applications: Open Questions and New Opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Bartsch, A.; Balzter, H.; George, C. The Influence of Regional Surface Soil Moisture Anomalies on Forest Fires in Siberia Observed from Satellites. Environ. Res. Lett. 2009, 4, 045021. [Google Scholar] [CrossRef]
- Hou, X.; Orth, R. Observational Evidence of Wildfire-Promoting Soil Moisture Anomalies. Sci. Rep. 2020, 10, 11008. [Google Scholar] [CrossRef]
- Kim, S.; Zhang, R.; Pham, H.; Sharma, A. A Review of Satellite-Derived Soil Moisture and Its Usage for Flood Estimation. Remote Sens. Earth Syst. Sci. 2019, 2, 225–246. [Google Scholar] [CrossRef]
- Xu, L.; Abbaszadeh, P.; Moradkhani, H.; Chen, N.; Zhang, X. Continental Drought Monitoring Using Satellite Soil Moisture, Data Assimilation and an Integrated Drought Index. Remote Sens. Environ. 2020, 250, 112028. [Google Scholar] [CrossRef]
- Ruff, M.S.; Krizek, D.T.; Mirecki, R.M.; Inouye, D.W. Restricted Root Zone Volume: Influence on Growth and Development of Tomato. J. Am. Soc. Hortic. Sci. 1987, 112, 763–769. [Google Scholar] [CrossRef]
- Leenaars, J.G.B.; Claessens, L.; Heuvelink, G.B.M.; Hengl, T.; Ruiperez González, M.; van Bussel, L.G.J.; Guilpart, N.; Yang, H.; Cassman, K.G. Mapping Rootable Depth and Root Zone Plant-Available Water Holding Capacity of the Soil of Sub-Saharan Africa. Geoderma 2018, 324, 18–36. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Lüthi, D.; Litschi, M.; Schär, C. Land–Atmosphere Coupling and Climate Change in Europe. Nature 2006, 443, 205–209. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Iturbe, I.; Porporato, A. Ecohydrology of Water-Controlled Ecosystems; Cambridge University Press: Cambridge, UK, 2005; ISBN 9780521819435. [Google Scholar]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; de Rosnay, P.; Jann, A.; Schneider, S.; et al. The ASCAT Soil Moisture Product: A Review of Its Specifications, Validation Results, and Emerging Applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Martinuzzi, J.; Font, J.; Berger, M. Soil Moisture Retrieval from Space: The Soil Moisture and Ocean Salinity (SMOS) Mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil Moisture Retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A Review of Spatial Downscaling of Satellite Remotely Sensed Soil Moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Tagesson, T.; Horion, S.; Nieto, H.; Zaldo Fornies, V.; Mendiguren González, G.; Bulgin, C.E.; Ghent, D.; Fensholt, R. Disaggregation of SMOS Soil Moisture over West Africa Using the Temperature and Vegetation Dryness Index Based on SEVIRI Land Surface Parameters. Remote Sens. Environ. 2018, 206, 424–441. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Dunbar, R.S.; Chaubell, M.J.; Colliander, A.; Yueh, S.; Jagdhuber, T.; Chen, F.; Crow, W.; O’Neill, P.E.; et al. The SMAP and Copernicus Sentinel 1A/B Microwave Active-Passive High Resolution Surface Soil Moisture Product. Remote Sens. Environ. 2019, 233, 111380. [Google Scholar] [CrossRef]
- Wei, Z.; Meng, Y.; Zhang, W.; Peng, J.; Meng, L. Downscaling SMAP Soil Moisture Estimation with Gradient Boosting Decision Tree Regression over the Tibetan Plateau. Remote Sens. Environ. 2019, 225, 30–44. [Google Scholar] [CrossRef]
- Nuñez-Olivieri, J.; Muñoz-Barreto, J.; Tirado-Corbalá, R.; Lakhankar, T.; Fisher, A. Comparison and Downscale of AMSR2 Soil Moisture Products with In Situ Measurements from the SCAN–NRCS Network over Puerto Rico. Hydrology 2017, 4, 46. [Google Scholar] [CrossRef]
- Vergopolan, N.; Chaney, N.W.; Beck, H.E.; Pan, M.; Sheffield, J.; Chan, S.; Wood, E.F. Combining Hyper-Resolution Land Surface Modeling with SMAP Brightness Temperatures to Obtain 30-m Soil Moisture Estimates. Remote Sens. Environ. 2020, 242, 111740. [Google Scholar] [CrossRef]
- Fischer, S.C. Assessing the Influence of Model Inputs on Performance of the EMT+VS Soil Moisture Downscaling Model for a Large Foothills Region in Northern Colorado; Colorado State University: Fort Collins, CO, USA, 2024. [Google Scholar]
- Dumedah, G.; Walker, J.P.; Merlin, O. Root-Zone Soil Moisture Estimation from Assimilation of Downscaled Soil Moisture and Ocean Salinity Data. Adv. Water Resour. 2015, 84, 14–22. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, G. Estimation of Soil Moisture from Optical and Thermal Remote Sensing: A Review. Sensors 2016, 16, 1308. [Google Scholar] [CrossRef]
- Carlson, T. An Overview of the “Triangle Method” for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Carlson, T.N.; Petropoulos, G.P. A New Method for Estimating of Evapotranspiration and Surface Soil Moisture from Optical and Thermal Infrared Measurements: The Simplified Triangle. Int. J. Remote Sens. 2019, 40, 7716–7729. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.N.; Wooster, M.J.; Islam, S. A Review of Ts/VI Remote Sensing Based Methods for the Retrieval of Land Surface Energy Fluxes and Soil Surface Moisture. Prog. Phys. Geogr. Earth Environ. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S.B. The Optical Trapezoid Model: A Novel Approach to Remote Sensing of Soil Moisture Applied to Sentinel-2 and Landsat-8 Observations. Remote Sens. Environ. 2017, 198, 52–68. [Google Scholar] [CrossRef]
- Wang, W.; Huang, D.; Wang, X.-G.; Liu, Y.-R.; Zhou, F. Estimation of Soil Moisture Using Trapezoidal Relationship between Remotely Sensed Land Surface Temperature and Vegetation Index. Hydrol. Earth Syst. Sci. 2011, 15, 1699–1712. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Masjedi, A.; Dehnavi, S. Temperature-Vegetation-Soil Moisture Dryness Index (TVMDI). Remote Sens. Environ. 2017, 197, 1–14. [Google Scholar] [CrossRef]
- Anderson, W.B.; Zaitchik, B.F.; Hain, C.R.; Anderson, M.C.; Yilmaz, M.T.; Mecikalski, J.; Schultz, L. Towards an Integrated Soil Moisture Drought Monitor for East Africa. Hydrol. Earth Syst. Sci. 2012, 16, 2893–2913. [Google Scholar] [CrossRef]
- Feng, H.; Chen, C.; Dong, H.; Wang, J.; Meng, Q. Modified Shortwave Infrared Perpendicular Water Stress Index: A Farmland Water Stress Monitoring Method. J. Appl. Meteorol. Climatol. 2013, 52, 2024–2032. [Google Scholar] [CrossRef]
- Ghulam, A.; Qin, Q.; Zhan, Z. Designing of the Perpendicular Drought Index. Environ. Geol. 2007, 52, 1045–1052. [Google Scholar] [CrossRef]
- Hu, T.; Renzullo, L.J.; van Dijk, A.I.J.M.; He, J.; Tian, S.; Xu, Z.; Zhou, J.; Liu, T.; Liu, Q. Monitoring Agricultural Drought in Australia Using MTSAT-2 Land Surface Temperature Retrievals. Remote Sens. Environ. 2020, 236, 111419. [Google Scholar] [CrossRef]
- Van doninck, J.; Peters, J.; De Baets, B.; De Clercq, E.M.; Ducheyne, E.; Verhoest, N.E.C. The Potential of Multitemporal Aqua and Terra MODIS Apparent Thermal Inertia as a Soil Moisture Indicator. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 934–941. [Google Scholar] [CrossRef]
- Amazirh, A.; Merlin, O.; Er-Raki, S.; Gao, Q.; Rivalland, V.; Malbeteau, Y.; Khabba, S.; Escorihuela, M.J. Retrieving Surface Soil Moisture at High Spatio-Temporal Resolution from a Synergy between Sentinel-1 Radar and Landsat Thermal Data: A Study Case over Bare Soil. Remote Sens. Environ. 2018, 211, 321–337. [Google Scholar] [CrossRef]
- Gao, X.; Zhao, X.; Brocca, L.; Huo, G.; Lv, T.; Wu, P. Depth Scaling of Soil Moisture Content from Surface to Profile: Multistation Testing of Observation Operators. Hydrol. Earth Syst. Sci. Discuss. 2017, 2017, 1–25. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Molden, D.J.; Makin, I.W. Remote Sensing for Irrigated Agriculture: Examples from Research and Possible Applications. Agric. Water Manag. 2000, 46, 137–155. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J. Evolution of Evapotranspiration Models Using Thermal and Shortwave Remote Sensing Data. Remote Sens. Environ. 2020, 237, 111594. [Google Scholar] [CrossRef]
- Hain, C.R.; Mecikalski, J.R.; Anderson, M.C. Retrieval of an Available Water-Based Soil Moisture Proxy from Thermal Infrared Remote Sensing. Part I: Methodology and Validation. J. Hydrometeorol. 2009, 10, 665–683. [Google Scholar] [CrossRef]
- Sahaar, S.A.; Niemann, J.D. Impact of Regional Characteristics on the Estimation of Root-Zone Soil Moisture from the Evaporative Index or Evaporative Fraction. Agric. Water Manag. 2020, 238, 106225. [Google Scholar] [CrossRef]
- Scott, C.A.; Bastiaanssen, W.G.M.; Ahmad, M.-D. Mapping Root Zone Soil Moisture Using Remotely Sensed Optical Imagery. J. Irrig. Drain. Eng. 2003, 129, 326–335. [Google Scholar] [CrossRef]
- Chauhan, N.S.; Miller, S.; Ardanuy, P. Spaceborne Soil Moisture Estimation at High Resolution: A Microwave-Optical/IR Synergistic Approach. Int. J. Remote Sens. 2003, 24, 4599–4622. [Google Scholar] [CrossRef]
- Merlin, O.; Rudiger, C.; Al Bitar, A.; Richaume, P.; Walker, J.P.; Kerr, Y.H. Disaggregation of SMOS Soil Moisture in Southeastern Australia. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1556–1571. [Google Scholar] [CrossRef]
- Piles, M.; Petropoulos, G.P.; Sánchez, N.; González-Zamora, Á.; Ireland, G. Towards Improved Spatio-Temporal Resolution Soil Moisture Retrievals from the Synergy of SMOS and MSG SEVIRI Spaceborne Observations. Remote Sens. Environ. 2016, 180, 403–417. [Google Scholar] [CrossRef]
- Portal, G.; Vall-Llosscra, M.; Piles, M.; Camps, A.; Chaparro, D.; Pablos, M.; Rossato, L.; Aabouch, K. Microwave and Optical Data Fusion for Global Mapping of Soil Moisture at High Resolution. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 341–344. [Google Scholar]
- Bai, L.; Long, D.; Yan, L. Estimation of Surface Soil Moisture with Downscaled Land Surface Temperatures Using a Data Fusion Approach for Heterogeneous Agricultural Land. Water Resour. Res. 2019, 55, 1105–1128. [Google Scholar] [CrossRef]
- Long, D.; Bai, L.; Yan, L.; Zhang, C.; Yang, W.; Lei, H.; Quan, J.; Meng, X.; Shi, C. Generation of Spatially Complete and Daily Continuous Surface Soil Moisture of High Spatial Resolution. Remote Sens. Environ. 2019, 233, 111364. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, X.; Chen, N.; Ma, H.; Zeng, J.; Fu, P.; Nam, W.-H.; Niyogi, D. Generating High-Accuracy and Cloud-Free Surface Soil Moisture at 1 Km Resolution by Point-Surface Data Fusion over the Southwestern U.S. Agric. For. Meteorol. 2022, 321, 108985. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Walker, J. A Methodology for Surface Soil Moisture and Vegetation Optical Depth Retrieval Using the Microwave Polarization Difference Index. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1643–1654. [Google Scholar] [CrossRef]
- Leng, P.; Li, Z.-L.; Liao, Q.-Y.; Gao, M.-F.; Duan, S.-B.; Zhang, X.; Shang, G.-F. Determination of All-Sky Surface Soil Moisture at Fine Spatial Resolution Synergistically Using Optical/Thermal Infrared and Microwave Measurements. J. Hydrol. 2019, 579, 124167. [Google Scholar] [CrossRef]
- Mishra, V.; Cruise, J.F.; Hain, C.R.; Mecikalski, J.R.; Anderson, M.C. Development of Soil Moisture Profiles through Coupled Microwave–Thermal Infrared Observations in the Southeastern United States. Hydrol. Earth Syst. Sci. 2018, 22, 4935–4957. [Google Scholar] [CrossRef]
- Wangemann, S.G.; Kohl, R.A.; Molumeli, P.A. Infiltration and Percolation Influenced by Antecedent Soil Water Content and Air Entrapment. Trans. ASAE 2000, 43, 1517–1523. [Google Scholar] [CrossRef]
- Tong, C.; Wang, H.; Magagi, R.; Goïta, K.; Zhu, L.; Yang, M.; Deng, J. Soil Moisture Retrievals by Combining Passive Microwave and Optical Data. Remote Sens. 2020, 12, 3173. [Google Scholar] [CrossRef]
- Zhang, Y.-K.; Schilling, K.E. Effects of Land Cover on Water Table, Soil Moisture, Evapotranspiration, and Groundwater Recharge: A Field Observation and Analysis. J. Hydrol. 2006, 319, 328–338. [Google Scholar] [CrossRef]
- Ranney, K.J.; Niemann, J.D.; Lehman, B.M.; Green, T.R.; Jones, A.S. A Method to Downscale Soil Moisture to Fine Resolutions Using Topographic, Vegetation, and Soil Data. Adv. Water Resour. 2015, 76, 81–96. [Google Scholar] [CrossRef]
- Takagi, K.; Lin, H.S. Temporal Dynamics of Soil Moisture Spatial Variability in the Shale Hills Critical Zone Observatory. Vadose Zone J. 2011, 10, 832–842. [Google Scholar] [CrossRef]
- Crow, W.T.; Berg, A.A.; Cosh, M.H.; Loew, A.; Mohanty, B.P.; Panciera, R.; de Rosnay, P.; Ryu, D.; Walker, J.P. Upscaling Sparse Ground-Based Soil Moisture Observations for the Validation of Coarse-Resolution Satellite Soil Moisture Products. Rev. Geophys. 2012, 50, RG2002. [Google Scholar] [CrossRef]
- Rosenbaum, U.; Bogena, H.R.; Herbst, M.; Huisman, J.A.; Peterson, T.J.; Weuthen, A.; Western, A.W.; Vereecken, H. Seasonal and Event Dynamics of Spatial Soil Moisture Patterns at the Small Catchment Scale. Water Resour. Res. 2012, 48, W10544. [Google Scholar] [CrossRef]
- Evans, J.G.; Ward, H.C.; Blake, J.R.; Hewitt, E.J.; Morrison, R.; Fry, M.; Ball, L.A.; Doughty, L.C.; Libre, J.W.; Hitt, O.E.; et al. Soil Water Content in Southern England Derived from a Cosmic-ray Soil Moisture Observing System—COSMOS-UK. Hydrol. Process. 2016, 30, 4987–4999. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Ryu, D.; Berg, A.A.; Rodell, M.; Jackson, T.J. Field Observations of Soil Moisture Variability across Scales. Water Resour. Res. 2008, 44, W01423. [Google Scholar] [CrossRef]
- Geroy, I.J.; Gribb, M.M.; Marshall, H.P.; Chandler, D.G.; Benner, S.G.; McNamara, J.P. Aspect Influences on Soil Water Retention and Storage. Hydrol. Process. 2011, 25, 3836–3842. [Google Scholar] [CrossRef]
- Coleman, M.L.; Niemann, J.D. Controls on Topographic Dependence and Temporal Instability in Catchment-scale Soil Moisture Patterns. Water Resour. Res. 2013, 49, 1625–1642. [Google Scholar] [CrossRef]
- Cowley, G.S.; Niemann, J.D.; Green, T.R.; Seyfried, M.S.; Jones, A.S.; Grazaitis, P.J. Impacts of Precipitation and Potential Evapotranspiration Patterns on Downscaling Soil Moisture in Regions with Large Topographic Relief. Water Resour. Res. 2017, 53, 1553–1574. [Google Scholar] [CrossRef]
- Abbaszadeh, P.; Moradkhani, H.; Zhan, X. Downscaling SMAP Radiometer Soil Moisture Over the CONUS Using an Ensemble Learning Method. Water Resour. Res. 2019, 55, 324–344. [Google Scholar] [CrossRef]
- Abowarda, A.S.; Bai, L.; Zhang, C.; Long, D.; Li, X.; Huang, Q.; Sun, Z. Generating Surface Soil Moisture at 30 m Spatial Resolution Using Both Data Fusion and Machine Learning toward Better Water Resources Management at the Field Scale. Remote Sens. Environ. 2021, 255, 112301. [Google Scholar] [CrossRef]
- Liu, Y.; Jing, W.; Wang, Q.; Xia, X. Generating High-Resolution Daily Soil Moisture by Using Spatial Downscaling Techniques: A Comparison of Six Machine Learning Algorithms. Adv. Water Resour. 2020, 141, 103601. [Google Scholar] [CrossRef]
- Peng, J.; Albergel, C.; Balenzano, A.; Brocca, L.; Cartus, O.; Cosh, M.H.; Crow, W.T.; Dabrowska-Zielinska, K.; Dadson, S.; Davidson, M.W.J.; et al. A Roadmap for High-Resolution Satellite Soil Moisture Applications—Confronting Product Characteristics with User Requirements. Remote Sens. Environ. 2021, 252, 112162. [Google Scholar] [CrossRef]
- Fathololoumi, S.; Karimi Firozjaei, M.; Biswas, A. Improving Spatial Resolution of Satellite Soil Water Index (SWI) Maps under Clear-Sky Conditions Using a Machine Learning Approach. J. Hydrol. 2022, 615, 128709. [Google Scholar] [CrossRef]
- Zhao, W.; Sánchez, N.; Lu, H.; Li, A. A Spatial Downscaling Approach for the SMAP Passive Surface Soil Moisture Product Using Random Forest Regression. J. Hydrol. 2018, 563, 1009–1024. [Google Scholar] [CrossRef]
- Fang, K.; Pan, M.; Shen, C. The Value of SMAP for Long-Term Soil Moisture Estimation with the Help of Deep Learning. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2221–2233. [Google Scholar] [CrossRef]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of Machine Learning Approaches for Biomass and Soil Moisture Retrievals from Remote Sensing Data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef]
- Greifeneder, F.; Notarnicola, C.; Wagner, W. A Machine Learning-Based Approach for Surface Soil Moisture Estimations with Google Earth Engine. Remote Sens. 2021, 13, 2099. [Google Scholar] [CrossRef]
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving Performance of Spatio-Temporal Machine Learning Models Using Forward Feature Selection and Target-Oriented Validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
- Rani, A.; Kumar, N.; Kumar, J.; Kumar, J.; Sinha, N.K. Machine Learning for Soil Moisture Assessment. In Deep Learning for Sustainable Agriculture; Elsevier: Amsterdam, The Netherlands, 2022; pp. 143–168. ISBN 9780323852142. [Google Scholar]
- Singh, A.; Gaurav, K. Deep Learning and Data Fusion to Estimate Surface Soil Moisture from Multi-Sensor Satellite Images. Sci. Rep. 2023, 13, 2251. [Google Scholar] [CrossRef]
- Fuentes, I.; Padarian, J.; Vervoort, R.W. Towards near Real-Time National-Scale Soil Water Content Monitoring Using Data Fusion as a Downscaling Alternative. J. Hydrol. 2022, 609, 127705. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Mishra, A.K. Multi-Layer High-Resolution Soil Moisture Estimation Using Machine Learning over the United States. Remote Sens. Environ. 2021, 266, 112706. [Google Scholar] [CrossRef]
- Liu, E.; Zhu, Y.; Lü, H.; Horton, R.; Gou, Q.; Wang, X.; Ding, Z.; Xu, H.; Pan, Y. Estimation and Assessment of the Root Zone Soil Moisture from Near-Surface Measurements over Huai River Basin. Atmosphere 2023, 14, 124. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Xaver, A.; Vreugdenhil, M.; Gruber, A.; Hegyiová, A.; Sanchis-Dufau, A.D.; Zamojski, D.; Cordes, C.; Wagner, W.; Drusch, M. Global Automated Quality Control of In Situ Soil Moisture Data from the International Soil Moisture Network. Vadose Zone J. 2013, 12, 1–21. [Google Scholar] [CrossRef]
- Cook, D.R. Soil Temperature and Moisture Profile (STAMP) System Handbook; Technical Reports; DOE Office of Science Atmospheric Radiation Measurement (ARM) Program: USA, 2016. Available online: https://www.osti.gov/biblio/1332724 (accessed on 1 November 2023).
- Zreda, M.; Desilets, D.; Ferré, T.P.A.; Scott, R.L. Measuring Soil Moisture Content Non-Invasively at Intermediate Spatial Scale Using Cosmic-Ray Neutrons. Geophys. Res. Lett. 2008, 35, L21402. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem–Scale Carbon Dioxide, Water Vapor, and Energy Flux Densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Osenga, E.C.; Vano, J.A.; Arnott, J.C. A Community-Supported Weather and Soil Moisture Monitoring Database of the Roaring Fork Catchment of the Colorado River Headwaters. Hydrol. Process. 2021, 35, e14081. [Google Scholar] [CrossRef]
- Schaefer, G.L.; Cosh, M.H.; Jackson, T.J. The USDA Natural Resources Conservation Service Soil Climate Analysis Network (SCAN). J. Atmos. Ocean. Technol. 2007, 24, 2073–2077. [Google Scholar] [CrossRef]
- Fleming, S.W.; Zukiewicz, L.; Strobel, M.L.; Hofman, H.; Goodbody, A.G. SNOTEL, the Soil Climate Analysis Network, and Water Supply Forecasting at the Natural Resources Conservation Service: Past, Present, and Future. JAWRA J. Am. Water Resour. Assoc. 2023, 59, 585–599. [Google Scholar] [CrossRef]
- Caldwell, T.G.; Bongiovanni, T.; Cosh, M.H.; Jackson, T.J.; Colliander, A.; Abolt, C.J.; Casteel, R.; Larson, T.; Scanlon, B.R.; Young, M.H. The Texas Soil Observation Network:A Comprehensive Soil Moisture Dataset for Remote Sensing and Land Surface Model Validation. Vadose Zone J. 2019, 18, 1–20. [Google Scholar] [CrossRef]
- Bell, J.E.; Palecki, M.A.; Baker, C.B.; Collins, W.G.; Lawrimore, J.H.; Leeper, R.D.; Hall, M.E.; Kochendorfer, J.; Meyers, T.P.; Wilson, T.; et al. U.S. Climate Reference Network Soil Moisture and Temperature Observations. J. Hydrometeorol. 2013, 14, 977–988. [Google Scholar] [CrossRef]
- Reichle, R.; De Lannoy, G.; Koster, R.D.; Crow, W.T.; Kimball, J.S.; Liu, Q.; Bechtold, M. SMAP L4 Global 3-Hourly 9 Km EASE-Grid Surface and Root Zone Soil Moisture Analysis Update, Version 7; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2022. [Google Scholar]
- Reichle, R.H.; De Lannoy, G.J.M.; Liu, Q.; Ardizzone, J.V.; Colliander, A.; Conaty, A.; Crow, W.; Jackson, T.J.; Jones, L.A.; Kimball, J.S.; et al. Assessment of the SMAP Level-4 Surface and Root-Zone Soil Moisture Product Using In Situ Measurements. J. Hydrometeorol. 2017, 18, 2621–2645. [Google Scholar] [CrossRef]
- Davis, B.N.; Werpy, J.; Friesz, A.; Impecoven, K.; Quenzer, R.L.; Maiersperger, T.; Meyer, D.J. Interactive Access to LP DAAC Satellite Data Archives Through a Combination of Open-Source and Custom Middleware Web Services. IEEE Geosci. Remote Sens. Mag. 2015, 3, 8–20. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Dorigo, W.; Himmelbauer, I.; Aberer, D.; Schremmer, L.; Petrakovic, I.; Zappa, L.; Preimesberger, W.; Xaver, A.; Annor, F.; Ardö, J.; et al. The International Soil Moisture Network: Serving Earth System Science for over a Decade. Hydrol. Earth Syst. Sci. 2021, 25, 5749–5804. [Google Scholar] [CrossRef]
- Dewitz, J. National Land Cover Database (NLCD) 2019 Products (Ver. 2.0, June 2021): U.S. Geological Survey Data Release. 2019. Available online: https://data.usgs.gov/datacatalog/data/USGS:60cb3da7d34e86b938a30cb9 (accessed on 1 June 2023).
- Dewitz, J.; U.S. Geological Survey. National Land Cover Database (NLCD) 2019 Products (Ver. 3.0, February 2024): U.S. Geological Survey Data Release. 2021. Available online: https://www.sciencebase.gov/catalog/item/5f21cef582cef313ed940043 (accessed on 1 June 2023).
- Didan, K. MODIS/Terra Vegetation Indices 16-Day L3 Global 250m SIN Grid. V061. 2021. Available online: https://ladsweb.modaps.eosdis.nasa.gov/missions-and-measurements/products/MOD13Q1 (accessed on 15 September 2023).
- Myneni, R.; Knyazikhin, Y.; Park, T. MODIS/Terra+Aqua Leaf Area Index/FPAR 4-Day L4 Global 500m SIN Grid. V061. 2021. Available online: https://ladsweb.modaps.eosdis.nasa.gov/missions-and-measurements/products/MCD15A3H (accessed on 1 June 2023).
- Soil Survey Staff Gridded National Soil Survey Geographic (GNATSGO) Database for the Conterminous United States. Available online: https://nrcs.app.box.com/v/soils (accessed on 5 January 2023).
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Jackson, T. GPM IMERG Final Precipitation L3 Half Hourly 0.1 Degree x 0.1 Degree V06; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2019. [Google Scholar]
- Hook, S.; Hulley, G. ECOSTRESS Swath Land Surface Temperature and Emissivity Instantaneous L2 Global 70 m v002 [Data Set]. NASA EOSDIS Land Processes Distributed Active Archive Center. 2022. Available online: https://lpdaac.usgs.gov/products/eco_l2_lstev002/ (accessed on 1 June 2023).
- Hook, S.; Fisher, J. ECOSTRESS Evapotranspiration PT-JPL Daily L3 Global 70 m V001 [Data Set]. NASA EOSDIS Land Processes Distributed Active Archive Center. 2019. Available online: https://lpdaac.usgs.gov/products/eco3etptjplv001/ (accessed on 1 June 2023).
- Zomer, R.J.; Xu, J.; Trabucco, A. Version 3 of the Global Aridity Index and Potential Evapotranspiration Database. Sci. Data 2022, 9, 409. [Google Scholar] [CrossRef] [PubMed]
- NASA; JPL. NASA Shuttle Radar Topography Mission Global 1 arc second [Data Set]. NASA EOSDIS Land Processes Distributed Active Archive Center. 2013. Available online: https://lpdaac.usgs.gov/products/srtmgl1v003/ (accessed on 1 June 2023).
- Theobald, D.M.; Harrison-Atlas, D.; Monahan, W.B.; Albano, C.M. Ecologically-Relevant Maps of Landforms and Physiographic Diversity for Climate Adaptation Planning. PLoS ONE 2015, 10, e0143619. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Yang, M.; Li, Z.; Shao, J.; Li, L.; Chen, P.; Li, S.; Zhao, R. Experimental Investigation of Relationship between Infiltration Rate and Soil Moisture under Rainfall Conditions. Water 2022, 14, 1347. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-Density Cypress Forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef]
- Xu, B.; Park, T.; Yan, K.; Chen, C.; Zeng, Y.; Song, W.; Yin, G.; Li, J.; Liu, Q.; Knyazikhin, Y.; et al. Analysis of Global LAI/FPAR Products from VIIRS and MODIS Sensors for Spatio-Temporal Consistency and Uncertainty from 2012–2016. Forests 2018, 9, 73. [Google Scholar] [CrossRef]
- Churkina, G.; Running, S.W. Contrasting Climatic Controls on the Estimated Productivity of Global Terrestrial Biomes. Ecosystems 1998, 1, 206–215. [Google Scholar] [CrossRef]
- Machado, R.; Serralheiro, R. Soil Salinity: Effect on Vegetable Crop Growth. Management Practices to Prevent and Mitigate Soil Salinization. Horticulturae 2017, 3, 30. [Google Scholar] [CrossRef]
- Yadav, D.S.; Jaiswal, B.; Gautam, M.; Agrawal, M. Soil Acidification and Its Impact on Plants. In Plant Responses to Soil Pollution; Springer: Singapore, 2020; pp. 1–26. ISBN 9789811549649. [Google Scholar]
- Rossiter, D.G.; Poggio, L.; Beaudette, D.; Libohova, Z. How Well Does Digital Soil Mapping Represent Soil Geography? An Investigation from the USA. SOIL 2022, 8, 559–586. [Google Scholar] [CrossRef]
- Krishnan, S.; Pradhan, A.; Indu, J. Estimation of High-Resolution Precipitation Using Downscaled Satellite Soil Moisture and SM2RAIN Approach. J. Hydrol. 2022, 610, 127926. [Google Scholar] [CrossRef]
- Farahani, A.; Moradikhaneghahi, M.; Ghayoomi, M.; Jacobs, J.M. Application of Soil Moisture Active Passive (SMAP) Satellite Data in Seismic Response Assessment. Remote Sens. 2022, 14, 4375. [Google Scholar] [CrossRef]
- Beck, H.E.; Pan, M.; Miralles, D.G.; Reichle, R.H.; Dorigo, W.A.; Hahn, S.; Sheffield, J.; Karthikeyan, L.; Balsamo, G.; Parinussa, R.M.; et al. Evaluation of 18 Satellite- and Model-Based Soil Moisture Products Using in Situ Measurements from 826 Sensors. Hydrol. Earth Syst. Sci. 2021, 25, 17–40. [Google Scholar] [CrossRef]
- Fisher, J.B.; Lee, B.; Purdy, A.J.; Halverson, G.H.; Dohlen, M.B.; Cawse-Nicholson, K.; Wang, A.; Anderson, R.G.; Aragon, B.; Arain, M.A.; et al. ECOSTRESS: NASA’s Next Generation Mission to Measure Evapotranspiration from the International Space Station. Water Resour. Res. 2020, 56, e2019WR026058. [Google Scholar] [CrossRef]
- Trabucco, A.; Zomer, R.J. Global Aridity Index and Potential Evapotranspiration (ET0) Climate Database V2. CGIAR Consort. Spat. Inf. 2019, 10, m9. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km Spatial Resolution Climate Surfaces for Global Land Areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Rudnicki, J.W.; Rodell, M. Variability in Surface Moisture Content along a Hillslope Transect: Rattlesnake Hill, Texas. J. Hydrol. 1998, 210, 259–281. [Google Scholar] [CrossRef]
- Western, A.W.; Grayson, R.B.; Blöschl, G.; Willgoose, G.R.; McMahon, T.A. Observed Spatial Organization of Soil Moisture and Its Relation to Terrain Indices. Water Resour. Res. 1999, 35, 797–810. [Google Scholar] [CrossRef]
- Burrough, P.A.; McDonnell, R.A. Principles of Geographical Information Systems; Oxford University Press: Oxford, UK, 1998; ISBN 0198233655. [Google Scholar]
- Celik, M.F.; Isik, M.S.; Yuzugullu, O.; Fajraoui, N.; Erten, E. Soil Moisture Prediction from Remote Sensing Images Coupled with Climate, Soil Texture and Topography via Deep Learning. Remote Sens. 2022, 14, 5584. [Google Scholar] [CrossRef]
- Luo, P.; Song, Y.; Huang, X.; Ma, H.; Liu, J.; Yao, Y.; Meng, L. Identifying Determinants of Spatio-Temporal Disparities in Soil Moisture of the Northern Hemisphere Using a Geographically Optimal Zones-Based Heterogeneity Model. ISPRS J. Photogramm. Remote Sens. 2022, 185, 111–128. [Google Scholar] [CrossRef]
- Iverson, L.R.; Prasad, A.M.; Rebbeck, J. A Comparison of the Integrated Moisture Index and the Topographic Wetness Index as Related to Two Years of Soil Moisture Monitoring in Zaleski State Forest, Ohio. In Proceedings of the 14th Central Hardwood Forest conference, Wooster, OH, USA, 16–19 March 2004. [Google Scholar]
- Bisong, E. Introduction to Scikit-Learn. In Building Machine Learning and Deep Learning Models on Google Cloud Platform; Apress: Berkeley, CA, USA, 2019; pp. 215–229. [Google Scholar]
- Jiang, D.; Lin, W.; Raghavan, N. A Novel Framework for Semiconductor Manufacturing Final Test Yield Classification Using Machine Learning Techniques. IEEE Access 2020, 8, 197885–197895. [Google Scholar] [CrossRef]
- Abiy, A.Z.; Wiederholt, R.P.; Lagerwall, G.L.; Melesse, A.M.; Davis, S.E. Multilayer Feedforward Artificial Neural Network Model to Forecast Florida Bay Salinity with Climate Change. Water 2022, 14, 3495. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Kornelsen, K.C.; Coulibaly, P. Root-zone Soil Moisture Estimation Using Data-driven Methods. Water Resour. Res. 2014, 50, 2946–2962. [Google Scholar] [CrossRef]
- Adab, H.; Morbidelli, R.; Saltalippi, C.; Moradian, M.; Ghalhari, G.A.F. Machine Learning to Estimate Surface Soil Moisture from Remote Sensing Data. Water 2020, 12, 3223. [Google Scholar] [CrossRef]
- Jamei, M.; Karbasi, M.; Malik, A.; Jamei, M.; Kisi, O.; Yaseen, Z.M. Long-Term Multi-Step Ahead Forecasting of Root Zone Soil Moisture in Different Climates: Novel Ensemble-Based Complementary Data-Intelligent Paradigms. Agric. Water Manag. 2022, 269, 107679. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, X.; Zhao, X. Series or Parallel? An Exploration in Coupling Physical Model and Machine Learning Method for Disaggregating Satellite Microwave Soil Moisture. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Demir-Kavuk, O.; Kamada, M.; Akutsu, T.; Knapp, E.-W. Prediction Using Step-Wise L1, L2 Regularization and Feature Selection for Small Data Sets with Large Number of Features. BMC Bioinform. 2011, 12, 412. [Google Scholar] [CrossRef] [PubMed]
- Thirumalaiah, K.; Deo, M.C. River Stage Forecasting Using Artificial Neural Networks. J. Hydrol. Eng. 1998, 3, 26–32. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. arXiv 2017, arXiv:1706.09516. [Google Scholar]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for Big Data: An Interdisciplinary Review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; p. 30. [Google Scholar]
- Sechidis, K.; Tsoumakas, G.; Vlahavas, I. On the Stratification of Multi-Label Data. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2011; pp. 145–158. ISBN 9783642238079. [Google Scholar]
- Paulik, C.; Dorigo, W.; Wagner, W.; Kidd, R. Validation of the ASCAT Soil Water Index Using in Situ Data from the International Soil Moisture Network. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 1–8. [Google Scholar] [CrossRef]
- Morales, P.; Sykes, M.T.; Prentice, I.C.; Smith, P.; Smith, B.; Bugmann, H.; Zierl, B.; Friedlingstein, P.; Viovy, N.; Sabaté, S.; et al. Comparing and Evaluating Process-based Ecosystem Model Predictions of Carbon and Water Fluxes in Major European Forest Biomes. Glob. Chang. Biol. 2005, 11, 2211–2233. [Google Scholar] [CrossRef] [PubMed]
- Entekhabi, D.; Reichle, R.H.; Koster, R.D.; Crow, W.T. Performance Metrics for Soil Moisture Retrievals and Application Requirements. J. Hydrometeorol. 2010, 11, 832–840. [Google Scholar] [CrossRef]
- Li, L.; Dai, Y.; Shangguan, W.; Wei, Z.; Wei, N.; Li, Q. Causality-Structured Deep Learning for Soil Moisture Predictions. J. Hydrometeorol. 2022, 23, 1315–1331. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- UNEP (United Nations Environment Programme). World Atlas of Desertification, 2nd ed.; UNEP: Nairobi, Kenya, 1997. [Google Scholar]
- Jamali, S.; Seaquist, J.W.; Ardo, J.; Eklundh, L. Investigating Temporal Relationships between Rainfall, Soil Moisture and MODIS-Derived NDVI and EVI for Six Sites in Africa. In Proceedings of the 34th International Symposium on Remote Sensing of Environment—The GEOSS Era: Towards Operational Environmental Monitoring, Sydney, Australia, 10–15 April 2011. [Google Scholar]
- Santos, W.J.R.; Silva, B.M.; Oliveira, G.C.; Volpato, M.M.L.; Lima, J.M.; Curi, N.; Marques, J.J. Soil Moisture in the Root Zone and Its Relation to Plant Vigor Assessed by Remote Sensing at Management Scale. Geoderma 2014, 221–222, 91–95. [Google Scholar] [CrossRef]
- Méndez-Barroso, L.A.; Vivoni, E.R.; Watts, C.J.; Rodríguez, J.C. Seasonal and Interannual Relations between Precipitation, Surface Soil Moisture and Vegetation Dynamics in the North American Monsoon Region. J. Hydrol. 2009, 377, 59–70. [Google Scholar] [CrossRef]
- Wang, T.; Franz, T.E.; Li, R.; You, J.; Shulski, M.D.; Ray, C. Evaluating Climate and Soil Effects on Regional Soil Moisture Spatial Variability Using EOFs. Water Resour. Res. 2017, 53, 4022–4035. [Google Scholar] [CrossRef]
- Zhang, Y.-Y.; Wu, W.; Liu, H. Factors Affecting Variations of Soil PH in Different Horizons in Hilly Regions. PLoS ONE 2019, 14, e0218563. [Google Scholar] [CrossRef]
- Song, Y.M.; Wang, Z.F.; Qi, L.L.; Huang, A.N. Soil Moisture Memory and Its Effect on the Surface Water and Heat Fluxes on Seasonal and Interannual Time Scales. J. Geophys. Res. Atmos. 2019, 124, 10730–10741. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; González-Zamora, A.; Almendra-Martín, L. Soil Moisture Memory and Soil Properties: An Analysis with the Stored Precipitation Fraction. J. Hydrol. 2021, 593, 125622. [Google Scholar] [CrossRef]
- Orth, R.; Seneviratne, S.I. Analysis of Soil Moisture Memory from Observations in Europe. J. Geophys. Res. Atmos. 2012, 117, 15115–15117. [Google Scholar] [CrossRef]
- Rong, L.; Duan, X.; Feng, D.; Zhang, G. Soil Moisture Variation in a Farmed Dry-Hot Valley Catchment Evaluated by a Redundancy Analysis Approach. Water 2017, 9, 92. [Google Scholar] [CrossRef]
- Jawson, S.D.; Niemann, J.D. Spatial Patterns from EOF Analysis of Soil Moisture at a Large Scale and Their Dependence on Soil, Land-Use, and Topographic Properties. Adv. Water Resour. 2007, 30, 366–381. [Google Scholar] [CrossRef]
- Senyurek, V.; Lei, F.; Boyd, D.; Kurum, M.; Gurbuz, A.C.; Moorhead, R. Machine Learning-Based CYGNSS Soil Moisture Estimates over ISMN Sites in CONUS. Remote Sens. 2020, 12, 1168. [Google Scholar] [CrossRef]
- Ren, Y.; Ling, F.; Wang, Y. Research on Provincial-Level Soil Moisture Prediction Based on Extreme Gradient Boosting Model. Agriculture 2023, 13, 927. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.S.; Bindlish, R.; Walker, J.P.; Watts, J.D. Local Scale (3-m) Soil Moisture Mapping Using SMAP and Planet SuperDove. Remote Sens. 2022, 14, 3812. [Google Scholar] [CrossRef]
- Park, S.; Im, J.; Park, S.; Rhee, J. AMSR2 Soil Moisture Downscaling Using Multisensor Products through Machine Learning Approach. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1984–1987. [Google Scholar]
- Huang, S.; Zhang, X.; Wang, C.; Chen, N. Two-Step Fusion Method for Generating 1 Km Seamless Multi-Layer Soil Moisture with High Accuracy in the Qinghai-Tibet Plateau. ISPRS J. Photogramm. Remote Sens. 2023, 197, 346–363. [Google Scholar] [CrossRef]
- Yang, Z.; He, Q.; Miao, S.; Wei, F.; Yu, M. Surface Soil Moisture Retrieval of China Using Multi-Source Data and Ensemble Learning. Remote Sens. 2023, 15, 2786. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Ngo, H.H.; Guo, W.; Chang, S.W.; Nguyen, D.D.; Nguyen, C.T.; Zhang, J.; Liang, S.; Bui, X.T.; Hoang, N.B. A Low-Cost Approach for Soil Moisture Prediction Using Multi-Sensor Data and Machine Learning Algorithm. Sci. Total Environ. 2022, 833, 155066. [Google Scholar] [CrossRef] [PubMed]
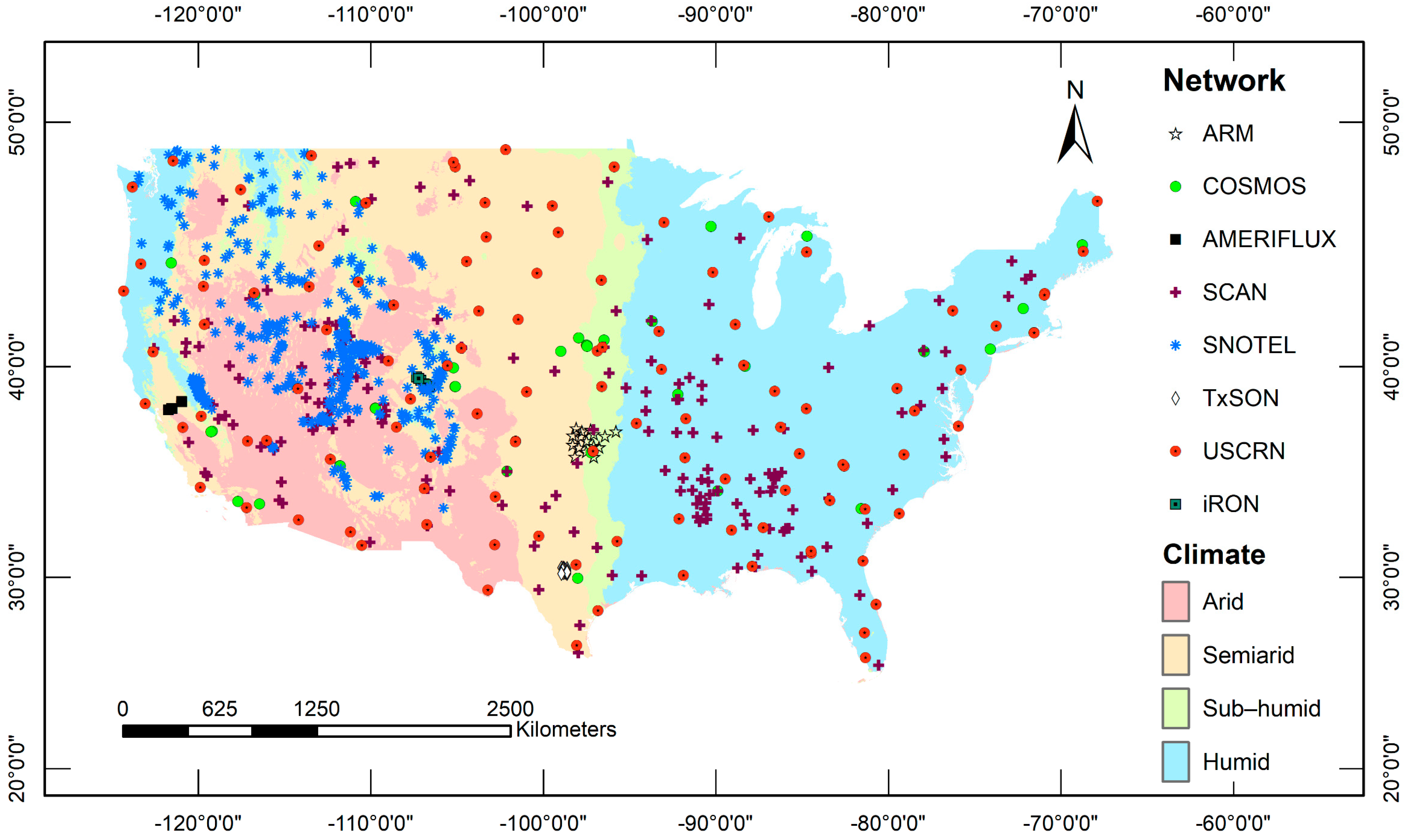




| Network | Stations | Reference |
|---|---|---|
| Atmospheric Radiation Measurement Climate Research Facility (ARM) | 17 | Cook [85] |
| Cosmic-Ray Soil Moisture Observing System (COSMOS) | 29 | Zreda et al. [86] |
| AMERIFLUX | 3 | Baldocchi et al. [87] |
| Roaring Fork Observation Network (iRON) | 8 | Osenga et al. [88] |
| Soil Climate Analysis Network (SCAN) | 168 | Schaefer et al. [89] |
| Snow Telemetry (SNOTEL) | 359 | Fleming et al. [90] |
| Texas Soil Observation Network (TxSON) | 40 | Caldwell et al. [91] |
| U.S. Climate Reference Network (USCRN) | 107 | Bell et al. [92] |
| Data Type | Variables | Product/Access | Spatial Resolution | Temporal Resolution | Reference |
|---|---|---|---|---|---|
| In Situ Soil Moisture | 0–5 cm 0–10 cm 0–20 cm 0–50 cm 0–100 cm | Soil moisture/ ISMN | Point or field measurements | Hourly | Dorigo et al. [97] |
| Satellite Soil Moisture | SSM (0–5 cm) RZSM (0–100 cm) PSM (0–bedrock) | SMAP SPL4SMGP.007/ GEE | 9 km | 3 h | Reichle et al. [93] |
| Landcover and Vegetation | NLCD | NLCD 2019/GEE | 30 m | Static | Dewitz [98,99] |
| NDVI EVI | MOD13Q1.061/ LPDAAC | 250 m | 16 Days | Didan [100] | |
| LAI fPAR | MCD15A3H.061/ LPDAAC | 500 m | 4 Days | Myneni et al. [101] | |
| Soil | Sand Silt Clay Organic Matter Bulk Density Electrical Conductivity pH Depth to Restrictive Layer | Soil layers/ USDA-NRCS (gNATSGO) | 30 m | Static | Soil Survey Staff [102] |
| Weather and Climate | Precipitation Measurement | GPM_3IMERGHH/GEE | 11 km | Half-hourly | Huffman et al. [103] |
| Instantaneous LST | ECO_L2_LSTE v002/LPDAAC | 70 m | Varies | Hook and Hulley [104] | |
| Instantaneous ET | ECO3ETPTJPLv001/LPDAAC | 70 m | Varies | Hook and Fisher [105] | |
| Instantaneous ESI, Instantaneous PET | ECO4ESIPTJPLv001/LPDAAC | 70 m | Varies | Hook and Fisher [105] | |
| Aridity Index AI | Climate Database v3/CGIAR-CSI | 1 km | Static | Zomer et al. [106] | |
| Topography | Elevation Slope Aspect Hillshade | SRTMGL1 v003/ GEE | 30 m | Static | NASA-JPL [107] |
| mTPI | Global SRTM mTPI/GEE | 270 m | Static | Theobald et al. [108] |
| Model | Hyperparameter | Optimal Value | Default |
|---|---|---|---|
| ANN | Number of hidden layers | 3 | 1 |
| Hidden layer sizes | 100 | 100 | |
| Activation function | Relu | Relu | |
| Training algorithm | Adam | Adam | |
| Regularization term | 0.01 | 0.0001 | |
| Learning rate | 0.001 | constant | |
| Maximum iterations | 100 | 200 | |
| RF | Number of trees | 200 | 100 |
| Maximum depth | 10 | None | |
| Min. samples for split | 5 | 2 | |
| Min. samples for leaf | 2 | 1 | |
| Max. features at split | sqrt | 1 | |
| Split criterion | Squared error | Squared error | |
| XGBoost | Learning rate | 0.3 | 0.3 |
| Maximum depth | 6 | 6 | |
| Number of trees | 500 | 100 | |
| Subsample for tree | 1 | 1 | |
| Depth sample fraction | 1 | 1 | |
| Min. child weight | 0.8 | 1 | |
| CatBoost | Number of trees | 1000 | 1000 |
| Learning rate | 0.05 | 0.03 | |
| Depth of tree | 10 | 6 | |
| Subsample for iteration | 1 | 1 | |
| Level feature proportion | 1 | 1 | |
| Regularization | 3 | 3 | |
| LightGBM | Number of boosting iterations | 1000 | 100 |
| Learning rate | 0.05 | 0.01 | |
| Number of leaves | 31 | 31 | |
| Maximum depth | 10 | −1 (unlimited) | |
| Min. data in leaf | 20 | 20 | |
| Regularization | 0.1 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahaar, S.A.; Niemann, J.D. Estimating Rootzone Soil Moisture by Fusing Multiple Remote Sensing Products with Machine Learning. Remote Sens. 2024, 16, 3699. https://doi.org/10.3390/rs16193699
Sahaar SA, Niemann JD. Estimating Rootzone Soil Moisture by Fusing Multiple Remote Sensing Products with Machine Learning. Remote Sensing. 2024; 16(19):3699. https://doi.org/10.3390/rs16193699
Chicago/Turabian StyleSahaar, Shukran A., and Jeffrey D. Niemann. 2024. "Estimating Rootzone Soil Moisture by Fusing Multiple Remote Sensing Products with Machine Learning" Remote Sensing 16, no. 19: 3699. https://doi.org/10.3390/rs16193699
APA StyleSahaar, S. A., & Niemann, J. D. (2024). Estimating Rootzone Soil Moisture by Fusing Multiple Remote Sensing Products with Machine Learning. Remote Sensing, 16(19), 3699. https://doi.org/10.3390/rs16193699








