Progressive Unsupervised Domain Adaptation for Radio Frequency Signal Attribute Recognition across Communication Scenarios
Abstract
1. Introduction
- (1)
- A noise perturbation consistency optimization learning method is introduced to utilize slight noise perturbations during training, enhancing the model’s robustness to various SNR conditions and improving the performance at low SNRs.
- (2)
- We propose a progressive label alignment training method, which, combined with optimization for maximizing sample-level correlation and distribution-level similarity, effectively enhances the similarity between the feature distributions of the source and target domains, thus increasing the cross-scenarios adaptability of RF signal attribute features.
- (3)
- Utilization of domain adversarial optimization learning methods to extract domain-invariant features, significantly reducing the impact of channel scenario differences on recognition outcomes.
- (4)
- Compared to baseline methods, the proposed method demonstrates superior performance in AMR and RFFI tasks across G2G and A2G channel scenarios.
2. Problem Formulation and Solution
2.1. Problem Formulation
2.2. Problem Solution
2.2.1. Traditional Deep Learning Paradigm
2.2.2. Deep Domain Adaptation Paradigm
3. Network Architectures for Task of Feature Extraction
3.1. Multi-Scale Correlation Networks for AMR Task
3.2. Multi-Periodicity Dependency Transformer for RFFI Task
4. Method
4.1. Noise Perturbation Consistency Learning
4.2. Sample-Level Maximum Correlation Learning
4.3. Distribution-Level Maximum Similarity Learning
4.4. Domain Adversarial Learning
4.5. Source-Domain Cross-Entropy Optimization Learning
4.6. Progressive Label Alignment Training Method
| Algorithm 1: Progressive label alignment training method | |||
| 1: | Input: Source domain signal data and labels ; | ||
| 2: | Target domain unlabeled signal data ; | ||
| 3: | Initialization of backbone, domain adversarial and MLP classifier networks; | ||
| 4: | Set key training parameters. | ||
| 5: | Output: Predicted labels for target domain signal sample . | ||
| 6: | begin | ||
| 7: | for epoch = 1 to 300 do | ||
| 8: | if convergence condition not met then | ||
| 9: | Randomly sample a set of source domain signal data and corresponding labels ; | ||
| 10: | Based on the batch of source domain labels, select pseudo-labeled signal data from the target domain that matches the source domain labels ; | ||
| 11: | Use the backbone network to extract features and from the source and target domain signals; | ||
| 12: | Use the task classification network to predict the labels and for the features of the source and target domains ; | ||
| 13: | Use the domain confusion classification network to predict the domain labels and for the features of the source and target domains ; | ||
| 14: | Compute the loss for the batch according to Equation (7); | ||
| 15: | Update the parameters of backbone network: ; | ||
| 16: | Update the parameters of task classification network: ; | ||
| 17: | Update the parameters of domain confusion classification network: ; | ||
| 18: | end if | ||
| 19: | end for | ||
| 20: | end | ||
5. Experimental Results and Analysis
5.1. Experimental Setup
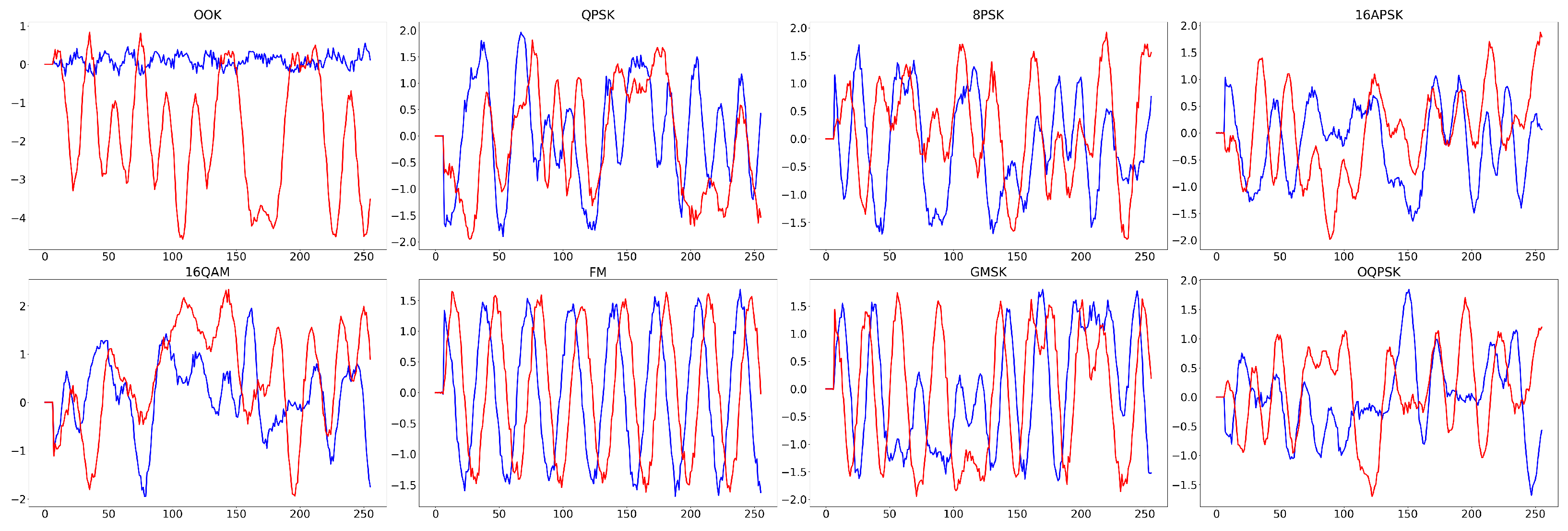
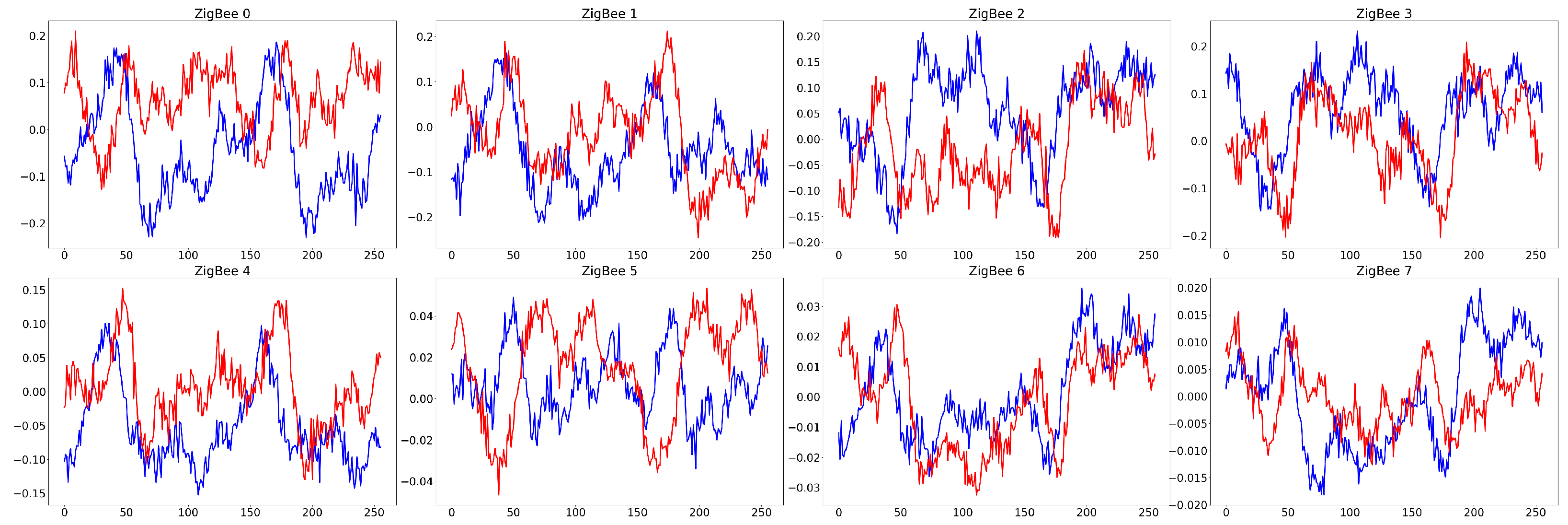
5.1.1. RF Signal Dataset
5.1.2. Experimental Setup
5.1.3. Experimental Performance Evaluation
5.1.4. Experimental Comparison of Baseline Methods
5.1.5. Experimental Settings
5.2. Results and Analysis
5.2.1. Performance Degradation across Various Communication Scenarios
5.2.2. Comparison of Unsupervised Domain Adaptation Methods
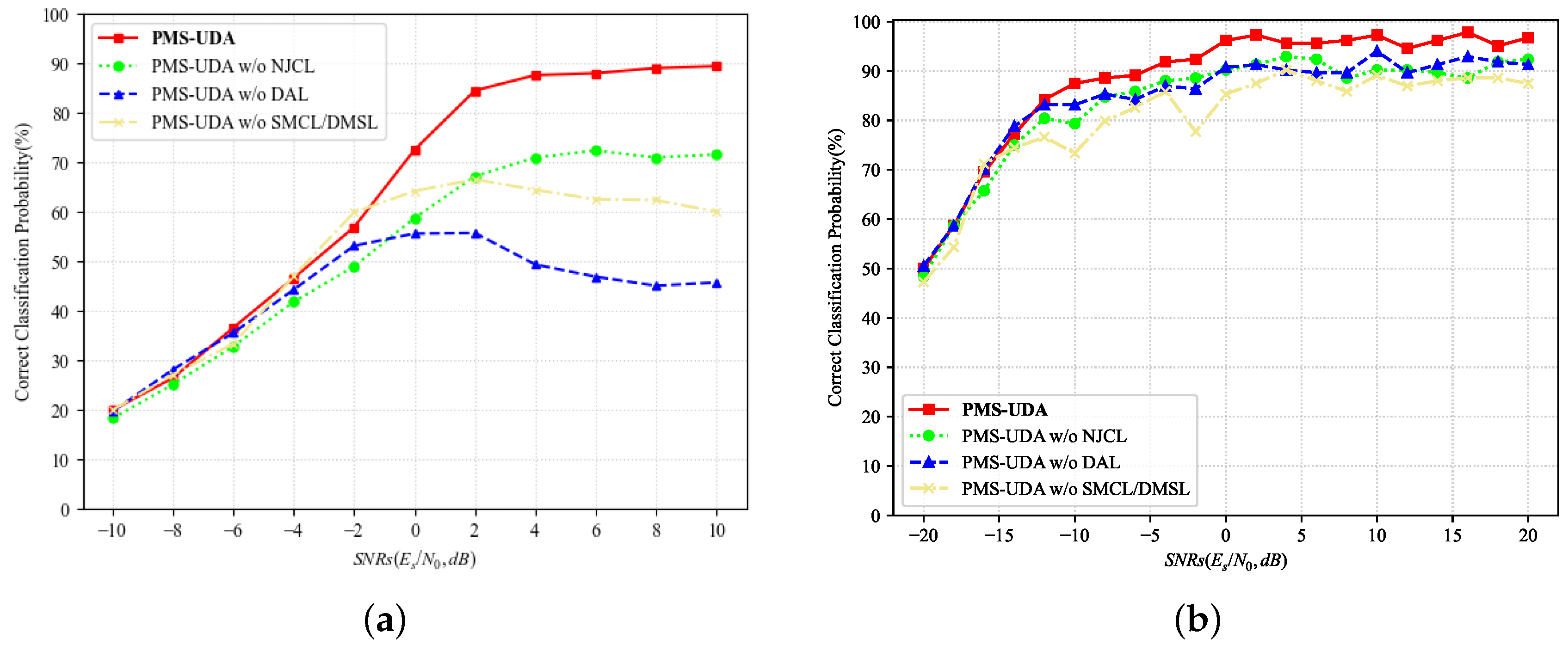
5.2.3. Ablation Study of the Optimization of Loss Functions
5.2.4. Ablation Study with Progressive Label Alignment Training Methods
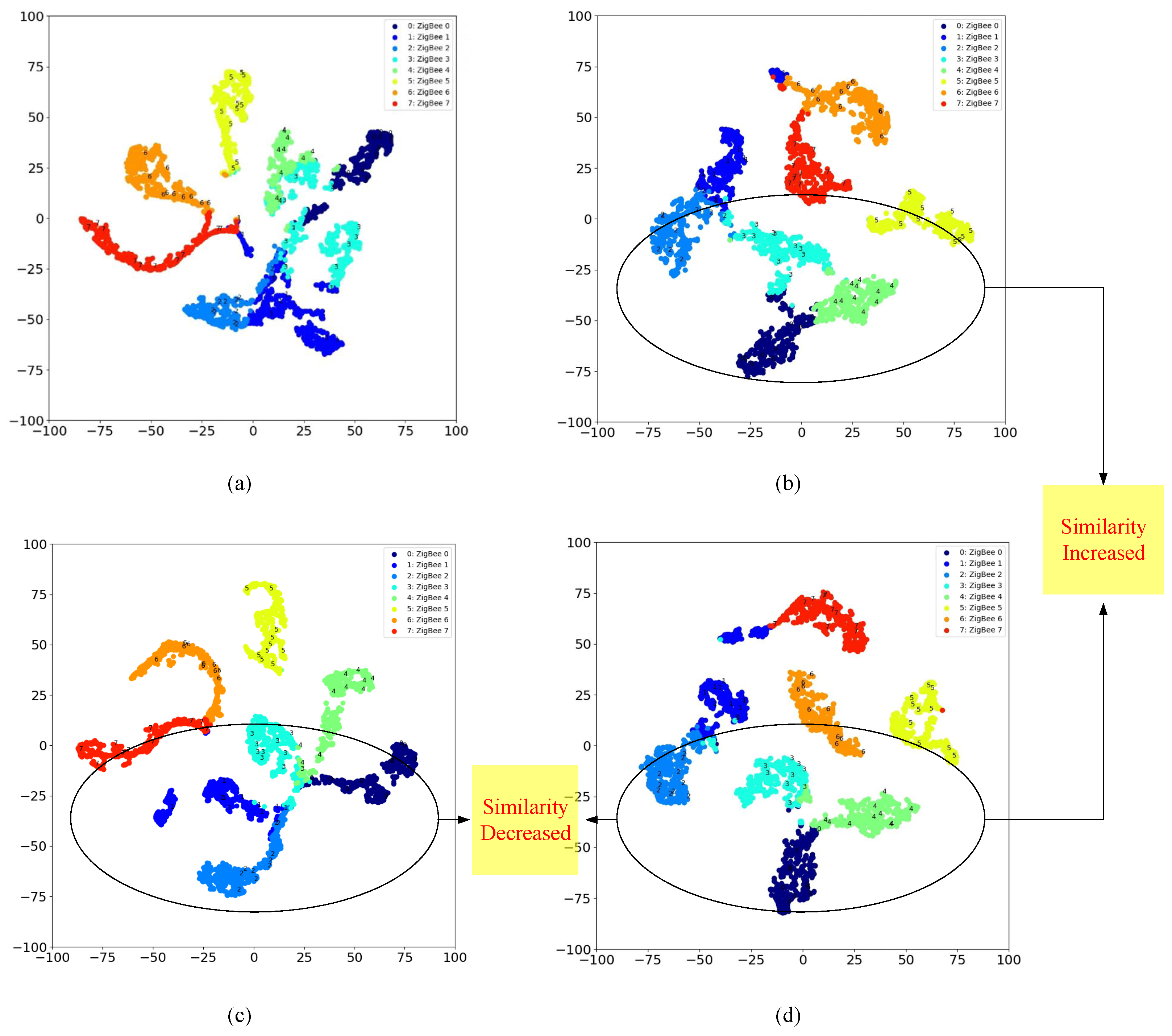
5.2.5. Similarity of Feature Distribution via T-SNE Visualization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Labib, N.S.; Danoy, G.; Musial, J.; Brust, M.R.; Bouvry, P. A Multilayer Low-Altitude Airspace Model for UAV Traffic Management. In Proceedings of the 9th ACM Symposium on Design and Analysis of Intelligent Vehicular Networks and Applications, DIVANet ’19, Miami Beach, FL, USA, 25–29 November 2019; ACM: New York, NY, USA, 2019; pp. 57–63. [Google Scholar] [CrossRef]
- Watson, T. Maximizing the Value of America’s Newest Resource, Low-Altitude Airspace: An Economic Analysis of Aerial Trespass and Drones. Indiana Law J. 2020, 95, 1399–1435. [Google Scholar]
- Zhang, H.; Wang, L.; Tian, T.; Yin, J. A Review of Unmanned Aerial Vehicle Low-Altitude Remote Sensing (UAV-LARS) Use in Agricultural Monitoring in China. Remote Sens. 2021, 13, 1221. [Google Scholar] [CrossRef]
- Yi, J.; Zhang, H.; Wang, F.; Ning, C.; Liu, H.; Zhong, G. An Operational Capacity Assessment Method for an Urban Low-Altitude Unmanned Aerial Vehicle Logistics Route Network. Drones 2023, 7, 582. [Google Scholar] [CrossRef]
- Guo, T.; Jiang, N.; Li, B.; Zhu, X.; Wang, Y.; Du, W. UAV Navigation in High Dynamic Environments: A Deep Reinforcement Learning Approach. Chin. J. Aeronaut. 2021, 34, 479–489. [Google Scholar] [CrossRef]
- Lyu, C.; Zhan, R. Global Analysis of Active Defense Technologies for Unmanned Aerial Vehicle. IEEE Aerosp. Electron. Syst. Mag. 2022, 37, 6–31. [Google Scholar] [CrossRef]
- Cai, J.; Gan, F.; Cao, X.; Liu, W.; Li, P. Radar Intra–Pulse Signal Modulation Classification with Contrastive Learning. Remote Sens. 2022, 14, 5728. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, T.; Feng, Z.; Yang, S. Towards the Automatic Modulation Classification with Adaptive Wavelet Network. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 549–563. [Google Scholar] [CrossRef]
- Paul, A.K.; Tachibana, A.; Hasegawa, T. An Enhanced Available Bandwidth Estimation Technique for an End-to-End Network Path. IEEE Trans. Netw. Serv. Manag. 2016, 13, 768–781. [Google Scholar] [CrossRef]
- Abdoush, Y.; Pojani, G.; Corazza, G.E. Adaptive Instantaneous Frequency Estimation of Multicomponent Signals Based on Linear Time–Frequency Transforms. IEEE Trans. Signal Process. 2019, 67, 3100–3112. [Google Scholar] [CrossRef]
- Huang, B.; Lin, C.L.; Chen, W.; Juang, C.F.; Wu, X. Signal Frequency Estimation Based on RNN. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 2030–2034. [Google Scholar] [CrossRef]
- Sun, L.; Ke, D.; Wang, X.; Huang, Z.; Huang, K. Robustness of Deep Learning-Based Specific Emitter Identification under Adversarial Attacks. Remote Sens. 2022, 14, 4996. [Google Scholar] [CrossRef]
- Zeng, Y.; Gong, Y.; Liu, J.; Lin, S.; Han, Z.; Cao, R.; Huang, K.; Letaief, K.B. Multi-Channel Attentive Feature Fusion for Radio Frequency Fingerprinting. IEEE Trans. Wirel. Commun. 2023, 23, 4243–4254. [Google Scholar] [CrossRef]
- Qi, X.; Hu, A.; Zhang, Z. Data-and-Channel-Independent Radio Frequency Fingerprint Extraction for LTE-V2X. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 905–919. [Google Scholar] [CrossRef]
- Qiu, Z.; Chu, X.; Calvo-Ramirez, C.; Briso, C.; Yin, X. Low Altitude UAV Air-to-Ground Channel Measurement and Modeling in Semiurban Environments. Wirel. Commun. Mob. Comput. 2017, 2017, 1587412. [Google Scholar] [CrossRef]
- Tu, K.; Rodríguez-Piñeiro, J.; Yin, X.; Tian, L. Low Altitude Air-to-Ground Channel Modelling Based on Measurements in a Suburban Environment. In Proceedings of the 2019 11th International Conference on Wireless Communications and Signal Processing (WCSP), Xi’an, China, 23–24 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Srivastava, A.; Prakash, J. Internet of Low-Altitude UAVs (IoLoUA): A Methodical Modeling on Integration of Internet of “Things” with “UAV” Possibilities and Tests. Artif. Intell. Rev. 2023, 56, 2279–2324. [Google Scholar] [CrossRef]
- Wang, M.; Lin, Y.; Tian, Q.; Si, G. Transfer Learning Promotes 6G Wireless Communications: Recent Advances and Future Challenges. IEEE Trans. Reliab. 2021, 70, 790–807. [Google Scholar] [CrossRef]
- Liu, C.; Wei, Z.; Ng, D.W.K.; Yuan, J.; Liang, Y.C. Deep Transfer Learning for Signal Detection in Ambient Backscatter Communications. IEEE Trans. Wirel. Commun. 2021, 20, 1624–1638. [Google Scholar] [CrossRef]
- Wong, L.J.; Michaels, A.J. Transfer Learning for Radio Frequency Machine Learning: A Taxonomy and Survey. Sensors 2022, 22, 1416. [Google Scholar] [CrossRef]
- Deng, W.; Xu, Q.; Li, S.; Wang, X.; Huang, Z. Cross-Domain Automatic Modulation Classification Using Multimodal Information and Transfer Learning. Remote Sens. 2023, 15, 3886. [Google Scholar] [CrossRef]
- Jing, Z.; Li, P.; Wu, B.; Yuan, S.; Chen, Y. An Adaptive Focal Loss Function Based on Transfer Learning for Few-Shot Radar Signal Intra-Pulse Modulation Classification. Remote Sens. 2022, 14, 1950. [Google Scholar] [CrossRef]
- Patel, V.M.; Gopalan, R.; Li, R.; Chellappa, R. Visual Domain Adaptation: A survey of recent advances. IEEE Signal Process. Mag. 2015, 32, 53–69. [Google Scholar] [CrossRef]
- Wang, M.; Deng, W. Deep Visual Domain Adaptation: A Survey. Neurocomputing 2018, 312, 135–153. [Google Scholar] [CrossRef]
- Wilson, G.; Cook, D. A Survey of Unsupervised Deep Domain Adaptation. ACM Trans. Intell. Syst. Technol. 2020, 11, 1–46. [Google Scholar] [CrossRef] [PubMed]
- Farahani, A.; Voghoei, S.; Rasheed, K.; Arabnia, H.R. A Brief Review of Domain Adaptation. In Advances in Data Science and Information Engineering; Transactions on Computational Science and Computational Intelligence; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Bu, K.; He, Y.; Jing, X.; Han, J. Adversarial transfer learning for deep learning based automatic modulation classification. IEEE Signal Process. Lett. 2020, 27, 880–884. [Google Scholar] [CrossRef]
- Liu, P.; Guo, L.; Zhao, H.; Shang, P.; Chu, Z.; Lu, X. A Long Time Span-Specific Emitter Identification Method Based on Unsupervised Domain Adaptation. Remote Sens. 2023, 15, 5214. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, Y.; Zhang, D.; Ma, Q.; Ding, W. Multiscale Correlation Networks Based On Deep Learning for Automatic Modulation Classification. IEEE Signal Process. Lett. 2023, 30, 633–637. [Google Scholar] [CrossRef]
- Xiao, J.; Ding, W.; Shao, Z.; Zhang, D.; Ma, Y.; Wang, Y.; Wang, J. Multi-Periodicity Dependency Transformer Based on Spectrum Offset for Radio Frequency Fingerprint Identification. arXiv 2024, arXiv:2408.07592. [Google Scholar] [CrossRef]
- Endres, D.M.; Schindelin, J.E. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Tu, Y.; Lin, Y.; Zha, H.; Zhang, J.; Wang, Y.; Gui, G.; Mao, S. Large-Scale Real-World Radio Signal Recognition with Deep Learning. Chin. J. Aeronaut. 2022, 35, 35–48. [Google Scholar] [CrossRef]
- Matolak, D.W.; Sun, R. Air–ground channel characterization for unmanned aircraft systems—Part III: The suburban and near-urban environments. IEEE Trans. Veh. Technol. 2017, 66, 6607–6618. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Roy, T.; Clancy, T.C. Over-the-Air Deep Learning Based Radio Signal Classification. IEEE J. Sel. Top. Signal Process. 2018, 12, 168–179. [Google Scholar] [CrossRef]




| Abbreviations | Notations |
|---|---|
| RF | Radio frequency |
| PMS-UDA | Progressive maximum similarity-based unsupervised domain adaptation |
| UAV | Unmanned aerial vehicle |
| A2G | Air-to-ground |
| G2G | Ground-to-ground |
| TL | Transfer learning |
| AMR | Automatic modulation recognition |
| RFFI | Radio frequency fingerprint identification |
| SNR | Signal-to-noise ratio |
| PLAT | Progressive label alignment training |
| AWGN | Additive white Gaussian noise |
| MSCNs | Multi-scale correlation networks |
| MPDFormer | Multi-periodicity dependency transformer |
| NPCL | Noise perturbation constancy loss |
| SMCL | Sample-level maximum correlation loss |
| DMSL | Distribution-level maximum similarity loss |
| KL | Kullback-Leibler |
| DAL | Domain adversarial loss |
| SDR | Software-defined radio |
| MPC | Multi-path component |
| t-SNE | t-distributed stochastic neighbor embedding |
| I,Q | in-phase and quadrature components of signal |
| Notation | Definition | Notation | Definition |
|---|---|---|---|
| Received signal | Trainable parameters of backbone model | ||
| Channel impulse response | , | Normalized signals of source and target domain | |
| Transmitted signal | Truth category labels from source domain | ||
| Additive white Gaussian noise | Normalized signals of target domain with noise perturbation | ||
| Amplitude of the k-th tap | norm | ||
| Path delay of the k-th tap | Additive white Gaussian noise | ||
| Frequency of the k-th tap | Feature map of original signal from target domain | ||
| Phase offset of the k-th tap | Feature map of perturbed signal from target domain | ||
| Loss function | Feature map of the signal samples | ||
| Noise perturbation consistency loss | Joint probability of G2G scenario | ||
| Sample-level maximum correlation loss | Joint probability of A2G scenario | ||
| Distribution-level maximum similarity loss | The expression for the mean distribution | ||
| Domain adversarial loss | KL divergence | ||
| Cross entropy loss | JS divergence | ||
| Balancing factor for | Mean of and , respectively | ||
| Balancing factor for | Trace of a matrix | ||
| Balancing factor for | n | Total number of signal samples | |
| Balancing factor for | Number of samples in the source and target domain | ||
| S, T | Source and target domain | Number of correctly recognized samples for the i-th attribute | |
| Joint probability distribution within the source domain | Weighting parameter of the squared correlation coefficient | ||
| Joint probability distribution within the target domain | Binary domain label | ||
| Aggregation across categorical labels | Domain adversarial network | ||
| Truth category labels | Trainable parameters of the adversarial network | ||
| Predicted category labels | Trainable parameters of the classification network | ||
| X, Y | Input and Label space of signal | Classifier of the RF signal attribute recognition | |
| Empirical risk within the source domain | C | Total number of attribute categories | |
| Empirical risk within the target domain | N | Total number of samples in the test set |
| Layer | Output Dimension | Number of Parameters | kFLOPs |
|---|---|---|---|
| Input | - | 0 | |
| LSWT | 120 | 245.8 | |
| MSC | - | 143.4 | |
| SAFS | 426 | 130.5 | |
| FS-ResNet | 2256 | 3313.3 | |
| FS-ResNet | 6544 | 5426.9 | |
| FS-ResNet | 23,312 | 10,675.1 | |
| GAP | 64 | - | 8.2 |
| Layers | Output Dimension | Parameters | kFLOPs |
|---|---|---|---|
| Input | 1024 × 2 | – | – |
| Periodic Embedding Representation | 16 × 128 | – | 13,799.4 |
| Projection | 16 × 128 | 16,512 | |
| Scaling | 16 × 128 | – | |
| Positional Encoding | 16 × 128 | – | |
| Encoding Layers | 16 × 128 | 1,193,472 | |
| Transpose | 128 × 16 | – | |
| GAP | 128 × 1 | – | |
| Squeeze | 128 | – | |
| Periodic Embedding Representation | 25 × 84 | – | 9626.4 |
| Projection | 25 × 84 | 7140 | |
| Scaling | 25 × 84 | – | |
| Positional Encoding | 25 × 84 | – | |
| Encoding Layers | 25 × 84 | 517,104 | |
| Transpose | 84 × 25 | – | |
| GAP | 84 × 1 | – | |
| Squeeze | 84 | – | |
| Periodic Embedding Representation | 8 × 256 | – | 27,004.9 |
| Projection | 8 × 256 | 65,792 | |
| Scaling | 8 × 256 | – | |
| Positional Encoding | 8 × 256 | – | |
| Encoding Layers | 8 × 256 | 4,746,240 | |
| Transpose | 256 × 8 | – | |
| GAP | 256 × 1 | – | |
| Squeeze | 256 | – | |
| Concatenation | 468 | – | 0.1 |
| Adaptive Fusion | 468 | 144 |
| Layer | Output Dimension | |
|---|---|---|
| AMR | RFFI | |
| Input | 64 | 468 |
| Linear | 128 | 128 |
| SELU | 128 | 128 |
| Dropout | 128 | 128 |
| Linear | 128 | 128 |
| SELU | 128 | 128 |
| Dropout | 128 | 128 |
| Linear | 2 | 2 |
| Layer | Output Dimension | |
|---|---|---|
| AMR | RFFI | |
| Input | 64 | 468 |
| Linear | 128 | 128 |
| SELU | 128 | 128 |
| Dropout | 128 | 128 |
| Linear | 64 | 64 |
| SELU | 64 | 64 |
| Dropout | 64 | 64 |
| Linear | 8 | 8 |
| Tap | |||
|---|---|---|---|
| 3 | 0.65 | −0.09 | 0.39 |
| 4 | −0.61 | −0.08 | 0.32 |
| 5 | −0.87 | −0.10 | 0.46 |
| 6 | −1.42 | −0.10 | 0.57 |
| 7 | −2.60 | −0.02 | 0.48 |
| 8 | −3.63 | 0.03 | 0.47 |
| 9 | −4.53 | 0.048 | 0.67 |
| Dataset Settings | Ground-to-Ground→Air-to-Ground (G2G→A2G) | Air-to-Ground→Ground-to-Ground (A2G→G2G) | ||
|---|---|---|---|---|
| Source | Target | Source | Target | |
| Sample size | 84,480 | 42,240 | 84,480 | 42,240 |
| Percentage with label | 100% | 0% | 100% | 0% |
| Signal dimension | 1024 × 2 | |||
| SNR | −10 dB to 10 dB, with a interval of 2 dB | |||
| Training: testing | 9:1 | |||
| Type of modulation | 8 modulation types: OOK, QPSK, 8PSK, 16APSK, 16QAM, FM, GMSK, OQPSK | |||
| Dataset Settings | Ground-to-Ground→Air-to-Ground (G2G→A2G) | Air-to-Ground→Ground-to-Ground (A2G→G2G) | ||
|---|---|---|---|---|
| Source | Target | Source | Target | |
| Sample size | 38,640 | 19,320 | 38,640 | 19,320 |
| Percentage with label | 100% | 0% | 100% | 0% |
| Signal dimension | 1024 × 2 | |||
| SNR | −20 dB to 20 dB, intervals 2 dB | |||
| Training: testing | 9:1 | |||
| Type of ZigBee devices | 8 ZigBee devices: 0, 1, 2, 3, 4, 5, 6, 7 | |||
| Tasks | Hyperparameters | ||||
|---|---|---|---|---|---|
| lr | |||||
| AMR | 1.0 | 0.1 | 1.0 | 2.0 | |
| RFFI | |||||
| Task | Accuracy (%) | ||||
|---|---|---|---|---|---|
| AMR | RFFI | ||||
| Test Scenario | G2G | A2G | G2G | A2G | |
| Train Scenario | |||||
| G2G | 72.9 | 34.9 | 95.9 | 79.3 | |
| A2G | 53.5 | 69.3 | 55.5 | 94.9 | |
| Method | Accuracy (%) | |||
|---|---|---|---|---|
| AMR | RFFI | |||
| G2G→A2G | A2G→G2G | G2G→A2G | A2G→G2G | |
| Lower limit | 34.9 | 53.5 | 79.3 | 55.5 |
| DANN | 62.6 | 68.3 | 83.8 | 58.3 |
| LTS-SEI | 63.7 | 70.2 | 86.7 | 69.7 |
| PMS-UDA (Ours) | 64.0 | 69.9 | 89.1 | 73.8 |
| Upper limit | 67.3 | 70.5 | 94.0 | 94.8 |
| Tasks | Accuracy (%) | |||
|---|---|---|---|---|
| PMS-UDA | PMS-UDA w/o NPCL | PMS-UDA w/o SMCL/DMSL | PMS-UDA w/o DAL | |
| AMR | 64.0 | 52.7 | 51.5 | 43.6 |
| RFFI | 89.1 | 83.4 | 80.4 | 84.4 |
| Progressive Label Alignment Training Method | Accuracy (%) | |||
|---|---|---|---|---|
| AMR | RFFI | |||
| G2G→A2G | A2G→G2G | G2G→A2G | A2G→G2G | |
| ✗ | 61.3 | 64.6 | 83.1 | 55.0 |
| ✓ | 64.0 | 69.9 | 89.1 | 73.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, J.; Zhang, H.; Shao, Z.; Zheng, Y.; Ding, W. Progressive Unsupervised Domain Adaptation for Radio Frequency Signal Attribute Recognition across Communication Scenarios. Remote Sens. 2024, 16, 3696. https://doi.org/10.3390/rs16193696
Xiao J, Zhang H, Shao Z, Zheng Y, Ding W. Progressive Unsupervised Domain Adaptation for Radio Frequency Signal Attribute Recognition across Communication Scenarios. Remote Sensing. 2024; 16(19):3696. https://doi.org/10.3390/rs16193696
Chicago/Turabian StyleXiao, Jing, Hang Zhang, Zeqi Shao, Yikai Zheng, and Wenrui Ding. 2024. "Progressive Unsupervised Domain Adaptation for Radio Frequency Signal Attribute Recognition across Communication Scenarios" Remote Sensing 16, no. 19: 3696. https://doi.org/10.3390/rs16193696
APA StyleXiao, J., Zhang, H., Shao, Z., Zheng, Y., & Ding, W. (2024). Progressive Unsupervised Domain Adaptation for Radio Frequency Signal Attribute Recognition across Communication Scenarios. Remote Sensing, 16(19), 3696. https://doi.org/10.3390/rs16193696







