Comparison and Optimization of Light Use Efficiency-Based Gross Primary Productivity Models in an Agroforestry Orchard
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Measurement of Environmental Variables
2.3. Flux Data Measurement, Processes, and Gap Filling
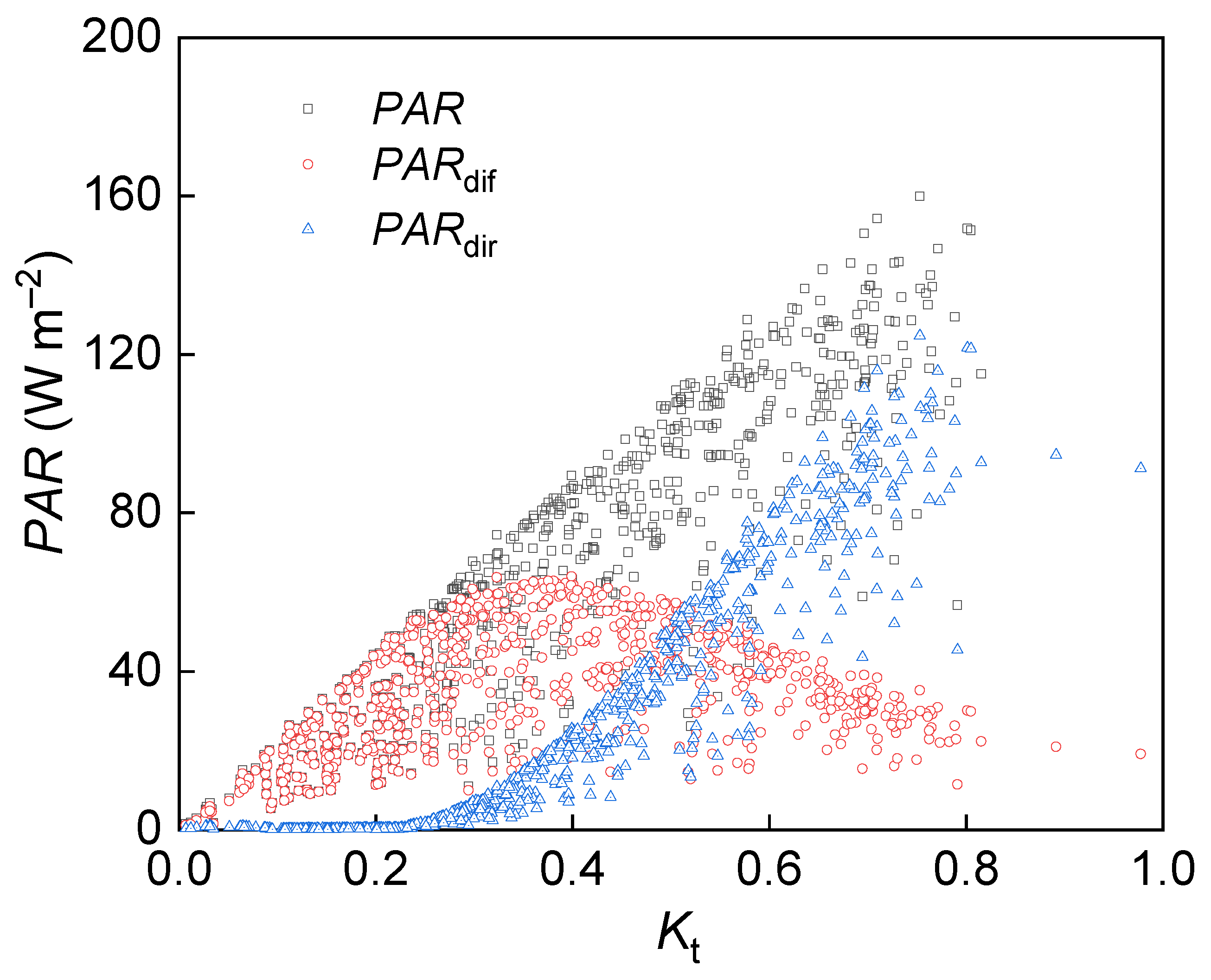
2.4. Calculation of Leaf Area Index and LSWI
2.5. Big-Leaf LUE-GPP Models
2.5.1. EC-LUE Model
2.5.2. MODIS Model
2.5.3. VPM
2.5.4. MVPM
2.5.5. Terrestrial Ecosystem Carbon Flux (TEC) Model
2.5.6. CASA Model
2.6. Two-Leaf LUE-GPP Model
2.7. Analysis of the Model Structure
2.8. Evaluation of Model Performances
3. Results
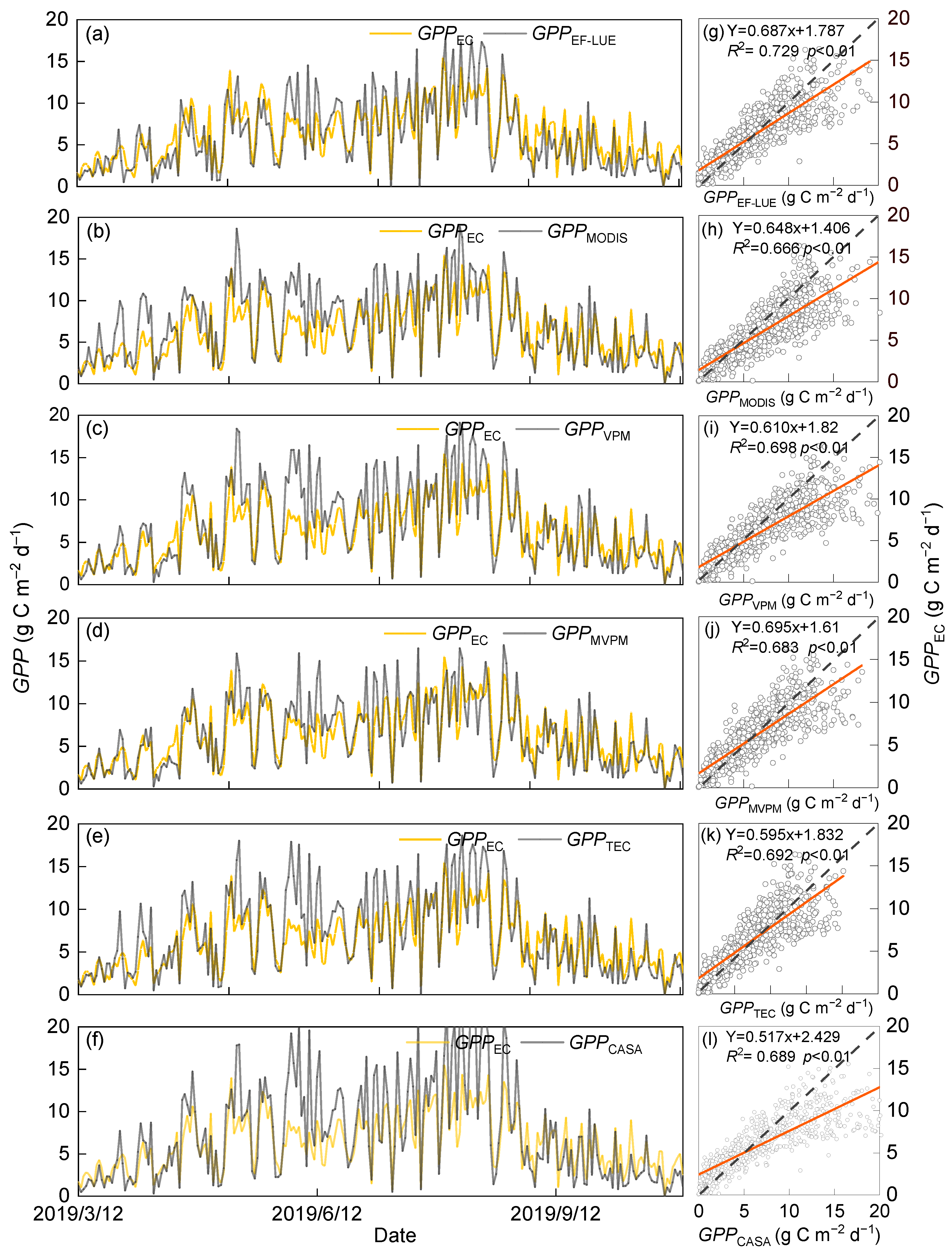
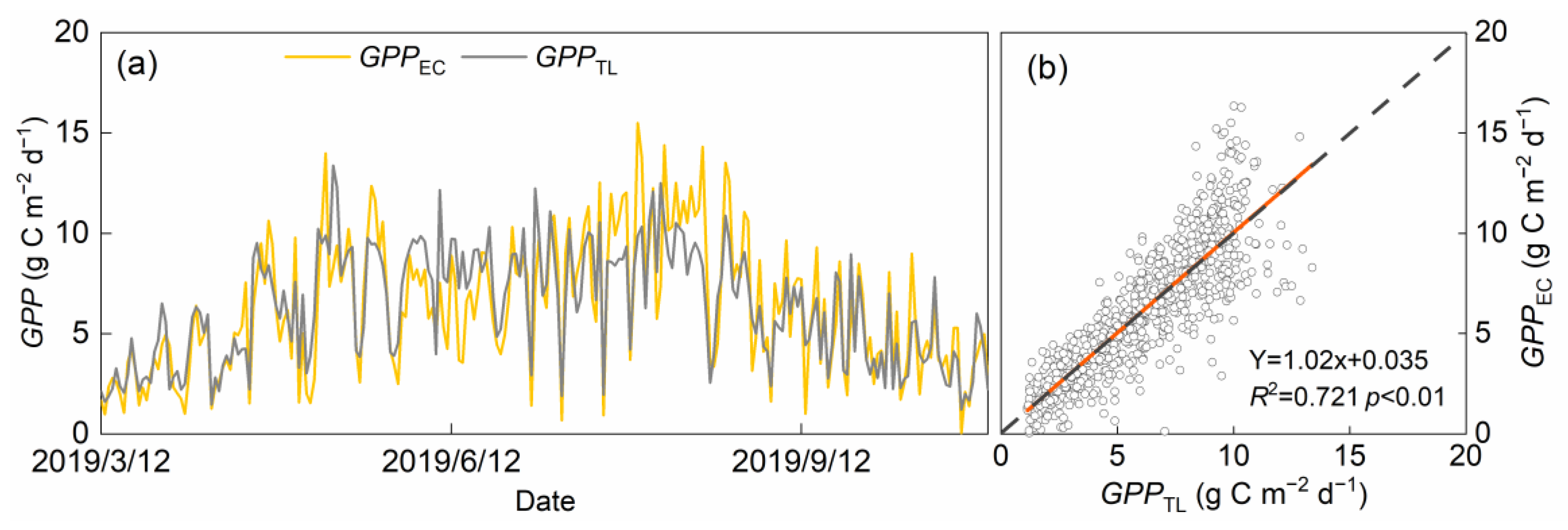
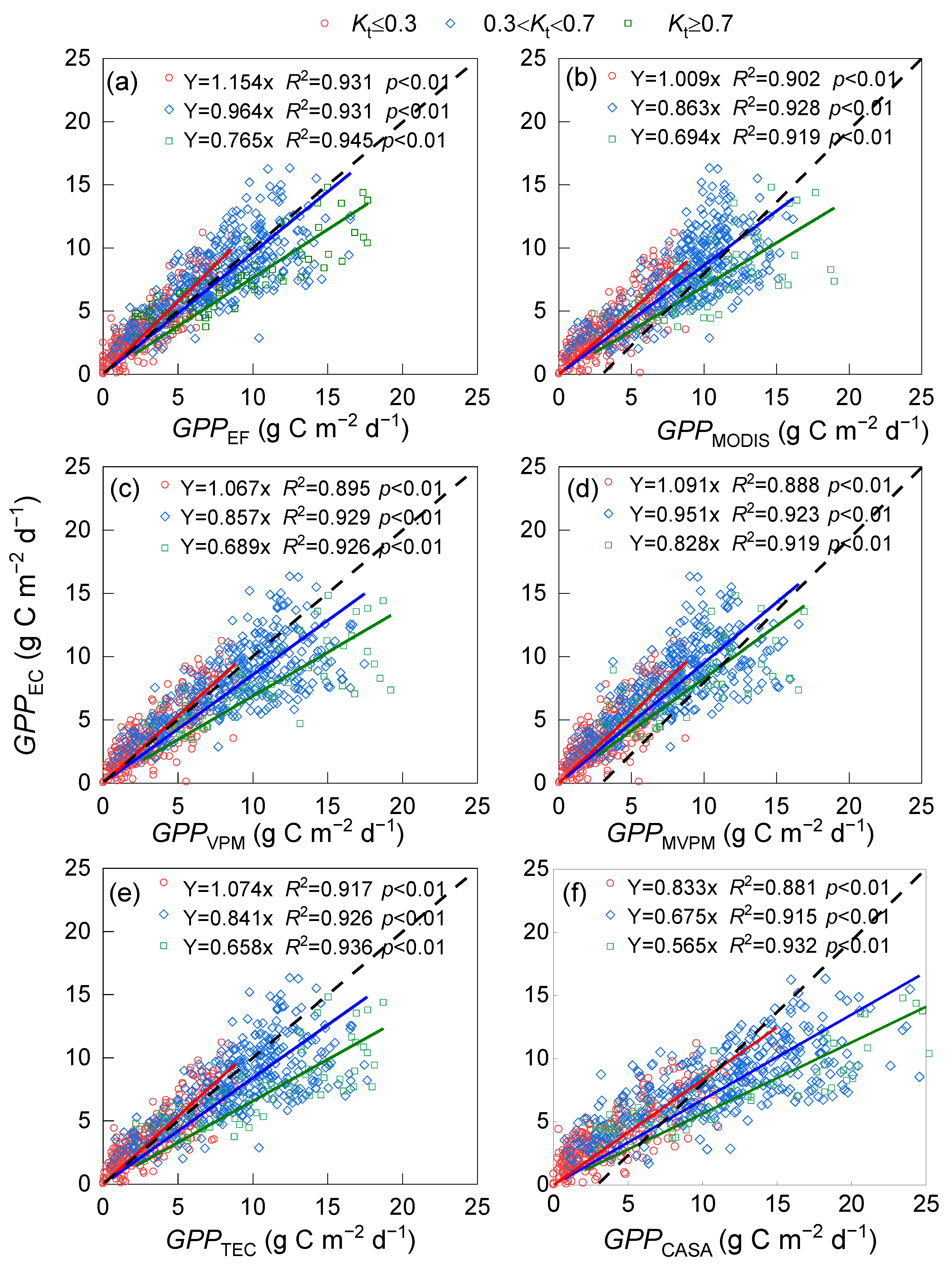
3.1. Performances of Various LUE-GPP Models
3.1.1. Six Big-Leaf LUE-GPP Models
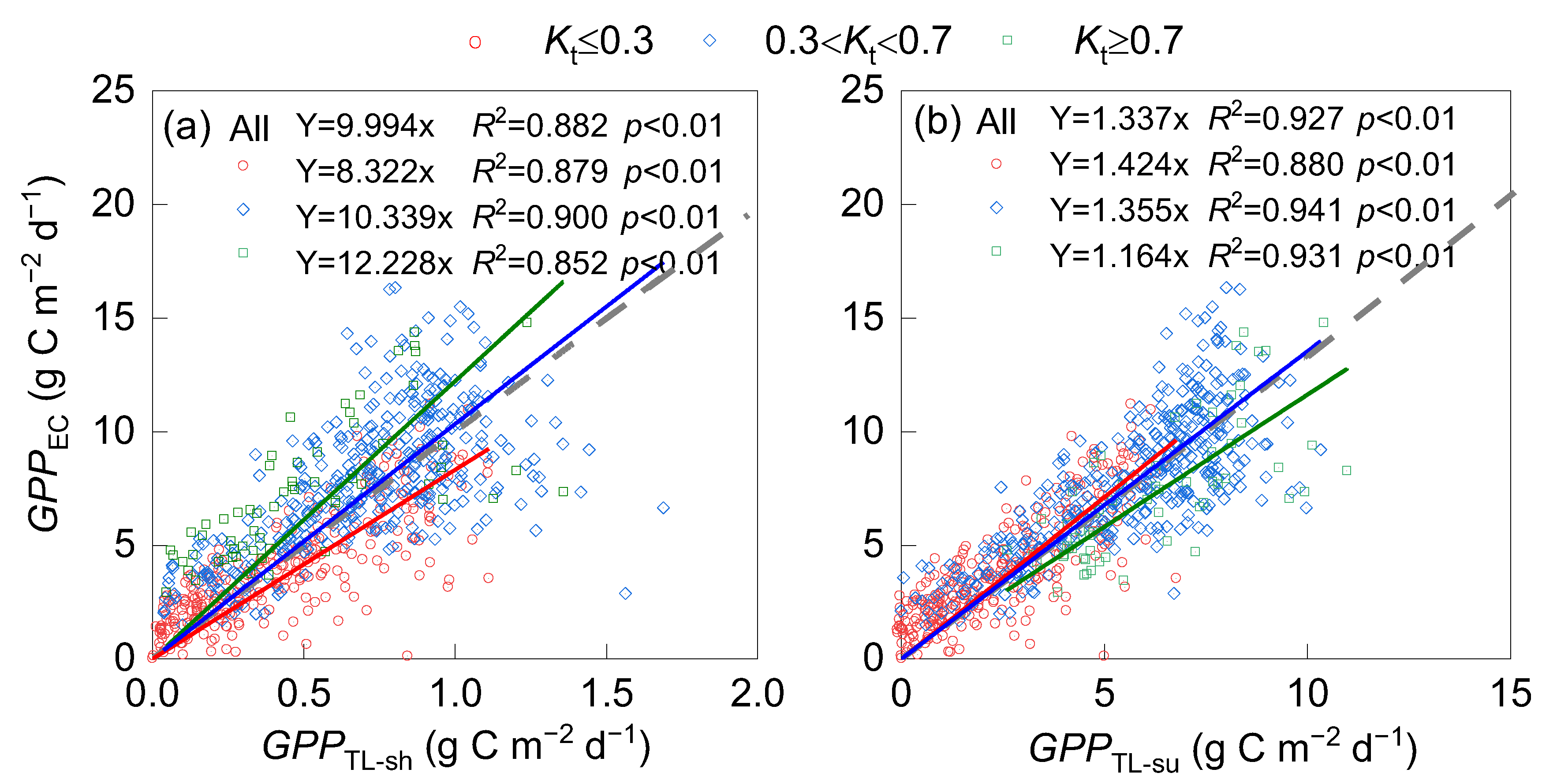
3.1.2. Two-Leaf LUE-GPP Models
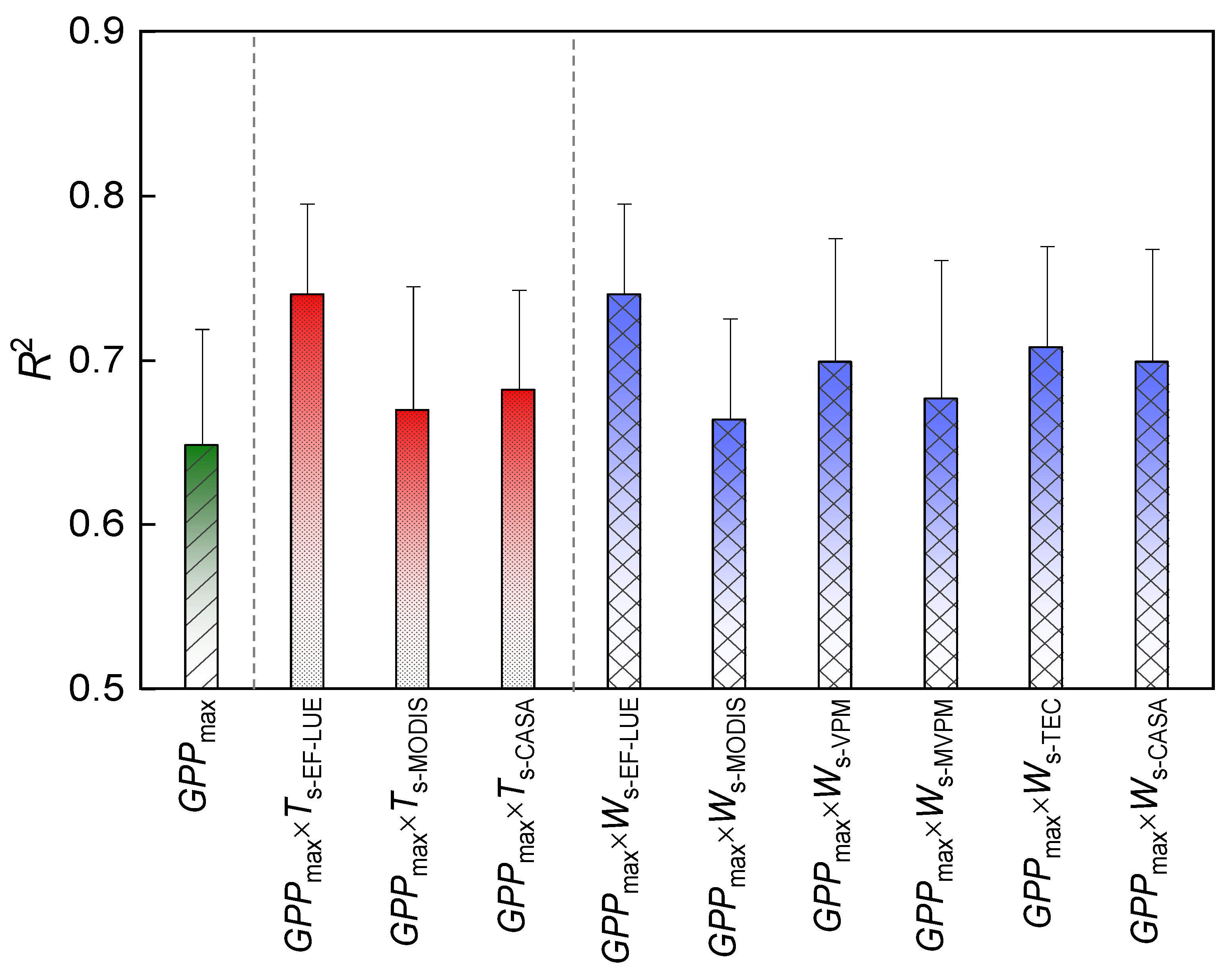
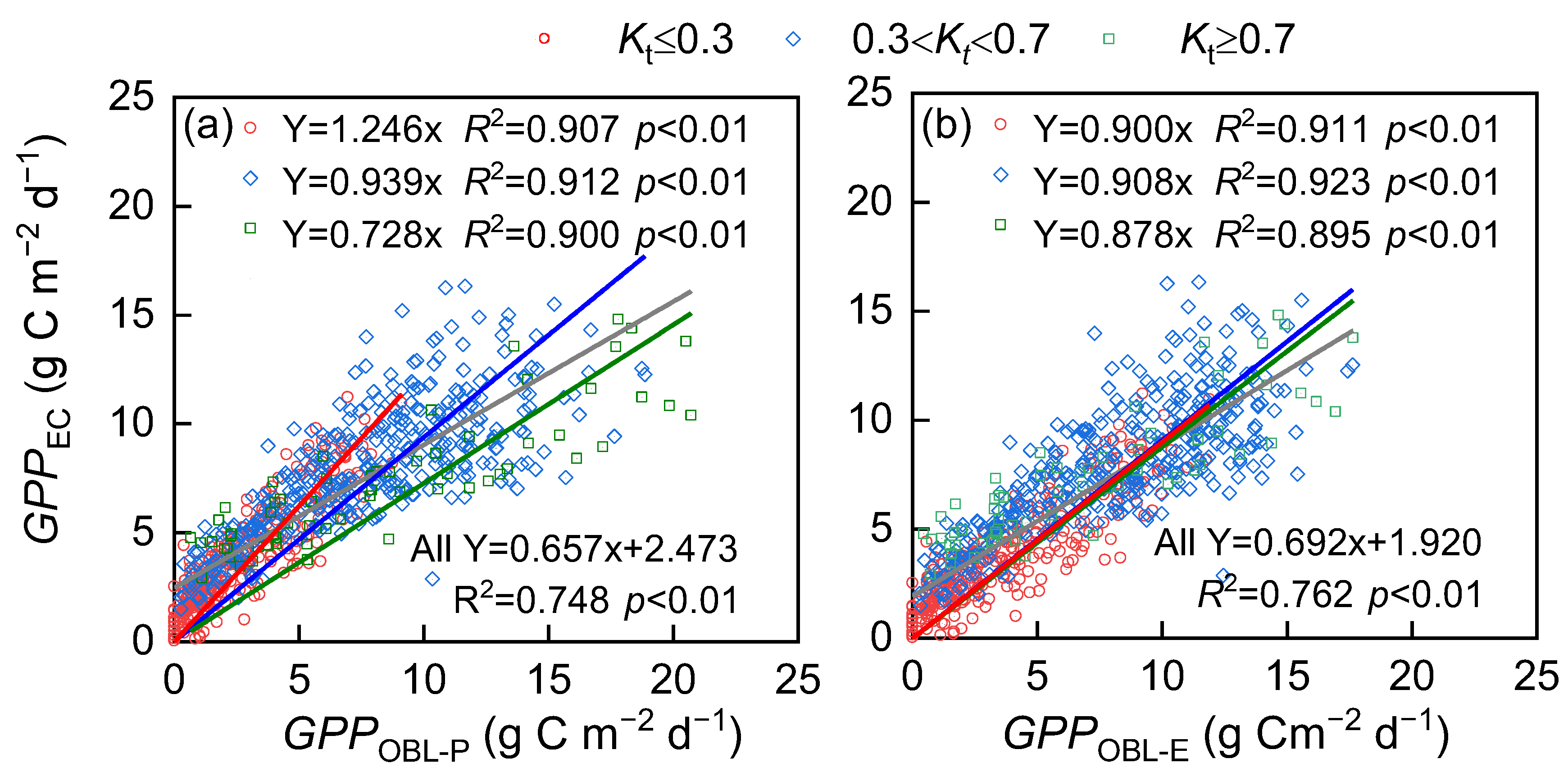
3.2. Influence of Model Structure on Model Performance
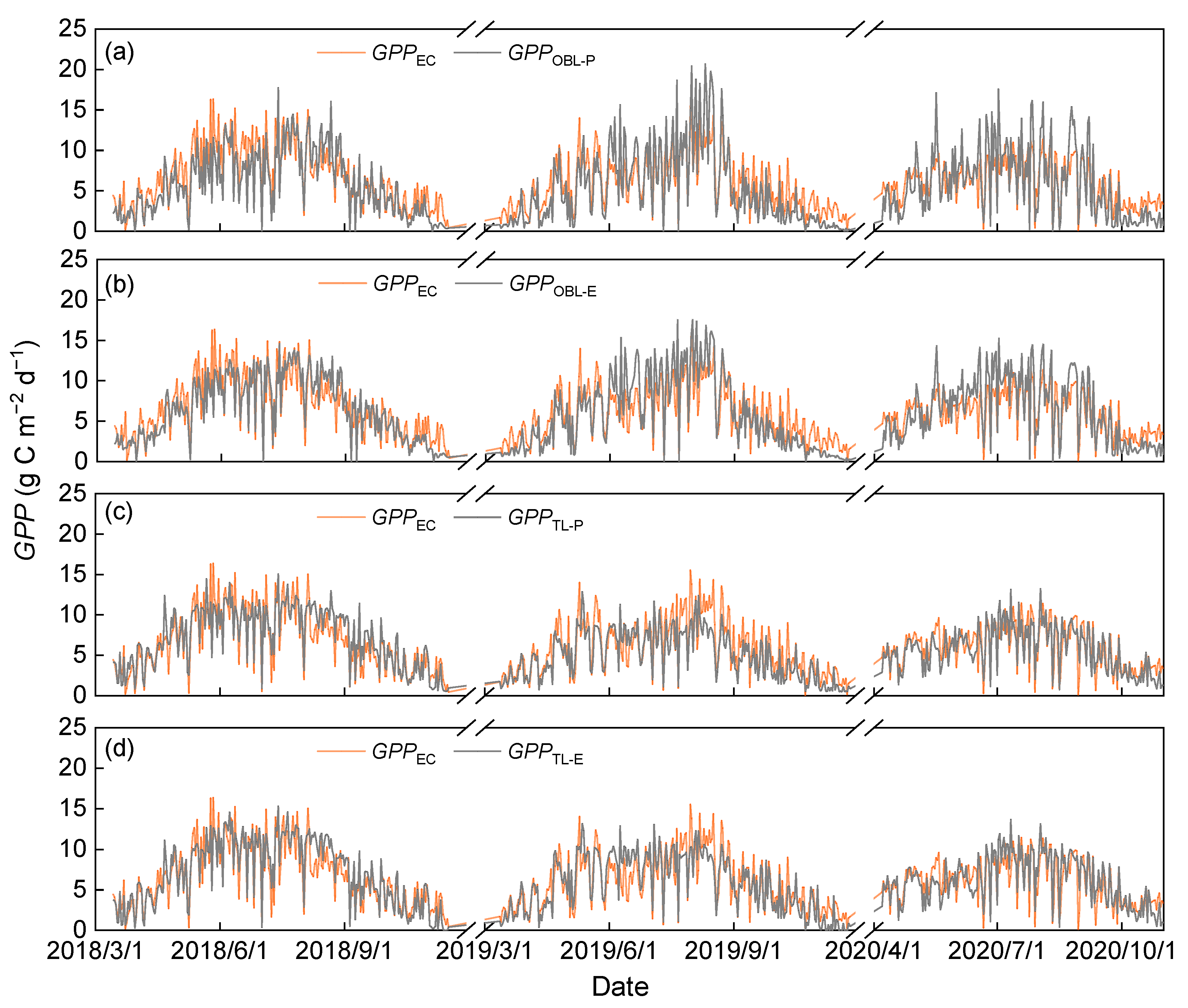
3.3. Model Performances under Different Weather Conditions
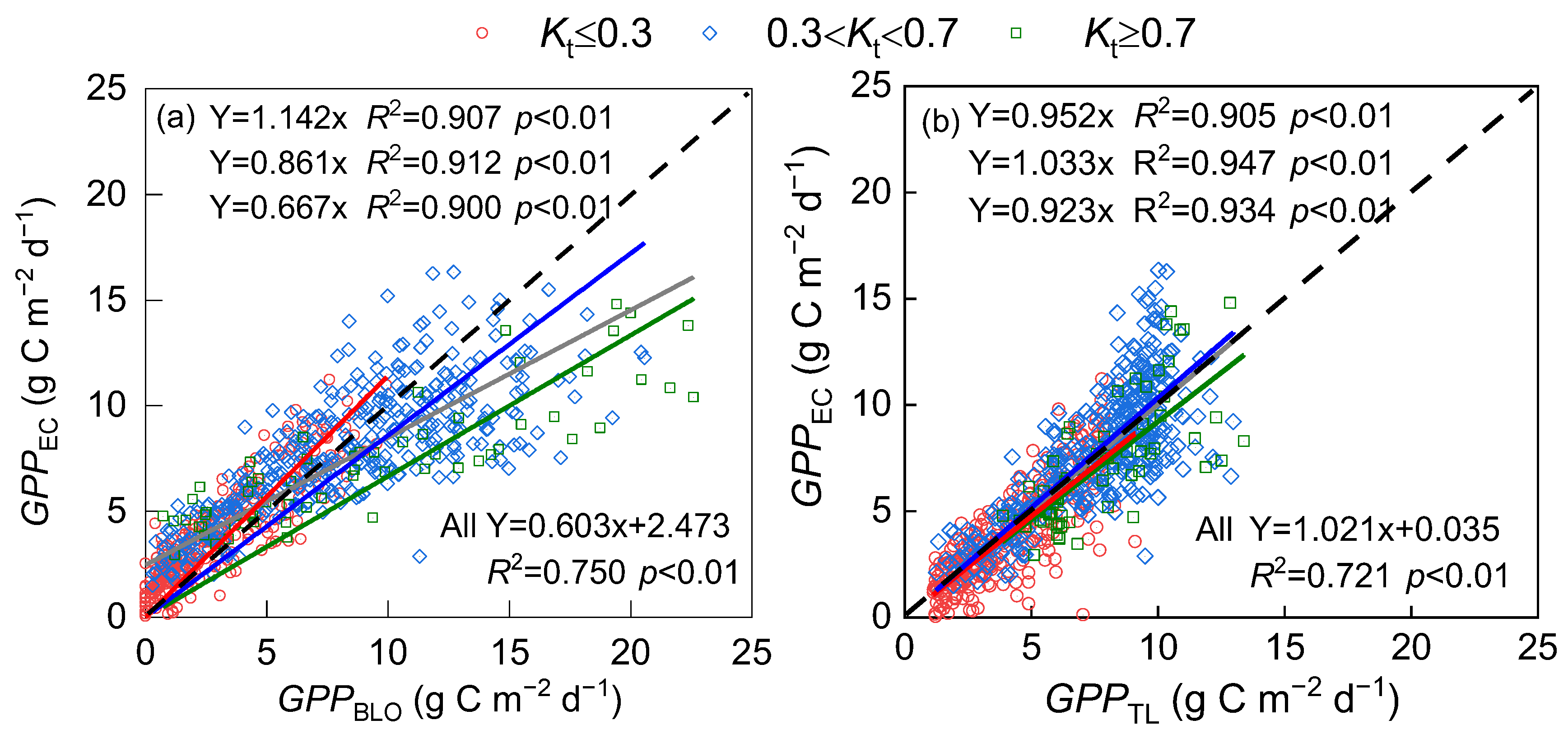
3.4. Optimization of the LUE-GPP Model by Introducing Kt
4. Discussion
4.1. Comparison of Big-Leaf LUE-GPP Models
4.2. Evaluation of LUE-GPP Model Performance under Different Weather Conditions
4.3. Limitations of the Study
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wellington, M.J.; Kuhnert, P.; Renzullo, L.J.; Lawes, R. Modelling Within-Season Variation in Light Use Efficiency Enhances Productivity Estimates for Cropland. Remote Sens. 2022, 14, 1495. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Z.; Wang, Z.; Zeng, Y.; Xue, P.; Zhang, M. Stability of the ecosystem gross primary productivity increasing in Chinese forestry ecological engineering area. Agric. Ecosyst. Environ. 2023, 356, 108636. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J.M.; Lombardozzi, D. Global vegetation productivity response to climatic oscillations during the satellite era. Glob. Chang. Biol. 2016, 2, 3414–3426. [Google Scholar] [CrossRef]
- Huang, L.X.; Lin, X.F.; Jiang, S.Z.; Liu, M.; Jiang, Y.Z.; Li, Z.L.; Tang, R.L. A two-stage light-use efficiency model for improving gross primary production estimation in agroecosystems. Environ. Res. Lett. 2022, 17, 104021. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.H.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Schmidt, M.; Reichenau, T.G.; Fiener, P.; Schneider, K. The carbon budget of a winter wheat field: An eddy covariance analysis of seasonal and inter-annual variability. Agric. For. Meteorol. 2012, 165, 114–126. [Google Scholar] [CrossRef]
- Hu, Z.M.; Shi, H.; Cheng, K.L.; Wang, Y.P.; Piao, S.L.; Li, Y.; Zhang, L.; Xia, J.Y.; Zhou, L.; Yuan, W.P.; et al. Joint structural and physiological control on the interannual variation in productivity in a temperate grassland: A data-model comparison. Glob. Chang. Biol. 2018, 24, 2965–2979. [Google Scholar] [CrossRef]
- Piao, S.L.; Sitch, S.; Ciais, P.; Friedlingstein, P.; Peylin, P.; Wang, X.H.; Ahlstrom, A.; Anav, A.; Canadell, J.G.; Cong, N.; et al. Evaluation of terrestrial carbon cycle models for their response to climate variability and to CO2 trends. Glob. Chang. Biol. 2013, 19, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- He, M.Z.; Ju, W.M.; Zhou, Y.L.; Chen, J.M.; He, H.L.; Wang, S.Q.; Wang, H.M.; Guan, D.X.; Yan, J.H.; Li, Y.N.; et al. Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary productivity. Agric. For. Meteorol. 2013, 173, 28–39. [Google Scholar] [CrossRef]
- Yan, H.; Wang, S.Q.; Yu, K.L.; Wang, B.; Yu, Q.; Bohrer, G.; Billesbach, D.; Bracho, R.; Rahman, F.; Shugart, H.H. A Novel Diffuse Fraction-Based Two-Leaf Light Use Efficiency Model: An Application Quantifying Photosynthetic Seasonality across 20 AmeriFlux Flux Tower Sites. J. Adv. Model. Earth Syst. 2017, 9, 2317–2332. [Google Scholar] [CrossRef]
- Zhang, L.X.; Zhou, D.C.; Fan, J.W.; Hu, Z.M. Comparison of four light use efficiency models for estimating terrestrial gross primary production. Ecol. Model. 2015, 300, 30–39. [Google Scholar] [CrossRef]
- Kalfas, J.L.; Xiao, X.M.; Vanegas, D.X.; Verma, S.B.; Suyker, A.E. Modeling gross primary production of irrigated and rain-fed maize using MODIS imagery and CO2 flux tower data. Agric. For. Meteorol. 2011, 151, 1514–1528. [Google Scholar] [CrossRef]
- Xiao, X.M.; Zhang, Q.Y.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Berrien, M.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Yuan, W.P.; Cai, W.W.; Xia, J.Z.; Chen, J.Q.; Liu, S.G.; Dong, W.J.; Merbold, L.; Law, B.; Arain, A.; Beringer, J.; et al. Global comparison of light use efficiency models for simulating terrestrial vegetation gross primary production based on the La Thuile database. Agric. For. Meteorol. 2014, 192, 108–120. [Google Scholar] [CrossRef]
- Chen, T.X.; van der Werf, G.R.; Dolman, A.J.; Groenendijk, M. Evaluation of cropland maximum light use efficiency using eddy flux measurements in North America and Europe. Geophys. Res. Lett. 2011, 38, L14707. [Google Scholar] [CrossRef]
- Du, D.; Zheng, C.; Jia, L.; Chen, Q.; Jiang, M.; Hu, G.; Lu, J. Estimation of Global Cropland Gross Primary Production from Satellite Observations by Integrating Water Availability Variable in Light-Use-Efficiency Model. Remote Sens. 2022, 14, 1722. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Nguy-Robertson, A.L.; Fang, H.; Andrew, E.S.; Chen, Y.; Dong, W.; Liu, S.; Zhang, H. Uncertainty in simulating gross primary production of cropland ecosystem from satellite-based models. Agric. For. Meteorol. 2015, 207, 48–57. [Google Scholar] [CrossRef]
- Wang, S.Q.; Huang, K.; Yan, H.; Yan, H.M.; Zhou, L.; Wang, H.M.; Zhang, J.H.; Yan, J.H.; Zhao, L.; Wang, Y.F.; et al. Improving the light use efficiency model for simulating terrestrial vegetation gross primary production by the inclusion of diffuse radiation across ecosystems in China. Ecol. Complex. 2015, 23, 1–13. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, Z.; Wu, X.; Wan, J. Light use efficiency models incorporating diffuse radiation impacts for simulating terrestrial ecosystem gross primary productivity: A global comparison. Agric. For. Meteorol. 2023, 332, 109376. [Google Scholar] [CrossRef]
- Jiang, S.Z.; Zhao, L.; Liang, C.; Cui, N.B.; Gong, D.Z.; Wang, Y.S.; Feng, Y.; Hu, X.T.; Zou, Q.Y. Comparison of satellite-based models for estimating gross primary productivity in agroecosystems. Agric. For. Meteorol. 2021, 297, 108253. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.S.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Wagle, P.; Zhang, Y.G.; Jin, C.; Xiao, X.M. Comparison of solar-induced chlorophyll fluorescence, light-use efficiency, and process-based GPP models in maize. Ecol. Appl. 2016, 26, 1211–1222. [Google Scholar] [CrossRef]
- Wagle, P.; Kakani, V.G. Environmental control of daytime net ecosystem exchange of carbon dioxide in switchgrass. Agric. Ecosyst. Environ. 2014, 186, 170–177. [Google Scholar] [CrossRef]
- Liu, P.; Tong, X.; Zhang, J.; Meng, P.; Li, J.; Zhang, J.; Zhou, Y. Effect of diffuse fraction on gross primary productivity and light use efficiency in a warm-temperate mixed plantation. Front. Plant Sci. 2022, 13, 966125. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, Z.Q.; Chen, J.Q.; Zhu, M.X.; Kang, M.C. Cloudiness regulates gross primary productivity of a poplar plantation under different environmental conditions. Can. J. For. Res. 2017, 47, 648–658. [Google Scholar] [CrossRef]
- Knohl, A.; Baldocchi, D.D. Effects of diffuse radiation on canopy gas exchange processes in a forest ecosystem. J. Geophys. Res. Biogeosci. 2008, 113, G02023. [Google Scholar] [CrossRef]
- Kanniah, K.D.; Beringer, J.; Hurley, L. Exploring the link between clouds, radiation, and canopy productivity of tropical savannas. Agric. For. Meteorol. 2013, 182, 304–313. [Google Scholar] [CrossRef]
- Gao, X.; Gu, F.; Mei, X.; Hao, W.; Li, H.; Gong, D.; Li, X. Light and Water Use Efficiency as Influenced by Clouds and/or Aerosols in a Rainfed Spring Maize Cropland on the Loess Plateau. Crop Sci. 2018, 58, 853–862. [Google Scholar] [CrossRef]
- Jiang, S.Z.; Liang, C.; Cui, N.B.; Zhao, L.; Du, T.S.; Hu, X.T.; Feng, Y.; Guan, J.; Feng, Y. Impacts of climatic variables on reference evapotranspiration during growing season in Southwest China. Agric. Water Manag. 2019, 216, 365–378. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, G.; Clement, R.; Dolman, H.; et al. Gap filling strategies for long term energy flux data sets. Agric. For. Meteorol. 2001, 107, 71–77. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Maisongrande, P.; Ruimy, A.; Dedieu, G.; Saugier, B. Monitoring seasonal and interannual variations of gross primary productivity, net primary productivity and net ecosystem productivity using a diagnostic model and remotely-sensed data. Tellus B Chem. Phys. Meteorol. 1995, 47, 178–190. [Google Scholar] [CrossRef]
- Lloyd, J.; Taylor, J.A. On the temperature-dependence of soil respiration. Funct. Ecol. 1994, 8, 315–323. [Google Scholar] [CrossRef]
- Ding, C.; Liu, X.; Huang, F.; Li, Y.; Zou, X. Onset of drying and dormancy in relation to water dynamics of semi-arid grasslands from MODIS NDWI. Agric. For. Meteorol. 2017, 234–235, 22–30. [Google Scholar] [CrossRef]
- Yan, H.; Wang, S.; Shugart, H.H. Large latitudinal difference in soil nitrogen limitation on global vegetation response to elevated CO2. Agric. For. Meteorol. 2023, 342, 109717. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Y.; Ju, W.; Chen, J.; Xiao, J. Accumulated soil moisture deficit better indicates the effect of soil water stress on light use efficiency of grasslands during drought years. Agric. For. Meteorol. 2023, 329, 109276. [Google Scholar] [CrossRef]
- Yuan, W.P.; Liu, S.; Zhou, G.S.; Zhou, G.Y.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Aber, J.D.; Reich, P.B.; Goulden, M.L. Extrapolating leaf CO2 exchange to the canopy: A generalized model of forest photosynthesis compared with measurements by eddy correlation. Oecologia 1996, 106, 257–265. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Wang, S.Q.; Billesbach, D.; Oechel, W.; Bohrer, G.; Meyers, T.; Martin, T.A.; Matamala, R.; Phillips, R.P.; Rahman, F.; et al. Improved global simulations of gross primary product based on a new definition of water stress factor and a separate treatment of C3 and C4 plants. Ecol. Model. 2015, 297, 42–59. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, X.; Ju, W.; Chen, J.M.; Wang, S.; Wang, H.; Yuan, W.; Black, T.A.; Jassal, R.; Ibrom, A.; et al. Global parameterization and validation of a two-leaf light use efficiency model for predicting gross primary production across FLUXNET sites. J. Geophys. Res.-Biogeosci. 2016, 121, 1045–1072. [Google Scholar] [CrossRef]
- Singarayer, J.S.; Ridgwell, A.; Irvine, P. Assessing the benefits of crop albedo bio-geoengineering. Environ. Res. Lett. 2009, 4, 045110. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Model. 1999, 124, 99–119. [Google Scholar] [CrossRef]
- Norman, J.M. Simulation of microclimates. In Biometeorology in Integrated Pest Management; Hatfield, J.L., Thomason, I.J., Eds.; Academic Press: New York, NY, USA, 1982; pp. 65–99. [Google Scholar]
- Wang, Y.; Zhou, L.; Jia, Q.Y.; Yu, W.Y. Water use efficiency of a rice paddy field in Liaohe Delta, Northeast China. Agric. Water Manag. 2017, 187, 222–231. [Google Scholar] [CrossRef]
- Tang, S.; Chen, J.M.; Zhu, Q.; Li, X.; Chen, M.; Sun, R.; Zhou, Y.; Deng, F.; Xie, D. LAI inversion algorithm based on directional reflectance kernels. J. Environ. Manag. 2007, 85, 638–648. [Google Scholar] [CrossRef]
- Raczka, B.M.; Davis, K.J.; Huntzinger, D.; Neilson, R.P.; Poulter, B.; Richardson, A.D.; Xiao, J.F.; Baker, I.; Ciais, P.; Keenan, T.F.; et al. Evaluation of continental carbon cycle simulations with North American flux tower observations. Ecol. Monogr. 2013, 83, 531–556. [Google Scholar] [CrossRef]
- Campoe, O.; Stape, J.L.; Albaugh, T.J.; A20llen, H.L.; Fox, T.R.; Rubilar, R.A.; Binkley, D. Fertilization and irrigation effects on tree level aboveground net primary production, light interception and light use efficiency in a loblolly pine plantation. Forest Ecol. Manag. 2013, 288, 43–48. [Google Scholar] [CrossRef]
- Cai, W.W.; Yuan, W.P.; Liang, S.L.; Liu, S.G.; Dong, W.J.; Chen, Y.; Liu, D.; Zhang, H.C. Large Differences in Terrestrial Vegetation Production Derived from Satellite-Based Light Use Efficiency Models. Remote Sens. 2014, 6, 8945–8965. [Google Scholar] [CrossRef]
- Yan, H.; Fu, Y.; Xiao, X.; Huang, H.Q.; He, H.; Ediger, L. Modeling gross primary productivity for winter wheat–maize double cropping system using MODIS time series and CO2 eddy flux tower data. Agric. Ecosyst. Environ. 2009, 129, 391–400. [Google Scholar] [CrossRef]
- Kurc, S.A.; Small, E.E. Dynamics of evapotranspiration in semiarid grassland and shrubland ecosystems during the summer monsoon season, central New Mexico. Water Resour. Res. 2004, 40, W09305. [Google Scholar] [CrossRef]
- Tong, Y.Q.; Wang, P.; Li, X.Y.; Wang, L.X.; Wu, X.C.; Shi, F.Z.; Bai, Y.; Li, E.G.; Wang, J.Q.; Wang, Y. Seasonality of the transpiration fraction and its controls across typical ecosystems within the Heihe River Basin. J. Geophys. Res. Atmos. 2019, 124, 1277–1291. [Google Scholar] [CrossRef]
- Watham, T.; Patel, N.R.; Kushwaha, S.P.S.; Dadhwal, V.K.; Kumar, A.S. Evaluation of remote-sensing-based models of gross primary productivity over Indian sal forest using flux tower and MODIS satellite data. Int. J. Remote Sens. 2017, 38, 5069–5090. [Google Scholar] [CrossRef]
- Leuning, R.; Cleugh, H.A.; Zegelin, S.J.; Hughes, D. Carbon and water fluxes over a temperate Eucalyptus forest and a tropical wet/dry savanna in Australia: Measurements and comparison with MODIS remote sensing estimates. Agric. For. Meteorol. 2005, 129, 151–173. [Google Scholar] [CrossRef]
- Berry, Z.C.; Goldsmith, G.R. Diffuse light and wetting differentially affect tropical tree leaf photosynthesis. New Phytol. 2020, 225, 143–153. [Google Scholar] [CrossRef]
- Alton, P.B.; Ellis, R.; Los, S.O.; North, P.R. Improved global simulations of gross primary product based on a separate and explicit treatment of diffuse and direct sunlight. J. Geophys. Res. Atmos. 2007, 112, D07203. [Google Scholar] [CrossRef]
- Reitz, O.; Bogena, H.; Neuwirth, B.; Sanchez-Azofeifa, A.; Graf, A.; Bates, J.; Leuchner, M. Environmental Drivers of Gross Primary Productivity and Light Use Efficiency of a Temperate Spruce Forest. J. Geophys. Res.-Biogeosci. 2023, 128, e2022JG007197. [Google Scholar] [CrossRef]
- Bao, S.; Wutzler, T.; Koirala, S.; Cuntz, M.; Ibrom, A.; Besnard, S.; Walther, S.; Sigut, L.; Moreno, A.; Weber, U.; et al. Environment-sensitivity functions for gross primary productivity in light use efficiency models. Agric. For. Meteorol. 2022, 312, 108708. [Google Scholar] [CrossRef]
- Williams, C.A.; Reichstein, M.; Buchmann, N.; Baldocchi, D.; Beer, C.; Schwalm, C.; Wohlfahrt, G.; Hasler, N.; Bernhofer, C.; Foken, T.; et al. Climate and vegetation controls on the surface water balance: Synthesis of evapotranspiration measured across a global network of flux towers. Water Resour. Res. 2012, 48, W06523. [Google Scholar] [CrossRef]



| Model | Model Structures | Required Parameters | Input Variables |
|---|---|---|---|
| Eddy covariance-light use efficiency model (EC-LUE) | PAR × fPAR × εmax × Min (Ts, Ws) | εmax, Tmin, Tmax, Topt | LAI, PAR, Ta, Rn, LE |
| Moderate resolution imaging spectroradiometer GPP algorithm (MODIS) | PAR × fPAR × εmax × Ts × Ws | εmax, Tmin, Topt, TMAXmin VPDmin, VPDmax | LAI, PAR, Ta, VPD |
| Vegetation photosynthesis model (VPM) | PAR × fPAR × εmax × Ts × Ws × Ps | εmax, Tmin, Tmax, Topt, LSWImax | LAI, PAR, Ta, LSWI |
| Modified vegetation photosynthesis model (MVPM) | PAR × fPAR × εmax × Min (Ts × Ws1 × Ws2) | εmax, Tmin, Tmax, Topt, VPDmax | LAI, PAR, Ta, LSWI, VPD |
| Terrestrial ecosystem carbon flux model (TEC) | PAR × fPAR × εmax × Ts × Ws | εmax, Tmin, Tmax, Topt, | LAI, PAR, Ta, Rn, λ, LE, G, Δ, γ |
| Carnegie-Ames-Stanford approach (CASA) | PAR × fPAR × εmax × Ts1 × Ts2 × Ws | εmax, Topt | LAI, PAR, Ta, Rn, λ, LE, G, Δ, γ |
| Two-leaf LUE-GPP model (TL) | (PAR × fPAR × εsu-max + PAR × fPAR × εsh-max) × Ts × Ws | εsu-max, εsh-max, Tmin, Topt, VPDmin, VPDmax | Ra, Rg, Ω, C, LAI, PAR, , Ta, VPD |
| Model Description | Model Structure |
|---|---|
| Estimated GPP without any environmental constraints | GPPNos = PAR × fPAR × LUEmax |
| Estimated GPP with Ts only | GPPTs = PAR × fPAR × LUEmax × Ts |
| Estimated GPP with Ws only | GPPWs = PAR × fPAR × LUEmax × Ws |
| Estimated GPP with the maximum limitation combination | GPPmin(Ts, Ws) = PAR × fPAR × LUEmax × min(Ts, Ws) |
| Estimated GPP with common limitation combination of Ts and Ws | GPP(Ts × Ws) =PAR × fPAR × LUEmax × Ts × Ws |
| Optimal Big-Leaf LUE-GPP Model | Two-Leaf LUE-GPP Model | |||
|---|---|---|---|---|
| Parameters | Power Function Form | Exponential Function | Power Function Form | Exponential Function |
| A1 | 1.536 | 2.703 | 1.315 | 9.776 × 10−10 |
| B1 | 3.010 × 10−9 | −1.011 | 0.391 | −1.999 |
| A2 | 1.447 | 2.9547 | ||
| B2 | 3.38 × 10−6 | −0.411 | ||
| Year | Models | R2 | MAE (g C m−2 d−1) | RMSE (g C m−2 d−1) | η | d1 | GPI | Ranking |
|---|---|---|---|---|---|---|---|---|
| 2018 | EF-LUE | 0.790 | 1.377 | 1.808 | 0.563 | 0.774 | 0.875 | 1 |
| MODIS | 0.721 | 1.574 | 2.025 | 0.501 | 0.739 | −0.748 | 4 | |
| VPM | 0.758 | 1.465 | 1.942 | 0.535 | 0.773 | 0.240 | 3 | |
| MVPM | 0.711 | 1.563 | 2.074 | 0.504 | 0.739 | −0.870 | 5 | |
| TEC | 0.773 | 1.403 | 1.852 | 0.555 | 0.776 | 0.602 | 2 | |
| CASA | 0.742 | 2.441 | 3.038 | 0.226 | 0.607 | −2.048 | 6 | |
| 2019 | EF-LUE | 0.772 | 1.636 | 2.100 | 0.429 | 0.746 | 1.373 | 2 |
| MODIS | 0.735 | 1.819 | 2.462 | 0.366 | 0.727 | −0.192 | 5 | |
| VPM | 0.747 | 1.869 | 2.685 | 0.348 | 0.730 | −0.062 | 4 | |
| MVPM | 0.759 | 1.511 | 2.083 | 0.473 | 0.764 | 1.451 | 1 | |
| TEC | 0.753 | 1.861 | 2.639 | 0.351 | 0.730 | 0.136 | 3 | |
| CASA | 0.759 | 2.123 | 2.511 | 0.260 | 0.665 | −1.834 | 6 | |
| 2020 | EF-LUE | 0.680 | 1.690 | 2.199 | 0.249 | 0.687 | 1.262 | 1 |
| MODIS | 0.615 | 1.957 | 2.645 | 0.130 | 0.655 | −0.184 | 6 | |
| VPM | 0.626 | 1.895 | 2.541 | 0.158 | 0.656 | 0.062 | 3 | |
| MVPM | 0.601 | 1.726 | 2.207 | 0.233 | 0.661 | 0.066 | 2 | |
| TEC | 0.650 | 2.168 | 2.995 | 0.136 | 0.643 | −0.145 | 5 | |
| CASA | 0.668 | 2.024 | 2.327 | 0.100 | 0.623 | 0.041 | 4 |
| Year | GPPEC | GPPEF-LUE | GPPMODIS | GPPVPM | GPPMVPM | GPPTEC | GPPCASA | GPPTL |
|---|---|---|---|---|---|---|---|---|
| 2018 | 6.77 | 6.27 | 7.03 | 6.99 | 6.40 | 6.99 | 7.46 | 6.43 |
| 2019 | 5.88 | 5.62 | 6.65 | 6.54 | 5.95 | 6.50 | 6.80 | 5.87 |
| 2020 | 6.00 | 6.09 | 7.05 | 6.51 | 5.79 | 7.09 | 7.84 | 6.28 |
| Year | R2 | MAE (g C m−2 d−1) | RMSE (g C m−2 d−1) | η | d1 | GPI |
|---|---|---|---|---|---|---|
| 2018 | 0.786 | 1.395 | 1.844 | 0.558 | 0.755 | 0.601 |
| 2019 | 0.733 | 1.329 | 1.751 | 0.537 | 0.758 | 1.185 |
| 2020 | 0.621 | 1.259 | 1.725 | 0.440 | 0.714 | 1.293 |
| Weather Conditions | BLO | OBL-P | OBL-E | TL | TL-P | TL-E |
|---|---|---|---|---|---|---|
| Kt ≤ 0.3 | 1.49 | 1.63 | 1.44 | 1.42 | 1.49 | 1.62 |
| 0.3 < Kt < 0.7 | 2.80 | 2.54 | 2.46 | 1.95 | 2.02 | 1.94 |
| Kt ≥ 0.7 | 4.47 | 3.72 | 2.73 | 2.10 | 2.16 | 2.02 |
| ALL | 2.58 | 2.36 | 2.14 | 1.78 | 1.84 | 1.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, N.; He, Z.; Wang, M.; Zhang, W.; Zhao, L.; Gong, D.; Li, J.; Jiang, S. Comparison and Optimization of Light Use Efficiency-Based Gross Primary Productivity Models in an Agroforestry Orchard. Remote Sens. 2024, 16, 3679. https://doi.org/10.3390/rs16193679
Cui N, He Z, Wang M, Zhang W, Zhao L, Gong D, Li J, Jiang S. Comparison and Optimization of Light Use Efficiency-Based Gross Primary Productivity Models in an Agroforestry Orchard. Remote Sensing. 2024; 16(19):3679. https://doi.org/10.3390/rs16193679
Chicago/Turabian StyleCui, Ningbo, Ziling He, Mingjun Wang, Wenjiang Zhang, Lu Zhao, Daozhi Gong, Jun Li, and Shouzheng Jiang. 2024. "Comparison and Optimization of Light Use Efficiency-Based Gross Primary Productivity Models in an Agroforestry Orchard" Remote Sensing 16, no. 19: 3679. https://doi.org/10.3390/rs16193679
APA StyleCui, N., He, Z., Wang, M., Zhang, W., Zhao, L., Gong, D., Li, J., & Jiang, S. (2024). Comparison and Optimization of Light Use Efficiency-Based Gross Primary Productivity Models in an Agroforestry Orchard. Remote Sensing, 16(19), 3679. https://doi.org/10.3390/rs16193679








