TE-LSTM: A Prediction Model for Temperature Based on Multivariate Time Series Data

Abstract

In the era of big data, prediction has become a fundamental capability. Current prediction methods primarily focus on sequence elements; however, in multivariate time series forecasting, time is a critical factor that must not be overlooked. While some methods consider time, they often neglect the temporal distance between sequence elements and the predicted target time, a relationship essential for identifying patterns such as periodicity, trends, and other temporal dynamics. Moreover, the extraction of temporal features is often inadequate, and discussions on how to comprehensively leverage temporal data are limited. As a result, model performance can suffer, particularly in prediction tasks with specific time requirements. To address these challenges, we propose a new model, TE-LSTM, based on LSTM, which employs a temporal encoding method to fully extract temporal features. A temporal weighting strategy is also used to optimize the integration of temporal information, capturing the temporal relationship of each element relative to the target element, and integrating it into the LSTM. Additionally, this study examines the impact of different time granularities on the model. Using the Beijing International Airport station as the study area, we applied our method to temperature prediction. Compared to the baseline model, our model showed an improvement of 0.7552% without time granularity, 1.2047% with a time granularity of 3, and 0.0953% when addressing prediction tasks with specific time requirements. The final results demonstrate the superiority of the proposed method and highlight its effectiveness in overcoming the limitations of existing approaches.

1. Introduction

In recent years, with the continuous development of internet technology and big data, people’s functional demands have evolved from merely detecting past events to real-time monitoring and further to predicting future occurrences [1,2,3,4,5]. By analyzing vast amounts of data, it is possible to predict the likelihood of events occurring, helping decision makers formulate practical plans and avoid one-sidedness and errors in decision making. In the context of expensive experiments or research, predictive analysis models can facilitate simulation experiments, thereby achieving cost savings. For example, in the machinery industry, accurate temperature prediction can ensure product quality, improve production efficiency, and ensure safety. In the field of ecology, sea surface temperature (SST) plays a crucial role in the energy balance at the Earth’s surface as well as in the exchange of energy, momentum, and moisture between the ocean and atmosphere [6]. Variations in SST can influence biological processes such as the distribution and reproduction of marine life; this has significant impacts on marine ecosystems [7]. In addition, in some industries, certain phenomena or numerical changes are extremely fast, such as high-precision experiments, so it is not only necessary to ensure the accuracy of the predicted results, but also to ensure the accuracy of the prediction method at specific times [8,9,10].

The core of prediction lies in identifying patterns embedded in time series data that are closely related to time [11,12]. Typically, data points that are closer in time have a greater impact on the results. However, the evolution of patterns within time series data is not fixed and can vary significantly over different periods [13,14,15]. Additionally, some entities undergo slow changes, such as the evolution of geological structures, which require a long time to capture. This means that if these entities undergo the same change twice, the magnitude of the change in a particular property value may be small, but the time span of the change may vary significantly. For example, it took 10 years for the height of a mountain to drop by 1 cm for the first time, and 20 years for it to drop by 1 cm for the second time. Thus, incorporating the time can help amplify subtle changes and capture more precise patterns. These considerations highlight the critical role of time in multivariate time series prediction tasks and underscore its indispensable nature.

Traditional prediction algorithms include Autoregressive Integrated Moving Average (ARIMA) [16], Logistic Regression, k-Nearest Neighbors (k-NN) [17], etc. These algorithms are suitable for simple relationships and small datasets but are not suitable for prediction tasks in the big data era. With the rapid development of deep learning, time series forecasting [18,19,20,21] models have shown excellent ability in handling nonlinear, high-frequency multidimensional, and discontinuous data, such as Recurrent Neural Networks (RNN) for time-series data modeling [22,23,24]. Each layer of the network utilizes the information from the previous layer, making it sensitive to sequence data. It can retain previous information to better understand the current information, but it cannot solve long-distance dependency issues. Gated Recurrent Unit (GRU) is based on RNN and also a chain-like neural network repeating module [25]. GRU adds update gates and reset gates, combining them into one update gate to control information updating and flow, solving the long-term dependency problem. Long Short-Term Memory (LSTM) is similar to GRU but includes three gates: forget gate, input gate, and output gate [26]. It uses a cell state and a hidden state to transmit information, which can better control what information is forgotten and what is remembered, thus more accurately controlling the transmission of long-term information. Bidirectional Long Short-Term Memory (BiLSTM) consists of forward LSTM and backward LSTM, solving the problem that LSTM can only predict from front to back and cannot predict from back to front.

The most commonly used methods for time series prediction currently include Recurrent Neural Network (RNN) architectures and their variants, particularly the combination of LSTM and other models. These approaches rely on the sequential order of time series data for prediction. The bidirectional LSTM-CRF model combines a bidirectional LSTM network with a Conditional Random Field (CRF) layer, utilizing LSTM to capture contextual dependencies in sequence data and CRF to manage dependencies between output labels, thereby enhancing the model’s robustness in sequence prediction tasks [12,27]. Mohammadi et al. combined a many-to-many LSTM (MTM-LSTM) and a Multilayer Perceptron (MLP), using MTM-LSTM to approximate the target at each step and MLP to integrate these approximations [28]. Wang et al. proposed a Graph Attention Network (GAT) method based on LSTM for vehicle trajectory prediction, where LSTM was used to encode vehicle trajectory information, and GAT was employed to represent vehicle interactions [29]. Ishida et al. integrated one-dimensional Convolutional Neural Networks (CNN) with LSTM to reduce input data size and improve computational efficiency and accuracy in hourly rainfall runoff modeling [30]. Wanigasekara et al. applied Fast Multivariate Ensemble Empirical Mode Decomposition Convolutional LSTM (Fast MEEMD ConvLSTM) for sea surface temperature prediction [31], where the Fast MEEMD method decomposed the SST spatiotemporal dataset [32,33]. Xu et al. proposed a novel approach for retrieving atmospheric temperature profiles using a Tree-structured Parzen Estimator (TPE) and a multi-layer perceptron (MLP) algorithm [34]. Long Short-Term Memory Neural Network (LSTNet) leverages CNN to capture short-term patterns and LSTM or GRU to retain longer-term dependencies [35]. Although these methods combine LSTM with other architectures, which offer inherent interpretability for sequential data such as language or speech, they exhibit poor interpretability for temporal data because the dependencies between time steps in the series are crucial, and the degree of reliance on variables at each time step varies. Some scholars have addressed this issue by introducing attention mechanisms. For instance, AT-LSTM assigns different weights to input features at each time step, effectively selecting relevant feature sequences as inputs to the LSTM neural network, using trend features for forecasting the next time frame [36]. EA-LSTM uses evolutionary attention-based LSTM training with competitive random search, where shared parameters allow LSTM to incorporate an evolutionary attention learning approach [37], which was ultimately applied to forecast PM2.5 levels and indoor temperatures in Beijing. These methods focus on enhancing the attention mechanism by quantitatively assigning attention weights to specific time steps within sequence features, enabling the model to prioritize key variables rather than time steps, thus addressing the instantaneous dispersion limitations of traditional LSTM models. However, these methods do not fully utilize temporal information, as the attention weights are solely based on the output of each time step, limiting their ability to explain temporal dependencies between different time steps. While they can distinguish the importance of various features at different time steps, they fall short in modeling temporal relationships. The Temporal Fusion Transformer (TFT) combines Transformers, LSTM, and other technological modules to incorporate time information as input features [38]. The LSTM module captures short-term dependencies, while the self-attention mechanism handles long-term dependencies, enabling time information to influence the model’s predictions. However, TFT does not consider the temporal distance between elements in the time series data and the target prediction time.

The general approach of these methods using LSTM and its variants is to first sort the dataset by time, select a fixed-length sequence, and use one or more subsequent elements as the prediction value for that sequence. For instance, the first thirty elements in a dataset might be selected as a sequence, with the thirty-first element serving as the prediction value. Subsequently, the sliding window method is employed to sequentially select sequences and prediction values according to a set step size. Based on this approach, existing prediction models are divided into two categories: (1) the vast majority of models do not consider time and only focus on how to improve the expression of input features in the model, such as Fast MEEMD–ConvLSTM. However, the time intervals between consecutive elements are different, and these time intervals can range from a few days to several months. This approach is clearly inadequate for addressing complex prediction problems in reality. (2) A small number of models do consider time, but they only use time to strengthen the input features of the sequence, neglecting the temporal distance between sequence elements and the predicted target time, a relationship essential for identifying patterns such as periodicity, trends, and other temporal dynamics. Moreover, the extraction of time features is often insufficient, and the utilization of time information is not comprehensive, as seen in models like LSTNet. Therefore, these limitations restrict the model to making predictions solely based on the order of occurrence, allowing it to only answer questions such as “What will happen next?”. Consequently, the model performs poorly when tasked with prediction questions with explicit time, such as “What will happen on 21 May 2024 12:00:00?”

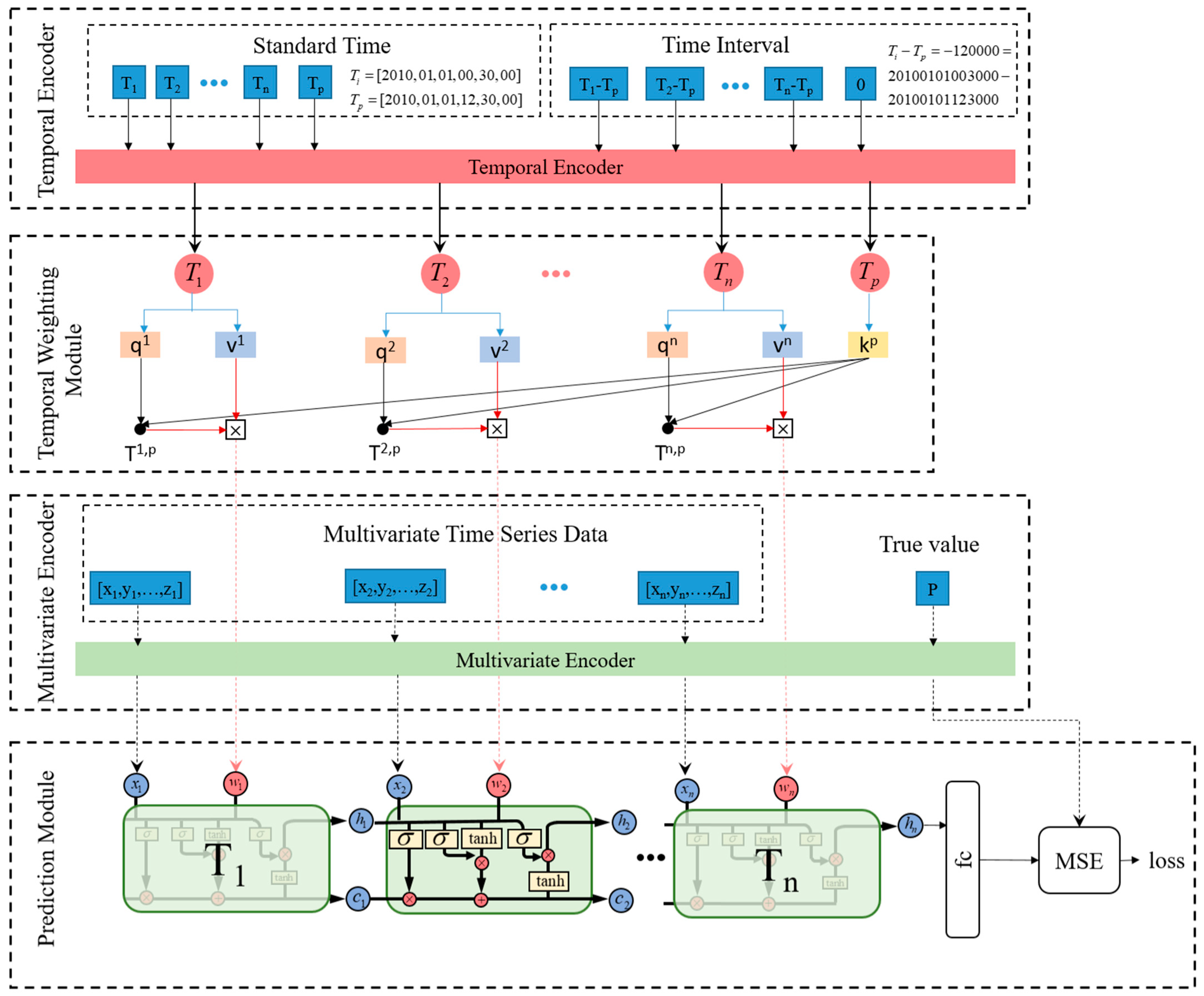
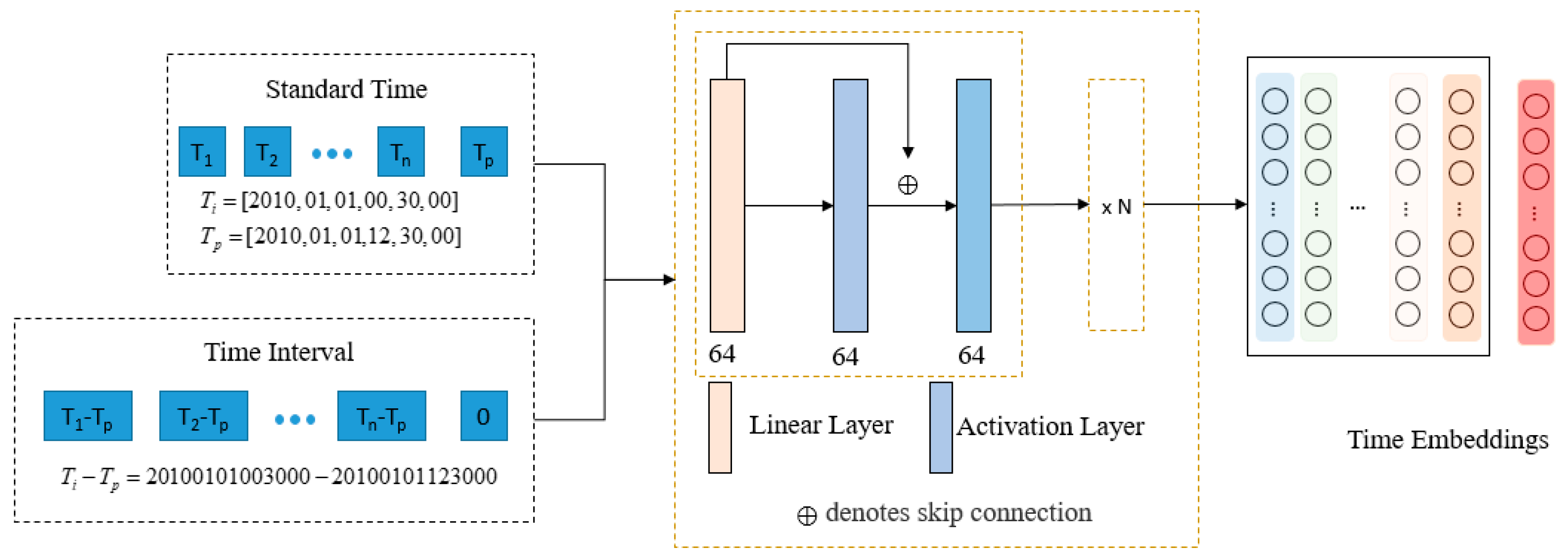
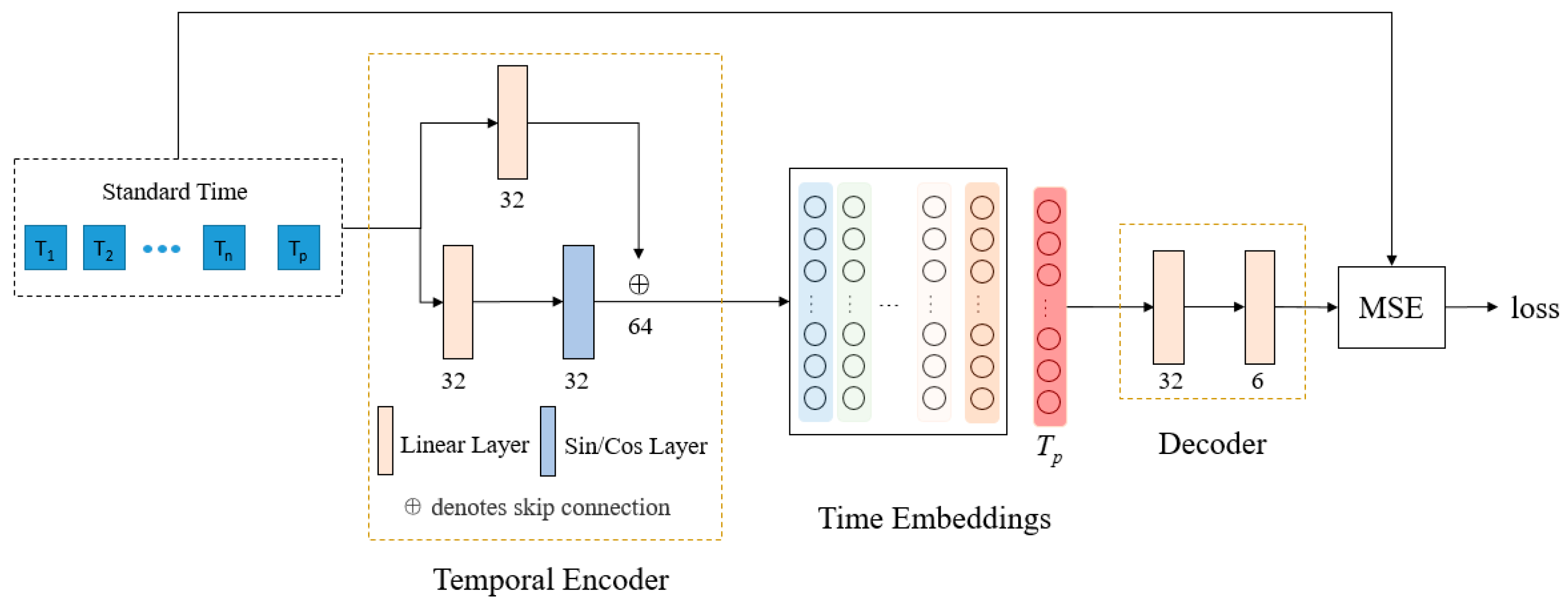
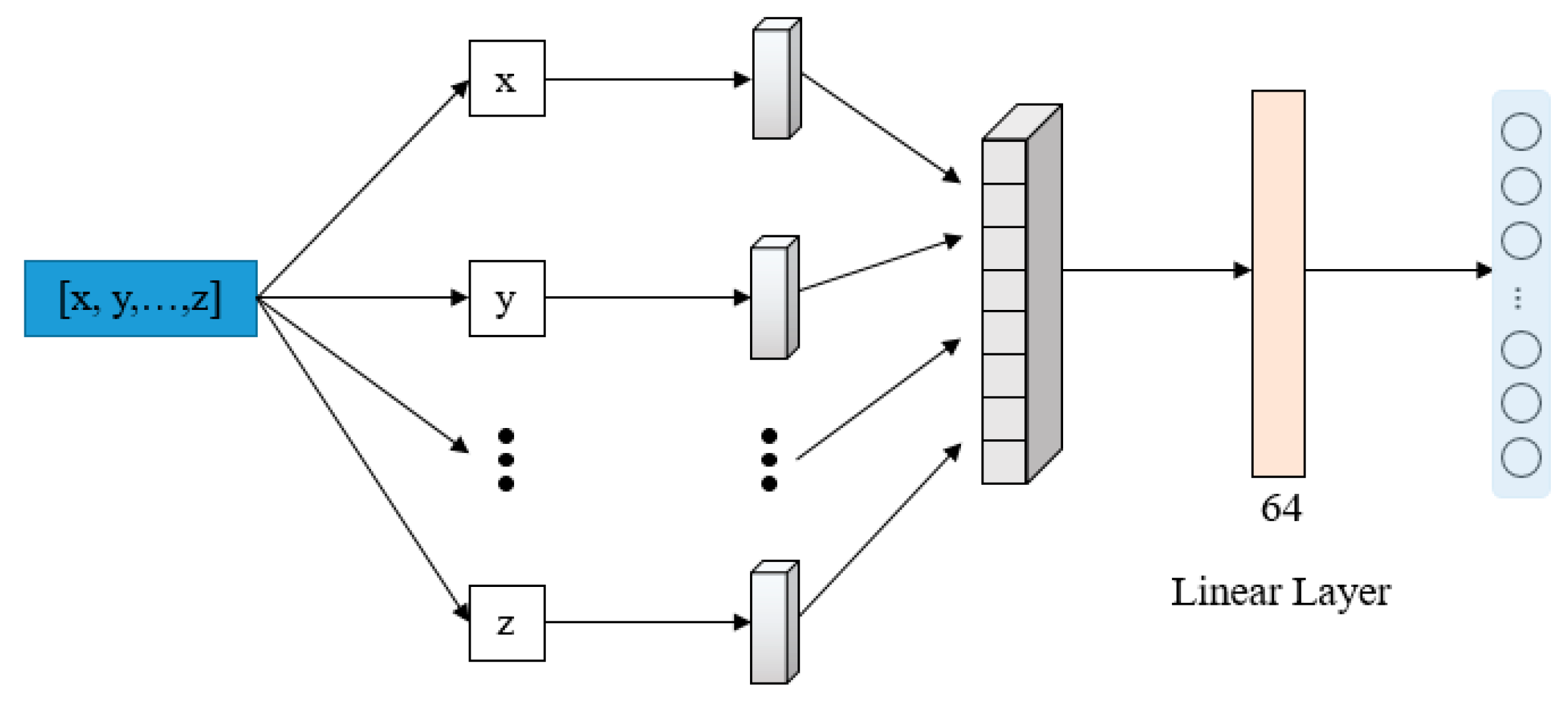
To address these issues, we propose TE-LSTM, an LSTM model that takes into account the temporal evolution of entities. This model is based on the LSTM model. First, to make full use of temporal information, we use two forms of time: the original time of the data and the time intervals between each element and the predicted target. The original time captures global patterns, while the time intervals capture local patterns. Then, we use FFN and Time2Vec to encode these two forms of time, fully extracting the temporal features. A temporal weighted strategy is employed to capture the time relationships between each element in the sequence and the target to be predicted. During each time step calculation of the LSTM, the corresponding temporal weights are integrated, replacing the original order positions to improve prediction accuracy. Finally, we analyze the model’s performance across different time granularities and validate its ability to answer prediction questions with explicit time.

Overall, this model incorporates time into the prediction process by combining LSTM with a temporal weighted strategy. By introducing a temporal weighted strategy, different temporal weights are dynamically calculated for each time step, which improves the model’s ability to process input sequences while enabling the model to consider the temporal information corresponding to these time steps and the temporal relationship with the target to be predicted. This combination not only demonstrates strong performance and flexibility in handling complex temporal tasks but also improves interpretability, enabling the model to excel in various tasks that require sequence data processing.

2. Materials and Methods

2.1. Experimental Data

Temperature prediction plays a crucial role in addressing climate change. By forecasting future temperature variations, it helps individuals and governments take proactive measures, reduce disaster losses, and enhance response capabilities. Therefore, we have chosen temperature prediction as the primary focus of our research. Additionally, the design of TE-LSTM incorporates the ability to capture both periodic and non-periodic patterns. Temperature fluctuations exhibit certain regularities, such as lower temperatures in the morning, higher temperatures at noon, and lower temperatures at night. Thus, selecting a temperature dataset provides an effective means to validate the performance and applicability of TE-LSTM on simple and periodic datasets. In parallel, we also selected the GDELT event dataset, where events are influenced by multiple factors and often occur unpredictably and suddenly. The GDELT dataset allows us to further assess the model’s performance on complex datasets characterized by high randomness and to test its applicability across different types of data.

This research applies the model to temperature prediction using climate data from the National Oceanic and Atmospheric Administration (NOAA). The NOAA provides global hourly/sub-hourly observational data for meteorological information. We used meteorological data from the Beijing Capital International Airport station from 2012 to 2020, comprising a total of 179,111 data points, as shown in Figure 1. The dataset includes several types of data:

• Total coverage: denotes the fraction of the total celestial dome covered by clouds or other obscuring phenomena.
• Total lowest cloud cover: represents the fraction of the celestial dome covered by all low clouds present. If no low clouds are present, it denotes the fraction covered by all middle-level clouds present.
• Low cloud genus: denotes a type of low cloud.
• Height: lowest cloud base height dimension.
• Mid cloud genus: denotes a type of middle-level cloud.
• High cloud genus: denotes a type of high cloud.
• Atmospheric pressure at the observation point.
• Temperature received from the Automated Weather Observing System (AWOS).
• Dew point received from the Automated Weather Observing System (AWOS).

We took temperature as the prediction target and used the other types of data as factors affecting temperature.

The GDELT project, supported by Google Jigsaw, monitors global broadcasts, print media, and online news from nearly every corner of every country in over 100 languages. It identifies the people, locations, organizations, themes, sources, emotions, counts, quotes, images, and events driving our global society, creating a free and open platform for computing the entire world. It is the largest, most comprehensive, and highest-resolution open database of human society ever created, with a total archive spanning over 215 years. For this study, we used events between two countries from the GDELT 1.0 simplified event database, covering all events from 1 January 1979, to 17 February 2014. There are a total of 164,255 events, spanning 412 event types. We performed a statistical analysis of the GDELT event dataset and visualized the results using a word cloud, as shown in Figure 2. In the word cloud, the font size corresponds to the frequency of events, with more frequent events represented by larger font sizes.

When creating the multivariate time series and predictive target dataset, the data are first sorted by occurrence time. In this experiment, the sequence length L is set to 30, and the X-th element after the sequence is selected as the prediction value. The dataset is divided into training, validation, and test sets in a ratio of 90:9:1. The dataset partitioning details are shown in

Table 1. Dataset statistics.

Dataset	NOAA	GDELT
Data Volume	179,111	164,255
Sequence Length L	30	30
Training	161,199	147,802
Validation	16,119	14,780
Testing	1793	1643

.

2.2. TE-LSTM

TE-LSTM builds upon the traditional LSTM, which is suitable for capturing data with long-term dependencies. To make the model suitable for processing multivariate time series data, it uses a temporal weighting strategy to optimize the integration of temporal information and capture the temporal relationship of each element relative to the target element. This combination allows the model to better focus on relevant parts of the input sequence and capture the time patterns inherent in the sequence, thereby improving the model’s performance.

The model consists of four main components, as shown in Figure 3. The first component is the temporal encoder, which encodes time in various ways to fully extract temporal features and determine the most suitable temporal encoding method for this model. The second component is the temporal weighting module, which employs a temporal weighting strategy to optimize time features and capture the relationship between the time of each element in the sequence and the predicted target time. The third component is the multivariate encoder. In multivariate time series data, each time step corresponds to multiple variables. This module encodes and recombines these variables into a tensor, serving as input for the prediction model. The fourth component is the prediction module, which is based on the traditional LSTM and consists of a chain neural network repeating module. Each chain neural network includes a forget gate, an input gate, an updated unit state, and a temporal weighting output gate. The inputs include the unit state and hidden state from the previous time step, the entity vector for the current time step, and the temporal weight for the current time step. The outputs are the unit state and hidden state of the current time step. This module ultimately generates prediction results through a fully connected layer and calculates the loss value using Mean Squared Error (MSE) and the true value.

2.2.1. Temporal Encoder

Time, as a crucial piece of information in the prediction process, has the following characteristics: (1) Fluidity: Time is linked to the motion of matter, passing second by second, minute by minute, continuously flowing and unaffected by human will; (2) irreversibility: Time cannot be reversed; once it has passed, it cannot be reclaimed; and (3) relativity: The progression of time is not absolutely constant.

Due to the inherent characteristics of time, entities exhibit evolutionary patterns such as periodicity, increase, or decrease. However, even for the same entity, these evolutionary patterns are not fixed and may vary across different periods. Additionally, the time span over which some entities evolve can be extraordinarily large; for instance, geological evolution may require hundreds, thousands, or even tens of thousands of years to discern patterns. These patterns are complex and strongly correlated with time, rather than solely dependent on the entity itself.

In reality, there are three types of time associated with entities: time points, time periods, and timelessness. In multivariate time series forecasting tasks, the type of time is typically a time point, and only a small portion of the data is timeless. In this paper, we classify the evolutionary patterns of elements into two categories: periodic and aperiodic. To capture these two types of patterns and fully extract temporal characteristics to better utilize time information, we employ two temporal encoding techniques: Feed Forward Networks (FFN) and Time2Vec [39].

(a)

Temporal Encoder (FFN)

The feedforward neural network principally comprises an input layer, hidden layers, and an output layer. The input layer receives external data, the hidden layers extract features from the data, and the output layer produces the calculation results. The skip connection structure introduced in the ResNet architecture proposed by He et al. effectively enhances network performance [40]. In this research, we utilize two forms of time:

• Standard Time of Each Element (ST): The standard time for each element is a 6-dimensional vector: [yyyy, MM, dd, HH, mm, ss] representing year, month, day, hour, minute, and second, respectively. This information captures the element’s absolute position on the timeline and its global evolutionary patterns, effectively identifying two types of evolutionary patterns. For elements whose evolutionary patterns require a long time span to be captured, the standard time helps in detecting global changes. When the patterns of elements continuously change, the standard time can pinpoint precise positions, allowing for the acquisition of information before and after that time point to capture finer details of the entity’s evolution. This time format is applicable to all types of datasets.
• The Time Interval between Each Element in the Sequence and the Element to Be Predicted (TI): The time interval between each element in the sequence and the element to be predicted is an exact value. This captures the relative position of each element in the sequence relative to the prediction target on the time axis. Additionally, as the model trains on sequences, using time intervals allows it to focus more on the sequence itself, reducing the emphasis on the global time position of elements and focusing more on local patterns. Thus, this method is better suited for capturing periodic patterns.

The overall structure of the temporal encoder is shown in Figure 4. A single hidden layer unit comprises a fully connected layer, LeakyReLU activation layer, and normalization layer. Each standard time or time interval in the time series data is fed into the encoder separately, where multiple hidden layers extract time features to generate the final time feature vector.

(b)

Temporal Encoder (Time2Vec)

Time2Vec is a method for time vector representation, designed to effectively incorporate time information into various machine learning architectures. Time2Vec captures periodic patterns and aperiodic trends by combining periodic functions, such as linear and sinusoidal functions. For a given time scalar t, the following Time2Vec(t) is defined as a vector of size k + 1, where the first component is a linear function of time, and the remaining components are periodic functions with learnable frequencies and phase offsets, allowing the Time2Vec model to learn and represent the complex time dynamics inherent in many real-world datasets:

$$Time2Vec\left(t\right)\left[i\right]=\left\{\begin{array}{cc}{\omega }_{i}t+{\varphi }_i& \left(i=0\right)\\ F\left({\omega }_{i}t+{\varphi }_i\right)& \left(1\le i\le k\right)\end{array}\right.$$

(1)

where $F()$ is the periodic activation function, ${\omega }_i$ and ${\varphi }_i$ is a learnable parameter.

Here, because Time2Vec can capture periodic and aperiodic trends, we only use the standard time of the element and convert standard time to a scalar: yyyyMMddHHmmss. We employ the encoder-decoder structure [41,42,43]. The encoder outputs a time vector with a dimension of 64, where the first 32 positions of the vector use linear layers and the last 32 positions use periodic activation functions:

$$\tau [i]=\left\{\begin{array}{cc}{\omega }_{i}t+{\varphi }_i& \left(0\le i<32\right)\hfill \\ F\left({\omega }_{i}t+{\varphi }_i\right)& \left(32\le i<64\right)\hfill \end{array}\right.$$

(2)

The following decoder uses two linear layers to decode the time vector into a six-dimensional vector, and calculates the loss value using the MSE function and standard time format time:

$$loss={\displaystyle \frac{1}{6}}{{\displaystyle {\sum }_{i=1}^6(L{(\tau )}_i-S{T}_i)}}^2$$

(3)

where L is a linear function, and ST is the standard time.

By calculating the loss, we ensure the decoded time is consistent with the standard time as much as possible. The overall structure of the temporal encoder is shown in Figure 5.

2.2.2. Temporal Weighting Module

Our objective is to understand the relationship between the time of each element and the target time being predicted. Inspired by the attention mechanism [44] and the use of spatial weighting strategy to optimize the integration of spatial information [45], we calculate the weights of each sequence element’s time and the target’s time to capture this relationship. For each element’s time in the sequence, a linear layer is used to generate the corresponding query matrix and value matrix. For time of target to be predicted, a linear layer generates the key matrix. Subsequently, the query matrix of each sequence element is multiplied by the key matrix of the predicted target time. Then, this result is multiplied by the value matrix to obtain the weight of that element relative to the predicted target time, as shown in Figure 3.

$$w_i={\displaystyle \frac{q^i{k}^p}{\sqrt{d_k}}}{v}^i$$

(4)

where $q,k,v$ represent the query matrix, key matrix, and value matrix, respectively. $d_k$ is the feature dimension of keys and queries.

2.2.3. Multivariate Encoder

In multivariate time series data, each time point or time step consists of multiple variables. For example, in the temperature dataset used in this study, there are nine variables at each time point, as described in Section 2.1. The input to the multivariate encoder is an array of multivariate variables: $[x,y,\cdot \cdot \cdot ,z]$ at each time point. The multivariate encoder uses a pre-trained Word2Vec model to encode each variable, obtaining the corresponding feature vector. Then, these feature vectors are concatenated to form a single feature vector. A linear layer is subsequently used to transform this feature vector into a vector of dimension 64, as specified by the model, as shown in Figure 6. The calculation process is as follows:

$$e=Linear(\underset{\mathrm{multivariable}:\left[x,y,\cdot \cdot \cdot ,z\right]}{\underbrace{W2V(x)\oplus W2V(y)\oplus \cdot \cdot \cdot \oplus W2V(z)}})$$

(5)

where W2V represents Word2Vec, and Linear represents linear transformation.

2.2.4. Prediction Module

The prediction module is based on the traditional LSTM architecture and consists of a chain neural network repeating module. Each chain neural network includes a forget gate, an input gate, a cell state layer, and a temporal weighting output gate. The calculation process of the forget gate, input gate, cell state layer, and output gate of the LSTM is as follows:

$$f_t=\sigma (W_f\cdot [h_{t-1},x_t]+b_f)$$

(6)

$$i_t=\sigma (W_i\cdot [h_{t-1},x_t]+b_i)$$

(7)

$${\tilde{C}}_t=\tanh (W_C\cdot [h_{t-1},x_t]+b_C)$$

(8)

$$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t$$

(9)

$$o_t=\sigma (W_o\cdot [h_{t-1},x_t]+b_o)$$

(10)

where $W$ represents the weight parameter, $b$ represents the bias parameter, $x_t$ represents input information, and $f,i,C,o$ represent the parameters of the forget gate, input gate, cell state layer, and out gate, respectively.

Here, we integrate the temporal weight into the output gate, as shown in Figure 3. This step aims to replace the original order positions with temporal weight. Then, we calculate the output using the current time step’s input information $x_t$, the current time step’s temporal weight $w_t$, and the hidden state from the previous time step $h_{t-1}$:

$$o_t=\sigma (W_o\cdot [h_{t-1},x_t]+w_t+b_o)$$

(11)

Then, the cell state is normalized to the [−1, 1] range using the tanh function, and the output at the current time step is calculated:

$$h_t=o_t\ast \tanh (C_t)$$

(12)

The model consists of n neural network modules described above, where n is the length of the sequence: n = L = 30. The output results of these n chain-like neural network repeating modules will finally enter a fully connected layer to obtain the final prediction result. The following Mean Squared Error (MSE) is used as the loss function:

$$loss={\displaystyle \frac{1}{n}}{{\displaystyle {\sum }_{i=1}^n(h_{p_i}-fc(h_{t_i}))}}^2$$

(13)

where n is the number of predictions, and $h_{p_i}$ is the true value.

3. Results and Discussion

We use probability (P) (P = 1 − MSE) as the evaluation metric.

3.1. Verify the Accuracy of TE-LSTM under Different Temporal Encoders

To verify the role of time in the model, we select the X-th (X = {1, 2, 3}) element after the sequence as the prediction value. Under the same conditions, the predicted data have the same occurrence order, but the time and time interval are different. For standard time, we use both FFN and Time2Vec time encoding methods, while for time interval, only FFN encoding is applicable. The model results are shown in

Table 2. Model results when using data with X = {1, 2, 3}.

Dataset	X	LSTM	ST (FFN)	ST (Time2Vec)	TI (FFN)
NOAA	1	0.909423	0.919506	0.908378	0.916457
	2	0.908807	0.924220	0.913982	0.916036
	3	0.908416	0.905575	0.907367	0.908263
GDELT	1	0.889572	0.892315	0.888130	0.887824
	2	0.889164	0.900982	0.896460	0.900762
	3	0.897718	0.900174	0.895819	0.889391

.

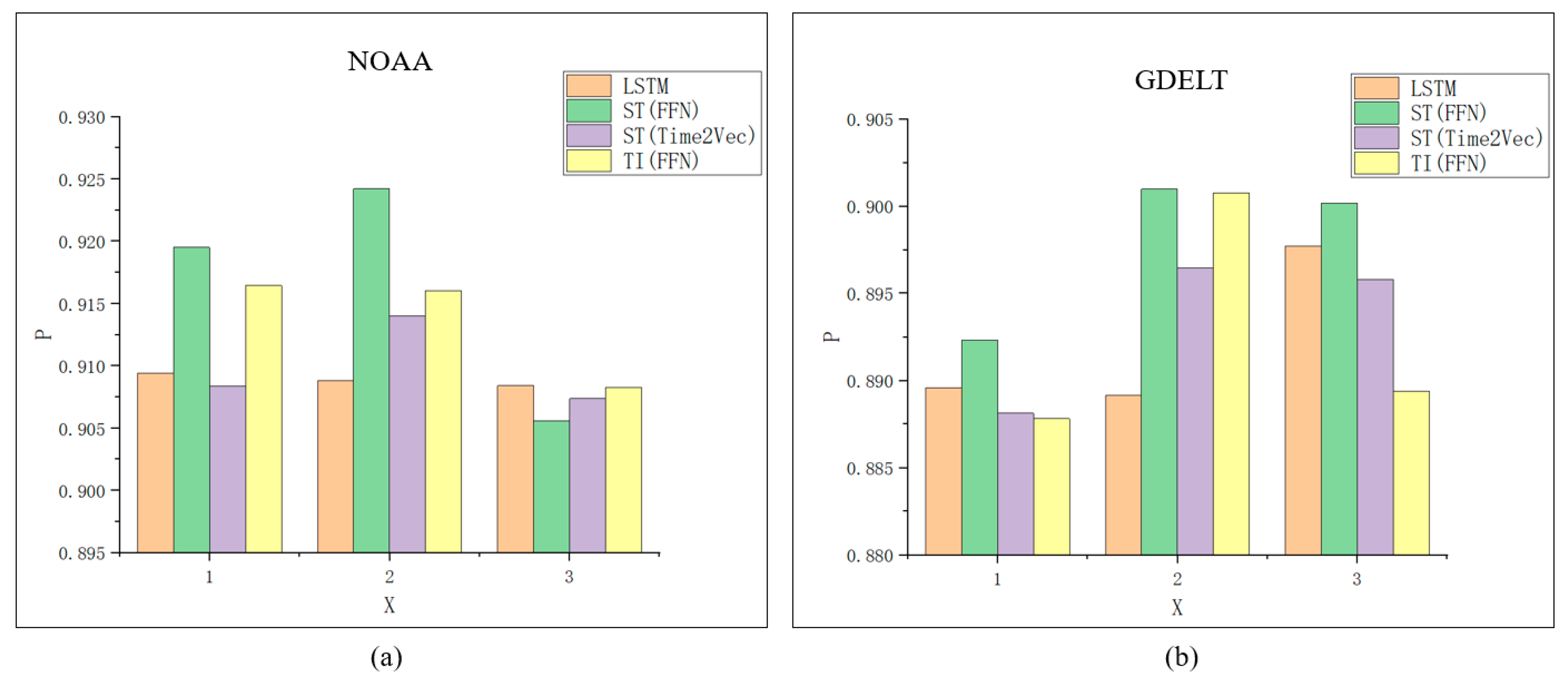
As shown in Figure 7, for the NOAA dataset, ST (FFN) demonstrates the best performance, with only a slight decrease in P at X = 3. In contrast, ST (Time2Vec) exhibits the worst performance, with a minor increase in P at X = 2. According to Table 2, when X = 1, ST (FFN) results increased by 1.0083%, TI (FFN) results increased by 0.7034%, and ST (Time2Vec) results decreased by 0.1045%. When X = 2, ST (FFN) results increased by 1.5413%, TI (FFN) results increased by 0.7229%, and ST (Time2Vec) results increased by 0.5175%. When X = 3, the performance of all three methods slightly decreased: ST (FFN) results decreased by 0.2841%, TI (FFN) results decreased by 0.0153%, and ST (Time2Vec) results decreased by 0.1049%. On average, ST (FFN) shows a mean increase of 0.7552%, TI (FFN) shows a mean increase of 0.4703%, and ST (Time2Vec) shows a mean increase of 0.1027%. For the GDELT dataset, ST (FFN) again demonstrates the best performance, while TI (FFN) performs the worst. According to Table 2, when X = 1, ST (FFN) results increased by 0.2743%, TI (FFN) results decreased by 0.1748%, and ST (Time2Vec) results decreased by 0.1442%. When X = 2, ST (FFN) results increased by 1.1818%, TI (FFN) results increased by 1.1598%, and ST (Time2Vec) results increased by 0.7296%. When X = 3, ST (FFN) results increased by 0.2456%, TI (FFN) results decreased by 0.8327%, and ST (Time2Vec) results decreased by 0.1899%. On average, ST (FFN) shows a mean increase of 0.5672%, TI (FFN) shows a mean increase of 0.0508%, and ST (Time2Vec) shows a mean increase of 0.1318%.

In conclusion, incorporating temporal information significantly enhances model prediction accuracy, with ST (FFN) being the most effective method for encoding time. The use of standard time facilitates the precise location of elements on the time axis, enabling the capture of comprehensive patterns, and is suitable for various types of datasets. Time interval captures the relative position between the time of elements in the current sequence and the target element, focusing solely on the evolution pattern of the sequence itself. This method is particularly suitable for datasets with short-term and periodic changes. In the NOAA dataset, where temperature is the prediction target, the periodic nature of temperature changes makes the TI (FFN) method more appropriate. Experimental results confirm the superiority of TI (FFN) in capturing periodicity. However, the TI (FFN) results still fall short compared to ST (FFN), indicating that the local information-focused approach of time interval is not the optimal solution. In the era of big data, datasets are characterized by large volumes, long time spans, and rich temporal information, necessitating comprehensive global information for more accurate predictions. The GDELT dataset, which uses events as prediction results, exhibits greater uncertainty, rendering the local pattern-focused TI (FFN) the worst performer. Therefore, for TE-LSTM, regardless of the type of dataset, the ST (FFN) temporal encoder can be used.

3.2. Verify the Accuracy of TE-LSTM under Different Time Granularities

The results of Experiment 1 verified the necessity and reliability of incorporating time information. Next, we evaluated the model’s performance under different time granularities. For NOAA data with richer time information, we set X = 1 and established five different time granularities G = {1, 2, 3, 6, 12}. For GDELT data, we set X = 1 and established three different time granularities G = {1, 2, 3}, due to the lesser time information in each sequence of GDELT data. Elements within the same time granularity are assigned the same time. For example, with a time granularity of G = 2 days, if 1 January 1979 and 2 January 1979 fall within the same time granularity, all elements within these two days are set to 1 January 1979. This approach is used to verify the model’s performance under different time granularities. The experimental results using the NOAA dataset are shown in

Table 3. The results of the models using the NOAA dataset with different time granularities.

Dataset	G (0.5 h)	LSTM	ST (FFN)	ST (Time2Vec)	TI (FFN)
NOAA	1	0.909423	0.919506	0.908378	0.916457
	2	0.910448	0.921464	0.905445	0.899359
	3	0.909430	0.921477	0.907413	0.914457
	6	0.904408	0.909433	0.910445	0.914428
	12	0.899278	0.902479	0.902379	0.899233

The results of the base LSTM model differ under different time granularities because the data are shuffled each time the dataset is created.

.

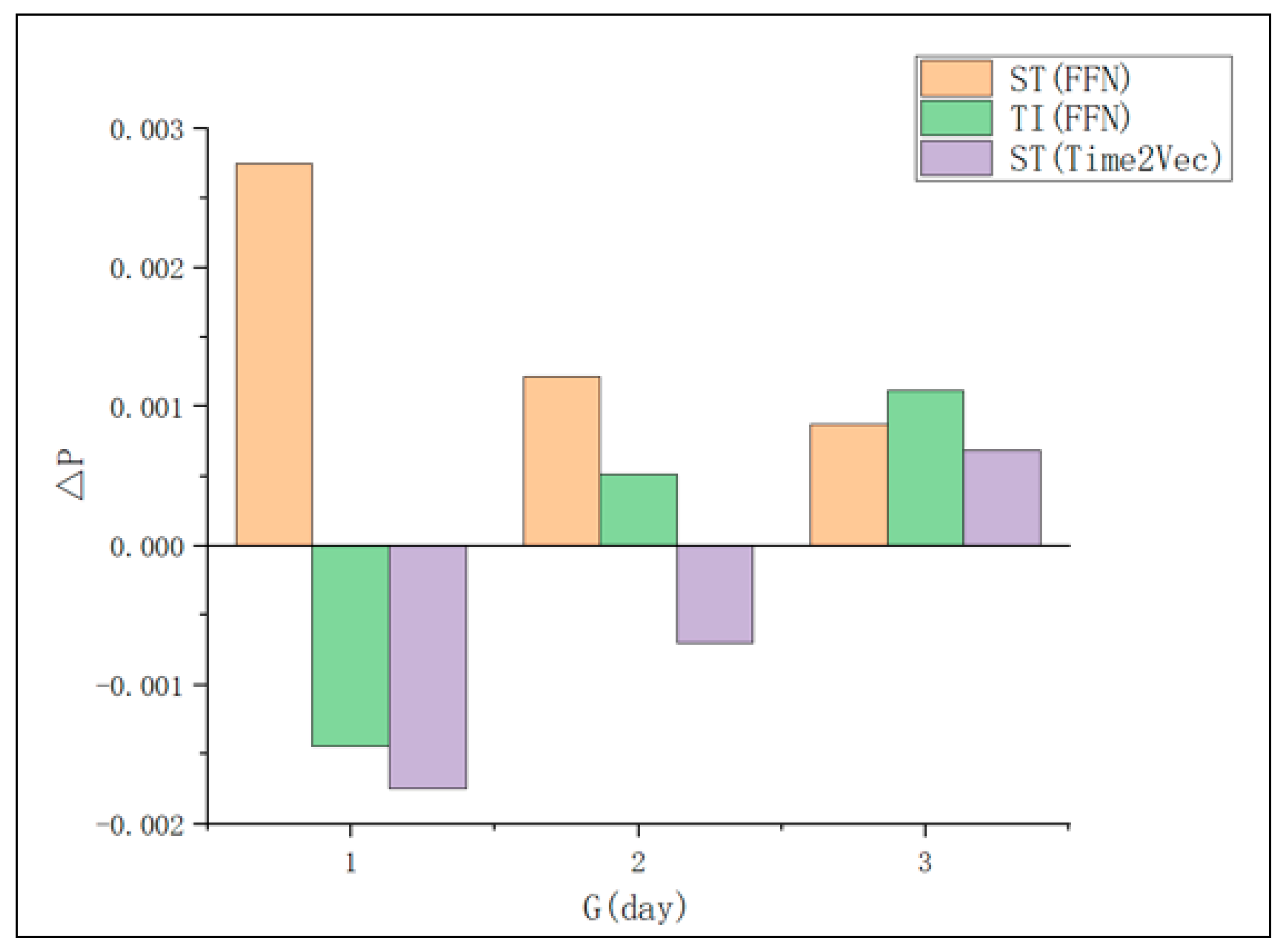
To comparatively analyze the impact of different time granularities on the model’s accuracy, we examined the probability changes $△P=P_{TE-LSTM}-P_{LSTM}$ between TE-LSTM, using different encoding methods, and LSTM at the same time granularity.

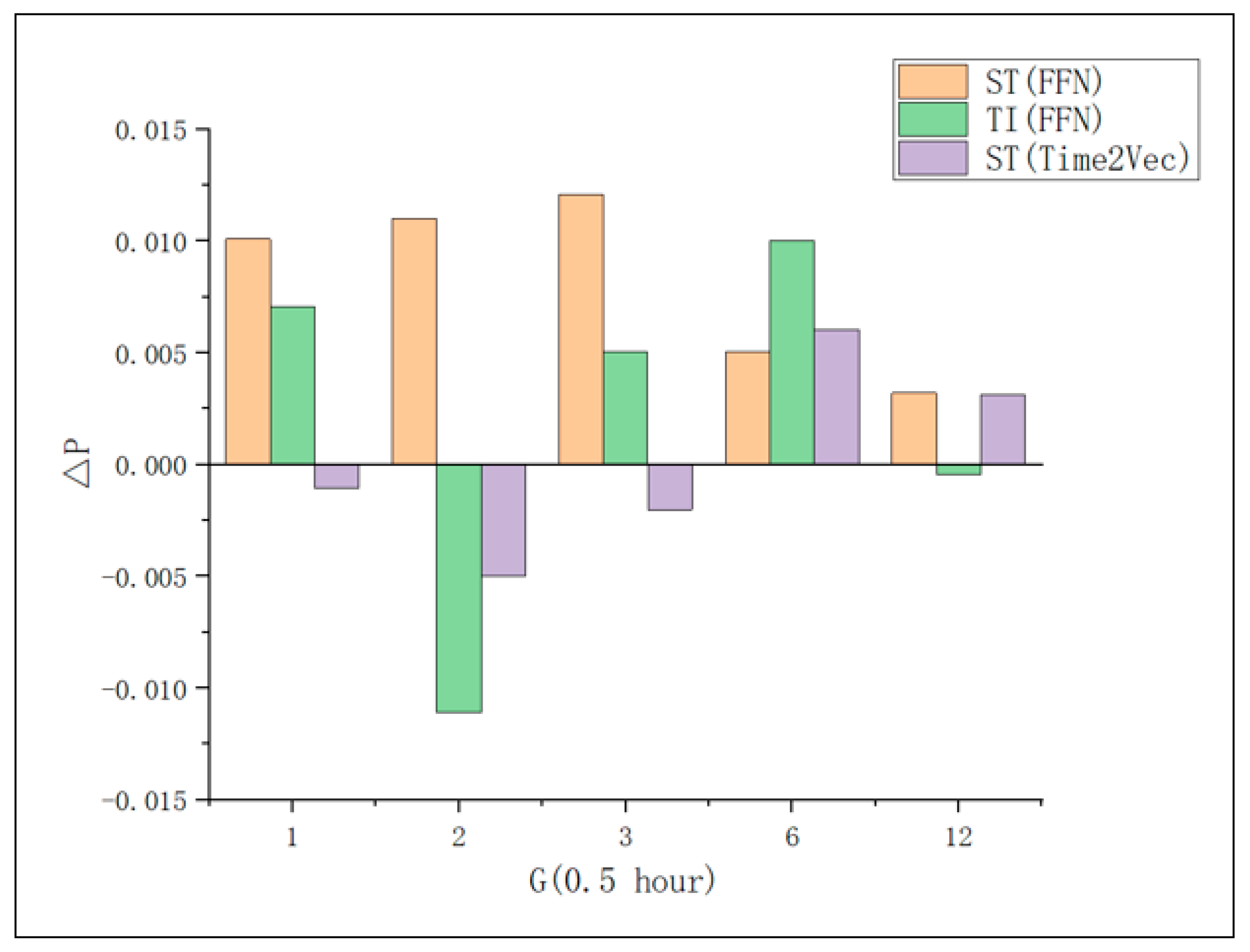
From Figure 8, it can be observed that as the time granularity increases, regardless of whether time fusion improves or degrades accuracy, the magnitude of change becomes smaller. This indicates that the influence of time in the model decreases. When analyzing the dataset itself, the multivariate time sequence length was set to 30 during dataset creation. 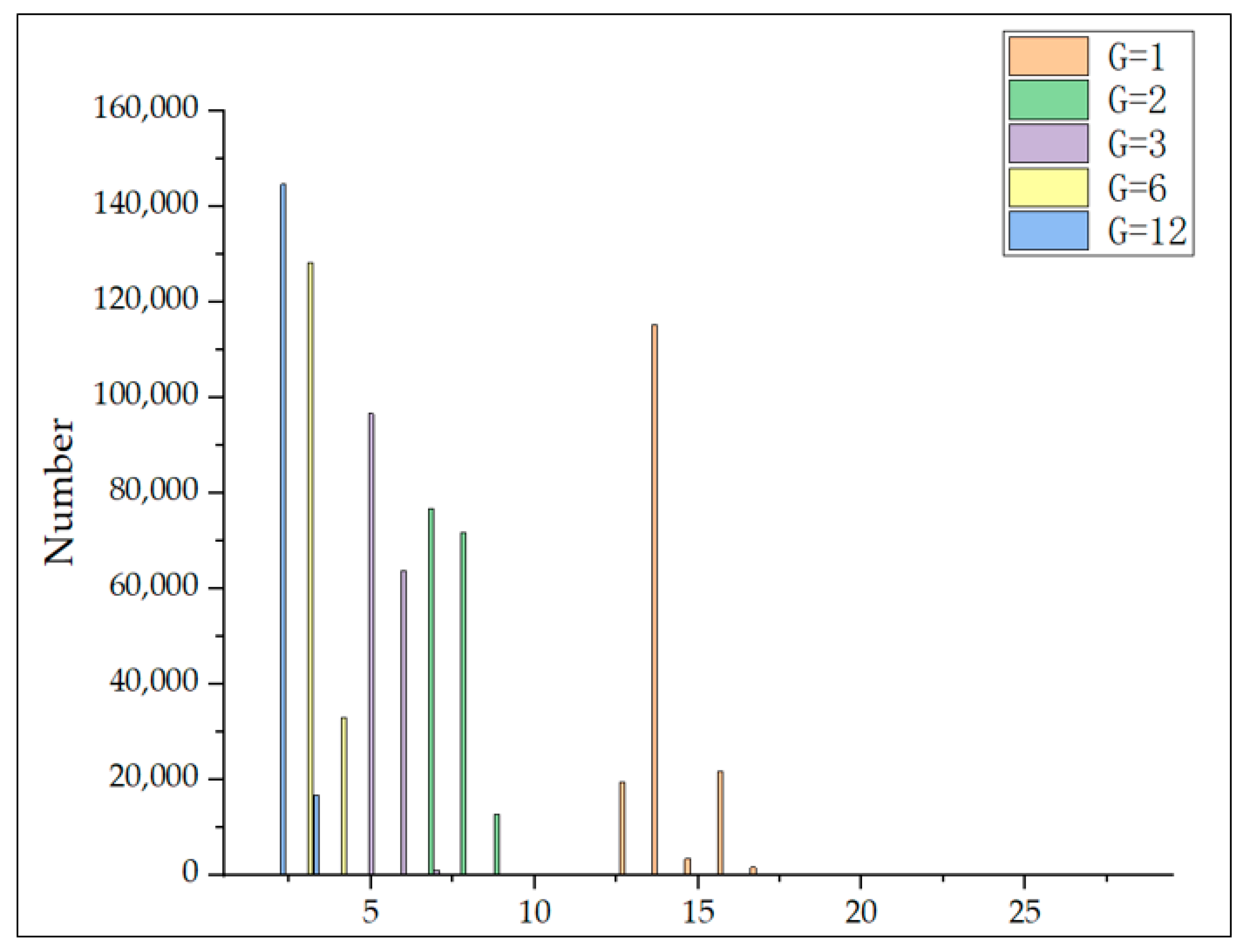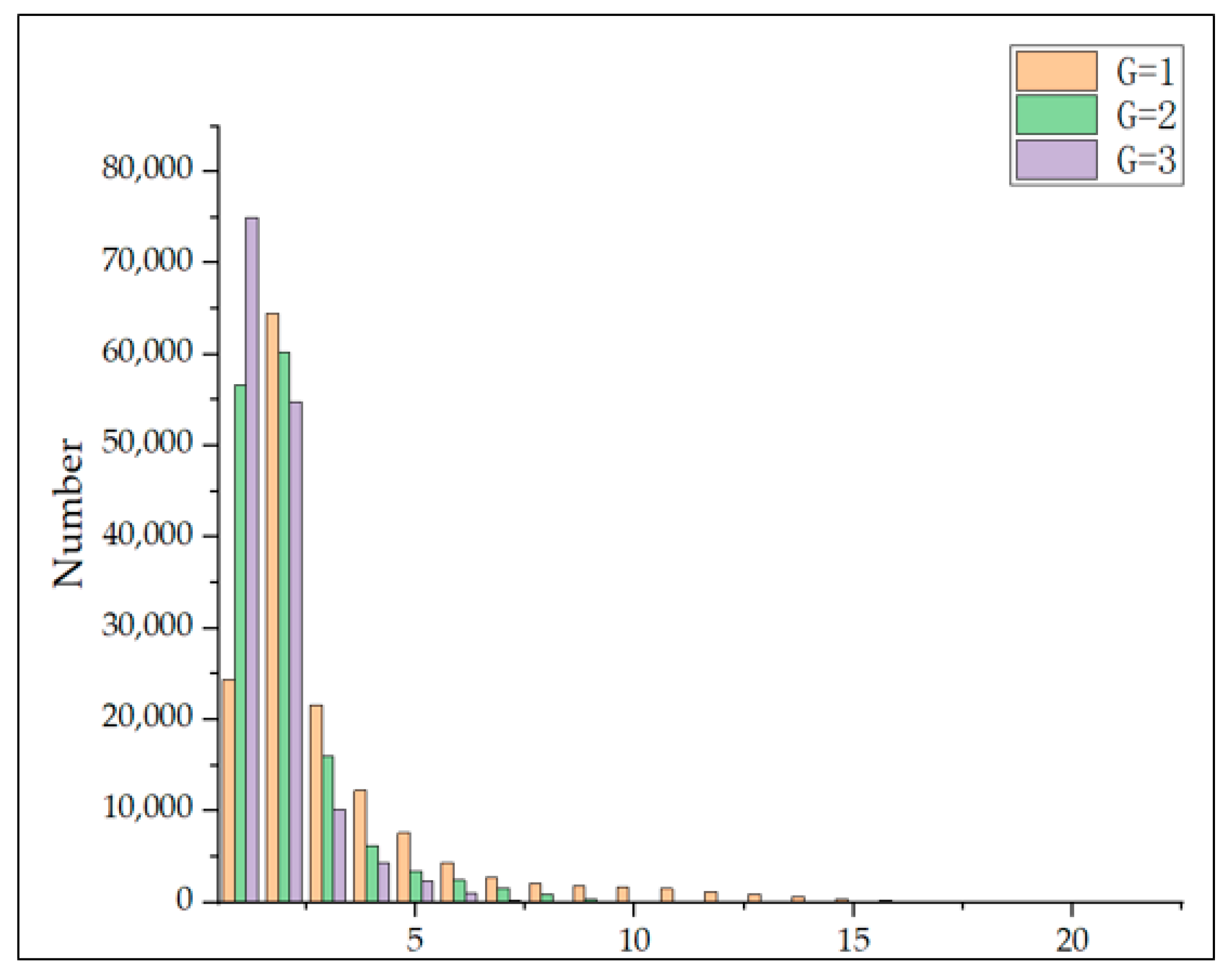We counted the occurrences of different time information in the sequences at various time granularities, as shown in Figure 9. The number of different times in the sequence is defined as follows: If a sequence contains 3 occurrences of 12:00:00 on 21 May 2024, 5 occurrences of 13:00:00 on 21 May 2024, 10 occurrences of 14:00:00 on 21 May 2024, and 2 occurrences of 15:00:00 on 21 May 2024, then this sequence has four non-repeating times.

From Figure 9, it can be observed that when G = 1, the time quantity is concentrated around 14; when G = 2, the time quantity is concentrated around 8; when G = 3, the time quantity is concentrated around 5; when G = 6, the time quantity is concentrated around 3; and when G = 12, the time quantity is concentrated around 2. As the time granularity increases, the number of time points in the sequence gradually decreases, leading to a decline in the richness of time information.

For ST (FNN), the pattern is captured through the absolute position of time. When the richness of time decreases, the model accuracy begins to decline. For ST (Time2Vec) and TI (FNN), both methods can capture periodicity. When the time granularity is small, too much time information introduces noise, making it difficult to capture patterns. As the time granularity increases, the model accuracy begins to slowly rise. Therefore, when the appropriate time granularity is chosen, the accuracy of these two methods will outperform the base model.

In summary, changes in time granularity significantly affect model accuracy. Appropriate time granularity can significantly enhance model performance. For ST (FNN), smaller time granularity yields better results, and larger time granularity should be avoided. For ST (Time2Vec) and TI (FNN), the model performs poorly with smaller time granularity. In this experiment, with a sequence length of 30, a time granularity of 6 or 12 is suitable, ensuring the number of time points in the sequence is around 3.

The experimental results using the GDELT dataset are shown in

Table 4. The results of the models using the GDELT dataset with different time granularities.

Dataset	G (Day)	LSTM	ST (FFN)	ST (Time2Vec)	TI (FFN)
GDELT	1	0.889572	0.892315	0.888130	0.887824
	2	0.888756	0.889969	0.889270	0.888060
	3	0.888272	0.889145	0.889386	0.888957

. We also examined the probability changes, as shown in Figure 10. From Figure 10, it can be observed that although the GDELT data do not exhibit a clear periodicity, the results of all three methods show a consistent pattern with those obtained using NOAA data. Similarly, the quantity of different time points in the sequence under different time granularities is also counted, as shown in Figure 11. When the complexity of time information is low, ST (Time2Vec) and TI (FNN) perform well. When the complexity of time information is high, ST (FFN) performs well.

3.3. Verify the Performance of TE-LSTM in Predicting Questions with Specific Times

We aimed to address the issue where existing models perform well in answering questions like “What will happen next?” but perform poorly in answering questions with specific times such as “What will happen on 21 May 2024 12:00:00?” Therefore, the model trained with X = 1, G = 1 was used as the baseline model. Then, this trained baseline model was used to predict data with X = {2, 3, 5, 10}, G = 1. When X is determined, the prediction target relative to the sequence order will be fixed, but the time of the prediction target will vary, and so will the time interval distance from the sequence. Therefore, this approach can be used to evaluate the performance of the proposed method in answering predictive questions with specific times. The results using the model trained with X = 1, G = 1 for X = {2, 3, 5, 10}, G = 1 data are shown in

Table 5. The results using the model trained with X = 1, G = 1 for X = {2, 3, 5, 10}, G = 1 data.

Dataset	X (G = 1)	LSTM	ST (FNN)	ST (Time2Vec)	TI (FNN)
NOAA	1	0.909423	0.919506	0.908378	0.916457
	2	0.909221	0.919213	0.908576	0.916178
	3	0.908810	0.917772	0.908639	0.912760
	5	0.907842	0.917608	0.907656	0.917809
	10	0.904270	0.913126	0.904135	0.912310
GDELT	1	0.889572	0.892315	0.888130	0.887824
	2	0.889554	0.891979	0.888211	0.887977
	3	0.889433	0.891608	0.887990	0.887809
	5	0.889310	0.891640	0.887870	0.887632
	10	0.889051	0.891354	0.887612	0.887407

.

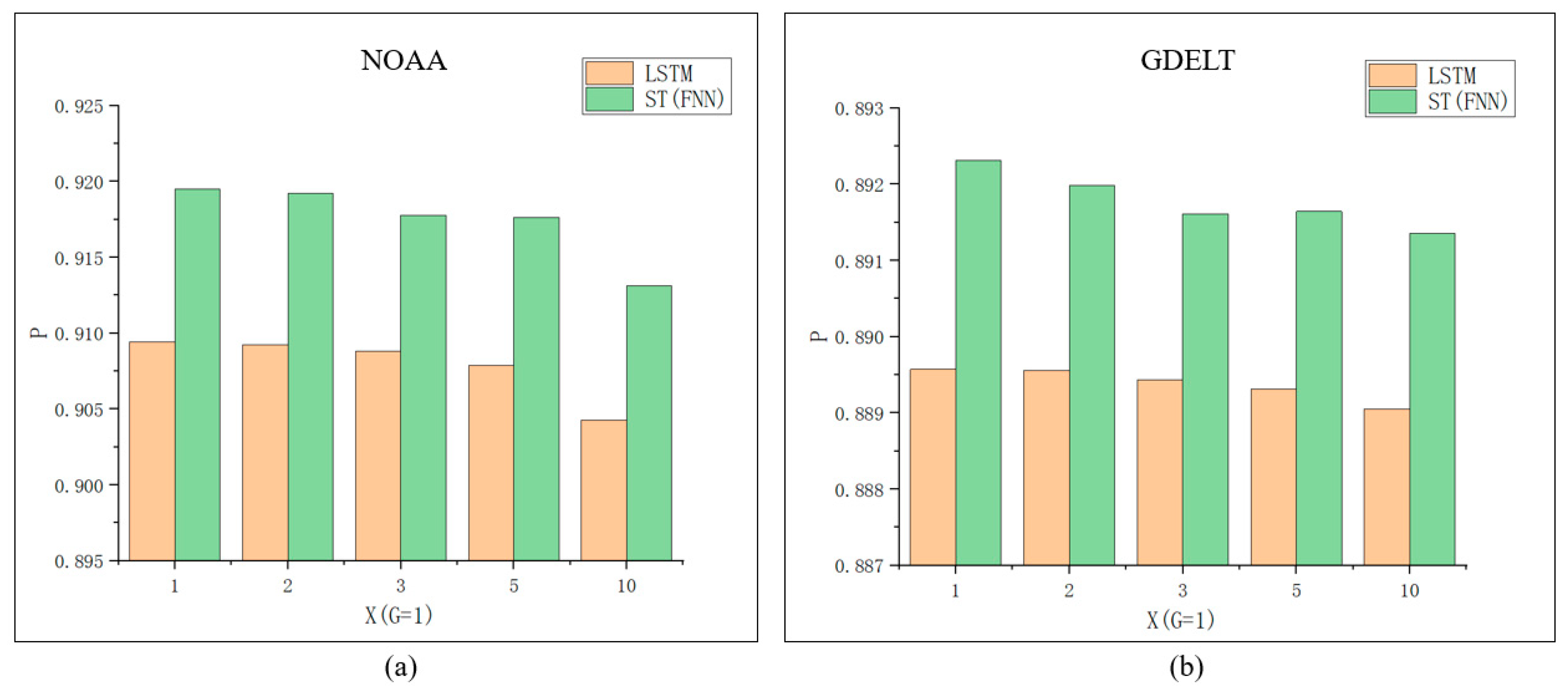
From the previous two experiments, we know that when X = 1, G = 1, ST (FFN) performs the best. Therefore, we only analyzed the comparison between TE-LSTM using ST (FFN) temporal encoder and LSTM. From Figure 12, for both two datasets, it can be seen that the performance of the ST (FFN) is significantly better than the baseline model. As the prediction steps increase, the probability P of the LSTM model shows a decreasing trend, indicating that the prediction results become less accurate. For the NOAA dataset, the ST (FFN)’s results remain stable around 91.55%. For GDELT data, the ST (FFN)’s results remain stable around 89.2%. This stability is because the ST (FFN) calculates the weight of each element’s time relative to the target’s time, capturing the time interval positions of each element with respect to the target element. This significantly enhances the results. However, when X = 10, both methods show a slight decrease. This is because the target to be predicted is too far from the corresponding sequence, weakening the regularity and correlation between the sequence and the target element. The role of temporal weight as an auxiliary enhancement diminishes. In contrast, LSTM treats all targets to be predicted as an element occurring at X = 1, and thus the prediction accuracy decreases. This result proves the excellent performance of TE-LSTM in answering questions with specific time predictions.

3.4. Comparison of TE-LSTM with State-of-the-Art (SOTA) Methods and Validation of TE-LSTM Performance on LSTM Variant Models

We chose two SOTA methods, TFT and Informer [38,46]. TFT is a hybrid model that combines the Transformer architecture with traditional LSTM, enabling it to capture long-term dependencies while handling both dynamic and static features. Moreover, TFT provides built-in interpretability, which is advantageous for understanding model predictions. Informer, an efficient Transformer variant specifically designed for long-term time series forecasting, reduces computational complexity through a sparse self-attention mechanism, significantly enhancing the efficiency of long-term series predictions. We first verified the ability of the three models to predict targets at different locations. In this experiment, the time granularity G is set to 1, and TE-LSTM employs the ST (FFN) time encoder, which demonstrated the best performance at this granularity. The final results are presented in

Table 6. The results of TE-LSTM and SOTA methods when using data with X = {1, 2, 3}.

Dataset	X	TE_LSTM	TFT	Informer
NOAA	1	0.919506	0.910564	0.916096
	2	0.924220	0.915774	0.913519
	3	0.905575	0.909956	0.914697
GDELT	1	0.892315	0.884865	0.895266
	2	0.900982	0.885409	0.906563
	3	0.900174	0.884908	0.893185

.

From Table 6, it can be observed that when using the NOAA dataset, the average accuracy of TE-LSTM is 0.916434, TFT is 0.912098, and Informer is 0.914771, with TE-LSTM showing the highest accuracy. When using the GDELT dataset, the average accuracy of TE-LSTM is 0.897824, TFT is 0.885061, and Informer is 0.898338, with Informer achieving the highest accuracy. TE-LSTM’s accuracy is 0.051433% lower than Informer’s. TE-LSTM is more suitable for datasets that exhibit regularity and simplicity. For datasets characterized by higher randomness and more complex patterns, traditional LSTM architectures and their variants tend to perform worse than Transformer architectures and their variants. This is because Transformers have a stronger capacity to capture long-range dependencies compared to LSTM. Due to its recursive nature, LSTM is more adept at capturing short-term dependencies and local patterns, such as trends and periodicity, which also explains why TE-LSTM outperforms Informer on datasets with certain periodic patterns. The GDELT dataset, with its high degree of randomness and weak local patterns, requires the ability to capture patterns over a longer time span. Therefore, Informer, with its superior ability to capture long-range dependencies, achieves the highest accuracy. However, across both datasets, TE-LSTM consistently outperforms TFT, indicating the effectiveness of TE-LSTM’s weighting strategy.

We also compare the ability of these three models to answer time-specific prediction questions, and the results are presented in

Table 7. The results of TE-LSTM and SOTA methods in predicting questions with specific times.

Dataset	X (G = 1)	TE_LSTM	TFT	Informer
NOAA	1	0.919506	0.910564	0.916096
	2	0.919213	0.908343	0.908897
	3	0.917772	0.907987	0.908554
	5	0.917608	0.907001	0.907603
	10	0.913126	0.903486	0.899208
GDELT	1	0.892315	0.884865	0.895266
	2	0.891979	0.884836	0.893274
	3	0.891608	0.884774	0.892185
	5	0.891640	0.884780	0.890133
	10	0.891354	0.884597	0.888894

. Neither the TFT nor Informer methods take into account the distance relationship between each time step in the time series and the target time to be predicted. When using a pre-trained model with X = 1 and G = 1 data to predict different positions, the model cannot adaptively adjust based on the predicted target time. As the predicted position increases, the model’s accuracy continues to decline, and the rate of decline is relatively rapid. TE-LSTM, on the other hand, uses the time weights of each time step and the predicted target time, instead of relying solely on the time sequence, which directly impacts the prediction results. This allows the model to make adaptive predictions based on the predicted target time, even when the predicted position changes. As a result, even if TE-LSTM’s pre-training accuracy is initially lower than Informer’s, its accuracy ultimately surpasses Informer’s as the predicted position increases. This demonstrates the effectiveness of the time-weighting method proposed via TE-LSTM, showcasing its superior performance in addressing time prediction problems with clear temporal constraints.

TE-LSTM uses LSTM as the base model and integrates time information into the prediction process, ultimately improving prediction accuracy. The model is not combined with other methods and has a relatively simple architecture. However, it is precisely this characteristic that allows TE-LSTM to be applied across all LSTM variant models. TE-LSTM can directly replace the LSTM module in these variants. In this study, we selected TFT as the base model and replaced the original LSTM module in TFT with TE-LSTM to evaluate the performance of different LSTM architectures and their variants under TE-LSTM. The experimental results are presented in

Table 8. The results of TFT and TFT using TE-LSTM. TFT-TE represents TFT using TE-LSTM.

Dataset	X	TFT	TFT-TE
NOAA	1	0.910564	0.911570
	2	0.915774	0.916166
	3	0.909956	0.910908
GDELT	1	0.884865	0.885147
	2	0.885409	0.896496
	3	0.884908	0.885809

. After replacing the original LSTM module in TFT with TE-LSTM, a slight improvement in model accuracy was observed. This demonstrates TE-LSTM’s strong compatibility, as it can be integrated into any LSTM variant model to enhance prediction accuracy.

3.5. Discussion

In this study, we introduce an innovative multivariate time series data prediction model: TE-LSTM, an LSTM variant that considers the temporal evolution of entities. To address the limitations of existing models that do not fully utilize the time dimension, we designed multiple time encoding methods for comparative experiments to comprehensively extract temporal features. Additionally, to account for the relationship between the time of each element in the time series and the predicted target time, we developed a time-weighting strategy that calculates the weight between each element’s time and the predicted target time. This weight is then incorporated into each time step, replacing the original sequence order, enabling the model to handle prediction tasks with explicit temporal constraints. Our study primarily focuses on temperature prediction, and we also validated the model’s performance on non-periodic and complex datasets using the GDELT dataset.

To validate the effectiveness of TE-LSTM, we predicted targets at different positions and compared the performance of three time encoders, as shown in Table 2. TE-LSTM, based on LSTM, leverages LSTM’s recursive nature to capture local changes in the sequence. The ST (FFN) encoder, which captures the absolute position of time, focuses on global changes, balancing long- and short-term dependencies. This made it suitable for various datasets, as demonstrated by its strong performance across both datasets. On the other hand, the TI (FFN) encoder uses time intervals between each element in the series and the predicted target time, focusing on local changes and strengthening the capture of short-term dependencies. This led to its particularly strong performance on the NOAA dataset, which exhibits periodicity, but it had weaker performance on the GDELT dataset, which lacks such periodic structures.

In environmental and meteorological research, time granularities of hours, days, or larger intervals can reveal vastly different patterns of change. Coarser time granularity may obscure key precursor changes, while finer granularity may introduce excessive noise, making it difficult to identify long-term trends. After verifying TE-LSTM’s effectiveness, we further investigated the impact of temporal richness on the results. We employed multi-scale analysis methods, exploring a range of time granularities from coarse to fine. Our findings indicate that the ST (FFN) method exhibits a negative correlation with time granularity, where larger granularities result in lower model accuracy. Consequently, ST (FFN) is more appropriate for datasets with rich temporal information. Both TI (FFN) and ST (Time2Vec) effectively capture periodicity, but they are less suitable when temporal information is abundant. As temporal granularity increases, the performance of these two methods initially improves but then declines, reaching peak accuracy at an optimal granularity. Therefore, selecting the appropriate time granularity is crucial for their application.

We also assessed the model’s ability to address time-specific prediction questions by pre-training it using a dataset with fixed prediction locations and then applying this pre-trained model to predict targets at other locations. The experimental results demonstrate that as the number of predicted positions increases, the accuracy of the TE-LSTM model remains relatively stable, with only a gradual decline, as shown in Table 5. Moreover, the performance of TE-LSTM was further validated by comparing it with SOTA methods such as TFT and Informer, as shown in Table 6 and Table 7. While TE-LSTM proved to be more effective for datasets with certain regularities, such as NOAA data, its accuracy on more complex and irregular datasets was lower than that of Informer. This difference is attributable to the inherent characteristics of TE-LSTM, which is based on LSTM. However, these characteristics also give TE-LSTM strong compatibility and applicability, allowing it to be integrated into various LSTM-based models. In this study, we replaced the original LSTM module in TFT with TE-LSTM, resulting in improved prediction accuracy and confirming the model’s compatibility and scalability.

The ability of TE-LSTM to answer time-specific prediction questions makes it applicable to multiple fields. In meteorological forecasting, for instance, it can be used to predict changes in temperature, rainfall, wind speed, and other meteorological variables at specific time points. This capability is critical for natural disaster warnings, such as for typhoons and rainstorms, as well as for agricultural production planning. Similarly, in environmental monitoring and disaster management, precise time prediction can forecast the occurrence of natural disasters such as earthquakes, landslides, and floods. This improves emergency response efficiency, minimizes losses, and provides a scientific basis for the formulation of more targeted response strategies. Additionally, in logistics and supply chain management, accurate time prediction can optimize transportation routes and inventory management, ensuring goods are delivered at the optimal time, thus reducing logistics costs and enhancing operational efficiency.

This study also has certain limitations. First, we were unable to obtain long-term data on temperature-related indicators such as solar radiation, wind speed, and wind direction. This limitation has a slight impact on the accuracy of temperature modeling. In future research, we aim to expand the inclusion of these indicators to improve the accuracy of the model’s temperature prediction. Additionally, we were unable to find datasets with ultra-long time spans, such as those related to geological evolution, to validate the model’s applicability. Datasets of this type require extended time periods to reveal accurate patterns. Since this method is based on LSTM, which excels at capturing short-term dependencies due to its recursive nature, its performance on datasets requiring long-term dependencies remains uncertain. Further validation is needed to accurately determine the model’s scope of applicability in such cases. Second, the study did not propose a unified method for determining the most appropriate time granularity. In environmental, meteorological, or geological research, the choice of time granularity—whether hours, days, or longer intervals—can reveal vastly different patterns of change. The optimal time granularity varies across different fields and requirements. Therefore, establishing a recommended framework or standard for selecting the appropriate time granularity based on data characteristics, research objectives, and prior experience is necessary to minimize the uncertainty caused by arbitrary selection. Additionally, the model did not consider spatial location, which can also affect prediction outcomes. Incorporating spatial information to develop spatiotemporal prediction models would be a promising direction for future research.

4. Conclusions

This study introduced a precise time point prediction method called TE-LSTM, a variant of the LSTM model designed to capture the temporal evolution of entities and used for temperature forecasting based on multivariate time-series data. This method extracts temporal features from multivariate time series data, automatically emphasizing features that are closer to the predicted target time, thus enhancing both the accuracy and reliability of predictions. The goal of TE-LSTM is to address the challenge of accurately predicting temperature or events at specific and reliable time points. The main contributions of this study are as follows:

(a)

Multiple encoders were designed to account for both the periodic and non-periodic nature of time, enabling the comprehensive extraction of temporal features. Additionally, the study examines the applicable datasets and optimal time granularity for each encoder.

(b)

A novel time weighting strategy based on LSTM was developed, which integrates the weight of each element in the time series relative to the predicted target time at each step. This approach allows the model to focus on features that are temporally closer to the target, transforming the model from sequence-based prediction to time-based prediction, thereby achieving more precise time point forecasting.

(c)

TE-LSTM was compared with the base LSTM model and two SOTA methods. The results demonstrate that TE-LSTM outperforms these models in terms of prediction accuracy, particularly for tasks requiring precise time point predictions.

(d)

The TE-LSTM method was applied to other LSTM variants, effectively improving their prediction accuracy, thereby validating the robustness and generalization capability of the proposed approach. The study also tested TE-LSTM on more complex GDELT datasets, further confirming the model’s applicability and generalizability.

This method can be applied to natural disaster warning systems (such as typhoons and rainstorms), agricultural production planning, and other fields. Currently, the model primarily focuses on temporal predictions and lacks the integration of spatial dynamics, which are essential for comprehensive forecasting. Moreover, the method may encounter challenges when applied to complex, multi-faceted scenarios due to data sparsity or variability in environmental conditions. In future research, we aim to overcome these limitations by incorporating spatial dimensions into the prediction process. By integrating both spatial and temporal data, we aspire to achieve more accurate and reliable predictions. Additionally, expanding the method’s applicability to a broader range of fields and exploring its scalability across different regions will be key objectives in our ongoing research.