Abstract
Biodiversity is a characteristic of ecosystems that plays a crucial role in the study of their evolution, and to estimate it, the species of all plants need to be determined. In this study, we used Unmanned Aerial Vehicles to gather RGB images of mid-to-high-altitude ecosystems in the Zao mountains (Japan). All the data-collection missions took place in autumn so the plants present distinctive seasonal coloration. Patches from single trees and bushes were manually extracted from the collected orthomosaics. Subsequently, Deep Learning image-classification networks were used to automatically determine the species of each tree or bush and estimate biodiversity. Both Convolutional Neural Networks (CNNs) and Transformer-based models were considered (ResNet, RegNet, ConvNeXt, and SwinTransformer). To measure and estimate biodiversity, we relied on the Gini–Simpson Index, the Shannon–Wiener Index, and Species Richness. We present two separate scenarios for evaluating the readiness of the technology for practical use: the first scenario uses a subset of the data with five species and a testing set that has a very similar percentage of each species to those present in the training set. The models studied reach very high performances with over 99 Accuracy and 98 F1 Score (the harmonic mean of Precision and Recall) for image classification and biodiversity estimates under 1% error. The second scenario uses the full dataset with nine species and large variations in class balance between the training and testing datasets, which is often the case in practical use situations. The results in this case remained fairly high for Accuracy at 90.64% but dropped to 51.77% for F1 Score. The relatively low F1 Score value is partly due to a small number of misclassifications having a disproportionate impact in the final measure, but still, the large difference between the Accuracy and F1 Score highlights the complexity of finely evaluating the classification results of Deep Learning Networks. Even in this very challenging scenario, the biodiversity estimation remained with relatively small (6–14%) errors for the most detailed indices, showcasing the readiness of the technology for practical use.
1. Introduction
Changes in vegetation patterns often indicate environmental stressors such as climate change, pollution, or disturbances such as invasive species, wildfires, and insect or disease outbreaks. Remote sensing approaches continue to have a significant role in tackling the detection and characterization of these and other changes in vegetation dynamics [1]. Continuous assessments of large forested areas is a necessary step toward a comprehensive understanding of forest structure, composition, function, and health thorough their phenological characteristics [2,3], with the final goal of improving forest-management strategies via informed decision making [4,5]. In particular, the continuous assessment of aspects such as tree species diversity [6,7] via remote sensing provides valuable insights into the evolution of forest ecosystems that biodiversity field measurements (conducted by fieldwork or manual monitoring systems) cannot produce [8].
Satellite images provide observations with many time points [3] over large areas and frequently include multispectral data [9] that are ideal for the continuous monitoring of diverse aspects such as biomass estimation [10], biodiversity estimation [6,7], or tree species classification [11,12]. Complementing them, other imaging modalities such as Unmanned Aerial Vehicles (from now on UAVs) present different characteristics that make it possible to develop other types of research. In particular, UAVs are better suited for studies where a high level of detail is important, for example, when identifying individual plants is necessary. UAV surveys are much faster than fieldwork and increase their range by reaching into zones that are hazardous or difficult to access. In this sense, UAVs have the potential to provide monitoring possibilities in areas of tenths of hectares with a very high level of detail, which is beyond the reach of fieldwork in terms of area and of satellite imaging in terms of resolution. Understanding the capacities and limitations of the different image modalities and fieldwork along with the possibilities of using them together [13,14] is a crucial step toward truly comprehensive studies of forests’ ecosystem evolution.
In this work, we will focus on the possibility of using UAV-acquired RGB images to estimate biodiversity using indices that require the number of plants of every species. As UAV-acquired images contain very detailed spatial information, with every pixel frequently representing around one centimeter in real life, automatic processing methods that include expert Forest Science knowledge need to be developed to extract as much information as possible from them. This expert-guided processing is automated through a branch of Artificial Intelligence known as Deep Learning (from now on DL), which is becoming an increasingly popular tool in Forestry applications [15,16]. Of particular interest for the current study, this technology offers highly effective image classification [17] and object-detection capabilities with applications in both short-term and long-term ecological studies. Utilizing DL for this purpose provides significant advantages, such as saving time and labor, comprehensive monitoring at different time points using stored data and a combination of diverse data sources, and allowing for the monitoring of large-scale areas across different regions and ecosystems. For example, Deep Learning has been used in ecological studies for tasks such as assessing the presence of invasive species [18,19], tracking insect outbreaks [20,21,22], mapping plant species in high-elevation ecosystems such as the one we will focus on in this study [23,24], as well as studying biodiversity [25] or ecosystem evolution [26].
In this work, we expand on our previous study [23] where we used Deep Learning Networks, from now on DLNs, to classify the subalpine bushes of six different species, focusing on the difficulty of the task even for human experts and on the ways in which DLNs could improve the study of bush species distribution. In this work, we expand the research area and examine different tree and bush species with a focus on the study of the biodiversity in the site. Specifically, the connection between image classification and the use of its results to estimate biodiversity indices is explored in detail and new DLNs are considered, with special interest in the level of readiness of the technology for practical use. Figure 1 illustrates, from a high-level perspective, the research steps and order. The final part of the paper contains links to the data and code used in the paper, which are publicly available.
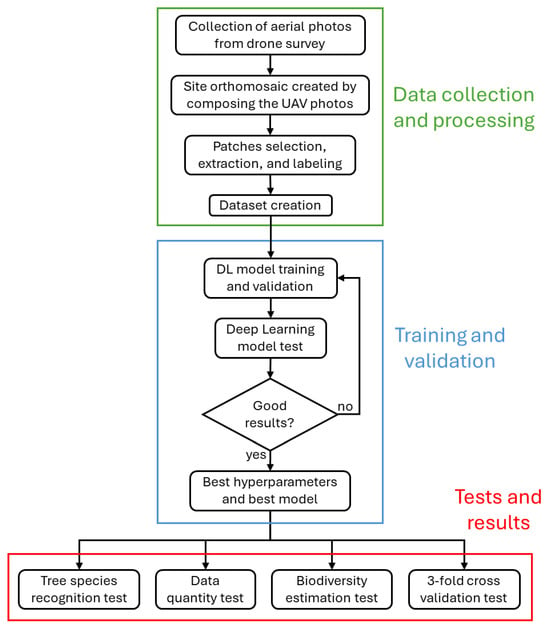
Figure 1.
Summary of all the tasks carried out during the course of this study. They are divided into three main categories: data collection and processing (green), model training (light blue), and experiments (red).
To sum up, the main goals of the current study are as follows:
- To determine the capacity of DLNs to classify images of the nine plant species considered. This includes comparing several state-of-the-art networks with several hyperparameter combinations.
- To estimate the biodiversity of the collected data using three well-known metrics: the Gini–Simpson Index (), the Shannon–Wiener Index (), and Species Richness ().
- To evaluate the level of readiness of the technology presented for practical use, including a study on the effect that the number of training images has on validation Accuracy as well as a real-use case scenario.
2. Materials and Methods
2.1. Data-Related Issues
In this section, we provide details regarding data collection with special emphasis on how the biodiversity information was recorded and annotated.
2.1.1. Study Site
The region of interest for this study is located in the Zao mountains. This volcanic area straddles the borders of Miyagi and Yamagata Prefectures in the northeastern region of the largest island of Japan (Honshu). The study area extends for ∼ 20 Ha, with an altitude ranging from 1334 m to 1733 m, and it is divided into sites. Data (vegetation photos) were collected from sites 1, 2, 3, and 5 (Figure 2 and Figure 3).
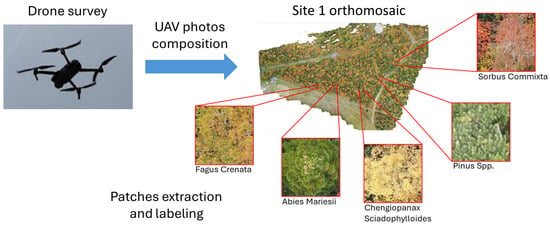
Figure 2.
Data-processing overview. Data were collected using UAV, from which orthomosaics for the four study sites were constructed. Trees and shrubs were annotated manually and then classified using Deep Learning Networks to estimate biodiversity. The figure shows one of the data-collection sites (site 1) with example images of species present.
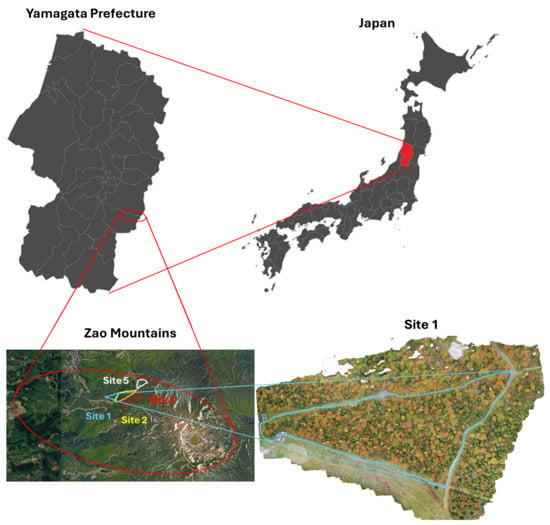
Figure 3.
Location of the four data-collection sites (Zao mountains, northeastern Japan). Expansion of Site 1 as an example (bottom-right image).
We considered the most commonly found tree and bush species in the environment with attention paid to their geographical distribution. For example, the experiment in Section 3.4 groups the plants from all species according to their geographical distribution in order to present a realistic use-case scenario where a team of researchers would train a DLN with plants from one data-collection site and then extend the study, using the trained model on a new site. Five of the species are the ones used in [23] (all of them with the exception of Sakura) and four new ones are added. We took advantage of the natural changes in vegetation coloration to make the problem of plant species classification less challenging: as the data collection in this study was performed exclusively in autumn, the plants are easier to classify than in the previous study, where both summer and autumn data were considered. We now present the names (Japanese, scientific, and English) of the nine species considered in this study along with a brief description of their appearance in autumn. Buna (Fagus crenata, Beech) is a deciduous tree species that presents large, round canopies and yellow coloration. Oshirabiso (Abies mariesii, Fir) is an evergreen conifer tree with a broadly conical canopy shape, branches that spread out horizontally from the trunk at different heights, and needle-like foliage. Koshiabura (Chengiopanax sciadophylloides, Koshiabura) is a small, deciduous tree with a very light yellow color and white flowers. Nanakamado (Sorbus commixta, Japanese Rowan) is a deciduous species, with a round or oval crown and red leaves. Matsu (Pinus spp., Pine) is an evergreen tree. The shape of its canopy is conical, similar to Fir, but the color is lighter, ranging from pale green to bluish green. Inutsuge (Ilex Crenata, Japanese Holly) is an evergreen bush with a relatively small and light green canopy and small, rounded leaves. Kyaraboku (Taxus cuspidata, Japanese Yew) is an evergreen species that can be found both as shrub or small tree and is dark green in color. It presents needle-shaped leaves and a crown with multiple layers. Minekaede (Acer tschonoskii, Butterfly Maple) is a deciduous species of shrub or small tree with yellow leaves and shrubs that grow close to one another and cover areas in which it is difficult to distinguish individual plants. Mizuki (Cornus controversa, Wedding Cake Tree) is a small deciduous tree with a round canopy, yellow–green in color. Figure 2 shows one of the four data-collection sites with examples of 5 species present in it. The plants described have different altitude intervals at which they are more concentrated and limits outside of which they are infrequently found.
Fir (Abies mariesii) covers about 87% of the area and can be found in both pure and mixed forests. The other most abundant tree species in the region are Fagus crenata, Acer japonicum, Ilex crenata, Chengiopanax sciadophylloides, Taxus cuspidata, Pinus spp., Acer tschonoskii, Cornus controversa, Quercus crispula, and Sorbus commixta. So, coniferous and deciduous species are present, with an average density of ∼400 trees per hectare. It can also be seen empirically that species proportion, tree density, and the size of individual plants change in relation to altitude (Table 1).

Table 1.
Species distribution of the dataset. The light green background highlights a subset of data which contain patches only from five plant species and only from two sites. This smaller group of images is used for the controlled experiment and for the data-quantity test.
2.1.2. Data Collection
All data collection was achieved by UAV flights over the study sites, except for occasional field surveys to double-check the manual labeling of patches for particularly difficult cases. The images of the forest were acquired using a Mavic 2 Pro UAV (DJI, Shenzen, China) with a nadir-pointing camera. The camera the UAV was equipped with is a Hasselblad L1D-20c (Gothenburg, Sweden), which takes 20-megapixel RGB photos. The “following terrain” flight plan function was used in order to keep a constant altitude of 90 m. The reason for this is to keep the relative sizes of trees in images constant. To keep the exposure values between 0 and 0.7, and to provide a ground sampling distance of 1.5–2.1 cm/pixel, the following camera settings were used:
- S priority (ISO-100).
- Shutter speed at 1/80–1/120 s in the case of favorable conditions.
- Shutter speed at 1/240–1/320 s in the case of worse conditions (strong sun or wind).
- A 90% image overlap in each direction.
2.1.3. Data Preprocessing
The images collected were used to build orthomosaics (one for each site) using the Agisoft Metashape [27] software. The Forestry experts in our group selected representative areas of the orthomosaics and then manually marked all the visible plants on them by placing a point at the center of each tree or bush. We automatically selected square pixel patches centered at every marked point. This corresponds to m areas in reality (at ground level). Each patch was selected so that it contains only one tree or, when they are difficult to tell apart, at least only one plant species. Figure 4 shows examples of patch selection, where the two subfigures come from nearby zones and have the same total area. In Figure 4a, individual trees are easy to tell apart, and in Figure 4b, it is still possible to identify the different species present, but telling apart individual trees is challenging.

Figure 4.
Two enlargements from the same orthomosaic, from which patches have to be manually extracted. Depending on plant species and image condition, it can be very difficult to distinguish individual trees when many canopies of the same species are close together (b). In this case, it is enough if the patches only contain one species. (a) Easy to identify trees. (b) Individual trees are hard to tell apart, but it is possible to ensure they all contain only one species (red contour).
The total number of patches labeled was 8583, with a strongly imbalanced dataset that reflects the distribution of species in the site. For example, Fir trees represent 41% of the whole dataset; meanwhile, Matsu patches are only 1% of the total (Table 1). The chosen species exhibit quite different characteristics (shape, size, and color), especially in the autumn season. This results in an easier classification problem for DLNs when compared to the shrubs of the previous study [23].
For some of the experiments, we selected a subset of the data to restrict the number of species and have an easier-to-control scenario with which to evaluate the basic performance of Deep Learning Networks. This smaller dataset is composed of 5 species (Buna, Koshiabura, Kyaraboku, Matsu, and Nanakamado) and only with patches from sites 1 and 2 (Table 1, green cells).
The patches thus built were separated into training, validation, and test sets consisting of 80%, 10%, and 10% of the total patches, respectively. The patches in the training set were fed to all DLNs along with their correct category (in this case, the plant species). This information was used to iteratively adjust the parameters in each DLN model in a process known as training.
The validation set was also used during the training process to prevent the overfitting of the models and to evaluate their performance. Overfitting is an issue with DLN training that occurs when the DLN model becomes too close to the training data being used but deviates from the general problem. The validation dataset images are fed to the network but their correct categories are not, so they are not used to adjust the parameters of the model. If at any point the model keeps improving its performance with the training images but plateaus for the validation images, overfitting becomes a concern, and training is stopped. The best parameters were found by considering the performances obtained with the validation set. Afterward, the testing set was used.
The testing set aims at assessing the performance of the model with previously unseen data. Just like for the validation set, its images are passed through every trained model without giving the model the correct categories, so they are not used to modify the parameters of the model. The main difference from the validation set is that the test set is only used after the training process is over and the best parameters of the model are set. The training process of DLNs is controlled and regulated through the use of training hyperparameters (the learning rate, number of epochs…). They differ from the parameters (or weights) in that they are manually set before training, not learned from data. Many combinations of hyperparameters are used to train different models, and the validation set is used to select the best combination, which results in the best model. The test set is only used after this selection to asses the best model performance.
Data Augmentation
As the number of parameters in DLNs is very high, the amount of data needed to train them is also large. Data augmentation is a commonly used technique aimed at slightly modifying the original data to obtain more training data. This procedure is primarily used to increase the available training data, but it also has the benefits of improving the models’ generalization capabilities and reducing the risk of overfitting. Simple image transformations such as rotations or small modifications in pixel intensity are applied to create realistic images that simulate different lighting conditions, new perspectives, etc. As the images thus created are artificial, it is important that the validation and test images are not augmented. Using augmented testing images would reduce the difficulty of the problem and thus overestimate the practical performance of the models trained.
In our case, the training patches underwent eight transformations with a 50% chance each (horizontal and vertical flip, rotations of 90, 180, or 270 degrees) or random small perturbations of the pixel values. Additionally, the patches in the training set are shuffled randomly at the beginning of training. Consequently, every time we train a DLN, the result has a random component. For this reason, when possible, the experiments are conducted multiple times, and we present and discuss the average of the results obtained to mitigate the effects of randomness. The discussion in Section 3 also includes comments on the variations between different training instances of the same model.
The total number of patches labeled was 8583 and the training set is always 80%. This means that for every training session, patches are extracted randomly. Since the best configuration uses a “data augmentation” value of 13 (see Section 3.1), models trained with those hyperparameters would use a training set of patches.
2.1.4. Biodiversity Data
We used eleven square plots, about 50 m on the side and situated at increasing altitudes, to assess changes in biodiversity by exhaustively tracking all trees and bushes. For each plot, all trees of the five selected species were manually marked and counted, and patches were extracted from them.
2.2. Deep Learning Networks for Species Classification and Biodiversity Estimation
This section provides details on the approach used for image classification and how its results were used for biodiversity estimation.
2.2.1. Tree-Species-Classification Task
The problem of image classification appears in many applied research areas, with DLNs being a very widespread option. Most popular among those are Convolutional Neural Networks (CNNs) [28]. These networks are very efficient at image-classification tasks and are responsible for the current popularity and success of Artificial Intelligence approaches (usually in its Deep Learning subcategory). Within the same research area, Transformer Networks [29], initially developed for natural language processing, have recently been adapted to image-processing tasks and are close to the performance of CNNs. As many models exist, it is not possible to anticipate their performance for every application. However, some indications can be extracted from the performance of the models in general-purpose image-classification benchmarks such as ImageNet [30], a database containing more than 14 million manually annotated images and over 20,000 classes. Considering all these factors as well as recent papers in drone-acquired Forestry image classification, the following four models were chosen:
- ResNet “Deep Residual Learning for Image Recognition” [31].
- RegNet “Designing Network Design Spaces” [32].
- ConvNeXt “A ConvNet for the 2020s” [33].
- SwinTransformer “Swin Transformer: Hierarchical Vision Transformer using Shifted Windows” [34,35].
ResNet, RegNet, and ConvNext are CNNs which have been used recently for a variety of UAV-acquired image-classification tasks in Forestry [16]. ResNet is slightly older but still widely popular and has obtained good results in classifying some of the species in the current study in [21,22,36]. RegNet and ConvNext are newer CNNs that have also obtained good results in related tasks [23,37,38]. The Swin network belongs to the Transformer family and has performed at the level of previous CNNs, for example in [23].
Transfer Learning
State-of-the-art image-classification models are large in the sense that they have a huge number of parameters; for example, the small version of Swin has 28 million weights. Training images are used to set the best values for these parameters. However, if the number of training images is too low, the models may underperform. To prevent this situation, the parameters of the model are initialized by copying the weights of a model trained for a “similar” classification task. This is a technique known as transfer learning [39,40]. First, a model is trained using a task that is considered “similar” and for which enough data are available. Then, the resulting parameters are used as the starting point for the training of the model with the (fewer) training images in the actual problem of interest. Often, the ImageNet dataset is used as the starting point. In some cases, transfer learning can be used repeatedly to progressively adapt from a more general problem to increasingly specific ones. See [41] for an example in Forestry.
The final step is often referred to as fine-tuning the model [42]. The main motivation here is that the classes in the larger (ImageNet in our case) dataset already contain some of the general features needed to classify the images in the smaller problem. The fine-tuning step is then dedicated to adapting the parameters to the particular characteristics of the smaller problem as well as changing structural parameters in the network such as the number of output classes, 9 in our case and 20,000 for ImageNet (Figure 5). Sometimes fine-tuning is performed on frozen networks, where all the parameters of the model except for the final (decision) layer are left unchanged and only the final layer is updated. In our case, better results were obtained by starting from the parameters obtained by pretraining on ImageNet and updating all the parameters in the model (in DL terminology, all models were fine-tuned with all their layers unfrozen).
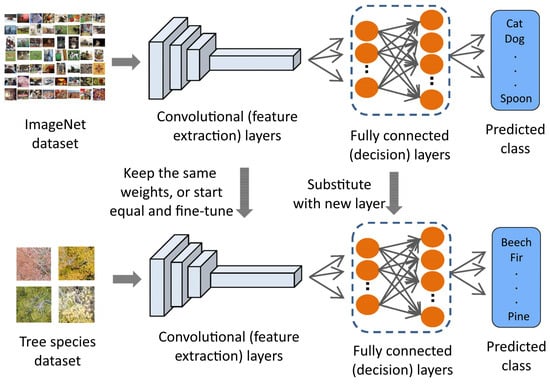
Figure 5.
Example of transfer learning and fine-tuning. An NN is trained with a very big generic dataset, ImageNet in this case (above). It is subsequently adapted to a new task by training on a small, specific dataset (below). Adapted from [43].
Setup for Finding the Best Model
Regardless of whether transfer learning is used, training DLNs is an iterative process that has a random component due to data shuffling and to the random nature of the data-augmentation algorithms that we used. Consequently, every time a model is trained, slightly different results are obtained. Frequently, the optimizer algorithm that guides the training process produces larger parameter variations in the initial steps to avoid local extremes. In problems such as the current one, where class distribution is uneven, this can bias the resulting model toward or away from the smaller classes.
For all the experiments in this paper, data augmentation was applied only for the training images. Then, the validation images were used during the training process to detect possible overfitting. The validation set was also used at the end of the training phase to choose the best among all the models trained.
For each architecture considered, an automatic procedure trained and tested a large number of hyperparameter values. This procedure had two steps. First, a “coarse” step, and then a second “fine” step where smaller variations were tested among the values obtaining the best results in the previous step. After this procedure, we decided to use the following hyperparameter values for all the architectures. The hyperparameters selected were 20 training epochs with an Adam optimizer, a learning rate of , and a Weight Decay of . Each image in the training set was augmented 13 times and no rebalancing between the different classes was performed. All the layers in all the models were retrained (unfrozen). After training was finished, the selected model was evaluated on the testing set, ensuring that the testing set had no influence on the training process.
Setup for Data-Quantity Test
In this section, we deal with the issue of how many data are necessary to effectively train a DLN. We considered the often-used situation where we started from DLNs with ImageNet weights, and we intended to retrain all their layers (unfrozen). We start with the same dataset as in the previous section, 5315 patches from five different classes (Table 1, green cells). This is a rather large number that may not be reachable in some studies. To assess the impact that the amount of available data had on the performance of DLNs, we used the Swin Transformer architecture and hyperparameters set that had obtained the best results in the previous test and retrained it using subsets of our image dataset.
Setup for Use-Case Test
In this section, we present an experiment aimed at evaluating the performance of the Swin Transformer Network (tiny version), which obtained the best results in the previous experiments, in a realistic scenario. While the dataset used in the previous section presented some difficulties such as a strong class imbalance, it could not be considered a test for real applications. The number of species considered was relatively low; the training, validation, and test sets had very similar class proportions due to the random partitioning of the data; and aspects such as data-collection season, data-collection area, lighting conditions, and camera settings during acquisitions were constant, limiting the variability expected in real-use situations.
Specifically, we considered all the data available (with 4 sites and 9 tree species (Table 1)) and broke them down into three sites (original sites 1, 2, and the combination of 3 and 5) and set up a 3-fold cross-testing experiment. In the first fold, site 1 was used for testing and sites 2, 3, and 5 for training. In the second fold, site 2 was used for testing and sites 1, 3, and 5 for training, and in the third fold, sites 3 and 5 were used for testing and sites 1 and 2 were used for training. The class balance between the 3 testing folds and from the training set to the testing set within every fold varied greatly, as can be seen in Table 1. For the sake of brevity, we made one single run with the Swin model for every fold.
2.2.2. Biodiversity Estimation
Biodiversity is a crucial indicator when studying forests. In this study, we used the results of our image-classification DLNs to estimate biodiversity. After the images from one particular site were automatically classified, we could then use one of the existing indices to compute biodiversity based on our automatic species classification. The algorithm calculates the biodiversity using a set of input images so they should cover the area being studied or be a representative sample. For each of the eleven biodiversity plots used, the species for all patches on the plots were predicted and the biodiversity indices were estimated using these predictions. Then, the expert annotations for the plots were used to compute the correct values for the biodiversity indices and compare them to the estimations. The indices that we used to measure biodiversity are as follows:
- Species Richness () [44], which stands for the number of different species represented in an ecological community.
- The Shannon–Wiener Index () [45], which stands for the uncertainty in predicting the species identity of an individual that is taken at random from the dataset. Higher values of this index thus represent higher biodiversity. See Equation (1):where is the ratio of trees of species i within the dataset: , with number of individuals of species i. Values between 1.5 and 3.5 are commonly considered as “high biodiversity”.
- The Gini–Simpson Index () [46], which is known in ecology as the probability of inter-specific encounters or the probability that two random trees in the dataset have different species. See Equation (2):This value ranges from 0 to 1, with higher values (closer to 1) representing higher biodiversity.
Setup for Biodiversity-Estimation Test
Biodiversity was calculated based on the same dataset as in Section 3.1 and using the three following metrics (the Gini–Simpson Index: , Shannon–Wiener Index: , and Species Richness: ) for each of the eleven plots considered. The three metrics are calculated using plant species count and the number of trees and shrubs of each species, so the ground truth was computed using manual counts. Additionally, the best-trained DLN model from Section 3.1 was also used to estimate biodiversity. In the reference plots, one patch was extracted for every existing tree and then classified and used to estimate the biodiversity indices.
2.2.3. Evaluation Metrics
Evaluating the results of Deep Learning models is a complex task as even though the training of DLNs is a process determined by a set of clearly defined metrics, the final goal of any trained model is to solve a practical problem. In applications with uneven class distribution, defining a “good performance” is often a nuanced issue. In particular, some metrics like Accuracy, defined as the percentage of correctly classified patches (), gives a good overall feel for the performance of DLNs. However, in applications where less-frequent classes are important, class-based metrics like Precision, Recall, and F1 Score [47,48] are better suited for the task. In particular, we consider the unweighted averages of class-wise metrics and we scale them from to percentages to make them easier to visualize along with Accuracy. These metrics are defined as follows:
n is the total number of different species and is the species index. (True Positives for species m) are elements of species m that are rightfully identified by the model. (False Negatives for species m) are elements of species m that are identified as a different, and thus incorrect, species. (True Negatives for species m) are elements that do not belong to species m and are correctly predicted as belonging to a different species. (False Positives for species m) are elements that do not belong to species m and are incorrectly identified as belonging to species m. These metrics consider each class as equally important, regardless of the number of its elements. This helps with detecting classification errors of underrepresented classes in imbalanced datasets. Notice that during the training process, these classes tend to have a smaller impact as the most commonly used loss functions are general-purpose and do not target specific classes but are global in nature. Finally, to provide as much insight as possible into the trained models, we also show confusion matrices [49] that indicate the number of elements predicted to be (x-axis) and actually belonging to each class (y-axis). These matrices are very helpful visual representations of the elements that were correctly classified (in the matrix diagonal) and of the mistakes made by the model (elements outside the diagonal) together with the classes that were confused.
3. Results
In this section, we evaluate the performance of DLNs for image classification and biodiversity estimation, first in a controlled scenario in terms of class balance in the data and then using a realistic use case.
3.1. Finding the Best Model
In this section, we aimed at finding the model that performed best at the task of classifying images of the five species considered when the training and testing sets contain a similar class distribution. The training, validation, and testing sets were all chosen randomly from the reduced dataset, which only uses sites 1 and 2 and five tree species (the green cells of Table 1). To minimize the effects of randomness in training, each type of model (architecture) was trained and tested 10 times for each hyperparameter combination.
The test set results are presented for all the architectures considered: First, Table 2 shows the mean, standard deviation, and confidence interval (95% confidence) for each group of the ten runs performed. Subsequently, Figure 6 provides a graphical summary by focusing on the F1 Score metric (the best and average values). Finally, Table 3 includes the top results for all the metrics.

Table 2.
Model comparison results on the test set. Mean, standard deviation (std), and confidence interval (ci) are shown for each metric. The values are calculated by running the same setup 10 times.
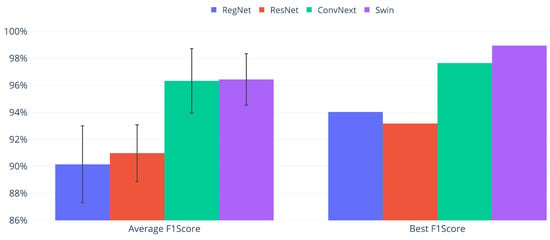
Figure 6.
Model comparison summary on the test set. Only average and best F1 Scores are displayed for each architecture. The confidence intervals are shown as error bars for the average F1 Score values.

Table 3.
Results of the best run (out of ten) for each architecture on the test set.
All the architectures considered are available with fewer or more layers and thus configurable parameters. The more challenging a task is, the larger a model needs to be to tackle it. Using larger models, however, requires more computation time and training data, and is more likely to produce overfitting, a phenomenon observed when models fail to capture the general features of the problem that the training images represent but can still provide the correct response for them, leading to poor practical performance. In our experiments, the best results were obtained by the smallest versions of the networks, so those are the ones included in this section.
All the architectures classified the five species satisfactorily, as exemplified by the Accuracy and F1 Score metrics close to or over 90% for both the best and average values. The results were consistent across the architectures and hyperparameter values tested, always within % of the average. Moreover, cases where a model failed to learn (Accuracy ∼, as expected from random predictions) were never observed.
Swin in its “tiny” version had the best overall performance, but ConvNext [33] produced virtually the same results, as the approximately 1% differences observed for best and average values in favor of Swin are smaller than their confidence intervals. ResNet and RegNet obtained slightly lower values, as visualized in Figure 6. Both presented a decrease of 9% for the average and 5% for the top F1 Score compared to Swin, while their Accuracy values were much closer to those of Swin, presenting a decrease of approximately 1.5%. This reflects an outstanding global performance with some problems classifying the smaller classes.
Regarding the statistical significance of the results, there are two groups of confidence intervals: Swin/ConvNext and ResNet/RegNet. While the confidence intervals of each pair overlap, showing no statistically significant difference in their performance, the two groups are clearly separated. Consequently, Swin and ConvNext perform equivalently and are better than the ResNet/RegNet pair at the 95% confidence level.
Swin has the overall top average and best values, and subsequently, we will focus the rest of the analysis on it. Taking practical use into account, we consider the peak result the most relevant. Since training is relatively fast, obtaining the best possible model for repeated use can be done by training many of them and selecting the best one. Even though this effectively increases the training time, it is a one-time endeavor that may be considered. In this case, the repeated training of the Swin network resulted in a 1.82% increase in the F1 Score, reflective of a marginally better performance for the smaller classes. This performance is best expressed in the confusion matrix, in the left part of Figure 7, while its right side presents the values of the metrics for the same matrix.
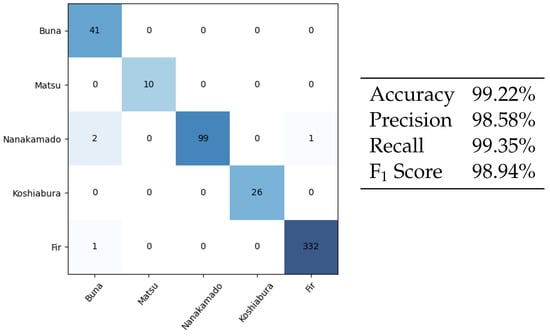
Figure 7.
Species classification confusion matrix (left) and classification metrics (right). These are results obtained with the test set, which the model never saw before. The rows of the matrix correspond to true labels, columns correspond to predicted labels. For example, the first cell in the Nanakamado row contains “2”. This means that 2 patches containing Nanakamado (true label) were classified as Buna (predicted label).
Notice how the number of misclassified images is very low: 4/512 for a 0.78% error. In total, three out of the four errors involve the Nanakamado species (Sorbus commixta) being confused with another class (Buna twice and Fir once).
In summary, the four networks studied obtained high Accuracy results, reaching 99.22% for Swin [45] and ConvNext [33]. The results are robust in the sense that even the average of ten executions was close to or over 98% for the four studied networks. The F1 Score values, defined to give more weight to the misclassification of less-frequent classes, were also very high with average values close to or over 90% for all the studied networks.
3.2. Data-Quantity Test
Figure 8 presents the results obtained with progressively smaller datasets. As the distribution of classes is uneven, we also used the reduction in the size of the training dataset to rebalance the training dataset. The species with the lowest number of patches is Matsu with 65 images, so the same number of patches from the other classes was selected and used to create a dataset of patches on the first reduced training step. Subsequently, five images from each class were removed at every step, maintaining smaller but balanced datasets. Every step was run five times to limit the influence of randomness in the final results, which is the average of the five training instances. As in the previous experiments, the training data are 80% of the reduced dataset (the first row of the x-axis labels, Figure 8), while the validation and test data are both 10% of the reduced dataset. Consequently, for this experiment, the training and test sets had the same balanced distribution of classes. In this setting, values over 90% on all metrics were achieved even with as few as 20 images per class (120/150 column). This is how, in this limited scenario, the Swin network was able to separate the five classes. From then on, the performance degraded rapidly, first for some of the classes as exemplified by the total Accuracy value lingering over 90% except for the final step and the rapidly decreasing values of the other metrics. These results showcase the capacity of DLNs to tackle new image-classification tasks even with very limited data to learn from.
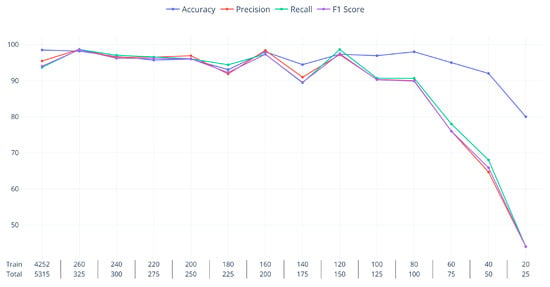
Figure 8.
The plot displays the performance of species-classification NNs on the test set. Each model is trained on progressively smaller datasets. The “Total” label indicates the number of patches that compose the current dataset, and the “Train” label is number of patches effectively used for training (80% of total).
3.3. Biodiversity-Estimation Test
Table 4 presents the comparison between the ground truth and estimated values for the three biodiversity indices in the eleven plots considered. Figure 9 depicts the differences between the estimated and real values for the Gini–Simpson and Shannon–Wiener biodiversity Indices.

Table 4.
Results of the biodiversity-estimation experiment on the biodiversity plots (see Section 2.1.4). For each of the 11 plots, the real value of the 3 biodiversity indices is shown alongside the one estimated by the algorithm.
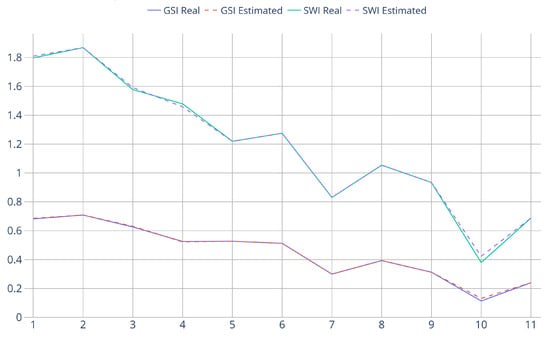
Figure 9.
Graphical representation of Table 4. X-axis indices represent the plots’ numbers. Y-axis is the metrics’ values (for all indices, higher values correspond to more biodiversity). Since the plots are chosen to be roughly increasing in altitude, the plot also represents the change in biodiversity depending on terrain elevation.
All biodiversity metrics rely on the number of trees from every species as predicted by the model trained. Consequently, it is possible for subsequent prediction errors to cancel each other out. Taking this into account, as well as the very high classification performance of the Swin model, for this controlled scenario, the biodiversity predictions were extremely close to the real values. Precisely, the number of species was correctly estimated for the 11 plots. For the and , exact values were obtained for 7 of the 11 plots, and their average real values are (0.449, 1.191), which are very close to the estimated average values (0.451, 1.194). Consequently, infrequent prediction errors resulted in a small overestimation of biodiversity in the 0.001 range. Both the ground truth and the estimated values show how, as expected, biodiversity decreases slightly as the altitude increases.
3.4. Use-Case Test
Table 5 and Figure 10 present the results of this experiment. The Table contains the details of the biodiversity and image-classification metrics for both the validation set (selected randomly as 10% of the training data) and the test set defined by the leave-one-out strategy. We provide the two sets of results to highlight the impact that class-distribution differences and origin in physically separate sites have on the performance of the model. The validation images present the same class balance as the training images and come from the same locations, acting as a baseline value. The testing images come from a separate site and present different class balances, providing us with insight into the performance of the model in real-use cases. We present the biodiversity index values as well as image-classification metrics. The confusion matrices presented provide granular insight into the sources of misclassification.

Table 5.
Results for the leave-one-out 3-fold cross-testing experiment. The upper section contains baseline results from the validation set, with a class balance similar to the training set. The lower section contains the proper results of the experiment from the test set. In this last case, class distribution between the training and test set varies significantly. The first three rows contain real and estimated values for the biodiversity metrics while the last two contain image-classification metrics.
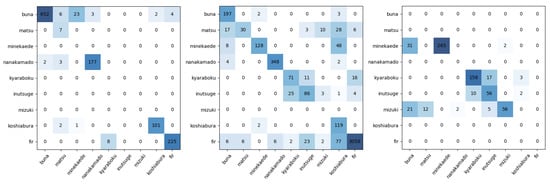
Figure 10.
Confusion matrices for the test sets of the leave-one-out 3-fold cross-testing experiment (fold 1 left, fold 2 center, and fold 3 right). Rows: true labels, columns: predicted labels.
On the one hand, the validation results are close to what we observed for the controlled-scenario experiment presented in Section 3.1. Specifically, the 97.83% average Accuracy value observed here is 1.36% lower than the 99.19% average Accuracy observed in Section 3.1. This small decrease is likely due to the fact that the current problem has more classes (nine compared to five previously), including some that are difficult to tell apart. This behavior is slightly more pronounced for the F1 Score with a 2.13% decrease from 97.12% to 94.00% here. The Swin model can thus classify the nine classes used in this experiment with high Accuracy in the “best case scenario” when the balance of classes is constant.
However, when the class balance differs between training and testing, the average Accuracy value drops by 7.19% to 90.64%. This is a clear decrease in the total Accuracy that is compounded by a severe reduction of over 40% in the average F1 Score down to 51.77%. This last value is slightly misleading. Ostensibly, 90% of the images are correctly predicted, and while there are problems with the smaller classes, the low number of images of some species in some of the folds results in a disproportionate effect on the F1 Score value. This happens because the F1 Score does not take into account the number of images in each class, but the overall performance of the class results in the missclassification of very few images. For example, the rightmost confusion matrix contains two cases of species not present (Koshiabura and Nanakamado) that were predicted a total of seven times. These mistaken predictions on roughly 1% of the images would have resulted in “0” F1 Scores for the two classes, reducing the overall F1 Score by 25%.
Regarding the biodiversity indices, their values for the validation set also follow a similar tendency as those observed in Section 3.1 with slightly less accurate predictions that are still very close (a second or third decimal value) to the ground truth. Differences between the predicted and real values are larger for the test set. In terms of each metric, is predicted perfectly for the validation set in the three folds but accumulates noticeable errors in the test set. These errors are a direct consequence of the differences in class balance as DLNs have a bias toward predicting the most frequent classes in the training set for those images that they cannot predict with high probability. For folds 1 and 3 in the testing set, where not all possible images are present, the Swin network makes a small number of predictions of non-present classes that result in a clear deviation from true values. The metric accumulates an average estimation error of around 6% of the real (0.5789) value, overestimating the index up to 0.619. The is also overestimated by approximately 14% of the original 1.6701 value up to 1.9087.
The confusion matrices presented in Figure 10 provide a granular view of the mistakes made by the Swin network. On the one hand, a large majority of the patches are correctly classified, as attested by the aforementioned 90% average Accuracy. On the other hand, there are some mistakes, especially with smaller classes and with classes that are very similar to each other. The former issue can be observed in the misclassification of Matsu, Inustuge, and Koshiabura (and to a minor extent Buna, Mizuki, and Nanakamado) to the extremely dominant Fir class in fold 2. In this case, the Swin model likely has too few examples to confidently predict the more difficult cases of the less-frequent species and is biased toward the dominant species. The main example of the latter effect is the confusion between Kyaraboku and Inutsuge that can be seen in folds 2 and 3.
The results clearly showcase the importance of the definition of the training sets for practical application as the class proportions between each of the training and testing sets were very different. The baseline results corresponding to the validation sets of this experiment presented in Table 5 showed how the Swin network was also able to achieve very high results, albeit slightly lower than for the previous problem (a 97.83% average Accuracy and 94.99% average F1 Score). However, once the testing set data were allowed to become more different from the training data, the values dropped notably to 90.64% and 51.77% for the same metrics. These values showcase a performance that is still very good in terms of image classification with under 10% errors for a much more challenging problem but also show some deficiencies, in particular in the classification of smaller classes. Figure 10 exemplifies issues such as the confusion between Kyaraboku and Inutsuge, which was also observed in [23], or the tendency toward overpredicting dominant classes.
Regarding the estimation of biodiversity metrics, the validation part of Table 5 shows that when the training and testing set have very similar class balances, the metric can be estimated without error and the and can be approximated with errors under 1%. When the training set is not as close to the balance of the testing set (Table 5, the test part), the and were estimated quite close to their actual value in the very challenging scenario used even if the estimation errors grew to 6% and 14%, respectively. On the other hand, the metric presented large deviations. Most of them were caused by wrong predictions of a very small number of images (see Figure 10). This could be addressed by modifying the metric to include a threshold, a minimum number of images that need to be classified as belonging to a species before it is considered as present in the site, or by asking users to validate the examples of extremely rare classes (23 images in the largest case in our experiment).
3.5. Hardware and Computational Time Considerations
Since we aim to provide a framework that is usable for practical applications, it is thus important to consider the requirements in terms of computational capacity and time. For this reason, we tested our code on different computers, and we present the results in Table 6. We show the results obtained by the best and worst computers that were tested. The upper half of the table lists the most relevant hardware specifications, while the lower half compares the duration of various tasks. A full dataset means that all the 8583 patches of Table 1 are used. Data preprocessing and augmentation consist of all the steps executed normally in our experiments to prepare the data, including the “standard” setting of 13X augmentation. Training time is the time needed to complete full training (including validation) of a new model. The last task is the time used by a trained model to examine 100 patches and give its response (the species of each patch).

Table 6.
Hardware specification of two computers that were used to run the experiments (top half). Time comparison for the most relevant operations (bottom half): preparing the dataset, training a model with the full dataset (Table 1), and examining 100 patches.
The difference between the two computers is evident; however, the slower Asus Zenbook is still able to complete training in under 1 day. This may seem like a long time, but training a model is not a routine activity, just a one-time endeavor in the beginning. Even in the case that more than one training session is planned to search for a better model, it is still a few days of waiting time for a DLN that can subsequently operate indefinitely.
The second consideration is about the faster MS-7E07 computer. While it is true that it is high-end equipment, this is relative to normal personal computers, and its market price is around 4600 euros. It is not comparable to specialized, multi-GPU supercomputers or entire data centers that are required by gigantic models like Chat GPT 4.
As a last note, we purposefully presented two extremes. A normal, GPU-equipped, desktop computer would cost less than the MS-7E07 and still have faster execution times than the Asus Zenbook. There are also other convenient alternatives; for example, the code can run on Colab Pro [50] without any problems for just 12 euros per month.
4. Discussion
In this study, we aimed at assessing the suitability of the combination of UAV-acquired images and image processing based on DLNs to estimate biodiversity. This type of study covers an area that is much larger than is possible for field studies, but small in terms of the monitoring studies performed using satellite imaging. At the same time, due to the very high gsd (1.5–2.1 cm/pixel), individual plants and even individual bush and tree branches are visible to experts and are processable by DLNs. This visual information is superior to what can be found in satellite imaging and close to what is observable in fieldwork (although some plant characteristics observable on the field, like tree trunks and leaves close to the ground, are obscured in UAV images due to the nadir-view aerial acquisition). Consequently, this type of study is complementary to existing approaches, and its main strength is that by using UAV-acquired images, we were able to consider information regarding individual trees and bushes in the study area rather than having to rely on interpolation as in large-area satellite-image-based studies [6,7] or in the extrapolation required in fieldwork after sample collection.
After collecting orthomosaics using UAVs and manually marking the locations of individual plants using single-point annotations, we classified images from individual plants using DLNs and then computed biodiversity indices from the automatic classifications. We compared the performance (in plant species classification) of different DLNs coupled with various hyperparameter combinations. Subsequently, we studied how the best-performing network transitions into practical use in biodiversity-estimation ecological studies. DLNs take advantage of the texture information present in high-spatial-resolution RGB images up to the point that they can tell apart bush and tree species, including accounting for some phenological changes and without needing information from non-visible (multispectral) channels, which is better than human experts [23]. In the current study, we first compared four DLNs, including the widely used ResNet network ([31], originally developed in 2014) and considered by us as a baseline for DLN image classification. In the first experiment in Section 3.1, five plant species’ Accuracy values reaching 99.22% were obtained by the best networks (Swin [45] and ConvNext [33]), but all the networks obtained high Accuracy values that were robust over repeated executions. The experiments with limited data in Section 3.2 showed how the best-performing DLN (Swin), thanks to the use of transfer learning, can perform image-classification tasks even with a very small training dataset. In Section 3.4, we aimed at assessing the level of readiness of the technology for use in practical applications. In a very challenging and realistic scenario, the comparison between validation results that maintain class balances and the test results (that do not) illustrates the need to carefully address the tricky problem of constructing representative training sets in practical applications. Nevertheless, the results obtained even in the worse cases still show Accuracy values over 90%, albeit with some problems in the classification of the smaller classes.
Concerning the comparison of our results to similar studies, first, it is important to note that the direct comparison of published numerical results is problematic due to differences in the evaluation methodology, the dataset particularities, and varying levels of difficulty, even in closely related problems. Nevertheless, some general tendencies can be observed. For example, it is clear that for studies such as this one, a very high spatial resolution is needed due to the small size of the plants being classified. In related research, satellite images have also been used to perform tasks related to biodiversity estimation, such as the estimation of the proportion of trees from different species in wide areas [6,13]; this is sometimes also in combination with Deep Learning Networks [51] but without the possibility of processing individual plants, which is required by the biodiversity indices that we use. Another common tendency refers to the correlation between the perception of human experts regarding the difficulty of a classification problem and the results obtained by DLNs. Even though humans and DLNs process images in fundamentally different ways, it is often the case that problems that appear simpler to experts also obtain better performances from DLNs. For example, ref. [19] reported a 98.10% classification Accuracy for a ResNet50 network when classifying an invasive blueberry species with salient purple coloration, and in [52,53], values of 77% (reaching 97.80% after post-processing) were reported when detecting a species of plant with bright white flowers. Following this trend, when the number of classes to be separated grows, the Accuracy percentages achieved by DLNs often decrease, as exemplified by the 90.64% reported in our experiment with nine classes. However, the most important factor in our experience is the variability within classes. The best example of this is the comparison between the current work and our previous study using data from some of the same data-collection sites in [23]. The current study considered more species in an equally realistic scenario as the previous work and used similar DLNs, but in the previous study, the data were acquired both in summer and autumn, increasing the variability within each class. As a result, the Accuracy achieved here in the most realistic scenario is about 20% higher than in the closest comparable scenario of the previous study.
The main goal of this paper was the estimation of biodiversity metrics, which, to the best of our knowledge, have not been estimated using UAV images and DLNs previously. Our results show that when the training and testing sets have very similar class balances, the metric can be estimated without error, and the and can be approximated with errors under 1%. These errors, while still probably within usable values for practical studies, grew to 6% for the and 14% for the when the training set deviated clearly from the testing set. This showcases the importance of defining data collection and study protocols for the creation of training datasets as representative of the problem that they aim to solve as possible. The estimation of obtained worse results in the more challenging case due to the mistaken predictions of a very small number of images. However, this could be addressed by simple adjustments (for example, a minimum number of patches necessary for a species to be considered present) in practical situations.
5. Conclusions
In this paper, we presented a method for biodiversity index estimation via semiautomatic UAV-acquired image classification. After data acquisition, the user would be asked to mark the trees in the sites manually for the algorithm to work and estimate the biodiversity. In our future work, we will consider the addition of further preprocessing steps for a fully automatic image-processing pipeline. Our results have shown how in ideal circumstances, DLNs can classify the images with an extremely low error rate and thus estimate biodiversity precisely. At the same time, we also showed how, in order to obtain optimal results in real-life use, an understanding of both the species being studied and the basics of DLNs is needed. In particular, it is always necessary to fine-tune the DLNs to be used for data from different species. Newer networks obtained small but noticeable improvements while the most important point was found to be creating a training set that is representative of the data that the network will be used on in practice. While achieving this is often not easy, our results have also shown how even with large variations in class distribution between training and testing sets, the and biodiversity indices can be estimated with a small degree of error, highlighting the readiness of the methodology for practical use.
Regarding possible future research directions, the current method is limited by the need to manually mark the position of bushes and trees. To overcome this, we will consider adding a “not vegetation” class and train with patches not specifically centered on plants as we did previously in [19,41]. The use of object-detection networks will also be considered. The current method was also shown to have problems with very small classes in the last experiment. To tackle this issue, we will improve the quality of the information gathered by considering multispectral data. At the same time, we will also consider how data-balancing techniques can improve biodiversity index estimation. Finally, we will continue to build on the work conducted in this and previous studies to collect data from all species during both summer and autumn to create a system that can continuously monitor vegetation throughout the year.
Author Contributions
Conceptualization, M.C., N.T.C.T., Y.D. and M.L.L.C.; methodology, M.C., N.T.C.T., Y.D., A.V. and M.L.L.C.; software, M.C., N.T.C.T. and Y.D.; validation, M.C., N.T.C.T., Y.D. and M.L.L.C.; formal analysis, M.C., Y.D. and A.V.; investigation, M.C., N.T.C.T., Y.D. and M.L.L.C.; resources, Y.D., A.S. and M.L.L.C.; data curation, M.C., N.T.C.T. and Y.D.; writing—original draft preparation, M.C. and Y.D.; writing—review and editing, M.C., N.T.C.T., Y.D., A.V. and M.L.L.C.; visualization, M.C., Y.D. and A.V.; supervision, Y.D., A.S. and M.L.L.C.; project administration, A.S. and M.L.L.C.; funding acquisition, A.S. and M.L.L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The code is available at the GitHub repository https://github.com/marco-conciatori-public/tree_classification (last access on 9 July 2024). It can also be experimented with online (no installation or setup required) on Google Colab [50] at the following link: https://colab.research.google.com/drive/1Pe9zkwzts3JIi80xxRfrBa-2Pqe87FlK (last access on 1 July 2024). The versions of ResNet, RegNet, ConvNeXt, and Swin Transformer pretrained on ImageNet are downloaded from Torchvision (https://pytorch.org/vision/stable/index.html, last access on 15 September 2024), a PyTorch (https://pytorch.org/) library. The data used for training, validation, and testing can be downloaded from this Dropbox link: https://www.dropbox.com/scl/fo/q532q2irrb5jv35s5it6h/APmTURD6u-dssLm6lKqpjHY/10Species?rlkey=ntuy2ph8sdg5mtttnk5v8339x&subfolder_nav_tracking=1&st=2c7zltbd&dl=0. Biodiversity plots and the patches extracted from them can be, respectively, found at these links: https://www.dropbox.com/scl/fo/q532q2irrb5jv35s5it6h/ADK4_e2AfV94bjtnAXCKmp4/Zao_sites_1-2/whole_plots?rlkey=ntuy2ph8sdg5mtttnk5v8339x&subfolder_nav_tracking=1&st=kngvj1c6&dl=0 and https://www.dropbox.com/scl/fo/q532q2irrb5jv35s5it6h/APopYIbmq_LRZiJrojWPx1A/Zao_sites_1-2/biodiversity_test?rlkey=ntuy2ph8sdg5mtttnk5v8339x&subfolder_nav_tracking=1&st=10n2f7pl&dl=0 Finally, a few of the best models obtained are also available for download from Dropbox: https://www.dropbox.com/scl/fo/q532q2irrb5jv35s5it6h/ABGd_YH3QKAs2Eb9LuQed00/models?rlkey=ntuy2ph8sdg5mtttnk5v8339x&subfolder_nav_tracking=1&st=yvz8n208&dl=0. All Dropbox links lastly accessed on 15 September 2024. The Neural Networks are pretrained Torchvision models, fine-tuned on the small dataset (Table 1, green cells). Each model consists of two files: the weights along with other necessary information, and a json file that contains the hyperparameters used and results obtained (each training epoch and test evaluation). The best model discussed in Section 3.1 is “swin_t_Weights-Swin_T_Weights.DEFAULT-2.pt”.
Acknowledgments
We would like to thank the members of the Smart Forest Laboratory (Lopez Lab) for their help during fieldwork and data collection.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Beck, P.S.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote. Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Jeganathan, C.; Dash, J.; Atzberger, C. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote. Sens. Environ. 2012, 123, 400–417. [Google Scholar] [CrossRef]
- Garioud, A.; Valero, S.; Giordano, S.; Mallet, C. Recurrent-based regression of Sentinel time series for continuous vegetation monitoring. Remote. Sens. Environ. 2021, 263, 112419. [Google Scholar] [CrossRef]
- Parisi, F.; Vangi, E.; Francini, S.; D’Amico, G.; Chirici, G.; Marchetti, M.; Lombardi, F.; Travaglini, D.; Ravera, S.; De Santis, E.; et al. Sentinel-2 time series analysis for monitoring multi-taxon biodiversity in mountain beech forests. Front. For. Glob. Chang. 2023, 6, 1020477. [Google Scholar] [CrossRef]
- Alterio, E.; Campagnaro, T.; Sallustio, L.; Burrascano, S.; Casella, L.; Sitzia, T. Forest management plans as data source for the assessment of the conservation status of European Union habitat types. Front. For. Glob. Chang. 2023, 5, 1069462. [Google Scholar] [CrossRef]
- Liu, X.; Frey, J.; Munteanu, C.; Still, N.; Koch, B. Mapping tree species diversity in temperate montane forests using Sentinel-1 and Sentinel-2 imagery and topography data. Remote. Sens. Environ. 2023, 292, 113576. [Google Scholar] [CrossRef]
- Rossi, C.; McMillan, N.A.; Schweizer, J.M.; Gholizadeh, H.; Groen, M.; Ioannidis, N.; Hauser, L.T. Parcel level temporal variance of remotely sensed spectral reflectance predicts plant diversity. Environ. Res. Lett. 2024, 19, 074023. [Google Scholar] [CrossRef]
- Madonsela, S.; Cho, M.A.; Ramoelo, A.; Mutanga, O.; Naidoo, L. Estimating tree species diversity in the savannah using NDVI and woody canopy cover. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 106–115. [Google Scholar] [CrossRef]
- Immitzer, M.; Neuwirth, M.; Böck, S.; Brenner, H.; Vuolo, F.; Atzberger, C. Optimal Input Features for Tree Species Classification in Central Europe Based on Multi-Temporal Sentinel-2 Data. Remote. Sens. 2019, 11, 2599. [Google Scholar] [CrossRef]
- Verrelst, J.; Halabuk, A.; Atzberger, C.; Hank, T.; Steinhauser, S.; Berger, K. A comprehensive survey on quantifying non-photosynthetic vegetation cover and biomass from imaging spectroscopy. Ecol. Indic. 2023, 155, 110911. [Google Scholar] [CrossRef]
- Lechner, M.; Dostálová, A.; Hollaus, M.; Atzberger, C.; Immitzer, M. Combination of Sentinel-1 and Sentinel-2 Data for Tree Species Classification in a Central European Biosphere Reserve. Remote. Sens. 2022, 14, 2687. [Google Scholar] [CrossRef]
- Yan, S.; Jing, L.; Wang, H. A New Individual Tree Species Recognition Method Based on a Convolutional Neural Network and High-Spatial Resolution Remote Sensing Imagery. Remote. Sens. 2021, 13, 479. [Google Scholar] [CrossRef]
- Wan, H.; Tang, Y.; Jing, L.; Li, H.; Qiu, F.; Wu, W. Tree Species Classification of Forest Stands Using Multisource Remote Sensing Data. Remote. Sens. 2021, 13, 144. [Google Scholar] [CrossRef]
- Iglseder, A.; Immitzer, M.; Dostálová, A.; Kasper, A.; Pfeifer, N.; Bauerhansl, C.; Schöttl, S.; Hollaus, M. The potential of combining satellite and airborne remote sensing data for habitat classification and monitoring in forest landscapes. Int. J. Appl. Earth Obs. Geoinf. 2023, 117, 103131. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote. Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Diez, Y.; Kentsch, S.; Fukuda, M.; Caceres, M.L.L.; Moritake, K.; Cabezas, M. Deep Learning in Forestry Using UAV-Acquired RGB Data: A Practical Review. Remote. Sens. 2021, 13, 2837. [Google Scholar] [CrossRef]
- Egli, S.; Höpke, M. CNN-Based Tree Species Classification Using High Resolution RGB Image Data from Automated UAV Observations. Remote. Sens. 2020, 12, 3892. [Google Scholar] [CrossRef]
- Kentsch, S.; Cabezas, M.; Tomhave, L.; Groß, J.; Burkhard, B.; Lopez Caceres, M.L.; Waki, K.; Diez, Y. Analysis of UAV-Acquired Wetland Orthomosaics Using GIS, Computer Vision, Computational Topology and Deep Learning. Sensors 2021, 21, 471. [Google Scholar] [CrossRef]
- Cabezas, M.; Kentsch, S.; Tomhave, L.; Gross, J.; Caceres, M.L.L.; Diez, Y. Detection of Invasive Species in Wetlands: Practical DL with Heavily Imbalanced Data. Remote. Sens. 2020, 12, 3431. [Google Scholar] [CrossRef]
- Dash, J.P.; Watt, M.S.; Pearse, G.D.; Heaphy, M.; Dungey, H.S. Assessing very high resolution UAV imagery for monitoring forest health during a simulated disease outbreak. ISPRS J. Photogramm. Remote. Sens. 2017, 131, 1–14. [Google Scholar] [CrossRef]
- Safonova, A.; Tabik, S.; Alcaraz-Segura, D.; Rubtsov, A.; Maglinets, Y.; Herrera, F. Detection of fir trees (Abies sibirica) damaged by the bark beetle in unmanned aerial vehicle images with deep learning. Remote. Sens. 2019, 11, 643. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Lopez Caceres, M.L.; Moritake, K.; Kentsch, S.; Shu, H.; Diez, Y. Individual Sick Fir Tree (Abies mariesii) Identification in Insect Infested Forests by Means of UAV Images and Deep Learning. Remote. Sens. 2021, 13, 260. [Google Scholar] [CrossRef]
- Moritake, K.; Cabezas, M.; Nhung, T.T.C.; Lopez Caceres, M.L.; Diez, Y. Sub-alpine shrub classification using UAV images: Performance of human observers vs. DL classifiers. Ecol. Inform. 2024, 80, 102462. [Google Scholar] [CrossRef]
- Zhang, C.; Atkinson, P.M.; George, C.; Wen, Z.; Diazgranados, M.; Gerard, F. Identifying and mapping individual plants in a highly diverse high-elevation ecosystem using UAV imagery and deep learning. ISPRS J. Photogramm. Remote. Sens. 2020, 169, 280–291. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, J.; Ao, Z.; Lao, D.; Xin, Q. Deep Learning Approaches for the Mapping of Tree Species Diversity in a Tropical Wetland Using Airborne LiDAR and High-Spatial-Resolution Remote Sensing Images. Forests 2019, 10, 1047. [Google Scholar] [CrossRef]
- Sylvain, J.D.; Drolet, G.; Brown, N. Mapping dead forest cover using a deep convolutional neural network and digital aerial photography. ISPRS J. Photogramm. Remote. Sens. 2019, 156, 14–26. [Google Scholar] [CrossRef]
- Agisoft LLC. Agisoft Metashape. Available online: https://www.agisoft.com/ (accessed on 15 September 2024).
- O’shea, K.; Nash, R. An introduction to convolutional neural networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5999–6009. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Radosavovic, I.; Kosaraju, R.P.; Girshick, R.; He, K.; Dollár, P. Designing network design spaces. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 10428–10436. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A ConvNet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Liu, Z.; Hu, H.; Lin, Y.; Yao, Z.; Xie, Z.; Wei, Y.; Ning, J.; Cao, Y.; Zhang, Z.; Dong, L.; et al. Swin Transformer V2: Scaling up Capacity and Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 12009–12019. [Google Scholar]
- Leidemer, T.; Gonroudobou, O.B.H.; Nguyen, H.T.; Ferracini, C.; Burkhard, B.; Diez, Y.; Lopez Caceres, M.L. Classifying the Degree of Bark Beetle-Induced Damage on Fir (Abies mariesii) Forests, from UAV-Acquired RGB Images. Computation 2022, 10, 63. [Google Scholar] [CrossRef]
- Xie, Y.; Ling, J. Wood defect classification based on lightweight convolutional neural networks. BioResources 2023, 18, 7663–7680. [Google Scholar] [CrossRef]
- Schiefer, F.; Kattenborn, T.; Frick, A.; Frey, J.; Schall, P.; Koch, B.; Schmidtlein, S. Mapping forest tree species in high resolution UAV-based RGB-imagery by means of convolutional neural networks. ISPRS J. Photogramm. Remote. Sens. 2020, 170, 205–215. [Google Scholar] [CrossRef]
- West, J.; Ventura, D.; Warnick, S. Spring Research Presentation: A Theoretical Foundation for Inductive Transfer; Brigham Young University, College of Physical and Mathematical Sciences: Provo, UT, USA, 2007; Volume 1. [Google Scholar]
- Bozinovski, S. Reminder of the first paper on transfer learning in neural networks, 1976. Informatica 2020, 44, 291–302. [Google Scholar] [CrossRef]
- Kentsch, S.; Lopez Caceres, M.L.; Serrano, D.; Roure, F.; Diez, Y. Computer Vision and Deep Learning Techniques for the Analysis of Drone-Acquired Forest Images, a Transfer Learning Study. Remote. Sens. 2020, 12, 1287. [Google Scholar] [CrossRef]
- Quinn, J.; McEachen, J.; Fullan, M.; Gardner, M.; Drummy, M. Dive into Deep Learning: Tools for Engagement; Corwin Press: Thousand Oaks, CA, USA, 2019. [Google Scholar]
- Mukhlif, A.A.; Al-Khateeb, B.; Mohammed, M.A. Incorporating a novel dual transfer learning approach for medical images. Sensors 2023, 23, 570. [Google Scholar] [CrossRef]
- Colwell, R.K., III. Biodiversity: Concepts, Patterns, and Measurement. In The Princeton Guide to Ecology; Princeton University Press: Princeton, NJ, USA, 2009; Chapter 3.1; pp. 257–263. [Google Scholar] [CrossRef]
- Spellerberg, I.F.; Fedor, P.J. A tribute to Claude Shannon (1916–2001) and a plea for more rigorous use of species richness, species diversity and the ‘Shannon–Wiener’ Index. Glob. Ecol. Biogeogr. 2003, 12, 177–179. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; Routledge: London, UK, 2017. [Google Scholar]
- Powers, D. Evaluation: From Precision, Recall and F-Factor to ROC, Informedness, Markedness & Correlation. Mach. Learn. Technol. 2008, 2, 37–63. [Google Scholar]
- Sasaki, Y. The truth of the F-measure. Teach Tutor Mater 2007, 1, 5. [Google Scholar]
- Ting, K.M. Confusion Matrix. In Encyclopedia of Machine Learning and Data Mining; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2017; p. 260. [Google Scholar] [CrossRef]
- Bisong, E. Google Colaboratory. In Building Machine Learning and Deep Learning Models on Google Cloud Platform: A Comprehensive Guide for Beginners; Chapter Google Colaboratory; Apress: Berkeley, CA, USA, 2019; pp. 59–64. [Google Scholar] [CrossRef]
- Bolyn, C.; Lejeune, P.; Michez, A.; Latte, N. Mapping tree species proportions from satellite imagery using spectral–spatial deep learning. Remote. Sens. Environ. 2022, 280, 113205. [Google Scholar] [CrossRef]
- Shirai, H.; Kageyama, Y.; Nagamoto, D.; Kanamori, Y.; Tokunaga, N.; Kojima, T.; Akisawa, M. Detection method for Convallaria keiskei colonies in Hokkaido, Japan, by combining CNN and FCM using UAV-based remote sensing data. Ecol. Inform. 2022, 69, 101649. [Google Scholar] [CrossRef]
- Shirai, H.; Tung, N.D.M.; Kageyama, Y.; Ishizawa, C.; Nagamoto, D.; Abe, K.; Kojima, T.; Akisawa, M. Estimation of the Number of Convallaria Keiskei’s Colonies Using UAV Images Based on a Convolutional Neural Network. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 1552–1554. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).