Hyperspectral Imaging for Phenotyping Plant Drought Stress and Nitrogen Interactions Using Multivariate Modeling and Machine Learning Techniques in Wheat
Abstract
1. Introduction
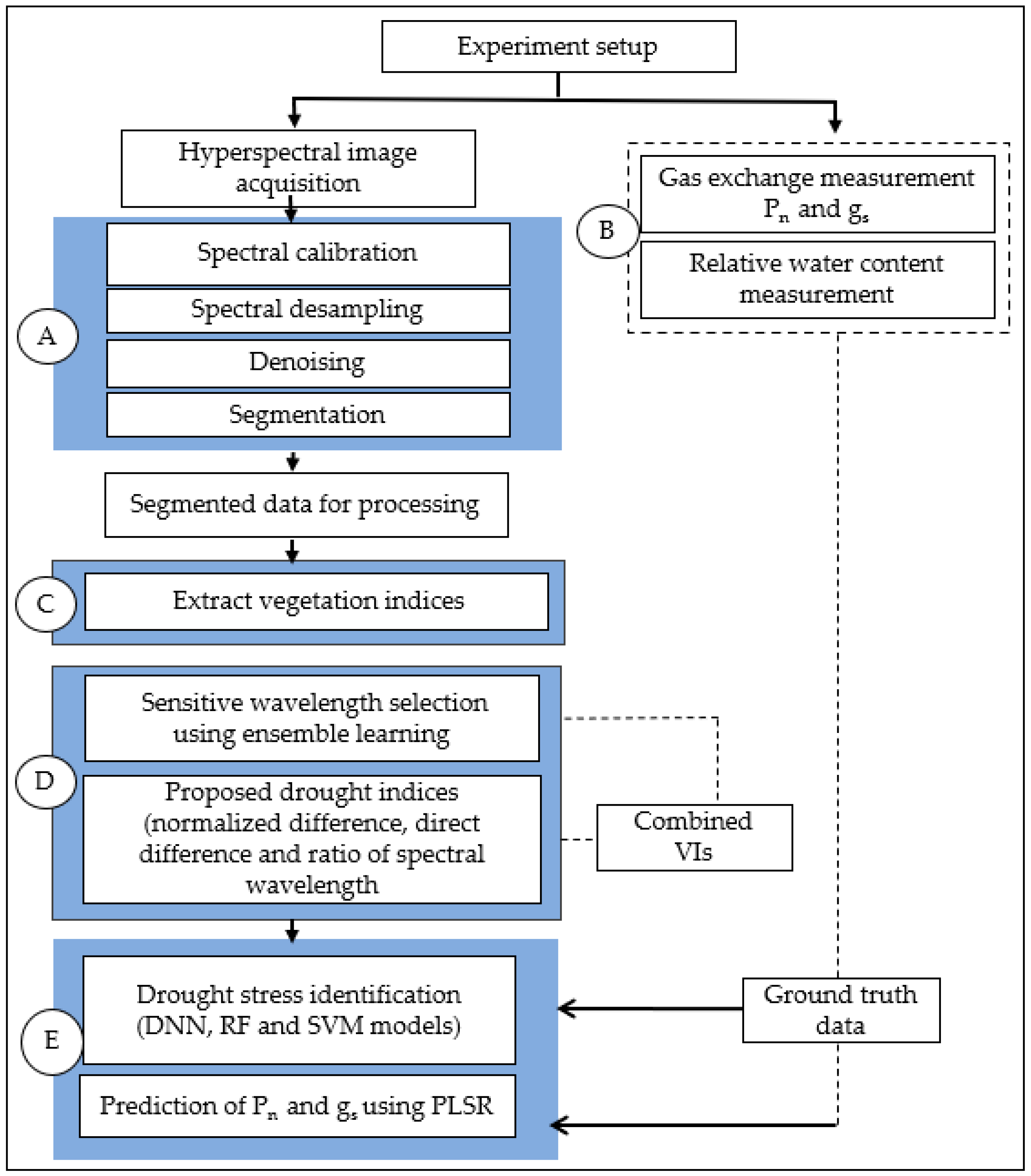
2. Materials and Methods
2.1. Experiment Setup
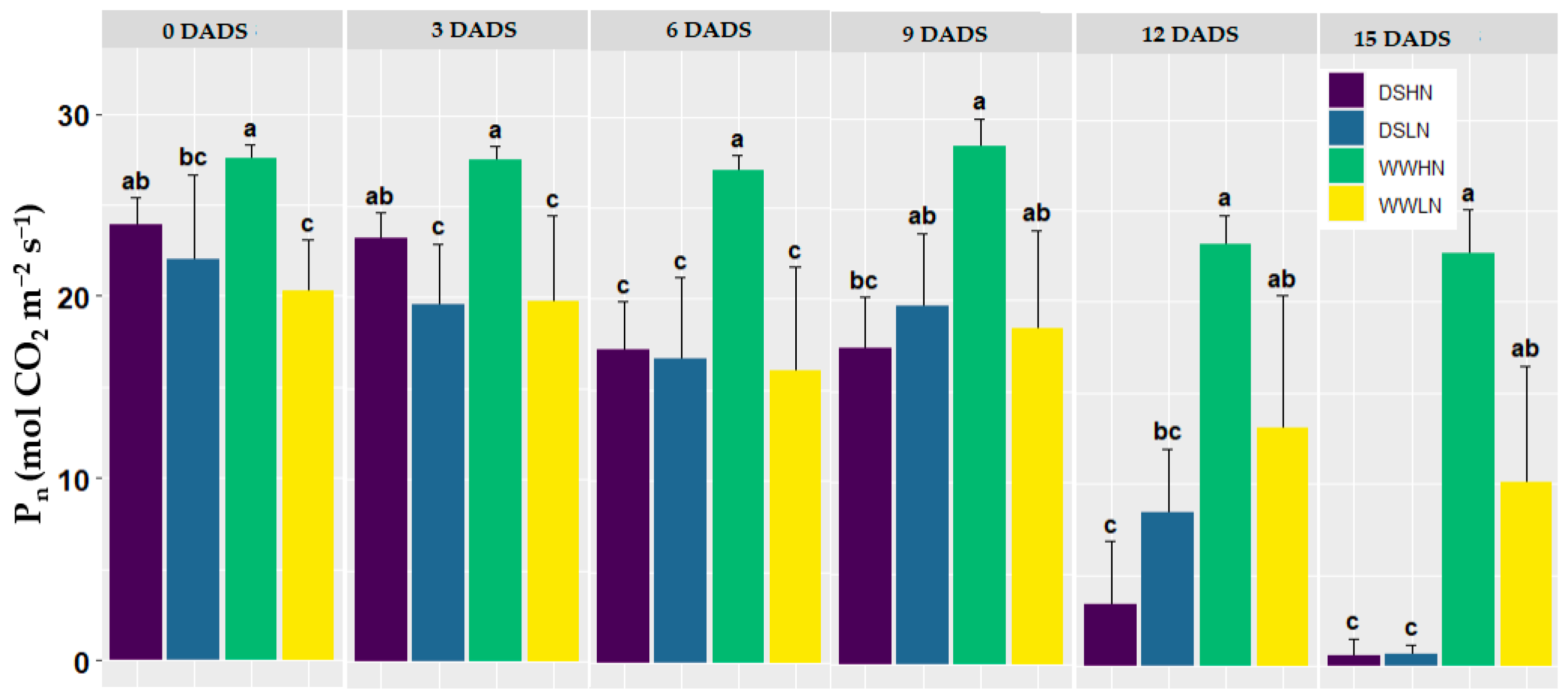
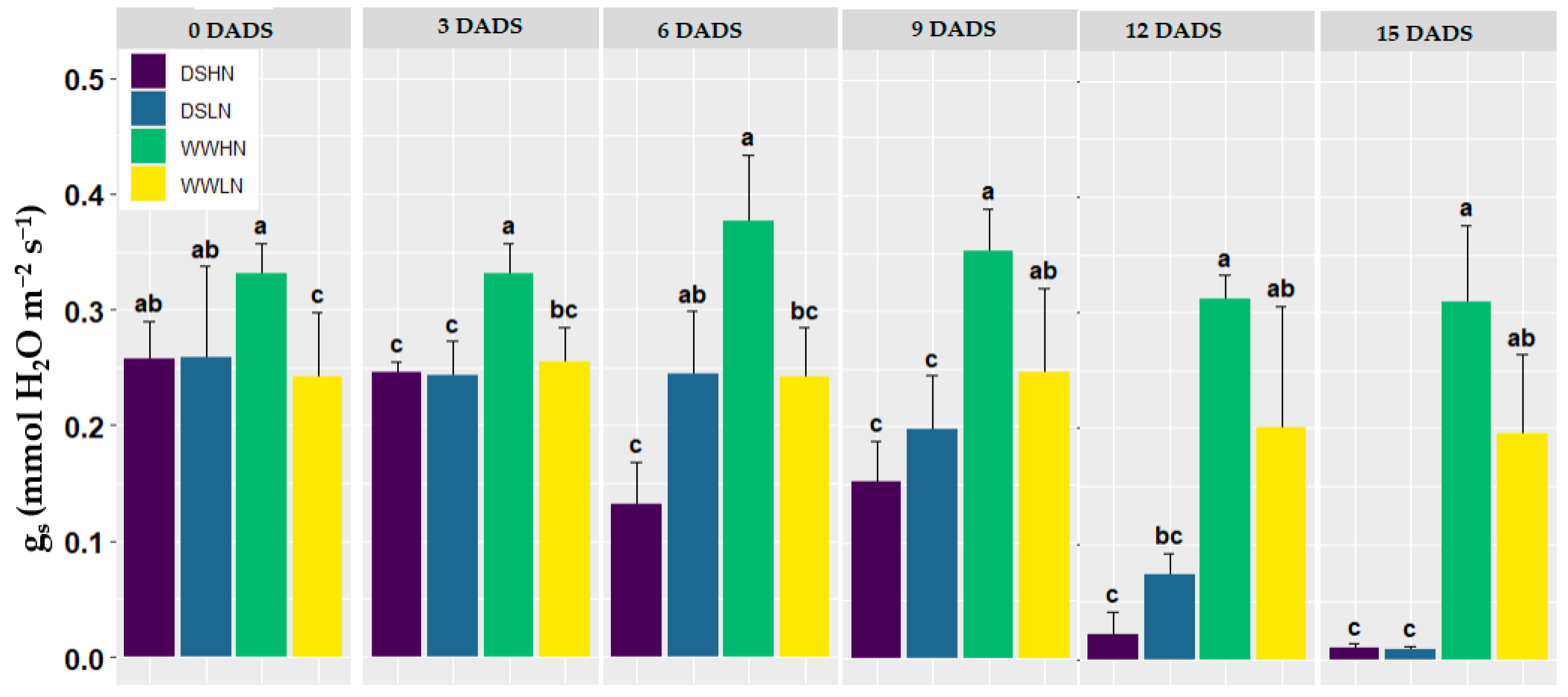
2.2. Physiological Measurements of Drought Stress
2.3. Hyperspectral Data Acquisition
2.4. Hyperspectral Image Pre-Processing
2.5. Segmenting the Hyperspectral Data
2.6. Extracting Known Vegetation Indices
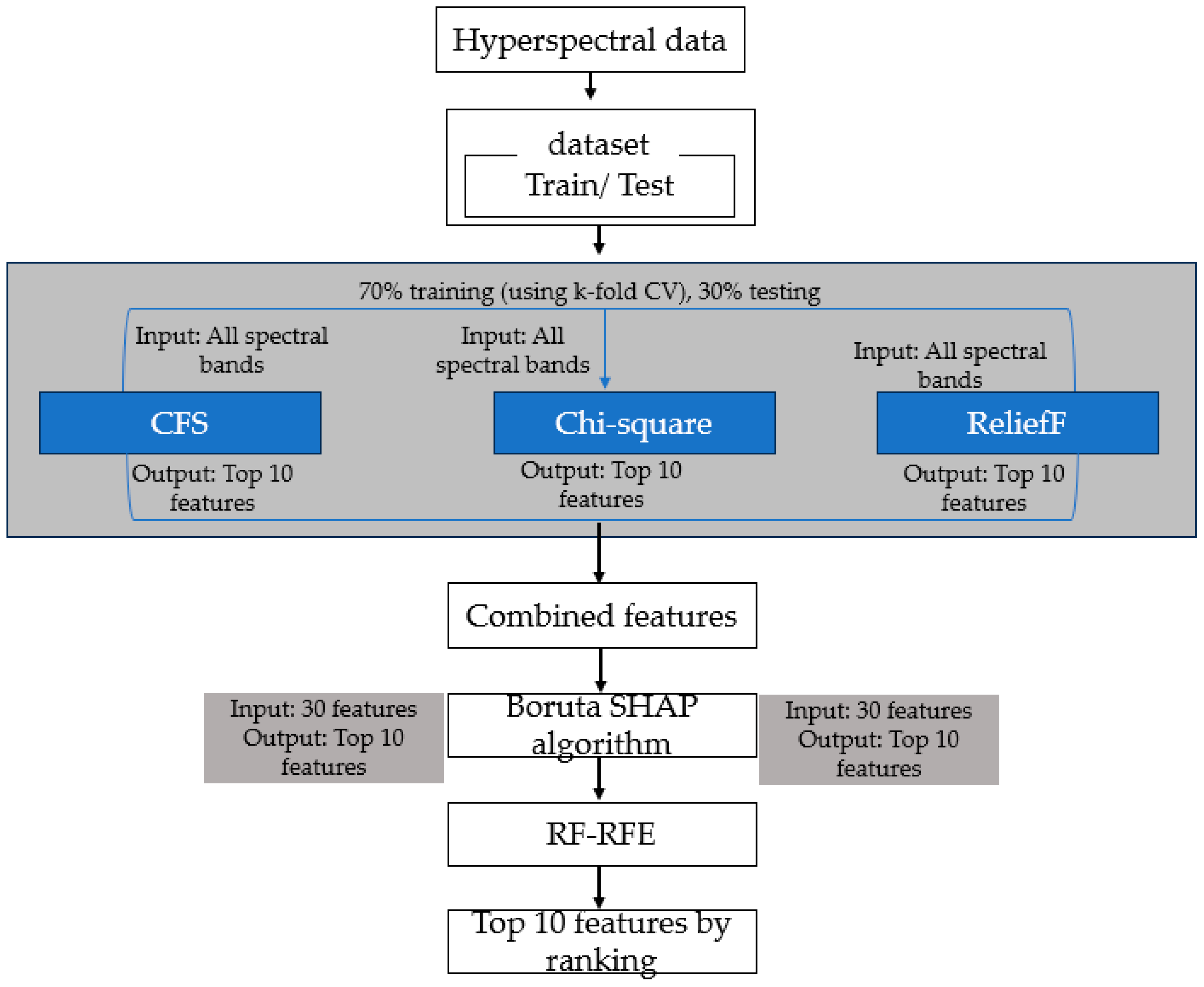
2.7. Wavelength Selection and New Drought Stress Indices
Wavelength Selection Using Ensemble Learning
2.8. Machine Learning Models for Drought Stress Identification
2.9. Multivariate Analysis for Stomatal Conductance and Photosynthetic Rate Predictions
2.10. Model Training and Testing
3. Results
3.1. Reference Data of Gas Exchange Measurements
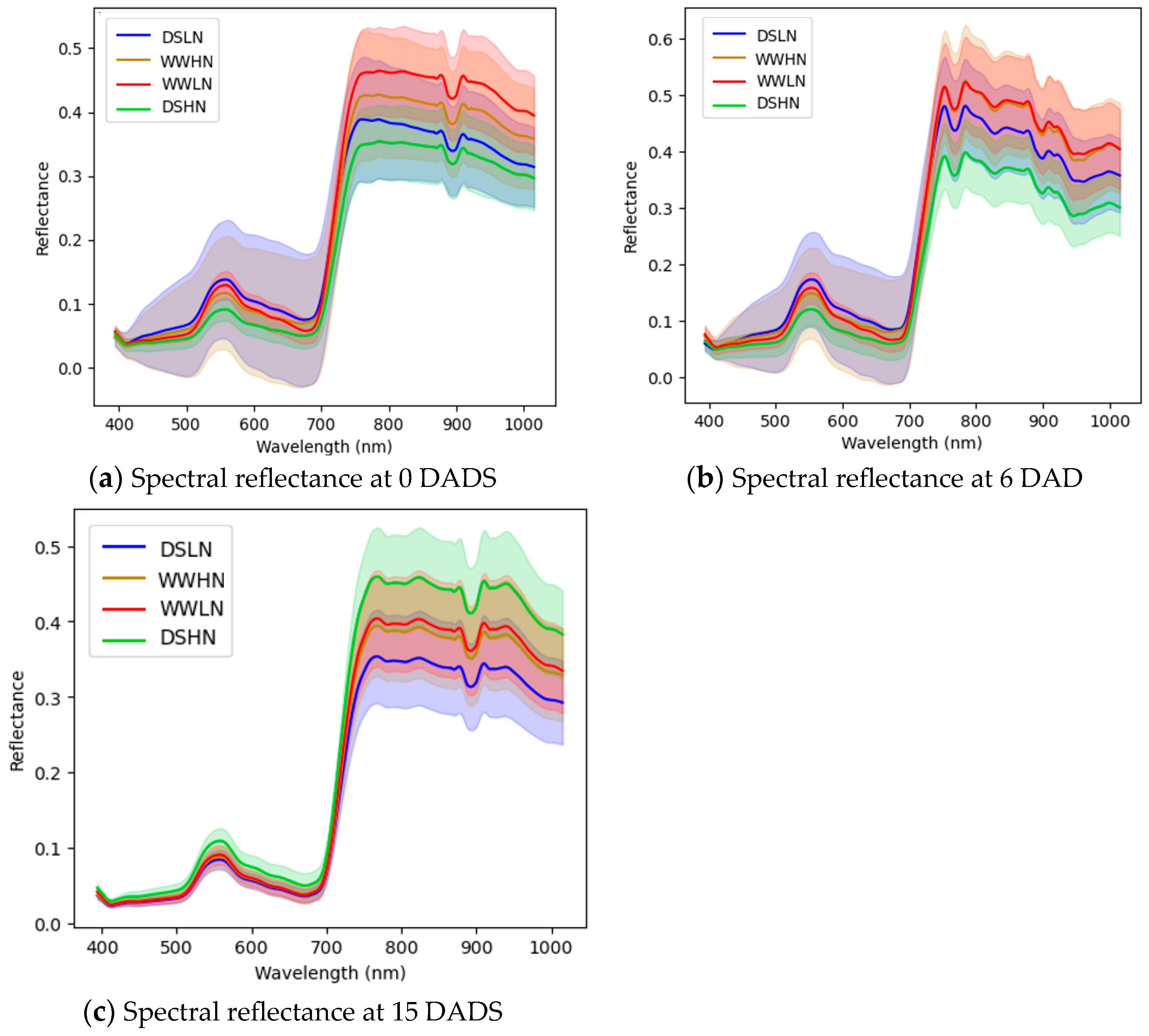
3.2. Spectral Reflectance Analysis
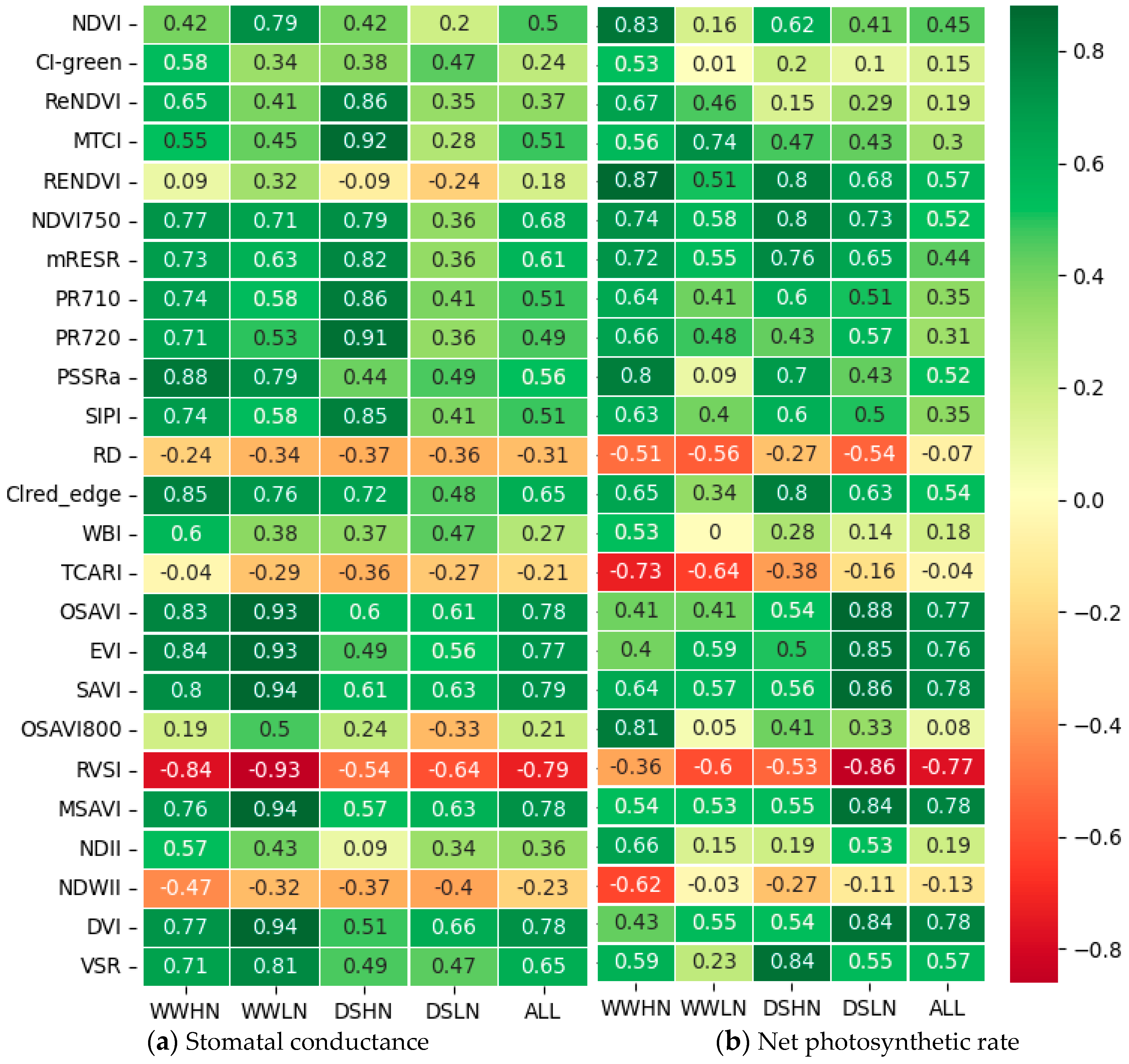
3.3. Correlation between the Known VIs and Gas Exchange Measurements (Pn and gs)
3.4. Waveband Selection and Proposed Indices
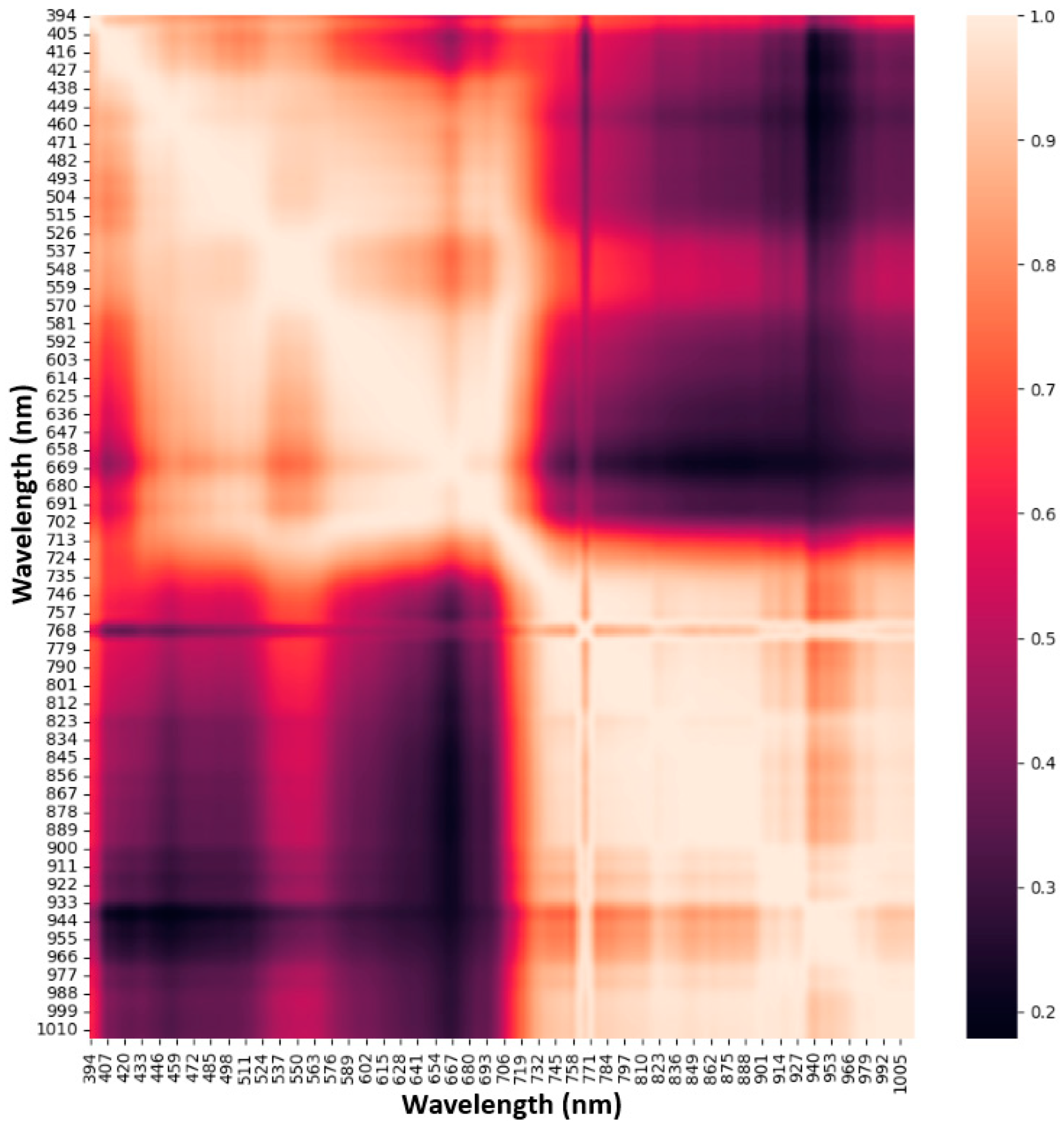
3.4.1. Spectral Band Pair Correlation
3.4.2. Output of the Ensemble Model Waveband Selection
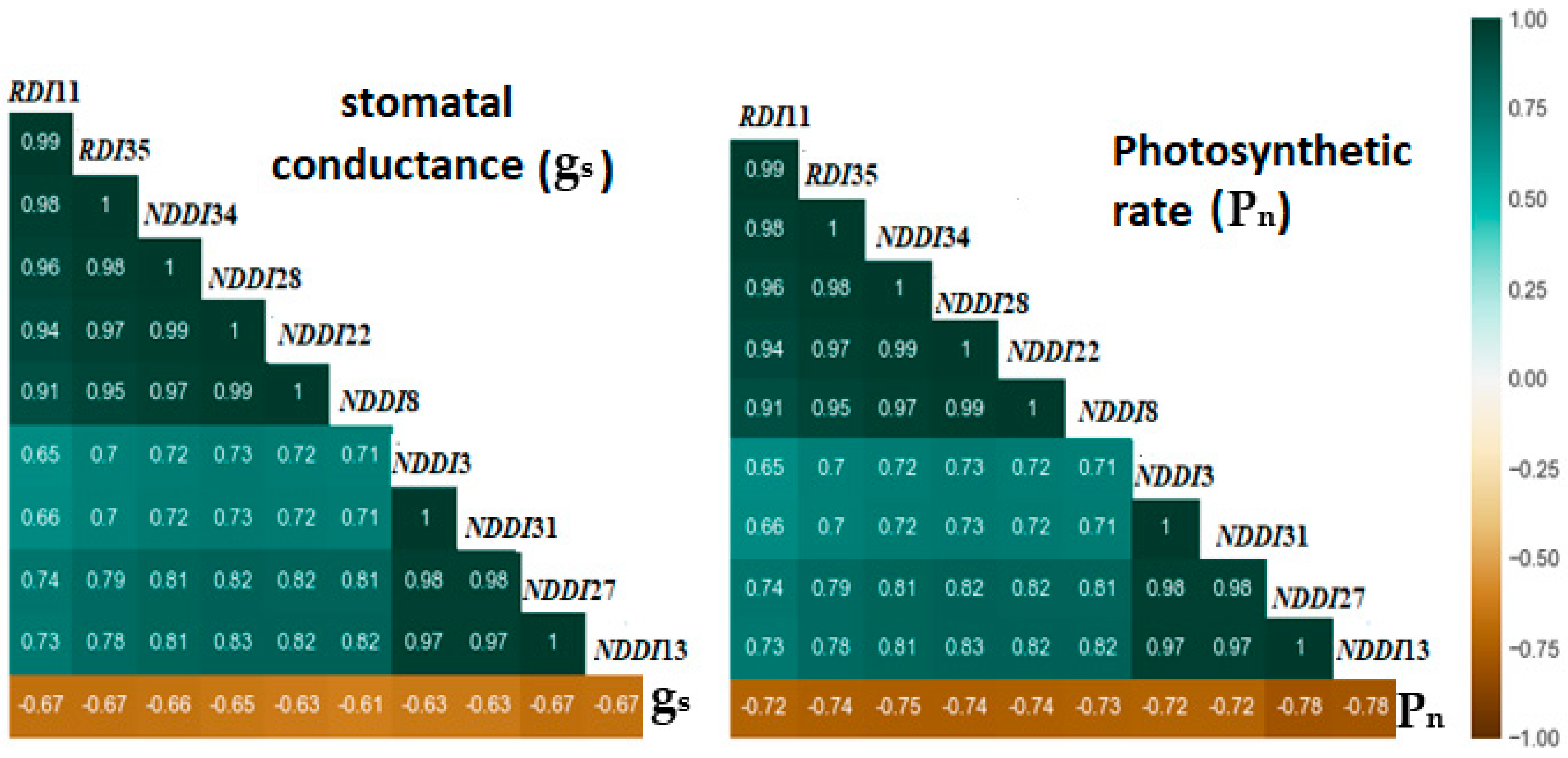
3.4.3. Proposed Drought Stress Indices
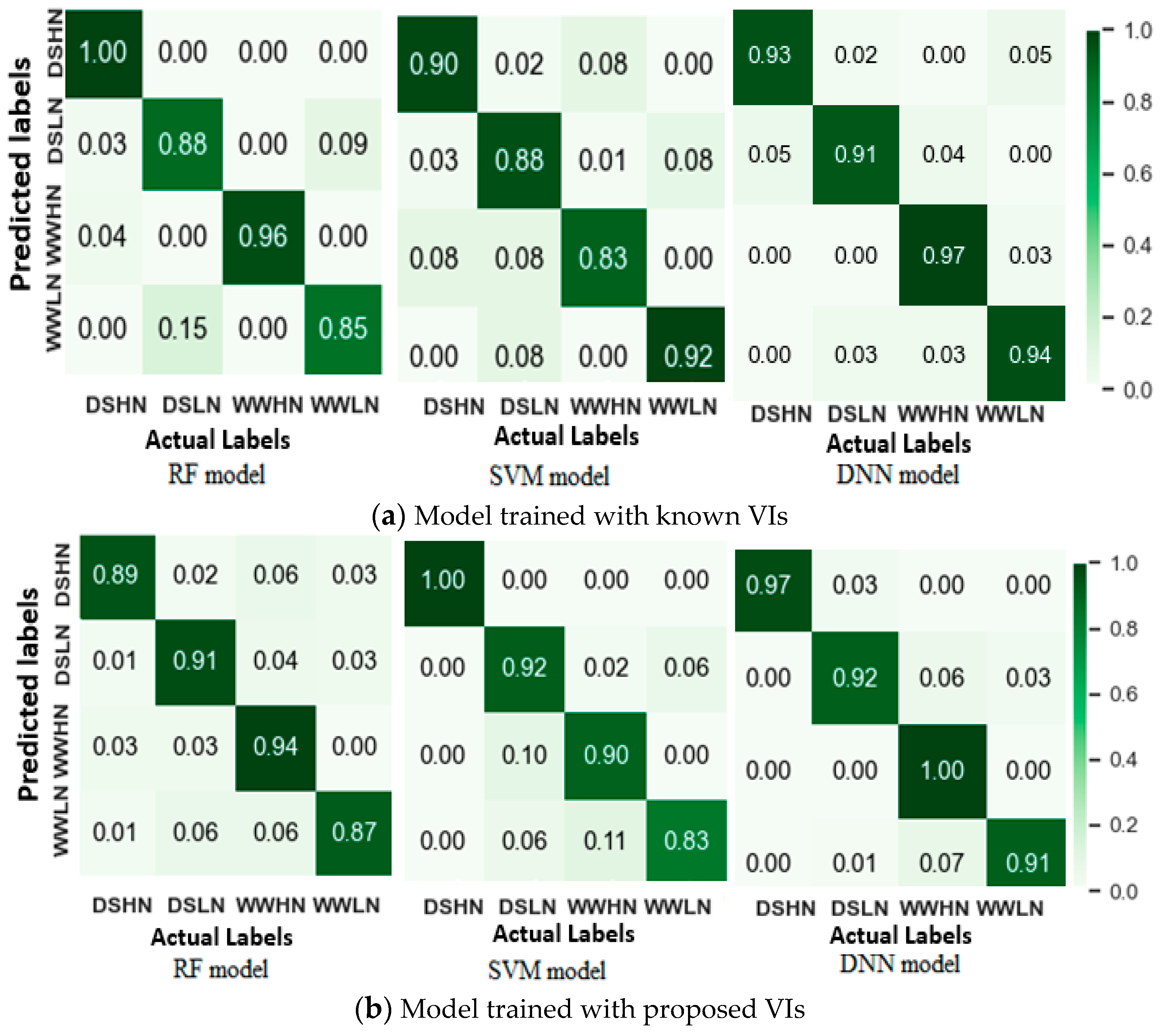
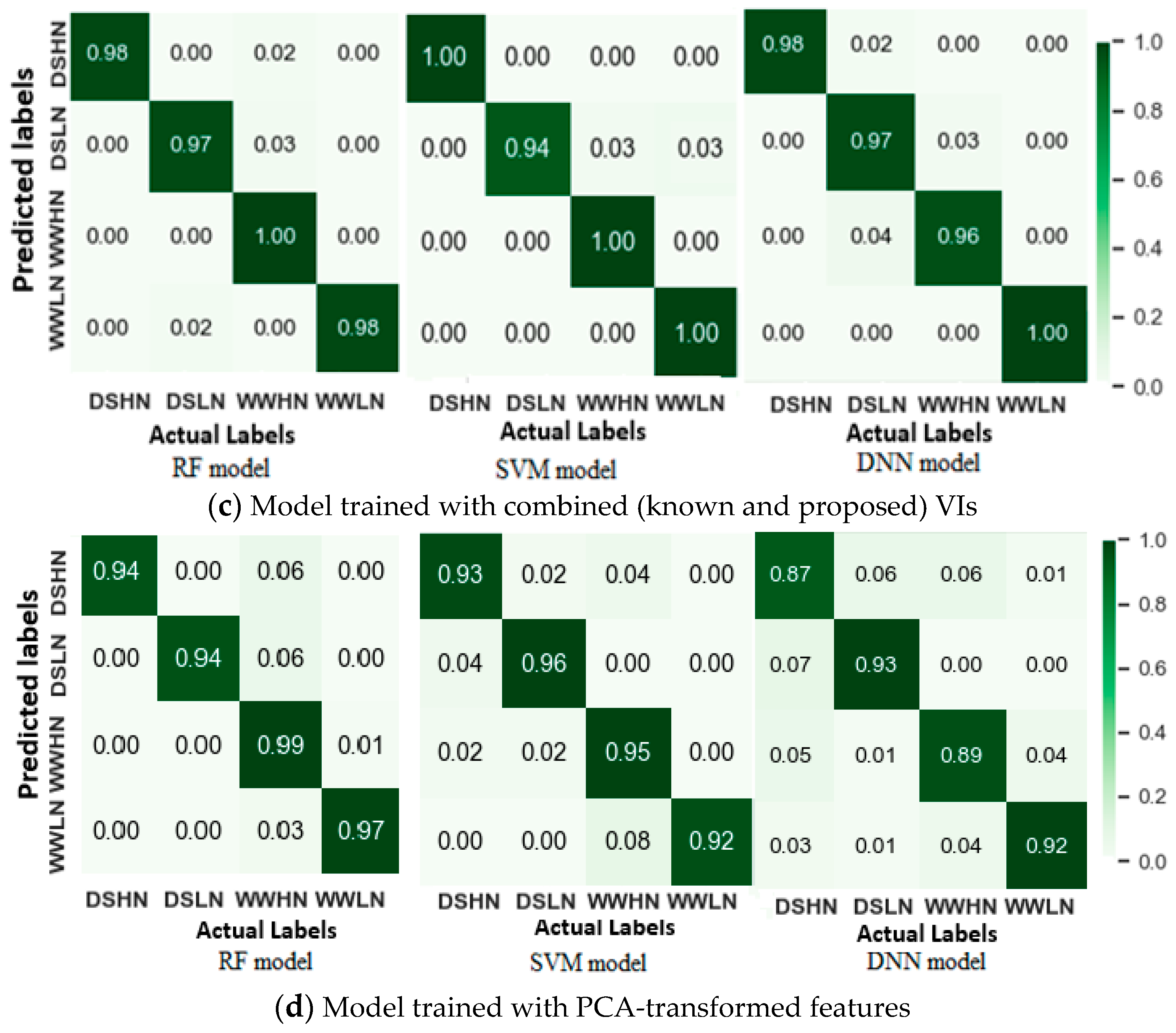
3.5. Machine Learning-Based Drought Detection
3.5.1. Drought Stress Identification Using Machine Learning Models
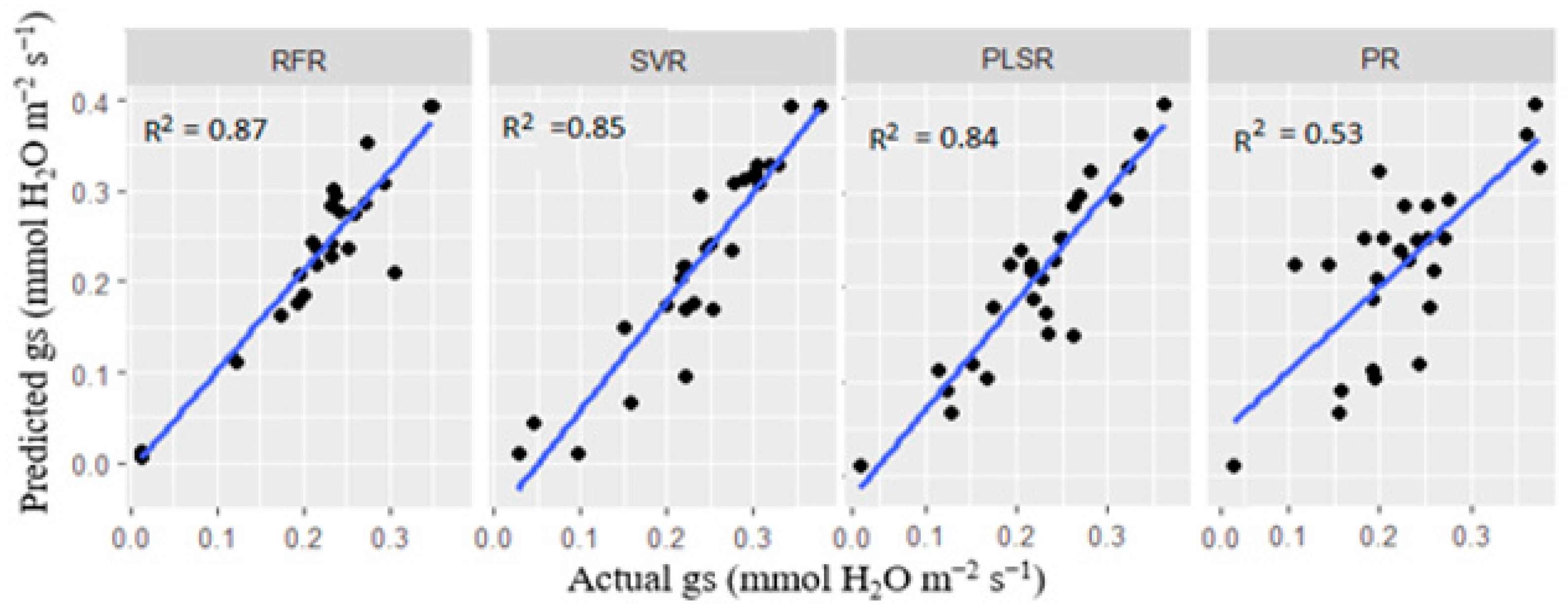
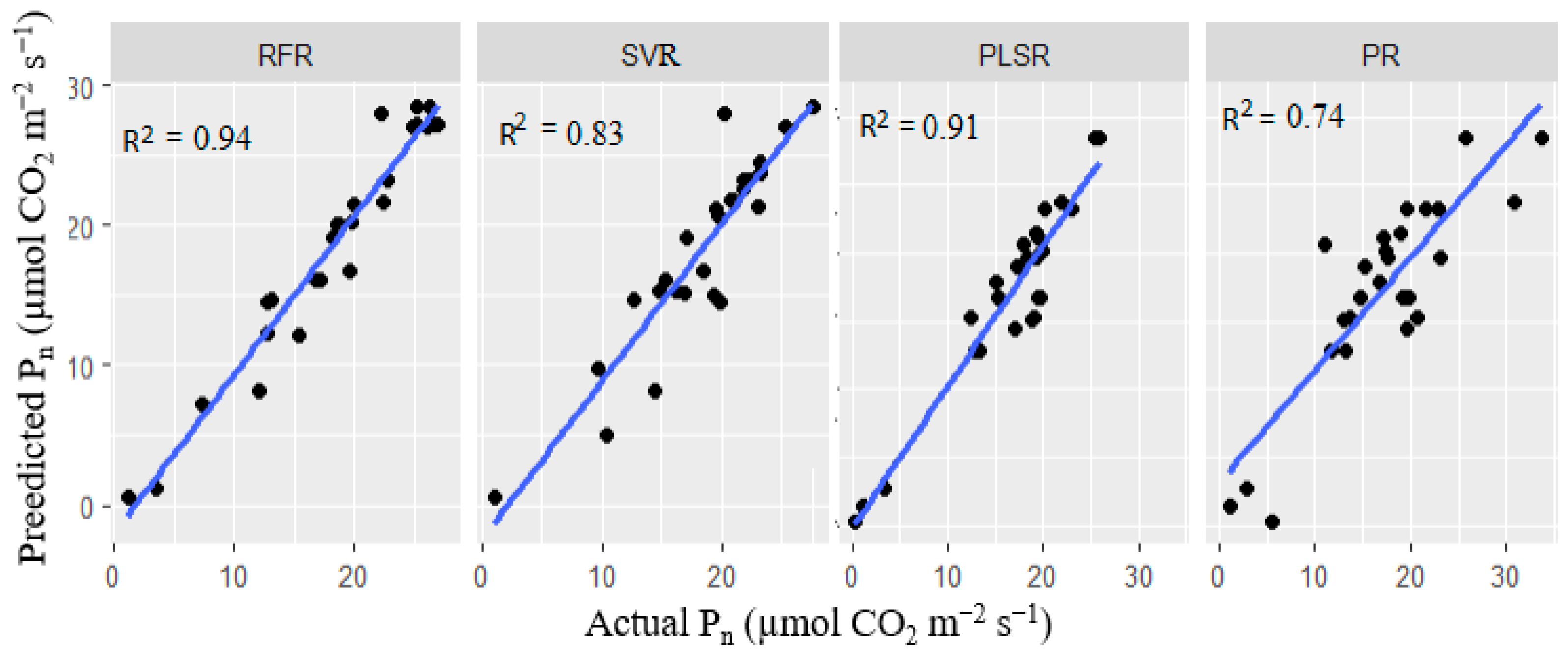
3.5.2. Multivariate Model Analysis for Stomatal Conductance and Photosynthetic Rate Predictions
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pirasteh-Anosheh, H.; Saed-Moucheshi, A.; Pakniyat, H.; Pessarakli, M. Stomatal responses to drought stress. In Water Stress and Crop Plants: A Sustainable Approach; Wiley: Hoboken, NJ, USA, 2016; Volume 1–2, pp. 24–40. [Google Scholar] [CrossRef]
- Duan, L.; Han, J.; Guo, Z.; Tu, H.; Yang, P.; Zhang, D.; Fan, Y.; Chen, G.; Xiong, L.; Dai, M.; et al. Novel digital features discriminate between drought resistant and drought sensitive rice under controlled and field conditions. Front. Plant Sci. 2018, 9, 492. [Google Scholar] [CrossRef]
- Xu, L.; Baldocchi, D. Seasonal trends in photosynthetic parameters and stomatal conductance of blue oak (Quercus douglasii) under prolonged summer drought and high temperature. Tree Physiol. 2003, 23, 865–877. [Google Scholar] [CrossRef] [PubMed]
- Leone, M. Advances in fiber optic sensors for soil moisture monitoring: A review. Results Opt. 2022, 7, 100213. [Google Scholar] [CrossRef]
- Grant, M.; Ochagavía, H.; Baluja, J.; Diago, P.; Tardáguila, J. Thermal imaging to detect spatial and temporal variation in the water status of grapevine (Vitis vinifera L.). J. Hortic. Sci. Biotechnol. 2016, 91, 43–54. [Google Scholar] [CrossRef]
- Zhang, Y.; Zha, Y.; Jin, X.; Wang, Y.; Qiao, H. Changes in Vertical Phenotypic Traits of Rice (Oryza sativa L.) Response to Water Stress. Front. Plant Sci. 2022, 13, 942110. [Google Scholar] [CrossRef]
- Mertens, S.; Verbraeken, L.; Sprenger, H.; Demuynck, K.; Maleux, K.; Cannoot, B.; De Block, J.; Maere, S.; Nelissen, H.; Bonaventure, G.; et al. Proximal Hyperspectral Imaging Detects Diurnal and Drought-Induced Changes in Maize Physiology. Front. Plant Sci. 2021, 12, 640914. [Google Scholar] [CrossRef]
- Proctor, C.; Dao, P.D.; He, Y. Close-range, heavy-duty hyperspectral imaging for tracking drought impacts using the PROCOSINE model. J. Quant. Spectrosc. Radiat. Transf. 2021, 263, 107528. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, L. Technical focus: Visible and near-infrared reflectance techniques for diagnosing plant physiological status. Trends Plant Sci. 1998, 3, 151–156. [Google Scholar] [CrossRef]
- Satterwhite, M.; Henley, J. Hyperspectral Signatures (400 to 2500 nm) of Vegetation, Minerals, Soils, Rocks, and Cultural Features: Laboratory and Field Measurements. 1990, p. 478. Available online: http://hdl.handle.net/11681/11316 (accessed on 23 September 2023).
- Asaari, M.S.M.; Mertens, S.; Dhondt, S.; Inzé, D.; Wuyts, N.; Scheunders, P. Analysis of hyperspectral images for detection of drought stress and recovery in maize plants in a high-throughput phenotyping platform. Comput. Electron. Agric. 2019, 162, 749–758. [Google Scholar] [CrossRef]
- Jay, S.; Gorretta, N.; Morel, J.; Maupas, F.; Bendoula, R.; Rabatel, G.; Dutartre, D.; Comar, A.; Baret, F. Estimating leaf chlorophyll content in sugar beet canopies using millimeter- to centimeter-scale reflectance imagery. Remote Sens. Environ. 2017, 198, 173–186. [Google Scholar] [CrossRef]
- Ihuoma, S.O.; Madramootoo, C.A. Recent advances in crop water stress detection. Comput. Electron. Agric. 2017, 141, 267–275. [Google Scholar] [CrossRef]
- Sun, Y.; Todorovic, S.; Goodison, S. Local-learning-based feature selection for high-dimensional data analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1610–1626. [Google Scholar] [CrossRef] [PubMed]
- Chutia, D.; Bhattacharyya, D.K.; Sarma, J.; Raju, P.N.L. An effective ensemble classification framework using random forests and a correlation based feature selection technique. Trans. GIS 2017, 21, 1165–1178. [Google Scholar] [CrossRef]
- Rady, A.; Ekramirad, N.; Adedeji, A.A.; Li, M.; Alimardani, R. Hyperspectral imaging for detection of codling moth infestation in GoldRush apples. Postharvest Biol. Technol. 2017, 129, 37–44. [Google Scholar] [CrossRef]
- Nagasubramanian, K.; Jones, S.; Singh, A.K.; Singh, A.; Ganapathysubramanian, B.; Sarkar, S. Explaining Hyperspectral Imaging Based Plant Disease Identification: 3D CNN and Saliency Maps. arXiv 2018, arXiv:1804.08831. [Google Scholar]
- Yang, P.; Liu, W.; Zhou, B.B.; Chawla, S.; Zomaya, A.Y. Ensemble-based wrapper methods for feature selection and class imbalance learning. In Advances in Knowledge Discovery and Data Mining, Proceedings of the 17th Pacific-Asia Conference, PAKDD 2013, Gold Coast, Australia, 14–17 April 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 544–555. [Google Scholar] [CrossRef]
- Remeseiro, B.; Bolon-Canedo, V. A review of feature selection methods in medical applications. Comput. Biol. Med. 2019, 112, 103375. [Google Scholar] [CrossRef]
- Damodaran, B.B.; Courty, N.; Lefevre, S. Sparse Hilbert Schmidt Independence Criterion and Surrogate-Kernel-Based Feature Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2385–2398. [Google Scholar] [CrossRef]
- Pandey, P.; Ge, Y.; Stoerger, V.; Schnable, J.C. High throughput in vivo analysis of plant leaf chemical properties using hyperspectral imaging. Front. Plant Sci. 2017, 8, 1348. [Google Scholar] [CrossRef]
- Anas, M.; Liao, F.; Verma, K.K.; Sarwar, M.A.; Mahmood, A.; Chen, Z.-L.; Li, Q.; Zeng, X.-P.; Li, Y.-R. Fate of nitrogen in agriculture and environment: Agronomic, eco-physiological and molecular approaches to improve nitrogen use efficiency. Biol. Res. 2020, 53, 47. [Google Scholar] [CrossRef]
- Gastal, F.; Lemaire, G.; Durand, J.-L.; Louarn, G. Quantifying crop responses to nitrogen and avenues to improve nitrogen-use efficiency. In Crop Physiology, 2nd ed.; Sadras, V.O., Calderini, D., Eds.; Academic Press: San Diego, CA, USA, 2015; pp. 161–206. [Google Scholar] [CrossRef]
- Lawlor, D.W. Limitation to photosynthesis in water-stressed leaves: Stomata vs. Metabolism and the role of ATP. Ann. Bot. 2002, 89, 871–885. [Google Scholar] [CrossRef]
- Gastal, F.; Lemaire, G. N uptake and distribution in crops: An agronomical and ecophysiological perspective. J. Exp. Bot. 2002, 53, 789–799. [Google Scholar] [CrossRef]
- Seleiman, M.F.; Al-Suhaibani, N.; Ali, N.; Akmal, M.; Alotaibi, M.; Refay, Y.; Dindaroglu, T.; Abdul-Wajid, H.H.; Battaglia, M.L. Drought stress impacts on plants and different approaches to alleviate its adverse effects. Plants 2021, 10, 259. [Google Scholar] [CrossRef] [PubMed]
- Masters-Clark, E.; Shone, E.; Paradelo, M.; Hirsch, P.R.; Clark, I.M.; Otten, W.; Brennan, F.; Mauchline, T.H. Development of a defined compost system for the study of plant-microbe interactions. Sci. Rep. 2020, 10, 1–9. [Google Scholar]
- Thameur, A.; Lachiheb, B.; Ferchichi, A. Drought effect on growth, gas exchange and yield, in two strains of local barley Ardhaoui, under water deficit conditions in southern Tunisia. J. Environ. Manag. 2012, 113, 495–500. [Google Scholar] [CrossRef]
- Keshtiban, R.K.; Carvani, V.; Imandar, M. Effects of salinity stress and drought due to different concentrations of sodium chloride and polyethylene glycol 6000 on germination and seedling growth characteristics of pinto bean (Phaseolus vulgaris L.). Adv. Environ. Biol. 2015, 237, 229–235. [Google Scholar]
- Nguyen, N.T.; Mohapatra, P.K.; Fujita, K.; Nakabayashi, K.; Thompson, J. Effect of nitrogen deficiency on biomass production, photosynthesis, carbon partitioning, and nitrogen nutrition status of Melaleuca and Eucalyptus species. Soil Sci. Plant Nutr. 2003, 49, 99–109. [Google Scholar] [CrossRef][Green Version]
- Virlet, N.; Sabermanesh, K.; Sadeghi-Tehran, P.; Hawkesford, M.J. Field Scanalyzer: An automated robotic field phenotyping platform for detailed crop monitoring. Funct. Plant Biol. 2016, 44, 143–153. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi-Tehran, P.; Virlet, N.; Hawkesford, M.J. A neural network method for classification of sunlit and shaded components of wheat canopies in the field using high-resolution hyperspectral imagery. Remote Sens. 2021, 13, 898. [Google Scholar] [CrossRef]
- LemnaTec. Digital Field Phenotyping. 2015, pp. 35–37. Available online: https://www.researchgate.net/publication/283706879_Digital_Field_Phenotyping_by_LemnaTec (accessed on 15 February 2023).
- Zhu, F.; Zhang, D.; He, Y.; Liu, F.; Sun, D.W. Application of Visible and Near Infrared Hyperspectral Imaging to Differentiate Between Fresh and Frozen-Thawed Fish Fillets. Food Bioprocess Technol. 2013, 6, 2931–2937. [Google Scholar] [CrossRef]
- Rinnan, A.; Van den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Koh, J.C.O.; Banerjee, B.P.; Spangenberg, G.; Kant, S. Automated hyperspectral vegetation index derivation using a hyperparameter optimisation framework for high-throughput plant phenotyping. New Phytol. 2022, 233, 2659–2670. [Google Scholar] [CrossRef] [PubMed]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Gamon, J.A.; Penuelas, J.; Field, C.B. A Narrow-Waveband Spectral Index That Tracks Diurnal Changes in Photosynthetic Efficiency. Remote Sens. Environ. 1992, 6, 22–42. [Google Scholar]
- Penuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Blackburn, G.A. Spectral indices for estimating photosynthetic pigment concentrations: A test using senescent tree leaves. Int. J. Remote Sens. 1998, 19, 657–675. [Google Scholar] [CrossRef]
- Podani, J.; Czárán, T. Individual-centered analysis of mapped point patterns representing multi-species assemblages. J. Veg. Sci. 1997, 8, 259–270. [Google Scholar] [CrossRef]
- Xu, H.R.; Ying, Y.B.; Fu, X.P.; Zhu, S.P. Near-infrared Spectroscopy in detecting Leaf Miner Damage on Tomato Leaf. Biosyst. Eng. 2007, 96, 447–454. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Buschmann, C.; Nagel, E. In vivo spectroscopy and internal optics of leaves as basis for remote sensing of vegetation. Int. J. Remote Sens. 1993, 14, 711–722. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Datt, B. A new reflectance index for remote sensing of chlorophyll content in higher plants: Tests using Eucalyptus leaves. J. Plant Physiol. 1999, 154, 30–36. [Google Scholar] [CrossRef]
- McFeeters, S.K. NDWI by McFEETERS. Remote Sens. Environ. 1996, 25, 687–711. [Google Scholar]
- Perry, C.R.; Lautenschlager, L.F. Functional equivalence of spectral vegetation indices. Remote Sens. Environ. 1984, 14, 169–182. [Google Scholar] [CrossRef]
- White, D.C.; Williams, M.; Barr, S.L. Detecting sub-surface soil disturbance using hyperspectral first derivative band ratios of associated vegetation stress. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2008, 37, 243–248. [Google Scholar]
- Okyere, F.G.; Cudjoe, D.; Sadeghi-Tehran, P.; Virlet, N.; Riche, A.B.; Castle, M.; Greche, L.; Simms, D.; Mhada, M.; Mohareb, F.; et al. Modeling the spatial-spectral characteristics of plants for nutrient status identification using hyperspectral data and deep learning methods. Front. Plant Sci. 2023, 14, 1209500. [Google Scholar] [CrossRef]
- Manikandan, G.; Pragadeesh, B.; Manojkumar, V.; Karthikeyan, A.L.; Manikandan, R.; Gandomi, A.H. Classification models combined with Boruta feature selection for heart disease prediction. Inform. Med. Unlocked 2024, 44, 101442. [Google Scholar] [CrossRef]
- Jackson, R.D.; Huete, A.R. Interpreting vegetation indices. Prev. Vet. Med. 1991, 11, 185–200. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Breiman, L. RFRSF: Employee Turnover Prediction Based on Random Forests and Survival Analysis. In Web Information Systems Engineering–WISE 2020, Proceedings of the 21st International Conference, Amsterdam, The Netherlands, 20–24 October 2020; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12343, pp. 503–515. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Helmholz, P.; Rottensteiner, F.; Heipke, C. Semi-automatic verification of cropland and grassland using very high resolution mono-temporal satellite images. ISPRS J. Photogramm. Remote Sens. 2014, 97, 204–218. [Google Scholar] [CrossRef]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API Design for Machine Learning Software: Experiences from the Scikit-Learn Project. arXiv 2013, arXiv:1309.0238. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Brochu, E.; Cora, V.M.; De Freitas, E. A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning. arXiv 2010, arXiv:1012.2599. [Google Scholar]
- Flexas, J.; Flexas, J.; Barón, M.; Bota, J.; Ducruet, J.M.; Gallé, A.; Galmés, J.; Jiménez, M.; Pou, A.; Ribas-Carbó, M.; et al. Photosynthesis limitations during water stress acclimation and recovery in the drought-adapted Vitis hybrid Richter-110 (V. berlandieri × V. rupestris). J. Exp. Bot. 2009, 60, 2361–2377. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Ayala-Silva, T.; Beyl, C.A. Changes in spectral reflectance of wheat leaves in response to specific macronutrient deficiency. Adv. Space Res. 2005, 35, 305–317. [Google Scholar] [CrossRef]
- Knipling, E.B. Physical and physiological basis for the reflectance of visible and near-infrared radiation from vegetation. Remote Sens. Environ. 1970, 1, 155–159. [Google Scholar] [CrossRef]
- Debnath, S.; Paul, M.; Motiur Rahaman, D.M.; Debnath, T.; Zheng, L.; Baby, T.; Schmidtke, L.M.; Rogiers, S.Y. Identifying individual nutrient deficiencies of grapevine leaves using hyperspectral imaging. Remote Sens. 2021, 13, 3317. [Google Scholar] [CrossRef]
- Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Moghimi, A.; Yang, C.; Marchetto, P.M. Integrating Hyperspectral Imaging and Artificial Intelligence to Develop Automated Frameworks for High-Throughput Phenotyping in Wheat. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2019. [Google Scholar]
- Thenkabail, P.S.; Smith, R.B.; Wiegand De Pauw, E. Richardson, † International Center for Agricultural Research in the Dry Areas 1990), natural vegetation (Friedl et al., 1994), and in (ICARDA). Environ 1995, 71, 158–182. [Google Scholar]
- Colovic, M.; Yu, K.; Todorovic, M.; Cantore, V.; Hamze, M.; Albrizio, R.; Stellacci, A.M. Hyperspectral Vegetation Indices to Assess Water and Nitrogen Status of Sweet Maize Crop. Agronomy 2022, 12, 2181. [Google Scholar] [CrossRef]
- Cheriyadat, A. Limitations of Principal Component Analysis for Dimensionality-Reduction for Classification of Hyperspectral Data. No. December. 2003. Available online: https://hdl.handle.net/11668/19123 (accessed on 12 September 2023).
| Vegetation Indices | Formula | Reference |
|---|---|---|
| Normalized difference vegetation index (NDVI) | (R800 − R680)/(R800 + R680) | [37] |
| Chlorophyll index green (Cl-green) | NIR/Green − 1 | [38] |
| Renormalized difference vegetation index (ReNDVI) | R800 − R670/(R800 + R670) ½ | [39] |
| MERIS terrestrial chlorophyll index (MTCI) | (R753 − R708)/(R708 − R681) | [40] |
| Red edge NDVI (RENDVI) | (R705 − R740)/(R705 + R740) | [37] |
| Normalized difference vegetation index (NDVI750) | (R750 − R680)/(R750 + R680) | [37] |
| Modified red edge simple ratio index (mRESR) | (R750 − R445)/(R750 + R445) | [39] |
| Photochemical reflectance index (PRI710) | (R531 − R710)/(R531 + R710) | [39] |
| Photochemical Reflectance Index (PRI720) | (R531 − R720)/(R531 + R720) | [41] |
| Structure insensitive pigment index (SIPI) | (R800 − R455)/(R800 + R705) | [42] |
| Pigment specific simple ratio (PSSRa) | R800/R680 | [43] |
| Reflectance difference (RD) | R800 − R680 | [43] |
| Chlorophyll index red edge (CI-red edge) | (R750 − R700)/(R700) | [44] |
| Water band index (WBI) | (R950/R900 | [45] |
| Transformed chlorophyll absorption in reflectance index (TCARI) | 3 × [(R705 − 665) − 0.2 × (R705 − R560) × (R705/R665)]) | [40] |
| Optimized soil-adjusted vegetation index (OSAVI) | ((1 + 0.16) × (R865 − R665)/(R865 − R665 + 0.16)) | [46] |
| Enhanced vegetation index (EVI) | 2.5 × [(R800 − R680)/(R800 + 6 × R680 − 7.5 × R450 + 1)] | [47] |
| Soil adjusted vegetation index (SAVI) | ((1 + 0.5) × (R801 − R670)/(R801 + R670 + 0.5) | [48] |
| Optimized soil adjusted vegetation index (OSAVI800) | (1 + 0.16) (R800 + R670)/(R800 + R670 + 0.61) | [46] |
| Red edge vegetation index (RSVI) | (NIR/Red)-1 | [48] |
| Improved SAVI with self-adjustment factor L (MSAVI) | 0.5 × {2 × R800 + 1 − (2 × R800 + 1)2 − 8 × (R800 − R670)} | [48] |
| Normalized difference infrared index (NDII) | (R780 − R710)/(R780 − R680) | [49] |
| Normalized difference water index (NDWI) | (R560 − R830)/(R560 + R830) | [50] |
| Difference vegetation index (DVI) | R800 − R670 | [51] |
| Vegetation stress ratio (VRS) | R725/R702 | [52] |
| Model | Parameters | Range |
|---|---|---|
| DNN | Hidden layers | 1,2,3,4,5 |
| Number of neurons | 50, 100, 150, 200, 300 | |
| Activation function | identity, logistics, tanh, ReLU | |
| Weight optimization | lbfgs, sgd, adam | |
| Regularization penalty (α) | 0.00001, 0.0001, 0.001, 0.01 | |
| Learning rate | constant, adaptive, in scaling | |
| Batch size | 200, 300, 400, 500, 600, 700 | |
| Momentum for gradient descent update | 0.9 | |
| Exponential decay rate (β) | 0.9 | |
| SVM | Kernel type | rbf, poly, linear |
| Degree of the polynomial kernel | 1, 2, 3 | |
| Regularization parameter (C) | 0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000 | |
| Kernel coefficient (gamma) | 0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, | |
| RF | Number of trees | 10, 30, 50, 70, 90, 110, 130, 150, 170, 190 |
| Maximum depth of the tree | 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 | |
| Number of features for the best split | sqrt (1 8 1), log2 (1 8 1), 181 | |
| Minimum samples for splitting | 2, 5, 10 | |
| Bootstrap samples for building tree | True, False |
| Selected Wavelengths (nm) | ||||
|---|---|---|---|---|
| Rank | Chi-Square | ReliefF | CFS | RFE |
| 1 | 555 | 680 | 669 | 553 |
| 2 | 554 | 689 | 674 | 557 |
| 3 | 556 | 949 | 939 | 669 |
| 4 | 553 | 722 | 936 | 674 |
| 5 | 557 | 683 | 957 | 722 |
| 6 | 552 | 674 | 949 | 940 |
| 7 | 636 | 940 | 671 | 957 |
| 8 | 673 | 670 | 547 | 636 |
| 9 | 674 | 669 | 546 | 683 |
| 10 | 672 | 957 | 542 | 542 |
| Metrics | ||||
|---|---|---|---|---|
| Features | Model | AA | F-Score | Kappa |
| Known VIs | RF | 0.921 | 0.925 | 0.893 |
| SVM | 0.887 | 0.881 | 0.882 | |
| DNN | 0.938 | 0.935 | 0.914 | |
| Proposed VIs | RF | 0.914 | 0.911 | 0.881 |
| SVM | 0.924 | 0.930 | 0.919 | |
| DNN | 0.948 | 0.949 | 0.933 | |
| Combined VIs | RF | 0.983 | 0.984 | 0.965 |
| SVM | 0.981 | 0.982 | 0.975 | |
| DNN | 0.977 | 0.979 | 0.969 | |
| PCA Features | RF | 0.961 | 0.962 | 0.960 |
| SVM | 0.941 | 0.940 | 0.921 | |
| DNN | 0.901 | 0.900 | 0.868 | |
| Stomatal Conductance (gs) | ||||
| Metrics | RFR | SVR | PR | PLSR |
| R2 | 0.871 | 0.845 | 0.534 | 0.842 |
| RMSE | 0.035 | 0.038 | 0.221 | 0.031 |
| MAE | 0.015 | 0.011 | 0.142 | 0.017 |
| Photosynthetic Rate (Pn) | ||||
| Metrics | RFR | SVR | PR | PLSR |
| R2 | 0.940 | 0.830 | 0.740 | 0.910 |
| RMSE | 0.015 | 0.063 | 0.144 | 0.018 |
| MAE | 0.004 | 0.013 | 0.127 | 0.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okyere, F.G.; Cudjoe, D.K.; Virlet, N.; Castle, M.; Riche, A.B.; Greche, L.; Mohareb, F.; Simms, D.; Mhada, M.; Hawkesford, M.J. Hyperspectral Imaging for Phenotyping Plant Drought Stress and Nitrogen Interactions Using Multivariate Modeling and Machine Learning Techniques in Wheat. Remote Sens. 2024, 16, 3446. https://doi.org/10.3390/rs16183446
Okyere FG, Cudjoe DK, Virlet N, Castle M, Riche AB, Greche L, Mohareb F, Simms D, Mhada M, Hawkesford MJ. Hyperspectral Imaging for Phenotyping Plant Drought Stress and Nitrogen Interactions Using Multivariate Modeling and Machine Learning Techniques in Wheat. Remote Sensing. 2024; 16(18):3446. https://doi.org/10.3390/rs16183446
Chicago/Turabian StyleOkyere, Frank Gyan, Daniel Kingsley Cudjoe, Nicolas Virlet, March Castle, Andrew Bernard Riche, Latifa Greche, Fady Mohareb, Daniel Simms, Manal Mhada, and Malcolm John Hawkesford. 2024. "Hyperspectral Imaging for Phenotyping Plant Drought Stress and Nitrogen Interactions Using Multivariate Modeling and Machine Learning Techniques in Wheat" Remote Sensing 16, no. 18: 3446. https://doi.org/10.3390/rs16183446
APA StyleOkyere, F. G., Cudjoe, D. K., Virlet, N., Castle, M., Riche, A. B., Greche, L., Mohareb, F., Simms, D., Mhada, M., & Hawkesford, M. J. (2024). Hyperspectral Imaging for Phenotyping Plant Drought Stress and Nitrogen Interactions Using Multivariate Modeling and Machine Learning Techniques in Wheat. Remote Sensing, 16(18), 3446. https://doi.org/10.3390/rs16183446












