Abstract
Radiative transfer models (RTMs) are often used to retrieve biophysical parameters from earth observation data. RTMs with multi-temporal and realistic forest representations enable radiative transfer (RT) modeling for real-world dynamic processes. To achieve more realistic RT modeling for dynamic forest processes, this study presents the 3D-explicit reconstruction of a typical temperate deciduous forest in 2015 and 2022. We demonstrate for the first time the potential use of bitemporal 3D-explicit RT modeling from terrestrial laser scanning on the forward modeling and quantitative interpretation of: (1) remote sensing (RS) observations of leaf area index (LAI), fraction of absorbed photosynthetically active radiation (FAPAR), and canopy light extinction, and (2) the impact of canopy gap dynamics on light availability of explicit locations. Results showed that, compared to the 2015 scene, the hemispherical-directional reflectance factor (HDRF) of the 2022 forest scene relatively decreased by 3.8% and the leaf FAPAR relatively increased by 5.4%. At explicit locations where canopy gaps significantly changed between the 2015 scene and the 2022 scene, only under diffuse light did the branch damage and closing gap significantly impact ground light availability. This study provides the first bitemporal RT comparison based on the 3D RT modeling, which uses one of the most realistic bitemporal forest scenes as the structural input. This bitemporal 3D-explicit forest RT modeling allows spatially explicit modeling over time under fully controlled experimental conditions in one of the most realistic virtual environments, thus delivering a powerful tool for studying canopy light regimes as impacted by dynamics in forest structure and developing RS inversion schemes on forest structural changes.
1. Introduction
Remote sensing (RS) observations can provide spatial and temporal information on essential climate variables (ECVs) and biophysical properties in forest ecosystems [1,2]. Multiple forest properties relevant to environmental applications (e.g., leaf area index (LAI), canopy cover, and biomass) can be derived from RS observations of reflected, emitted, or scattered radiation using physically-based or empirical models. In this context, a comprehensive understanding of the interaction between light (i.e., electromagnetic radiation) and forests is essential for the accurate interpretation of vegetation RS observations [3].
Radiative transfer models (RTMs) simulate the interactions between forest structure and light using physically described mechanisms [4,5]. RTMs can facilitate our comprehension of light reflection, transmission, and absorption in forests and help interpret RS data. Therefore, RTMs are often used to retrieve biophysical parameters from EO data and are critical in improving the calibration and validation of RS products. Furthermore, RTMs enable a precise quantification of scattering and absorption within canopies, which is valuable for studying fundamental ecosystem processes such as photosynthesis and transpiration.
RTMs calculate the interaction between landscapes and radiation using the radiative transfer equation (RTE). The RTE describes the differential change of the radiance along a given direction in the medium [6,7]. The RTE lacks an analytical solution, necessitating our reliance on some form of approximation to make the equation numerically solvable [7]. The turbid medium approximation is a widely applied approach to describe the radiative transfer (RT) in vegetation [8,9,10]. This approach simplifies the vegetation canopy as a horizontal one-dimensional medium consisting of spatially homogeneous scatterers. It uses the Beer-Lambert law to describe the transmission of radiation through the vegetation canopy [11] as a function of the cumulative LAI [12] and possibly accounting for the leaf angle [8], scattering and diffuse solar radiation transfer [13,14], heterogeneity/clumping [15,16,17,18], and the hot spot effect [19,20,21].
Many methods have been developed to solve the RTE. The discrete ordinate method assumes radiation propagates along a fixed number (N) of discrete directions corresponding to N RTEs [22,23]. The RT anisotropy can be taken into account by using a large number of propagation directions (e.g., N > 100). The radiosity method uses the radiation balance equation on a finite number of discrete scatterers [24]. The Successive Orders of Scattering method calculates the total radiance vector as the summation of contributions from multi-scattered photons and pre-defines the maximum scattering number [25].
With the advancement in computer power, the Monte Carlo Ray Tracing (MCRT) method has become another viable method for RTMs to simulate the interaction between landscapes and radiation. The MCRT method is derived from computer graphics [26]. It traces the paths of an enormous number of photons (rays) and simulates a sequence of scattering events of photons between the light source and the receiver [27,28,29]. Some MCRT methods can simulate RT in fully explicit 3D scenes with structural detail at the individual leaf level [27,28,30,31,32]. Such RT modeling on structurally explicit 3D scenes (of arbitrary complexity) provides the opportunity to simulate RS observations with minimal structural assumptions [33].
The representation of forest structure is an important input that affects RTM accuracy [2,5,34,35,36]. In one-dimensional RT models such as PROSAIL [37], the canopy structure is assumed to be a spatially homogeneous layer, i.e., the turbid medium layer. In 3D RTMs, simple 3D geometries (e.g., ellipsoid or cone archetypes) are most often used to represent the 3D structure of trees [38,39,40,41]. When inferring biophysical properties from these abstract representations, care is needed because such crown archetypes typically do not fully consider within-canopy clumping [5,42,43]. Some studies built more detailed 3D tree structures using observed structural parameters and ecological properties [44,45,46,47,48,49]. Their tree models were built using field inventories, canopy information extracted from airborne laser scanning (ALS), parametric modeling of plant anatomy, topology, and software such as OnyxTree (www.onyxtree.com, accessed on 22 August 2023). However, the above 3D models do not necessarily represent tree structure of individuals in the forest stand sufficiently.
Using fewer assumptions and approximations about physical parameters in the forest structure reconstruction process generally results in more realistic forest representations. RTMs with more precise 3D forest structure representations enable more accurate radiative transfer (RT) modeling at a finer resolution. Widlowski et al. [5] and Liu et al. [2] proved that the choice of the architectural abstraction for canopies (voxel-based or 3D-explicit) can result in significant biases in RT modeling. Janoutová et al. [34] showed that compared to the explicit needle representation, the turbid needle representation could not well reproduce reflectance around the hot spot and in the extreme zenith angles in RT modeling. Based on the terrestrial laser scanning (TLS) point cloud, the 3D-explicit structural model first uses geometric 3D models to reconstruct the woody tree structure. The resulting woody components are subsequently employed as attractors to rebuild the leaves by incorporating field-measured structural characteristics and geometric 3D models [50]. Widlowski et al. built 3D models of three shea trees from TLS data and replicated them to reconstruct a savanna scene [5]. They employed a ray-casting algorithm to determine the number of leaves to be placed along the branches inside the canopy for trees with high LAI values. Calders et al. reconstructed a complete temperate deciduous forest stand using quantitative structure modeling (QSM) and TLS data [51]. They used the FANNI algorithm to add leaves to the reconstructed woody structure. Janoutová et al. reconstructed a 3D spruce tree model from TLS data and tested different levels of leaf representations [34]. These leaf representations included detailed needle shoots transformed into turbid medium, simplified shoots retained as facets, and detailed needle shoots retained as facets.
3D-explicit forest representations will guarantee that the relations between forest properties and satellite/airborne RS signatures at high or very high spatial resolutions can still be properly understood and adequately exploited [5]. Such realistic 3D forest representations are of great value for the realistic calibration and validation of earth observation (EO) data, as well as to provide useful uncertainty assessment [51]. Moreover, 3D-explicit forest representations are likely to be the most promising way to accurately simulate the response of in-situ instruments [5]. However, reconstructing the 3D-explicit forest structure at stand scale (≥1-ha) is time-consuming and labor-intensive [52,53]. Performing RT modeling using a 3D-explicit structure typically also requires a considerable amount of computational resources. Considering the above challenges, only a few studies have reconstructed 3D-explicit models from TLS data incorporating all trees within the forest stand. In some studies, only a small number of trees (less than five) were 3D-explicitly modeled and then replicated to create a forest stand that was used as input for the RTM [5,34,54]. Instead of collecting in-situ scanned data, some studies utilized simulated forest point cloud data or virtual tree models [35,36]. So far, there was only one stand-scale 3D-explicit forest model for RTM purposes, which individually reconstructed all trees within a forest stand in Wytham Woods (UK) [51].
Using the multi-temporal forest representation as the structural input for RTMs enables realistic RT modeling for real-world forest dynamic processes such as tree growth, mortality, and disturbances. Such multi-temporal RT modeling can help us not only comprehend the underlying relation behind forest structure changes and RS signal changes that have occurred in the past but also generate plausible projections of such changes in the future. Bitemporal forest representation (summer and winter) of a 1.12-ha Järvselja Birch stand was reconstructed by Widlowski et al. [48] based on inventory data and the subsampling approach. The forest dynamic change between summer and winter was represented by trees with and without leaves and differences in ground spectral properties. The temperate mixed forest located on the southern slope of the Laegern mountain in Switzerland was scanned by TLS in 2014 [55] and helicopter-based LiDAR in 2010 [43]. 3D forest scenes made of voxels (2010 and 2014 scenes) and simple 3D geometries (2010 scene) were reconstructed based on the LiDAR data for RT modeling [43,55]. In addition to forest structure, Lukes et al. [56] used varying spectral properties to represent the temporal changes in forests. However, the above 3D forest scenes in RT modeling were either not reconstructed in fully explicit (e.g., based on approximations of subsampling reconstruction or voxel-based representations) or static. There are no structurally explicit and multi-temporal 3D forest scenes for RT modeling, which limits our capability to model dynamic RT processes of forests in a spatially explicit way and to investigate the impact of forest structural dynamics on RT at fine spatial scales.
Based on recent advances in TLS hardware and processing, multi-temporal and 3D-explicit forest structure models could be built for RT modeling to aid research and applications in RS, climate change, and ecology. To this end, this study aims to: (1) reconstruct the 3D-explicit scene of a typical temperate deciduous forest at two time stamps, 2015 and 2022, to achieve physically realistic and process-traceable RT modeling of forest dynamics; (2) demonstrate the potential use of this bitemporal 3D-explicit RT modeling on the forward modeling and quantitative interpretation of: RS observations of LAI, fraction of absorbed photosynthetically active radiation (FAPAR), and stand-level canopy light regimes; and the impact of canopy gap dynamics on light availability at explicit locations within the canopy under different illumination conditions (diffuse light, midday direct light, and morning direct light); (3) evaluate the computational efficiency of the bitemporal 3D-explicit RT modeling presented. We intend to demonstrate that the bitemporal 3D-explicit RT modeling presented allows spatially explicit modeling of canopy light regimes over time to study key ecosystem processes related to canopy light distribution and to aid in the interpretation of RS data on forest structural dynamics. If successful, this study would provide the first 3D-explicit forest model with bitemporal structural representations, which is one of the most realistic forest scenes for bitemporal 3D RT modeling to date.
2. Materials and Methods
2.1. Study Area and Data Collection
The study site is Wytham Woods [57,58], a typical temperate forest located in the southern UK (Figure 1). The research was conducted within a 1-ha area (100 × 100 m) of mixed deciduous forest, which is a part of the ForestGEO global network of forest inventory plots nested within an 18-ha long-term forest inventory plot run by Oxford University [51,59]. Sycamore (Acer pseudoplatanus), common ash (Fraxinus excelsior), and common hazel (Corylus avellana) were the dominant species.
Figure 1.
Geographic location and map of Wytham Woods with plot indicated by ‘X’ [60].
Calders et al. [51] collected the 3D structural information of the study area in 2015 using TLS. The forest inventory census data was also used in Calders et al. [51], which showed that in 2015, the average diameter at breast height (DBH) of the individual tree in the site was 35.2 cm and the median DBH was 24 cm. In the census, the smallest DBH was 2.9 cm and the largest DBH was 141.2 cm. This study repeated the TLS data collection in leaf-off (February and March 2022) and leaf-on (June 2022) conditions. The 1-ha plot was scanned in a regular 20 × 20 m grid. There were 36 scan locations in total. A 0.04° angular sampling was used for both zenith and azimuth angles during scanning, with the scanning range spanning from 0° to 130° for zenith and 0° to 360° for azimuth. An upright and a tilted scan were conducted at each scan location for better scanning coverage. Spectral properties of leaves, bark, and understorey in the study area measured by Calders et al. [51] using a FieldSpec (ASD Spectrometer) (Malvern Panalytical, Malvern, UK) were used in this study for RT modeling. The TLS data of the study area in 2015 was collected using a RIEGL VZ-400 scanner (RIEGL, Horn, Austria) [51], whereas a RIEGL VZ-400i TLS was used in 2022. In 2015 and 2022, the scanners were both operated with a scanning frequency of 300 khZ, and the operating wavelength of the two instruments was both 1550 nm. These two terrestrial laser scanners record different lower reflectance thresholds (−20 dB in VZ-400 and −25 dB in VZ-400i) in the raw data. The data from both scanners were compared, indicating similar raw data when reflectance values below −20 dB were filtered out.
2.2. 3D-Explicit Reconstruction of 2022 Forest Stand Structure
The 3D-explicit model of the 2022 forest stand was reconstructed in this study. This reconstructed forest scene, together with the scene reconstructed in 2015 [51], were used as structural inputs for bitemporal RT modeling. Similar to the approach used to reconstruct the 2015 scene [51], our forest stand reconstruction was conducted in four main steps: (1) tree segmentation; (2) quantitative structure modeling; (3) leaf addition; and (4) digital terrain model (DTM) generation and forest stand assembling. TLS data of the leaf-off condition was used for tree extraction and QSM modeling (steps 1 and 2). Both leaf-on and leaf-off data were used for the leaf addition step (step 3). The DTM was generated based on the leaf-off point cloud of the plot.
2.2.1. Tree Extraction
Point clouds from all scan locations were first co-registered to a single point cloud using RIEGL’s RiSCAN PRO software package (v2.17). In 2015, the colored iron flags were put at the scan locations. When conducting scanning in 2022, by using these flags as the reference, we put the scanners at the same scan locations as in 2015. Therefore, the TLS plot scans were aligned between 2015 and 2022. Similar to the reconstruction of the 2015 model, the registered plot point cloud was downsampled to 0.026 m resolution. Calders et al. [51] extracted individual trees of the forest stand from 2015 leaf-off point cloud data using the treeseg open-source software (v0.1.0) [61] with manual quality control. This study used these 2015 extracted trees as a starting base to manually segment individual trees from the 2022 leaf-off point cloud data. Manual segmentation can be time-consuming but guarantees the highest quality control for segmentation [62].
2.2.2. Quantitative Modeling of Tree Structure
This study built a QSM [63] for each tree based on their segmented leaf-off point cloud. The QSM workflow [62] using treeqsm v2.0 was used. Based on the skeleton of the tree leaf-off point cloud, this QSM workflow fitted cylinders to the point cloud data. More specifically, we first built multiple QSMs from the individual tree point cloud using different cover patch sizes (from 0.03 m to 0.08 m at an increment of 0.005 m). Under each cover patch size, ten QSMs were built. Then we used the optimal workflow from Calders et al. [51] and the visual quality check with the original point cloud as the reference to choose the optimal tree QSM from the multiple QSMs reconstructed.
2.2.3. Leaf Addition
The modeled tree QSM was used as an attractor to rebuild the leaves using the Foliage and Needles Naïve Insertion (FaNNI) algorithm [50]. The leaf area density distribution depended on the branch height and order. The reconstructed leaves mostly faced upwards with some random variations. The assumed leaf shape was a tetragon, and the length was distributed uniformly between 25 cm and 30 cm. The above leaf shape assumptions could reduce the number of triangular facets modeled with acceptable realism, thus providing a feasible computational efficiency for RT modeling. This study used the same leaf structural simplifications as in the 2015 scene [51] when reconstructing leaf models for 2022 to remain similar leaf shapes in the bitemporal comparison of RT modeling.
The LAI was obtained based on leaf-on and leaf-off scans of 2022. LAI is defined as half the total developed area of leaves per unit horizontal surface area [64]. The directional gap fraction was used with the raw TLS data to calculate the mean effective wood area index (eWAI, from leaf-off data) and effective plant area index (ePAI, from leaf-on data) based on methods from Calders et al. [65,66], and methods from Jupp et al. [67] that were implemented in the pylidar package (https://www.pylidar.org/, accessed on 9 June 2023). The directional gap fraction was the gap fraction of the canopy in a certain hinge region at each scan location. The zenith ring between 55° and 60° was used as the hinge region in this study to convert the gap fraction model without making assumptions about the foliage and wood orientation function [65]. The eWAI was defined as one-half of the total area of light that can be intercepted by stems and branches per unit of horizontal ground surface area, which was extracted from leaf-off scan data. The ePAI was defined as one-half of the total area of light intercepted by plants per unit of horizontal ground surface area, which was extracted from leaf-on scan data.
The effective leaf area Index (eLAI) was defined as one-half of the total area that light can be intercepted by leaves per unit of horizontal ground surface area [68]. Similar to the 2015 model, the eLAI of the 2022 model was estimated using a linear regression between ePAI, eWAI, and eLAI (eLAI = 0.552 + 1.069 × (ePAI − eWAI), R2 = 0.87) [65]. The eLAI of the plot was the average value of the eLAI calculated from every scan location. Based on Ryu et al. [69], a clumping index Ω of 0.98 was used to estimate the total stand leaf area: total leaf area = 10,000 × eLAI/Ω. The 10,000 is the total area of the plot in m2 (i.e., 1-ha). We conducted this empirical calibration of LAI to ensure consistency with the processing of the 2015 models, thereby justifying the comparative analysis. The total stand leaf area was distributed over all trees according to the relative tree branch length obtained from the tree QSM.
2.2.4. DTM Generation and Forest Stand Assembling
We used the Triangulated Irregular Network (TIN) algorithm [70] to build DTM from the 2022 leaf-off point cloud data. The TIN algorithm created the DTM by the iterative densification of the triangulated irregular network. The spatial resolution of the DTM was 1 m. After DTM generation, the 3D-explicit forest stands were reconstructed by placing all 3D-explicit modeled trees on the DTM. The spectral properties of leaves and wood (Figure 2) were assigned to each tree in the reconstructed 2022 forest stand based on the individual tree species. The reflectance of DTM was set as in-situ measured understorey reflectance.
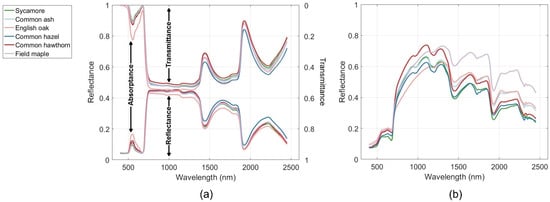
Figure 2.
Spectral properties of different tree species in the plot [2,51]. (a) Reflectance and transmittance of leaves; (b) reflectance of bark.
2.3. Radiative Transfer Modeling
2.3.1. Canopy Light Regimes at the Stand Scale
The DART model [31,71] was used to conduct RT modeling. DART can simulate the Earth-atmosphere radiation interactions from visible to thermal infrared wavelengths. A comprehensive benchmarking between DART and other RTMs for simulating vegetation canopy reflectance has been conducted by Pinty et al. [72,73] and Widlowski et al. [4,48,74]. Liu et al. [75] also benchmarked DART modeling against UAV-measured images using the 2015 Wytham Woods model. DART modeling showed agreement with UAV RS imagery in both pixel level with Pearson’s r = 0.6 at NIR band and stand scale (normalized deviation +1.9% at NIR band) [75].
The 3D-explicit forest scenes of the 2015 and 2022 Wytham Woods forest stand were used as structural inputs for DART. The scenes were duplicated around themselves eight times to ensure energy conservation in the RT modeling. In this duplication process, the height of DTM’s edge was slightly shifted to preserve the continuity of the scene and slope (see “infinite slope” in [76,77]). The atmosphere characteristics were based on the MODTRAN atmosphere model [78]. The Mid-Latitude Summer gas model and the Rural aerosol model with a visibility of 23 km were used in this study [79]. The sky was assumed to be cloud-free in the modeling [43]. The solar zenith and azimuth angles were 38.4° and 125.2°, respectively. These solar angles were the same as in the DART benchmarking work against UAV RS imagery [75], corresponding to the solar angles at Wytham Woods at 10 a.m. on the 30 June 2015, which corresponds to the period of data collection in 2015.
We simulated multiple forest biophysical properties and biosphere ECVs at two time stamps (2015 and 2022) in this study. These simulated variables include top-of-canopy variables (HDRF at nadir viewing direction), inside-canopy variables (the vertical profiles of light extinction, absorption, and LAI), and stand-level variables (canopy cover and FAPAR). LAI, canopy cover, and FAPAR are biosphere ECVs that critically contribute to the characterization of Earth’s climate [80]. The vertical profiles of light extinction and absorption are essential for understanding forest processes and ecosystem functions because light interception is a driving variable for many key ecosystem processes [81]. The HDRF is the reflectance product of space-based RS instruments that have an IFOV with a full cone angle of approximately 0.1° (e.g., MODIS, AVHRR) [82]. We simulated these variables to demonstrate the potential of this bitemporal 3D-explicit RT modeling on the forward modeling and quantitative interpretation of observations on important forest variables.
The HDRF was simulated using the DART-Lux mode. The DART-Lux mode allowed rapid simulation of spectral images of complex landscapes. The comparison in a variety of scenarios showed that DART-Lux mode was consistent with DART-FT mode (relative differences < 1%), with image simulation time and memory reduced by a hundredfold [31]. The FAPAR and the vertical profiles of light extinction and absorption were simulated using the DART-FT mode, as the DART-Lux mode was less efficient than the DART-FT mode in radiative budget modeling.
The spatial resolution of the DART-FT modeling was 1 m (i.e., the cell dimension in the modeling was 1 × 1 × 1 m3, and the vertical profiles of light extinction and absorption were documented every 1 m along height). In the modeling, the amounts of PAR absorbed by every object in the scene were recorded and used to calculate different types of FAPAR by dividing by the amount of PAR reaching the scene. More specifically, leaf FAPAR, wood FAPAR, understorey FAPAR, and total FAPAR were recorded in the modeling for better analysis of radiative transfer processes within the canopy. The leaf, wood, understorey, and total FAPAR were the fraction of photosynthetically active radiation absorbed by leaves, woody components, understorey, and whole forest scene, respectively. The canopy cover and the vertical profile of LAI of the virtual forest scenes in RT modeling were calculated from the reconstructed bitemporal 3D-explicit forest stand. The canopy cover refers to the ratio of vertically projected canopy-covered area to the total area of the given site [83]. We also documented the leaf cover and wood cover in this study to better analyze the RT process within the forest. The leaf cover and wood cover refer to the ratio of vertically projected leaf-covered and wood-covered area to the total area of the given site, respectively. The bitemporal RS images were simulated for Sentinel-2 MSI bands using a flat sensor spectral response for each waveband. We simulated the top of the canopy HDRF at nadir viewing direction. HDRF simulations at moderate (10 m), high (25 cm), and ultra-high resolutions (1 cm) were conducted to match the Sentinel-2, commercial high-resolution (e.g., Planet), and possible ultra-high resolution EO missions in the future.
Light extinction and absorption inside the canopy were 3D-explicitly simulated at PAR (400–700 nm), blue (457.5–522.5 nm), green (542.5–577.5 nm), red (650–680 nm), and NIR (784.5–899.5 nm) bands. The amount of downward radiation (zenithal range 90–180°, azimuthal range 0–360°) at a certain height layer above the ground at stand scale was recorded in the simulation and used to calculate the canopy light extinction at that height by comparing to the solar irradiance.
2.3.2. Canopy Light Availability at Explicit Locations
We selected 4 locations in the forest stand that represent typical examples of gap dynamics (Figure 3 and Figure 4). The horizontal locations of selected canopy gap dynamics were shown in Figure 3. Figure 4 shows the vertical profiles of selected canopy gap dynamics observed by terrestrial laser scanning. The first location was a gap located at a dead tree fall. At this location, the dead tree fall increased the gap fraction within the canopy, while the growth of the neighboring tree canopy reduced the gap fraction. The gap fraction was calculated as the fraction of the sky visible through the canopy [84]. The second location was a new canopy gap caused by the branch damage of a living tree. It was used to study the impact of canopy damage on light availability within the canopy and at ground level. The third location was a closing gap due to neighboring canopy growth. The fourth location was a reference location for comparison where only natural canopy growth occurred.
Figure 3.
Locations of canopy gap dynamics and photosynthetically active radiation (PAR) sensors simulated, shown in the TLS point cloud (top view): (a) 2015; (b) 2022.
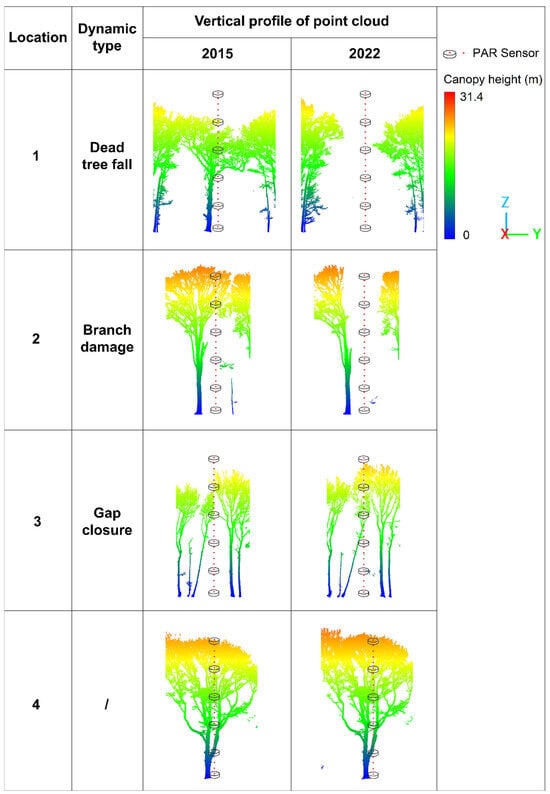
Figure 4.
Vertical profiles of different types of canopy gap dynamics observed by terrestrial laser scanning, and the position of simulated PAR sensors.
To investigate the impact of gap dynamics on light availability within the canopy, three illumination conditions were used in this simulation of explicit locations: perfectly diffuse light, midday direct light, and morning direct light. Diffuse light arose from the scattering of sunlight by the atmosphere and arrived at the scene equally from all directions, whereas direct light arrived in a straight line from the sun without being scattered [85]. The illumination zenith and azimuth angles for the midday direct light were 28.4° and 180°, respectively. This illumination angle corresponded to the solar angle of 1 p.m. at the study site on the summer solstice (i.e., the maximum solar altitude angle for the year). The illumination zenith and azimuth angles for the morning direct light were 81.3° and 62.7°, respectively. This illumination angle corresponded to the sun’s position at 6 a.m. on the summer solstice at the study site.
The canopy light availability at the above locations was simulated. The photosynthetically active radiation (PAR) sensor measurements of downward radiation at 400 to 700 nm wavelengths were simulated at each location. The simulated PAR sensors measured all downward PAR (i.e., zenithal range 90–180°, azimuthal range 0–360°) passing through the intercepting area. The radius of the sensor intercepting area was 3 cm. The spectral response of the sensor was assumed to be flat. The sensors were placed every 1 m along the height, starting at 1 m above ground up to the top of the canopy (25 m above ground) (Figure 4), to simulate canopy light availability below, inside, and above the canopy. The sensor’s field of view was assumed to be the entire hemisphere (i.e., zenith viewing angle 0–90°, azimuth viewing angle 0–360°). To account for the light extinction, the downward radiation recorded by the simulated PAR sensor was normalized by dividing by the solar irradiance. The solar irradiance was obtained above the canopy, from sensor simulations at 40 m height. Finally, the simulated bitemporal light extinction profiles at each location were used to study the impact of gap dynamics on forest light regimes.
2.4. Evaluation of Computational Efficiency of Bitemporal 3D-Explicit Radiative Transfer Modeling
The computational efficiency of the presented bitemporal 3D-explicit radiative transfer modeling was evaluated by the time and RAM consumption. We documented the time and RAM consumption of different types of RT simulations conducted, including simulations of optical remote sensing observation, canopy light distribution, and light availability at explicit locations (PAR sensor simulation). The RT simulations were conducted at the HPC facility of Ghent University. The hardware and simulation settings related to efficiency are listed in Table 1.

Table 1.
Hardware condition and simulation settings related to computational efficiency.
2.5. Flowchart of Research Methodology
The methodology flowchart of this research is shown in Figure 5.
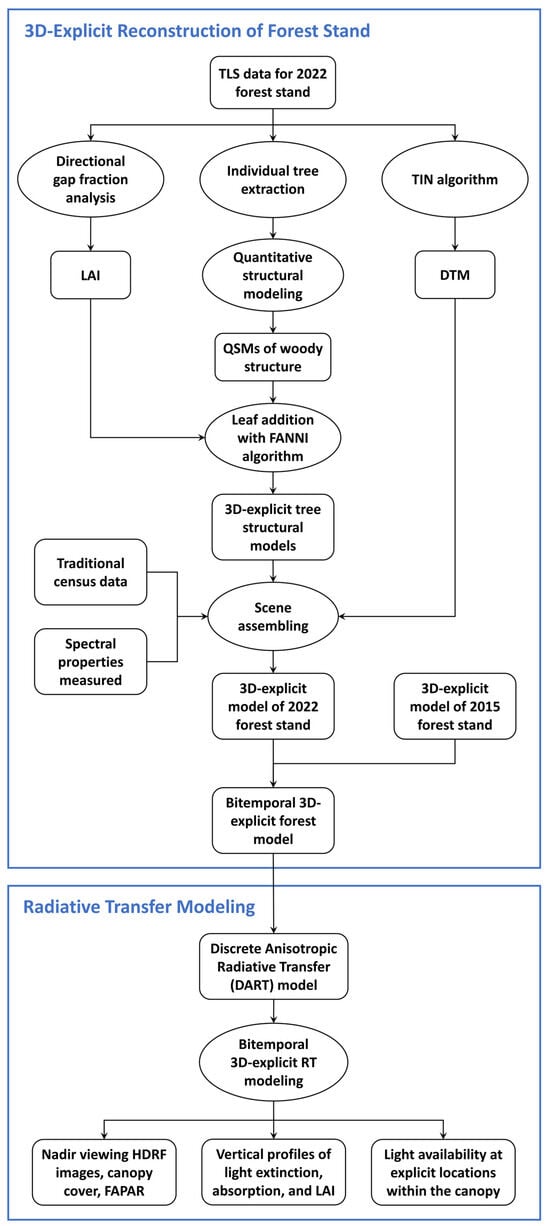
Figure 5.
Flowchart of research methodology. QSMs of woody structure were reconstructed using leaf-off TLS data.
3. Results
3.1. 3D-Explicit Reconstruction of 2022 Forest Stand
Leaf-off point clouds of 520 individual trees were segmented from the 1-ha leaf-off 2022 TLS data (Figure 6). The dynamics in the wood structure of an individual tree from 2015 to 2022 are illustrated in Figure 7. At stand scale, 30 trees have fallen since 2015, including 20 living and ten dead trees. QSMs of 520 trees in the stand were reconstructed individually based on their segmented point cloud data. Figure 8c shows an example of the optimized QSM for a Sycamore tree.
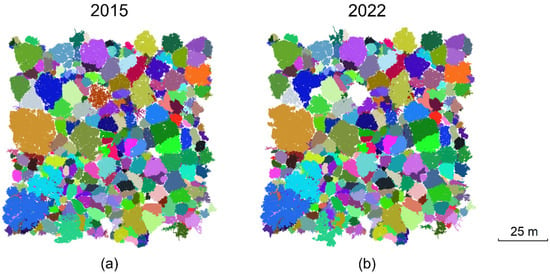
Figure 6.
Segmented TLS leaf-off point cloud of 1-ha Wytham Woods forest stand (top view): (a) 2015; (b) and 2022. Each color represents an individual tree.
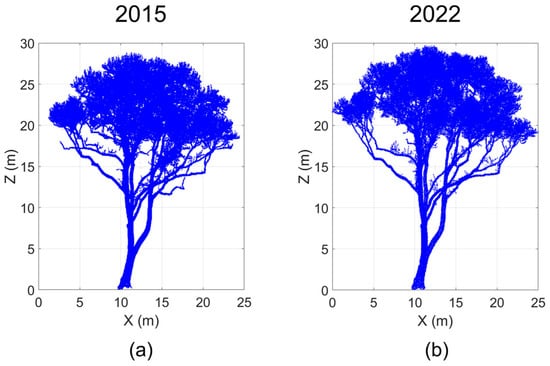
Figure 7.
The dynamic change of wood structure of a Common ash (Fraxinus excelsior) tree from 2015 to 2022. (a) 2015 leaf-off point cloud; (b) 2022 leaf-off point cloud.

Figure 8.
3D-explicit reconstruction of a Sycamore (Acer pseudoplatanus) tree. (a) TLS point cloud colored by height (leaf-off); (b) QSM overlaid with TLS leaf-off point cloud; (c) QSM, the modeled branch length was 3863.3 m; (d) Fully reconstructed tree: QSM + leaves, the leaf area assigned to this tree was 888.2 m2.
Directional gap fraction analysis in leaf-on and leaf-off conditions obtained a stand-level ePAI of 5.7 and an eWAI of 1.9 by calculating the average ePAI and eWAI values from all scan locations. Thus, the eLAI and LAI were estimated to be 4.6 and 4.7, respectively. The 509 living trees had a total branch length of 202.7 km, according to QSM. The branch length of the individual living trees ranged from 2 m to 9.3 km, with the median branch length per tree being 195.5 m. The total leaf area of 47,000 m2 was distributed over the individual trees based on the relative branch length (tree branch length divided by total stand branch length). Figure 8d shows a fully reconstructed 3D-explicit model of a Sycamore tree. The complete 1-ha 3D-explicit models for the 2022 and 2015 forest stands are shown in Figure 9.
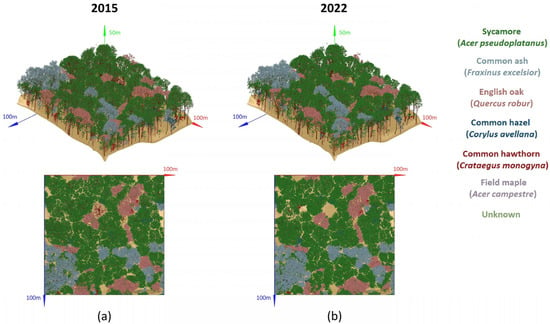
Figure 9.
The 3D-explicit models of the complete 1-ha Wytham Woods forest stand in (a) 2015 and (b) 2022. The different leaf colors represent the different tree species present in Wytham Woods. The stems and branches of all trees are shown in brown.
3.2. Bitemporal Radiative Transfer Modeling
3.2.1. Vertically Resolved Radiative Transfer
The vertical distribution of LAI in the 2022 forest scene shifted upward compared to the 2015 scene (2022 vertical LAI peak: 20 m above ground, 2015 vertical LAI peak: 19 m above ground) (Figure 10c). The simulated vertical light absorption profile for the 2022 scene also shifted upwards from the 2015 scene (Figure 10b): the absorption peak of the 2022 scene was 21 m above ground, which was one meter higher than in the 2015 scene. Correspondingly, the light availability decreased faster from top-of-canopy to ground level in the 2022 scene compared to 2015 (Figure 10a). The above trends also apply to NIR, blue, green, and red bands (Figure 11). While the LAI increased from 2015 to 2022 (from 3.8 to 4.7), the canopy cover and leaf/wood cover did not show a big change (Table 2). The leaf cover remained the same, and the wood cover decreased by 5% because 30 trees fell between 2015 and 2022. The forest’s total FAPAR also did not change along with vertical and total LAI (Table 2). The leaf FAPAR increased by 0.037, the wood FAPAR decreased by 0.033, and the understorey FAPAR remained the same from 2015 to 2022.
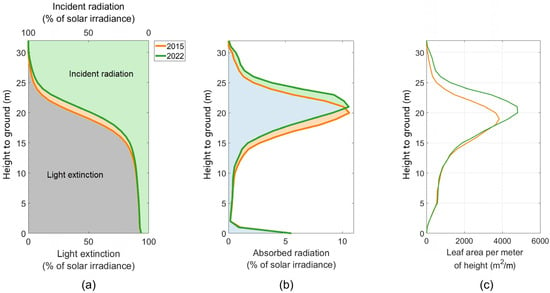
Figure 10.
The vertical profiles of simulated (a) light extinction, (b) light absorption, and (c) leaf area per meter of height in 2015 and 2022 forest scenes. The results of light extinction and absorption were based on the PAR band. The illumination zenith angle (IZA) was 38.4° and the illumination azimuth angle (IAA) was 125.2°.
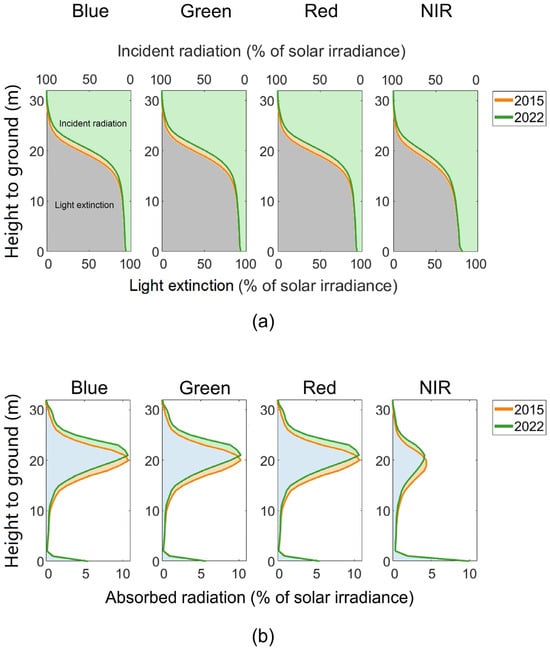
Figure 11.
The vertical profiles of simulated (a) light extinction and (b) light absorption in the blue, green, red, and NIR bands for the 2015 and 2022 forest scenes. Illumination zenith angle (IZA) 38.4°, illumination azimuth angle (IAA) 125.2°.

Table 2.
The LAI, vegetation cover, and simulated FAPAR in 2015 and 2022 forest scenes.
3.2.2. Forward Modeling of Hemispherical-Directional Reflectance Factor
The simulated bitemporal HDRF images at the spatial resolution of Sentinel-2 observation, high-resolution commercial RS observation, and potential ultra-high-resolution RS observation were shown in Figure 12. The HDRF of the 2022 scene at nadir viewing direction was on average 3.8% lower than the 2015 scene, in Sentinel-2 RGB bands. In contrast, in the NIR band, the 2022 forest scene reflected more radiation than the 2015 scene. The HDRF at nadir viewing direction was 4.2% higher in 2022 compared to 2015. These changes in HDRF were caused by the forest structure dynamics from 2015 to 2022.
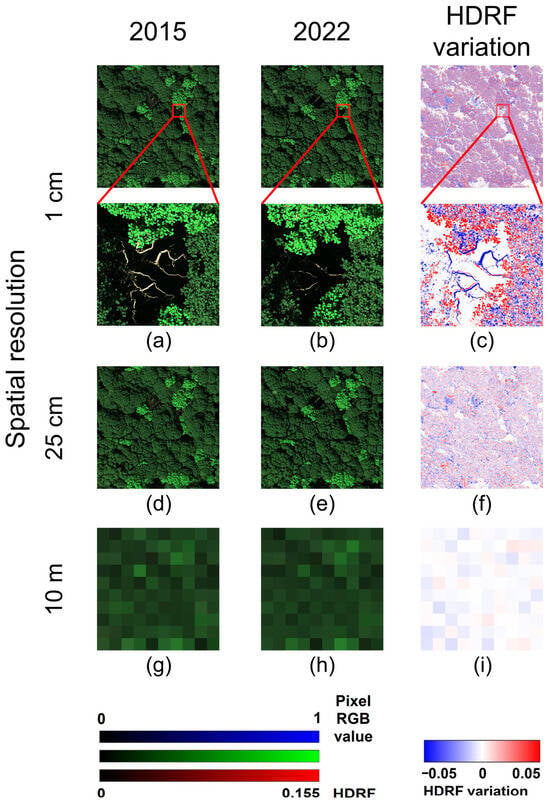
Figure 12.
Simulated top of canopy images of Wytham Woods forest scenes in 2015 and 2022. The images were simulated under nadir viewing directions and Sentinel-2 RGB bands. IZA 38.4°, IAA 125.2°. (a,b) Ultra-high resolution images in 2015 and 2022 (spatial resolution: 1 cm); (d,e) 25 cm resolution images in 2015 and 2022; (g,h) 10 m resolution images in 2015 and 2022; (c,f,i) Spatial pattern of HDRF variation from 2015 to 2022 (red band).
3.2.3. Impacts of Canopy Gap Dynamics on Light Availability
Results showed that the canopy gap dynamics had important impacts on the simulated local light availability. These impacts were also different depending on the illumination conditions (Figure 13, Figure 14, Figure 15 and Figure 16).
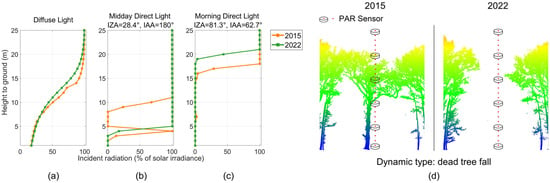
Figure 13.
Light extinction profiles of downward PAR at location 1: (a) diffuse light; (b) midday direct light (IZA 28.4°, IAA 180°); (c) morning direct light (IZA 81.3°, IAA 27.3°). The X axis is the local light availability represented as the percentage of incident solar irradiance. The Y axis is the height from the simulated sensors to the ground. (d) The canopy gap dynamic at this location.
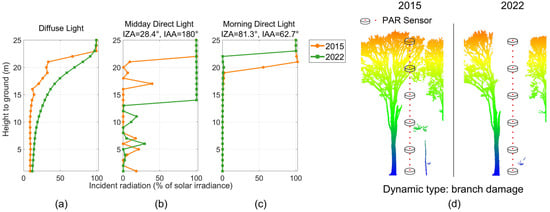
Figure 14.
Light extinction profiles of downward PAR at location 2: (a) diffuse light; (b) midday direct light (IZA 28.4°, IAA 180°); (c) morning direct light (IZA 81.3°, IAA 27.3°). The X axis is the local light availability represented as the percentage of incident solar irradiance. The Y axis is the height from the simulated sensors to the ground. (d) The canopy gap dynamic at this location.
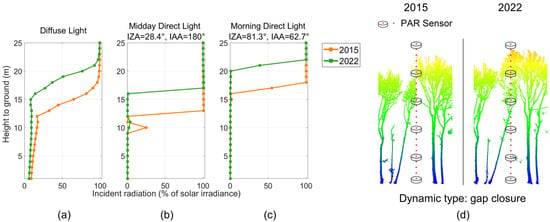
Figure 15.
Light extinction profiles of downward PAR at location 3: (a) diffuse light; (b) midday direct light (IZA 28.4°, IAA 180°); (c) morning direct light (IZA 81.3°, IAA 27.3°). The X axis is the local light availability represented as the percentage of incident solar irradiance. The Y axis is the height from the simulated sensors to the ground. (d) The canopy gap dynamic at this location.
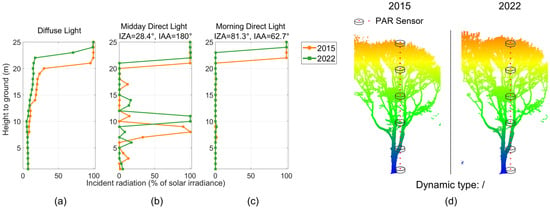
Figure 16.
Light extinction profiles of downward PAR at location 4: (a) diffuse light; (b) midday direct light (IZA 28.4°, IAA 180°); (c) morning direct light (IZA 81.3°, IAA 27.3°). The X axis is the local light availability represented as the percentage of incident solar irradiance. The Y axis is the height from the simulated sensors to the ground. (d) The canopy gap dynamic at this location.
The canopy gap dynamic at location 1 was caused by a dead tree fall and the growth of the neighboring canopy. Under diffuse light, the downward PAR at 9 to 20 m above ground at location 1 decreased by 7.8% of solar irradiance from 2015 to 2022 (Figure 13a). The largest reduction happened at 14 m height, where the downward PAR decreased by 15% of solar irradiance. At 9 to 20 m above ground, the tree canopy growth near the gap had a greater impact on the gap fraction than the dead tree fall. Hence, the downward PAR at these heights decreased under diffuse light.
Under midday direct light, the downward PAR increased significantly from 2015 to 2022 at 5 to 10 m above ground (Figure 13b). The downward PAR at 5 to 10 m heights in the 2022 scene increased by 84.8% of solar irradiance on average compared to the 2015 scene. Moreover, there was a brief increase of downward PAR at 4 m height in the 2015 scene compared to other heights, which was caused by sunflecks at this location. Under more oblique direct light in the morning, the downward PAR at 17 to 20 m heights in 2022 decreased by 70.3% of solar irradiance compared to 2015 (Figure 13c). In 2015 forest scene location 1, the midday direct light can reach sensors higher than 10 m without being intercepted by the canopy. Then, the incident light began to be partially intercepted by the dead tree before reaching the sensor at 10 m height and was fully obscured before reaching the sensor at 8 m height. In the 2022 scene, due to the fall of a dead tree, the midday direct light can reach the sensors at 5 m height and above without being intercepted. As a result, there was an increase in downward PAR at 5 to 10 m heights in 2022 under midday direct light, compared to 2015. The morning direct light passed more horizontally through the canopy than the midday direct light (zenith angle 81.3° vs. 28.4°). As a result, it had a longer path through the canopy and was intercepted more by the top of the canopy compared to midday direct light. In the 2015 scene, the morning direct light can reach sensors at 18 m height and above without being intercepted by the canopy. While in the 2022 scene, the morning direct light was intercepted by the canopy at higher positions (20 m height) than in the 2015 scene due to the canopy growth, which resulted in the decrease of downward PAR at 17 to 20 m heights from 2015 to 2022.
The gap formation at location 2 (Figure 14d) was caused by branch damage in the upper canopy. This gap dynamic led to a greater gap fraction and increased the light availability inside the canopy. Under diffuse light, the downward PAR at 1 to 22 m heights in location 2 increased by 15.5% of solar irradiance on average from 2015 to 2022 (Figure 14a). The maximum increase occurred at 21 m height (47% of solar irradiance), and this downward PAR difference between 2015 and 2022 scenes gradually declined to 3% of solar irradiance as one moved from the interior of the canopy to the understory (sensor height decreased from 21 m to 1 m). The gap dynamic of location 2 occurred at the upper canopy (Figure 14d). This gap dynamic had less impact on the gap fraction at more distant positions (i.e., closer to the ground) due to the field of view. Therefore, under diffuse illumination, the downward PAR difference under the canopy between 2015 and 2022 was smaller than the difference within the canopy.
Under midday direct light, the downward PAR at 14 to 21 m heights in location 2 increased significantly (93.2% of solar irradiance on average) from 2015 to 2022 (Figure 14b). The branch damage at location 2 happened at the upper canopy. In the 2022 scene, the midday direct light can reach the sensor at 14 m height without being intercepted because of this gap dynamic. In the 2015 scene, the midday direct light was intercepted by the upper canopy (at 21 m height). As a result, the downward PAR at 14 to 21 m heights in the 2022 scene increased significantly than in the 2015 scene, under midday direct light. As the height decreased, there was also some brief increase of light availability at several heights below and within the canopy (fluctuations in Figure 14b, at 1 to 11 m heights, and 17, 19 m heights of the 2015 scene). Sunflecks caused these brief increases in light availability, as midday direct light can better penetrate the canopy than diffuse and morning direct light. Under more oblique direct light of morning, the downward PAR at 20 to 22 m heights decreased by 85.3% of solar irradiance from 2015 to 2022 (Figure 14c). This was because the morning direct light was obscured by the top of the canopy before reaching the canopy gap caused by branch damage. Due to the growth of the neighboring canopy, the 2022 canopy was taller than the 2015 canopy and the light was intercepted at higher positions in the 2022 scene.
The closing gap in location 3 (Figure 15d) resulted in a decrease in gap fraction, which led to less downward PAR within the canopy under diffuse light. Under diffuse light, the downward PAR at 1 to 22 m heights in location 3 decreased by 20.3% of solar irradiance on average from 2015 to 2022 (Figure 15a). The largest reduction occurred at 16 m height (decreased by 67.3% of solar irradiance). The closing gap also caused direct light to be intercepted by the canopy at higher positions. In the 2015/2022 scene, the midday direct light can reach the sensors at 13/17 m height without being intercepted, respectively. Hence, the downward PAR at 13 to 16 m heights in the 2022 scene decreased by 99.9% of solar irradiance compared to the 2015 scene (Figure 15b). Similarly, under morning direct light, the downward PAR at 17 to 21 m heights decreased by 82.7% of solar irradiance from 2015 to 2022 (Figure 15c). Moreover, there was a brief increase of downward PAR in the 2015 scene at 10 m height under midday direct light (Figure 15b).
Location 4 was a reference point without gap dynamics apart from natural tree growth (Figure 16d). Under diffuse light, the downward PAR at 8 to 23 m heights of location 4 decreased by 16.5% of solar irradiance on average from 2015 to 2022 (Figure 16a). The largest reduction occurred at the top of the canopy (22 m height, decreased by 82.1% of solar irradiance).
Due to the tree growth, the 2022 canopy was higher than the 2015 canopy and thus intercepted the direct light at higher positions. Under morning direct light, the downward PAR at 22 to 23 m heights decreased by 99.7% of solar irradiance from 2015 to 2022 (Figure 16c). Under midday direct light, the downward PAR at 21 m height decreased by 99.6% of solar irradiance from 2015 to 2022. Meanwhile, the height of sunflecks within the canopy shifted upwards (6 to 8 m heights in the 2015 scene, 10 to 11 m heights in the 2022 scene), causing significant differences in light availability within the canopy between the 2015 and 2022 scenes (Figure 16b).
Under diffuse light, the ground PAR availability at location 2 relatively increased by 33% (from 9.1% of solar irradiance to 12.1% of solar irradiance) due to the branch damage (Figure 14a, 1 m height). At location 3, the ground PAR availability relatively decreased by 31.9% (from 9.1% of solar irradiance to 6.2% of solar irradiance) because of the closing gap. Under direct light, as mentioned above, the PAR availability at the ground mainly depended on whether the incident light could reach the ground unhindered. Since the direct light, whether in the morning or midday, was all intercepted by the canopy before reaching the ground, the canopy gap dynamics in this study had no significant impact on the ground light availability under direct light. Only at location 2 in the 2015 scene, under midday direct light, did the downward PAR at 1 m height show a brief increase (Figure 14b). This increase in ground PAR availability was caused by the sunflecks.
3.2.4. Computational Efficiency of Bitemporal 3D-Explicit Radiative Transfer Modeling
Even though there were about 1.8 million individual objects in each of the 2015 and 2022 forest scenes, the RT modeling required little computational resources (Table 3). Our bitemporal 3D-explicit forest scene combined with the DART model can achieve highly realistic forest RT modeling with a feasible computational resource cost. It is a novel and promising approach to modeling RT for RS and ecology research.

Table 3.
Computational resource consumption for different types of bitemporal 3D-explicit radiative transfer modeling.
4. Discussion
4.1. Impacts of Forest Structural Dynamics on Radiative Transfer
The Wytham Woods forest is a mature forest. From 2015 to 2022, its canopy cover did not substantially change. Therefore, the leaf FAPAR only increased by 0.037 (a relative increase of 5.4%) while the LAI increased by 23.7%. Meanwhile, the nadir HDRF relatively decreased by 3.8% in visible bands. The absorption was the dominant canopy-light interaction in visible bands. With the increase of LAI (3.8 to 4.7), the canopy absorbed more radiation at visible bands this might cause less radiation to be reflected to the sensor by the canopy due to energy conservation.
In the NIR band, in contrast to the visible bands, the scene nadir HDRF increased (+4.2%) with increasing LAI. In the NIR band, canopy reflection is the dominant canopy-light interaction, as little radiation was absorbed by the canopy. Therefore, the increase of LAI caused more reflections of NIR radiation from the canopy, which resulted in the higher nadir NIR HDRF in the 2022 scene than in the 2015 scene.
4.2. Impacts of Canopy Gap Dynamics on Local Light Availability
Under diffuse light, the canopy PAR availability decreased gradually from the top of the canopy to the ground level (Figure 13a, Figure 14a, Figure 15a and Figure 16a). Diffuse light came homogenously from the sky in multiple directions. Therefore, the gap fraction at a position determined how much diffuse light could reach this position without being intercepted. The canopy gap dynamics impacted the PAR availability within the canopy by changing the gap fraction of locations underneath it. The closing gap (location 3), tree growth (location 4), and canopy growth near the fallen tree (location 1) reduced the gap fraction, causing the decrease in PAR availability inside the canopy (Figure 13a, Figure 15a and Figure 16a). The branch damage (location 2) increased the gap fraction and PAR availability within the canopy (Figure 14a).
Diffuse light could better penetrate the canopy [86] and reach the ground than the direct light (Figure 13a, Figure 14a, Figure 15a and Figure 16a vs. Figure 13b,c, Figure 14b,c, Figure 15b,c and Figure 16b,c, 1 m height). Therefore, the vertical profile of canopy PAR availability was more homogeneous under diffuse light compared to direct light. Since the photosynthetic rate of single leaves shows a non-linear response to the light flux density [86], the canopy can use diffuse light more efficiently than direct light. This is important for optimal canopy photosynthesis.
Under direct light, the PAR availability within the canopy decreased sharply at a certain height (Figure 13b,c, Figure 14b,c, Figure 15b,c and Figure 16b,c). The vertical profile of PAR availability within the canopy mainly depended on the position the incident direct light could reach before being intercepted. Under midday direct light, the dead tree fall (location 1) and the branch damage (location 2) allowed the light to reach the deeper canopy unhindered. This increased the PAR availability inside the canopy (Figure 13b and Figure 14b). In contrast, the closing gap (location 3) and the canopy growth (location 4) caused the light to be intercepted by the canopy at higher positions. This led to the decrease in PAR availability within the canopy (Figure 15b and Figure 16b). Moreover, midday direct light was more vertical (zenith angle 28.4°) than the morning light. Hence, midday direct light can better penetrate the canopy and cause sunflecks within and below the canopy. These sunflecks were impacted by the canopy gap dynamics and briefly increased the PAR availability within and below the canopy (Figure 13b, Figure 14b, Figure 15b and Figure 16b). Such sunflecks may contribute up to 80% of the total irradiance in the understorey [87]. These sunflecks can greatly impact the growth of understory plants [88]; the utilization of sunflecks has been credited for up to 60% of the carbon gain by understory plants [89].
The morning direct light was more oblique than the midday direct light (zenith angle 81.3° vs. 28.4°). The morning direct light had a longer path through the canopy and was intercepted more by the top of the canopy, compared to midday direct light. Therefore, the canopy growth in the upper canopy had the greatest impact on the interception of morning direct light compared to other canopy gap dynamics. Due to the canopy growth, from 2015 to 2022, the morning direct light was intercepted higher up in the canopy at all four locations. This resulted in a decrease in PAR availability in the top canopy layer from 2015 to 2022 (Figure 13c, Figure 14c, Figure 15c and Figure 16c).
Some classic light extinction models used the exponential assumption for the vertical light availability within the canopy [90,91,92]. Our results showed that, at fine spatial scales, the canopy light availability might be different from the classic light extinction model, and this difference highly depended on the local canopy structure and its dynamics, as well as the illumination condition (Figure 13, Figure 14, Figure 15 and Figure 16). The differences in the spatial scales investigated and the structural representations might be the reason for the different results between the classic light extinction models and the bitemporal 3D-explicit RT modeling. These differences between models should be considered in future research when modeling the canopy light availability with gap dynamics.
4.3. Outlook
This study is important for modeling the impact of forest canopy dynamics on RT at high resolution so that the RT modeling can be matched to the temporal dynamics observed by UAV RS. Based on bitemporal 3D-explicit forest structure representation, RT modeling could explicitly match with bottom-of-atmosphere RS observations spatially and temporally. However, there are still challenges in (1) matching RT modeling with top-of-atmosphere (i.e., satellite) RS observations, such as accurate modeling of atmospheric effects and its temporal variations (e.g., clouds) and precise registration of geolocation between images; (2) the feasibility of conducing multi-temporal 3D-explicit RT modeling with more sufficient input parameters, in different forest types, and at a landscape level that aligns with the scale of EO to obtain more generalizable conclusions about canopy light regimes. Such challenges need to be investigated in the future.
Different TLS instruments (RIEGL VZ400 and VZ400i) were used to estimate the LAI of the forest stand at two time stamps. Since their difference in lower reflectance thresholds could cause uncertainties in the bitemporal LAI estimation, we filtered the raw TLS data of both instruments to minimize the impact of different TLS equipment on LAI estimation. As a wider range of TLS equipment is commercially available, including that of other manufacturers, future work should include benchmarking studies to guarantee proper use of TLS data in the context of time-series forest dynamics.
This study reconstructed the bitemporal 3D-explicit model for a typical temperate deciduous forest using the QSM and FANNI algorithms and TLS data. Further studies in structurally different forests are needed to obtain the 3D-explicit models of different types of forests and environmental conditions, i.e., forests of different latitudes (tropical, boreal), canopy cover (e.g., savanna), understory (e.g., different ground reflectance due to rain, seasonal leaf litter, or undergrowth), or disturbances (fire, insect infestation). However, due to the diversity of forests, there are multiple difficulties in performing structural modeling for different forest types based on QSM and FANNI algorithms and TLS data. In many forests, only leaf-on TLS data can be used for structural modeling because of their evergreen nature. However, the spatial information of the top of the canopy is incomplete in leaf-on TLS data because of the canopy occlusion on the laser beam. Hence, it is difficult for QSM and FANNI to reconstruct the complete structural model. In addition, accurate leaf-wood separation from TLS point clouds is also a challenge in both tropical and boreal forests. It is difficult to develop an accurate wood-leaf separation algorithm broadly applicable across different tropical forest types because of their structural complexity and diversity [93,94]. In boreal forests, it is challenging to distinguish individual needles in any tree- or plot-level TLS point cloud because conifers have small needles and densely clustered leaves [95]. Often, it is even very difficult to recognize individual needles and branches in point clouds. Moreover, accurate and efficient individual tree segmentation from point clouds has been a pressing problem due to the overlap between tree canopies. The above challenges make it difficult to conduct structural modeling for different forest types based on QSM and FANNI algorithms and TLS data. LiDAR data with more detailed canopy structural information could help to address the above challenges. These LiDAR data might be acquired from, but are not limited to, the full waveform hyperspectral LiDAR [96], LiDAR with greater penetration, or multi-source LiDAR data fusion [97]. If these challenges could be solved, the 3D-explicit model could be reconstructed for diverse forest types based on QSM and FANNI algorithms and LiDAR data.
This study currently uses a general assumption on the spatial heterogeneity of the leaf structure (leaf angle, leaf size, leaf area density distribution) in the leaf reconstruction [50]. The leaf area distribution was based on branch height and order; the leaf orientation was mostly faced upwards with some random variations; the leaf shape was a tetragon, and the leaf length was distributed uniformly between 25 cm and 30 cm. These assumptions on leaf structure in the bitemporal 3D-explicit model produced some errors in the 3D structure compared to the real canopy with leaves. For more precise RT modeling, ground sampling of actual leaf shapes and distributions, such as leaf form, curvature, and arrangement, should be considered in future studies. Moreover, a key issue in quantifying these errors was that explicitly measuring and reconstructing leaf structure at stand scale (>1-ha) was a great challenge for now. The explicit reconstruction of individual leaves was only possible if the leaves in the upper canopy could be fully scanned, i.e., there was no canopy occlusion on the laser beam. To do so, the above-mentioned full waveform hyperspectral LiDAR [96], LiDAR with smaller beam divergence for greater canopy penetration, different TLS scanning strategies [98], or multi-source LiDAR data fusion [97] should be further explored in future research to overcome the canopy occlusion on the laser beam, obtain the complete canopy leaf structural information, and improve the realism of canopy leaf reconstructions.
The spectral properties of trees and understory plants change across seasons. Leaf spectral properties change through the season as leaves age [99]. The reflectance of understorey, leaf, and wood also changes after rain due to water content change. Since this study focused on the impact of long-term forest structural dynamics on RT modeling, we used spectral properties measured in 2015 for RT modeling of the two time stamps. Future multi-temporal RTM studies should consider the effect of the above temporal heterogeneity of forest spectral properties on RT modeling.
The Illumination condition determines the ratio of direct/diffuse incident light and the direction of direct light, thus impacting the canopy light distribution. This study tested three illumination conditions: diffuse light, midday direct light, and morning direct light in the light availability simulation of explicit locations. Further studies with a wider range of illumination conditions are needed to better investigate the impact of illumination conditions on canopy light availability. Comparisons between bitemporal 3D-explicit RT modeling, in-situ PAR sensor measurements, or the classic light extinction model (e.g., the exponential assumption [90,91,92]) are also needed. Such comparisons could help us better understand the light regime inside the canopy.
To improve the value of 3D RTMs in the calibration and validation of RS products, a proper validation method should be designed to validate the 3D RT modeling with in-situ measurements and actual RS observation, possibly starting from using bottom-of-atmosphere RS data (e.g., UAV images) as reference [34,43,75,100], then validating the 3D RT modeling with top-of-atmosphere RS data (i.e., satellite EO). More complex forest elements should also be reconstructed for more precise RT modeling. These elements include, but are not limited to, lianas in tropical forests [101], grasses, and shrubs. The combination of UAV-LiDAR and TLS is a promising way to improve the scale of 3D RT modeling to align with the scale of EO. Forest structural properties at a landscape level can be efficiently obtained from UAV-LiDAR data. Such forest properties of large scale can be used as the quality index [75] to guide the TLS-based tree library reconstruction method [34,48,75]. In this way, it is possible to conduct 3D forest RT modeling at a landscape level with feasible storage and computational resource consumptions.
5. Conclusions
This study provides the first 3D-explicit forest model with bitemporal structural representations, which is one of the most realistic forest scenes for bitemporal 3D RT modeling to date. We reconstructed the 3D-explicit scene of 2022 Wytham Woods forest based on TLS measurement and quantitative structural modeling. Together with the existing 2015 Wytham Woods forest model, we created the most explicit bitemporal 3D forest scene to date for RT modeling. This study demonstrated the potential of this bitemporal 3D-explicit RT modeling on the forward modeling and quantitative interpretation of RS observations of LAI, FAPAR, and canopy light regimes. Results showed that, compared to the 2015 scene, the leaf FAPAR of the 2022 forest scene relatively increased by 5.4%, and the HDRF at nadir viewing direction relatively decreased by 3.8%. This study also quantified the impact of canopy gap dynamics on forest light regimes of explicit locations. The results showed that, in this bitemporal 3D-explicit forest scene reconstructed, only under diffuse light did the branch damage and closing gap significantly impact ground light availability. Under direct light, the vertical profile of PAR availability within the canopy mainly depended on the position the incident direct light could reach before being intercepted. This position was impacted by the canopy gap dynamics.
This study demonstrates that bitemporal 3D-explicit RT modeling is a powerful tool for studying canopy light regimes as impacted by dynamics in forest structure and its subsequent ecological implications. This bitemporal 3D-explicit RT modeling allows spatially explicit modeling of canopy light regimes over time to study key ecosystem processes such as photosynthesis, regeneration, and competition, and to aid in the interpretation of RS data on forest structural dynamics. By using virtually reconstructed forests, we can place virtual sensors anywhere in the canopy. This way we can measure light regimes at a much finer spatial resolution, or at locations that are often impractical in the field (e.g., high up in the canopy).
Author Contributions
Conceptualization, C.L., K.C. and H.V.; Data curation, C.L., K.C., N.O., L.T. and J.A. (John Armston); Formal analysis, C.L., K.C., Y.W. and H.V.; Funding acquisition, C.L., K.C. and N.O.; Investigation, C.L., K.C., N.O. and H.V.; Methodology, C.L., K.C., Y.W. and H.V.; Project administration, K.C. and N.O.; Resources, C.L., K.C., N.O., L.T., M.D. and J.N.; Software, C.L., K.C., J.-P.G.-E., Y.W. and J.A. (John Armston); Supervision, K.C. and H.V.; Validation, C.L. and K.C.; Visualization, C.L., K.C., L.T., J.-P.G.-E., Y.W., F.M. and H.V.; Writing—original draft, C.L., K.C. and H.V.; Writing—review and editing, C.L., K.C., N.O., L.T., J.A. (Jennifer Adams), J.-P.G.-E., Y.W., F.M., J.A. (John Armston), M.D., W.W., J.N. and H.V. All authors have read and agreed to the published version of the manuscript.
Funding
C.L. was funded by the China Scholarship Council (CSC) (No. 201906600031). N.O. was funded by the MetEOC4 project; this project (19ENV07 MetEOC-4) has received funding from the EMPIR program co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation program. L.T. was supported by a special research fund (BOF) from Ghent University. M.D. was supported by the Natural Environment Research Council (NERC grant reference number NE/X019071/1, “UK EO Climate Information Service”). F.M. was funded by the FWO as a junior/senior postdoc and is thankful to this organization for its financial support (FWO grant no. 1214720N/1214723N).
Data Availability Statement
The Wytham Woods bitemporal 3D-explicit forest model is available from https://bitbucket.org/tree_research/wytham_woods_3d_model/, accessed on 30 August 2024.
Acknowledgments
We thank Yves Govaerts for the elaborate discussions and constructive comments on the manuscript. We thank the support of computer scientists in the DART team: Nicolas Lauret, Jordan Guilleux, and Eric Chavanon. We also acknowledge funding for capital equipment from UCL and from NERC NCEO.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The Concept of Essential Climate Variables in Support of Climate Research, Applications, and Policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Liu, C.; Calders, K.; Meunier, F.; Gastellu-Etchegorry, J.P.; Nightingale, J.; Disney, M.; Origo, N.; Woodgate, W.; Verbeeck, H. Implications of 3D Forest Stand Reconstruction Methods for Radiative Transfer Modeling: A Case Study in the Temperate Deciduous Forest. J. Geophys. Res. Atmos. 2022, 127, e2021JD036175. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Grau, E.; Lauret, N. DART: A 3D Model for Remote Sensing Images and Radiative Budget of Earth Surfaces. In Modeling and Simulation in Engineering; IntechOpen: London, UK, 2012. [Google Scholar]
- Widlowski, J.L.; Pinty, B.; Lopatka, M.; Atzberger, C.; Buzica, D.; Chelle, M.; Disney, M.; Gastellu-Etchegorry, J.P.; Gerboles, M.; Gobron, N.; et al. The Fourth Radiation Transfer Model Intercomparison (RAMI-IV): Proficiency Testing of Canopy Reflectance Models with ISO-13528. J. Geophys. Res. Atmos. 2013, 118, 6869–6890. [Google Scholar] [CrossRef]
- Widlowski, J.L.; CÔté, J.F.; Béland, M. Abstract Tree Crowns in 3D Radiative Transfer Models: Impact on Simulated Open-Canopy Reflectances. Remote Sens. Environ. 2014, 142, 155–175. [Google Scholar] [CrossRef]
- Modest, M.F.; Mazumder, S. Radiative Heat Transfer; Academic Press: Cambridge, MA, USA, 2021; ISBN 032398407X. [Google Scholar]
- Verhoef, W. Theory of Radiative Transfer Models Applied in Optical Remote Sensing of Vegetation Canopies. Ph.D. Thesis, Wageningen University and Research, Wageningen, The Netherlands, 1998. [Google Scholar]
- Ross, J. The Radiation Regime and Architecture of Plant Stands, 3rd ed.; Springer Science & Business Media: Berlin, Germany, 1981. [Google Scholar]
- Myneni, R.B.; Ross, J.; Asrar, G. A Review on the Theory of Photon Transport in Leaf Canopies. Agric. For. Meteorol. 1989, 45, 1–153. [Google Scholar] [CrossRef]
- Liang, S. Quantitative Remote Sensing of Land Surfaces; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 0471723711. [Google Scholar]
- Monsi, M. Uber Den Lichtfaktor in Den Pflanzengesellschaften Und Seine Bedeutung Fur Die Stoffproduktion. Jap. J. Bot. 1953, 14, 22–52. [Google Scholar]
- Bailey, B.N.; Fu, K. The Probability Distribution of Absorbed Direct, Diffuse, and Scattered Radiation in Plant Canopies with Varying Structure. Agric. For. Meteorol. 2022, 322, 109009. [Google Scholar] [CrossRef]
- Goudriaan, J. Crop Micrometeorology a Simulation Study. Ph.D. Thesis, Wageningen University and Research, Wageningen, The Netherlands, 1977. [Google Scholar]
- Norman, J.M.M. Modeling the Complete Crop Canopy. In Modification of the Aerial Environment of Plants; American Society of Agricultural Engineers: St. Joseph, MO, USA, 1979. [Google Scholar]
- Bailey, B.N.; Ponce de León, M.A.; Scott Krayenhoff, E. One-Dimensional Models of Radiation Transfer in Heterogeneous Canopies: A Review, Re-Evaluation, and Improved Model. Geosci. Model Dev. 2020, 13, 4789–4808. [Google Scholar] [CrossRef]
- Smith, N.J.; Chen, J.M.; Black, T.A. Effects of Clumping on Estimates of Stand Leaf Area Index Using the LI-COR LAI-2000. Can. J. For. Res. 1993, 23, 1940–1943. [Google Scholar] [CrossRef]
- Nilson, T. A Theoretical Analysis of the Frequency of Gaps in Plant Stands. Agric. Meteorol. 1971, 8, 25–38. [Google Scholar] [CrossRef]
- Pinty, B.; Lavergne, T.; Dickinson, R.E.; Widlowski, J.L.; Gobron, N.; Verstraete, M.M. Simplifying the Interaction of Land Surfaces with Radiation for Relating Remote Sensing Products to Climate Models. J. Geophys. Res. Atmos. 2006, 111, D2. [Google Scholar] [CrossRef]
- Verstraete, M.M.; Pinty, B.; Dickinson, R.E. A Physical Model of the Bidirectional Reflectance of Vegetation Canopies: 1. Theory. J. Geophys. Res. 1990, 95, 11755–11765. [Google Scholar] [CrossRef]
- Kuusk, A. The Hot Spot Effect of a Uniform Vegetative Cover. Sov. J. Remote Sens. 1985, 3, 645–658. [Google Scholar]
- Kuusk, A. The Hot Spot Effect in Plant Canopy Reflectance. In Photon-Vegetation Interactions; Springer: Berlin, Germany, 1991. [Google Scholar]
- Gastellu-Etchegorry, J.P.; Yin, T.; Lauret, N.; Cajgfinger, T.; Gregoire, T.; Grau, E.; Feret, J.B.; Lopes, M.; Guilleux, J.; Dedieu, G.; et al. Discrete Anisotropic Radiative Transfer (DART 5) for Modeling Airborne and Satellite Spectroradiometer and LIDAR Acquisitions of Natural and Urban Landscapes. Remote Sens. 2015, 7, 1667–1701. [Google Scholar] [CrossRef]
- Verhoef, W. Light Scattering by Leaf Layers with Application to Canopy Reflectance Modeling: The SAIL Model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Borel, C.C.; Gerstl, S.A.W.; Powers, B.J. The Radiosity Method in Optical Remote Sensing of Structured 3-D Surfaces. Remote Sens. Environ. 1991, 36, 13–44. [Google Scholar] [CrossRef]
- Duan, M.; Min, Q.; Lü, D. A Polarized Radiative Transfer Model Based on Successive Order of Scattering. Adv. Atmos. Sci. 2010, 27, 891–900. [Google Scholar] [CrossRef]
- Glassner, A.S. An Introduction to Ray Tracing; Morgan Kaufmann: Burlington, MA, USA, 1989; ISBN 0122861604. [Google Scholar]
- Govaerts, Y.M.; Verstraete, M.M. Raytran: A Monte Carlo Ray-Tracing Model to Compute Light Scattering in Three-Dimensional Heterogeneous Media. IEEE Trans. Geosci. Remote Sens. 1998, 36, 662732. [Google Scholar] [CrossRef]
- Lewis, P. Three-Dimensional Plant Modelling for Remote Sensing Simulation Studies Using the Botanical Plant Modelling System. Agronomie 1999, 19, 185–210. [Google Scholar] [CrossRef]
- North, P.R.J. Three-Dimensional Forest Light Interaction Model Using a Monte Carlo Method. IEEE Trans. Geosci. Remote Sens. 1996, 34, 946–956. [Google Scholar] [CrossRef]
- España, M.; Baret, F.; Aries, F.; Andrieu, B.; Chelle, M. Radiative Transfer Sensitivity to the Accuracy of Canopy Structure Description. The Case of a Maize Canopy. Agronomie 1999, 19, 241–254. [Google Scholar] [CrossRef]
- Wang, Y.; Kallel, A.; Yang, X.; Regaieg, O.; Lauret, N.; Guilleux, J.; Chavanon, E.; Gastellu-Etchegorry, J.P. DART-Lux: An Unbiased and Rapid Monte Carlo Radiative Transfer Method for Simulating Remote Sensing Images. Remote Sens. Environ. 2022, 274, 112973. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Lavergne, T.; Pinty, B.; Verstraete, M.; Gobron, N. Rayspread: A Virtual Laboratory for Rapid BRF Simulations over 3-D Plant Canopies. Lect. Notes Comput. Sci. Eng. 2006, 211–231. [Google Scholar] [CrossRef]
- Disney, M.; Lewis, P.; Saich, P. 3D Modelling of Forest Canopy Structure for Remote Sensing Simulations in the Optical and Microwave Domains. Remote Sens. Environ. 2006, 100, 114–132. [Google Scholar] [CrossRef]
- Janoutová, R.; Homolová, L.; Malenovskỳ, Z.; Hanuš, J.; Lauret, N.; Gastellu-Etchegorry, J.P. Influence of 3D Spruce Tree Representation on Accuracy of Airborne and Satellite Forest Reflectance Simulated in DART. Forests 2019, 10, 292. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Tao, S.; Su, Y. VBRT: A Novel Voxel-Based Radiative Transfer Model for Heterogeneous Three-Dimensional Forest Scenes. Remote Sens. Environ. 2018, 206, 318–335. [Google Scholar] [CrossRef]
- Van der Zande, D.; Stuckens, J.; Verstraeten, W.W.; Mereu, S.; Muys, B.; Coppin, P. 3D Modeling of Light Interception in Heterogeneous Forest Canopies Using Ground-Based LiDAR Data. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 792–800. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL Models: A Review of Use for Vegetation Characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Cescatti, A. Modelling the Radiative Transfer in Discontinuous Canopies of Asymmetric Crowns. I. Model Structure and Algorithms. Ecol. Modell. 1997, 101, 263–274. [Google Scholar] [CrossRef]
- García, M.; North, P.; Viana-Soto, A.; Stavros, N.E.; Rosette, J.; Martín, M.P.; Franquesa, M.; González-Cascón, R.; Riaño, D.; Becerra, J.; et al. Evaluating the Potential of LiDAR Data for Fire Damage Assessment: A Radiative Transfer Model Approach. Remote Sens. Environ. 2020, 247, 111893. [Google Scholar] [CrossRef]
- Kobayashi, H.; Iwabuchi, H. A Coupled 1-D Atmosphere and 3-D Canopy Radiative Transfer Model for Canopy Reflectance, Light Environment, and Photosynthesis Simulation in a Heterogeneous Landscape. Remote Sens. Environ. 2008, 112, 173–185. [Google Scholar] [CrossRef]
- Ni, W.; Li, X.; Woodcock, C.E.; Caetano, M.R.; Strahler, A.H. An Analytical Hybrid GORT Model for Bidirectional Reflectance over Discontinuous Plant Canopies. IEEE Trans. Geosci. Remote Sens. 1999, 37, 987–999. [Google Scholar] [CrossRef]
- Calders, K.; Lewis, P.; Disney, M.; Verbesselt, J.; Herold, M. Investigating Assumptions of Crown Archetypes for Modelling LiDAR Returns. Remote Sens. Environ. 2013, 134, 39–49. [Google Scholar] [CrossRef]
- Schneider, F.D.; Leiterer, R.; Morsdorf, F.; Gastellu-Etchegorry, J.P.; Lauret, N.; Pfeifer, N.; Schaepman, M.E. Simulating Imaging Spectrometer Data: 3D Forest Modeling Based on LiDAR and in Situ Data. Remote Sens. Environ. 2014, 152, 235–250. [Google Scholar] [CrossRef]
- Disney, M.I.; Lewis, P.; Gomez-Dans, J.; Roy, D.; Wooster, M.J.; Lajas, D. 3D Radiative Transfer Modelling of Fire Impacts on a Two-Layer Savanna System. Remote Sens. Environ. 2011, 115, 1866–1881. [Google Scholar] [CrossRef]
- Disney, M.I.; Kalogirou, V.; Lewis, P.; Prieto-Blanco, A.; Hancock, S.; Pfeifer, M. Simulating the Impact of Discrete-Return Lidar System and Survey Characteristics over Young Conifer and Broadleaf Forests. Remote Sens. Environ. 2010, 114, 1546–1560. [Google Scholar] [CrossRef]
- Disney, M.I.; Lewis, P.E.; Bouvet, M.; Prieto-Blanco, A.; Hancock, S. Quantifying Surface Reflectivity for Spaceborne Lidar via Two Independent Methods. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3262–3271. [Google Scholar] [CrossRef]
- Stuckens, J.; Somers, B.; Delalieux, S.; Verstraeten, W.W.; Coppin, P. The Impact of Common Assumptions on Canopy Radiative Transfer Simulations: A Case Study in Citrus Orchards. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 1–21. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Mio, C.; Disney, M.; Adams, J.; Andredakis, I.; Atzberger, C.; Brennan, J.; Busetto, L.; Chelle, M.; Ceccherini, G.; et al. The Fourth Phase of the Radiative Transfer Model Intercomparison (RAMI) Exercise: Actual Canopy Scenarios and Conformity Testing. Remote Sens. Environ. 2015, 169, 418–437. [Google Scholar] [CrossRef]
- Woodgate, W.; Disney, M.; Armston, J.D.; Jones, S.D.; Suarez, L.; Hill, M.J.; Wilkes, P.; Soto-Berelov, M.; Haywood, A.; Mellor, A. An Improved Theoretical Model of Canopy Gap Probability for Leaf Area Index Estimation in Woody Ecosystems. For. Ecol. Manag. 2015, 358, 303–320. [Google Scholar] [CrossRef]
- Åkerblom, M.; Raumonen, P.; Casella, E.; Disney, M.I.; Danson, F.M.; Gaulton, R.; Schofield, L.A.; Kaasalainen, M. Non-Intersecting Leaf Insertion Algorithm for Tree Structure Models. Interface Focus 2018, 8, 20170045. [Google Scholar] [CrossRef] [PubMed]
- Calders, K.; Origo, N.; Burt, A.; Disney, M.; Nightingale, J.; Raumonen, P.; Åkerblom, M.; Malhi, Y.; Lewis, P. Realistic Forest Stand Reconstruction from Terrestrial LiDAR for Radiative Transfer Modelling. Remote Sens. 2018, 10, 933. [Google Scholar] [CrossRef]
- Åkerblom, M.; Kaitaniemi, P. Terrestrial Laser Scanning: A New Standard of Forest Measuring and Modelling? Ann. Bot. 2021, 128, mcab111. [Google Scholar] [CrossRef]
- Disney, M. Terrestrial LiDAR: A Three-Dimensional Revolution in How We Look at Trees. New Phytol. 2019, 222, 1736–1741. [Google Scholar] [CrossRef] [PubMed]
- Côté, J.F.; Widlowski, J.L.; Fournier, R.A.; Verstraete, M.M. The Structural and Radiative Consistency of Three-Dimensional Tree Reconstructions from Terrestrial Lidar. Remote Sens. Environ. 2009, 113, 1067–1081. [Google Scholar] [CrossRef]
- Kükenbrink, D.; Schneider, F.D.; Schmid, B.; Gastellu-Etchegorry, J.P.; Schaepman, M.E.; Morsdorf, F. Modelling of Three-Dimensional, Diurnal Light Extinction in Two Contrasting Forests. Agric. For. Meteorol. 2021, 296, 108230. [Google Scholar] [CrossRef]
- Lukeš, P.; Neuwirthová, E.; Lhotáková, Z.; Janoutová, R.; Albrechtová, J. Upscaling Seasonal Phenological Course of Leaf Dorsiventral Reflectance in Radiative Transfer Model. Remote Sens. Environ. 2020, 246, 111862. [Google Scholar] [CrossRef]
- Kirby, K.J.; Bazely, D.R.; Goldberg, E.A.; Hall, J.E.; Isted, R.; Perry, S.C.; Thomas, R.C. Changes in the Tree and Shrub Layer of WythamWoods (Southern England) 1974-2012: Local and National Trends Compared. Forestry 2014, 87, cpu026. [Google Scholar] [CrossRef]
- Savill, P.; Perrins, C.; Kirby, K.; Fisher, N. Wytham Woods: Oxford’s Ecological Laboratory; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Calders, K.; Verbeeck, H.; Burt, A.; Origo, N.; Nightingale, J.; Malhi, Y.; Wilkes, P.; Raumonen, P.; Bunce, R.G.H.; Disney, M. Laser Scanning Reveals Potential Underestimation of Biomass Carbon in Temperate Forest. Ecol. Solut. Evid. 2022, 3, e12197. [Google Scholar] [CrossRef]
- The ECN Data Centre Site Information: Wytham. Available online: https://ecn.ac.uk/sites/site/terr/wytham (accessed on 1 April 2019).
- Burt, A.; Disney, M.; Calders, K. Extracting Individual Trees from Lidar Point Clouds Using Treeseg. Methods Ecol. Evol. 2019, 10, 438–445. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive Estimates of Above-Ground Biomass Using Terrestrial Laser Scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Markku, Å.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast Automatic Precision Tree Models from Terrestrial Laser Scanner Data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.A. Defining Leaf Area Index for Non-flat Leaves. Plant. Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Calders, K.; Origo, N.; Disney, M.; Nightingale, J.; Woodgate, W.; Armston, J.; Lewis, P. Variability and Bias in Active and Passive Ground-Based Measurements of Effective Plant, Wood and Leaf Area Index. Agric. For. Meteorol. 2018, 252, 231–240. [Google Scholar] [CrossRef]
- Calders, K.; Schenkels, T.; Bartholomeus, H.; Armston, J.; Verbesselt, J.; Herold, M. Monitoring Spring Phenology with High Temporal Resolution Terrestrial LiDAR Measurements. Agric. For. Meteorol. 2015, 203, 158–168. [Google Scholar] [CrossRef]
- Jupp, D.L.B.; Culvenor, D.S.; Lovell, J.L.; Newnham, G.J.; Strahler, A.H.; Woodcock, C.E. Estimating Forest LAI Profiles and Structural Parameters Using a Ground-Based Laser Called ’Echidna®. Tree Physiol. 2009, 29, 171–181. [Google Scholar] [CrossRef]
- Black, T.A.; Chen, J.-M.; Lee, X.; Sagar, R.M. Characteristics of Shortwave and Longwave Irradiances under a Douglas-Fir Forest Stand. Can. J. For. Res. 1991, 21, 1020–1028. [Google Scholar] [CrossRef]
- Ryu, Y.; Nilson, T.; Kobayashi, H.; Sonnentag, O.; Law, B.E.; Baldocchi, D.D. On the Correct Estimation of Effective Leaf Area Index: Does It Reveal Information on Clumping Effects? Agric. For. Meteorol. 2010, 150, 463–472. [Google Scholar] [CrossRef]
- Axelsson, P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models. Int. Arch. Photogramm. Remote Sens. 2000, 23, 110–117. [Google Scholar]
- Gastellu-Etchegorry, J.P.; Demarez, V.; Pinel, V.; Zagolski, F. Modeling Radiative Transfer in Heterogeneous 3-D Vegetation Canopies. Remote Sens. Environ. 1996, 58, 131–156. [Google Scholar] [CrossRef]
- Pinty, B.; Gobron, N.; Widlowski, J.; Gerstl, S.A.W.; Verstraete, M.M.; Antunes, M.; Bacour, C.; Gascon, F.; Gastellu, J.; Goel, N. Radiation Transfer Model Intercomparison (RAMI) Exercise. J. Geophys. Res. Atmos. 2001, 106, 11937–11956. [Google Scholar] [CrossRef]
- Pinty, B.; Widlowski, J.L.; Taberner, M.; Gobron, N.; Verstraete, M.M.; Disney, M.; Gascon, F.; Gastellu, J.P.; Jiang, L.; Kuusk, A.; et al. Radiation Transfer Model Intercomparison (RAMI) Exercise: Results from the Second Phase. J. Geophys. Res. Atmos. 2004, 109, D6. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Taberner, M.; Pinty, B.; Bruniquel-Pinel, V.; Disney, M.; Fernandes, R.; Gastellu-Etchegorry, J.P.; Gobron, N.; Kuusk, A.; Lavergne, T.; et al. Third Radiation Transfer Model Intercomparison (RAMI) Exercise: Documenting Progress in Canopy Reflectance Models. J. Geophys. Res. Atmos. 2007, 112, D9. [Google Scholar] [CrossRef]
- Liu, C.; Calders, K.; Origo, N.; Disney, M.; Meunier, F.; Woodgate, W.; Gastellu-Etchegorry, J.P.; Nightingale, J.; Honkavaara, E.; Hakala, T.; et al. Reconstructing the Digital Twin of Forests from a 3D Library: Quantifying Trade-Offs for Radiative Transfer Modeling. Remote Sens. Environ. 2023, 298, 113832. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P. DART User’s Manua (5.7.9). Available online: https://dart.omp.eu/Public/documentation/contenu/documentation/DART_User_Manual.pdf (accessed on 11 May 2021).
- Wang, Y.; Lauret, N.; Gastellu-Etchegorry, J.P. DART Radiative Transfer Modelling for Sloping Landscapes. Remote Sens. Environ. 2020, 247, 111902. [Google Scholar] [CrossRef]
- Berk, A.; Bernstein, L.S.; Robertson, D.C. MODTRAN: A Moderate Resolution Model for LOWTRAN; Geophysics Laboratory: Lakewood, CA, USA, 1989; Volume 7. [Google Scholar]
- Grau, E.; Gastellu-Etchegorry, J.P. Radiative Transfer Modeling in the Earth-Atmosphere System with DART Model. Remote Sens. Environ. 2013, 139, 149–170. [Google Scholar] [CrossRef]
- Zemp, M.; Chao, Q.; Han Dolman, A.J.; Herold, M.; Krug, T.; Speich, S.; Suda, K.; Thorne, P.; Yu, W. GCOS 2022 Implementation Plan; World Meteorological Organization: Geneva, Switzerland, 2022. [Google Scholar]
- Mariscal, M.J.; Martens, S.N.; Ustin, S.L.; Chen, J.; Weiss, S.B.; Roberts, D.A. Light-Transmission Profiles in an Old-Growth Forest Canopy: Simulations of Photosynthetically Active Radiation by Using Spatially Explicit Radiative Transfer Models. Ecosystems 2004, 7, 454–467. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance Quantities in Optical Remote Sensing-Definitions and Case Studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Zhang, J.; Khoshbakht, M.; Liu, J.; Gou, Z.; Xiong, J.; Jiang, M. A Clustering Review of Vegetation-Indicating Parameters in Urban Thermal Environment Studies towards Various Factors. J. Therm. Biol. 2022, 110, 103340. [Google Scholar] [CrossRef]
- Welles, J.M.; Norman, J.M. Instrument for Indirect Measurement of Canopy Architecture. Agron. J. 1991, 83, 818–825. [Google Scholar] [CrossRef]
- Iqbal, M. An Introduction to Solar Radiation; Elsevier: Amsterdam, The Netherlands, 2012; ISBN 0323151817. [Google Scholar]
- Li, T.; Yang, Q. Advantages of Diffuse Light for Horticultural Production and Perspectives for Further Research. Front. Plant Sci. 2015, 6, 704. [Google Scholar] [CrossRef] [PubMed]
- Chazdon, R.L.; Pearcy, R.W. The Importance of Sunflecks for Forest Understory Plants. Bioscience 1991, 41, 760–766. [Google Scholar] [CrossRef]
- Pearcy, R.W. Photosynthetic Utilisation of Lightflecks by Understory Plants. Aust. J. Plant Physiol. 1988, 15, 223–238. [Google Scholar] [CrossRef]
- Pearcy, R.W.; Chazdon, R.L.; Gross, L.J.; Mott, K.A. Photosynthetic Utilization of Sunflecks: A Temporally Patchy Resource on a Time Scale of Seconds to Minutes. In Exploitation of Environmental Heterogeneity by Plants; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Alton, P.B.; North, P.R.; Los, S.O. The Impact of Diffuse Sunlight on Canopy Light-Use Efficiency, Gross Photosynthetic Product and Net Ecosystem Exchange in Three Forest Biomes. Glob. Chang. Biol. 2007, 13, 776–787. [Google Scholar] [CrossRef]
- Denning, A.S.; Nicholls, M.; Prihodko, L.; Baker, I.; Vidale, P.L.; Davis, K.; Bakwin, P. Simulated Variations in Atmospheric CO2 over a Wisconsin Forest Using a Coupled Ecosystem-Atmosphere Model. Glob. Chang. Biol. 2003, 9, 1241–1250. [Google Scholar] [CrossRef]
- Sitch, S.; Smith, B.; Prentice, I.C.; Arneth, A.; Bondeau, A.; Cramer, W.; Kaplan, J.O.; Levis, S.; Lucht, W.; Sykes, M.T.; et al. Evaluation of Ecosystem Dynamics, Plant Geography and Terrestrial Carbon Cycling in the LPJ Dynamic Global Vegetation Model. Glob. Chang. Biol. 2003, 9, 161–185. [Google Scholar] [CrossRef]
- Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Calders, K.; Woodgate, W. Leaf and Wood Classification Framework for Terrestrial LiDAR Point Clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef]
- Wang, D.; Momo Takoudjou, S.; Casella, E. LeWoS: A Universal Leaf-Wood Classification Method to Facilitate the 3D Modelling of Large Tropical Trees Using Terrestrial LiDAR. Methods Ecol. Evol. 2020, 11, 376–389. [Google Scholar] [CrossRef]
- Du, S.; Lindenbergh, R.; Ledoux, H.; Stoter, J.; Nan, L. AdTree: Accurate, Detailed, and Automatic Modelling of Laser-Scanned Trees. Remote Sens. 2019, 11, 2074. [Google Scholar] [CrossRef]
- Hakala, T.; Suomalainen, J.; Kaasalainen, S.; Chen, Y. Full Waveform Hyperspectral LiDAR for Terrestrial Laser Scanning. Opt. Express 2012, 20, 7119–7127. [Google Scholar] [CrossRef]
- Terryn, L.; Calders, K.; Bartholomeus, H.; Bartolo, R.E.; Brede, B.; D’hont, B.; Disney, M.; Herold, M.; Lau, A.; Shenkin, A.; et al. Quantifying Tropical Forest Structure through Terrestrial and UAV Laser Scanning Fusion in Australian Rainforests. Remote Sens. Environ. 2022, 271, 112912. [Google Scholar] [CrossRef]
- Schneider, F.D.; Kükenbrink, D.; Schaepman, M.E.; Schimel, D.S.; Morsdorf, F. Quantifying 3D Structure and Occlusion in Dense Tropical and Temperate Forests Using Close-Range LiDAR. Agric. For. Meteorol. 2019, 268, 249–257. [Google Scholar] [CrossRef]
- Chavana-Bryant, C.; Malhi, Y.; Anastasiou, A.; Enquist, B.J.; Cosio, E.G.; Keenan, T.F.; Gerard, F.F. Leaf Age Effects on the Spectral Predictability of Leaf Traits in Amazonian Canopy Trees. Sci. Total Environ. 2019, 666, 1301–1315. [Google Scholar] [CrossRef] [PubMed]
- Ebengo, D.M.; De Boissieu, F.; Vincent, G.; Weber, C.; Féret, J.B. Simulating Imaging Spectroscopy in Tropical Forest with 3d Radiative Transfer Modeling. Remote Sens. 2021, 13, 2120. [Google Scholar] [CrossRef]
- Krishna Moorthy, S.M.; Raumonen, P.; Van den Bulcke, J.; Calders, K.; Verbeeck, H. Terrestrial Laser Scanning for Non-Destructive Estimates of Liana Stem Biomass. For. Ecol. Manag. 2020, 456, 117751. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).