Abstract
Fractional vegetation cover (FVC) is a crucial indicator for measuring the growth of surface vegetation. The changes and predictions of FVC significantly impact biodiversity conservation, ecosystem health and stability, and climate change response and prediction. Southwest China (SWC) is characterized by complex topography, diverse climate types, and rich vegetation types. This study first analyzed the spatiotemporal variation of FVC at various timescales in SWC from 2000 to 2020 using FVC values derived from pixel dichotomy model. Next, we constructed four machine learning models—light gradient boosting machine (LightGBM), support vector regression (SVR), k-nearest neighbor (KNN), and ridge regression (RR)—along with a weighted average heterogeneous ensemble model (WAHEM) to predict growing-season FVC in SWC from 2000 to 2023. Finally, the performance of the different ML models was comprehensively evaluated using tenfold cross-validation and multiple performance metrics. The results indicated that the overall FVC in SWC predominantly increased from 2000 to 2020. Over the 21 years, the FVC spatial distribution in SWC generally showed a high east and low west pattern, with extremely low FVC in the western plateau of Tibet and higher FVC in parts of eastern Sichuan, Chongqing, Guizhou, and Yunnan. The determination coefficient R2 scores from tenfold cross-validation for the four ML models indicated that LightGBM had the strongest predictive ability whereas RR had the weakest. WAHEM and LightGBM models performed the best overall in the training, validation, and test sets, with RR performing the worst. The predicted spatial change trends were consistent with the MODIS-MOD13A3-FVC and FY3D-MERSI-FVC, although the predicted FVC values were slightly higher but closer to the MODIS-MOD13A3-FVC. The feature importance scores from the LightGBM model indicated that digital elevation model (DEM) had the most significant influence on FVC among the six input features. In contrast, soil surface water retention capacity (SSWRC) was the most influential climate factor. The results of this study provided valuable insights and references for monitoring and predicting the vegetation cover in regions with complex topography, diverse climate types, and rich vegetation. Additionally, they offered guidance for selecting remote sensing products for vegetation cover and optimizing different ML models.
1. Introduction
The Intergovernmental Panel on Climate Change (IPCC) Sixth Assessment Report (AR6) revealed that the global average surface temperature was 1.09 °C higher than the average from 1850 to 1900 over the past decade (2011–2020). Moreover, each decade over the past 40 years experienced higher global average surface temperatures than any previous decade [1,2]. Vegetation is an essential component of terrestrial ecosystems, which plays a critical role in maintaining ecosystem stability. It responds to and influences climate change as an “indicator” of regional environmental change [3,4]. The fractional vegetation cover (FVC) reflects the surface distribution of vegetation and varies significantly seasonally and across regions, influenced by climate, topography, and human activities. Satellite remote sensing data offers various advantages, such as low cost, high reliability, and numerous product options, making it an important data source for analyzing various vegetation indices. The advancement of remote sensing technology has created favorable conditions for accurate monitoring of FVC over large areas [5]. In particular, the Earth Observing System Moderate Resolution Imaging Spectroradiometer (EOS-MODIS) normalized difference vegetation index (NDVI) data product offers several advantages compared with the Global Inventory Modelling and Mapping Studies (GIMMS) NDVI, the Advanced Very High Resolution Radiometer (AVHRR) NDVI, and the Systeme Probatoire d’Observation de la Terre (SPOT-VGT) NDVI. These advantages include simultaneously observing multiple channels, higher spatiotemporal resolution, large-scale observation capabilities, and high accuracy. Additionally, the dataset has undergone processes such as radiometric calibration, atmospheric correction, and cloud detection, ensuring a certain level of quality assurance. Consequently, it is widely used in the studies of the changes in vegetation cover [6,7,8,9,10].
Domestic and international scholars monitored and analyzed the changes in FVC in various regions. For example, Wu et al. (2014) [11] used GIMMS NDVI data to estimate global FVC from 1982 to 2011, revealing significant seasonal variations. High-latitude regions showed a marked increase in FVC due to global warming. Shobairi et al. (2018) [12] analyzed the changes in FVC and drivers in Guangdong Province, China, from 2000 to 2010 using MODIS-NDVI data. Their trend analysis indicated that FVC was higher in the less economically developed northern mountainous regions with minimal human disturbance. In contrast, industrialization and urbanization in the southern coastal regions led to lower FVC. They also detected a positive correlation between FVC and sunshine hours. Hill and Guerschman (2020) [13] developed a global FVC product and investigated FVC levels and trends across grassland ecoregions globally. Their findings revealed significant positive and negative FVC trends in many ecoregions. East Africa, Patagonia, and Australia’s Mitchell Grasslands experienced substantial declines in non-photosynthetic vegetation and increases in bare soil, reflecting the interactions between prolonged drought, heavy livestock use, agricultural expansion, and other land use changes. Li et al. (2022) [14] used trend analysis, the Google Earth Engine (GEE) platform, and a random forest classifier to examine vegetation dynamics during the growing seasons from 2001 to 2020 in the China–Myanmar Economic Corridor. They quantified the spatial distribution, change patterns, and driving factors of FVC, discovering a 0.68% decrease in the average FVC of forests and grasslands. However, cropland, which was concentrated in the south–central region, contributed 50.4% to the FVC increase, highlighting the offsetting effect of increased cultivated crops on natural vegetation loss. Wang et al. (2022) [15] used the GEE platform to retrieve FVC in the Yellow River Basin from 1999 to 2019. They showed significant FVC improvements, particularly in the central basin, with precipitation, sunshine duration, and relative humidity being the most influential factors. Eisfelder et al. (2023) [16] analyzed seasonal vegetation trends in Europe from 1981 to 2018 using AVHRR NDVI data. Their trend analysis identified distinct vegetation cover patterns for spring, summer, and autumn across different European regions. They found positive trends in vegetation cover over large areas of Europe when considering the entire growing season. Dastigerdi et al. (2024) [17] examined the changes in vegetation cover in northeastern Iran from 2001 to 2020 using MODIS-NDVI time-series data (MOD13Q1). The trend analysis revealed significant increases in vegetation cover in 32% of the region and decreases in 26%. The increasing trends were mainly observed in highland areas.
Approaches for estimating FVC include field measurements and satellite-based observations. While field measurements provide higher accuracy and spatial resolution, they are constrained by high costs, intermittent observation times, and limited coverage areas. In contrast, remote sensing observations are more cost-effective, cover extensive areas, and allow for long-term FVC estimation. Methods based on remote sensing include empirical models, pixel unmixing models, physical methods, and machine learning (ML) techniques. Among these, pixel unmixing models are widely adopted due to their simplicity and practicality [18,19,20,21]. These models assume that each pixel in a remotely sensed image consists of two or more components, and FVC is determined by decomposing these mixed components. The pixel dichotomy model, a linear variant of the pixel unmixing model, assumes that each pixel comprises vegetation and non-vegetation components, and it estimates FVC based on this decomposition. This model does not rely on field-measured FVC data, making it well-suited for regional vegetation monitoring [22].
In recent decades, several global-scale FVC products have been developed using remote sensing data, including the Global LAnd Surface Satellite (GLASS) FVC, VGT bioGEOphysical product Version 1 (GEOV1) FVC, VGT bioGEOphysical product Version 2 (GEOV2) FVC, PROBA-V bioGEOphysical product Version 3 (GEOV3) FVC, the Carbon CYcle and Change in Land Observational Products from an Ensemble of Satellites (CYCLOPES) FVC, and the Multi-source Synergized Quantitative (MuSyQ) FVC [23,24]. These products are generated based on different satellite sensors, resolutions, revisit intervals, spatial ranges, temporal scopes, and algorithms. Numerous comparative and evaluative studies have been conducted on these FVC products. For instance, Liu et al. (2019) [25] performed a spatiotemporal comparison and validation of three global FVC products (GEOV2, GEOV3, GLASS). The results indicated general spatiotemporal consistency across most regions. The GLASS and GEOV2 FVC products demonstrated reliable spatiotemporal completeness, whereas the GEOV3 FVC product exhibited significant data gaps in high-latitude regions, particularly in winter. The GEOV3 product also showed higher FVC values compared to GEOV2 and GLASS products near the equator. Differences between GEOV2 and GLASS FVC products were most pronounced in deciduous forests, where GLASS reported slightly higher FVC values during winter. Temporal profiles of GEOV2 and GLASS were more consistent than those of GEOV3, with GLASS showing greater accuracy when compared to reference FVC datasets. Therefore, different FVC products demonstrate variations in FVC values with respect to different geographical regions, seasons, and types of underlying land surfaces.
FVC is a crucial indicator for assessing surface vegetation growth. Research on the changes in FVC significantly impacts regional ecosystem health and stability, climate change monitoring and prediction, biodiversity conservation, land use planning, agricultural production and food security, water resource management, carbon cycling, global change, disaster risk assessment, and environmental policy and planning. Therefore, predicting FVC is of great practical significance. The prediction methods for FVC include traditional regression models [26], trend extrapolation [27], cellular automata (CA)–Markov [9], rescaled range analysis (Hurst exponent) [28], gray models [29], and future multi-scenario simulations [30,31]. Kumar et al. (2014) [26] used a logistic regression model (LRM) to predict the changes in forest cover in the Bhanupratappur forest division of Kanker district, Chhattisgarh State, India. The forest cover data from 1990 and 2000 were used to predict forest cover for 2010, with the LRM achieving reasonably high accuracy (receiver-operating characteristic = 87%). Cui et al. (2021) [9] predicted vegetation coverage grades for 2025 using data from 2008, 2010, and 2013. Their results indicated an upward trend in vegetation coverage in the Qinling Mountains under policy guidance, especially in urban areas. Ahmad et al. (2023) [28] tracked the spatiotemporal changes in vegetation in Pakistan from 2000 to 2020, using the Hurst exponent to estimate future trends. Values above 0.5 suggested consistent future vegetation trends in all four provinces. Wang et al. (2024) [31] used MODIS-NDVI data and a pixel dichotomy model to estimate FVC. Then, they analyzed the spatiotemporal evolution of vegetation cover in Shenyang City, China, from 2000 to 2020 using trend and deviation analyses. They employed the patch-generating land use simulation model, based on land use data from 2010, 2015, and 2020, to simulate vegetation cover scenarios for 2030 in Shenyang City.
The rapid development of big data and artificial intelligence technologies in recent years has led to the increasing application of machine learning methods, such as k-nearest neighbor (KNN), random forest (RF), deep neural network (DNN), support vector regression (SVR), multiple linear regression (MLR), support vector machine (SVM), artificial neural network (ANN), and long short-term memory, for estimating and predicting FVC [32,33,34,35,36,37,38]. For instance, Jia et al. (2021) [34] used rainfall and temperature as input variables. They employed MLR, ANN, and SVM models to predict the changes in vegetation cover in the tributaries of the Wei River Basin. The results indicated that the prediction accuracies of the three models ranked as SVM > ANN > MLR, revealing a complex nonlinear relationship between meteorological factors and FVC. Roy (2021) [35] extracted NDVI and enhanced vegetation index (EVI) values from the MODIS dataset (2001–2018) to predict vegetation indices for 2019, testing four supervised ML algorithms (SVR, RF, linear, and polynomial regression). The models predicted NDVI with an error range of 1.51–5.73% and EVI with an error range of 4.33–6.99%. An upward linear trend was observed in the data, suggesting increasing vegetation cover. Ahmad et al. (2023) [36] introduced a convolutional long short-term memory (ConvLSTM) model for more comprehensive and detailed NDVI forecasts. They compared the ConvLSTM network with the parametric crop growth model (PCGM) using the root mean square error (RMSE) metric on the same set of soybean crop field pixels. The ConvLSTM model, with its best training configuration, achieved an RMSE of 0.0782, outperforming the PCGM’s RMSE of 0.0989. Peng (2023) [37] developed aquatic FVC retrieval models using KNN, RF, and DNN algorithms based on Landsat-8 satellite images of Wuliangsuhai Lake. The results indicated that all three models performed well, with the DNN model showing the best performance. The DNN model achieved an R2 score of 0.873, an RMSE of 0.118, and a slope of 0.856 in the univariate linear fit between estimated and actual values. ML is a method that simulates human learning using knowledge from probability theory and statistics to establish the relationships from existing data, extracting valuable information from large and complex datasets for forecasting, predicting change trends, and improving learning efficiency [39,40]. ML offers several advantages compared with other FVC prediction methods: It can handle complex relationships and nonlinear correlations, adapt to large-scale and multidimensional data, and has data-driven and automated feature learning capabilities. Additionally, it provides high flexibility, strong generalization ability, and high prediction accuracy when combining multi-source data. Thus, ML has become a popular strategy for FVC prediction with significant application potential.
Southwest China (SWC) is a crucial ecological security barrier and also an area characterized by ecological fragility and climate sensitivity. Zheng et al. (2016) [41] used MODIS-NDVI data to estimate the annual maximum FVC at a 250 m resolution in SWC from 2000 to 2010, analyzing the changes in vegetation cover in forests, shrubs, and grasslands. Peng et al. (2017) [42] employed the mean method, coefficient of variation, and correlation analysis to examine the changes in FVC in forest and grassland areas and their relationship with precipitation in the five southwestern provinces (Guizhou, Yunnan, Sichuan, Guangxi, and Chongqing) from 2009 to 2015, considering terrain and vegetation types. Their findings indicated that FVC in these regions decreased from 0.87 to 0.78, signifying obvious vegetation degradation, with precipitation effects showing significant spatial variability. Feng and Dong (2022) [43] and He et al. (2021) [44] used MODIS-NDVI data to investigate the spatiotemporal evolution of FVC in Yunnan Province and Chongqing municipality, respectively. The results showed that FVC in Yunnan Province exhibited a “single peak” distribution and an increasing trend from 2010 to 2020, whereas Chongqing municipality witnessed an overall improvement in FVC from 2000 to 2015. Huang et al. (2023) [45] evaluated the differences between two global FVC products, GEOLAND2 Version 3 and Global Land Surface Satellite, in SWC. They discovered significant spatiotemporal and seasonal discrepancies between the products, with large variations in values across different land use types, slopes, and altitudes. The study concluded that, when selecting FVC product data, the influences of season, terrain, and surface type should be considered when choosing the most appropriate remote sensing data products based on specific research objectives.
The literature review shows that the current studies on FVC in SWC primarily focus on the overall analysis of spatiotemporal variation characteristics for areas excluding Tibet. These studies are not sufficiently specific and comprehensive regarding the spatiotemporal variation characteristics of FVC within specific provinces (Sichuan, Yunnan, Guizhou) and municipalities (Chongqing, Tibet) in SWC. Furthermore, the temporal scale of the research is relatively outdated, with a significant lack of studies on FVC estimation and prediction based on ML methods in SWC. Given the complexities of the topography, climate sensitivity, and diverse vegetation types in SWC, several questions arise regarding global warming: What are the recent overall spatiotemporal variation trends of FVC in SWC? How do the spatiotemporal variation trends and differences in FVC manifest across the five provinces and municipalities, including Tibet? What is the prediction accuracy and effectiveness of using different ML models based on MODIS-NDVI data for the growing-season FVC? These questions necessitate a more comprehensive and integrated analysis, particularly considering the high-altitude region of Tibet, which is significantly impacted by global warming. The present study addresses these issues, aiming to provide a scientific understanding of the changes in the ecological environment in SWC. The results offer critical theoretical and technical support for ecological environment protection and the construction of ecological civilization in SWC.
2. Materials and Methods
2.1. Study Areas
In this study, SWC mainly refers to five provinces and municipalities in China: Sichuan, Guizhou, Yunnan, Chongqing, and Tibet (78°25′E–110°11′E, 21°8′N–36°53′N), covering an area of 2.37 × 106 km2, which accounts for 24.6% of the total land area in China. The region is characterized by complex topography, with elevations ranging from 46 to 8569 m above sea level, and generally slopes from high in the west to low in the east. The western part of Sichuan and Tibet is mainly a plateau, whereas the eastern part of Sichuan and Chongqing consists of basins and hilly mountains. The region has an annual average temperature of −2.8 °C to 23.9 °C and annual precipitation of 600 to 2300 mm, exhibiting diverse climatic types [46]. The eastern part has a mostly subtropical monsoon climate, whereas the western part is dominated by a plateau mountain climate. The southern Yunnan area features a tropical monsoon climate [47,48]. SWC has a rich diversity of vegetation types, including coniferous forests, broad-leaved forests, grasslands, meadows, shrubs, herbaceous plants, and cultivated vegetation. It is also a crucial source and transit area for many rivers, making its ecological protection vital for the downstream ecosystems. Generally, the vegetation cover and precipitation levels are lower in the high-altitude areas of the western plateau compared with the low-altitude areas in the east [42,49]. The geographical location, elevation distribution, and the average NDVI values in 2020 are shown in Figure 1.
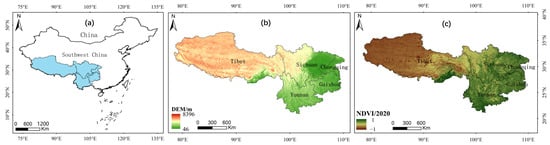
Figure 1.
Geographical location (a), elevation distribution (b) and the average NDVI values for 2020 (c) in Southwest China.
2.2. Data
2.2.1. Data Sources
The dataset included NDVI and digital elevation model (DEM) remote sensing data, along with the fifth-generation European Centre for Medium-Range Weather Forecasts atmospheric reanalysis of the global climate (ERA5) reanalysis data from the European Centre for Medium-Range Weather Forecasts. The NDVI data included MODIS-MOD13A3 NDVI data from 2000 to 2023 (http://www.nasa.gov/, accessed on 20 June 2023) and FY3D-Medium Resolution Spectral Imager (MERSI) NDVI data from 2021 to 2023 (http://www.nsmc.org.cn/, accessed on 10 January 2024), with spatial resolutions of 1 and 5 km, respectively. The DEM primarily originated from the National Tibetan Plateau Data Center (https://data.tpdc.ac.cn/, accessed on 15 March 2023), with a spatial resolution of 500 m. The ERA5 data comprised monthly datasets from 2000 to 2023, including surface temperature at 2 m (T-2m), net surface solar radiation (NSSR), soil surface water retention capacity (SSWRC), total precipitation (Total-Prec), and vegetation evapotranspiration (VET), with a spatial resolution of 0.1° × 0.1°, available at https://cds.climate.copernicus.eu/, accessed on 10 September 2023. The GLASS FVC product used for comparison and validation was sourced from the National Earth System Science Data Sharing Infrastructure, National Science and Technology Infrastructure of China (http://www.geodata.cn/thematicView/GLASS.html, accessed on 18 July 2023), spanning the period from 2000 to 2020. It features an 8-day temporal resolution, a 0.5 km spatial resolution, and is projected in a sinusoidal grid, provided in HDF format.
2.2.2. Data Preprocessing
With the exception of the GLASS FVC product, all data were interpolated to a uniform spatial resolution of 0.1° × 0.1° for analysis to account for the varying spatial resolutions of data from different sources. The NDVI dataset underwent the following preprocessing steps: (1) The MODIS Reprojection Tool was used to convert the downloaded Hierarchical Data Format into Tag Image File Format, extract monthly NDVI data, and convert the geographic coordinate system into World Geodetic System (WGS1984). (2) The monthly NDVI data for this region were clipped using ESRI Shapefile format boundary files of the five provinces and municipalities in SWC. (3) Preprocessing and quality control of the MODIS-MOD13A3 NDVI data were performed, which included noise removal, outlier detection, and handling of missing values, considering the specific conditions of SWC. (4) The FVC values were calculated from the NDVI pixel values and interpolated to a spatial resolution of 0.1° × 0.1°. A total of 324 NDVI images were processed. The preprocessing of the ERA5 and DEM data involved converting data formats and downscaling the spatial resolution of DEM data. Finally, the calculated FVC data and the processed ERA5 and DEM data were converted into Comma Separated Values format files to facilitate data reading and model training in Python 3.9.
2.3. Methods
2.3.1. Estimation of FVC
FVC is defined as the percentage of the ground area vertically projected by vegetation within a given statistical area. This can be estimated using the pixel dichotomy model, which assumes that each pixel comprises both vegetated and non-vegetated surface areas. The formula used for calculating FVC is as follows [5,50,51]:
where NDVI represents the NDVI of a mixed pixel, NDVIsoil represents the NDVI of the non-vegetated endmember, and NDVIveg represents the NDVI of the vegetated endmember. NDVIsoil, which mainly corresponds to bare ground, theoretically remains constant over time. The estimates for NDVIveg and NDVIsoil are derived using a confidence interval method, selecting the values at the 5% and 95% cumulative frequency of NDVI pixels as the NDVIsoil and NDVIveg endmembers, respectively. These values are then used in Formula (1) to calculate the FVC for each pixel. Since NDVIsoil values are close to zero, the calculated FVC values may occasionally be less than zero or greater than one. In such cases, the FVC values less than zero are set to zero, and those greater than one are set to one [52].
2.3.2. Classification and Validation of FVC
Based on the “Soil Erosion Classification and Grading Standards” (SL 190-2007) [53], issued by the Ministry of Water Resources of the People’s Republic of China in 2008, and considering the actual conditions of the study area, the FVC was categorized into five classes [54,55,56]. Table 1 provides a breakdown of the five FVC classifications and their corresponding main land use/cover types.

Table 1.
Classification of FVC in the study area.
The assessment and validation of moderate spatial resolution FVC datasets are generally challenging because ground-based point measurements are often unsuitable for direct comparisons due to surface heterogeneity. Based on ground measurement data and data from reference validation sites in relevant publications, some scholars, after comparing the current mainstream international global-scale FVC products, concluded that the GLASS FVC product was optimal in terms of spatiotemporal continuity, consistency, and accuracy [25,57,58,59]. Therefore, this study used scatter plots to cross-validate the MODIS-MOD13A3-FVC, calculated using the pixel dichotomy method, against the GLASS FVC product, providing indirect validation of the effectiveness and accuracy of the MODIS-MOD13A3-FVC data calculated in this study.
2.3.3. Theil–Sen Slope Estimation
The time trend analysis of FVC primarily employs Theil–Sen slope estimation. Theil–Sen regression uses the statistic of median slopes for parameter estimation, enhancing the robustness of the regression model. Additionally, it is a nonparametric method that does not require assumptions about data distribution, providing greater flexibility. The formula used for calculating Theil–Sen slope β is as follows [60,61]:
where xi and xj represent the FVC sample sequence values at times i and j, respectively (j > i). The median function is denoted as “median”. The parameter β indicates the average rate of change and trend of the sequence: β > 0 signifies an increasing FVC trend, β = 0 indicates no significant trend, and β < 0 signifies a decreasing trend. The significance level of this trend change was determined using the t test.
2.3.4. Mann–Kendall Test
The Mann–Kendall test is a nonparametric hypothesis test method not influenced by the overall distribution of the sample or a few outliers. It is used to assess the significance of the FVC variation trend over different timescales. Given a set of time-series data X = (x1, x2, …, xn), the first step is to determine the relative ranking between xi and xj for all values, which is denoted as S. The formula used for calculating the test statistic S is as follows [62,63]:
where xi and xj are the data values at time i and j, respectively, n is the length of the dataset, that is, the number of data points, and sgn ( ) is the interpolation function. A positive value of S indicates an increasing trend, a negative value indicates a decreasing trend, and a value of zero indicates no change. The variance of S, denoted as Var(S), is calculated as follows:
where m represents the number of tied groups in the time-series data and tk denotes the number of data points in the kth tied group. The test statistic Z value, used for trend analysis, was constructed based on the values of S and Var(S) as follows:
Using Formula (6) and referring to the critical values in the normal distribution table at a given significance level, the absolute value of Z greater than 1.65, 1.96, and 2.58 indicates that the trend passes the significance level tests at confidence levels of 90%, 95%, and 99%, respectively. The spatial variation trend can then be classified into nine levels: very significant increase and very significant decrease (p < 0.01), significant increase and significant decrease (p < 0.05), slightly significant increase and slightly significant decrease (p < 0.1), no significant increase and no significant decrease (p > 0.1), and no change (Z = 0). The p-value represents the probability of observing the difference between the sample mean and the population mean, assuming that the null hypothesis is true.
2.3.5. ML Model
Numerous studies have shown that the climate and topographic factors are closely related to FVC and exhibit nonlinear relationships. ML can automatically learn from data samples to uncover internal patterns and use these patterns to predict new samples, effectively addressing the nonlinear relationship between independent and dependent variables, thus significantly improving prediction accuracy. Given the wide variety of ML methods and the differing computational principles of various algorithms, this study primarily selected four individual models—LightGBM, SVR, KNN, and RR—and an ensemble model constructed based on the optimal selection of these four individual models to predict FVC in SWC.
- A.
- LightGBM model
LightGBM is an efficient gradient-boosting tree algorithm developed by Microsoft Research Asia. It is an improved version of the Gradient Boosting Decision Tree algorithm, offering significant enhancements in both performance and efficiency. LightGBM is widely used in the ML field and has achieved excellent results in numerous data science competitions. LightGBM offers several advantages, including high efficiency, low memory consumption, accuracy, support for parallel training, and scalability [64,65]. Despite these benefits, it also presents certain limitations, such as the risk of overfitting, complexity of parameter tuning, and sensitivity to outliers.
Defining the training sample set as M = [(z1, y1), …, (zn, yn)], the function of LightGBM is:
where represents the true label value, represents the corresponding predicted value, f(k) represents the kth tree model, and is the regularization term. The difference between the predicted value and the true label value is calculated using the loss function:
The second-order Taylor expansion of the loss function is as follows:
For the ith sample, the first-order derivative of the loss function is and the second-order derivative of the loss function is The objective function can be further transformed into:
where represents the set of data points in leaf node j.
- B.
- SVR model
SVR is a powerful ML algorithm used for regression analysis. Similar to SVM, SVR is specifically designed for regression problems. SVR exhibits several advantages, including effectiveness in high-dimensional spaces, the ability to perform nonlinear mapping, strong robustness, good flexibility, and superior generalization capability. However, it also has notable drawbacks, such as sensitivity to parameter tuning, high computational complexity, inefficiency when applied to large-scale datasets, and challenges in interpreting the results [66].
Assuming the training sample set S = {si = (xi, yi), xi ∈ Rn, yi ∈ Rn}. SVR applies a mapping function φ to map the data and then models it as follows [67,68]:
where ω is the weight vector and b is the bias term. By introducing the penalty parameter C, the insensitive loss function ε, the Lagrange multipliers, and the kernel function K (x, xj) to replace (φ(xi), φ(x)), the decision function can be expressed as follows:
where is a kernel function that satisfies the Mercer condition, and are sample vectors, and and are the Lagrange multipliers in the quadratic programming problem.
- C.
- KNN model
KNN is a simple yet powerful supervised learning algorithm suitable for classification and regression problems. KNN offers several advantages, including simplicity and ease of understanding, suitability for multi-class classification problems, broad applicability, low training time complexity, and strong adaptability. Nonetheless, it has notable limitations, such as high computational cost, large memory requirements, slow prediction speed, and sensitivity to outliers.
The core idea of the KNN regression algorithm is to predict a sample’s value by identifying the K-nearest samples in the feature space based on similarity measures and using their weighted average. In the KNN model, the distance between two measured points in the feature space (χ, generally an n-dimensional real vector feature space ) reflects the similarity between the two points. Distance metrics such as Euclidean distance, Manhattan distance, and Mahalanobis distance can be used. Considering the Euclidean distance, the calculation formula is as follows [69,70]:
In this formula, After finding the K-nearest samples, the predicted value of the sample can be obtained using the Formula (14):
where is the predicted value of the sample to be estimated and is the actual value of the KNN training samples.
- D.
- RR model
RR is an extended linear regression technique designed to handle multicollinearity issues. RR provides several advantages, including the capacity to manage multicollinearity, a reduced risk of overfitting, retention of all features, mathematical stability, and ease of implementation. However, its drawbacks include the necessity of manually tuning the regularization parameter, limited applicability to nonlinear models, challenges when the number of features exceeds the number of samples, and sensitivity to outliers [71].
In the case of collinearity, the parameters estimated by RR are more robust than those estimated by the least squares approach. Specifically, RR addresses the matrix inverse problem by adding a nonzero value k to the diagonal elements of . Hence, the ridge estimator for the linear coefficients is calculated as [72]:
where represents an identity matrix and k is the ridge or shrinkage parameter determining the strength of the penalty imposed on the regression coefficients.
- E.
- Heterogeneous ensemble ML model
Local optima are easily encountered due to the different focus of individual ML models on capturing various features. Single models have limitations and poor generalization ability. The advantages and disadvantages of different ML methods also vary. Ensemble learning can combine the advantages of individual models to fully learn the sample features and potentially achieve better predictive performance. The principle of ensemble learning is to combine multiple base classifiers through a certain strategy to construct a new classifier for completing the learning task. Ensemble learning is of two types: homogeneous and heterogeneous ensemble learning [73]. Homogeneous ensemble algorithms select the same learner as the base classifier, with a high correlation between models, thus making them prone to overfitting. In contrast, heterogeneous ensemble algorithms select diverse and different models as base classifiers, extracting features from different data space perspectives. This approach allows for complementary strengths and weaknesses among models, thereby improving model accuracy [74,75]. Typical heterogeneous ensemble models include stacking, blending, and weighted averaging. Among these, the weighted averaging method is a common and simple heterogeneous ensemble learning method, where the prediction result is the weighted average of the prediction results of each base learner [76,77]. This is calculated as:
where represents the weight of the individual learner , and and . In the weighted averaging method, the weights can generally be learned from the training data. This study primarily used this method to create the weighted average heterogeneous ensemble of the selected individual models. The performance of each base learner on the training dataset was used as the relative weight of the model during prediction.
2.3.6. Indicators of Model Accuracy Assessment
In regression tasks, evaluation indicators primarily focus on the differences between predicted and true values. The accuracy of different models was assessed by computing and comparing statistical measures based on the discrepancies between actual inversion values and predicted values. These metrics included RMSE, mean absolute error (MAE), explained variance score (EVS), correlation coefficient (CC), and mean absolute percentage error (MAPE), which were calculated using Equations (17)–(21) [46,78]. In addition, a tenfold cross-validation method was used to measure the performance of the model by averaging the coefficient of determination (R2) from 10 cross-validations. The formula for calculating R2 for each cross-validation is depicted in Equation (22) [79]:
where i refers to the index of the ith sample point, denotes the true value of the sample, denotes the predicted value of the sample, and and represent the average true value and predicted value, respectively. The symbol n indicates the number of samples, and Var denotes the sample variance. Among the five indicators, RMSE, MAE, and MAPE values range from 0 to ∞; these indices are always greater than zero, with values closer to 0 indicating better model performance. The EVS value ranges from 0 to 1, with values closer to 1 indicating better model performance. CC measures the correlation between two variables, with values ranging from −1 to 1; the closer the value is to 1 or −1, the stronger the relationship between the true and predicted values [80,81].
The R2 score from tenfold cross-validation reflects the fitting performance of the model on different data subsets. Specifically, the R2 score indicates how well the predicted values of the model fit the true values, ranging from 0 to 1, with values closer to 1 indicating stronger predictive ability. Using tenfold cross-validation helps avoid biases from a single training or test set division, offering a more comprehensive and reliable evaluation of the performance of the model.
3. Results
3.1. FVC Validation
The GLASS FVC validation data were resampled to a spatial resolution of 1 km and a temporal resolution of 1 month to match the spatiotemporal resolution of the MODIS-MOD13A3-FVC data calculated in this study. Figure 2 shows density scatter plots comparing the annual average FVC for 2000, 2007, 2014, and 2020 between the FVC dataset calculated in this study (MODIS-MOD13A3-FVC) and the published GLASS FVC product. The analysis indicated R2 values close to unity for all four years, ranging from 0.92 to 0.94, with both the MAE and RMSE nearly zero. These suggest a strong correlation between the MODIS-MOD13A3-FVC and the GLASS FVC product, highlighting their consistency and validating the reliability of the MODIS-MOD13A3-FVC data in capturing FVC variations. Moreover, since the MODIS-MOD13A3-FVC in this study was calculated within SWC, it is likely more accurate in reflecting the vegetation conditions of the study area.
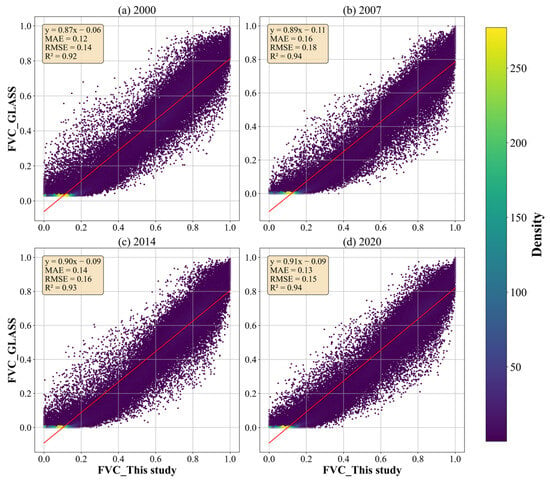
Figure 2.
Density scatter plots of the annual average FVC during 2000–2020 between the FVC dataset calculated in this study and the published GLASS FVC product. (a) 2000, (b) 2007, (c) 2014, (d) 2020.
3.2. Spatiotemporal Variability of FVC
3.2.1. Analysis of FVC Variation Trends at Different Timescales
Table 2 shows the multi-year average FVC values from 2000 to 2020 for the entire SWC and its five provinces and municipalities, categorized by the year, four seasons, and growing season (May to September). The table also includes the standard errors, which measure the dispersion of the average FVC values. The annual average FVC values were as follows: Yunnan (0.78) > Guizhou (0.75) > Chongqing (0.74) > Sichuan (0.66) > southwest China overall (0.46) > Tibet (0.22), indicating significant regional differences. Seasonally, Tibet had the lowest average FVC in all four seasons and the growing season. Therefore, it was classified as a low-coverage area, with the highest summer FVC being only 0.27. Chongqing and Guizhou had similar FVC values, with the highest summer values of 0.84 and 0.86 and the lowest winter values of 0.60 and 0.61, respectively. The FVC values of Yunnan were all above 0.70, showing the best FVC status with minimal variation across different timescales. The FVC of Sichuan was 0.80 in summer, whereas it was relatively low in winter due to the western part being the Sichuan–Tibet Plateau and adjacent to Tibet. The average growing-season FVC was higher than that of Tibet but lower than that of Chongqing, Guizhou, and Yunnan. The standard error values for the entire SWC and the five provinces and municipalities were all ≤ 0.05, indicating good stability of the sample means with minor differences from the true population means.

Table 2.
Average FVC and standard error across various timescales from 2000 to 2020 in southwest China.
Table 3 shows the FVC trend changes at different timescales. Since 2000, the overall FVC in SWC displayed an increasing trend. The annual variation rates were as follows: winter (0.16/100a) > autumn (0.11/100a) > annual (0.09/100a) > spring (0.07/100a) > growing season (0.03/100a) > summer (0.02/100a). However, the trends in summer and the growing season did not pass the p < 0.05 significance level t test. Among the five provinces and municipalities, all provinces and municipalities showed an increasing trend in the annual, seasonal, and growing season scales, except for Tibet, where the FVC showed a decreasing trend. Chongqing and Guizhou both passed the p < 0.01 significance level t test, indicating a significant increasing trend. The R2 score of Chongqing’s multi-year fitted trend line equation was as high as 0.88, indicating the best fit. The fitted trend line equations for Sichuan in summer, Yunnan in spring, summer, and the growing season, and Tibet in summer and autumn did not pass the p < 0.05 significance level t test, indicating that the trends in these seasons were not significant. The interannual variation trends for the administrative regions were in the order Chongqing (0.54/100a) > Guizhou (0.47/100a) > Sichuan (0.19/100a) > Yunnan (0.16/100a) > southwest China overall (0.09/100a) > Tibet (−0.06/100a), reflecting that Chongqing had the most significant FVC increasing trend from 2000 to 2020.

Table 3.
FVC trend line equation and significance level (t test) from 2000 to 2020 in southwest China.
3.2.2. Spatial Variation Trends
Figure 3 shows the spatial distribution of FVC at different timescales from 2000 to 2020, which was obtained using the Theil–Sen slope estimation method and Mann–Kendall test. The overall FVC in SWC was higher in the east and lower in the west. The FVC was extremely low in the western plateau of Tibet but relatively high in parts of Sichuan, Chongqing, Guizhou, and Yunnan. The FVC was relatively high across different timescales in southeastern Tibet, where the altitude is generally below 4000 m, latitude is lower, and rainfall is abundant. In Sichuan Province, the western part lies on the eastern Tibetan Plateau whereas the eastern part is the Sichuan Basin, showing a similar pattern of higher FVC in the east and lower in the west. The annual average FVC value (0.46) was close to that of spring (0.46) and autumn (0.44), with the value in the growing season (0.51) slightly lower than that in summer (0.53). The overall FVC in the eastern part of SWC improved in spring with revival of vegetation compared with that in winter but was still lower in the Tibetan Plateau and central Yunnan compared with that in summer (Figure 3c). In summer, the vegetation growth was more significant in central Yunnan, western Sichuan, and eastern Tibet (Figure 3d). In autumn, apart from a large-scale decline in FVC in the Sichuan Basin and western Sichuan, Yunnan and Guizhou also experienced a decline (Figure 3e). In winter, a significant widespread decline in FVC was observed across the region, except in southeastern Tibet and southern Yunnan, where the FVC remained almost unchanged (Figure 3f). The steep terrain was unfavorable for vegetation growth in the Hengduan Mountains, where the altitude is mostly 4000–5000 m and the elevation difference between valleys and peaks can reach 2000 m, resulting in low FVC at any timescale.
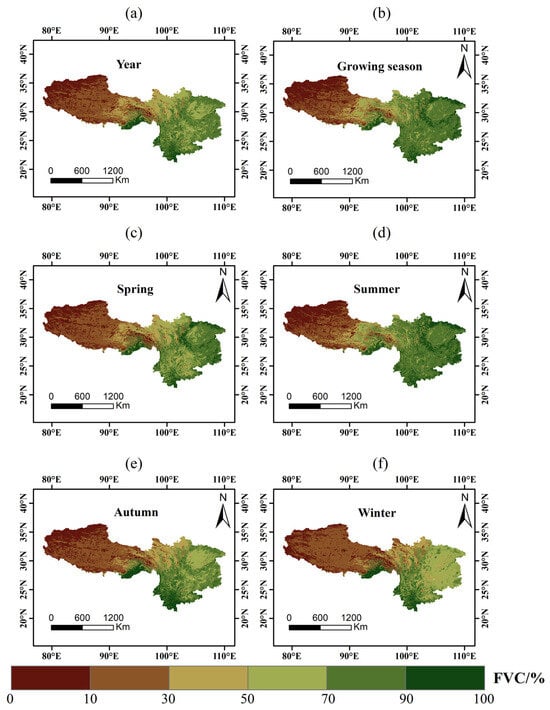
Figure 3.
Spatial distribution of FVC across different timescales from 2000 to 2020 in southwest China. (a) Annual, (b) growing season, (c) spring, (d) summer, (e) autumn, and (f) winter.
Figure 4 shows the spatial variation trends of FVC at different timescales in SWC from 2000 to 2020. During this period, the interannual spatial variation (Figure 4a) indicated a significant degradation of FVC in central and western Tibet; however, southeastern Tibet showed no significant trend. The vegetation improvement was relatively good in the eastern part of SWC, including the Sichuan Basin, Chongqing, Guizhou, and eastern Yunnan, whereas the area of Hengduan Mountains showed an overall decreasing trend. The spatial variation trend of the growing season lay between summer and autumn (Figure 4b), with the most significant vegetation degradation occurring in central Tibet. The areas with increasing FVC were mainly concentrated in the Sichuan Basin, Chongqing, Guizhou, and eastern Yunnan in spring, with slight increases in northwestern and southeastern Tibet. The areas with decreasing FVC were mainly in the Hengduan Mountains and plateau regions (Figure 4c). The FVC trend in summer was similar to that in spring, but the vegetation degradation in western Sichuan and the improvement in northern Tibet were more significant (Figure 4d). The FVC trend in Tibet was not significant in autumn, whereas the improvement in the eastern regions was better than that in summer (Figure 4e). The overall degradation in Tibet was quite significant in winter, with no significant trend in southeastern Tibet; however, the FVC degradation trend in the Hengduan Mountains was more pronounced (Figure 4f).
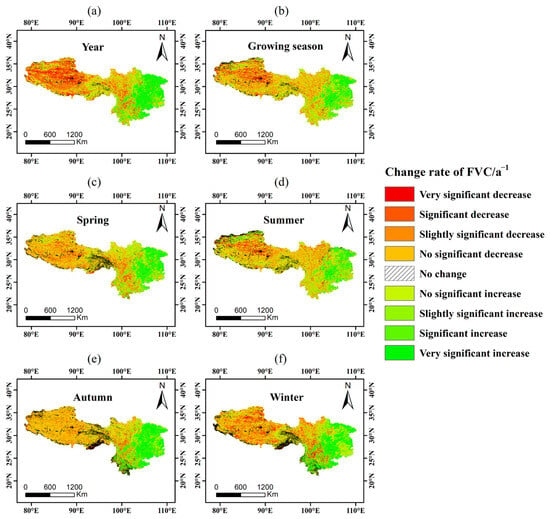
Figure 4.
Spatial change trend of FVC across different timescales from 2000 to 2020 in southwest China. (a) Annual, (b) growing season, (c) spring, (d) summer, (e) autumn, and (f) winter.
Table 4 presents the area proportion statistics for the spatial variation trends of FVC at different timescales. Regarding the interannual spatial variation, areas with very significant, significant, and slightly significant increasing trends accounted for 25.3% of the total area of SWC, primarily in Chongqing, Guizhou, southeastern Sichuan, eastern Yunnan, and southeastern and northern Tibet. Areas with very significant, significant, and slightly significant decreasing trends accounted for 25.8%, mainly in western Tibet, northern Yunnan, and western Sichuan. Overall, the interannual FVC spatial variation trend in Tibet was decreasing, with some increases in southeastern and northern Tibet. The FVC improvement in northern Tibet was relatively good in summer and the growing season, but areas with no significant change had the highest proportion. The areas with no change or no significant decrease accounted for 77.4%, mainly in the Qinghai–Tibet Plateau and the Hengduan Mountains, indicating minimal FVC change in the plateau during autumn since 2000. Degradation occurred in the plateau region and northern Yunnan in winter, whereas the areas with no change were mainly located in the Hengduan Mountains. The total area with no interannual change in winter was only 2.7%, also mainly in the Hengduan Mountains.

Table 4.
Area proportion of spatial variation trend of FVC across different timescales from 2000 to 2020.
3.2.3. Changes in FVC Classification during the Growing Season
Figure 5 shows the spatial classification maps for the five FVC categories during the growing seasons of 2000, 2007, 2014, and 2020, based on the FVC classification thresholds listed in Table 1. Figure 6 depicts the changes in the area proportions of different FVC classifications from 2000 to 2020 during the growing season.
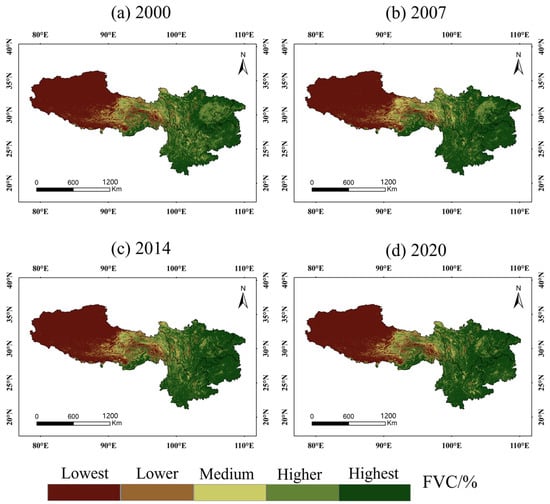
Figure 5.
Spatial variation of FVC classification in growing season from 2000 to 2020. (a) 2000, (b) 2007, (c) 2014, (d) 2020.
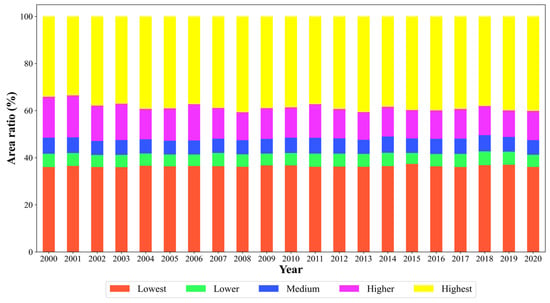
Figure 6.
The area ratio changes in FVC classification during the growing season from 2000 to 2020.
The comprehensive analysis of Figure 5 and Figure 6 indicates that the average FVC values for the five categories—lowest FVC, lower FVC, medium FVC, higher FVC, and highest FVC—remained relatively stable over the observed four-year periods. Specifically, the FVC values ranged from 0.10 to 0.13 for the lowest FVC, 0.30 to 0.38 for the lower FVC, 0.53 to 0.58 for the medium FVC, 0.68 to 0.69 for the higher FVC, and 0.86 to 0.87 for the highest FVC. Among these, the highest FVC category had the largest area ratio, averaging 38.46% over a 21-year period, followed by the lowest FVC at 36.40%. Together, these two categories accounted for 74.86% of SWC. The area ratio for lower FVC was the smallest, averaging 5.35%, while medium FVC followed at 6.32%. The higher FVC category had an intermediate area ratio of 13.46%. Spatially, the distribution of these FVC categories varied: lowest and lower FVCs were predominantly found in western Tibet, medium FVCs were mainly in eastern and northwestern Tibet and southwestern Sichuan, higher and highest FVCs were concentrated in southeastern Tibet, much of Sichuan, Yunnan, Guizhou, and Chongqing. Due to human activities, the FVC in eastern Tibet and western Sichuan decreased from high to low vegetation coverage between 2000 and 2007. Conversely, following the implementation of reforestation and grassland restoration policies, the Sichuan Basin and the Yunnan–Guizhou Plateau experienced an increase in vegetation coverage from low to high between 2007 and 2014.
From 2015 to 2020, while the area ratio of the highest FVC category significantly declined, the other four FVC categories exhibited a slight increase in their area ratios. Specifically, the area ratio for lowest FVC peaked at 37.38% in 2015 and reached a low of 35.96% in 2003; for lower FVC, it was highest at 5.88% in 2018 and lowest at 4.66% in 2015; for medium FVC, it peaked at 6.89% in 2014 and was lowest at 5.84% in 2005; for higher FVC, it was highest at 17.81% in 2001 and lowest at 11.29% in 2019; for highest FVC, it peaked at 40.68% in 2008 and was lowest at 33.54% in 2001. These FVC changes were closely related to the climate, geographical environment, and human activities in SWC.
3.3. ML-Based Prediction and Performance Evaluation of FVC during the Growing Season in SWC
3.3.1. Construction of Prediction Model and Determination of Optimal Parameters
As climate and terrain factors are closely related to the changes in FVC, this study first selected six factors—T-2m, NSSR, SSWRC, Total-Prec, VET, and DEM—from the growing season of 2000–2020 as input variables. The prediction models were initially constructed with the MODIS-MOD13A3-FVC, derived from the MOD13A3 NDVI product, as the output variable using single and ensemble models based on LightGBM, SVR, KNN, and RR. The FVC for the growing seasons of 2021–2023, predicted using these models, was then evaluated and compared with the actual MODIS-MOD13A3-FVC values and the FY3D-MERSI-FVC, derived from the FY3D-MERSI NDVI product, for result assessment and spatiotemporal cross-validation analysis. The six factors from historical data and the corresponding year were used for predicting the FVC for 2022 and 2023.
When constructing the model, the dataset from 21 years was divided into a 60% training set, a 20% validation set, and a 20% test set, comprising a total of 3,198,720 raster data points. Each raster data point included six input variables and one output variable, with each year’s data containing 21,760 rasters. Based on these data, training, validation, and testing analyses were conducted using four different ML models. The Grid Search method, which can exhaustively search for the best hyperparameter combination, involves defining the hyperparameter space, constructing the parameter grid, model training and evaluation, selecting the optimal hyperparameter combination, and retraining the model. This method ensures that the hyperparameters optimizing the model’s performance within the specified hyperparameter space are identified [82]. Therefore, the Grid Search and tenfold cross-validation were primarily used to determine the optimal parameters for different ML models, as shown in Table 5. The construction and operation of the ML models were performed on a computer with a Python 3.9 environment.

Table 5.
Optimal parameter values for four different ML models.
Specifically, the LightGBM model’s parameters needed careful adjustment to enhance predictive performance. The configuration included n_estimators = 200 to ensure sufficient boosting stages, max_depth = 15 to prevent overfitting, and learning_rate = 0.2 to balance convergence and training speed. Min_child_weight = 5 and num_leaves = 9 controlled tree growth to avoid complexity, colsample_bytree = 1.0 and subsample = 1.0 were used for full data training without random sampling, and reg_lambda = 0.5 was used for L2 regularization to reduce overfitting risk. For the SVR model, the parameter adjustments focused on regression accuracy. In this case, c = 1 set the penalty strength for errors, kernel = ‘RBF’ handled nonlinear patterns, gamma = 1 defined the influence range of the kernel function, and epsilon = 0.1 set the tolerance of the loss function. The KNN model’s parameters balanced prediction accuracy and computational efficiency. Algorithm = ‘auto’ selected the best neighborhood search algorithm, metric = ‘Manhattan’ managed data geometry, and n_neighbors = 15, determined by cross-validation, balanced bias and variance. Weights = ‘Distance’ assigned higher weights to closer neighbors for accuracy, and p = 2 used the Euclidean distance measure. The RR model used alpha = 0.1 as the regularization parameter to handle collinearity, with L2 regularization to reduce complexity and prevent overfitting.
3.3.2. R2 Scores from Tenfold Cross-Validation
Figure 7 shows the R2 scores of the four models in tenfold cross-validation, calculated using Equation (22). The LightGBM model achieved an R2 score of 0.9, close to 1, indicating a strong fit between predicted and true values and demonstrating strong predictive ability. The SVR model followed with an R2 score of 0.83, which was slightly lower than LightGBM but still showed good predictive ability. The KNN and RR models exhibited similar R2 scores of 0.75 and 0.74, respectively, indicating moderate predictive ability. R2 scores were crucial for understanding and selecting the most suitable model for a specific task, highlighting the potential of these four ML models in prediction problems. They helped researchers find the best balance between prediction accuracy and model complexity. In constructing the weighted average heterogeneous ensemble model (WAHEM), the selection of models and the setting of weights comprehensively considered various factors, including the R2 score, the characteristics of the models themselves, and the model performance evaluation metrics.
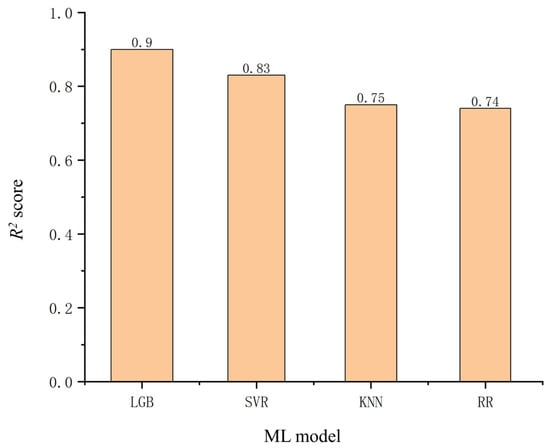
Figure 7.
R2 score from tenfold cross-validation for various models.
3.3.3. Performance Evaluation of Different ML Models
Table 6 shows the performance evaluation metrics of four individual ML models and the WAHEM on the training, validation, and test sets. The main metrics included RMSE, MAE, EVS, and CC. As the RR model is an improvement and extension of the linear regression model and a nonlinear relationship exists between the input and output variables in this study, we considered various characteristics of the four models and their evaluation values on the three datasets (Table 6), as well as the R2 scores in Figure 7 (with the RR model having the lowest R2 scores). Based on this, we constructed a WAHEM using LightGBM, SVR, and KNN to further improve prediction accuracy and reduce model uncertainty by integrating the advantages of different algorithms. The ensemble weights were set as LightGBM = 0.5, SVR = 0.3, and KNN = 0.2.

Table 6.
Performance evaluation metrics of different ML models across various datasets.
In the training set, the WAHEM showed the best performance with the lowest RMSE (0.0048) and MAE (0.0535) and the highest EVS (0.960) and CC (0.9856), thus outperforming the four individual models. This indicated the strongest correlation between predicted and true values, with minimal bias, the highest accuracy, and the best overall performance. WAHEM was followed by the LightGBM, SVR, and KNN models. The RR model performed the worst, with the highest RMSE (0.0309) and MAE (0.1372) and the lowest EVS (0.7410) and CC (0.8608). The performance trends remained consistent in the validation and test sets. The LightGBM model had the lowest RMSE and MAE and the highest EVS and CC, making it the best-performing model. Among the other three models, SVR performed better in terms of RMSE, MAE, and EVS. In contrast, WAHEM displayed better performance in terms of CC, with values of 0.9394 and 0.9401 in the validation and test sets, respectively, indicating a significant correlation. Overall, WAHEM exhibited the best performance across all evaluation metrics in the training set, indicating the highest prediction accuracy, followed by LightGBM, SVR, and KNN models. The RR model performed the worst. LightGBM had the best performance and highest prediction accuracy in the validation and test sets, followed by SVR, WAHEM, and KNN models, with the RR model showing the poorest performance and lowest prediction accuracy across all three datasets.
3.4. Comparative Analysis of FVC Predictions Using Different ML Models and Satellite Product Retrievals
Figure 8 shows the spatial distribution maps of FVC predictions for the growing seasons of 2021–2023 from four individual ML models and the WAHEM, compared with MODIS-MOD13A3-FVC and FY3D-MERSI-FVC. The spatial variation trends of FVC predicted using all models were quite consistent, showing lower values in the west, higher values in the east, and decreasing values from south to north in the central region. The FVC values changed significantly and inversely with the changes in altitude in the central region, the transition area from eastern Tibet to western Sichuan (Figure 1). The model predictions were closer to MODIS-MOD13A3-FVC (true values) compared with MODIS-MOD13A3-FVC and FY3D-MERSI-FVC, showing consistent spatial distribution trends. However, the predicted FVC values were relatively higher. The spatial distribution was also consistent with FY3D-MERSI-FVC; however, the value differences were larger, with FY3D-MERSI-FVC generally having lower values, especially in the eastern region.
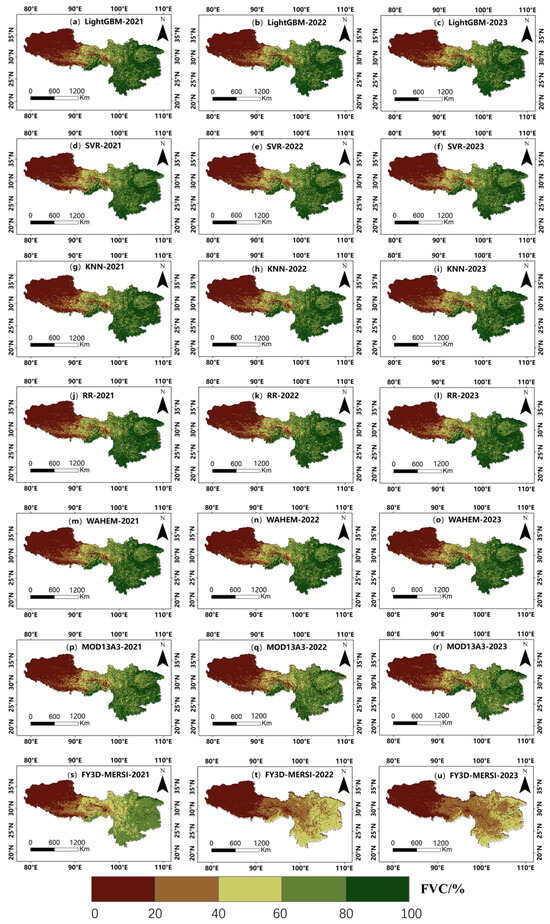
Figure 8.
Spatial distribution of FVC predicted by different ML models and retrieved calculation from satellite products during the growing seasons from 2021 to 2023. (a) LightGBM-2021, (b) LightGBM-2022, (c) LightGBM-2023, (d) SVR-2021, (e) SVR-2022, (f) SVR-2023, (g) KNN-2021, (h) KNN-2022, (i) KNN-2023, (j) RR-2021, (k) RR-2022, (l) RR-2023, (m) WAHEM-2021, (n) WAHEM-2022, (o) WAHEM-2023, (p) MOD13A3-2021, (q) MOD13A3-2022, (r) MOD13A3-2023, (s) FY3D-MERSI-2021, (t) FY3D-MERSI-2022, (u) FY3D-MERSI-2023.
Figure 9 shows the spatial variation comparison of FVC predictions for the growing seasons of 2021–2023 using different ML models in various regions of SWC, compared with MODIS-MOD13A3-FVC and FY3D-MERSI-FVC. All ML models predicted higher FVC values for the entire SWC, Sichuan, Chongqing, Guizhou, Yunnan, and Tibet compared with MODIS-MOD13A3-FVC and FY3D-MERSI-FVC. The predicted spatial distribution of FVC was similar across models, with smaller deviations from the true values and larger deviations from FY3D-MERSI-FVC values. For the entire SWC, the predictions of the SVR model were closest to the actual values, with FVC differences of 0.01 (2021), 0.0452 (2022), and 0.0315 (2023). The RR model displayed the largest differences, with values of 0.025 (2021), 0.051 (2022), and 0.058 (2023). For Sichuan, the predictions of the SVR model were closest to the actual values in 2021 (FVC difference of 0.034). The WAHEM’s predictions in 2022 and 2023 were the closest, with differences of 0.069 and 0.059, respectively. The largest differences were found in RR (0.05 in 2021), KNN (0.079 in 2022), and LightGBM (0.075 in 2023). For Chongqing and Guizhou, the SVR model’s predictions were the closest to the actual values, with differences of 0.00 (2021, Chongqing), 0.072 (2022, Chongqing), 0.029 (2023, Chongqing), 0.022 (2021, Guizhou), 0.066 (2022, Guizhou), and 0.037 (2023, Guizhou). The RR model showed the largest differences, with values of 0.029 (2021, Chongqing), 0.094 (2022, Chongqing), 0.068 (2023, Chongqing), 0.045 (2021, Guizhou), 0.085 (2022, Guizhou), and 0.078 (2023, Guizhou). For Yunnan, the SVR model’s predictions were the closest to the actual values in 2021 and 2022, with FVC differences of 0.027 and 0.046, respectively. In 2023, the KNN model’s predictions were the closest, with a difference of 0.052. The RR model showed the largest difference of 0.047 in 2021 and 0.066 in 2022, whereas the LightGBM model showed the largest difference of 0.079 in 2023. For Tibet, the LightGBM model’s predictions were the closest to the actual values in 2021 and 2022, with FVC differences of 0.013 and 0.029, respectively. In 2023, the WAHEM’s predictions were the closest, with a difference of 0.012. The largest differences were found in SVR (0.018 in 2021), KNN (0.036 in 2022), and RR (0.024 in 2023). Overall, the SVR model’s predictions were the closest to the true values in the annual average predictions for each region, whereas the RR model showed the largest differences. The smallest deviations between model predictions and actual values occurred in 2021, followed by 2023, with the largest deviations in 2022.
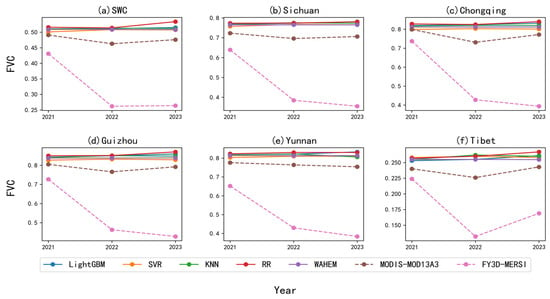
Figure 9.
Comparison of FVC changes derived from different ML model predictions and satellite product calculations across various regions during the growing seasons from 2021 to 2023. (a) SWC, (b) Sichuan, (c) Chongqing, (d) Guizhou, (e) Yunnan, and (f) Tibet.
The predicted values of different ML models for 2021–2023 showed large deviations from the FY3D-MERSI-FVC values, generally being higher. The FVC values were the closest in 2021, followed by 2022. The FVC value deviations in 2023 were the largest in other regions, except for Tibet. Compared with MODIS-MOD13A3-FVC, the overall FVC values of SWC were lower by 0.06 (2021), 0.201 (2022), and 0.212 (2023). In Sichuan Province, the FVC values were lower by 0.084, 0.311, and 0.351 for the aforementioned 3 years, respectively. In Chongqing, they were lower by 0.06, 0.30, and 0.38, respectively. In Guizhou, they were lower by 0.078, 0.303, and 0.364, respectively. In Yunnan, they were lower by 0.124, 0.334, and 0.37, respectively. In Tibet, they were lower by 0.016, 0.094, and 0.074, respectively. In 2021, the largest FVC value deviation was observed in Sichuan Province; in 2022, it was in Yunnan, and in 2023, it was in Chongqing. Tibet showed the smallest deviations in all 3 years.
Table 7 shows the RMSE and MAPE evaluation comparison results between the predicted values of different ML models and the actual values for 2021–2023. In 2021, the WAHEM had the smallest deviation, with RMSE and MAPE of 5.81 × 10−3 and 14.97%, respectively. The LightGBM model followed with RMSE and MAPE of 5.95 × 10−3 and 15.26%, respectively. The RR model had the largest deviation, with RMSE and MAPE of 10.70 × 10−3 and 18.80%, respectively. In 2022 and 2023, the LightGBM model had the smallest deviation, with RMSE of 5.95 × 10−3 and MAPE of 14.41% for both years, followed by the WAHEM. The RR model had the largest deviation, with RMSE of 13.70 × 10−3 and 20.45 × 10−3 and MAPE of 20.05% and 32.75%, respectively. Overall, the comprehensive statistical evaluation of each pixel over these 3 years revealed that the LightGBM model performed the best, followed by the WAHEM, whereas the RR model performed the worst.

Table 7.
Comparison of evaluations between different ML models and MODIS-MOD13A3-FVC (true values) from 2021 to 2023.
3.5. Analysis of the Feature Importance of the LightGBM Model
The LightGBM model is a gradient-boosting framework based on efficient decision trees that can automatically evaluate and output feature importance scores during training. This feature allows researchers to directly identify the features most significantly impacting the predictive performance of the model. In contrast, the KNN model, which is a lazy learning algorithm based on nearest points for prediction, does not involve feature importance. Although the SVR model can build nonlinear models, its coefficients do not directly reflect feature importance. The RR model includes regularization to prevent overfitting. However, its coefficients are influenced by the regularization strength and feature scale, making it difficult to interpret feature importance directly from the coefficients. As analyzed in Figure 7, Table 6 and Table 7, the LightGBM model provided the best predictive results. Therefore, this study used the feature importance scores from the LightGBM model to determine the influence of different input features. The specific importance scores are shown in Figure 10. The horizontal axis represents all the input features of the LightGBM model, whereas the vertical axis represents the importance score of each feature. A higher score indicates a greater impact of that feature on the predictive results of the model.
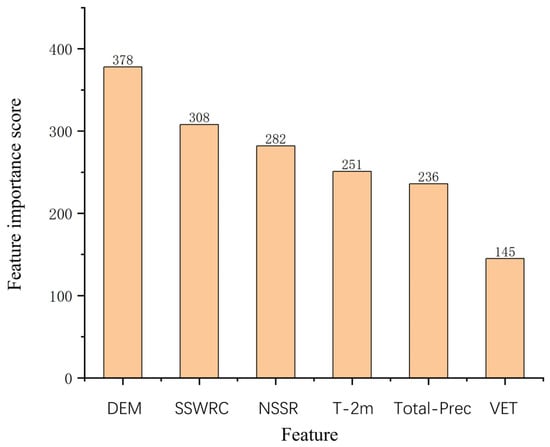
Figure 10.
Feature importance scores in the LightGBM model.
Figure 10 shows the importance scores of each feature, ranked as follows: DEM (378) > SSWRC (308) > NSSR (282) > T-2m (251) > Total-Prec (236) > VET (145). DEM had the highest feature importance score, indicating that elevation had the closest relationship with FVC and the greatest influence among the six input features. SSWRC ranked second, which is crucial for water supply to plants and particularly important for seed germination and seedling rooting. NSSR, which provides energy for plant growth and drives photosynthesis, ranked third. T-2m, which directly affects vegetation growth and the rates of photosynthesis and respiration, ranked fourth. Total-Prec, which is essential for providing water to vegetation and a fundamental condition for plant growth, ranked fifth. VET, the process of plants releasing water into the atmosphere through leaf stomata and an important part of the plant water cycle, ranked sixth in this study, also significantly impacting FVC.
4. Discussion
This study analyzed the spatiotemporal variation characteristics of FVC in SWC from 2000 to 2020. The results were consistent with the findings of some scholars in previous studies within the corresponding timescales for the region. For example, Zheng et al. (2017) [83] used MODIS-NDVI data to analyze the dynamic changes in FVC in SWC (Guangxi, Guizhou, Chongqing, Yunnan, Sichuan, and parts of western Qinghai and southeastern Tibet) from 2000 to 2014. The FVC in SWC showed a decreasing trend from southeast to northwest. Over the 15 years, the annual maximum FVC showed an overall increasing trend, with the largest increase from 2009 to 2014. During this period, FVC showed a fluctuating upward trend, and the overall vegetation cover improved. FVC increased in all seasons except for a decreasing trend in summer. This study found that the FVC in all seasons showed an increasing trend. However, the increasing trend in summer was not significant and did not pass the significance level test at p = 0.05. Additionally, the rate of increase varied due to the differences in the study area scope and timescale. Xiong et al. (2019) [84] investigated the spatiotemporal variation characteristics of vegetation cover in the growing season (April to September) in SWC from 2000 to 2016. They indicated that MODIS-NDVI showed an increasing trend over the 17 years, with the most significant increase in April. The area showing an increasing trend accounted for 71.49% of the total study area, mainly in the eastern and southeastern regions. Compared with the results of this study, the interannual increasing trend and the spatial distribution of the increasing trend were generally consistent. However, significant differences in the rate of increase over time and the spatial proportion of the increasing trend were observed due to the differences in the study area scope and the division of the growing-season timescale. Li (2019) [85] analyzed the spatiotemporal variation characteristics of GIMMS FVC in SWC from 1982 to 2016 and found an increasing overall trend of FVC, with vegetation conditions showing positive development in different seasons and the growing season. Most areas had good vegetation cover, with an annual FVC average of 0.46. Despite the differences in the study area and timescale, these results are basically consistent with the findings of this study. Additionally, SWC generally displayed a moderately stable (34.1%) and a less stable (31.1%) development trend, which corresponded to the results of this study revealing a relatively large area of slightly significant increase and slightly significant decrease in spatial variation trends in different seasons, interannually, and in the growing season. Furthermore, Zhang et al. (2020) [86], Yan et al. (2021) [87], and Duan et al. (2022) [88] also examined the vegetation cover in SWC (Sichuan, Yunnan, Guizhou, Chongqing, and Guangxi) using SPOT NDVI (2000–2015), GIMMS NDVI (1982–2015), and AVHRR and GIMMS NDVI (1982–2015), respectively, all revealing an overall increasing trend in vegetation. Compared with the aforementioned studies, which focused on timescales up to 2016, this study addressed the spatiotemporal variation characteristics in recent years with the intensification of global warming. Previous studies did not extensively cover the spatiotemporal variation trends and differences in FVC across the five provinces and municipalities, including Tibet, resulting in relatively less comprehensive analyses.
ML methods are increasingly used to estimate and predict vegetation changes due to their ability to handle complex relationships and nonlinear associations, adaptation to large-scale and multidimensional data, and features such as data-driven and automated feature learning, high flexibility, and strong generalization ability. Among the four individual ML models selected in this study, the LightGBM model stood out due to its histogram-based optimization and flexible tree growth strategy, offering high efficiency and accuracy. It also excelled in handling complex interactions and nonlinear relationships between features, making it the best-performing model with the highest prediction accuracy. The RR model, which is a linear regression extension technique used to address multicollinearity issues, struggled with the nonlinear relationships between vegetation cover and terrain and climate factors, resulting in the poorest overall evaluation performance and the lowest prediction accuracy. A WAHEM was constructed in this study by weighting the selected individual ML models, aiming to leverage their strengths to better learn the sample features and achieve superior prediction results. However, the WAHEM performed the best in all four evaluation metrics on the training set. The performance of the WAHEM was not as good as that of the LightGBM and SVR models on the validation and test sets. Nonetheless, the differences in comprehensive evaluation metrics were not significant. This might be attributed to factors such as the random division of the dataset, the relative weight settings of different ML methods, and the choice of heterogeneous ensemble learning strategies.
The MOD13A3 NDVI data, which are provided by the MODIS satellite, are a crucial operational product for monitoring the changes in surface vegetation. They include global monthly data with a spatial resolution of 1 km, which are primarily generated based on the NDVI 16-day composite algorithm. This product features high clarity and minimal cloud impact. The MOD13A3 product also includes a pixel reliability band to assess pixel imaging quality, allowing the exclusion of NDVI pixels affected by ice/snow and cloud cover during preprocessing. The atmospheric correction is performed using surface bidirectional reflectance to ensure data accuracy, thus removing the effects of water, clouds, heavy aerosols, and cloud shadows. The FY3D satellite, launched in December 2017, carries the MERSI instrument, which is capable of obtaining seamless global true-color images at a 250 m resolution and images from two infrared split-window regions daily. It is considered one of the most advanced wide-swath imaging remote sensing instruments today, with performance similar to that of the MODIS satellite sensor [89,90]. MERSI’s NDVI data, available from May 2019 onward, are an important product for deriving global vegetation parameters and monitoring vegetation changes [91]. As the MODIS satellite approaches retirement, FY3D is expected to succeed it, continuing to provide products with different temporal and spatial scales. However, its products still require further evaluation and validation.
The MODIS satellite sensor achieves high calibration accuracy due to its advanced on-orbit calibration equipment and regularly updated calibration coefficients. The absolute radiometric calibration accuracy can reach 5%, and the relative radiometric calibration accuracy can reach 1%. This excellent performance has established MODIS as a standard satellite for sensor calibration, which is extensively used in cross-calibration studies of other global sensors. In contrast, the performance of the FY satellite series sensors degrades more significantly with longer on-orbit operation time [92]. In this study, we compared the FVC predictions of four individual ML models and the WAHEM for the growing seasons of 2021–2023 with MODIS-MOD13A3-FVC and FY3D-MERSI-FVC. The spatial variation trends predicted using all ML models were consistent over the three years, showing lower values in the west, higher values in the east, and a decreasing trend from south to north in the central region. All model predictions were closer to MODIS-MOD13A3-FVC, with high consistency in spatial distribution trends, although the predicted FVC values were relatively higher. The spatial distribution was also consistent with FY3D-MERSI-FVC; however, the value differences were larger, with FY3D-MERSI-FVC values generally lower. MODIS-MOD13A3-FVC values were generally higher than FY3D-MERSI-FVC values. As the output variable for constructing prediction models using different ML methods was MODIS-MOD13A3-FVC, the predictions for 2021–2023 were expected to be closer to MODIS-MOD13A3-FVC values. This bias was determined by the learning capabilities of the ML models. The comparison results of the two data products aligned with the findings of Wang and Li (2022) and Zhang (2023) [93,94]. Wang and Li (2022) [93] evaluated the quality and usability of FY3D-MERSI NDVI data by comparing it with MODIS-Terra NDVI data from May 2019 to December 2020, based on spatial patterns and time series. The results showed high consistency in spatial distribution and time-series characteristics. On a global average level, FY3D-MERSI NDVI was systematically lower than MODIS-Terra NDVI, with a tendency to underestimate high values and overestimate low values, resulting in a slightly narrower dynamic range. The linear regression model using MODIS-Terra NDVI as the independent variable and FY3D-MERSI NDVI as the dependent variable showed high accuracy (R2 of 0.91–0.95, RMSE of 0.048–0.068), with regression coefficients showing some temporal variation (slope of 0.87–0.94, intercept of 0.02–0.04). Zhang (2023) [94] compared FY3D-MERSI NDVI with MODIS-NDVI products from 2020–2023 in terms of spatial patterns, processing methods, time series, and site-scale comparisons. The results also showed a strong spatiotemporal correlation in NDVI, with consistent seasonal variation trends for different underlying surface types. The scatter plots were mostly distributed around 1:1, with an average RMSE of less than 0.06. Overall, MODIS-NDVI values were higher than FY3D-MERSI NDVI values, with FY3D-MERSI NDVI being lower than MODIS-NDVI in high vegetation cover areas and higher in low vegetation cover areas, especially in desert sites. This discrepancy was attributed to the differences in their spectral response functions and atmospheric corrections. Although the spectral response functions of FY3D and MODIS for vegetation monitoring were extremely similar in terms of bandwidth and peak response, FY3D MERSI had a slightly wider lower limit in the red band and a wider upper limit in the near-infrared band compared with MODIS. The spectral response functions were relatively wider, and the central wavelengths of the red and near-infrared bands were different, with MODIS at 0.645 μm (red) and 0.858 μm (near-infrared), and FY3D at 0.650 μm (red) and 0.865 μm (near-infrared), leading to saturation in high vegetation cover areas. The differences in the original bands used for NDVI calculation between the two satellites could cause certain biases ([95]; http://www.nsmc.org.cn/, accessed on 16 July 2024). Previous studies showed that the MERSI bands were more susceptible to atmospheric water vapor, and their signal-to-noise ratio was still slightly lower than that of MODIS, leading to some differences in monitoring values. Additionally, the interpolation methods used to unify the spatial resolutions also caused calculation biases due to the different spatial resolutions of the NDVI data from the two satellites.
In the LightGBM model, DEM had the highest feature importance score, indicating that the relationship between FVC and elevation was the closest and significantly influenced the six input features. The topography of SWC is complex. The terrain in mountainous and hilly areas became more rugged with an increase in elevation, making soil and water conservation more difficult. Additionally, the temperature gradually decreased, leading to a decrease in the FVC in these areas with increasing elevation. This underscored the close relationship between FVC and elevation in SWC [84]. The authors previously found that the elevation and FVC at different timescales were significantly correlated, with a notable downward trend. FVC at different timescales increased significantly with the slope, but when the slope exceeded 25°, FVC gradually decreased, highlighting the impact of elevation and slope on FVC in SWC [96]. SSWRC had the second-highest feature importance score, indicating the importance of SSWRC to FVC. Bao et al. (2023) [97] found that, when the thermal conditions for plateau vegetation growth were sufficiently met, the soil moisture conditions surpassed temperature and other thermal factors to become the most crucial climatic factor affecting plateau vegetation growth. Therefore, the importance score of SSWRC was the highest among the five climatic factors selected in this study, which was consistent with our results. In summary, the six factors selected in this study had varying degrees of importance to FVC and played a key role in maintaining ecosystem health and ecological balance.
5. Summary and Conclusions
FVC is a crucial indicator for assessing surface vegetation conditions and a key factor affecting soil erosion, water loss, and ecosystem health. The changes in FVC are essential for monitoring regional ecological environments and hold significant importance for the research on climate, hydrology, ecology, and global changes. SWC is characterized by complex topography, diverse climate types, and rich vegetation types. It is also the source and flowing area of numerous rivers. The changes in vegetation have a significant impact on the environment, ecosystems, and socio-economic conditions in the region and related downstream areas. This study aimed to calculate the average annual, seasonal, and growing-season FVC for the entire SWC and its five constituent provinces/municipalities from 2000 to 2020 using the pixel dichotomy model and the NDVI data from the MODIS–MOD13A3. The study also analyzed the spatiotemporal variation characteristics of FVC at various timescales. We selected four ML models: LightGBM, SVR, KNN, and RR, by integrating five climate factors from ERA5 data, DEM, and FY3D-MERSI NDVI data. Additionally, a WAHEM optimized from these single ML models was also constructed to predict growing-season FVC in SWC. The performance of the different ML models was comprehensively evaluated using tenfold cross-validation and multiple performance metrics. The models were then used to predict FVC for the growing seasons of 2021–2023. The predicted results were evaluated and compared with their actual values and FY3D-MERSI-FVC through result assessment and spatiotemporal cross-validation analysis.
The results indicated that the FVC calculated using the pixel dichotomy model in this study had an R2 value close to 1, with MAE and RMSE values near 0 when compared to the GLASS FVC product. This demonstrated a high degree of correlation and consistency between the two datasets and provided indirect validation of the reliability and effectiveness of the FVC data calculated in this study. The overall FVC in SWC predominantly increased from 2000 to 2020. Among the five provinces/municipalities, all except Tibet showed an increasing trend annually, seasonally, and during the growing season, with Chongqing (0.54/100a) exhibiting the most significant increase. Over the 21 years, the FVC spatial distribution in SWC generally showed a high east and low west pattern, with extremely low FVC in the western plateau of Tibet and higher FVC in parts of eastern Sichuan, Chongqing, Guizhou, and Yunnan. The annual average FVC value (0.46) was close to that of spring (0.46) and autumn (0.44), whereas the value of the growing season (0.51) was slightly lower than that of summer (0.53). The interannual spatial variation indicated a significant degradation of FVC in central and western Tibet; however, southeastern Tibet showed no significant trend. The vegetation improvement was relatively good in the eastern part of SWC, including the Sichuan Basin, Chongqing, Guizhou, and eastern Yunnan, whereas the area of Hengduan Mountains showed an overall decreasing trend. Areas with very significant, significant, and slightly significant increasing trends accounted for 25.3% of the total area of SWC, primarily in Chongqing, Guizhou, southeastern Sichuan, eastern Yunnan, and southeastern and northern Tibet. Areas with very significant, significant, and slightly significant decreasing trends accounted for 25.8%, mainly in western Tibet, northern Yunnan, and western Sichuan. Overall, the interannual FVC spatial variation trend in Tibet was decreasing, with some increases in southeastern and northern Tibet. The average FVC values for the five categories remained relatively stable from 2000 to 2020. However, due to human activities, vegetation coverage in eastern Tibet and western Sichuan decreased from high to low between 2000 and 2007. In contrast, following the implementation of reforestation and grassland restoration policies, the Sichuan Basin and the Yunnan–Guizhou Plateau experienced an increase in vegetation coverage from low to high between 2007 and 2014. From 2015 to 2020, while the area ratio of the highest FVC category significantly decreased, the other four categories exhibited a modest increase in their area ratios.
The determination coefficient R2 scores from tenfold cross-validation for the four ML models were 0.9 (LightGBM), 0.83 (SVR), 0.75 (KNN), and 0.74 (RR), respectively. The LightGBM model achieved an R2 score of 0.9, close to 1, indicating a strong fit between predicted and true values and demonstrating strong predictive ability. WAHEM exhibited the best performance across all evaluation metrics in the training set, RMSE, MAE, EVS, and CC were 0.0048, 0.0535, 0.960, and 0.9856, respectively, indicating the highest prediction accuracy, followed by LightGBM, SVR, and KNN models. The RR model performed the worst. LightGBM had the best performance and highest prediction accuracy in the validation and test sets, followed by SVR, WAHEM, and KNN models, with the RR model showing the poorest performance and lowest prediction accuracy across all three datasets. The spatial distribution maps of FVC predictions for the growing seasons of 2021–2023 from four individual ML models and the WAHEM, compared with MODIS-MOD13A3-FVC and FY3D-MERSI-FVC, showed that the spatial variation trends of FVC predicted using all models were quite consistent, showing lower values in the west, higher values in the east, and decreasing values from south to north in the central region. The FVC values changed significantly and inversely with the changes in altitude in the central region, the transition area from eastern Tibet to western Sichuan. The model predictions were closer to MODIS-MOD13A3-FVC (true values) compared with MODIS-MOD13A3-FVC and FY3D-MERSI-FVC, showing consistent spatial distribution trends. However, the predicted FVC values were relatively higher. The spatial distribution was also consistent with FY3D-MERSI-FVC; however, the value differences were larger, with FY3D-MERSI-FVC generally having lower values, especially in the eastern region.
Based on a comprehensive comparison of FVC predicted values by different ML models with actual values over 3 years, the SVR model’s predictions were the closest to the true values in the annual average predictions for each region, whereas the RR model showed the largest differences. The smallest deviations between model predictions and actual values occurred in 2021, followed by 2023, with the largest deviations in 2022. When comparing the predicted values of different ML models with FY3D-MERSI-FVC data over 3 years, in 2021, the largest FVC value deviation was observed in Sichuan Province. In 2022, it was in Yunnan, and in 2023, it was in Chongqing. Tibet showed the smallest deviations in all 3 years. The RMSE and MAPE evaluation results comparing the predicted values of different ML models with actual values from 2021 to 2023 indicated that the comprehensive statistical evaluation of each pixel over these 3 years revealed that the LightGBM model performed the best, followed by the WAHEM, whereas the RR model performed the worst. In the LightGBM model, the highest feature importance score was assigned to DEM, indicating a strong correlation with FVC. Among the five selected climatic factors, SSWRC was identified as having the most significant impact on FVC.
The results of this study might aid in understanding the spatiotemporal characteristics of vegetation cover change in SWC under global warming, particularly in the high-altitude Tibetan region. Validating moderate spatial resolution FVC datasets poses challenges due to the difficulty of directly comparing ground-based point measurements with these datasets because of surface heterogeneity. This study validated the FVC calculated using the pixel dichotomy model against the widely used and highly accurate GLASS FVC product, but the validation is still somewhat limited. Despite the availability of many ML methods, this study only examined four. Future research should incorporate additional FVC validation methods and explore a broader range of ML techniques, especially deep learning and hybrid models combining different advantages. In terms of ML input variables, this study considered only DEM and some climate factors. Future studies should incorporate additional features, including both natural and human activity factors, to improve prediction accuracy. While constructing heterogeneous ensemble models, future studies should also explore stacking and blending ensemble methods. Additionally, attempts should be made to achieve more refined FVC predictions by improving the overall spatiotemporal resolution of the data. Hence, potential directions exist for further research. In conclusion, the prediction of FVC for the growing season in this study provides a solid theoretical basis and data foundation for ML-based prediction methods and also offers valuable reference and guidance for other similar studies.
Author Contributions
X.L.: Conceptualization, data curation, visualization, writing—original draft, funding acquisition, supervision, writing—review; Y.L.: data curation, investigation, software, code, methodology, writing—original draft; L.W.: conceptualization, supervision, writing—review. All authors have read and agreed to the published version of the manuscript.
Funding
This study was jointly supported by the Key Research and Development (R&D) Project of the Department of Science and Technology of Yunnan Province (202203AC100005 and 202203AC100006), the Open Project of the Research Center for Meteorological Disaster Prediction, Early Warning and Emergency Management at the Key Research Base of Humanities and Social Sciences of the Sichuan Provincial Department of Education (ZHYJ23-ZD01), the Second Tibetan Plateau Scientific Expedition and Research Program (2019QZKK0105), and the Drought Meteorological Science Research Fund of the China Meteorological Administration (IAM202201).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Masson-Delmotte, V.; Zhai, P.M.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Huang, M.T.; Yelekçi, O.; Yu, R.; Zhou, B.Q. Climate Change 2021: The Physical Science Basis. In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2021; Volume 2. [Google Scholar]
- Ma, Z.Y.; Ren, J.X.; Chen, H.T.; Jiang, H.; Gao, Q.X.; Liu, S.L.; Yan, W.; Li, Z.M. Analysis and Recommendations of the IPCC Working Group I Assessment Report. Resour. Environ. Sci. 2022, 35, 2550–2558. [Google Scholar]
- Fu, Y.H.; Zhao, H.; Piao, S.; Peaucelle, M.; Peng, S.; Zhou, G.; Ciais, P.; Huang, M.; Menzel, A.; Peñuelas, J.; et al. Declining Global Warming Effects on the Phenology of Spring Leaf Unfolding. Nature 2015, 526, 104–107. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Du, G.; Bi, H.; Li, Z.; Zhang, X. Normal Difference Vegetation Index Simulation and Driving Analysis of the Tibetan Plateau Based on Deep Learning Algorithms. Forests 2024, 15, 137. [Google Scholar] [CrossRef]
- Gao, L.; Wang, X.; Johnson, B.A.; Tian, Q.; Wang, Y.; Verrelst, J.; Mu, X.; Gu, X. Remote Sensing Algorithms for Estimation of Fractional Vegetation Cover Using Pure Vegetation Index Values: A review. ISPRS J. Photogramm. Remote Sens. 2020, 159, 364–377. [Google Scholar] [CrossRef]
- Filipponi, F.; Valentini, E.; Xuan, A.N.; Guerra, C.A.; Wolf, F.; Andrzejak, M.; Taramelli, A. Global MODIS Fraction of Green Vegetation Cover for Monitoring Abrupt and Gradual Vegetation Changes. Remote Sens. 2018, 10, 653. [Google Scholar] [CrossRef]
- Mustafa, Y. Spatiotemporal Analysis of Vegetation Cover in Kurdistan Region-Iraq Using MODIS Image Data. J. Appl. Sci. Technol. Trends 2020, 1, 1–7. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Liu, H.; Zuo, Q.T.; Yu, J.T.; Li, Y. Spatiotemporal Changes of Fractional Vegetation Coverage in the Yellow River Basin during 2000–2019. Resour. Sci. 2021, 43, 849–858. [Google Scholar]
- Cui, L.; Zhao, Y.; Liu, J.; Wang, H.; Han, L.; Li, J.; Sun, Z. Vegetation Coverage Prediction for the Qinling Mountains Using the CA–Markov Model. ISPRS Int. J. Geo-Inf. 2021, 10, 679. [Google Scholar] [CrossRef]
- Wang, X.L.; Jiang, Y.Y.; Zhang, Y.F.; Chen, J.Z.; Ao, Z.J.; Ji, Z.J. Characteristics and Driving Factors of Vegetation Changes in the Gannan Plateau from 2001 to 2020. Pratacultural. Sci. 2023, 40, 2185–2198. [Google Scholar]
- Wu, D.H.; Wu, H.; Zhao, X.; Zhou, T.; Tang, B.; Zhao, W.; Jia, K. Evaluation of Spatiotemporal Variations of Global Fractional Vegetation Cover Based on GIMMS NDVI Data from 1982 to 2011. Remote Sens. 2014, 6, 4217–4239. [Google Scholar] [CrossRef]
- Shobairi, S.O.R.; Usoltsev, V.A.; Chasovskikh, V.P. Dynamic Estimation Model of Vegetation Fractional Coverage and Drivers. Int. J. Adv. Appl. Sci. 2018, 5, 60–66. [Google Scholar] [CrossRef]
- Hill, M.J.; Guerschman, J.P. The MODIS Global Vegetation Fractional Cover Product 2001–2018: Characteristics of Vegetation Fractional Cover in Grasslands and Savanna Woodlands. Remote Sens. 2020, 12, 406. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.L.; Zhang, J. Growing-Season Vegetation Coverage Patterns and Driving Factors in the China-Myanmar Economic Corridor Based on Google Earth Engine and Geographic Detector. Ecol. Indic. 2022, 136, 108620. [Google Scholar] [CrossRef]
- Wang, X.L.; Shi, S.H.; Chen, J.Z.X. Changes and Driving Factors of Vegetation Coverage in the Yellow River Basin. China Environ. Sci. 2022, 42, 5358–5368. [Google Scholar]
- Eisfelder, C.; Asam, S.; Hirner, A.; Reiners, P.; Holzwarth, S.; Bachmann, M.; Gessner, U.; Dietz, A.; Huth, J.; Bachofer, F. Seasonal Vegetation Trends for Europe over 30 Years from A Novel Normalised Difference Vegetation Index (NDVI) Time-Series—The Timeline NDVI Product. Remote Sens. 2023, 15, 3616. [Google Scholar] [CrossRef]
- Dastigerdi, M.; Nadi, M.; Sarjaz, M.R.; Kiapasha, K. Trend Analysis of MODIS NDVI Time Series and Its Relationship to Temperature and Precipitation in Northeastern of Iran. Environ. Monit. Assess. 2024, 196, 346. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.; Mao, F.; Zhang, M.; Zhu, D.; He, S.; Huang, Z.; Du, H. Spatiotemporal Evolution of Fractional Vegetation Cover and Its Response to Climate Change Based on MODIS Data in the Subtropical Region of China. Remote Sens. 2021, 13, 913. [Google Scholar] [CrossRef]
- Feng, F.; Yang, X.; Jia, B.; Li, X.; Li, X.; Xu, C.; Wang, K. Variability of Urban Fractional Vegetation Cover and Its Driving Factors in 328 Cities in China. Sci. China Earth Sci. 2024, 67, 466–482. [Google Scholar] [CrossRef]
- Li, Y.; Sun, J.; Wang, M.; Guo, J.; Wei, X.; Shukla, M. Spatiotemporal Variation of Fractional Vegetation Cover and Its Response to Climate Change and Topography Characteristics in Shaanxi Province, China. Appl. Sci. 2023, 13, 11532. [Google Scholar] [CrossRef]
- Li, F.; Chen, W.; Zeng, Y.; Zhao, Q.; Wu, B. Improving Estimates of Grassland Fractional Vegetation Cover Based on a Pixel Dichotomy Model: A Case Study in Inner Mongolia, China. Remote Sens. 2014, 6, 4705–4722. [Google Scholar] [CrossRef]
- Han, H.; Yin, Y.; Zhao, Y.; Qin, F. Spatiotemporal Variations in Fractional Vegetation Cover and Their Responses to Climatic Changes on the Qinghai–Tibet Plateau. Remote Sens. 2023, 15, 2662. [Google Scholar] [CrossRef]
- Zhao, T.; Mu, X.; Song, W.; Liu, Y.; Xie, Y.; Zhang, B.; Xie, D.; Jiang, L.; Yan, G. Mapping Spatially Seamless Fractional Vegetation Cover over China at a 30-m Resolution and Semimonthly Intervals in 2010–2020 Based on Google Earth Engine. J. Remote Sens. 2023, 3, 0101. [Google Scholar] [CrossRef]
- Liu, D.; Jia, K.; Jiang, H.; Xia, M.; Tao, G.; Wang, B.; Chen, Z.; Yuan, B.; Li, J. Fractional Vegetation Cover Estimation Algorithm for FY-3B Reflectance Data Based on Random Forest Regression Method. Remote Sens. 2021, 13, 2165. [Google Scholar] [CrossRef]
- Liu, D.; Jia, K.; Wei, X.; Xia, M.; Zhang, X.; Yao, Y.; Zhang, X.; Wang, B. Spatiotemporal Comparison and Validation of Three Global-Scale Fractional Vegetation Cover Products. Remote Sens. 2019, 11, 2524. [Google Scholar] [CrossRef]
- Kumar, R.; Nandy, S.; Agarwal, R.; Kushwaha, S.P.S. Forest Cover Dynamics Analysis and Prediction Modeling Using Logistic Regression Model. Ecol. Indic. 2014, 45, 444–455. [Google Scholar] [CrossRef]
- Bai, J.J.; Xu, M.D.; Bai, B.; Zhao, W.J.; Zhang, Y.T. Research on the Regionalization and Prediction Model of Vegetation Status. J. Taiyuan Univ. Technol. 2019, 50, 76–81. [Google Scholar]
- Ahmad, A.; Zhang, J.; Bashir, B.; Mahmood, K.; Mumtaz, F. Exploring Vegetation Trends and Restoration Possibilities in Pakistan by Using Hurst Exponent. Environ. Sci. Pollut. Res. 2023, 30, 91915–91928. [Google Scholar] [CrossRef]
- Zhang, X.L.; Zhang, J.; Liu, H.J.; Liu, J.H. The Application of Gray GM(1,N) Self-Memory Coupling Model in Grassland Vegetation Coverage. J. Inn. Mong. Agric. Univ. (Nat. Sci. Ed.) 2023, 44, 68–78. [Google Scholar]
- Zarei, A.; Asadi, E.; Ebrahimi, A.; Jafari, M.; Malekian, A.; Nasrabadi, H.M.; Chemura, A.; Maskell, G. Prediction of Future Grassland Vegetation Cover Fluctuation under Climate Change Scenarios. Ecol. Indic. 2020, 119, 106858. [Google Scholar] [CrossRef]
- Wang, L.Y.; Jiang, H.L.; Zhang, S.H. Spatial and Temporal Evolution of Vegetation Cover and Multi-Scenario Simulation Prediction in Shenyang from 2000–2020. Remote Sens. Technol. Appl. 2024, 39, 1–10. [Google Scholar]
- Vidal-Macua, J.J.; Nicolau, J.M.; Vicente, E.; Heras, M.M. Assessing Vegetation Recovery in Reclaimed Opencast Mines of the Teruel Coalfield (Spain) Using Landsat Time Series and Boosted Regression Trees. Sci. Total Environ. 2020, 717, 137250. [Google Scholar] [CrossRef] [PubMed]
- Van Klompenburg, T.; Kassahun, A.; Catal, C. Crop Yield Prediction Using Machine Learning: A Systematic Literature Review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Jia, S.T.; Huang, S.Z.; Wang, H.; Li, Z.Y.; Huang, Q.; Liang, H. Simulation of Vegetation Change Based on BP-SVM Mode. Arid Zone Res. 2021, 38, 1085–1093. [Google Scholar]
- Roy, B. Optimum Machine Learning Algorithm Selection for Forecasting Vegetation Indices: MODIS NDVI & EVI. Remote Sens. Appl. Soc. Environ. 2021, 23, 100582. [Google Scholar]
- Ahmad, R.; Yang, B.; Ettlin, G.; Berger, A.; Rodríguez-Bocca, P. A Machine-Learning Based ConvLSTM Architecture for NDVI Forecasting. Int. Trans. Oper. Res. 2023, 30, 2025–2048. [Google Scholar] [CrossRef]
- Peng, Q.Y. Remote Sensing Estimation of Aquatic Vegetation Fractional Vegetation Cover in Wuliangsuhai Based on Machine Learning. Master’s Thesis, Inner Mongolia University, Hohhot, China, 2023. [Google Scholar]
- Gou, Y.; Jin, Z.; Kou, P.; Tao, Y.; Xu, Q.; Zhu, W.; Tian, H. Mechanisms of Climate Change Impacts on Vegetation and Prediction of Changes on the Loess Plateau, China. Environ. Earth Sci. 2024, 83, 234. [Google Scholar] [CrossRef]
- Shan, Z.D.; Luo, H.; Liu, D. Evaporation Model Evaluation Based on Machine Learning Algorithm. Res. Soil Water Conserv. 2023, 30, 289–294. [Google Scholar]
- Van Jaarsveld, B.; Hauswirth, S.M.; Wanders, N. Machine Learning and Global Vegetation: Random Forests for Downscaling and Gap Filling. Hydrol. Earth Syst. Sci. 2024, 28, 2357–2374. [Google Scholar] [CrossRef]
- Zheng, Z.J.; Zeng, Y.; Zhao, Y.J.; Gao, W.W.; Zhao, D.; Wu, B.F. Analysis of Land Cover Changes in Southwestern China Since the 1990s. Acta Ecol. Sin. 2016, 36, 7858–7869. [Google Scholar]
- Peng, R.W.; Luo, Y.; Yu, J.L.; Zhao, Z.L. Changes in Vegetation Coverage and Its Relationship with Rainfall in Southwest China from 2009 to 2015. J. Guizhou Norm. Univ. (Nat. Sci.) 2017, 35, 15–23. [Google Scholar]
- Feng, B.; Dong, Y. Spatial-Temporal Changes of Vegetation Coverage and Topographic Effects in Yunnan Province from 2010 to 2020. J. Zhejiang For. Sci. Technol. 2022, 42, 23–32. [Google Scholar]
- He, Q.; Mou, F.; Li, Q.; Yang, M. Geography Study on Spatiotemporal Evolution of Fractional Vegetation Coverage and the Driving Forces in Chongqing. Sci. Technol. Eng. 2021, 21, 11955–11962. [Google Scholar]
- Huang, R.J.; Chen, J.J.; Lin, X.C.; You, H.T.; Han, X.W. Spatio-Temporal Differences and Influencing Factors of GEOV3 and GLASS Fractional Vegetation Cover Products in Southwest China. Remote Sens. Technol. Appl. 2023, 38, 708–717. [Google Scholar]
- Li, X.; Jia, H.; Wang, L. Remote Sensing Monitoring of Drought in Southwest China Using Random Forest and eXtreme Gradient Boosting Methods. Remote Sens. 2023, 15, 4840. [Google Scholar] [CrossRef]
- Zeng, X.L.; Chen, T.T. Analysis of the Driving Forces of Vegetation Dynamic Changes in Southwest China. China Environ. Sci. 2023, 43, 6561–6570. [Google Scholar]
- Li, X.; Chen, Z.; Wang, L. Analysis of the Spatiotemporal Variation Characteristics of Main Extreme Climate Indices in Sichuan Province of China from 1968 to 2017. Appl. Ecol. Environ. Res. 2020, 18, 3211–3242. [Google Scholar] [CrossRef]
- Chen, X.M.; Pan, Y.C.; Xu, Y.; Guo, Z.D.; Dai, Q.Y. Spatio-Temporal Variation of Fractional Vegetation Coverage and Its Relationship with Climate and Topographic Factors in Southwest China. Southwest China J. Agric. Sci. 2023, 36, 1307–1317. [Google Scholar]
- Li, M.M. The Method of Vegetation Fraction Estimation by Remote Sensing. Master’s Thesis, Institute of Remote Sensing Applications, Chinese Academy Sciences, Beijing, China, 2003. [Google Scholar]
- Japery, G.; Chen, X.; Bao, A. A Comparison of Methods for Estimating Fractional Vegetation Cover in Arid Regions. Agric. For. Meteorol. 2011, 151, 1698–1710. [Google Scholar] [CrossRef]
- Zhao, H.F.; Cao, X.Y. Vegetation Cover Changes and Its Climate Driving in Three-River-Source National Park. Plateau Meteorol. 2022, 41, 328–337. [Google Scholar]
- SL 190-2007; Water Resources Industry Standard of the People’s Republic of China—Standards for Classification and Gradation of Soil Erosion. Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2008.
- Gao, Y.; Xie, Y.; Qian, D.; Zhang, L.; Gong, J. Dynamic Variations of Vegetation Coverage and Landscape Pattern in Bailongjiang Basin of Southern Gansu. Res. Soil Water Conserv. 2015, 22, 181–187. [Google Scholar]
- Zhao, N.; Zhao, Y.H.; Zou, H.F.; Bai, X.; Zhen, Z. Spatial and Temporal Trends and Drivers of Fractional Vegetation Cover in Heilongjiang Province, China During 1990–2020. Chin. J. Appl. Ecol. 2023, 34, 1320–1330. [Google Scholar]
- Wei, C.; Su, K.; Jiang, X.; You, Y.; Zhou, X.; Yu, Z.; Chen, Z.; Liao, Z.; Zhang, Y.; Wang, L. Increase in Precipitation and Fractional Vegetation Cover Promote Synergy of Ecosystem Services in China’s Arid Regions—Northern Sand-Stabilization Belt. Front. Ecol. Evol. 2023, 11, 1116484. [Google Scholar] [CrossRef]
- Jia, K.; Liang, S.; Wei, X.; Yao, Y.; Yang, L.; Zhang, X.; Liu, D. Validation of Global Land Surface Satellite (GLASS) Fractional Vegetation Cover Product from MODIS Data in an Agricultural Region. Remote Sens. Lett. 2018, 9, 847–856. [Google Scholar] [CrossRef]
- Liu, D.; Jia, K.; Xia, M.; Wei, X.; Yao, Y.; Zhang, X.; Tao, G. Fractional Vegetation Cover Estimation Algorithm Based on Recurrent Neural Network for MODIS 250 m Reflectance Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6532–6543. [Google Scholar] [CrossRef]
- Yang, L.; Jia, K.; Liang, S.; Liu, M.; Wei, X.; Yao, Y.; Zhang, X.; Liu, D. Spatio-Temporal Analysis and Uncertainty of Fractional Vegetation Cover Change over Northern China during 2001–2012 Based on Multiple Vegetation Data Sets. Remote Sens. 2018, 10, 549. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, X.; Zhang, Y.; Zhang, H.; Li, L. Vegetation Degradation and Its Driving Factors in the Farming–pastoral Ecotone over the Countries along Belt and Road Initiative. Sustainability 2019, 11, 1590. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, S.; Wang, H.Y.; Yang, X.; Zhang, F.L.; Wang, N.; Tao, F. Spatio-Temporal Variation Characteristics of NDVI in the Three Northeast Provinces and Their Responses to Climatic Factors. J. Meteorol. Environ. 2024, 40, 71–78. [Google Scholar]
- Wei, F.Y. Modern Climate Statistical Diagnosis and Prediction Techniques; Meteorological Press: Beijing, China, 2007. [Google Scholar]
- Wang, T.; Yilinuer, A.; Li, S.Y.; Ayshemguli, Z.; Zhang, X.R.; Gao, T.F. Three Trend Analysis Methods in Precipitation Characteristic Analysis of Eastern Pamirs. Meteorol. Mon. 2022, 48, 1312–1320. [Google Scholar]
- Zhang, B.; Xiang, X.; Jia, J.L.; Zhang, X.H.; Li, C.Q.; Peng, J. Landslide Disaster Prediction Method Around Natural Gas Pipelines Based on LightGBM. J. Jilin Univ. 2023, 61, 338–346. [Google Scholar]
- Zhuo, Y.C.; Hao, H.B. Intelligent Flow Detection in Hospital Microservice Platform Security Operation and Maintenance Management System Based on Genetic Algorithm Optimized LightGBM Algorithm. Chin. J. Med. Phys. 2024, 41, 788–792. [Google Scholar]
- Buthelezi, M.N.M.; Lottering, R.T.; Peerbhay, K.Y.; Onisimo, M. A Machine Learning Approach to Mapping Suitable Areas for Forest Vegetation in the eThekwini Municipality. Remote Sens. Appl. Soc. Environ. 2024, 35, 101208. [Google Scholar] [CrossRef]
- Zhou, Q.; Luo, F.; Chai, B.; Zhou, A.G. Comparative Study of Machine Learning Algorithms for Predicting the Geothermal Temperatures in Deep and Long Tunnels. Saf. Environ. Eng. 2024, 1–10. [Google Scholar] [CrossRef]
- Gan, R.; Ma, C.; Gao, Y.; Guo, L.; Hou, X.; Lu, X. Monthly Runoff Prediction Method Based on Secondary Decomposition and Support Vector Machine. J. Zhengzhou Univ. (Eng. Sci.) 2024, 1–8. [Google Scholar] [CrossRef]
- Liu, H.; Ma, J.; Li, R. Simulation of the Water-Thermal Features within the Surface Soil in Tanggula Region, Qinghai-Tibet Plateau, by Using KNN Model. J. Glaciol. Geocryol. 2021, 42, 1243–1252. [Google Scholar]
- Dai, J.; Wang, Z.; Zhang, Y.; Si, L.; Wei, D.; Zhou, W.; Gu, J.; Zou, X.; Song, Y. Research on Influencing Factors for Drilling Rate in Coal Mines and Its Intelligent Prediction Methods. Coal Sci. Technol. 2024, 52, 209–221. Available online: https://link.cnki.net/urlid/11.2402.TD.20240118.1633.002 (accessed on 18 January 2024).
- Sharma, M.; Kumar, B.; Mahajan, V.; Bhat, M. Ridge Regression Model for the Estimation of Total Carbon Sequestered by Forest Species. In Statistical Methods and Applications in Forestry and Environmental Sciences; Springer: Berlin/Heidelberg, Germany, 2020; pp. 181–191. [Google Scholar]
- Yang, Q.; Jiang, C.; Ding, T. Impacts of Extreme-High-Temperature Events on Vegetation in North China. Remote Sens. 2023, 15, 4542. [Google Scholar] [CrossRef]
- Polykretis, C.; Grillakis, M.G.; Argyriou, A.V.; Papadopoulos, N.; Alexakis, D.D. Integrating Multivariate (GeoDetector) and Bivariate (IV) Statistics for Hybrid Landslide Susceptibility Modeling: A Case of the Vicinity of Pinios Artificial Lake, Ilia, Greece. Land 2021, 10, 973. [Google Scholar] [CrossRef]
- Dietterich, T.G. An Experimental Comparison of Three Methods for Constructing Ensembles of Decision Trees: Bagging, Boosting, and Randomization. Mach. Learn. 2000, 40, 139–157. [Google Scholar] [CrossRef]
- Zhou, C.; Gan, L.L.; Wang, Y.; Wu, H.Y.; Yu, J.; Cao, Y.; Yin, K.L. Landslide Susceptibility Prediction Based on Non-Landslide Samples Selection and Heterogeneous Ensemble Machine Learning. J. Geo-Inf. Sci. 2023, 25, 1570–1585. [Google Scholar]
- Tien Bui, D.; Ho, T.C.; Pradhan, B.; Pham, B.; Nhu, V.; Revhaug, I. GIS-based Modeling of Rainfall-Induced Landslides Using Data Mining-based Functional Trees Classifier with AdaBoost, Bagging, and MultiBoost Ensemble Frameworks. Environ. Earth Sci. 2016, 75, 1101. [Google Scholar] [CrossRef]
- Jiang, B.D.; Li, X.C.; Luo, H.Y.; Song, Y.W. A Comparative Analysis of Heterogeneous Ensemble Learning Methods for Landslide Susceptibility Assessment. China Civ. Eng. J. 2023, 56, 170–179. [Google Scholar]
- Guo, Q.; Yan, J.; Hao, Q.P.; Han, D.; Yang, Z.H.; Yan, X.Y.; Zhang, H.P.; Li, R. Short-Term Wind Power Prediction Method Based on Closed-Loop Clustering and Multi-Objective Optimization. J. Shanghai Jiaotong Univ. 2014, 1–20. [Google Scholar] [CrossRef]
- Malakouti, S.M.; Menhaj, M.B.; Suratgar, A.A. The Usage of 10-fold Cross-validation and Grid Search to Enhance ML Methods Performance in Solar Farm Power Generation Prediction. Clean. Eng. Technol. 2023, 15, 100664. [Google Scholar] [CrossRef]
- Gu, Q.Y.; Han, Y.; Xu, Y.P.; Yao, H.Y.; Niu, H.F.; Huang, F. Laboratory Research on Polarized Optical Properties of Saline-alkaline Soil Based on Semi-empirical Models and Machine Learning Methods. Remote Sens. 2022, 14, 226. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, L.X.; Yu, D.S.; Feng, K.Y.; Wang, X.; Song, J. Improving Leaf Area Index Retrieval Using Multi-Sensor Images and Stacking Learning in Subtropical Forests of China. Remote Sens. 2021, 14, 148. [Google Scholar] [CrossRef]
- Ogunsanya, M.; Isichei, J.; Desai, S. Grid Search Hyperparameter Tuning in Additive Manufacturing Processes. Manuf. Lett. 2023, 35, 1031–1042. [Google Scholar] [CrossRef]
- Zheng, Z.J.; Zeng, Y.; Zhao, Y.J.; Zhao, D.; Wu, B.F. Monitoring and Dynamic Analysis of Fractional Vegetation Cover in Southwestern China over the Past 15 Years Based on MODIS Data. Remote Sens. Land Resour. 2017, 29, 128–136. [Google Scholar]
- Xiong, Q.L.; He, Y.L.; Li, T.Y.; Yu, L. Spatiotemporal Patterns of Vegetation Coverage and Response to Climatic and Topographic Factors in Growing Season in Southwest China. Res. Soil Water Conserv. 2019, 26, 259–266. [Google Scholar]
- Li, T.Y. Spatio-Temporal Characteristics and Influence Factors of Vegetation Coverage in Southwest China. Master’s Thesis, Yunnan University, Kunming, China, 2019. [Google Scholar]
- Zhang, Y.; Liu, Q.; Wang, Y.; Huang, J. Assessing the Impacts of Climate Change and Anthropogenic Activities on Vegetation in Southwest China. J. Mt. Sci. 2022, 19, 2678–2692. [Google Scholar] [CrossRef]
- Yan, W.; Wang, H.; Jiang, C.; Jin, S.; Ai, J.; Sun, O.J. Satellite View of Vegetation Dynamics and Drivers over Southwestern China. Ecol. Indic. 2021, 130, 108074. [Google Scholar] [CrossRef]
- Duan, C.; Li, J.; Chen, Y.; Ding, Z.; Ma, M.; Xie, J.; Yao, L.; Tang, X. Spatiotemporal Dynamics of Terrestrial Vegetation and Its Driver Analysis over Southwest China from 1982 to 2015. Remote Sens. 2022, 14, 2497. [Google Scholar] [CrossRef]
- Xu, N.; Niu, X.; Hu, X.; Wang, X.; Wu, R.; Chen, S.; Chen, L.; Sun, L.; Ding, L.; Yang, Z.; et al. Prelaunch Calibration and Radiometric Performance of the Advanced MERSI II on FengYun-3D. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4866–4875. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, P.; Gu, S.; Hu, X.; Tang, S.; Yang, L.; Xu, N.; Zhen, Z.; Wang, L.; Wu, Q.; et al. Capability of Fengyun-3D Satellite in Earth System Observation. J. Meteorol. Res. 2019, 33, 1113–1130. [Google Scholar] [CrossRef]
- Han, X.; Yang, J.; Tang, S.; Han, Y. Vegetation Products Derived from Fengyun-3D Medium Resolution Spectral Imager-II. J. Meteorol. Res. 2020, 34, 775–785. [Google Scholar] [CrossRef]
- Wang, M.Y.; Luo, Y.; Zhang, Z.Y.; Xie, Q.Y.; Wu, X.D.; Ma, X.L. Recent Advances in Remote Sensing of Vegetation Phenology: Retrieval Algorithm and Validation Strategy. Natl. Remote Sens. Bull. 2022, 26, 431–455. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Li, G.C. Assessment of FY-3D MERSI/NDVI Global Product. Acta Meteorol. Sin. 2022, 80, 124–135. [Google Scholar]
- Zhang, Z.Y. VI Quality Assessment and Application of Fengyun Polar-Orbiting Satellites. Master’s Thesis, Lanzhou University, Lanzhou, China, 2023. [Google Scholar]
- Sun, M.H. Research on NDVI Time Series Reconstruction Method Based on FY-3D Data—A Case Study of North China Plain. Master’s Thesis, Hebei GEO University, Shijiazhuang, China, 2022. [Google Scholar]
- Liu, Y.T.; Wang, L.; Li, X.H.; Guo, L. Analysis on Spatio-Temporal Variability of Fractional Vegetation Cover and Influencing Factors from 2000 to 2020 in Southwestern China. Plateau Meteorol. 2024, 43, 264–276. [Google Scholar]
- Bao, Y.; Wang, Y.Q.; Nan, S.L.; Yu, M. Response of Vegetation over the Qinghai-Xizang Plateau to Projected Warming Climate. Plateau Meteorol. 2023, 42, 553–563. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).