Opposing Impacts of Greenspace Fragmentation on Land Surface Temperature in Urban and Surrounding Rural Areas: A Case Study in Changsha, China
Abstract
1. Introduction
2. Materials and Methods
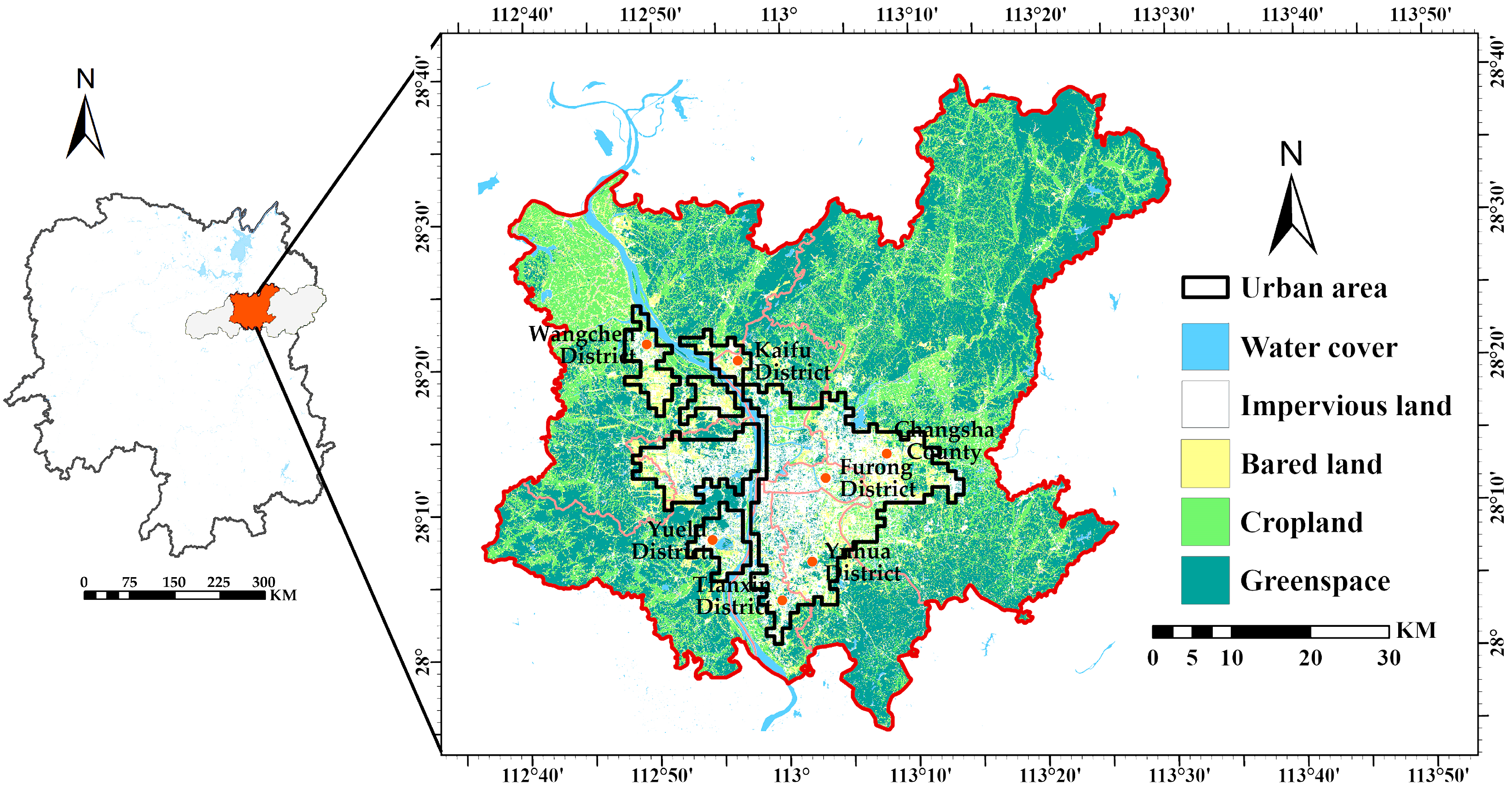
2.1. Study Area
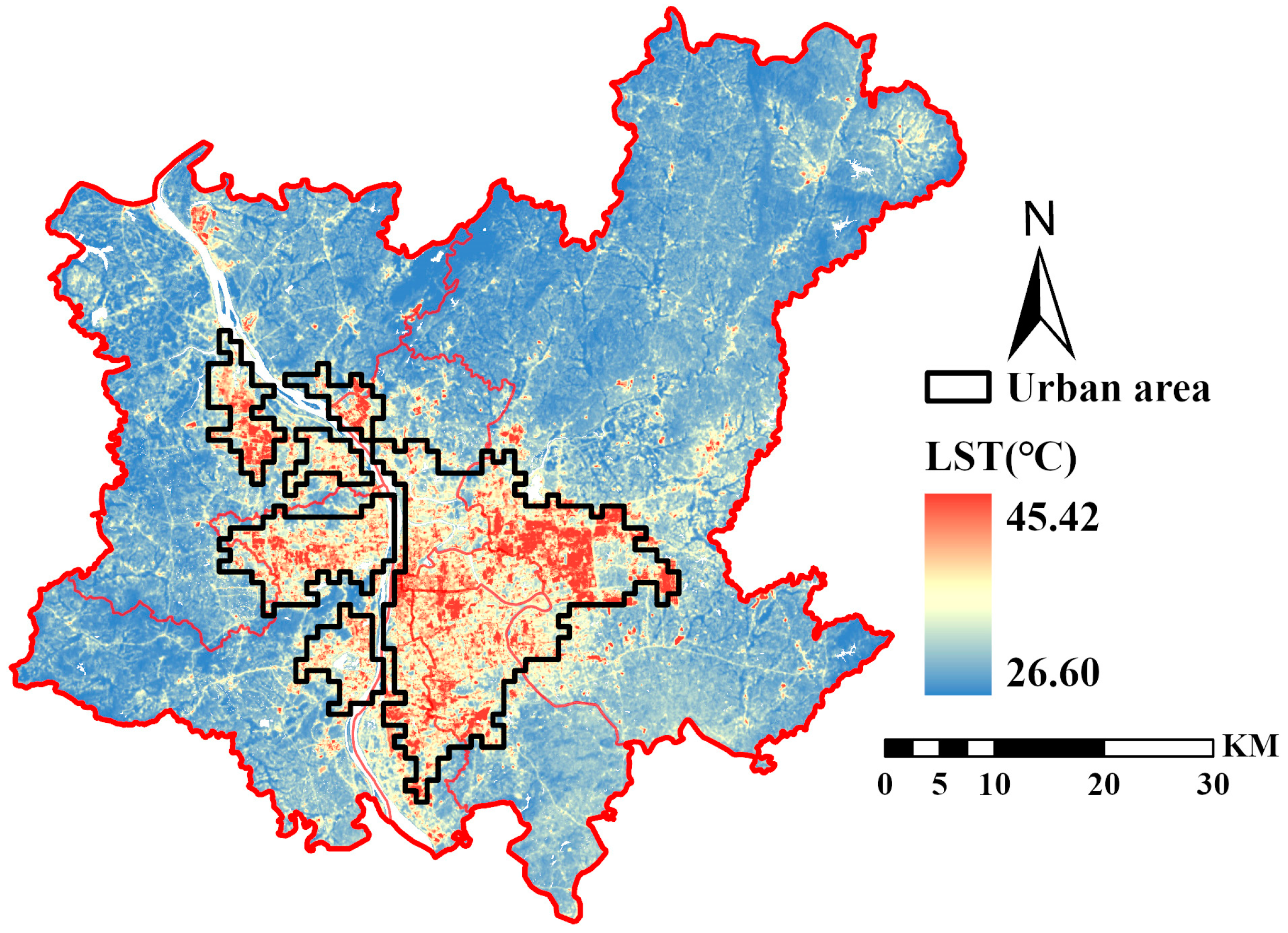
2.2. Land Surface Temperature
2.3. Quantifying Landscape Composition and Greenspace Fragmentation
2.4. Statistical Analysis
3. Results
3.1. Descriptive Statistics
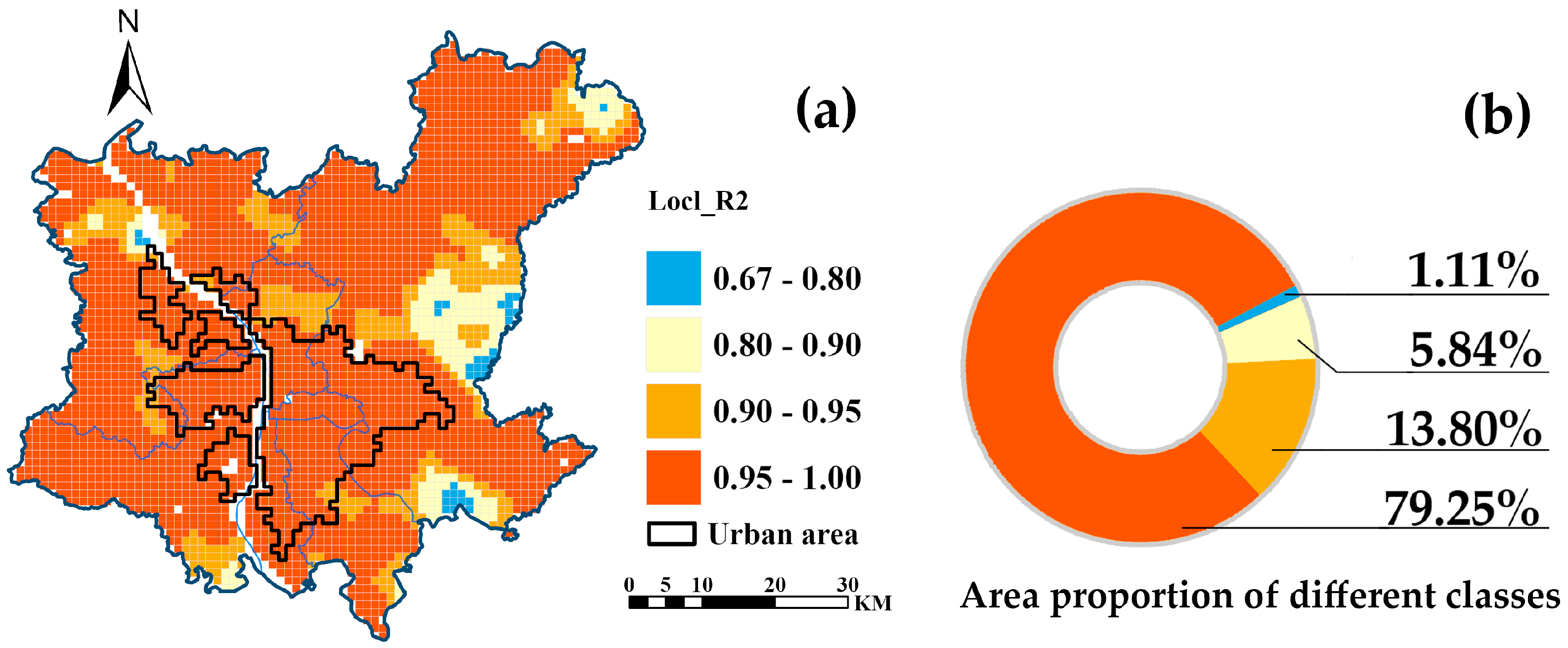
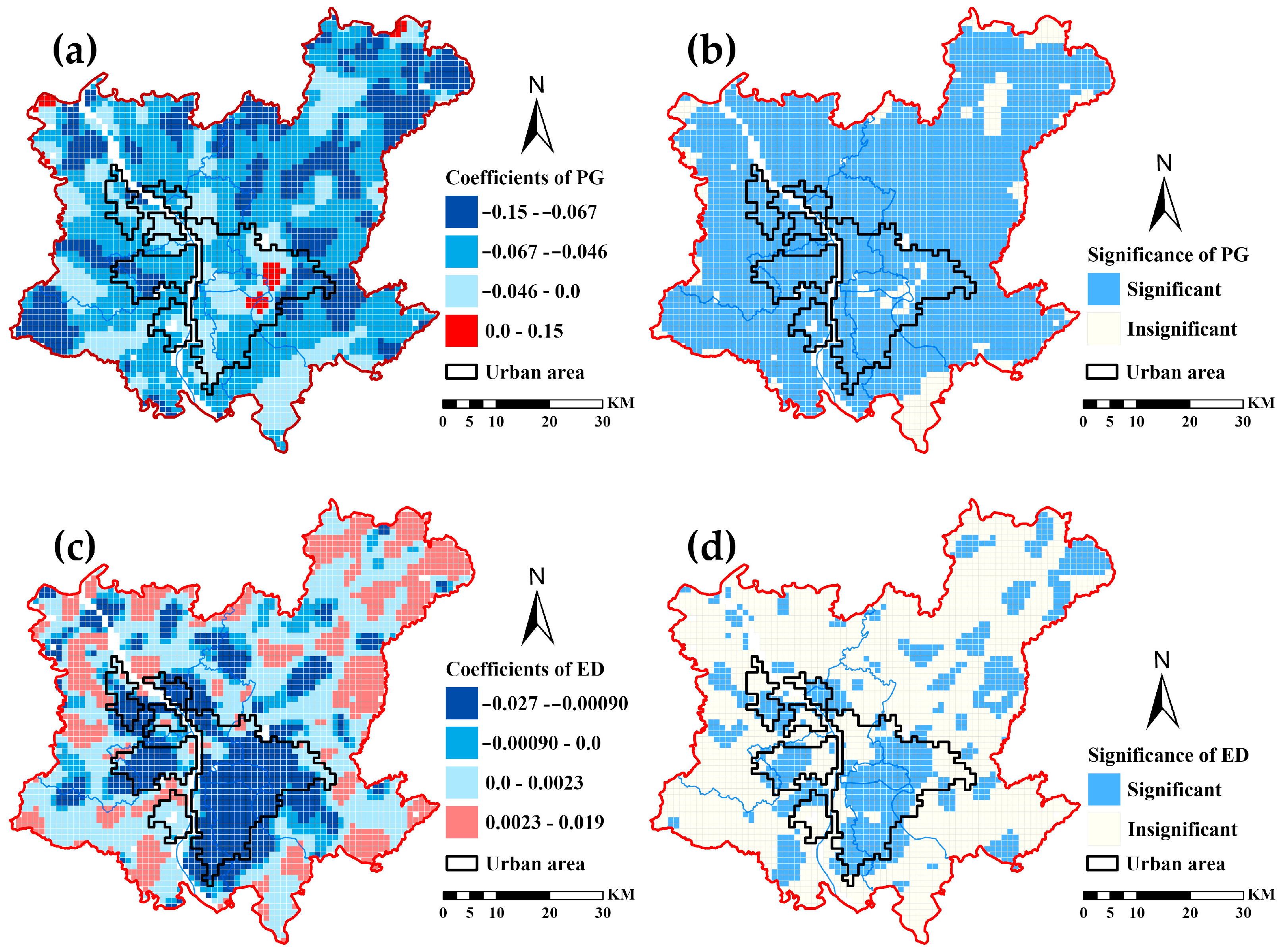
3.2. Spatial Variation of Greenspace Fragmentation Impacts on LST
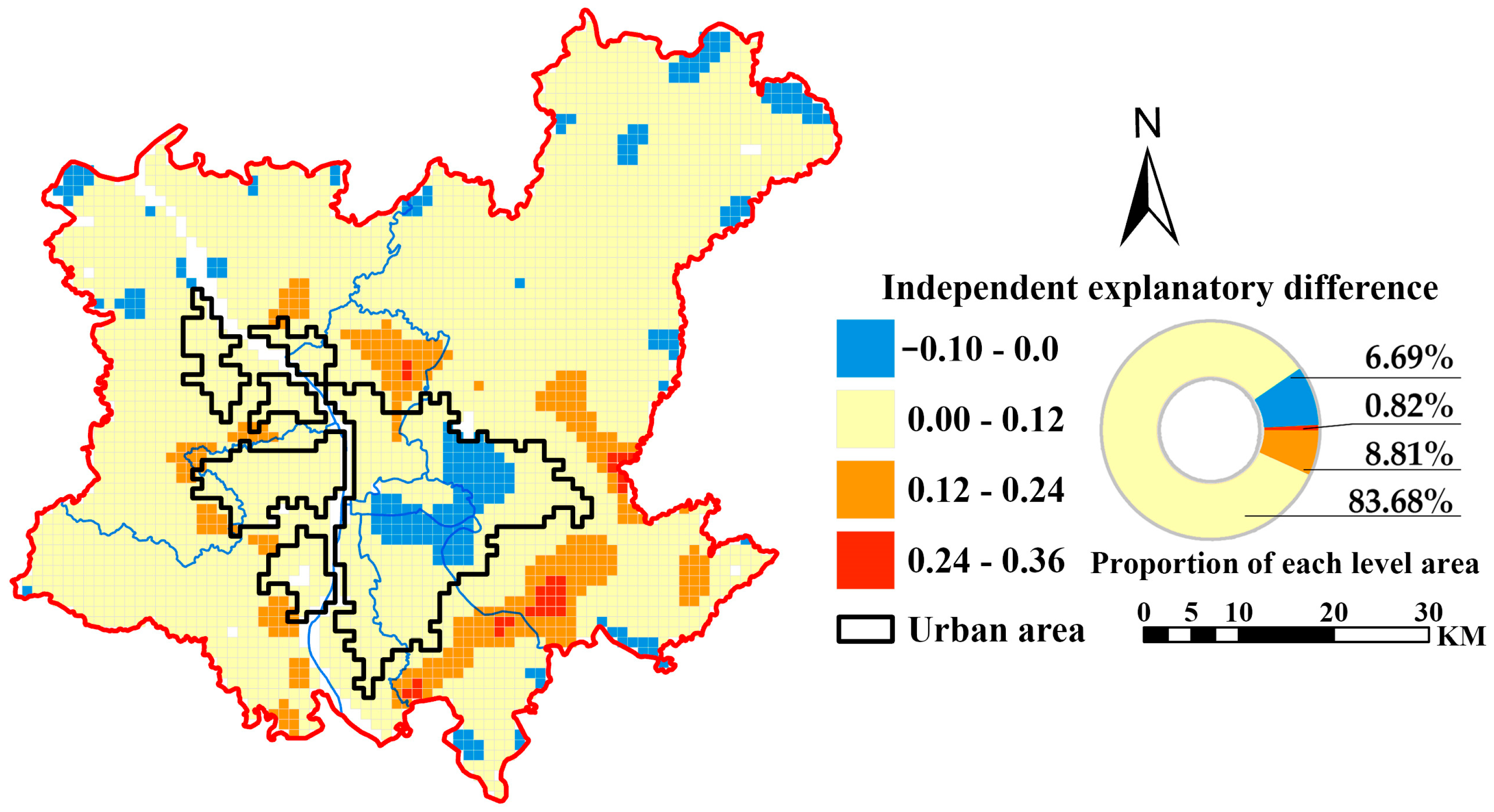
3.3. Spatial Variation of the Relative Importance of Greenspace Coverage and Fragmentation
4. Discussion
4.1. Spatial Variation of the Greenspace Fragmentation Impacts on LST
4.2. Management Implementations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, M.; Ren, C.; Wang, H.; Wang, J.; Feng, Z.; Kumar, P.; Haghighat, F.; Cao, S.-J. Mitigating urban heat island through neighboring rural land cover. Nat. Cities 2024, 1, 522–532. [Google Scholar] [CrossRef]
- Chen, J.; Zhan, W.; Du, P.; Li, L.; Li, J.; Liu, Z.; Huang, F.; Lai, J.; Xia, J. Seasonally disparate responses of surface thermal environment to 2D/3D urban morphology. Build. Environ. 2022, 214, 108928. [Google Scholar] [CrossRef]
- Chen, J.; Zhan, W.; Jin, S.; Han, W.; Du, P.; Xia, J.; Lai, J.; Li, J.; Liu, Z.; Li, L.; et al. Separate and combined impacts of building and tree on urban thermal environment from two- and three-dimensional perspectives. Build. Environ. 2021, 194, 107650. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Yu, S.; Jia, G.; Li, H.; Li, W. Urban heat island impacts on building energy consumption: A review of approaches and findings. Energy 2019, 174, 407–419. [Google Scholar] [CrossRef]
- Habibullah, M.S.; Din, B.H.; Tan, S.-H.; Zahid, H. Impact of climate change on biodiversity loss: Global evidence. Environ. Sci. Pollut. Res. 2021, 29, 1073–1086. [Google Scholar] [CrossRef] [PubMed]
- Mora, C.; Dousset, B.; Caldwell, I.R.; Powell, F.E.; Geronimo, R.C.; Bielecki, C.R.; Counsell, C.W.W.; Dietrich, B.S.; Johnston, E.T.; Louis, L.V.; et al. Global risk of deadly heat. Nat. Clim. Chang. 2017, 7, 501–506. [Google Scholar] [CrossRef]
- Yu, Z.; Yao, Y.; Yang, G.; Wang, X.; Vejre, H. Spatiotemporal patterns and characteristics of remotely sensed region heat islands during the rapid urbanization (1995–2015) of Southern China. Sci. Total Environ. 2019, 674, 242–254. [Google Scholar] [CrossRef]
- Zhou, D.; Bonafoni, S.; Zhang, L.; Wang, R. Remote sensing of the urban heat island effect in a highly populated urban agglomeration area in East China. Sci. Total Environ. 2018, 628, 415–429. [Google Scholar] [CrossRef]
- Wong, N.H.; Tan, C.L.; Kolokotsa, D.D.; Takebayashi, H. Greenery as a mitigation and adaptation strategy to urban heat. Nat. Rev. Earth Environ. 2021, 2, 166–181. [Google Scholar] [CrossRef]
- Jay, O.; Capon, A.; Berry, P.; Broderick, C.; de Dear, R.; Havenith, G.; Honda, Y.; Kovats, R.S.; Ma, W.; Malik, A.; et al. Reducing the health effects of hot weather and heat extremes: From personal cooling strategies to green cities. Lancet 2021, 398, 709–724. [Google Scholar] [CrossRef]
- Akbari, H.; Damon Matthews, H.; Seto, D. The long-term effect of increasing the albedo of urban areas. Environ. Res. Lett. 2012, 7, 024004. [Google Scholar] [CrossRef]
- Fang, Y.; Zhao, L. Assessing the environmental benefits of urban ventilation corridors: A case study in Hefei, China. Build. Environ. 2022, 212, 108810. [Google Scholar] [CrossRef]
- Cui, Y.; Yin, M.; Cheng, X.; Tang, J.; He, B.-J. Towards cool cities and communities: Preparing for an increasingly hot future by the development of heat-resilient infrastructure and urban heat management plan. Environ. Technol. Innov. 2024, 34, 103568. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, P.; Hu, Y.; Ouyang, L.; Zhu, L.; Ni, G. Canopy transpiration and its cooling effect of three urban tree species in a subtropical city- Guangzhou, China. Urban For. Urban Green. 2019, 43, 126368. [Google Scholar] [CrossRef]
- Qiu, G.Y.; Zou, Z.; Li, X.; Li, H.; Guo, Q.; Yan, C.; Tan, S. Experimental studies on the effects of green space and evapotranspiration on urban heat island in a subtropical megacity in China. Habitat Int. 2017, 68, 30–42. [Google Scholar] [CrossRef]
- Winbourne, J.B.; Jones, T.S.; Garvey, S.M.; Harrison, J.L.; Wang, L.; Li, D.; Templer, P.H.; Hutyra, L.R. Tree Transpiration and Urban Temperatures: Current Understanding, Implications, and Future Research Directions. BioScience 2020, 70, 576–588. [Google Scholar] [CrossRef]
- Jiao, M.; Zhou, W.; Zheng, Z.; Wang, J.; Qian, Y. Patch size of trees affects its cooling effectiveness: A perspective from shading and transpiration processes. Agric. For. Meteorol. 2017, 247, 293–299. [Google Scholar] [CrossRef]
- Kong, F.; Yan, W.; Zheng, G.; Yin, H.; Cavan, G.; Zhan, W.; Zhang, N.; Cheng, L. Retrieval of three-dimensional tree canopy and shade using terrestrial laser scanning (TLS) data to analyze the cooling effect of vegetation. Agric. For. Meteorol. 2016, 217, 22–34. [Google Scholar] [CrossRef]
- Wang, Z.-H.; Zhao, X.; Yang, J.; Song, J. Cooling and energy saving potentials of shade trees and urban lawns in a desert city. Appl. Energy 2016, 161, 437–444. [Google Scholar] [CrossRef]
- Schwaab, J.; Meier, R.; Mussetti, G.; Seneviratne, S.; Bürgi, C.; Davin, E.L. The role of urban trees in reducing land surface temperatures in European cities. Nat. Commun. 2021, 12, 6763. [Google Scholar] [CrossRef]
- Trlica, A.; Hutyra, L.R.; Schaaf, C.L.; Erb, A.; Wang, J.A. Albedo, Land Cover, and Daytime Surface Temperature Variation Across an Urbanized Landscape. Earths Future 2017, 5, 1084–1101. [Google Scholar] [CrossRef]
- Livesley, S.J.; McPherson, E.G.; Calfapietra, C. The Urban Forest and Ecosystem Services: Impacts on Urban Water, Heat, and Pollution Cycles at the Tree, Street, and City Scale. J. Environ. Qual. 2016, 45, 119–124. [Google Scholar] [CrossRef] [PubMed]
- Turner-Skoff, J.B.; Cavender, N. The benefits of trees for livable and sustainable communities. Plants People Planet 2019, 1, 323–335. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z. Relationship between land surface temperature and spatial pattern of greenspace: What are the effects of spatial resolution? Landsc. Urban Plan. 2013, 114, 1–8. [Google Scholar] [CrossRef]
- Liao, W.; Guldmann, J.-M.; Hu, L.; Cao, Q.; Gan, D.; Li, X. Linking urban park cool island effects to the landscape patterns inside and outside the park: A simultaneous equation modeling approach. Landsc. Urban Plan. 2023, 232, 104681. [Google Scholar] [CrossRef]
- Peng, J.; Jia, J.; Liu, Y.; Li, H.; Wu, J. Seasonal contrast of the dominant factors for spatial distribution of land surface temperature in urban areas. Remote Sens. Environ. 2018, 215, 255–267. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.; Singh, V.P.; Liu, C. Impacts of Spatial Configuration of Land Surface Features on Land Surface Temperature across Urban Agglomerations, China. Remote Sens. 2021, 13, 4008. [Google Scholar] [CrossRef]
- Guo, G.; Wu, Z.; Chen, Y. Complex mechanisms linking land surface temperature to greenspace spatial patterns: Evidence from four southeastern Chinese cities. Sci. Total Environ. 2019, 674, 77–87. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Tiyip, T.; Pla, F.; Latorre-Carmona, P.; Halik, U.; Sawut, M.; Caetano, M. Effects of green space spatial pattern on land surface temperature: Implications for sustainable urban planning and climate change adaptation. ISPRS J. Photogramm. Remote Sens. 2014, 89, 59–66. [Google Scholar] [CrossRef]
- Nastran, M.; Kobal, M.; Eler, K. Urban heat islands in relation to green land use in European cities. Urban For. Urban Green. 2019, 37, 33–41. [Google Scholar] [CrossRef]
- Basu, T.; Das, A. Urbanization induced degradation of urban green space and its association to the land surface temperature in a medium-class city in India. Sustain. Cities Soc. 2023, 90, 104373. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z.; Xu, W.; Zheng, H. Spatial pattern of greenspace affects land surface temperature: Evidence from the heavily urbanized Beijing metropolitan area, China. Landsc. Ecol. 2012, 27, 887–898. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, J.; Cadenasso, M.L. Effects of the spatial configuration of trees on urban heat mitigation: A comparative study. Remote Sens. Environ. 2017, 195, 1–12. [Google Scholar] [CrossRef]
- Li, B.; Shi, X.; Wang, H.; Qin, M. Analysis of the relationship between urban landscape patterns and thermal environment: A case study of Zhengzhou City, China. Environ. Monit. Assess. 2020, 192, 540. [Google Scholar] [CrossRef]
- Yin, J.; Wu, X.; Shen, M.; Zhang, X.; Zhu, C.; Xiang, H.; Shi, C.; Guo, Z.; Li, C. Impact of urban greenspace spatial pattern on land surface temperature: A case study in Beijing metropolitan area, China. Landsc. Ecol. 2019, 34, 2949–2961. [Google Scholar] [CrossRef]
- Masoudi, M.; Tan, P.Y.; Liew, S.C. Multi-city comparison of the relationships between spatial pattern and cooling effect of urban green spaces in four major Asian cities. Ecol. Indic. 2019, 98, 200–213. [Google Scholar] [CrossRef]
- Zhou, L.; Hu, F.; Wang, B.; Wei, C.; Sun, D.; Wang, S. Relationship between urban landscape structure and land surface temperature: Spatial hierarchy and interaction effects. Sustain. Cities Soc. 2022, 80, 103795. [Google Scholar] [CrossRef]
- Guo, G.; Wu, Z.; Cao, Z.; Chen, Y.; Zheng, Z. Location of greenspace matters: A new approach to investigating the effect of the greenspace spatial pattern on urban heat environment. Landsc. Ecol. 2021, 36, 1533–1548. [Google Scholar] [CrossRef]
- Wu, Y.; Hou, H.; Wang, R.; Murayama, Y.; Wang, L.; Hu, T. Effects of landscape patterns on the morphological evolution of surface urban heat island in Hangzhou during 2000–2020. Sustain. Cities Soc. 2022, 79, 103717. [Google Scholar] [CrossRef]
- Wang, L.; Hou, H.; Weng, J. Ordinary least squares modelling of urban heat island intensity based on landscape composition and configuration: A comparative study among three megacities along the Yangtze River. Sustain. Cities Soc. 2020, 62, 102381. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Z.; Xie, M.; Wang, Y. Investigating spatial non-stationary and scale-dependent relationships between urban surface temperature and environmental factors using geographically weighted regression. Environ. Model. Softw. 2010, 25, 1789–1800. [Google Scholar] [CrossRef]
- Tu, J.; Xia, Z. Examining spatially varying relationships between land use and water quality using geographically weighted regression I: Model design and evaluation. Sci. Total Environ. 2008, 407, 358–378. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Jensen, J.; Weng, Q.; Weaver, R. A Geographically Weighted Regression Analysis of the Underlying Factors Related to the Surface Urban Heat Island Phenomenon. Remote Sens. 2018, 10, 1428. [Google Scholar] [CrossRef]
- Guo, A.; Yang, J.; Sun, W.; Xiao, X.; Cecilia, J.X.; Jin, C.; Li, X. Impact of urban morphology and landscape characteristics on spatiotemporal heterogeneity of land surface temperature. Sustain. Cities Soc. 2020, 63, 102443. [Google Scholar] [CrossRef]
- Changsha Statistics Bureau. Changsha Statistical Yearbook; China Statistic Press: Beijing, China, 2021. [Google Scholar]
- Yu, X.; Guo, X.; Wu, Z. Land Surface Temperature Retrieval from Landsat 8 TIRS—Comparison between Radiative Transfer Equation-Based Method, Split Window Algorithm and Single Channel Method. Remote Sens. 2014, 6, 9829–9852. [Google Scholar] [CrossRef]
- Ali, S.A.; Parvin, F.; Ahmad, A. Retrieval of Land Surface Temperature from Landsat 8 OLI and TIRS: A Comparative Analysis Between Radiative Transfer Equation-Based Method and Split-Window Algorithm. Remote Sens. Earth Syst. Sci. 2022, 6, 1–21. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jimenez-Munoz, J.C.; Soria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martinez, P. Land Surface Emissivity Retrieval From Different VNIR and TIR Sensors. IEEE Trans. Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS; NASA: Washington, DC, USA, 1974; Volume 351, p. 309. [Google Scholar]
- Chen, J.; Jin, S.; Du, P. Roles of horizontal and vertical tree canopy structure in mitigating daytime and nighttime urban heat island effects. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102060. [Google Scholar] [CrossRef]
- Herse, M.R.; With, K.A.; Boyle, W.A. Grassland fragmentation affects declining tallgrass prairie birds most where large amounts of grassland remain. Landsc. Ecol. 2020, 35, 2791–2804. [Google Scholar] [CrossRef]
- Fahrig, L. Ecological Responses to Habitat Fragmentation Per Se. Annu. Rev. Ecol. Evol. Syst. 2017, 48, 1–23. [Google Scholar] [CrossRef]
- Crompton, O.; Correa, D.; Duncan, J.; Thompson, S. Deforestation-induced surface warming is influenced by the fragmentation and spatial extent of forest loss in Maritime Southeast Asia. Environ. Res. Lett. 2021, 16, 114018. [Google Scholar] [CrossRef]
- Hesselbarth, M.H.; Sciaini, M.; With, K.A.; Wiegand, K.; Nowosad, J. landscapemetrics: An open-source R tool to calculate landscape metrics. Ecography 2019, 42, 1648–1657. [Google Scholar] [CrossRef]
- Yang, W.; Deng, M.; Tang, J.; Luo, L. Geographically weighted regression with the integration of machine learning for spatial prediction. J. Geogr. Syst. 2023, 25, 213–236. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W. Optimizing urban greenspace spatial pattern to mitigate urban heat island effects: Extending understanding from local to the city scale. Urban For. Urban Green. 2019, 41, 255–263. [Google Scholar] [CrossRef]
- Hsieh, C.-M.; Li, J.-J.; Zhang, L.; Schwegler, B. Effects of tree shading and transpiration on building cooling energy use. Energy Build. 2018, 159, 382–397. [Google Scholar] [CrossRef]
- Rahman, M.A.; Stratopoulos, L.M.; Moser-Reischl, A.; Zölch, T.; Häberle, K.-H.; Rötzer, T.; Pretzsch, H.; Pauleit, S. Traits of trees for cooling urban heat islands: A meta-analysis. Build. Environ. 2020, 170, 106606. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y. Investigating the effects of 3D urban morphology on the surface urban heat island effect in urban functional zones by using high-resolution remote sensing data: A case study of Wuhan, Central China. ISPRS J. Photogramm. Remote Sens. 2019, 152, 119–131. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, W.; Zheng, Z.; Jiao, M.; Qian, Y. Interactions among spatial configuration aspects of urban tree canopy significantly affect its cooling effects. Sci. Total Environ. 2023, 864, 160929. [Google Scholar] [CrossRef]
- Yu, Z.; Guo, X.; Jørgensen, G.; Vejre, H. How can urban green spaces be planned for climate adaptation in subtropical cities? Ecol. Indic. 2017, 82, 152–162. [Google Scholar] [CrossRef]
- Soltanifard, H.; Kashki, A.; Karami, M. Analysis of spatially varying relationships between urban environment factors and land surface temperature in Mashhad city, Iran. Egypt. J. Remote Sens. Space Sci. 2022, 25, 987–999. [Google Scholar] [CrossRef]
- Scalenghe, R.; Marsan, F.A. The anthropogenic sealing of soils in urban areas. Landsc. Urban Plan. 2009, 90, 1–10. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, T.; Li, X.; Li, X. Effects of percent green cover on the relationship between greenspace fragmentation and land surface temperature: A case study in Changsha. Ecol. Environ. Sci. 2024, 32, 242–248. [Google Scholar] [CrossRef]
- Jiang, T.; Yang, C.; Liao, W.; Li, H.; Liu, H.; Ren, B.; Li, X. Path analysis of the urban greenspace landscape pattern impacts on land surface temperature: A case study in Changsha. Ecol. Environ. Sci. 2023, 32, 18–25. [Google Scholar] [CrossRef]


| Variables (Unit) | Mean | SD | Min | Max |
|---|---|---|---|---|
| LST (°C) | 30.468 | 1.448 | 27.316 | 38.334 |
| Percent of greensapce (%) | 49.073 | 28.252 | 0.102 | 100.00 |
| Percent of cropland (%) | 24.161 | 19.394 | 0.00 | 90.658 |
| Percent of bare land (%) | 12.085 | 9.605 | 0.00 | 71.092 |
| Elevation (m) | 59.478 | 44.2 | 8.986 | 464.05 |
| Edge density of greenspace (m·hm−2) | 136.752 | 59.651 | 0.00 | 287.979 |
| Factors | OLS | GWR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | Std. Error | t Value | VIF | Mean | Min | 1st Qu | 3rd Qu | Max | |
| (Intercept) | 35.17 *** | 0.057 | 617.11 | / | 35.25 | 25.84 | 34.22 | 36.28 | 45.77 |
| PG | −0.055 *** | 0.00060 | −94.28 | 3.11 | −0.056 | −0.15 | −0.067 | −0.046 | 0.15 |
| PC | −0.064 *** | 0.00060 | −104.76 | 1.62 | −0.061 | −0.16 | −0.073 | −0.048 | 0.029 |
| PB | −0.021 *** | 0.0013 | −16.26 | 1.72 | −0.033 | −0.20 | −0.047 | −0.017 | 0.090 |
| ED | 0.00030 | 0.00020 | 1.79 | 1.37 | 0.00030 | −0.027 | −0.00090 | 0.0023 | 0.019 |
| ELE | −0.0041 *** | 0.00030 | −12.21 | 2.49 | 0.0011 | −0.073 | −0.0062 | 0.0039 | 0.13 |
| R-squared | 0.87 | 0.98 | |||||||
| Diagnostics | OLS | GWR | |||||||
| Residual sum of squares | 875.55 | 139.93 | |||||||
| log Lik | −2457.89 | 1201.22 | |||||||
| Classic AIC | 4929.79 | −12.38 | |||||||
| AICc | 4929.82 | 1547.36 | |||||||
| Adjusted R-squared: | 0.87 | 0.97 | |||||||
| Moran’s I | 0.67 *** | 0.0047 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Li, X.; Li, C.; Gan, D. Opposing Impacts of Greenspace Fragmentation on Land Surface Temperature in Urban and Surrounding Rural Areas: A Case Study in Changsha, China. Remote Sens. 2024, 16, 3609. https://doi.org/10.3390/rs16193609
Wang W, Li X, Li C, Gan D. Opposing Impacts of Greenspace Fragmentation on Land Surface Temperature in Urban and Surrounding Rural Areas: A Case Study in Changsha, China. Remote Sensing. 2024; 16(19):3609. https://doi.org/10.3390/rs16193609
Chicago/Turabian StyleWang, Weiye, Xiaoma Li, Chuchu Li, and Dexin Gan. 2024. "Opposing Impacts of Greenspace Fragmentation on Land Surface Temperature in Urban and Surrounding Rural Areas: A Case Study in Changsha, China" Remote Sensing 16, no. 19: 3609. https://doi.org/10.3390/rs16193609
APA StyleWang, W., Li, X., Li, C., & Gan, D. (2024). Opposing Impacts of Greenspace Fragmentation on Land Surface Temperature in Urban and Surrounding Rural Areas: A Case Study in Changsha, China. Remote Sensing, 16(19), 3609. https://doi.org/10.3390/rs16193609







