MAFNet: Multimodal Asymmetric Fusion Network for Radar Echo Extrapolation

Abstract

Radar echo extrapolation (REE) is a crucial method for convective nowcasting, and current deep learning (DL)-based methods for REE have shown significant potential in severe weather forecasting tasks. Existing DL-based REE methods use extensive historical radar data to learn the evolution patterns of echoes, they tend to suffer from low accuracy. This is because data of radar modality face difficulty adequately representing the state of weather systems. Inspired by multimodal learning and traditional numerical weather prediction (NWP) methods, we propose a Multimodal Asymmetric Fusion Network (MAFNet) for REE, which uses data from radar modality to model echo evolution, and data from satellite and ground observation modalities to model the background field of weather systems, collectively guiding echo extrapolation. In the MAFNet, we first extract overall convective features through a global shared encoder (GSE), followed by two branches of local modality encoder (LME) and local correlation encoders (LCEs) that extract convective features from radar, satellite, and ground observation modalities. We employ an multimodal asymmetric fusion module (MAFM) to fuse multimodal features at different scales and feature levels, enhancing radar echo extrapolation performance. Additionally, to address the temporal resolution differences in multimodal data, we design a time alignment module based on dynamic time warping (DTW), which aligns multimodal feature sequences temporally. Experimental results demonstrate that compared to state-of-the-art (SOTA) models, the MAFNet achieves average improvements of 1.86% in CSI and 3.18% in HSS on the MeteoNet dataset, and average improvements of 4.84% in CSI and 2.38% in HSS on the RAIN-F dataset.

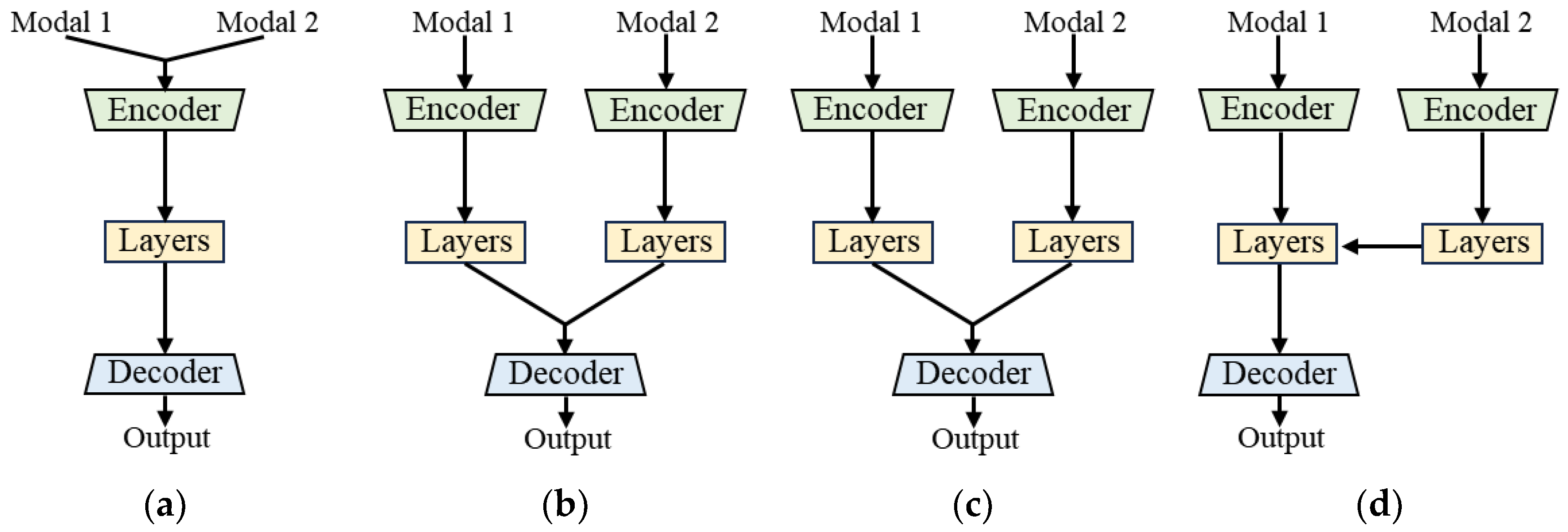
1. Introduction

Convective nowcasting aims to provide convective system predictions for a local region over relatively short time scales (e.g., 0–2 h), including type, intensity, and location [1]. It provides timely weather forecasting and impacts residents’ daily life greatly [2]. Weather forecasting based on Numerical Weather Prediction (NWP) used to serve as the foundation for severe weather forecasting. However, NWP models suffer from spin-up problems, struggling to provide convective nowcasting with high accuracy [3,4].

Traditional REE models such as centroid tracking and cross-correlation methods rely on kinematic approaches for echo extrapolation. Due to their inadequate capability for handling the complex nonlinearity of atmospheric systems [5,6], they suffer from low prediction accuracy. In recent years, deep learning (DL)-based methods have drawn great attention and emerged as a novel driving force for innovation in weather forecasting. In comparison to NWP-based methods, DL-based radar echo extrapolation (REE) methods have increasingly become the primary techniques for convective nowcasting, attributed to their robust nonlinear modeling capability and proficiency in handling complex data [7]. They predict future echo sequences based on given historical sequences, without reliance on solving complex formulas of physical evolution laws by high-performance computers (HPC). As a data-driven methodology, the DL-based REE method inputs historical meteorological data into neural networks to uncover the laws of convective evolution. The extrapolation performance is primarily determined by the network architecture, which extracts features and learns laws, and the input data, which provide convective information. A number of studies have been conducted to enhance REE performance by improving the architectures of networks. Existing DL-based REE methods can be broadly classified into four categories: convolution neural network (CNN)-based methods [8,9,10], recurrent neural network (RNN)-based methods [11,12,13,14,15], generative adversarial network (GAN)-based methods [16,17,18], and Transformer-based methods [19,20,21]. However, convective nowcasting is not merely a spatiotemporal sequence prediction task, and improvements at the neural network architecture level struggle to utilize meteorological principles for constraining model predictions. Therefore, there is an urgent need to enhance meteorological data inputs by utilizing the interrelationships among various meteorological elements, which promises to significantly improve the performance of convective nowcasting.

Modern weather observation involves a variety of instruments, encompassing ground observation stations, weather radars, and meteorological satellites spanning from the surface to the upper atmosphere [22]. Multimodal data provide information on the same weather system from different aspects and possess potential correlations, despite disparities in their observational orientations and data organization [23]. Recently, there has been growing attention to studies focusing on improving REE accuracy by incorporating multimodal data inputs. Zhang et al. [24] proposed a multi-input multi-output recurrent neural network, which uses precipitation grid data, radar echo data, and reanalysis data as input to simultaneously predict precipitation amount and intensity. Ma et al. [25] introduced ground observation data and radar data into an RNN-based framework and adopted a late fusion strategy to incorporate the features of ground meteorological elements into radar features. The extrapolation results are superior to those of common RNN using only radar modal data. Niu et al. [26] devised a two-stage network framework for precipitation nowcasting, in which the spatial-channel attention and the generative adversarial module are used to fuse features and generate radar echo sequences. Although the aforementioned research based on multimodal data has made progress in improving the accuracy of convective nowcasting, there are still limitations in the alignment of spatiotemporally heterogeneous data and the fusion strategy of multimodal data. Firstly, there exists a significant disparity in both the temporal and spatial resolutions of multimodal heterogeneous data (as illustrated in

Table 1. Parameter information of different datasets.

Dataset	Modality	Time Resolution	Spatial Resolution
HKO-7 [29]	Radar	6 min	1 km
SEVIR [30]	Radar	5 min	0.5 km
	Satellite (vis/ir/lght)	5 min	0.5/2/8 km
RainBench [31]	SimSat	3 h	10 km
	ERA5	1 h	30 km
	IMERG	30 min	10 km
RAIN-F [32]	Radar	1 h	0.5 km
	Ground Observations	1 h	10 km
	IMERG	1 h	10 km
RAIN-F+ [33]	Radar	5 min	0.5 km
	Ground Observations	1 h	10 km
	IMERG	30 min	10 km
	Himawari-8	10 min	2 km
MeteoNet [34]	Radar	5 min	1 km
	Ground Observations	6 min	10 km
	Satellite	1 h	3 km
	AROME	1 h	10 km
	ARPEGE	1 h	1 km

), where the interpolation methods employed for data alignment often introduce errors. Second, existing multimodal symmetric fusion strategy treats modality-specific and modality-shared features equivalently, potentially leading to the loss of high-frequency detailed information contained within modality-specific features during the propagation process of the fusion network [27,28].

Recently, novel advancements have been made in multimodal data fusion strategies, particularly in addressing the fusion of heterogeneous and diverse data. In [35], an attention-based nonlinear diffusion module is proposed, which increases the spatial resolution and temporal resolution of sparse NWP forecast data and facilitates the fusion with spatiotemporally heterogeneous radar data. Chen et al. [36] propose a dynamic time warping (DTW)-based method for time series assessment, which improves the precision of time series data generated by time–space fusion. These two methods offer valuable insights into time series alignment that do not rely on interpolation. Moreover, recent works explore the inter-modal correlation and complementary in multimodal data. To decompose modality-specific features, modality-shared features, and model cross-modality features, Zhao et al. [37] propose a novel correlation-driven feature decomposition method, which adopts a dual-branch structure and achieves promising results in multimodal image fusion tasks. In [38], an asymmetric multilevel alignment module is designed for refining the feature alignment between images and text. Xu et al. [39] propose an asymmetric attention fusion module to dynamically adjusts to the informativeness of each modality, which allows for a dynamic fusion of modalities and enhances the integration of information.

In the field of convective nowcasting based on REE, different data modalities contribute significantly differently, with radar data often exerting a more pronounced influence than data from satellite and ground observations modalities. For instance, weather radar typically exhibits higher temporal and spatial resolution, enabling accurate detection of the dynamic variations within local convective systems [40,41]. In addition to its broad detection range, weather radar can also detect the vertical structure of convective systems [42,43]. We are inspired to propose a multimodal asymmetric fusion network (MAFNet) for REE. When considering multimodal REE tasks, radar modality provides the ground truth labels and exhibits strong correlations with the prediction outputs. High-frequency detailed information within modality-specific features of the radar modality aids in predicting the evolution details of echoes more effectively. Furthermore, low-frequency basic information within modality-shared features among other modalities provides insights into the overall evolutionary trends of convective systems, thus serving as a supplement to radar modality. Our framework employs a multi-branch structure and equips each modality branch with global–local encoders. Thus, the low-frequency basic information within modality-shared features and high-frequency detailed information within modality-specific can be separately extracted. Then, multimodal features with temporal resolution distinction are aligned by the DTW-based alignment module (DTW-AM), where the errors introduced by interpolation can be alleviated. Finally, the multimodal features are integrated by the multimodal asymmetric fusion module (MAFM) and achieve a more nuanced fusion of convective information. The MAFNet exploits the convective complementary information inherent in multimodal data, leveraging the advantages of multiple modalities while mitigating the weaknesses of individual modalities, thereby improving the overall performance of REE. In summary, the primary contributions of the MAFNet are as follows:

(1) We propose a multimodal asymmetric fusion network (named the MAFNet) for REE, which incorporates a multi-branch architecture and a global–local feature encoding and fusion structure. This framework allows for the extraction and integration of effective convective complementary information from multimodal data, thereby enhancing the accuracy of REE.

(2) Inspired by non-interpolative alignment methods, we have designed a DTW-based alignment module (DTW-AM) in the feature encoding stage, which aligns multimodal data with temporal resolution distinction by computing the correlation of features at different positions between multimodal feature sequences.

(3) Considering the varying contributions of multimodal data to REE, we have designed a multimodal asymmetric fusion module (MAFM), which fused the modality-specific features of radar modality and the modality-shared feature among multiple modalities to guide REE, thus leveraging their respective strengths and improving the accuracy of REE.

The remainder of this article is organized as follows. In Section 2, we review the DTW algorithm and multimodal fusion strategies. Section 3 introduces the definition of multimodal spatiotemporal prediction and the architecture of the MAFNet. Experimental results and analysis are presented in Section 4. Finally, conclusions are drawn in Section 5.

2. Related Work

2.1. DTW Algorithm

The dynamic time warping (DTW) algorithm was initially proposed by Itakura to align words in speech recognition tasks [44]. As research progresses, the DTW algorithm has shown promising performance in tasks related to time series. DTW enables the comparison of similarity between sequences of different lengths and sequences that are stretched or compressed, thereby achieving alignment of elements at different positions, which serves as a basis for alignment, classification, clusters, and other related tasks [45,46].

In multimodal meteorological data, the data sequences within the same period often vary in length due to the different temporal resolutions of the sensing instruments. When performing multimodal feature fusion, aligning feature sequences with different lengths and extending them to a uniform length is necessary. Therefore, DTW-based alignment holds promise in this regard and we propose a DTW-AM to align other modalities to the radar modality, which facilitates subsequent multimodal fusion. The principles of the proposed DTW-AM are elucidated in Section 3.4.

2.2. Asymmetric Fusion Strategy

Existing methods for multimodal data fusion can be broadly classified into four categories based on the fusion stage and feature hierarchy: early fusion, middle fusion, late fusion, and asymmetric fusion (as depicted in Figure 1). The early fusion strategy performs concatenation of multiple modalities before the encoder. The middle fusion strategy fuses multimodal feature branches’ output by feature encoders. The late fusion strategy integrates the output of multimodal branches for final decoding. However, these three symmetrical fusion strategies consider the importance of each modality to be equal, and this may lead to the loss of information from certain modalities. In contrast, within an asymmetric fusion strategy, a specific modal branch takes precedence, while other modal branches provide supplementary information to facilitate the accomplishment of the final task. From a structural perspective, the asymmetric fusion strategy bears a resemblance to the late fusion strategy, as it occurs before the decoder. However, at the feature level, the information hierarchy within different modal branches varies, and a specific branch tends to dominate.

Several representative multimodal models designed for specific spatiotemporal prediction tasks are enumerated in

Table 2. Representative multimodal models for spatiotemporal prediction.

Model	Fusion Strategy	Prediction Target
EF-ConvLSTM [30]	Early fusion	Precipitation nowcasting
MCGLN [47]	Early fusion	Lightning nowcasting
RN-Net [2]	Middle fusion	Rainfall nowcasting
MFSP-Net [30]	Middle fusion	Precipitation nowcasting
MM-RNN [31]	Late fusion	Precipitation nowcasting
LightNet [48]	Late fusion	Lightning nowcasting
LGRF [49]	Late fusion	Autonomous navigation
FURENet [50]	Late fusion	Convective nowcasting
HST-AFP [35]	Asymmetric fusion	Precipitation nowcasting

. In the EF-ConvSLTM [30], MCGLN [47], RN-Net [2], and MFSP-Net [30], the early fusion and middle fusion strategies are adopted, and the multimodal input is fused by channel concatenation or convolution in the very first layers of the model. However, the early fusion and middle fusion strategies are often affected by information entanglement, which potentially weakens the performance of the model. In [31,48,49,50], the late fusion strategy integrates multimodal branches as input to the decoder, which effectively preserves the information from each branch and facilitates learning data from each modality better. However, these symmetric fusion strategies treat each modality equally, and different modalities struggle to interact dynamically. The asymmetric fusion strategy employed in [35,39] offers valuable insights, assigning weights to different modal branches and integrating multimodal features at different scales, thereby fully exploiting the contributions of different modalities to the final task. In Section 3.5, we present the considerations and implementation of the multimodal asymmetric fusion module (MAFM) in the MAFNet.

3. Methodology

This section provides a detailed description of the MAFNet. Section 3.1 presents the formulation of multimodal REE. The overall architecture of the MAFNet is described in Section 3.2, and mainly includes three modules: global–local encoders, DTW-AM, and MAFM. Section 3.3 introduces the components of the global–local encoders. In Section 3.4, we introduce the DTW-AM that was specifically designed for aligning radar modality and other modalities. Section 3.5 illustrates the structure of MAFM and the propagation of multimodal features within it. Section 3.6 gives a detailed introduction to the loss function used in model training.

3.1. Problem Description

REE typically refers to the prediction of the radar echoes in the forthcoming 0–2 h, encompassing attributes such as intensity, morphology, and location. REE is essentially a spatiotemporal sequence predicting problem, where the sequence of past radar maps serves as the input and the sequence of future radar maps is the output [11]. As for multimodal REE tasks, they involve the sequences of multiple modalities as the input, with the sequence of radar maps as the output.

Let us use the tensors $R_t,S_t,G_t\in {\mathbb{R}}^{C\times H\times W}$ to denote the radar map, satellite map, and ground observation map observed at time $t$, respectively, where $C, W$, and $H$ denote the number of channels, the width, and the height of the data observed within the same region in each modality. Suppose that there are three input sequences, namely radar maps, satellite maps, and ground observation maps, $R=\{R_{t-m+1},R_{t-m+2},...{,R}_t\}$, $S=\{S_{t-m+1},S_{t-m+2},...{,S}_t\}$, $G=\{G_{t-m+1},G_{t-m+2},...{,G}_t\}$, where $m$ is the length of the input sequence. The REE problem is to predict the most probable output sequence of radar maps, $\widehat{R}=\{{\widehat{R}}_{t+1},{\widehat{R}}_{t+2},...,{\widehat{R}}_{t+n}\}$, where $n$ is the length of the output sequence. Specifically, we train the MAFNet parameterized as $\theta$ by batch gradient descent for REE tasks, and maximize the likelihood of predicting the sequence of the true radar map, $R^{\ast }=\{R_{t+1},R_{t+2},...,R_{t+n}\}$. The formulation can be described as:

$$\widehat{R}=\arg \underset{R^{\ast }}{\max }P\left(R^{\ast }\right|R,S,G;\theta )$$

(1)

where P is the conditional probability. In contrast to unimodal REE, where only R is used for parameterization, multimodal REE involves R, S, and G to jointly parameterize θ.

3.2. Overview of the MAFNet

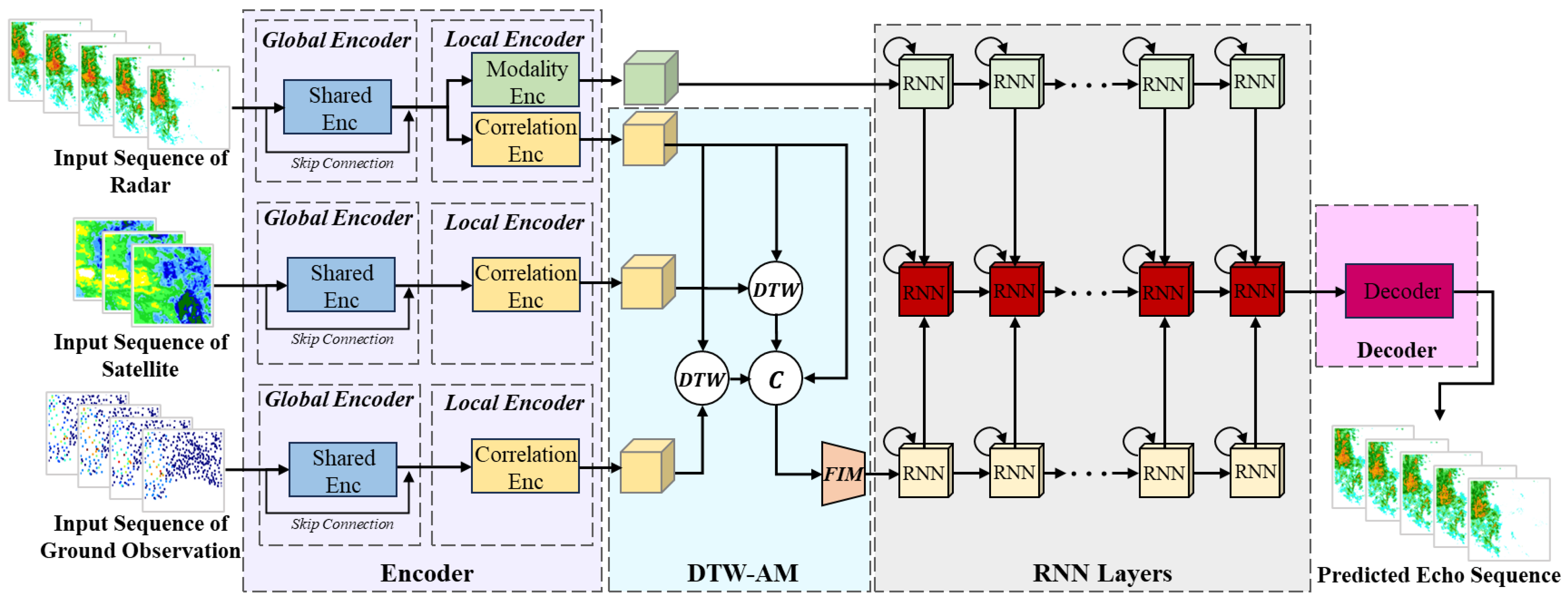
The workflow of our proposed MAFNet is presented in Figure 2, employing a multi-branch structure and global–local encoders. The MAFNet consists structurally of global–local encoders, DTW-AM, MAFM (integrated within RNN layers), and a decoder.

First, the global encoder extracts shallow features from the multimodal inputs, where the parameters of this encoder are shared. Subsequently, multimodal features undergo local encoding to extract modality-specific and modality-shared features. Among these, the modality-shared features of different lengths are aligned by the DTA-AW before being concatenated. Afterward, modality-specific and modality-shared features are fused in the MAFM of the RNN layers and propagated forward. During this process, as modality-specific features and modality-shared features do not share parameters, their feature hierarchies differ, making the fusion process asymmetric. Finally, the fused multimodal features are decoded to obtain the predicted echo sequences.

3.3. Global–Local Encoders

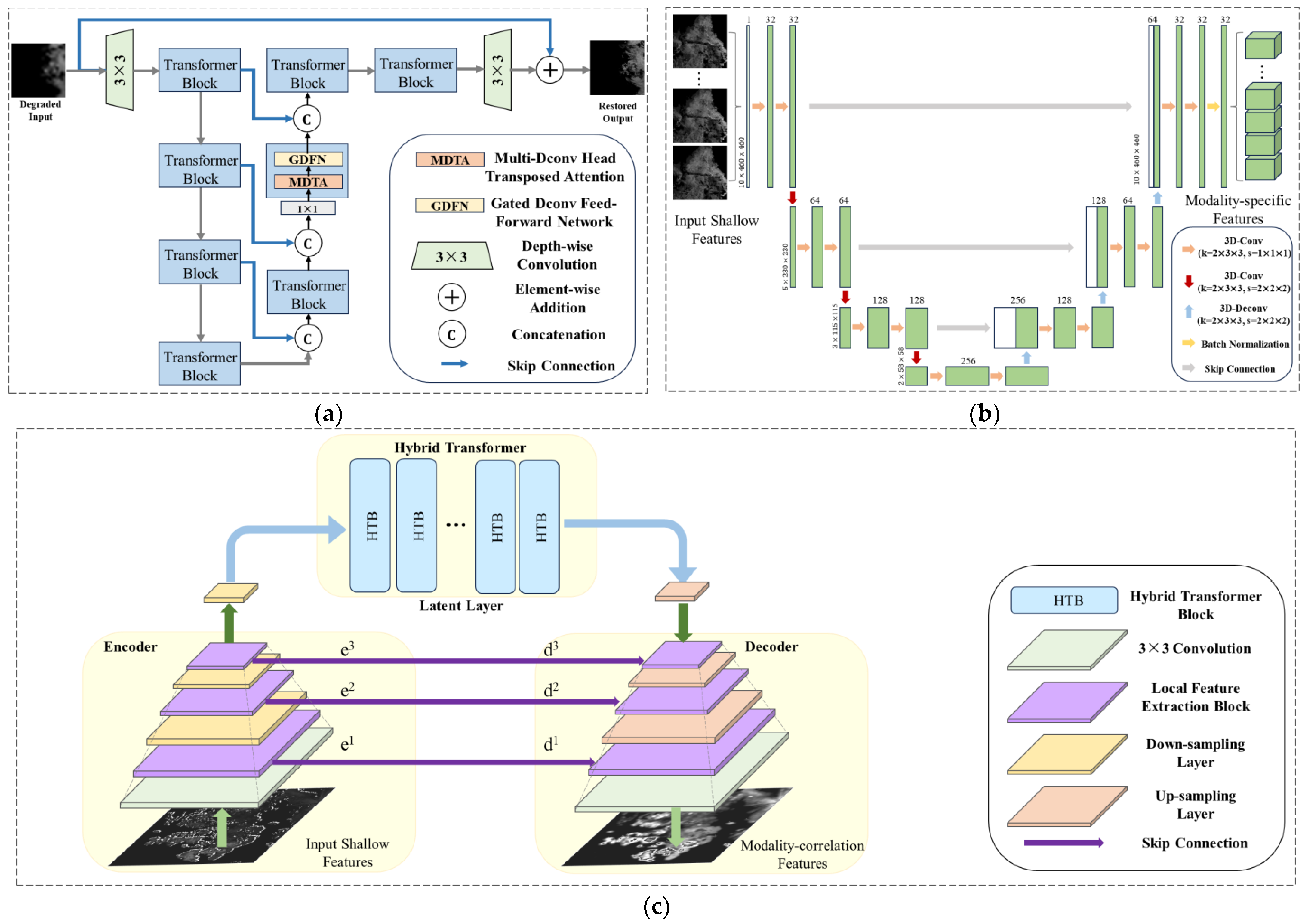
The encoders consist of three components: the Restormer block [51]-based global shared encoder (GSE), the 3D-U-Net [52]-based local modality encoder (LME), and the Dual-former block [53]-based local correlation encoder (LCE). In multimodal branches, the weights of GSE are shared, while the weights of LME and LCE are private.

For clarity in formulations, some symbols are defined. The input sequences of radar modality, satellite modality, and ground observation modality are denoted as $R\in {\mathbb{R}}^{C\times H\times W\times L_1}$, $S\in {\mathbb{R}}^{C\times H\times W\times L_2}$, $G\in {\mathbb{R}}^{C\times H\times W\times L_3}$, where $L_1, L_2, L_3$ denote the lengths of the sequences, respectively. The GSE, LME, and LCE are represented by $GSE(\cdot ), LME(\cdot ), LCE(\cdot )$, respectively.

3.3.1. Global Shared Encoder

GSE is a shared encoder across multimodal branches, which aims to extract shallow features from multimodal inputs and map them into a unified feature space at an initial stage. The encoding process can be formulated as:

$${\mathrm{F}}_R^{GSE}=GSE\left(R\right), {\mathrm{F}}_S^{GSE}=GSE\left(S\right), {\mathrm{F}}_G^{GSE}=GSE\left(G\right)$$

(2)

where ${\mathrm{F}}_R^{GSE}$, ${\mathrm{F}}_S^{GSE}$ and ${\mathrm{F}}_G^{GSE}$ are shallow features extracted from radar, satellite, and ground observation inputs $R$, $S$, and $G$, respectively.

GSE employs a computationally efficient Restormer block, which can extract shallow features and achieve cross-modality feature extraction through weight sharing across multiple branches. According to the original paper [51], the simplified architecture of the Restormer block in GSE is represented in Figure 3a.

3.3.2. Local Modality Encoder

LME aims to extract modality-specific features from the shallow features of the radar modality branch, which is formulated as:

$${\mathrm{F}}_R^{LME}=LME\left({\mathrm{F}}_R^{GSE}\right)$$

(3)

where ${\mathrm{F}}_R^{GSE}$ and ${\mathrm{F}}_R^{LME}$ are the shallow features and modality-specific features, respectively.

The reason we choose 3D-U-Net in LME is that it can effectively extract multi-scale features from radar modality. The unique symmetric structure of 3D-U-Net facilitates feature reuse and parameter sharing, and its adoption of skip connections helps to capture information at different scales without increasing computation too much. The architecture of LME is shown in Figure 3b.

In LME, one assumption is that the high-frequency detailed information in modality-specific features is modality-irrelevant and represents the unique characteristics of the radar modality (e.g., the texture details of local echoes and the strength of echo reflectivity make it challenging to directly relate to the information from other modalities). Therefore, modality-specific features of radar input can be effectively preserved during forward propagation, facilitating the subsequent stage of asymmetric feature fusion.

3.3.3. Local Correlation Encoder

Contrary to LME, the LCE is designed to extract low-frequency basic information in modality-correlated features from multimodal inputs, which can be expressed as:

$$\left\{\begin{array}{c}{\mathrm{F}}_R^{LCE}=LCE\left({\mathrm{F}}_R^{GSE}\right)\\ {\mathrm{F}}_S^{LCE}=LCE\left({\mathrm{F}}_S^{GSE}\right)\\ {\mathrm{F}}_G^{LCE}=LCE\left({\mathrm{F}}_G^{GSE}\right)\end{array}\right.$$

(4)

where ${\mathrm{F}}_R^{LCE}$, ${\mathrm{F}}_S^{LCE}$ and ${\mathrm{F}}_G^{LCE}$ are the correlated features extracted from radar, satellite, and ground observation modalities, respectively.

The Dual-former is an efficient feature encoder, which combines the Hybrid Transformer and local feature extraction modules to model local features and long-distance relationships while maintaining a small computational cost. The structure of the Dual-former-based LCE is illustrated in Figure 3c.

Figure 3. The structures of global–local encoders: (a) The Restormer block-based GSE, (b) The 3D-U-Net- based LME, (c) The Dual-former-based LCE.

Figure 3. The structures of global–local encoders: (a) The Restormer block-based GSE, (b) The 3D-U-Net- based LME, (c) The Dual-former-based LCE.

We assume that the modality-shared features containing low-frequency basic information are modality-relevant, multimodal features. The modality-shared features collectively reveal the inherent patterns and evolution trends of the convective systems (e.g., despite different observational orientations in multimodal inputs, the evolution trends of the convective system within the same background field remain consistent across multi-modalities). By leveraging the relevant information embedded in the modality-shared features, the utilization of convective evolution laws is enhanced and the performance of REE can be improved.

3.4. DTW-Alignment Module (DTW-AM)

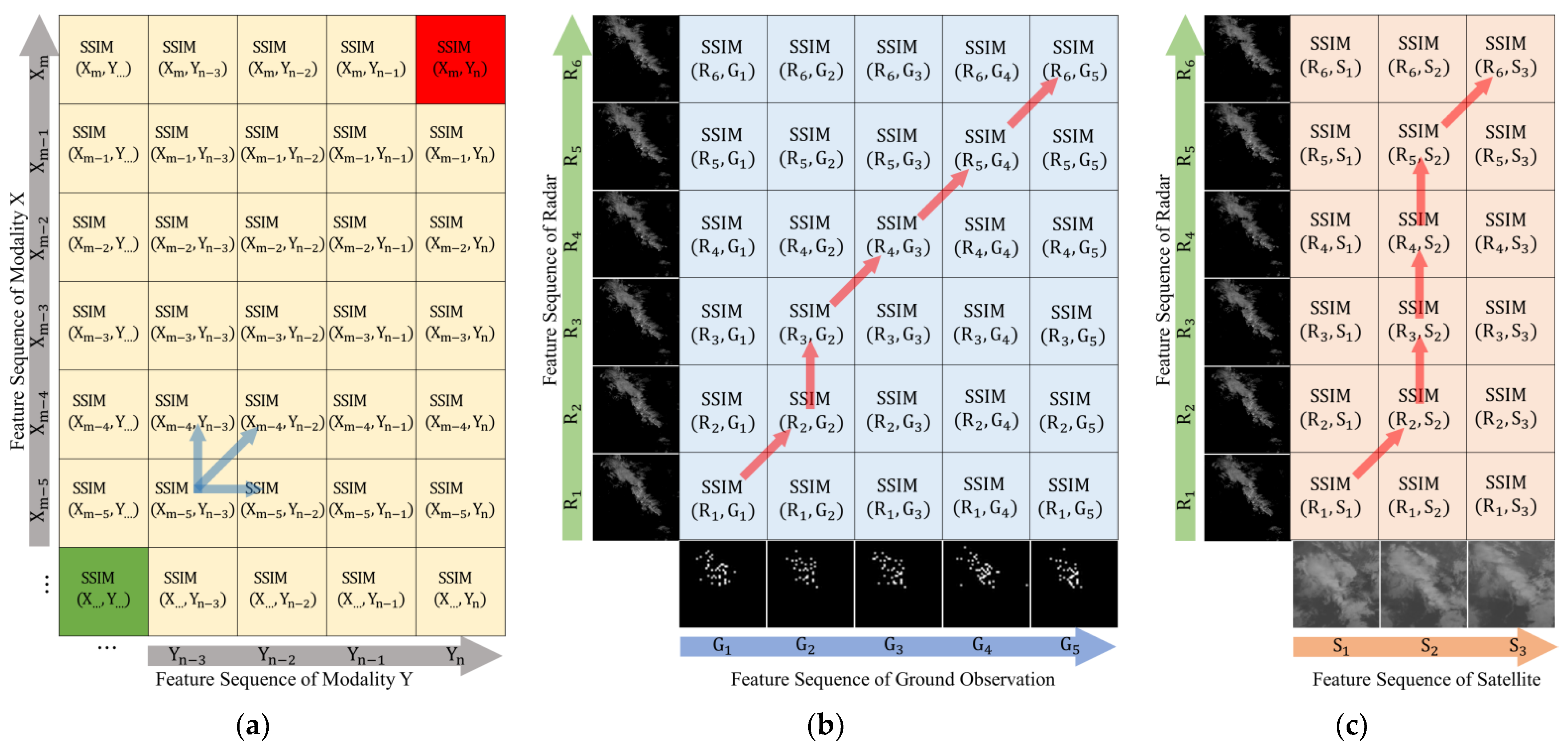
The DTW-AM is designed to align modality-correlated features from LCEs’ outputs, which comprise two DTW units and one feature interaction module (FIM). For temporally inconsistent multimodal feature sequences, DTW units first calculate pairwise similarities between their sequences and identify the optimal time alignment paths. They then extend the feature sequences of different lengths to the same length and concatenate them together. The concatenated feature sequence is fed into the FIM for interaction among modality-correlated features.

As illustrated in Figure 4, DTW-AM measures the similarity between feature maps of each frame in different modal feature sequences by SSIM scores [54], which comprehensively evaluates similarity across luminance, contrast, and structure of the feature maps. The task of the DTW-AM is to find the shortest alignment path that maximizes the sum of feature map similarities. We assume that there are two feature sequences of lengths $\mathrm{m}$ and $\mathrm{n}$, denoted as $\mathrm{X}$ and $\mathrm{Y}$, respectively. For any frame of feature at a given time, they are represented as ${\mathrm{X}}_{\mathrm{i}}$ and ${\mathrm{Y}}_{\mathrm{j}}$. The alignment path of length $\mathrm{K}$ is denoted as $\mathrm{W}$. Therefore, the $\mathrm{k}$-th point in $\mathrm{W}$ can be represented as ${\mathrm{W}}_{\mathrm{k}}=({\mathrm{X}}_{\mathrm{i}},{\mathrm{Y}}_{\mathrm{j}})$. The alignment path is subject to the following three constraints:

(1)

Boundary condition: The alignment path must start from $({\mathrm{X}}_0,{\mathrm{Y}}_0)$, and end at $({\mathrm{X}}_{\mathrm{m}},{\mathrm{Y}}_{\mathrm{m}})$.

(2)

Continuity condition: For any point $({\mathrm{X}}_{\mathrm{i}},{\mathrm{Y}}_{\mathrm{j}})$ on the alignment path and its subsequent point $({\mathrm{X}}_{\mathrm{i}\prime },{\mathrm{Y}}_{\mathrm{j}\prime })$, they must satisfy $\mathrm{i}\prime -\mathrm{i}\le 1$, and $\mathrm{j}\prime -\mathrm{j}\le 1$.

(3)

Monotonicity condition: For any point $({\mathrm{X}}_{\mathrm{i}},{\mathrm{Y}}_{\mathrm{j}})$ on the alignment path and its subsequent point $({\mathrm{X}}_{\mathrm{i}\prime },{\mathrm{Y}}_{\mathrm{j}\prime })$, they must satisfy $\mathrm{i}\prime -\mathrm{i}\ge 0$, and $\mathrm{j}\prime -\mathrm{j}\ge 0$.

Figure 4. The principles of DTW-AM: (a) matrix of similarity measures; (b) an example of aligning radar modal features with ground modal features; (c) an example of aligning radar modal features with satellite modal features. (The arrows represent progression along the temporal sequences).

Figure 4. The principles of DTW-AM: (a) matrix of similarity measures; (b) an example of aligning radar modal features with ground modal features; (c) an example of aligning radar modal features with satellite modal features. (The arrows represent progression along the temporal sequences).

Consequently, as illustrated in Figure 4a, the alignment path is constrained to start from the green point in the bottom-left corner and end at the red point in the top-right corner; each point can only progress in one of the three directions indicated by the blue arrows. This ensures that the two feature sequences are aligned in a forward temporal process, without skipping any frame of feature maps, and the path does not revisit or backtrack. The optimization process of the alignment path can be formalized as follows:

$$\mathrm{D}\mathrm{T}\mathrm{W}(\mathrm{X},\mathrm{Y})=\underset{\mathrm{K}}{\mathrm{arg\; min}}(\sum _{\mathrm{k}=1}^{\mathrm{K}}({\displaystyle \frac{1}{\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}\left({\mathrm{W}}_{\mathrm{k}}\right)}}))$$

(5)

where the higher the SSIM score, the more similar the two feature maps are. We take the reciprocal to represent the difference between the two feature maps.

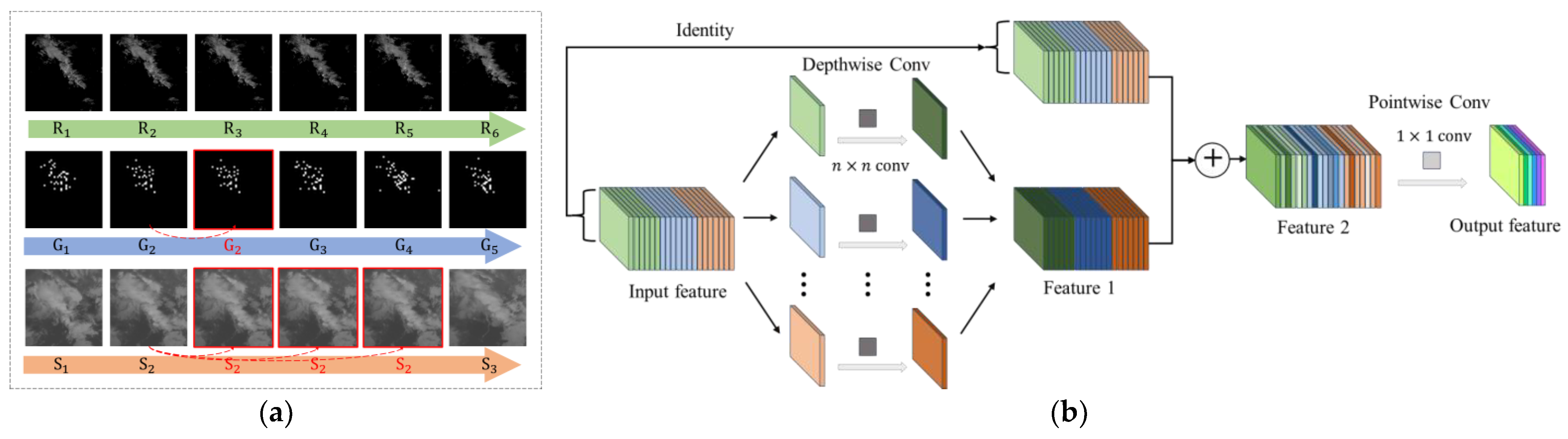
In Figure 4b,c, there are two examples of aligning radar feature sequences with ground observation feature sequences and satellite feature sequences, respectively. Here, R, G, and S denote the radar, ground observation, and satellite feature sequences, with the optimal alignment path indicated by red arrows. It is noteworthy that in DTW-AM, we fixed the length of the radar feature sequence, aligning the ground observation and satellite feature sequences with the radar feature sequence. Specifically, the alignment from R to G/S is a one-to-one mapping, while from G/S to R is a one-to-many mapping. There is an example of the output of DTW-AM in Figure 5a, where the aligned multimodal feature sequences are extended to the same length. Subsequently, the multimodal feature sequences are concatenated and fed into the FIM.

The FIM is a feature interaction module based on Maintaining the Original information-Deeply Separable Convolution (MODSConv) [55], which helps maintain original information after depthwise separable convolution. The architecture of FIM is shown in Figure 5b. In the FIM, one branch of the input feature undergoes a grouped depthwise convolution, while another branch maintains the original information. Then, they are added together to supplement missing information between channels. Subsequently, pointwise convolution integrates information between the channels of the multimodal feature and reduces the dimension of the channels.

We denote the output of the DTW unit and FIM as $DTW(\cdot ), FIM(\cdot )$, respectively. The outcome of DTW-AM can be expressed as:

$${\mathrm{F}}_R^{DTA-AM}=FIM\left(\right[DTW({\mathrm{F}}_R^{LCE},{\mathrm{F}}_S^{LCE});DTW({\mathrm{F}}_R^{LCE},{\mathrm{F}}_G^{LCE})\left]\right)$$

(6)

where ${\mathrm{F}}_R^{DTW-AM}$ is the output feature sequence of DTW-AM, ‘;’ indicates feature concatenation.

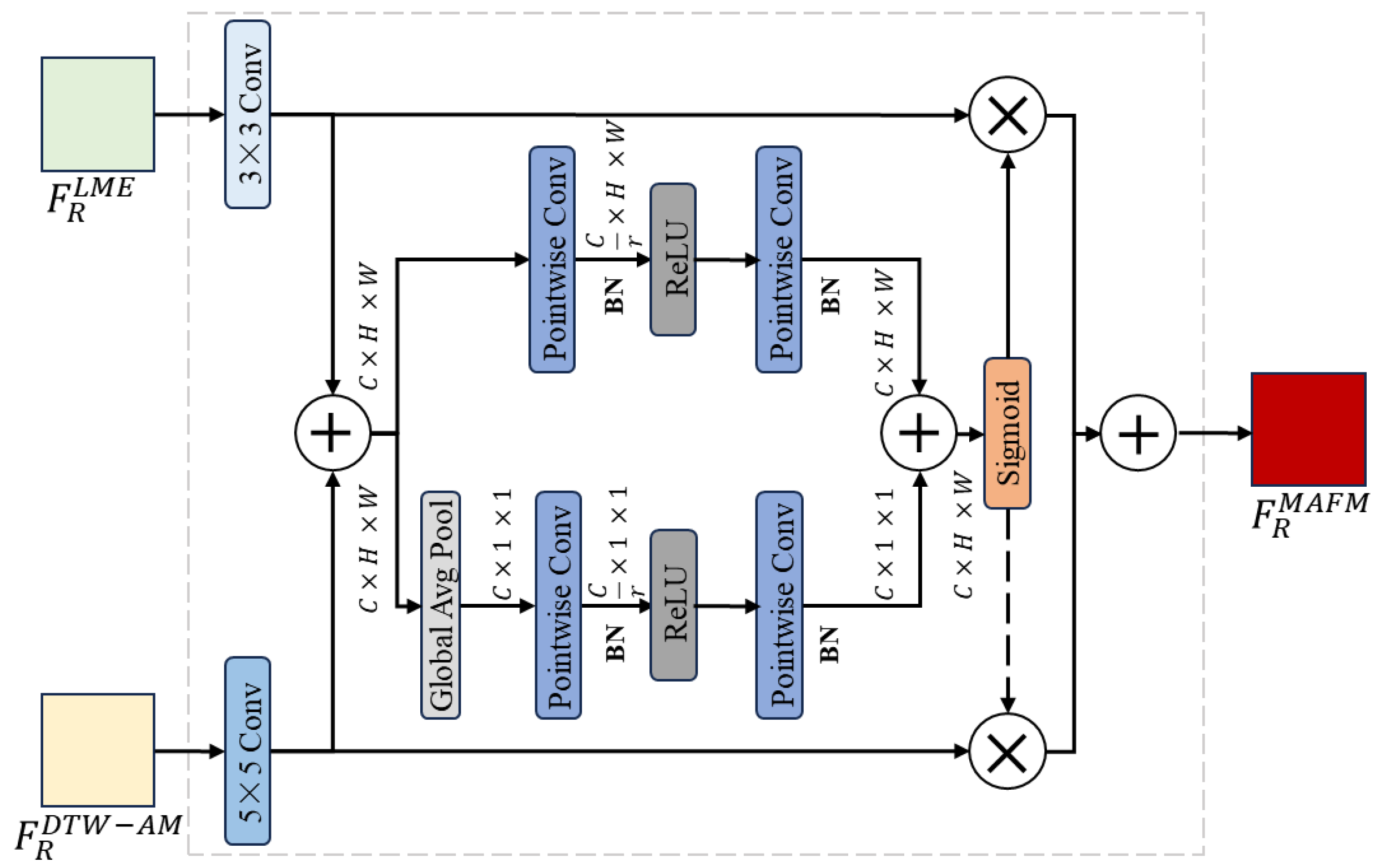
3.5. Multimodal Asymmetric Fusion Module (MAFM)

The MAFM is a plug-and-play component integrated within the RNN layers, which is employed to fuse modality-specific features and modality-correlated features from different encoding branches during the forward propagation process. The MAFM is based on attentional feature fusion (AFF) [56] and its architecture is illustrated in Figure 6.

The MAFM receives two streams of feature inputs. The modality-specific feature sequences and modality-correlated feature sequences undergo 3 × 3 and 5 × 5 convolution, respectively, generating multi-scale abstract features. Subsequently, the two sequences are summed up, and it is passed through the global average pool layer to compress its spatial size, while another branch maintains its dimensions. Following this, both feature branches undergo pointwise convolutional layers and activation layers individually, and the outcomes are summed up. Next, the activated sum is used as a weight and distributed to the two original feature input branches in different proportions. Finally, a weighted average is calculated to obtain the multimodal asymmetric fused feature. If we denote the weights as $\mathrm{M}$, the formulation of MAFM can be expressed as:

$${\mathrm{F}}_R^{MAFM}=\mathrm{M}({\mathrm{F}}_R^{LME}⨄{\mathrm{F}}_R^{DTW-AM})\otimes {\mathrm{F}}_R^{LME}+(1-\mathrm{M}({\mathrm{F}}_R^{LME}⨄{\mathrm{F}}_R^{DTW-AM}\left)\right)\otimes {\mathrm{F}}_R^{DTW-AM}$$

(7)

where a ${\mathrm{F}}_R^{MAFM}$ is the multimodal asymmetric fused feature, ‘$⨄$’ denotes the initial feature integration, and ‘$\otimes$’ denotes the Hadamard product.

Figure 6. The architecture of the MAFM.

Figure 6. The architecture of the MAFM.

3.6. Loss Function

During the training of the models, we employ a combination of mean absolute error (MAE) and mean square error (MSE) as the loss function, which is a common approach in regression tasks [31]. Furthermore, to enhance the model’s perception and predictive capability of intense convective echoes, we assign greater weights to echoes of higher intensity. The loss function can be formulated as:

$${\mathrm{L}}_{\mathrm{M}\mathrm{A}\mathrm{E}}={\displaystyle \frac{1}{H\times W}}\sum _{i=1}^H\sum _{j=1}^W\left|y_{i,j}-{\tilde{y}}_{i,j}\right|$$

(8)

$${\mathrm{L}}_{\mathrm{M}\mathrm{S}\mathrm{E}}={\displaystyle \frac{1}{H\times W}}\sum _{i=1}^H\sum _{j=1}^W{(y}_{i,j}-{\tilde{y}}_{i,j}{)}^2$$

(9)

$$\mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}={\omega }_{i,j}[\lambda {\mathrm{L}}_{\mathrm{M}\mathrm{A}\mathrm{E}}+(1-\lambda \left){\mathrm{L}}_{\mathrm{M}\mathrm{S}\mathrm{E}}\right]$$

(10)

$${\omega }_{i,j}=\left\{\begin{array}{l} 1, if y_{i,j}\le 20 \mathrm{dBZ}\\ 5, if 20 \mathrm{dBZ}<y_{i,j}\le 35 \mathrm{dBZ}\\ 10, if 35 \mathrm{dBZ}<y_{i,j}\le 45 \mathrm{dBZ}\\ 20, if 45 \mathrm{dBZ}<y_{i,j} \end{array}\right.$$

(11)

where the intensity of the radar echo is expressed in dBZ; $y_{i,j}$, ${\tilde{y}}_{i,j}$ are the ground truth and prediction of the echoes; and $H,W$ are the height and width of the echo image, respectively. ${\omega }_{i,j}$ is the weight assigned to echoes of different intensities. $\lambda$ is a constant to adjust the proportion of MAE and MSE, which is 0.5 in our experiments.

4. Experiment

In this section, the experimental setup and results are presented. Section 4.1 describes the datasets used in experiments. In Section 4.2, the evaluation metrics are introduced. In Section 4.3, we present the implementation details. In Section 4.4 and Section 4.5, the experimental results on two datasets are displayed. In Section 4.6, the ablation study of the MAFNet is analyzed.

4.1. Datasets

Due to the stochastic nature of weather phenomena and limitations in detection capabilities and locations of meteorological instruments, existing multimodal datasets are rare and limited in variety. The MeteoNet [29] provided by Meteo France and the RAIN-F [27] provided by SI-Analytics are two representative publicly available multimodal meteorological datasets. Their contributions are highly significant for research in multimodal weather forecasting.

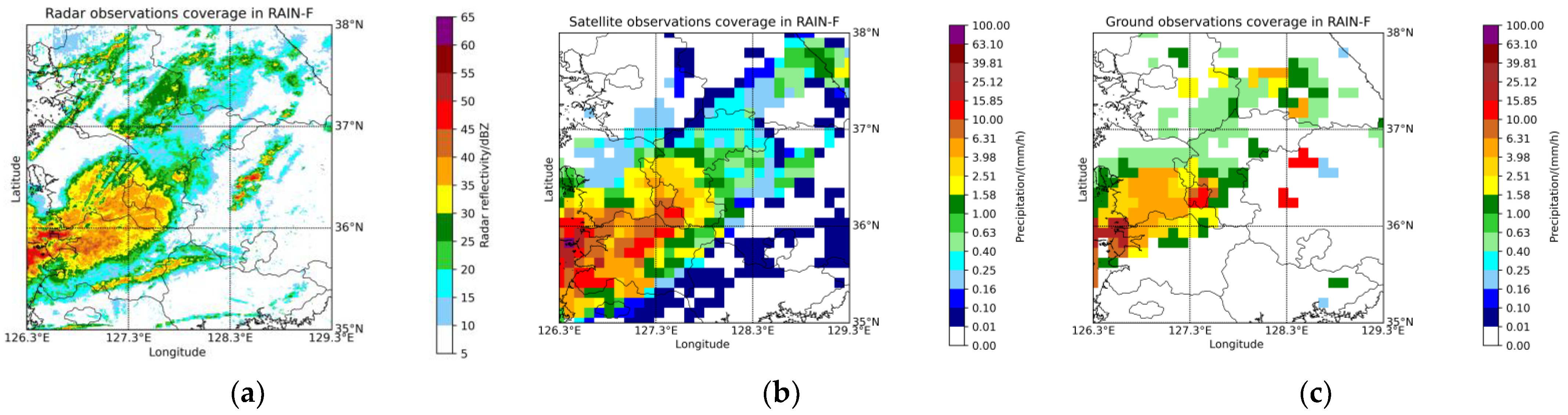
(1) MeteoNet: This dataset provides multimodal meteorological data from southeastern (SE) France from 2016 to 2018, including ground observations, rain radar data, satellite remote sensing data, weather forecast models, and land–sea and terrain masks. In experiments performed on MeteoNet, we have delineated a study area of $460 \mathrm{k}\mathrm{m}\times 460 \mathrm{k}\mathrm{m}$ within the SE region (see Figure 7). We conduct experiments using radar data, ground-observed precipitation, and IR108 data of satellites from the SE region. The spatial resolutions of radar, ground observations, and satellite data are 1 km, 10 km, and 3 km, respectively, with temporal resolutions of 5 min, 6 min, and 1 h, respectively. The preprocessed dataset consists of 19,000 samples, partitioned in a ratio of 13,000:2000:4000 for training, validation, and test subsets, respectively.

(2) RAIN-F: This dataset offers ground observations, radar, and satellite data collected by the Korea Meteorological Administration (KMA) and the National Aeronautics and Space Administration (NASA), which cover an area of the Korean Peninsula from 2017–2019 (see Figure 8). The spatial resolutions of radar, satellite data, and ground observations are 0.5 km, 10 km, 10 km, respectively, with a temporal resolution of 1 h. The preprocessed dataset consists of 12,000 samples, with the training, validation, and testing subsets containing 9000, 1500, and 1500 samples respectively.

4.2. Evaluation Metrics and Implementation Details

We employ both quantitative and qualitative evaluations to compare the REE performance of the MAFNet with other models. Quantitative evaluation metrics include convective nowcasting evaluation metrics and image quality evaluation indexes, which are the critical success index (CSI) [57], Heidke Skill Score (HSS) [58], peak signal-to-noise ratio (PSNR) [59], structural similarity index measure (SSIM), and mean square error (MSE).

The CSI and HSS are calculated at the radar echo intensity threshold of $\mathrm{\tau }=\{20,35,45\} \mathrm{d}\mathrm{B}\mathrm{Z}$, respectively corresponding to incrementally increasing precipitation intensities. The prediction results and ground truth are first converted to 0/1 according to the intensity thresholds (0 denotes the absence of precipitation, 1 denotes the presence of precipitation), and distinct labels are assigned accordingly (as shown in

Table 3. The labels of confusion matrix.

	Prediction = 1	Prediction = 0
Ground Truth = 1	TP	FN
Ground Truth = 0	FP	TN

).

Therefore, the CSI and HSS can be formulated as:

$$\mathrm{C}\mathrm{S}\mathrm{I}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}+\mathrm{F}\mathrm{P}}}$$

(12)

$$\mathrm{H}\mathrm{S}\mathrm{S}={\displaystyle \frac{2\ast (\mathrm{T}\mathrm{P}\ast \mathrm{T}\mathrm{N}-\mathrm{F}\mathrm{N}\ast \mathrm{F}\mathrm{P})}{\left(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}\right)\left(\mathrm{F}\mathrm{N}+\mathrm{T}\mathrm{N}\right)+(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P})(\mathrm{F}\mathrm{P}+\mathrm{T}\mathrm{N})}}$$

(13)

The CSI and HSS collectively measure the accuracy of convective nowcasting, reflecting the model’s predictive capability regarding the location, morphology, and intensity of radar echoes. The PSNR and SSIM quantify the visual similarity between predicted radar echo images and ground truth, where higher scores indicate better visual performance of the predicted radar echo images. MSE is a commonly used statistical metric that assesses the general predictive capability of the model.

4.3. Implementation Details

Considering the differences between MeteoNet and RAIN-F datasets, we employ different experimental configurations on them, respectively.

In experiments performed on the MeteoNet dataset, multimodal data of different sizes are resized to $460\times 460$ for analysis. We use multimodal data as inputs, including radar data and ground observations from the previous hour, along with satellite data from the past three hours, with the radar echoes for the next hour serving as the prediction target. This setup is motivated by the capability of DTW-AM to align multimodal features with different time intervals. Moreover, we have implemented an asymmetric fusion strategy in the MAFNet, where radar data include modality-specific features crucial for detailed echo evolution, while ground observations and satellite data contain modality-correlated features, providing atmospheric motion background fields.

The experimental setup on RAIN-F is slightly different from those on MeteoNet. Since the temporal resolution of multimodal data is uniformly 1 h, experiments conducted on the RAIN-F dataset no longer involve DTW-AM, as the temporal alignment of data is unnecessary. All of the multimodal data are preprocessed and resized to $300\times 300$. We use multimodal data including radar reflectivity, satellite-observed precipitation, and ground-observed precipitation, where the first two steps serve as inputs and the subsequent three steps are prediction targets. Given that the lifecycle of short-lived convective systems typically spans only a few hours, the temporal resolution of 1 h poses a significant challenge for convective nowcasting. This configuration is more closely aligned with the practical demands of convective nowcasting.

In experiments conducted on two datasets, the MAFNet uses MotionRNN [60] as the backbone RNN unit. The MAFNet is compared with representative DL-based REE methods, including CNN-based SmaAt-UNet [61], RNN-based PredRNN [12] and MIM [14], Transformer-based Rainformer [21], and Earthformer [62]. The above DL-based REE models have configurations similar to those of the MAFNet. Specifically, all models use the Adam optimizer [63] with momentum ${\beta }_1=0.5$, ${\beta }_2=0.999$, and an initial learning rate of 1 $\times {10}^{-4}$. The maximum epoch of training is set to 200, and an early stop will be implemented if the validation scores do not improve for more than 5 epochs. The number of feature channels is 32, and the number of hidden states channels is 256. Their training is performed on four RTX 3090 GPUs, with a batch size of eight. The quantitative evaluation scores are averaged over all samples in the test set. Specifically, CSI and HSS are computed at thresholds of $\mathrm{\tau }=\{20,35,45\} \mathrm{d}\mathrm{B}\mathrm{Z}$, while PSNR, SSIM, and MSE are calculated without restriction of echo intensity thresholds. For a fair comparison, the comparative models use temporally interpolated multimodal data aligned and concatenated along the channel dimension as input, with radar echoes as the output.

4.4. Experimental Results on MeteoNet

For the MeteoNet dataset, the quantitative evaluation results of comparison experiments are shown in

Table 4. Quantitative evaluation results on MeteoNet.

Models	CSIτ ↑			HSSτ ↑			$\mathbf{PSNR} \uparrow$	SSIM ↑	MSE ↓
	$\mathbf{\tau }=20$	$\mathbf{\tau }=35$	$\mathbf{\tau }=45$	$\mathbf{\tau }=20$	$\mathbf{\tau }=35$	$\mathbf{\tau }=45$
PredRNN	0.5304	0.3367	0.1587	0.6132	0.4291	0.2135	27.2192	0.8441	22.376
MIM	0.5376	0.3478	0.1633	0.6154	0.4349	0.2192	27.3685	0.8483	21.985
SmaAt-UNet	0.5463	0.3536	0.1689	0.6204	0.4427	0.2251	29.1214	0.8605	21.297
Rainformer	0.5561	0.3588	0.1753	0.6318	0.4503	0.2318	28.5453	0.8524	20.446
Earthformer	0.5782	0.3645	0.1814	0.6375	0.4626	0.2367	28.9346	0.8567	20.139
MAFNet	0.5819	0.3769	0.1842	0.6521	0.4852	0.2423	29.4568	0.8649	19.854

where ‘τ’ denotes threshold of radar echo intensity. ↑ indicates that higher scores are better, while ↓ indicates that lower scores are better. The best and the second-best scores are respectively denoted by bold and underlined markers.

.

From Table 4, we can see that the MAFNet outperforms other DL-based models on all convective nowcasting evaluation metrics. Specifically, compared to the representative RNN-based MIM, the MAFNet demonstrates improvements of 8.24%, 8.37%, 12.80%, 5.96%, 11.57%, and 10.54% on CSI²⁰, CSI³⁵, CSI⁴⁵, HSS²⁰, HSS³⁵, and HSS⁴⁵, respectively. Furthermore, compared to the CNN-based SmaAt-UNet, the MAFNet shows improvements of 6.52%, 6.59%, 9.06%, 5.11%, 9.6%, and 7.64% on CSI metrics and HSS metrics, respectively. Particularly, compared to the state-of-the-art (SOTA) Earthformer, the MAFNet achieves enhancements of 0.64%, 3.40%, 1.54%, 2.29%, 4.89% and 2.37% on CSI²⁰, CSI³⁵, CSI⁴⁵, HSS²⁰, HSS³⁵, and HSS⁴⁵, respectively. In addition, the MAFNet exhibits superior scores across PSNR and SSIM metrics, as well as the lowest MSE, indicating not only its effectiveness in convective nowcasting evaluation metrics but also its competitiveness in the quality of predicted images. Furthermore, SmaAt-UNet achieves the second-best scores in PSNR and SSIM, which may be attributed to its robust CNN-based image feature processing capabilities.

The qualitative evaluation results of different models are shown in Figure 9. Two convective weather event cases selected from the SE region of France are presented here to visually demonstrate the REE performance of the MAFNet and compare it with other models. In Figure 9a, a convective system is moving from central to northeastern parts, with its convective core region highlighted in red boxes. The MAFNet exhibits the closest prediction to the ground truth across all forecast results, which predicts not only the movement of the echo region but also its shape and intensity to a considerable degree. In contrast, PredRNN, MIM, and SmaAt-UNet exhibit significant deviations in predicting the trend of echo movement, while Rainformer and Earthformer show deficiencies in predicting echo morphology and intensity. Furthermore, we can analyze the variations in the convective systems from the perspective of multimodal data. From the satellite modality input, variations in the cloud-top brightness temperature indicate a trend of the convective system moving towards the northeast. The decrease in brightness temperature and the expansion in area suggest an intensification and broadening of convection, which is consistent with the information contained in the radar modality. From the ground observation modality input, precipitation sites are predominantly concentrated in the northeastern region, indicating vigorous convective development in that area. This often corresponds to continuous precipitation cloud layers, which aligns with the radar input as well.

In Figure 9b, a convective system is intensifying gradually, and predictions from different methods are highlighted with red boxes for visual comparison of discrepancies. The MAFNet is capable of forecasting adjacent and continuous areas of strong echoes (yellow regions exceeding 30 dBZ), whereas other models exhibit deficiencies in predicting echo shape and intensity. Furthermore, from the perspective of satellite modality input, the region with lower cloud-top brightness temperatures in the lower part of the image has merged from several smaller areas into a contiguous region (yellow areas), indicating the coalescence and growth of the convective core. This observation is consistent with the distribution of the elongated strong convective area observed at time T = 0 in the radar modality input. From the ground observation modality input, the locations of precipitation sites show minimal variation; however, there is a significant increase in precipitation intensity (with areas changing from blue and green to orange and red). This increase is significantly correlated with the intensification of convection observed in the radar modality input.

Based on the comprehensive quantitative and qualitative assessment, it can be concluded that integrating detailed echo information from radar modality with convective background field information from satellite and ground observational modalities and fusing them asymmetrically at different feature levels, effectively improves the performance of REE. This suggests that supplementing single radar modal data with other modal data is feasible and features at different levels can collectively contribute to REE.

4.5. Experimental Results on RAIN-F

The quantitative evaluation results on the RAIN-F dataset are presented in

Table 5. Quantitative evaluation results on RAIN-F.

Models	CSIτ ↑			HSSτ ↑			$\mathbf{PSNR} \uparrow$	SSIM ↑	MSE ↓
	$\mathbf{\tau }=20$	$\mathbf{\tau }=35$	$\mathbf{\tau }=45$	$\mathbf{\tau }=20$	$\mathbf{\tau }=35$	$\mathbf{\tau }=45$
PredRNN	0.3961	0.2922	0.0783	0.4489	0.3483	0.1205	25.2198	0.7325	26.944
MIM	0.4010	0.2980	0.0872	0.4563	0.3654	0.1256	25.4547	0.7379	25.621
SmaAt-UNet	0.4185	0.3074	0.0935	0.4625	0.3768	0.1319	26.8326	0.7482	24.837
Rainformer	0.4219	0.3103	0.0984	0.4793	0.3937	0.1358	26.4342	0.7466	24.258
Earthformer	0.4247	0.3177	0.1031	0.4856	0.4024	0.1447	26.7683	0.7537	23.776
MAFNet	0.4368	0.3286	0.1116	0.4913	0.4139	0.1492	27.1432	0.7584	23.245

where ‘τ’ denotes threshold of radar echo intensity. ↑ indicates that higher scores are better, while ↓ indicates that lower scores are better. The best and the second-best scores are respectively denoted by bold and underlined markers.

, while the qualitative assessment results are illustrated in Figure 10.

From Table 5, it is observed that the quantitative evaluation scores on the RAIN-F dataset are generally lower compared to those on the MeteoNet dataset. This is because experiments on RAIN-F focus on predicting radar echoes for only the next three time steps, but due to longer time intervals, the lead time can extend to three hours, resulting in greater extrapolation difficulty. In comparison to MIM, the MAFNet shows improvements of 8.92%, 10.27%, 27.98%, 7.67%, 13.27%, and 18.79% on CSI²⁰, CSI³⁵, CSI⁴⁵, HSS²⁰, HSS³⁵, and HSS⁴⁵, respectively. Furthermore, compared to the latest Earthformer (2023), the MAFNet exhibits enhancements of 2.85%, 3.43%, 8.24%, 1.17%, 2.86%, and 3.11% in the corresponding CSI and HSS metrics. The quantitative evaluation results indicate that experimental conclusions on the RAIN-F dataset align with those on the MeteoNet dataset, demonstrating the effectiveness of the MAFNet in improving REE, particularly with more notable improvements at the thresholds of 35 dBZ and 45 dBZ.

Figure 10. The two study cases in the Korean Peninsula. (a) case time T = 10 July 2017, 22:00 UTC+9, (b) case time T = 17 May 2019, 23:00 UTC+9. (Key areas are highlighted by the red box).

Figure 10. The two study cases in the Korean Peninsula. (a) case time T = 10 July 2017, 22:00 UTC+9, (b) case time T = 17 May 2019, 23:00 UTC+9. (Key areas are highlighted by the red box).

In Figure 10, there are two examples illustrating the movement of convective systems over the Korean Peninsula. In Figure 10a, the convective system moves from west to east, with its intensity initially increasing and subsequently decreasing. Due to the extended forecast lead time causing significant prediction uncertainty, all models struggle to forecast the process of radar echo intensity decrease. However, the MAFNet still demonstrates superiority in predicting radar echo movement and morphology. As highlighted by the red boxes, PredRNN and MIM fail to predict the elongated north-south extension of radar echoes. While SmaAt-UNet, Rainformer, and Earthformer forecast the originally continuous radar echo region as two separate parts. Despite overestimating the radar echo intensity in some areas, the MAFNet provides more accurate predictions of the overall radar echo morphology. Additionally, from the satellite modality input, the convective system is observed to be moving eastward with a tendency for intensification. Concurrently, the ground observation modality input reveals that the convective system is evolving into a narrow, north-south oriented shape. Together, these observations provide supplementary information to the radar modality regarding the movement direction and morphological changes of the convective system.

In Figure 10b, there is a process of an eastward-moving convective system, where the connected radar echo areas gradually increase in size. The predictions of PredRNN and MIM indicate a decrease in the radar echo area, while SmaAt-UNet forecasts radar echo shapes that diverge significantly from the ground truth. Rainformer and Earthformer correctly capture the movement trends of radar echoes, but they exhibit less accuracy in intensity and morphological details compared to the MAFNet. Moreover, from the inputs of both satellite and ground observation modalities, there is a high degree of similarity observed: the strong convective center is slowly moving toward the northeast while its intensity significantly increases. This observation is strongly correlated with the inputs from the radar modality.

In the convective storm nowcast experiments conducted on the RAIN-F dataset with a lead time of 3 h, which exceeds the 1-h lead time on the MeteoNet dataset, slightly lower CSI and HSS scores were obtained. However, in comparative extrapolation experiments across different models, our proposed MAFNet consistently achieved superior performance. This proves the effectiveness of our multimodal asymmetric fusion strategy, which supplements convective information with satellite and ground modalities, integrating them at hierarchical feature levels to enhance REE accuracy.

4.6. Ablation Study Results

In the MAFNet, LCE is utilized to extract modality-relevant, multimodal features from multimodal data, particularly the atmospheric background field information. It supplements the developmental insight into convective systems with perspectives from satellite and ground observations, exploring correlations and complementarities among multimodal information. MAFM asymmetrically integrates multimodal features to fuse radar modality-specific features from the LME branch and modality-relevant, multimodal features from the LCE branch at different levels and scales, thereby alleviating the limitations of single radar-mode information. Therefore, we designed ablation experiments to separately evaluate the effectiveness of LCE and MAFM in extracting multimodal features and asymmetrically fusing features.

The quantitative evaluation results of the ablation experiments are presented in

Table 6. Ablation experiment results on MeteoNet.

Models	CSIτ ↑			HSSτ ↑			$\mathbf{PSNR} \uparrow$	SSIM ↑	MSE ↓
	$\mathbf{\tau }=20$	$\mathbf{\tau }=35$	$\mathbf{\tau }=45$	$\mathbf{\tau }=20$	$\mathbf{\tau }=35$	$\mathbf{\tau }=45$
w/o LCE AND MAFM	0.5682	0.3597	0.1724	0.6342	0.4604	0.2274	28.5617	0.8536	20.976
w/o MAFM	0.5743	0.3613	0.1789	0.6439	0.4741	0.2385	28.8356	0.8584	20.364
MAFNet	0.5819	0.3769	0.1842	0.6521	0.4852	0.2423	29.4568	0.8649	19.854

where ‘τ’ denotes threshold of radar echo intensity. ↑ indicates that higher scores are better, while ↓ indicates that lower scores are better. The best and the second-best scores are respectively denoted by bold and underlined markers.

and

Table 7. Ablation experiment results on RAIN-F.

Models	CSIτ ↑			HSSτ ↑			$\mathbf{PSNR} \uparrow$	SSIM ↑	MSE ↓
	$\mathbf{\tau }=20$	$\mathbf{\tau }=35$	$\mathbf{\tau }=45$	$\mathbf{\tau }=20$	$\mathbf{\tau }=35$	$\mathbf{\tau }=45$
w/o LCE AND MAFM	0.4256	0.3082	0.0973	0.4796	0.3945	0.1364	26.4528	0.7489	24.688
w/o MAFM	0.4281	0.3145	0.1025	0.4827	0.3986	0.1412	26.6511	0.7529	24.125
MAFNet	0.4368	0.3286	0.1116	0.4913	0.4139	0.1492	27.1432	0.7584	23.245

where ‘$\mathrm{\tau }$’ denotes threshold of radar echo intensity. ↑ indicates that higher scores are better, while ↓ indicates that lower scores are better. The best and the second-best scores are respectively denoted by bold and underlined markers.

, while the qualitative assessment results are illustrated in Figure 11. Since LCE and MAFM are sequentially connected network components, with MAFM reliant on LCE, we have designed two variant models (without LCE AND MAFM and MAFM) to separately evaluate the effects of LCE and MAFM. From Table 6, the model without MAFM shows average improvements of 1.76% and 3.13% over the model without LCE AND MAFM on CSI and HSS metrics, respectively. Compared to the model without MAFM, the MAFNet shows average improvements of 2.87% and 1.73% on CSI and HSS scores. In Table 7, the model without MAFM shows an average improvement of 2.66% in CSI and 1.74% in HSS compared to the model without LCE AND MAFM. The MAFNet demonstrates a 5.27% improvement in CSI and a 3.76% improvement in HSS compared to the model without MAFM.

In Figure 11, there are two ablation study cases selected from the MeteoNet dataset and the RAIN-F dataset, respectively. The model without LCE AND MAFM exhibits the poorest predictive performance, which significantly underestimates the echo intensity in its predictions. It also faces insufficient representation of detailed internal features within the echoes, along with positional bias and ambiguity in predictions. The performance of the model without MAFM has shown slight improvement, as it can predict areas of higher echo intensity. However, it still struggles with location inconsistencies between predictions and ground truth. The MAFNet is equipped with both LCE and MAFM, and demonstrates superior performance across all three models. It not only predicts strong echo centers (red areas exceeding 45 dBZ), but also forecasts echo shapes closer to ground truth.

The ablation experiments on LCE and MAFM reveal that LCE extracts convective-related features from multimodal data, uncovering correlations and complementarities among these features. MAFM asymmetrically integrates convective features from different encoders, enhancing the model’s utilization of multimodal convective features and improving REE accuracy.

5. Conclusions

Radar echo extrapolation based on deep learning is emerging as a promising technique for convective nowcasting, demonstrating significant application potential. Previous DL-based methods face challenges such as error introduction during data alignment, and difficulties in feature representation and fusion when integrating spatiotemporally heterogeneous multimodal data. This paper proposes a multimodal asymmetric fusion network for radar echo extrapolation. Our proposed MAFNet employs a global–local encoder architecture to model convective system dynamics from three perspectives: overall convective features, dynamic echo features from radar modality, and top and bottom convective features from satellite and ground observation modalities, thereby leveraging the correlation and complementarity of multimodal data. Notably, DTW-AM provides new insights into non-interpolative data alignment methods by dynamically aligning multimodal data sequences through feature map similarity calculation. Additionally, MAFM is designed to asymmetrically fuse multimodal convective features across various levels and scales, thereby enhancing REE performance. Through comparative and ablation experiments, we have demonstrated that the MAFNet outperforms representative CNN-based, RNN-based, and Transformer-based radar echo extrapolation models on two multimodal meteorological datasets. Furthermore, visualized radar echo extrapolation cases clearly illustrate the superiority of the MAFNet, affirming the enhancement in extrapolation performance achieved through multimodal input and asymmetric fusion strategy.

In future work, we will further investigate the underlying mechanisms by which different modalities improve REE performance, enhance the interpretability of multimodal data studies, explore the role of physical products from different modalities in REE, and incorporate atmospheric physics constraints into model training.