Abstract
This work presents two pre-processing patches to automatically correct the residual local misalignment of datasets acquired by very/extremely high resolution (VHR/EHR) satellite multispectral (MS) scanners, one for, e.g., GeoEye-1 and Pléiades, featuring two separate instruments for MS and panchromatic (Pan) data, the other for WorldView-2/3 featuring three instruments, two of which are visible and near-infra-red (VNIR) MS scanners. The misalignment arises because the two/three instruments onboard GeoEye-1 / WorldView-2 (four onboard WorldView-3) share the same optics and, thus, cannot have parallel optical axes. Consequently, they image the same swath area from different positions along the orbit. Local height changes (hills, buildings, trees, etc.) originate local shifts among corresponding points in the datasets. The latter would be accurately aligned only if the digital elevation surface model were known with sufficient spatial resolution, which is hardly feasible everywhere because of the extremely high resolution, with Pan pixels of less than 0.5 m. The refined co-registration is achieved by injecting the residue of the multivariate linear regression of each scanner towards lowpass-filtered Pan. Experiments with two and three instruments show that an almost perfect alignment is achieved. MS pansharpening is also shown to greatly benefit from the improved alignment. The proposed alignment procedures are real-time, fully automated, and do not require any additional or ancillary information, but rely uniquely on the unimodality of the MS and Pan sensors.
1. Introduction
The ever increasing availability of image data featuring a spectral diversity (visible and near-infra-red (VNIR), short-wave infra-red (SWIR), thermal infra-red (TIR), X-band, C-band and L-band microwave data, also with multiple polarizations) and complementary spectral and spatial resolutions, together with the characteristics of the various imaging modalities, have promoted the study of fusion methodologies tailored to remote-sensing images of the Earth. Fusion aims to produce an added value besides those available from the individual data sets. Although fusion results are often interpreted by humans to solve application-oriented tasks (detection of landslides, floods, and burning events, to mention some examples), semi-supervised and even fully automated systems (e.g., thematic classifiers) benefit from fusion products instead of separate datasets.
Extensive studies on the fusion of remotely sensed images for Earth observation (EO) have been accomplished in recent decades, and a significant number of methods has been developed [1]. Image fusion can be labeled according to several criteria. One is based on sensors’ homogeneity. Homogeneous image fusion means that the images that shall be combined are provided by instruments that exploit the same physical mechanism. This class is also known as unimodal image fusion. The fusion of a multispectral (MS) and a panchromatic (Pan) image is referred to as MS pansharpening, and is a typical unimodal fusion. The images subject to unimodal fusion are results of measurements of solar radiation reflected by the scene, though they may span different wavelengths and exhibit different spatial resolutions. Conversely, the fusion of heterogeneous image data, also known as multimodal fusion, pertains to cases in which the data are captured by instruments that do not share the same physical imaging features.
A further way to discriminate among fusion methods is the content level subject to fusion: (a) pixel level (or area-based), (b) feature level, or (c) decision level [1]. Fusion at the pixel level combines the values of pixels in the images that are merged; the goal is to produce a fused image. Feature-level fusion combines specific descriptors, or features, extracted from the individual images that are to be merged. For the fusion of optical and synthetic aperture radar (SAR) images [2], a direct combination of the two datasets is not recommended, in order to avoid contaminating the fused image with the poor signal-to-noise ratio (SNR) of the SAR data. To do so, features calculated from the SAR images (e.g., texture and spatial heterogeneity [3]) can be implanted into the optical images, thus relaxing the tight co-registration requirements peculiar of pixel-level fusion. Decision-level fusion combines the classification maps obtained from each dataset separately, or from different classification algorithms working on the same dataset. The output of decision-based fusion is a classification map.
Among pixel-based methods, MS pansharpening is an established methodology, and is still receiving an ever increasing attention [1,4], especially after the launch of very high resolution (VHR) and extremely high resolution (EHR) spaceborne imaging systems. Pansharpening benefits from the complementary spatial and spectral resolutions of MS and Pan, due to the physical SNR constraints of broad and narrow bands [5]. The goal of pansharpening is the synthesis of a unique product featuring as many spectral bands as are those the original MS image, each having spatial resolution same as that of the Pan image.
After the interpolated MS bands have been overlapped to the Pan image [6], the first step is to check the co-registration between the datasets. This issue is crucial because pixel-based fusion is generally sensitive to misalignment, feature-based fusion is to a lower extent [7], and decision-based fusion is even less sensitive [8]. Then, the geometric details are extracted from the Pan image and added to the MS bands, following a certain injection model. The first step of detail extraction may follow the spectral criterion, originally referred to as component substitution (CS), or the spatial criterion, relying on separable [9,10] or non-separable [11] multiresolution analysis (MRA). Following the spectral criterion, the detail is given as a difference between the original Pan image and a little-detailed intensity component, generated by a pixel-based combination of interpolated MS bands. According to the spatial criterion, the detail is calculated as the difference between the original Pan image and the Pan image smoothed by a lowpass filter, retaining the same content of spatial frequency as the MS bands. Spectral and spatial methods are complementary concerning their tolerance to spatial and spectral artifacts, respectively [12,13]. In principle, all CS methods are intrinsically shift-tolerant [12], though the same property may be obtained by sophisticated convex optimization techniques [14]. It should be noted that, for multimodal fusion, an intensity component makes no sense and, therefore, cannot be defined [15], and the registration of the datasets that will be merged cannot be implicitly achieved by the fusion itself, and should be carried out otherwise [16].
Before fusion is accomplished, the Pan image is radiometrically transformed by an affine grayscale transformation, such that the lowpass-filtered Pan exhibits mean and variance equal to those of the component that shall be substituted [17]. The detail injection model rules the combination of the latter with the interpolated MS image. The injection model is stated between each resampled MS band and a lowpass version of the Pan image. The multiplicative injection model with haze correction [18,19] is essential for improving the fusion performance by leveraging atmospheric imaging mechanisms [20]. The design of injection models is a key topic for multimodal fusion, where the two dataset are the outcomes of different physical mechanisms, like for thermal sharpening [21].
The basic categorization of CS and MRA has been updated considering other methods that have recently been introduced [4], relying on Bayesian inference [22], total variation (TV) regularization [23], and sparse representations [24]. Recently, machine learning paradigms have been exploited: from the pioneering approach based on convolutional neural networks (CNN) [25], to more sophisticated architectures, such as generative adversarial networks (GAN) [26]. For learning-based methods, histogram matching and detail injection modeling are automatically learned from the training data and implicitly performed by the network. However, GANs are capable of controlling each other and, thus, are invaluable, for example, for multimodal fusion [27].
Here, we present two totally unsupervised procedures for the fine co-registration of interpolated MS bands to Pan image. The former is suitable for systems featuring a unique instrument for all MS bands, e.g., GeoEye-1 and Pléiades, as well as GeoEye-2 (which ceased operations in 2019), IKONOS-2, and QuickBird-2 (both dismissed in 2015). The latter is suitable for the two MS instruments of WorldView-2/3. This occurs because the Pan channel is statistically correlated with the MS channels. The fact that a unimodal fusion, as pansharpening is, was potentially capable of overcoming MS-to-Pan misalignment was recognized several years ago [28]. However, until 2020, no alignment of spectral diversity (color hues) was feasible, only of spatial structures [29]. A previous approach is totally different because it is based on the model of the instrument [30], and works with four MS bands and Pan. Another valuable effort is fully automatic, and works with submetric Pan [31], but requires considerable processing resources. The proposed method is real-time, fully automatic, may be used for any satellite system and, in principle, extended to more than three onboard instruments, e.g., WorldView-3.
The organization of the article is the following. Section 2 investigates the causes of misalignment in VHR and EHR satellite MS scanners, and lays the foundation of the fine alignment procedures, one suitable for most systems, featuring two separate instruments, one for MS and another for Pan, and another suitable for WorldView-2/3, having two separate VNIR scanners. Section 3 presents extensive results on the analysis of residues, correction of shifts, and pansharpening for the GeoEye-1 and WorldView-2 datasets. Section 4 discusses the main issues encountered, and explains the advantages of the alignment procedure. Section 5 suggests possible application scenarios.
2. Materials and Methods
2.1. Materials
Since the pioneering very high resolution (VHR) imager IKONOS-2, launched in 1999, MS scanners onboard satellites have attained submetric resolutions in the VNIR wavelengths of the Pan image. The present generation of WorldView satellites for EO features extremely high resolution (EHR) acquisition capability: up to 1.24 m for MS and 0.31 m for Pan, at nadir. The resolution capability of less than one meter from an orbit of heights greater than 600 km is obtained thanks to extremely cumbersome and heavy optics. Constraints in the system design have motivated the adoption of a unique optics for both the MS and Pan scanners. MS bands have a lower spatial resolution, and are acquired with a somewhat elevated value of the modulation transfer function (MTF) at Nyquist frequency (half the sampling frequency). Conversely, the Pan image, typically having four times greater Nyquist frequency, for an MS-to-Pan scale ratio equal to four, is captured with a lower MTF value at Nyquist, but a higher SNR, thanks to the time-delayed integration (TDI), directly implemented on the charge coupled device (CCD). The on-orbit Pan image, being only a little noisy and practically aliasing-free, is then postprocessed for restoration of the MTF to a value similar to those of the MS bands. An edge-crispening filter, i.e., an all-pass filter plus a high-pass filter, is usually applied during the geocoding process, which includes a resampling. The characteristics of the MTF, with shape of a Chinese hat with broad flaps, produces typical values at Nyquist frequency around 0.3 for the MS channels, and less than 0.1, on orbit, for the Pan. Figure 1 illustrates the laboratory MTF of an MS channel of the Pléiades instrument. Note that the spatial frequency response is squeezed along track due to the motion of the platform [32]. Due to diffraction of the optics, the MTF is slightly shrunk as the wavelength increases. Thus, the spatial resolution is slightly better for the leftmost part of the visible spectrum, corresponding to the violet color [33].
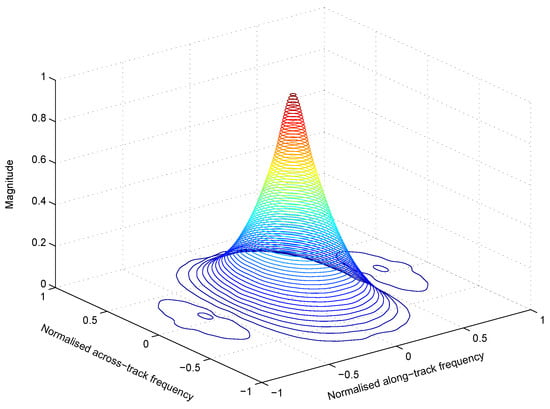
Figure 1.
Laboratory MTF of a spectral channel of the Pléiades instrument.
In parallel to spatial resolution, the number of spectral channels of new-generation MS scanners has been increased to finely cover the VNIR wavelengths. Figure 2 displays the spectral responsivity channels of a typical 4-band MS + Pan system (GeoEye-1) and the nine spectral channels (4 + 4 + Pan) of WorldView-2.
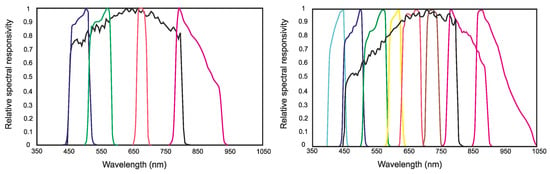
Figure 2.
Spectral responsivity functions of: (left) GeoEye-1, bands: blue, Pan, green, red, NIR. Left to right; (right) WorldView-2, bands coastal, blue, Pan, green, yellow, red edge, NIR1, NIR2, with one MS scanner (MS1) taking the same four bands as GeoEye-1; another MS scanner (MS2) capturing coastal, yellow, red edge and NIR2.
The MS and Pan instruments share the same optics and, hence, a unique focal plane. Thus, they cannot have strictly parallel axes, but have a small angle that is contained in the orbit plane. The consequence is that the instruments scan different areas at the same instant; equivalently, they scan the same area at different times. Thus, moving objects, e.g., vehicles, appear displaced in the MS and in the Pan images. The MS instrument, however, simultaneously captures all of the bands in a bundle under the same perspective. So, the MS bands are rigidly shifted from one another, a misalignment easily corrected before the data are distributed, but not locally warped by an extent depending on the relief of the terrain.
The Pan instrument images the same scene as the MS instrument does, from a different viewpoint along the orbit, which determines a parallax view. In the presence of discontinuities of the ground surface, and of terrain relief in general, the same object is imaged at different positions in the MS and Pan images. Figure 3, left panel, illustrates acquisition of two separate instruments across the swath. The small angle between the axes of the two instruments is magnified along the orbit, for displaying convenience. The across-track angle encompasses the width of the swath captured by the CCD detector.
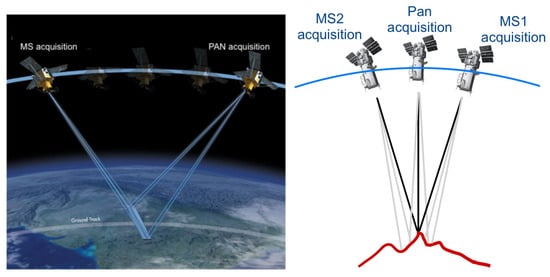
Figure 3.
Acquisition geometries of GeoEye-1 (left) and WorldView-2/3 (right) MS scanning systems. In the former case, there are two separate instruments, one for the four MS bands and another for Pan, whose optical axes are not perfectly parallel. The acquisition of the same scan line orthogonal to the ground track of the platform occurs on different instants; hence, from different points along the orbit, the acquisition angles from the orbit are deliberately exaggerated. In the latter case, the plot is simplified: the optical axis of the one out of three instruments that performs the acquisition from the respective positions along the orbit is shown with a solid dark line.
The displacement of the same point imaged from different viewpoints is referred to as disparity, and depends on the quote of the point. Whereas in computer stereo vision, disparity is exploited to estimate the quote, in order to reset the disparity to align the same point framed in the two images, its ground height must be previously known. This operation, inverse to stereo restitution, is performed by orthorectification, whose goal is to yield an image same as if it were acquired with the zenith satellite position at infinity distance, which can be exactly superimposed onto a chart. Once the MS and Pan images have been orthorectified, perfect overlap is possible with a rigid shift. The precision of orthorectification, however, depends on the accuracy of the digital elevation model (DEM) used for its calculation [34,35,36]. If the spatial sampling of DEM is too coarse with respect to the pixel size, the quote-driven local warping is insufficient, and a residual shift survives. Another possible cause of error is that DEM usually represents the height of the bare soil, and not of possible natural and human-made structures, typically buildings.
Another viable solution for MS and Pan co-registration is the use of a coordinate transformation based on ground control points (GCP), which are points whose positions in the two images are easily detectable with supervised or semi-supervised techniques. This procedure does not require an accurate DEM, but requires a large number of GCPs, especially if the scene is large and the terrain relief is variable. The sensitiveness to operator’s skill is mitigated by the use of semi-supervised techniques [37]. In any case, these procedures are scarcely reproducible, and may be insufficient for the extremely high-resolution characteristics of modern satellite scanning systems.
The situation described before is even more complicated for satellites equipped with more than two instruments, such as the WorldView-2/3 platforms, in which eight MS bands are taken by two separate instruments. In WorldView-2, three instruments are present on the platform: the classical 4-band MS instrument (MS1), and the new MS instrument (MS2) featuring four more bands, partially interleaved with the others. WorldView-3 is also equipped with a short-wave infra-red (SWIR) scanner. Now, the three instruments acquire different areas at the same instant, or equivalently, they scan the same area at different times. Consequently, moving objects and points at different heights in the scene appear not only shifted in the two sets of MS bands towards the Pan images [38], but the two sets of MS bands are also captured at different moments from distinct positions along the orbit; hence, under different viewing perspectives. Figure 3, right panel, illustrates the acquisition geometry of the WorldView-2 platform. For the sake of clarity, the angles between the optical axes have been intentionally exaggerated.
2.2. Methods
Whenever pansharpening is accomplished, co-registration is usually assumed between the datasets. An inaccurate MS-to-Pan overlap may severely impair the quality of the fusion, depending on the adopted class of methods. CS methods damp small shifts and prevent the geometry of the scene from fading [12,39]. Depending on the injection model, there may be a small residual color change, but not in the structures [29,40]. Instead, the class of methods based on MRA is sensitive to spatial mismatches that cause a loss of synchronization of lowpass and highpass spatial frequency components and the consequent fading of sharp edges and structures. The duality of the classes of spectral (CS) and spatial (MRA) pansharpening algorithms makes the latter robust to spectral impairments, i.e., MS and Pan datasets taken from different satellites and/or at different times [13]. This property is invaluable for multiplatform fusion [41]. Generally speaking, the fusion of heterogeneous datasets (multi-modal fusion), such as thermal and optical datasets, cannot be approached as a problem of CS [21].
For a unimodal fusion, as pansharpening is, a multivariate linear regression between lowpass-filtered Pan, , and interpolated MS bands, , in which the phase of the linear interpolating kernel should match the acquisition geometry to avoid introducing systematic shifts [6], has been used to model the spectral and spatial relationships between the channels of the two instruments [42]:
in which is the kth MS band interpolated to the size of Pan, is the LS intensity component, and the space-varying residue. The set of LS weights, , is calculated as the LS solution of Equation (1). A measure of the matching success in Equation (1) is provided by the coefficient of determination, , defined as
in which and indicate the variance of LS residue and of lowpass-filtered Pan image, respectively.
2.2.1. Alignment of GeoEye-1 Data (4-Bands + Pan)
In the seminal article on the spatial properties of MS pansharpening methods [12], the shift-tolerance of CS methods has been mathematically proven. However, no idea was presented of how to exploit these properties in contexts other than those of fusion. It was also unclear how to extend the shift-invariance to the spectral component (color hues), and not only to the spatial structures. In a subsequent short paper [28], the properties of CS methods were analyzed in depth. It was found that the spatial detail injected by CS methods has a lowpass component that has the effect of aligning the expanded MS bands over the Pan image and a highpass component that provides the actual sharpening. In MRA methods, the lowpass component, and hence the alignment, are missing. If the CS method features an intensity component, like that defined in Equation (1), the lowpass component is exactly given by the LS residue, which can be calculated as difference between and . The problem was finding an injection model suitable for the shift of both structures and colors. The multiplicative injection model, derived from the transfer model of solar radiation through the atmosphere [20], was first proposed in [29].
With the aim of correcting the interpolated MS bands, we used the space-varying multiplicative gain [43], instead of the projection-based injection gain used in [40], to drive the injection of the residue, , into the interpolated MS bands:
in which is the corrected that overlaps onto . Equation (3) highlights that the injection of the residue, , multiplied by the multiplicative gain, i.e., the ratio , into the resampled MS band is equal to its multiplication by .
2.2.2. Alignment of WorldView-2/3 Data (4 + 4 + Pan)
Though never explicitly addressed, the set of MS bands in Equation (1) are implicitly supposed to be aligned to each other. This condition was satisfied until the first satellite of the WorldView MS scanner generation was successfully launched in 2009 [44]. Whenever WorldView-2/3 data are concerned (WorldView-4, which is no longer operational since 2019, featured a unique MS instrument), the geometry of the view allows for the eight spectral bands to be imaged from two different positions along the orbit, both different from Pan, as shown in Figure 3. The lack of an accurate digital surface model (DSM) can cause local shifts between the old bands (blue (B), green (G), red (R), and near-infra-red 1 (NIR1)), and the four bands imaged by the new MS instrument, coastal (C), i.e., violet, yellow (Y), red-edge (RE), and outermost NIR, namely, NIR2. The presence of desynchronization among the components of Equation (1) is expected to locally increase their mismatch with the lowpass Pan.
The problem can be solved by considering the eight MS bands of WorldView-2/3 as produced by two separate instruments, and by splitting Equation (1) between the datasets while, in principle, Equation (1) might be written for all eight bands together. Let and denote the subscripts of the bands of the old and new MS scanners, respectively. Based on the sequence of the bands arranged by ascending wavelength, and . Equation (1) can be divided into
in which , including the offsets and , are the LS space-constant spectral weights, and and are the space-varying residues of the matching of old and new instruments towards the unique Pan.
In the case of two separate MS instruments, the correction in Equation (3) is split across MS1 and MS2 and the residues in Equation (4), either or , are injected into the interpolated MS bands of the old and new MS scanners, respectively:
in which and is the corrected version of overlapped onto . Equation (5) states that the residue of each scanner, , should be multiplied by the ratio before being injected into the interpolated MS band. This equals the multiplication of by the ratio .
3. Experimental Results
3.1. GeoEye-1 Dataset
A GeoEye-1 image has been acquired over the area of Trenton NJ, USA, on 27 September 2019. The on-orbit limit sampling interval at nadir (half the system resolution) is 1.64 m for MS and 0.41 m for Pan. The spatial sampling interval (SSI) of the resampled geocoded product is 2 m for MS and 0.5 m for Pan; thus, the scale ratio is equal to four. The MS image comprises four bands: blue (B), green (G), red (R), and near-infra-red (NIR). The test image size is 512 × 512 pixels for MS, and 2048 × 2048 for Pan. The radiometric resolution of the packed DN format is 11 bits; the conversion coefficients to top-of-atmosphere (TOA) spectral radiance have been extracted from the metadata. The Pan image and a true color composition of the MS bands (B3, B2, B1) are displayed in Figure 4.

Figure 4.
512 × 512 portion of test GeoEye-1 image at 0.5 m: (a) Pan; (b) interpolated MS B3-B2-B1 (true color).
Figure 5 presents the residue of the multivariate regression of the four MS bands towards the lowpass-filtered Pan, both before and after the four bands have been corrected, as in Equation (3). The residue is mostly concentrated on the top of buildings, whose height is presumably unspecified in the available DEM used for the geometric corrections. After correction, the coefficient of determination of the multivariate regression increases from to .

Figure 5.
Residue of multivariate regression to lowpass-filtered Pan of: (a) resampled MS bands, ; (b) corrected MS bands, .
Once the MS bands have been overlapped over the Pan image, simulations of MS pansharpening have been carried out. The goal is to check possible benefits of the alignment for the main class of MRA or spatial methods. From Ref. [12], CS (or spectral) methods are known to be insensitive to spatial impairments of the data. The popular and performing fusion methods that are compared are:
- Gram–Schmidt with spectral adaptivity (GSA) [42], perhaps the most popular among CS methods;
- Brovey transform with haze correction (BT-H) [17], an optimized version of the popular Brovey transform CS method;
- Adaptive wavelet luminance proportional with haze correction (AWLP-H) [45], an optimized version of a popular MRA method;
- Modulation transfer function generalized Laplacian pyramid with full scale (MTF-GLP-FS) injection gains [46], an optimized version of an MRA method based on GLP.
Implementations of pansharpening methods have been taken from the Pansharpening Toolbox.
The results of the fusion of the original (uncorrected) dataset are depicted in Figure 6. What immediately stands out is that, due to the presence of MS-to-Pan shifts on the top of buildings, the two CS methods yield clearer and sharper images than those of the two MRA methods, which are known to be unable to compensate for local misalignment. Instead, once the data have been corrected following Equation (3), the fused images are almost identical to one another. Figure 7 highlights that the two MRA methods recover their top performance, which had been diminished by local shifts.

Figure 6.
Visual results of fusion without correction for MS-to-Pan alignment: (a) BT-H without alignment; (b) GSA without alignment; (c) AWLP-H without alignment; (d) MTF-GLP-FS without alignment.

Figure 7.
Visual results of fusion with correction for MS-to-Pan alignment: (a) BT-H with alignment; (b) GSA with alignment; (c) AWLP-H with alignment; (d) MTF-GLP-FS with alignment.
To provide a deeper understanding of the nature of fusion, Table 1 and Table 2 report the values of established full-scale quality indexes [47] on the fused datasets. Full-scale quality assessment means that there is no reference, as in reduced resolution assessment [48], and quality measurement is brought back to the fulfillment of the two consistencies between the fused image and the original MS and Pan, respectively [49]. In fact, it has recently been noted that full-scale quality indexes may be sensitive to shifts in the original datasets [50]. Spatial consistency is crucial in the presence of misalignment [51], depending on the class of methods, either CS or MRA. When the MS bands are overlapped over Pan, they become the new starting point for fusion, but also for carrying out the consistency checks. Therefore, for uncorrected data, the quality reference is provided by the original MS bands that are fused; for corrected data, the new MS bands overlapped to Pan are implicitly the quality assessment reference.

Table 1.
GE-1 Trenton: full scale quality indexes without alignment for fusion/assessment.

Table 2.
GE-1 Trenton: full scale quality indexes with alignment for fusion/assessment.
The entry labeled as EXP denotes the absence of injected details. In the case of no alignment, the original data are simply resampled with bicubic interpolation. In the case of realignment, the corrected data are generated at the spatial scale of Pan, and resampling is implicit in the correction procedure. The values of the quality indexes for the fusion of uncorrected data in Table 1 reveal that all CS methods are poorer than the MRA methods, despite the fact that the visual appearance is exactly the opposite. The fusion of corrected MS data with the latter as a reference of consistency turns the situation upside down: all methods, except EXP, are pretty comparable to each other, with AWLP-H being slightly better, according to all indexes. The explanation of this is very simple. If CS methods force the fused image to overlap over Pan, they shift the fused image from the original MS, which is the reference for spectral consistency. Hence, the latter becomes poorer. Instead, with the automatic pre-alignment, both CS and MRA methods do not change the alignment of the data, which is the same as the alignment of the data that are fused. Therefore, consistency measurements are not altered, because all MS data (initial, fused, and reference) are aligned. Eventually, we cannot help noting that the index QNR, dating back to 2008, is moderately sensitive to shifts, and has the asset of recognizing AWLP-H as the best method, but also, the drawback is that the perfect spectral consistency of EXP conceals its poor spatial consistency; hence, EXP is always the best fusion method, which is puzzling. We wish to recall that each index is normalized in [0,1], but in such an interval, the mapping of scales is nonlinear. The indexes are suitable for relatively ranking methods, rather than for providing an absolute quality measure.
3.2. WorldView-2 Dataset
A WorldView-2 image was acquired on the area of Sydney, Australia, on 21 August 2012. The spatial sampling interval (SSI) is 2 m for MS and 0.5 m for Pan. The area is 2048 × 2048 Pan and 512 × 512 MS. Both MS and Pan have been orthonormalized using a DEM available at 10 m. Figure 8 shows the 0.5 m Pan, the true color composition of the bicubically interpolated bands acquired by the MS1 instrument, and the false color composition of the interpolated MS2 bands. The three icons display the data captured by each of the three instruments in Figure 3. There is no misalignment of bands within the same bitmap, corresponding to a unique instrument, but there is misregistration between bands taken by different instruments. The roofs of the buildings are framed with slightly different perspectives, partially corrected during cartographic resampling.

Figure 8.
512 × 512 portion of test WorldView-2 image at 0.5 m: (a) Pan; (b) interpolated B5-B3-B2 (true color); (c) interpolated B6-B4-B1 (false color). Each image displayed is taken by a unique instrument without combining the spectral bands of different scanners.
Figure 9 shows the map of the LS residue of the multivariate regression of MS to lowpass-filtered Pan and the related values of matching success, given by , defined in Equation (2). The residue is mostly concentrated in built-up structures, for which the DEM used for the orthonormalization was not of adequate spatial resolution. What immediately stands out, however, is the presence of moving vehicles along the main road, whose motion can be detected by looking at Figure 8. The variance of the zero-mean residue is large for the match of MS2, and slightly lower for MS1, which better encompasses Pan, while the outermost bands of MS2 lie outside the bandwidth of Pan. If regression is carried out on the corrected bands of Equation (3), the residue almost vanishes: more for MS1 only, less for MS2 only, due to the different layouts of the bands of the two instruments. Using the eight corrected bands in Equation (5), the regression achieves a value of of 0.99999. Few non-zero residues, due to interpolation errors of moving cars, appear on the road.

Figure 9.
Residue of multivariate regression to lowpass-filtered Pan of: (a) the four bands of MS1, ; (b) the four bands of MS2, ; (c) the eight bands together (MS1 + MS2), ; (d) the corrected bands of MS1, ; (e) the corrected bands of MS2, ; (f) MS1+MS2 after correction, . All residue maps have been linearly stretched by the same factor for displaying convenience.
The fusion results of BT-H [43] are presented for the original MS data and the MS data corrected for misalignment of the MS instruments. Figure 10 shows two color compositions of the uncorrected and corrected MS data where all eight bands have been fused together. When the fused data are displayed in true color, only data from MS1 are displayed and the shift towards Pan is almost completely absorbed by BT-H (a CS method), analogously to what happened in [29]. The effect of the correction is hardly perceivable in the magnified detail of the car. When the bands displayed are taken from both instruments, the intersensor shift is not completely canceled by the unique residue calculated on all eight bands. The surviving misalignment is visible in the magnified box as a desynchronization of the color hues of the car. After applying the correction in Equation (3), the alignment is recovered. The problem originating with the presence of two separate MS scanners imaging from different parallaxes is that the alignment of MS over Pan cannot be implicitly recovered by CS pansharpening methods, as it happens with only two onboard instruments.

Figure 10.
Fusion results of a CS method (BT-H): (a) B5-B3-B2 composition without alignment; (b) B5-B3-B2 with alignment; (c) B6-B3-B1 without alignment; (d) B6-B3-B1 with alignment.
The comparison of the four methods in Section 3.1 on the detail of the main road with moving vehicles is reported in Figure 11, Figure 12, Figure 13 and Figure 14. Without correction, MRA is far poorer than CS on moving cars. With the full correction (see Equation (5)), all methods perform well. In the challenging case of inter-instrument color composition, the bleeding of colors is restrained. According to the proof stated in [12], only shifts of moderate extents can be recovered. The high speed of cars on the main road originates shifts of MS towards Pan of extent up to five-six pixels at the scale of Pan. Such a shift cannot be well approximated by the first-order development of the mathematical function representing the moving vehicle.

Figure 11.
Visual results of BT-H fusion with and without correction for MS-to-Pan alignment: (a) 5-3-2 composition (R-G-B true color captured by MS1) without alignment; (b) 6-4-1 composition (RE-Y-C false color captured by MS2) without alignment; (c) 6-3-1 composition (RE-G-C false color captured by MS1 and MS2 together) without alignment; (d) 5-3-2 composition (R-G-B true color captured by MS1) with alignment; (e) 6-4-1 composition (RE-Y-C false color captured by MS2) with alignment; (f) 6-3-1 composition (RE-G-C false color captured by MS1 and MS2 together) with alignment.

Figure 12.
Visual results of GSA fusion with and without correction for MS-to-Pan alignment: (a) 5-3-2 composition (R-G-B true color captured by MS1) without alignment; (b) 6-4-1 composition (RE-Y-C false color captured by MS2) without alignment; (c) 6-3-1 composition (RE-G-C false color captured by MS1 and MS2 together) without alignment; (d) 5-3-2 composition (R-G-B true color captured by MS1) with alignment; (e) 6-4-1 composition (RE-Y-C false color captured by MS2) with alignment; (f) 6-3-1 composition (RE-G-C false color captured by MS1 and MS2 together) with alignment.

Figure 13.
Visual results of AWLP-H fusion with and without correction for MS-to-Pan alignment: (a) 5-3-2 composition (R-G-B true color captured by MS1) without alignment; (b) 6-4-1 composition (RE-Y-C false color captured by MS2) without alignment; (c) 6-3-1 composition (RE-G-C false color captured by MS1 and MS2 together) without alignment; (d) 5-3-2 composition (R-G-B true color captured by MS1) with alignment; (e) 6-4-1 composition (RE-Y-C false color captured by MS2) with alignment; (f) 6-3-1 composition (RE-G-C false color captured by MS1 and MS2 together) with alignment.

Figure 14.
Visual results of MTF-GLP-FS fusion with and without correction for MS-to-Pan alignment: (a) 5-3-2 composition (R-G-B true color captured by MS1) without alignment; (b) 6-4-1 composition (RE-Y-C false color captured by MS2) without alignment; (c) 6-3-1 composition (RE-G-C false color captured by MS1 and MS2 together) without alignment; (d) 5-3-2 composition (R-G-B true color captured by MS1) with alignment; (e) 6-4-1 composition (RE-Y-C false color captured by MS2) with alignment; (f) 6-3-1 composition (RE-G-C false color captured by MS1 and MS2 together) with alignment.
4. Discussion
After presenting the results on the two datasets of two different instruments, in which the acquisition geometry is progressively complicated by the presence of two and then three separate instruments, a series of considerations can be made. For scanners with decametric resolution, e.g., Sentinel-2 and the operational land imager (OLI), the problem of misalignment does not exist, either with a unique instrument capturing all the MS bands (Sentinel-2) or also with three separate instruments (OLI), because the pixel size, SSI, is comparable with the spatial scale at which the DEM is generally available (10 m). If the scale of DEM is 10 m, and the scale of Pan is less than 1 m, it becomes impossible to correct the parallaxes with sufficient accuracy. In the presence of discontinuities of the ground surface, the registration error turns out to be a fraction of the scale of DEM, say 25%, with an optimistic view. Thus, a misalignment of up to three pixels of Pan is produced, spread over the height discontinuities of the surface. This problem has been recognized since full-scale quality assessments have become widespread. With fusion and assessment performed on spatially degraded data, typically by a factor of four, all pixel shifts are divided by four and do not produce appreciable misalignment effects. This is the reason why the proposed approach regards datasets that are at least VHR, corresponding to 1 m Pan.
Once the resampled MS bands have been automatically and accurately overlaid onto the Pan image, established MRA pansharpening algorithms recover their original top performance, which had been diminished in the passage from HR to VHR and EHR datasets. Performance is intended both in the visual sense and also according to widespread statistical quality indexes based on consistency measurements of fusion products towards unfused MS and Pan. In other words, the same resampled MS bands corrected for shift compensation should be used as input to the fusion and quality assessment procedures.
According to the theoretical development reported in [12], the proposed pre-processing patches are intrinsically capable of removing possible aliasing artifacts, originated by insufficient sampling step size, from the resampled MS bands, provided that the Pan image is aliasing-free. This is true because the Pan image is taken by sampling the same MTF in Figure 1 with a step size four times greater.
It should be noted that preprocessing patches are independent of the measure unit of the data, e.g., top of atmosphere (TOA) spectral radiance, TOA reflectance, surface reflectance, in floating-point or packed fixed-point formats, due to multivariate regression, whose degree of matching, namely , does not change with the data units or formats [52]. In other words, the dataset are correctly realigned, whichever is their initial format, and the corrected datasets retain their original formats.
The proposed method does not require either training datasets or ancillary data (DEM, GCP, etc.), and may work on a unique MS + Pan image. Last but not least, its computational complexity is quite moderate, comparable to that of pansharpening methods that exploit multivariate regression, such as GSA [42] and BT-H [17].
We wish to note that this is a tool to improve the usability of MS and Pan datasets for a variety of possible applications. The datasets are provided by the distributor in a geocoded format. The geo-localization accuracy is stated to be 3 m for GeoEye-1 (the same as for WorldView-2), and is obtained using “a GPS receiver, a gyroscope and a star tracker, without any GCP (Ground Control Points)”. Since an error of 3 m (six Pan pixels!) is too large for crucial tasks, like MS pan-sharpening, we devised a procedure for the fine co-registration of the MS and Pan datasets. We wish to stress the fact that the data have been already co-registered by the provider by using a digital elevation model (DEM) and the geo-localization accuracy measured, e.g., by means of a GPS receiver, is 3 m for both MS and Pan. Unfortunately, a DEM may not contain buildings, or trees, on the top of which most of shifts are concentrated. So, unless a high spatial resolution digital surface model (DSM) calculated via laser scanners is available, as happens for the skyscrapers of the down-towns of most cities, local shifts due to uncompensated parallaxes are unavoidable. In order check whether the procedure is capable of compensating shifts of 3 m, we used information of moving cars, whose shifts can be measured with a certain accuracy. We are not concerned about measuring or improving the geo-localization accuracy, but we want to have interpolated MS and Pan that overlap everywhere as much as possible, because the performance of fusion depends on that.
5. Conclusions
The study has presented a simple idea that has lead to two fully automated real-time procedures. One for the fine co-registration of MS and Pan datasets produced by systems featuring two separate onboard instruments, like GeoEye-1 and Pléiades, among systems that are currently operative. Another, for the MS1, MS2 and Pan datasets produced by the three instruments onboard WorldView-2/3. The key point to detect and correct shifts is the space-varying residue of the multivariate linear regressions between the interpolated MS bands and the lowpass-filtered Pan. Simulations performed on a 4-band GeoEye-1 image and an 8-band WorldView-2 image, both having 2 m MS and 50 cm Pan, show that local shifts up to at least 2 m are compensated, both in geometry and in colors.
The proposed strategy relies on the unimodality of MS and Pan instruments, thanks to which the lowpass filtered Pan image can be synthesized as weighted combination of the four interpolated MS bands of each MS scanner, if there is more than one. The spatial residue of the multivariate regression locally measures the misalignment between the intensity component of the MS bands captured by one instrument and the lowpass-filtered Pan. If such a residue is weighted by the pixel ratio of the interpolated MS band to the synthetic intensity and injected into the interpolated MS band, the latter is aligned to the Pan image, in terms of both spatial structures and color hues. In practice, the correction consists of pixel-by-pixel multiplying the interpolated MS band by the ratio of lowpass-filtered Pan and synthetic LS intensity component.
As a possible development, the effects of haze correction, beneficial for pansharpening [19,43,53], are worth investigating. Specifically, the correction of atmospheric path radiance should be applied to the multiplicative injection gain by which the residue is modulated before being injected to correct the shift of the current MS band.
The proposed automatic fine co-registration procedure can be extended to a fourth onboard instrument: the SWIR MS scanner mounted on WorldView-3. The residue-based alignment procedure might in principle be utilized to finely co-register hyperspectral (HS) and Pan; in addition to fusion, this issue is also relevant for a spectral unmixing that is driven by Pan [54].
As a final remark, it would be intriguing to investigate the behaviors of fusion methods based on learning, when they are trained on correctly aligned MS and Pan data. In fact, there are methods that are capable of learning and compensating for small misalignments [55,56], as happens to all CS methods that operate without learning, but nobody has ever checked the improvements in learning carried out on perfectly aligned MS and Pan datasets.
Author Contributions
Conceptualization and methodology: L.A. and A.G.; validation and software: A.A.; data curation: A.A. and A.G.; writing: L.A. and A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The image datasets analyzed in this study can be found here: https://resources.maxar.com/product-samples/pansharpening-benchmark-dataset/ (subject to authorization by Maxar, accessed on 10 September 2024) and https://eoiam-idp.eo.esa.int/ (subject to authorization by ESA, accessed on 10 September 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Remote Sensing Image Fusion; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Iervolino, P.; Guida, R.; Riccio, D.; Rea, R. A novel multispectral, panchromatic and SAR data fusion for land classification. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2019, 12, 3966–3979. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S. Information-theoretic heterogeneity measurement for SAR imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 619–624. [Google Scholar] [CrossRef]
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Restaino, R.; Scarpa, G.; Ulfarsson, M.O.; Alparone, L.; Chanussot, J. A new benchmark based on recent advances in multispectral pansharpening: Revisiting pansharpening with classical and emerging pansharpening methods. IEEE Geosci. Remote Sens. Mag. 2021, 9, 53–81. [Google Scholar] [CrossRef]
- Thomas, C.; Ranchin, T.; Wald, L.; Chanussot, J. Synthesis of multispectral images to high spatial resolution: A critical review of fusion methods based on remote sensing physics. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1301–1312. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M.; Alparone, L. Bi-cubic interpolation for shift-free pan-sharpening. ISPRS J. Photogramm. Remote Sens. 2013, 86, 65–76. [Google Scholar] [CrossRef]
- Alparone, L.; Garzelli, A.; Zoppetti, C. Fusion of VNIR optical and C-band polarimetric SAR satellite data for accurate detection of temporal changes in vegetated areas. Remote Sens. 2023, 15, 638. [Google Scholar] [CrossRef]
- D’Elia, C.; Ruscino, S.; Abbate, M.; Aiazzi, B.; Baronti, S.; Alparone, L. SAR image classification through information-theoretic textural features, MRF segmentation, and object-oriented learning vector quantization. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 1116–1126. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Argenti, F.; Baronti, S. Wavelet and pyramid techniques for multisensor data fusion: A performance comparison varying with scale ratios. In Image and Signal Processing for Remote Sensing V; Serpico, S.B., Ed.; SPIE: Bellingham, WA, USA, 1999; Volume 3871, pp. 251–262. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. Advantages of Laplacian pyramids over ”à trous” wavelet transforms for pansharpening of multispectral images. In Image and Signal Processing for Remote Sensing XVIII; Bruzzone, L., Ed.; SPIE: Bellingham, WA, USA, 2012; Volume 8537, pp. 12–21. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Alparone, L.; Baronti, S. Multiresolution fusion of multispectral and panchromatic images through the curvelet transform. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seoul, Republic of Korea, 25–29 July 2005; pp. 2838–2841. [Google Scholar] [CrossRef]
- Baronti, S.; Aiazzi, B.; Selva, M.; Garzelli, A.; Alparone, L. A theoretical analysis of the effects of aliasing and misregistration on pansharpened imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 446–453. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R.; Garzelli, A.; Santurri, L. Sensitivity of pansharpening methods to temporal and instrumental changes between multispectral and panchromatic data sets. IEEE Trans. Geosci. Remote Sens. 2017, 55, 308–319. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Liu, W.; Huang, J. SIRF: Simultaneous satellite image registration and fusion in a unified framework. IEEE Trans. Image Process. 2015, 24, 4213–4224. [Google Scholar] [CrossRef]
- Santarelli, C.; Carfagni, M.; Alparone, L.; Arienzo, A.; Argenti, F. Multimodal fusion of tomographic sequences of medical images: MRE spatially enhanced by MRI. Comput. Meth. Progr. Biomed. 2022, 223, 106964. [Google Scholar] [CrossRef] [PubMed]
- Uss, M.L.; Vozel, B.; Lukin, V.V.; Chehdi, K. Multimodal remote sensing image registration with accuracy estimation at local and global scales. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6587–6605. [Google Scholar] [CrossRef]
- Alparone, L.; Garzelli, A.; Vivone, G. Intersensor statistical matching for pansharpening: Theoretical issues and practical solutions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4682–4695. [Google Scholar] [CrossRef]
- Li, H.; Jing, L. Improvement of a pansharpening method taking into account haze. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2017, 10, 5039–5055. [Google Scholar] [CrossRef]
- Lolli, S.; Alparone, L.; Garzelli, A.; Vivone, G. Haze correction for contrast-based multispectral pansharpening. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2255–2259. [Google Scholar] [CrossRef]
- Pacifici, F.; Longbotham, N.; Emery, W.J. The importance of physical quantities for the analysis of multitemporal and multiangular optical very high spatial resolution images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6241–6256. [Google Scholar] [CrossRef]
- Addesso, P.; Longo, M.; Restaino, R.; Vivone, G. Sequential Bayesian methods for resolution enhancement of TIR image sequences. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 233–243. [Google Scholar] [CrossRef]
- Fasbender, D.; Radoux, J.; Bogaert, P. Bayesian data fusion for adaptable image pansharpening. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1847–1857. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. A new pansharpening algorithm based on total variation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 318–322. [Google Scholar] [CrossRef]
- Vicinanza, M.R.; Restaino, R.; Vivone, G.; Dalla Mura, M.; Chanussot, J. A pansharpening method based on the sparse representation of injected details. IEEE Geosci. Remote Sens. Lett. 2015, 12, 180–184. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Ma, J.; Yu, W.; Chen, C.; Liang, P.; Guo, X.; Jiang, J. Pan-GAN: An unsupervised pan-sharpening method for remote sensing image fusion. Inform. Fusion 2020, 62, 110–120. [Google Scholar] [CrossRef]
- Ma, J.; Yu, W.; Liang, P.; Li, C.; Jiang, J. FusionGAN: A generative adversarial network for infrared and visible image fusion. Inform. Fusion 2019, 48, 11–26. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Arienzo, A.; Baronti, S.; Garzelli, A.; Santurri, L. Deployment of pansharpening for correction of local misalignments between MS and Pan. In Image and Signal Processing for Remote Sensing XXIV; Bruzzone, L., Bovolo, F., Eds.; SPIE: Bellingham, WA, USA, 2018; Volume 10789. [Google Scholar] [CrossRef]
- Arienzo, A.; Alparone, L.; Aiazzi, B.; Garzelli, A. Automatic fine alignment of multispectral and panchromatic images. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Waikoloa, HI, USA, 26 September–2 October 2020; pp. 228–231. [Google Scholar] [CrossRef]
- Lee, C.; Oh, J. Rigorous co-registration of KOMPSAT-3 multispectral and panchromatic images for pan-sharpening image fusion. Sensors 2020, 20, 2100. [Google Scholar] [CrossRef]
- Xie, G.; Wang, M.; Zhang, Z.; Xiang, S.; He, L. Near real-time automatic sub-pixel registration of panchromatic and multispectral images for pan-sharpening. Remote Sens. 2021, 13, 3674. [Google Scholar] [CrossRef]
- Aiazzi, B.; Selva, M.; Arienzo, A.; Baronti, S. Influence of the system MTF on the on-board lossless compression of hyperspectral raw data. Remote Sens. 2019, 11, 791. [Google Scholar] [CrossRef]
- Coppo, P.; Chiarantini, L.; Alparone, L. End-to-end image simulator for optical imaging systems: Equations and simulation examples. Adv. Opt. Technol. 2013, 2013, 295950. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Aguera, F.; Aguilar, F.J.; Carvajal, F. Geometric accuracy assessment of the orthorectification process from very high resolution satellite imagery for Common Agricultural Policy purposes. Int. J. Remote Sens. 2008, 29, 7181–7197. [Google Scholar] [CrossRef]
- Shepherd, J.D.; Dymond, J.R.; Gillingham, S.; Bunting, P. Accurate registration of optical satellite imagery with elevation models for topographic correction. Remote Sens. Lett. 2014, 5, 637–641. [Google Scholar] [CrossRef]
- Xin, X.; Liu, B.; Di, K.; Jia, M.; Oberst, J. High-precision co-registration of orbiter imagery and digital elevation model constrained by both geometric and photometric information. ISPRS J. Photogramm. Remote Sens. 2018, 144, 28–37. [Google Scholar] [CrossRef]
- Le Moigne, J.; Netanyahu, N.S.; Eastman, R.D. (Eds.) Image Registration for Remote Sensing; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Kääb, A.; Léprince, S. Motion detection using near-simultaneous satellite acquisitions. Remote Sens. Environ. 2014, 154, 164–179. [Google Scholar] [CrossRef]
- Jing, L.; Cheng, Q. An image fusion method for misaligned panchromatic and multispectral data. Int. J. Remote Sens. 2011, 32, 1125–1137. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Garzelli, A.; Santurri, L. Blind correction of local misalignments between multispectral and panchromatic images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1625–1629. [Google Scholar] [CrossRef]
- Restaino, R.; Vivone, G.; Addesso, P.; Chanussot, J. Hyperspectral sharpening approaches using satellite multiplatform data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 578–596. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS+Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Garzelli, A.; Aiazzi, B.; Alparone, L.; Lolli, S.; Vivone, G. Multispectral pansharpening with radiative transfer-based detail-injection modeling for preserving changes in vegetation cover. Remote Sens. 2018, 10, 1308. [Google Scholar] [CrossRef]
- Updike, T.; Comp, C. Radiometric Use of WorldView-2 Imagery; Technical report; DigitalGlobe: Longmont, CO, USA, 2010. [Google Scholar]
- Vivone, G.; Alparone, L.; Garzelli, A.; Lolli, S. Fast reproducible pansharpening based on instrument and acquisition modeling: AWLP revisited. Remote Sens. 2019, 11, 2315. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. Full scale regression-based injection coefficients for panchromatic sharpening. IEEE Trans. Image Process. 2018, 27, 3418–3431. [Google Scholar] [CrossRef]
- Arienzo, A.; Vivone, G.; Garzelli, A.; Alparone, L.; Chanussot, J. Full-resolution quality assessment of pansharpening: Theoretical and hands-on approaches. IEEE Geosci. Remote Sens. Mag. 2022, 10, 2–35. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R. Assessment of pyramid-based multisensor image data fusion. In Image and Signal Processing for Remote Sensing IV; Serpico, S.B., Ed.; SPIE: Bellingham, WA, USA, 1998; Volume 3500, pp. 237–248. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O.; Benediktsson, J.A. Quantitative quality evaluation of pansharpened imagery: Consistency versus synthesis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1247–1259. [Google Scholar] [CrossRef]
- Alparone, L.; Garzelli, A.; Lolli, S.; Zoppetti, C. Full-scale assessment of pansharpening: Why literature indexes may give contradictory results and how to avoid such an inconvenience. In Image and Signal Processing for Remote Sensing XXIX; Bruzzone, L., Bovolo, F., Eds.; SPIE: Bellingham, WA, USA, 2023; Volume 12733, p. 1273302. [Google Scholar] [CrossRef]
- Alparone, L.; Garzelli, A.; Vivone, G. Spatial consistency for full-scale assessment of pansharpening. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 5132–5134. [Google Scholar] [CrossRef]
- Arienzo, A.; Aiazzi, B.; Alparone, L.; Garzelli, A. Reproducibility of pansharpening methods and quality indexes versus data formats. Remote Sens. 2021, 13, 4399. [Google Scholar] [CrossRef]
- Arienzo, A.; Alparone, L.; Garzelli, A.; Lolli, S. Advantages of nonlinear intensity components for contrast-based multispectral pansharpening. Remote Sens. 2022, 14, 3301. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, Y.; Jia, J.; Shu, M.W.R.; Wang, J. The effects of misregistration between hyperspectral and panchromatic images on linear spectral unmixing. Int. J. Remote Sens. 2020, 41, 8862–8889. [Google Scholar] [CrossRef]
- Seo, S.; Choi, J.S.; Lee, J.; Kim, H.H.; Seo, D.; Jeong, J.; Kim, M. UPSNet: Unsupervised pan-sharpening network with registration learning between panchromatic and multi-spectral images. IEEE Access 2020, 8, 201199–201217. [Google Scholar] [CrossRef]
- Kim, H.H.; Kim, M. Deep spectral blending network for color bleeding reduction in PAN-sharpening images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5403814. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).