Abstract
Off-grid issues and high computational complexity are two major challenges faced by sparse Bayesian learning (SBL)-based compressive sensing (CS) algorithms used for random frequency pulse interval agile (RFPA) radar. Therefore, this paper proposes an off-grid CS algorithm for RFPA radar based on Root-SBL to address these issues. To effectively cope with off-grid issues, this paper derives a root-solving formula inspired by the Root-SBL algorithm for velocity parameters applicable to RFPA radar, thus enabling the proposed algorithm to directly solve the velocity parameters of targets during the fine search stage. Meanwhile, to ensure computational feasibility, the proposed algorithm utilizes a simple single-level hierarchical prior distribution model and employs the derived root-solving formula to avoid the refinement of velocity grids. Moreover, during the fine search stage, the proposed algorithm combines the fixed-point strategy with the Expectation-Maximization algorithm to update the hyperparameters, further reducing computational complexity. In terms of implementation, the proposed algorithm updates hyperparameters based on the single-level prior distribution to approximate values for the range and velocity parameters during the coarse search stage. Subsequently, in the fine search stage, the proposed algorithm performs a grid search only in the range dimension and uses the derived root-solving formula to directly solve for the target velocity parameters. Simulation results demonstrate that the proposed algorithm maintains low computational complexity while exhibiting stable performance for parameter estimation in various multi-target off-grid scenarios.
1. Introduction
Radar, as an active remote sensing device, is an electronic system that utilizes radio waves to detect the locations of targets and measure their ranges and velocities. In the increasingly complex electromagnetic environment, the use of new technologies and novel systems to enhance radar detection and electronic counter-countermeasure (ECCM) performance has become a critical topic [1]. Random frequency pulse repetition interval agile (RFPA) radar, as a new type of radar system, features each pulse having a randomly agile carrier frequency distributed across a given frequency band and a pulse repetition interval (PRI) that varies within a jitter range based on a probability density function [2]. Meanwhile, the characteristic of the RFPA radar, which transmits narrowband signals instantaneously while synthesizing a wideband spectrum from the transmitted signals, enhances its anti-jamming capability and achieves high-range resolution [3,4]. In addition, the random PRI helps to avoid the inherent range or velocity ambiguities associated with a fixed PRI in traditional radar systems [5]. These advantages make RFPA radar highly anticipated for applications such as target parameter estimation and imaging [6,7,8].
However, the agility of the carrier frequency in RFPA radar results in the received echo of each pulse being narrowband, causing information loss in the frequency domain. The information loss from RFPA radar results in a high sidelobe plateau and floor when traditional matched-filtering methods are used to estimate the range–velocity parameters of targets [9,10], thereby significantly affecting the accuracy of estimating target parameters. Moreover, in the observation scenarios of RFPA radar, the number of targets is typically quite small within the coarse resolution range cell for a given fast-time sampling, resulting in noticeable sparsity. Therefore, scholars have extensively researched sparse reconstruction algorithms based on a theory named compressive sensing (CS); these algorithms are particularly well-suited for exploiting the information loss and sparsity characteristics [11], to partially mitigate the high sidelobe problem, and to achieve target parameter estimation for agile radar [12,13].
Currently, typical CS algorithms for sparse reconstruction in agile radar include greedy algorithms, convex optimization algorithms, and sparse Bayesian learning (SBL) algorithms. Specifically, greedy algorithms find the global optimal solution by iteratively seeking local optimal solutions, as exemplified by the classic orthogonal matching pursuit (OMP) algorithm [14,15]. In 2018, Quan firstly applied the OMP algorithm for target parameter estimation for frequency agile and PRF-jittering radar (i.e., the RFPA radar) based on the CS theory, achieving high resolution while demonstrating the feasibility of applying CS theory in the field of RFPA radar [6]. The core principle of convex optimization algorithms is to convert the originally complex norm nondeterministic polynomial (NP) problem into a norm optimization problem [16], as illustrated by algorithms such as the Alternating Direction Method of Multipliers (ADMM) [17] and Basis Pursuit (BP) [18]. The fundamental idea of SBL algorithms is to first establish a prior distribution for the target echoes, regarded as a random vector, and to subsequently reconstruct the target echo by Bayesian inference [19]. In 2019, Yao employed an SBL algorithm based on complex Gaussian distributions in frequency agile radars, achieving effective sidelobe suppression and target parameter estimation [20]. The aforementioned sparse reconstruction algorithms based on CS theory [14,15,16,17,18,20] first discretize the range–velocity parameter space into a uniform grid of points and then assume that the target parameters are accurately positioned at these grid points. However, the real parameters of the target may be located at any point within the continuous parameter space, causing mismatches between the true target positions and the grid points, known as off-grid issues. In instances of off-grid issues, the energy of signals may spread to adjacent discrete grids [21], directly influencing the performance of parameter estimation of range–velocity when utilizing the aforementioned algorithms for agile radar [22]. To address off-grid issues and enhance the robustness of the algorithm, grid refinement and dictionary learning are currently the two strategies. Grid refinement methods still utilize a predefined observation matrix based on the scenario information and aim to mitigate the impact of off-grid issues by refining the grid size of the predefined observation matrix. In 2013, Huang introduced an algorithm called Adaptive Matching Pursuit with Constrained Total Least Squares (AMP-CTLS) for frequency agile radar based on the combination of a grid refinement method and a greedy algorithm, which searches for atoms that are not actually present in the initial observation matrix by adaptively updating grids and the observation matrix [23]. In 2022, Liu proposed an Improved Orthogonal Matching Pursuit (IOMP) algorithm for frequency agile radar, which significantly reduces computational complexity while achieving comparable performance to the OMP algorithm in [6] by selecting the most relevant atoms from the refined observation matrix instead of traversing every column of the refined matrix [24]. Dictionary learning methods [25] achieve sparse reconstruction by optimizing a dictionary matrix without any predefined structural constraints, thereby overcoming off-grid issues. This approach has been widely applied in the fields of channel estimation [26,27], direction-of-arrival (DOA) estimation [28], and radar imaging [29]. In 2019, Zhang combined the dictionary learning method with the convex optimization algorithm to partially address the cross-term and mismatch issues encountered when using the atomic norm minimization algorithm in frequency agile radar, thereby estimating target parameters in the continuous domain [30]. However, dictionary learning methods require comprehensive training samples, and when these samples are insufficient, it becomes more challenging to understand the underlying causes of the signal or to extract relevant information from observations [25]. Additionally, due to practical implementation constraints, RFPA radar lacks sufficient training samples to support dictionary learning. Therefore, it is necessary to explore more innovative and suitable parameter iteration estimation algorithms within the grid refinement method that better align with the current agile radar conditions. Currently, off-grid CS algorithms for agile radar mainly rely on greedy algorithms and convex optimization algorithms due to their superior computational feasibility and simpler implementation methods [23,24,30]. However, the increased correlation between columns of the observation matrix due to scenarios with closely spaced targets significantly impacts the performance of these algorithms. In contrast, SBL algorithms fully account for the correlation between columns of the observation matrix in scenarios with closely spaced targets, thereby exhibiting stable parameter estimation performance [31].
For one-dimensional target parameter estimation with radar, off-grid SBL algorithms are primarily applied for DOA estimation. In 2017, Dai presented a Root-SBL algorithm, which, unlike existing off-grid SBL methods that linearly approximate the true DOA, updates grid points by solving the roots of a parameter polynomial, thus overcoming grid constraints and relatively reducing off-grid errors [32]. In 2021, the Grid Interpolation Multi-Snapshot SBL (GI-MSBL) algorithm was proposed by Wang and utilized grid interpolation methods to optimize the grid-point set and addressed the DOA problem involving closely spaced targets through the estimation of noise variance and signal power in two rounds [33].
In the realm of two-dimensional estimation of range–velocity parameters for RFPA radar, there has been limited research on SBL-based CS algorithms applied to RFPA radar. In 2023, Wang proposed an SBL-based CS algorithm for RFPA radar, which leveraged the Laplace distribution to enhance sparsity and improve the dynamic range of the algorithm [34]. But this algorithm did not account for off-grid scenarios, and its performance would significantly degrade when dealing with off-grid targets. Hence, there is a necessity to investigate off-grid SBL-based CS algorithms for RFPA radar. However, the application of off-grid SBL-based CS algorithms encounters significant challenges due to the large number of pulses and a considerable amount of refined grid points in the range and velocity dimension. Therefore, we delved into off-grid SBL-based CS algorithms for RFPA radar, with the focus on harmonizing algorithmic computational efficiency with performance stability. In our previous work, we introduced the grid refinement and generalized double-Pareto (GDP) distribution based on the SBL (RGDP-SBL) algorithm [35], which utilizes a GDP distribution with strong sparsity to perform searches over the coarse and fine grids and applies a partial grid refinement technique during the fine search stage to compute the energy and noise variance for each grid, enabling accurate target parameter estimation. Meanwhile, the RGDP-SBL algorithm reduces computational complexity to some extent by efficiently utilizing the diagonal elements of matrices. However, despite its efficient utilization of diagonal elements to slightly reduce computational complexity, the extent of reduction offered by the RGDP-SBL algorithm remains relatively constrained. Furthermore, when efforts are made to enhance the computational feasibility of the RGDP-SBL algorithm by reducing the number of search grid points, a decline in the estimation performance of the target parameters can be observed. Hence, there exists a necessity to explore a novel off-grid CS algorithm based on SBL to significantly reduce computational complexity while mitigating any potential loss in algorithmic performance for RFPA radar systems.
This paper proposes an off-grid CS algorithm based on Root-SBL for RFPA radar and aimed at maintaining robust performance for target parameter estimation while achieving superior computational feasibility. To alleviate the impact posed by the off-grid issue, this paper derives a root-solving formula for velocity parameters specific to RFPA radar, enabling the proposed algorithm to overcome the limitation of grids and directly solve for the target velocity parameters during the fine search stage. Meanwhile, the proposed algorithm utilizes the single-level hierarchical complex Gaussian prior distribution model with fewer and simpler parameters for updating the hyperparameters and employs the derived root-solving formula to negate the necessity of grid refinement in the velocity dimension, thereby reducing the computational complexity. Moreover, the proposed algorithm accelerates the convergence rate during the fine search stage by incorporating a fixed-point strategy into the Expectation-Maximization (EM) algorithm, thus further reducing the computational complexity significantly. In the specific implementation, the proposed algorithm performs hyperparameter updating based on the complex Gaussian prior distribution during the coarse search stage to approximate values for the range and velocity parameters. Subsequently, during the fine search stage, the grid search in the range dimension is conducted. Concurrently, the proposed algorithm incorporates the fixed-point strategy into the EM algorithm to update the hyperparameters for the velocity dimension. After each update, the algorithm utilizes the derived root-solving formula to directly determine the target velocity parameters. Simulation results demonstrate that the proposed algorithm is superior in terms of accuracy, convergence speed, and computational complexity in various scenarios. Moreover, this paper provides specific results for simulations in different multi-target off-grid scenarios and detailed computational complexity analyses from both computational complexity expression and runtime perspectives.
2. Materials and Methods
2.1. Signal Model
Assume that in an RFPA radar observation scenario there are H point targets moving radially, where the velocity and initial range of the h-th target is denoted as and , respectively. Then, it is supposed that within a coherent processing interval (CPI), N pulse signals are transmitted. Therefore, based on the transmitted signal of the RFPA radar, the n-th echoes can be modeled as
where denotes the complex backscatter coefficient, which represents the scattering intensity of the h-th target, and denote the unit rectangular function and the time at which the radar receives the echoes from the h-th target, respectively, represents random PRI jittering, which follows a uniform distribution, while denotes the pulse width, and indicates the average PRI of the RFPA radar. The function denotes the carrier frequency of the n-th pulse, where is the center frequency, is the frequency-hopping sequence and is uniformly distributed over , with M being the total number of frequency agility points, and indicates the bandwidth of the minimum frequency-hopping step. The terms and respectively represent the time delay and the Doppler frequency, while c represents the speed of light.
After receiving the echo, the n-th echo is discretized by sampling at time , where , with L denoting the total number of fast-time snapshots and representing the sampling frequency. For convenience of signal processing, this paper assumes that in the observed scenario, there is at most one target within the range cell corresponding to adjacent sampling times. In this context, the range migration of targets can be neglected [36]. Therefore, by isolating the stage term of Formula (1) separately, simultaneously adding the envelope , and ignoring fast-time, the n-th sampled echo can be expressed as
Here, the term contains the range information of targets and is dependent on the frequency-hopping code sequence . The term contains velocity information of targets and varies with the pulse sequence n.
According to the CS theory model [11], the echoes can be expressed in matrix form:
where and represents the observed data of echoes, and are the target echoes that contain unknown range and velocity information. For convenience, the observation matrix is pre-constructed based on the RFPA radar observation scenario rather than being obtained through dictionary learning methods [37]. According to the actual observation scenarios for RFPA radar, the number of targets is significantly less than the number of grid points [38]. Consequently, the echoes of the RFPA radar exhibit sparsity in the range–velocity plane. Hence, it is feasible to discretize the range–velocity values into grid points. The range dimension is divided into P grid points, and the velocity dimension is divided into Q grid points, resulting in a total of grid points. Then, we can obtain the observation matrix for the range dimension R and the observation matrix for the velocity dimension V. Their specific expressions are as follows:
Performing the Kronecker operation on the constructed observation matrices and yields the final observation matrix :
Subsequently, the final observation matrix will be utilized for the sparse reconstruction of the target echoes in RFPA radar [39].
2.2. Proposed Method
The proposed algorithm in this paper aims to mitigate the impact of off-grid issues in the CS algorithm based on SBL for RFPA radar while ensuring the computational feasibility. The proposed algorithm employs a simple single-level hierarchical complex Gaussian prior distribution for hyperparameter updating and integrates the fixed-point strategy with the EM algorithm to reduce computational complexity. Meanwhile, it utilizes the derived root-solving formula to solve for the target velocity parameters during the fine search stage; it achieves stable performance for estimating the velocity parameters of targets. Specifically, the use of the derived root-solving formula avoids grid refinement, further significantly reducing the computational complexity. The specific derivation process of the root-solving formula is presented in Section 2.2.2. In detail, the proposed algorithm comprises two distinct stages: a coarse search and a fine search. During the coarse search stage, the proposed improved algorithm updates the hyperparameters of the signal based on the complex Gaussian prior distribution to rapidly approximate the range and velocity parameters of targets. Subsequently, in the fine search stage, the proposed improved algorithm utilizes a grid search in the range dimension while integrating the fixed-point strategy into the EM algorithm to update the hyperparameters in the velocity dimension. After each hyperparameter is updated, the algorithm directly solves the velocity parameters of targets using the derived root-solving formula. To provide a more intuitive representation, the flowchart of the proposed algorithm is depicted in Figure 1.
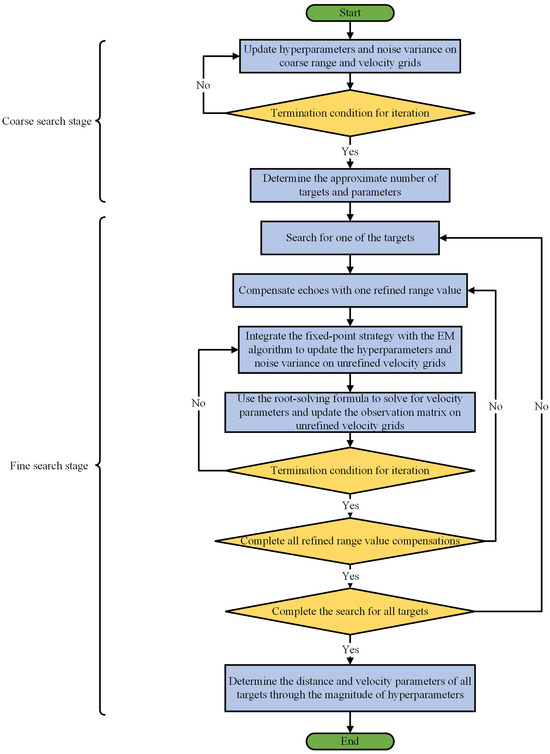
Figure 1.
Top-level figure: flowchart of the proposed algorithm.
According to the flowchart in Figure 1, it is possible to consider using the Zynq-7000 All Programmable System-on-Chip (SoC), abbreviated Zynq, for hardware-level implementation. The Zynq chip includes programmable logic (PL) resources and processing system (PS) resources. The PL resources and PS resources used by the proposed algorithm module are described in Figure 2.
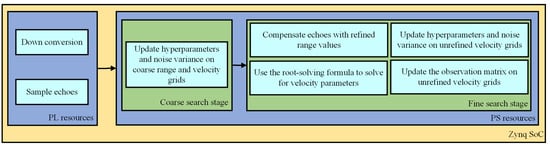
Figure 2.
The division of labor within the Zynq SoC.
2.2.1. Coarse Search for Targets
The fundamental concept of the SBL algorithm for RFPA radar is to assume that the target echoes follow a given prior distribution and to then reconstruct the target echoes through Bayesian inference [40,41]. In the field of radar signal recovery, widely used prior distributions include the complex Gaussian distribution, Laplace distribution, and GDP distribution. Specifically, the single-level hierarchical complex Gaussian distribution model is simple and involves few parameters, resulting in lower computational complexity. The Laplace distribution requires the consideration of a few more parameters, enhancing sparsity to some extent but also increasing computational complexity. The GDP distribution is a three-level hierarchical prior model with many parameters and strong sparsity, but it incurs very high computational complexity. Therefore, this paper selects the simple and parameter-efficient complex Gaussian prior distribution [20] as the prior distribution for the target echoes to reduce the computational complexity of the proposed algorithm. It is worth noting that the low sparsity of the complex Gaussian distribution would result in performance degradation in the estimation of target range–velocity parameters when directly applying traditional SBL methods. Therefore, during the fine search stage, the proposed improved algorithm requires compensatory measures to address this performance loss. The detailed steps of the fine search will be elaborated on in Section 2.2.2. Assuming that each element in the columns of the target echoes of RFPA follows a complex Gaussian distribution with a mean of 0 and variance , its probability density function (PDF) is expressed as:
Here, denotes the covariance matrix of target echoes , and represents the variance of the j-th row, corresponding to the signal power at the j-th grid point of the observation matrix. Additionally, serves as a signal hyperparameter and indicates the sparsity of the target echoes . Meanwhile, assume that the noise also follows an independent complex Gaussian distribution, i.e., , where represents the reciprocal of the noise variance, and denotes the identity matrix. The PDF of the RFPA radar echoes is obtained as follows:
According to Bayesian inference, the posterior PDF of the target echoes is given by the following equation [19]:
Here, and denote the posterior mean and posterior variance of , respectively. This paper employs the Type II objective function [42] to estimate the signal hyperparameter and the noise variance , where the Type II objective function in this paper is represented by . Meanwhile, to derive the iterative formulas for and , the EM algorithm [43,44] is employed. The EM algorithm consists of the Expectation step stage and the Maximization step stage. During the Expectation step stage, by taking the natural logarithm of the objective function following the complex Gaussian distribution and computing its expectation, the objective function can be obtained. By utilizing Formula (10) for variable substitution and employing the integral value of the complex Gaussian distribution, the objective function can be derived as:
The detailed derivation process is presented in Appendix A.1. During the Maximization step stage, partial derivatives of Formula (11) with respect to and are calculated, and they are shown as:
The specific derivation processes for Formulas (12) and (13) are shown in Appendix A.2. Setting each partial derivative to zero yields the update formulas for and , respectively. Hence, the iterative formulas for and under the multi-snapshot scenario are given by:
It can be observed that in the calculation of Formula (14), only the diagonal elements of sigma are required, making the computation of the entire sigma unnecessary, which can slightly reduce the computational complexity. Through a predetermined number of iterations on and , the algorithm achieves convergence in the coarse search stage. Subsequently, the maximum value of the posterior mean is searched. Utilizing the remainder theorem, the grid points corresponding to the positions of targets can be computed, thus obtaining the approximate range and velocity information of the targets through a transformation.
2.2.2. Fine Search for Targets
Performing a fine search within the grids where the targets are located, as determined during the coarse search stage, enables a more accurate estimation of the range–velocity parameters of targets. The fine search stage involves three steps:
- (1)
- Fine searching in the range dimension: For each target, the coarse search range grids corresponding to the approximate locations identified during the coarse search stage and the two adjacent coarse search range grids are refined into total grids. Subsequently, each grid value in the range dimension is used to sequentially compensate for the range term in the expression of the RFPA radar echoes.
- (2)
- Fine searching in the velocity dimension: During each compensation iteration of the range term of the RFPA radar echoes, by updating the hyperparameters and reconstructing the observation matrix of the velocity dimension, estimation of the velocity parameter v in the velocity term can be achieved.
- (3)
- Range–velocity parameter estimation: Upon completion of the fine search, the maximum value within the search range in the two-dimensional range–velocity plane is identified and then converted into the target range–velocity values.
Since the fine search in the range dimension employs a straightforward grid search, further elaboration is unnecessary. Therefore, the remaining part of this section will detail the method for the fine search in the velocity dimension during each range grid search.
For the fine search in the velocity dimension, the first step involves determining the total number of velocity grid points associated with each target based on the coarse search results, thereby mitigating the influence of other targets on the target of interest. Assume that the number of targets determined after the coarse search is K, which ideally should be equal to the actual number of targets H. Assume that there are a total of velocity grid points associated with each target, where these grid points include one velocity grid point obtained through the coarse search and grid points adjacent to this grid point in the velocity dimension. The observation matrix of the velocity dimension corresponding to each target can be reconstructed using the same approach as in Formula (4), where . To reduce the computational complexity, the proposed algorithm avoids refining the velocity grid and only considers the coarse search velocity grids corresponding to the approximate location identified during the coarse search stage and the two adjacent coarse search velocity grids. Moreover, to eliminate energy leakage from targets to surrounding velocity grid points, the process of hyperparameter updating is still necessary. During hyperparameter updating, it is assumed that the target echoes follow a complex Gaussian prior distribution. Therefore, similar to the derivation in the coarse searching part, after eliminating the influence of other irrelevant grids, the signal posterior mean and posterior covariance matrix are defined as:
where denotes the covariance matrix of the target echoes after eliminating the influence of other irrelevant grids, , is the variance of the -th row, corresponding to the power at the k-th grid point in the newly constructed k-th observation matrix of the velocity dimension, and is the noise variance for the k-th target. When conducting the fine search in the velocity dimension, the Type II objective function is still utilized. By taking the natural logarithm and finding the expectation of K objective functions, the following equation is obtained:
Taking the partial derivative of Formula (18) with respect to yields the following formula:
To accelerate the convergence rate of the proposed algorithm and, consequently, to reduce computational complexity during hyperparameter updating, a fixed-point strategy is incorporated into the EM algorithm to solve for the hyperparameters . Let , where represents the hyperparameters obtained from the previous iteration, and denotes the diagonal elements of the posterior covariance matrix . Setting Formula (19) to zero and substituting can solve for the updating formula for . Therefore, the iterative formulas for signal hyperparameters are given by:
Here, is the l-th column of the signal posterior mean after eliminating the influence of other irrelevant grid points. Taking the partial derivative of yields the following equation:
Setting Formula (21) to zero yields the update formula for :
After each update of the signal hyperparameters and noise variance , it is necessary to update the observation matrix of the velocity dimension . This is equivalent to maximizing the expectation function containing only velocity information, as formulated in Formula (18). The expectation function can be expressed as:
Taking the derivative of Formula (23) with respect to the velocity parameter v results in the following expression:
The detailed derivation of Formula (24) is included in Appendix A.3. Simplify Formula (24) and set it to zero:
Let , and , where denotes the element in the i-th row and -th column of , and represents the -th element of . Consequently, the first term comprises and its coefficient , the second term consists of and its coefficient vector , and the third term consists of and its coefficient vector . Simultaneously, denotes the -th column of the observation matrix of the velocity dimension , and represents the derivative of with respect to . By approximation, it can be obtained that . It is noteworthy that , where represents the 1-norm of returning the sum of elements in a vector, and . Therefore, by substituting , and into Formula (25) while performing simplification and linear operations, the following equation can be obtained:
Let . Writing the above equation in the form of a linear combination gives
Here, and represent the n-th element in the vectors and , respectively. The Root algorithm [32] is employed to solve for parameter in the above equation. Since the polynomial above is of order N, there exist N corresponding roots in the complex plane. These roots have unit circle absolute values in the absence of noise, but in the presence of noise, these roots may not lie on the unit circle. Among the N roots, the one closest to the unit circle is selected as the solution and corresponds to the updated velocity grid point . The following equation transforms the root into a velocity grid point:
Meanwhile, it is necessary to verify whether the updated grid point falls within the corresponding update range. If the updated grid point is within the interval , the observation matrix is reconstructed. Otherwise, the grid point position remains unchanged, and the next iteration is initiated. The method for reconstructing the observation matrix is as follows:
Hence, updating the velocity dimension observation matrix at each iteration enables a gradual convergence toward the true value of the velocity parameter, thereby facilitating accurate estimation of the velocity of the target. For clarity, the specific steps of the proposed algorithm are shown in Algorithm 1.
| Algorithm 1 The Proposed Algorithm |
| 1: Input: observation matrix , observed data composed of echoes , the number of |
| range–velocity grid points J, the number of snapshots L, pulse number N |
| fine search step of range dimension , the number of velocity grid points |
| in fine search , maximum iterations of coarse search , maximum |
| iterations of fine search . |
| 2: Initialization: , , , error threshold , |
| , , . |
| 3: while do |
| 4: |
| 5: Update and by Formulas (9) and (10). |
| 6: Update and by Formulas (14) and (15). |
| 7: end while |
| 8: Identify the top K maximum values in . |
| 9: for do |
| 10: for do |
| 11: Use each range value to compensate for echoes |
| 12: while do |
| 13: |
| 14: Update and by Formulas (16) and (17). |
| 15: Incorporate the fixed-point strategy into the EM algorithm to update |
| by Formula (20). |
| 16: Update by Formula (22). |
| 17: for do |
| 18: Use the derived root-solving formula to solve by Formula (27). |
| 19: Convert to velocity grid point by Formula (28). |
| 20: if |
| 21: Reconstruction of by Formula (29). |
| 22: else |
| 23: continue |
| 24: end |
| 25: end for |
| 26: if |
| 27: break |
| 28: end |
| 29: end while |
| 30: end for |
| 31: end for |
| 32: Output: and , find the position where the maximum amplitude value of the |
| range–velocity plane is located and convert it to the range and velocity |
| parameters of targets. |
3. Simulation Results
In this section, a comprehensive series of simulations is conducted to demonstrate the superior performance of the proposed algorithm. The structure of this section is outlined as follows:
- (1)
- Section 3.1 provides an overview of the simulation parameters and scenario parameter settings.
- (2)
- Section 3.2 presents a detailed analysis conducted to assess the performance of the proposed algorithm.
- (3)
- Section 3.3 conducts a comprehensive performance comparison of the proposed algorithm against other algorithms, including the convex optimization-based ADMM algorithm from [17], the greedy OMP algorithm in [6], the SBL algorithm from [20], the GI-MSBL algorithm mentioned in [33], and the RGDP-SBL algorithm proposed in [35].
It is noteworthy that the OMP, ADMM, and SBL algorithms employed for comparison lack corresponding off-grid algorithms. Consequently, to objectively compare the performance of various algorithms, we developed off-grid algorithms for these algorithms using grid refinement methods, and the corresponding algorithms are applied on refined grids following coarse searches.
3.1. Simulation Parameter Settings
The specific settings for the parameters of the RFPA radar are detailed in Table 1.

Table 1.
Simulation parameters for RFPA radar.
During the simulation process, 20 snapshots are selected, the maximum number of iterations of the proposed algorithm during the coarse search is 300, and the error threshold is 0.1. The performance of the algorithm is evaluated using the root mean square error (RMSE), denoted as for the range dimension and for the velocity dimension and defined as follows:
Here, denotes the total number of Monte Carlo simulations, and respectively denote the estimated values for the velocity and range of targets, while v and r represent the true values for the velocity and range of targets. Based on the radar parameter settings in Table 1, the range resolution of the RFPA radar in this study is m, and the velocity resolution is m/s. Therefore, the range and velocity resolutions are used as performance metrics for and in the statistical analysis, respectively, with the objective that and should be lower than the range and velocity resolutions and as close to zero as possible, indicating super-resolution. Additionally, we use the success rate of range and velocity parameter estimation as another metric for statistical analysis. The specific method for success rate calculation is as follows: during each Monte Carlo simulation, the differences between the estimated range–velocity parameters from each algorithm and the actual values are recorded. If the difference between the estimated range parameter and the actual range value is below the corresponding resolution, the estimation of the range parameter is considered a successful estimation. The same method is applied for calculating the success rate of velocity parameter estimation.
In this paper, seven distinct observation scenarios are established to facilitate the assessment of the performance of the proposed algorithm: (1) Scenario S1 comprises just one target. (2) Scenario S2 includes two closely spaced targets with identical signal-to-noise ratios (SNRs). (3) Scenario S3 contains three targets with the same SNRs, among which two targets are located in the same range–velocity grid while another target is located precisely in a coarse search grid. (4) In Scenario S4, two targets are closely spaced, and the SNR of target T3 is higher than that of the other two targets. (5) In Scenario S5, two targets are closely spaced, and the SNR of target T2 is higher than that of the other two targets. (6) Scenarios S6 and S7 involve closely spaced targets and include four and five targets, respectively, that share an identical SNR, with one target positioned precisely in a coarse search grid in each scenario. The range and velocity of the targets located precisely at coarse search grid points are 1080 m and 420 m/s, respectively. The specific scenario configurations are summarized in Table 2.

Table 2.
Specific parameter settings for observation scenarios.
Notably, the proposed algorithm uses the root-solving formula from Formula (27) to directly solve the velocity parameters during the fine search stage, eliminating the need for velocity grid refinement. To determine the range and velocity step sizes for both the coarse and fine search stages, a performance analysis and comparison of different combinations of coarse and fine search step sizes is required. Through a preliminary analysis, coarse search steps of 2 m or 5 m for the range and 10 m/s for the velocity can be selected, while fine search steps of 0.1 m or 0.5 m for the range can be adopted. Accordingly, the proposed algorithm is applied to S3 with these search steps across 200 Monte Carlo simulations. A performance comparison is made to determine the optimal search step combination, with the results shown in Table 3.

Table 3.
Performance of the proposed algorithm under different search step combinations for S3.
Based on the results shown in Table 3, subsequent simulations use 2 m and 10 m/s as the range and velocity search steps for the coarse search and 0.1 m as the range search step for the fine search.
3.2. Performance Analysis of the Proposed Algorithm
In this section, two simulations are designed to analyze the performance of the proposed algorithm: (1) simulation using the proposed algorithm applied to a single-target scenario and scenarios with multiple closely spaced targets and (2) simulation using the proposed algorithm in scenarios with different SNRs (strong and weak targets).
3.2.1. Simulation in Single-Target Scenario and Scenarios with Multiple Closely Spaced Targets
To analyze the performance of the proposed improved algorithm in scenarios with one target and multiple closely spaced targets, 200 Monte Carlo simulations are carried out for S1, S2, and S3, and the RMSE for each scenario is computed. The simulation results are presented in Table 4.

Table 4.
Performance of the proposed algorithm for S1, S2 and S3.
As depicted in Table 4, the RMSE of the proposed improved algorithm is proportional to the complexity of the scenario. For the simple single-target S1, the performance of the proposed algorithm is excellent. Conversely, S2 and S3 are more complex scenarios involving closely spaced targets, leading to increases in the RMSE. Despite this, owing to the grid search in the range dimension and the utilization of the derived root-solving formula for accurate velocity parameter estimation, the RMSE of the proposed algorithm can be maintained at a low value when it is applied to relatively complex S2 and S3.
To intuitively investigate the specific effects of the proposed algorithm during its application, this section details its simulation results in S3. reveals high-energy false targets scattered across the range–velocity plane during the coarse search, potentially interfering with true target identification. However, these false targets occur randomly. To mitigate this, this paper employs a multiple detection method: initially, three coarse searches are performed, followed by retaining targets that appear at the same location at least twice and discarding those that appear randomly at any location. Figure 3 showcases the simulation results, including the coarse search result after eliminating false targets, local fine search results for each target, and a final result in the range–velocity plane.
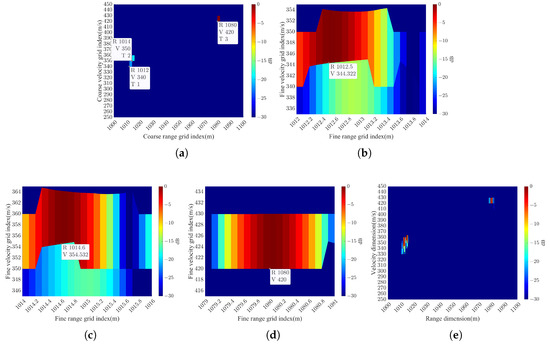
Figure 3.
Detailed results of parameter estimation for targets in S3 using the proposed algorithm: (a) Result of the coarse search. (b) Result of the fine search for T1. (c) Result of the fine search for T2. (d) Result of the fine search for T3. (e) The final result on the range–velocity plane.
As shown in Figure 3, the proposed algorithm determines the approximate positions of three targets through a coarse search, and then it obtains detailed range–velocity parameters for each target by a fine search. Notably, Figure 3b–d exhibit a large and uneven division of the velocity dimension grids. This is because the proposed algorithm directly utilizes the root-solving formula to update the velocity dimension grid during the fine search stage, causing uneven grid division. Meanwhile, the proposed algorithm avoids refinement of velocity dimension grids, contributing to a larger size of velocity dimension grids.
3.2.2. Simulation in Scenarios with Both Strong and Weak Targets
In S4, the distant sidelobe floor of the strong T3 may overshadow T1 and T2, while in S5, the near sidelobe plateau of the strong T2 may overshadow T1, and the distant sidelobe floor may mask T3. These issues will impact the estimation of the target range–velocity parameters. Therefore, in this section, the proposed algorithm is simulated for S4 and S5 to evaluate its performance in scenarios with both strong and weak targets. The simulation results of the proposed algorithm for S4 and S5 are depicted in Figure 4 and Figure 5, respectively.
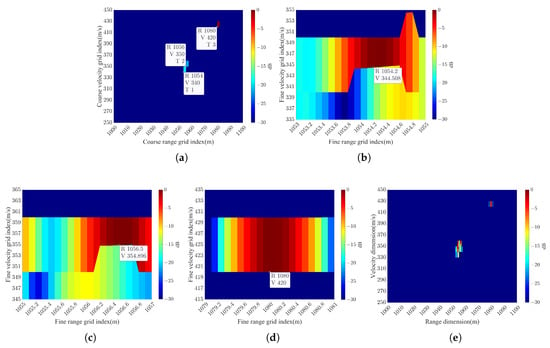
Figure 4.
Detailed results for parameter estimation for targets in S4 using the proposed algorithm: (a) Result of the coarse search. (b) Result of the fine search for T1. (c) Result of the fine search for T2. (d) Result of the fine search for T3. (e) The final result on the range–velocity plane.
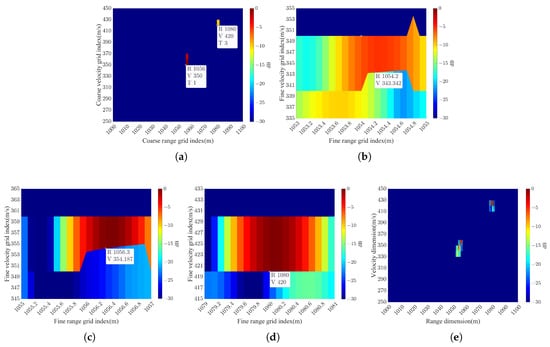
Figure 5.
Detailed results for parameter estimation for targets in S5 using the proposed algorithm: (a) Result of the coarse search. (b) Result of the fine search for T1. (c) Result of the fine search for T2. (d) Result of the fine search for T3. (e) The final result on the range–velocity plane.
As depicted in Figure 4, due to obscuration by the distant sidelobe floor of the strong T3, the energies of T1 and T2 decrease after the coarse search, which poses a challenge for accurately estimating the range–velocity parameters. However, after the fine search, the proposed algorithm can estimate the range–velocity parameters of T1 and T2 with small errors. As shown in Figure 5, the coarse search stage of the algorithm is limited to identifying only two targets. However, upon conducting the subsequent fine search, the range–velocity parameters of all three targets can be precisely estimated. This observation suggests that during the coarse search, the distant sidelobe floor of T2 attenuates the energy of T3, thereby increasing the likelihood of its failure to be detected. Meanwhile, the near sidelobe plateau of T2 obscures T1 completely. Nonetheless, the fine search stage effectively overcomes these challenges and enables accurate estimation of the range–velocity parameters for all three targets.
3.3. Comparison of the Performance of Different Algorithms
In this section, we establish three simulation frameworks aimed at comprehensively contrasting the performance of the proposed algorithm with that of other CS algorithms (OMP [6], ADMM [17], SBL [20], GI-MSBL [33], and RGDP-SBL [35]) in scenarios involving closely spaced targets under various off-grid conditions: (1) simulation under different SNRs, (2) simulation under different numbers of targets, and (3) simulation under different numbers of iterations.
3.3.1. Simulation under Different SNRs
To explore the influence of varying SNRs on the performance of algorithms in scenarios characterized by closely spaced targets, this simulation employs all of the algorithms mentioned above for S3. The SNR increases incrementally by 1dB from −12 dB to 8 dB. At each SNR value, 200 Monte Carlo simulations are conducted, and results of the simulations are illustrated in Figure 6.
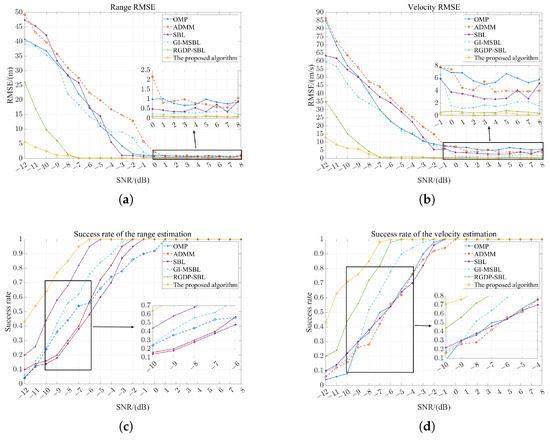
Figure 6.
Algorithm performance under varying SNRs in S3: (a) RMSE for the range dimension. (b) RMSE for the velocity dimension. (c) Success rate for range estimation. (d) Success rate for velocity estimation.
As shown in Figure 6a,b, during the gradual increase in the SNR from −12 dB to 8 dB, the performance of all algorithms improves, reaching saturation after a certain level of SNR. Additionally, the proposed algorithm demonstrates superior adaptability to low-SNR conditions, while other algorithms exhibit poorer performance under low SNRs. At saturation, the proposed algorithm achieves performance comparable to that of the RGDP-SBL algorithm. This can be attributed to the accuracy-enhancing methods adopted in the proposed algorithm, such as the direct solution of the velocity parameters in the velocity dimension and the grid search in the range dimension. Meanwhile, at saturation, it is evident that the RMSE values of the OMP, SBL, and ADMM algorithms are relatively high in the range and velocity dimensions. This is because the increased correlation between columns of the observation matrix caused by closely spaced targets affects the performance of these three algorithms. Moreover, although the GI-MSBL algorithm maintains relatively stable performance at saturation, its performance is still inferior compared to both the RGDP-SBL algorithm and the proposed algorithm. Therefore, the proposed algorithm demonstrates stable performance in response to SNR variations. And in Figure 6c,d, with increasing an SNR, the estimation success rates for both the range and velocity improve across all algorithms, eventually reaching one after a certain SNR value. Notably, even under low-SNR conditions, the proposed algorithm demonstrates higher estimation success rates compared to the other algorithms and rapidly reaches one as the SNR increases. These observations indicate that the proposed algorithm exhibits strong robustness to variations in the SNR.
3.3.2. Simulation under Different Numbers of Targets
To assess the influence of different target numbers on performance for the six aforementioned algorithms, simulations are sequentially conducted for S1, S2, S3, S6, and S7, corresponding to the number of targets ranging from 1 to 5. For each target number, 200 Monte Carlo simulations are conducted. The simulation results are illustrated in Figure 7.
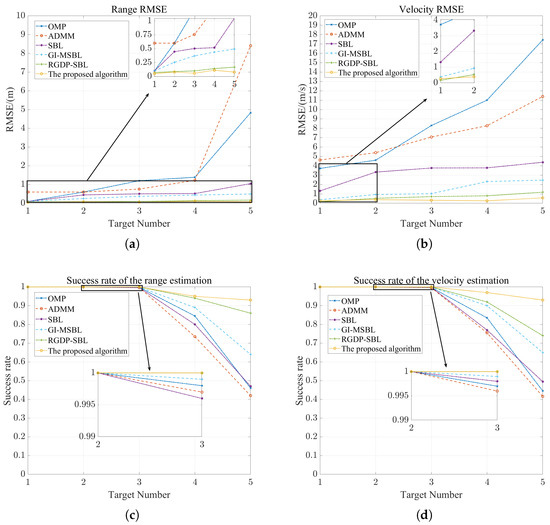
Figure 7.
Algorithm performance under varying numbers of targets: (a) RMSE for the range dimension. (b) RMSE for the velocity dimension. (c) Success rate for range estimation. (d) Success rate for velocity estimation.
In Figure 7a,b, as the number of targets increases, both the range RMSEs and the velocity RMSEs of all of the algorithms show an upward trend. This phenomenon is mainly attributed to the reduced sparsity of radar echoes resulting from the increased number of targets, which consequently impacts the performance of range–velocity parameter estimation for the targets. It is worth noting that as the number of targets increases, the range RMSEs and the velocity RMSEs of the OMP, ADMM, SBL, and GI-MSBL algorithms increase more significantly, indicating a greater impact on their performance. In contrast, the proposed algorithm can maintain lower RMSEs in both dimensions, and its performance is comparable to that of the RGDP-SBL algorithm. As shown in Figure 7c,d, when the number of targets is between 1 and 3, the success rates for range and velocity estimation for all algorithms reach or approach one. However, as the number of targets increases to 4–5, the success rates for all of the algorithms decrease to varying extents due to reduced sparsity. In this case, while the success rates of the proposed algorithm also decrease, they remain higher than those of the other algorithms and stay above 0.9. Consequently, the performance of the proposed algorithm remains relatively stable despite both the increase in the number of targets and the off-grid issue.
3.3.3. Simulation under Different Numbers of Iterations
To evaluate the convergence rates of the different algorithms, it is necessary to investigate the performance of each algorithm under varying numbers of iterations. Therefore, S3, with closely spaced targets, is selected as the simulation scenario in this section, and the number of iterations for each algorithm is gradually increased from 1 to 15. For each number of iterations, 200 Monte Carlo simulations are conducted for each algorithm, and the RMSE is recorded accordingly. During the simulation, it is important to note that each iteration of the OMP algorithm is influenced by the sparsity of the scenario. Since the sparsity of S3 is three, the parameters of the targets that correspond to the number of iterations can only be obtained in the first two iterations. Consequently, calculating the RMSE of the OMP algorithm in these initial iterations is not meaningful. Therefore, when applying the OMP algorithm to S3, the RMSE is only calculated starting from the third iteration. The simulation results are shown in Figure 8.
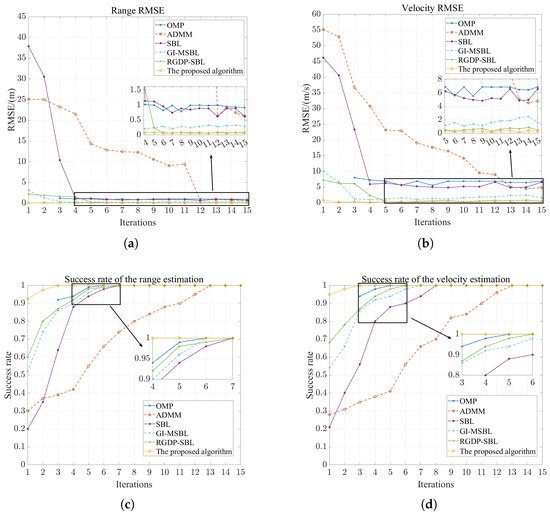
Figure 8.
Algorithm performance under varying numbers of iterations: (a) RMSE for the range dimension. (b) RMSE for the velocity dimension. (c) Success rate for range estimation. (d) Success rate for velocity estimation.
As shown in Figure 8a,b, the performance of each algorithm progressively improves with an increasing number of iterations and eventually stabilizes within its convergence domain after reaching convergence. It is observed that ADMM requires at least 13 iterations to converge, while the OMP, SBL, and GI-MSBL algorithms need 3–5 iterations for convergence. Additionally, the RMSE values of these algorithms are higher than those of the RGDP-SBL algorithm and the proposed algorithm, reflecting inferior performance at estimating range–velocity parameters. Although the RMSE value in the convergence domain of the RGDP-SBL algorithm is minimal, it still necessitates at least five iterations to achieve convergence. In contrast, the proposed algorithm converges almost instantaneously, typically within a single iteration, while maintaining an RMSE value in the convergence domain that is comparable to that of the RGDP-SBL algorithm. As illustrated in Figure 8c,d, with an increasing number of iterations, the success rates for range and velocity estimation improve for all algorithms and eventually converge, reaching two success rates of 1 after a certain number of iterations. For the ADMM algorithm, convergence is slower, requiring more iterations for its parameter estimation success rates to reach 1. The other compared algorithms require 4–7 iterations to achieve two success rates of 1. In contrast, the proposed algorithm demonstrates rapid convergence with a very low number of iterations, achieving two success rates above 0.9 with just one iteration. This indicates that the proposed algorithm has a significant advantage in scenarios requiring real-time parameter estimation.
4. Discussion
In the aforementioned simulations in Section 3, both the proposed algorithm and the RGDP-SBL algorithm demonstrated comparable accuracy in parameter estimation across varying SNR levels and different target counts. Therefore, this section provides a comprehensive comparison and discussion of the computational complexities of these two algorithms. Since both algorithms consist of two stages—namely, a coarse search and a fine search—this section compares the computational complexity of each stage individually.
4.1. Analysis of Computational Complexity in the Coarse Search Stage
In the derivation outlined in Section 2.2.1, it becomes apparent that the proposed algorithm in the coarse search stage primarily entails computations denoted by Formulas (9), (10), (14) and (15), with corresponding parameters labeled as , , , and , respectively. Conversely, in [35], it is observed that the computations associated with the coarse search stage of the RGDP-SBL algorithm primarily stem from parameters , , , , , and . To provide a detailed comparison of the computational complexity, this paper utilizes the number of complex multiplications as a metric. The detailed expressions for the computational complexity involving the parameters of these two algorithms in the coarse search are presented in Table 5.

Table 5.
The expression of computational complexity involving parameters in the coarse search stage.
From Table 5, it is evident that the computational complexity of the coarse search stage in the proposed algorithm is lower compared to that of the RGDP-SBL algorithm. This can be attributed to the fact that during the coarse search stage, the RGDP-SBL algorithm, which is based on the complex three-level hierarchical GDP distribution model, involves multiple hyperparameters with complex expressions. In contrast, the proposed algorithm updates hyperparameters based on the simple single-level hierarchical complex Gaussian distribution model that involves fewer hyperparameters with simpler expressions, thereby reducing the computational complexity during the coarse search stage.
4.2. Analysis of Computational Complexity in the Fine Search Stage
Due to significant differences between the proposed algorithm and the RGDP-SBL algorithm in the fine search stage, this section will discuss in detail the computational complexity of the fine search stage for each algorithm separately. For the proposed algorithm, based on the derivation in Section 2.2.2 for the fine search part, the computations involved in each iteration mainly stem from Formulas (16), (17), (20), (22), (27) and (28). It is noteworthy that in previous simulations, we observed that superior performance of the algorithm could be achieved by solely utilizing and in Formula (27) for root-solving. Hence, only and from Formula (27) are employed in our simulations, rather than incorporating all of , , and , and this approach further reduced the computational complexity. Consequently, the parameters involved are , , , , , , and . The specific expression for the computational complexity of the parameters involved in the fine search stage of the proposed algorithm is presented in Table 6.

Table 6.
The expression of computational complexity involving parameters in the fine search stage of the proposed algorithm.
For the RGDP-SBL algorithm, each iteration involves computations primarily from , , , and . Therefore, the computational complexity of the parameters involved in the fine search stage of the RGDP-SBL algorithm is shown in Table 7.

Table 7.
The expression of computational complexity involving parameters in the fine search stage of the RGDP-SBL algorithm.
During algorithm execution, both the proposed algorithm and the RGDP-SBL algorithm require fine searching for each of the H targets in the scenario. It is noteworthy that during the fine search for each target, the RGDP-SBL algorithm requires the conducting of a grid search over grids, where represents the number of velocity grid points the RGDP-SBL algorithm needs to search for when fine searching for each target. Conversely, the proposed algorithm necessitates a grid search over grids for each target during the fine search, and it accomplishes fewer iterations. Meanwhile, since the proposed algorithm eliminates the need for refining the velocity grids, the number of velocity grid points in the proposed algorithm is substantially smaller than the number of refined velocity grid points in the RGDP-SBL algorithm. Furthermore, in contrast to the RGDP-SBL algorithm, which utilizes the three-level hierarchical GDP distribution, the proposed algorithm still updates hyperparameters based on the single-level hierarchical complex Gaussian distribution during the fine search, and it integrates a fixed-point strategy with the EM algorithm to accelerate the convergence rate, thereby further reducing computational complexity. Consequently, the computational complexity of the proposed algorithm during the fine search is lower than that of the RGDP-SBL algorithm.
To provide a more intuitive and comprehensive comparison of computational complexity, this study applies the proposed algorithm and other algorithms for comparison (OMP [6], ADMM [17], SBL [20], GI-MSBL [33], and RGDP-SBL [35]) in Section 3.3 separately for scenarios S1, S2, and S3, conducting 200 Monte Carlo simulations in each scenario and statistically analyzing the algorithm’s runtime. The detailed total runtimes of these algorithms during the coarse and fine search stages are presented in Table 8.

Table 8.
Runtimes of the proposed algorithms and the RGDP-SBL algorithm.
In summary, the proposed algorithm, employing a simple single-level hierarchical complex Gaussian distribution model and eliminating the need for velocity grid refinement during the fine search process, results in lower computational complexity in both the coarse and fine search stages compared to the RGDP-SBL algorithm. Additionally, the computational complexity of the proposed algorithm is lower than that of most other algorithms used for comparison. Although its complexity is slightly higher than that of the OMP algorithm, the proposed algorithm demonstrates superior accuracy and robustness in Section 3.3, making this minor drawback acceptable.
5. Conclusions
This paper proposes a new SBL-based off-grid CS algorithm for RFPA radar based on the Root-SBL algorithm, with the aim of achieving both stable accuracy and superior computational feasibility for estimating the range–velocity parameters of targets. To cope with the off-grid issue, this paper derives a root-solving formula applicable to RFPA radar, thus accurately solving the target velocity parameter during the fine search stage. Meanwhile, to substantially reduce computational complexity, the proposed algorithm utilizes a single-level hierarchical complex Gaussian distribution with few and simple parameters and uses the derived root-solving formula to avoid grid refinement in the velocity dimension. Furthermore, the proposed algorithm incorporates the fixed-point strategy into the EM algorithm to update the hyperparameters during the fine search stage to accelerate the convergence rate. Results of comprehensive simulations indicate that the proposed algorithm exhibits superior performance in scenarios involving closely spaced targets and scenarios with strong and weak targets. Additionally, compared to other CS algorithms, the proposed algorithm exhibits excellent accuracy in terms of handling different SNRs, dealing with varying numbers of targets, and achieving faster convergence rates. Furthermore, while maintaining superior performance, the proposed algorithm also exhibits lower computational complexity. Since the frequency agility range of the RFPA radar in our simulation is relatively limited and the performance of the proposed algorithm notably deteriorates with too many targets, in future research, we will focus on improving these two aspects.
Author Contributions
Conceptualization, J.W.; methodology, J.W. and B.S.; software, B.S.; writing—original draft preparation, B.S. and S.D.; writing—review and editing, J.W. and Q.Z.; supervision, J.W.; funding acquisition, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number 61971043).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ECCM | Electronic Counter-CounterMeasures |
| RFPA | Random Frequency and Pulse Repetition Interval Agile |
| PRI | Pulse Repetition Interval |
| CS | Compressive Sensing |
| SBL | Sparse Bayesian Learning |
| OMP | Orthogonal Matching Pursuit |
| NP | Nondeterministic Polynomial |
| ADMM | Alternating Direction Method of Multipliers |
| BP | Basis Pursuit |
| AMP-CTLS | Adaptive Matching Pursuit with Constrained Total Least Squares |
| IOMP | Improved Orthogonal Matching Pursuit |
| DOA | Direction-of-Arrival |
| GI-MSBL | Grid Interpolation–Multiple-snapshot SBL |
| GDP | Generalized Double-Pareto |
| RGDP-SBL | grid Refinement and GDP distribution based on SBL |
| EM | Expectation-Maximization |
| CPI | Coherent Processing Interval |
| Probability Density Function | |
| RMSE | Root Mean Square Error |
| SNR | Signal-to-Noise Ratio |
Appendix A
Appendix A.1
The detailed derivation process for Formula (11) is as follows:
According to , the objective function can be derived as:
In the derivation process, an approximation method is employed: , and is the constant term. It is noted that can be calculated from the integral value of the PDF of the complex Gaussian distribution; thus, . Therefore, the function can be simplified as:
Appendix A.2
Appendix A.3
The detailed process for obtaining Formula (24) is described as follows:
Let ; we can obtain that
Evidently, Formula (A6) consists of two parts, so the partial derivatives of the first part can be derived as:
And the partial derivatives of the second part can be derived as:
Therefore, by integrating Formulas (A7) and (A8), we can obtain the form of Formula (24), which is:
References
- Richards, M.A. Fundamentals of Radar Signal Processing; McGraw-Hill Professional: New York, NY, USA, 2022. [Google Scholar]
- Long, X.W.; Li, K.; Tian, J.; Wang, J.; Wu, S.L. Ambiguity Function Analysis of Random Frequency and PRI Agile Signals. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 382–396. [Google Scholar] [CrossRef]
- Nuss, B.; Fink, J.; Jondral, F. Cost efficient frequency hopping radar waveform for range and doppler estimation. In Proceedings of the 2016 17th International Radar Symposium (IRS), Krakow, Poland, 10–12 May 2016; pp. 1–4. [Google Scholar]
- Axelsson, S.R.J. Analysis of random step frequency radar and comparison with experiments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 890–904. [Google Scholar] [CrossRef]
- Blunt, S.D.; Mokole, E.L. Overview of radar waveform diversity. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 2–42. [Google Scholar] [CrossRef]
- Quan, Y.H.; Wu, Y.J.; Li, Y.C.; Sun, G.C.; Xing, M. Range Doppler reconstruction for frequency agile and PRF-jittering radar. IET Radar Sonar Navig. 2018, 12, 348–352. [Google Scholar] [CrossRef]
- Jiang, H.; Zhao, C.; Zhao, Y. Coherent integration algorithm for frequency-agile and PRF-jittering signals in passive localization. Chin. J. Electron. 2021, 30, 781–792. [Google Scholar]
- Wei, S.; Zhang, L.; Liu, H. Joint frequency and PRF agility waveform optimization for high-resolution ISAR imaging. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5100723. [Google Scholar] [CrossRef]
- Kulpa, J.S. Noise radar sidelobe suppression algorithm using mismatched filter approach. Int. J. Microw. Wirel. Technol. 2016, 8, 865–869. [Google Scholar] [CrossRef]
- Long, X.W.; Wu, W.; Li, K.; Wang, J.; Wu, S.L. Multi-timeslot Wide-Gap Frequency-Hopping RFPA Signal and Its Sidelobe Suppression. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 634–649. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Quan, Y.H.; Fang, W.; Sha, M.H.; Chen, X.D.; Ruan, F.; Li, X.H.; Meng, F.; Wu, Y.J.; Xing, M.D. Present situation and prospects of frequency agility radar waveform countermeasures. Syst. Eng. Electron. 2021, 43, 3126–3136. [Google Scholar]
- Yang, J.G. Research on Sparsity-Driven Regularization Radar Imaging Theory and Method. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2013. [Google Scholar]
- Fang, H.; Yang, H. Greedy Algorithms and Compressed Sensing. Acta Autom. Sin. 2011, 37, 1413–1421. (In Chinese) [Google Scholar]
- Quan, Y.H. Study on Sparse Signal Processing for Radar Detection and Imaging Application. Ph.D. Dissertation, Xidian University, Xi’an, China, 2012. [Google Scholar]
- Liu, Z.; Wei, X.Z.; Li, X. Low sidelobe robust imaging in random frequency-hopping wideband radar based on compressed sensing. J. Cent. South Univ. 2013, 20, 702–714. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Wang, W. A Study of Convex Relaxation Algorithms for Compressed Sensing Reconstruction Problem. Master’s Dissertation, Xidian University, Xi’an, China, 2014. [Google Scholar]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Tao, Y.J.; Zhang, G.; Tao, T.B.; Leng, Y.; Leung, H. Frequency-agile Coherent Radar Target Sidelobe Suppression Based on Sparse Bayesian Learning. In Proceedings of the 2019 IEEE MTT-S International Microwave Biomedical Conference (IMBioC), Nanjing, China, 6–8 May 2019; Volume 1, pp. 1–4. [Google Scholar]
- Chae, D.H.; Sadeghi, P.; Kennedy, R.A. Effects of Basis-Mismatch in Compressive Sampling of Continuous Sinusoidal Signals. In Proceedings of the 2010 2nd International Conference on Future Computer and Communication, Wuhan, China, 21–24 May 2010; Volume 2, pp. V2-739–V2-743. [Google Scholar]
- Chi, Y.J.; Scharf, L.L.; Pezeshki, A.; Calderbank, A.R. Sensitivity to Basis Mismatch in Compressed Sensing. IEEE Trans. Signal Process. 2011, 59, 2182–2195. [Google Scholar] [CrossRef]
- Huang, T.Y.; Liu, Y.M.; Meng, H.D.; Wang, X.Q. Adaptive Matching Pursuit for Off-Grid Compressed Sensing. arXiv 2013, arXiv:13084273. [Google Scholar]
- Liu, Z.X.; Quan, Y.H.; Wu, Y.J.; Xu, K.J.; Xing, M.D. Range and Doppler reconstruction for sparse frequency agile linear frequency modulation-orthogonal frequency division multiplexing radar. IET Radar Sonar Navig. 2022, 16, 1014–1025. [Google Scholar] [CrossRef]
- Tošić, I.; Frossard, P. Dictionary Learning. IEEE Signal Process. Mag. 2011, 28, 27–38. [Google Scholar] [CrossRef]
- Ding, Y.; Rao, B.D. Compressed downlink channel estimation based on dictionary learning in FDD massive MIMO systems. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Zhou, Z.; Cai, B.; Chen, J.; Liang, Y. Dictionary learning-based channel estimation for RIS-aided MISO communications. IEEE Wirel. Commun. Lett. 2022, 11, 2125–2129. [Google Scholar] [CrossRef]
- Guo, Q.; Xin, Z.; Zhou, T.; Yin, J.; Cui, H. Adaptive compressive beamforming based on bi-sparse dictionary learning. IEEE Trans. Instrum. Meas. 2021, 71, 6501011. [Google Scholar] [CrossRef]
- Liu, Q.; Cheng, Y.; Cao, K.; Liu, K.; Wang, H. Radar Forward-Looking Imaging for Complex Targets Based on Sparse Representation with Dictionary Learning. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4026605. [Google Scholar] [CrossRef]
- Zhang, G.B.; Huang, T.Y.; Liu, Y.M.; Eldar, Y.C.; Wang, X.Q. Frequency Agile Radar Using Atomic Norm Soft Thresholding with Modulations. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Wipf, D. Sparse estimation with structured dictionaries. Adv. Neural Inf. Process. Syst. 2011, 24, 2016–2024. [Google Scholar]
- Dai, J.S.; Bao, X.; Xu, W.C.; Chang, C.Q. Root Sparse Bayesian Learning for Off-Grid DOA Estimation. IEEE Signal Process. Lett. 2017, 24, 46–50. [Google Scholar] [CrossRef]
- Wang, Q.S.; Yu, H.; Li, J.; Dong, C.; Ji, F.; Chen, Y.K. Sparse Bayesian Learning Based Algorithm for DOA Estimation of Closely Spaced Signals. J. Electron. Inf. Technol. 2021, 43, 708–716. [Google Scholar]
- Wang, J.; Zhao, Y.; Shan, B.; Zhong, Y. An improved compressive sensing algorithm based on sparse Bayesian Learning for RFPA radar. In Proceedings of the IET International Radar Conference (IRC 2023), Chongqing, China, 3–5 December 2023; pp. 3957–3963. [Google Scholar]
- Wang, J.; Shan, B.; Duan, S.; Zhao, Y.; Zhong, Y. An Off-Grid Compressive Sensing Algorithm based on Sparse Bayesian Learning for RFPA Radar. Remote Sens. 2024, 16, 403. [Google Scholar] [CrossRef]
- Huang, T.Y. Coherent Frequency-Agile Radar Signal Processing by Solving an Inverse Problem with a Sparsity Constraint. Ph.D. Thesis, Tsinghua University, Beijing, China, 2014. [Google Scholar]
- Chen, W.; Rodrigues, M. Dictionary Learning with Optimized Projection Design for Compressive Sensing Applications. IEEE Signal Process. Lett. 2013, 20, 992–995. [Google Scholar] [CrossRef]
- Anitori, L.; Maleki, A.; Otten, M.; Baraniuk, R.G.; Hoogeboom, P. Design and Analysis of Compressed Sensing Radar Detectors. IEEE Trans. Signal Process. 2012, 61, 813–827. [Google Scholar] [CrossRef]
- Gerstoft, P.; Mecklenbräuker, C.F.; Xenaki, A.; Nannuru, S. Multisnapshot Sparse Bayesian Learning for DOA. IEEE Signal Process. Lett. 2016, 23, 1469–1473. [Google Scholar] [CrossRef]
- Wipf, D.P. Bayesian Methods for Finding Sparse Representations; University of California: San Diego, CA, USA, 2006. [Google Scholar]
- Ji, S.H.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Giri, R.; Rao, B. Type I and Type II Bayesian Methods for Sparse Signal Recovery Using Scale Mixtures. IEEE Trans. Signal Process. 2016, 64, 3418–3428. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D. Maximum Likelihood from Incomplete Data Via the EM Algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Wang, A.P.; Zhang, G.Y.; Liu, F. Research and Application of EM Algorithm. Comput. Technol. Dev. 2009, 19, 108–110. (In Chinese) [Google Scholar]
- Schott, J.R. Matrix Analysis for Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).