Incorporating Effects of Slope Units and Sliding Areas into Seismically Induced Landslide Risk Modeling in Tectonically Active Mountainous Areas
Abstract
1. Introduction
2. Materials and Methods
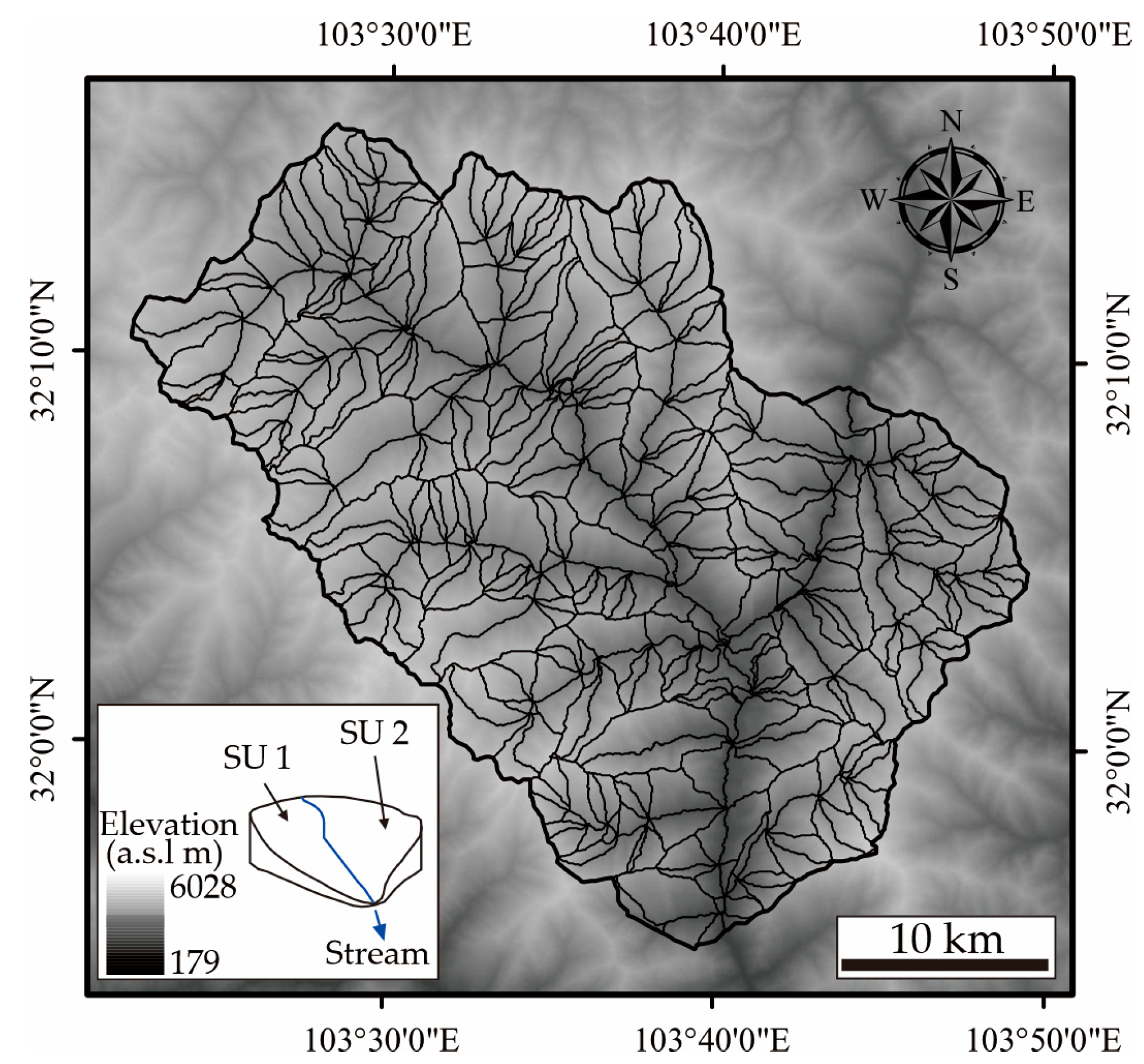
2.1. Study Area
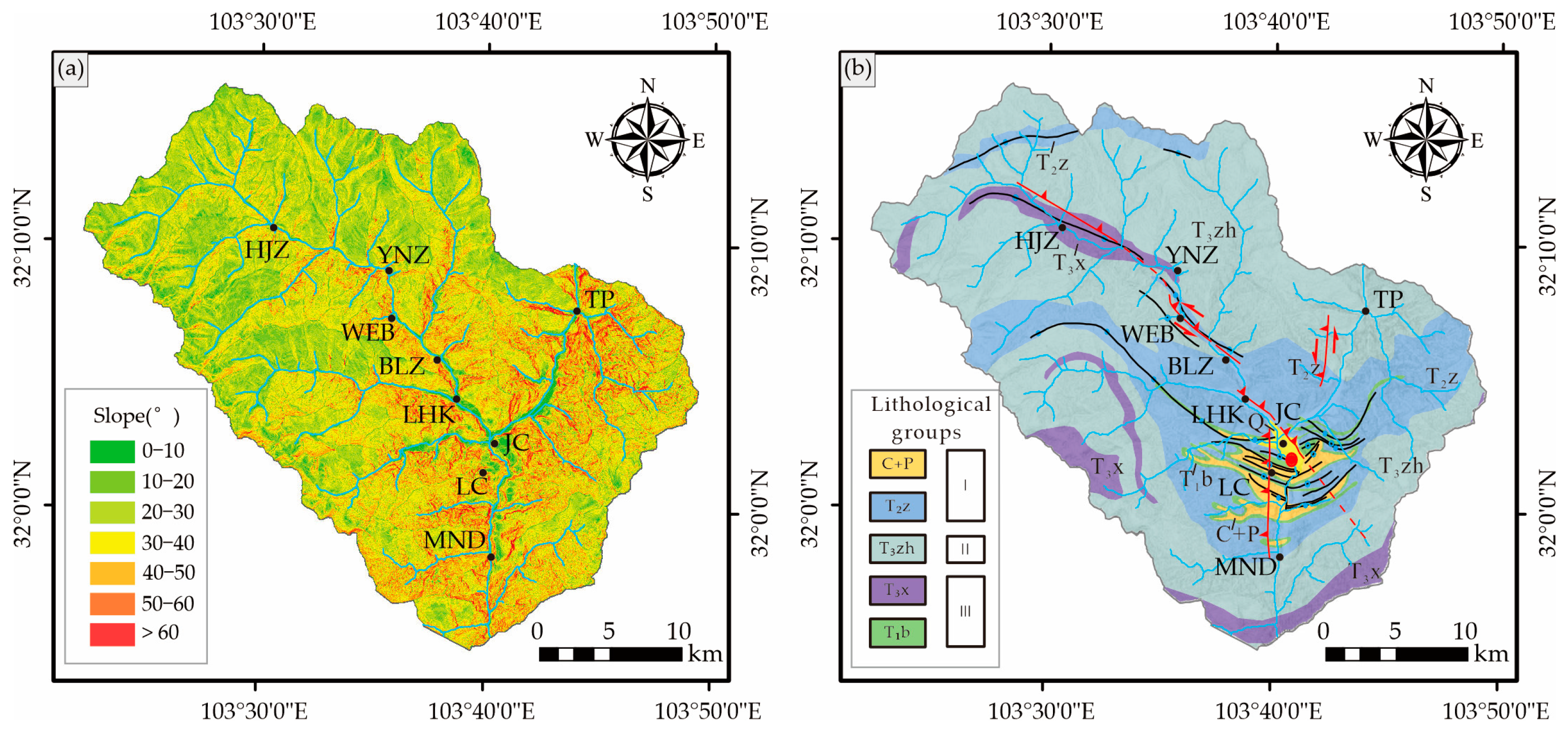
2.1.1. Geomorphological Setting
2.1.2. Geological Setting

2.1.3. Historical Earthquakes
2.2. Methods
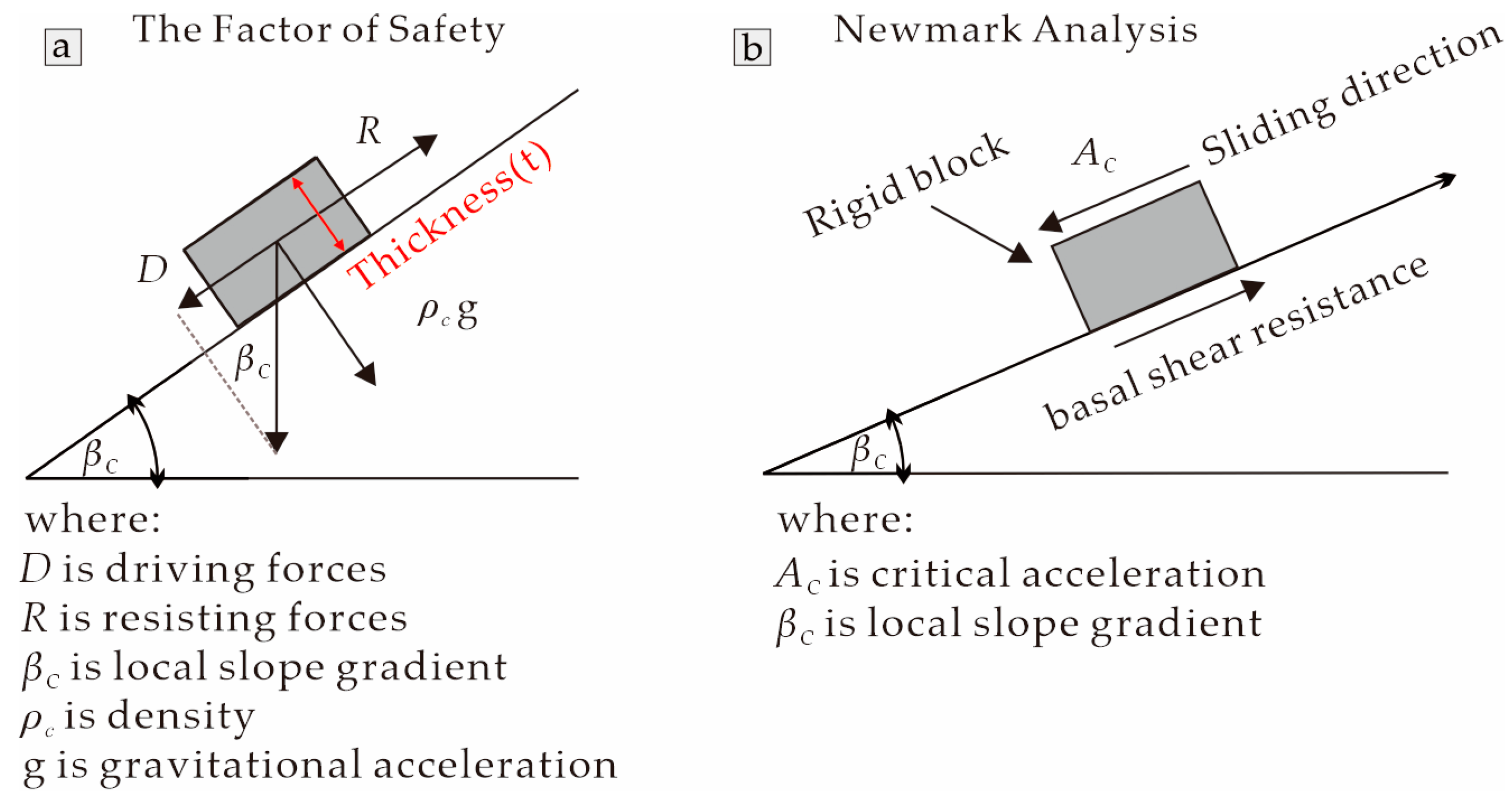
2.2.1. Review of the Newmark Model
2.2.2. Description of the Newmark Model’s Inputs
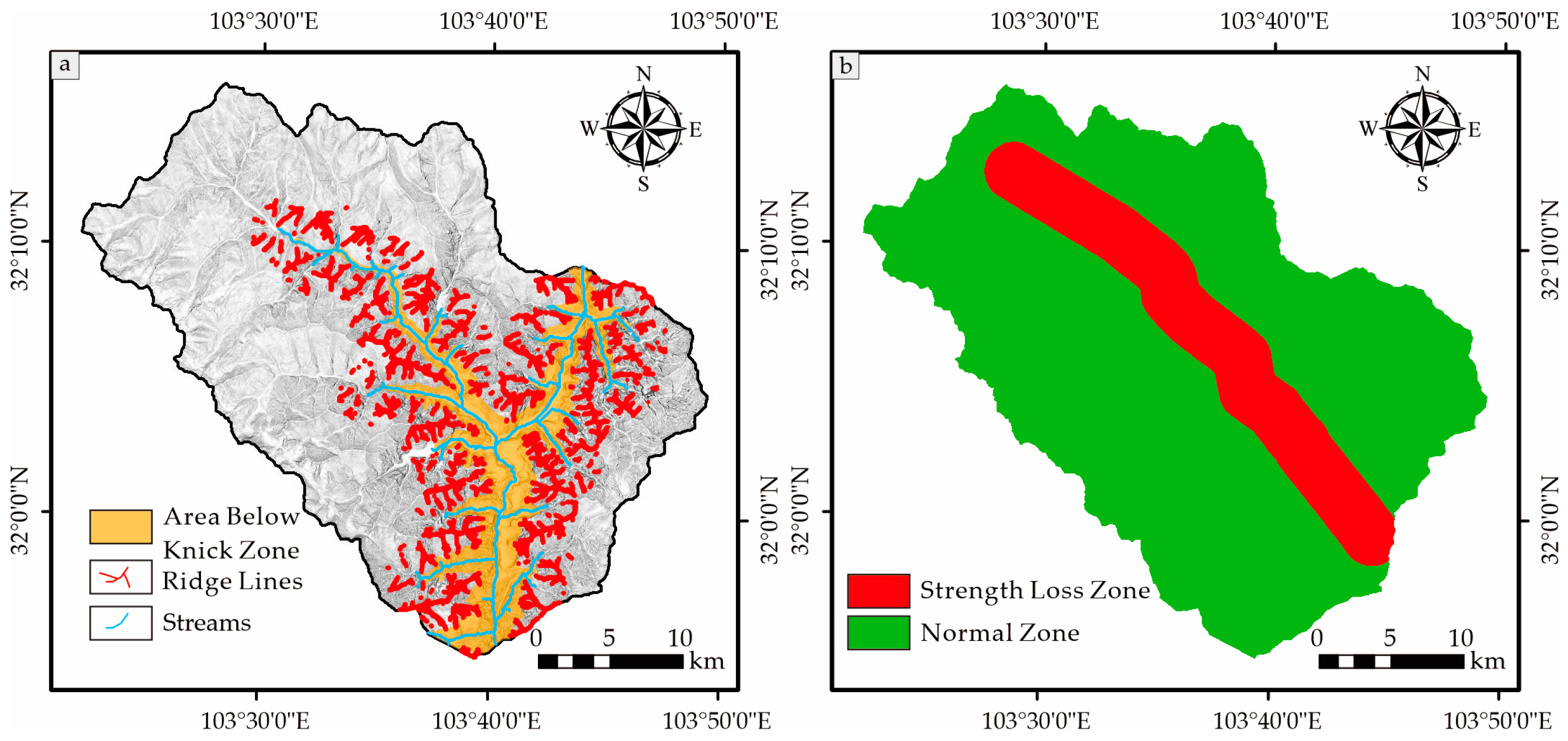
2.2.3. Optimization of Newmark Model’s Inputs
2.2.4. Automatic Extraction of Slope Units
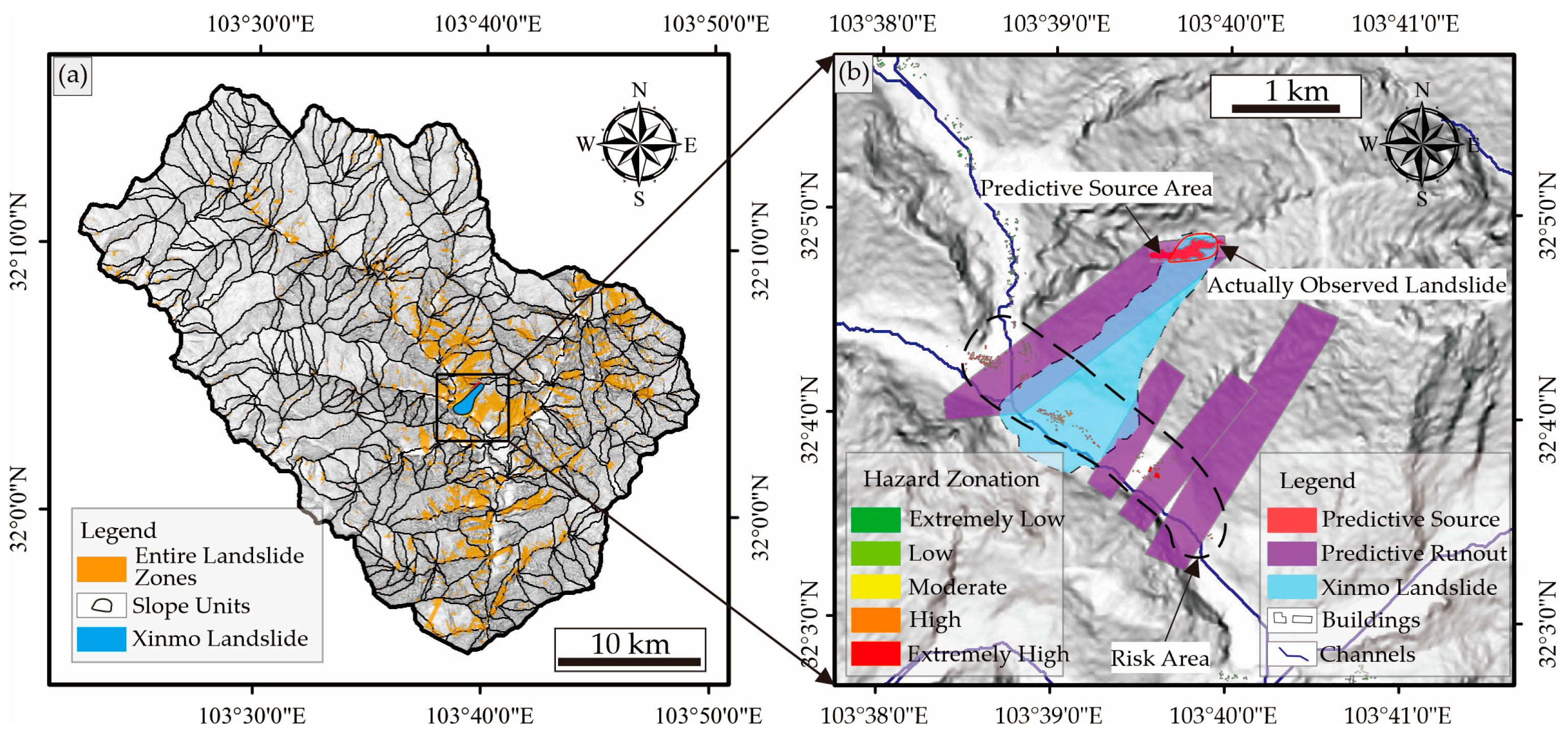
2.2.5. Procedure of Slope-Unit-Based Landslide Runout
2.2.6. Kernel-Density-Based Risk Identification
2.2.7. Application and Verification
3. Results
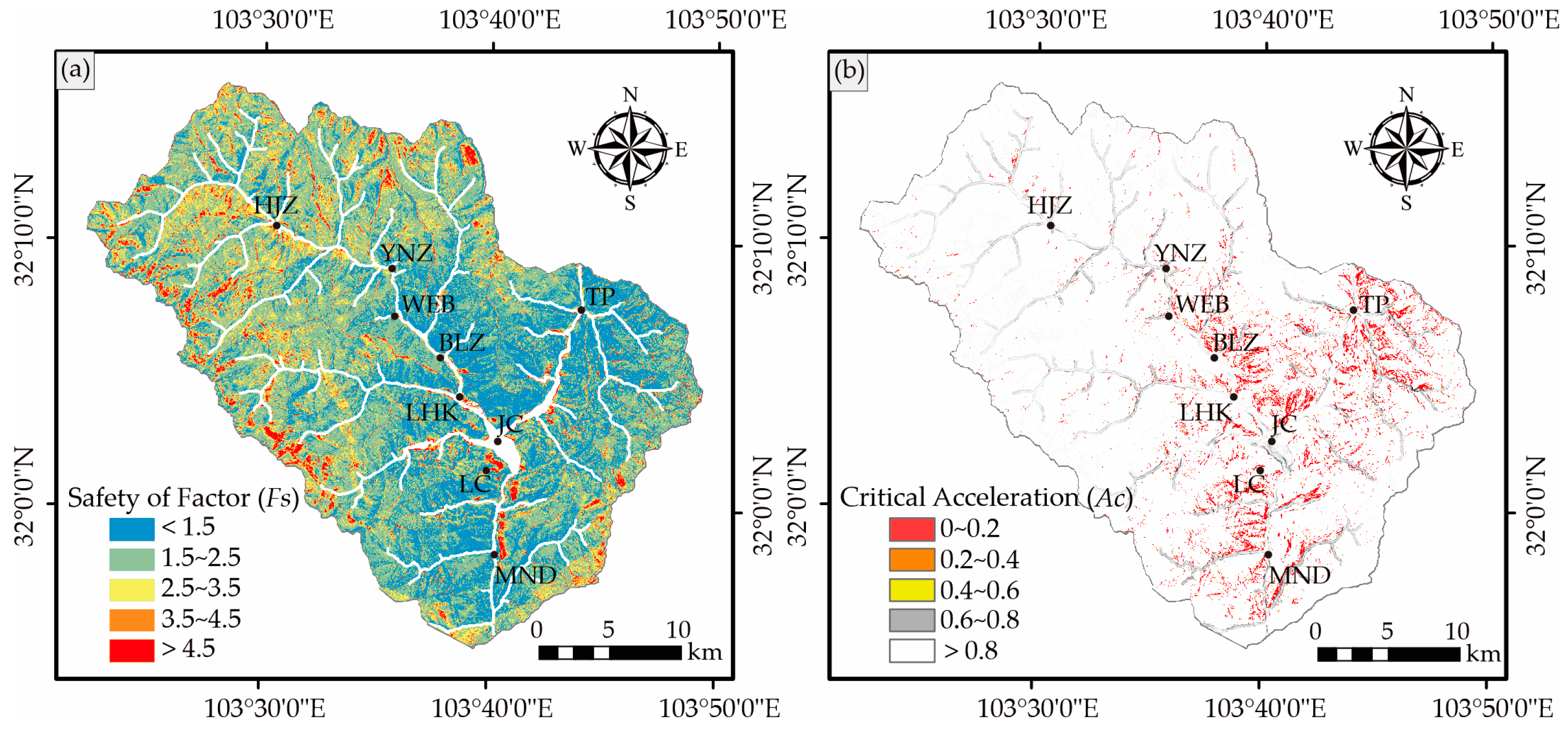
3.1. Newmark-Based Landslide Hazard Estimations
3.1.1. Generation of the Static Slope Stability and the Critical Acceleration Maps
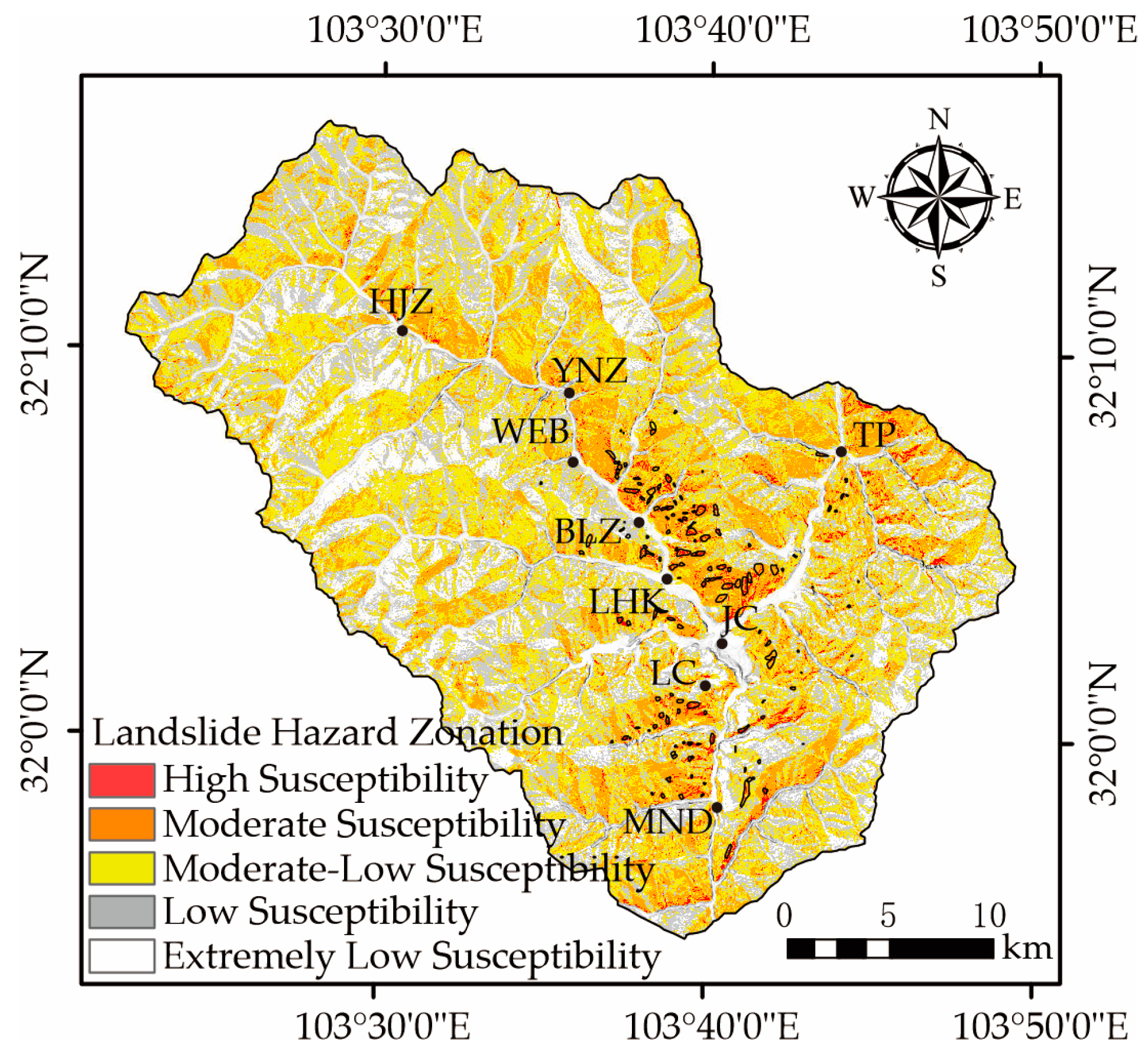
3.1.2. Landslide Hazard Zonation
3.2. Newmark-Runout-Based Infrastructural Risk Estimations
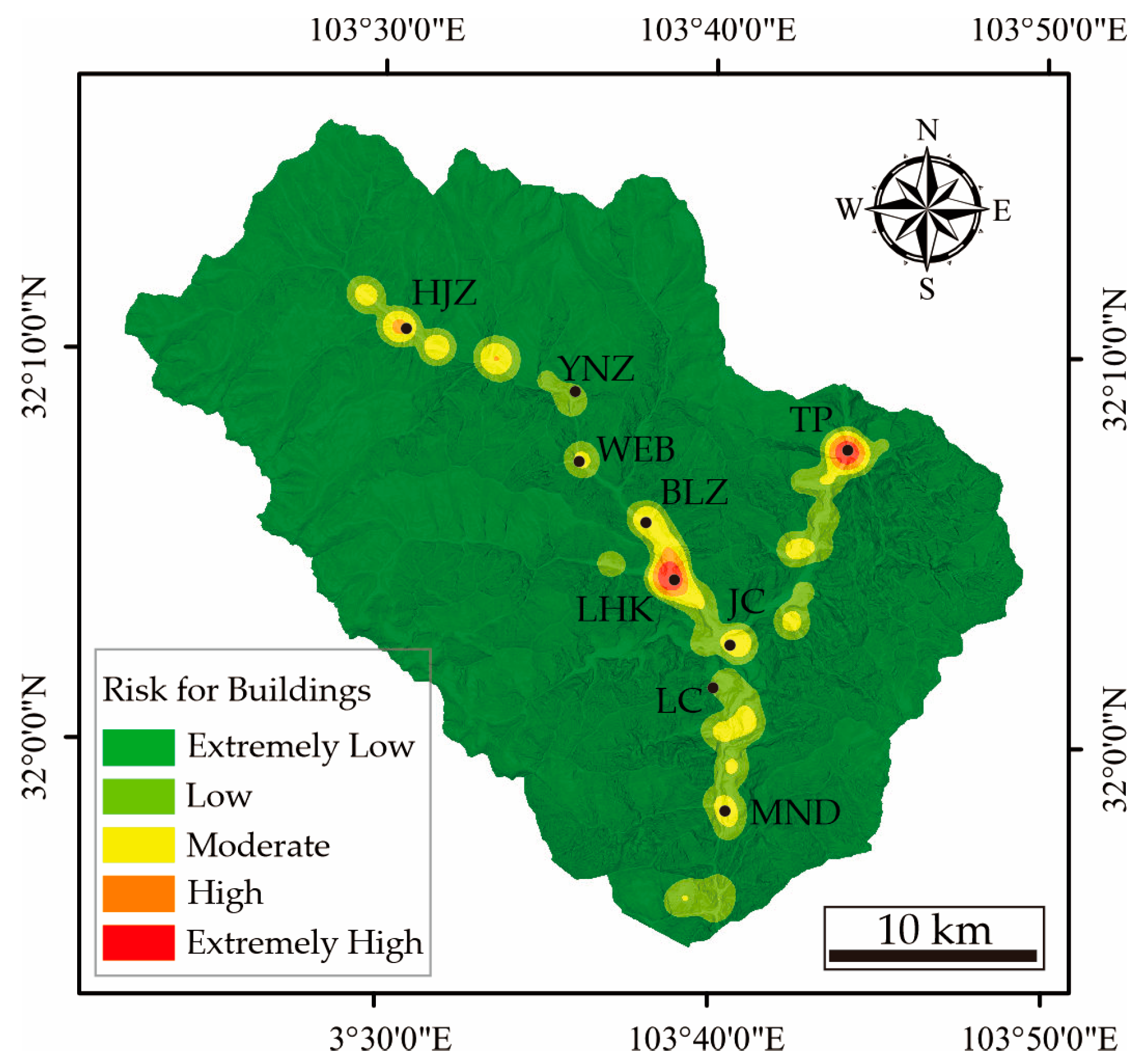
3.2.1. Risk Estimation of Buildings
3.2.2. Risk Estimation of Roads
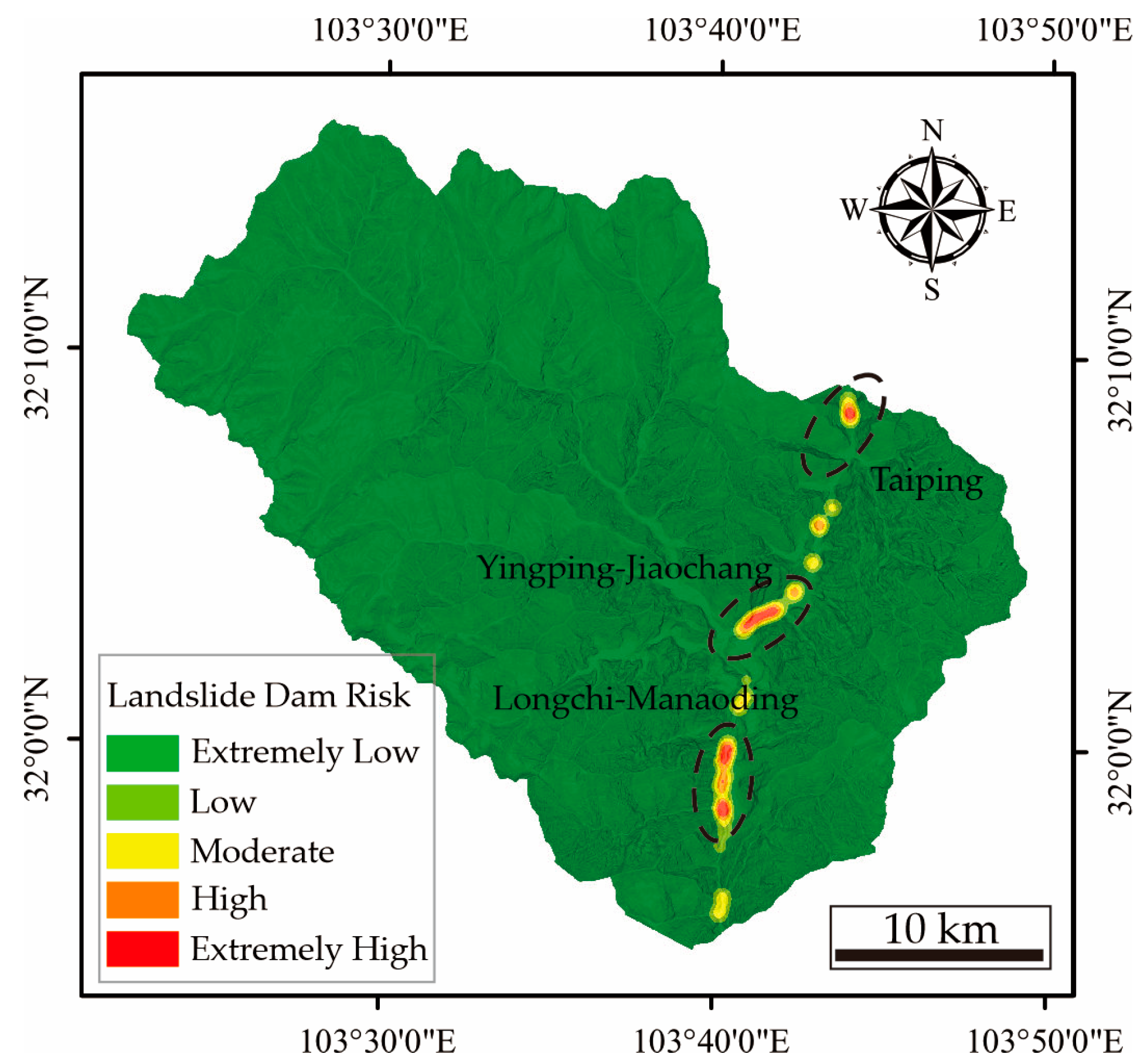
3.3. Landslide Dam Risk Estimations
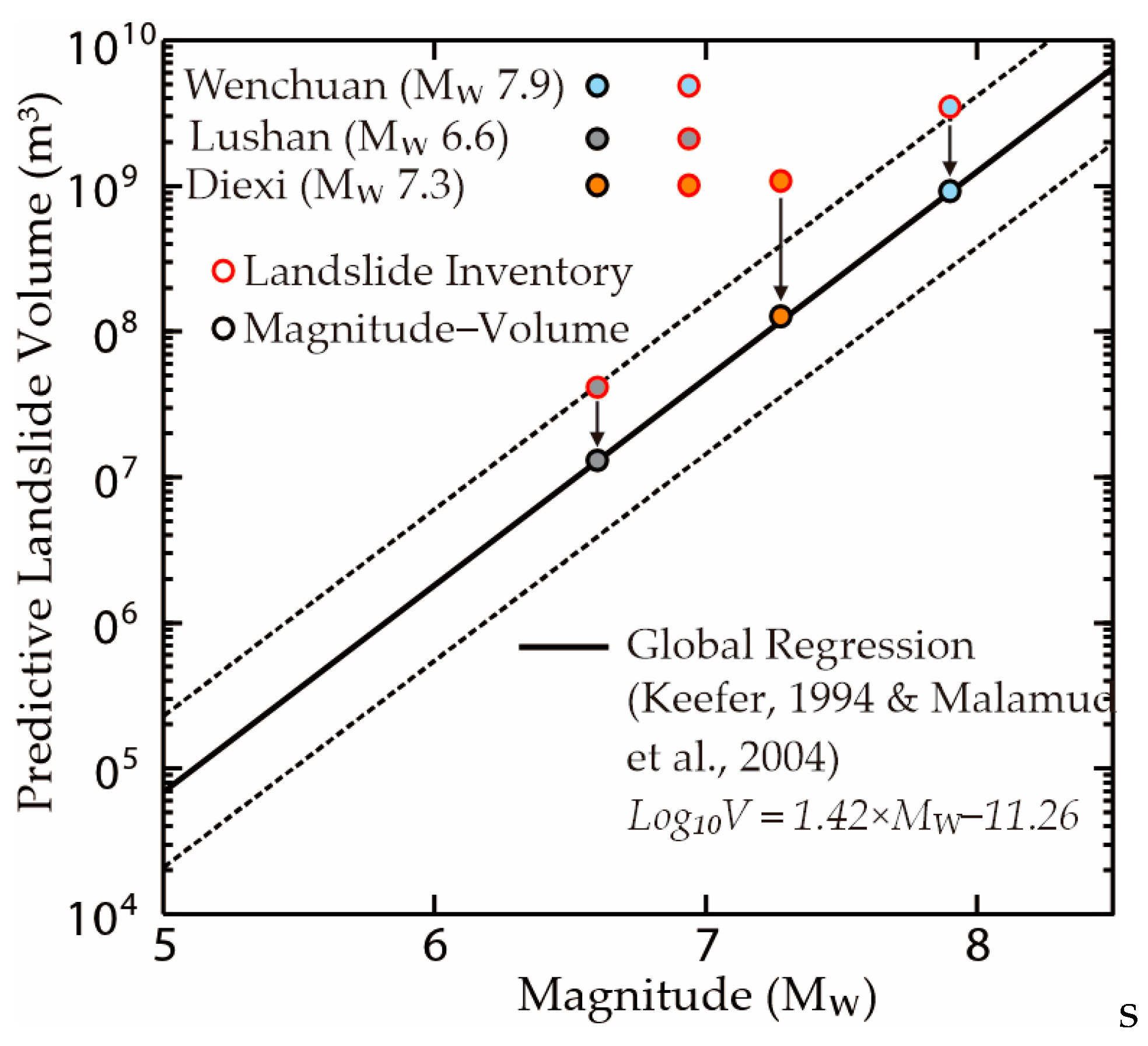
3.3.1. Estimation of Landslide Dam Volume
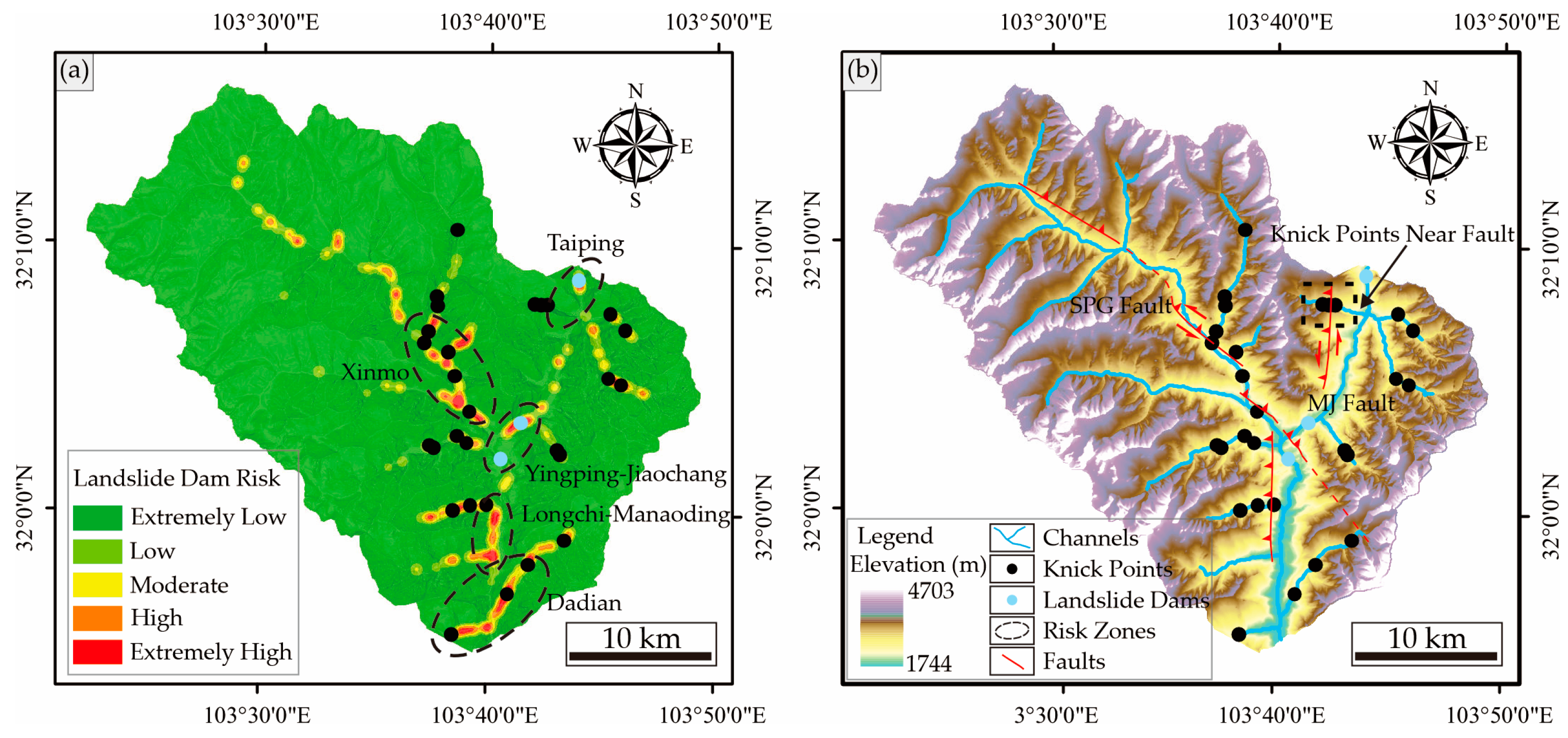
3.3.2. Spatial Distribution of Landslide Dams
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, X.M.; Scaringi, G.; Korup, O.; West, A.J.; Van Westen, C.J.; Tanyas, H.; Hovius, N.; Hales, T.C.; Jibson, R.W.; Allstadt, K.E.; et al. Earthquake-Induced Chains of Geologic Hazards: Patterns, Mechanisms, and Impacts. Rev. Geophys. 2019, 57, 421–503. [Google Scholar] [CrossRef]
- Cui, P.; Ge, Y.; Li, S.; Li, Z.; Xu, X.; Zhou, G.; Chen, H.; Wang, H.; Lei, Y.; Zhou, L.; et al. Scientific challenges in disaster risk reduction for the Sichuan–Tibet Railway. Eng. Geol. 2020, 309, 106837. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.W.; Yao, X.; Dai, F.C. Three (nearly) complete inventories of landslides triggered by the May 12, 2008 Wenchuan Mw 7.9 earthquake of China and their spatial distribution statistical analysis. Landslides 2014, 11, 441–461. [Google Scholar] [CrossRef]
- Xi, C.; Tanyas, H.; Lombardo, L.; He, K.; Hu, X.; Jibson, R. Estimating weakening on hillslopes caused by strong earthquakes. Commun. Earth Environ. 2024, 5, 81. [Google Scholar] [CrossRef]
- Yi, S.; Wu, C.; Cui, P.; Li, Y.; Lei, M. Cause of the Baige Landslides: Long-Term Cumulative Coupled Effect of Tectonic Action and Surface Erosion. Lithosphere 2022, 7, 7784535. [Google Scholar] [CrossRef]
- Livio, F.; Ferrario, M.F. Assessment of attenuation regressions for earthquake-triggered landslides in the Italian Apennines: Insights from recent and historical events. Landslides 2020, 17, 2825–2836. [Google Scholar] [CrossRef]
- Fan, X.M.; Domenech, G.; Scaringi, G.; Huang, R.Q.; Xu, Q.; Hales, T.; Dai, L.X.; Yang, Q.; Francis, O. Spatio-temporal evolution of mass wasting after the 2008 M-w 7.9 Wenchuan earthquake revealed by a detailed multi-temporal inventory. Landslides 2018, 15, 2325–2341. [Google Scholar] [CrossRef]
- Li, G.; West, A.J.; Densmore, A.L.; Jin, Z.; Zhang, F.; Wang, J.; Clark, M.; Hilton, R.G. Earthquakes drive focused denudation along a tectonically active mountain front. Earth Planet. Sci. Lett. 2017, 472, 253–265. [Google Scholar] [CrossRef]
- Ma, S.; Xu, C.; Shao, X. Spatial prediction strategy for landslides triggered by large earthquakes oriented to emergency response, mid-term resettlement and later reconstruction. Int. J. Disaster Risk Reduct. 2020, 43, 101362. [Google Scholar] [CrossRef]
- Gallen, S.; Clark, M.; Godt, J.; Roback, K.; Niemi, N. Application and evaluation of a rapid response earthquake-triggered landslide model to the 25 April 2015 Mw 7.8 Gorkha earthquake, Nepal. Tectonophysics 2016, 714, 173–187. [Google Scholar] [CrossRef]
- Saade, A.; Abou-Jaoude, G.; Wartman, J. Regional-scale co-seismic landslide assessment using limit equilibrium analysis. Eng. Geol. 2016, 204, 53–64. [Google Scholar] [CrossRef]
- Grant, A.; Wartman, J.; Abou-Jaoude, G. Multimodal method for coseismic landslide hazard assessment. Eng. Geol. 2016, 212, 146–160. [Google Scholar] [CrossRef]
- Newmark, N. Effects of Earthquakes on Dams and Embankments. Geotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Jibson, R.W. Predicting earthquake-induced landslide displacements using Newmark’s sliding block analysis. Transp. Res. Rec. 1993, 1411, 9–17. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Peng, W.F.; Wang, C.L.; Chen, S.T.; Lee, S.T. Incorporating the effects of topographic amplification and sliding areas in the modeling of earthquake-induced landslide hazards, using the cumulative displacement method. Comput. Geosci. 2009, 35, 946–966. [Google Scholar] [CrossRef]
- Yue, X.L.; Wu, S.H.; Yin, Y.H.; Gao, J.B.; Zheng, J.Y. Risk Identification of Seismic Landslides by Joint Newmark and RockFall Analyst Models: A Case Study of Roads Affected by the Jiuzhaigou Earthquake. Int. J. Disaster Risk Sci. 2018, 9, 392–406. [Google Scholar] [CrossRef]
- Huang, F.M.; Tao, S.Y.; Chang, Z.L.; Huang, J.S.; Fan, X.M.; Jiang, S.H.; Li, W.B. Efficient and automatic extraction of slope units based on multi-scale segmentation method for landslide assessments. Landslides 2021, 18, 3715–3731. [Google Scholar] [CrossRef]
- Alvioli, M.; Guzzetti, F.; Marchesini, I. Parameter-free delineation of slope units and terrain subdivision of Italy. Geomorphology 2020, 358, 107124. [Google Scholar] [CrossRef]
- Alvioli, M.; Marchesini, I.; Reichenbach, P.; Rossi, M.; Ardizzone, F.; Fiorucci, F.; Guzzetti, F. Automatic delineation of geomorphological slope units with r.slopeunits v1.0 and their optimization for landslide susceptibility modeling. Geosci. Model Dev. 2016, 9, 3975–3991. [Google Scholar] [CrossRef]
- Deng, B.; Liu, S.G.; Liu, S.; Li, Z.W. The micro-strain mechanism of Jiaochang arc structure in Songpan-Garze fold belt, Sichuan, China. Geol. Bull. China 2010, 29, 697–706. (In Chinese) [Google Scholar]
- Cook, K.L.; Royden, L.H.; Burchfiel, B.C.; Lee, Y.-H.; Tan, X. Constraints on Cenozoic tectonics in the southwestern Longmen Shan from low-temperature thermochronology. Lithosphere 2013, 5, 393–406. [Google Scholar] [CrossRef]
- Chen, Y.L.; Li, D.P.; Zhou, J.; Liu, F.; Zhang, H.F.; Nie, L.S.; Jiang, L.T.; Song, B.; Liu, X.M.; Wang, Z. U-Pb dating, geochemistry, and tectonic implications of the Songpan-Ganzi block and the Longmen Shan, China. Geochem. J. 2009, 243, 77–99. [Google Scholar] [CrossRef]
- Li, Y.; Cao, S.; Zhou, R.; Densmore, A.L.; Aellis, M. Late Cenozoic Minjiang Incision Rate and Its Constraint on the Uplift of the Eastern Margin of the Tibetan Plateau. Acta Geol. Sin. 2005, 79, 28–37. [Google Scholar] [CrossRef]
- Zhao, S.; Chigira, M.; Wu, X. Gigantic rockslides induced by fluvial incision in the Diexi area along the eastern margin of the Tibetan Plateau. Geomorphology 2019, 338, 27–42. [Google Scholar] [CrossRef]
- Xu, Z.Q.; Hou, L.W.; Wang, Z.X. Mountain Building Processes of the Songpan-Ganzi Orogency; Geological Publishing House: Beijing, China, 1992. (In Chinese) [Google Scholar]
- Shao, C.J.; Li, Y.; Lan, H.X.; Li, P.Y.; Zhou, R.J.; Ding, H.R.; Yan, Z.K.; Dong, S.L.; Yan, L.; Deng, T. The role of active faults and sliding mechanism analysis of the 2017 Maoxian postseismic landslide in Sichuan, China. Bull. Eng. Geol. Environ. 2019, 78, 5635–5651. [Google Scholar] [CrossRef]
- Cui, S.H.; Wu, H.; Pei, X.J.; Yang, Q.W.; Huang, R.Q.; Guo, B. Characterizing the spatial distribution, frequency, geomorphological and geological controls on landslides triggered by the 1933 Mw 7.3 Diexi Earthquake, Sichuan, China. Geomorphology 2022, 403, 108177. [Google Scholar] [CrossRef]
- Chen, J.H.; Liu, Q.Y.; Li, S.C.; Guo, B.; Wang, J.; Qi, S.H. Seismotectonic study by relocation of the Wenchuan M(S)8.0 earthquake sequence. Chin. J. Geophys. Chin. Ed. 2009, 52, 390–397. (In Chinese) [Google Scholar]
- Jones, L.M.; Han, W.; Hauksson, E.; Jin, A.; Zhang, Y.; Luo, Z. Focal mechanisms and aftershock locations of the Songpan earthquakes of August 1976 in Sichuan, China. J. Geophys. Res. Solid Earth 1984, 89, 7697–7707. [Google Scholar] [CrossRef]
- Huang, Z.; Tang, R.; Liu, S. Re-discussion of the Seismogenic Structure of the Diexi Large Earthquake in 1933 and the Arc Tectonics on Jiaochang, Sichuan Province. Earthq. Res. China 2002, 18, 183–192. [Google Scholar] [CrossRef]
- Jibson, R.; Harp, E.; Michael, J. A method for producing digital probabilistic seismic landslide hazard maps. Eng. Geol. 2000, 58, 271–289. [Google Scholar] [CrossRef]
- Dreyfus, D.; Rathje, E.M.; Jibson, R.W. The influence of different simplified sliding-block models and input parameters on regional predictions of seismic landslides triggered by the Northridge earthquake. Eng. Geol. 2013, 163, 41–54. [Google Scholar] [CrossRef]
- Chen, X.L.; Liu, C.G.; Yu, L.; Lin, C.X. Critical acceleration as a criterion in seismic landslide susceptibility assessment. Geomorphology 2014, 217, 15–22. [Google Scholar] [CrossRef]
- Gallen, S.F.; Clark, M.K.; Godt, J.W. Coseismic landslides reveal near-surface rock strength in a high-relief, tectonically active setting. Geology 2015, 43, 11–14. [Google Scholar] [CrossRef]
- Chen, L.X.; Mei, L.; Zeng, B.; Yin, K.L.; Shrestha, D.P.; Du, J. Failure probability assessment of landslides triggered by earthquakes and rainfall: A case study in Yadong County, Tibet, China. Sci. Rep. 2020, 10, 16531. [Google Scholar] [CrossRef]
- GB/T 50218-2014; Standard for Engineering Classification of Rock Mass. Standards Press of China: Beijing, China, 2014. (In Chinese)
- Li, C.; Su, L.J. Influence of critical acceleration model on assessments of potential earthquake-induced landslide hazards in Shimian County, Sichuan Province, China. Landslides 2021, 18, 1659–1674. [Google Scholar] [CrossRef]
- Meunier, P.; Hovius, N.; Haines, J. Topographic site effects and the location of earthquake induced landslides. Earth Planet. Sci. Lett. 2008, 275, 221–232. [Google Scholar] [CrossRef]
- Kirkpatrick, H.M.; Moon, S.; Yin, A.; Harrison, T.M. Impact of fault damage on eastern Tibet topography. Geology 2021, 49, 30–34. [Google Scholar] [CrossRef]
- Dunham, A.; Kiser, E.; Kargel, J.; Haritashya, U.; Watson, C.S.; Shugar, D.; Hughes, A.; DeCelles, P. Topographic Control on Ground Motions and Landslides From the 2015 Gorkha Earthquake. Geophys. Res. Lett. 2022, 49, e2022GL098582. [Google Scholar] [CrossRef]
- Caccavale, M.; Matano, F.; Sacchi, M. An integrated approach to earthquake-induced landslide hazard zoning based on probabilistic seismic scenario for Phlegrean Islands (Ischia, Procida and Vivara), Italy. Geomorphology 2017, 295, 235–259. [Google Scholar] [CrossRef]
- Xu, W.; Wu, J.; Gao, M. Seismic Hazard Analysis of China’s Mainland Based on a New Seismicity Model. Int. J. Disaster Risk Sci. 2023, 14, 280–297. [Google Scholar] [CrossRef]
- Legros, F. The mobility of long-runout landslides. Eng. Geol. 2002, 63, 301–331. [Google Scholar] [CrossRef]
- Crosta, G.B.; De Blasio, F.V.; Frattini, P. Global Scale Analysis of Martian Landslide Mobility and Paleoenvironmental Clues. J. Geophys. Res. Planets 2018, 123, 872–891. [Google Scholar] [CrossRef]
- Larsen, I.J.; Montgomery, D.R.; Korup, O. Landslide erosion controlled by hillslope material. Nat. Geosci. 2010, 3, 247–251. [Google Scholar] [CrossRef]
- Fan, X.; Van Westen, C.J.; Korup, O.; Gorum, T.; Xu, Q.; Dai, F.; Huang, R.; Wang, G. Transient water and sediment storage of the decaying landslide dams induced by the 2008 Wenchuan earthquake, China. Geomorphology 2012, 171, 58–68. [Google Scholar] [CrossRef]
- Baddeley, A.; Turner, R. Spatstat: An R package for analyzing spatial point patterns. J. Stat. Softw. 2005, 12, 1–42. [Google Scholar] [CrossRef]
- Huang, D.; Li, Y.Q.; Song, Y.X.; Xu, Q.; Pei, X.J. Insights into the catastrophic Xinmo rock avalanche in Maoxian county, China: Combined effects of historical earthquakes and landslide amplification. Eng. Geol. 2019, 258, 105158. [Google Scholar] [CrossRef]
- Dai, L.X.; Fan, X.M.; Jansen, J.D.; Xu, Q. Landslides and fluvial response to landsliding induced by the 1933 Diexi earthquake, Minjiang River, eastern Tibetan Plateau. Landslides 2021, 18, 3011–3025. [Google Scholar] [CrossRef]
- Zhao, S.; Chigira, M.; Wu, X. Buckling deformations at the 2017 Xinmo landslide site and nearby slopes, Maoxian, Sichuan, China. Engineering Geology 2018, 246, 187–197. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.; Shyu, J.B.H. Database and spatial distribution of landslides triggered by the Lushan, China Mw 6.6 earthquake of 20 April 2013. Geomorphology 2015, 248, 77–92. [Google Scholar] [CrossRef]
- Li, G.; West, A.J.; Densmore, A.L.; Hammond, D.E.; Jin, Z.; Zhang, F.; Wang, J.; Hilton, R.G. Connectivity of earthquake-triggered landslides with the fluvial network: Implications for landslide sediment transport after the 2008 Wenchuan earthquake. J. Geophys. Res. Earth Surf. 2016, 121, 703–724. [Google Scholar] [CrossRef]
- Keefer, D.K. The importance of earthquake-induced landslides to long-term slope erosion and slope-failure hazards in seismically active regions. Geomorphology 1994, 10, 265–284. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L.; Guzzetti, F.; Reichenbach, P. Landslide inventories and their statistical properties. Earth Surf. Process. Landf. 2004, 29, 687–711. [Google Scholar] [CrossRef]
- Parker, R.N.; Densmore, A.L.; Rosser, N.J.; De Michele, M.; Li, Y.; Huang, R.Q.; Whadcoat, S.; Petley, D.N. Mass wasting triggered by the 2008 Wenchuan earthquake is greater than orogenic growth. Nat. Geosci. 2011, 4, 449–452. [Google Scholar] [CrossRef]
- Fan, X.M.; Yunus, A.P.; Jansen, J.D.; Dai, L.X.; Strom, A.; Xu, Q. Comment on ‘Gigantic rockslides induced by fluvial incision in the Diexi area along the eastern margin of the Tibetan Plateau’ by Zhao et al. (2019) Geomorphology 338, 27–42. Geomorphology 2019, 402, 106963. [Google Scholar] [CrossRef]
- Liu, F.; Li, J.; Yang, S. Landslide erosion associated with the Wenchuan earthquake in the Minjiang River watershed: Implication for landscape evolution of the Longmen Shan, eastern Tibetan Plateau. Nat. Hazards 2015, 76, 1911–1926. [Google Scholar] [CrossRef]
- Xie, M.W.; Esaki, T.; Cai, M.F. A time-space based approach for mapping rainfall-induced shallow landslide hazard. Environ. Geol. 2004, 46, 840–850. [Google Scholar] [CrossRef]
- Wang, H.; Wang, G.; Wang, F.; Sassa, K.; Chen, Y. Probabilistic modeling of seismically triggered landslides using Monte Carlo simulations. Landslides 2008, 5, 387–395. [Google Scholar] [CrossRef]
- Guo, D.; Hamada, M.; He, C.; Wang, Y.; Zou, Y. An empirical model for landslide travel distance prediction in Wenchuan earthquake area. Landslides 2014, 11, 281–291. [Google Scholar] [CrossRef]

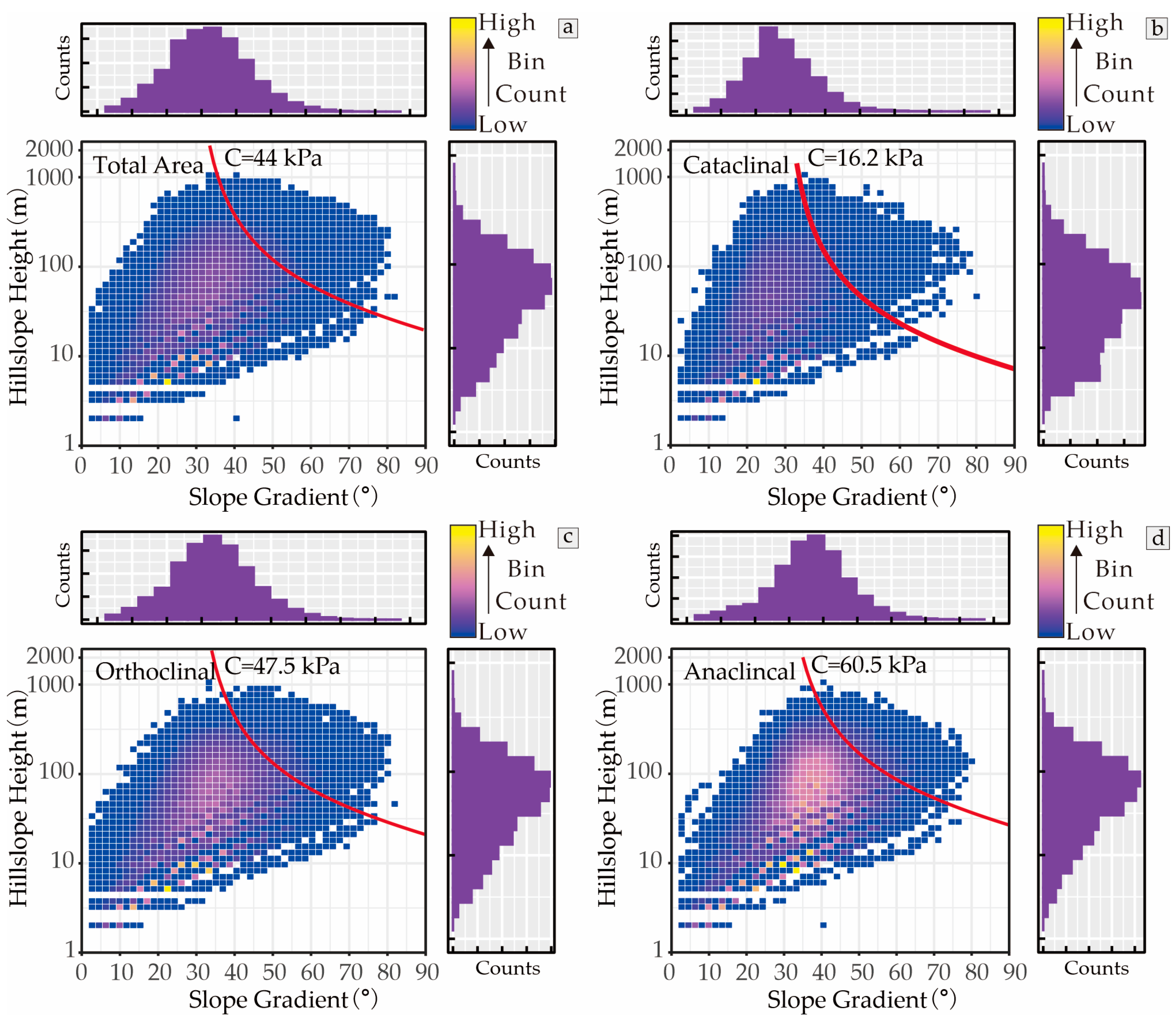






| Lithological Group | Lithological Description | Units | c (kPa) | φ (°) | γ (kN/m3) | t (m) | Area (km2) | Proportion (%) |
|---|---|---|---|---|---|---|---|---|
| Type I | Thick-bedded quartz sandstone interbedded with limestone, slate, and phyllite | ZGN C + P | 32 | 33 | 25 | 3.0 | 269 | 30.40 |
| Type II | Medium-thick-bedded quartz sandstone interbedded with limestone | ZWU | 30 | 31 | 24 | 2.5 | 528 | 59.66 |
| Type III | Thin-bedded slate and phyllite | BCG XDQ | 28 | 29 | 23 | 2.0 | 88 | 9.94 |
| Infrastructural Type | Hazard Levels | ||||
|---|---|---|---|---|---|
| Extremely Low | Low | Moderate | High | Extremely High | |
| Buildings | <500 m | 300~500 m | 200~300 m | 100~200 m | ≤100 m |
| Roads | <400 m | 250~400 m | 150~250 m | 50~150 m | ≤50 m |
| Value | 1 | 2 | 3 | 4 | 5 |
| Newmark Model (AC/PGA) | High | Moderate | Moderate–Low | Low | Extremely Low |
|---|---|---|---|---|---|
| <4.06 | 4.06~14.12 | 14.12~22.27 | 22.27~30.63 | >30.63 | |
| Exceedance probability of 2% (km2) | 13.47 | 176.96 | 283.94 | 224.67 | 104.33 |
| Evaluation Parameter | Newmark Model (Exceedance Probability of 2%) |
|---|---|
| Correctly predicted source area (A) (km2) | 1.53 |
| Falsely predicted source area (B) (km2) | 11.94 |
| Total predicted source area (A + B) (km2) | 13.47 |
| Correctly predicted stable area (C) (km2) | 784.07 |
| Actual landslide source area (D) (km2) | 5.13 |
| Total study area (E) (km2) | 803.37 |
| Landslide failure capture (LFC) (A/D) (%) | 29.83 |
| Total landslide prediction proportion (TLPP) (A + B)/E (%) | 1.68 |
| Efficiency (LFC-TLPP) (%) | 28.15 |
| Accuracy (A + C)/E (km2) | 97.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Ye, C.; Pei, X.; Oguchi, T.; He, Z.; Yang, H.; Huang, R. Incorporating Effects of Slope Units and Sliding Areas into Seismically Induced Landslide Risk Modeling in Tectonically Active Mountainous Areas. Remote Sens. 2024, 16, 3517. https://doi.org/10.3390/rs16183517
Wu H, Ye C, Pei X, Oguchi T, He Z, Yang H, Huang R. Incorporating Effects of Slope Units and Sliding Areas into Seismically Induced Landslide Risk Modeling in Tectonically Active Mountainous Areas. Remote Sensing. 2024; 16(18):3517. https://doi.org/10.3390/rs16183517
Chicago/Turabian StyleWu, Hao, Chenzuo Ye, Xiangjun Pei, Takashi Oguchi, Zhihao He, Hailong Yang, and Runqiu Huang. 2024. "Incorporating Effects of Slope Units and Sliding Areas into Seismically Induced Landslide Risk Modeling in Tectonically Active Mountainous Areas" Remote Sensing 16, no. 18: 3517. https://doi.org/10.3390/rs16183517
APA StyleWu, H., Ye, C., Pei, X., Oguchi, T., He, Z., Yang, H., & Huang, R. (2024). Incorporating Effects of Slope Units and Sliding Areas into Seismically Induced Landslide Risk Modeling in Tectonically Active Mountainous Areas. Remote Sensing, 16(18), 3517. https://doi.org/10.3390/rs16183517







