Abstract
Conventional altimetry has greatly advanced our understanding of mesoscale eddies but falls short in studying fine-scale eddies (<150 km). The newly launched Surface Water and Ocean Topography (SWOT) altimeter, however, with its unprecedented high-resolution capabilities, offers new opportunities to observe these fine-scale eddies. In this study, we use SWOT data to explore these previously elusive fine-scale eddies in the Kuroshio Extension. During SWOT’s fast sampling phase from 29 May 2023 to 10 July 2023, we identified an average of 4.5 fine-scale eddies within each 120 km wide swath. Cyclonic eddies, which are slightly more frequent than the anticyclonic ones (ratio of 1.16), have a similar mean radius of 23.4 km. However, cyclonic eddies exhibit higher amplitudes, averaging 3.5 cm compared to 2.8 cm for anticyclonic eddies. In contrast to the mesoscale eddies detected by conventional altimeters, the fine-scale eddies revealed by SWOT are characterized by smaller sizes and weaker amplitudes. This study offers a preliminary view of fine-scale eddy characteristics from space, highlighting SWOT’s potential to advance our understanding of these dynamic processes. Nonetheless, it also emphasizes the necessity for comprehensive analysis to fully exploit the satellite’s capabilities in monitoring and interpreting complex eddy behaviors.
1. Introduction
Oceanic eddies are persistent, circular features in the ocean, typically ranging in size from tens to hundreds of kilometers [1]. These eddies are integral to ocean circulation, impacting both larger- and smaller-scale movements [2,3]. They contain a significant portion of the oceanic kinetic energy [4,5] and are crucial for transporting water mass, heat, dissolved carbon, and other biogeochemical tracers [6,7,8].
Historically, the sparse resolution of in situ observations has limited our understanding of eddies on a global level. The advent of satellite altimeters has greatly addressed this issue by providing continuous sea surface height (SSH) measurements globally [1,9]. Many studies have used the gridded SSH maps from the Data Unification and Altimeter Combination System (DUACS) to identify and characterize eddies [1,10,11,12,13,14,15,16,17,18]. However, conventional altimeters only measure SSH along their nadir tracks, meaning they can resolve only mesoscale eddies with a spatial scale of approximately 150–200 km due to the large gaps between satellite tracks [19,20]. As a result, these products capture only 6–16% of the total number of eddies, leaving the most abundant fine-scale eddies beneath 150 km unresolved [21]. While this indicates that satellite-based products may struggle to detect the full range of eddy sizes, these findings are based on pseudo-observation experiments from realistic numerical ocean models [21]. Given that many studies use altimetry data to validate or constrain ocean models [22,23], the accuracy of these high-resolution “realistic” ocean models in representing the ground truth of oceanic eddies remains uncertain, necessitating further investigation into the “missed” eddies under 150 km.
To enhance our understanding of fine-scale eddies below 150 km from space, the Surface Water and Ocean Topography (SWOT) mission was developed [24,25] and successfully launched in December 2022 [26]. The primary instrument of the SWOT mission is a Ka-band radar interferometer (KaRIn), which offers high-resolution SSH observations over a 120 km wide swath centered on the SWOT nadir track. However, a 20 km gap exists in the middle of the swath due to measurement errors [24], which is complemented by the conventional nadir altimeter onboard SWOT. SWOT provides two-dimensional level-3 SSH maps with a 2 km grid spacing [26,27]. Preliminary analysis shows that instrumental noise has a standard deviation of less than 0.4 cm, enabling the resolution of ocean signals with wavelengths down to 5 km, an order of magnitude finer than the previous nadir altimeters (~50 km) [26]. Moreover, SWOT initially operated in a fast calibration and validation phase with a 1-day repeat orbit (Cal/Val orbit) before transitioning to its science orbit with a 21-day repeat cycle. This high temporal resolution is particularly valuable for examining fine-scale processes, which typically have a shorter time scale, associated with their spatial scale [28,29].
Therefore, the unprecedented spatial and temporal resolution of SWOT allows for a deeper understanding of fine-scale oceanic eddies that were previously undetectable from space. By concurrently using SWOT observation and a mooring array, Zhang et al. [30] successfully captured two fine-scale eddies in the northwestern Pacific Subtropical Countercurrent (STCC) region during spring 2023. This discovery not only confirms the presence of fine-scale eddies in the STCC region, but also demonstrates SWOT’s capability to detect fine-scale eddies with scales around 10 km. Despite these case studies, further investigation is needed to understand the characteristics of the fine-scale eddies.
The Kuroshio Extension (KE, black box in Figure 1) is the extension of the western boundary current of the North Pacific Ocean Subtropical Gyre, occurring after the Kuroshio Current separates from the coast of Japan. Known for its strong meanders and formation of energetic eddies (Figure 1) [31,32,33], eddies in this region have been extensively studied using the DUACS SSH dataset on the identification, properties, variability, and dynamics of mesoscale eddies [34,35,36,37]. However, as previously noted, the DUACS SSH dataset is insufficient for accurately capturing fine-scale eddies ranging from 10 to 150 km. In contrast, SWOT has the capability to observe these features.
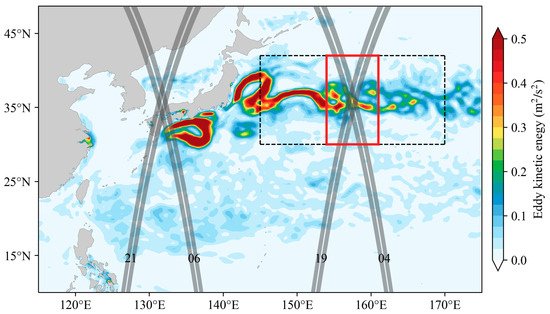
Figure 1.
Eddy kinetic energy averaged over the SWOT Cal/Val period. The gray swaths denote the SWOT Cal/Val orbit in the northwest Pacific. The number of orbit passes are labeled at the bottom of the figure. The black box represents the KE region. The red box denotes the study region of the fine-scale eddies.
In this study, we use SSH data from SWOT and traditional nadir altimeters to investigate fine-scale eddies that are missed by conventional SSH products but detectable with the new-generation SWOT satellite. The paper is structured as follows: Section 2 describes the altimetry datasets, data processing methods, and eddy identification schemes; Section 3 presents the results of eddy detection using both conventional altimetry and SWOT data; Section 4 offers a brief discussion on the prospects and challenges of using SWOT in the future; and finally, Section 5 summarizes the key findings.
2. Materials and Methods
2.1. Altimetry Data
In this study, we utilized level-4 sea level anomaly (SLA) data from the DUACS to represent conventional altimeter measurements. The DUACS provides a comprehensive sea level product through the European Copernicus Marine Service (CMS), integrating along-track measurements from multiple altimetry satellites since 1993. The SLA dataset offers a temporal resolution of 1 day and a spatial resolution of 0.25°, computed using optimal interpolation relative to a twenty-year mean (1993–2012). Due to the limited coverage of the SWOT Cal/Val orbit, we selected SLA data from 29 March 2023 to 10 July 2023. The DOI of the product is 10.48670/moi-00149.
For the new-generation altimeter measurements, we used the level-3 KaRIn low-rate sea surface height (SSH) data product, version 1.0. Specifically, we employed the variable “ssha_noiseless”, which represents sea surface height anomalies with all corrections applied and denoised using the U-Net model and Gomez algorithm [38,39]. During the Cal/Val orbit between 29 March and 11 July 2023, the 004 pass and 019 pass of SWOT crossed through the KE region and intersected around 37.5°N (gray lines in Figure 1). This product provides along-swath SSH measurements with a spatial resolution of 2 km along-track and 2 km cross-track. Within the KE region, the temporal resolution for data from the same pass is approximately 1 day. However, the temporal resolution between different passes, passes 004 and 019, is about half a day. This product is freely available on 10.24400/527896/A01-2023.017.
2.2. Data Processing
To highlight the fine-scale eddy features detected by SWOT measurements, we use the DUACS dataset to represent the background information, regarding it as representative of the mesoscale SSH fluctuations. We explore fine-scale eddies by examining the differences in sea level anomalies (SLA) between SWOT and DUACS data, following methods established in previous studies [30,40]. However, due to differences in data structure between the two datasets, several processing steps are required before calculating SLA differences.
The level-3 SWOT data include measurements from both the nadir altimeter and the KaRIn (Figure 2a). The nadir altimeter is intended to fill the large gap in the middle of the swath. However, combining measurements from the two different instruments appears problematic, particularly around 34.2°N (black ellipse in Figure 2b), indicating potential systematic errors between the nadir and KaRIn measurements. Consequently, the gap was filled by linearly interpolating only the KaRIn measurements in the cross-track direction, as shown in Figure 2c.
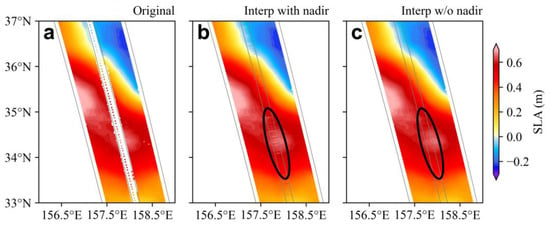
Figure 2.
(a) A snapshot of SWOT-observed SSH anomalies, including both the nadir altimeter (scattered points in the middle) and KaRIn measurements (filled color on the sides). (b) Linear interpolation across the swath with both the nadir and KaRIn measurements. (c) Linear interpolation across the swath with only the KaRIn measurements. The black ellipse highlights the significant differences between (b) and (c).
Considering the possibility of systematic biases between SWOT and its nadir altimeter, similar biases may be present between SWOT and DUACS data. To ensure a fair comparison, we computed SLAs by subtracting the corresponding time means from the Cal/Val period (29 March to 11 July 2023) following Zhang et al. [30]. The DUACS SLA data were then bilinearly interpolated onto the SWOT grid and subtracted from the SWOT data to obtain the SLA differences between SWOT and the DUACS.
2.3. Eddy Identification Method for DUACS Data
Version 3.6.1 of the py-eddy-tracker, a method for identifying eddies based on SSH [41], was applied to the daily SLA fields from the DUACS. Prior to applying the method, individual SLA field was first spatially high-pass filtered using a Gaussian filter within a 5° 5° box. The key identifying parameters are based on the following criteria:
- SLA contours are computed at 0.1 cm intervals.
- The number of internal grids is ≥1 and <4000. Since we focus on the fine-scale eddies in this study, we do not limit the minimum eddy size, but the maximum eddy size is constrained by the total pixel count in the KE region.
- Pass a shape test with error ≤ 55%, where the error is defined as the ratio between the areal sum of closed SLA contour deviations from its fitted circle and the area of that circle.
- The amplitude of the eddy is ≥3 cm for avoiding the interference of SSH noise.
Following these criteria, eddies in the KE region can be identified, along with their quantified amplitudes and radii. It worth noting that only ~100 days of SLA snapshots were available, the eddy tracking method was not applied, and the lifespan of the identified eddies was not calculated. Although SLA snapshots are consecutive, they were treated as individual observations for eddy identification. The python package of this method can be found via: 10.5281/zenodo.7197432.
2.4. Eddy Identification Method for SWOT Data
Fine-scale eddies were identified based on the SLA differences between SWOT and DUACS data using the same method [41]. Before applying the identification method, the SLA differences were interpolated onto a uniformed grid with a 0.02° interval. To eliminate interpolation-induced noise, a low-pass filter with 10 km of cut-off wavelength was applied to the uniformed gridded data. The eddy identification criteria are as follows:
- SLA contours are computed at 0.05 cm intervals. Because the mesoscale signals were filtered out by subtracting the DUACS data, the remaining SLA magnitude is reduced. Therefore, the contour intervals are adjusted to 0.05 cm.
- The number of internal grids is ≥225 and <3600. Although SWOT data has a spatial resolution of 2 km, the estimated SWOT scale in the KE region is about 30 km in wavelength (~15 pixels) [42]. This threshold is used to determine the minimum eddy size, with the maximum eddy size constrained by the wide of the swath (~60 pixels).
- Pass a shape test with error ≤ 55%.
- No additional restrictions are applied to the eddy amplitude. Due to limited familiarity with the properties of fine-scale eddies, no specific amplitude restrictions are imposed.
3. Results
3.1. Revisiting the Mesoscale Eddy Information by DUACS
Before examining the fine-scale eddies detected by SWOT, we first revisited the mesoscale eddy characteristics using conventional altimetry data. We applied our eddy identification method to the KE region (145°E–170°E, 30°N–42°N, black box in Figure 1). Figure 3 provides an overview of the eddies in the KE region during the Cal/Val period. Since we did not consider eddies with lifetimes exceeding a certain threshold, multiple eddies were detected daily in the SLA field. Figure 3a displays a snapshot of the SLA, surface geostrophic velocity, and eddy identification. It implies that most eddies in the KE region are caused by flow shear instability [35], resulting in anticyclonic eddies north of the main stream and cyclonic eddies to the south. These eddies generally have lifetimes shorter than 20 weeks, with their radii reflecting the sheer scale of the Kuroshio. Eddies with opposite distribution characteristics are primarily pinched off from the meander, as evident in the case of the three strong anticyclonic eddies near 37°–38°N. These eddies are long-live eddies with larger sizes compared to the aforementioned eddy type. On average, there are about 41.3 eddies detected per day during the Cal/Val period, including 19.9 cyclonic eddies and 21.3 anticyclonic eddies. The temporal variation in eddy numbers (Figure 3b) shows a slight decrease in early summer compared to spring, aligning with previous studies suggesting that changes in baroclinic instability are a primary factor [43].
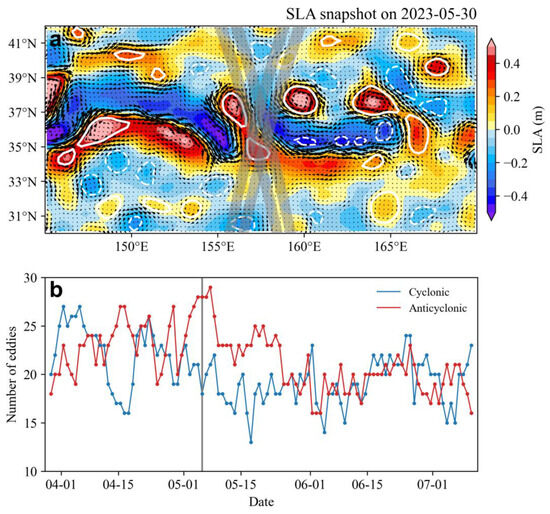
Figure 3.
(a) Snapshot of the SLA (color), surface geostrophic velocity (black quiver), and eddy identification results (white circle) on 30 May 2023. The solid circles represent anticyclonic eddies while dashed circles denote cyclonic eddies. The gray swaths denote the SWOT Cal/Val orbit in this region. (b) The timeseries of the eddy numbers identified per day, with cyclonic eddies colored in blue while anticyclonic eddies colored in red. The vertical gray line denotes the date of the snapshot shown in (a).
We then employed a heatmap to visualize the relationship between an eddy’s radius and its amplitude (Figure 4a). Although we have not imposed a limit on the minimum eddy size, over 96% of the identified eddy radii are larger than 30 km. This indicates that our choice of not setting a minimum eddy size has a limited impact on the overall results. Specifically, about 74% of eddies have a radius ranging from 30 to 70 km and 64% of eddies have an amplitude less than 10 cm. However, there are notable differences between cyclonic and anticyclonic eddies. The cyclonic eddies generally have a larger size but weaker amplitude compared to the anticyclonic eddies. Dimensionality reduction provided a more detailed analysis of eddy radius and amplitude distribution (Figure 4b,c). For cyclonic eddies, the mean radius is 54.8 km with a standard deviation of 20.4 km, indicating a moderate average size with some variability. The distribution of cyclonic eddies exhibits a positive skewness of 1.04, suggesting a tendency toward larger radii with a longer tail on the right side. The kurtosis of 0.95 indicates that the distribution is relatively flat compared to a normal distribution, with fewer extreme values and a more even spread across the range of observed radii. In contrast, anticyclonic eddies have a mean radius of 60.2 km, which is larger than that of cyclonic eddies. The standard deviation for anticyclonic eddies is 24.0 km, reflecting greater variability in size. The anticyclonic eddies’ distribution is more positively skewed (1.28) and has a higher kurtosis (1.95), indicating a flatter distribution with a higher presence of extreme values compared to cyclonic eddies. Overall, while both eddy types show positive skewness, anticyclonic eddies generally have larger mean radii and greater variability. The platykurtic nature of anticyclonic eddies’ distribution suggests a more uniform size distribution with fewer extreme values compared to cyclonic eddies.
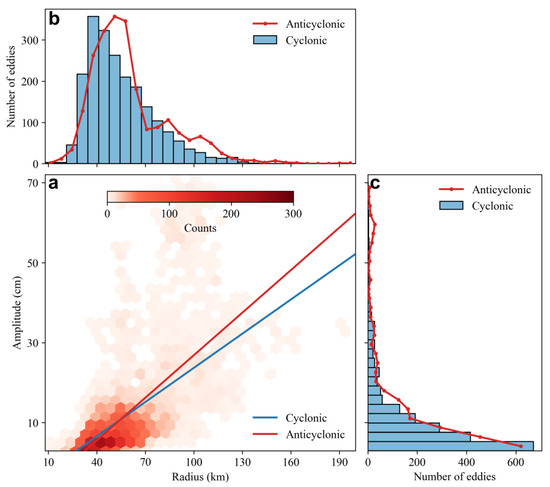
Figure 4.
(a) Heatmap of the relationship between mesoscale eddy radius and amplitude. The blue and red line denote the linear regression of cyclonic eddies and anticyclonic eddies, respectively. (b,c) demonstrate the histogram of eddy radius and amplitude. Blue bars and red lines stand for cyclonic and anticyclonic eddies, respectively.
Similar differences are observed in the amplitudes of the eddies (Figure 4c). The cyclonic eddies have an average amplitude of 10.8 cm with a standard deviation of 10.1 cm, while anticyclonic eddies exhibit a higher average amplitude of 12.7 cm and greater variability (13.1 cm). Despite this, the skewness and kurtosis provide a different perspective compared to the radius. Cyclonic eddies display more extreme variability with higher skewness and kurtosis, indicating a tendency toward larger amplitude values and a more peaked distribution. In contrast, anticyclonic eddies, although larger on average, show a more evenly spread amplitude distribution with lower skewness and kurtosis. This suggests that while anticyclonic eddies generally have larger amplitudes, their distribution is less extreme and more uniform compared to cyclonic eddies. These findings suggest that anticyclonic eddies are generally larger and more variable in both radius and amplitude than cyclonic eddies, reflecting their distinct dynamic behavior in the KE region during the Cal/Val period.
3.2. Fine-Scale Eddy Information by SWOT
3.2.1. The Scale-Resolving Capability of SWOT
After revisiting the mesoscale eddy properties in the KE region, how will SWOT expand our knowledge? Since the spatial scales resolved by SWOT could vary seasonally and spatially [42], we first estimated SWOT’s capability to resolve spatial scales in the KE region during the Cal/Val period. The along-swath SLA power spectral density (PSD) is shown in Figure 5. For comparison, the DUACS SLA spectrum was calculated after linear interpolation onto the SWOT swath. The PSD results reveal that SWOT and DUACS exhibit similar density levels above 150 km. However, at wavelengths below 150 km, where traditional altimetry is often dominated by noise [19], the spectra diverge, with DUACS’s spectrum showing a steeper slope. This is understandable as the DUACS slope is extrapolated to shorter wavelengths, which still reflects the original geostrophic turbulence theory [44]. In contrast, the SWOT-derived spectral slope between 50–120 km aligns closely with the k−11/3 power law. This observation supports predictions from surface quasi-geostrophic theory [45], which suggests that the ocean dynamics in this energetic region should be governed by fine-scale features. As the wavenumber approaches approximately 20 km, it intersects with the SWOT baseline error requirement, indicating that SWOT can resolve processes with scales larger than 20 km in the KE region. The two SWOT passes in this region (passes 004 and 019 as shown in Figure 1) display similar features (dashed line in Figure 5), further confirming SWOT’s capability to resolve fine-scale eddies effectively.
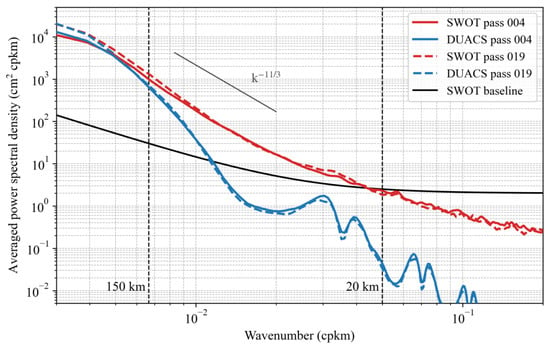
Figure 5.
SLA spectrum from SWOT (red) and DUACS (blue) data averaged over the Cal/Val period. The solid and dashed colored lines represent the results from SWOT passes 004 and 019, respectively. The black line denotes the baseline of the SWOT error requirement. The power law of k−11/3 is displayed in the figure. The two vertical dashed lines denote the reference wavenumbers of 150 km and 20 km.
In summary, SWOT offers potential opportunities to advance our understanding of fine-scale oceanic features by providing ultra-high-resolution data that extend beyond the capabilities of traditional altimetry. This enhanced resolution allows for a more detailed exploration of fine-scale eddies ranging from 150 km to 20 km in the KE region, which were previously less accessible.
3.2.2. Cases of Fine-Scale Eddies Detected by SWOT
By examining the SLA differences between SWOT and DUACS during the Cal/Val period, we present two snapshots of eddy identification results. In the first case, dated 15 May 2023 (Case I), the DUACS data clearly show an anticyclonic mesoscale eddy with a positive SLA around 156°E, 36°N (Figure 6a). This anticyclonic eddy has a diameter exceeding 200 km and a maximum SLA over 50 cm. The SWOT data, while displaying a similar spatial pattern, reveal enhanced SLA values and a more intricate distribution. This discrepancy arises because DUACS data, which transfer the one-dimensional measurements to a gridded product, tend to smooth out fine-scale features. In contrast, SWOT data, which directly observe two-dimensional data, capture these fine-scale structures more distinctly. The SLA differences (Figure 6c) highlight five fine-scale eddies within the SWOT swath, including one cyclonic and one anticyclonic fine-scale eddy (marked by white circles) located on the edge of the mesoscale anticyclonic eddy. The fine-scale cyclonic eddy, with an amplitude of 5.3 cm and a radius of 19.7 km, is relatively weak and small, whereas the fine-scale anticyclonic eddy has a higher amplitude of 9.3 cm and a larger radius of 39.0 km.
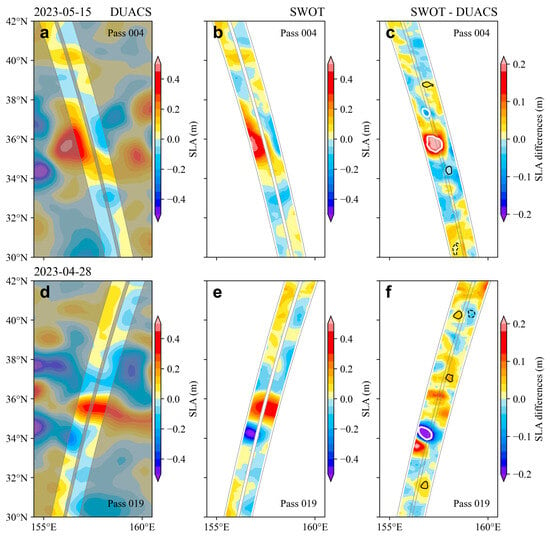
Figure 6.
Maps of SLAs from (a) the DUACS product and (b) SWOT data on 15 May 2023 from pass 004. (c) The differences between (a,b). Gray lines indicate the extent of SWOT’s swath, with gaps between two swaths filled through linear interpolation. Circles denote the eddy identification results, with the white circles being particular fine-scale eddies that are reinforced in the main text. (d–f) Same as (a–c) but for results on 28 April 2023 from pass 019.
In the second case, dated 28 April 2023 (Case II), the DUACS SLA field displays a prominent eddy front beneath the SWOT orbit (Figure 6d). A relatively weak cyclonic mesoscale eddy is evident near 156°E, 34°N. The SWOT SLA, while also showing a strong eddy front, reveals much stronger localized SLA values compared to DUACS (Figure 6e). The SLA differences (Figure 6f) highlight a cyclonic fine-scale eddy with an amplitude reaching 14.7 cm and a radius of 31.2 km, superimposed on the frontal region. These comparisons underscore SWOT’s capability to detect fine-scale eddies with radii smaller than 50 km that traditional nadir-looking altimeters like DUACS may miss.
To further explore these fine-scale eddies, we analyzed the time evolution of the two strongest detected fine-scale eddies: the anticyclonic eddy from Case I and the cyclonic eddy from Case II. In Case I (Figure 7a–c), the anticyclonic eddy’s amplitude increased from 7.1 cm on 13 May to 9.3 cm on 15 May, before decreasing to 5.9 cm on 17 May. Concurrently, its radius grew from 29.0 km to 43.3 km during these five days. Similarly, in Case II (Figure 7d–f), the cyclonic eddy’s amplitude intensified from 4.0 cm on 24 April to 14.7 cm by 28 April, with its radius nearly doubling from 24 April to 26 April and then stabilizing from 26 April to 28 April.
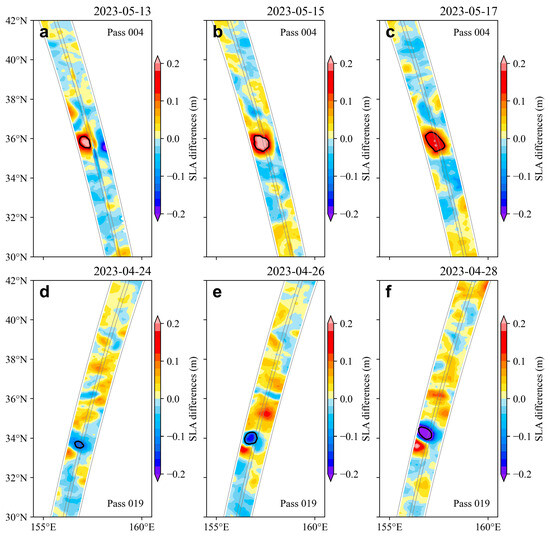
Figure 7.
The case-selected fine-scale eddies and SLA differences evolve with time. (a–c) Results from pass 004 from 13 May 2023 to 17 May 2023. The black circles represent the case-selected eddy. (d–f) Same as (a–c) but for results from pass 019 from 24 April 2023 to 28 April 2023.
The above two case studies highlight SWOT’s enhanced capability to detect fine-scale eddies compared to conventional altimetry. However, besides these case-selected eddies, SWOT also identifies other fine-scale eddies with lower amplitudes that DUACS data might miss. In the subsequent analysis, we will consider all of the identified fine-scale eddies to provide a comprehensive view of the characteristics and distribution of fine-scale eddies detectable by SWOT but not captured by DUACS.
3.2.3. Properties of Fine-Scale Eddies Detected by SWOT
Figure 8 displays the numbers of fine-scale eddies detected by SWOT during the Cal/Val period, combining results from two passes to achieve a temporal resolution of 12 h. It is worth mentioning that the detection regions of the two passes differ slightly, introducing some variation between adjacent times in the timeseries. Nevertheless, the overall continuity of the timeseries indicates minimal impact from these deviations. A total of 858 fine-scale eddies were identified during the Cal/Val period, with a ratio of cyclonic to anticyclonic eddies of 1.16, suggesting a higher prevalence of fine-scale cyclonic eddies in the KE region. However, the timeseries also has some missing values, which are further filled by the nearest interpolation. On average, under the 120 km wide narrow swath, SWOT is capable of capturing approximately 4.5 fine-scale eddies per visit. This ability to detect features that traditional altimeters might miss highlights SWOT’s enhanced capability to reveal finer-scale eddy structures.
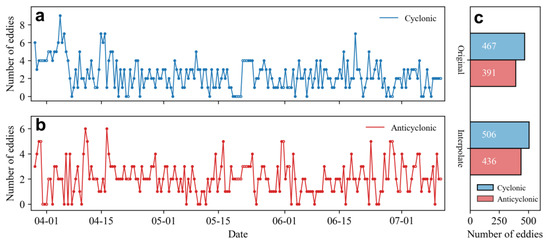
Figure 8.
The timeseries of identified (a) cyclonic and (b) anticyclonic fine-scale eddy numbers during the Cal/Val period. White circles denote missing values but are filled using the nearest interpolation. (c) The total number of fine-scale eddies during the Cal/Val period, with blue and red representing the cyclonic and anticyclonic eddies, respectively. The original result denotes the eddy numbers with SWOT’s missing values, with the interpolate representing the result after filling the missing values.
Figure 9 illustrates the distribution and characteristics of fine-scale eddies detected by SWOT. The majority of these eddies have radii below 25 km and amplitudes below 4 cm. This is expected since mesoscale eddies, which are detectable by conventional altimeters (Figure 4a), are excluded from this dataset. Similar to the results derived from conventional altimeters, the cyclonic and anticyclonic fine-scale eddies also illustrate some notable differences. Cyclonic eddies have an average radius of 23.3 km with a standard deviation of 5.1 km. This indicates a higher variability in the size of cyclonic eddies. The distribution of their radii is positively skewed (skewness = 1.5) and shows a pronounced peak (kurtosis = 2.8), suggesting that while most cyclonic eddies cluster around the average size, there is a tendency for some to be significantly larger. The anticyclonic eddies almost have the same distribution with minimum differences. They have an average radius of 23.5 km with a standard deviation of 5.0 km. Their distribution is also positively skewed but less pronounced (skewness = 1.3) and flatter (kurtosis = 2.1), implying a more uniform distribution with fewer extreme values compared to cyclonic eddies. In terms of amplitude, cyclonic eddies have an average of 3.5 cm with a standard deviation of 2.5 cm. This distribution is more variable and skewed (skewness = 1.5) with a pronounced peak (kurtosis = 2.8), which indicates greater amplitude variability and a tendency toward larger amplitude values. Conversely, anticyclonic eddies have a lower average amplitude of 2.8 cm and a smaller standard deviation of 1.7 cm. Their amplitude distribution is less skewed (skewness = 1.3) and flatter (kurtosis = 2.1), reflecting a more consistent and lower range of amplitude values compared to cyclonic eddies. To conclude, these findings highlight that cyclonic fine-scale eddies are characterized by greater amplitude variability and more extreme values, while anticyclonic fine-scale eddies tend to be more uniform with generally lower amplitudes.
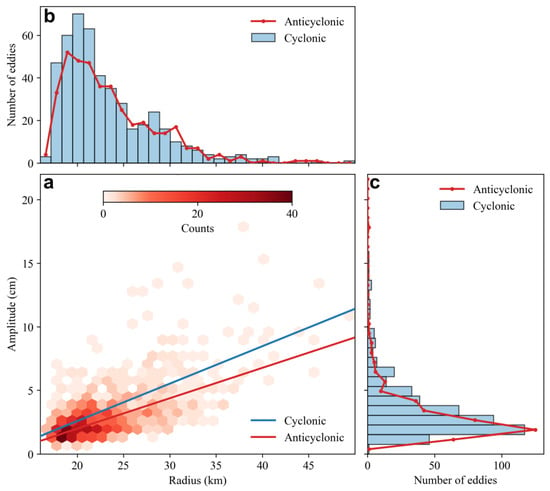
Figure 9.
Same as Figure 4, but for fine-scale eddy properties detected by SWOT.
Comparing the findings from SWOT with DUACS data (Figure 4 and Figure 9) reveals significant differences that highlight the enhanced capabilities of SWOT in detecting fine-scale eddies. The DUACS, with its broader-scale focus, captures larger eddies and higher amplitudes, reflecting the larger, more generalized features of the oceanic eddy field. In contrast, SWOT’s ability to resolve fine-scale eddies reveals a more detailed and comprehensive picture of eddy dynamics. This finer resolution allows SWOT to uncover variations and subtleties in the eddy field that conventional altimeters might overlook, providing a more nuanced view of the eddy population.
4. Discussion
4.1. Prospect of Detecting Eddies with SWOT on Science Orbit
Our study leveraged SWOT data from the Cal/Val orbit to achieve higher temporal resolution. However, the large gaps between satellite tracks pose a significant challenge for studying eddy properties. The Cal/Val orbit lasted only three months, after which SWOT transitioned to a global mapping phase on 26 July 2023. In this science orbit phase, SWOT covers nearly the entire Earth in approximately 21 days, potentially providing an opportunity for new insights into fine-scale eddy studies. Previous observing system simulation experiments (OSSEs) have indicated that SWOT could identify over 66% of eddies [46], a substantial improvement compared to the 6–16% detected by DUACS. Here, we preliminarily tested this potential with real SWOT measurement.
We selected SWOT data from 25 May 2024 to 14 June 2024 as a case study. During this period, SWOT passes 013 and 014 covered nearly the entire KE region with minimal gaps (Figure 10a). We also compared the DUACS data averaged over the same period, the processed SWOT SLA fields, and the SLA differences between SWOT and DUACS (Figure 10b–d). To minimize the influence of extrapolation, our analysis focuses on the central region (black box in Figure 10), excluding the edges of our initial selection. The large-scale oceanic patterns from both data sources are consistent, with a high pattern correlation coefficient of 0.96 (Figure 10b,c). However, the SWOT SLA map (Figure 10c) exhibits some discontinuities, resulting in irregularities in the SLA differences (Figure 10d). These irregularities are mainly due to sampling time differences caused by SWOT’s orbital characteristics. The measuring time differences between neighboring tracks can reach up to 10 days, leading to drastic changes in the SLA field [47].
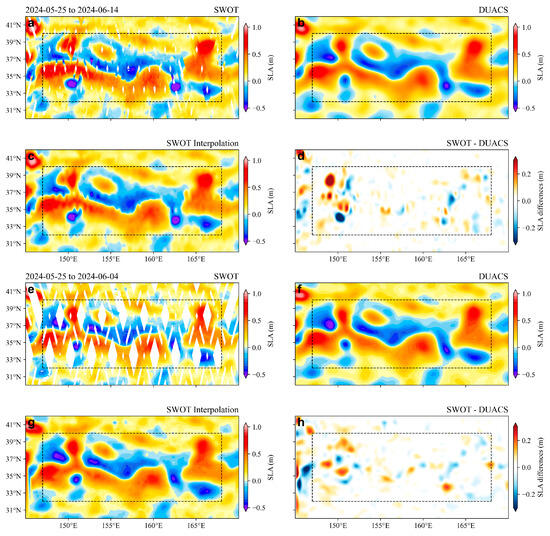
Figure 10.
(a) Along-swath SLA derived from SWOT within a 21-day repeat cycle from 25 May 2024 to 14 June 2024. (b) The averaged SLA results during the same period derived from DUACS. (c) The mapped SLA field from (a) using linear interpolation. (d) The SLA differences between SWOT and DUACS. The black dashed box denotes the central region range. (e–h) Same as (a–d), but for one subcycle from 25 May 2024 to 4 June 2024.
To address this issue, Qiu et al. [47] propose temporally dividing the 21-day repeat cycle into two subcycles in the KE region. In each subcycle, the time difference among neighboring tracks is less than 2 days. However, this approach also introduces large diamond-shaped gaps between adjacent swaths within a subcycle (Figure 10e). Spatially, these gaps are filled by the measurements from another subcycle about 10 days later/earlier. By focusing on data from a single subcycle, rather than the entire repeat cycle, we can significantly reduce the time differences between SLA measurements, leading to a more continuous SLA field as shown in Figure 10g. The SLA differences (Figure 10h) reveal numerous fine-scale circular and elliptical structures, highlighting SWOT’s potential for detailed investigation of fine-scale eddies during its science orbit.
However, there are still challenges with using science orbit data for eddy detection. One major issue is merging along-swath data onto a uniform grid for scientific analysis. The most common method, optimal interpolation (OI), provides performance only equivalent to that of 2–4 conventional altimeters due to the limited temporal resolution of SWOT’s science orbit [48]. Some new methods have been proposed recently [49,50,51,52,53], but their effectiveness with real SWOT data requires further assessment. Besides, blending SWOT data with existing conventional altimeters is another challenging task, although efforts are underway to address this [54].
4.2. Caveats for the Identification of Fine-Scale Eddies
Despite the promising capabilities of SWOT for studying fine-scale eddies, several limitations must be considered. Most importantly, the eddies identified in this study are more accurately described as eddy-like structures. Various factors can produce signals that mimic eddies, such as deviations in the DUACS product. Due to its sampling and mapping procedures, DUACS often misinterprets eddy signals, which can be erroneously aliased as larger eddies [21]. This misrepresentation can lead to inaccurate background information on mesoscale eddies and generate artifact fine-scale eddies when analyzing SLA differences.
In addition to the deviations in the DUACS product, SWOT data also has its own limitations. The high-resolution measurements from SWOT capture not only balanced geostrophic motions but also unbalanced wave motions, such as near-inertial flows and internal tides. Although the transition scale from balanced to unbalanced motions is relatively low in the KE region [55,56], the highly inhomogeneous property of the transition scale necessitates caution when interpreting SWOT data for eddy detection. Furthermore, the sampling errors of SWOT could affect the accuracy of eddy detection [46]. Fortunately, the SWOT Science Team has worked to denoise the data, mitigating some of these issues [38,39].
Moreover, apart from the issues with DUACS and SWOT data themselves, simply subtracting the DUACS data from SWOT data may introduce additional errors. DUACS accounts for time differences between altimeters [57], whereas SWOT provides instantaneous measurements. To address this, we have spatially smoothed the SWOT data within a 10 km × 10 km box to minimize the impact of these time differences. Nonetheless, further research is needed to either correct these time differences or assess their impact on the results.
Finally, given SWOT’s ultra-high resolution, there is an urgent need for more in situ ocean observations to validate the identified eddies [30]. Independent observations, such as from mooring arrays, Argos, and chlorophyll satellites, are essential to confirm that the detected features are true eddies rather than artifacts of the data or features induced by other dynamical factors. In our study, the balanced motion signals in the KE region are significantly stronger than the unbalanced signals, suggesting that the identified features are more likely genuine eddies. However, due to the current limitations of DUACS and SWOT data, we must remain cautious about the statistical results, as they may include non-eddy characteristics.
5. Conclusions
The advent of the new-generation satellite altimeter, SWOT, has provided unprecedented high-resolution SSH data for exploring oceanic fine-scale eddies that conventional altimeters have missed. Here, focusing on the eddy-energetic KE region, we show that during the SWOT Cal/Val orbit (29 March to 11 July 2023), a substantial number of fine-scale eddies were visible within the 120 km wide narrow swath beneath the SWOT satellite.
On average, approximately 4.5 fine-scale eddies were detected per visit. These eddies, which are superimposed on mesoscale structures, have a mean radius of 23.4 km and a mean amplitude of 3.2 cm. Cyclonic eddies have a slightly more frequent occurrence than anticyclonic ones, with a ratio of 1.16. While both types of eddies exhibit similar radii and variability, cyclonic eddies tend to have higher amplitudes, averaging 3.5 cm compared to 2.8 cm for anticyclonic eddies. A more intuitive and detailed breakdown of these properties is presented in Table 1.

Table 1.
Fine-scale eddy properties detected by SWOT.
In contrast to current altimetry data which generally reflect broader and larger features of the oceanic eddy field, the new-generation SWOT altimeter offers a more detailed and comprehensive picture of a smaller-scale eddy field. This finer resolution allows SWOT to uncover variations and subtleties in the eddy field that conventional altimeters might overlook, thereby providing a deeper understanding of full-scale eddy dynamics.
As SWOT has transitioned from its Cal/Val orbit to its science orbit, it now provides an opportunity for global observation of fine-scale eddies. However, our analysis reveals challenges associated with the mismatch between the time differences of neighboring tracks and the timescales of fine-scale processes. Although dividing the 21-day repeat cycle into shorter subcycles can partially address this issue, overcoming these challenges also requires advancements in technology and methods. Ongoing efforts are focused on developing solutions to enhance the effectiveness of SWOT data for fine-scale eddy studies. Continued innovation in satellite technology and data processing methods will be crucial in fully realizing the potential of SWOT to transform our understanding of ocean dynamics.
In summary, the new-generation SWOT altimeter represents a significant leap forward in ocean observation, providing unprecedented detail on fine-scale eddies that were previously elusive. While challenges remain, the insights gained from SWOT data are invaluable, offering a deeper and more nuanced view of the ocean’s fine-scale processes. As we refine our methodologies and integrate new technologies, SWOT will undoubtedly continue to advance our knowledge of ocean dynamics and enhance our ability to monitor and understand the complex behavior of fine-scale eddies on a global scale.
Author Contributions
Conceptualization, T.D. and Z.J.; methodology, T.D.; software, T.D.; validation, T.D.; formal analysis, T.D.; investigation, T.D.; resources, T.D.; data curation, T.D.; writing—original draft preparation, T.D.; writing—review and editing, T.D. and Z.J.; visualization, T.D.; supervision, Z.J.; project administration, Z.J.; funding acquisition, Z.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Laoshan Laboratory Science and Technology Innovation Projects, LSKJ202201406-3. T.D. is founded by the National Key Research and Development Program of China, 2023YFB3907704, and Laoshan Laboratory Science and Technology Innovation Projects, LSKJ202400203.
Data Availability Statement
All data used in this study are publicly accessible. The SWOT Level-3 KaRIn SSH data can be found in https://doi.org/10.24400/527896/A01-2023.017 (AVISO/DUACS, 2024). The gridded altimetry data are available from https://doi.org/10.48670/moi-00149 (E.U. Copernicus Marine Service Information).
Acknowledgments
We would like to express our gratitude to Mingfang Miao for discussing some details of the data processing method. We also appreciated Man Yuan and Yingzhe Cui for the guidance on eddy identification.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global Observations of Nonlinear Mesoscale Eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Capet, X.; Campos, E.J.; Paiva, A.M. Submesoscale Activity over the Argentinian Shelf. Geophys. Res. Lett. 2008, 35, L15605. [Google Scholar] [CrossRef]
- Farneti, R.; Delworth, T.L.; Rosati, A.J.; Griffies, S.M.; Zeng, F. The Role of Mesoscale Eddies in the Rectification of the Southern Ocean Response to Climate Change. J. Phys. Oceanogr. 2010, 40, 1539–1557. [Google Scholar] [CrossRef]
- Klein, P.; Lapeyre, G.; Siegelman, L.; Qiu, B.; Fu, L.; Torres, H.; Su, Z.; Menemenlis, D.; Le Gentil, S. Ocean-Scale Interactions from Space. Earth Space Sci. 2019, 6, 795–817. [Google Scholar] [CrossRef]
- Ferrari, R.; Wunsch, C. Ocean Circulation Kinetic Energy: Reservoirs, Sources, and Sinks. Annu. Rev. Fluid Mech. 2009, 41, 253–282. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic Mass Transport by Mesoscale Eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global Heat and Salt Transports by Eddy Movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef] [PubMed]
- Chelton, D.B.; Gaube, P.; Schlax, M.G.; Early, J.J.; Samelson, R.M. The Influence of Nonlinear Mesoscale Eddies on Near-Surface Oceanic Chlorophyll. Science 2011, 334, 328–332. [Google Scholar] [CrossRef]
- Fu, L.-L.; Chelton, D.; Le Traon, P.-Y.; Morrow, R. Eddy Dynamics From Satellite Altimetry. Oceanography 2010, 23, 14–25. [Google Scholar] [CrossRef]
- Chaigneau, A.; Le Texier, M.; Eldin, G.; Grados, C.; Pizarro, O. Vertical Structure of Mesoscale Eddies in the Eastern South Pacific Ocean: A Composite Analysis from Altimetry and Argo Profiling Floats. J. Geophys. Res. Ocean. 2011, 116, C11025. [Google Scholar] [CrossRef]
- Escudier, R.; Renault, L.; Pascual, A.; Brasseur, P.; Chelton, D.; Beuvier, J. Eddy Properties in the Western Mediterranean Sea from Satellite Altimetry and a Numerical Simulation. J. Geophys. Res. Ocean. 2016, 121, 3990–4006. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Q.; Sun, L.; Li, S.; Yang, Y.; Liu, S. The Most Typical Shape of Oceanic Mesoscale Eddies from Global Satellite Sea Level Observations. Front. Earth Sci. 2015, 9, 202–208. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Wang, W.; Huang, R.X. Universal Structure of Mesoscale Eddies in the Ocean. Geophys. Res. Lett. 2013, 40, 3677–3681. [Google Scholar] [CrossRef]
- You, Z.; Liu, L.; Bethel, B.J.; Dong, C. Feature Comparison of Two Mesoscale Eddy Datasets Based on Satellite Altimeter Data. Remote Sens. 2022, 14, 116. [Google Scholar] [CrossRef]
- Gaube, P.; McGillicuddy, D.J., Jr.; Chelton, D.B.; Behrenfeld, M.J.; Strutton, P.G. Regional Variations in the Influence of Mesoscale Eddies on Near-Surface Chlorophyll. J. Geophys. Res. Ocean. 2014, 119, 8195–8220. [Google Scholar] [CrossRef]
- Kubryakov, A.A.; Kozlov, I.E.; Manucharyan, G.E. Large Mesoscale Eddies in the Western Arctic Ocean from Satellite Altimetry Measurements. J. Geophys. Res. Ocean. 2021, 126, e2020JC016670. [Google Scholar] [CrossRef]
- Erickson, Z.K.; Fields, E.; Johnson, L.; Thompson, A.F.; Dove, L.A.; D’Asaro, E.; Siegel, D.A. Eddy Tracking from In Situ and Satellite Observations. J. Geophys. Res. Ocean. 2023, 128, e2023JC019701. [Google Scholar] [CrossRef]
- Cheng, Y.-H.; Ho, C.-R.; Zheng, Q.; Kuo, N.-J. Statistical Characteristics of Mesoscale Eddies in the North Pacific Derived from Satellite Altimetry. Remote Sens. 2014, 6, 5164–5183. [Google Scholar] [CrossRef]
- Ducet, N.; Le Traon, P.Y.; Reverdin, G. Global High-Resolution Mapping of Ocean Circulation from TOPEX/Poseidon and ERS-1 and -2. J. Geophys. Res. Ocean. 2000, 105, 19477–19498. [Google Scholar] [CrossRef]
- Dufau, C.; Orsztynowicz, M.; Dibarboure, G.; Morrow, R.; Le Traon, P. Mesoscale Resolution Capability of Altimetry: Present and Future. J. Geophys. Res. Ocean. 2016, 121, 4910–4927. [Google Scholar] [CrossRef]
- Amores, A.; Jordà, G.; Arsouze, T.; Le Sommer, J. Up to What Extent Can We Characterize Ocean Eddies Using Present-Day Gridded Altimetric Products? J. Geophys. Res. Ocean. 2018, 123, 7220–7236. [Google Scholar] [CrossRef]
- Nagai, T.; Gruber, N.; Frenzel, H.; Lachkar, Z.; McWilliams, J.C.; Plattner, G.-K. Dominant Role of Eddies and Filaments in the Offshore Transport of Carbon and Nutrients in the California Current System. J. Geophys. Res. Ocean. 2015, 120, 5318–5341. [Google Scholar] [CrossRef]
- Cipollone, A.; Masina, S.; Storto, A.; Iovino, D. Benchmarking the Mesoscale Variability in Global Ocean Eddy-Permitting Numerical Systems. Ocean. Dyn. 2017, 67, 1313–1333. [Google Scholar] [CrossRef]
- Fu, L.-L.; Ubelmann, C. On the Transition from Profile Altimeter to Swath Altimeter for Observing Global Ocean Surface Topography. J. Atmos. Ocean. Technol. 2014, 31, 560–568. [Google Scholar] [CrossRef]
- Durand, M.; Fu, L.-L.; Lettenmaier, D.P.; Alsdorf, D.E.; Rodriguez, E.; Esteban-Fernandez, D. The Surface Water and Ocean Topography Mission: Observing Terrestrial Surface Water and Oceanic Submesoscale Eddies. Proc. IEEE 2010, 98, 766–779. [Google Scholar] [CrossRef]
- Fu, L.-L.; Pavelsky, T.; Cretaux, J.-F.; Morrow, R.; Farrar, J.T.; Vaze, P.; Sengenes, P.; Vinogradova-Shiffer, N.; Sylvestre-Baron, A.; Picot, N.; et al. The Surface Water and Ocean Topography Mission: A Breakthrough in Radar Remote Sensing of the Ocean and Land Surface Water. Geophys. Res. Lett. 2024, 51, e2023GL107652. [Google Scholar] [CrossRef]
- Morrow, R.; Fu, L.-L.; Ardhuin, F.; Benkiran, M.; Chapron, B.; Cosme, E.; d’Ovidio, F.; Farrar, J.T.; Gille, S.T.; Lapeyre, G.; et al. Global Observations of Fine-Scale Ocean Surface Topography with the Surface Water and Ocean Topography (SWOT) Mission. Front. Mar. Sci. 2019, 6, 232. [Google Scholar] [CrossRef]
- d’Ovidio, F.; Pascual, A.; Wang, J.; Doglioli, A.M.; Jing, Z.; Moreau, S.; Grégori, G.; Swart, S.; Speich, S.; Cyr, F.; et al. Frontiers in Fine-Scale In Situ Studies: Opportunities during the SWOT Fast Sampling Phase. Front. Mar. Sci. 2019, 6, 168. [Google Scholar] [CrossRef]
- McWilliams, J.C. Submesoscale Currents in the Ocean. Proc. R. Soc. A. 2016, 472, 20160117. [Google Scholar] [CrossRef]
- Zhang, Z.; Miao, M.; Qiu, B.; Tian, J.; Jing, Z.; Chen, G.; Chen, Z.; Zhao, W. Submesoscale Eddies Detected by SWOT and Moored Observations in the Northwestern Pacific. Geophys. Res. Lett. 2024, 51, e2024GL110000. [Google Scholar] [CrossRef]
- Qiu, B.; Kelly, K.A.; Joyce, T.M. Mean Flow and Variability in the Kuroshio Extension from Geosat Altimetry Data. J. Geophys. Res. Ocean. 1991, 96, 18491–18507. [Google Scholar] [CrossRef]
- Kida, S.; Mitsudera, H.; Aoki, S.; Guo, X.; Ito, S.; Kobashi, F.; Komori, N.; Kubokawa, A.; Miyama, T.; Morie, R.; et al. Oceanic Fronts and Jets around Japan: A Review. J. Oceanogr. 2015, 71, 469–497. [Google Scholar] [CrossRef]
- Sasaki, Y.N.; Minobe, S. Climatological Mean Features and Interannual to Decadal Variability of Ring Formations in the Kuroshio Extension Region. J. Oceanogr. 2015, 71, 499–509. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S. Variability of the Kuroshio Extension Jet, Recirculation Gyre, and Mesoscale Eddies on Decadal Time Scales. J. Phys. Oceanogr. 2005, 35, 2090–2103. [Google Scholar] [CrossRef]
- Ji, J.; Dong, C.; Zhang, B.; Liu, Y.; Zou, B.; King, G.P.; Xu, G.; Chen, D. Oceanic Eddy Characteristics and Generation Mechanisms in the Kuroshio Extension Region. J. Geophys. Res. Ocean. 2018, 123, 8548–8567. [Google Scholar] [CrossRef]
- Yang, H.; Qiu, B.; Chang, P.; Wu, L.; Wang, S.; Chen, Z.; Yang, Y. Decadal Variability of Eddy Characteristics and Energetics in the Kuroshio Extension: Unstable Versus Stable States. J. Geophys. Res. Ocean. 2018, 123, 6653–6669. [Google Scholar] [CrossRef]
- Jing, Z.; Chang, P.; Shan, X.; Wang, S.; Wu, L.; Kurian, J. Mesoscale SST Dynamics in the Kuroshio–Oyashio Extension Region. J. Phys. Oceanogr. 2019, 49, 1339–1352. [Google Scholar] [CrossRef]
- Gómez-Navarro, L.; Cosme, E.; Sommer, J.L.; Papadakis, N.; Pascual, A. Development of an Image De-Noising Method in Preparation for the Surface Water and Ocean Topography Satellite Mission. Remote Sens. 2020, 12, 734. [Google Scholar] [CrossRef]
- Tréboutte, A.; Carli, E.; Ballarotta, M.; Carpentier, B.; Faugère, Y.; Dibarboure, G. KaRIn Noise Reduction Using a Convolutional Neural Network for the SWOT Ocean Products. Remote Sens. 2023, 15, 2183. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Wang, J.; Fu, L.-L. Seasonal and Fortnight Variations in Internal Solitary Waves in the Indonesian Seas from the SWOT Measurements. J. Geophys. Res. Ocean. 2024, 129, e2024JC021086. [Google Scholar] [CrossRef]
- Mason, E.; Pascual, A.; McWilliams, J.C. A New Sea Surface Height–Based Code for Oceanic Mesoscale Eddy Tracking. J. Atmos. Ocean. Technol. 2014, 31, 1181–1188. [Google Scholar] [CrossRef]
- Wang, J.; Fu, L.-L.; Torres, H.S.; Chen, S.; Qiu, B.; Menemenlis, D. On the Spatial Scales to Be Resolved by the Surface Water and Ocean Topography Ka-Band Radar Interferometer. J. Atmos. Ocean. Technol. 2019, 36, 87–99. [Google Scholar] [CrossRef]
- Yang, Y.; Liang, X.S. On the Seasonal Eddy Variability in the Kuroshio Extension. J. Phys. Oceanogr. 2018, 48, 1675–1689. [Google Scholar] [CrossRef]
- Charney, J.G. Geostrophic Turbulence. J. Atmos. Sci. 1971, 28, 1087–1095. [Google Scholar] [CrossRef]
- Held, I.M.; Pierrehumbert, R.T.; Garner, S.T.; Swanson, K.L. Surface Quasi-Geostrophic Dynamics. J. Fluid Mech. 1995, 282, 1–20. [Google Scholar] [CrossRef]
- Ma, C.; Guo, X.; Zhang, H.; Di, J.; Chen, G. An Investigation of the Influences of SWOT Sampling and Errors on Ocean Eddy Observation. Remote Sens. 2020, 12, 2682. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Klein, P.; Ubelmann, C.; Fu, L.-L.; Sasaki, H. Reconstructability of Three-Dimensional Upper-Ocean Circulation from SWOT Sea Surface Height Measurements. J. Phys. Oceanogr. 2016, 46, 947–963. [Google Scholar] [CrossRef]
- Pujol, M.-I.; Dibarboure, G.; Traon, P.-Y.L.; Klein, P. Using High-Resolution Altimetry to Observe Mesoscale Signals. J. Atmos. Ocean. Technol. 2012, 29, 1409–1416. [Google Scholar] [CrossRef]
- Ubelmann, C.; Klein, P.; Fu, L.-L. Dynamic Interpolation of Sea Surface Height and Potential Applications for Future High-Resolution Altimetry Mapping. J. Atmos. Ocean. Technol. 2015, 32, 177–184. [Google Scholar] [CrossRef]
- Rogé, M.; Morrow, R.; Ubelmann, C.; Dibarboure, G. Using a Dynamical Advection to Reconstruct a Part of the SSH Evolution in the Context of SWOT, Application to the Mediterranean Sea. Ocean. Dyn. 2017, 67, 1047–1066. [Google Scholar] [CrossRef]
- Archer, M.R.; Li, Z.; Fu, L. Increasing the Space–Time Resolution of Mapped Sea Surface Height From Altimetry. J. Geophys. Res. Ocean. 2020, 125, e2019JC015878. [Google Scholar] [CrossRef]
- Ballarotta, M.; Ubelmann, C.; Rogé, M.; Fournier, F.; Faugère, Y.; Dibarboure, G.; Morrow, R.; Picot, N. Dynamic Mapping of Along-Track Ocean Altimetry: Performance from Real Observations. J. Atmos. Ocean. Technol. 2020, 37, 1593–1601. [Google Scholar] [CrossRef]
- Guillou, F.L.; Metref, S.; Cosme, E.; Ubelmann, C.; Ballarotta, M.; Sommer, J.L.; Verron, J. Mapping Altimetry in the Forthcoming SWOT Era by Back-and-Forth Nudging a One-Layer Quasigeostrophic Model. J. Atmos. Ocean. Technol. 2021, 38, 697–710. [Google Scholar] [CrossRef]
- Dibarboure, G.; Anadon, C.; Briol, F.; Cadier, E.; Chevrier, R.; Delepoulle, A.; Faugère, Y.; Laloue, A.; Morrow, R.; Picot, N.; et al. Blending 2D Topography Images from SWOT into the Altimeter Constellation with the Level-3 Multi-Mission DUACS System. EGUsphere 2024, 2024, 1–64. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Klein, P.; Wang, J.; Torres, H.; Fu, L.-L.; Menemenlis, D. Seasonality in Transition Scale from Balanced to Unbalanced Motions in the World Ocean. J. Phys. Oceanogr. 2018, 48, 591–605. [Google Scholar] [CrossRef]
- Callies, J.; Wu, W. Some Expectations for Submesoscale Sea Surface Height Variance Spectra. J. Phys. Oceanogr. 2019, 49, 2271–2289. [Google Scholar] [CrossRef]
- Pujol, M.-I.; Faugère, Y.; Taburet, G.; Dupuy, S.; Pelloquin, C.; Ablain, M.; Picot, N. DUACS DT2014: The New Multi-Mission Altimeter Data Set Reprocessed over 20 Years. Ocean Sci. 2016, 12, 1067–1090. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).