GPP of a Chinese Savanna Ecosystem during Different Phenological Phases Simulated from Harmonized Landsat and Sentinel-2 Data
Abstract
1. Introduction
2. Materials and Methods
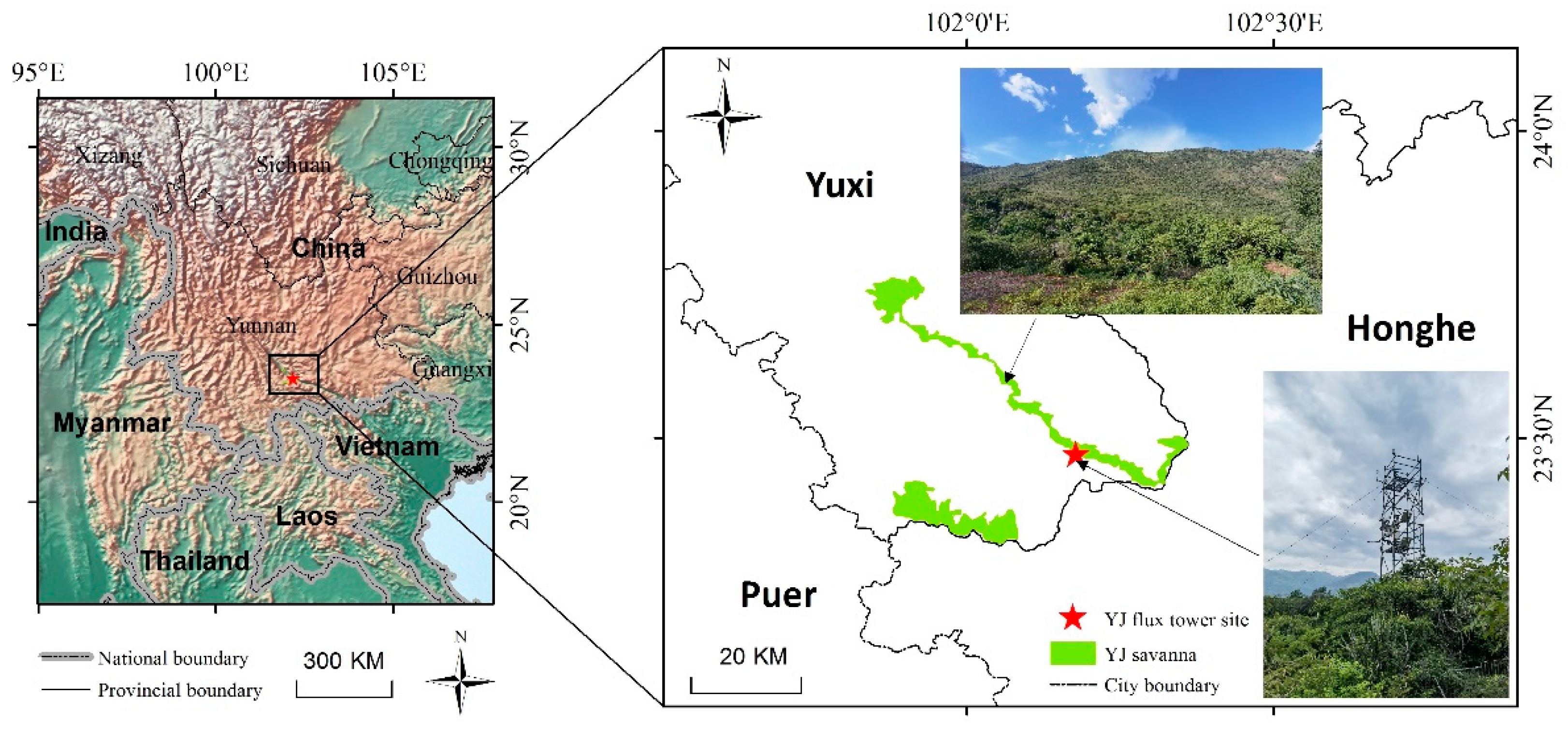
2.1. Study Area
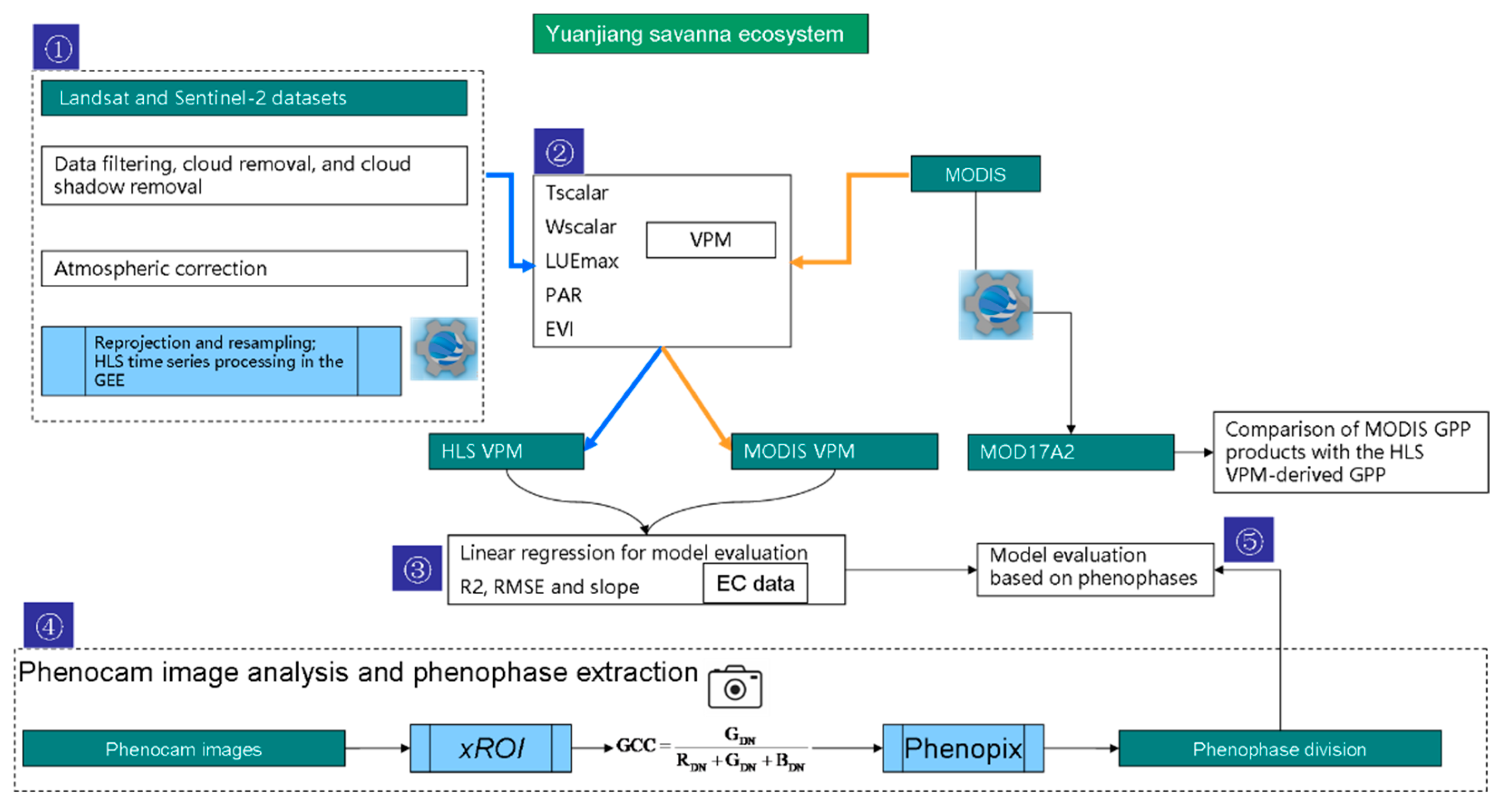
2.2. Workflow Overview
2.3. Flux and Meteorological Data
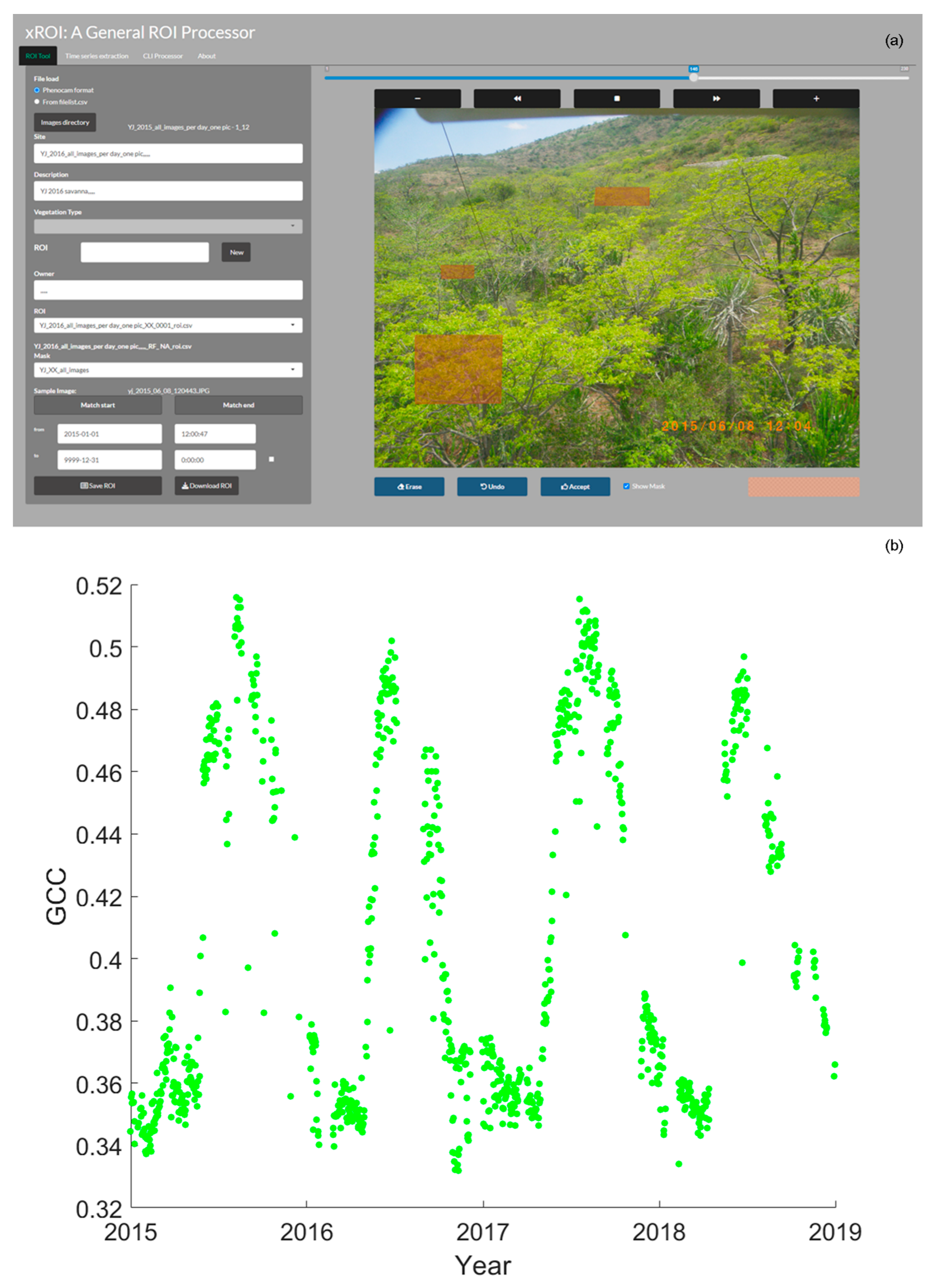
2.4. Phenocam Data and Canopy Phenology Analysis
2.4.1. Phenocam Settings
2.4.2. Image Analysis and Identification of Phenophase Transition Dates
2.4.3. Identifying Phenophase Transition Dates from GCC Values
2.5. Harmonization of Landsat and Sentinel-2 in the Google Earth Engine
2.5.1. Cloud and Cloud Shadow Masking
2.5.2. Radiometric Difference Correction of Multisensor TOA Data
2.5.3. SIAC Atmospheric Correction
2.6. MODIS Land Surface Reflectance and GPP Product Data
2.7. VPM and Model Parameters
2.8. VPM Performance Evaluation
3. Results
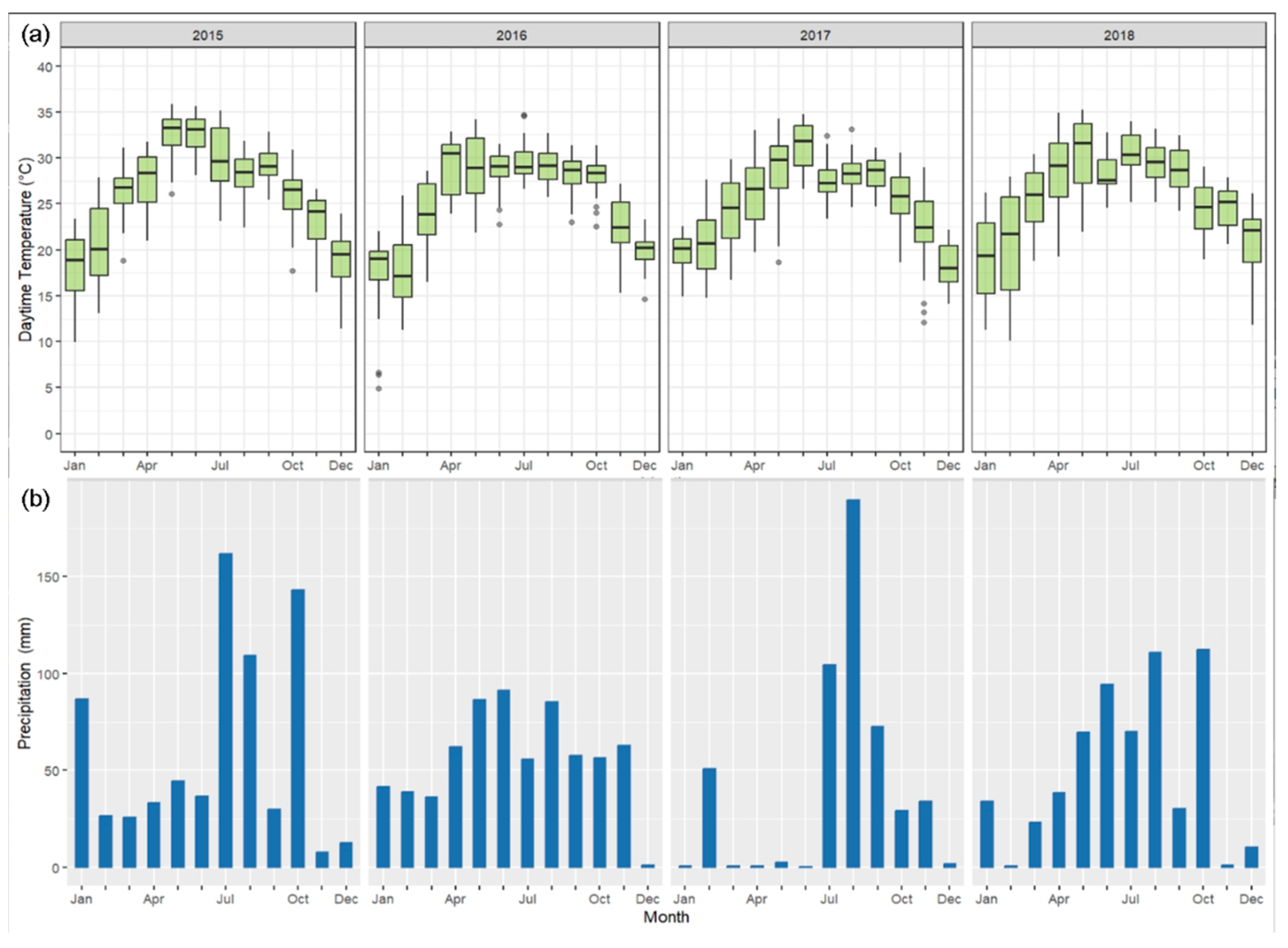
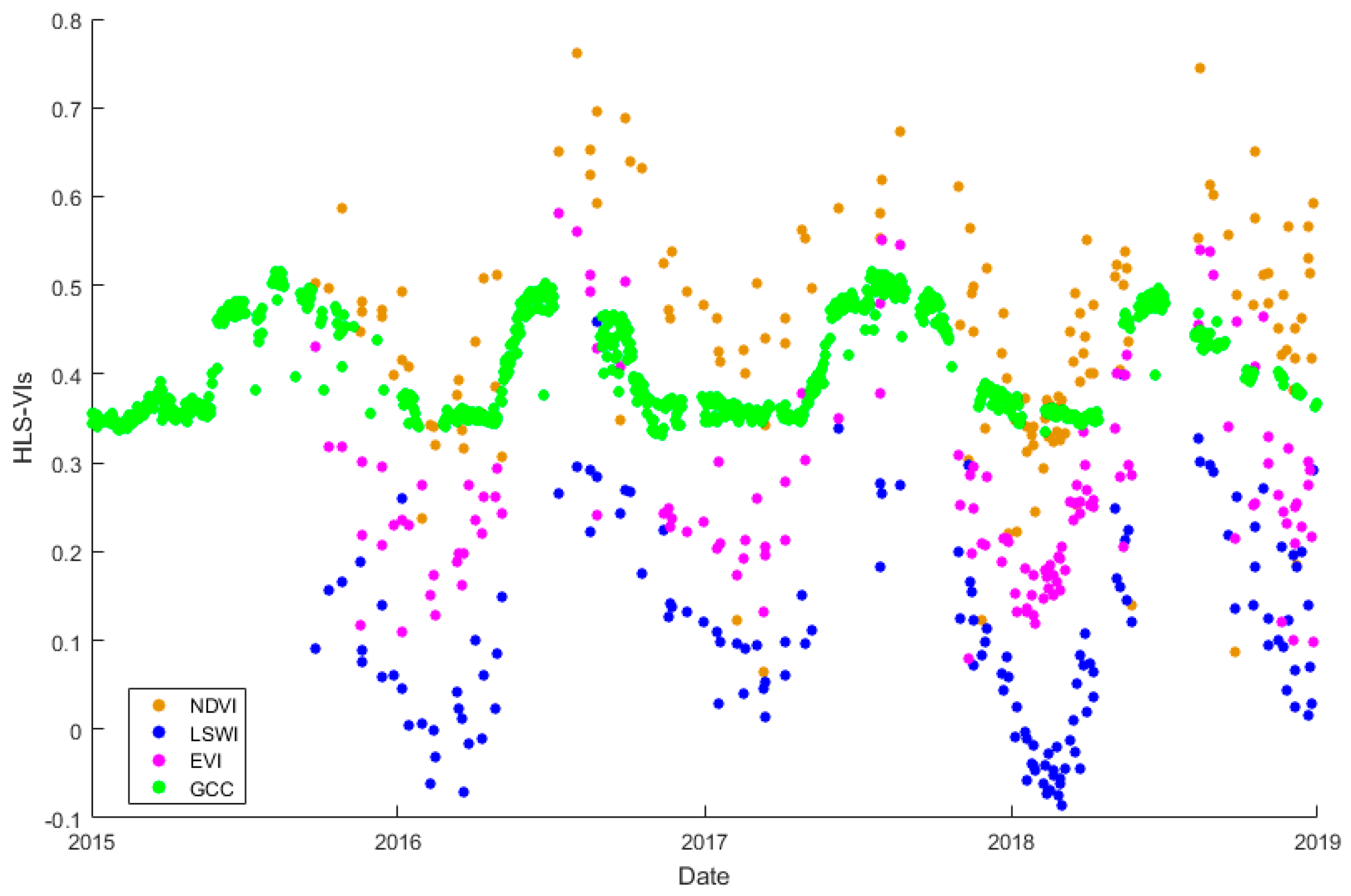
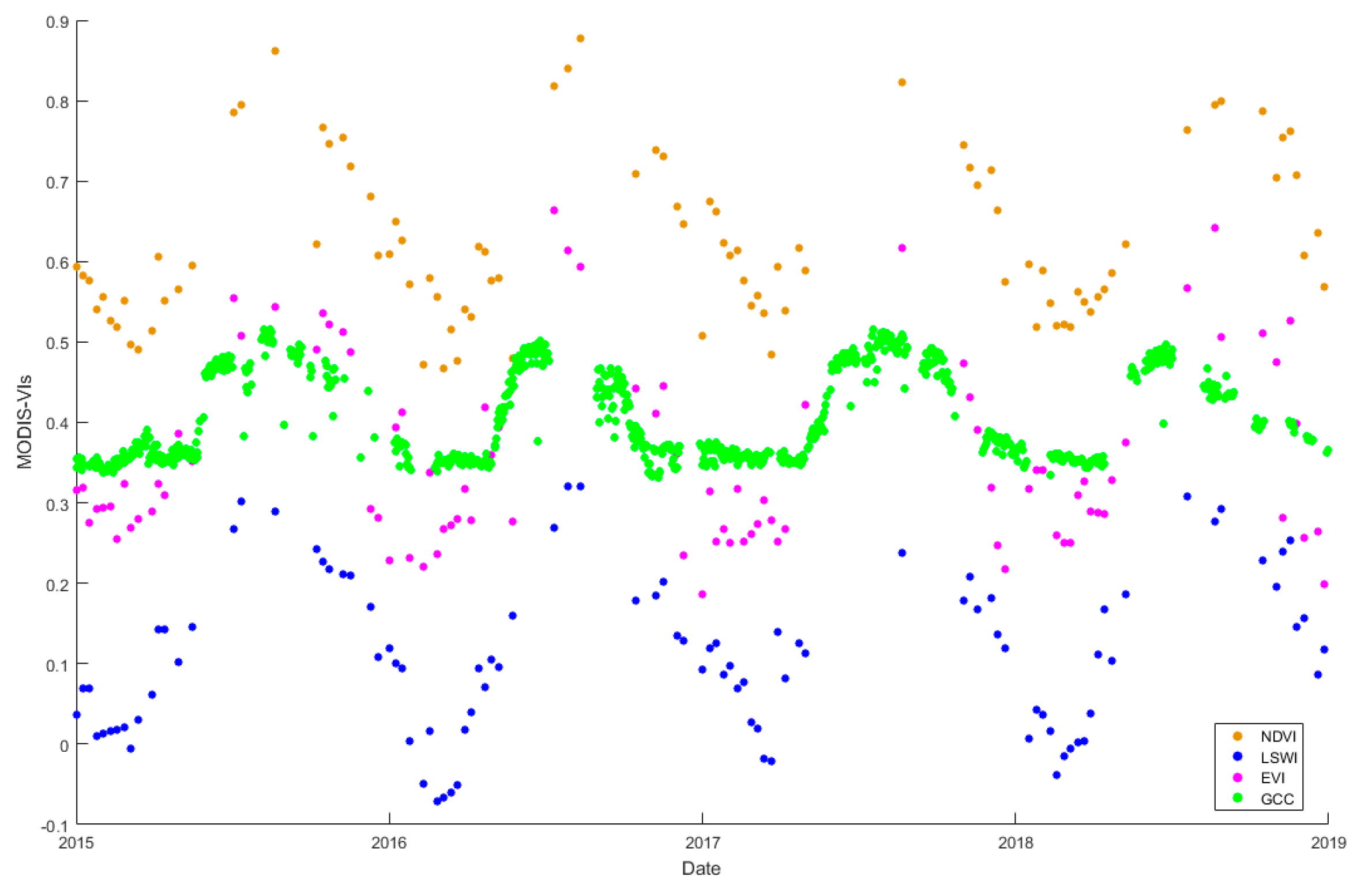
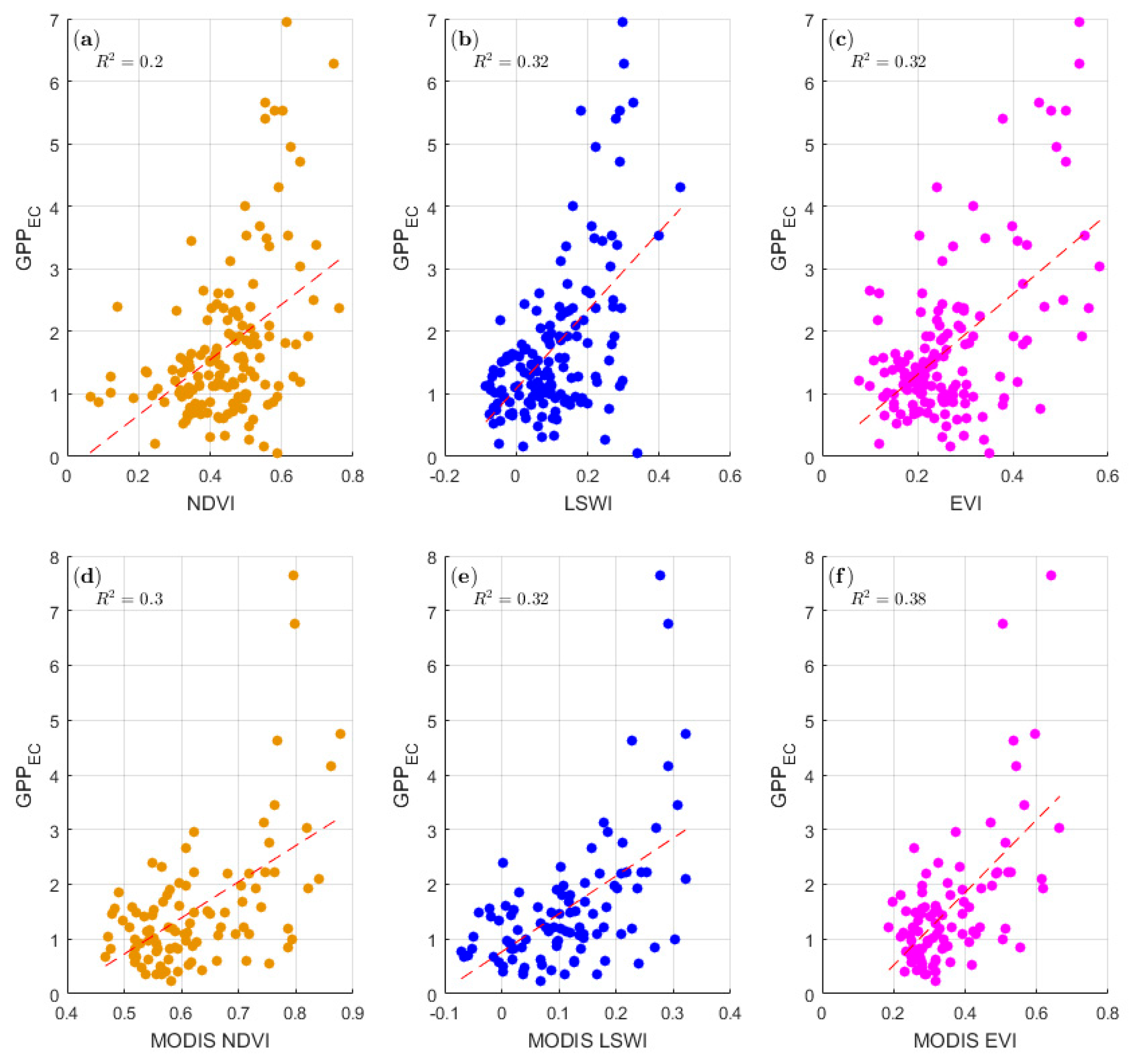
3.1. Temperature and Precipitation and the Relationship between the GPPEC and Remote Sensing VIs at the Yuanjiang Station
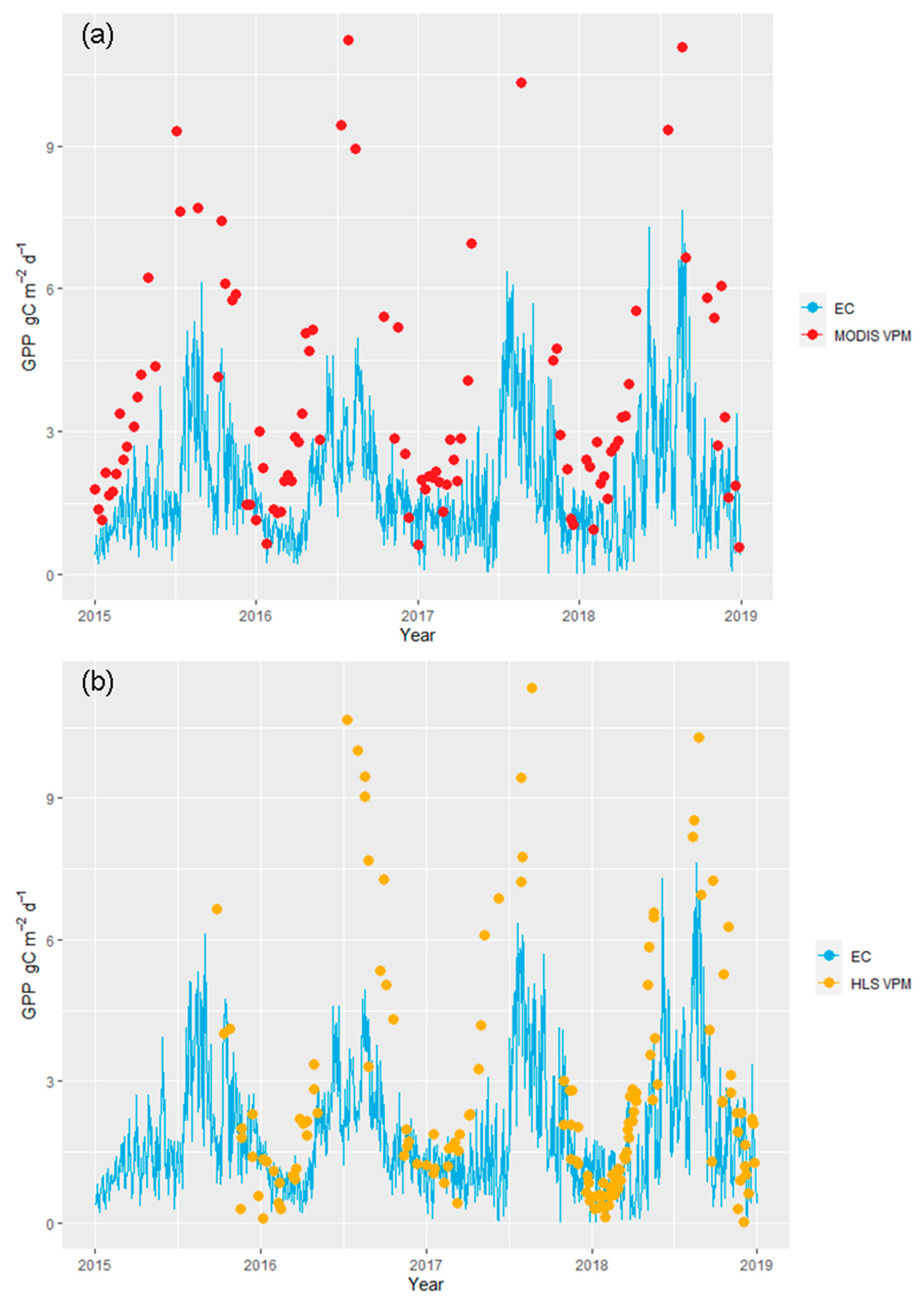
3.2. Comparison of the EC Dynamics and Trends of the HLS and MODIS VPM Results
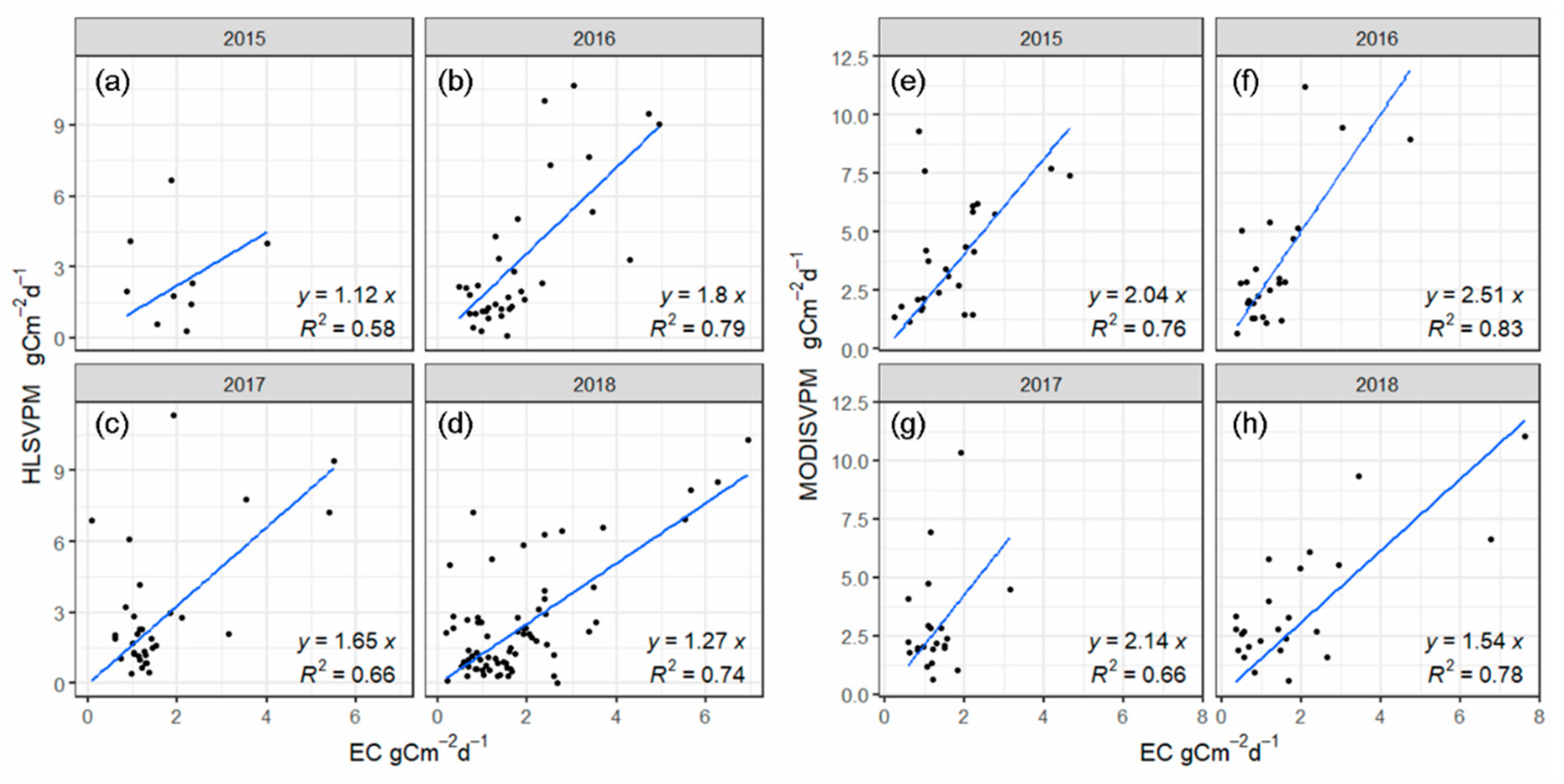
3.3. Evaluation of the HLS and MODIS VPM Results
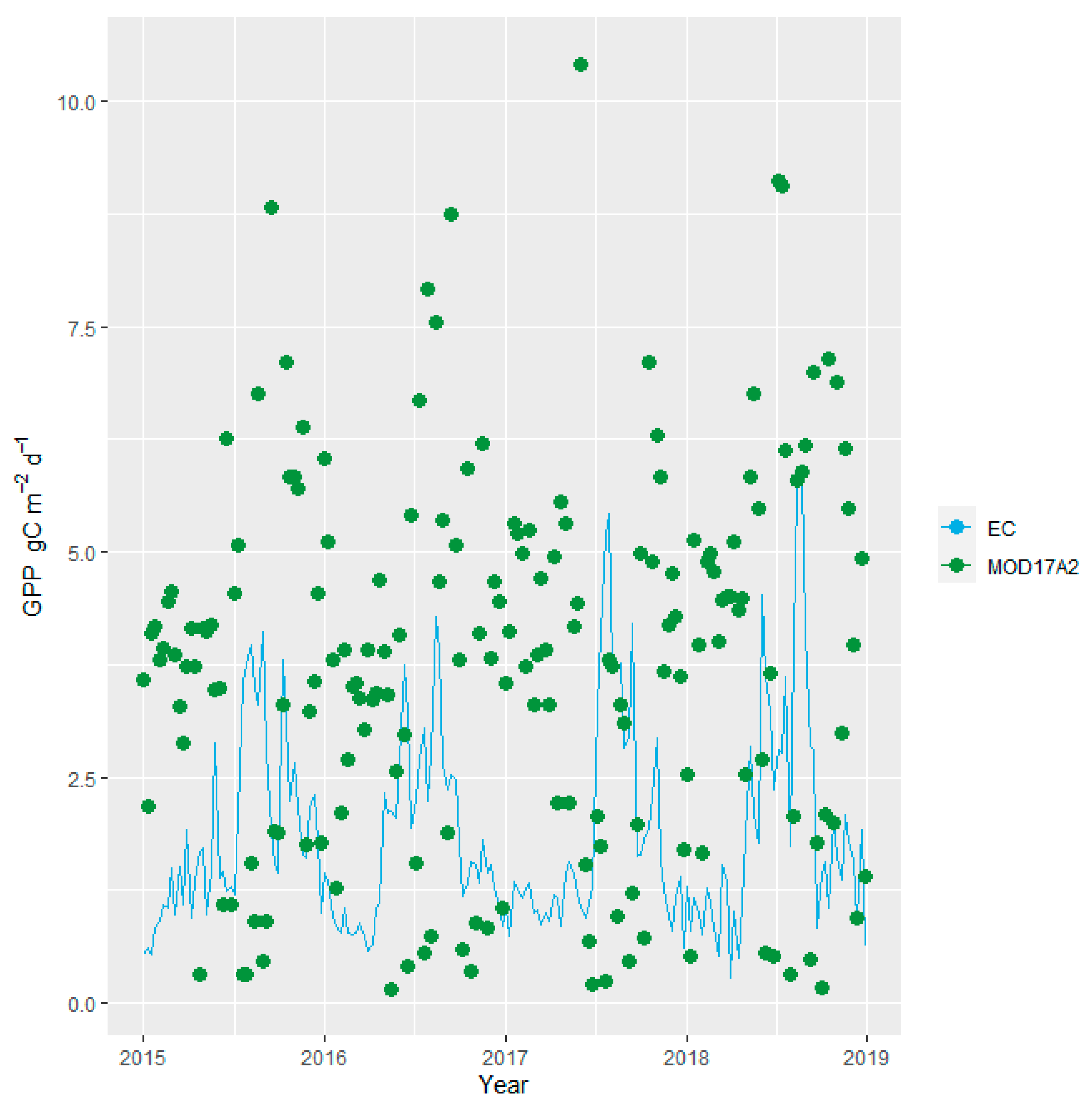
3.4. Comparison of the Conventional MODIS Products and GPPEC
3.5. Extraction of Phenophases and Changes in the GPP during Different Phenophases via Remote Sensing Simulations
3.5.1. Phenophase Division
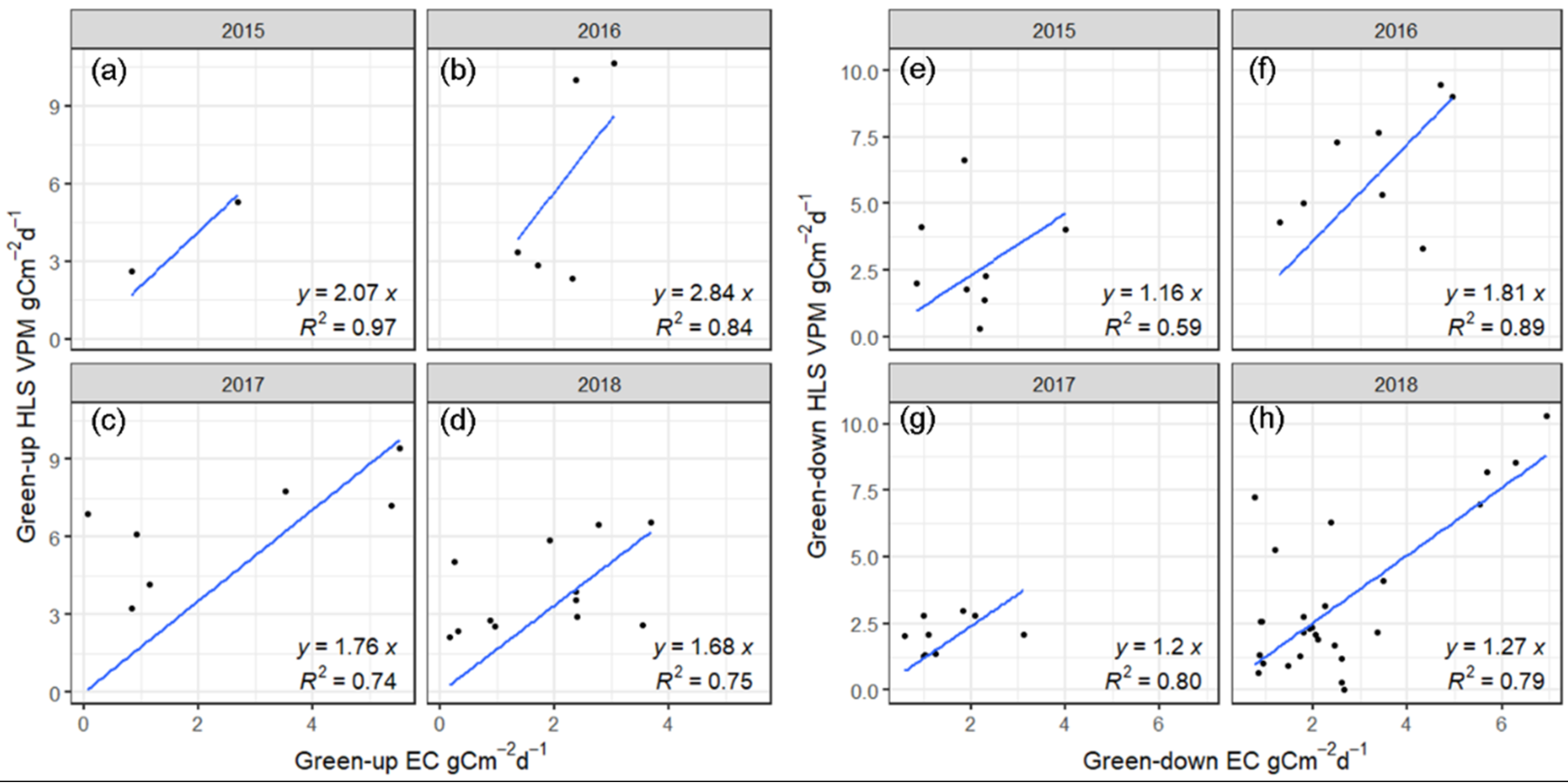
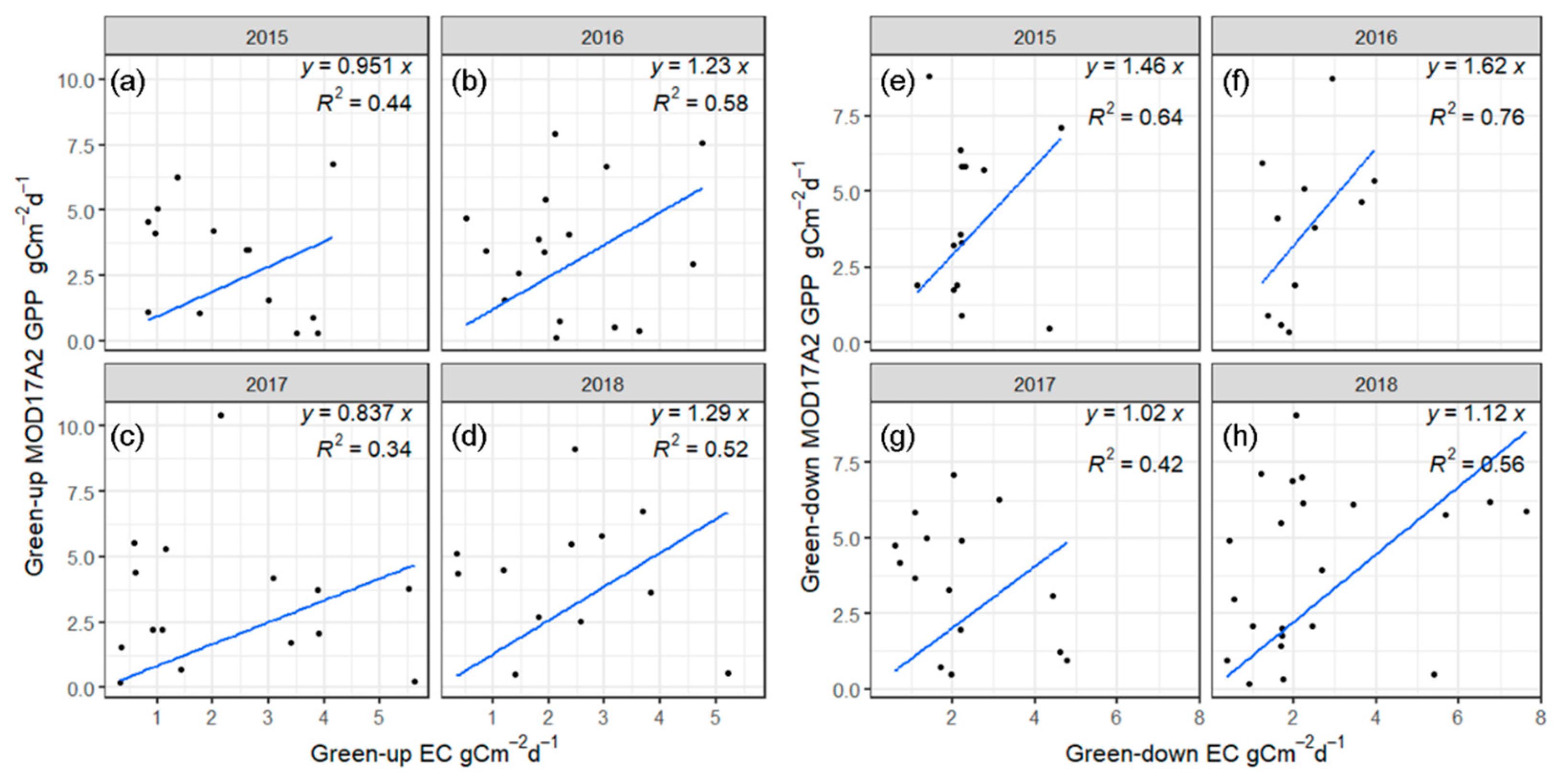
3.5.2. Comparison of the Simulated GPP Values during the Different Phenophases
4. Discussion
4.1. HLS Data Play a Significant Role in Improving Savanna GPP Estimation
4.2. Relationship between Phenophases and GPP Remote Sensing Modeling in Savanna Ecosystems
4.3. Advantages of the VPM over Conventional Remote Sensing Products in Savanna GPP Studies
4.4. Uncertainties, Limitations, and Implications of GPP Simulation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdi, A.M.; Brandt, M.; AbelR, C. Fensholt. Satellite Remote Sensing of Savannas: Current Status and Emerging Opportunities. J. Remote Sens. 2022, 2022, 9835284. [Google Scholar] [CrossRef]
- Hutley, L.B.; Beringer, J.; Fatichi, S.; Schymanski, S.J.; Northwood, M. Gross primary productivity and water use efficiency are increasing in a high rainfall tropical savanna. Glob. Chang. Biol. 2022, 28, 2360–2380. [Google Scholar] [CrossRef]
- Grace, J.; Jose, J.S.; Meir, P.; Miranda, H.S.; Montes, R.A. Productivity and carbon fluxes of tropical savannas. J. Biogeogr. 2006, 33, 387–400. [Google Scholar] [CrossRef]
- Alberton, B.; Almeida, J.; Helm, R.; da Torres, R.S.; Menzel, A.; Morellato, L.P.C. Using phenological cameras to track the green up in a cerrado savanna and its on-the-ground validation. Ecol. Inform. 2014, 19, 62–70. [Google Scholar] [CrossRef]
- Ma, X.L.; Huete, A.; Moore, C.E.; Cleverly, J.; Hutley, L.B.; Beringer, J.; Leng, S.; Xie, Z.Y.; Yu, Q.; Eamus, D. Spatiotemporal partitioning of savanna plant functional type productivity along NATT. Remote Sens. Environ. 2020, 246, 111855. [Google Scholar] [CrossRef]
- Myo, S.T.Z.; Zhang, Y.P.; Song, Q.H.; Chen, A.G.; Yang, D.X.; Zhou, L.G.; Lin, Y.X.; Phyo, Z.; Fei, X.H.; Liang, N.S. Assessing Canopy Phenological Variations and Gross Primary Productivity in A Savanna Ecosystem in Yuanjiang, Yunnan Province of Southwest China. J. Environ. Inform. 2023, 42, 75–89. [Google Scholar] [CrossRef]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Hutley, L.B.; Setterfield, S.A. Savanna. In Encyclopedia of Ecology, 2nd ed.; Fath, B., Ed.; Elsevier: Oxford, UK, 2019; pp. 623–633. [Google Scholar]
- Lapuz, R.S.; Jaojoco, A.K.M.; Reyes, S.R.C.; De Alban, J.D.; Tomlinson, T.K.W. Greater loss and fragmentation of savannas than forests over the last three decades in Yunnan Province, China. Environ. Res. Lett. 2022, 17, 014003. [Google Scholar] [CrossRef]
- Li, J.; Jin, Y.; Liu, Y.; Zhang, Y.; Grace, J.; Song, Q.; Sha, L.; Lin, Y.; Chen, A.; Li, P.; et al. Effects of precipitation exclusion on N2O emissions in a savanna ecosystem in SW China. Atmos. Environ. 2018, 187, 1–8. [Google Scholar] [CrossRef]
- Pei, Y.; Dong, J.; Zhang, Y.; Yuan, W.; Doughty, R.; Yang, J.; Zhou, D.; Zhang, L.; Xiao, X. Evolution of light use efficiency models: Improvement, uncertainties, and implications. Agric. For. Meteorol. 2022, 317, 108905. [Google Scholar] [CrossRef]
- Sjöström, M.; Ardö, J.; Arneth, A.; Boulain, N.; Cappelaere, B.; Eklundh, L.; de Grandcourt, A.; Kutsch, W.L.; Merbold, L.; Nouvellon, Y.; et al. Exploring the potential of MODIS EVI for modeling gross primary production across African ecosystems. Remote Sens. Environ. 2011, 115, 1081–1089. [Google Scholar] [CrossRef]
- Wagle, P.; Zhang, Y.G.; Jin, C.; Xiao, X.M. Comparison of solar-induced chlorophyll fluorescence, light-use efficiency, and process-based GPP models in maize. Ecol. Appl. 2016, 26, 1211–1222. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, X.; Wu, X.; Zhou, S.; Zhang, G.; Qin, Y.; Dong, J. Data Descriptor: A global moderate resolution dataset of gross primary production of vegetation for 2000–2016. Sci. Data 2017, 4, 170165. [Google Scholar] [CrossRef]
- Ahmad, S.; Pandey, A.C.; Kumar, A.; Lele, N.V.; Bhattacharya, B.K. Primary productivity estimation of forest based on in-situ biophysical parameters and sentinel satellite data using vegetation photosynthesis model in an eastern Indian tropical dry deciduous forest. Trop. Ecol. 2022, 63, 409–422. [Google Scholar] [CrossRef]
- Yang, J.; Dong, J.; Xiao, X.; Dai, J.; Wu, C.; Xia, J.; Zhao, G.; Zhao, M.; Li, Z.; Zhang, Y.; et al. Divergent shifts in peak photosynthesis timing of temperate and alpine grasslands in China. Remote Sens. Environ. 2019, 233, 111395. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, X.M.; Wagle, P.; Ma, S.Y.; Baldocchi, D.; Carrara, A.; Zhang, Y.; Dong, J.W.; Qin, Y.W. Canopy and climate controls of gross primary production of Mediterranean-type deciduous and evergreen oak savannas. Agric. For. Meteorol. 2016, 226, 132–147. [Google Scholar] [CrossRef]
- Biudes, M.S.; Vourlitis, G.L.; Velasque, M.C.S.; Machado, N.G.; de Morais Danelichen, V.H.; Pavao, V.M.; Ar-ruda, P.H.; Nogueira, Z.J.D.S. Gross primary productivity of Brazilian Savanna (Cerrado) estimated by different remote sensing-based models. Agric. For. Meteorol. 2021, 307, 108456. [Google Scholar] [CrossRef]
- Song, G.; Wang, J.; Zhao, Y.; Yang, D.; Lee, C.K.F.; Guo, Z.; Detto, M.; Alberton, B.; Morellato, P.; Nelson, B.; et al. Scale matters: Spatial resolution impacts tropical leaf phenology characterized by multi-source satellite remote sensing with an ecological-constrained deep learning model. Remote Sens. Environ. 2024, 304, 114027. [Google Scholar] [CrossRef]
- Mas, J.F.; de Araujo, R.S. Assessing Landsat Images Availability and Its Effects on Phenological Metrics. Forests 2021, 12, 574. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Raj, R.; Bayat, B.; Lukes, P.; Sigut, L.; Homolova, L. Analyzing Daily Estimation of Forest Gross Primary Production Based on Harmonized Landsat-8 and Sentinel-2 Product Using SCOPE Process-Based Model. Remote Sens. 2020, 12, 3773. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; Moreno-Martínez, Á.; García-Haro, F.; Camps-Valls, G.; Robinson, N.; Kattge, J.; Running, S. Global Estimation of Biophysical Variables from Google Earth Engine Platform. Remote Sens. 2018, 10, 1167. [Google Scholar] [CrossRef]
- Moore, C.E.; Beringer, J.; Evans, B.; Hutley, L.B.; Tapper, N.J. Tree-grass phenology information improves light use efficiency modelling of gross primary productivity for an Australian tropical savanna. Biogeosciences 2017, 14, 111–129. [Google Scholar] [CrossRef]
- Kooistra, L.; Berger, K.; Brede, B.; Graf, L.V.; Aasen, H.; Roujean, J.-L.; Machwitz, M.; Schlerf, M.; Atzberger, C.; Prikaziuk, E.; et al. Reviews and syntheses: Remotely sensed optical time series for monitoring vegetation productivity. Biogeosciences 2024, 21, 473–511. [Google Scholar] [CrossRef]
- Sonnentag, O.; Hufkens, K.; Teshera-Sterne, C.; Young, A.M.; Friedl, M.; Braswell, B.H.; Milliman, T.; O’Keefe, J.; Richardson, A.D. Digital repeat photography for phenological research in forest ecosystems. Agric. For. Meteorol. 2012, 152, 159–177. [Google Scholar] [CrossRef]
- Ma, X.; Huete, A.; Yu, Q.; Coupe, N.R.; Davies, K.; Broich, M.; Ratana, P.; Beringer, J.; Hutley, L.B.; Cleverly, J.; et al. Spatial patterns and temporal dynamics in savanna vegetation phenology across the North Australian Tropical Transect. Remote Sens. Environ. 2013, 139, 97–115. [Google Scholar] [CrossRef]
- Alberton, B.; Martin, T.C.M.; Da Rocha, H.R.; Richardson, A.D.; Moura, M.S.B.; Torres, R.S.; Morellato, L.P.C. Relationship between tropical leaf phenology and ecosystem productivity using phenocameras. Front. Environ. Sci. 2023, 11, 1223219. [Google Scholar] [CrossRef]
- Richardson, A.D.; Jenkins, J.P.; Braswell, B.H.; Hollinger, D.Y.; Ollinger, S.V.; Smith, M.-L. Use of digital webcam images to track spring green-up in a deciduous broadleaf forest. Oecologia 2007, 152, 323–334. [Google Scholar] [CrossRef]
- Baldocchi, D.D. How eddy covariance flux measurements have contributed to our understanding of Global Change Biology. Glob. Chang. Biol. 2019, 26, 242–260. [Google Scholar] [CrossRef]
- Cleverly, J.; Eamus, D.; Van Gorsel, E.; Chen, C.; Rumman, R.; Luo, Q.; Coupe, N.R.; Li, L.; Kljun, N.; Faux, R.; et al. Productivity and evapotranspiration of two contrasting semiarid ecosystems following the 2011 global carbon land sink anomaly. Agric. For. Meteorol. 2016, 220, 151–159. [Google Scholar] [CrossRef]
- Jin, C.; Xiao, X.; Merbold, L.; Arneth, A.; Veenendaal, E.; Kutsch, W.L. Phenology and gross primary production of two dominant savanna woodland ecosystems in Southern Africa. Remote Sens. Environ. 2013, 135, 189–201. [Google Scholar] [CrossRef]
- Cernusak, L.A. Gas exchange and water-use efficiency in plant canopies. Plant Biol. 2020, 22 (Suppl. S1), 52–67. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Tian, F.; Huang, K.; Wang, Y.; Wu, Z.; Fensholt, R. Asymmetric patterns and temporal changes in phenology-based seasonal gross carbon uptake of global terrestrial ecosystems. Glob. Ecol. Biogeogr. 2020, 29, 1020–1033. [Google Scholar] [CrossRef]
- Jin, J.; Hou, W.; Ma, X.; Wang, H.; Xie, Q.; Wang, W.; Zhu, Q.; Fang, X.; Zhou, F.; Liu, Y.; et al. Improved estimation of gross primary production with NIRvP by incorporating a phenophase scheme for temperate deciduous forest ecosystems. For. Ecol. Manag. 2024, 556, 121742. [Google Scholar] [CrossRef]
- Higgins, S.I.; Delgado-Cartay, M.D.; February, E.C.; Combrink, H.J. Is there a temporal niche separation in the leaf phenology of savanna trees and grasses? J. Biogeogr. 2011, 38, 2165–2175. [Google Scholar] [CrossRef]
- El-Madany, T.S.; Reichstein, M.; Perez-Priego, O.; Carrara, A.; Moreno, G.; Martín, M.P.; Pacheco-Labrador, J.; Wohlfahrt, G.; Nieto, H.; Weber, U.; et al. Drivers of spatio-temporal variability of carbon dioxide and energy fluxes in a Mediterranean savanna ecosystem. Agric. For. Meteorol. 2018, 262, 258–278. [Google Scholar] [CrossRef]
- Huang, D.; Chi, H.; Xin, F.F.; Miyata, A.; Kang, M.; Liu, K.W.; Li, R.D.; Dang, H.S.; Qin, Y.W.; Xiao, X.M. Improved estimation of gross primary production of paddy rice cropland with changing model parameters over phenological transitions. Ecol. Model. 2021, 445, 109492. [Google Scholar] [CrossRef]
- Ma, X.; Zhu, X.; Xie, Q.; Jin, J.; Zhou, Y.; Luo, Y.; Liu, Y.; Tian, J.; Zhao, Y. Monitoring nature’s calendar from space: Emerging topics in land surface phenology and associated opportunities for science applications. Glob. Chang. Biol. 2022, 28, 7186–7204. [Google Scholar] [CrossRef]
- Jin, Y.; Li, J.; Liu, C.; Liu, Y.; Zhang, Y.; Song, Q.; Sha, L.; Balasubramanian, D.; Chen, A.; Yang, D.; et al. Precipitation reduction alters herbaceous community structure and composition in a savanna. J. Veg. Sci. 2019, 30, 821–831. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Fei, X.; Song, Q.; Zhang, Y.; Liu, Y.; Sha, L.; Yu, G.; Zhang, L.; Duan, C.; Deng, Y.; Wu, C.; et al. Carbon exchanges and their responses to temperature and precipitation in forest ecosystems in Yunnan, Southwest China. Sci. Total Environ. 2018, 616, 824–840. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H.; et al. Gap filling strategies for defensible annual sums of net ecosystem exchange. Agric. For. Meteorol. 2001, 107, 43–69. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Tenhunen, J.; Aubinet, M.; Bakwin, P.; Berbigier, P.; Bernhofer, C.; Burba, G.; Clement, R.; Davis, K.J.; et al. Seasonality of ecosystem respiration and gross primary production as derived from FLUXNET measurements. Agric. For. Meteorol. 2002, 113, 53–74. [Google Scholar] [CrossRef]
- Seyednasrollah, B.; Milliman, T.; Richardson, A.D. Data extraction from digital repeat photography using xROI: An interactive framework to facilitate the process. ISPRS J. Photogramm. Remote Sens. 2019, 152, 132–144. [Google Scholar] [CrossRef]
- Richardson, A.D.; Hollinger, D.Y.; Aber, J.D.; Ollinger, S.V.; Braswell, B.H. Environmental variation is directly responsible for short- but not long-term variation in forest-atmosphere carbon exchange. Glob. Chang. Biol. 2007, 13, 788–803. [Google Scholar] [CrossRef]
- Filippa, G.; Cremonese, E.; Migliavacca, M.; Galvagno, M.; Forkel, M.; Wingate, L.; Tomelleri, E.; di Cella, U.M.; Richardson, A.D. Phenopix: A R package for image-based vegetation phenology. Agric. For. Meteorol. 2016, 220, 141–150. [Google Scholar] [CrossRef]
- Beck, P.S.A.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Klosterman, S.T.; Hufkens, K.; Gray, J.M.; Melaas, E.; Sonnentag, O.; Lavine, I.; Mitchell, L.; Norman, R.; Friedl, M.A.; Rich-ardson, A.D. Evaluating remote sensing of deciduous forest phenology at multiple spatial scales using PhenoCam imagery. Biogeosciences 2014, 11, 4305–4320. [Google Scholar] [CrossRef]
- Kline, M. Calculus: An Intuitive and Physical Approach, 2nd ed.; Dover Publications: Mineola, NY, USA, 1998. [Google Scholar]
- Chastain, R.; Housman, I.; Goldstein, J.; Finco, M.; Tenneson, K. Empirical cross sensor comparison of Sentinel-2A and 2B MSI, Landsat-8 OLI, and Landsat-7 ETM + top of atmosphere spectral characteristics over the conterminous United States. Remote Sens. Environ. 2019, 221, 274–285. [Google Scholar] [CrossRef]
- Yin, F.; Lewis, P.E.; Gómez-Dans, J.L. Bayesian atmospheric correction over land: Sentinel-2/MSI and Landsat 8/OLI. Geosci. Model Dev. 2022, 15, 7933–7976. [Google Scholar] [CrossRef]
- Xiao, X.M.; Zhang, Q.Y.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Berrien, M.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Jin, Y.Q.; Li, J.; Liu, C.G.; Liu, Y.T.; Zhang, Y.P.; Song, Q.H.; Sha, L.Q.; Chen, A.G.; Yang, D.X.; Li, P.G. Response of net primary productivity to precipitation exclusion in a savanna ecosystem. For. Ecol. Manag. 2018, 429, 69–76. [Google Scholar] [CrossRef]
- Cho, S.; Kang, M.; Ichii, K.; Kim, J.; Lim, J.-H.; Chun, J.-H.; Park, C.-W.; Kim, H.S.; Choi, S.-W.; Lee, S.-H.; et al. Evaluation of forest carbon uptake in South Korea using the national flux tower network, remote sensing, and data-driven technology. Agric. For. Meteorol. 2021, 311, 108653. [Google Scholar] [CrossRef]
- Wagle, P.; Gowda, P.H.; Northup, B.K. Annual dynamics of carbon dioxide fluxes over a rainfed alfalfa field in the U.S. Southern Great Plains. Agric. For. Meteorol. 2019, 265, 208–217. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Zhu, H.; Tan, Y.; Yan, L.; Liu, F. Flora of the Savanna-like Vegetation in Hot Dry Valleys, Southwestern China with Implications to their Origin and Evolution. Bot. Rev. 2020, 86, 281–297. [Google Scholar] [CrossRef]
- Tran, K.H.; Zhang, X.; Ketchpaw, A.R.; Wang, J.; Ye, Y.; Shen, Y. A novel algorithm for the generation of gap-free time series by fusing harmonized Landsat 8 and Sentinel-2 observations with PhenoCam time series for detecting land surface phenology. Remote Sens. Environ. 2022, 282, 113275. [Google Scholar] [CrossRef]
- Cai, Z.; Junttila, S.; Holst, J.; Jin, H.; Ardö, J.; Ibrom, A.; Peichl, M.; Mölder, M.; Jönsson, P.; Rinne, J.; et al. Modelling Daily Gross Primary Productivity with Sentinel-2 Data in the Nordic Region-Comparison with Data from MODIS. Remote Sens. 2021, 13, 469. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, L.; Xiao, J.; Yuan, W.; Yan, M.; Li, T.; Zhang, Z. Sources of uncertainty in gross primary productivity simulated by light use efficiency models: Model structure, parameters, input data, and spatial resolution. Agric. For. Meteorol. 2018, 263, 242–257. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Google Earth Engine Applications Since Inception: Usage, Trends, and Potential. Remote Sens. 2018, 10, 1509. [Google Scholar] [CrossRef]
- Christian, B.; Joshi, N.; Saini, M.; Mehta, N.; Goroshi, S.; Nidamanuri, R.R.; Thenkabail, P.; Desai, A.R.; Krishnayya, N.S.R. Seasonal variations in phenology and productivity of a tropical dry deciduous forest from MODIS and Hyperion. Agric. For. Meteorol. 2015, 214, 91–105. [Google Scholar] [CrossRef]
- Lin, S.R.; Li, J.; Liu, Q.H.; Li, L.H.; Zhao, J.; Yu, W.T. Evaluating the Effectiveness of Using Vegetation Indices Based on Red-Edge Reflectance from Sentinel-2 to Estimate Gross Primary Productivity. Remote Sens. 2019, 11, 1303. [Google Scholar] [CrossRef]
- Fei, X.; Jin, Y.; Zhang, Y.; Sha, L.; Liu, Y.; Song, Q.; Zhou, W.; Liang, N.; Yu, G.; Zhang, L.; et al. Eddy covariance and biometric measurements show that a savanna ecosystem in Southwest China is a carbon sink. Sci. Rep. 2017, 7, srep41025. [Google Scholar] [CrossRef] [PubMed]
- Ustin, S.L.; Middleton, E.M. Current and near-term advances in Earth observation for ecological applications. Ecol. Process. 2021, 10, 1. [Google Scholar] [CrossRef]
- Restrepo-Coupe, N.; Huete, A.; Davies, K.; Cleverly, J.; Beringer, J.; Eamus, D.; van Gorsel, E.; Hutley, L.B.; Meyer, W.S. MODIS vegetation products as proxies of photosynthetic potential along a gradient of meteorologically and biologically driven ecosystem productivity. Biogeosciences 2016, 13, 5587–5608. [Google Scholar] [CrossRef]
- Kanniah, K.D.; Beringer, J.; Hutley, L.B.; Tapper, N.J.; Zhu, X. Evaluation of Collections 4 and 5 of the MODIS Gross Primary Productivity product and algorithm improvement at a tropical savanna site in northern Australia. Remote Sens. Environ. 2009, 113, 1808–1822. [Google Scholar] [CrossRef]
- Wagle, P.; Xiao, X.M.; Torn, M.S.; Cook, D.R.; Matamala, R.; Fischer, M.L.; Jin, C.; Dong, J.W.; Biradar, C. Sensitivity of vegetation indices and gross primary production of tallgrass prairie to severe drought. Remote Sens. Environ. 2014, 152, 1–14. [Google Scholar] [CrossRef]
- Zhang, L.X.; Zhou, D.C.; Fan, J.W.; Guo, Q.; Chen, S.P.; Wang, R.H.; Li, Y.Z. Contrasting the Performance of Eight Satellite-Based GPP Models in Water-Limited and Temperature-Limited Grassland Ecosystems. Remote Sens. 2019, 11, 1333. [Google Scholar] [CrossRef]
- Rossini, M.; Cogliati, S.; Meroni, M.; Migliavacca, M.; Galvagno, M.; Busetto, L.; Cremonese, E.; Julitta, T.; Siniscalco, C.; di Cella, U.M.; et al. Remote sensing-based estimation of gross primary production in a subalpine grassland. Biogeosciences 2012, 9, 2565–2584. [Google Scholar] [CrossRef]
- Fei, X.H.; Song, Q.H.; Zhang, Y.P.; Yu, G.R.; Zhang, L.M.; Sha, L.; Liu, Y.; Xu, K.; Chen, H.; Wu, C.S.; et al. Patterns and Controls of Light Use Efficiency in Four Contrasting Forest Ecosystems in Yunnan, Southwest China. J. Geophys. Res.-Biogeosciences 2019, 124, 293–311. [Google Scholar] [CrossRef]
- Lin, S.; Huang, X.; Zheng, Y.; Zhang, X.; Yuan, W. An Open Data Approach for Estimating Vegetation Gross Primary Production at Fine Spatial Resolution. Remote Sens. 2022, 14, 2651. [Google Scholar] [CrossRef]
- Chen, R.; Liu, L.; Liu, X.; Liu, Z.; Gu, L.; Rascher, U. Improving estimates of sub-daily gross primary production from solar-induced chlorophyll fluorescence by accounting for light distribution within canopy. Remote Sens. Environ. 2024, 300, 113919. [Google Scholar] [CrossRef]
- Schaefer, K.; Schwalm, C.R.; Williams, C.; Arain, M.A.; Barr, A.; Chen, J.M.; Davis, K.J.; Dimitrov, D.; Hilton, T.W.; Hollinger, D.Y.; et al. A model-data comparison of gross primary productivity: Results from the North American Carbon Program site synthesis. J. Geophys. Res. Biogeosciences 2012, 117, G03010. [Google Scholar] [CrossRef]
- Gelybo, G.; Barcza, Z.; Kern, A.; Kljun, N. Effect of spatial heterogeneity on the validation of remote sensing based GPP estimations. Agric. For. Meteorol. 2013, 174, 43–53. [Google Scholar] [CrossRef]

| Spectral Bands | From OLI to MSI | From ETM+ to MSI |
|---|---|---|
| Blue | MSI = −0.0107 + 1.0946 × OLI | MSI = −0.0139 + 1.1060 × ETM+ |
| Green | MSI = 0.0026 + 1.0043 × OLI | MSI = 0.0041 + 0.9909 × ETM+ |
| Red | MSI = −0.0015 + 1.0524 × OLI | MSI = −0.0024 + 1.0568 × ETM+ |
| Near-infrared (NIR) | MSI = −0.0021 + 1.0283 × OLI | MSI = −0.0140 + 1.1515 × ETM+ |
| Shortwave infrared (SWIR1) | MSI = 0.0065 + 1.0049 × OLI | MSI = 0.0041 + 1.0361 × ETM+ |
| SWIR2 | MSI = 0.0046 + 1.0002 × OLI | MSI = 0.0086 + 1.0401 × ETM+ |
| GPPHLS-VPM | GPPMODIS-VPM | |||||
|---|---|---|---|---|---|---|
| Year | Slope | R2 | RMSE | Slope | R2 | RMSE |
| 2015 | 1.12 | 0.58 | 1.54 | 2.04 | 0.76 | 3.04 |
| 2016 | 1.8 | 0.79 | 2.65 | 2.51 | 0.83 | 3.1 |
| 2017 | 1.65 | 0.66 | 2.64 | 2.14 | 0.66 | 2.62 |
| 2018 | 1.27 | 0.74 | 1.80 | 1.54 | 0.78 | 2.49 |
| 2015–2018 | 1.46 | 0.71 | 2.25 | 1.91 | 0.74 | 2.83 |
| Year | Slope | R2 | RMSE |
|---|---|---|---|
| 2015 | 1.39 | 0.01 | 2.82 |
| 2016 | 1.57 | 0.03 | 2.81 |
| 2017 | 1.14 | 0.05 | 3.2 |
| 2018 | 1.26 | 0.03 | 3.25 |
| 2015–2018 | 1.32 | 0.001 | 3.03 |
| Year | SOSDOY (Green-Up) | POPDOY | EOSDOY (Green-Down) |
|---|---|---|---|
| 2015 | 128 | 176 | 296 |
| 2016 | 105 | 186 | 265 |
| 2017 | 102 | 169 | 268 |
| 2018 | 91 | 158 | 220 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xie, S.; Zhang, Y.; Song, Q.; Filippa, G.; Qi, D. GPP of a Chinese Savanna Ecosystem during Different Phenological Phases Simulated from Harmonized Landsat and Sentinel-2 Data. Remote Sens. 2024, 16, 3475. https://doi.org/10.3390/rs16183475
Zhang X, Xie S, Zhang Y, Song Q, Filippa G, Qi D. GPP of a Chinese Savanna Ecosystem during Different Phenological Phases Simulated from Harmonized Landsat and Sentinel-2 Data. Remote Sensing. 2024; 16(18):3475. https://doi.org/10.3390/rs16183475
Chicago/Turabian StyleZhang, Xiang, Shuai Xie, Yiping Zhang, Qinghai Song, Gianluca Filippa, and Dehua Qi. 2024. "GPP of a Chinese Savanna Ecosystem during Different Phenological Phases Simulated from Harmonized Landsat and Sentinel-2 Data" Remote Sensing 16, no. 18: 3475. https://doi.org/10.3390/rs16183475
APA StyleZhang, X., Xie, S., Zhang, Y., Song, Q., Filippa, G., & Qi, D. (2024). GPP of a Chinese Savanna Ecosystem during Different Phenological Phases Simulated from Harmonized Landsat and Sentinel-2 Data. Remote Sensing, 16(18), 3475. https://doi.org/10.3390/rs16183475






