High-Efficiency Forward Modeling of Gravitational Fields in Spherical Harmonic Domain with Application to Lunar Topography Correction
Abstract
1. Introduction
2. Theory and Methods
2.1. Spatial Domain Forward Modeling Method
2.2. Forward Method in Spherical Harmonic Domain
| Algorithm 1: Gravity forward modeling in spherical harmonic domain |
| Input: 3D density distributions of each layer |
| 1. Do k = 1 to Nz, and initialize gz = 0 |
| 2. Calculate and ; |
| 3. Multiply the factor to step 1; |
| 4. Spherical harmonic synthesis of the result in step 3 to obtain the gz(k); |
| 5. gz = gz + gz(k); |
| 6. End Do |
| Output: 2D distribution of the gz component. |
3. Synthetic Forward Model Tests
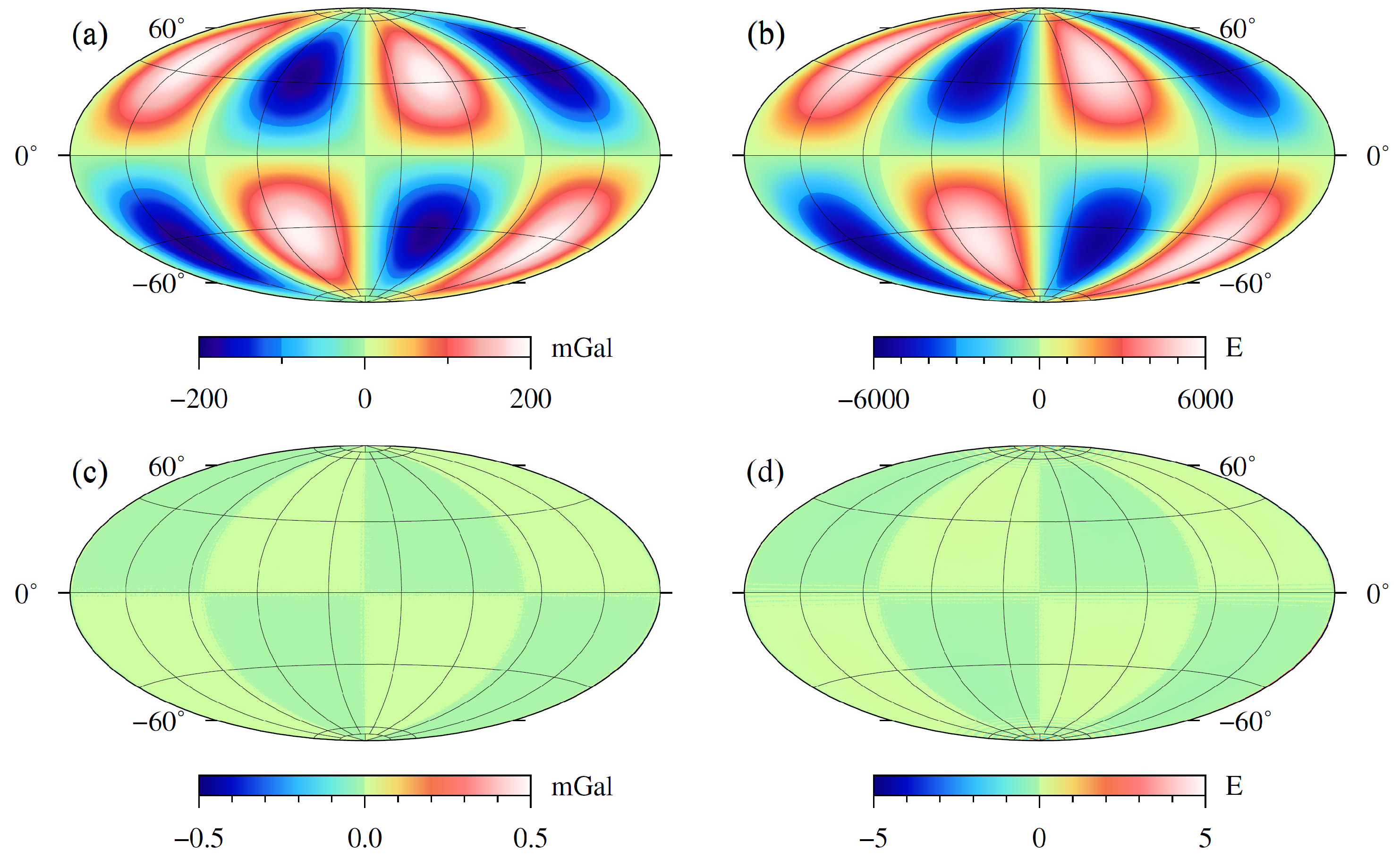
3.1. Sphere Shell Model
3.2. Complex Synthetic Model
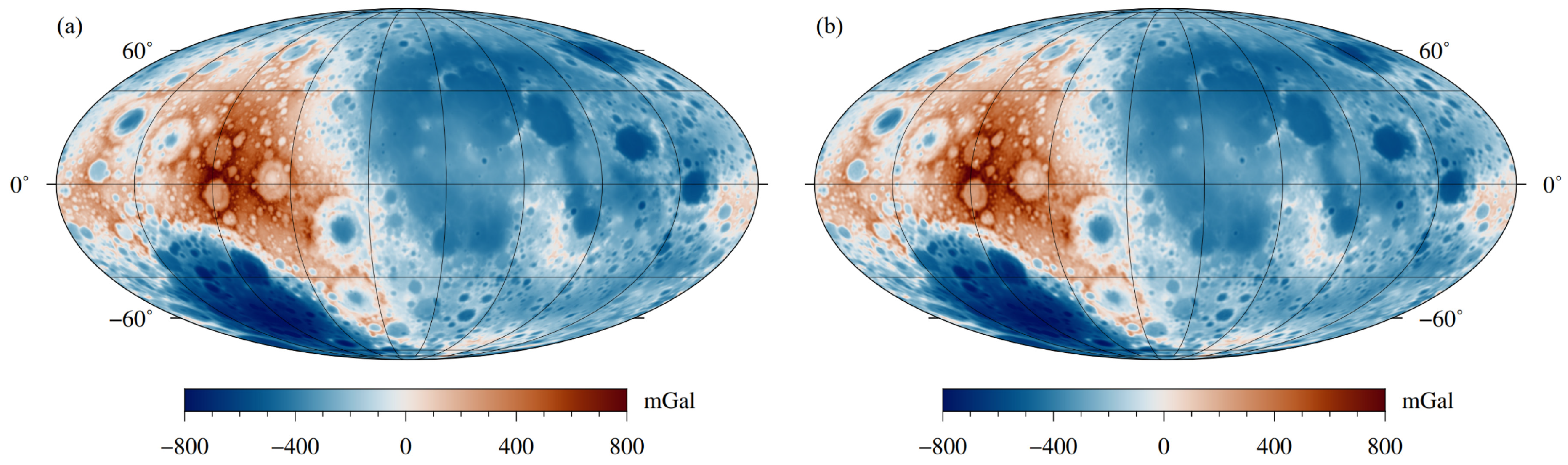
4. Application to Lunar Topography Correction
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roy, A.; Wu, L. Generalized Gauss-FFT 3D forward gravity modeling for irregular topographic mass having any 3D variable density contrast. Comput. Geosci. 2023, 172, 105297. [Google Scholar] [CrossRef]
- Tenzer, R.; Hamayun, K.; Vajda, P. Global maps of the CRUST 2.0 crustal components stripped gravity disturbances. J. Geophys. Res. Solid Earth 2009, 114, B05408. [Google Scholar] [CrossRef]
- Tenzer, R.; Gladkikh, V.; Novák, P.; Vajda, P. Spatial and spectral analysis of refined gravity data for modelling the crust–mantle interface and mantle-lithosphere structure. Surv. Geophys. 2012, 33, 817–839. [Google Scholar] [CrossRef]
- Zhao, G.; Chen, B.; Uieda, L.; Liu, J.; Kaban, M.K.; Chen, L.; Guo, R. Efficient 3-D large-scale forward modeling and inversion of gravitational fields in spherical coordinates with application to lunar mascons. J. Geophys. Res. Solid Earth 2019, 124, 4157–4173. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, J.; Chen, B.; Kaban, M.K.; Du, J. 3-D Density Structure of the Lunar Mascon Basins Revealed by a High-Efficient Gravity Inversion of the GRAIL Data. J. Geophys. Res. Planets 2021, 126, e2021JE006841. [Google Scholar] [CrossRef]
- Kaban, M.K.; Mooney, W.D.; Petrunin, A.G. Cratonic root beneath North America shifted by basal drag from the convecting mantle. Nat. Geosci. 2015, 8, 797–800. [Google Scholar] [CrossRef]
- Kaban, M.K.; Stolk, W.; Tesauro, M.; El Khrepy, S.; Al-Arifi, N.; Beekman, F.; Cloetingh, S.A. 3D density model of the upper mantle of Asia based on inversion of gravity and seismic tomography data. Geochem. Geophys. Geosystems 2016, 17, 4457–4477. [Google Scholar] [CrossRef]
- Tenzer, R.; Chen, W. Mantle and sub-lithosphere mantle gravity maps from the LITHO1. 0 global lithospheric model. Earth-Sci. Rev. 2019, 194, 38–56. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, J.; Chen, B.; Kaban, M.K.; Zheng, X. Moho beneath Tibet based on a joint analysis of gravity and seismic data. Geochem. Geophys. Geosystems 2020, 21, e2019GC008849. [Google Scholar] [CrossRef]
- Boulanger, O.; Chouteau, M. Constraints in 3D gravity inversion. Geophys. Prospect. 2001, 49, 265–280. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Jiang, L.; Lin, Q.; Wan, L. Polynomial-based density inversion of gravity anomalies for concealed iron-deposit exploration in North China. Geophysics 2019, 84, B325–B334. [Google Scholar] [CrossRef]
- Kamm, J.; Lundin, I.A.; Bastani, M.; Sadeghi, M.; Pedersen, L.B. Joint inversion of gravity, magnetic, and petrophysical data—A case study from a gabbro intrusion in Boden, Sweden. Geophysics 2015, 80, B131–B152. [Google Scholar] [CrossRef]
- Deng, Y.; Levandowski, W.; Kusky, T. Lithospheric density structure beneath the Tarim basin and surroundings, northwestern China, from the joint inversion of gravity and topography. Earth Planet. Sci. Lett. 2017, 460, 244–254. [Google Scholar] [CrossRef]
- Liang, Q.; Chen, C.; Li, Y. 3-D inversion of gravity data in spherical coordinates with application to the GRAIL data. J. Geophys. Res. Planets 2014, 119, 1359–1373. [Google Scholar] [CrossRef]
- Zhong, Y.; Ren, Z.; Tang, J.; Lin, Y.; Chen, B.; Deng, Y.; Jiang, Y. Constrained gravity inversion with adaptive inversion grid refinement in spherical coordinates and its application to mantle structure beneath Tibetan Plateau. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022916. [Google Scholar] [CrossRef]
- Li, X.; Chouteau, M. Three-Dimensional Gravity Modeling in All Space. Surv. Geophys. 1998, 19, 339–368. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.; Benedek, J. The gravitational potential and its derivatives for the prism. J. Geod. 2000, 74, 552–560. [Google Scholar] [CrossRef]
- Foerste, C.; Bruinsma, S.L.; Abrikosov, O.; Lemoine, J.-M.; Marty, J.C.; Flechtner, F.; Balmino, G.; Barthelmes, F.; Biancale, R. EIGEN-6C4 The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. GFZ Data Serv. 2014. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, B04406. [Google Scholar] [CrossRef]
- Goossens, S.; Matsumoto, K.; Liu, Q.; Kikuchi, F.; Sato, K.; Hanada, H.; Ishihara, Y.; Noda, H.; Kawano, N.; Namiki, N. Lunar gravity field determination using SELENE same-beam differential VLBI tracking data. J. Geod. 2011, 85, 205–228. [Google Scholar] [CrossRef]
- Konopliv, A.S.; Park, R.S.; Yuan, D.N.; Asmar, S.W.; Watkins, M.M.; Williams, J.G.; Fahnestock, E.; Kruizinga, G.; Paik, M.; Strekalov, D. High-resolution lunar gravity fields from the GRAIL primary and extended missions. Geophys. Res. Lett. 2014, 41, 1452–1458. [Google Scholar] [CrossRef]
- Zuber, M.T.; Smith, D.E.; Watkins, M.M.; Asmar, S.W.; Konopliv, A.S.; Lemoine, F.G.; Melosh, H.J.; Neumann, G.A.; Phillips, R.J.; Solomon, S.C. Gravity field of the Moon from the Gravity Recovery and Interior Laboratory (GRAIL) mission. Science 2013, 339, 668–671. [Google Scholar] [CrossRef] [PubMed]
- Genova, A.; Goossens, S.; Lemoine, F.G.; Mazarico, E.; Neumann, G.A.; Smith, D.E.; Zuber, M.T. Seasonal and static gravity field of Mars from MGS, Mars Odyssey and MRO radio science. Icarus 2016, 272, 228–245. [Google Scholar] [CrossRef]
- Konopliv, A.S.; Park, R.S.; Folkner, W.M. An improved JPL Mars gravity field and orientation from Mars orbiter and lander tracking data. Icarus 2016, 274, 253–260. [Google Scholar] [CrossRef]
- Anderson, E.G. The Effect of Topography on Solutions of Stokes’ Problem. Ph.D. Thesis, UNSW Sydney, Kensington, Australia, 1976. [Google Scholar]
- Deng, X.L.; Sneeuw, N. Analytical Solutions for Gravitational Potential up to Its Third-order Derivatives of a Tesseroid, Spherical Zonal Band, and Spherical Shell. Surv. Geophys. 2023, 44, 1125–1173. [Google Scholar] [CrossRef]
- Grombein, T.; Seitz, K.; Heck, B. Optimized formulas for the gravitational field of a tesseroid. J. Geod. 2013, 87, 645–660. [Google Scholar] [CrossRef]
- Heck, B.; Seitz, K. A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. J. Geod. 2007, 81, 121–136. [Google Scholar] [CrossRef]
- Asgharzadeh, M.; Von Frese, R.; Kim, H.; Leftwich, T.; Kim, J. Spherical prism gravity effects by Gauss-Legendre quadrature integration. Geophys. J. Int. 2007, 169, 1–11. [Google Scholar] [CrossRef]
- Ouyang, F.; Chen, L.-W.; Shao, Z.-G. Fast calculation of gravitational effects using tesseroids with a polynomial density of arbitrary degree in depth. J. Geod. 2022, 96, 97. [Google Scholar] [CrossRef]
- Wild-Pfeiffer, F. A comparison of different mass elements for use in gravity gradiometry. J. Geod. 2008, 82, 637–653. [Google Scholar] [CrossRef]
- Uieda, L.; Barbosa, V.C.; Braitenberg, C. Tesseroids: Forward-modeling gravitational fields in spherical coordinates. Geophysics 2016, 81, F41–F48. [Google Scholar] [CrossRef]
- Zeng, X.; Wan, X.; Lin, M.; Wang, W. Gravity field forward modelling using tesseroids accelerated by Taylor series expansion and symmetry relations. Geophys. J. Int. 2022, 230, 1565–1584. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Li, J. Fast 3D magnetic anomaly forward modelling based on integral equation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–8. [Google Scholar]
- Eshagh, M. Non-singular expressions for the vector and the gradient tensor of gravitation in a geocentric spherical frame. Comput. Geosci. 2008, 34, 1762–1768. [Google Scholar] [CrossRef]
- Petrovskaya, M.; Vershkov, A. Non-singular expressions for the gravity gradients in the local north-oriented and orbital reference frames. J. Geod. 2006, 80, 117–127. [Google Scholar] [CrossRef]
- Parker, R. The rapid calculation of potential anomalies. Geophys. J. Int. 1973, 31, 447–455. [Google Scholar] [CrossRef]
- Oldenburg, D.W. The inversion and interpretation of gravity anomalies. Geophysics 1974, 39, 526–536. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Phillips, R.J. Potential anomalies on a sphere: Applications to the thickness of the lunar crust. J. Geophys. Res. Planets 1998, 103, 1715–1724. [Google Scholar] [CrossRef]
- Ishihara, Y.; Goossens, S.; Matsumoto, K.; Noda, H.; Araki, H.; Namiki, N.; Hanada, H.; Iwata, T.; Tazawa, S.; Sasaki, S. Crustal thickness of the Moon: Implications for farside basin structures. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Neumann, G.A.; Nimmo, F.; Kiefer, W.S.; Taylor, G.J.; Melosh, H.J.; Phillips, R.J.; Solomon, S.C.; Andrews-Hanna, J.C.; Asmar, S.W. The crust of the Moon as seen by GRAIL. Science 2013, 339, 671–675. [Google Scholar] [CrossRef]
- Root, B.; Novák, P.; Dirkx, D.; Kaban, M.; van der Wal, W.; Vermeersen, L. On a spectral method for forward gravity field modelling. J. Geodyn. 2016, 97, 22–30. [Google Scholar] [CrossRef]
- Šprlák, M.; Han, S.C.; Featherstone, W.E. Forward modelling of global gravity fields with 3D density structures and an application to the high-resolution (similar to 2 km) gravity fields of the Moon. J. Geod. 2018, 92, 847–862. [Google Scholar] [CrossRef]
- Šprlák, M.; Han, S.-C.; Featherstone, W. Spheroidal forward modelling of the gravitational fields of 1 Ceres and the Moon. Icarus 2020, 335, 113412. [Google Scholar] [CrossRef]
- Rexer, M.; Hirt, C.; Claessens, S.; Tenzer, R. Layer-Based Modelling of the Earth’s Gravitational Potential up to 10-km Scale in Spherical Harmonics in Spherical and Ellipsoidal Approximation. Surv. Geophys. 2016, 37, 1035–1074. [Google Scholar] [CrossRef]
- Ramillien, G. Density interface topography recovered by inversion of satellite gravity gradiometry observations. J. Geod. 2017, 91, 881–895. [Google Scholar] [CrossRef]
- Álvarez, O.; Gimenez, M.; Braitenberg, C.; Folguera, A. GOCE satellite derived gravity and gravity gradient corrected for topographic effect in the South Central Andes region. Geophys. J. Int. 2012, 190, 941–959. [Google Scholar] [CrossRef]
- Casotto, S.; Fantino, E. Gravitational gradients by tensor analysis with application to spherical coordinates. J. Geod. 2009, 83, 621–634. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Du, J.; Chen, C.; Lesur, V.; Wang, L. Non-singular spherical harmonic expressions of geomagnetic vector and gradient tensor fields in the local north-oriented reference frame. Geosci. Model Dev. Discuss. 2014, 7, 8477–8503. [Google Scholar] [CrossRef]
- Wu, L.; Tian, G. High-precision Fourier forward modeling of potential fields. Geophysics 2014, 79, G59–G68. [Google Scholar] [CrossRef]
- Zhao, G.; Chen, B.; Chen, L.; Liu, J.; Ren, Z. High-accuracy 3D Fourier forward modeling of gravity field based on the Gauss-FFT technique. J. Appl. Geophys. 2018, 150, 294–303. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Meschede, M. SHTools: Tools for working with spherical harmonics. Geochem. Geophys. Geosystems 2018, 19, 2574–2592. [Google Scholar] [CrossRef]
- Frigo, M.; Johnson, S.G. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef]
- Ditmar, P.; Kusche, J.; Klees, R. Computation of spherical harmonic coefficients from gravity gradiometry data to be acquired by the GOCE satellite: Regularization issues. J. Geod. 2003, 77, 465–477. [Google Scholar] [CrossRef]
- Neumann, G.A.; Zuber, M.T.; Wieczorek, M.A.; Head, J.W.; Baker, D.M.; Solomon, S.C.; Smith, D.E.; Lemoine, F.G.; Mazarico, E.; Sabaka, T.J. Lunar impact basins revealed by Gravity Recovery and Interior Laboratory measurements. Sci. Adv. 2015, 1, e1500852. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G.; Mazarico, E.; Torrence, M.H.; McGarry, J.F.; Rowlands, D.D.; Head, J.W., III; Duxbury, T.H. Initial observations from the lunar orbiter laser altimeter (LOLA). Geophys. Res. Lett. 2010, 37, L18204. [Google Scholar] [CrossRef]
- Haines, G. Spherical cap harmonic analysis. J. Geophys. Res. Solid Earth 1985, 90, 2583–2591. [Google Scholar] [CrossRef]
- Korte, M.; Holme, R. Regularization of spherical cap harmonics. Geophys. J. Int. 2003, 153, 253–262. [Google Scholar] [CrossRef]
- Thébault, E.; Schott, J.; Mandea, M. Revised spherical cap harmonic analysis (R-SCHA): Validation and properties. J. Geophys. Res. Solid Earth 2006, 111, B01102. [Google Scholar] [CrossRef]
- Zhao, G.; Liang, S. High-Efficient Forward Modeling Method of Gravitational Fields in Spherical Harmonic Domain with Application to Lunar Topography. Figshare Dataset 2024. [Google Scholar] [CrossRef]
- Wessel, P.; Luis, J.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.; Tian, D. The generic mapping tools version 6. Geochem. Geophys. Geosystems 2019, 20, 5556–5564. [Google Scholar] [CrossRef]









| Methods | Computational Time (s) | Maximum Relative Error (%) | ||
|---|---|---|---|---|
| gz | gzz | gz | gzz | |
| Uieda et al. [32] | 1,850,759.53 | 2,256,446.96 | 3.12 × 10−2 | 5.15 × 10−4 |
| Zhao et al. [5] | 1880.19 | 2148.41 | 3.12 × 10−2 | 5.15 × 10−4 |
| The proposed method | 1.96 | 1.96 | 6.15 × 10−6 | 3.38 × 10−6 |
| Observation Heights (km) | Computational Time for gzz (s) | ||
|---|---|---|---|
| Uieda et al. [32] | Zhao et al. [5] | The Proposed Method | |
| 0.01 | 11,631.53 | 36.81 | 0.016 |
| 0.1 | 9831.45 | 32.20 | 0.016 |
| 1.0 | 8143.89 | 28.14 | 0.016 |
| 10.0 | 6588.89 | 23.33 | 0.016 |
| 100.0 | 5428.82 | 19.79 | 0.016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Liang, S. High-Efficiency Forward Modeling of Gravitational Fields in Spherical Harmonic Domain with Application to Lunar Topography Correction. Remote Sens. 2024, 16, 3414. https://doi.org/10.3390/rs16183414
Zhao G, Liang S. High-Efficiency Forward Modeling of Gravitational Fields in Spherical Harmonic Domain with Application to Lunar Topography Correction. Remote Sensing. 2024; 16(18):3414. https://doi.org/10.3390/rs16183414
Chicago/Turabian StyleZhao, Guangdong, and Shengxian Liang. 2024. "High-Efficiency Forward Modeling of Gravitational Fields in Spherical Harmonic Domain with Application to Lunar Topography Correction" Remote Sensing 16, no. 18: 3414. https://doi.org/10.3390/rs16183414
APA StyleZhao, G., & Liang, S. (2024). High-Efficiency Forward Modeling of Gravitational Fields in Spherical Harmonic Domain with Application to Lunar Topography Correction. Remote Sensing, 16(18), 3414. https://doi.org/10.3390/rs16183414





