On-Orbit Wavelength Calibration Error Analysis of the Spaceborne Hyperspectral Greenhouse Gas Monitoring Instrument Using the Solar Fraunhofer Lines
Abstract
1. Introduction
2. Materials and Methods
2.1. Instrument Design Parameters
2.2. Solar Reference Spectrum
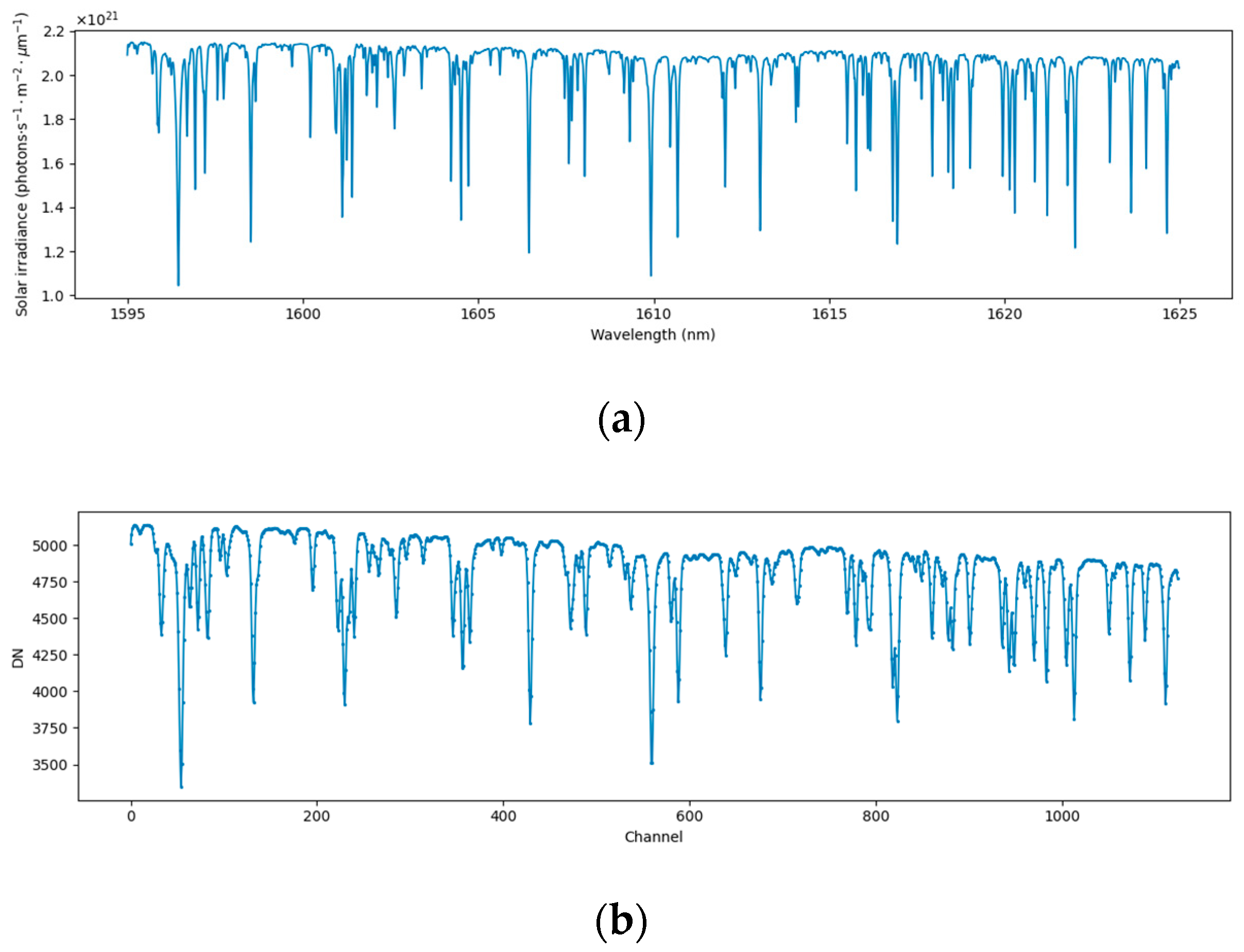
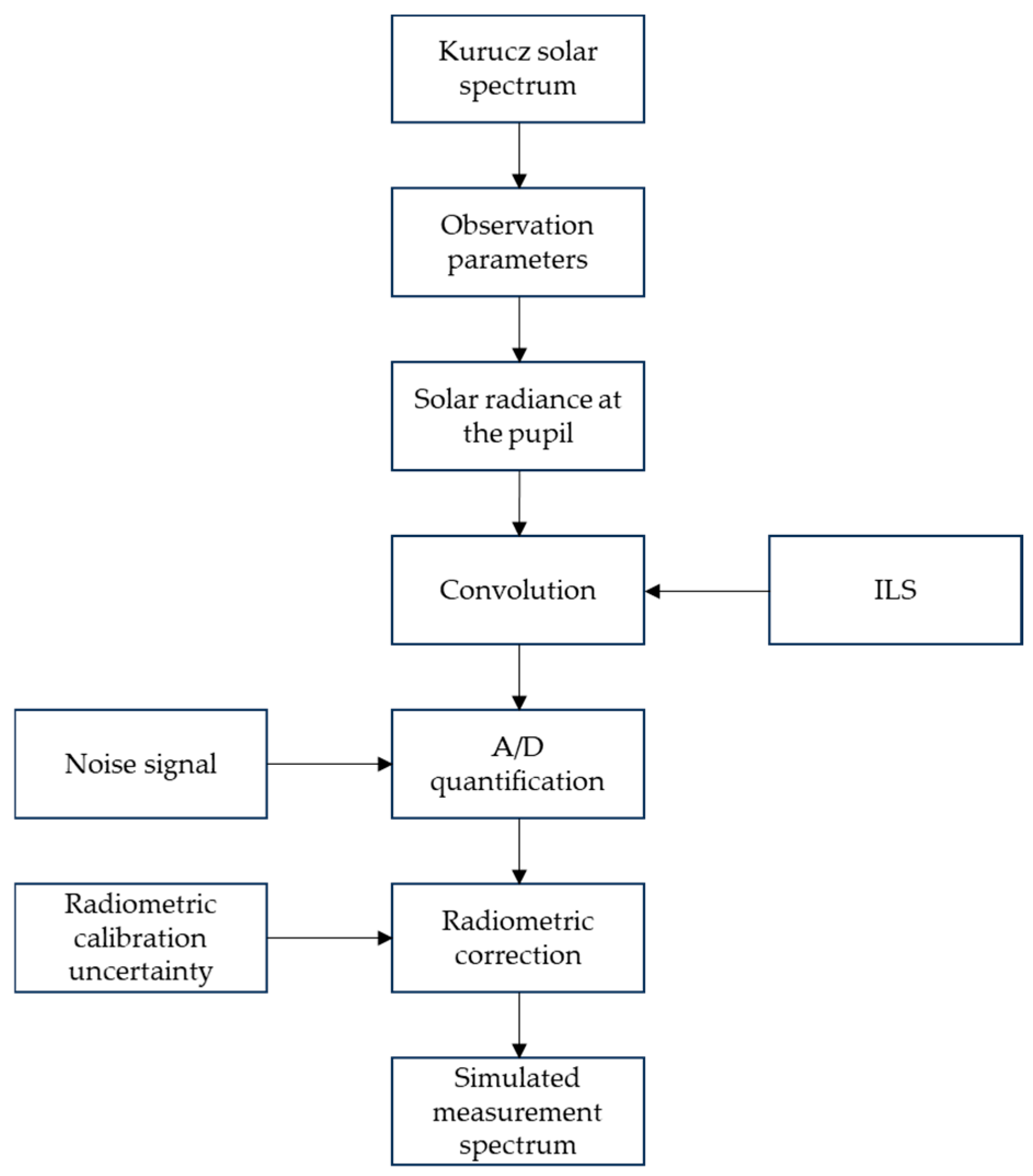
2.3. Simulation of Measurement Spectrum
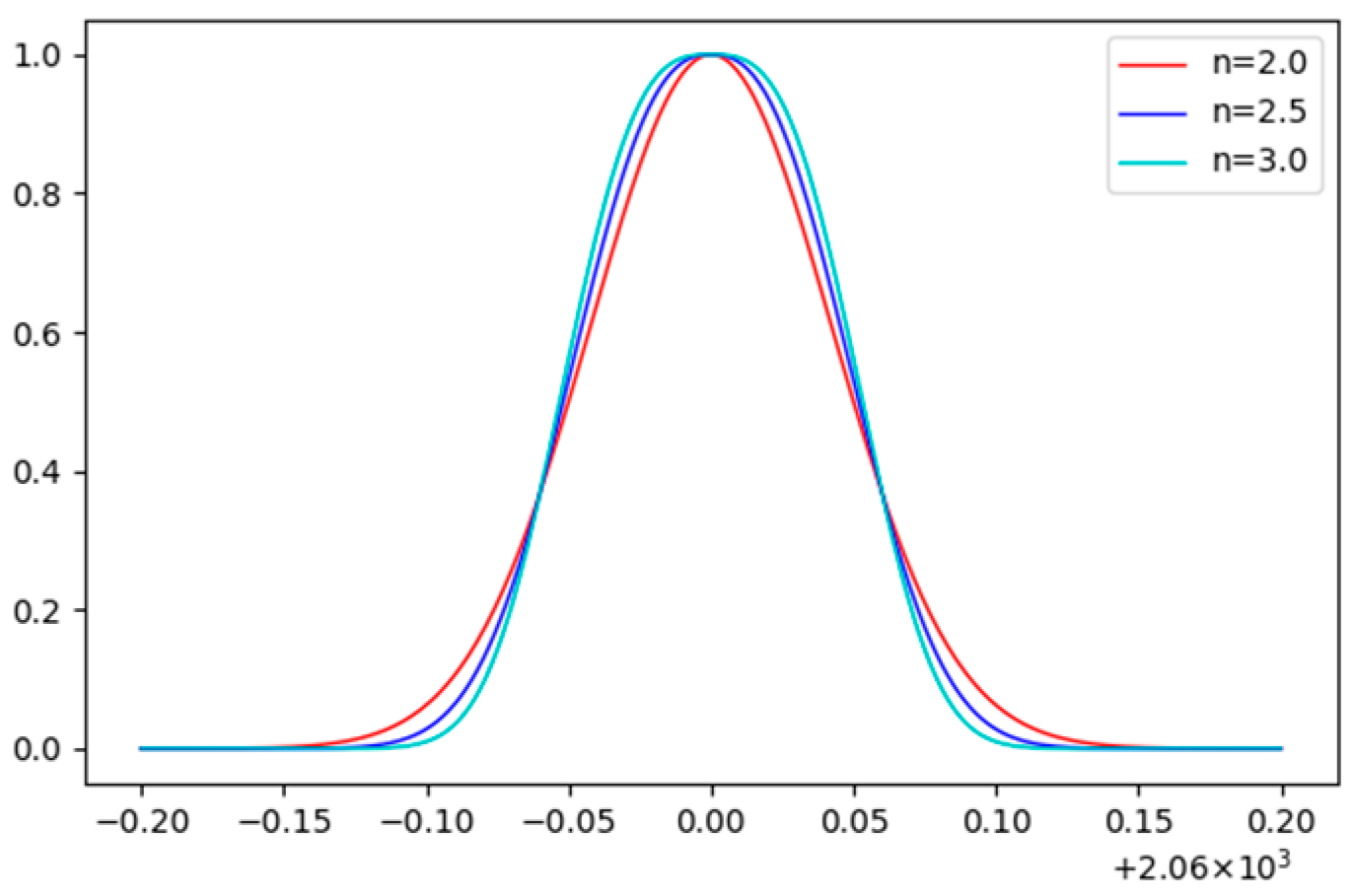
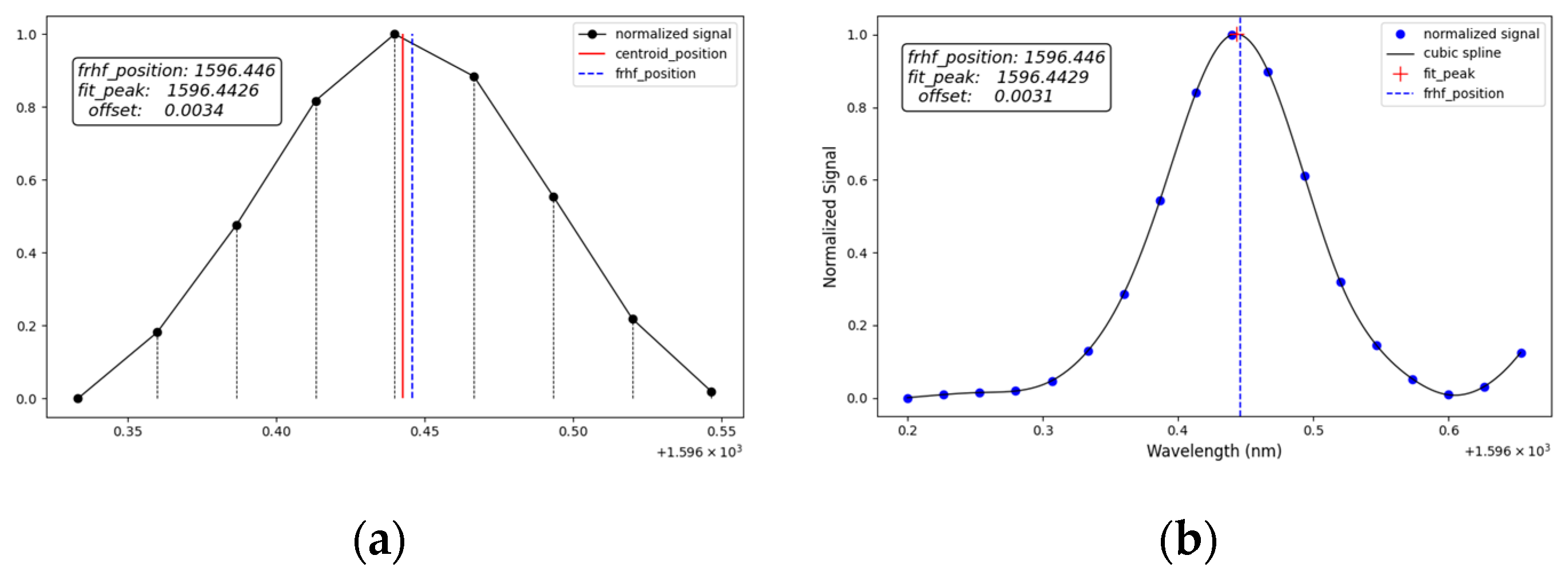
2.4. Wavelength Calibration Method
3. Results and Discussions
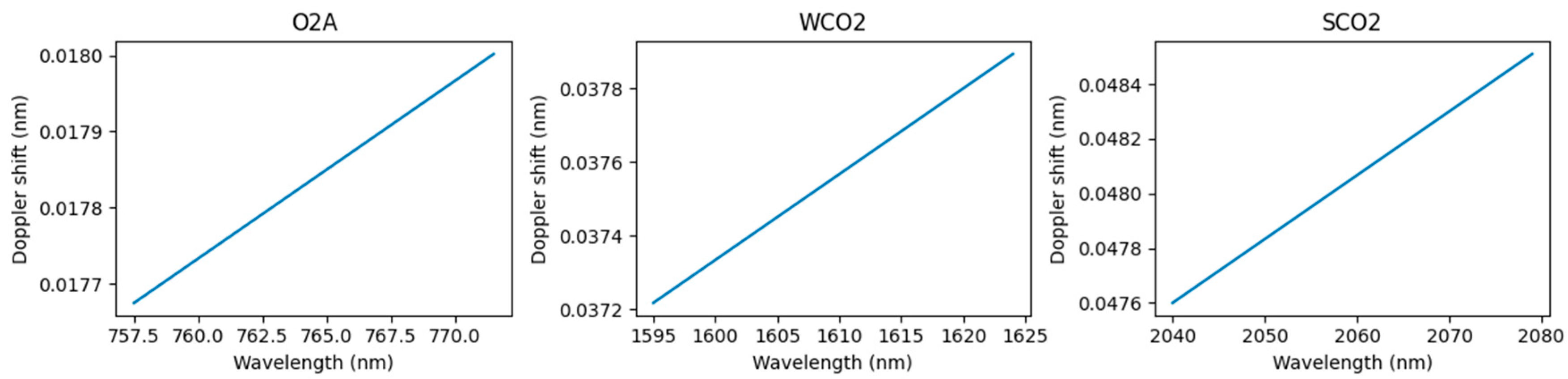
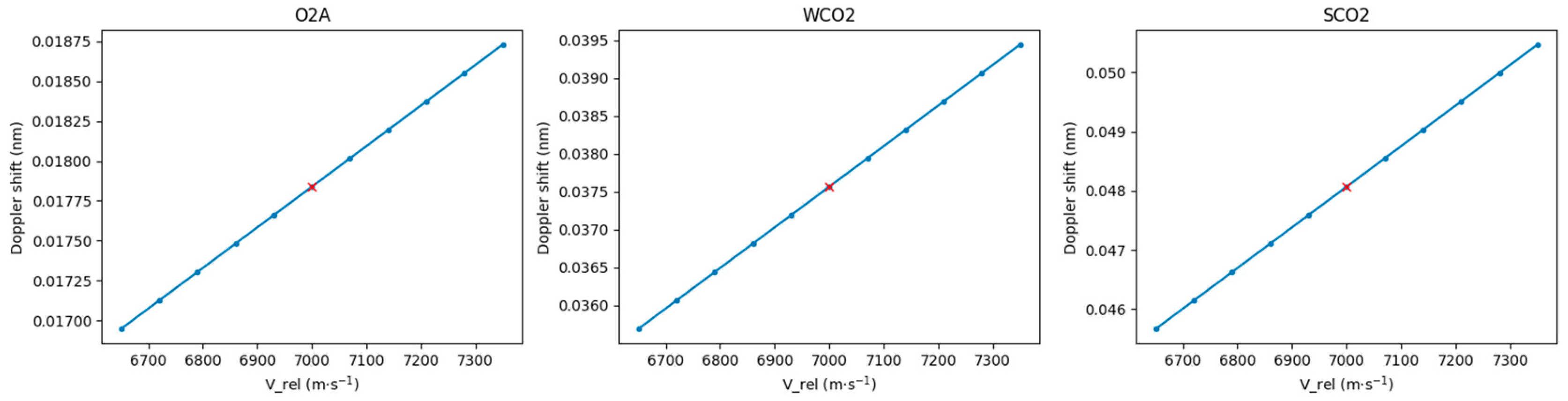
3.1. Doppler Shift Correction Error
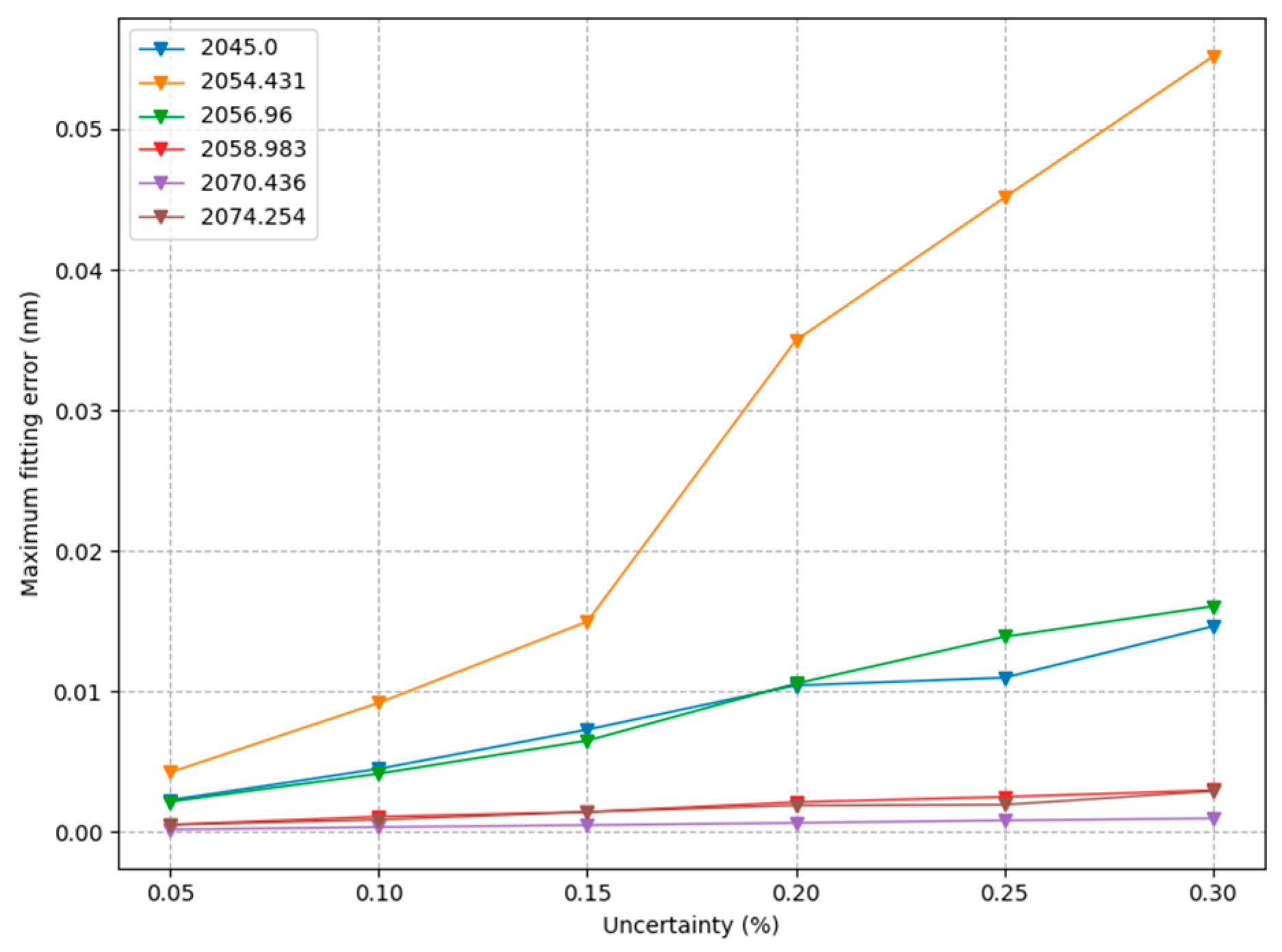
3.2. Systematic Error
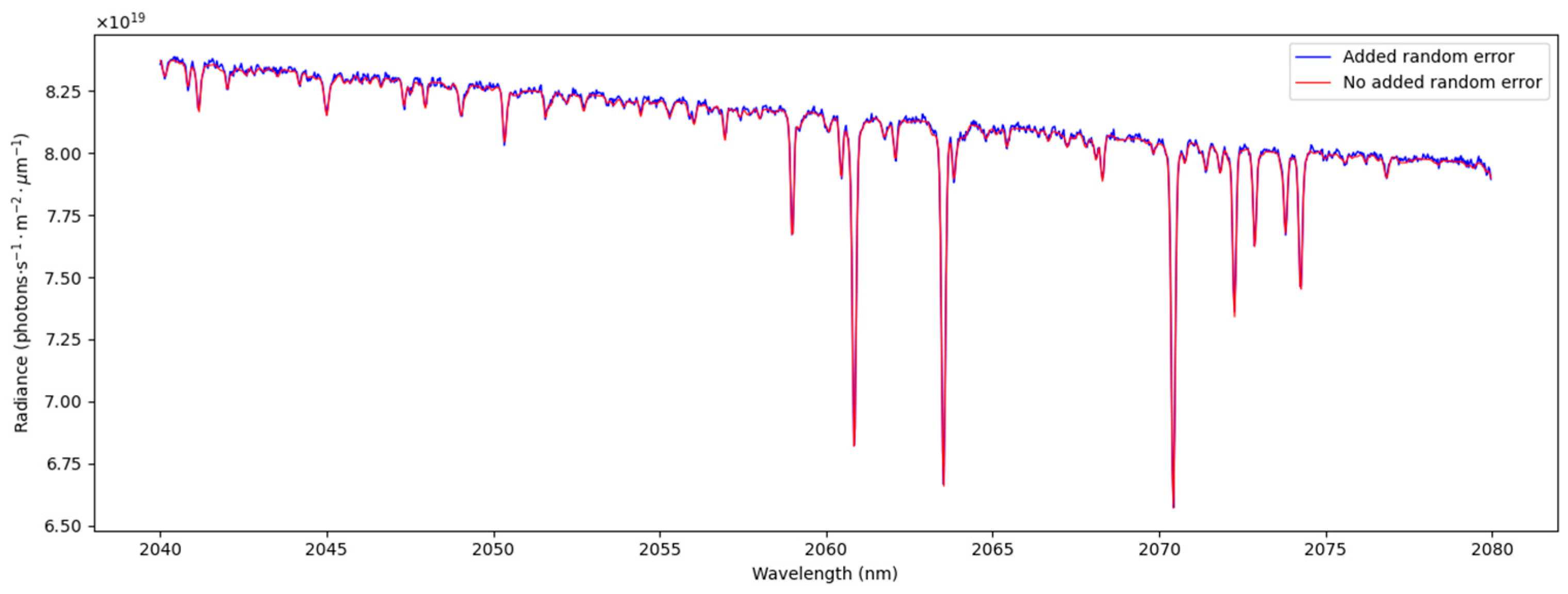
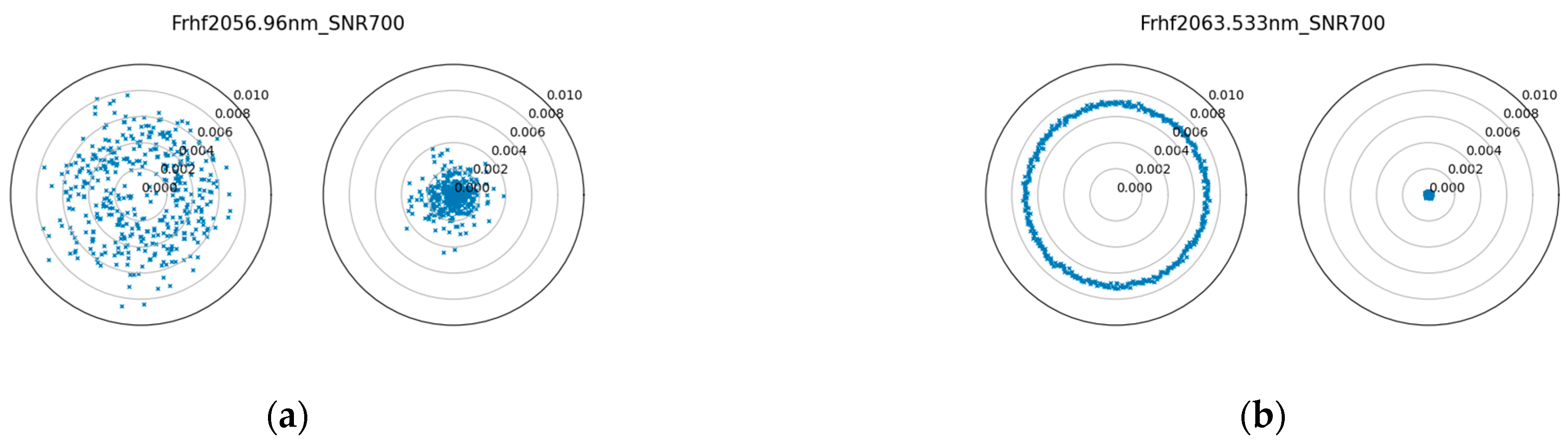
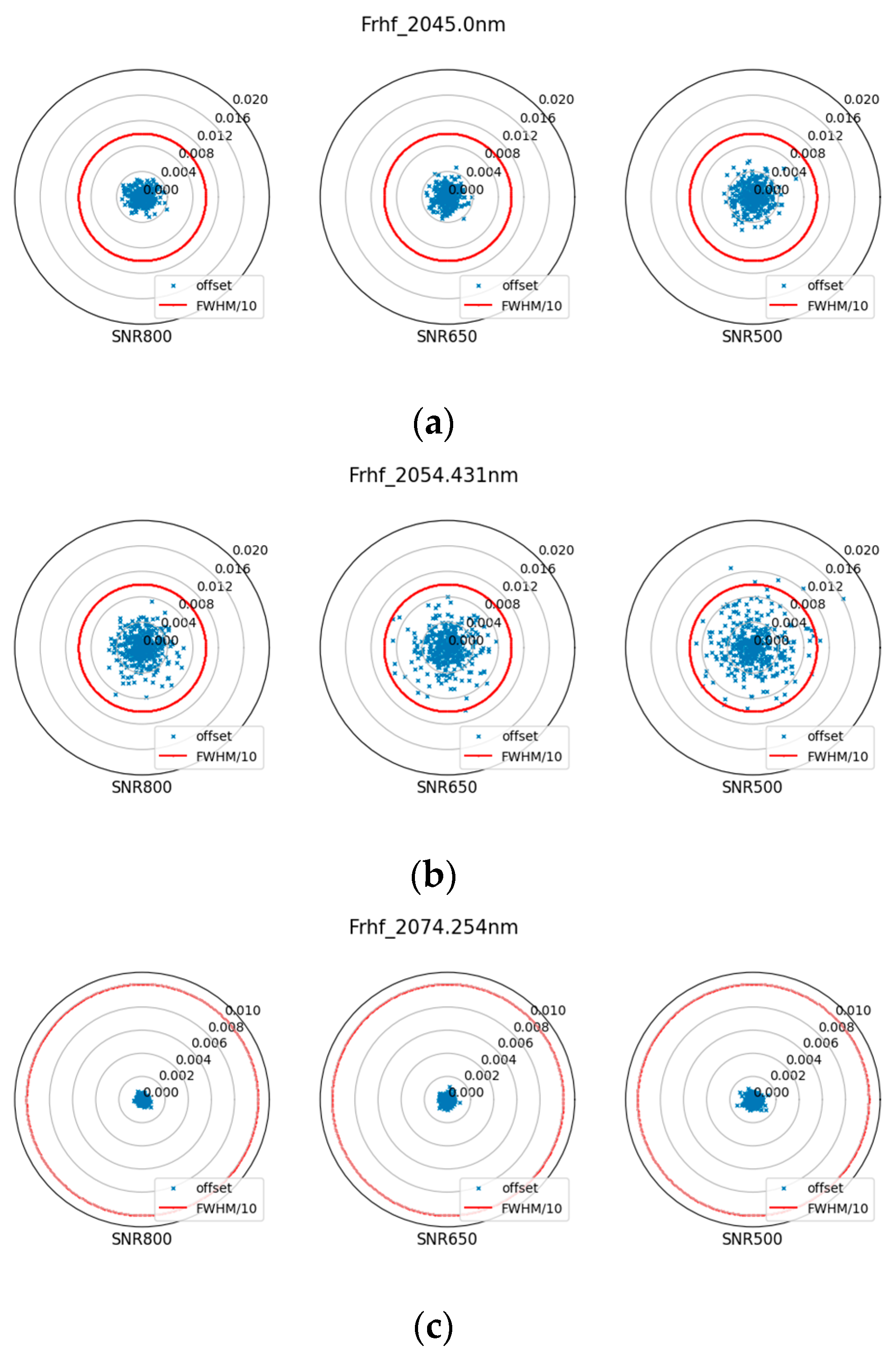
3.3. Random Error
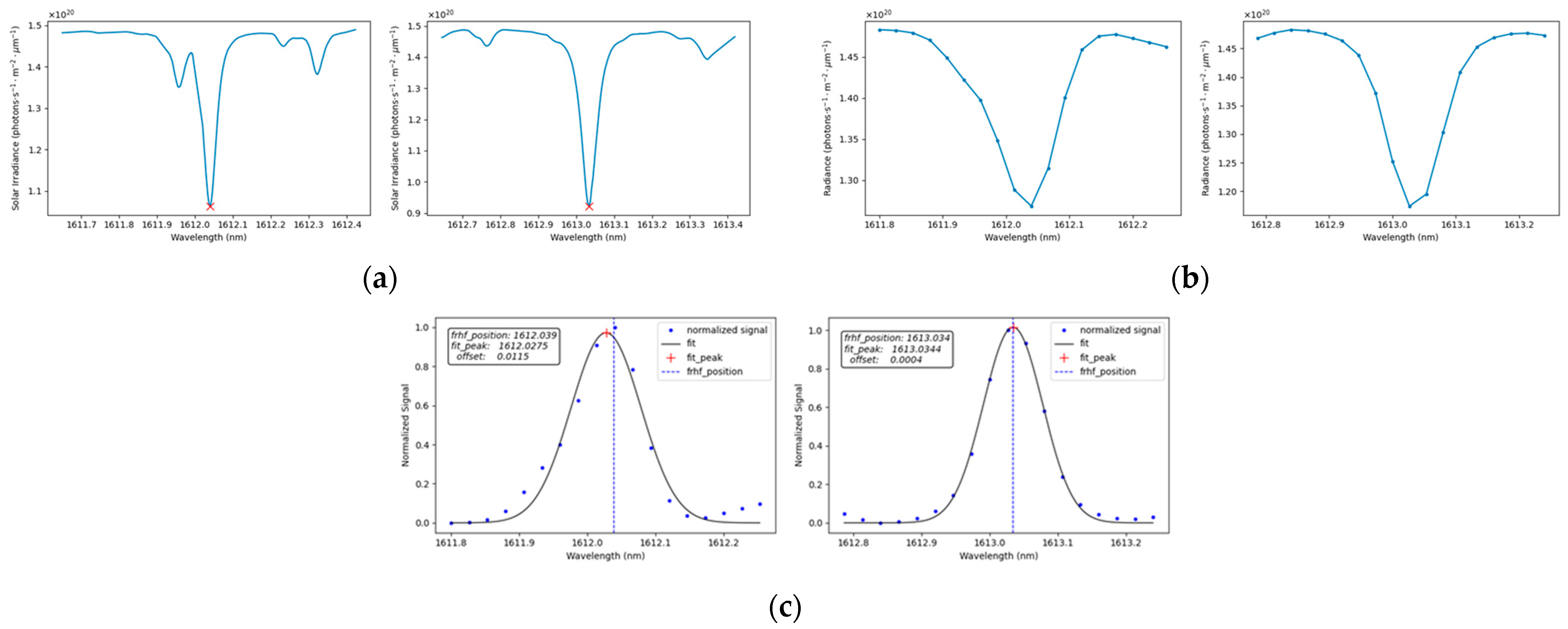
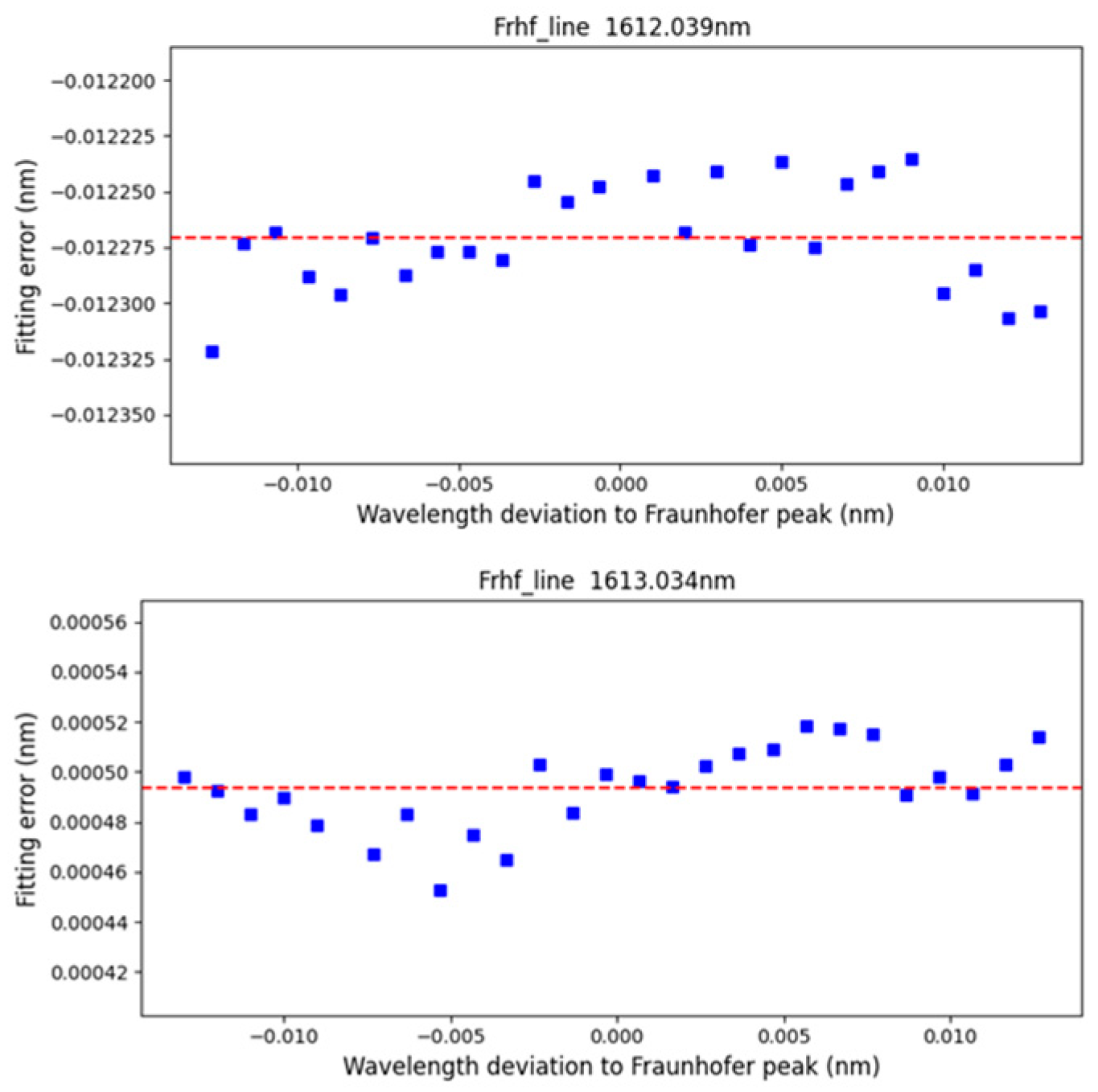
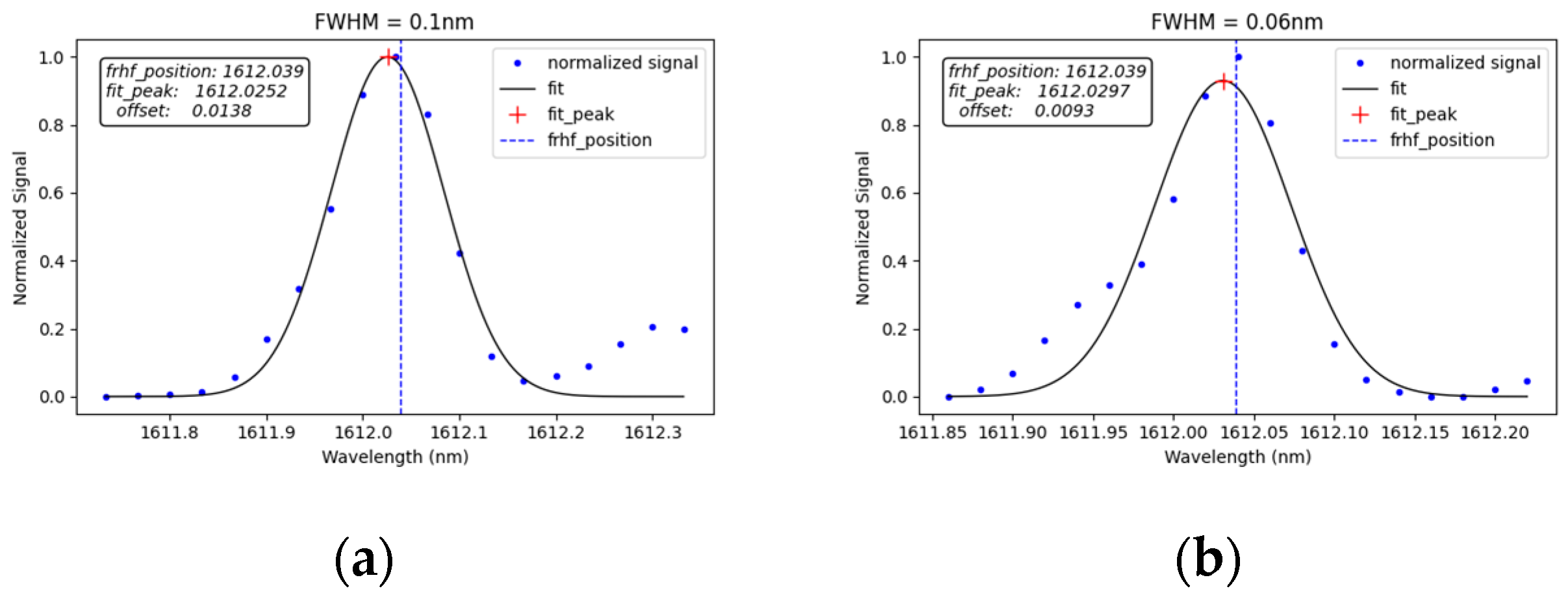
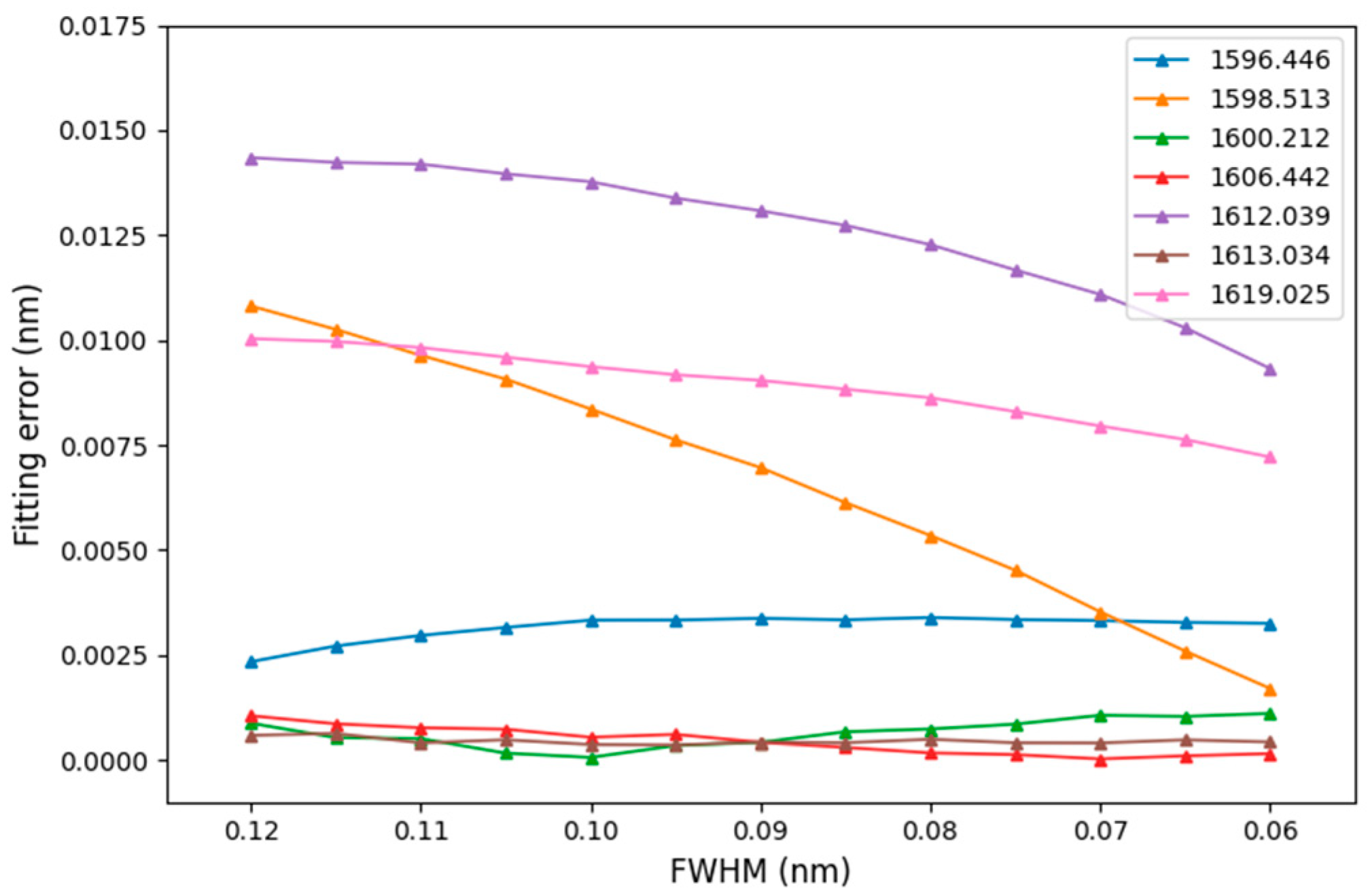
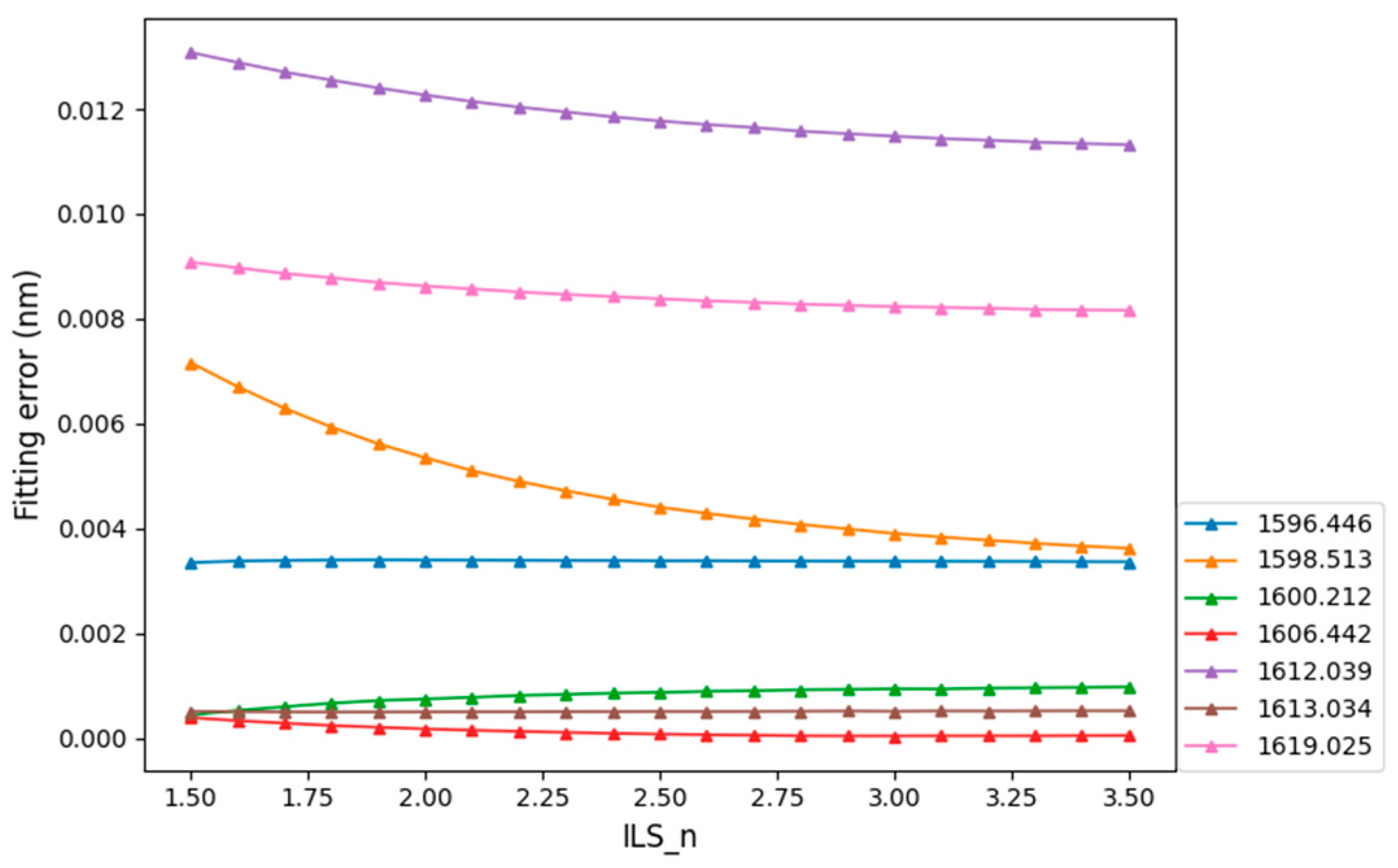
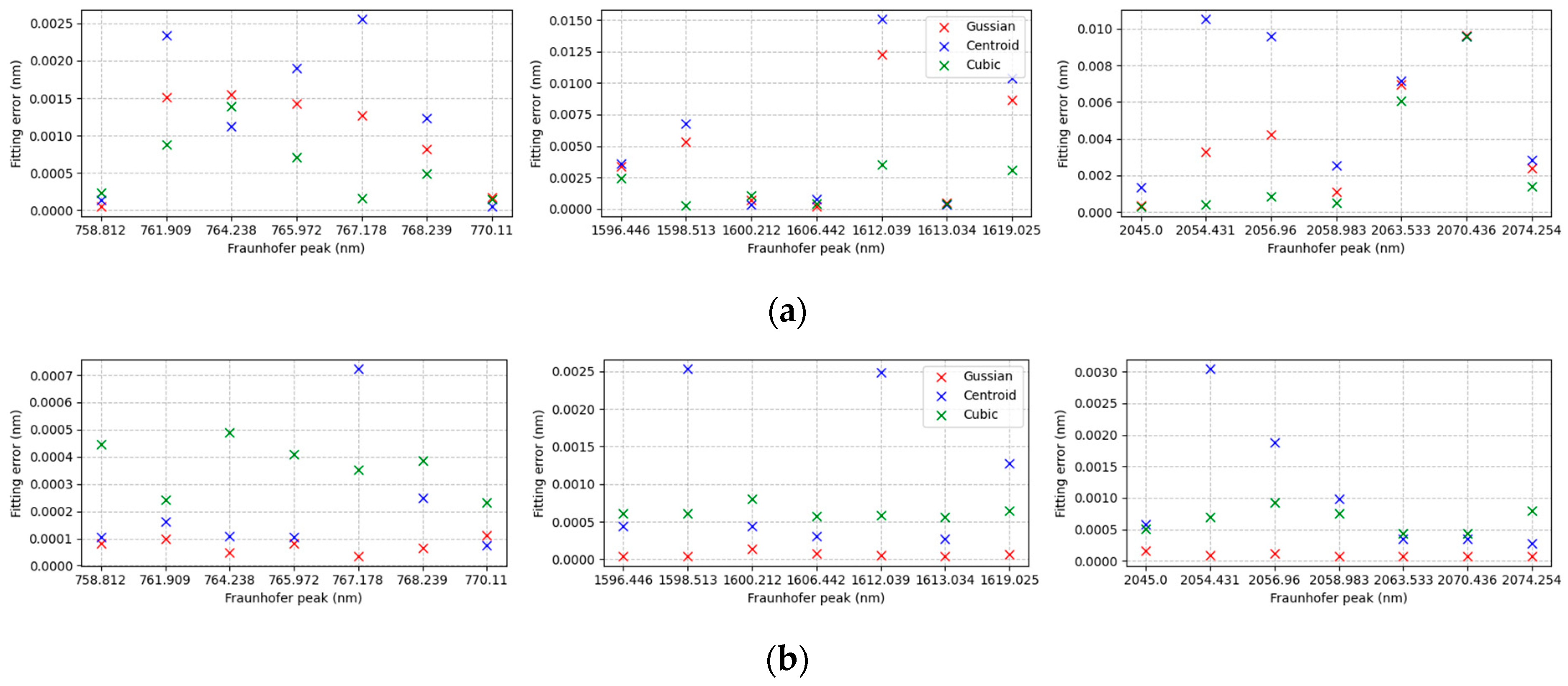
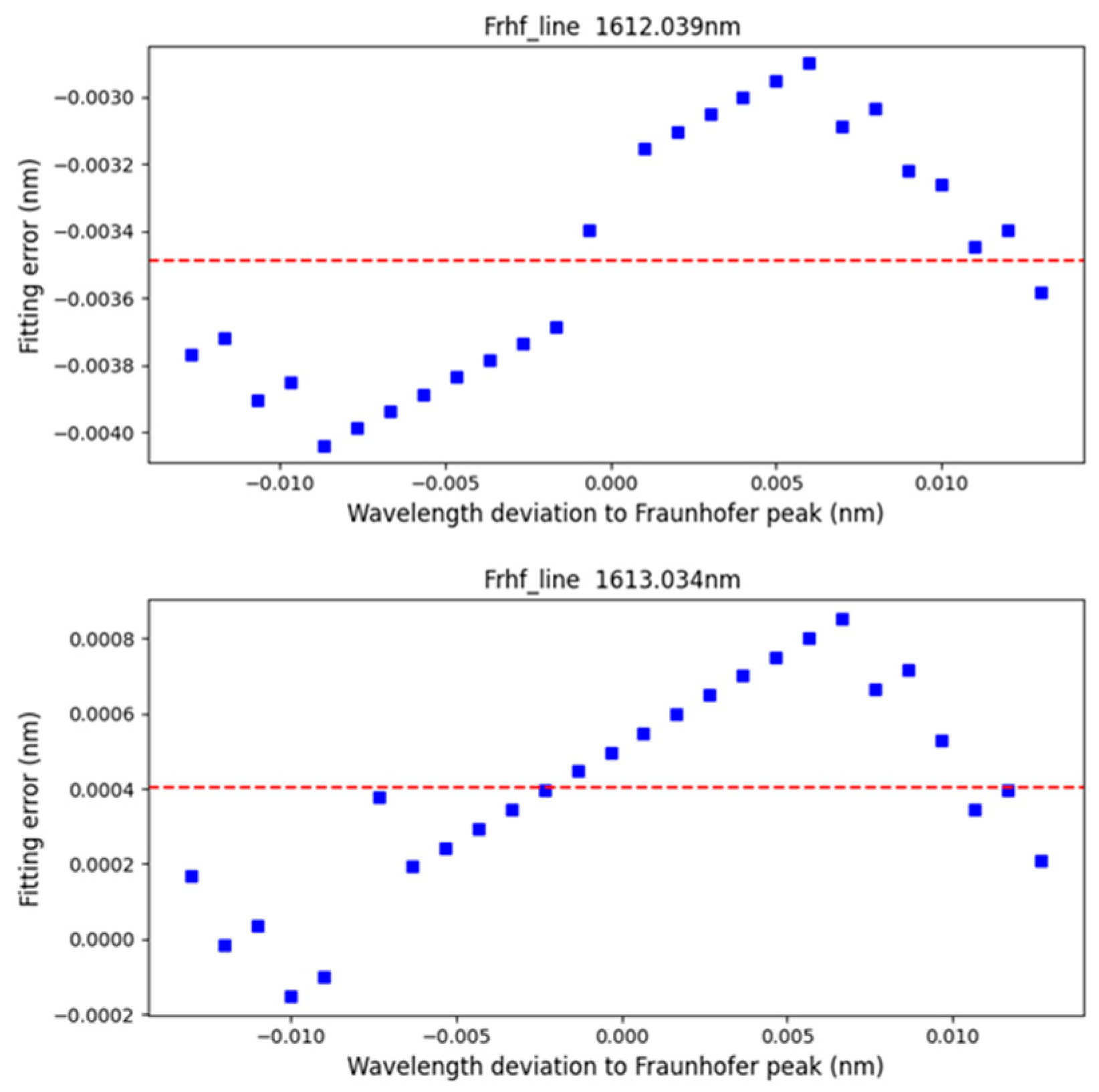
3.4. Peak-Seek Algorithm Error
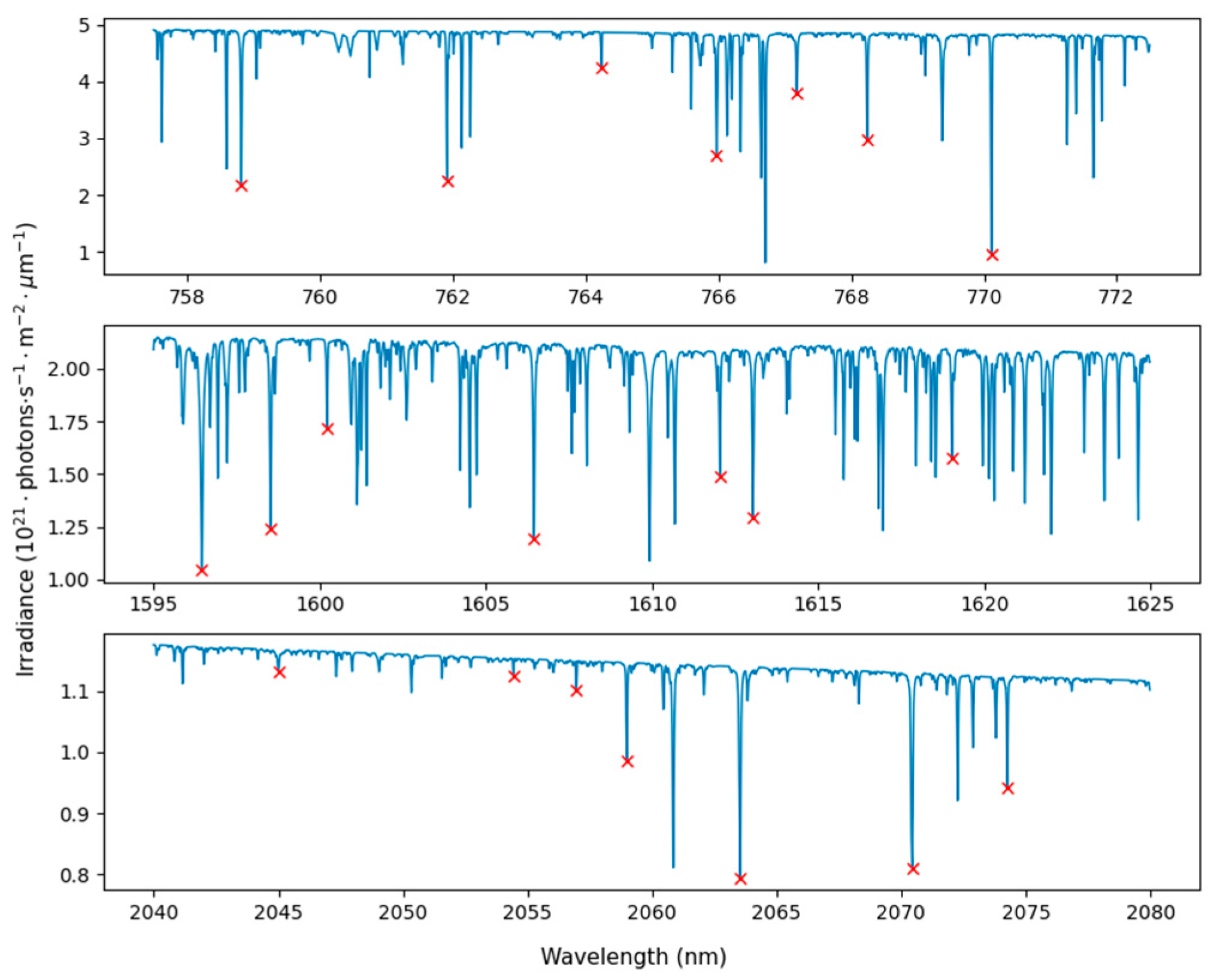
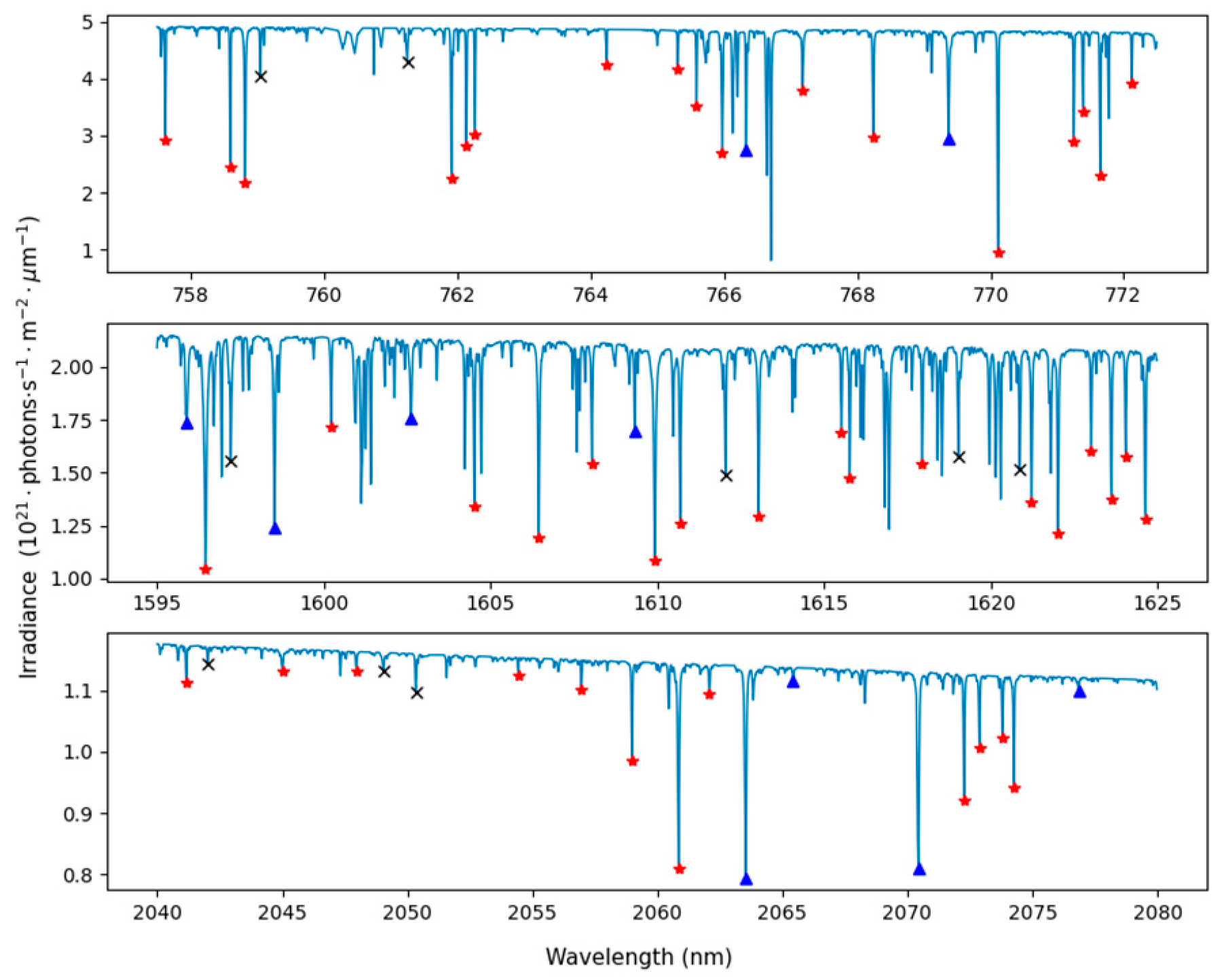
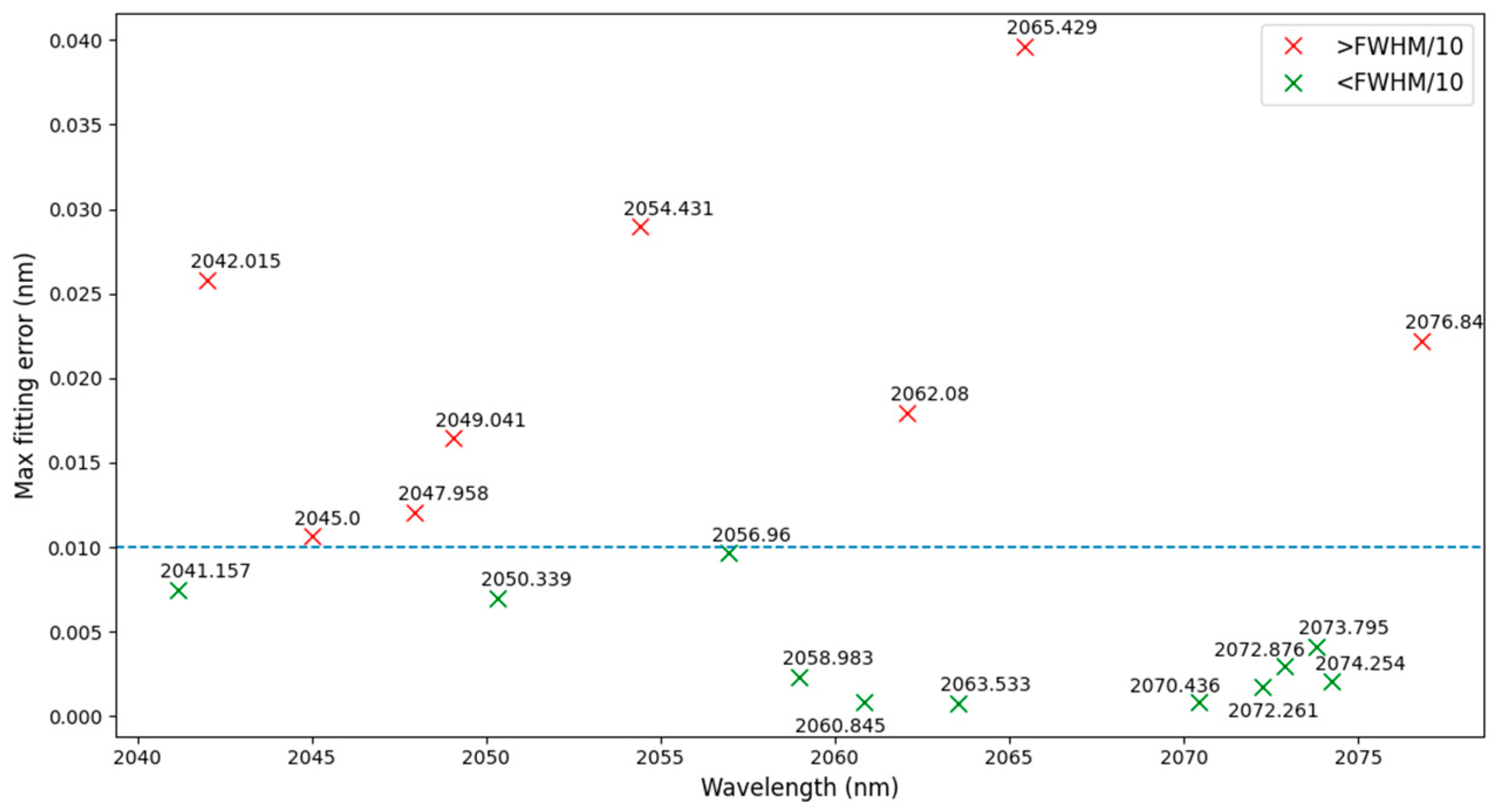
3.5. Results of Screening
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Hauck, J.; Olsen, A.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S.; et al. Global Carbon Budget 2020. Earth Syst. Sci. Data 2020, 12, 3269–3340. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Zhu, S.H.; Parker, R.J.; Liu, Y. Tropical methane emissions explain large fraction of recent changes in global atmospheric methane growth rate. Nat. Commun. 2022, 13, 1378. [Google Scholar] [CrossRef]
- Bruhwiler, L.; Basu, S.; Butler, J.H.; Chatterjee, A.; Dlugokencky, E.; Kenney, M.A.; McComiskey, A.; Montzka, S.A.; Stanitski, D. Observations of greenhouse gases as climate indicators. Clim. Chang. 2021, 165, 12. [Google Scholar] [CrossRef] [PubMed]
- Gautam, Y.K.; Sharma, K.; Tyagi, S.; Ambedkar, A.K.; Chaudhary, M.; Singh, B.P. Nanostructured metal oxide semiconductor-based sensors for greenhouse gas detection: Progress and challenges. R. Soc. Open Sci. 2021, 8, 201324. [Google Scholar] [CrossRef]
- Chatterjee, A.; Gierach, M.M.; Sutton, A.J.; Feely, R.A.; Crisp, D.; Eldering, A.; Gunson, M.R.; O’Dell, C.W.; Stephens, B.B.; Schimel, D.S. Influence of El Nino on atmospheric CO over the tropical Pacific Ocean: Findings from NASA’s OCO-2 mission. Science 2017, 358, eaam5776. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wang, J.; Che, K.; Cai, Z.; Yang, D.; Wu, L. Satellite remote sensing of greenhouse gases: Progress and trends. Natl. Remote Sens. Bull. 2021, 25, 53–64. [Google Scholar] [CrossRef]
- Liu, J.J.; Baskaran, L.; Bowman, K.; Schimel, D.; Bloom, A.A.; Parazoo, N.C.; Oda, T.; Carroll, D.; Menemenlis, D.; Joiner, J.; et al. Carbon Monitoring System Flux Net Biosphere Exchange 2020 (CMS-Flux NBE 2020). Earth Syst. Sci. Data 2021, 13, 299–330. [Google Scholar] [CrossRef]
- Cai, B.; Zhu, S.; Yu, S.; Dong, H.; Zhang, C.; Wang, C.; Zhu, J.; Gao, Q.; Fang, S.; Pan, X.; et al. The interpretation of 2019 refinement to the 2006 IPCC guidelines for national greenhouse gas inventory. Environ. Eng. 2019, 37, 1–11. [Google Scholar]
- Buchwitz, M.; Schneising, O.; Burrows, J.P.; Bovensmann, H.; Reuter, M.; Notholt, J. First direct observation of the atmospheric CO year-to-year increase from space. Atmos. Chem. Phys. 2007, 7, 5341–5342. [Google Scholar] [CrossRef][Green Version]
- Yokota, T.; Yoshida, Y.; Eguchi, N.; Ota, Y.; Tanaka, T.; Watanabe, H.; Maksyutov, S. Global Concentrations of CO2 and CH4 Retrieved from GOSAT: First Preliminary Results. Sola 2009, 5, 160–163. [Google Scholar] [CrossRef]
- Frankenberg, C.; Pollock, R.; Lee, R.A.M.; Rosenberg, R.; Blavier, J.F.; Crisp, D.; O’Dell, C.W.; Osterman, G.B.; Roehl, C.; Wennberg, P.O.; et al. The Orbiting Carbon Observatory (OCO-2): Spectrometer performance evaluation using pre-launch direct sun measurements. Atmos. Meas. Tech. 2015, 8, 301–313. [Google Scholar] [CrossRef]
- Suto, H.; Kataoka, F.; Kikuchi, N.; Knuteson, R.O.; Butz, A.; Haun, M.; Buijs, H.; Shiomi, K.; Imai, H.; Kuze, A. Thermal and near-infrared sensor for carbon observation Fourier transform spectrometer-2 (TANSO-FTS-2) on the Greenhouse gases Observing SATellite-2 (GOSAT-2) during its first year in orbit. Atmos. Meas. Tech. 2021, 14, 2013–2039. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Yao, L.; Chen, X.; Cai, Z.N.; Yang, D.X.; Yin, Z.S.; Gu, S.Y.; Tian, L.F.; Lu, N.M.; et al. The TanSat mission: Preliminary global observations. Sci. Bull. 2018, 63, 1200–1207. [Google Scholar] [CrossRef] [PubMed]
- Jervis, D.; McKeever, J.; Durak, B.O.A.; Sloan, J.J.; Gains, D.; Varon, D.J.; Ramier, A.; Strupler, M.; Tarrant, E. The GHGSat-D imaging spectrometer. Atmos. Meas. Tech. 2021, 14, 2127–2140. [Google Scholar] [CrossRef]
- Veefkind, J.P.; Aben, I.; McMullan, K.; Förster, H.; de Vries, J.; Otter, G.; Claas, J.; Eskes, H.J.; de Haan, J.F.; Kleipool, Q.; et al. TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications. Remote Sens. Environ. 2012, 120, 70–83. [Google Scholar] [CrossRef]
- Xiong, W. Greenhouse gases Monitoring Instrument (GMI) on GF-5 satellite (invited). Infrared Laser Eng. 2019, 48, 0303002. [Google Scholar] [CrossRef]
- Shao, C.; Gu, M.; Qi, C.; Wu, C. Detection of zero path difference position for FY-3D hyper-spectral infrared atmospheric sounder. Opt. Precis. Eng. 2020, 28, 2573–2580. [Google Scholar] [CrossRef]
- Crisp, D.; Fisher, B.M.; O’Dell, C.; Frankenberg, C.; Basilio, R.; Bösch, H.; Brown, L.R.; Castano, R.; Connor, B.; Deutscher, N.M.; et al. The ACOS CO2 retrieval algorithm—Part II: Global XCO2 data characterization. Atmos. Meas. Tech. 2012, 5, 687–707. [Google Scholar] [CrossRef]
- Green, R.O. Spectral calibration requirement for earth-looking imaging spectrometers in the solar-reflected spectrum. Appl. Opt. 1998, 37, 683–690. [Google Scholar] [CrossRef]
- Li, S.Z.; Cheng, L.; Yang, H.C.; Wang, Z.W.; Ding, L. Assessment of the Influence of Instrument Parameters on the Detection Accuracy of Greenhouse-Gases Absorption Spectrometer-2 (GAS-2). Atmosphere 2023, 14, 1418. [Google Scholar] [CrossRef]
- Crisp, D.; Pollock, H.R.; Rosenberg, R.; Chapsky, L.; Lee, R.A.M.; Oyafuso, F.A.; Frankenberg, C.; O’Dell, C.W.; Bruegge, C.J.; Doran, G.B.; et al. The on-orbit performance of the Orbiting Carbon Observatory-2 (OCO-2) instrument and its radiometrically calibrated products. Atmos. Meas. Tech. 2017, 10, 59–81. [Google Scholar] [CrossRef]
- Bi, Y.; Wang, Q.; Yang, Z.; Liu, C.; Lin, C.; Tian, L.; Zhang, N.; Wang, Y. TanSat ACGS On-orbit Wavelength Calibration Using the Solar Fraunhofer Lines. Chin. J. Atmos. Sci. 2022, 46, 645–652. [Google Scholar]
- Voors, R.; Dobber, M.; Dirksen, R.; Levelt, P. Method of calibration to correct for cloud-induced wavelength shifts in the Aura satellite’s Ozone Monitoring Instrument. Appl. Opt. 2006, 45, 3652–3658. [Google Scholar] [CrossRef]
- Xian, G.; Yan, C.; Wu, C.; Zhang, J. Effect of temperature on airborne imaging spectrometer optical properties. Infrared Laser Eng. 2015, 44, 1647–1653. [Google Scholar]
- Santantonio, N.; Bartoloni, A.; Bini, A.; Esposito, P.G.; Lorenzini, S. A Multi Parameter Retrieval Approach to HypSEO Spectral and Radiometric Calibration. In IEEE International Geoscience and Remote Sensing Symposium, Proceedings of IGARSS 2002, Toronto, ON, Canada, 24–28 June 2002; IEEE: New York, NY, USA, 2002; pp. 2735–2737. [Google Scholar]
- Mao, Y.L.; He, T.; Ren, F.; Huang, J. The On-orbit Calibration Method of Hyper-Spectral Fluorescence Imaging Spectrometer. In Fifth Symposium on Novel Optoelectronic Detection Technology and Application, Xi’an, China, 24–26 October 2018; SPIE: Bellingham, WA, USA, 2019; p. 11023. [Google Scholar]
- Li, B.; Li, M.; Xu, P. High Precision On-board Calibration for Spaceborne Atmospheric Monitoring Spectrometer. Spacecr. Recovery Remote Sens. 2018, 39, 60–69. [Google Scholar]
- Wang, T.X.; Yan, G.J.; Ren, H.Z.; Mu, X.H. Improved Methods for Spectral Calibration of On-Orbit Imaging Spectrometers. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3924–3931. [Google Scholar] [CrossRef]
- Sornig, M.; Fischer, S.; Chlebek, C.; Muecke, M.; Honold, H.P.; Heider, B. The Hyperspectral Instrument Onboard EnMAP, Overview and Current Status. In International Conference on Space Optics-Icso 2018, Chiania, Greece, 9–12 October 2018; SPIE: Bellingham, WA, USA, 2018; p. 11180. [Google Scholar]
- Wang, Y.; Shi, E.; Wang, H. Method of in-flight wavelength calibration for wide band hyper-spectral imager. Infrared Laser Eng. 2019, 48, 303006. [Google Scholar] [CrossRef]
- Mori, S.; Cho, Y.C.R.; Tabata, H.; Yumoto, K.; Böttger, U.; Buder, M.; Dietz, E.; Hagelschuer, T.; Hübers, H.W.; Kameda, S.; et al. Fraunhofer line-based wavelength-calibration method without calibration targets for planetary lander instruments. Planet. Space Sci. 2024, 240, 105835. [Google Scholar] [CrossRef]
- Delwart, S.; Preusker, R.; Bourg, L.; Santer, R.; Ramon, D.; Fischer, J. MERIS in-flight spectral calibration. Int. J. Remote Sens. 2007, 28, 479–496. [Google Scholar] [CrossRef]
- Kuli-Zade, D.M.; Mamedov, S.G.; Aliyeva, Z.F. The fraunhofer lines classifications by asymmetry changes inside the profiles in the spectrum of the Sun. Astrophys. Bull. 2017, 72, 337–339. [Google Scholar] [CrossRef]
- Heath, D.F.; Georgiev, G. A New Approach for Spectroradiometric Calibration Consistency on the Ground and in Space. In Earth Observing Missions and Sensors: Development, Implementation, and Characterization, 2nd ed.; SPIE: Bellingham, WA, USA, 2012; p. 8528. [Google Scholar]
- O’Brien, D.M.; Mitchell, R.M.; English, S.A.; Da Costa, G.A. Airborne measurements of air mass from OA-band absorption spectra. J. Atmos. Ocean. Technol. 1998, 15, 1272–1286. [Google Scholar] [CrossRef]
- Mao, J.P.; Kawa, S.R. Sensitivity studies for space-based measurement of atmospheric total column carbon dioxide by reflected sunlight. Appl. Opt. 2004, 43, 914–927. [Google Scholar] [CrossRef] [PubMed]
- Kuang, Z.M.; Margolis, J.; Toon, G.; Crisp, D.; Yung, Y. Spaceborne measurements of atmospheric CO by high-resolution NIR spectrometry of reflected sunlight: An introductory study: Art. no. 1716. Geophys. Res. Lett. 2002, 29, 11. [Google Scholar] [CrossRef]
- Fontenla, J.; White, O.R.; Fox, P.A.; Avrett, E.H.; Kurucz, R.L. Calculation of solar irradiances. I. Synthesis of the solar spectrum. Astrophys. J. 1999, 518, 480–499. [Google Scholar] [CrossRef]
- Chance, K.; Kurucz, R.L. An improved high-resolution solar reference spectrum for earth’s atmosphere measurements in the ultraviolet, visible, and near infrared. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1289–1295. [Google Scholar] [CrossRef]
- Li, S.; Li, C.L.; Xu, S.Y.; Zhang, H.; Zheng, Y.Q. Preflight radiometric calibration of a carbon dioxide spectrometer. Meas. Sci. Technol. 2019, 30, 055401. [Google Scholar] [CrossRef]
- Yang, Z.D.; Zhen, Y.Q.; Yin, Z.S.; Lin, C.; Bi, Y.M.; Liu, W.; Wang, Q.; Wang, L.; Gu, S.Y.; Tian, L.F. Prelaunch Radiometric Calibration of the TanSat Atmospheric Carbon Dioxide Grating Spectrometer. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4225–4233. [Google Scholar] [CrossRef]







| Band | O2A | WCO2 | SCO2 |
|---|---|---|---|
| Detection Objective | Aerosol, surface air pressure | CO2 | CO2, H2O |
| Wavelength (nm) | 757.5~772.5 | 1595~1625 | 2040~2080 |
| Spectral Resolution (nm) | 0.04 | 0.08 | 0.10 |
| Sampling Rate | 3 | ||
| SNR ) | 350:1@3.8 × 1019 | 340:1@1.55 × 1019 | 230:1@8.4 × 1018 |
| Dynamic Range ) | 1.1 × 1017~1.4 × 1021 | 5.7 × 1016~4.9 × 1020 | 3.1 × 1016~1.7 × 1020 |
| Spatial Resolution (km) | <3 | ||
| Wavelength Calibration Accuracy | <FWHM/10 | ||
| Absolute Calibration Accuracy | 5% | ||
| Inter-channel Relative Calibration Accuracy | 0.2% | ||
| Band | Fraunhofer Lines/nm | ||||||
|---|---|---|---|---|---|---|---|
| O2A | 758.812 | 761.909 | 764.238 | 765.972 | 767.178 | 768.239 | 770.110 |
| WCO2 | 1596.446 | 1598.513 | 1600.212 | 1606.442 | 1612.039 | 1613.034 | 1619.025 |
| SCO2 | 2045.000 | 2054.431 | 2056.960 | 2058.983 | 2063.533 | 2070.436 | 2074.254 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Gong, C.; Hu, Y.; Zheng, F.; Liu, Y. On-Orbit Wavelength Calibration Error Analysis of the Spaceborne Hyperspectral Greenhouse Gas Monitoring Instrument Using the Solar Fraunhofer Lines. Remote Sens. 2024, 16, 3367. https://doi.org/10.3390/rs16183367
Guo Y, Gong C, Hu Y, Zheng F, Liu Y. On-Orbit Wavelength Calibration Error Analysis of the Spaceborne Hyperspectral Greenhouse Gas Monitoring Instrument Using the Solar Fraunhofer Lines. Remote Sensing. 2024; 16(18):3367. https://doi.org/10.3390/rs16183367
Chicago/Turabian StyleGuo, Yulong, Cailan Gong, Yong Hu, Fuqiang Zheng, and Yunmeng Liu. 2024. "On-Orbit Wavelength Calibration Error Analysis of the Spaceborne Hyperspectral Greenhouse Gas Monitoring Instrument Using the Solar Fraunhofer Lines" Remote Sensing 16, no. 18: 3367. https://doi.org/10.3390/rs16183367
APA StyleGuo, Y., Gong, C., Hu, Y., Zheng, F., & Liu, Y. (2024). On-Orbit Wavelength Calibration Error Analysis of the Spaceborne Hyperspectral Greenhouse Gas Monitoring Instrument Using the Solar Fraunhofer Lines. Remote Sensing, 16(18), 3367. https://doi.org/10.3390/rs16183367







