Four-Dimensional Parameter Estimation for Mixed Far-Field and Near-Field Target Localization Using Bistatic MIMO Arrays and Higher-Order Singular Value Decomposition
Abstract
1. Introduction
2. Preliminaries
3. Tensor-Based 4D Parameter Estimation for Mixed FF and NF Target Localization
3.1. Signal Model
3.2. Algorithm
| Algorithm 1 Four-dimensional parameter estimation algorithm for mixed FF and NF target localization |
| 1: Calculate the sample covariance tensor using (21) based on . |
| 2: Perform the truncated HOSVD of to obtain according to (24), and obtain its left singular vector matrices and . |
| 3: Construct a selection matrix , and calculate the function based on (26). |
| 4: Construct spectral function using , then perform one-dimensional search for AOD estimation according to (27). |
| 5: Perform a one-dimensional spectral peak search using according to (28) to obtain the estimate of ROD. |
| 6: Construct a selection matrix , calculate the function using (30), and estimate AOA according to (31). |
| 7: Perform a one-dimensional spectral peak search using to estimate ROA based on (32). |
| 8: Match according to the parameter pairing criterion in (33). |
4. Performance Analysis
4.1. The Cramér–Rao Lower Bound
4.2. The Number of Detectable Targets
4.3. Computational Complexity
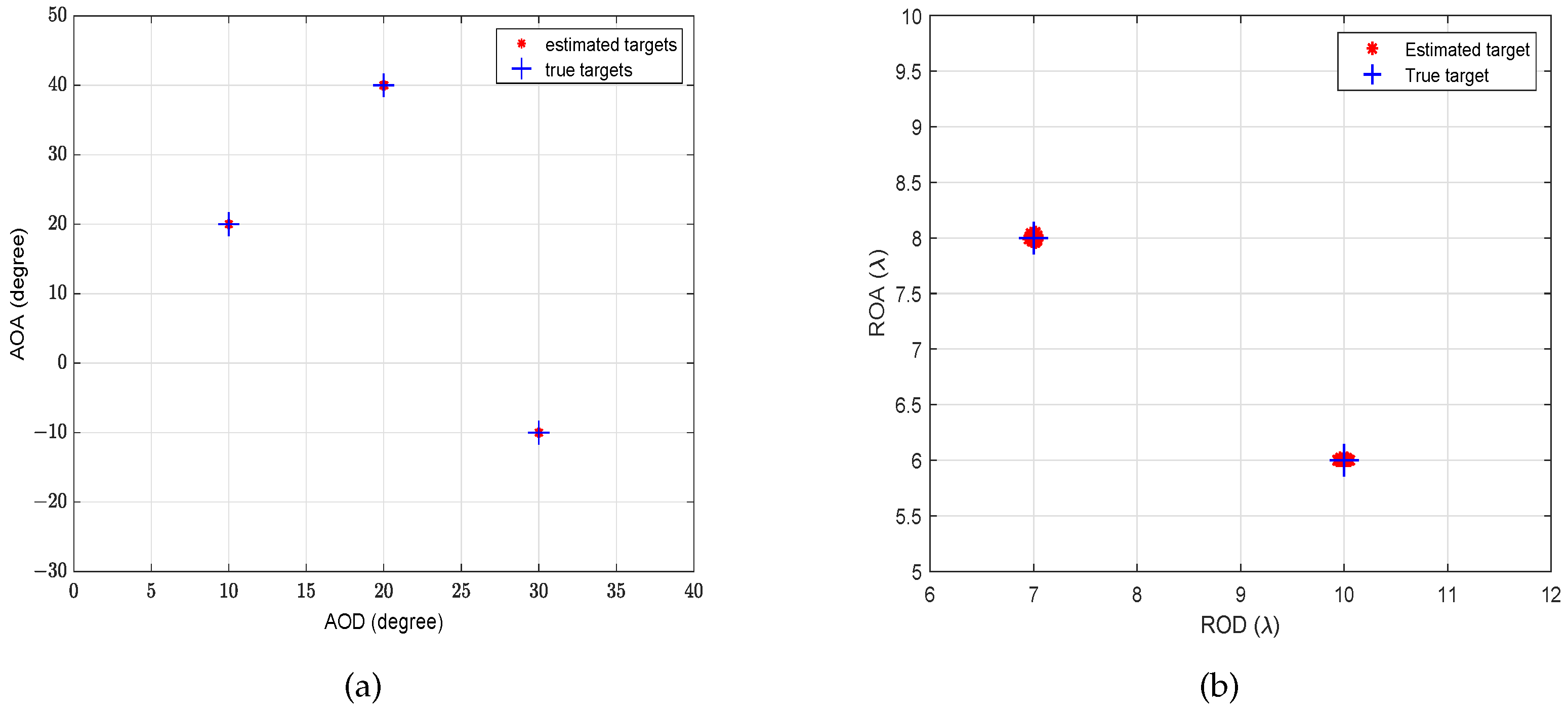
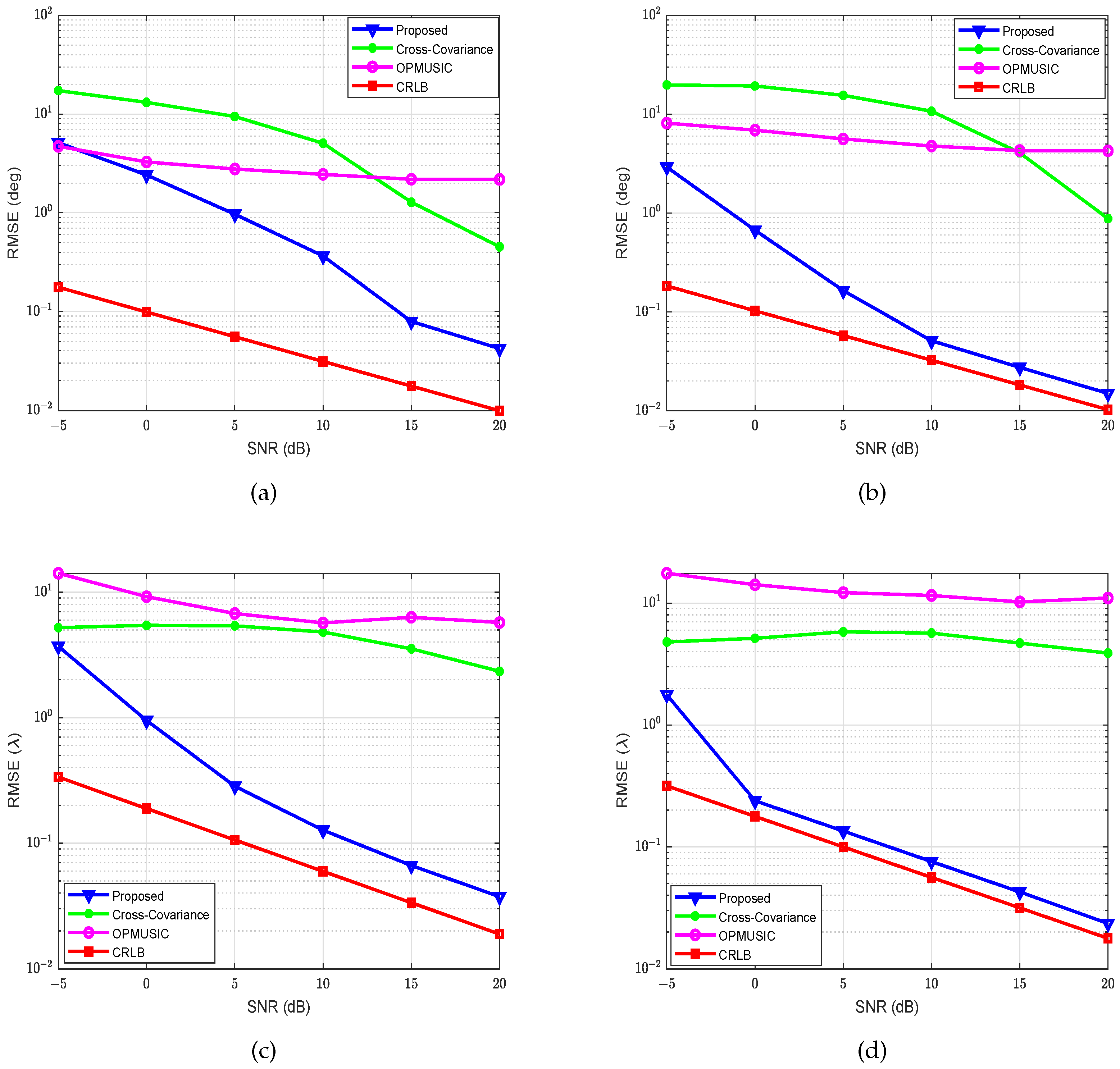
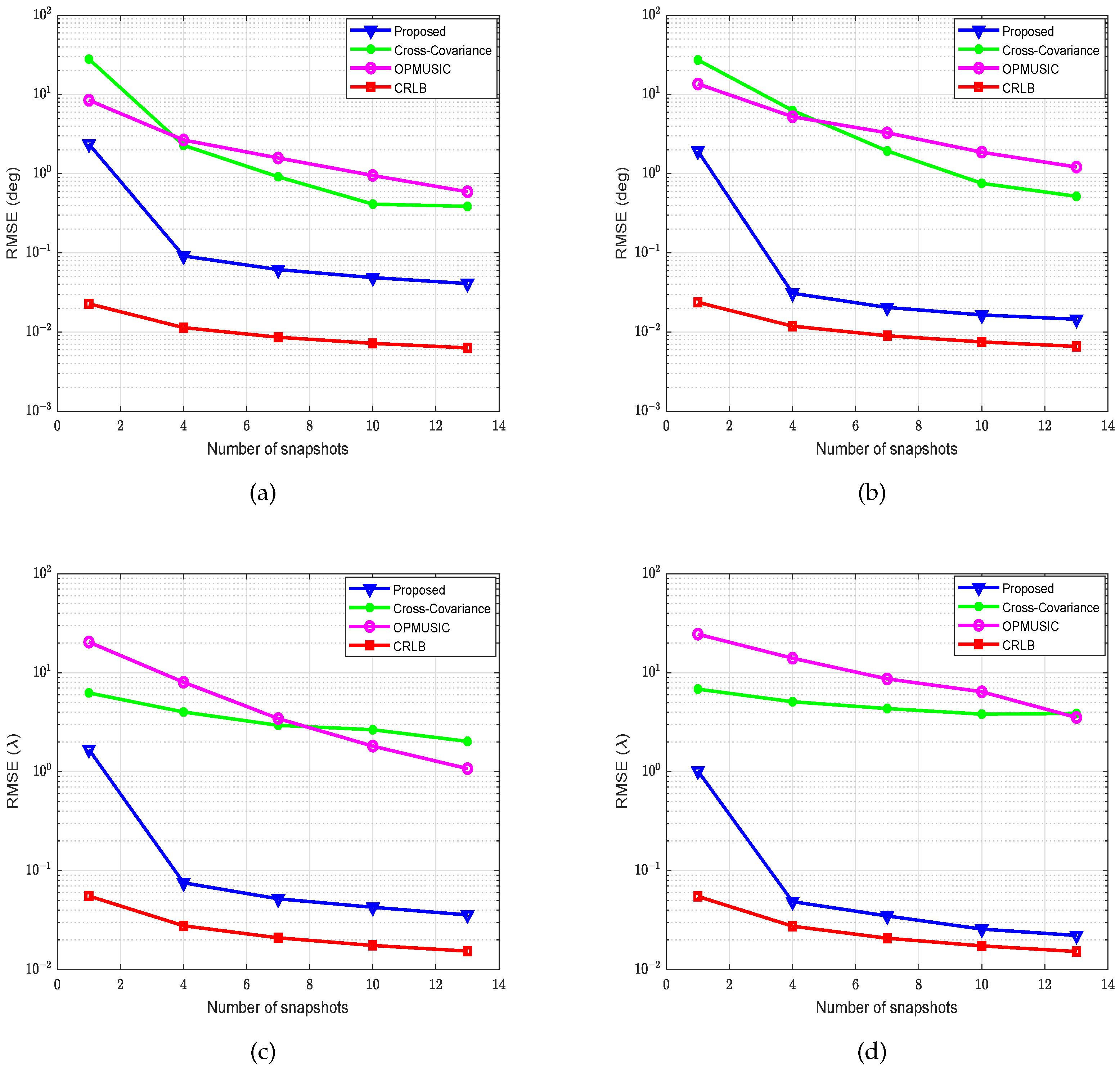
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiao, M.; Mumtaz, S.; Huang, Y. Millimeter wave communications for future mobile networks. IEEE J. Sel. Areas Commun. 2017, 35, 1909–1935. [Google Scholar] [CrossRef]
- Bjrnson, E.; Sanguinetti, L.; Wymeersch, H. Massive MIMO is a reality—What is next? Five promising research directions for antenna arrays. Digi. Signal Process 2019, 94, 3–20. [Google Scholar] [CrossRef]
- Fang, Y.; Zhu, S.; Liao, B.; Li, X.; Liao, G. Target localization with bistatic MIMO and FDA-MIMO dual-mode radar. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 952–964. [Google Scholar] [CrossRef]
- Ahmad, M.; Zhang, X.; Lai, X.; Ali, F.; Shi, X. Low-complexity 2D-DOD and 2D-DOA estimation in bistatic MIMO radar systems: A reduced-dimension MUSIC algorithm approach. Sensors 2024, 24, 2801. [Google Scholar] [CrossRef]
- Shi, J.; Hu, G.; Zhang, X. Sparsity-based DOA estimation of coherent and uncorrelated targets with flexible MIMO radar. IEEE Trans. Veh. Technol. 2019, 68, 5835–5848. [Google Scholar] [CrossRef]
- Xie, Q.; Pan, X.; Huang, M. Sparsity-based direction-of-departure and direction-of-arrival estimation for bistatic multiple-input multiple-output radar. IEEE Access 2019, 7, 118826–118838. [Google Scholar] [CrossRef]
- Liu, D.; Zhao, Y.; Zhang, T. Sparsity-based two-dimensional DOA estimation for co-prime planar array via enhanced matrix completion. Remote Sens. 2022, 14, 4690. [Google Scholar] [CrossRef]
- Zhang, R.; Shim, B.; Wu, W. Direction-of-arrival estimation for large antenna arrays with hybrid analog and digital architectures. IEEE Trans. Signal Process. 2021, 70, 72–88. [Google Scholar] [CrossRef]
- Wei, X.; Jiang, Y.; Liu, Q. Calibration of phase shifter network for hybrid beamforming in mmWave massive MIMO systems. IEEE Trans. Signal Process. 2020, 68, 2302–2315. [Google Scholar] [CrossRef]
- Elbir, A.M.; Mishra, K.V.; Chatzinotas, S. Spherical wavefront near-field DoA estimation in THz automotive radar. In Proceedings of the 18th European Conference on Antennas and Propagation (EuCAP), Glasgow, UK, 17–22 March 2024; pp. 1–5. [Google Scholar]
- Wu, J.; Kim, S.; Shim, B. Near-field channel estimation for RIS-assisted wideband Terahertz systems. In Proceedings of the 2022 IEEE Global Communications Conference (GLOBECOM 2022), Rio de Janeiro, Brazil, 4 December 2022; pp. 3893–3898. [Google Scholar]
- Singh, P.R.; Wang, Y.; Charge, P. Near field targets localization using bistatic MIMO system with symmetric arrays. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 2403–2407. [Google Scholar]
- Singh, P.R.; Wang, Y. Near field targets localization using bistatic MIMO system with spherical wavefront based model. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 2408–2412. [Google Scholar]
- Chen, C.; Zhong, W.D.; Yang, H. On the performance of MIMO-NOMA-based visible light communication systems. IEEE Photonics Technol. Lett. 2017, 30, 307–310. [Google Scholar] [CrossRef]
- Hong, J.; Erning, H.Z.; Han, Q. 4-D Parameter Estimation in Bistatic MIMO Radar for Near-Field Target Localization. In Proceedings of the IEEE International Wireless Symposium (IWS), Shenzhen, China, 30 March–1 April 2015; pp. 1–4. [Google Scholar]
- Zhao, T.; Chen, H.; Tian, Y. An algorithm for 5-D parameters estimation of near-field sources using parallel factor analysis. Multidimens. Syst. Signal Process. 2022, 33, 1139–1150. [Google Scholar] [CrossRef]
- He, J.; Swamy, M.N.S.; Ahmad, M.O. Efficient application of MUSIC algorithm under the coexistence of far-field and near-field sources. IEEE Trans. Signal Process. 2012, 60, 2066–2070. [Google Scholar] [CrossRef]
- Zheng, Z.; Fu, M.; Wang, W.Q. Mixed far-field and near-field source localization based on subarray cross-cumulant. Signal Process. 2018, 150, 51–56. [Google Scholar] [CrossRef]
- Wang, K.; Wang, L.; Shang, J.R. Mixed near-field and far-field source localization based on uniform linear array partition. IEEE Sensors J. 2016, 16, 8083–8090. [Google Scholar] [CrossRef]
- Ma, H.; Tao, H.; Xie, J. Mixed far-field and near-field source localization using a linear tripole array. IEEE Wirel. Commun. Lett. 2020, 9, 889–892. [Google Scholar] [CrossRef]
- He, Q.; Cheng, Z.; Wang, Z. Mixed far-field and near-field source separation and localization based on FOC matrix differencing. Digit. Signal Process. 2022, 131, 103753. [Google Scholar] [CrossRef]
- Zuo, W.; Xin, J.; Zheng, N. Subspace-based localization of far-field and near-field signals without eigendecomposition. IEEE Trans. Signal Process. 2018, 66, 4461–4476. [Google Scholar] [CrossRef]
- Yang, J.; Hao, C.; Zheng, Z. Localization of mixed near-field and far-field multi-band sources based on sparse representation. Multidimens. Syst. Signal Process. 2020, 31, 173–190. [Google Scholar] [CrossRef]
- Wang, B.; Liu, J.; Sun, X. Mixed sources localization based on sparse signal reconstruction. IEEE Signal Process. Lett. 2012, 19, 487–490. [Google Scholar] [CrossRef]
- Wu, X.; Yan, J. Gridless mixed sources localization based on low-rank matrix reconstruction. IEEE Wirel. Commun. Lett. 2020, 9, 1748–1752. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, W.; Dong, F. A One-snapshot localization algorithm for mixed far-field and near-field sources. IEEE Commun. Lett. 2020, 24, 1010–1014. [Google Scholar] [CrossRef]
- Huang, Z.; Xue, B.; Wang, W.; Dong, F.; Wang, D. A low complexity localization algorithm for mixed far-field and near-field sources. IEEE Commun. Lett. 2021, 12, 3838–3842. [Google Scholar] [CrossRef]
- Tian, Y.; Lian, Q.; Xu, H. Mixed near-field and far-field source localization utilizing symmetric nested array. Digit. Signal Process. 2017, 73, 16–23. [Google Scholar] [CrossRef]
- Wu, X. Localization of far-field and near-field signals with mixed sparse approach: A generalized symmetric arrays perspective. Signal Process. 2020, 175, 107665. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, W.-P. Single far-field or near-field source localization with sparse or uniform cross array. IEEE Trans. Veh. Technol. 2020, 69, 9135–9139. [Google Scholar] [CrossRef]
- Su, X.; Hu, P.; Liu, Z.; Liu, T.; Peng, B.; Li, X. Mixed near-field and far-field source localization based on convolution neural networks via symmetric nested array. IEEE Trans. Veh. Technol. 2021, 70, 7908–7920. [Google Scholar] [CrossRef]
- Zheng, Z.; Fu, M.; Wang, W.-Q.; So, H.C. Symmetric displaced coprime array configurations for mixed near- and far-Field source localization. IEEE Trans. Antennas Propag. 2021, 69, 465–477. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Qi, J.; Li, Y. Symmetric extended nested array for passive localization of mixture near-and far-field sources. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 1244–1248. [Google Scholar] [CrossRef]
- Wu, X.; Yan, J. 3-D Mixed far-field and near-field sources localization with cross array. IEEE Trans. Veh. Technol. 2020, 69, 6833–6837. [Google Scholar] [CrossRef]
- Chen, H.; Ahmad, F.; Vorobyov, S.V.; Porikli, F. Tensor decompositions in wireless communications and MIMO radar. IEEE J. Sel. Top. Signal Process. 2021, 15, 438–453. [Google Scholar] [CrossRef]
- Mao, C.; Shi, J.; Wen, F. Target localization in bistatic EMVS-MIMO radar using tensor subspace method. IEEE Access 2019, 7, 163119–163127. [Google Scholar] [CrossRef]
- Xu, F.; Yang, X.; Lan, T. Search-free direction-of-arrival estimation for transmit beamspace multiple-input multiple-output radar via tensor modeling and polynomial rooting. IET Radar Sonar Navig. 2021, 15, 574–580. [Google Scholar] [CrossRef]
- Xu, F.; Morency, M.W.; Vorobyov, S.A. DOA estimation for transmit beamspace MIMO radar via tensor decomposition with vandermonde factor matrix. IEEE Trans. Signal Process. 2021, 70, 2901–2917. [Google Scholar] [CrossRef]
- Shi, J.; Wen, F.; Liu, T. Nested MIMO radar: Coarrays, tensor modeling, and angle estimation. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 573–585. [Google Scholar] [CrossRef]
- Singh, P.R.; Wang, Y.; Charge, P. Bistatic MIMO radar for near field source localization using PARAFAC. Electron. Lett. 2016, 52, 1060–1061. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Lathauwer, L.D.; Moor, B.D.; Vandewalle, J. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 2000, 21, 1253–1278. [Google Scholar] [CrossRef]
- Barrar, R.B.; Wilcox, C.H. On the fresnel approximation. IRE Trans. Antennas Propag. 1958, 6, 43–48. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Pesavento, M.; Gershman, A.B. Maximum-likelihood direction-of-arrival estimation in the presence of unknown nonuniform noise. IEEE Trans. Signal Process. 2001, 49, 1310–1324. [Google Scholar]
- Stoica, P.; Larsson, E.G.; Gershman, A.B. The stochastic CRB for array processing: A textbook derivation. IEEE Signal Process. Lett. 2001, 8, 148–150. [Google Scholar] [CrossRef]

| Method | Computational Complexity |
|---|---|
| Cross-Covariance algorithm | |
| OPMUSIC algorithm | |
| Proposed algorithm | |
| Method | Running Time (s) |
|---|---|
| Cross-Covariance algorithm | 0.152716 |
| OPMUSIC algorithm | 30.318917 |
| Proposed algorithm | 0.965869 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Jiang, H.; Zheng, H. Four-Dimensional Parameter Estimation for Mixed Far-Field and Near-Field Target Localization Using Bistatic MIMO Arrays and Higher-Order Singular Value Decomposition. Remote Sens. 2024, 16, 3366. https://doi.org/10.3390/rs16183366
Zhang Q, Jiang H, Zheng H. Four-Dimensional Parameter Estimation for Mixed Far-Field and Near-Field Target Localization Using Bistatic MIMO Arrays and Higher-Order Singular Value Decomposition. Remote Sensing. 2024; 16(18):3366. https://doi.org/10.3390/rs16183366
Chicago/Turabian StyleZhang, Qi, Hong Jiang, and Huiming Zheng. 2024. "Four-Dimensional Parameter Estimation for Mixed Far-Field and Near-Field Target Localization Using Bistatic MIMO Arrays and Higher-Order Singular Value Decomposition" Remote Sensing 16, no. 18: 3366. https://doi.org/10.3390/rs16183366
APA StyleZhang, Q., Jiang, H., & Zheng, H. (2024). Four-Dimensional Parameter Estimation for Mixed Far-Field and Near-Field Target Localization Using Bistatic MIMO Arrays and Higher-Order Singular Value Decomposition. Remote Sensing, 16(18), 3366. https://doi.org/10.3390/rs16183366







