Abstract
Aerosols in the atmosphere significantly reduce the solar radiation reaching the Earth’s surface through scattering and absorption processes. Knowing their properties becomes essential when we are interested in measuring solar radiation at a given location on the ground. The commonly used parameters that characterize their effects are the Aerosol Optical Depth , the Angstrom exponent , and the Angstrom coefficient . One method for estimating these parameters is to fit ground-based measurements of clear-sky direct solar radiation using a model on which it depends. However, the choice of model depends on its suitability to the atmospheric conditions of the site considered. Eleven empirical solar radiation models depending on and were thus chosen and tested with solar radiation measurements recorded between 2005 and 2014 in Tamanrasset in southern Algeria. The results obtained were compared to measurements made with the AERONET solar photometer on the same site during the same period. Among the 11 models chosen, the best performing ones are REST2 and CPCR2. They proved to be the best suited to estimate with approximately the same RMSE of 0.05 and a correlation coefficient R with respect to AERONET of 0.95. The results also highlighted good performances of these models for the estimation of with an of 0.05 and 0.04, and an R of 0.95 and 0.96, respectively. The values of obtained from the fitting of these models were, however, less good, with R around 0.38. Additional treatments based on a Recurrent Neural Network (RNN) were necessary to improve its estimation. They provided promising results showing a significant improvement in estimates with R reaching 0.7 when referring to AERONET data. Furthermore, this parameter made it possible to identify different types of aerosols in Tamanrasset such as the presence of maritime, dust, and mixed aerosols representing, respectively, 31.21%, 3.25%, and 65.54%, proportions calculated over the entire period studied. The seasonal analysis showed that maritime aerosols are predominant in the winter in Tamanrasset but decrease with the seasons to reach a minimum in the summer (JJA). Dust aerosols appear in February and persist mainly in the spring (MAM) and summer (JJA), then disappear in September. These results are also consistent with those obtained from AERONET.
1. Introduction
Radiation reaching the Earth’s surface under all sky conditions is highly dependent on multiple atmospheric factors that introduce various absorption and scattering processes. Gases and aerosols are the key parameters that govern solar radiation reaching the ground under clear skies. The main absorbing gases are ozone, oxygen, water vapor, and carbon dioxide, while all other atmospheric gases scatter solar radiation at all wavelengths [1,2]. The presence of aerosols in the atmosphere in the liquid or solid phase also decreases the amount of solar radiation reaching the Earth’s surface [3] through absorption and scattering processes. The loss will be approximately 25–35% for a PhotoVoltaic (PV) energy conversion system. This justifies the importance of quantifying and studying the temporal properties of aerosol effects on solar radiation, particularly in areas considered suitable for the exploitation of solar energy using PV conversion systems. More generally, aerosols play a crucial role in the radiation budget of the Earth by affecting its temperature at different time and space scales. Generally, ground-based active and passive remote sensing instruments offer reliable measurements to study aerosol properties. Their long-term, continuous observations enhance our understanding of both global and regional properties and their impact on the Earth’s climate. Among the passive methods, sun-photometers and sky-radiometers are recognized as particularly effective for aerosol measurements [4,5,6]. Consequently, various global and regional observation networks, such as AERONET, have been established. For the active method, LIDAR and RADAR remote sensing instruments are widely used due to their advantages of detecting the vertical distribution of aerosols [6,7].
Aerosols have different shapes, size distributions, and residence times. They come from different sources such as the condensation of gases, the action of the wind on the surface of the Earth, volcanoes, fires, and human activity. Aerosol turbidity or atmospheric turbidity can define the state of the atmosphere with suspended aerosols [8,9]. The Aerosol Optical Depth (AOD), the Angstrom exponent , and the Angstrom coefficient are the parameters usually used to characterize them. The AOD, which is wavelength-dependent, measures the extinction of sunlight due to scattering and absorption by aerosols in the atmosphere [4], while the Angstrom coefficient is related to their quantity [1]. The parameter is normally between 0.0 and 0.5 but can exceed this upper limit in the case of a highly charged atmosphere. The Angstrom turbidity equation given hereafter expresses the dependence of AOD with the wavelength , the number of particles (), and their sizes ():
where the wavelength is in micrometers.
The Angstrom coefficient therefore corresponds to AOD at 1 m wavelength. AOD is related to the Angstrom coefficient through Equation (1) for other wavelengths. The Angstrom coefficient can be obtained from aerosol spectral transmissions at two wavelengths [10] and appears to be independent of air mass [11]. The experimental determination of can be obtained from spectral measurements of direct solar radiation (sun-photometer) but measurements are generally not easy to implement. Several authors have proposed different parametric models to obtain from integrated measurements of solar irradiance [12,13].
The Angstrom exponent is a reliable index of the particle size distribution of aerosols, i.e., it is a good indicator of the dominant size of atmospheric particles [14,15]. Its values vary from 0 to 4. It takes values around 4 when the aerosol particles are very small, of the order of air molecules, while it approaches 0 for large particles. The Angstrom formula (Equation (1)) applied to two AOD measurements allows one to obtain this indicator by
where and are the AOD values obtained, respectively, at the two wavelengths and .
Knowing the properties of aerosols through these parameters is very useful in the field of renewable energies because, depending on their nature, they affect the propagation of solar energy in the atmosphere differently. Indeed, aerosols coming from various sources have different optical and physicochemical properties, in addition to being wavelength-dependent [16]. The classification of aerosols therefore proves to be an important step in quantifying these effects. For this reason, many studies were conducted to classify aerosols [14,17,18]. The correlation between aerosol properties facilitates their characterization, although, in the majority of cases, well-mixed aerosol types are quite difficult to classify [19]. The most common scatter plot for discriminating aerosol types is between the AOD and Angstrom exponent [20]. Other techniques have also been used, such as the wavelength dependence of Single Scattering Albedo (SSA), the correlation between the fine-mode fraction and SSA [21], and the correlation between the absorption and extinction of the Angstrom exponent [22]. Most research studies classify aerosols in the atmosphere into four main types, namely biomass-burning aerosols, urban aerosols, maritime aerosols, and dust aerosols [16,21,23,24,25]. The remaining cases that do not belong to the threshold proposed in the literature are characterized as mixed type (MT or undetermined aerosols). These aerosols have different physicochemical, optical, and radiative characteristics depending on their origin. Certain types of aerosols can interact with cloud droplets and, therefore, modify their micro-physical properties, influencing the radiative properties and precipitation processes. Thus, the relationship between and will be used in this paper to classify aerosol types for the studied site. High values of are affected by biomass burning, dust, or urban aerosols where values close to zero correspond to sea spray and dust, and values above 1.5 indicate the significant presence of smokes or urban aerosols [22].
This paper has two main parts. The first concerns the estimation of aerosol parameters (, , and ) from measurements of direct solar radiation recorded during the period 2005–2014 at Tamanrasset, in the south of Algeria, and different empirical clear-sky models of direct solar radiation. Eleven empirical models based on the parameters of interest were chosen and tested to select the best one(s) relative to the measurements. The results obtained were then compared to AERONET (AErosol RObotic NETwork) data to select the model best suited to the Tamanrasset site. The second part of the article discusses and presents the method to improve the results, mainly the poor estimate of obtained from the model fitting. An innovative method based on a Recurrent Neural Network (RNN) was therefore developed to improve its estimation thanks to AERONET measurements. This method will be presented, as well as the results obtained, which now make it possible to classify the aerosols present in the atmosphere of Tamanrasset.
2. Materials and Methods
This section presents the data and models used in this work and, then, the methods developed to estimate the Angstrom parameters.
2.1. Materials
2.1.1. Ground Measurements of Solar Radiation
Solar radiation data were collected between 2005 and 2014 at the Regional Meteorological Center (Direction Régionale de la Météo Sud, National Meteorological Office, ONM, Dar El Beida, Algeria) located in Tamanrasset (22.79°N, 5.53°E, 1377 m altitude) in southern Algeria (see Figure 1 on the left). The data correspond to direct, global, and diffuse solar radiation measurements. Instruments and methods for data collection are the same as those described in detail by Zaiani et al. (2021) [9].
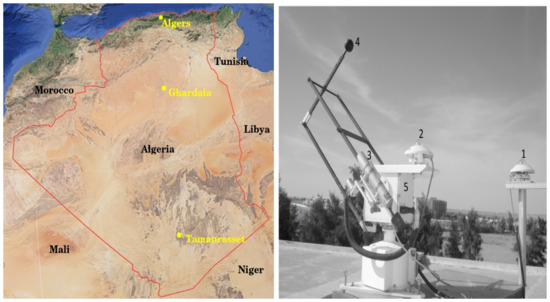
Figure 1.
(Left): Tamanrasset location. (Right): radiometric station for measuring the global, direct, and diffuse solar radiation: (1) Pyranometer for measuring the global solar irradiance. (2) Pyranometer for measuring the diffuse irradiance component. (3) Peryheliometer for measuring the direct irradiance component. (4) The ball is used to permanently hide the pyranometer (2). (5) The two-axis solar tracker.
The measurement of the direct, global, and diffuse components of solar radiation was carried out with EKO-type instruments (see Figure 1 on the right). They are calibrated every three years and cleaned two to three times a week depending on weather conditions. The dataset used in this work corresponds to 3287 days of solar radiation measurements. However, only clear days were considered to study the aerosols’ properties. They were selected from the dataset with an appropriate method [26]. The number of useful days was thus reduced after selection to 1369, i.e., 42% of the weather conditions in Tamanrasset were clear days.
2.1.2. AERONET and MODIS Data
Photometer spectral measurements of the direct (collimated) solar radiation from the AERONET network (http://AERONET.gsfc.nasa.gov, accessed on 1 March 2021) provided the information to calculate the columnar Aerosol Optical Depth () at different wavelengths (). and are used to calculate the Angstrom turbidity ( exponent and coefficient) thanks to the Angstrom relationship (Equation (1)). Two data versions (1 and 2) and three levels (1.0, 1.5, and 2.0) exist for each AERONET product. The highest quality data can be found in version 2, level 2.0, after a delay of 12 months or more (due to final calibration and manual inspection). This product exists for Tamanrasset, where an AERONET station is installed and operational. It was, therefore, used in this work to obtain at different wavelengths for the Tamanrasset region. There are 2828 measurements over the period from 1 January 2006 to 31 December 2014, except for 2010, where no measurements are available. This study also used MOD07 products created from measurements of the MODIS instrument onboard the TERRA satellite. These are level 2.0 products of column-integrated total ozone at a 10 km resolution. They cover the period between 2005 and 2014.
2.1.3. Clear-Sky Models
Eleven clear-sky models were considered for this study. They were selected from various studies providing their complete formulation and validation [27,28,29,30]. The main criterion for model selection was primarily its dependence on Angstrom parameters and . Table 1 gives the selected clear-sky models with the other required variables, namely solar constant [W/m2], zenith angle [degrees], the elevation of the site above sea level [m], local barometric pressure p [mb], surface albedo , the total amount of ozone [atm-cm], the total amount of nitrogen-dioxide [atm-cm] (a value of 0.0002 atm-cm was taken when the measurement was not available), the total precipitable water vapor [cm], the Angstrom exponent , and the Angstrom coefficient . All these variables were relevant for clear-sky modeling of direct normal irradiances (DNIcs) and diffuse horizontal irradiances (DIFcs), except , which was only useful for determining DNIcs.

Table 1.
Clear-sky models and their required inputs. The variables displayed are the solar constant [W/m2], zenith angle [degrees], site elevation above sea level [m], surface albedo , local barometric pressure p [mb], Angstrom exponent , Angstrom coefficient , total ozone amount [atm-cm], total nitrogen dioxide amount [atm-cm], and total precipitable water vapor [cm].
The models selected are empirical models that translate atmospheric attenuation processes by a simplified parameterization. They express solar radiation in clear skies with analytical expressions, taking atmospheric components as input (Table 1). Each empirical model expresses the atmospheric transmittance relative to solar radiation, i.e., the ratio between what impinges the top of the atmosphere and what remains at ground level. It can be parameterized in terms of air mass and concentration or amount of constituents present in the atmosphere. The components of solar radiation are calculated from the total atmospheric transmittance T, defined as the product of the different transmittance terms:
where , and are, respectively, the different transmittances due to stratospheric ozone, optical properties of gases, water vapor, Rayleigh scattering, and aerosol properties.
2.2. Methods
2.2.1. Estimation of Angstrom Parameters Using Model Fitting
The first objective of the study was the estimation of Angstrom parameters from ground-based measurements of direct solar radiation under clear skies and one of the chosen models. This means that the aerosol parameters and were obtained by least-squares fitting of the clear-sky model to the selected solar radiation measurements, i.e., clear-sky measurements. The AOD parameter was then calculated from Equation (1).
The different steps of the methodology that was implemented to achieve this objective are presented in Algorithm 1.
| Algorithm 1 Different steps of the methodology. | |
| Step 1: | Construct the solar radiation dataset from 2006 to 2014 with 10 min sampling as well as the ozone data with the same sampling over the same period. |
| Step 2: | Selection of solar radiation data corresponding to clear-sky conditions according to the method proposed by Zaiani et al., (2020) [26] |
| Step 3: | Using the least-squares algorithm to fit solar radiation measurements with the selected model to obtain the Angstrom parameters. |
| Step 4: | Comparison of the results to those measured with the solar photometer AERONET |
| Step 5: | Conclusions on model performance with respect to the best estimation of Angstrom parameters. |
Several metric parameters were used for comparison purposes, since this study focused on the performance of radiation models under clear-sky conditions to estimate Angstrom parameters. These are the root mean square error (RMSE), the mean absolute percentage error (MAPE), the dependence of model error (MBE), and the correlation coefficient (R) (see Zaiani et al., (2017) [39] for definitions).
2.2.2. Prediction Model Using RNN
Machine Learning techniques were also applied to regression tasks to improve the results if needed. Indeed, the integration of a Recurrent Neural Network (RNN) model can be useful if the least-squares fitting method of the clear-sky model to the data does not give conclusive results (see Section 2.2.1). This option was possible thanks to the AERONET measurements of the aerosol parameters that we wanted to obtain on the same site. The RNN model took the Angstrom coefficient as input to provide a better estimate of the Angstrom exponent as output. The database that contained and obtained from the AERONET measurements was split for this purpose in order to create the predicted model. A total of 70% of the database was used for training and 30% for testing. Figure 2 shows the steps of creating this predicted model.
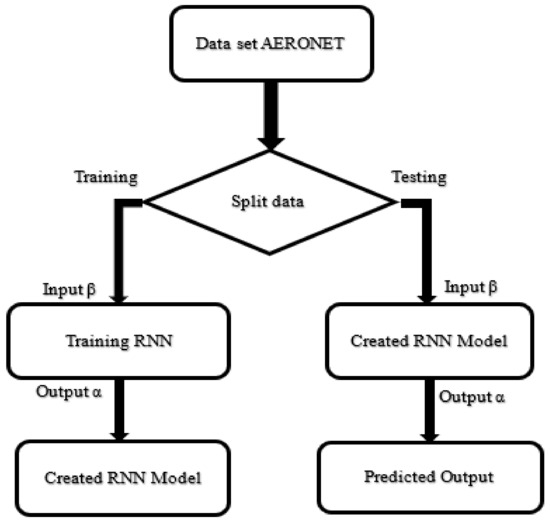
Figure 2.
Diagram of creating the predicted model.
3. Results
The solar radiation measurements described in Section 2.1.1 were processed using the eleven clear-sky models (see Section 2.1.3). The methodology for the estimation of the Angstrom parameters and for Tamanrasset (see Algorithm 1) was implemented to process data corresponding to direct solar radiation.
3.1. Estimation of Angstrom Coefficient ()
The model fitting method was used with direct solar radiation measurements and the eleven models. The obtained Angstrom coefficient was then compared to what AERONET measured.
3.1.1. Model Pre-Ranking
The histograms giving the distribution of the Angstrom coefficient obtained are a good indicator to evaluate, as a first approach, how close the results from the different models were to the measurements. Indeed, Figure 3 plots the histograms of the eleven models and clearly shows the differences between the distributions. An obvious bias is observed between the values, as confirmed by the shape and maximum occurrence of the different histograms. These histograms are then used to classify the models, since the differences essentially reflect their performance in estimating the Angstrom coefficient. Thus, the BASHAHU, CPCR2, IDERIAH, JANJAI, MIQBALC, and REST2 models, which have approximately the same distribution shape, were retained, unlike the other models, BIRD, DAI, IQBALA, IQBALC, and MAC2, which can now be rejected. The histogram of AERONET measurements confirms the hypothesis of choice by shape, as can be seen at the bottom-right of Figure 3.
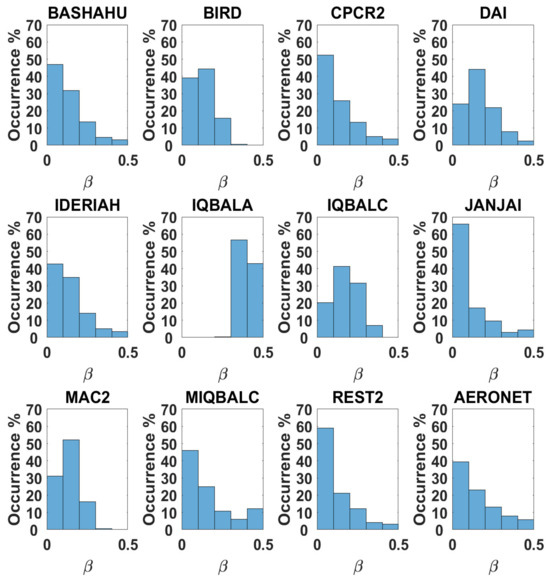
Figure 3.
Histograms of Angstrom coefficients () obtained with the 11 models from direct solar radiation measurements recorded during the period 2005–2014. The histogram of AERONET measurements made on the same site and during the same period is also plotted on the bottom-right.
3.1.2. Evaluation of Pre-Selected Models
The second selection step consisted of comparing the values of obtained from the six models selected previously with the measurements of carried out on the same site and during the same period with the AERONET solar photometer. Figure 4, on the left, shows the temporal variation of the Angstrom parameter obtained from AERONET and three models selected from the six according to their a priori quality (from good to less good). The correlation between daily measurements from AERONET and from clear-sky models is plotted in Figure 4 on the right. A good correlation can already be observed in the figures on which the regression line allowing the statistical errors to be obtained is calculated. They are given in Table 2 in descending order according to the performance of the fitting models, i.e., the overall goodness of fit, defined as the sum of all the absolute values of statistical errors plus (). The models are thus classified by the values of the overall goodness of fit, from the lowest to the highest. The obtained ranking shows that CPCR2 and REST2 are the clear-sky models best suited to estimate the Angstrom coefficient at Tamanrasset. The left plot of Figure 4 indeed shows that estimated with the CPCR2 model presents temporal variations similar to those of AERONET and that there is also a very good correlation between them compared to other models (Figure 4, on the right).
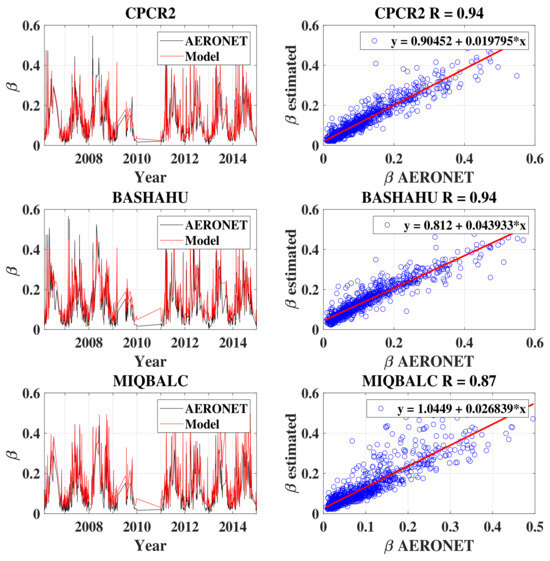
Figure 4.
(Left): temporal variation of Angstrom coefficient obtained from radiometric (red line) and AERONET (black line) measurements. (Right): correlation between daily values of Angstrom coefficient estimated using clear-sky models and AERONET.

Table 2.
Statistical errors on estimated using clear-sky models and AERONET measurements. The overall goodness of fit is inferred from statistical errors and used for model ranking (see text).
The estimation of the Angstrom coefficient therefore requires no additional processing.
3.2. Estimation of Angstrom Exponent ()
The same method as for , comparing the results of the six models with the AERONET measurements, was used for the estimation of the Angstrom exponent .
Figure 5, on the left, shows the temporal variation of obtained from three models and AERONET where the wavelengths 440 and 870 nm were used to calculate it with Equation (2). The three models are CPCR2 and REST2, which gave the best estimates of and JANJAI, which has the best overall goodness of fit for (see Table 3). The correlation between the daily values of estimated with the three models and measured with AERONET is illustrated in Figure 5, on the right. These curves show that is poorly estimated, regardless of the model. There is just a weak correlation with AERONET for obtained from CPCR2 and REST2, which is 0.38 and 0.35, respectively. Table 3 gives the statistical errors of the six models and confirms the poor estimation of the Angstrom exponent.
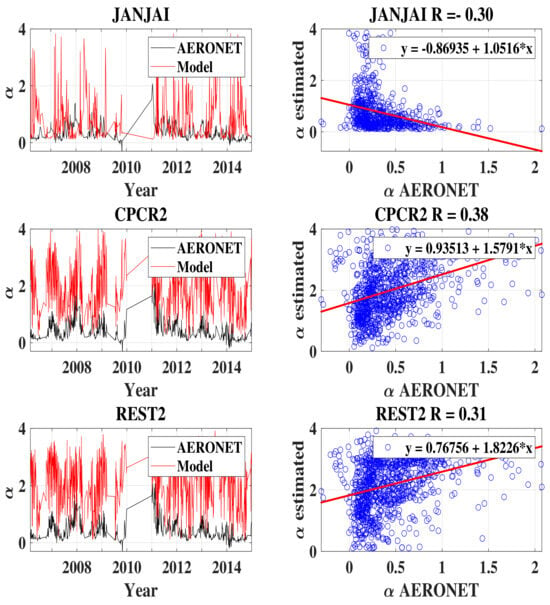
Figure 5.
(Left): temporal variation of the Angstrom exponent from radiometric (red) and AERONET (black) measurements. (Right): correlation between daily values of Angstrom exponent obtained from AERONET and estimated using three clear-sky models.

Table 3.
Statistical errors between obtained from AERONET and estimated with clear-sky models.
The difficulty in estimating the Angstrom exponent largely arises from the complexity and reliability of the fitting method, particularly the nonlinear least-squares algorithm. In addition, the clear-sky model used in this estimation involves at least three parameters (as shown in Table 1). This complexity can lead to overfitting, as the algorithm may struggle to find the global minimum during the optimization process, often settling for local minima, resulting in the observed deviations. Additional treatments are, therefore, necessary to improve the results in order to make them more significant. Figure 6, on the left, plots, in red again, the Angstrom exponent , which is poorly estimated with the fitting method using the CPCR2 model and, in black, the AERONET measurements of .
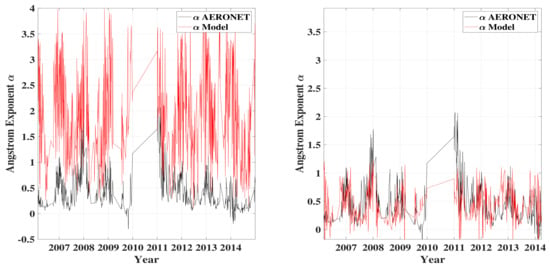
Figure 6.
(Left): Angstrom exponent measured by AERONET (black line) superposed to that estimated from radiometric data using the model CPCR2 (red line). (Right): the same plot with obtained with the model predicted with RNN (red line).
Figure 6, on the right, shows the same parameters but with obtained from the model predicted with RNN using estimated from the CPCR2 model (red line). We can clearly see a notable improvement in the values of this estimated parameter. Indeed, the predicted Angstrom exponent follows the same trend as AERONET measurements, with a calculated correlation factor (R) of 0.60.
4. Discussion
This section will discuss the results obtained in comparison with AERONET measurements as well as other aerosol parameters derived from them (AOD and types).
4.1. Comparison of and Obtained from Radiometric and AERONET Measurements
The monthly variations of the Angstrom coefficient obtained at Tamanrasset from AERONET and from radiometric measurements with the two selected models CPCR2 and REST2 are shown in Figure 7. We note that the monthly curves obtained from the models are very similar to each other, as expected, and also to that of AERONET. They have the same trend throughout the year, with maximum values in June. A similar result had already been obtained in a previous study on turbidity in Tamanrasset covering the same period [9]. The explanation put forward for the peak of aerosols observed in June is the winds coming from the southern sectors (Sirocco) during the summer season that characterizes the Sahara of North Africa. Indeed, this kind of wind brings particles of dust and sand with it, which increases the Angstrom coefficient [9]. Seasonal variations of the Angstrom coefficient can be explained by high temperatures in June in Tamanrasset (around 30 °C) combined with low values of humidity (around 10%) and also the presence of dust storms during that month.
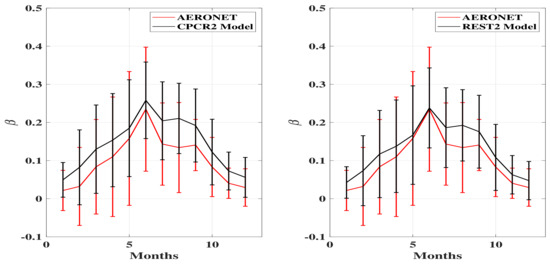
Figure 7.
Monthly average of estimated Angstrom coefficients () for the period 2005–2014 superposed to those obtained from AERONET.
Concerning the Angstrom exponent, the use of the RNN algorithm has allowed a clear improvement in the estimation of this parameter (see Section 3.2). However, discrepancies between the estimated and measured values were still observed, which required the improvement of the RNN model. So, the strategy adopted for this was to take data selection windows of 1 or 2 years in order to carry out the training. The final result was then the concatenation of the outputs of all the models created over each of the selected periods. Figure 8 shows the results when using 1- (left) and 2-year periods (right) in the AERONET dataset to perform the training of the used model. We note that the results obtained were more consistent than those presented in the right plot of Figure 6. Indeed, the variations of the extremum values of are clearly visible, unlike the previous results, when the training was carried out using the entire dataset. A better correlation factor R between alpha estimates and AERONET measurements is observed, reaching 0.66 using the 1-year selection window and 0.69 for 2 years (Figure 9).
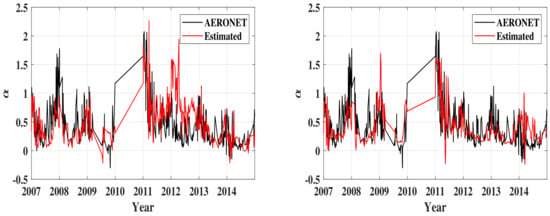
Figure 8.
Predicted Angstrom exponent using 1- (left) and 2-year (right) periods in AERONET dataset for training.
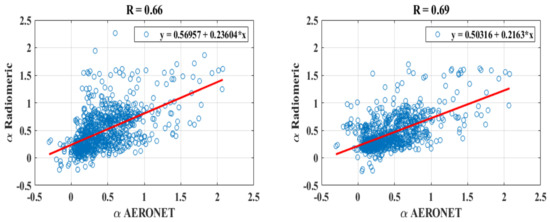
Figure 9.
Regression of estimated with the measured one when using 1 (left) and 2 (right) years of AERONET data in training.
4.2. Estimation of Aerosol Optical Depth ()
The spectral AOD was calculated with the Angstrom relation (Equation (1)) and the parameters and obtained with the CPCR2-RNN models using direct solar radiation. The wavelengths 0.870 µm, 0.675 µm, 0.500 µm, and 0.440 µm of AERONET were used in Equation (1). The results obtained were then compared to the AOD measurements made with AERONET. Figure 10 shows the daily variation of obtained from the CPCR2-RNN models at the selected wavelengths superimposed on the spectral AOD measurements of AERONET.
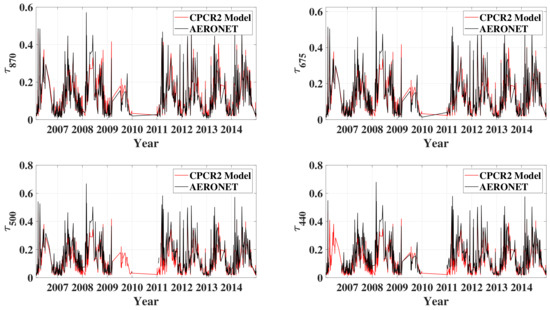
Figure 10.
AOD estimated using direct solar radiation (red) superimposed to AERONET measurements (black) for each AERONET wavelength.
We see, in this figure, that all the curves have the same trend regardless of the wavelength, as also clearly shown in Figure 11 with the regression lines plotted in the scatter plot of the AOD estimated with the CPCR2-RNN models for the selected wavelengths versus measurements made with AERONET. These regression lines then allow us to calculate the statistical errors and the correlation factors R for each wavelength (see Table 4). We can see that it is at 0.870 µm that the estimated AOD and that measured with AERONET are the closest compared to the other wavelengths. Indeed, we obtain RMSE = 0.05, MAPE = 0.36, and MBE = 0.02 for the wavelength of 0.870 µm with a strong correlation R of 0.95 between the estimates and the measurements.
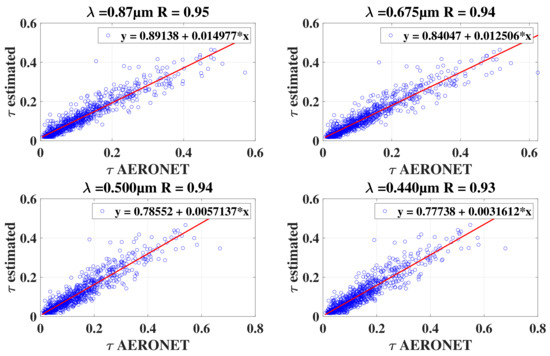
Figure 11.
AOD estimated from the CPCR2-RNN models using direct solar radiation versus measured with AERONET: the regression lines (red) allow the calculation of statistical errors and the correlation factor R.

Table 4.
Statistical error between estimated and obtained from AERONET.
Radiometric measurements are obtained from the integration of solar radiation over the large part of the solar spectrum permitted by the instrument. The aerosol parameters deduced from the models are, therefore, primarily linked to a broad spectral range. It therefore makes sense to calculate the Broadband Aerosol Optical Depth, i.e., the BAOD. Gueymard (1998) [40] developed a model to calculate this parameter but it was obtained here by integrating the AOD spectral data on the part of the solar spectrum in which they were acquired or calculated. In this case, BAOD was calculated by applying a numerical integration technique of the AOD values over the spectral range from 440 to 870 nm. This consisted of using a mathematical method to estimate the area under the curve of the AOD values measured at different wavelengths in this range. AOD spectral data from AERONET and their estimates obtained with the CPCR2-RNN models and the Angstrom relationship were thus used for this purpose. Figure 12, on the left, shows the temporal variation of BAOD obtained from the CPCR2-RNN models (red line) and AERONET (black line). The curves are very similar, as confirmed by Figure 12, on the right, showing a strong correlation between the two BAODs (R = 0.93). Statistical errors given in Table 4 also consolidate the BAOD calculation obtained by spectral integration. However, as before for the AOD spectral study, we also find that BAODs obtained from radiometric measurements are very close to the AODs measured with AERONET at 0.870 µm with the same very strong correlation (R = 0.95).
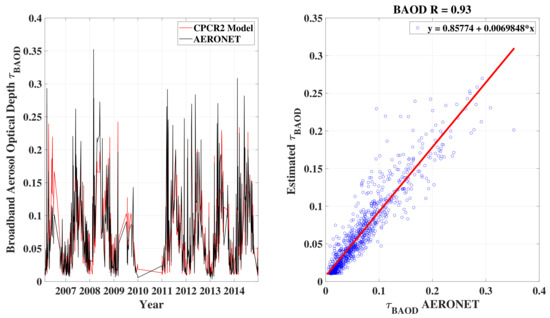
Figure 12.
(Left): estimated BAOD obtained from direct solar radiation measurements (red) superposed to that from AERONET (black). (Right): correlation between estimated with CPCR2 model using radiometric measurements and from AERONET.
4.3. Aerosol Types in Tamanrasset Region
Four main types of aerosols can be classified in the atmosphere, namely biomass-burning aerosols, urban aerosols, maritime aerosols, and dust aerosols (see Section 1). The most commonly used method to discriminate them is based on the relationship between the values of the AOD and the Angstrom exponent . Dust aerosols exhibit the characteristic of high in longer wavelengths due to low values of , which is then very useful in identifying this type. Unlike dust aerosols, urban and biomass-burning aerosols are better identified by short wavelengths. According to the frequency distribution of , a threshold value is usually chosen to separate coarse and fine aerosols. Many studies in the literature have used different thresholds of versus for the cluster analysis approach, as shown in Table 5 [17,23,24,25,41,42,43,44].

Table 5.
Thresholds for aerosol cluster analysis.
The Angstrom exponent as a function of the Aerosol Optical Depth is shown in Figure 13. We have calculated from the data in Figure 13, on the left, which correspond to the entire period studied, that the presence of maritime, dust, and mixed aerosols represents, respectively, 31.21%, 3.25%, and 65.54%. The same types of aerosols were identified using the AERONET data (Figure 13 on the right), which give, respectively, 34.33%, 3.01%, and 62.66% of maritime, dust, and mixed aerosols. These aerosol percentages are very similar to those obtained from radiometric data.
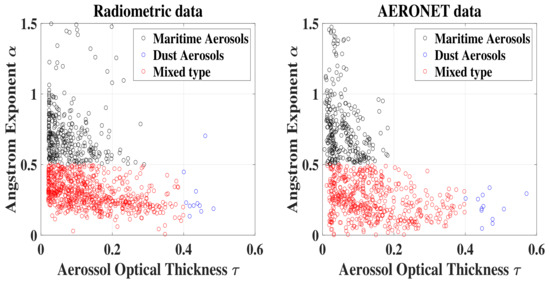
Figure 13.
Identification of aerosol types in Tamanrasset.
Figure 14, on the top, shows the monthly occurrences of the different aerosol types (maritime, dust, and mixed) found over the period from 2006 to 2014 from radiometric data (left) and AERONET (right). We see that the two bar graphs are also very similar. The aerosols detected are the same but with some differences in the percentiles, probably due to the different number of samples in the month. The seasonal occurrences were, therefore, calculated and present a greater similarity, as shown at the bottom of Figure 14. This bar graph shows that mixed aerosols are present during all seasons but have a slightly lower occurrence in the winter (DJF). In contrast, maritime aerosols are more important but decrease during the other seasons to reach their minimum in the summer (JJA). Dust aerosols start their appearance in February to be mainly present in the spring (MAM) and summer (JJA), then disappear in September. Table 6 summarizes the seasonal occurrences of the different aerosol types obtained from radiometric and AERONET data.
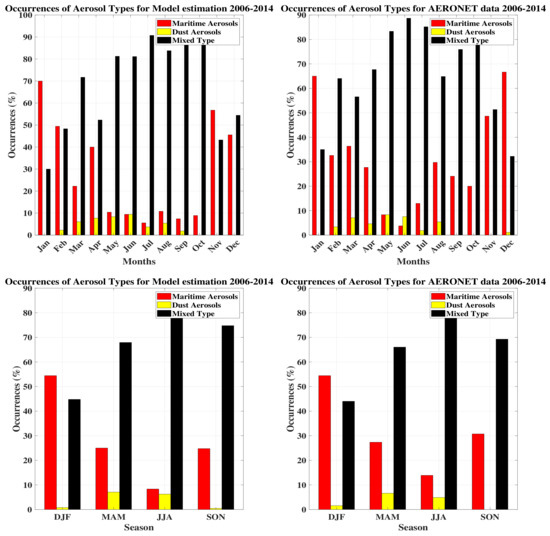
Figure 14.
Monthly (top) and seasonal (bottom) occurrences of identified aerosol types in Tamanrasset.

Table 6.
Seasonal percentiles of each aerosol type.
5. Conclusions
This article dealt with the estimation of aerosol parameters (Angstrom coefficient , Angstrom exponent , and Aerosol Optical Depth AOD ) in cloudless conditions using clear-sky models and ground measurements of direct solar radiation. The radiometric measurements used were those collected in Tamanrasset, in southern Algeria, during the period from 2005 to 2014. AERONET measurements carried out on the same site were used for comparison and validation purposes. The Tamanrasset radiometric measurements were first processed by considering eleven clear-sky models to estimate the aerosol parameters on which they depend, mainly and . A least-squares fitting method was used to find the best-suited model to approximate the solar radiation measurements. The best estimate of the two parameters and was then used to calculate the spectral and Broadband Aerosol Optical Depth using the Angstrom relationship.
The study first focused on the estimation of the Angstrom coefficient considering the 11 models and the direct solar radiation measurements. The best estimation of this parameter was obtained with the REST2 or CPCR2 models with, respectively, 0.04 and 0.03 for RMSE and 0.91 and 0.95 for the correlation factor R. Moreover, the monthly variation of plotted throughout the year showed a maximum value in June, which is consistent with AERONET data and the result found in a previous study on turbidity in Tamanrasset covering the same period [9].
The second step of this work then continued with the estimation of the Angstrom exponent . The results were not conclusive with the method of fitting the model to the data when the comparison was made with the AERONET data, even in the case of using the best models that provided the best estimate for . There was just a weak correlation with the AERONET measurements, which did not exceed 0.38 at best. A complement to the fitting method was, therefore, necessary. This led us to employ and exploit an unsupervised predicted algorithm, namely the Recurrent Neural Network (RNN). The model predicted with RNN used the Angstrom coefficient as input and the Angstrom exponent as output. The results obtained revealed that the predicted Angstrom exponent was more conclusive with a correlation R of 0.69 with AERONET data.
The spectral AOD was then calculated using the Angstrom relation and the values estimated with the CPCR2 model and the RNN complement. The Angstrom parameters used showed good consistency of the estimated spectral AOD with AERONET measurements taken at different wavelengths. The closest coherence was obtained at the wavelength 0.870 µm, at which low statistical errors (RMSE = 0.05, MAPE = 0.36, and MBE = 0.02) were observed with a strong correlation (R = 0.95). The radiometric observations were performed over a wide spectral range, so the integration of the spectral AOD data was calculated to estimate the Broadband Aerosol Optical Depth, the BAOD. A strong correlation between data obtained from CPCR2-RNN models and AERONET measurements was also found (), confirming the reliability of these models for estimating aerosols’ optical properties. However, we found, as for the spectral AOD, that BAODs obtained from the radiometric measurements were very close to the AODs measured with AERONET at 0.870 µm, with the same very strong correlation (R = 0.95).
Finally, a classification of aerosol types was carried out from the estimated parameters ( and ) and those measured by the AERONET photometer. We observed in Tamanrasset the presence of maritime, dust, and mixed aerosols, both with radiometric data or AERONET. We found that mixed aerosols are present during all seasons, but with a slightly lower occurrence in the winter (DJF), when maritime aerosols are predominant but decrease with the other seasons to reach a minimum in the summer (JJA). Dust aerosols begin their appearance in February to be mainly present in the spring (MAM) and summer (JJA), then disappear in September.
Author Contributions
Methodology, M.Z. and A.I.; validation, M.Z., A.I. and J.D.; formal analysis, M.Z.; investigation, M.Z., A.I. and J.D.; resources, M.Z.; data curation, M.Z.; writing—original draft preparation, M.Z.; writing—review and editing, A.I.; supervision, A.I.; funding acquisition, A.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The AERONET data used in this study are available at http://aeronet.gsfc.nasa.gov (accessed on 14 January 2024). The MODIS products used in this work are available at https://earthdata.nasa.gov/ (accessed on 3 November 2023). For the meteorological and solar radiation data, the authors were unable to find a valid data repository for the data used in this study. The data are available at the Regional Meteorological Center (Direction météo Régional Sud, Office National de la Météorologie, ONM, Algeria).
Acknowledgments
The authors thank URAER and LATMOS (CNRS) for their support, which made this publication possible, as well as ONM of Tamanrasset for providing the data used in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Iqbal, M. Chapter 6—Solar Spectral Radiation Under Cloudless Skies. In An Introduction to Solar Radiation; Academic Press: Cambridge, MA, USA, 1983; pp. 107–168. [Google Scholar] [CrossRef]
- Bilbao, J. Global, Diffuse, Direct, and Ultraviolet Solar Irradiance Recorded in Malta and Atmospheric Component Influences. Energy Procedia 2014, 57, 1206–1210. [Google Scholar] [CrossRef]
- Li, X.; Mauzerall, D.L.; Bergin, M.H. Global reduction of solar power generation efficiency due to aerosols and panel soiling. Nat. Sustain. 2020, 3, 720–727. [Google Scholar] [CrossRef]
- Xun, L.; Lu, H.; Qian, C.; Zhang, Y.; Lyu, S.; Li, X. Analysis of Aerosol Optical Depth from Sun Photometer at Shouxian, China. Atmosphere 2021, 12, 1226. [Google Scholar] [CrossRef]
- Zheng, Y.; Che, H.; Xia, X.; Wang, Y.; Yang, L.; Chen, J.; Wang, H.; Zhao, H.; Li, L.; Zhang, L.; et al. Aerosol optical properties and its type classification based on multiyear joint observation campaign in north China plain megalopolis. Chemosphere 2021, 273, 128560. [Google Scholar] [CrossRef]
- Liu, J.; Guo, Z.; Zhou, L.; Wang, L.; Wang, J.; Yan, Q.; Hua, D. Inversion and analysis of aerosol optical properties and lidar ratios based on sky-radiometer and Raman lidar measurements in Xi’an, China. Front. Environ. Sci. 2022, 10, 1039559. [Google Scholar] [CrossRef]
- Ji, H.; Zhang, Y.; Chen, S.; Chen, H.; Guo, P. Aerosol characteristics inversion based on the improved lidar ratio profile with the ground-based rotational Raman–Mie lidar. Opt. Commun. 2018, 416, 54–60. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Psiloglou, B.E. Climatology of the Linke and Unsworth–Monteith Turbidity Parameters for Greece: Introduction to the Notion of a Typical Atmospheric Turbidity Year. Appl. Sci. 2020, 10, 4043. [Google Scholar] [CrossRef]
- Zaiani, M.; Irbah, A.; Djafer, D.; Listowski, C.; Delanoe, J.; Kaskaoutis, D.; Boualit, S.B.; Chouireb, F.; Mimouni, M. Study of Atmospheric Turbidity in a Northern Tropical Region Using Models and Measurements of Global Solar Radiation. Remote Sens. 2021, 13, 2271. [Google Scholar] [CrossRef]
- Ångström, A. Techniques of Determinig the Turbidity of the Atmosphere. Tellus 1961, 13, 214–223. [Google Scholar] [CrossRef]
- Grenier, J.C.; De La Casinière, A.; Cabot, T. A spectral model of Linke’s turbidity factor and its experimental implications. Solar Energy 1994, 52, 303–313. [Google Scholar] [CrossRef]
- Louche, A.; Maurel, M.; Simonnot, G.; Peri, G.; Iqbal, M. Determination of Ångström’s turbidity coefficient from direct total solar irradiance measurements. Solar Energy 1987, 38, 89–96. [Google Scholar] [CrossRef]
- Pinazo, J.M.; Cañada, J.; Boscá, J.V. A new method to determine Ångström’s turbidity coefficient: Its application for Valencia. Solar Energy 1995, 54, 219–226. [Google Scholar] [CrossRef]
- Toledano, C.; Cachorro, V.E.; Berjon, A.; de Frutos, A.M.; Sorribas, M.; de la Morena, B.A.; Goloub, P. Aerosol optical depth and Ångström exponent climatology at El Arenosillo AERONET site (Huelva, Spain). Q. J. R. Meteorol. Soc. 2007, 133, 795–807. [Google Scholar] [CrossRef]
- Basart, S.; Pérez, C.; Cuevas, E.; Baldasano, J.M.; Gobbi, G.P. Aerosol characterization in Northern Africa, Northeastern Atlantic, Mediterranean Basin and Middle East from direct-sun AERONET observations. Atmos. Chem. Phys. 2009, 9, 8265–8282. [Google Scholar] [CrossRef]
- Kaskaoutis, D.G.; Kambezidis, H.D.; Hatzianastassiou, N.; Kosmopoulos, P.G.; Badarinath, K.V.S. Aerosol climatology: Dependence of the Angstrom exponent on wavelength over four AERONET sites. Atmos. Chem. Phys. Discuss. 2007, 7, 7347–7397. [Google Scholar] [CrossRef]
- Khademi, F.; Bayat, A. Classification of aerosol types using AERONET version 3 data over Kuwait City. Atmos. Environ. 2021, 265, 118716. [Google Scholar] [CrossRef]
- Raptis, I.P.; Kazadzis, S.; Amiridis, V.; Gkikas, A.; Gerasopoulos, E.; Mihalopoulos, N. A Decade of Aerosol Optical Properties Measurements over Athens, Greece. Atmosphere 2020, 11, 154. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J.; Song, C.H.; Kim, S.B.; Chun, Y.; Sohn, B.J.; Holben, B.N. Characteristics of aerosol types from AERONET sunphotometer measurements. Atmos. Environ. 2010, 44, 3110–3117. [Google Scholar] [CrossRef]
- Giles, D.; Holben, B.; Tripathi, S.; Eck, T.; Newcomb, W.; Slutsker, I.; Dickerson, R.; Thompson, A.; Mattoo, S.; Wang, S.H.; et al. Aerosol Properties Over the Indo-Gangetic Plain: A Mesoscale Perspective from the TIGERZ Experiment. J. Geophys. Res. Atmos. 2011, 116, D18203. [Google Scholar] [CrossRef]
- Ichoku, C.; Kaufman, Y.J.; Remer, L.A.; Levy, R. Global aerosol remote sensing from MODIS. Adv. Space Res. 2004, 34, 820–827. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Kaskaoutis, D.G. Aerosol climatology over four AERONET sites: An overview. Atmos. Environ. 2008, 42, 1892–1906. [Google Scholar] [CrossRef]
- B.AL-Taie, K.; Rajab, J.M.; Al-Salihi, A.M. Climatology and classification of aerosols based on optical properties over selected stations in Iraq. In Proceedings of the International Conference of Numerical Analysis and Applied Mathematics ICNAAM 2019, Rhodes, Greece, 23–28 September 2020; p. 050041. [Google Scholar] [CrossRef]
- Kumar, K.R.; Kang, N.; Yin, Y. Classification of key aerosol types and their frequency distributions based on satellite remote sensing data at an industrially polluted city in the Yangtze River Delta, China. Int. J. Climatol. 2018, 38, 320–336. [Google Scholar] [CrossRef]
- Pawar, G.V.; Devara, P.C.S.; Aher, G.R. Identification of aerosol types over an urban site based on air-mass trajectory classification. Atmos. Res. 2015, 164–165, 142–155. [Google Scholar] [CrossRef]
- Zaiani, M.; Djafer, D.; Chouireb, F.; Irbah, A.; Hamidia, M. New method for clear day selection based on normalized least mean square algorithm. Theor. Appl. Climatol. 2020, 139, 1505–1512. [Google Scholar] [CrossRef]
- Sun, X.; Bright, J.M.; Gueymard, C.A.; Bai, X.; Acord, B.; Wang, P. Worldwide performance assessment of 95 direct and diffuse clear-sky irradiance models using principal component analysis. Renew. Sustain. Energy Rev. 2021, 135, 110087. [Google Scholar] [CrossRef]
- Sun, X.; Bright, J.M.; Gueymard, C.A.; Acord, B.; Wang, P.; Engerer, N.A. Worldwide performance assessment of 75 global clear-sky irradiance models using Principal Component Analysis. Renew. Sustain. Energy Rev. 2019, 111, 550–570. [Google Scholar] [CrossRef]
- Antonanzas-Torres, F.; Urraca, R.; Polo, J.; Perpiñán-Lamigueiro, O.; Escobar, R. Clear sky solar irradiance models: A review of seventy models. Renew. Sustain. Energy Rev. 2019, 107, 374–387. [Google Scholar] [CrossRef]
- Gueymard, C.A. Clear-sky irradiance predictions for solar resource mapping and large-scale applications: Improved validation methodology and detailed performance analysis of 18 broadband radiative models. Solar Energy 2012, 86, 2145–2169. [Google Scholar] [CrossRef]
- Bashahu, M.; Laplaze, D. An atmospheric model for computing solar radiation. Renew. Energy 1994, 4, 455–458. [Google Scholar] [CrossRef]
- Ideriah, F.J.K. A model for calculating direct and diffuse solar radiation. Solar Energy 1981, 26, 447–452. [Google Scholar] [CrossRef]
- Dai, Q.; Fang, X. A simple model to predict solar radiation under clear sky conditions. Adv. Space Res. 2014, 53, 1239–1245. [Google Scholar] [CrossRef]
- Janjai, S.; Sricharoen, K.; Pattarapanitchai, S. Semi-empirical models for the estimation of clear sky solar global and direct normal irradiances in the tropics. Appl. Energy 2011, 88, 4749–4755. [Google Scholar] [CrossRef]
- Davies, J.A.; McKay, D.C. Estimating solar irradiance and components. Solar Energy 1982, 29, 55–64. [Google Scholar] [CrossRef]
- Bird, R.; Hulstrom, R. A Simplified Clear Sky Model for Direct and Diffuse Insolation on Horizontal Surfaces; SERI/TR-642-761; Solar Energy Research Institute (Now NREL): Golden, CO, USA, 1981; p. 46. [Google Scholar]
- Iqbal, M. Chapter 7—Total Broadband Radiation Under Cloudless Skies. In An Introduction to Solar Radiation; Academic Press: Cambridge, MA, USA, 1983; pp. 169–213. [Google Scholar] [CrossRef]
- Gueymard, C. REST2: High-performance solar radiation model for cloudless-sky irradiance, illuminance, and photosynthetically active radiation—Validation with a benchmark dataset. Solar Energy 2008, 82, 272–285. [Google Scholar] [CrossRef]
- Zaiani, M.; Djafer, D. New Approach to Establish a Clear Sky Global Solar Irradiance Model. Int. J. Renew. Energy Res. 2017, 7, 1454–1462. [Google Scholar]
- Gueymard, C.A. Turbidity Determination from Broadband Irradiance Measurements: A Detailed Multicoefficient Approach. J. Appl. Meteorol. Climatol. 1998, 37, 414–435. [Google Scholar] [CrossRef]
- Chen, Q.X.; Yuan, Y.; Shuai, Y.; Tan, H.P. Graphical aerosol classification method using aerosol relative optical depth. Atmos. Environ. 2016, 135, 84–91. [Google Scholar] [CrossRef]
- Pathak, B.; Bhuyan, P.K.; Gogoi, M.; Bhuyan, K. Seasonal heterogeneity in aerosol types over Dibrugarh-North-Eastern India. Atmos. Environ. 2012, 47, 307–315. [Google Scholar] [CrossRef]
- Ali, M.A.; Nichol, J.E.; Bilal, M.; Qiu, Z.; Mazhar, U.; Wahiduzzaman, M.; Almazroui, M.; Islam, M.N. Classification of aerosols over Saudi Arabia from 2004 to 2016. Atmos. Environ. 2020, 241, 117785. [Google Scholar] [CrossRef]
- Sabetghadam, S.; Alizadeh, O.; Khoshsima, M.; Pierleoni, A. Aerosol properties, trends and classification of key types over the Middle East from satellite-derived atmospheric optical data. Atmos. Environ. 2021, 246, 118100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).