Comparative Study on the Vertical Column Concentration Inversion Algorithm of Tropospheric Trace Gas Based on the MAX-DOAS Measurement Spectrum
Abstract
1. Introduction
2. Processing of Spectral Data
3. Inversion Algorithm
3.1. Geometric Method (Geometric)
3.2. Simplified Model Method (Model)
3.3. Look-Up Table Method (Table)
4. Results and Discussion
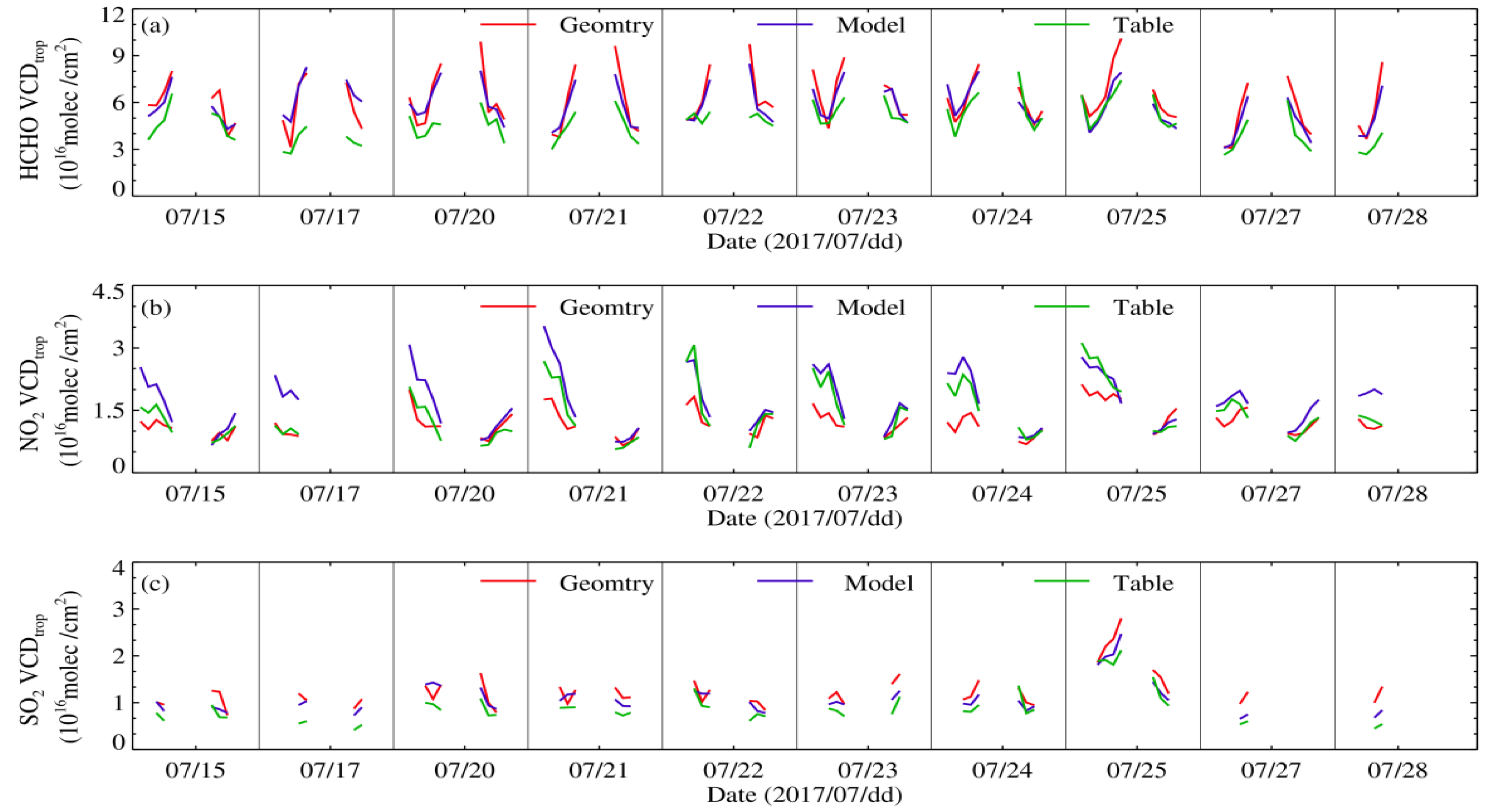
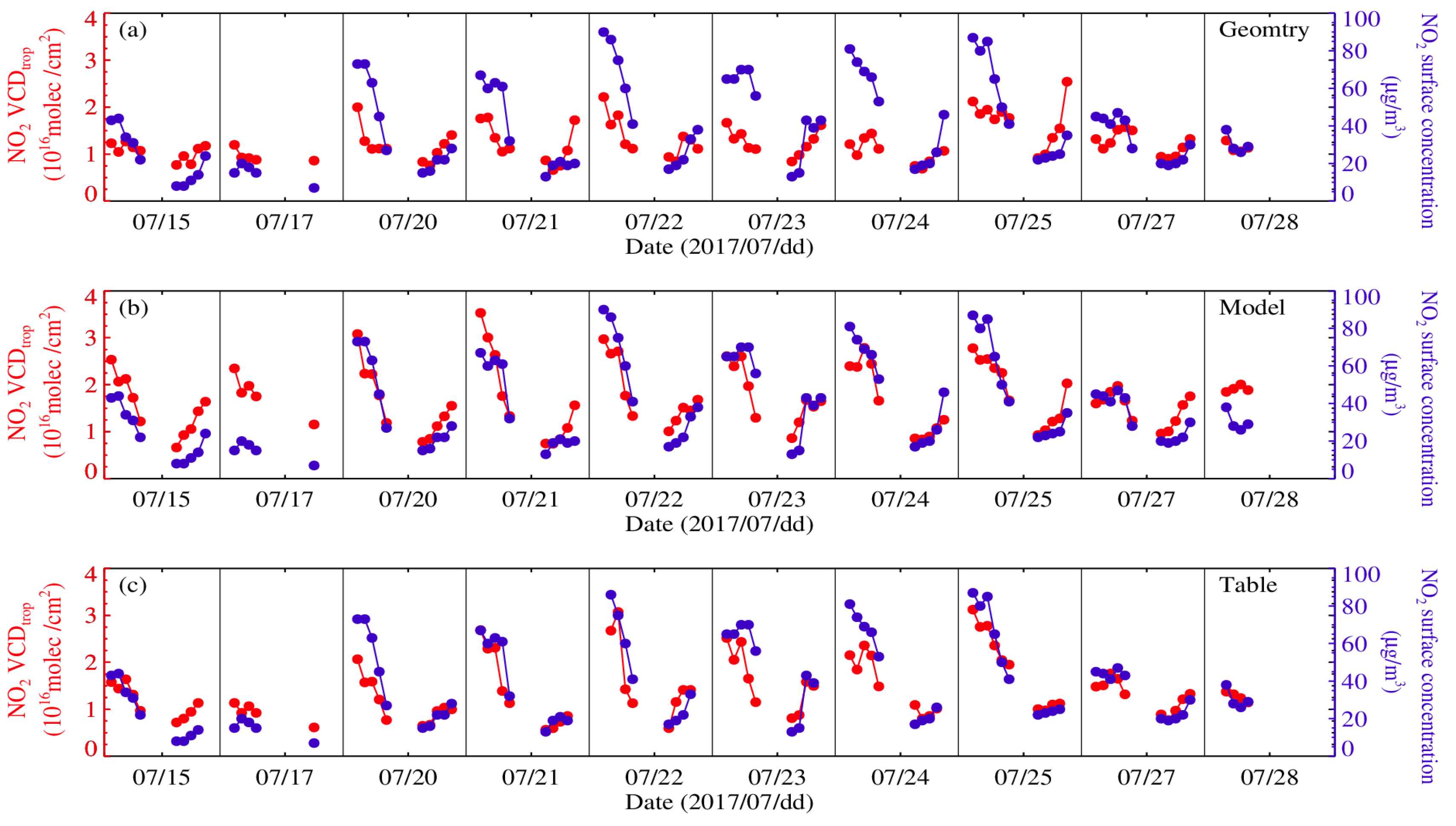
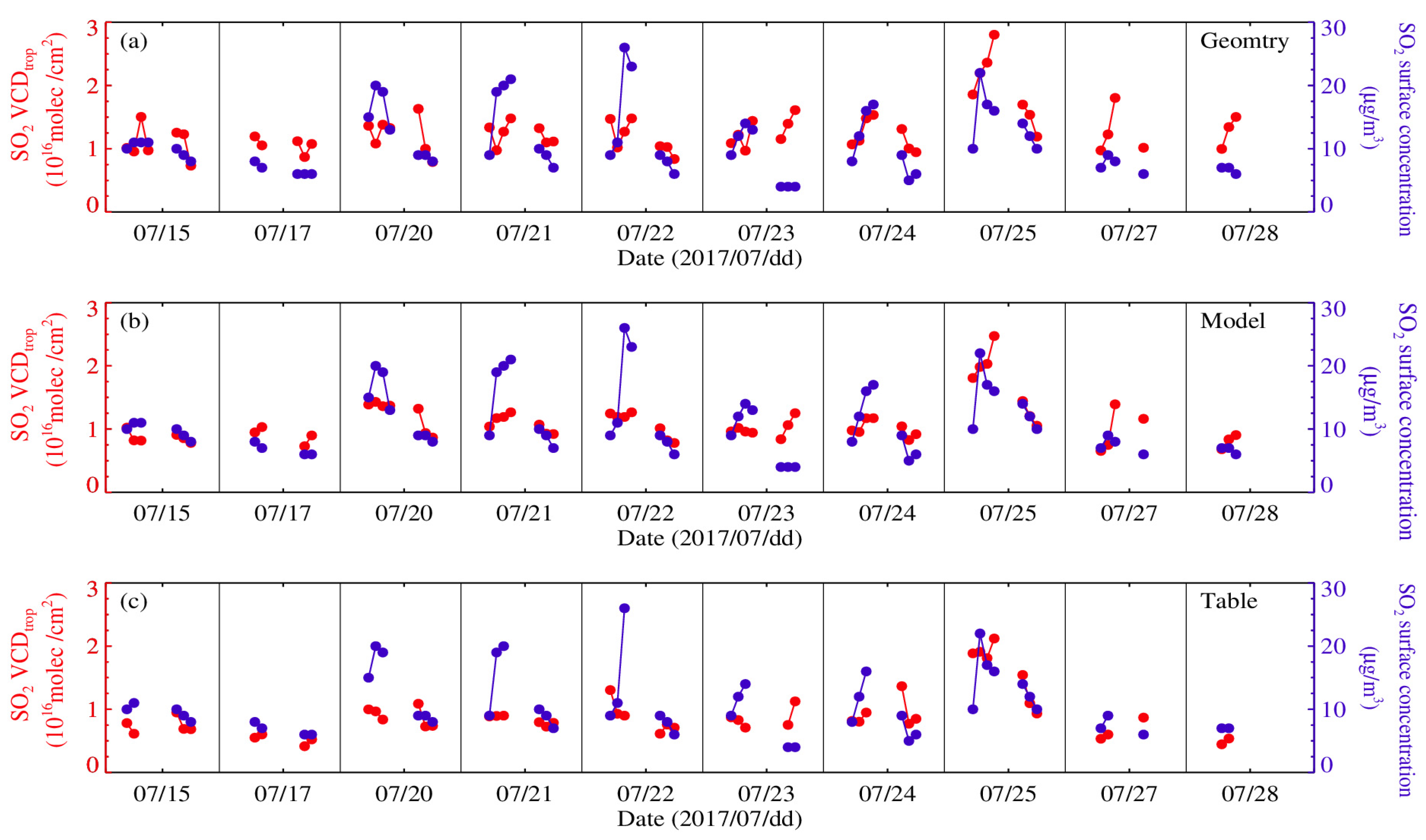
4.1. The Diurnal Variation of Column Concentration
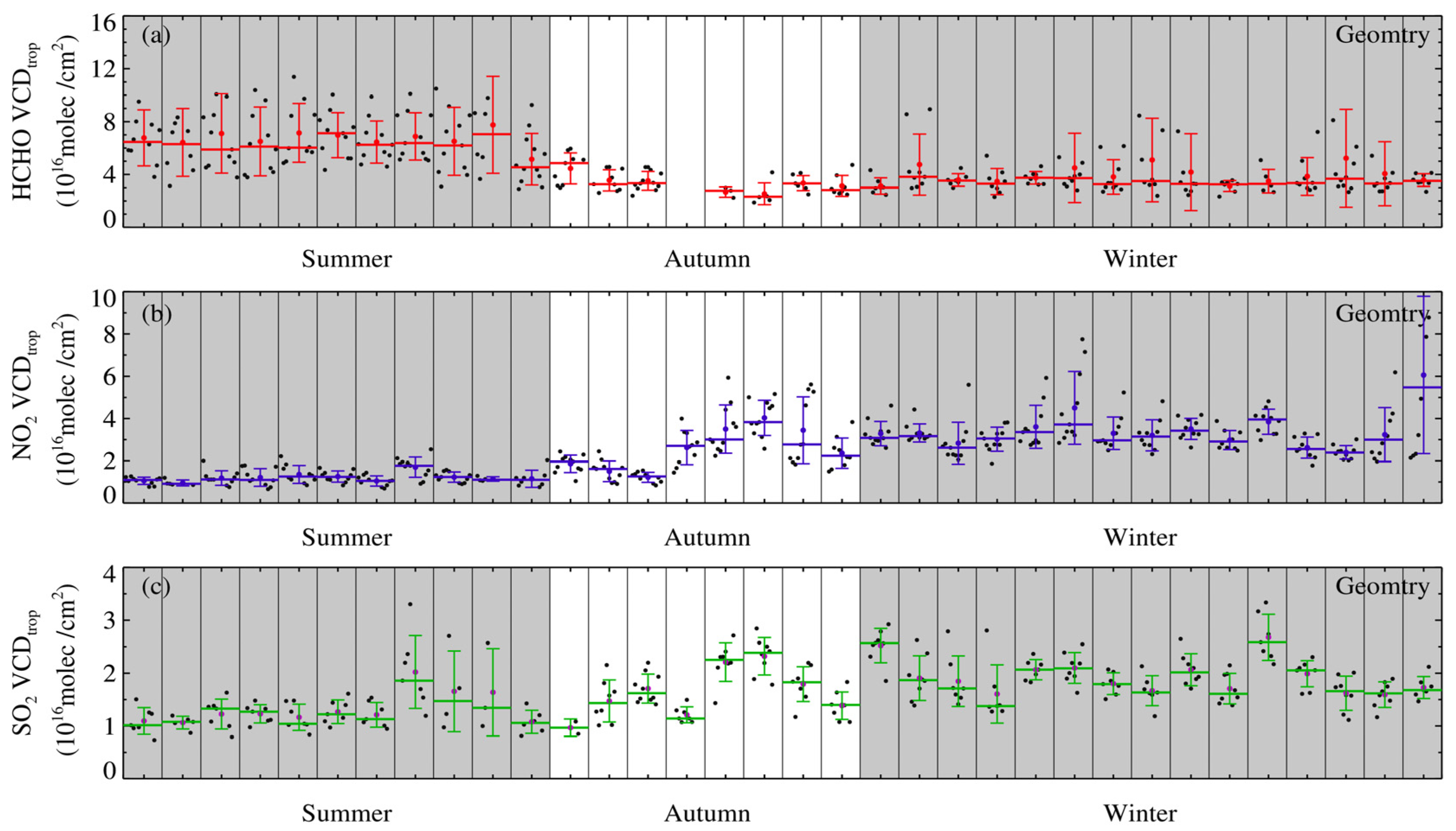
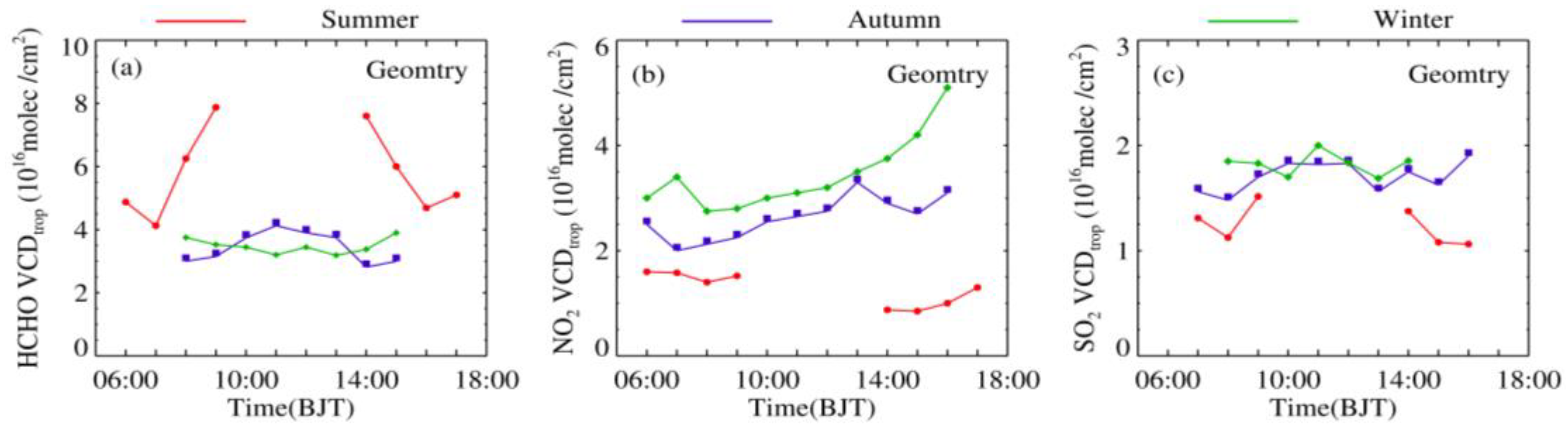
4.2. Seasonal Variation of Column Concentration
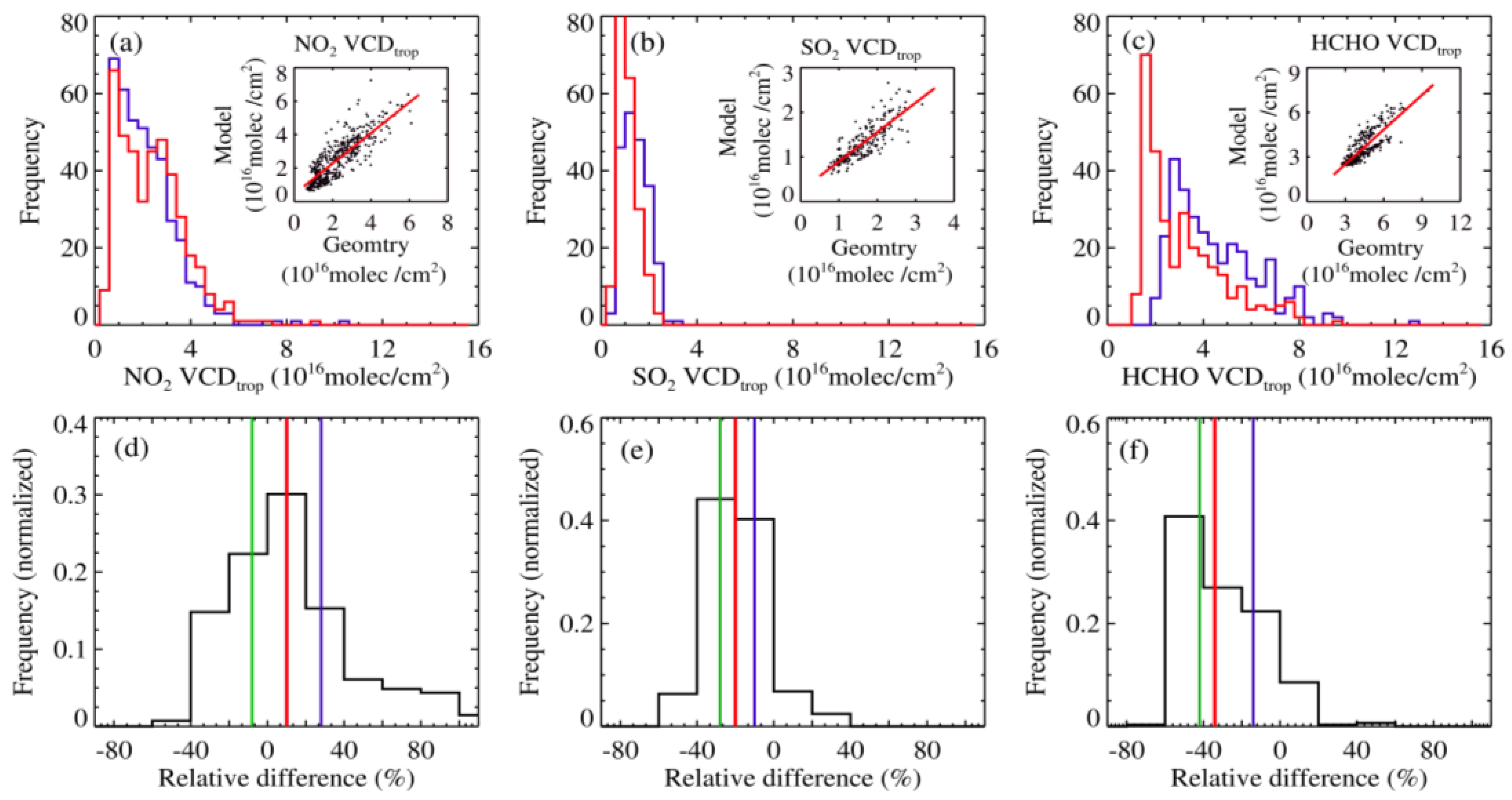
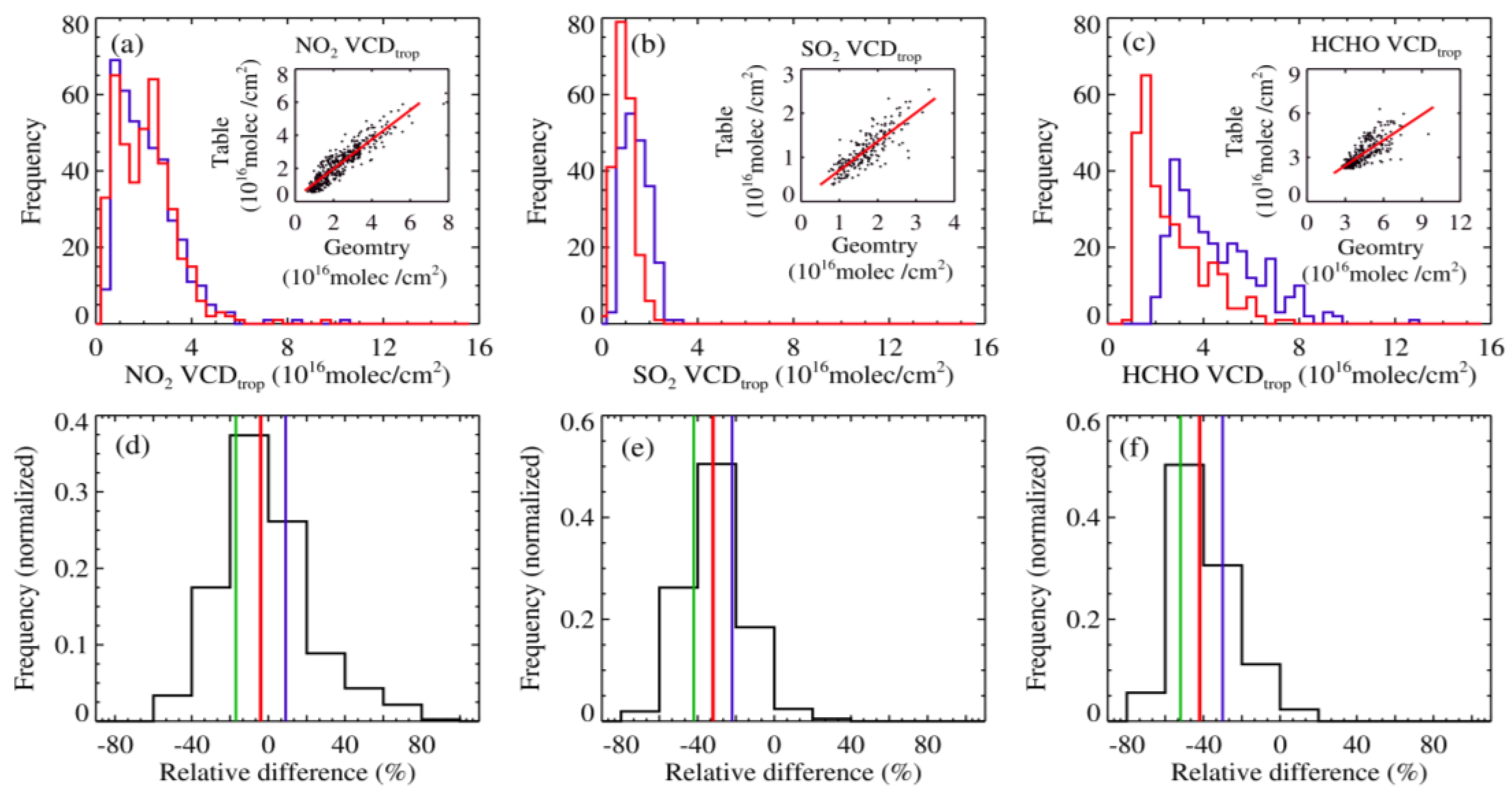
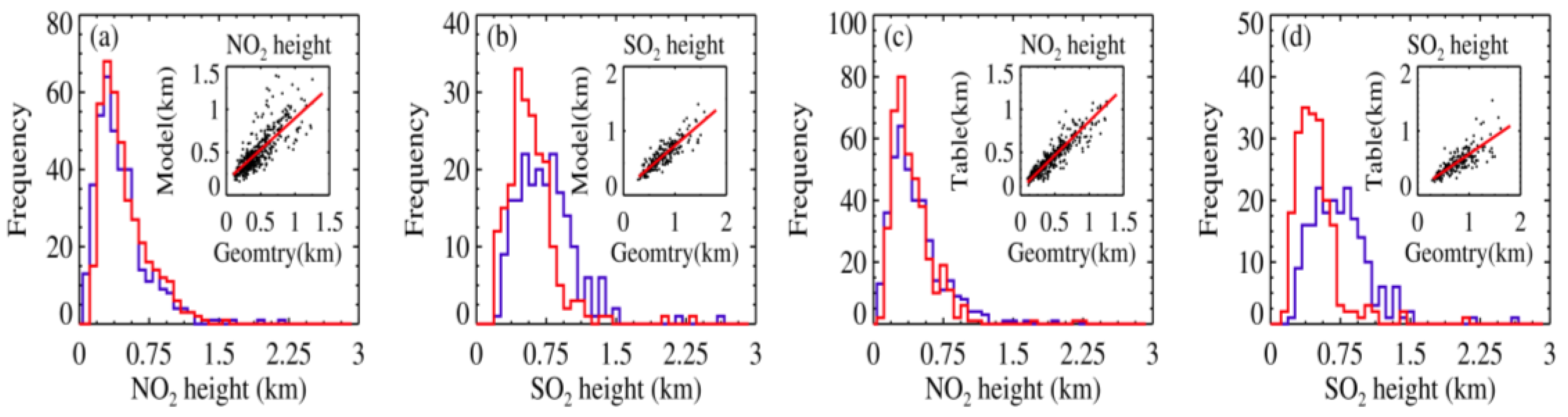
4.3. Statistic and Analysis
4.3.1. Variation in Relative Differences
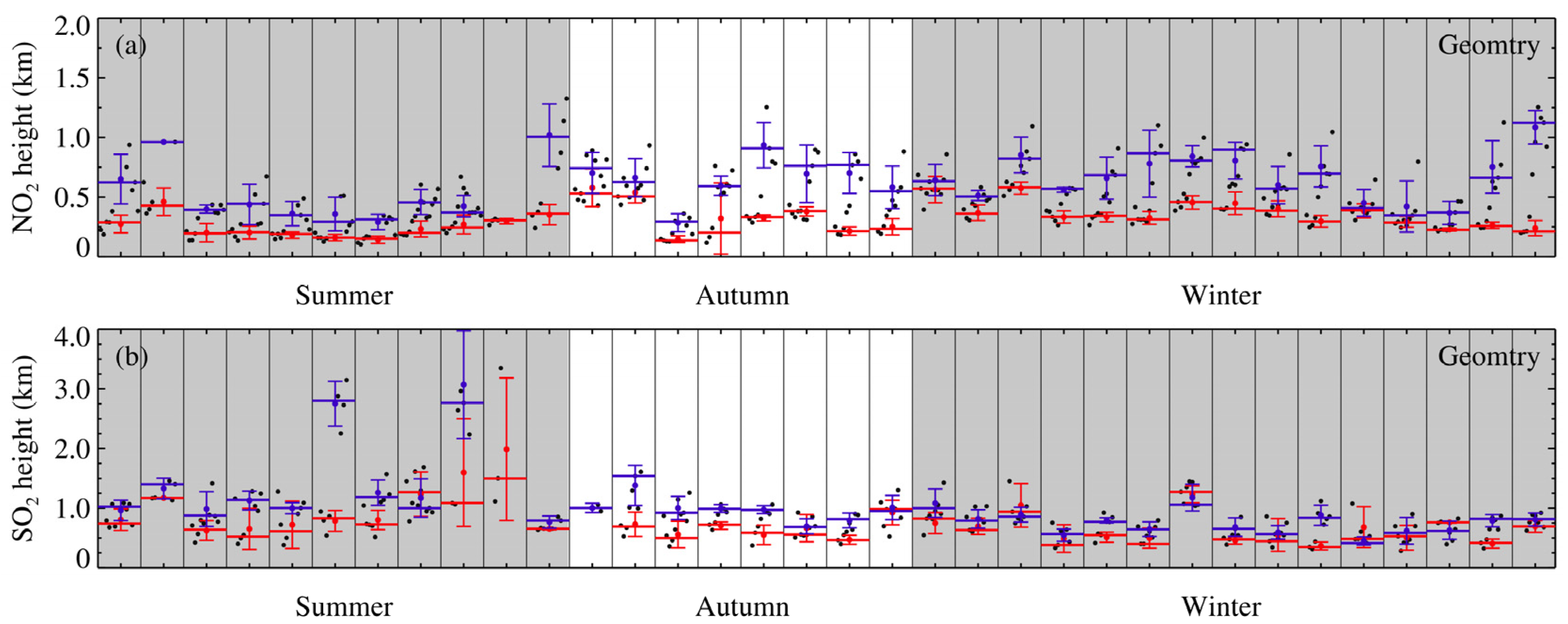
4.3.2. The Variation of Distribution Height
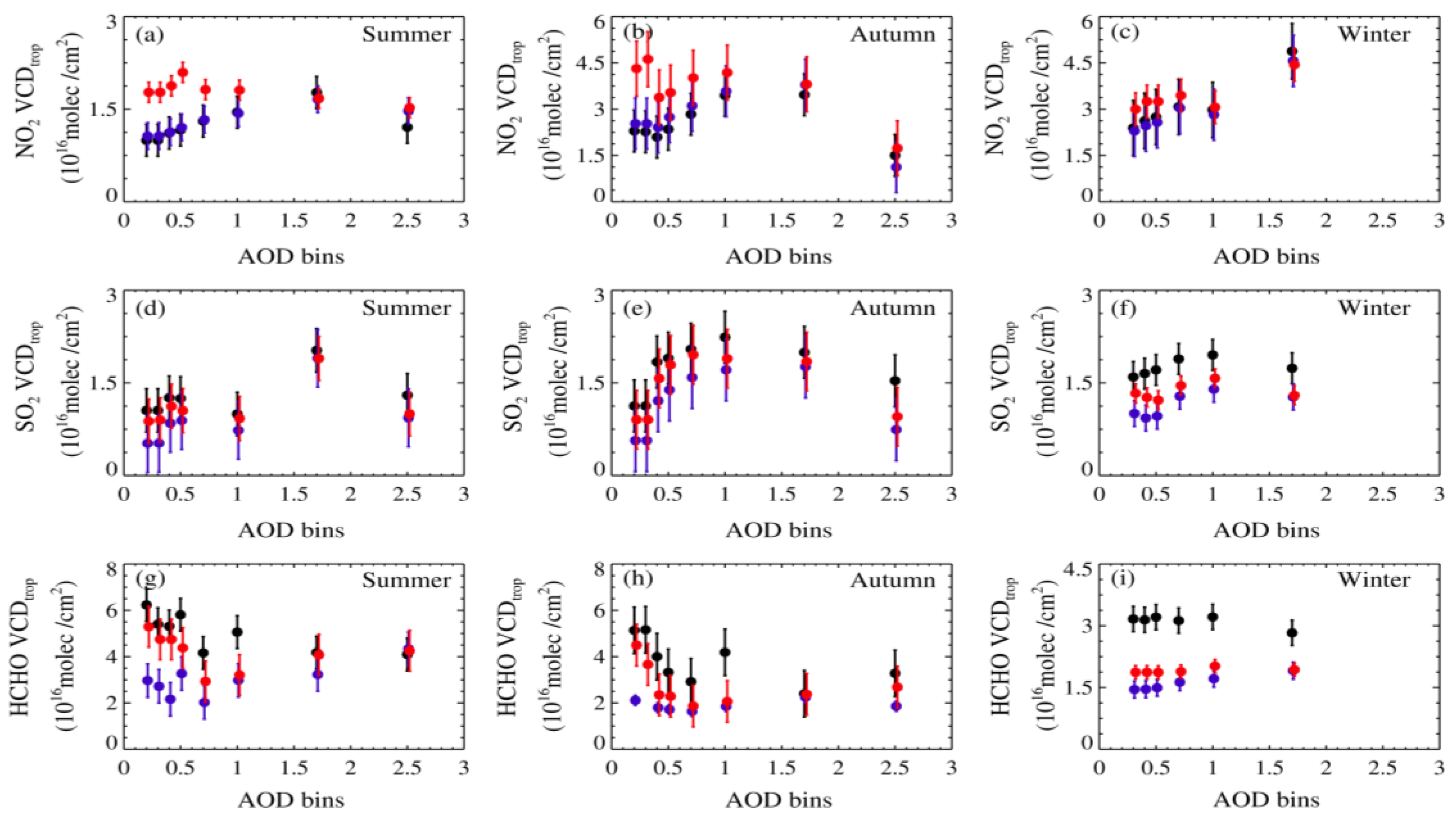
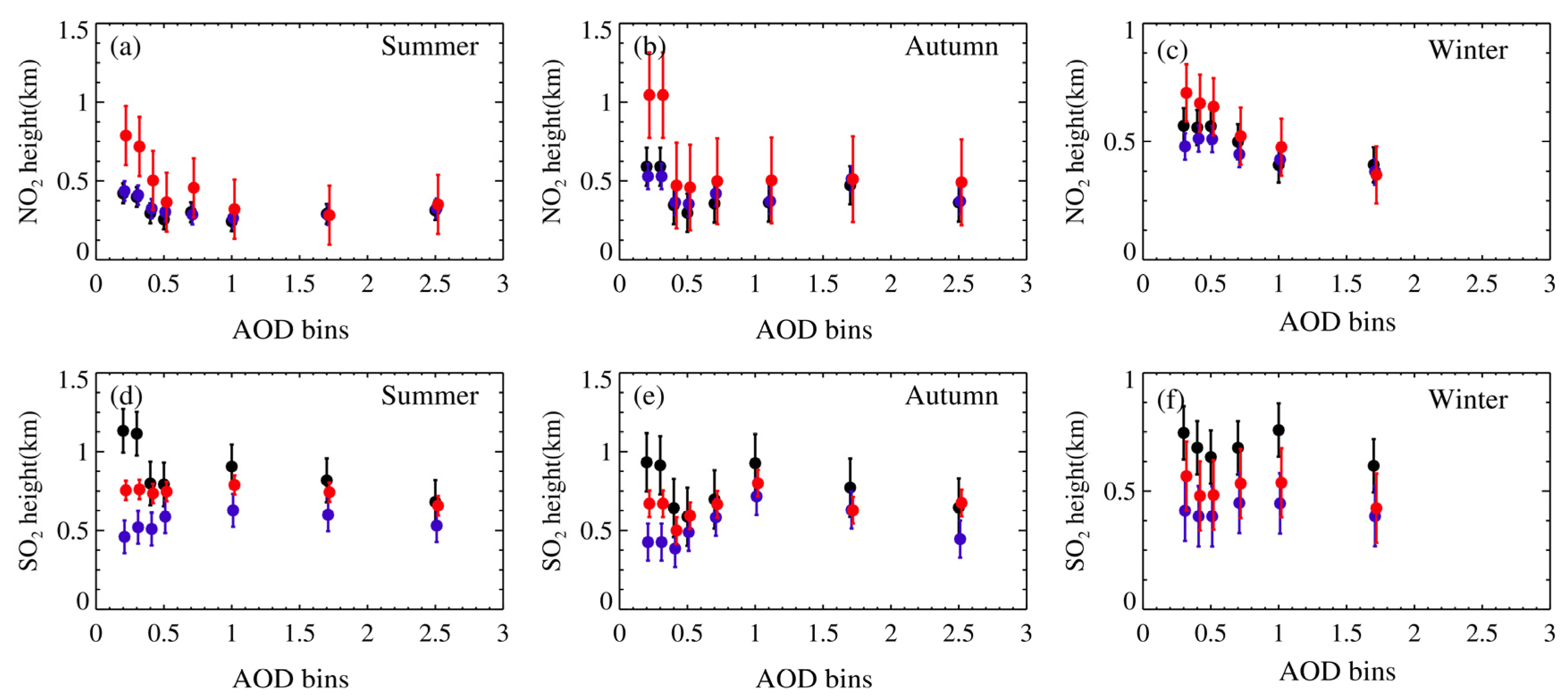
4.4. Analysis of Inversion Characteristics of Algorithms
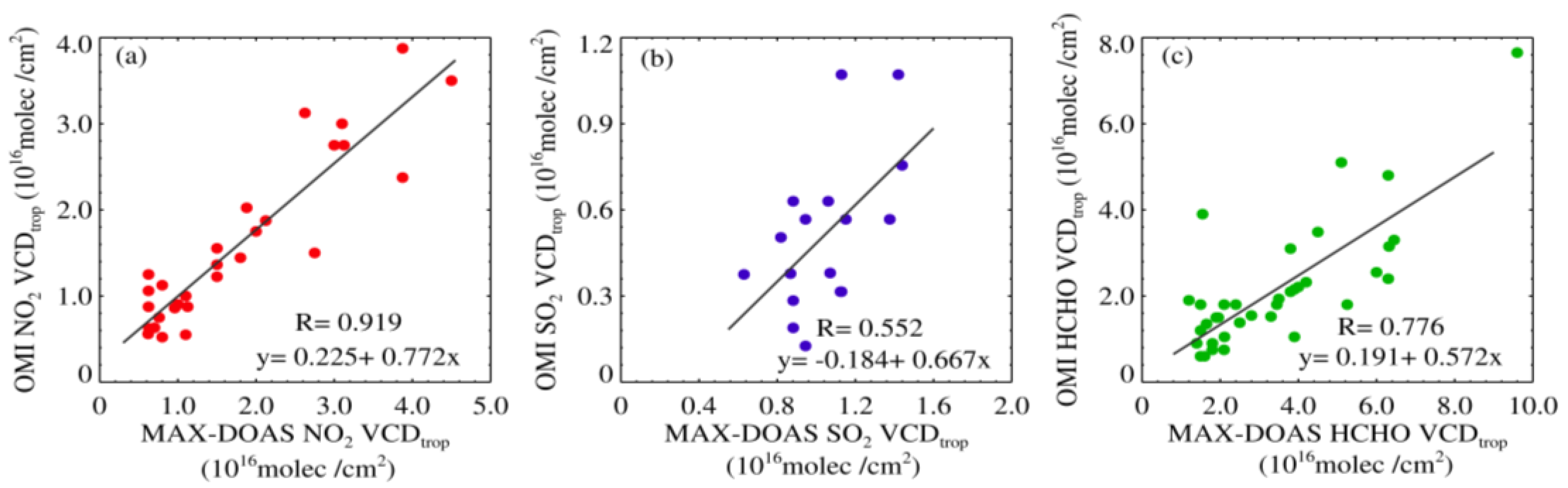
4.5. The Verification and Comparison of MAX-DOAS and the OMI Satellite
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.Y.; Wei, W.L.; Che, H.Z.; Tang, X.; Bian, J.C.; Yu, K.; Wang, W.G. Ground-based MAX-DOAS measurements of tropospheric aerosols, NO2 and HCHO distributions in the urban environment of Shanghai, China. Remote Sens. 2022, 14, 1726. [Google Scholar] [CrossRef]
- Javed, Z.; Liu, C.; Khokhar, M.F.; Xing, C.; Tan, W.; Subhani, M.A.; Rehman, A.; Tanvir, A. Investigating the impact of Glyoxal retrieval from MAX-DOAS observations during haze and non-haze conditions in Beijing. J. Environ. Sci. 2019, 80, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Benaventa, N.; Garcia-Nieto, D.; Wang, S.S.; Saiz-Lopez, A. MAX-DOAS measurements and vertical profiles of glyoxal and formaldehyde in Madrid, Spain. Atmos. Environ. 2019, 199, 357–367. [Google Scholar] [CrossRef]
- Drosoglou, T.; Koukouli, M.E.; Kouremeti, N.; Bais, A.F.; Zyrichidou, I.; Balis, D.; van der A, R.J.; Xu, J.; Li, A. MAX-DOAS NO2 observations over Guangzhou, China; ground-based and satellite comparisons. Atmos. Meas. Tech. 2018, 11, 2239–2255. [Google Scholar] [CrossRef]
- Wagner, T.; Beirle, S.; Brauers, T.; Deutschmann, T.; Frieß, U.; Hak, C.; Halla, J.D.; Heue, K.P.; Junkermann, W.; Li, X.; et al. Inversion of tropospheric profiles of aerosol extinction and HCHO and NO2 mixing ratios from MAX-DOAS observations in Milano during the summer of 2003 and comparison with independent data sets. Atmos. Meas. Tech. 2011, 254, 2685–2715. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, C.; Chan, K.L.; Hu, Q.; Liu, H.; Li, B.; Xing, C.; Tan, W.; Zhou, H.; Si, F.; et al. First observation of tropospheric nitrogen dioxide from the Environmental Trace Gases Monitoring Instrument onboard the GaoFen-5 satellite. Light Sci. Appl. 2020, 9, 677–685. [Google Scholar]
- Khan, W.A.; Khokhar, M.F.; Shoaib, A.; Nawaz, R. Monitoring and analysis of formaldehyde columns over Rawalpindi-Islamabad, Pakistan using MAX-DOAS and satellite observation. Atmos. Pollut. Res. 2018, 9, 840–848. [Google Scholar] [CrossRef]
- Tong, Z.P.; Li, Y.H.; Liu, Y.; Hou, X.G. Spatiotemporal distribution of NO2 in oasis cities between south and north Tianshan Mountains during heavy air pollution. Environ. Pollut. Control. 2018, 41, 125–132. [Google Scholar]
- Lee, H.; Ryu, J.; Irie, H.; Jang, S.-H.; Park, J.; Choi, W.; Hong, H. Investigations of the Diurnal Variation of Vertical HCHO Profiles Based on MAX-DOAS Measurements in Beijing: Comparisons with OMI Vertical Column Data. Atmosphere 2015, 6, 1816–1832. [Google Scholar] [CrossRef]
- Wagner, T.; Dix, B.; Friedeburg, C.V.; Frieß, U.; Sanghavi, S.; Sinreich, R.; Platt, U. MAX-DOAS O4 measurements: A new technique to derive information on atmospheric aerosols—Principles and information content. J. Geophys. Res. Atmos. 2004, 109, D22205. [Google Scholar] [CrossRef]
- Frieß, U.; Monks, P.S.; Remedios, J.J.; Rozanov, A.; Sinreich, R.; Wagner, T.; Platt, U. MAX-DOAS O4 measurements: A new technique to derive information on atmospheric aerosols: 2. Modeling studies. J. Geophys. Res. Atmos. 2006, 111, 3007–3021. [Google Scholar] [CrossRef]
- Irie, H.; Boersma, F.; Kanaya, Y.; Takashima, H.; Xiaole, P.; Wang, Z. Quantitative bias estimates for tropospheric NO2 columns retrieved from SCIAMACHY, OMI, and GOME-2 using a common standard for East Asia. AGU Fall Meet. 2012, 5, 2403–2411. [Google Scholar]
- Vlemmix, T.; Hendrick, F.; Pinardi, G.; Smedt, I.D.; Fayt, C.; Hermans, C.; Piters, A.; Wang, P.; Levelt, P.; Roozendael, M.V. MAX-DOAS observations of aerosols, formaldehyde and nitrogen dioxide in the Beijing area: Comparison of two profile retrieval approaches. Atmos. Meas. Tech. 2015, 8, 941–963. [Google Scholar] [CrossRef]
- Friedeburg, C.V.; Pundt, I.; Mettendorf, K.U.; Wagner, T.; Platt, U. Multi-axis-DOAS measurements of NO2 during the BAB II motorway emission campaign. Atmos. Environ. 2005, 39, 977–985. [Google Scholar] [CrossRef]
- Brinksma, E.J.; Pinardi, G.; Volten, H.; Braak, R.; Richter, A.; Schönhardt, A.; Van Roozendael, M.; Fayt, C.; Hermans, C.; Dirksen, R.J.; et al. The 2005 and 2006 DANDELIONS NO2 and aerosol intercomparison campaigns. J. Geophys. Res. Atmos. 2008, 113, 762–770. [Google Scholar] [CrossRef]
- Honninger, G.; Von Friedeburg, C.; Platt, U. Multi axis differential optical absorption spectroscopy (MAX-DOAS). Atmos. Chem. Phys. 2004, 4, 231–254. [Google Scholar] [CrossRef]
- Ma, J.Z.; Beirle, S.; Jin, J.L.; Shaiganfar, R.; Yan, P.; Wagner, T. Tropospheric NO2 vertical column densities over Beijing: Results of the first three years of ground-based MAX-DOAS measurements (2008–2011) and satellite validation. Atmos. Chem. Phys. 2013, 13, 1547–1567. [Google Scholar] [CrossRef]
- Wang, T.; Wang, P.C.; Yu, H.; Zhang, X.Y.; Zhou, B.; Si, F.Q.; Wang, S.S.; Bai, W.G.; Zhou, H.J.; Zhao, H. Intercomparison of slant column measurements of NO2 by ground-based MAX-DOAS. Acta Phys. Sin. 2013, 62, 054206. [Google Scholar] [CrossRef]
- Wang, T.; Wang, P.C.; Yu, H.; Sun, L. Analysis of the Characteristics of tropospheric NO2 in Xianghe based on MAX-DOAS measurement. Clim. Environ. Res. 2014, 19, 51–60. [Google Scholar]
- Fu, Q.; Liu, W.Q.; Ci, F.Q.; Zhang, Y.H.; Xie, P.H. Determination of the vertical column density of trace gas measured by MAX-DOAS. Acta Photonica Sin. 2009, 38, 1216–1220. [Google Scholar]
- Wu, F.C.; Li, A.; Xie, P.H.; Chen, H.; Ling, L.Y.; Xu, J.; Mou, F.S.; Zhang, J.; Shen, J.C.; Liu, J.G.; et al. Dectection and distribution of tropospheric NO2 vertical column density based on mobile multi-axis differential optical absorption spectroscopy. Acta Phys. Sin. 2015, 64, 198–208. [Google Scholar] [CrossRef]
- Li, X.; Brauers, T.; Hofzumahaus, A.; Lu, K.; Li, P.Y.; Shao, M.; Wanger, T.; Wahner, A. MAX-DOAS measurements of NO2, HCHO and CHOCHO at a rural site in Southern China. Atmos. Chem. Phys. 2013, 13, 2133–2151. [Google Scholar] [CrossRef]
- Li, X.; Brauers, T.; Shao, M.; Garland, R.M.; Wagner, T.; Deutschmann, T.; Wahner, A. MAX-DOAS measurements in southern China: Retrieval of aerosol extinctions and validation using ground-based in-situ data. Atmos. Chem. Phys. 2010, 10, 2079–2089. [Google Scholar] [CrossRef]
- Platt, U.; Stutz, J. Differential Optical Absorption Spectroscopy, Physics of Earth and Space Environments; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hendrick, F.; Müller, J.F.; De Mazière, M.; Fayt, C.; Gielen, C.; Hermans, C.; Ma, J.Z.; Pinardi, G.; Stavrakou, T.; Vlemmix, T.; et al. Four Years of Ground-based MAX-DOAS Observations of HONO and NO2 in the Beijing Area. Atmos. Chem. Phys. 2013, 14, 765–781. [Google Scholar] [CrossRef]
- Jin, J.; Ma, J.; Lin, W.; Zhao, H.; Shaiganfar, R.; Beirle, S.; Wagner, T. MAX-DOAS measurements and satellite validation of tropospheric NO2 and SO2 vertical column densities at a rural site of North China. Atmos. Environ. 2016, 133, 12–25. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, G.; Wang, D.; Si, F.K. Analysis on change characteristic of autumn relative humidity in China. Mod. Agric. Sci. Technol. 2017, 6, 173–174. [Google Scholar]
- Wang, Y.D.; Wang, Z.X. Characteristics of PM2.5 concentration variability and its meteorological factors in Shanghai. Arid. Land Geogr. 2018, 41, 1088–1096. [Google Scholar] [CrossRef]
- Wang, S.S. Inversion Study of NO2 and Aerosol Pollution in Shanghai Urban Area Based on Passive DOAS. Master’s Thesis, Fudan University, Shanghai, China, 2012. [Google Scholar]
- Duan, Y.S. Shanghai Atmospheric Visibility Study. Master’s Thesis, East China Normal University, Shanghai, China, 2005. [Google Scholar]
- Shi, H.; Chen, M.; Han, J.J. Analysis of factors affecting visibility and its variation features in Pudong area of Shanghai. Atmos. Sci. Res. Appl. 2008, 2, 1–8. [Google Scholar]
- Li, Y.J.; Shu, J. Study of horizontal visibility in Shanghai by PWD22. Adm. Tech. Environ. Monit. 2010, 22, 24–28. [Google Scholar]
- Yao, J.; Liu, W.; Wang, G.H.; Zeng, Y.S.; Huang, Y.; Liu, S.Q.; Yuan, N. The variation characteristics of atmospheric visibility in Jiading District, Shanghai. Environ. Pollut. Control. 2013, 35, 36–41. [Google Scholar]
- Fried, A.; Crawford, J.; Olson, J.; Walega, J.; Potter, W.; Wert, B.; Jordan, C.; Anderson, B.; Shetter, R.; Lefer, B.; et al. Airborne tunable diode laser measurements of formaldehyde during TRACE-P: Distributions and box model comparisons. J. Geophys. Res. 2003, 108, 8798. [Google Scholar] [CrossRef]
- Junkermann, W. On the distribution of formaldehyde in the western Po-Valley, Italy, during FORMAT 2002/2003. Atmos. Chem. Phys. 2009, 9, 9187–9196. [Google Scholar] [CrossRef]
- Klippel, T.; Fischer, H.; Bozem, H.; Lawrence, M.G.; Butler, T.; Jöckel, P.; Tost, H.; Martinez, M.; Harder, H.; Regelin, E.; et al. Distribution of hydrogen peroxide and formaldehyde over Central Europe during the HOOVER project. Atmos. Chem. Phys. 2011, 11, 4391–4410. [Google Scholar] [CrossRef]
- Tian, X.; Xie, P.; Xu, J.; Li, A.; Wang, Y.; Qin, M.; Hu, Z. Long-term observations of tropospheric NO2, SO2 and HCHO by MAX-DOAS in Yangtze River Delta area, China. J. Environ. Sci. 2018, 71, 210–224. [Google Scholar] [CrossRef]
- Jin, J.L.; Ma, J.Z.; Lin, W.Z.; Zhao, H.R. Characteristics of NO2 tropospheric column density over a Rural area in the North China Plain. J. Appl. Meteorol. Sci. 2016, 27, 303–311. [Google Scholar]
- Fu, T.M.; Jacob, D.J.; Palmer, P.I.; Chance, K.; Wang, Y.X.; Barletta, B.; Blake, D.R.; Stanton, J.C.; Pilling, M.J. Space-based formaldehyde measurements as constraints on volatile organic compound emissions in east and south Asia and implications for ozone. J. Geophys. Res. Atmos. 2007, 112, D06312. [Google Scholar] [CrossRef]
- Barkley, M.P.; Kurosu, T.P.; Chance, K.; Smedt IDe Roozendael, M.V.; Arneth, A.; Hagberg, D.; Guenther, A. Assessing sources of uncertainty in formaldehyde air mass factors over tropical South America: Implications for top-down isoprene emission estimates. J. Geophys. Res. Atmos. 2012, 117, D13304. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Zhou, R.; Zhou, B. Urban atmospheric formaldehyde concentrations measured by a differential optical absorption spectroscopy method. Environ. Sci. Process. Impacts 2014, 16, 291–297. [Google Scholar] [CrossRef]
- Chen, D. Study on Atmospheric Trace Gas Measurements Using Zenith-Sky Scattered Light-DOAS Technique. Master’s Thesis, Fudan University, Shanghai, China, 2008. [Google Scholar]
- Yang, S.N. Study on Atmospheric Pollution in Shanghaiusing Zenith-Sky Passive DOAS Technique. Master’s Thesis, Fudan University, Shanghai, China, 2011. [Google Scholar]
- Chan, K.L.; Hartl, A.; Lam, Y.F.; Xie, P.H.; Liu, W.Q.; Cheung, H.M.; Lampel, J.; Pohler, D.; Li, A.; Xu, J.; et al. Observations of tropospheric NO2 using ground based MAX-DOAS and OMI in measurements during the Shanghai World Expo 2010. Atmos. Environ. 2015, 119, 45–58. [Google Scholar] [CrossRef]
- Tian, X.; Xu, J.; Xie, P.H.; Li, A.; Hu, Z.K.; Li, X.M.; Ren, B.; Wu, Z.Y. Retrieving tropospheric vertical distribution in HCHO by multi-Axis differential optical absorption spectroscopy. Spectrosc. Spectr. Anal. 2019, 39, 2325–2331. [Google Scholar]
- Cheng, T.; Xu, C.; Duan, J.; Wang, Y.; Leng, C.; Tao, J.; Che, H.; He, Q.; Wu, Y.; Zhang, R.; et al. Seasonal variation and difference of aerosol optical properties in columnar and surface atmospheres over Shanghai. Atmos. Environ. 2015, 123, 315–326. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, S.; Guo, Y.; Zhang, R.; Qina, X.; Huang, K.; Wang, D.; Fud, Q.; Wang, J.; Zhou, B. Aerosol vertical profile retrieved from ground-based MAX-DOAS observation and characteristic distribution during wintertime in Shanghai, China. Atmos. Environ. 2018, 192, 193–205. [Google Scholar] [CrossRef]
- Xing, C.; Liu, C.; Wang, S.; Chan, K.L.; Gao, Y.; Huang, X.; Su, W.; Zhang, C.; Dong, Y.; Fan, G.; et al. Observations of the vertical distributions of summertime atmospheric pollutants and the corresponding ozone production in Shanghai, China. Atmos. Chem. Phys. 2017, 17, 14275–14289. [Google Scholar] [CrossRef]
- Wang, Y.; Lampel, J.; Xie, P.; Beirle, S.; Li, A.; Wu, D.; Wagner, T. Ground-based MAX-DOAS observations of tropospheric aerosols, NO2, SO2 and HCHO in Wuxi, China, from 2011 to 2014. Atmos. Chem. Phys. 2017, 17, 2189–2215. [Google Scholar]
- Leitao, J.; Richter, A.; Vrekoussis, M.; Kokhanovsky, A.; Zhang, Q.J.; Beekmann, M.; Burrows, J.P. On the improvement of NO2 satellite retrievals—Aerosol impact on the airmass factors. Atmos. Meas. Tech. 2010, 3, 475–493. [Google Scholar] [CrossRef]
- Liu, C.; Bai, W.G.; Zhang, X.Y.; Zhang, P. An improvement of retrieving carbon monoxide from SCIAMACHY Part I: With respect to the instrumenta1 issues. Chin. J. Geophys. 2013, 56, 758–769. (In Chinese) [Google Scholar]
- Jin, J.L. MAX-DOAS measurements of tropospheric NO2 and SO2 vertical column densities over atypical polluted area in North China. Ph.D. Thesis, Chinese Academy of Meteorological Sciences, Beijing, China, 2016. [Google Scholar]


| Target Gas | Interfering Gas | Temperature (K) | Source of Absorption Cross-Section Data a | Inverted Wavelength (nm) |
|---|---|---|---|---|
| O4 | 293 | Thalman Volkamer (2013) | ||
| HCHO | 298 | Meller Moortgat (2000) | ||
| BrO | 224 | Fleischmann (2004) | ||
| NO2, O4 | NO2 | 294, 220 | Vandaele (1998) | 338~370 |
| O3 | 223, 293 | Serdyuchenko (2014) | ||
| Ring | — | QDOAS | ||
| O4 | 293 | Thalman Volkamer (2013) | ||
| HCHO | 298 | Meller Moortgat (2000) | ||
| HCHO | BrO | 224 | Fleischmann (2004) | 338~357 |
| NO2 | 294, 220 | Vandaele (1998) | ||
| O3 | 223, 293 | Serdyuchenko (2014) | ||
| Ring | — | QDOAS | ||
| O3 | 223, 293 | Serdyuchenko (2014) | ||
| SO2 | 293 | Bogumil (2003) | ||
| SO2 | NO2 | 294, 220 | Vandaele (1998) | 305~317.5 |
| HCHO | 298 | Meller Moortgat (2000) | ||
| Ring | — | QDOAS |
| LOWTRAN Parameterization | ||
|---|---|---|
| Altitude | Spring and Summer | Autumn and Winter |
| Boundary layer 0~2 km | Urban aerosol | Urban aerosol |
| Visibility of 10 km | Visibility of 10 km | |
| Relative humidity is 80% | Relative humidity is 70% | |
| Troposphere 2~10 km | Visibility of 23 km | Visibility of 23 km |
| Relative humidity is 80% | Relative humidity is 70% | |
| Stratosphere 10~30 km | Background aerosol | Background aerosol |
| Background load | Background load | |
| Middle layer 30~100 km | Standard mesosphere aerosol | Standard mesosphere aerosol |
| Parameter | Unit | Assignment |
|---|---|---|
| Solar zenith angle (SZA) | Degree (°) | Measured value |
| Relative azimuth | Degree (°) | Measured value |
| F | — | 0.10~1.00 (interval:0.10) |
| τ | — | 0.10~1.00 (interval:0.10) |
| 1.15~1.30 (interval:0.15) | ||
| 1.50~3.00 (interval:0.25) | ||
| 3.50~4.00 (interval:0.50) | ||
| H | km | 0.20~1.20 (interval:0.05) |
| 1.30~1.50 (interval:0.10) | ||
| z | km | 0.10~3.00 (interval:0.25) |
| 3.50~4.00 (interval:0.50) | ||
| 5.00~9.00 (interval:1.00) | ||
| 11.00~15.0 (interval:2.00) | ||
| ξ | km | 5 |
| The total number of aerosol extinction coefficient profiles | Strip | 5040 |
| Geomtry | Model | Table | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Factor | HCHO VCDtrop | NO2 VCDtrop | SO2 VCDtrop | HCHO VCDtrop | NO2 VCDtrop | SO2 VCDtrop | HCHO VCDtrop | NO2 VCDtrop | SO2 VCDtrop |
| DSRF | 0.564 | −0.198 | −0.235 | 0.442 | −0.208 | −0.065 | 0.498 | −0.152 | −0.222 |
| RH | −0.428 | 0.405 | −0.265 | −0.361 | 0.712 | −0.205 | −0.431 | 0.531 | −0.268 |
| T | 0.402 | −0.326 | 0.300 | 0.322 | −0.690 | 0.284 | 0.473 | −0.452 | 0.335 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Lu, Y.; Yu, K.; Xiao, F.; Guo, R.; Yan, N.; Wang, W. Comparative Study on the Vertical Column Concentration Inversion Algorithm of Tropospheric Trace Gas Based on the MAX-DOAS Measurement Spectrum. Remote Sens. 2024, 16, 3359. https://doi.org/10.3390/rs16183359
Wang H, Lu Y, Yu K, Xiao F, Guo R, Yan N, Wang W. Comparative Study on the Vertical Column Concentration Inversion Algorithm of Tropospheric Trace Gas Based on the MAX-DOAS Measurement Spectrum. Remote Sensing. 2024; 16(18):3359. https://doi.org/10.3390/rs16183359
Chicago/Turabian StyleWang, Haoyue, Yuehua Lu, Ke Yu, Feihong Xiao, Rongzhi Guo, Naicong Yan, and Weiguo Wang. 2024. "Comparative Study on the Vertical Column Concentration Inversion Algorithm of Tropospheric Trace Gas Based on the MAX-DOAS Measurement Spectrum" Remote Sensing 16, no. 18: 3359. https://doi.org/10.3390/rs16183359
APA StyleWang, H., Lu, Y., Yu, K., Xiao, F., Guo, R., Yan, N., & Wang, W. (2024). Comparative Study on the Vertical Column Concentration Inversion Algorithm of Tropospheric Trace Gas Based on the MAX-DOAS Measurement Spectrum. Remote Sensing, 16(18), 3359. https://doi.org/10.3390/rs16183359




