Abstract
The upcoming European Space Agency (ESA) satellite mission GENESIS is an Earth-orbiting satellite carrying instruments of all four space geodetic techniques. The onboard transmitter for Very Long Baseline Interferometry (VLBI) will allow the observation of the satellite with VLBI radio telescopes. The objective of this study is to investigate the integration of VLBI observations of GENESIS into the operations of the VLBI Global Observing System (VGOS). Based on both current and foreseeable modern VGOS antenna networks, we consider the realistic observability of both geodetic radio sources and GENESIS. We conduct a comprehensive scheduling and perform extensive simulations of the VLBI observations. We assume that observations of GENESIS are scheduled within regular, geodetic experiments. The integration of GENESIS as an additional source in the scheduling results in a minimal degradation in the geodetic parameter estimation of station positions and dUT1 of less than 0.09 mm and 0.06 μs, respectively. The results suggest to schedule scans of GENESIS at intervals of about 5 min to limit the decrease in the number of observations of geodetic sources to less than 5% with respect to schedules containing only geodetic radio sources. The schedules for 24 h experiments comprise about 150 to 200 scans and 1000 to 5000 observations of GENESIS, depending on the size of the utilized network. The frame tie accuracy between the VLBI and GENESIS frames is assessed in the form of station positions, which are solely estimated from observations of GENESIS. Multiple 24 h experiments are simulated over 52 weeks with assumed session cadences of two to three experiments per week. By stacking the normal equations from three months of experiments, we obtain station position estimates with a precision of less than 10 mm. After 12 months, the repeatabilites are reduced to less than 5 mm.
1. Introduction
Under the Global Geodetic Observing System (GGOS) initiative, the International Association of Geodesy (IAG) set the accuracy and stability requirements for a Terrestrial Reference Frame (TRF) at 1 mm and mm/year to meet the scientific needs of various Earth science disciplines [1]. The ITRF2020 is the latest realization of the International Terrestrial Reference Frame (ITRF) [2]. It is established by observations from four space geodetic techniques: Very Long Baseline Interferometry (VLBI), Global Navigation Satellite Systems (GNSS), Satellite Laser Ranging (SLR), and Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS). These techniques are combined with terrestrial local tie measurements at co-location sites. Despite representing the most accurate realization of a TRF, the long-term position and time evolution of the ITRF2020 is estimated to be on the order of 5 mm and mm/year, respectively, [2].
In the ITRF2020, a large fraction of discrepancies between terrestrial local ties and space geodesy estimates exceed 5 mm. A useful tool to improve the combination of the individual techniques is the concept of space ties [3], the co-locations of several space geodetic techniques on satellites, with the aim of strengthening inter-technique ties. Mission proposals, such as GRASP [4] and E-GRASP [5], which aimed to combine instruments of GNSS, SLR, VLBI, and DORIS on a single Earth-orbiting satellite, have not been approved in the past.
In November 2022, the European Space Agency’s (ESA) Ministerial Council approved the GENESIS satellite mission as a component of the FutureNAV program [6]. Scheduled for launch in 2028, GENESIS will be a satellite platform flying in a polar orbit at an altitude of about 6000 km. It will carry instruments of all four space geodetic techniques. These instruments will be co-located with carefully calibrated reference points on board the satellite. The ground stations of all space geodetic techniques will be indirectly interconnected through observations of the instruments on the GENESIS satellite (see Figure 1). The primary objective of the mission is the implementation of in-orbit space ties, which have the potential to improve the accuracy and stability of future realizations of the ITRF. With the GENESIS mission approved, it is now up to the geodetic community to develop optimal observing and analysis strategies. At the time of writing, the design of the VLBI transmitter onboard the GENESIS satellite is still under development. As part of the GENESIS Science Exploitation Team (GSET), Working Group 3, which includes experts in the field of VLBI, is providing advice and assistance to ESA in this design process. The key factors driving the antenna design include regulations set forth by the International Telecommunication Union (ITU), radio frequency interference (RFI), and the compatibility with legacy S/X and VLBI Global Observing System (VGOS) stations.
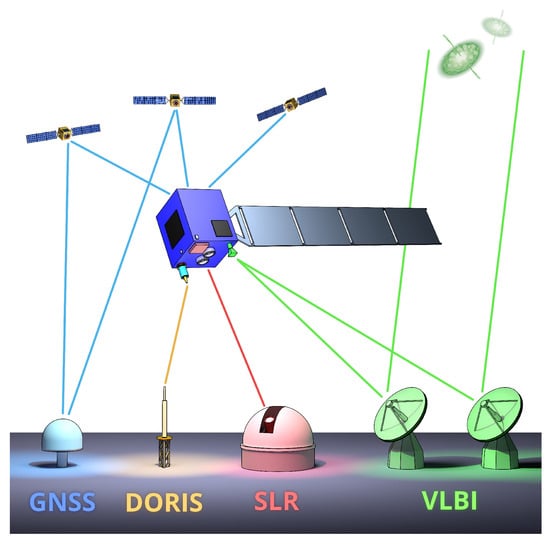
Figure 1.
Visualization of the GENESIS satellite. The satellite will be equipped with a Global Navigation Satellite Systems (GNSS) receiver, Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) receiver, Satellite Laser Ranging (SLR) reflector, and Very Long Baseline Interferometry (VLBI) transmitter.
VLBI observations of Earth-orbiting satellites are not standard and are not performed routinely yet. However, in several test experiments (e.g., [7,8,9]) it was demonstrated that the technical challenges inherent to VLBI observations of near-field targets can be overcome by adjustments to the standard VLBI processing pipeline [10]. In addition to real observations, several simulation studies were conducted to assess the potential of VLBI observations of Earth-orbiting satellites. For example, Plank et al. [11], Männel [12], and Schunck et al. [13] estimated the VLBI station positions from simulated observations of GNSS satellite constellations utilizing the satellites’ navigation signals in L-band. Other studies assume a VLBI transmitter on satellites, as is the case for GENESIS. Plank et al. [14] estimated VLBI station positions from simulated observations of a co-location satellite with orbital parameters following the proposed GRASP mission as well as LAGEOS-1. Anderson et al. [15] simulated and assessed the frame tie performance with a GENESIS-like satellite. Wolf and Böhm [16] presented a simulation study on the optimal distribution of VLBI transmitters on the Galileo space segment for frame ties. The most recent numerical simulations for a GENESIS-like co-location satellite were presented by Pollet et al. [17]. The authors followed a more extensive approach, simulating observations for all four space geodetic techniques and combining them at the observation level. Klopotek et al. [18] evaluated the potential of VLBI observations of Earth-orbiting satellites for precise orbit determination. Based on combined schedules with both geodetic radio sources and either LAGEOS-1/-2 or a set of Galileo satellites, the authors derive orbit solutions as well as geodetic parameters, i.e., VLBI stations positions, Earth rotation parameters, and geocenter offsets.
Despite previous efforts in this area, further investigations and simulations are required with regard to the integration of GENESIS into VLBI operations [19]. In addition to deficiencies in the employed antenna networks and the error modeling of observations, existing studies that consider a co-location satellite do not undertake a dedicated scheduling of experiments. Instead, scans of geodetic sources are replaced at regular intervals using standard VLBI schedules, or scans are simply assumed to be performed at regular intervals. This results in abstruse numbers of scans and observations, which are challenging to interpret and do not reflect realistic numbers in schedules with a co-location satellite.
In VLBI experiments, the participating stations are coordinated to observe a list of geodetic sources in an optimized sequence. In this manuscript, the term “geodetic sources” is used to refer to compact extragalactic radio sources observed in VLBI experiments. When integrating GENESIS as an additional source, two principal consideration must be taken into account. On the one hand, a certain number of scans of GENESIS should be scheduled to link the VLBI frame to the GENESIS frame with high accuracy. However, on the other hand, a substantial number of scans of geodetic sources are required to estimate geodetic parameters, including station positions, Earth Orientation Parameters (EOPs), and geodetic source positions, with consistent accuracy. Given that the geodetic sources and GENESIS compete for the observing time of the participating stations, it is essential to conduct a thorough analysis to determine the amount of allocated observing time for GENESIS.
This work addresses the uncertainties of the integration of GENESIS into global VGOS operations. VLBI experiments with the modern VGOS antennas are currently not running continuously as envisaged in Petrachenko et al. [20], but only two to four times per month. At present, data storage, data transfer, and correlation time are the bottlenecks of VGOS operations [21]. Therefore, we assess the feasibility of integrating observations of GENESIS within the 24 h experiments of the regular VGOS operations, rather than conducting additional dedicated experiments that would further strain the limited resources. Building upon previous simulation studies [13,14,15,16], we present a dedicated simulation study from a VLBI perspective. We show a comprehensive analysis on the integration of GENESIS into VGOS experiments. The scheduling is conducted with the well-established scheduling software VieSched++ v1.34 [22], taking into account actual antenna characteristics. Based on realistic schedules with current and projected VGOS antenna networks, we perform extensive Monte Carlo simulations of VLBI observations of GENESIS and geodetic sources. The investigations focus on the development of an optimal scheduling strategy and the evaluation of the impact of integrating GENESIS into VGOS experiments on the estimation of geodetic parameters. In a previous study, Klopotek et al. [18] integrated observations of LAGEOS-1/-2 into VLBI experiments with a legacy S/X antenna network. The authors notice no negative impact on the estimation of geodetic parameters. In comparison, this work significantly enhances the investigation of the integration of GENESIS by considering its actual orbit, utilizing a modern VGOS antenna network, and conducting comprehensive scheduling. In contrast to prior studies, this investigation addresses the trade-off between the negative impact of GENESIS on geodetic parameter estimates and the estimated frame tie accuracy between the VLBI and GENESIS frames. The frame tie accuracy is evaluated in the form of station position estimates from observations of GENESIS. It is established from 24 h experiments as well as over an extended period of up to 12 months. Section 2 outlines the concept of this work, while Section 3 presents the methodology. Section 4 shows the results, which are then discussed in Section 5.
2. Concept
The concept of this work comprising four main steps is visualized in Figure 2. In step 1, we perform a schedule optimization following the work by Schartner and Böhm [23]. VLBI scheduling is a complex optimization problem in which scheduling weight factors play a crucial role. For example, they determine whether stations slew long distances between scans to benefit from evenly distributed sky coverage or keep the slew time between scans short to maximize the number of observations. Because scheduling weight factors decisively impact the results, they should be optimized for each VLBI experiment. The VGOS schedule optimization performed in step 1 uses schedules which only contain geodetic radio sources, further referred to as VGOS schedules. Based on sets of scheduling weight factors, schedules are created and simulations are performed to estimate station position, EOPs, and source positions. The result is a set of optimal scheduling weight factors that correspond to the best estimation precision. In the following steps 2, 3, and 4, these optimal scheduling weight factors are applied to the generation of schedules using both geodetic sources and GENESIS, further referred to as mixed schedules. We assume that the optimal scheduling weight factors for VGOS schedules are also optimal for the estimation of geodetic parameters for mixed schedules.
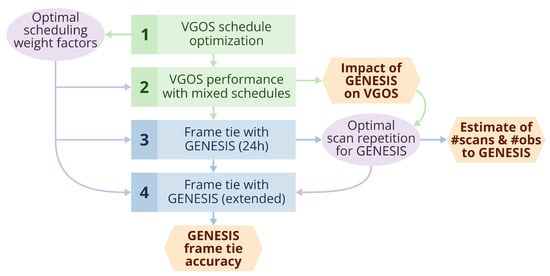
Figure 2.
Concept of this work. Four main steps will be performed to investigate the impact of GENESIS on VLBI Global Observing System (VGOS) operations, the valid estimate of the number of scans and observations of GENESIS, as well as the achievable frame tie accuracy.
In step 2, we analyze the VGOS performance in mixed schedules. Or, in other words, we investigate to what extent the integration of GENESIS into VGOS experiments impacts the estimation of geodetic parameters. Applying the optimal scheduling weight factors from step 1, we generate schedules containing both geodetic sources and GENESIS. Consequently, the number of scans and observations of geodetic sources is reduced in mixed schedules compared to VGOS schedules. From the mixed schedules, the geodetic parameters are estimated solely from the observations of geodetic sources. In this step, observations of GENESIS do not contribute to the analysis and are disregarded. The simulated results are compared to step 1 to derive the degradation of the parameter estimates.
In step 3, the mixed schedules from step 2 are used to estimate the frame tie between the VLBI frame and the GENESIS frame from 24 h VLBI experiments. We assume that the GENESIS orbit is determined through observations of the satellite techniques (GNSS, SLR, and DORIS). As this orbit is assumed to be imperfect, we simulate orbital errors as further detailed in Section 3. In this study, the VLBI frame is then attached to the GENESIS frame through observations of the satellite. We define the frame tie as the VLBI station positions derived only from VLBI observations of GENESIS. It is assumed that with a set of VLBI station positions given in the initial VLBI frame and a set of estimated VLBI station positions given in the GENESIS frame, a frame tie can be established to link the frames. The repeatability of the station position estimates is a measure for the expected frame tie accuracy. This analysis builds upon previous studies by Plank et al. [14], Anderson et al. [15], Wolf and Böhm [16], and Schunck et al. [13]. The optimal scan repetition rate with which GENESIS will be integrated into mixed schedules is derived from a compromise between the results from steps 2, the impact of GENESIS on VGOS, and 3, the estimated frame tie accuracy. On the one hand, GENESIS ideally does not degrade the estimation of geodetic parameters. A low repetition rate for GENESIS scans leads to larger numbers of observations of geodetic sources. On the other hand the GENESIS mission and its goals are supported by performing large numbers of VLBI observations of the satellite. A high repetition rate might be required to do so. From the resulting optimal scan repetition, we derive valid estimates for the expected numbers of scans and observations of GENESIS in real experiments. A scan refers to the time period during which multiple VLBI antennas observe the same radio source. An observation refers to the measured delay observable from a single baseline pair of VLBI antennas from a scan.
In step 4, we investigate the expected frame tie accuracy over an extended period of time. The optimal scheduling weight factors and the optimal scan repetition for GENESIS are used to generate mixed schedules for several months of VGOS operations. Here, we take into account the expected cadence of two to three 24 h VGOS experiments per week for the launch year of GENESIS in 2028. The normal equations of the simulated 24 h sessions are stacked and solved for the VLBI station position. These estimates are a measure of the expected frame tie accuracy over a period of up to 12 months of VGOS experiments.
Processing Strategies
In this work, we utilize two processing strategies contrasted in Figure 3. The simulation and estimation of geodetic parameters from observations of geodetic sources performed in steps 1 and 2 follow the VGOS Processing. The simulation and estimation of the frame tie from observations of GENESIS performed in steps 3 and 4 follow the GENESIS Processing.

Figure 3.
Processing strategies. Simulation configuration of the two processing strategies applied in this work: VGOS Processing and GENESIS Processing. Visualized are the considered source types, simulated error sources, applied constraints, and estimated parameters.
VGOS Processing represents the standard procedure for geodetic VLBI simulations. Only observations of geodetic sources are considered. The observations are simulated including tropospheric turbulence, clock inaccuracies, and measurement noise. To solve the rank deficiency in the normal equations datum constraints are necessary. We apply a no-net-translation (NNT) and a no-net-rotation (NNR) constraint. The estimation of the parameters is performed in a least squares fit. The quality of the schedule is evaluated by the precision of the estimates of station positions and EOPs. Tropospheric delays and station clocks are estimated as a by-product. This procedure is well established and has been used in several previous studies, such as Petrachenko et al. [20], Pany et al. [24], Schartner and Böhm [23], and Schartner et al. [25].
GENESIS Processing represents a procedure for the evaluation of inter-technique frame ties. Observations of both geodetic sources and GENESIS are considered. Again, the observations are modeled with errors for tropospheric turbulence, clock inaccuracies, and measurement noise. Additionally, orbit errors are simulated for GENESIS. No NNT or NNR constraints are used. The VLBI station positions are estimated only from observations of GENESIS. Observations of geodetic sources are used to improve the estimation of the troposphere and the station clocks. EOPs and geodetic source positions are fixed because we assume that they can be derived with high accuracy following the VGOS Processing strategy. We do not perform an orbit determination for GENESIS. The concept of the GENESIS Processing strategy was applied to the simulation of VLBI observations of satellites in recent studies by Wolf and Böhm [16] and Schunck et al. [13].
3. Materials and Methods
The foundation of this work is the utilization of global networks of modern VGOS antennas. Based on Behrend et al. [21], we consider three global networks consisting of stations that are either currently operational, expected to be operational soon, or in the planning stage. These networks are shown in Figure 4. Operational stations are already participating in VGOS experiments of the International VLBI Service for Geodesy and Astrometry (IVS, [26]). Stations expected to be operational soon have built antennas with a working signal chain. Stations in planning stage are expected to be operational before the launch of the GENESIS mission in 2028, with the exception of Tahiti, which is scheduled for operations later. Based on the status of the stations, we form the networks A, B, and C, representing a 12-, 20-, and 29-station network, respectively.

Figure 4.
Current status of VGOS station network based on Behrend et al. [21]. Blue circles (●) mark the telescopes in the operational 12-station network. Red diamonds (◆) mark the additional 8 telescopes that are expected to be operational soon, building a 20-station network. Black triangles (▲) depict another 9 additional telescopes, representing a future 29-station VGOS network.
3.1. Scheduling
In the VLBI technique, individual stations are only able to make one observation of one radio source on the sky at any given time. To form a radio interferometer, it has to be guaranteed that two or more stations simultaneously observe the same source. In geodetic VLBI experiments, the participating stations actively need to be coordinated to observe sources in a certain sequence and for a certain duration to achieve an optimal geometric stability and highest possible precision for the estimated geodetic parameters during analysis. At the same time, individual antenna characteristics, such as slew speeds, sensitivities, and source visibility, need to be accounted for. The concept of subnetting, where the network is divided into subnetworks and multiple sources are observed simultaneously, increases the complexity of this optimization problem exponentially [22]. Scheduling plays a crucial role as it significantly impacts the precision of geodetic parameter estimates (e.g., [23,25]). Therefore, comprehensive scheduling is an integral element of this work. We use the well-established scheduling software VieSched++. The software generates a schedule scan after scan using a brute force approach, calculating all possible next scans and evaluating them. The best next scan is selected based on weight factors. Weight factors can compete against each other, and there is no ideal combination of weight factors that is optimal for all experiments in general. Therefore, they must be determined individually for each experiment. In this work, four weight factors are tested following the recommendations by Schartner and Böhm [22]. These are the idle time of stations, the improvement in sky-coverage per scan, the number of observations per scan, and the duration of a scan. The idle time criterion gives stations that have not observed a higher weight in a while. The sky-coverage criterion favors an even distribution of scans across the sky of stations, leading to a better estimation of tropospheric delays [27]. The weight factor for the number of observations maximizes the number of observations. The weight factor on the duration of a scan reduces the duration between the end of the previous scan and the end of the tested scans. It includes time for the field system commands, slew time, possible idle time, calibration time, and observation time. Further details on weight factors and their impact on scheduling are available in Schartner and Böhm [22] and Schartner and Böhm [23].
As is typical for VLBI experiments, we create schedules with lengths of 24 h. VieSched++ is capable of including observations of satellites together with observations of geodetic sources in a common schedule. As commonly performed in current VGOS schedules, we choose a fixed scan length of 30 s for observations of geodetic sources [25]. For GENESIS observations, we choose a fixed scan length of 10 s. Based on the values given in [28], we assume that this is a sufficient integration time. For the generation of mixed schedules, scans of GENESIS are always prioritized over scans of geodetic sources if the satellite is visible from at least two stations. At the same time, a minimum repeat time, further referred to as MRT, is introduced for the satellite. Once a scan of GENESIS has been scheduled, the next scan of GENESIS can only be scheduled once the MRT has elapsed. That way we include observations of GENESIS in regular intervals while ensuring we include scans of geodetic sources in between. In this work, we evaluate MRTs from 1 to 10 min in 1 min intervals. Figure 5 visualizes the ground track of the GENESIS satellite for a duration of 24 h. The position is given as small dots in intervals of min. Every hour is marked with a big dot. The orbit shows about revolutions per day, which is equivalent to h per one revolution. Due to the polar orbit and frequent overflights in the polar regions, longer visibility times are expected for stations at high latitudes.

Figure 5.
Ground track of the GENESIS orbit over a 24 h period. The small dots represent the position of the satellite over the Earth in a min interval. The big dots show the position every hour from 0 h to 24 h.
3.2. Simulations
We use the Vienna VLBI and Satellite Software v3.3 (VieVS; [29]) to perform Monte Carlo simulations. Each 24 h schedule is simulated 1000 times. The observed minus computed observation delay is composed of four parts: tropospheric turbulence, clock error, measurement noise, and errors in the orbit determination of the GENESIS satellite. The delays in the troposphere include temporal and spatial correlation. A refractive index structure constant of and a scale height of 2000 m are assumed at all stations, along with an eastward wind velocity of 8 m/s [30]. Clock drifts are characterized by random walk and integrated random walk processes, with an Allan Standard Deviation of s after 50 min. Measurement noise is simulated as white noise with a standard deviation of 10 ps (≈1.2 mm) for both geodetic sources and GENESIS [16,28]. We assume that the orbit determined through satellite techniques contains errors in the satellite positions at the time of scans. For the simulation of orbit errors, we added a module to VieVS which is described in Section Orbit Errors. The simulated effects are put together to form the reduced observations
where is the tropospheric delay at station i, is the clock drift at station i, is the measurement noise per baseline observation, and is the delay due to an error in the satellite orbit position. Orbit errors are only simulated for observations of GENESIS.
Orbit Errors
We assume that the satellite techniques are utilized for a precise orbit determination of the GENESIS satellite with orbit solutions of 1-day arcs. We also assume that the determined GENESIS orbit is erroneous. In the orbit error simulation module, this is implemented by a modification of the orbital elements. For each of the 1000 simulation runs, the orbital elements are changed randomly by reasonable values to generate a set of erroneous orbital elements. The unchanged orbit parameters and positions are further referred to as true. At the time of each scan, the true and erroneous orbit positions are determined. Each erroneous orbit position is then transformed into the corresponding local coordinate frame of the true orbit position as offset in along-track-, cross-track-, and radial-direction. For scan i, the offset vector is given by
To describe the accuracy of the erroneous orbit in each component the root-mean-square (rms) values of the along-track-, cross-track-, and radial-direction are calculated from all scans. The rms value for the along-track component is given by
where N is the total number of scans. The values and are calculated accordingly. In VLBI observations of satellites, the measured delay is significantly less sensitive to changes in the satellite position in the radial direction as compared to the cross-track- and along-track-direction [31]. This is because the VLBI technique is inherently more sensitive to variations that cause changes in the angle of arrival of the signal rather than just the distance. Meanwhile, in precise orbit determination of medium Earth orbit satellites the radial component is typically determined with higher accuracy than the along-track and cross-track components. To account for this, the along-track and cross-track components of all offset positions are scaled to exceed the offsets in the radial direction. A scale factor of three is selected to ensure that a considerable portion of the orbit error is reflected in the simulated delay. The scaled along-track offsets are given by
The scaled cross-track offsets are derived similarly. The radial offsets remain unchanged,
The modulated offset vector at scan i contains the scaled components , and . The 3D-accuracy of the orbit offsets over all scans is given by the rms value
where is the Euclidean vector norm. The orbit errors are assumed to have a certain target orbit accuracy with the value . The offset vectors are scaled to meet the orbit accuracy
For the updated offsets of the erroneous orbit positions, the radial component is three times smaller than the along-track and cross-track components. Furthermore, the sizes of the offsets of the erroneous orbit positions meet the target orbit accuracy,
In this work, we consider three different orbit accuracies . Delva et al. [6] state that the GENESIS orbit could be determined with accuracies better than 1 cm. For Low-Earth Orbit missions, GNSS data usually provide one of the strongest contributions to precise orbit determination due to the almost continuous tracking of GNSS satellites. However, Montenbruck et al. [32] underline that at an altitude of 6000 km, the GNSS tracking coverage for a spaceborne receiver is significantly reduced. Furthermore, the authors underline that GENESIS will receive GNSS signals outside the Terrestrial Service Volume. A lack of detailed data on antenna transmit patterns in this region currently hinders a precise evaluation of the potential measurement and orbit-determination accuracy. Given that the expected final orbit accuracy is unclear, we consider three different levels of orbit accuracies. Figure 6 shows three exemplary sample realizations of offsets in along-track-, cross-track-, and radial-direction over a period of 24 h. The target orbit accuracy is 3 cm. The offsets oscillate around the true satellite position. Additionally, trends and constant offsets are present. For each simulation, orbit errors over 24 h are simulated 1000 times.
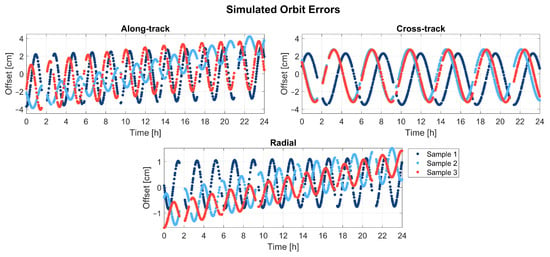
Figure 6.
Three exemplary sample realizations of a thousand simulated orbit errors in along-track-, cross-track-, and radial-direction over a period of 24 h. The 3D target orbit accuracy is 3 cm.
In the following, we calculate the delay difference resulting from the offset between the true and erroneous satellite positions as observed by the stations. For each observation, the true satellite position, the offset satellite position, as well as the positions of station 1 and station 2 are determined as absolute coordinates in a common coordinate frame. The geometric configuration is illustrated in Figure 7. The delays are calculated on the pure geometric delay described in the formalism by Klioner [33]. We neglect other effects like the retarded baseline effect and relativistic effects. As this is a simulation study and we are considering the differences between the true and observed delay, the simulation results are hardly affected. The geometric delay observed from the stations to the true satellite position is given by
where c is the speed of light and is the geometric distance between station i and the true satellite position. Similarly, the geometric delay observed from the stations to the erroneous offset satellite position is given by
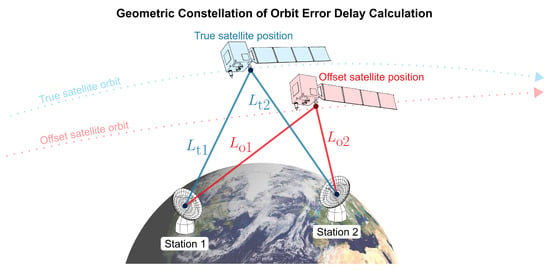
Figure 7.
The orbit error delay calculation takes into account the geometric configuration of the true satellite position, the offset satellite position, station 1, and station 2. The distances between station 1 and station 2 to the true satellite position are and , respectively. The distances to the erroneous offset satellite position are and .
The delay difference resulting from an erroneous orbit determination of GENESIS is calculated by
The value is added to the observed minus computed value as described in Section 3.2.
3.3. Analysis
In the analysis, the target parameters are estimated from the simulated observations with a least-squares adjustment. As presented in Section 2, we follow two processing strategies with individual analysis. In the VGOS processing, the troposphere is estimated as zenith wet delays every 10 min as piece-wise linear offsets (PWLO) with a relative constraints of cm. North and east gradients are estimated as PWLO every 20 min with relative constraints of cm. The clock behavior is parameterized with a quadratic term and PWLO every 60 min with relative constraint of cm. All five EOPs, namely two polar motion parameters, two nutation parameters, and dUT1, as well as the station positions are estimated with a single value per session. To resolve the rank deficiency, the datum definition is realized using NNT and NNR constraints over all stations. The source positions are estimated for sources observed in at least three scans and with at least 25 observations [25]. The GENESIS processing considers observations of both geodetic sources and GENESIS. In contrast to VGOS processing, EOPs and geodetic source positions are not estimated but fixed to a priori values. Furthermore, station position estimates are only derived from observations of GENESIS. That way, the coordinates are defined through the satellite frame. No datum constraints are necessary. The estimates of the 1000 simulation runs are used to calculate repeatability values for each parameter. These repeatability values are calculated as standard deviation and represent the expected accuracy of a parameter.
4. Results
4.1. VGOS Schedule Optimization
For the VGOS schedule optimization, we test variations in weight factors used in the scheduling to evaluate each set of weights based on the estimates of geodetic parameters. For all three networks, we generate schedules containing only geodetic sources. The tested weight factors refer to the duration of a scan, the number of observations per scan, and the improvement in sky-coverage per scan. Each weight factor was tested with the values . The idle time weight factor was fixed to with an interval of 300 s. This leads to a total of 64 tested schedules for each network.
We consider the schedules that show the best estimates for station positions, dUT1, polar motion parameters (XPO and YPO), and nutation parameters (NUTX and NUTY). Figure 8 shows the five best results from schedules for Network A. Schedule 1 shows the best repeatabilities for station positions and YPO. Schedules 2, 3, 4, and 5 show the best repeatabilities for dUT1, XPO, NUTX, and NUTY, respectively. Additionally, the numbers of scans and observations are presented. The results underline that large numbers of scans and observations do not necessarily lead to the best results. For example, schedule 2 shows about 100 fewer scans and fewer observations than schedule 4; however, schedule 2 shows better results for station positions and dUT1. In general, there is not one schedule that provides the best results for all parameters. The results vary strongly between the smallest and largest value for each parameter. For the station position repeatability, the worst result of mm for schedule 4 is an increase of about with respect to the best result of mm for schedule 1. The percentage increase between the smallest and largest values for the repeatabilities in dUT1, XPO, YPO, NUTX, and NUTY are about , , , , and , respectively. This shows that among the best five of the 64 tested schedules, relative changes in the estimated parameters of about 7–10% are a normal variation. Although not shown here, this analysis was equivalently performed with networks B and C. For network B, the relative changes in the station position repeatability and dUT1 repeatability across the best schedules are and , respectively. For network C, they are and . We choose the best schedule based on the performance across all estimated parameters. Consequently, the best schedule for network A is schedule 1. The weight factors used to create this schedule were used in the further investigations of this work.
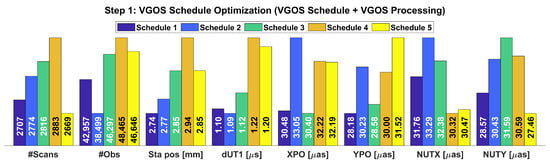
Figure 8.
VGOS schedule optimization for network A. Out of 64 tested schedules, the results from the five schedules showing the best repeatability values in the average station position and Earth orientation parameters (EOPs) are shown for network A. Additionally, the corresponding number of scans and observations are given.
4.2. Mixed Schedules
For the generation of mixed schedules, GENESIS is added as an additional source in the scheduling with MRTs from 1 to 10 min in 1 min intervals. The weight factors determined in Section 4.1 are applied in the scheduling. Figure 9 shows the distribution of satellite and geodetic source scans on local skies for selected stations based on a 24 h schedule with an MRT of 2 min for network C. It can be seen that scans of GENESIS are scheduled at regular intervals if the satellite is visible from at least two stations. The skyplot for Ny-Ålesund, which is located at a latitude of about north, shows a large number and the most equal distribution of satellite scans among the selected stations. Wettzell, located at a latitude of about north, has many GENESIS scans towards the north. In the other directions, scans of GENESIS are more sparsely scheduled. Katherine and Kokee show significantly fewer and less equally distributed scans of GENESIS compared to Ny-Ålesund. Due to the nature of the orbit, the stations Katherine and Kokee, located at latitudes of about south and north, respectively, exhibit shorter visibilities to the satellite. The total visibility of GENESIS, calculated by the time the satellite is above elevation and visible from at least one other station, is h per day for Ny-Ålesund when averaging over 10 days. For Katherine and Kokee, the visibility is h and h. This underlines that even the station with the most visibility to GENESIS has on average about 17 h a day in which regular VLBI observations can be performed. However, it also shows that there is a strong bias between observation times across different latitudes, potentially leading to a bias in the determination of the frame tie.

Figure 9.
Distribution of satellite and geodetic source observations on local skies for (a) Ny-Ålesund, (b) Wettzell, (c) Katherine, and (d) Kokee based on a 24 h schedule with a minimum repeat time (MRT) of 2 min for network C.
Figure 10 shows the number of stations with visibility to GENESIS above elevation for networks A, B, and C within 24 h. It also visualizes whether GENESIS is in the northern hemisphere (NH) or the southern hemisphere (SH) during the time. The imbalance between the number of stations between NH and SH is caused by the antenna networks. The majority of stations are located in the NH. Only a maximum of seven stations are located in the SH for network C. The figure shows that for all three networks, there are periods where GENESIS is visible from only one station. During these times, no observations can be performed, as no baseline observation is possible.
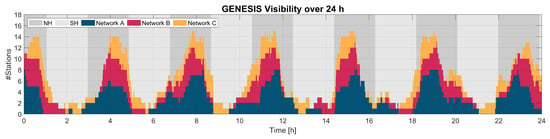
Figure 10.
Number of stations with visibility to GENESIS in 24 h with an elevation mask of for networks A, B, and C. The background shows whether GENESIS is in the northern hemisphere (NH) or the southern hemisphere (SH) during the time.
GENESIS is visible from different surface areas of the Earth with every satellite orbit revolution. This leads to the effect that the geometric configuration of stations and satellites vary from one day to another. By conducting VLBI experiments on different days, each 24 h session will provide different numbers of scans and observations. Therefore, the analysis investigating the VGOS performance with mixed schedules (step 2), presented in Section 4.3, and the frame tie with GENESIS for 24 h sessions (step 3), presented in Section 4.4, are not based on a single experiment, but on four experiments, each separated by one week, to account for this variation in the geometric configuration between stations and satellite.
4.3. VGOS Performance with Mixed Schedules
In the following, we investigate to what extent GENESIS degrades VGOS results when being included in the scheduling. The mixed schedules are analyzed following the VGOS processing. The results are averaged over four 24 h experiments on different days. Figure 11 presents the station position repeatabilities, dUT1 repeatabilities, number of scans, and number of observations of geodetic sources for networks A, B, and C. The values are given as absolute numbers as well as percentage with respect to the VGOS schedule reference.
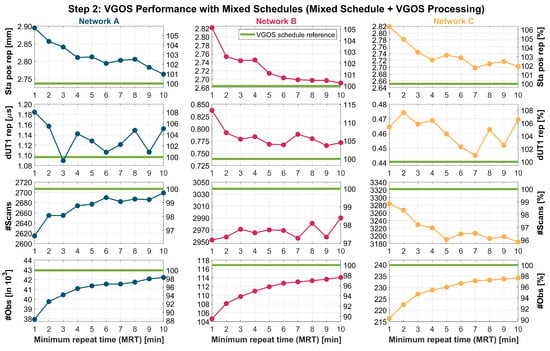
Figure 11.
Degradation of VGOS results due to GENESIS. For each network A, B, and C, the station position repeatability, dUT1 repeatability, number of scans, and number of observations are shown when analyzing mixed schedules with MRTs for GENESIS between 1 and 10 min in 1 min intervals. The values are given as absolute values as well as percentages relative to the VGOS schedule reference. The analysis follows the VGOS processing. The number of scans and observations only refers to geodetic sources.
The average station position repeatability tends to improve with larger MRTs for all three networks. This was to be expected, as with longer repeat times between scans of GENESIS, more observations of geodetic sources are performed, and the VLBI station positions are estimated with higher precision. At 1 min MRT, the degradation of the station position repeatability with respect to the VGOS schedule reference is at the level of mm for the three networks. This is an equivalent percentage increase of about . With MRTs equal to or larger than 4 min, the increase is less than mm or across all networks. In comparison, the variation in the station position repeatability across the best schedules presented in the VGOS schedule optimization in Section 4.1 is for network A, for network B, and for network C. This shows that the scheduling and optimization of the scheduling weight factors lead to larger differences in the station position repeatabilities than the integration of GENESIS in VGOS schedules with MRTs of 4 min or more. Similar observations can be made for dUT1. The repeatabilities for dUT1 are more noisy than for the station position and no clear improvement of the estimation can be detected with increasing MRT. With MRTs equal to or larger than 3 min, the increase with respect to the VGOS schedule reference is less than s or for networks A, B, and C. The differences in the dUT1 estimates across the best schedules of the VGOS schedule optimization are for network A, for network B, and for network C. Similar to the station position repeatability, the optimization of the scheduling weight factors shows larger differences across the best schedules in the dUT1 estimate than the degradation of the results due to integration of GENESIS into the schedules with MRTs larger than 3-min.
For network A, the number of scans increases for larger MRTs. For network B, an increase can be seen with exceptions for 7 min and 9 min MRT. For network C, the most scans are at short MRTs. This is due to the effect of subnetting; while a part of the network observes GENESIS, another subnetwork observes geodetic sources. Because of the size of network C, several subnetworks are built leading to a larger number of scans with a fewer number of observations overall. As mentioned above, for all three networks, the number of observations of geodetic sources increases with larger MRTs for GENESIS. A significant decrease can be observed at first. At 1 min MRT, the number of observations drops by about %, %, and % with respect to the reference from the VGOS schedule for networks A, B, and C, respectively. At 5 min MRT, it drops by about %, %, and %. Based on the station position and dUT1 repeatabilities, and in order to maintain a reasonably large number of observations, the results suggest implementing GENESIS in VGOS schedules with MRTs of about 4 to 5 min or longer.
4.4. Frame Tie with GENESIS in 24 h Experiments
To investigate the expected frame tie accuracy, the mixed schedules are analyzed following the GENESIS processing. We evaluate the estimated station positions from observations of GENESIS. Figure 12 shows the station position repeatability of selected stations averaged over four 24 h sessions with network C, an MRT of 5 min, and orbit errors at the level of 3 cm. The stations are sorted from left to right by their latitude with Ny-Ålesund representing the most northern and Hobart the most southern station. Ny-Ålesund shows the best station position repeatability. It also has a large number of scans and observations. Among the selected stations, Hobart shows the worst station position repeatability with the up-component being determined significantly worse than the north- and east-components. Although Hobart shows a similar number of scans as Ishioka, the number of observations is significantly less. This indicates that on average Hobart does not share many baselines with other stations per scan. The repeatabilities for Wettzell and Ishioka underline that the number of scans and observations are not the only elements affecting the station position repeatability. Wettzell shows more scans and observations than Ishioka. However, the station position repeatability is larger than for Ishioka. The reason for this could be the favorable antenna network geometry and connectivity for Ishioka leading to more advantageous baselines. With the stations sorted by their latitude, the number of scans underlines the general increase in visibility of GENESIS close to the polar regions due to the nature of the orbit.
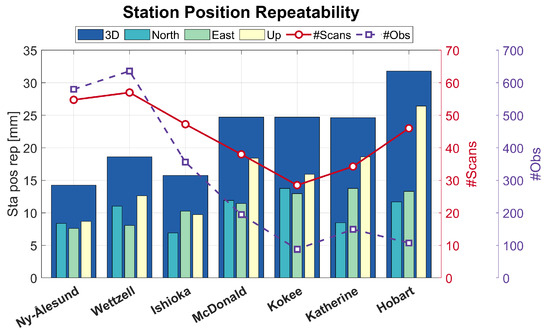
Figure 12.
Station position repeatability for selected stations from network C and an MRT of 5 min derived from observations of GENESIS with an orbit error of 3 cm. The stations are sorted from left to right by their latitude. The station position repeatability is given as 3D as well as the individual north-, east-, and up-components. The number of scans and observations refers to GENESIS only.
Figure 13 visualizes the station position repeatability averaged over all stations, the number of GENESIS scans, and the number of GENESIS observations for the three networks A, B, and C with MRTs from 1 min to 10 min in 1 min intervals. The four different orbit error magnitudes are at 0 cm (no orbit errors), 1 cm, 3 cm, and 5 cm. For all three networks, the station position repeatability deteriorates with larger MRTs. This is simply explicable by a decreasing number of scans and observations. Furthermore, as to be expected, the station position repeatability decreases with larger orbit errors of the satellite. The number of scans ranges from about 100 to 400 for network A, about 100 to 450 for network B, and about 100 to 500 for network C. With the increasing size of the utilized antenna network, GENESIS is visible from at least two stations for longer periods of time if newly added stations cover areas that were not previously seen by other stations. The improved visibility of networks B and C as compared to network A eventually leads to more scans at the same MRT, and while the difference in the number of scans between network A and C is at maximum about 100 scans, the number of observations differs significantly. The networks B and C show more than 3–4 times more observations than network A.
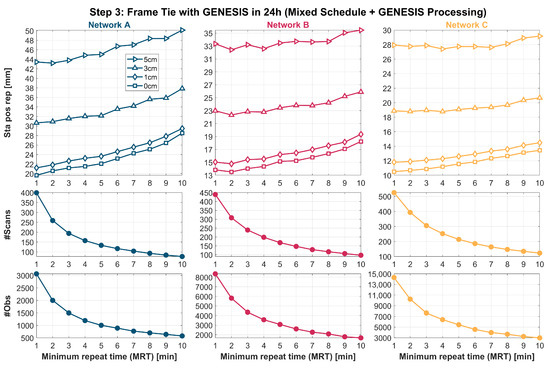
Figure 13.
GENESIS performance with mixed schedules. For each network A, B, and C, the station position repeatability, number of scans, and number of observations are shown when analyzing mixed schedules with MRTs for GENESIS between 1 and 10 min in 1 min intervals. Orbit errors are simulated at different magnitudes at 0 cm (no orbit errors), 1 cm, 3 cm, and 5 cm. The analysis follows the GENESIS processing. The station positions are derived only from GENESIS observations. The number of scans and observations only refers to observations of GENESIS.
Although not shown here, we tested shorter MRTs at 30 s, even removing the MRT. Instead of an improvement of the station position repeatability, the results are significantly worse. This is because the frequent observation of GENESIS leads to too few geodetic source observations and, consequently, a poor distribution of sources across the local skies of stations. This compromises the estimation of the troposphere and station positions. An MRT of 1 min leads to the best estimation of station positions. However, the analysis presented in Section 4.3 shows that MRTs shorter than 4 min lead to a significant decrease in the number of geodetic source observations in mixed schedules as compared to VGOS schedules. In this work, the main focus of the experiments with mixed schedules should remain on ensuring high-precision estimates of geodetic parameters derived from observations of geodetic sources. Therefore, in the further analysis of this work, we choose an MRT for GENESIS of 5 min.
4.5. Long-Term Frame Tie with GENESIS over 12 Months of Experiments
To investigate the long-term frame tie accuracy, we combine multiple experiments into a global solution, estimating the parameters from a common adjustment of all available observations. The experiments are scheduled with the scheduling weight factors determined in Section 4.1 and the optimal MRT of 5 min determined in Section 4.3 and Section 4.4. We simulate 24 h experiments following a cadence of two or three experiments per week. The experiments following the cadence of two experiments per week are performed on Monday and Friday. The experiments following the cadence of three experiments per week are conducted on Monday, Wednesday, and Friday. Following these cadences, experiments are conducted over a period of 52 weeks resulting in 104 and 156 experiments, respectively. Figure 14 shows the results of the derived frame tie with GENESIS over an extended period of time. The station position repeatabilities are derived by stacking the normal equations of multiple experiments of mixed schedules evaluated with the GENESIS processing. The values are given for networks A, B, and C with orbit errors of 0 cm (no orbit errors), 1 cm, 3 cm, and 5 cm. For each network, a cadence of 2 and 3 experiments per week over time periods of 3, 6, 9, and 12 months is shown. The number of conducted experiments is given as well.

Figure 14.
Station position repeatabilities with mixed schedules following the GENESIS processing. The repeatabilities are given for the three networks A, B, and C with orbit errors at the level of 0 cm (no orbit errors), 1 cm, 3 cm, and 5 cm. The results are shown for the cadence 2 (2 experiments per week) and cadence 3 (3 experiments per week) after 3, 6, 9, and 12 months, respectively. Additionally, the number of performed experiments is given in brackets.
Compared to the results based on single 24 h experiments, the stacking of multiple sessions leads to significant improvements. As expected, with the increasing number of conducted experiments, the improvements are large at first and slow down with higher numbers. For all three networks and orbit error levels, station position repeatabilities of below 1 cm can already be determined after 3 months with cadence 2. Similar to the results presented in Section 4.4, the size of the utilized network plays a large role in the results. In contrast to network A, the station position repeatability for network C improves with fewer numbers of experiments and performs better with larger satellite orbit errors. After 12 months of experiments, the differences between cadences 2 and 3 are small for orbit errors of 0 cm and 1 cm. However, with larger orbit errors of 3 cm and 5 cm, the additional experiments of cadence 3 become more important. With cadence 3 and orbit errors of 5 cm, the station position repeatabilities reach mm, mm, and mm for networks A, B, and C, respectively. In contrast, the values are mm, mm, and mm for cadence 2. Overall, the station position repeatability can be improved by a factor of about 10 after 12 months of experiments with cadence 2 or 9 months of experiments with cadence 3, as compared to the results from the single 24 h experiments.
5. Discussion
This study investigates the integration of VLBI observations with the upcoming ESA mission GENESIS into VGOS operations. The results demonstrate that the negative impact of GENESIS on the precision of geodetic parameter estimates is minimal. These findings are consistent with those of previous simulation studies that incorporated additional artificial radio sources into VLBI experiments [18,34]. The results presented herein provide further enhancement to the findings of previous studies by implementing the planned GENESIS orbit parameters, utilizing both the current and projected VGOS antenna networks, and conducting comprehensive scheduling. In contrast to prior studies, this investigation addresses the trade-off between the negative impact of GENESIS on geodetic parameter estimates and the estimated frame tie accuracy between the VLBI and GENESIS frames. The findings suggest integrating GENESIS into VGOS schedules with MRTs of at least 5 min. As a result, the degradation of the station position and dUT1 repeatabilities are less than mm and s, respectively. Furthermore, the number of observations is reduced by less than . A comparison is presented between the degradation of the parameters due to GENESIS and the variation within the VGOS schedule optimization. It was demonstrated that no single schedule provides the best estimates for all geodetic parameters. Rather, each schedule shows strengths in the estimation of different parameters. It was found that the geodetic parameter estimates exhibited a variation of between and among the best-tested schedules. In comparison, the change in the station position and dUT1 estimation due to GENESIS is less than and , respectively, while the impact of GENESIS on VGOS schedules is not negligible, especially considering the decrease in the number of observations; the results suggest that GENESIS can be included into regular VGOS experiments.
A significant aspect of this work is the application of comprehensive scheduling. We utilized the well-established scheduling software VieSched++. The software assesses the anticipated orbit of GENESIS and creates realistic observability with the global antenna network. With an MRT of 5 min, the mixed schedules comprise about 150 to 200 scans and about 1000 to 5000 observations of GENESIS, depending on the VGOS network. In this study, we present the first numbers of scans and observations of GENESIS with current and projected VGOS networks that are based on profound scheduling. The given numbers in this work can contribute to further studies by other groups within the geodetic community in preparation for the GENESIS mission.
We employed a two-step approach to establish the frame tie between the VLBI and GENESIS frames. In the first step, the GENESIS orbit is determined with satellite-based techniques. In the second step, VLBI observations with VGOS networks serve to establish a tie between the two frames. The results indicate that the frame tie can be achieved with an accuracy of several millimeters after a few months of observations. After 12 months of experiments with GENESIS for all three networks, a frame tie can be achieved with an accuracy of 2–4 mm, assuming orbit errors of 5 cm and a session cadence of three experiments per week. A cadence of two experiments per week results in a decrease in frame tie accuracy to approximately 3–5 mm. As expected, the results improve further when assuming smaller orbit errors of 3 cm or 1 cm. However, these values warrant cautious interpretation. The modeling of orbit errors applied in this work is simplified. The errors are derived from disturbances at the level of orbital elements, rather than from the forces acting on the satellite. Consequently, they may not fully reflect the anticipated errors for real observations. Therefore, our simulations should be regarded as lower limits.
We perform frame tie realization from a VLBI perspective. The simulations presented here reflect standard practices for VLBI simulation studies. It should be noted, however, that the displayed frame tie realization based on a two-step approach represents merely one possible method of combining the space geodetic techniques via the GENESIS satellite. At this stage, several working groups are engaged in conceptualizing an optimal strategy for rigorously combining and commonly analyzing observations of the four space geodetic techniques at the observation level. Prior research has demonstrated that VLBI has the potential to contribute to the orbit determination of satellites equipped with VLBI transmitters (e.g., [18,31]). Consequently, VLBI observations of GENESIS could play a significant role in the satellite’s orbit determination.
For observations of geodetic sources, we assume scan lengths of 30 s, as this is the common practice currently employed in VGOS experiments. However, VGOS operations are still developing and the implementation of adaptive scan lengths could reduce the duration antennas observe each source. Theoretically, scan lengths of 10 s or less are feasible with VGOS. Shorter scan lengths would increase the number of scans of geodetic sources in between GENESIS scans while maintaining unchanged MRTs. This could further decrease the impact of GENESIS on VGOS operations. Another aspect of VGOS that could develop more significance in the future is the concept of twin telescopes. At present, the three space geodetic observatories in Ny-Ålesund, Onsala, and Wettzell are equipped with twin telescopes. The advantages are obtained by assuming that the tropospheric activity above the two antennas is identical and that they are connected to the same clock. An additional observing mode inherent to twin telescopes is multidirectional observing, whereby the two antennas point in different directions to observe different sources. In this way, each antenna is part of a different subnetwork. The advantage of this observing mode for observations of VLBI transmitters on board satellites, such as GENESIS, is that geodetic sources can be observed with no interruptions. With regard to GENESIS, the signal characteristics are currently the subject of discussion. Consequently, the signal-to-noise ratio, scan length, and precision of actual observations of GENESIS may deviate from the assumptions presented in this study.
Prior to the launch of GENESIS in 2028, the VLBI technique still requires further development in the processing of observations of near-field targets to actually support the mission with dedicated VLBI observations [35]. In particular, the generation of the schedule files and station-specific control files need to be modified to seamlessly implement satellites in experiments with geodetic sources. Furthermore, due to the lack of tracking support of the antenna control units, some antennas are unable to continuously track GENESIS across the sky. Instead, stepwise or static tracking could be viable alternatives that require further investigation. These adjustments primarily necessitate software changes rather than hardware updates.
In this study, we limited our analysis to VLBI observations of GENESIS with VGOS networks. It is intended that the legacy S/X network will continue its operations with the weekly R1 and R4 experiments, thus maintaining the time series of observations. By additionally integrating GENESIS in these experiments, the legacy antenna network can contribute with observations of be tied to the GENESIS frame and contribute to a common analysis of VLBI and the other space geodetic techniques. Typically legacy antennas exhibit slower slew speeds in comparison to VGOS antennas. This could result in a reduced number of scans of geodetic sources in between scans of GENESIS, which could in turn lead to a larger degradation of geodetic parameter estimates.
Author Contributions
Conceptualization, D.S., L.M. and G.M.C.; methodology, D.S. and L.M.; software, D.S. and L.M.; validation, D.S. and L.M.; formal analysis, D.S.; investigation, D.S.; resources, D.S. and L.M.; data curation, D.S.; writing—original draft preparation, D.S.; writing—review and editing, D.S., L.M. and G.M.C.; visualization, D.S.; supervision, D.S., L.M. and G.M.C.; project administration, D.S., L.M. and G.M.C.; funding acquisition, L.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Australian Research Council (ARC), grant number DE180100245.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the corresponding author on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Plag, H.P.; Pearlman, M. Global Geodetic Observing System: Meeting the Requirements of a Global Society on a Changing Planet in 2020, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Collilieux, X.; Métivier, L.; Chanard, K. ITRF2020: An augmented reference frame refining the modeling of nonlinear station motions. J. Geod. 2023, 97, 47. [Google Scholar] [CrossRef]
- Rothacher, M.; Beutler, G.; Behrend, D.; Donnellan, A.; Hinderer, J.; Ma, C.; Noll, C.; Oberst, J.; Pearlman, M.; Plag, H.P.; et al. The future Global Geodetic Observing System. In Global Geodetic Observing System; Plag, H.P., Pearlman, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Bar-Sever, Y.; Haines, B.; Bertiger, W.; Desai, S.; Wu, S. Geodetic Reference Antenna in Space (GRASP)—A Mission to Enhance Space-based Geodesy. In Proceedings of the COSPAR Colloquium: Scientific and Fundamental Aspects of the Galileo Program, Padua, Italy, 14–16 October 2009; Available online: https://gssc.esa.int/education/galileo-science-colloquium/ (accessed on 12 July 2024).
- Biancale, R. E-GRASP/Eratosthenes: Proposal for Earth Explorer Opportunity Mission EE-9. In Proceedings of the First International Workshop on VLBI Observations of Near-Field Targets, Bonn, Germany, 5–6 October 2016; Available online: http://www3.mpifr-bonn.mpg.de/div/meetings/vonft/pdf-files/talks/E-GRASP_Eratosthenes_Biancale (accessed on 12 July 2024).
- Delva, P.; Altamimi, Z.; Blazquez, A.; Blossfeld, M.; Böhm, J.; Bonnefond, P.; Boy, J.-P.; Bruinsma, S.; Grzegorz, B.; Chatzinikos, M.; et al. GENESIS: Co-location of geodetic techniques in space. Earth Planets Space 2023, 75, 5. [Google Scholar] [CrossRef]
- Haas, R.; Hobinger, T.; Klopotek, G.; Kareinen, N.; Yang, J.; Comnrinck, L.; De Witt, A.; Nickola, M. VLBI with GNSS–signals on an Intercontinental Baseline—A progress report. In Proceedings of the 23rd European VLBI Group for Geodesy and Astrometry Working Meeting, Gothenburg, Sweden, 15–19 May 2017; Haas, R., Elgered, G., Eds.; Chalmers University of Technology: Gothenburg, Sweden, 2017; pp. 117–121. [Google Scholar]
- Plank, L.; Hellerschmied, A.; McCallum, J.; Böhm, J.; Lovell, J. VLBI observations of GNSS-satellites: From scheduling to analysis. J. Geod. 2017, 91, 867–880. [Google Scholar] [CrossRef] [PubMed]
- Hellerschmied, A.; McCallum, L.; McCallum, J.; Sun, J.; Böhm, J.; Cao, J. Observing APOD with the AuScope VLBI Array. Sensors 2018, 18, 1587. [Google Scholar] [CrossRef] [PubMed]
- Nothnagel, A. Elements of Geodetic and Astrometric Very Long Baseline Interferometry; TU Wien, Department of Geodesy and Geoinformation: Vienna, Austria, 2021; Available online: https://www.vlbi.at/data/publications/Nothnagel_Elements_of_VLBI.pdf (accessed on 12 July 2024).
- Plank, L.; Böhm, J.; Schuh, H. Simulated VLBI Satellite Tracking of the GNSS Constellation: Observing Strategies. In IAG 150 Years—Proceedings of the 2013 IAG Scientific Assembly, Potsdam, Germany, 1–6 September 2013; Rizos, C., Willis, P., Eds.; Springer: Cham, Switzerland, 2016; Volume 143, pp. 85–90. [Google Scholar] [CrossRef]
- Männel, B. Co-location of Geodetic Observation Techniques in Space. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2016. [Google Scholar]
- Schunck, D.; McCallum, L.; Calves, G.M. Simulating VLBI observations to BeiDou and Galileo satellites in L-band for frame ties. J. Geod. Sci. 2024, 14, 20220168. [Google Scholar] [CrossRef]
- Plank, L.; Böhm, J.; Schuh, H. Precise station positions from VLBI observations to satellites: A simulation study. J. Geod. 2014, 88, 659–673. [Google Scholar] [CrossRef]
- Anderson, J.M.; Beyerle, G.; Glaser, S.; Liu, L.; Männel, B.; Nilsson, T.; Heinkelmann, R.; Schuh, H. Simulations of VLBI observations of a geodetic satellite providing co-location in space. J. Geod. 2018, 92, 1023–1046. [Google Scholar] [CrossRef]
- Wolf, H.; Böhm, J. Optimal distribution of VLBI transmitters in the Galileo space segment for frame ties. Earth Planets Space 2023, 75, 173. [Google Scholar] [CrossRef] [PubMed]
- Pollet, A.; Coulot, D.; Biancale, R.; Pérosanz, F.; Loyer, S.; Marty, J.C.; Glaser, S.; Schott-Guilmault, V.; Lemoine, J.-M.; Mercier, F.; et al. GRGS numerical simulations for a GRASP-like mission. J. Geod. 2023, 97, 45. [Google Scholar] [CrossRef]
- Klopotek, G.; Hobiger, T.; Haas, R.; Otsubo, T. Geodetic VLBI for precise orbit determination of Earth satellites: A simulation study. J. Geod. 2020, 94, 56. [Google Scholar] [CrossRef]
- Böhm, J.; Wolf, H. Opportunities with VLBI Transmitters on Satellites. In International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar] [CrossRef]
- Petrachenko, B.; Niell, A.; Behrend, D.; Corey, B.; Böhm, J.; Charlot, P.; Collioud, A.; Gipson, J.; Haas, R.; Hobiger, T.; et al. Design Aspects of the VLBI2010 System. In IVS 2008 Annual Report; Behrend, D., Baver, K.D., Eds.; NASA/TP-2009-214183; NASA Technical Publications: Washington, DC, USA, 2009; pp. 13–67. [Google Scholar]
- Behrend, D.; Ruszczyk, C.; Elosegui, P.; Neidhardt, A. The VGOS High Road: From Inception and Prototyping to Operations to Maturation and Beyond. In Proceedings of the 26th European VLBI Group for Geodesy and Astronomy Working Meeting; Bad Kötzting, Germany, 11–15 June 2023. Available online: https://ntrs.nasa.gov/api/citations/20230016286/downloads/evga2023_behrend.pdf?attachment=true (accessed on 12 July 2024).
- Schartner, M.; Böhm, J. VieSched++: A New VLBI Scheduling Software for Geodesy and Astrometry. PASP 2019, 131, 084501. [Google Scholar] [CrossRef]
- Schartner, M.; Böhm, J. Optimizing schedules for the VLBI global observing system. J. Geod. 2020, 94, 12. [Google Scholar] [CrossRef] [PubMed]
- Pany, A.; Böhm, J.; MacMillan, D.; Schuh, H.; Nilsson, T.; Wresnik, J. Monte Carlo simulations of the impact of troposphere, clock and measurement errors on the repeatability of VLBI positions. J. Geod. 2011, 85, 39–50. [Google Scholar] [CrossRef]
- Schartner, M.; Collioud, A.; Charlot, P.; Xu, M.H.; Soja, B. Bridging astronomical, astrometric and geodetic scheduling for VGOS. J. Geod. 2023, 97, 17. [Google Scholar] [CrossRef]
- Nothnagel, A.; Artz, T.; Behrend, D.; Malkin, Z. International VLBI Service for Geodesy and Astrometry. J. Geod. 2017, 91, 711–721. [Google Scholar] [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Jaradat, A.; Jaron, F.; Gruber, J.; Nothnagel, A. Considerations of VLBI transmitters on Galileo satellites. Adv. Space Res. 2021, 68, 1281–1300. [Google Scholar] [CrossRef]
- Böhm, J.; Böhm, S.; Boisits, J.; Girdiuk, A.; Gruber, J.; Hellerschmied, A.; Krasna, H.; Landskorn, D.; Madzak, M.; Mayer, D.; et al. Vienna VLBI and Satellite Software (VieVS) for Geodesy and Astrometry. PASP 2018, 130, 044503. [Google Scholar] [CrossRef]
- Nilsson, T.; Haas, R.; Elgered, G. Simulations of atmospheric path delays using turbulence models. In Proceedings of the 18th European VLBI for Geodesy and Astrometry Working Meeting, Vienna, Austria, 12–13 April 2007; Böhm, J., Pany, A., Schuh, H., Eds.; Geowissenschaftliche Mitteilungen, Heft Nr. 79, Schriftenreihe der Studienrichtung Vermessung und Geoinformation, Technische Universität Wien: Vienna, Austria, 2007; pp. 175–180, ISSN 18118380. [Google Scholar]
- Wolf, H.; Böhm, J.; Schartner, M.; Hugentobler, U.; Soja, B.; Nothnagel, A. Dilution of Precision (DOP) Factors for Evaluating Observations to Galileo Satellites with VLBI. In Geodesy for a Sustainable Earth: Proceedings of the 2021 Scientific Assembly of the International Association of Geodesy, Beijing, China, 28 June–2 July 2021; Freymueller, J.T., Sanchez, L., Eds.; Springer: Cham, Switzerland, 2022; Volume 154, pp. 305–312. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Thoelert, S.; Arnold, D.; Bury, G. GNSS visibility and performance implications for the GENESIS mission. J. Geod. 2023, 97, 96. [Google Scholar] [CrossRef] [PubMed]
- Klioner, S. General Relativistic Model of VLBI Observables. In Proceedings of the AGU Chapman Conference on Geodetic VLBI: Monitoring Global Change, Washington, DC, USA, 22–26 April 1991; Alef, W., Bernhart, A., Nothnagel, A., Eds.; NOAA Technical Report NOS 137 NGS49. The U.S. Department of Commerce and the National Oceanic and Atmospheric Administration, National Ocean Service: Silver Spring, MD, USA, 1991; pp. 188–202. [Google Scholar]
- Klopotek, G.; Hobiger, T.; Haas, R. Geodetic VLBI with an artificial radio source on the Moon: A simulation study. J. Geod. 2018, 92, 457–469. [Google Scholar] [CrossRef]
- Schunck, D.; McCallum, L.; Molera Calvés, G. Practical Considerations of VLBI Observations to the GENESIS Mission. In International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).